Introduction

With the continuous iterative development of motor vehicles, the overall rate of of traffic accidents is on the rise, which seriously affects social security and stability. Furthermore, the increasing number of accidents has affected the economy, productivity, and social personnel. Accurate traffic accident prediction is essential in preventive measures and optimization of road management. Therefore, it is urgent to develop effective methods to predict accident severity, identify key risk factors (e.g., infrastructure improvements, optimized signal timing), and thereby enhance overall roadway safety.

At present, the field of predicting the severity of traffic accidents employs statistical models and machine learning (ML) techniques mainly. The former primarily derives statistical values by conducting statistical modeling on the collected datasets. Refs.1,2 establish relationship models between the features and accident levels utilizing the polynomial Logit model. In3, the generalized ordered Logit model is used to extract the relevant features of non-motorized vehicles in the severity of accidents, and the binary logarithm model4 is used to analyze the collision risk and severity of motor vehicles. The drawback of these methods lies in their requirement for prior assumptions, which tends to enlarge the prediction error of the model. Furthermore, due to their reliance on strong assumptions, these models are prone to overfitting or decreased prediction accuracy on large-scale data. Conversely, in the application of machine learning methods, the final relationship model is derived by leveraging the unique nonlinear mapping capabilities embedded within the network. This requires clearly defining the network’s inputs and outputs, along with configuring its specific hyperparameters. For instance, the SST-DHL framework for sparse spatiotemporal dynamic hypergraph learning is employed to derive high-order dependencies related to traffic accidents5, while utilizing a cross-regional dynamic hypergraph learning model to detect global spatiotemporal dependencies. Similarly, Ref6. applies convolutional neural networks to extract spatial features and patterns from accident samples, and employs a bidirectional long short-term memory network to capture the temporal dependence among influencing factors.

While existing methods have yielded good results, several challenges remain that require immediate attention. Firstly, the distribution of traffic accident data is extremely unbalanced: despite large volumes of data, severe accidents are scarce, yet they carry the greatest societal impact. This also leads to difficulty in extracting the information of the characteristics of major accidents and accurately predicting it during the establishment of the accident severity prediction model. Secondly, the distribution characteristics of accident samples are mostly integer type, which will affect the quality of sample generation. Finally, complex interactions and correlations among samples can elude traditional neural networks, limiting their ability to capture these nuanced relationships.

To address the aforementioned challenges, this paper proposes a method for processing and accurately predicting unbalanced traffic accident datasets using a VAE-attention and GCN network. We construct a relationship model that links different accident characteristics to risk levels. Specifically, we first segment the samples using a sliding window to ensure dataset quality. Given the imbalanced distribution of accident samples, we employ a Variational Autoencoder (VAE) to augment underrepresented samples. This VAE incorporates a self-attention mechanism to capture interdependencies among traffic features and learn associated contextual information within the dataset. To generate plausible integer traffic accident samples, new synthetic samples are produced using a smooth L1 loss function. Subsequently, both the synthetic and real samples are fed into the input layer of a Graph Convolutional Network (GCN). The GCN is designed to learn the internal relationships between accident characteristics and severity, capture hidden sample relationships, and ultimately establish an accident severity prediction model. The main contributions of this paper are summarized as follows:

  1. (a)

    The sliding window is used to segment the original samples. To generate the newly synthetic samples that are close to the integer value, a smooth L1 function is used as the reconstruction loss function of the VAE method.

  2. (b)

    To learn the hidden correlations among sample features, the hidden information of the input features is obtained by incorporating the self-attention mechanism. A VAE-attention method is proposed to generate minority samples, thereby improving the precision of traffic accident prediction.

  3. (c)

    The GCN network is used to establish the topology structure of accident samples, and the multi-node graph structure is used to predict the traffic accident severity in complex environments combined with the swish activation function. The experimental effect is improved by about 10% in the traffic accident prediction results.

The organization of this paper is as follows: The related work of sample generation and prediction is summarized in Sect. “Related work”. The specific data preprocessing and data generating with the VAE method are described in Sect. “The traffic accident data preprocessing and generating”. The traffic accident severity prediction model is constructed in Sect. “The traffic accident severity prediction by the GCN model”. Sect. “The experiment results and analysis” shows the experiment results and analysis based on the traffic accident datasets. Finally, the paper is summarized in the Conclusion.

Related work

Prediction of traffic accident severity plays a crucial role in both road safety7,8 and social stability. However, because severe accidents are far fewer in number than minor ones, the resulting accident dataset is highly imbalanced. Therefore, it is necessary to first preprocess the data distribution to achieve balance before building a severity prediction model. At present, traditional statistical–probabilistic methods are constrained by their prior assumptions and tend to incur large errors; by contrast, machine learning approaches—capable of directly analyzing real-time monitoring data and uncovering latent distribution patterns—have been widely adopted in this domain.

In the field of sample generation, generative adversarial networks, variational autoencoders (VAEs), and stream models are mainstream methods. Among them, VAE9 is based on the probability graph generation process, and compared with Generative Adversarial Networks (GANs)10,11, sample generation is more stable and interpretable. Therefore, a series of VAE variants have been proposed successively, such as Conditional Variational Autoencoder (CVAE)12,13,14, Vector Quantization Variational Autoencoder (VQ-VAE)15,16, etc. For example, the SC-VAE proposed in reference17 embeds sparse encoding into the VAE framework, achieving effective representation of sparse data; The DCD-VAE in reference18 decoupled different types of information through distributed constraint decomposition; The dynamic VAE network in reference19 can learn continuous zero samples. In addition, the fusion of VAE and GAN has also shown potential in fields such as image generation20,21. These studies indicate the advantages of VAE in sample generation and processing of data distribution characteristics, especially in improving the imbalance problem of traffic accident data. However, a single VAE still has limitations in capturing complex feature associations in the data.

After obtaining the balanced traffic accident data, it is needed to construct a traffic predictive model22,23. Several scholars have adopted deep learning networks for traffic accident prediction24,25,26,27,28. However, Convolutional Neural Networks (CNNs) exhibit limitations in processing global information and capturing deep-level correlations. In 2016, Kipf and Welling proposed the Graph Convolutional Network (GCN)29, which offers a novel solution to this challenge. The GCN excels at extracting hidden features and topological information within data, and has found widespread application in traffic flow prediction within the transportation domain.Thereby, GCN has been widely used because it can extract hidden features and topological information in the data. A series of methods combined with GCN networks have been applied to the field of transportation, and most of the research focuses on traffic flow prediction30,31,32,33. Ref34 proposed RT-GCN spatiotemporal convolution network to predict traffic flow, Gaussian distribution node representation, and variance-based attention mechanism are used to deal with noise disturbance and missing data. In response to the problem of insufficient accuracy in existing multivariate time series anomaly detection models due to neglecting variable associations or the importance of time dimension variables. In35, the MUTANT framework, which captures variable time-varying associations through GCN are proposed and the attention mechanism are combined to model variable importance. REF.36 notes that time series networks in the process industry face limitations due to sparse labeled data. To address this challenge, a novel semi-supervised strategy based on Variational Autoencoders (VAE) and Wasserstein Generative Adversarial Networks (WGAN) is proposed. Specifically, the SVAE is first trained to derive the zₛ distribution. Subsequently, the UVAE extracts the zu distribution, which is then aligned with the SVAE’s distribution using the WGAN framework. Finally, these components are integrated into the SS-VAE architecture. In Ref37, the MVGCVAE model is proposed to address the issues of information loss and insufficient feature fusion in microbial disease association prediction. This model integrates multi-view GCN, VAE, and dynamic kernel matrix weighting, while multi-view information is fused through an attention mechanism.

In summary, the advantages of VAE method in balancing data distribution and generating high-quality samples are highly complementary to GCN’s ability to capture feature topological relationships and explore deep correlations. However, for imbalanced and discrete integer traffic accident data, there are complex multi factor correlations within it. In addition to combining VAE with GCN, sample balancing processing is also required based on the characteristics of the data itself. Based on the above-mentioned methods, this article combines self attention mechanism with VAE to extract sample features. Due to the inherent characteristics of the data, this article adopts a smooth L1 function as the reconstruction loss of VAE, and uses the Swish function as the activation function of the GCN network, thus fully leveraging the advantages of VAE and GCN in traffic accident generation and prediction.

The traffic accident data preprocessing and generating

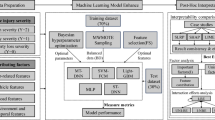
This paper is structured into three main parts to address the challenges of imbalanced traffic accident data and complex latent feature construction. Firstly, original samples undergo preprocessing via a sample mapping method to convert them into numerical traffic data. Subsequently, the mapped samples are segmented using a sliding window technique, which serves to expand the input sample size and enhance the efficiency of subsequent sample generation processes. Secondly, the characteristic distribution of minority samples is modeled, and newly synthetic samples are generated through a Variational Autoencoder (VAE) approach. Within this generative model, the smooth L1 function is employed as the reconstruction loss to yield new integer samples. Moreover, a self-attention mechanism is integrated with the encoder of the VAE to facilitate latent information learning of traffic features. Finally, a Graph Convolutional Network (GCN) is utilized to predict accident severity levels, with the swish function adopted as the activation function (AC). By establishing relationships between feature nodes and edges, the topological structure linking environmental features and accident severity can be derived. The overall framework of the paper is illustrated in Fig. 1.

Fig. 1
figure 1

The overall accident severity prediction framework based on the proposed methods.

Full size image

In Fig. 1, the black arrow indicates the data flow direction. The input samples are first preprocessed as sub-samples, and then the VAE method combined with the self-attention mechanism and smooth L1 function is used to generate synthetic minority samples (major accident). Then, the 2-dimension (2D) traffic datasets are transformed as graph datasets, the topological structure of accident data is established by the GCN method, and the accident severity under different features can be predicted.

In this paper, the original accident datasets are recorded as \(D^{\prime} = \{ {\mathbf{x}}^{\prime},{\mathbf{y}}^{\prime}\}\), the expansion form is as follows.

\({\mathbf{x}}^{\prime} = \left[ \begin{gathered} x^{\prime}_{1,1} \;\; \cdots \;\;x^{\prime}_{1,q} \;\; \cdots \;\;\;x^{\prime}_{1,n} \hfill \\ \; \vdots \;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ x^{\prime}_{p,1} \;\; \cdots \;\;x^{\prime}_{p,q} \;\;\; \cdots \;\;x^{\prime}_{p,n} \hfill \\ \; \vdots \;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ x^{\prime}_{m,1} \;\; \cdots \;\;x^{\prime}_{m,q} \; \cdots \;\;x^{\prime}_{m,n} \hfill \\ \end{gathered} \right]\), \({\mathbf{y}}^{\prime} = \left[ \begin{gathered} y^{\prime}_{1} \hfill \\ \; \vdots \hfill \\ y^{\prime}_{p} \hfill \\ \; \vdots \hfill \\ y^{\prime}_{m} \hfill \\ \end{gathered} \right],\)

Among them, \({\mathbf{x}}^{\prime}\) is the overall environment features, \(q = 1,...,n\) indicate the q-th features and n is the number of features. \(p = 1,...,m\) represents the traffic accident, m is the number of accidents. \(x^{\prime}_{p,q}\) represents the q-th environment features of p-th traffic accident. \({\mathbf{y}}^{\prime}\) are the overall samples of traffic accident severity, \(y^{\prime}_{p}\) indicates the severity of p-th traffic accidents.

Data mapping and segmentation

Since the traffic accident datasets monitored are all text data, it greatly affects the implementation effect of the later generation and prediction model. Hence, this paper uses the sample mapping process to change the original form of traffic data. By classifying different environmental features and setting the category of each feature to a numerical value, a group of numerical samples can be obtained. By the discrete mapping coding, the results corresponding to each environmental factor and the severity of the accident are mapped into a number. For instance, among the weather factors: rainy day = 1, sunny day = 2, wind day = 3, snow day = 4, fog day = 5, frost day = 6, others = 7; road surface: dry = 1, wet = 2, ice = 3, silt = 4, snow melting = 5, ponding 6, others = 7; Accident severity mapping: minor accident = 1, ordinary accident = 2, major accident = 3, devastating accident = 4. Discretize all environmental features \({\mathbf{x}}^{\prime}\) and accident severity samples \({\mathbf{y}}^{\prime}\), where, \({\mathbf{x}}^{\prime}_{n}\) represents the n-th environmental features corresponding to the accident severity, \({\mathbf{y}}^{\prime}\) indicates the discrete accident severity, and the mapped datasets are \(D_{M} = \left\{ {X_{N} ,Y} \right\}\). The specific mapping process is shown in Fig. 2.

Fig.2
figure 2

The mapping process of traffic accident datasets.

Full size image

After 2D numerical samples are obtained through data mapping, the efficiency of dataset generation can be improved. However, the learning efficiency of sample distribution will be affected due to the excessive length of the original data. Hence, the samples are segmented by sliding window to establish a high-quality training dataset. According to the sliding window step and window size, the mapped original samples are segmented. Figure 3 shows the specific process of sample division.

Fig. 3
figure 3

The processes of data segmentation and conversion.

Full size image

In Fig. 3, assuming that the size of original traffic datasets is \({D}_{M}=\left\{{X}_{M*N},{Y}_{M}\right\}\), M is the number of samples, and N is the number of features.

The datasets DM are divided into P sub-samples by sliding window, and the size of each sub-sample is L*N. L is the size of a sliding window, and the step size is k, indicating the number of bits the window moves. Hence, through the dataset segmentation technique, the P sub-samples \({dd}_{i}=\left\{{X}_{L*N,i=1,\dots P},{Y}_{L}\right\}\) of traffic accident datasets can be obtained.

The few samples generation process based on VAE method

After obtaining sub-samples of traffic accident datasets through data mapping and segmentation, the synthetic minority samples should be generated. Generally, the frequency of major accidents is relatively lower than minor accidents. This also leads to an extremely unbalanced distribution of the traffic accident severity dataset and skewed data distribution, then, the accuracy of subsequent accident severity prediction will be further affected.

Hence, to improve the performance of traffic accident prediction, the VAE generative model is used, which can expand the minority samples, so that the overall dataset can be balanced. The VAE method is a generation model, which maps the data to the distribution parameters in the potential space through the encoder, and then generates new data from the samples in the potential space through the decoder. Additionally, considering that the original data has integer characteristics after data mapping, to make the newly generated samples more consistent with the integer characteristics, the smooth L1 function is used as the reconstruction function in this paper, which makes the model produce output values closer to the integer and improves the robustness of the model. By combining with self-attention mechanism in VAE, the key feature information can be collected, the efficiency of sample generation must be enhanced. Furthermore, the hidden features of sample and the association among the traffic features are extracted.

In the synthetic samples generation process, the P sub-samples \(dd^{\prime}_{i} = \left\{ {X_{L*N,i = 1, \ldots P} ,Y_{L} } \right\}\) should input into the Encoder module of the VAE method, which follows the probability distribution p(X). Then, the output \(X_{L*N}^{Enc}\) of the Encoder module can be obtained after mapping by the neural network. The self-attention mechanism is combined in the encoder of VAE. There are three main variables, the query vector Q, key vector K and value V, which can capture the internal relationship between input samples. The calculation formula of Q, K, and V is shown in (1).

$$\begin{gathered} Q = W^{Q} X_{L*N}^{Enc} \hfill \\ K = W^{K} X_{L*N}^{Enc} \hfill \\ V = X_{L*N}^{Enc} \hfill \\ \end{gathered}$$
(1)

In formula (1), \(W^{Q}\) and \(W^{K}\) is the weight parameter respectively, which is obtained by the neural network training.

Then, the dot product is calculated and the softmax function is used to obtain the attention weight value \(a_{L}\), the calculation process is shown in (2).

$$a_{L} (Q,K,V) = soft\max (\frac{{Q*K^{T} }}{\sqrt d })$$
(2)

where, d is the dimension of the Query vector Q or key vector K, and the size of it is (L*L).

Finally, the output value \(h_{i,j}\) is obtained by the dot product of the attention weight value and V value. The specific calculation process is shown in (3).

$$h_{i,j} = \sum\limits_{k = 1}^{L} {a_{i,k} *V_{k,j} }$$
(3)

Among them, i is the position of the output sequence, j is the feature dimension, j = 1,…, N, k is the position of the input sequence.

By combining with the self-attention mechanism in the Encoder module, the important features can be noticed when processing the overall input samples, so as to capture the dependence between the traffic features. The overall output vector sequence after self-attention calculation is \(H_{L*N}\). Then, the mean \(\mu (H_{L*N} )\) and variance \(\Sigma (H_{L*N} )\) of the output vector sequence trained by the neural network are obtained. The samples are sampled in the standard normal distribution \(N(0,I)\) and the hidden variable Z can be further obtained, then the generating sub-samples \({X{\prime}}_{L*N,i=1,\dots P}\) are obtained.

Optimizations are conducted on the model, its parameters, and other components through the loss function to improve the generation efficiency of the generative model. The loss function of the VAE model consists of two parts: the KL divergence \(L_{LOSS}^{1}\) and the reconstruction loss \(L_{LOSS}^{2}\). Generally, the latter is calculated by Mean Squared Error(MSE) which is too simplistic and lacks specificity in the problems of sample characteristics. To enhance the ability of the generated samples to approximate integer characteristics, the smooth L1 function is used as the reconstruction error in this paper. Hence, the loss function of the VAE model that combined the self-attention is shown in (4).

$$\begin{gathered} LOSS = L_{LOSS}^{1} + L_{LOSS}^{2} \hfill \\ \;\;\;\;\;\;\;\;\; = KL\left( {N(\mu (H_{L*N} ),\Sigma (H_{L*N} )))||N(0,1)} \right) + L_{2} \hfill \\ \end{gathered}$$
(4)

where, the calculation process of KL divergence is \(L_{LOSS}^{1}\), which is the similarity between the relationship between posterior distribution after the self-attention mechanism and standard normal distribution. By minimizing the loss of KL divergence \(L_{LOSS}^{1}\), the latent variable Z will have better distribution characteristics. \(L_{LOSS}^{2}\) is the reconstruction error between the generated and original samples, which is calculated by the smooth L1 loss function, and the formula is shown in (5).

$$L_{LOSS}^{2} = \left\{ \begin{gathered} 0.5 \cdot (X - X^{\prime})^{2} \;\left| {X - X^{\prime}} \right|{ < 1} \hfill \\ \left| {X - X^{\prime}} \right| - 0.5\;\;\;\left| {X - X^{\prime}} \right| \ge {1} \hfill \\ \end{gathered} \right.$$
(5)

Utilizing the smooth L1 loss function as the reconstruction error \(L_{LOSS}^{2}\) can enhance the robustness of the generation model, addressing the issue where synthetic samples fails to closely adhere to integer characteristics. Conversely, the smooth L1 loss function computes errors in a piecewise manner, which dampens the sensitivity of the loss function calculation to aberrant values, thereby reducing the possibility of gradient explosion or disappearance.

In summary, the overall structure of the VAE generation model integrated with the self-attention mechanism is shown in Fig. 4, including four parts: Encoder, Attention Mechanism, Resampling, and Decoder. Based on the sample generation process, the effectiveness of sample generation can be enhanced and the accuracy of subsequent predictions on traffic accident severity datasets can be further improved.

Fig. 4
figure 4

The synthetic data generation process of VAE-Self-Attention method.

Full size image

The traffic accident severity prediction by the GCN model

After solving the problem of unbalanced distribution of original samples through the VAE model, it is necessary to establish the accident severity prediction model. To more effectively represent the hidden internal relationship between various accident features and severity, this paper uses the graph convolution network model for predictive process modeling. \(G = \left( {V^{\prime},E} \right)\) is the network model structure, where \(V^{\prime}\) is the sample node, representing each accident severity sample, and E is the edge connecting the nodes, representing the relationship between different samples.

This paper constructs graph data based on the Euclidean distance between nodes. Suppose the sample size input into the Graph Convolutional Network (GCN) is \({D}_{U}=\left\{{X}_{U*N},{Y}_{U}\right\}\), where U = \(M+C\), M represents the original sample size, C represents the generated sample size, and N represents the sample features.\(Y_{U}\) denotes the data nodes, with each node’s features being \(X_{U*N}\). The relationships between nodes form an adjacency matrix A, the size of it is U*U. The Euclidean distance between any two nodes (\(X_{i}\), \(X_{j}\)) is calculated, and when the distance is less than a threshold \(\varepsilon (l < \varepsilon )\), it is considered that there is an edge between the two nodes. The edge indices are stored in an edge list, which is then converted into a tensor.

The graph convolution network structure still contains input layer, output layer and hidden layer. The sample X is fed into the input layer, the hidden layer is convoluted through the GCN module of the hidden layer, and the accident severity results corresponding to different samples X is output. The propagation mode of each network layer in the GCN structure is formula (6).

$$H^{(l + 1)} = f\left( {\tilde{D}^{ - 1/2} \tilde{A}\tilde{D}^{ - 1/2} H^{(l)} W^{(l)} } \right)$$
(6)

where, W is the weight parameter in each layer of the model, and \(\tilde{A}\) is the sum of the adjacency matrix A and the identity matrix, that is, the edge connection is calculated for each node. \(\tilde{D}\) is the degree matrix of \(\tilde{A}\), that is, the number of connected edges of nodes. l indicates the number of layers in the network structure. When l = 0, it indicates that it is currently the input layer. \(f( \cdot )\) is the activation function in neurons.

To make the nonlinear mapping process stable and reduce the problem of gradient explosion or disappearance, the Swish function and log-softmax function are used for graph convolution processing. The calculation process of Swish function is as shown in (7), and the log-softmax function is as shown in formula (8).

$$\begin{aligned} S{\text{wish}}(x) = & x \cdot sigmoid(\beta x) \\ = & \frac{x}{{1 + e^{ - (\beta x)} }} \\ \end{aligned}$$
(7)
$$LogSoft\max (x_{i} ) = \log (\frac{{e^{{x_{i} }} }}{{\sum\nolimits_{j} {e^{{x_{j} }} } }})$$
(8)

In this paper, the multi-level neighborhood information is transmitted by superimposing two-layer convolution layers, and the spatial characteristics of the input samples are extracted. The process of convolution calculation of two-layer graph is as shown in formula (9).

$$\begin{aligned} O = & f(X,A) \\ = & LogSoft\max (\tilde{A}Swish(\tilde{A}XW^{(0)} )W^{(1)} ) \\ \end{aligned}$$
(9)

Hence, the unbalanced traffic accident severity prediction model constructed by the GCN method is shown in Fig. 5.

Fig. 5
figure 5

The accident severity prediction modelling process based on the GCN method.

Full size image

Through the above process, the relationship model between environmental features and accident severity can be established, then the prediction results can be obtained. Predicting results can provide decision support for relevant road management departments and improve the safety characteristics of traffic operation.

The experiment results and analysis

To evaluate the availability of the proposed method in sample generation and accident severity prediction, two groups of real accident data were tested. First, the datasets were mapped by numerical map method and segmented by the sliding window. Then the VAE method was used to generate synthetic minority accident samples, expanding the minority samples, so that the overall datasets reached a balanced state and distribution. Finally, the prediction model is established by the GCN network, and the relationship model between accident characteristics and severity was obtained.

Datasets description

Traffic accident severity datasets

This paper utilizes two sets of traffic accident data for verification, sourced primarily from 12,182, 1112 and 31,636 accidents that transpired within a district of NEW YORK, CHILI and BRONX, respectively, spanning the years 2014 to 2016. The datasets encompass characteristics of the accident sites’ surrounding environments. Specifically, this paper selects nine characteristics, along with the severity of the accidents, which are subsequently categorized into four distinct groups. The concrete sample distribution of the traffic accident datasets is shown in Table 1.

Table 1 The sample distribution of traffic accident severity on different datasets.
Full size table

In Table 1, the severity of the accident is divided into four categories: minor accident L1, ordinary accident L2, major accident L3, and devastating accident L4. Obviously, the distribution of different types of accident severity is extremely unbalanced. For example, there are only 41 devastating accidents in New York, accounting for 0.3% of the total number of accidents, while the number of devastating accidents L4 in CHILI only accounts for 0.6% of the total number. However, despite the number of devastating accidents is relatively small, most of them are minor accidents, but devastating accidents will cause more dangerous consequences, including the loss of personnel and property. Therefore, it is urgent to generate samples of accident data to obtain balanced datasets.

Firstly, through the data mapping method, the original text data is mapped into numerical samples that can be processed directly by the computer. Due to page restrictions, taking the New York dataset as an example, Table 2 shows the mapping and distribution results corresponding to some features of the New York dataset. Figure 6 shows the visualization results of partial feature distribution.

Table 2 Partial feature distribution and mapping results of NEW YORK accident features.
Full size table
Fig. 6
figure 6

A part of accident features of NEWYORK datasets.

Full size image

In Table 2, there are different classes in the monitored environmental features, and the accident data corresponding to different categories can simply show which are the accident characteristics with greater impact. For example, in the light intensity factor, the accident distribution monitored in the daytime is much higher than that at night; When the road surface is dry, the data distribution of accidents accounts for the largest proportion. In these monitoring sample characteristics, some factors are easy to couple and affect the later accident prediction results, such as monitoring the road conditions and road conditions.

In Fig. 6, the green bars represent the accident volume corresponding to L3, the blue bars represent the sample size corresponding to L1, and the red bars show the devastating accident samples L4. Apparently, the proportion of red is very small, while the proportion of green is the largest, followed by the number of blue bars. This indicates that the number of major and minor accidents accounts for a larger proportion, while the number of devastating accidents is the smallest. This results in a highly unbalanced data distribution, which seriously affects the accuracy of subsequent accident severity predictions. Therefore, this paper first uses Variational Autoencoders (VAE) to augment the samples of severe accidents, to balance the overall sample distribution and thereby improve the effectiveness of subsequent accident predictions.

The training network setting and generation results

By configuring the network hyper-parameters as outlined in Table 3, the sample generation outcomes and prediction results can be obtained.

Table 3 The hyper-parameters of the proposed method.
Full size table

Effective sample generation and prediction results can be obtained through the network settings in Table 3. The sample distribution corresponding to different features has also been significantly improved. The visualization results of features after generation corresponding to Fig. 6 are shown in Fig. 7.

Fig. 7
figure 7

Data feature distribution generation results of NEW YORK datasets.

Full size image

Compared with Fig. 6, the sample distribution corresponding to the features depicted in Fig. 7 has undergone an overall improvement, particularly in terms of the proportion of L4 samples across various features. Furthermore, the method introduced in this paper can addresses the integer nature of the original samples, ensuring that the newly generated samples maintain the integer characteristic. In addition to merely replicating the exact values found in the original sample features, some other samples are also generated. For instance, the ‘Day of Week’ feature has values exceeding 8, albeit with a very low distribution frequency. Despite being included in the training and prediction processes, these exceptional values could not be accurately forecasted. Consequently, the inclusion of these newly generated exceptional samples does not significantly impact the overall accident prediction model.

To demonstrate whether the method proposed in this paper has alleviated the data quality and class imbalance issues after augmenting the sample data, comparisons were conducted using different generation methods. Quantitative metrics (Jensen-Shannon Divergence JSD, Kullback–Leibler Divergence KLD, Wasserstein Distance WD) were employed to evaluate different datasets, complemented by t-SNE for dimensionality reduction to visualize the enhancement effects of various generation methods. Figures 8, 9 and 10 display the t-SNE plots corresponding to different datasets, while Table 4 presents the quantitative results of data generation quality.

Fig. 8
figure 8

The T-SNE results of CHILI datasets under different generation ethods (a) GAN (b) VAE (c) DCGAN (d) ADASYN (e) proposed method.

Full size image
Fig. 9
figure 9

The T-SNE results of NEWYORK datasets under different generation ethods (a) GAN (b) VAE (c) DCGAN (d) ADASYN (e) proposed method.

Full size image
Fig. 10
figure 10

The T-SNE results of BRONX datasets under different generation ethods (a) GAN (b) VAE (c) DCGAN (d) ADASYN (e) proposed method.

Full size image
Table 4 The generation indexes of different methods.
Full size table

Figures 8, 9 and 10 illustrate the enhancement effects of different generation methods on three datasets. The generated data (red points) and original data (blue points) were separately reduced to a 2D plane using t-SNE. Different shapes represent distinct classes (four in total). As shown in the figures, the proposed method successfully generates samples within the distribution of the original data. It is obvious that DCGAN can easily generate more samples but do not match the original data type, resulting in the problem of data imbalance still existing.

To quantify the quality of generated data, this paper employs three key distance metrics—JSD, KLD, WD—to assess the discrepancy between the distribution of generated data and that of the original data, as presented in Table 4. A smaller value for each of these metrics typically suggests a higher degree of similarity between the generated and original data distributions. However, it is important to note that while smaller values of these metrics generally indicate a closer resemblance between the two distributions, this does not always equate to superior quality of the generated data. For instance, issues like mode collapse, lack of diversity in critical substructures, or poor performance on task-specific metrics might persist even when the overall distributional distance is small.

Prediction and analysis results

The minority samples are generated by the VAE model constructed in the above section, and the proportion of different accident severity are balanced. Then, the traffic accident severity prediction model based on the GCN method should be established. In this paper, the input datasets of the GCN network consist of generation and original samples, which are processed as graph data G. Since the connection of graph datasets are complex, this paper shows the accident graph data corresponding to 500 samples in the CHILI dataset, as shown in Fig. 11.

Fig. 11
figure 11

The graph datasets of CHILI accident samples.

Full size image

In Fig. 11, samples belonging to distinct categories exhibit varied colors. Obviously, it is evident that there are precisely four categories in total, among which only one is represented by purple. This scarcity of purple-colored samples arises due to the limited number of instances pertaining to devastating accidents. Furthermore, some samples overlap due to their spatial proximity, thereby exacerbating this representation issue.

In the process of converting accident data to graph data, specifically, an empty graph is first created. Then, the traffic accident severity samples are added as a node to the graph by traversing each sample in the dataset, and the sample label is used as the attribute of the node to form graph accident data G. Furthermore, to obtain the adjacency matrix, the distance between two nodes is calculated and the distance threshold \(\varepsilon\) is set as 2.5(\(\varepsilon { = 2}{\text{.5}}\)). When the distance between nodes is less than the threshold value \(\varepsilon\), determine that there is an edge between the two nodes and record it as a sample pair. The sample pair whose distance is less than the threshold value is added to the graph as an edge, and the distance is used as the weight of the edge to obtain the adjacency matrix A. Combining with Eqs. (6–9), the relationship model between different accident features and accident severity is obtained, and the hidden internal topological structure is obtained.

The traffic accident severity based on the GCN prediction network is established in combination with Table 3, and two sets of traffic accident data sets are processed by taking the data generated by the VAE model that combined with the self-attention mechanism and smooth L1 function as the input. The ratio of the training set and test set is 9:1. Confusion matrix and can show the classification results clearly. Figures 12 and 13 show the accident severity prediction results and comparison results corresponding to the two datasets.

Fig. 12
figure 12

The Confusion results of CHILI dataset based on GCN model. (a) CHILI datasets, (b) NEWYORK datasets (c) BRONX datasets.

Full size image
Fig. 13
figure 13

The ROC curve of CHILI dataset. (a) CHILI datasets, (b) NEWYORK datasets (c) BRONX datasets.

Full size image

In Fig. 12, the confusion matrix can clearly show the effectiveness of prediction process for different categories of samples. The darker the color on the diagonal, the better the prediction effect. Hence, the minority samples: class 3 (devastating accident L4) or class 2 (major accident L3) can also be accurately predicted, and the severity of the accident can be determined according to the input environmental characteristics. It shows that the method proposed in this paper greatly improves the prediction efficiency of minority samples after effective expansion. The closer the ROC curve value is to 1, the better the model’s classification effect. Therefore, the more the curve is biased toward the upper left corner of Fig. 13, the higher the accuracy. In Fig. 13, the curves of different types corresponding to our proposed method are all biased toward the upper left corner, and in particular, the accuracy of Class 3 (severe accident type) is the highest. This indicates that our proposed method can effectively address the problem of extreme imbalance in the original data, improve data quality, and thereby enhance the accuracy of downstream accident prediction tasks.

To further verify the effectiveness of the combination of VAE and GCN network in the process of accident severity prediction, the samples generated by VAE that combined with the self-attention mechanism and smooth L1 function are taken as input, and different prediction methods are compared, including K-nearest neighbor (KNN), random forest (RF), support vector machine (SVM), Adaptive Synthetic Sampling (ADASYN) and Convolutional neural network (CNN). Simultaneously, to show that the method proposed in this paper improves the effect of sample generation, the quantitative indicators are shown in Tables 5 and 6 by taking the original sample as input and comparing different prediction methods, and the visual comparison results are shown in Fig. 14.

Table 5 The comparison results under different generation methods.
Full size table
Table 6 The quantitative indexes on different classifier.
Full size table
Fig. 14
figure 14

The classification comparison based on different classifier. (a) CHILI datasets, (b) NEWYORK datasets (c) BRONX datasets.

Full size image

On the other hand, Although ADASYN’s generation metrics were slightly higher than those of the method proposed in this paper in the previous generation quality metric calculation, its generation quality has very low accuracy in downstream classification tasks, and the imbalance problem is still evident, as shown in Table 5.

In Table 5, for DCGAN, VAE, and GAN, only the Accuracy value of their corresponding accident prediction results is high, while the values of other metrics such as Precision, Recall, and F1-score are all very low. This is because the models only learn the features of majority-class samples in such data, and minority-class samples are not processed. Therefore, it is evident that the data quality generated by these generative methods is not high, leading to extremely imbalanced classification results. This indicates that although the above generative methods have augmented the data, they have not solved the problem of imbalanced data distribution. Secondly, although the generative metrics of ADASYN are better than those of our proposed method, the accuracy of accident prediction using the data generated by ADASYN on the three datasets is 19.06%, 36.03%, and 42.22% lower than that of our proposed method, respectively.

To further clarify the effectiveness of our proposed method in addressing the problem of imbalanced accident data and improving accident prediction, the augmented data generated by our proposed method is used as the input to classifiers. Comparisons are made with different classifiers, with the input data for verification being the dataset generated by our proposed method. The results are shown in Table 6 and Fig. 14.

In Table 6, apparently, the method proposed in this paper has the highest accuracy of accident severity prediction. In CHILI datasets, the Adaboost method has the lowest accuracy, while the prediction accuracy of the KNN and Random Forest methods are close to that of the method proposed in this paper. Compared with the SVM, KNN, Random Forest, Adaboost, CNN methods, the accuracy of the proposed method are improved by about 13.79%, 0.99%, 1.03%, 56.39%, 3.86%, respectively. In the NEWYORK datasets, the accuracy of the proposed method improved by 30.96% and 9.21% compared to SVM and ADAboost methods, but slightly decreased by an average of 1.71% compared to KNN, RF, and CNN methods.Since the size of the New York and BRONX datasets are larger than that of the CHILI datasets, it is also reasonable that the New York and BRONX datasets are not as effective as the CHILI datasets.

In Fig. 14, by validating different datasets in various classifiers, four classification metrics—Accuracy, Precision, Recall, and F1-score—are used to verify the effectiveness of the proposed method in enhancing the quality of accident data and improving accident prediction. The input data for other comparative classifiers are all generated by the method proposed in this paper. For the datasets generated through the proposed method, the prediction accuracy is improved regardless of which classifier is used for accident prediction. Among them, the GCN in the CHILI dataset achieves the highest accuracy of 0.86, and the Precision, Recall, and F1-score metrics also show balanced performance, indicating that the proposed method has solved the problem of imbalanced distribution in the original accident data.

Ablation experiment

To systematically assess the impact of different modules on the overall performance of the proposed method, this paper employs ablation experiments: specific modules are incrementally removed, and the contribution of each module to the overall framework is quantitatively evaluated. These ablation experiments primarily validate the roles of the self-attention mechanism, smooth L1 loss function, and Swish activation function within the proposed method. Table 7 presents a comprehensive ablation analysis, quantifying how the removal of individual modules affects the distributional similarity between generated and original data via three key metrics: JSD, KLD, and WD.

Table 7 The generation quality indexes under different ablation modules of proposed method.
Full size table

In Table 7, after removing the attention mechanism module, the KLD, JSD, WD value are all increased significantly, indicating that the distribution of the original data was significantly different from that of the generation data, with JSD, KLD,WD increasing by 33.4% (± 0.117), 49.5%(± 0.297) and 45.9%(± 0.765)), respectively.

On the other hand, the results reveal that the Smooth-L1 function and Swish activation function modules leads to the most significant performance degradation, with JSD increasing by 0.4094, KLD increasing by 0.4455, and WD rising by 0.3666, indicating its critical role in preserving data discreate integer and unbalanced distribution characteristics. In view of the above situation, it shows that the discrete integer characteristics of the original data need to integrate these modules to make the newly generated samples conform to the original distribution characteristics. Moreover, Smooth-L1 function and Swish activation function can further solve the problems of unbalanced distribution and discrete-integer of samples, so the removal of activation function and reconstruction loss function modules makes the distribution distance indexes fluctuate the most. Regarding the afore-mentioned results, it indicates that the discrete integer characteristics inherent in the original data require the integration of these modules to ensure that newly generated samples conform to the original distribution properties.

To sum up, the proposed method effectively addresses the imbalanced distribution issue of discrete integer-type samples and is capable of synthesizing new samples that align with the original sample characteristics. The proposed approach enhances data quality, further improves the accuracy of downstream classification tasks, and thereby increases data utilization rates.

Conclusion

To improve the accuracy of road traffic accident severity prediction, this paper proposes a model that integrates VAE-attention and GCN. First, data mapping encoding is applied to digitize the original samples. Then, a Variational Autoencoder (VAE) with a self-attention mechanism is used to capture the distribution of minority class samples, uncover internal correlations among features, and generate samples that better align with the original data distribution, using the Smooth L1 loss function. Finally, a Graph Convolutional Network (GCN) is employed to classify the severity of accidents. Experimental results show that after sample augmentation, the proposed method improves prediction accuracy by 19.06–42%, outperforming other models and effectively addressing the data imbalance issue. In the future work, the incorporating spatiotemporal information or multimodal features (e.g., images, text) will explore into accident prediction. The model can also be extended to more real-world traffic scenarios, such as highways or urban intersections, to enhance the efficiency of traffic management and risk warning systems.