Abstract
The paper presents a lightweight hybrid image encryption scheme for IoT applications. The method performs secure key exchange using ECC, derives random keys using the CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195], and encrypts the image using AES-128. The secret shared via ECC serves as the seed for the CA rule vector [90, 90, 51, 51, 92, 195, 195, 195], facilitating the generation of a highly dispersed and secure session key. The system generates a highly diffused key through CA and then uses it in the AES encryption process. The framework has been tested on standard images from the SIPI database and has shown strong security results with NPCR of 99.6461, UACI of 49.9927, and entropy of 7.9991 for the Baboon Image. The method has passed all NIST randomness tests and shows a superior execution time, making it highly suitable for lightweight encryption in resource-constrained IoT environments.
Similar content being viewed by others
Introduction
The existing cryptographic models highlight the challenge of achieving efficient, secure and scalable key diffusion in strong information security1. RSA and ECC systems provide good protection; however, they often face key sharing problems, especially in environments vulnerable to cyber threats2,3. This proposal introduces a new solution that uses parallelism CA to enhance security and efficiency in key sharing within a hybrid cryptographic framework4.
‘Cellular Automata (CA)’, known for its simplicity and powerful features, has been widely applied in fields such as image processing, random number generation, and cryptography5. Cryptographic systems improve encryption by using one-dimensional and two-dimensional cellular automata (CA) to introduce randomness and distribution6. The proposed method combines ‘cellular automata (CA)’ with ‘Elliptic Curve Cryptography (ECC)’ to create a hybrid secure data model based on cellular automata, which improves the security and integrity of cryptographic processes7.
The proposed algorithm uses dynamic Cellular Automata to handle secret key exchanges in a typical two-party setup. It integrates small and secure key sizes through ECC and embeds chaotic properties in CA, which strengthens protection against attacks such as cryptanalysis. The proposed work uses CA for key distribution, improving efficiency even when an attacker attempts to intercept it.
This paper discusses the design and implementation of the suggested algorithm, as well as a comparison with alternative key distribution methods. Simulation and analysis show that the proposed method improves security while being significantly less complex than SHA-3, making it a practical option for use in modern cryptography.
-
Hybrid Encryption Approach: The proposed method uses the ECC and CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] for secure image encryption on low-resource devices.
-
Strong Security Results: The proposed method achieves NPCR of 99.6261 and UACI of 49.9758, showing a high resistance to attacks.
-
Future use flexibility: Future implementations can adapt the proposed work to other cryptographic methods and CA rules for different security applications.
The next part of the proposed research work is described in the following way. In the first section of this proposed work, Section "Related works" looks at some of the previous research work done in this field. To avoid losing readers, some preliminary concepts are discussed in Section "Preliminaries" before presenting the proposed scheme in Section "The proposed scheme". The performance analysis of the proposed plan, the experiments and their results is presented in Section "Experimental results and analysis" of the paper. Lastly, Section "Conclusion" concludes the entire process.
Related works
We reviewed the existing literature by grouping it into three categories: Cellular Automata (CA)-based encryption, ECC-based encryption, and Hybrid encryption combining ECC, CA, and other methods.
Cellular automata-based encryption
Stuanicua et al.8 studied the use of Cellular Automata in cryptography. They showed that stream ciphers and hardware implementations of CA improve data security. Their work supports the concept of using Linear Hybrid Cellular Automata (LHCA) for real-time processing.
Das et al.9 explored traditional cryptographic methods such as DES and AES. They combined CA Rules 32 and 2 with XOR operations to improve symmetric key encryption and decryption. This approach increased the efficiency and strength of the cryptosystem.
Banerjee et al.10 developed a hardware-based encryption model using CA for wireless networks. Their model used multiple encryption layers, captured environmental noise, and adapted to real-time changes. This design improved resistance against code breaking and reduced the encryption time.
Parashar et al.11 used non-complemented CA rules and a hybrid rule vector for symmetric key cryptography. They implemented the method in C language to improve security during digital data transmission.
Chakraborty et al.12 introduced a new way to select hybrid CA rule sets that provide stronger cryptographic properties. They used graph theory to evaluate features like nonlinearity and algebraic degree. Their approach passed NIST randomness tests and outperformed earlier CA-based models.
ECC-based encryption
Gupta et al.13 used ECC for image encryption on 3G devices. They converted image pixels into elliptic curve points to create cipher images. ECC provided smaller key sizes, faster speed, and stronger security compared to RSA.
Toughi et al.14 applied ECC with AES for image encryption. They used a dynamic generator point G and ECC-based random number generators defined by NIST. Their method offered small key sizes, strong randomness, and reliable security.
Fang et al.15 combined ECC with a 5D hyperchaotic system and DNA coding for asymmetric colour image encryption. Their multi-layer scrambling and diffusion steps improved resistance to attacks and provided high entropy and large key space.
Jasra et al.16 integrated ECC with DNA encoding and a 4D hyperchaotic system. Their method included mutual authentication and digital signatures for image verification. It improved randomness, reduced complexity, and resisted multiple forms of cryptanalysis.
Hybrid ECC, CA, and chaotic systems
Kumar et al.17 proposed an image encryption method using chaotic maps, ECC, and a genetic algorithm. They achieved an entropy score of 7.99 and a key space of \(2^{511}\). Their model encrypted a \(512\times 512\) image in 0.5634 seconds.
Chowdhary et al.18 analyzed hybrid encryption methods such as ECC with Hill Cipher, ECC with AES, and ElGamal with Double Playfair Cipher. They tested combinations for encryption time, entropy, PSNR, NPCR, and UACI. They found that ECC with AES is effective for small images sent over long distances.
Zheng et al.19 introduced a method that used a combined chaotic map with an improved zigzag transform. The improved chaotic system produced better shuffling and mixing of pixels. They also used SHA-256 to protect against chosen plaintext attacks.
Li et al.20 enhanced image encryption with a modified lifting structure and a cross-plane zigzag transform. Their method overcame coupling problems in traditional zigzag methods and improved information entropy21,22.
The limitations of the proposed work are:
-
The ECC algorithm requires time for key generation, which may be a concern for very low-power IoT devices.
-
The method uses a fixed Cellular Automata Rule (CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195]), which may not be strong against all types of attacks.
-
Distributed systems complicate the secure storage of private keys and IVs.
-
The study tested the system on small grayscale images, and its behaviour may differ with larger or colour images.
Table 1 presents a detailed comparison of related image encryption schemes, covering methods such as DNA coding, chaotic maps, Cellular Automata, and elliptic curve-based encryption, along with their respective strengths and drawbacks.
Preliminaries
In the following section, the proposed work will conduct an in-depth analysis of the challenges in the mathematical foundations and theoretical frameworks that play a key role in defining the architecture of the proposed work. The proposed work begins by introducing the basics of “Cellular Automata (CA)” and exploring the field of “Elliptic Curve Cryptography (ECC)”. These theoretical concepts form the foundation for a detailed, step-by-step introduction to the proposed cryptosystem in the following section.
Cellular automata rule number 51, 90, 92, 195
John von Neumann, a leading figure in the domain of ‘Cellular Automata’ (CA), is acknowledged as the father of CA28. The concept of self-replication, which describes a system’s ability to produce an identical replica of itself, significantly stimulated his strong interest29.
Rule 90
Rule 90 is a 1D Cellular Automaton defined by the update rule of the Eq. (1).
where \(C_{i}^{t+1}\) denotes the state of cell i at time step \(t+1\), and \(\oplus\) denotes the bitwise XOR operation.
Starting from a simple pattern, such as a single one among 0s, Rule 90 generates a fractal-like Sierpinski triangle. Due to its structured complexity and deterministic yet chaotic behaviour, it makes it useful for applications in random number generation, fractal creation, and cryptographic systems.
Rule 51
Rule 51 is a 1D Cellular Automaton defined by the update rule shown in Eq. (2).
Here, \(C_{i}^{t+1}\) denotes the state of cell i at time step \(t+1\), and \(\overline{C_{i}^{t}}\) represents the bitwise NOT (logical inversion) of the cell’s current state.
Rule 51 functions as a simple inversion rule, where each cell flips its state at every time step, independent of its neighbours. This results in a blinking behaviour with a period of two. While not complex on its own, this rule can contribute to diversity and unpredictability in hybrid Cellular Automata systems used in encryption and pseudo-random bit generation.
Rule 92
Rule 92 is a 1D Cellular Automaton defined by the update rule in Eq. (3).
where \(C_{i}^{t+1}\) denotes the state of cell i at time step \(t+1\), and \(\oplus\) denotes the bitwise XOR operation.
Rule 92 creates patterns based on the XOR of the left and right neighbouring cells. It produces semi-chaotic structures with alternating complexity, which makes it valuable when used alongside other rules in cryptographic systems, particularly in key stream generation or diffusion stages.
Rule 195
Rule 195 is a 1D Cellular Automaton defined by the update rule of Eq. (4).
where \(\overline{C_{i-1}^{t}}\) is the bitwise NOT of the left neighbor, and \(\vee\) denotes the bitwise OR operation.
Rule 195 introduces conditional behaviour based on the negation of the left neighbour and the current cell’s state. The combination of inversion and logical OR creates asymmetric transitions, which enhance diffusion and add unpredictability in lightweight encryption applications.
Table 2 shows the 10-step evolution of a one-dimensional cellular automaton (CA) using the 8-bit seed 11010011 under a null boundary. The rule vector [90, 90, 51, 51, 92, 195, 195, 195] defines the update rule for each bit position. The CA shows a repeating pattern starting at iteration 8, indicating cyclic behaviour. Such periodicity is advantageous in image encryption, as it supports reversible and secure bit-level transformations in the diffusion process.
Cellular automaton evolution process
The proposed method uses a one-dimensional cellular automaton (CA) for bit-level transformation, using an 8-bit seed and a rule vector under null boundary conditions. The following section describes the step-by-step process.:
-
1.
Initialization:
-
Seed: The initial 8-bit binary state is 11010011, equivalent to decimal 211.
-
Rule Vector: Each bit position is assigned a specific Wolfram rule as follows:
$$\begin{aligned} [90, 90, 51, 51, 92, 195, 195, 195] \end{aligned}$$ -
Boundary Condition: The proposed work applies a null boundary condition, treating the non-existing neighbours (to the left of bit 0 and right of bit 7) as 0.
-
2.
Neighborhood Extraction: To update each bit i in the 8-bit string (\(i = 0\) to 7), the proposed work construct a 3-bit neighborhood \((x_{i-1}, x_i, x_{i+1})\), substituting missing neighbors beyond the string limits with 0, as per the null boundary rule.
-
3.
Rule Application: For each bit i, apply its designated Wolfram rule (from the rule vector) to the 3-bit neighbourhood. Each rule corresponds to an 8-bit output pattern, where each bit specifies the next state for one of the eight possible 3-bit combinations (111, 110, ..., 000).
-
4.
Bit Update: For all \(i \in [0,7]\), compute the next bit value using the rule assigned to position i, and concatenate the results to form the updated 8-bit state.
-
5.
Iteration: Repeat the rule application process for a fixed number of iterations (e.g., 8 times). For each iteration, record the:
-
Updated 8-bit binary value
-
Decimal equivalent
-
6.
Pattern Observation: This cyclic behaviour is particularly useful for diffusion in image encryption. Each pixel value (ranging from 0 to 255) is represented as an 8-bit binary string and transformed through successive CA iterations, enabling strong, yet reversible, bit-level transformations.
-
7.
Application to Encryption:
Elliptic curve cryptography
“Elliptic Curve Cryptography” (ECC)30 represents an advanced public-key cryptographic scheme that uses the mathematical structure of elliptic curves situated over finite fields. ECC delivers a substantial degree of security with reduced key dimensions compared to traditional methodologies such as RSA31.
Equation (5) mathematically characterizes an elliptic curve:
where the constants \(\alpha\) and \(\beta\) must satisfy
To ensure that the curve has no singular points.
In the context of ECC key generation, one chooses a private key k and computes the corresponding public key Q as
where B is the designated base point on the curve, and \(k \cdot B\) denotes the scalar multiplication of B.
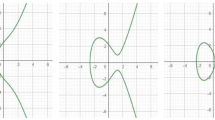
Systems employ ECC for secure communications, digital signatures, and key exchange protocols. It provides strong security32 with less computational power. This makes it well-suited for resource-constrained devices, such as mobile phones. Figure 1 shows the following procedures in Elliptic Curve Cryptography (ECC).
Elliptic Curve Cryptography (ECC) plot with parameters \(a = -1.8\) and \(b = 2\): The figure shows the elliptic curve defined by the Weierstrass equation \(y^2 = x^3 + ax + b\), which forms the foundation for elliptic curve cryptographic systems. The shape of the curve ensures the group structure required for secure key generation and exchange.
Example of ECC encryption and decryption
Consider two parties, Alice and Bob, who aim to share image data securely.
Step 1: Key Generation (ECC)
-
The elliptic curve is SECP256R1 with the base point B.
-
Alice selects a private key \(k_A = 15\) and computes her public key as \(Q_A = k_A \cdot B\).
-
Bob selects a private key \(k_B = 27\) and computes his public key as \(Q_B = k_B \cdot B\).
Step 2: Key Exchange (ECDH)
-
Alice computes the shared secret as \(S_A = k_A \cdot Q_B\).
-
Bob computes the shared secret as \(S_B = k_B \cdot Q_A\).
-
The elliptic curve properties ensure \(S_A = S_B = k_A \cdot k_B \cdot B\).
Step 3: Key Transformation using CA
-
Convert the shared secret into an 8-bit seed.
-
Process the seed through the CA rule vector [90, 90, 51, 51, 92, 195, 195, 195] for 100 iterations.
-
Generate the CA-derived session key as the output.
Step 4: Encryption (AES-128)
-
Alice encrypts the image with AES-128 in CBC mode using the CA-derived session key.
-
Alice sends the encrypted image C and the initialization vector (IV) to Bob.
Step 5: Decryption
-
Bob uses his ECC private key and Alice’s ECC public key to recompute the shared secret.
-
Bob applies the same CA transformation to regenerate the session key.
-
Bob decrypts C with AES-128 and the regenerated key to recover the original image.
This example demonstrates how ECC secures key exchange, while the CA transformation adds another layer of randomness before AES encryption, resulting in a secure and lightweight method for IoT devices.
The proposed scheme
The hybrid cryptographic system implements an image encryption framework, where Elliptic Curve Cryptography (ECC) is used to exchange private keys securely, Cellular Automata (CA) Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] is used to derive these private keys randomly, and AES-128 acts as an image encryptor. This triple-layered solution aims to provide top-notch security, with the system operating efficiently in a manner suited for resource-constrained IoT devices.
Starting with encryption, both parties generate an ECC key pair on the SECP256R1 (P-256) curve. The public keys are exchanged via the Elliptic Curve Diffie-Hellman (ECDH) to arrive at a shared secret. The system does not use this secret value directly. It feeds the value into the Cellular Automata Rule Vector [90, 90, 51, 51, 92, 195, 195, 195], which transforms it into a complex pseudorandom session key, called the CA key.
The system converts this CA-derived key into a form suitable for AES-128 encryption to secure image data. AES is used in the system because it ensures strong encryption, and embedded devices widely support it. By integrating CA as a key transformation layer, the system maximises entropy and diffusion before encryption, strengthening resistance against statistical and brute-force attacks.
Decryption is performed precisely as the encryption process. Using their private key and the sender’s public key, the receiver regenerates a shared secret, then generates the same CA key using Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] and ultimately decrypts the image using AES-128.
Figures 2 and 3 illustrate the encryption and decryption workflows. The complete setup consists of four core steps.
-
1.
ECC Key Generation and Exchange: Generate ECC key pairs and derive the shared secret through ECDH.
-
2.
Key Derivation with CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195]: Use the shared secret as a seed in the Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] and run it for 100 iterations with a 32-cell automaton to generate a pseudorandom CA key.
-
3.
Image Encryption Using AES-128: Encrypt the grayscale image using AES in CBC mode with a 128-bit IV and the CA key.
-
4.
Secure Decryption: Decrypt the encrypted image using the same key and IV derived earlier
Hence, this approach uses ECC for lightweight key exchange, CA for efficient randomness generation, and AES for strong symmetric encryption to realise a compact, secure, and scalable encryption system for the IoT platform.
In the proposed framework, the Cellular Automata CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] is used to derive the key from the ECC-generated shared secret. The CA Rule Vector [90, 90, 51, 51, 92, 195, 195, 195] was chosen due to its low computational overhead, straightforward bitwise XOR evolution, and suitability for real-time applications in resource-constrained IoT devices. Although Rule 90 is a linear rule that generally produces symmetrical patterns, the system does not apply it directly for encryption but uses it for dynamic key generation. When seeded with a truly large-entropy input (i.e., the ECC shared secret), the CA evolution produces outputs that are sufficiently diffused to be used as derivatives in session-based AES keys. Rule 90 is too simple, elegantly hardware-friendly, and very fast. That said, we do acknowledge that a combination of multiple CA rules or a good non-linear one, such as Rule 30 or some hybrid CA switching strategies, would improve randomness and resistance to key prediction. The study discusses this disadvantage and includes it in the proposed future work.
Currently, the design uses ECC-based key exchange to establish a shared secret between the two communicating parties. Although secure and efficient enough for the initial key agreement, we recognise that performing ECC operations for every single encryption instance will be computationally expensive, especially for constrained IoT devices. In a practical implementation of the schemes, the ECC key exchange may be performed once per session, after which the shared secret derived from it may be reused (periodically refreshed, for example, or used for multiple images). This session key approach reduces computational requirements while retaining security properties.
Algorithm 1, GenerateECCKeyPair generates a pair of keys for ‘Elliptic Curve Cryptography’ (ECC) without any external input. It outputs a tuple that contains a private key and a public key. The algorithm begins by generating a private key using the SECP256R1 curve and the default_backend() for cryptographic operations. Next, it derives the corresponding public key from the generated private key. The process returns both the private and public keys as a tuple. It keeps the private key secret to ensure secure communication, while the public key is shared openly.
Algorithm 2, DeriveSharedSecret derives a shared secret between two parties using “Elliptic Curve Diffie-Hellman” (ECDH). It begins by using the private key to perform the ECDH exchange with the peer’s public key, which allows both parties to compute the same shared secret. The resulting shared secret is then returned as the algorithm’s output, enabling secure communication between the two parties while keeping the private keys confidential.
Algorithm 3, CAFE_Encrypt, is a hybrid image encryption procedure that combines Elliptic Curve Cryptography (ECC) for secure key exchange, Cellular Automata (CA) Rule 90 for key derivation, and AES-128 as the main encryption algorithm. The algorithm accepts two inputs: image_path (the path to the original image) and output_path (the location where the encrypted image will be saved). It begins by generating ECC key pairs for both the sender and the receiver, resulting in (PrivateKey_A, PublicKey_A) and (PrivateKey_B, PublicKey_B). The system establishes a shared secret via Elliptic Curve Diffie–Hellman (ECDH) using the sender’s private key and the receiver’s public key. This shared secret is converted into an integer and used as seed input for a Cellular Automata Rule 90 process, producing a session key, CA_Key. The grayscale image is then loaded from image_path into ImageArray. The actual encryption is performed using the AES-128 algorithm in the CBC mode, with the CA_Key and a randomly generated Initialisation Vector (IV). Finally, the resulting encrypted image and the IV are saved in output_path, and the algorithm returns a confirmation message indicating successful encryption and storage.
Algorithm 4, CAFE_Decrypt, is a hybrid image decryption procedure that complements the CAFE encryption process. It integrates Elliptic Curve Cryptography (ECC) for secure key reconstruction, Cellular Automata (CA) Rule vector (90,90,51,51,92,195,195,195) for session key derivation, and AES-128 for decrypting image data. The algorithm takes four inputs: encrypted_path (the location of the encrypted image), output_path (the destination path for the decrypted image), PrivateKey_A (the receiver’s ECC private key), and PublicKey_B (the sender’s ECC public key). The process begins by loading the encrypted image from the specified path and extracting both the Initialisation Vector (IV) and the encrypted image content (EncryptedImage). The shared secret is then computed using the ECC Diffie–Hellman key exchange method, based on PrivateKey_A and PublicKey_B. This shared secret is converted into an integer and used as a seed in the Cellular Automata Rule vector (90,90,51,51,92,195,195,195), generating the session decryption key CA_Key. The AES-128 decryption algorithm is then applied using the derived CA_Key and IV to recover the original image data, stored in DecryptedImage. Finally, the decrypted image is saved in output_path, and the algorithm returns a message confirming successful decryption and storage.
Computational complexity
The proposed encryption scheme involves several steps that contribute to its overall computational complexity. The key generation using ‘Elliptic Curve Cryptography’ (ECC) with the secp256r1 curve has a fixed complexity of O(1). This is because it uses a fixed key size of 256 bits and the operations are independent of the image size. The key exchange using Elliptic Curve Diffie-Hellman (ECDH) also takes O(1) time. It uses the same scalar multiplication technique as the ECC key generation. The Cellular Automata (CA)-based key transformation uses the rule vector (90,90,51,51,92,195,195,195). It runs on a grid that matches the image size. If the image is \(n \times n\), the time required for this step is \(O(n^2)\). The number of iterations in CA is constant, so it does not significantly affect the overall complexity. Encryption and decryption are performed using the Advanced Encryption Standard (AES) algorithm. AES works on fixed-size blocks. Since the number of blocks increases with the size of the image, the time complexity is \(O(n^2)\). In total, both the encryption and decryption processes take \(O(n^2)\) time and space. This is shown in Table 3. The method is simple, fast, and suitable for devices with limited resources.
Key sharing process
Table 4 shows the key sharing steps used in the proposed method. In Step 1, both Alice and Bob create ECC key pairs. Each pair has a private key and a public key. The private key is kept secret, and the public key is shared. In Step 2, Alice and Bob exchange their public keys, but keep their private keys hidden. In Step 3, each person uses their private key and the public key of the other person to compute a shared secret. This shared secret is never sent over the network. In Step 4, the shared secret is converted into a number, which is used as input for the Cellular Automata Rule vector (90,90,51,51,92,195,195,195). This generates a new key called CA_Key. In Step 5, the CA_Key is used to start the encryption and decryption of AES-128 of image data. This process ensures security and is suitable for lightweight devices.
Table 5 presents the main building blocks of the proposed encryption scheme and their functions and security advantages. The Private Key is a secret 256-bit value that is never exchanged. It protects against man-in-the-middle (MITM) attacks. The Public Key is derived from the private key and may be exchanged freely. It assists in secure key exchange via ECDH, but is worthless without the private key. Each party uses its keys through ECDH to generate the Shared Secret. The system never transmits this secret and remains session-specific, ensuring forward secrecy. The CA Key is derived using the Cellular Automata Rule vector (90,90,51,51,92,195,195,195). It enhances randomness, and the encryption is secured against statistical attacks. The AES-IV is a 128-bit initialisation vector. It ensures that even if the same image is encrypted multiple times, the output is distinct every time.
Table 6 describes an example of the key-exchange procedure. Alice generates a private key and a public key first. Bob generates his own private key and public key. Alice transmits her public key to Bob. Bob obtains Alice’s public key. Subsequently, Bob sends his public key to Alice. Alice obtains Bob’s public key. Finally, Alice computes the shared secret using her private key and Bob’s public key. Bob also uses his private key and Alice’s public key to calculate the same shared secret. Both use this shared secret to generate the CA_Key. This CA_Key is employed for AES encryption.
Difference from existing key exchange approaches
Many existing secret key exchange methods use only public-key cryptography, such as RSA or Elliptic Curve Cryptography (ECC), to create a session key, or they depend on symmetric keys that are shared in advance. These methods often have higher processing needs, face risks if part of the key is leaked, or do not add enough randomness to the session key. The proposed method first uses ECC with the SECP256R1 curve to create a shared secret between two parties. This shared secret is not used directly. Instead, it passes through an 8-bit Cellular Automata (CA) rule vector [90, 90, 51, 51, 92, 195, 195, 195]. This step changes the bits and adds more randomness before making the final AES-128 session key. This two-step process gives better protection against guessing and statistical attacks, while keeping the processing light for IoT devices.
Experimental results and analysis
The experimental results are performed in Python 3.7 and executed on an HP laptop with an Intel Core i5-8250U CPU (1.80 GHz) and 8 GB of RAM. In this proposed work, the elliptic curve secp256r1 (P-256) has been used. The input test images are “Baboon,” of size \(512\times 512\) pixels and “House,” and “Female”, each of size \(256\times 256\) pixels, while one clock image of size \(512 \times 512\) pixels has been used in JPG format from the SIPI database33, as shown in Fig. 4. It provides a clear test environment to evaluate the performance and compatibility of the model with standard hardware. It is one of the most widely used types of elliptic curve cryptography.
Visual comparison of original, encrypted, and decrypted images for four standard test cases using the proposed encryption scheme. The results show the effectiveness of the encryption in obscuring visual content and the accuracy of the decryption in restoring the original images without perceptible loss. (Image Source 33).
Table 7 presents a set of benchmark test images selected from the USC-SIPI image database33, which is widely adopted in image processing and encryption research. The images represent diverse categories such as highly textured patterns (Baboon), biometric content (Female), objects with sharp edges (Clock), and architectural structures (House). This diversity enables a comprehensive evaluation of the proposed encryption system in terms of texture preservation, edge sensitivity, and statistical measures including PSNR, SSIM, NPCR, UACI, and entropy.
The encryption quality of the proposed framework is measured using four standard images from the USC-SIPI image database33. The chosen images differ in content, structure, and complexity and are suitable for serving as standards to evaluate the performance of statistical and perceptual operations.
Key space exploration
This section evaluates the per-session brute-force space for the proposed scheme.
ECC secret and security level: ECDH over secp256r1 (P-256) produces a 256-bit shared secret. In practical terms, P-256 provides approximately a 128-bit security level.
Key derivation: The scheme derives a 128-bit AES session key from the ECDH shared secret using a CA-based transform. This transform does not add new entropy; it deterministically maps the shared secret to a 128-bit key.
IV is public: AES-CBC uses a 128-bit IV that is random and publicly transmitted. Because the IV is not secret, it does not contribute to brute-force key space.
Effective key space: An attacker must guess the 128-bit AES session key to break a single session:
This key space aligns with the security level of P-256 and resists brute-force attacks.
Note on ECC private keys: Breaking the long-term ECC private keys requires solving the elliptic-curve discrete logarithm problem, which has an estimated work factor of roughly \(2^{128}\) operations. This attack is distinct from per-session AES key guessing.
Brute-force resistance
Brute force resistance refers to a system’s ability to survive attacks in which an attacker tries every possible key to find the correct one. In this encryption system, the use of Elliptic Curve Cryptography (ECC) with a 256-bit private key creates a huge key space. This key space is \(2^{256}\), making it extremely difficult to guess the correct key through brute-force attacks. The use of Cellular Automata and AES encryption adds an extra layer of security. These techniques enhance the system’s security, making brute-force attacks practically impossible.
Histogram analysis
Histogram analysis examines the spatial arrangement of pixel intensity values within a visual representation to assess its contrast, brightness, and overall quality34. The histogram graphically represents the frequency of each intensity level and highlights image characteristics such as under- or overexposure35. This analytical approach is instrumental in a variety of applications, including image enhancement, thresholding, and segmentation, thereby facilitating improved visualisation and interpretation of image data. Figures 5, 6, 7, and 8 display histograms of the pixel distributions for the Baboon, House, Female and clock images, respectively, for the original and encrypted versions.
Comparison of the original and encrypted Baboon images. Subplots: (a) Histogram of original image showing non-uniform pixel distribution, (b) Histogram of encrypted image showing nearly uniform distribution, (d) Circular histogram of original image, and (d) Circular histogram of encrypted image demonstrating uniform pixel diffusion. (Image Source:33).
Comparison of the original and encrypted House images. Subplots: (a) Histogram of original image showing non-uniform pixel distribution, (b) Histogram of encrypted image showing flattened distribution, (c) Circular histogram of original image, and (d) Circular histogram of encrypted image demonstrating uniform pixel diffusion. (Image Source:33).
Comparison of the original and encrypted Female images. Subplots: (a) Histogram of original image showing non-uniform pixel distribution, (b) Histogram of encrypted image showing uniform distribution, (c) Circular histogram of original image, and (d) Circular histogram of encrypted image demonstrating effective diffusion and encryption. (Image Source:33).
Histogram comparison of the original and encrypted Clock images. The encrypted histogram is highly uniform, indicating strong resistance to statistical analysis. (Image Source33).
Test of cipher image quality
MSE calculates the average square difference between the pixel values of the two images. The MSE formula between an original image and a cipher image is as follows36:
Here, X and Y are the height and width of the image, respectively, while A(x, y) and B(x, y) represent the pixel values of the plain image and the cipher images at position (x, y), respectively. The MSE needs to be greater than or equal to 30 for an algorithm to be considered generally secure. Table 8 presents the MSE values between the plain or original image and the cipher images obtained after the proposed algorithm.
PSNR gives the ratio of noise between plain and cipher images. The PSNR formula between plain and cipher image is37:
Here, \(Z_p\) denotes the maximum possible pixel value (255 for 8-bit images), and MSE represents the mean square error obtained from Eqs. (7) and (8). The high value of PSNR indicates a good quality of an image and similarity to the original image. A small value of PSNR indicates high encryption quality. Table 8 presents the PSNR values of the encrypted images obtained by the proposed algorithm.
In table 8, the MSE values for the encrypted images are around 105.44 for Female, 105.26 for Clock, 105.48 for House, and 105.69 for Baboon. These \(\text {PSNR}\) values indicate that the image quality is largely preserved, with only moderate distortion introduced by the encryption process.
The PSNR values for these images are 27.90 for Female, 27.91 for Clock, 27.90 for House, and 27.90 for Baboon. These \(\text {PSNR}\) values indicate that the image quality is largely preserved, with only moderate distortion introduced by the encryption process. These values indicate that the encryption process introduces only minimal distortion between the original and encrypted images, as expected for secure image encryption schemes.
Differential analysis
Differential analysis examines the response of encrypted visual data to minor alterations in the input, using two main metrics, “Number of Pixels Change Rate” (NPCR) and “Unified Average Changing Intensity” (UACI)38.
The method computes NPCR and UACI using the following equations.
Here \(I_1\) and \(I_2\) are two encrypted images: one generated from the original image and the other from a version in which only one pixel has been altered39. Let the width of the image be M and the height be N. Table 9 presents the NPCR and UACI values computed for the proposed method using Eqs. (9), (10), and (11).
In table 9, the NPCR values for the encrypted images are 99.6461 for Baboon, 99.5992 for Female, 99.6419 for Clock, and 99.6068 for House. These values indicate that the encryption method is highly sensitive to pixel changes, as the NPCR is close to 100, which is desirable to ensure security by producing significant differences in the encrypted image.
The UACI values for the images are 49.9927 for Baboon, 49.9561 for Female, 49.9823 for Clock and 49.9787 for House. These figures show that the encryption method produces a significant difference in the intensity of the pixels, with UACI values approaching 50, which is ideal to ensure that the encrypted images differ substantially from the original images.
Information entropy analysis
Image randomness is measured using information entropy40, defined by the formula 12:
Here, \(P(x_i)\) is the probability of each grayscale intensity value \(x_i\). For grayscale images, an entropy value close to 8 indicates high randomness41. In our experiment, we encrypted grayscale medical images using our algorithm, and the entropy values shown in Table 10 are close to 8, confirming strong randomness in the encrypted images.
In table 10, the Information Entropy for the original images is 7.7845 for Baboon, 7.6763 for Female, 7.7477 for Clock and 7.5231 for House. These values show the amount of randomness or unpredictability in the pixel values of the original images.
For encrypted images, the Information Entropy values are 7.9991 for Baboon, 7.9991 for Female, 7.9990 for Clock, and 7.9997 for House. These values are very close to 8, which is the maximum possible entropy for an 8-bit image. This indicates that the encryption method increases the randomness, making the encrypted images highly unpredictable and secure.
Correlation coefficient tests
Correlation Coefficient Tests examine the interplay between pixel values in both original and encrypted images, illustrating the extent to which the encryption process maintains or modifies spatial information42 using Pearson’s Equation (13), (14) and (15). The method uses the following formulae to calculate the correlation coefficient between two adjacent pixels.
Here, x and y are the grey values of two adjacent image pixels.
- t is the total number of pairs of adjacent pixels selected, where each pair is represented as (x, y). - E(x) is the mean grey value of all pixels x. - D(x) is the variance of the grey values of the pixels x.
Table 11 presents the values of the correlation coefficient in the horizontal, vertical and diagonal directions for the gray test images and their encrypted versions. The correlation values for the original test images are close to one, indicating a high similarity between adjacent pixels. In contrast, the correlation values for the encrypted images are close to zero, showing low similarity and high randomness43.
Figures 9, 12, 10 and 11 show correlation coefficients for the Baboon, Clock, House, and Female images. Table 11 shows the correlation coefficient linked with the proposed methodology.
RGB pixel correlation scatter plots of the Baboon image. The left column of each channel (R, G, B) shows the original image correlation, while the right column shows the encrypted image correlation. The three rows represent horizontal, vertical, and diagonal pixel correlations, respectively. The encrypted images show low correlation, demonstrating effective diffusion and encryption.
RGB pixel correlation scatter plots of the House image. The left column of each channel (R, G, B) shows the original image correlation, while the right column shows the encrypted image correlation. The three rows represent horizontal, vertical, and diagonal pixel correlations, respectively. The encrypted images show low correlation, demonstrating effective diffusion and encryption.
RGB pixel correlation scatter plots of the Female image. The left column of each channel (R, G, B) shows the original image correlation, while the right column shows the encrypted image correlation. The three rows represent horizontal, vertical, and diagonal pixel correlations, respectively. The encrypted images show low correlation, demonstrating effective diffusion and encryption.
In table 11, the correlation values of the original images are very high. This means that the pixels in the original images are closely related to each other. For example, Baboon has 0.8246 in the horizontal direction, 0.7649 in the vertical direction, and 0.7591 in the diagonal direction.
The encrypted images show correlation values close to zero. This means that the pixel relationships break after encryption. For example, Baboon has 0.0050 in the horizontal direction, -0.0002 in the vertical direction, and -0.0035 in the diagonal direction. This indicates that the encryption method eliminates pixel similarity. This is a sign of a secure encryption scheme.
Comparative analysis
Table 12 provides a comparative analysis of the proposed method about other scholarly studies, using metrics such as “Mean Squared Error” (MSE), “Peak Signal-to-Noise Ratio” (PSNR), “Number of Pixel Change Rate” (NPCR), “Unified Average Changing Intensity” (UACI), information entropy, and the correlation coefficient.
The table compares the proposed method to existing methodologies, showing that it achieves higher NPCR and UACI values. It also has a high information entropy, close to eight. The correlation coefficients are almost zero. This means that the encrypted image is relatively safe. The MSE and PSNR values are both satisfactory. These findings support the good encryption performance of the suggested method.
The line graph (Fig. 13) presents a comparative assessment of four encryption protocols—the proposed work, PRESENT, SPECK, and ChaCha20—on six major evaluation factors: security, performance, memory footprint, computational overhead, energy expenditure, and scalability. Each approach is scored on a scale from 1 (Low) to 5 (Excellent), with an easy-to-follow visual line indicating its strengths and weaknesses. The proposed work consistently achieves high scores in all categories, making it suitable for lightweight, efficient, and scalable encryption. ChaCha20, on the other hand, is highly secure, but falls behind in terms of energy and computational efficiency, showing resource trade-offs.
Line chart representation of encryption algorithms—Proposed work, PRESENT, SPECK, and ChaCha20—evaluated across key criteria: security, performance, memory usage, computational cost, energy consumption, and scalability. The scores were obtained through a hybrid approach: PRESENT and SPECK metrics were adapted from47, ChaCha20 values from48, and proposed method values from our experimental evaluation on a Python 3.7 environment (Intel Core i5-8250U, 8GB RAM). All criteria were normalized to a five-point rating scale for consistency.
The radar graph Fig. 14 displays the multidimensional performance overview of the same four encryption methods. The circular viewpoint highlights the well-balanced excellence of the suggested work, which is evident in its strong performance across all six areas. The form and space covered by each polygon point out the general efficiency of each method. Although PRESENT and SPECK offer efficient and lightweight cryptography, they lack security compared to the proposed work. ChaCha20 is superior in terms of security but suboptimal in terms of energy consumption and computational cost; therefore, it is better suited for high-performance devices rather than resource-constrained IoT devices. The radar chart uses data taken from Table 13.
Radar chart comparing proposed method with PRESENT, SPECK, and ChaCha20 based on normalized values for speed, memory, energy, security, and scalability. The method derives the raw values from benchmark studies and experimental results presented in Table 15. Higher scores indicate better performance.
Table 14 presents a comparative evaluation of the proposed work scheme against existing lightweight encryption techniques: PRESENT, SPECK, and ChaCha20. The proposed method offers high security, low computational cost, and minimal energy consumption, making it an ideal solution for IoT and constrained environments. In contrast, ChaCha20 offers strong security, but at the expense of higher resource requirements, while PRESENT and SPECK provide moderate security with low memory usage.
The study takes the benchmark values for PRESENT and SPECK from their original specifications and from the hardware evaluation reported by47.. For ChaCha20, performance statistics were taken according to Bernstein’s analysis48. The study uses these results as normalization scores on the radar chart (Fig. 14) and summarizes them in Table 15.
NIST test
The “National Institute of Standards and Technology”49, also known as NIST, is a federal agency in the United States that focuses on measurement, standards, technology, adoption, and best practices throughout the country. NIST was founded in 1901 and serves as one of the key agencies providing a reliable measurement system essential in various fields, including cybersecurity, manufacturing, and scientific research. It has established several frameworks and guidelines for information security, including the NIST Cybersecurity Framework and the NIST Special Publication50. NIST promotes innovation and provides access to valuable resources that improve the quality and safety of government and commercial systems, benefiting the public and the economy. Table 16 shows the evaluation results. These statistics demonstrate the strong performance of the proposed work in all tests and its effectiveness in generating high image insecurity.
In Table 16, we present the results of the NIST statistical test suite applied to the encrypted Baboon grayscale image. Each p-value exceeds the significance threshold of 0.01, which confirms that the encryption process introduces high randomness into the image data. The tests, including Frequency, Runs, Approximate Entropy, and Serial variations, demonstrate the absence of detectable patterns. Furthermore, the results of Random Excursions and Random Excursions Variant show consistent statistical uniformity, reinforcing the robustness of the proposed encryption method against randomness-related vulnerabilities.
Encryption and decryption time and memory usage for Baboon (\(512\times 512\)) Image
Table 17 presents a performance comparison of the proposed ECC and Cellular Automata-based image encryption and decryption algorithms using the standard Baboon image (\(512 \times 512\) pixels). The encryption procedure took 0.000813 seconds, using 332,622 bytes of memory, while the decryption procedure took even less time, 0.000378 seconds, and used 198,693 bytes of memory. These findings demonstrate the efficiency of both the computational speed and memory requirements of the algorithm, thus qualifying it for lightweight security applications.
Performance justification for AES in IoT
Though AES is not generally classified as a lightweight cipher compared to specialised lightweight block ciphers such as PRESENT or SPECK, this choice is dictated first by practical and then technical considerations. AES-128 is a NIST-approved standard encryption, well accepted worldwide, and by far the most secure cipher established against the very best cryptographic attacks. It is best suited for crucial IoT applications such as medical imaging, smart surveillance, and secure sensor networks. However, several modern IoT processors implement AES support in hardware (emphatically the ARMv8 Cryptography Extensions and Intel AES-NI), which creates a speedy implementation for AES transmissions, so the potential computational burden is mostly gone. In the experimental evaluation scheme, this framework is encrypted in 0.000813 seconds. It requires only 332,622 bytes of memory for a \(512 \times 512\) grayscale image, which indeed attests that AES is well-suited in terms of efficiency even on resource-constrained devices if harnessed and designed cleverly. Moreover, AES is coupled with a CA-based key derivation scheme.
Comparative analysis of CA rules
Table 18 shows the comparative study of the frequently used CA rules for cryptography. Rule 90 and Rule 150, which are linear and predictable, are used for lightweight key derivation in our model, not for genuine encryption. It is simple and fast enough for implementation in constrained environments. However, nonlinear or hybrid rules (like Rule 30, Rule 45 or Hybrid CA) provide greater randomness and thus better security. Such rules could eventually be incorporated to enhance the unpredictability of the key scheduling operation.
Comparison of encryption frameworks for IoT in terms of security and efficiency
Table 19 gives a high-level comparison of different encryption frameworks suited for IoT environments. Our proposed framework (ECC + CA + AES) strikes a balance between security and computational efficiency, with the CA Rule vector introducing lightweight key derivation; however, performing ECC operations in every encryption cycle can result in some overhead. The system can minimize this overhead by adopting session-based key negotiation or integrating lightweight cipher techniques such as PRESENT. Along such lines, future work is foreseen to include benchmarking on constrained IoT hardware.
Conclusion
The proposed work is a hybrid image encryption system that integrates key exchange based on elliptic curve cryptography (ECC), cellular automata (CA) Rule Vector-based session key derivation, and AES-128 encryption. The main novelty is the use of CA to transform the ECC dynamically shared secret into a cryptographically strong and diffused session key. AES-128, which is not a lightweight cipher in theory, has demonstrated performance efficiency in this framework, illustrating its practical feasibility for IoT implementations. The scheme performs excellently in statistical tests (NPCR 99.6461, UACI 49.9927, entropy \(\approx 7.9991\)) and passes all NIST tests. Subsequent work will consider alternative lightweight cipher algorithms, such as SPECK or PRESENT, and adaptive CA rule systems for further enhancement in resource savings and scalability.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- CA:
-
Cellular Automata
- ECC:
-
Elliptic Curve Cryptography
- AES:
-
Advanced Encryption Standard
- CBC:
-
Cipher Block Chaining
- NPCR:
-
Number of Pixels Change Rate
- UACI:
-
Unified Average Changing Intensity
- IV:
-
Initialization Vector
- PSNR:
-
Peak Signal-to-Noise Ratio
- MSE:
-
Mean Squared Error
- NIST:
-
National Institute of Standards and Technology
References
Ramakrishna, D. & Shaik, M.A. A comprehensive analysis of cryptographic algorithms: Evaluating security, efficiency, and future challenges. IEEE Access 13, 11576-11593 (2024)
Dalal, Y.M., Supreeth, S., Amuthabala, K., Satheesha, T., Asha, P. & Somanath, S. Optimizing security: A comparative analysis of rsa, ecc, and dh algorithms. In: 2024 IEEE North Karnataka Subsection Flagship International Conference (NKCon), IEEE, pp. 1–6 (2024).
Mallouli, F., Hellal, A., Saeed, N.S. & Alzahrani, F.A. A survey on cryptography: comparative study between rsa vs ecc algorithms, and rsa vs el-gamal algorithms. In: 2019 6th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2019 5th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom) IEEE, pp. 173–176 (2019).
Ahmad, S., Mehfuz, S. & Beg, J. Hybrid cryptographic approach to enhance the mode of key management system in cloud environment. J. Supercomput. 79(7), 7377–7413 (2023).
Nandi, S., Kar, B. K. & Chaudhuri, P. P. Theory and applications of cellular automata in cryptography. IEEE Trans. Comput. 43(12), 1346–1357 (1994).
Packard, N. H. & Wolfram, S. Two-dimensional cellular automata. J. Stat. Phys. 38(5), 901–946 (1985).
Branstad, D. K. & Smid, M. E. Integrity and security standards based on cryptography. Comput. Secur. 1(3), 255–260 (1982).
Stănică, G.C. & Anghelescu, P. Encryption algorithm using linear hybrid cellular automaton. In: 2022 International Semiconductor Conference (CAS) IEEE, pp. 257–260 (2022).
Das, M., Das, K.R., Sahu, M. & Dash, R. Application of cellular automata for an efficient symmetric key cryptosystem. In: 2019 International Conference on Applied Machine Learning (ICAML) IEEE, pp. 21–26 (2019).
Banerjee, A. & Kundu, A. Cellular automata based cryptography model for reliable encryption using state transition in wireless network optimizing data security. Wirel. Pers. Commun. 119(1), 877–918 (2021).
Parashar, D., Roy, S., Dey, N., Jain, V. & Rawat, U. Symmetric key encryption technique: A cellular automata based approach. In: Cyber Security: Proceedings of CSI 2015 Springer, pp. 59–67 (2018).
Chakraborty, K. & Chowdhury, D.R. Cshr: Selection of cryptographically suitable hybrid cellular automata rule. In: Cellular Automata: 10th International Conference on Cellular Automata for Research and Industry, ACRI 2012 Springer, Santorini Island, Greece, September 24-27, 2012. Proceedings 10, pp. 591–600 (2012).
Gupta, K., Silakari, S., Gupta, R. & Khan, S.A. An ethical way of image encryption using ecc. In: 2009 First International Conference on Computational Intelligence, Communication Systems and Networks IEEE, pp. 342–345 (2009).
Toughi, S., Fathi, M. H. & Sekhavat, Y. A. An image encryption scheme based on elliptic curve pseudo random and advanced encryption system. Signal Process. 141, 217–227 (2017).
Fang, J., Zhao, K. & Liang, W. A novel color image encryption scheme using elliptic curve cryptography and hyperchaotic system. Physica Scripta 98(11), 115257 (2023).
Jasra, B. & Moon, A. H. Color image encryption and authentication using dynamic dna encoding and hyper chaotic system. Expert Syst. Appl. 206, 117861 (2022).
Kumar, S. & Sharma, D. A chaotic based image encryption scheme using elliptic curve cryptography and genetic algorithm. Artif. Intell. Rev. 57(4), 87 (2024).
Chowdhary, C. L. et al. Analytical study of hybrid techniques for image encryption and decryption. Sensors 20(18), 5162 (2020).
Zheng, J. & Lv, T. Image encryption algorithm based on cascaded chaotic map and improved zigzag transform. IET Image Process. 16(14), 3863–3875 (2022).
Li, H., Hu, Y., Shi, Z., Wang, B. & Zheng, P. An image encryption algorithm based on improved lifting-like structure and cross-plane zigzag transform. IEEE Access 10, 82305–82318 (2022).
Salim, S. K., Msallam, M. M. & Olewi, H. I. Hide text in an image using blowfish algorithm and development of least significant bit technique. Indones. J. Electr. Eng. Comput. Sci 29(1), 339–347 (2023).
Olewi, H.I., Msallam, M.M., Salim, S.K. & Al-Behadili, H.A. Enhanced security through integrated morse code encryption and lsb steganography in digital communications. Traitement du signal 41(1), 519-524 (2024)
Enayatifar, R., Abdullah, A. H. & Isnin, I. F. Chaos-based image encryption using a hybrid genetic algorithm and a dna sequence. Opt. Lasers Eng. 56, 83–93 (2014).
Pourjabbar Kari, A., Habibizad Navin, A., Bidgoli, A. M. & Mirnia, M. A new image encryption scheme based on hybrid chaotic maps. Multimed. Tools Appl. 80(2), 2753–2772 (2021).
Kumar, A. & Raghava, N. An efficient image encryption scheme using elementary cellular automata with novel permutation box. Multimed. Tools Appl. 80(14), 21727–21750 (2021).
Alawida, M. A novel image encryption algorithm based on cyclic chaotic map in industrial iot environments. IEEE Trans. Ind. Inform. 20(8), 10530–10541 (2024).
Tanksale, V. Efficient elliptic curve diffie-hellman key exchange for resource-constrained iot devices. Electronics 13(18), 3631 (2024).
Von Neumann, J. The general and logical theory of automata. In: Systems Research for Behavioral Science, pp. 97–107. Routledge, (2017)
Von Neumann, J. et al. Theory of self-reproducing automata (1966)
Koblitz, N., Menezes, A. & Vanstone, S. The state of elliptic curve cryptography. Des. Codes Cryptogr. 19, 173–193 (2000).
Sahoo, A., Mohanty, P. & Sethi, P.C. Image encryption using rsa algorithm. In: Intelligent Systems: Proceedings of ICMIB 2021, pp. 641–652. Springer, (2022)
Singh, S.R., Khan, A.K. & Singh, T.S. A critical review on elliptic curve cryptography. In: 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), pp. 13–18 IEEE, (2016).
Weber, A. The usc-sipi image database 2014. URL http://sipi.usc.edu/database (2018)
Somaraj, S. & Hussain, M. A. Performance and security analysis for image encryption using key image. Indian journal of science and technology 8(35), 1 (2015).
Kolivand, H., Hamood, S.F., Asadianfam, S. & Rahim, M.S. Image encryption techniques: A comprehensive review. Multimed. Tools Appl. 27, https://doi.org/10.1007/s11042-023-17896-0 (2024).
Himanshu, H., Hooda, R. & Poply, V. Image enhancement in fourier domain using mse and psnr. In: AIP Conf. Proc. 3081, 060001 (2024).
Setyaningsih, E. & Wardoyo, R. Review of image compression and encryption techniques. Int. J. Adv. Comput. Sci. Appl. 8(2) (2017)
Wu, Y. et al. Npcr and uaci randomness tests for image encryption. Cyber journals: multidisciplinary journals in science and technology. Journal of Selected Areas in Telecommunications (JSAT) 1(2), 31–38 (2011)
Abdullah, R. M. & Abrahim, A. R. Review of image encryption using different techniques. Academic Journal of Nawroz University 11(3), 170–177 (2022).
Lin, J. Divergence measures based on the shannon entropy. IEEE Trans. Inf. Theory 37(1), 145–151 (1991).
Sparavigna, A.C. Entropy in image analysis. MDPI (2019)
Bahrami, S. & Naderi, M. Image encryption using a lightweight stream encryption algorithm. Advances in Multimedia 2012(1), 767364 (2012).
Khan, J. S. & Ahmad, J. Chaos based efficient selective image encryption. Multidimens. Syst. Signal Process. 30, 943–961 (2019).
Es-Sabry, M., El Akkad, N., Merras, M., Saaidi, A. & Satori, K. A new image encryption algorithm using random numbers generation of two matrices and bit-shift operators. Soft Comput. 24(5), 3829–3848 (2020).
Zhu, S., Deng, X., Zhang, W. & Zhu, C. Image encryption scheme based on newly designed chaotic map and parallel dna coding. Mathematics 11(1), 231 (2023).
Allawi, S. T. & Alshibani, D. R. Color image encryption using lfsr, dna, and 3d chaotic maps. Int. J. Electr. Comput. Eng. Syst. 13(10), 885–893 (2022).
Muhammed, R.K. et al. Comparative analysis of aes, blowfish, twofish, salsa20, and chacha20 for image encryption. arXiv preprint arXiv:2407.16274 (2024)
Dey, S. Advancing the idea of probabilistic neutral bits: first key recovery attack on 7.5 round chacha. IEEE Trans. Inf. Theory 70 (8), 6091-6106 (2024)
Standard, D.E. National institute of standards and technology. Federal Information Processing Standard (FIPS) Publication 46(1) (2002)
Glinka, C. et al. The 30 m small-angle neutron scattering instruments at the national institute of standards and technology. J. Appl. Crystallogr. 31(3), 430–445 (1998).
Funding
Open access funding provided by Manipal University Jaipur.
Author information
Authors and Affiliations
Contributions
Biswarup Yogi contributed to the conceptualization, methodology design, software development, and execution of experiments. Ajoy Kumar Khan supervised the research process, provided critical insights into data analysis, and contributed to manuscript review and editing. Satyabrata Roy provided overall supervision, guided the project direction, contributed to result interpretation, and was responsible for the final revision and approval of the manuscript. All the authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Yogi, B., Khan, A.K. & Roy, S. Cellular automata based key distribution for lightweight hybrid image encryption with elliptic curve cryptography. Sci Rep 15, 34437 (2025). https://doi.org/10.1038/s41598-025-17536-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-17536-7