A novel extraction model optimization with effective separation coefficient for rare earth extraction process using improve differential evolution

Abstract

The mechanistic model of the rare earth extraction process neglects the efficacy of the agitator within the extraction extractor. This oversight results in a significant discrepancy between the theoretical solute concentration at each stage and the actual process data. To rectify this issue, we introduce an effective separation coefficient, thereby enabling the creation of a model capable of accurately determining the concentration of rare earth elements (REE) within each extraction extractor. This model also facilitates the construction of an optimized objective function for determining the effective separation coefficient. Taking into account the multi-modal and multi-variable characteristics of the optimized objective function, we put forth an enhanced version of the improved differential evolution algorithm, the Linear-Chaos and Two Mutation Strategies of Adaptive Differential Evolution (LCTADE)with Covariance Matrix and Cauchy Perturbation(CC-LCTADE). First, a chaotic sequence is embedded into the improved algorithm to generate the initial population, enhancing population diversity. Next, during the mutation and crossover processes, a new feature coordinate system is established, and covariance matrices and Cauchy disturbances are added to enhance the algorithm’s accuracy and its ability to avoid premature convergence. Additionally, recognizing the different performance requirements for mutation strategies at various stages of evolution, we introduce a dual-mutation strategy method based on DE/current-to-pbest/1 and DE/rand/1. Finally, a parameter-adaptive method is used to set the values of F, CR, and NP. In the simulation experiments, the proposed CC-LCTADE method and LCTADE method are first tested against the CEC2017 function and compared with other algorithms, demonstrating their superiority. CC-LCTADE is then used to solve the effective separation coefficient based objective function for rare earth extraction process. The experiments shows CC-LCTADE is effective and can be applied to the actual the rare earth extraction simulation system.

Introduction

The mechanism of rare earth extraction process is complex, and the component content distribution of each rare earth elements (REE) is the key point of control in extraction process, which has certain rules, and in the 1970s, Xu¹ summarized a substantial quantity of experimental data on rare earth extraction, laying the groundwork for a theory of two-component rare earth extraction. Subsequently, many scholars have do some research on the component content model of REE in the extraction process. For example, Wu² introduced iterative correction parameters, optimizing the separation process of multi-component systems through the stepwise recursive and iterative computation of component concentrations at each stage. Nevertheless, the application of these two methodologies in the industrial sphere has indicated that the derived technological parameters frequently prove to be impractical. Wang³ designed parameters based on the separation coefficients of different adjacent REE, taking into account the cutting positions. However, this approach yielded significant design errors. Zhong⁴ formulated the average fraction method to determine the effective separation coefficient, based on the average molar fraction of the aqueous phase in the extraction extractor. This method, however, exhibits decreased accuracy when the molar fraction of easily extracted components is smaller. Ding⁵ suggested the relative separation coefficient model, but failed to account for actual separation efficacy, resulting in discrepancies between the steady-state component concentration model output and the actual values. And also, the REE recovery process flow sheet is relatively complex⁶.

When devising new processes, factories typically utilize the aforementioned methods to estimate the number of extraction extractors necessary for a production process under ideal conditions. In practice, to achieve the production target, additional extraction extractors are incorporated into the stage (one stage equates to one extraction extractor) calculated during the actual construction process. However, without consideration of the on-site efficacy of the extraction extractor, the component concentrations computed by the mechanistic model^2,3,4 exhibit significant discrepancies with actual values. These can be several or even dozens of stages behind the actual site, diverging considerably from the actual production target. For instance, the theoretical component concentration (the process production index) in the 20th stage of the extraction extractors in the Ce/Pr production process is 0.85, which corresponds to the component concentration in the 26th stage of the actual production process.Therefore,a component concentration computation model that aligns with practical production must be proposed. Given that the parameters derived from the aforementioned methods are idealized, they cannot reliably guide the actual operation of production.To address this limitation, we propose the concept of an effective separation coefficient, which takes into account the impact of the extraction efficacy of extractors on the calculation of component concentrations in real-world production. This concept builds upon the relative separation coefficient model suggested by previous researchers. By incorporating this new approach, we can establish a more accurate computation model for component concentrations under actual working conditions and optimally calculate the effective separation coefficient, thereby improving the reliability of rare earth extraction production processes on site⁷ are characterized by multi-variability, non-linearity, and strong coupling, leading to a multi-peak, multi-variable objective optimization function for component concentration. Compared to Particle Swarm, Ant Colony, and Genetic algorithms, the Differential Evolution (DE) algorithm^8,9 stands out due to its simple structure, superior performance, straightforward parameters, and low time complexity, thus establishing it as a competitive evolutionary algorithm^10,11,12. Various improvements on the DE algorithm have been proposed to address engineering optimization problems^13,14. The DE algorithm optimizes the entire search space by treating random vectors in the population as individual optimizations¹⁵ and using the scaling, addition, and subtraction between vectors as mutation strategies. However, optimizing a high-dimension, multi-peak objective function with this method is often unstable, as the scaling factor of the parameter (F), crossover probability (CR), population number (NP), and the selection of mutation strategies may result in search stagnation and local optimal values only¹⁶.

JADE¹⁷ proposed a new mutation strategy–DE/ current-to-pBest /1–where individuals are randomly selected from the top 100$\times$p% with the optimal fitness value balance population diversity and convergence speed. Parameters F and CR are adaptively updated through normal distribution and Cauchy distribution, respectively. In SHADE¹⁸, the historical data of successful individuals adaptively update F and CR after the selection operation. Based on SHADE, L-SHADE^19,20,21 dynamically adjusts the NP and proposes a linear population reduction scheme to enhance population diversity in the early stages of evolution. O-L-SHADE²² introduces a new mutation strategy–DE/ current-to-pbest-2Order /1–which randomly selects two individuals in the population and sorts their fitness values to advance the L-SHADE algorithm. COBiDE²³ incorporates a covariance matrix and uses population distribution information to establish a characteristic coordinate system between population individuals and the parameters, within which crossover operation occurs. $\eta \_$CODE²⁴ introduces a new $\eta$_ Cauchy operator to improve the global and local search capability of COBiDE. DEwDVR²⁵ innovatively utilizes the information of differential vectors in each generation of successful individuals to reduce algorithm complexity. DSDE²⁶ designs a two-strategy mutation scheme to balance the exploration and utilization of the descendants. AGDE²⁷ introduces a new mutation rule to utilize the information in the DE population.

From the above discourse, it is evident that the selection of mutation strategies and the generation of F, CR, and NP parameters significantly impact optimization results. SNDE²⁸ proposes a new method to improvement the search accuracy, it built a grid of interconnect individuals with superior fitness instead of in rank order. BWDE²⁹ improved the performance by use a five-layer hierarchical structure and based on four types of individual information. And many algorithm are evident that the selection of mutation strategies and the generation of F, CR, and NP parameters significantly impact optimization results^30,31. Hence, choosing appropriate mutation strategies and parameters according to the objective function’s characteristics becomes crucial.

In summary, we propose optimizing the effective separation coefficient of the rare earth extraction process using an improved differential evolution algorithm. First, we analyze the traditional calculation model of the relative separation coefficient based on the mechanistic model. Accounting for the efficacy of the extraction extractor, we propose the effective separation coefficient of the extractor and establish the objective function of the effective separation coefficient using the least squares method. To obtain the effective separation coefficient that aligns with working conditions, we propose an improved differential evolution algorithm (CC-LCTADE). This approach embeds a chaotic sequence to generate the initial population, enhancing population diversity, and adds a covariance matrix framework to articulate the correlation between variables during variation crossover, optimizing the evolutionary process. We propose a double mutation strategy method based on DE/current-to-pbest/1 and DE/rand/1, considering the varying performance requirements of the mutation strategy at different evolution stages. Finally, we employ different parameter adaptive methods to set the F, CR, and NP values. And finally we successfully applies the CC-LCTADE to predict the component content of the REE on-site.

Methods

Classical differential evolution(DE) algorithm

Differential Evolution (DE) is an evolutionary algorithm that employs mutation, crossover, and selection operations to generate a new population. In DE, each individual in the population undergoes these operations, and their fitness, evaluated by the objective function, determines their quality. The best individual is tracked throughout the evolutionary process. The dimensionality of individuals is represented by ’D’. The algorithm starts with an initial population size of ’NP’. The symbol ${\vec {X}_{i,G}}$ represents the ith individual in the Gth generation, which is also one of the candidate solutions. It can be expressed as³²:

$$\begin{aligned} {\vec {X}_{i,G}} = \left( {{x_{1,i,G}},{x_{2,i,G}},{x_{3,i,G}}, \cdots {x_{D,i,G}}} \right) ,\quad i = 1,2, \cdots ,NP \end{aligned}$$

(1)

Initialization: For each individual, since it is related to a specific objective function, the initial population ($G=0$) in the algorithm is supposed to override specified range as much as possible. Then the jth dimensional component of the ith vector is randomly initialized , which is:

$$\begin{aligned} {x_{ji,0}} = {x_{j,\min }} + ran{d_{i,j}}[0,1] \cdot \left( {{x_{j,\max }} - {x_{j,\min }}} \right) \end{aligned}$$

(2)

In which, $ran{d_{i,j}}\left[ {0,1} \right]$ denotes a uniform random number in the range of 0 to 1, ${x_{j,\min }}$ and ${x_{j,\max }}$ are the minimum and maximum values of each dimension of the vector, respectively.

Mutation: After initialization, the individual ${\overrightarrow{X} _{i,G}}$, generates donor vector ${\overrightarrow{V} _{i,G}}$ through a mutation acting. The simplest form of mutation “DE/rand/1” is expressed as⁸:

$$\begin{aligned} {\vec {V}_{i,G}} = {\vec {X}_{q_1^i}} + F \cdot \left( {{{\vec {X}}_{q_2^i}} - {{\vec {X}}_{q_3^i}}} \right) \end{aligned}$$

(3)

where ${\overrightarrow{X} _{q_1^i}},{\overrightarrow{X} _{q_2^i}},{\overrightarrow{X} _{q_3^i}}$ are individuals randomly selected from the current population, and the index $q_1^i \ne q_2^i \ne q_3^i \ne i$ are mutually exclusive integers, which are randomly selected from 1 to NP.

Crossover: To obtain abundant potential diversity of the population, crossover is conducted to obtain trial vector ${\overrightarrow{U} _{i,G}}$ by selecting the components both from the donor vector ${\overrightarrow{V} _{i,G}}$ and target vector ${\overrightarrow{X} _{i,G}}$ after mutation. The crossover operation is:

$$\begin{aligned} {u_{j,i,G}} = {\left\{ \begin{array}{ll} v_{j,i,G} & \text { if}\ {\left( {{{{\mathop {rand}\nolimits } }_{i,j}}[0,1] \le CR \ { or} \ j = {j_{{rand }}}} \right) } \\ x_{j,i,G} & \text { otherwise} \end{array}\right. } \end{aligned}$$

(4)

where the symbol $v_{j,i,G}$ represent the ith operating variable within the jth mutant vector, whereas $u_{j,i,G}$ symbolizes the ith operating variable within the jth trial vector during the nth generation G. The term CR is employed to signify the probability of crossover. The binomial crossover is conducted on each of D variables, contingent on the generation of a random number, confined within the range of 0 to 1, that doesn’t exceed the value of CR.

Selection: The descendants of the individual is always better than or equal to the paternal individuals by General Greed. Determine whether the target vector ${\overrightarrow{X} _{i,G}}$ and the corresponding trial vector ${\overrightarrow{U} _{i,G}}$ after evolution can be stocked to the $G+1$ generation³³:

$$\begin{aligned} {\vec {X}_{i,G + 1}} = \left\{ {\begin{array}{*{20}{l}} {{{\vec {U}}_{i,G}}}& {{\textrm{if }}f\left( {{{\vec {U}}_{i,G}}} \right) \le f\left( {{{\vec {X}}_{i,G}}} \right) }\\ {{{\vec {X}}_{i,G}}}& {{\textrm{if }}f\left( {{{\vec {U}}_{i,G}}} \right) > f\left( {{{\vec {X}}_{i,G}}} \right) } \end{array}} \right. \end{aligned}$$

(5)

where $f( \cdot )$ is the objective function or fitness value.

When the iteration number is the maximum during the population evolution, then final population is obtained, meanwhile, the smallest fitness value of the individual in population is the solution of the objective function.

The Improved differential evolution algorithm

Differential Evolution (DE) is prone to several challenges, including search stagnation, sensitivity to parameter selection, and premature convergence, among others. These issues limit the algorithm’s adaptability across a wide range of optimization objectives. To address these challenges, we have proposed an enhanced DE algorithm,the block diagram of which is present in Fig. 1. This improvement incorporates advancements in the initialization phase, as well as the introduction of a covariance matrix and a Cauchy perturbation framework. These modifications enhance both the convergence speed and the precision of the algorithm, leading to more optimal optimization results.

Figure 1

Simple operational block diagram of CC-LCTADE.

Initialization of the chaotic sequence

The initial population, generated through the initialization process, exerts considerable influence on the evolutionary progression of population-based heuristic algorithms, thereby affecting the attainment of the optimal solution³². Traditional differential evolution algorithms randomly generate the initial population, which may lead to uneven spatial distribution of individual solutions within the population. Given its heightened sensitivity to initial values, chaos can traverse all states under specific rules in a random, bounded, and non-repetitive manner. Consequently, embedding a chaotic sequence to generate the initial population could enhance the diversity of the population. This procedural adjustment is anticipated to contribute to the algorithm’s overall efficiency.

With the initialized population of the cubic mapping in the chaos mode, the chaotic sequence distribution is more uniform than that of the commonly used Logistic mapping³⁴. It can be expressed as:

$$\begin{aligned} h(n + 1) = 4h{(n)^3} - 3h(n); - 1 \le h(n) \le 1;n = 0,1,2,... \end{aligned}$$

(6)

Mapping the chaotic space to the objective function solution space is as follows:

• 1) Randomly generate a D-dimensional chaotic variable $H = \left( {{h_1},{h_2}, \cdots ,{h_i}, }\right.$ $\left. {\ldots {h_d}} \right)$ in the range of $- 1 \le {h_i} \le 1,1 \le i \le d$;

• 2) Use Eq. (6) to iterate H in each dimension $NP-1$ times to obtain $NP-1$ chaotic variables;

• 3) Based on the equation ${x_{id}} = {x_{\min ,d}} + \left( {1 + {h_{id}}} \right) \cdot \frac{{{x_{\max ,d}} - {x_{\min ,d}}}}{2}$, in which ${x_{\min ,d}},{x_{\max ,d}}$ are the value range of the target vector, we map the generated NP chaotic variables to the objective function solution space to get NP initial populations.

Framework of the covariance matrix

The mutation and crossover operations in classical Differential Evolution (DE) algorithms are implemented within the original coordinate system. However, this fails to capture the correlation between distinct variables. To rectify this, we propose the usage of a covariance matrix to delineate the correlation among these variables. Subsequently, sample data is mapped onto a novel space via the application of eigenvectors and eigenvalues to eliminate any identical characteristics between variables. The original coordinate system, in certain search stages, falls short of generating feasible solutions that satisfy the requirements of one or multiple application environments³⁵. Information regarding population distributions reveals the solution space’s characteristics across different evolutionary stages. Therefore, this information can be employed to establish a characteristic coordinate system, thereby enhancing the efficacy of the algorithm.

The equation used in covariance calculation of the $i-th$ dimension and the $j-th$ dimension in the current $G-th$ generation population is:

$$\begin{aligned} {\mathop {\textrm{cov}}} \left( {i,j} \right) = \frac{{\sum \limits _{\kappa = 1}^{NP} {\left( {X_{i,\kappa }^G - \bar{X}_i^G} \right) \left( {X_{j,\kappa }^G - {\bar{X}}_j^G} \right) } }}{{NP - 1}} \end{aligned}$$

(7)

where ${\bar{X}}_i^G$ and ${\bar{X}}_j^G$ represent the mean values of all vectors in the $i-th$ dimension and $j-th$ dimension respectively. $X_{i,\kappa }^G$ and $X_{j,\kappa }^G$ represent the variable values of the $i-th$ dimension and the jth dimension of the individual $\kappa$, respectively. The covariance matrix C, is consist of the $i-th$ dimension and the $j-th$ dimension covariance which is calculated by the individuals in the population, is as follows:

$$\begin{aligned} C = \left\{ {{c_{i,j}}|{c_{i,j}} = {\mathop {\textrm{cov}}} \left( {i,j} \right) } \right\} \end{aligned}$$

(8)

We establish the characteristic coordinate with the distribution information of individuals in population, and obtain the canonical orthonormal bases composed of eigenvectors by decomposing the covariance matrix C. It can be described as:

$$\begin{aligned} C = B{D_c}^2{B^T} \end{aligned}$$

(9)

in which, B is orthogonal matrix composed of eigenvectors whose column vector is C, $D_c$ represents the diagonal matrix, and the diagonal elements of $D_c$ are the eigenvalues of C.

After establishing the characteristics coordinate system, we perform mutation and crossover under the framework of the covariance matrix, and then map the individuals from the most original coordinate to the characteristic coordinate, which is:

$$\begin{aligned} \vec {X}_{i,G}' = {B^T}{\vec {X}_{i,G}} \end{aligned}$$

(10)

in which, $\vec {X}_{i,G}'$ is the individual obtained in characteristic coordinate system, $\vec {X}_{i,G}$ is the individual in the original coordinate system.

We obtain the trial vector $\vec {U}_{i,G}'$ under characteristic coordinate system based on above operation. Then re-transform $\textbf{U}_{i,G}'$ to the original coordinate system in following way:

$$\begin{aligned} {\vec {U}_{i,G}} = B\vec {U}_{i,G}' \end{aligned}$$

(11)

Double mutation strategy

Mutation strategies differ in their suitability for addressing various optimization functions. Furthermore, the optimal mutation strategy might vary at different stages of a specific optimization problem’s evolution. Consequently, selecting a mutation strategy that effectively adapts to diverse optimization functions is critical. Research indicates that the ’DE/rand/1’ mutation strategy can facilitate random individual mutations, offering robust global search capabilities throughout the evolutionary process. This strategy can enhance population diversity during the early stages of evolution. However, it lacks guidance from the optimal individual and can consequently slow convergence^36,37. On the other hand, the ’DE/current-to-pbest/1’ mutation strategy enables mutations between paternal and optimal individuals with high convergence precision. However, this strategy is prone to becoming trapped in local optimization, which can limit its overall effectiveness³⁸.

Because the performance requirements of the mutation strategies are different at different evolution stages. And for the sake of the convergence speed and accuracy, we propose a double mutation strategy based on the two multi-scale mutation strategies, one of them is DE/current-to-pbest/1’, the other is ‘DE/rand/1’.

$$\begin{aligned} {\vec {V}_{i,G}} = \gamma \cdot {\vec {V}_{i1,G}} + (1 - \gamma ) \cdot {\vec {V}_{i2,G}} \end{aligned}$$

(12)

where ${\vec {V}_{i1,G}}$ and ${\vec {V}_{i2,G}}$ are respectively obtained by the two mutation strategies.

$$\begin{aligned} & {\vec {V}_{i1,G}} = {\vec {X}_{i,G}} + {F_i} \cdot \left( {\vec {X}_{best,G}^p - {{\vec {X}}_{i2,G}}} \right) + {F_i} \cdot \left( {{{\vec {X}}_{r_4^i,G}} - {{\vec {X}}_{r_5^i,G}}} \right) \end{aligned}$$

(13)

$$\begin{aligned} & {\vec {V}_{i2,G}} = {\vec {X}_{q_1^i,G}} + {F_i} \cdot \left( {{{\vec {X}}_{q_2^i,G}} - {{\vec {X}}_{q_3^i,G}}} \right) \end{aligned}$$

(14)

in which, ${F_i}$ is the scale factor corresponding to the ith individual. $\vec {X}_{best,G}^p$ is randomly selected from the first $NP \times p(p \in \left[ {0,1} \right] )$ individuals with better fitness values in the ${G-th}$ generation. ${\vec {X}_{q_1^i,G}},{\textbf{X}_{q_2^i,G}},{\vec {X}_{q_3^i,G}},{\vec {X}_{q_4^i,G}}$ are randomly selected from the Gth generation. When the fitness value of an evolved individual is better than the pre-evolved one, which is stored in the external archive A. ${\vec {X}_{q_5^i,G}}$ is randomly selected from the union set between the current population and A. ${q_1} \ne {q_2} \ne {q_3} \ne {q_4} \ne {q_5} \ne i$ are the mutually exclusive indices randomly selected from the range [1,NP].

$\gamma \in \left[ {0,1} \right]$is the variation scale control factor, which is becoming smaller in the optimization process. The search process of most evolutionary algorithms of the early stage is more important than that of the later stages. It is necessary to increase the proportion of the mutation vector which generated by the mutation strategy–DE/current-to-pbest/1 ,then make the search range closer to the optimum solution and speed up the convergence, so the value of $\gamma$ in the beginning is larger. And later in the evolutionary , due to poor population diversity, the algorithm is liable to trap in a local optimum solution, and should increase the proportion of the variation vector generated by the mutation strategy–DE/rand/1, and the value of $\gamma$ should be smaller in the later of evolution. According to evolutionary characteristics, the dynamic adjustment strategy of $\gamma$ can be defined as:

$$\begin{aligned} \gamma = \frac{{a}}{{\sqrt{1 + \mathop {^{\left( {\frac{{5 \cdot G}}{{Maxgem}}} \right) }}\nolimits ^{10} } }} + b \end{aligned}$$

(15)

in which, G represents the number of current evolution generation, Maxgem the maximum iteration generation, and in which, $a + b = 1$.

The frame of Cauchy perturbation

As the differential evolution algorithm is applied iteratively to address the objective function, there is a gradual decrease in population diversity, leading to a propensity towards local optimum traps, a phenomenon known as precocious convergence. Precocious convergence is characterized by a halt in population evolution and an almost null diversity. Additionally, the error between the function value at a given moment and the global optimum solution becomes significant. The function error and overall diversity of the nth generation population can be expressed with the following mathematical formulations:

$$\begin{aligned} & erro{r_G} = f\left( {{{\vec {X}}_{best,G}}} \right) - f({\vec {X}^*}) \end{aligned}$$

(16)

$$\begin{aligned} & di{v_G} = \frac{1}{{NP}}\sum \limits _{i = 1}^{NP} {\left\| {{{\vec {X}}_{i,G}} - \frac{1}{{NP}}\sum \limits _{i = 1}^{NP} {{{\vec {X}}_{i,G}}} } \right\| } \end{aligned}$$

(17)

where ${\vec {X}^*}$ represents the solution vector when the optimization function obtains the theoretical optimum fitness value.

When $erro{r_G} > 0$ and $di{v_G} = 0$, the population can be judged in a precocious convergence state. When solving the optimization function for the practical problems, $erro{r_G} > 0$ cannot be used to determine whether the population is precocious since ${\vec {X}^*}$ is unknown. Obviously, a simple and effective method is needed to judge precocious convergence of population.

Following the mutation and crossover of the generation population, a comparative analysis of the resultant offspring population and the parental one is performed to scrutinize the evolutionary process. If the fitness values of the majority of individuals in the offspring population surpass those of the parent population, it indicates that the evolutionary process is still underway.

Conversely, if the fitness values of most individuals in the offspring population are equal to or less than those in the parental population, it suggests that the evolutionary process has reached a standstill. Therefore, the parameters $erro{r_G} > 0$ and $di{v_G} = 0$ can serve as critical indicators to ascertain whether the current population is experiencing precocious convergence.

Define S as the total number of the offspring individuals which are not as good as the parental ones in population at present. The correlation between the $G-th$ parent population and the $i-th$ offspring individuals can be described as:

$$\begin{aligned} & {S_i} = {\left\{ \begin{array}{ll} 1 & f\left( {{{\vec {U}}_{i,G}}} \right) \ge f\left( {{{\vec {X}}_{i,G}}} \right) \\ 0 & { otherwise } \end{array}\right. } \end{aligned}$$

(18)

$$\begin{aligned} & S = sum({S_i}),i = 1,2,\ldots ,NP \end{aligned}$$

(19)

Define T as the total generation value of offspring individuals of successive generations that are inferior to or equal to the parental individuals, is larger than P:

$$\begin{aligned} T = {\left\{ \begin{array}{ll} T + 1 & { S \ge P }\\ 0 & { otherwise } \end{array}\right. } \end{aligned}$$

(20)

where $P = 0.5*NP$. Supposing $S \ge P$, it indicates that the population at present deviates from the global optimal value in evolution, and T increases. Otherwise, the value of T is 0.

Consider Q as the threshold for determining whether the evolution process has ceased. If the condition $T > Q$ is met, it can be concluded that the current population’s evolution is stagnant. Experimental validation suggests that the optimal value for Q is $1.5*D$.

Taking $T > Q$ and $di{v_G} = 0$ as the preconditions for judging whether the population of the moment is in precocious convergence. The state of the current population can be judged by:

$$\begin{aligned} SL = {\left\{ \begin{array}{ll} 1 & { di{v_G}> \varepsilon \ and\ T > Q }\\ 0 & { otherwise } \end{array}\right. } \end{aligned}$$

(21)

If $SL=1$, the population is in a precocious convergence state, and $\varepsilon$ is a very small value which is larger than 0.

If the population finds itself in a state of precocious convergence, the concept of disturbance can be employed to disentangle the population from the confines of the local optimum range. In this study, we utilize Cauchy perturbation to extricate the population from the grasp of precocious convergence.

The pNP individuals boasting superior fitness values are selected and subjected to this perturbation. This process ensures the preservation of the most advantageous direction for the entire population, thus mitigating the risk of entrapment within a local optimum.

Cauchy perturbation is executed on the pNP individuals through the following mathematical operation:

$$\begin{aligned} cNP = pNP + \varsigma *\tan \left( {\pi *rand\left( {pNP,D} \right) - 0.5} \right) \end{aligned}$$

(22)

where cNP is the pNP population after perturbation; $\varsigma$ is the perturbation parameter, generally set to ${10^{ - 6}}$.

Instead of pNP, cNP is a new population. The cNP and the offspring generated before the disturbance preform select operation to obtain a new generation population. Then the new population evolution process is continuously executed until the optimum fitness value of the optimization function, then its corresponding optimum solution are obtained.

The parameter adaptive strategy

In contemporary research, numerous effective self-adaptive parameter methods have been proposed. However, for optimization problems, differing parameter adaptation methods can yield varying results. This paper investigates the setting of F, CR and NP using distinct parameter adaptation strategies.

Crossover Probability (CR) dictates the likelihood that the trial vector inherits from the target vector. We utilize the historical information of successful individuals from each iteration to adaptively generate the current CR. The CR for each individual within the population is generated via a normal distribution with a standard deviation of 0.1 and an average of $\mu CR$. This process is as follows:

$$\begin{aligned} C{R_i} = {\mathop {\textrm{randi}}\nolimits } (\mu CR,0.1) \end{aligned}$$

(23)

The starting value of $\mu CR$ is set to 0.5. And after each iteration, the updated $\mu CR$ can be described as:

$$\begin{aligned} \mu CR = \left( {1 - {c_{CR}}} \right) \times \mu CR + {c_{CR}} \times {{\mathop {\textrm{mean}}\nolimits } _{WL}}\left( {{S_{CR}}} \right) \end{aligned}$$

(24)

where $S_{CR}$ denotes the CR value of each successful individual. The range of $\mu CR$ is [0,1], $mae{n_{WL}}({S_{CR}})$ represents the weighted average of all CR in $S_{CR}$, and $c_{CR}$ is a constant value, which is set to 0.5.

$$\begin{aligned} & mea{n_{WL}}({S_{CR}}) = \frac{{\sum \nolimits _{k = 1}^{\left| {{S_{CR}}} \right| } {{\omega _k} \cdot S_{k,CR}^2} }}{{\sum \nolimits _{k = 1}^{\left| {{S_{CR}}} \right| } {{\omega _k} \cdot {S_{k,CR}}} }} \end{aligned}$$

(25)

$$\begin{aligned} & {\omega _k} = \frac{{\Delta {f_k}}}{{\sum \nolimits _{k = 1}^{\left| {{S_{CR}}} \right| } {\Delta {f_k}} }} \end{aligned}$$

(26)

$$\begin{aligned} & \Delta {f_k} = \left| {f\left( {{{\vec {U}}_{i,G}}} \right) - f\left( {{{\vec {X}}_{i,G}}} \right) } \right| \end{aligned}$$

(27)

in which, $\omega _k$ is the weight coefficient, and $\Delta {f_k}$ is the absolute value of the error between the fitness values of individuals after evolution and those before evolution.

The mutation vector is depend on the scale factor F. For better adapt to the effect of evolutionary process, update F according to the fitness value of each generation during evolution:

$$\begin{aligned} F_i = {\left\{ \begin{array}{ll} rand{c_i}\left( {0.5,0.1} \right) & { if(f({X_{best}}) = f({X_{worst}})) }\\ \frac{{f({X_{worst}}) - f({X_i})}}{{f({X_{worst}}) - f({X_{best}})}} & { otherwise } \end{array}\right. } \end{aligned}$$

(28)

where ${X_{worst}},{X_{best}}$ are the individuals with the worst and best fitness values in the Gth generation population.

In the initial stage of evolution, when the population size is larger, we employ a linear decrease of the population number (NP) to enhance the diversity of the population. Conversely, in the later evolutionary stages when the population size is smaller, this approach can be used to augment the convergence rate. The number of individuals evolving into the next generation can be represented as follows:

$$\begin{aligned} N{P_{G + 1}} = round\left[ {\left( {\frac{{N{P_{\max }} - N{P_{\min }}}}{{MAX\_NFE}}} \right) \cdot NFE + N{P_{\min }}} \right] \end{aligned}$$

(29)

where $N{P_{\max }}$ is the maximum population, which is generally set to $18 * D$ generally, $N{P_{\min }}$ is the minimum population, which is set to 4. NFE represents the assessment times of fitness value, and $MAX\_NFE$ represents the maximal assessment times of fitness value, which is generally set to $1000*D$.

The pseudo-code of algorithm CC-LCTADE is in Algorithm 1.

Algorithm 1

The pseudo-code of algorithm CC-LCTADE

Analysis of the algorithm complexity

The computational complexity of an algorithm primarily hinges on the number of times the fitness value needs to be evaluated. When comparing the Cross-Correlation Local Coordinate Transformation and Adaptive Differential Evolution (CC-LCTADE) algorithm with classical Differential Evolution (DE) and Just Another Differential Evolution (JADE), the complexities of the algorithms are found to be quite different.

The complexity of DE is ${\textrm{O}}\left( {NP \times D \times {G_{\max }}} \right)$, in which ${G_{\max }}$ is the maximum value of running generations, and the complexity of JADE is $O\left( {NP \times \left[ {D + \log (NP)} \right] \times {G_{\max }}} \right)$. Comparing with JADE, the framework of the algorithm and the evaluation times of maximal fitness $Max\_nfe$ are almost the same, although CC-LCTADE makes some changes in variation and parameter adaptation. Besides, the covariance matrix framework incorporated into CC-LCTADE is primarily used for coordinate system transformation, thereby not adding significant computational complexity. Moreover, the Cauchy perturbation framework only functions when certain conditions are met, specifically when the population experiences precocious convergence. As such, additional calculations are only required during chaos initialization, resulting in a complexity of for LCTADE which is $O\left( {NP \times \left[ {2D + \log (NP)} \right] \times {G_{\max }}} \right)$.

Results and discussion

To validate the feasibility of the proposed method outlined in the paper, the CC-LCTADE algorithm is employed to solve benchmark functions sourced from the CEC2017 function library. The performance of CC-LCTADE is then compared to that of other enhanced DE algorithms.The CC-LCTADE algorithm is then utilized to optimize the rare earth extraction objective function, enabling the determination of the effective separation coefficient for each extractor. Subsequently, the obtained effective separation coefficients are used to calculate the component content of each extractor, allowing for the realistic simulation of the REEP process.

Ablation experiments

First, we evaluated the performance of the differential evolution algorithm and the improved algorithm using non-parametric tests, specifically the Wilcoxon rank test and the Friedman test, across various dimensions. Subsequent analysis focused on the distinctions and advantages of the proposed algorithm compared to traditional differential evolution algorithms, as detailed in Table 1. The symbols “+/=/-” in the table indicate whether the performance of the improved algorithm is better than, equal to, or worse than the original algorithm. The ’p’ values, derived from the Wilcoxon rank test, signify the statistical significance of the differences in performance at significance levels of $\delta$ = 0.05 and $\delta$ = 0.1, respectively.

Table 1 Comparison of CC-LCTADE with LCTADE and DE at different dimension.

In Table 1, the enhanced version of the differential evolution algorithm, which includes improvements in initialization, mutation strategy, and parameter selection, demonstrates superior convergence speed and precision compared to the classical differential evolution algorithm. These enhancements are particularly effective in multi-dimensional scenarios, leading to notable optimization effects. In Fig. 2, we can see the convergence curve of DE, CC-DE and LCTADE, CC-LCTADE on function 11, 15, 26, 29. The convergence rate and accuracy of DE and LCTADE with covariance matrix and cauchy perturbation is better than the DE and LCTADE, and the CC-LCTADE is the best.

Figure 2

Error convergence curves of DE and CC-DE, LCTADE, CC-LCTADE on different functions.

Methods comparison

In our study of the CEC2017 benchmark, we considered all dimensions. However, we eliminated function 2 due to its instability³⁹. We applied the Cross-Correlation Local Coordinate Transformation and Adaptive Differential Evolution (CC-LCTADE) algorithm to the remaining 29 optimized benchmark functions from the CEC2017 function library. These functions encompass a range of types, including unimodal, simple multimodal, hybrid, and composition functions, serving as a comprehensive tested to evaluate the performance and feasibility of CC-LCTADE.

The performance of CC-LCTADE was compared to that of various established algorithms: PSO⁴⁰, JADE¹⁷, APSM-jSO, COBiDE²³, SNDE²⁸, DEwDVR²⁵, and LCTADE (which is the version of CC-LCTADE without the covariance matrix framework and Cauchy perturbation framework). Our comprehensive evaluation aimed to demonstrate the relative efficacy of these methods.

We set the parameter values of the six comparison medthods in accordince with the references, also the experimental environment is all the same. And the number of population size in CC-LCTADE was 100. We set the parameters of CC-LCTADE: $N{P_{\max }}$=18*D, $N{P_{\min }}$=4, $\mu CR = 0.5$, $Max\_nfe = D*1000$, $Maxgem = 3000$, the value repeated cross validation by experiments is $a = 0.87,b = 0.13$.

The CC-LCTADE and LCTADE are compared with PSO and five other algorithms (JADE, APSM-jSO, COBiDE, SNDE, DEwDVR) across 29 test functions using experimental analysis in all dimensions (D=10, 30, 50 and 100). The number of superior results is provided in Table 2.

Table 2 Performance comparison of different algorithms across various dimensions.

In the experimental framework, the performance of the methodology is evaluated by comparing the error between the mean value and standard deviation of the function $f\left( x \right) - f\left( {{{{\hat{x}}}^ * }} \right)$. Here, x represents the optimal solution achieved by the algorithm in one run, and is the established optimal solution of the benchmark function. Both error value and standard deviation less than 1E-8 are considered as zero. The solution dimension, denoted as D, is set to 30 for all 29 test functions. Each algorithm and each test function independently run 51 times, all culminating at the termination criterion of 300,000 function evaluations (FES). To evaluate the quality of the optimal solutions from a statistical perspective, two hypothesis testing methods are employed: the Wilcoxon signed rank test and the Friedman test.

The proposed algorithm, alongside PSO, JADE, APSM-jSO, COBiDE, SNDE, DEwDVR, and LCTADE, are examined within the function space of CEC2017. The comparative data collected is presented in Table 3. In the table, MeanS denotes the mean error value, STD represents the standard deviation, and Nob corresponds to the number of best results obtained by a particular algorithm.

According to Wilcoxon’test and the Friedman test, the difference between the improved DE and PSO are singniaficant for benchamarks CEC2017. In low dimension, the PSO algorithm gets 2 better results , but the rank of Friedman test is the largest. With the increase of dimensions, it can be seen that the processing power of PSO algorithm is greatly reduced, far less than that of the improved differential evolution algorithm. Perhaps due to the influence of population and control parameter settings, PSO algorithm can not adapt to higher dimensional problems.

Moreover, PSO, these five improved algorithms and LCTADE are subjected to Wilcoxon rank and Friedman tests alongside CC-LCTADE. The results of the Wilcoxon rank test (as displayed in Tables 2) reveal that under the significance levels of $\delta$=0.05 and $\delta$=0.1, the values derived from the comparison of CC-LCTADE with the other algorithms are consistently below the significance level. This confirms a statistically significant difference between the CC-LCTADE algorithm and the other improved algorithms. Furthermore, the Friedman test, a non-parametric method used for comparing the performance of all algorithms, ranks CC-LCTADE first, indicating its superior performance.

Table 3 Result of the algorithms in the functions in CEC2017 as D = 30.

Table 3 reveals that the proposed CC-LCTADE algorithm yields the best results for 24 test functions. Specifically, for unimodal ${f_1}{\mathrm{- }}{f_3}$ and simple multimodal functions ${f_4}{\mathrm{- }}{f_{10}}$, JADE achieves the best results for 2 functions, APSM-jSO for 5, SNDE for 3, DEwDVR for 2, LCTADE for 6, and CC-LCTADE for 7. Regarding the more complex mixed functions ${f_{11}}{\mathrm{- }}{f_{30}}$, JADE does not produce the best results for any function, APSM-jSO excels at 3, COBiDE at 5, SNDE at 3, DEwDVR at 3, LCTADE at 11, and CC-LCTADE at 16. Thus, it is apparent that CC-LCTADE offers superior optimization for unimodal, multimodal, and mixed functions.

The comparative evaluation provides further evidence of the effectiveness of the double mutation strategies proposed by CC-LCTADE, and these algorithms include JADE and SHADE (utilize the DE/current-to-pbest/1 mutation strategy), COBiDE (incorporates the covariance matrix into DE/rand/1), and O-L-SHADE (introduce the novel mutation strategy DE/current-to-pbest-2 Order/1). Based on DE/ current-to-pbbest /1 and DE/ /1, these strategies effectively circumvent local optima by controlling the variation scale factor, thereby enhancing convergence speed and accuracy. Compared to LCTADE, the CC-LCTADE algorithm boosts the capacity to address premature convergence through the incorporation of the covariance matrix and the Cauchy perturbation frame.

Lastly, to vividly demonstrate the superior performance of CC-LCTADE, five test functions were selected from the CEC2017 benchmark set with the dimensional complexity set to 30D. Convergence curves were plotted to represent the correlation between the fitness value errors of the six algorithms (including CC-LCTADE) on functions 5, 8, 13, 21, 26, and 30, and the number of evolutionary generations.

The analysis of convergence curves for various algorithms, as shown in Fig. 3, demonstrates that the advantage of DE-based variants is superior to PSO ones, and JADE produces the least effective optimization results across different test functions. O-L-SHADE, on the other hand, initiates the evolutionary process with a rapid convergence rate. COBiDE, however, tends to yield local optimal values more frequently due to significant fluctuations that affect the optimization process during the evolution of the multi-peak test function. In contrast, CC-LCTADE exhib superior convergence accuracy across a range of functions compared to other algorithms. It also shows a high convergence rate, second only to O-L-SHADE, at the beitsginning of the evolutionary process. However, it should be noted that CC-LCTADE’s convergence rate is relatively slow in the early stages. Despite this, it achieves the minimum fitness value error faster than other algorithms in the later stages of evolution. This unique characteristic can be attributed to the use of “DE/RAND/1” as an exploratory tool, which allows the algorithm to explore a larger portion of the solution space and thus avoid premature convergence to local optimal values. In the later stages, the “DE/current-to-pbest/1” strategy accelerates the convergence rate. Furthermore, CC-LCTADE demonstrates improved convergence performance and superior optimal performance in high-dimensional optimization problems, facilitated by the integration of a covariance matrix and a Cauchy perturbation framework.

Figure 3

Error iteration comparison diagram of each improved algorithm on different functions.

Solve the effective separation coefficient of the REEP

Rare earth extraction process

The rare earth extraction process (REEP) is typically a sequential cascade extraction operation, comprising a series of mixed extractors. These extractors facilitate the contact between REE and the organic and aqueous phases, enabling extraction and separation of distinct elements. As illustrated in Fig. 4, the REEP consists of ’m-stage’ scrubbing and ’n-stage’ extraction²⁸. In this system, under the action of agitators within the extraction extractor, the extraction agent is introduced at the first extractor and injectsed from left to right. Simultaneously, the detergent is added at the ’n+m-th’ extractor, injected from right to left. The feed liquid is introduced to the organic phase at the ’n-th’ extractor, moving from right to left. Through continuous interaction with the extractant, distinct REEs are selectively extracted into different solvents, achieving separation. Ultimately, at the first stage, the less readily extracted component B, with a component content of ${Y_B}$, is obtained, while at the ’(n+m)-th’ stage, the easy-to-extracteasily extracted component A, with a component content of ${Y_A}$, is secured. The relative separation coefficient $\beta _{1/l}$ is that the component content of the l-th $\left( {l = 1,2, \cdots ,N} \right)$ rare earth element (REE) divided by the component content of the first (difficult-to-extract )rare earth element, which is:

$$\begin{aligned} \beta _{1/l} = \frac{{{Y_l} \times {X_1}}}{{Y_1} \times {X_l}} \end{aligned}$$

(30)

Figure 4

Rare earth cascade extraction production process.

Similarly, the expression of the relative separation coefficient $\beta _{l/N}$ of the l-th $\left( {l = 1,2, \cdots ,N} \right)$ component relative to the last (easy-to-extract) component is:

$$\begin{aligned} \beta _{l/N} = \frac{{{Y_N} \times {X_l}}}{{{Y_l} \times {X_N}}} \end{aligned}$$

(31)

where $X_l$ and $Y_l$ are the component content of the l-th $\left( {l = 1,2, \cdots ,N} \right)$ REE of the two phase(aqueous and organic) when extraction process is stable.

When the rare earth extraction system reaches stable state, the calculation formula of the relative separation coefficient is shown in Table 4. In Table 4, L is the number of elements that are used to distinguish the difficult-to-extract and easy-to-extract components, and C is the current element number.

Table 4 The relative separation coefficient in each stage.

Extraction process objective function based on effective separation coefficient

In⁵, the relative separation coefficients calculated by formulas (30) and (31) can be applied to derive the component content of each REE of each extractor.

In each extractor with two-phase component composition, the content of REE in the organic phase at extraction extractors is calculated by:

$$\begin{aligned} {\textrm{Y}}_{cl} = \left( {{X_{cl}} \times \prod \limits _{k = 1}^l {{\beta _{k/1}}} } \right) /\sum \limits _{\alpha = 1}^N {\left( {{X_{{\textrm{c}}\alpha }} \times \prod \limits _{k = 1}^l {{\beta _{k/1}}} } \right) } \end{aligned}$$

(32)

where ${Y_{cl}}$ is the l-th component content in the organic phase, ${X_{cl}}$ is the l-th component content in the aqueous phase, ${X_{c\alpha }}$ is the $\alpha -th\left( {\alpha = 1,2, \cdots ,N} \right)$ component content in the aqueous phase, ${\beta _{k/1}}$ and ${\beta _{k/N}}$ is the relative separation coefficient in the extraction section and scrubbing section. Similarly, the component content of the aqueous phase in the scrubbing section is calculated by:

$$\begin{aligned} {{\textrm{X}}_{wl}} = \left( {{Y_{wl}} \times \prod \limits _{k = 1}^l {{\beta _{k/{\textrm{N}}}}} } \right) /\sum \limits _{\alpha = 1}^N {\left( {{Y_{w\alpha }} \times \prod \limits _{k = 1}^l {{\beta _{k/{\textrm{N}}}}} } \right) } \end{aligned}$$

(33)

where ${X_{wl}}$ is the l-th component content in the aqueous phase, ${Y_{wl}}$ is the l-th component content in the organic phase, ${Y_{w\alpha }}$ is the $\alpha -th\left( {\alpha = 1,2, \cdots ,N} \right)$ component content in the organic phase.

Building upon Eqs. (32) and (33), the component content of each element between different phases in each extractor can be theoretically calculated with the use of the separation coefficient. It must be noted that the actual extraction industry incurs specific energy consumption, especially from agitators within the extractor. Consequently, the effectiveness of extraction across extractors varies, implying that the component content in each extractor might not align with the actual component content. This clear discrepancy indicates that the relative separation coefficient computed using Eqs. (30) and (31) lacks accuracy. This inaccuracy results in the component content of each element as calculated by Eqs. (32) and (33), not being consistent with actual working conditions.

In the actual production process, ${\beta _{k/1}}$ is known. Considering the effective of the agitator, so $\eta$ is supposed to be the effective coefficient of the agitator.And then the formula (32) and (33) can be rewritten to :

$$\begin{aligned} & {{\textrm{Y}}_{cl}} = \left( {{X_{cl}} \times \prod \limits _{k = 1}^l {(\eta . \times {\beta _{k/1}})} } \right) /\sum \limits _{\alpha = 1}^N {\left( {{X_{c\alpha }} \times \prod \limits _{k = 1}^l {(\eta . \times {\beta _{k/1}})} } \right) } \end{aligned}$$

(34)

$$\begin{aligned} & {X_{wl}} = \left( {{Y_{wl}} \times \prod \limits _{k = 1}^l {(\eta . \times {\beta _{k/N}})} } \right) /\sum \limits _{\alpha = 1}^N {\left( {{Y_{w\alpha }} \times \prod \limits _{k = 1}^l {(\eta . \times {\beta _{k/N}})} } \right) } \end{aligned}$$

(35)

where $\eta (0< \eta < 1)$ is the effective coefficient, when $\eta = 1$, the effective is 100%, which is an ideal state, when $\eta = 0$, the effective is 0, indicating that the agitator is not working. To derive the effective separation coefficient, the least squares method is employed, seeking to minimize the sum of squared differences between the component content as calculated by Eqs. (34) and (35) and the actual component content observed in each extractor.

${\beta '}_{k/i}=\eta \cdot {\beta _{k/i}}$ is defined as the effective separation coefficient of the extraction extractor, and the optimized objective function of the organic phase and that of the aqueous phase is respectively:

$$\begin{aligned} & \min {\textrm{J}} = \sum \limits _{l = 1}^N {{{\left( {Y_{cl}^* - \left( {{X_{cl}} \times \prod \limits _{k = 1}^l {\beta _{k/1}^\prime } } \right) /\sum \limits _{\alpha = 1}^N {\left( {{X_{c\alpha }} \times \prod \limits _{k = 1}^l {\beta _{k/1}^\prime } } \right) } } \right) }^2}} \end{aligned}$$

(36)

$$\begin{aligned} & \min W = \sum \limits _{l = 1}^N {{{\left( {X_{wl}^* - \left( {{Y_{wl}} \times \prod \limits _{k = 1}^l {\beta _{k/1}^\prime } } \right) /\sum \limits _{\alpha = 1}^N {\left( {{Y_{w\alpha }} \times \prod \limits _{k = 1}^l {\beta _{k/1}^\prime } } \right) } } \right) }^2}} \end{aligned}$$

(37)

where $Y_{cl}^ *$ and $X_{wl}^ *$ respectively represent the actual value of the component content of the l-th rare earth element. Obviously, we adopt optimization algorithms to calculate the effective separation coefficient ${\beta '}$ of formulas (36) and (37).

On the basis of the actual data from the REEP in site, we adopt the least square method to establish optimization function (36) and (37) based on effective separation coefficient. The improved DE algorithm CC-LCTADE is used to solve the optimization effective separation coefficient in each extractor to solve minJ and minW with the fitness function. We solve the effective separation coefficient ${\beta '}_{k/1}$ of problem (36), in which the element group N is 3. When $K=1$, $\beta _{1/1}' = 1$ is known, then when $k = 2,3$, the solution of the objective function should be $\beta _{2/1}'$ and $\beta _{3/1}'$.

Set the dimension of the feasible solution of problem (36) is 2, the effective separation coefficient $\beta _{2/1}'$ of Ce/Pr and $\beta _{3/1}'$ of Pr/Nd are the first and second dimensions of the optimization solution, which are the individuals with the smallest fitness value in population after evolution process with CC-LCTADE. Solve problem (37) with the same way. CC-LCTADE algorithm was used to optimize and solve the effective separation coefficients of each extractor for 20 times, and get the average vale of the 20 times, which are exhibited in Fig. 5.

Figure 5

Effective separation coefficients of each extractor in the extraction and scrubbing sections.

As illustrated in Fig. 6, the separation effect of the extractor around the 26-th stage in the feed stage is superior to that of the outlets at both ends. This aligns with the highest effective separation coefficient at the 26th stage. Moreover, the effective separation coefficient of Ce/Pr exhibits minor fluctuations in the scrubbing section and is proximate to 1, signifying an excessive scrubbing state. This analysis affirms the rationality of the effective separation coefficient introduced in this paper, which is congruent with actual industrial conditions. Using the aforementioned effective separation coefficients for each extractor, formulas (36) and (37) are employed to compute the component content of the REEs Ce, Pr, and Nd in each extractor. These are then compared with actual data. As indicated in Fig. 6, the component content for each rare earth element, as calculated by the proposed model, aligns closely with actual values. This demonstrates that the process simulation of the REEP, established by introducing the proposed effective separation coefficient, adheres to actual working conditions. Three evaluation indicators - maximum relative error (MAXRE), average relative error (MEANRE), and root mean square error (RMSE) - are employed to precisely assess the reliability of the model presented in this paper.

Figure 6

Comparison between model and actual component content.

The component content of Ce, Pr, and Nd are computed separately, with the results displayed in Table 5 and Fig. 7. The discrepancy between the component content calculated by the proposed method and the actual field data is remarkably small, with the absolute value of the maximum relative error consistently within 5%. The relative error remains relatively stable during the intermediate process but exhibits significant fluctuations near the exports at both ends. The component content of the rare earth element, which constitutes a minor fraction in extraction, demonstrates significant fluctuations. Thus, even minor changes in the production process may induce substantial variations in its relative error.

Compared with other enhanced DE algorithms, its performance indicators are superior, corroborating the effectiveness of the proposed methods.

Figure 7

The relative error absolute value between model component content and actual value.

Table 5 Performance indicators with different optimization algorithms.

Industrial application

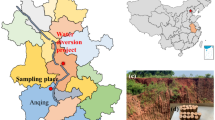
We conducted an industrial experiment of rare earth extraction at a manufacturing company in Ganzhou, Jiangxi Province, as shown in Fig. 8. To depict the REEP, we introduced the effective separation coefficients as discussed in this paper and utilized the optimal algorithms to predict the REE component content at each extractor. Its feasibility was validated on the REEP simulation platform. By comparing with actual conditions, the best optimization method was selected to predict the REE component content and process parameters in the onsite control process.

Figure 8

The field of REEP and supervisory control system.

The composition of the feed liquid and primary process parameters were derived from the onsite CePr/Nd extraction process, as depicted in Table 6. A simulation system for the REEP was established, which enables the optimization of REEP process parameters and facilitates the visualization of the REE component content distribution. The system was evaluated in the REEP and is employed in conjunction with the field control system to guide actual extraction production.

Table 6 Main process indexes of CePr/Nd extraction process.

Figure 9 depicts the boundary conditions for the CePr/Nd extraction within the developed simulation system,covering aspects such as the elemental composition in the liquid phase, separation coefficients between elements, the chosen feeding method, conditions of the extraction agent, and the use of detergent, among other factors. Subsequently, the proposed CC-LCTADE method was employed to derive the predicted component content of the REE in both phases at each extractor, thus clarifying the distribution of the component content. Moreover, optimal process parameters, such as the ideal extraction amount in the aqueous and organic phases, were determined.

Figure 9

Simulation platform of the rare earth extraction process.

Utilizing the simulation system of the REEP, the proposed algorithms were applied to predict the component content of the REE at each extractor. We compared the performance indicators obtained with different algorithms and further analyzed the influence on the component content distribution under various working conditions. Applying alternative optimization methods within our developed simulation system can accelerate the development cycle for rare earth element processing (REEP), lower production costs, and increase efficiency. As a result, this study holds considerable practical importance, offering essential guidance for actual process production.

Conclusion

The conventional calculation approach based on the mechanistic model overlooks the impact of the extraction extractor, leading to a substantial discrepancy between the component content derived for at each extractor and the actual plant data. Such discrepancies are inadequate for accurately simulating the real extraction process. In response, this paper introduces the concept of the effective separation coefficient and employs the CC-LCTADE algorithm alongside the least square method to construct the objective function and solve for the effective separation coefficients in each extractor. The calculation model developed to determine the optimal component content has been specifically designed to reflect real-world operating conditions. This model has been successfully implemented in a simulation system for the REEP, enabling the prediction of the distribution of REE at each extraction point. The effectiveness of the proposed method has been rigorously validated by comparing the predicted results with actual process data. The findings provide a valuable reference for the development of new technologies, the restructuring of existing REEPs, and the re-optimization of technological parameters, underscoring the practical significance of this research.