Multi skill project scheduling optimization based on quality transmission and rework network reconstruction

Abstract

Quality deficiencies are widely acknowledged as a primary driver of project rework, with personnel skill levels serving as a critical determinant of activity quality. This study presents a scheduling model that integrates quality transmission mechanisms and dynamic rework subnet reconstruction within the Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP) framework. The proposed model aims to optimize project duration while mitigating rework risks. To address the computational complexity of the model, an Improved Gazelle Optimization Algorithm (GOAIP) was developed, incorporating dynamic operators, shuffle crossover, and Gaussian mutation strategies to balance global and local optimization. Experimental validation across diverse case scales demonstrates that the proposed model and algorithm outperform mainstream optimization techniques in solution accuracy and convergence efficiency, highlighting their robust applicability and practical significance.

Introduction

Amid rapid technological advancements, heightened competition among enterprises has made project success rates a crucial indicator of organizational competitiveness. Ensuring the timely delivery of projects within budget while meeting both quality and functional requirements is a fundamental determinant of project success¹. However, project management often faces significant challenges, especially due to rework resulting from quality deficiencies and design changes. Such challenges have a profound impact on project schedules and costs, leading to resource wastage and decreased efficiency². According to The Chaos Report published by The Standish Group (2020), only 31% of projects globally are completed on time, while over 50% experience delays primarily due to rework. Consequently, minimizing rework and improving project quality and efficiency have become pressing priorities in the field of project management^3,4,5.

The Resource-Constrained Project Scheduling Problem (RCPSP), a classical framework in project management, provides theoretical foundations and methodologies for optimizing project activity scheduling and resource allocation⁶. The primary objective of RCPSP is to minimize project duration and cost by efficiently scheduling activities under resource constraints. However, traditional RCPSP models often overlook the heterogeneity of personnel skill levels, which directly affects task quality and is frequently a major cause of rework^7,8,9.

To overcome these limitations, recent research has incorporated personnel skill factors into RCPSP, leading to the development of the Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP). MSRCPSP focuses on optimizing the scheduling of multi-skilled personnel to enhance resource utilization while balancing skill alignment and project duration optimization¹⁰. Existing studies have examined skill heterogeneity, stochastic resignation, and the dynamics of learning and forgetting effects^11,12,13. Weighted average functions have also been utilized to model the relationship between skill levels and task quality¹⁴. However, most studies remain confined to evaluating the quality of individual activities, overlooking the cascading quality transmission effects within project networks.

In practical projects, activity quality is rarely isolated; rather, it is directly influenced by the quality of preceding activities. This quality transmission mechanism can trigger cascading rework effects, significantly impacting overall project duration and resource allocation¹⁵. Despite this critical dependency, many existing models fail to systematically capture these cascading effects, resulting in limited applicability to real-world project networks.

To bridge these gaps, this study proposes a project scheduling model within the MSRCPSP framework that systematically incorporates personnel skill levels and quality transmission mechanisms. The model integrates a dynamic rework reconstruction process to mitigate the cascading effects of quality deficiencies. A Mixed-Integer Linear Programming (MILP) model is formulated to facilitate solution derivation by linearizing nonlinear constraints. To address the computational complexity of the model, this study introduces an Improved Gazelle Optimization Algorithm (GOAIP), which combines dynamic operators, shuffle crossover, and Gaussian mutation mechanisms. This approach achieves a dynamic equilibrium between global search and local optimization.

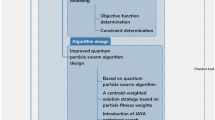
 In summary, this study investigates the impacts of quality transmission and personnel skill levels on project scheduling, proposing an efficient optimization framework. Experimental results validate the effectiveness of the proposed model and algorithm in reducing rework rates and shortening project durations. Figure 1 illustrates the research framework, encompassing the research objectives and background, core components (quality transmission mechanisms, dynamic rework reconstruction, and multi-skilled personnel allocation), algorithmic solutions, and experimental results. This framework provides systematic theoretical support and practical tools for resource scheduling in complex project environments.

Fig. 1

Framework for Quality Propagation and Multi-Skilled Project Scheduling.

Related research review

Development and research of uncertainty in RCPSP

Project scheduling techniques were initially developed using the Critical Path Method (CPM) and the Program Evaluation and Review Technique (PERT), which played a pivotal role in early projects such as the Manhattan Project and the Apollo Moon Landing Program¹⁶. However, these methods failed to account for resource constraints, resulting in a disconnect between project plans and their practical implementation. To address this gap, Pritsker et al.¹⁷ introduced the Resource-Constrained Project Scheduling Problem (RCPSP), which optimizes activity start times to minimize project duration while adhering to both resource and precedence constraints. As project management environments become more complex, uncertainties such as fluctuating activity durations and unstable resource costs have become more pronounced. Traditional RCPSP models face significant challenges in managing uncertainties in real-world projects.

Researchers have developed uncertainty-based RCPSP approaches that employ probabilistic distributions, robust optimization, and stochastic programming. For instance, Ortiz-Pimiento et al.¹⁸ proposed a critical chain-based heuristic algorithm to dynamically optimize uncertainties in multi-mode scheduling. Wang et al.¹⁹ developed a robust multi-objective scheduling model that balances cost-effectiveness and stability by incorporating resource transfer costs and schedule stability. Similarly, Yuan et al.²⁰ proposed a hybrid co-evolutionary algorithm tailored for prefabricated building environments to mitigate the negative effects of duration uncertainty. Despite these advancements, most studies focus on time and cost uncertainties, while the dynamic effects of activity quality, particularly quality transmission effects, remain underexplored.

Research on rework risk and quality transmission effects

Rework risk is a critical source of uncertainty in project scheduling and is widely recognized as a major contributor to project delays. Studies have shown that the allocation of multi-skilled labor and effective activity quality management significantly mitigate rework risks. For example, Maghsoudlou et al.²¹ designed a multi-objective optimization algorithm to address rework risks, while Wang et al.²² quantified the impact of stochastic rework on schedules using a mixed-integer programming model. Ju et al.²³ developed a reactive scheduling approach to mitigate schedule delays induced by rework-related deviations.

Moreover, previous research has highlighted the intrinsic relationship between rework risk and quality management. Through empirical investigation, Ye et al.²⁴ identified unclear project management processes and subpar construction quality as the primary causes of rework. Ran et al.²⁵ proposed a quality management strategy based on threshold control, optimizing resource allocation and risk management through a dynamic scheduling model with minimum quality thresholds. Liberatore et al.²⁶ introduced the concept of "project cumulative quality" to monitor project quality and determine the need for rework or repairs.

Further studies indicate that project activity quality is interdependent and significantly influenced by the quality of preceding activities. These effects often lead to cascading rework impacts, further exacerbating overall project delays. For example, Zhu et al.¹⁵ found that rework in preceding activities directly impacts subsequent activities in assembly manufacturing projects, leading to quality transmission that amplifies delay risks. Ellinas et al.²⁷ emphasized that failures in preceding activities within a project network can lead to quality degradation in subsequent activities, triggering cascading risk amplification.

Nevertheless, most existing studies treat rework as an isolated event, failing to account for the interdependence of quality transmission across activities. While the cascading effects of rework risks underscore the importance of quality transmission, current research often treats rework as an independent event, lacking systematic modeling. Particularly in multi-skilled scheduling problems, the systematic modeling of quality transmission mechanisms, dynamic rework subnet reconstruction, and the quantification of their impact on project scheduling remain challenging research areas.

Optimization algorithms in project scheduling and beyond: classical, metaheuristic, and hybrid approaches

Classical optimization algorithms in project scheduling

Various heuristic and metaheuristic optimization algorithms have been proposed to address complex optimization problems in project scheduling. Each algorithm presents distinct advantages in practical applications. For example, Genetic Algorithms (GA) conduct global searches using crossover and mutation operations, which makes them suitable for large-scale optimization problems; however, they are susceptible to premature convergence²⁸. Ant Colony Optimization (ACO), which simulates ant pathfinding through pheromone mechanisms, excels in combinatorial optimization; however, it suffers from high computational complexity²⁹. Particle Swarm Optimization (PSO) converges rapidly but lacks adequate local search capabilities, rendering it vulnerable to local optima³⁰.

Hybrid metaheuristics in project scheduling and beyond

In recent years, hybrid metaheuristic algorithms have demonstrated remarkable versatility in addressing complex optimization problems across various domains, providing valuable insights for resource-constrained project scheduling (RCPSP). In the core area of RCPSP, hybrid approaches have evolved to tackle stochastic, multi-objective, and sustainability-driven challenges. For example, simulation-based hybrid genetic algorithms³¹, integrated with resource-based (RB) scheduling policies, significantly reduce financial risks in stochastic multi-mode RCPSP by optimizing the conditional net present value at risk (CNPVaR), achieving a 13% improvement in solution stability compared to traditional methods. Similarly, the integration of non-dominated sorted genetic algorithms with magnet-based crossover operators³² reduces greenhouse gas emissions by 13.6% in multi-site projects, addressing the long-overlooked environmental aspects of RCPSP. Furthermore, reinforcement learning, hybridized with agent-based modeling³³, provides adaptive decision-making frameworks for dynamic construction scheduling, resulting in a 15% reduction in project delays under resource uncertainty.

Beyond RCPSP, hybrid metaheuristics exhibit cross-industry adaptability through methodological synergies. In logistics, a two-stage hybrid ant colony algorithm³⁴ optimizes electric vehicle routing under time-dependent energy constraints, with its cluster-based resource allocation logic paralleling RCPSP’s multi-skill resource scheduling. In cloud computing, spider-honeybee hybrid optimization³⁵ is used to balance container deployment costs and network latency, a strategy that can potentially be applied to RCPSP’s virtual resource allocation in cloud-enabled project management. Notably, in manufacturing, multi-fidelity deep learning hybrids³⁶ are employed for real-time defect prediction in laser welding, demonstrating how data-driven hybrid frameworks can enhance RCPSP’s responsiveness to dynamic disruptions.

Game theory-driven collaborative resource optimization

In recent years, game theory models have provided a novel theoretical framework for resource competition and collaboration in distributed manufacturing environments, particularly demonstrating unique advantages in cloud manufacturing and sustainable production systems. For example, Renna³⁷ highlighted in a systematic review that game theory effectively coordinates production planning, scheduling, and resource-sharing objectives by modeling multi-agent strategic interactions. This coordination reduces manufacturing cycles and enhances system resilience. In cloud resource allocation scenarios, a hybrid model combining double auctions and evolutionary games³⁸ simulates resource exchange strategies among Cloud Service Providers (CSPs). The model increases social welfare by 5% and reduces redundant contracts by 3%, significantly outperforming traditional auction methods. The mechanism dynamically adjusts CSP bidding strategies through evolutionary games and incorporates default penalty mechanisms (e.g., resource reclamation rights) to strengthen cooperation incentives, offering solutions to trust issues in multi-agent resource scheduling.

Additionally, research on resource-sharing strategies in cloud manufacturing environments has revealed the potential of game theory in managing multi-objective trade-offs. Li³⁹constructed a two-stage dynamic decision-making model based on the Stackelberg Game, analyzing the impact of three strategies—independent supplier operations, alliance cooperation, and collaboration with cloud platforms—on system profits. The study found that low-margin cost suppliers have a competitive advantage in task allocation, while the alliance strategy is opposed by cloud platforms due to reduced overall profits. This insight provides analogous implications for multi-contractor collaboration in RCPSP, particularly in resolving responsibility allocation and profit conflicts. For instance, modeling the cost-sharing problem of rework due to activity quality defects using a leader—follower game framework can be an effective approach.

These interdisciplinary advances highlight critical trends in optimizing the Resource-Constrained Project Scheduling Problem (RCPSP), showcasing the integration of hybrid metaheuristics with multi-paradigm approaches. For example, combining metaheuristics with simulation, deep learning, or multi-agent systems such as ABM-RL hybrids enables context-aware optimization capabilities in stochastic environments. Additionally, game-theoretic coordination and conflict resolution techniques—such as auction mechanisms and Stackelberg game-based strategies—formalize multi-agent interactions, offering equilibrium solutions for conflicting objectives, such as individual profit maximization versus collective carbon reduction. Furthermore, sustainability-driven adaptability, exemplified by emission-aware scheduling and dynamic penalty mechanisms like resource reclamation in cloud manufacturing, enhances system resilience against environmental and operational disruptions. Real-time responsiveness is further facilitated by techniques such as magnet-based crossover and flexible energy estimation, which enable rapid policy adjustments to address dynamic resource failures. Together, these trends expand the methodological toolkit for RCPSP, bridging algorithmic optimization with strategic decision-making in multi-stakeholder environments.

However, existing studies still exhibit significant limitations. Traditional hybrid algorithms (e.g., GA, ACO) struggle to effectively balance global exploration and local exploitation in complex dependency scenarios, such as dynamic quality transmission and rework subnet reconstruction. Furthermore, most models decouple quality control from scheduling decisions, resulting in an inability to accurately model cascading delays caused by quality defects.

To address these challenges, this study proposes an improved Gazelle Optimization Algorithm (GOAIP), which integrates shuffle crossover and Gaussian mutation mechanisms to dynamically balance global search and local exploitation, thereby enhancing both solution quality and efficiency. By embedding the quality transmission mechanism within the dynamic scheduling model, GOAIP can simultaneously optimize resource allocation and defect prevention, overcoming the limitations of traditional decoupling approaches. Experimental results demonstrate that GOAIP reduces project duration by an average of 22% across multiple RCPSP benchmark tests, significantly outperforming existing algorithms (GA, ACO, GWO).

Research gaps and contributions

The following gaps have been identified based on the existing literature:

• 1. Inadequate modeling of the dynamic impact of activity quality: Existing RCPSP and MSRCPSP studies primarily focus on time and cost factors, with limited consideration of the cascading effects of quality transmission and rework.

• 2. Lack of a systematic approach for quantifying quality transmission mechanisms: Current research has not modeled the interdependence of activity quality, hindering an accurate description of the propagation characteristics of quality issues.

• 3. Limited applicability of optimization algorithms: Traditional algorithms exhibit insufficient global and local search capabilities when addressing quality transmission and rework risks.

Contributions of this paper are as follows:

• 1. Proposing a dynamic quality management model that integrates quality transmission mechanisms and personnel skill levels, while quantifying the cascading effects of activity quality.

• 2. Developing a Mixed-Integer Linear Programming (MILP) model for optimizing scheduling and dynamic rework subnet reconstruction.

• 3. Presenting the Improved Gazelle Optimization Algorithm (GOAIP) and validating its effectiveness through comparisons with mainstream algorithms for solving complex scheduling problems.

Problem definition and model construction

This study investigates the Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP) concerning quality transmission, incorporating various components, including activities (both original and rework), personnel, skill types, skill levels, and quality grades. The impact of the rework subnet on the structure of the original project network is considered, and the original project network is represented as $G\left( {V,\,E} \right)$, where the set of activities is denoted as $V=\left\{0,\,1,\,2,\,\cdots ,\,\left|V\right|,\,\left|V\right|+1\right\}$. Activity 0 and activity $\left|V\right|+1$ are dummy activities that represent the start and end of the project, respectively. These dummy activities do not consume time or resources. All other activities, except for zero and $\left|V\right|+1$, are actual activities, and the numbering of each activity is greater than or equal to its preceding activity. $E$ represents the set of precedence relationships among the original activities, where any $\left(i,j\right)\in E$ indicates that activity $i$ must be completed before activity $j$.

Each actual activity has specific skill-type requirements and minimum skill standards. Each individual possesses specific skill types and levels, which can be applied to suitable activities to meet the activity’s skill requirements. Individual skill levels are assessed by a dedicated expert group based on factors such as background, knowledge, experience, and past performance. Skill levels are represented by real numbers ranging from 0 to 1. The expert group comprises R&D managers, project managers, industry experts, and HR evaluation specialists. During activity execution, the overall quality of an activity is influenced by the personnel’s skill levels and the quality transmission between successive activities. The project network contains several critical quality control activities, including inspections, testing, and acceptance tasks. Professional inspectors evaluate various project metrics to determine whether the quality of preceding activities meets the required standards. Based on inspection results and quality traceability information, certain upstream activities may require rework to ensure that the interim project quality meets specified standards. Rework activities form a rework subnet that integrates with the original project network, thus altering the structure of the project network.

The reconstructed network is represented as $G\left( {V^{\prime } ,E^{\prime } } \right)$, which includes all activities, retaining the numbering of the original network activities. Any rework activity corresponding to an original activity $j$ is denoted as ${O}_{j}$ and represents the precedence relationships of the reconstructed project network, encompassing the relationships among original activities, relationships among rework activities, and relationships between original and rework activities. Figure 2 illustrates a project network comprising seven activities. In this network, activities 0 and 6 are defined as dummy activities, representing the start and end of the project, respectively. Activity 5 is critical, triggering quality inspection of preceding activities immediately after execution. Assume that activity 2 has quality issues. Due to quality transmission, the low quality of activity 2 affects its immediate successors, activities 3 and 4, which further influence activity 5, resulting in a cascading rework effect²⁷. Consequently, rework activities ${O}_{2}\text{ to }{O}_{5}$ are introduced into the original project network, thus reconstructing the network structure. This indicates that the original activities’ completion times and the rework activities’ durations influence the overall project duration. Therefore, under multi-skilled human resource constraints, the core research problem of this study is to optimize the allocation of multi-skilled personnel and schedule activity timings to minimize rework durations, thus achieving project duration minimization.

Fig. 2

Project network with cascading effects of rework.

To simplify practical problems, it is essential to align the design of the multi-skill project scheduling model, which incorporates quality transmission, with relevant theoretical literature and the practical needs of modern enterprise projects. Otherwise, the problem would become overly complex, rendering computations inefficient and making solutions challenging. Furthermore, such results may not be broadly applicable to the diverse requirements of enterprises. Based on a review of the existing literature, this study operates under the following assumptions:

• 1. Project activities are carried out continuously, with each participant utilizing a single, defined skill level for each specific activity.

• 2. Activity quality is quantified as a number between 0 and 1, with higher values corresponding to better quality. Quality consists of two components: (i) partial quality, influenced by the skill level of the executing personnel, and (ii) upward-transferred quality, which is directly affected by preceding activities.

• 3. Each activity undergoes rework only once. After rework, the activity’s quality is assumed to meet the required standards, meaning that no further rework is required.

• 4. The resource requirements for rework activities are identical to those of the original activities, and the addition of rework activities does not impact the personnel allocation decisions for the original activities.

This study is based on known project network parameters, such as activity skill requirements, personnel skill types, and skill levels. The objective is to allocate personnel efficiently and determine the required execution skills while scheduling the execution times of project activities, including rework activities. To minimize the total project duration, this must be achieved under various constraints, including precedence relationships, skill supply–demand balance, and minimum skill requirements.

The following sections will present the construction of a mathematical model, with a focus on personnel allocation and project scheduling. All symbols used in the model are defined below (Table 1):

Table 1 Relevant parameters and their meanings.

Multi-skilled personnel allocation submodel

This study optimizes the assignment of personnel and their respective skill types to activities within the original project network, taking into account the specific skill requirements of each activity and the skill proficiency of the personnel. The goal is to ensure efficient and rational workflows throughout the allocation process. The multi-skilled personnel allocation submodel is defined as follows:

$$\begin{array}{*{20}c} {\mathop \sum \limits_{h \in H} y_{ihs} = N_{is} ,\quad \forall i \in V{ \setminus }\left\{ {0,\left| V \right| + 1} \right\},\quad s \in S} \\ \end{array}$$

(1)

$$\begin{array}{*{20}c} {y_{ihs} G_{hs} \ge L_{is} - M\left( {1 - y_{ihs} } \right),\quad \forall i \in V{ \setminus }\left\{ {0,\left| V \right| + 1} \right\},\quad s \in S,\quad h \in H} \\ \end{array}$$

(2)

$$\begin{array}{c}\sum_{j\in V} {x}_{0jh}=1,\quad \forall h\in H\end{array}$$

(3)

$$\begin{array}{c}\sum_{i\in V} {x}_{i,\,\left|V\right|+1,\,h}=1,\quad \forall h\in H\end{array}$$

(4)

$$\begin{array}{c}\sum_{j\in V} {x}_{ijh}=\sum_{{j}^{{^{\prime}}}\in V} {x}_{{j}^{{^{\prime}}}ih},\quad \forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\quad h\in H\end{array}$$

(5)

$$\begin{array}{c}{x}_{iih}=0,\quad i\in V,\quad h\in H\end{array}$$

(6)

$$\begin{array}{c}{v}_{ij}\ge {E}_{ij},\quad \forall i,\quad j\in V\end{array}$$

(7)

$$\begin{array}{c}{v}_{ij}+{v}_{ji}\le 1,\quad \forall i,\quad j\in V,\quad i<j\end{array}$$

(8)

$$\begin{array}{c}{v}_{ip}\ge {v}_{ij}+{v}_{jp}-1,\quad \forall i,\quad j,\quad p\in V,\quad i\ne j\ne p\end{array}$$

(9)

$$\begin{array}{c}{x}_{ijh}\le {v}_{ij},\,\forall i,\,j\in V,\,h\in H\end{array}$$

(10)

$$\begin{array}{c}\sum_{j\in V} {x}_{ijh}\le \sum_{s\in S} {y}_{ihs},\quad \forall i\in V,\quad h\in H\end{array}$$

(11)

Decision Variables

The model involves two binary decision variables: ${x}_{ijh}$ and ${y}_{ihs}$:

• ${x}_{ijh}=1$: Indicates that worker $h$ moves from activity $i$ to activity $j$. Otherwise, ${x}_{ijh}=0$. This variable ensures that workers continue their tasks in sequence, maintaining the flow of activities.

• ${y}_{ihs}=1$: Indicates that worker $h$ applies skill $s$ to activity $i$. Otherwise, ${y}_{ihs}=0$. This variable ensures that workers are assigned the appropriate skills for the corresponding activities.

Constraint Descriptions

• Constraint (1): Skill Supply–Demand Balance – This constraint ensures that the total skill supply allocated to each activity $i$ for skill $s$ meets the skill demand ${N}_{is}$. It guarantees that the required number of workers with the necessary skills is assigned to each task.

• Constraint (2): Minimum Skill Requirement – This constraint ensures that the skill level ${G}_{hs}$ of worker $h$ assigned to activity $i$ meets or exceeds the minimum skill requirement ${L}_{is}$​ for skill $s$. If worker $h$ does not apply skill $s$, the constraint is relaxed using a large constant $M$.

• Constraints (3)–(6): Resource Flow Balance – These constraints ensure that each worker $h$ begins at the dummy start activity (activity 0) and returns to the dummy end activity (activity $\left|V\right|+1$). Each worker must follow a continuous flow from the start to the end of the schedule, thereby ensuring the correct sequence of task execution.

• Constraint (7): Precedence Relationships – This constraint ensures that task $i$ is completed before task $j$, adhering to the precedence constraints of the project and preventing any violations of task dependencies..

• Constraints (8) and (9): Avoidance of Cyclic Resource Flow –These constraints prevent cyclic resource flows within the project network, ensuring that workers do not return to already completed tasks, thereby avoiding resource flow cycles and conflicts in task execution.

• Constraints (10) and (11): Variable Relationships – The first constraint ensures that workers only proceed to the next task $j$ if there is a precedence relationship between tasks $i$ and $j$. The second constraint ensures that the allocation of workers to tasks follows the required skill sets for each task.

These constraints ensure the efficient allocation of multi-skilled personnel, while meeting skill requirements, maintaining task priority sequences, and ensuring balanced resource flow. This guarantees the optimal scheduling of tasks and the effective utilization of resources throughout the project.

Project scheduling submodel considering quality transmission

Activity quality measurement model with quality transmission

Research and practical experience in project management have shown that the quality of activities within a project network is interdependent rather than isolated. If a particular activity encounters quality issues, these problems can negatively impact the quality of subsequent activities. In this study, the total quality of an activity’s completion is divided into two components:

• 1. Sub-quality (${Q}_{i}^{Sub})$: This reflects the quality of the activity itself, considering factors such as task difficulty and the efficiency of resource allocation.

• 2. Incoming quality (${Q}_{j}^{In})$: This represents the influence of the quality of preceding activities on the current activity.

Together, these components determine the total quality of an activity’s completion (${Q}_{j}^{Out})$. Figure 3 illustrates the structure of activity quality and the transmission relationships among activities.

Fig. 3

Framework of Activity Quality Components and Flow Relationships.

In the figure, ${TQ}_{1}$, ${TQ}_{2}$, and ${TQ}_{3}$ r represent the total output quality of the three preceding activities. These qualities are transmitted through the project network and form the “input quality” (${IQ}_{4)}$ for activity 4. The incoming quality directly influences the execution of activity 4. The sub-quality (${SQ}_{4})$ of activity 4 is primarily determined by its own execution, including factors such as resource allocation and task complexity. The total output quality $({TQ}_{4)}$ of activity 4 is the combined result of ${IQ}_{4}$ and ${SQ}_{4}$.

This framework models the quality transmission mechanism among activities, illustrating how the quality of preceding activities influences the completion quality of subsequent ones.

General Formula for Activity Quality Measurement

The relationship between total quality, sub-quality, and incoming quality can be expressed using the following general formula:

$$\begin{array}{c}{Q}_{i}^{\text{out }}=f\left({Q}_{i}^{\text{Sub }},\,{Q}_{j}^{\text{out }}\mid j\in {V}_{i}^{\text{Pre }}\right),\quad \forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

(12)

Focusing on the influence of personnel skill levels on an activity’s sub-quality, the following formula calculates the sub-quality:

$$\begin{array}{c}\\ {Q}_{i}^{\text{Sub }}=\sum_{s\in S} {w}_{is}\frac{\sum_{h\in H} {y}_{ihs}{G}_{hs}}{{N}_{is}},\quad \forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

(13)

Here:

• The term $\frac{\sum_{h\in H} {y}_{ihs}{G}_{hs}}{{N}_{is}}$ represents the average skill level of personnel using skill $s$.

• The weight ${w}_{is}$ adjusts the influence of different skill types on activity quality. For instance, if an activity requires both skill 1 (primary) and skill 2 (auxiliary), skill 1 will have a higher weight.

Formula (12) defines the total output quality ${Q}_{i}^{\text{out}}$ of an activity, which is determined by two components: the sub − quality ${Q}_{i}^{\text{Sub}}$ of the activity itself and the output quality ${Q}_{j}^{\text{out}}$ from the preceding activities, where $j$ belongs to the set of preceding activities ${V}_{i}^{\text{Pre}}$ of activity $i$ The function $f()$ describes how these two components interact to determine the overall quality of activity $i$.

Formula (13) calculates the sub-quality ${Q}_{i}^{\text{Sub}}$ of an activity, taking into account the influence of personnel skill levels. It sums over all skill types $s$ used in the activity. The term $\frac{\sum_{h\in H} {y}_{ihs}{G}_{hs}}{{N}_{is}}$ represents the average skill level of the personnel assigned to activity $i$ using skill $s$ , where ${y}_{ihs}$ is a binary variable indicating whether worker $h$ applies skill $s$ in activity $i$, ${G}_{hs}$ is the skill level of worker $h$ for skill $s$, and ${N}_{is}$ is the number of workers required for skill $s$ in task $i$. The weight ${w}_{is}$ adjusts the contribution of each skill type to the overall sub-quality of the activity.

Quality Transmission Mechanisms

Based on a review of relevant studies, three theoretical quality transmission mechanisms are proposed to describe the relationships among total quality, sub-quality, and incoming quality:

• 1. Quality Transmission Based on System Reliability Drawing from system reliability theory, the quality transmission mechanism is defined as follows:

  $${Q}_{i}^{In}=1-\prod_{j\in {V}_{i}^{\text{Pre }}} \left(1-{Q}_{j}^{\text{Out }}\right),\quad \forall i\in V\setminus \{0,\,|V|+1\}$$

  (14)
  $${Q}_{i}^{\text{Out }}={Q}_{i}^{\text{Sub }}\cdot {Q}_{i}^{\text{In }},\quad \forall i\in V\setminus \{0,\,|V|+1\}$$

  (15)

Formula (14) represents the incoming quality ${Q}_{i}^{In}$ of activity $i$ . It is calculated based on the output quality ${Q}_{j}^{\text{Out}}$ of preceding activities. Specifically, ${Q}_{i}^{In}$ is the complement of the product of the output quality of all preceding activities. That is, if the output quality of any preceding activity is 1 (indicating it has reached the highest quality standard), the incoming quality of the current activity will not be affected and will depend entirely on its sub-quality.

Formula (15) defines the total output quality ${Q}_{i}^{\text{Out}}$ of activity $i$ , which is determined by the product of its sub-quality ${Q}_{i}^{\text{Sub }}$ and incoming quality ${Q}_{i}^{\text{In}}$. The total output quality reflects the actual completion quality of the activity, incorporating both the quality of the activity’s execution (sub-quality) and the influence of preceding activities on the quality of the current activity.

The system reliability-based quality transmission mechanism was selected for its ability to capture the interdependence of tasks in complex projects, where the quality of one activity depends on the performance of preceding tasks. This mechanism is particularly effective in managing the uncertainty and risks inherent in multi-stage projects, such as research and development (R&D) projects, where failures in earlier tasks can cascade, negatively affecting the quality of subsequent activities. By modeling how the quality of preceding activities influences the input quality of later tasks, this mechanism helps identify and address the weakest links in the project, thereby improving resource allocation, adaptability, and resilience to quality-related issues. Overall, it provides valuable insights for more effective resource management and decision-making in complex and uncertain environments.

• 2. Quality Transmission Based on Weighted Averages Given that the quality contribution of activities to the overall project can vary, the weighted average method is commonly applied⁴⁰. This mechanism is expressed as follows:

  $$\begin{array}{c}{Q}_{i}^{\text{In }}=\sum_{j\in {V}_{i}^{\text{Pre }}} {\alpha }_{j}{Q}_{j}^{\text{Out }},\quad \forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

  (16)
  $$\begin{array}{c}{Q}_{i}^{\text{Out }}=\left(1-\sum_{j\in {V}_{i}^{\text{Pre }}} {\alpha }_{j}\right){Q}_{i}^{\text{Sub }}+{Q}_{i}^{\text{In }},\quad \forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

  (17)

Formula (16) represents the incoming quality ${Q}_{i}^{\text{In}}$ of activity $i$ , which is the weighted average of the output quality ${Q}_{j}^{\text{Out }}$ of all preceding activities. The contribution of each preceding activity to the quality of the current activity is represented by the weight ${\alpha }_{j}$​, which reflects the extent to which the preceding activity influences the quality of the current activity. The total incoming quality is the weighted sum of the output qualities of the preceding activities and their corresponding weights.

Formula (17) defines the total output quality ${Q}_{i}^{\text{Out}}$ of activity iii. The output quality of the current activity consists of two parts: one part is based on the weighted value of the current activity’s sub-quality ${Q}_{i}^{\text{Sub}}$, and the other part is the incoming quality ${Q}_{i}^{\text{In}}$ from the preceding activities. The weighted sum of these two components determines the overall quality of the activity.

The quality transmission mechanism based on weighted averages was chosen because it effectively quantifies the varying contributions of different activities to the overall project quality. In practical projects, where the influence of each task on quality can differ, this mechanism uses weighted averages to reflect the varying importance of each activity, allowing for flexible adjustments to the quality propagation model. This adaptability is particularly useful in multi-stage projects, where the impact of tasks on quality is uneven, as it enhances the accuracy of quality control across the entire project. Additionally, if preceding activities have little impact on the current task, the mechanism simplifies by relying solely on the sub-quality of the current activity. Overall, this mechanism provides a flexible and precise framework for modeling quality propagation in complex projects, ensuring both adaptability and accuracy in quality management.

• 3. Quality Transmission Based on the “Weakest Link Effect” In many cases, the weakest activity in a project network determines the overall quality level²⁶. For instance, in scheduling problems for assembly manufacturing projects, Zhu et al.¹⁵ assumed that if any preceding activity requires rework, the current activity must also undergo rework, thereby triggering cascading rework effects. This mechanism is expressed as follows:

  $${Q}_{i}^{\text{In }}=min\left\{{Q}_{j}^{\text{out }}\mid j\in {V}_{i}^{\text{Pre }}\right\},\quad \forall i\in V\setminus \{0,\,|V|+1\}$$

  (18)
  $${Q}_{i}^{\text{Out }}=min\left\{{Q}_{i}^{\text{Sub }},\,{Q}_{i}^{\text{In }}\right\},\quad \forall i\in V\setminus \{0,\,|V|+1\}$$

  (19)

Formula (18) defines the incoming quality ${Q}_{i}^{\text{In }}$ of activity $i$ . In this model, the incoming quality is determined by the minimum output quality ${Q}_{j}^{\text{out}}$ of all preceding activities. This means that the incoming quality of the current activity is constrained by the activity with the lowest quality among the preceding activities, reflecting the "weakest link effect" in the quality propagation across the project network.

Formula (19) represents the total output quality ${Q}_{i}^{\text{Out}}$ of activity $i$ . The total output quality is the smaller value between the current activity’s sub-quality ${Q}_{i}^{\text{Sub}}$ and its incoming quality ${Q}_{i}^{\text{In}}$. This formula highlights that even if the sub-quality of the current activity is high, its total output quality is still limited by the lowest quality of the preceding activities, further reflecting the cascading effect in quality propagation.

The "weakest link effect" quality transmission mechanism was chosen because it effectively models situations where the overall quality of a project is constrained by the weakest activity in the network, particularly in environments with highly interdependent tasks, such as manufacturing or assembly projects. In these contexts, defects or delays in one task can negatively impact the entire project, and this mechanism captures the cascading effects that occur when a preceding task with low quality (requiring rework) affects subsequent tasks. This cascading impact is especially critical in rework scenarios, where a single defective task can cause further delays and quality degradation. By focusing on the minimum quality among preceding tasks, this mechanism provides a simple yet effective way to model quality transmission, making it particularly useful in projects with limited resources or high task interdependencies. It mirrors real-world scenarios where overall project performance is often constrained by the weakest or most critical task, aligning with the understanding that improving or addressing these weak points is crucial for enhancing project outcomes. In summary, this mechanism was selected for its ability to capture cascading quality effects in complex projects, providing a clear and practical approach to ensuring quality control across interconnected tasks.

Project network reconstruction

In this study, rework operations are triggered when the quality of an activity does not meet the required standards. Unlike previous studies, which treat rework as a mere extension of the original activity’s duration, this study considers rework independent. In this framework, each activity $i$ is assigned a unique identifier, ${O}_{i}$, for its corresponding rework activity. Additionally, due to the cascading effects of quality transmission, rework issues may propagate, creating a network of multiple rework activities. At the project level, integrating the rework subnet significantly alters the structure of the original project network, resulting in the fusion of original and rework activities into a reconstructed network.

The duration of a rework activity is determined by the associated rework workload. Specifically, the higher the completion quality of the original activity, the lower the rework workload, leading to a shorter rework duration. This study specifically addresses rework triggered by quality issues, where quality levels are typically quantified as the percentage of compliance with a set of quality indicators, represented on a scale from 0 to 1. Lower quality levels (i.e., lower compliance rates) correspond to a higher degree of rework.

In practice, quality assessments are often discrete. Therefore, this study adopts a threshold model to define quality thresholds for varying rework levels and their corresponding rework durations. A piecewise, monotonically decreasing function is employed to characterize the relationship between activity quality and rework levels. As illustrated in Fig. 4, the $[0,\,1]$ quality interval is divided into levels, each corresponding to a specific quality range $[L{Q}_{il},\,M{Q}_{il}]$. The rework level for each quality level is denoted as ${\delta }_{il}\in (0,\,1)$,and the duration of rework activity ${O}_{i}$ is calculated as ${K}_{{O}_{i}l}=\lceil{\delta }_{il}{D}_{i}\rceil$.

Fig. 4

Calculation function of rework level.

For products or components, quality levels are commonly classified as "qualified," "minor defects," "general defects," and "severe defects." By analyzing defect types, quantities, and rework outcomes, based on historical data or expert assessments, the corresponding rework level for each quality classification can be predicted. For example:

• Severe defects Full rework is required, leading to a rework level of 100%.

• General or minor defects Partial rework, such as reinforcement or repair, is required, resulting in lower rework levels.

• Qualified No rework is required, resulting in a rework level of 0%.

Mathematical Formulation

To incorporate the quality level into the project scheduling model, a binary variable ${z}_{il}$ is introduced to indicate whether activity $i$ falls into quality level $l$ . The following formulas apply:

$$\begin{array}{l}\left\{\begin{array}{l}{z}_{il}=1,\, \, {\text{i}}{\text{f}} \, L{Q}_{il}\le {Q}_{i}^{\text{out }}<M{Q}_{il}\\ {z}_{il}=0,\,\\ \, {\text{o}}{\text{t}}{\text{h}}{\text{e}}{\text{r}}{\text{w}}{\text{i}}{\text{s}}{\text{e}} \, \end{array},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\,l\in L\right.\end{array}$$

(20)

$$\begin{array}{c}{d}_{i}={D}_{i},\quad \forall i\in V\end{array}$$

(21)

$$\begin{array}{c}{d}_{i}=\sum_{l\in L} {z}_{{O}_{i}l}{B}_{{O}_{i}l},\quad \forall i\in {V}^{{^{\prime}}}\setminus V\end{array}$$

(22)

Here:

• ${z}_{il}:$ Binary variable indicating whether activity $i$ belongs to quality level $l$.

• ${Q}_{i}^{\text{out }}:$ Total output quality of activity $i$.

• ${d}_{i}:$ Duration of activity $i$.

• ${B}_{{O}_{i}l}:$ Base duration of rework activity ${O}_{i}$ at quality level $l$.

Formula (20) introduces the binary variable ${z}_{il}$ , which indicates whether activity $i$ belongs to quality level $l$ . If the output quality of activity $i$ ${Q}_{i}^{\text{out}}$ lies between the minimum quality standard $L{Q}_{il}$ and the maximum quality standard $M{Q}_{il}$ , then ${z}_{il}=1$ , indicating that activity $i$ meets quality level; otherwise, ${z}_{il}=0$.

Formula (21) defines the duration ${d}_{i}$ of activity $i$ . For original activities, the duration ${d}_{i}$ is equal to its fixed original duration ${D}_{i}$ .

Formula (22) calculates the duration ${d}_{i}$ of rework activity ${O}_{i}$, where the duration is the weighted sum based on quality levels. ${z}_{{O}_{i}l}$ is the binary variable indicating whether rework activity ${O}_{i}$ meets quality level $l$, and ${B}_{{O}_{i}l}$ is the baseline duration of rework activity ${O}_{i}$ at quality level $l$ . By weighting the durations for different quality levels according to their corresponding quality levels, the duration of the rework activity can be dynamically adjusted.

These three formulas ensure that the duration of rework activities is dynamically adjusted according to their quality levels, reflecting the impact of quality defects on project scheduling.

Activity scheduling model

To schedule activities within the reconstructed project network, the following equations and constraints are proposed:

$$\begin{array}{c}{F}^{T}=s{t}_{\left|V\right|+1}\end{array}$$

(23)

$$\begin{array}{c}{{E}^{{^{\prime}}}}_{ij}\left(s{t}_{i}+{d}_{i}\right)\le s{t}_{j},\quad \forall i,\quad j\in {V}^{{^{\prime}}}\end{array}$$

(24)

$$\begin{array}{c}s{t}_{i}+{d}_{i}+{v}_{ij}M\le s{t}_{j},\quad \forall i,\quad j\in V\end{array}$$

(25)

Explanation of Formulas and Constraints

• 1. Equation (23): The project completion time (${F}^{T}$) is determined by the start time of the dummy end activity ($s{t}_{\left|V\right|+1}$). This formula defines the overall project duration as the start time of the final activity in the schedule.

• 2. Constraint (24): This constraint ensures that the precedence relationships within the reconstructed project network are maintained. Specifically, for any two activities $i$ and $j$, the start time of activity $j$ must be later than or equal to the end time of activity $i$, considering both the duration of activity $i$ and its associated delays.

• 3. Constraint (25): This constraint models the sequencing of activities based on resource flow. It ensures that the start time of activity $j$ is at least the end time of activity $i$ plus the necessary resource flow time (represented by ${v}_{ij}$), while accounting for potential delays (denoted by $M$).

Summary of the Model

This study presents a multi-skill resource-constrained project scheduling model (MSRCPSP) that incorporates the effects of quality transmission. The primary objective of the model, as outlined in Eq. (23), is to minimize the total project completion time. The model is subject to the constraints defined in Eqs. (1)–(13), (20)–(22), and (24)–(25).

This nonlinear integer programming model aims to minimize the overall project duration by optimizing the scheduling process. Specific quality transmission mechanisms can be incorporated by substituting Eq. (12) with the corresponding expressions to better align with practical project scenarios.

Basis for selecting the improved algorithm

Traditional optimization algorithms, such as the Genetic Algorithm (GA) and Ant Colony Optimization (ACO), exhibit several limitations when applied to complex multi-skill project scheduling problems:

• 1. Inefficient at handling nonlinear constraints and complex quality transmission mechanisms.

• 2. Prone to slow convergence and the tendency to become trapped in local optima.

• 3. Limited adaptability when dealing with combinatorial optimization problems.

In contrast, the Improved Gazelle Optimization Algorithm (GOAIP) provides distinct advantages:

• 1. Balancing Global Exploration and Local Exploitation

GOAIP is inspired by gazelle foraging behavior, which dynamically balances global exploration and local exploitation. The integration of Brownian motion and Lévy flight mechanisms enhances diversity in the early stages of the search process, while refining local solutions in the later stages. Studies have shown that this dynamic search strategy significantly improves convergence speed and solution quality⁴¹.

• 2. Efficient Management of Discrete and Combinatorial Optimization Problems

Continuous optimization algorithms often experience efficiency losses after discretization. GOAIP incorporates shuffle crossover and Gaussian mutation operators, providing exceptional flexibility in adapting to combinatorial optimization problems⁴². This adaptability makes it especially well-suited for project scheduling scenarios involving complex task interdependencies and multi-skill requirements.

• 3. Enhanced Convergence Speed and Solution Precision

Dynamic stochastic factors and adaptive update strategies improve GOAIP’s robustness and efficiency, allowing for the rapid identification of high-quality solutions. Compared to algorithms such as GA and Grey Wolf Optimizer (GWO), GOAIP demonstrates superior performance in solving complex multi-objective optimization tasks⁴³.

• 4. Flexibility in Handling Complex Constraints

The shuffle crossover and Gaussian mutation strategies of GOAIP further improve its ability to manage complex constraints, offering crucial support for dynamic quality transmission modeling in multi-skill project scheduling problems⁴⁴.

Algorithm design

Building upon the rationale for selecting the Improved Gazelle Optimization Algorithm (GOAIP), this study presents an enhanced optimization framework aimed at addressing complex constraints and dynamic quality transmission in multi-skill project scheduling problems.

The Gazelle Optimization Algorithm (GOA), introduced in 2022, has gained widespread adoption as an intelligent optimization algorithm⁴⁵. GOA simulates the survival behaviors of gazelles, including foraging and predator evasion, through a mechanism that combines Brownian motion and Lévy flights, dynamically balancing global search and local exploitation. The algorithm demonstrates exceptional global exploration capabilities and efficient search performance. However, the standard GOA algorithm is limited in its adaptability to discrete optimization problems and complex constraints.

To overcome these limitations, the Improved Gazelle Optimization Algorithm (GOAIP) is introduced in this study. GOAIP is specifically designed for multi-skill personnel allocation and project scheduling, integrating innovative operators, such as shuffle crossover and Gaussian mutation, to enhance adaptability and computational efficiency. GOAIP retains the global search capabilities of the original algorithm while refining its local search mechanisms, effectively tackling complex nonlinear constraints and combinatorial optimization challenges.

Adapting continuous algorithms to discrete problems

Discrete optimization problems, such as multi-skill project scheduling, are complicated by combinatorial constraints, including task sequencing and resource allocation. Traditional discrete optimization methods, such as Ant Colony Optimization and Simulated Annealing, are prone to becoming trapped in local optima. To overcome these challenges, this study employs the continuous optimization algorithm, GOAIP, to address discrete problems. It employs discretization techniques, such as binary encoding and shuffle crossover, to adapt effectively to discrete solution spaces.

• 1. Advantages of Continuous Optimization Algorithms

Continuous optimization algorithms, such as Genetic Algorithms (GA) and Gazelle Optimization Algorithms (GOA), offer significant advantages in terms of global search capabilities and flexibility. These algorithms efficiently explore solution spaces and avoid local optima in high-dimensional, complex constraint environments. By incorporating discretization techniques, their applicability is extended to discrete optimization problems.

• 2. Discretization Techniques

To apply continuous optimization algorithms to discrete problems, the following key discretization techniques were employed:

Binary Encoding Continuous variables are normalized and converted into fixed-length binary strings, enabling effective searches within discrete solution spaces. For instance, a value of 0.75 can be represented as the binary string "1011," enabling continuous optimization algorithms to operate within discrete spaces and identify optimal solutions⁴⁶.

Shuffle Crossover Shuffle crossover is an operator designed for discrete permutation problems. It generates new offspring solutions by randomly rearranging parts of parent solutions, thus enhancing solution diversity and significantly improving global exploration capabilities. This method is particularly effective for complex problems, such as multi-skill project scheduling, as it enhances search efficiency.

The improved GOAIP algorithm successfully adapts continuous optimization algorithms to discrete optimization problems, such as multi-skill project scheduling, by incorporating discretization techniques, such as shuffle crossover and binary encoding. As illustrated in Fig. 4, a comparative analysis of shuffle crossover, before and after applying it to test cases with 30, 60, 90, and 120 activities, demonstrates that these discretization techniques not only assist GOAIP in identifying better solutions in complex discrete solution spaces but also significantly enhance convergence speed and solution quality.

Gazelle Optimization Algorithm (GOA)

The survival behavior of gazelles inspires the optimization process of the Gazelle Optimization Algorithm (GOA) during foraging. The process is divided into two phases: the foraging (exploitation) phase, which occurs when no predators are present, and the fleeing (exploration) phase, which is triggered upon predator detection.

Exploitation phase

During the foraging phase, gazelles forage calmly when no predators are nearby, and their positions are assumed to follow Brownian motion. The position update for Gazelle $i$ is calculated as follows:

$$\begin{array}{c}{x}_{i}^{p1}={x}_{i}+v\cdot {r}_{1}\cdot {R}_{b}\left(\text{ Elite }-{R}_{b}\times {x}_{i}\right)\end{array}$$

(26)

where:

• ${x}_{i}^{p1}$ and ${x}_{i}$ represent the positions of gazelle $i$ before and after the first update.

• $v$: Foraging speed.

• ${r}_{1}$:A random number, ${r}_{1}\in [0,\,1]$.

• ${\text{Elite}}$: The position of the best-performing gazelle.

• ${R}_{b}$: Brownian motion vector, calculated as:

  $$\begin{array}{c}{f}_{b}\left(x,\,\mu ,\,\sigma \right)=\frac{1}{\sqrt{2\pi }\sigma }\text{exp}\left(-\frac{\left(x-{\mu }^{2}\right)}{2{\sigma }^{2}}\right)=\frac{1}{\sqrt{2\pi }}\text{exp}\left(-\frac{{x}^{2}}{2}\right)\end{array}$$

  (27)

Here,${f}_{b}(x,\,\mu ,\,\sigma )$ is the Gaussian probability distribution function of ${R}_{b}$,with $\mu =0$ and ${\sigma }^{2}=1$.

Equation (26) describes the position update strategy for gazelles during predator-free foraging, where individual positions are optimized through the synergy of stochastic perturbations and elite guidance. The velocity term $v$ regulates the global movement intensity, the uniform random number ${r}_{1}\in [0,\,1]$ controls local stochasticity, and the Brownian motion vector ${R}_{b}$ introduces multidimensional Gaussian perturbations. The core of the update mechanism lies in the directional guidance term $\left(\text{Elite }-{R}_{b}\times {x}_{i}\right)$, where ${R}_{b}$ synchronously perturbs both the current position ${x}_{i}$ and the elite individual’s position ${\text{Elite}}$ to generate a difference. This term is then scaled by the stochastic factor  $v\cdot {r}_{1}$ , ensuring adaptive balance across dimensions. The formulation preserves the exploration capability of random walks (driven by ${R}_{b}$ and ${r}_{1}$) while enhancing convergence efficiency through elite attraction.

Equation (27) defines the probabilistic distribution of the Brownian motion vector  ${R}_{b}$ : each dimension independently follows a standard normal distribution ($\mu =0,{\sigma }^{2}=1$), with the probability density function ${f}_{b}\left(x\right)= \frac{1}{\sqrt{2\pi }}\text{exp}\left(-\frac{{x}^{2}}{2}\right)$. This symmetric distribution ensures equal likelihood of perturbations in all directions, where small displacements occur with higher probability than large mutations, consistent with the physical properties of Brownian motion. By embedding ${R}_{b}$ into Eq. (26), the algorithm naturally incorporates Gaussian noise-driven exploration during position updates, providing mathematical guarantees for global optimization.

Exploration phase

When predators are detected, gazelles rapidly wag their tails, stomp their feet, and flee. The movements during this phase involve abrupt directional changes:

• In odd iterations, gazelles escape in one direction.

• In even iterations, gazelles escape in the opposite direction.

Gazelles that detect predators first and react more promptly update their positions using Lévy flight, while those that react later initially follow Brownian motion before transitioning to Lévy flight. The position update equations for this phase are as follows:

$$\begin{array}{c}{x}_{i}^{p2.1}={x}_{i}+v\cdot {\mu }_{g}\cdot {r}_{2}\cdot {R}_{l}\left(\text{ Elite }-{R}_{l}\times {x}_{i}\right)\end{array}$$

(28)

$$\begin{array}{c}\\ {x}_{i}^{p2.2}={x}_{i}+v\cdot {\mu }_{g}\cdot {c}_{f}\cdot {R}_{b}\left(\text{ Elite }-{R}_{l}\times {x}_{i}\right)\#\end{array}$$

(29)

where:

• ${x}_{i}^{p2.1}$ and ${x}_{i}^{p2.2}$:Position of gazelle $i$ after the second update.

• ${\mu }_{g}:$ Direction characteristic variable.

• ${r}_{2}:$ A random variable, ${r}_{2}\in [0,\,1]$.

• ${c}_{f}:$ Cumulative effect of the predator, calculated as:

  $$\begin{array}{c}{c}_{f}={\left(1-\frac{m}{M}\right)}^\frac{2m}{M}\end{array}$$

  (30)

Here, $m$ and $M$ represent the current and maximum number of iterations, respectively.

The escape success of a gazelle is determined as follows:

$${x}_{i}^{p2.3}=\left\{\begin{array}{c}{x}_{i}+{c}_{f}\left[{l}_{b}+{r}_{3}\cdot \left({u}_{b}-{l}_{b}\right)\right]\cdot Q \, {\text{i}}{\text{f}} \, {r}^{{^{\prime}}}\le psrs\\ {x}_{i}+\left[\text{ psrs }\left(1-{r}_{4}\right)+{r}_{4}\right]\left({x}_{{r}_{1}}-{x}_{{r}_{2}}\right) \, {\text{e}}{\text{l}}{\text{s}}{\text{e}}\end{array}\right.$$

(31)

where:

• ${u}_{b}and {l}_{b}:$ Upper and lower bounds of the gazelles’s position.

• ${r}_{3,\,4}$: Random numbers,${r}_{3},{r}_{4}\in [0,\,1]$.

• $psrs:$ Escape rate, set to 0.34.

• $Q:$ A binary vector of random numbers from $[{0,1}]$.

The binary variable $U$ determines the escape decision:

$$\begin{array}{l}U=\left\{\begin{array}{l}0,\, \, {\text{i}}{\text{f}} \, {r}_{4}<0.34\\ 1,\, \, {\text{e}}{\text{l}}{\text{s}}{\text{e}}\end{array}\right.\end{array}$$

(32)

Equations (28)–(32) model the dynamic predator-evasion strategies of gazelles. Equation (28) governs proactive individuals that adopt Lévy flight ${R}_{l}$ for long-jump exploration, where directional variability ${\mu }_{g}$ and stochastic scaling ${r}_{2}\in [0,\,1]$ enhance escape diversity. Equation (29) applies to delayed responders, initially leveraging Brownian motion ${R}_{b}$ for localized search, modulated by a quadratically decaying predator-cumulative factor ${c}_{f}$ (Eq. 30: ${c}_{f}={\left(1-\frac{m}{M}\right)}^\frac{2m}{M}$), which mimics diminishing predation pressure over iterations. Equation (31) determines escape success: gazelles either relocate near positional bounds ${(l}_{b},{u}_{b})$ with probability $psrs=0.34$ (controlled by a binary vector $Q$ ) or follow social cues via differential learning $\left({x}_{{r}_{1}}-{x}_{{r}_{2}}\right)$ . Equation (32) finalizes the binary escape decision $U$ through threshold ${r}_{4}<0.34$. This framework integrates adaptive stochasticity (Lévy-Brownian hybridization), predation-pressure decay ${c}_{f}$, and social-cue exploitation, balancing urgent evasion with systematic exploration while maintaining dimensional consistency in vector-scalar operations.

This exploration phase allows gazelles to dynamically adapt to predator pursuits, effectively balancing global and local search processes.

Improved gazelle optimization algorithm (GOAIP)

The standard Gazelle Optimization Algorithm (GOA) demonstrates strong global search capabilities, making it effective for tackling complex project scheduling problems. However, it faces several limitations when applied to discrete problems and complex constraints:

• 1. Fixed Perturbation Mechanism This limits diversity during the initial search stages and hampers convergence in later stages.

• 2. Simplistic Local Search Updates The lack of sufficient gene exchange between individuals heightens susceptibility to local optima.

• 3. Limited Fine-Tuning Capability The inadequate precision in identifying high-quality solutions affects the accuracy of the final results.

To address these challenges, this study introduces the Improved Gazelle Optimization Algorithm (GOAIP), which incorporates three key enhancements: dynamic random factors, shuffle crossover, and Gaussian mutation mechanisms.

Dynamic random factors and optimized perturbation mechanism

The disturbance mechanism in the standard GOA is fixed, which limits its adaptability to the varying requirements of different search stages. In this paper, a dynamic stochastic factor $r{s}_{1}$ is introduced to balance global search and local exploitation dynamically. The dynamic random factor is introduced to achieve a dynamic balance between global exploration and local exploitation.

The dynamic stochastic factor is defined as follows:

$$\begin{array}{c}r{s}_{1}=rand\cdot 0.3+0.01,{s}_{1}\in \left[{0.01,0.31}\right]\end{array}$$

(33)

$$\begin{array}{c}{X}_{i}^{t+1,j}={X}_{i}^{t,j}+{\text{s}}{\text{t}}{\text{e}}{\text{p}}\end{array}$$

(34)

Equation (33) defines a dynamic stochastic threshold $r{s}_{1}=\text{rand}\cdot 0.3+0.01$(where rand $\in [{0,1}]$), confining $r{s}_{1}\in \left[{0.01,0.31}\right]$ to adaptively regulate perturbation probability. In Eq. (34), the position update ${X}_{i}^{t+1,j}={X}_{i}^{t,j}+{\text{step}}$ introduces a stochastic ${\text{step}}$, generated by either Brownian motion (Gaussian steps) or Lévy flight (heavy-tailed steps). For each dimension, a perturbation is triggered only if a uniformly distributed random number ${R}_{d}\in [{0,1}]$ satisfies ${R}_{d}<r{s}_{1}$; otherwise, the current solution is retained. This mechanism dynamically suppresses unnecessary noise by narrowing the perturbation window (via $r{s}_{1}$’s bounded range) while preserving critical exploratory behaviors through context-aware step generation ${\text{step}}$. The framework achieves a self-adaptive balance between global exploration and local exploitation across iterative search stages, ensuring dimensional consistency in vector-scalar operations.

This improvement is inspired by chaotic optimization methods⁴⁷, with similar concepts having been successfully applied in Particle Swarm Optimization (PSO)⁴⁸ and Differential Evolution (DE)⁴⁹ algorithms. By introducing the dynamic stochastic factor, the GOA enhances its search control flexibility when addressing complex optimization problems, thus laying a solid foundation for efficient global exploration and precise local optimization.

Shuffle crossover mechanism

The standard GOA (Gazelle Optimization Algorithm) relies on simple position updates during the local search phase, lacking an effective information exchange mechanism. This deficiency often leads to insufficient population diversity and a tendency to fall into local optima. To address this limitation, this paper introduces a shuffle crossover mechanism, which enhances gene exchange among individuals to optimize population diversity and improve global search capability:

• 1. Select Parent Individuals Two superior parent individuals, ${X}_{j}$ and ${X}_{k}$,are selected through a binary tournament, ensuring that high-quality individuals are chosen for crossover.

• 2. Random Gene Shuffle Gene indices of the parent individuals are randomly shuffled to generate crossover points. This step uses $\text{randperm}$ to generate random indices, ensuring the production of diverse combinations through crossover.

• 3. Generation of New Offspring A new candidate solution ${X}_{\text{new}}$ is generated by exchanging the genes of parent individuals ${X}_{j}$ and ${X}_{k}$ according to the shuffled indices. This process forms a new offspring through recombination of parent genes.

• 4. Fitness Comparison The newly generated solution ${X}_{\text{new}}$ is compared with the parent solutions in terms of fitness. The solution with higher fitness is retained for the next generation.

Crossover Operation Formulas:

Let the genes of parent individuals ${X}_{j}$ and ${X}_{k}$ be represented as follows:

$$\begin{array}{c}{X}_{j}=\left[{x}_{j1},{x}_{j2},\dots ,{x}_{jn}\right],{X}_{k}=\left[{x}_{k1},{x}_{k2},\dots ,{x}_{kn}\right]\end{array}$$

(35)

The crossover operation involves generating random gene indices ${x}_{1}$ and ${x}_{2}$ to exchange the genes of the parent individuals:

$$\begin{array}{c}{X}_{\text{new }}=\text{crossover}\left({X}_{j},{X}_{k}\right)=\left[{X}_{j}\left({x}_{1}\right),{X}_{k}\left({x}_{2}\right)\right]\end{array}$$

(36)

Equation (35) defines the gene vectors of parent individuals ${X}_{j}$ and ${X}_{k}$ as $n$ -dimensional arrays: ${X}_{j}=\left[{x}_{j1},{x}_{j2},\dots ,{x}_{jn}\right]$ and ${X}_{k}=\left[{x}_{k1},{x}_{k2},\dots ,{x}_{kn}\right]$. Equation (36) describes the crossover operation: two distinct positional indices $({x}_{1},{x}_{2})$, generated via the random permutation function $\text{randperm}$, are used to exchange genetic segments between parents, producing an offspring ${X}_{\text{new }}=\left[{X}_{j}\left({x}_{1}\right),{X}_{k}\left({x}_{2}\right)\right]$ . Here, ${x}_{1}$ and ${x}_{2}$ correspond to randomly selected subsets of positional indices, ensuring stochastic yet structurally preserved recombination. This mechanism systematically explores the solution space through dimension-wise hybridization while avoiding disruptive gene permutations, thereby maintaining population diversity and preventing premature convergence.

Mechanism Impact:

The shuffle crossover mechanism operates through the steps of gene shuffling, offspring generation, and fitness evaluation (as shown in Fig. 5), effectively enhancing gene exchange diversity. This prevents premature convergence to local optima, significantly improving both global search capabilities and solution quality. As a result, the algorithm can explore the solution space more comprehensively and converge more efficiently to the global optimum when addressing complex optimization problems⁵⁰.

Fig. 5

Schematic Diagram of the Shuffle Crossover Mechanism.

Gaussian mutation mechanism

In the standard GOA (Gazelle Optimization Algorithm), the local search phase primarily relies on simple position updates of individuals, which lacks the capability for fine adjustments to local solutions, thereby affecting the final solution accuracy. To address this issue, this paper introduces a Gaussian mutation mechanism during the local search phase. By dynamically adjusting the standard deviation $\sigma$, the mutation amplitude is effectively controlled, thereby optimizing the precision of the solution.

Core Equations of Gaussian Mutation:

$$\begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+randn()\cdot \sigma \end{array}$$

(37)

$$\begin{array}{c}\sigma =\left(ub-lb\right)\cdot {\text{g}}{\text{a}}{\text{m}}{\text{p}}\end{array}$$

(38)

Here:

• $randn()$ is a random number following a standard normal distribution.

• '${\text{gamp}}$' is a dynamic adjustment parameter controlling the size of the standard deviation.

• $ub$ and $lb$ are the upper and lower bounds of the variable, ensuring that the mutation amplitude matches the problem’s search space.

• $\sigma$ represents the mutation amplitude and is determined by the dynamically adjusted parameter.

Equation (37) governs the Gaussian mutation mechanism: ${X}_{i}^{t+1}={X}_{i}^{t}+randn()\cdot \sigma$ , where $randn()$ generates standard normally distributed noise, and $\sigma$ controls the mutation amplitude. Equation (38) defines $\left(ub-lb\right)\cdot {\text{gamp}}$, dynamically adapting the mutation range to the search space $\left(ub,lb\right)$ through a tunable parameter ${\text{gamp}}$. This dual mechanism achieves scale-awareness (via $\left(ub-lb\right)$ normalization) and adaptive regulation (via iteration-dependent ${\text{gamp}}$). By coupling bounded exploration ($\sigma$- constrained steps) with Gaussian stochasticity $randn()$,the method balances local refinement and global exploration while ensuring solution feasibility within the predefined domain $\left([lb,ub]\right)$.

Mechanism Process:

• 1. Large-Scale Variation In the early stages of the search, a large mutation amplitude $\sigma$ is applied to enhance global exploration capabilities and prevent premature convergence to local optima.

• 2. Gradual Convergence As iterations progress, the mutation amplitude gradually decreases, allowing the algorithm to focus on searching near potential global optima. During this phase, mutations transition into finer adjustments, enhancing local search capabilities.

• 3. Fine-Tuning In the later stages of the search, very small perturbations in $\sigma$ are applied to achieve precise localization of high-quality solutions. The small mutation amplitude minimizes unnecessary perturbations while refining solution quality.

Mutation Probability and Mutation Attempts:

• 1. Mutation Probability For each mutation operation, each dimension of the solution has a probability $\text{prob}$ of being mutated. In general, the mutation probability is higher in the early stages to increase diversity, while it gradually decreases in later stages to ensure stability and convergence.

• 2. Mutation Attempts Each individual typically undergoes multiple mutation attempts in each generation. The parameter $\text{Gentimes}$ (number of mutation attempts) controls the number of mutation trials per individual. More mutation attempts are applied in the early stages to enhance population diversity, whereas fewer attempts are used in the later stages to refine solution quality.

By dynamically adjusting the mutation amplitude $\sigma$, the Gaussian mutation mechanism performs broad global searches in the early stages and fine local optimizations in the later stages. This prevents premature convergence and improves the final solution quality. Through the process of large-scale variation → gradual convergence → fine-tuning (as shown in Fig. 6), the mechanism successfully balances global exploration and local exploitation. It significantly enhances the algorithm’s performance in exploring the solution space, particularly demonstrating clear advantages in solving complex optimization problems⁵¹.

Fig. 6

Gaussian Mutation Mechanism and Dynamic Adjustment Process.

Summary of algorithm improvements

This study improves the core structure of the standard Gazelle Optimization Algorithm (GOA) by incorporating dynamic random factors, a shuffle crossover mechanism, and a Gaussian mutation mechanism. These improvements significantly enhance global search capabilities, population diversity, and the precision of local exploitation. Table 2 presents a detailed comparison between the standard GOA and the improved version, highlighting the specific enhancements and their corresponding impacts:

Table 2 Improved Mechanisms and Comparison of GOA.

Figure 7 presents the structural framework of the Improved Gazelle Optimization Algorithm (GOAIP), where three key enhancements—dynamic stochastic factors, the shuffle crossover mechanism, and the Gaussian mutation mechanism—are integrated across various stages of the main loop to synergistically improve algorithm performance:

• 1. Dynamic Stochastic Factor and Perturbation Mechanism Generated dynamically within the main loop, this component adjusts the perturbation intensity to balance global exploration with local exploitation, ensuring the algorithm adapts to varying search requirements at each stage.

• 2. Shuffle Crossover Mechanism By introducing random gene shuffling and selection, this mechanism enhances information exchange among individuals during the population update phase, leading to superior solutions while maintaining population diversity.

• 3. Gaussian Mutation Mechanism Focused on local exploitation, this mechanism dynamically adjusts mutation amplitude to refine solutions and achieve fine-tuned optimization, thus improving solution precision.

Fig. 7

Structural Diagram of Improved Gazelle Optimization Algorithm.

These three improvements are closely interrelated: the dynamic stochastic factor operates throughout the process, providing flexible support for crossover and mutation; the shuffle crossover mechanism emphasizes global population optimization; and the Gaussian mutation mechanism focuses on local search refinement. Through this multi-stage synergistic approach, GOAIP rapidly converges to high-quality solutions in complex search tasks.

Algorithm performance testing

Adjustment of test cases

The Project Scheduling Problem Library (PSPLIB) is a globally recognized standard repository for evaluating project scheduling algorithms. However, the existing cases in PSPLIB do not sufficiently address the specific needs of this study, particularly for Multi-Skill Resource-Constrained Project Scheduling Problems (MSRCPSP) that involve activity-based quality transmission. To address this gap, the original test cases were adjusted and extended to better simulate resource constraints and quality transmission characteristics in MSRCPSP.

New test cases were developed based on foundational PSPLIB cases by modifying resource constraints, task durations, dependencies, and the quality transmission between activities. The adjustment process adhered to the following principles:

• 1. Resource Constraints Task requirements and available resources were redistributed to align with real-world project management scenarios.

• 2. Task Distribution Task durations, start times, end times, and dependencies were redesigned to reflect actual project execution sequences and priorities.

• 3. Quality Transmission Resource allocation and task priorities were adjusted to account for quality impacts between activities, considering quality transmission mechanisms.

• 4. Data Generation Methods Test cases were generated through manual adjustments and predefined rules. For example, resource requirements were randomly or proportionally assigned to existing tasks, while task dependencies and quality transmission mechanisms were modeled based on fundamental engineering scenarios.

The adjusted dataset provides a robust foundation for algorithm performance comparisons. It serves as a testing platform for evaluating algorithms (e.g., GOAIP, GA, PSO, GWO, COA, GOA, and COOT) in MSRCPSP, ensuring experimental reproducibility and facilitating the validation of results by other researchers.

Algorithm parameter settings

To evaluate the advantages of the Improved Gazelle Optimization Algorithm (GOAIP) in terms of solution quality and convergence speed, six algorithms (GOAIP, GA, PSO, GWO, COA, GOA, and COOT) were implemented in MATLAB R2023a and tested on a mainstream commercial computer (Windows 11 OS, AMD Ryzen 7 7840H CPU @ 3.80 GHz, 16 GB RAM, Radeon 780 M Graphics). The specific parameter settings for each algorithm are as follows:

Parameters for GOAIP:

• Population size: 100

• Gravitational parameter update coefficient: 20

• Velocity range: 0.5

• Maximum iterations: 100

• Independent runs: 500 (with the best solution retained for each run)

Parameters for Comparison Algorithms:

• Population size: 100

• Maximum iterations: 100

• Independent runs: 500 (retaining the best solution for each run)

These settings ensure a fair comparison of algorithm performance and highlight the improvements achieved by GOAIP in complex optimization problems.

Algorithm performance verification

Effectiveness of dynamic operators

In comparative experiments, cases with 30, 60, 90, and 120 activities were selected to systematically evaluate the performance differences between the standard GOA and the improved GOAIP, which incorporates dynamic operators. The analysis was conducted across three dimensions: convergence performance, statistical metrics, and the impact of dynamic operators.

• 1. Convergence Performance (Fig. 8):

  • 30-Activity Case GOAIP achieves stability at approximately 50 iterations, while GOA takes longer to reach similar convergence. The curve for GOAIP is smoother, demonstrating higher solution quality and greater stability.

  • 60- and 90-Activity Cases As the problem size increases, the advantages of GOAIP become more pronounced. In the 90-activity case, GOAIP stabilizes before 80 iterations, while GOA shows more significant fluctuations and slower convergence.

  • 120-Activity Case GOAIP quickly identifies high-quality solutions in the early iterations, while GOA stagnates, particularly in the later stages, failing to achieve further optimization.

• 2. Statistical Metrics (Table 3):

  • Mean Objective Value GOAIP outperforms GOA in all cases. For example, in the 30-activity case, GOA’s mean objective value is 157.23, while GOAIP achieves 151.76, indicating a significant improvement.

  • Standard Deviation GOAIP exhibits lower standard deviations, reflecting more stable solutions. For instance, in the 60-activity case, GOA’s standard deviation is 5.12, compared to GOAIP’s 3.89.

  • Best and Worst Objective Values GOAIP achieves superior best-case and worst-case values, demonstrating its superior global search capabilities. In the 120-activity case, GOAIP’s best objective value is 634.15, significantly better than GOA’s 663.37.

• 3. Impact of Dynamic Operators:

Fig. 8

Comparison of Dynamic Operators for Different Case Sizes.

Table 3 Impact of Dynamic Operators on GOA vs GOAIP.

The introduction of dynamic operators facilitates extensive global exploration during the early search phase and precise local exploitation in later phases. Initially, dynamic operators broaden the search space, preventing premature convergence, while later phases refine solutions and accelerate convergence to high-quality solutions. Dynamic operators significantly enhance performance in complex cases (e.g., 90- and 120-activity cases), demonstrating their adaptability to challenging search tasks.

• 4. Comprehensive Conclusion:

Experimental results confirm that GOAIP outperforms the standard GOA in terms of solution quality, convergence speed, and stability. The introduction of dynamic operators is a key factor in enhancing algorithm performance. Table 3 and Fig. 8 together validate the effectiveness of dynamic operators, providing a more efficient solution for complex optimization problems.

Effectiveness analysis of shuffle crossover mechanism

To assess the impact of the shuffle crossover mechanism on convergence speed and solution quality, this study compares the performance of the original Gazelle Optimization Algorithm (GOA) with its improved version (GOAIP), which integrates the shuffle crossover mechanism. Experiments were conducted using test cases with 30, 60, 90, and 120 activities. The analysis is presented from both qualitative and quantitative perspectives:

• 1. Convergence Performance Comparison

  Figure 9 demonstrates that the shuffle crossover mechanism significantly improves GOAIP’s convergence speed, solution stability, and objective value optimization:

  • 30-Activity Case GOAIP achieved near-optimal objective values within 50 iterations, while GOA required approximately 70 iterations to reach comparable optimization levels.

  • 60- and 90-Activity Cases As problem complexity increased, the convergence advantage of GOAIP became more pronounced. In the 60-activity case, GOAIP’s convergence curve stabilized after 70 iterations, while GOA exhibited persistent fluctuations. In the 90-activity case, GOAIP achieved an objective value of approximately 456.67, compared to 498.28 for GOA, demonstrating a significant optimization advantage.

  Fig. 9

  

  Comparison of Shuffle Crossover Effect for Different Cases.

• 2. Quantitative Metrics Comparison

Experimental data further quantified the optimization effects of the shuffle crossover mechanism, showing that GOAIP outperformed GOA in objective value optimization, solution stability, and achieving optimal results, as shown in Table 4:

• Average Objective Value GOAIP consistently achieved superior average objective values across all cases. For example, in the 30-activity case, GOA’s average objective value was 151.15, while GOAIP improved it to 140.28, a 7.2% improvement. Similarly, in the 90-activity case, GOAIP reduced the average objective value from 486.53 to 450.93, a reduction of 7.3%.

• Standard Deviation GOAIP exhibited significantly lower standard deviations, indicating superior solution stability. For example, in the 60-activity case, GOAIP’s standard deviation was 4.31, compared to GOA’s 5.62.

• Best and Worst Objective Values GOAIP consistently achieved superior best-case and worst-case values. In the 90-activity case, GOAIP’s best objective value was 456.67, significantly outperforming GOA’s 475.15, while GOAIP’s worst objective value was 480.34, significantly better than GOA’s 498.28.

Table 4 Shuffle Crossover Impact Comparison.

• 3. Comprehensive Conclusion

Experimental results confirm that the shuffle crossover mechanism significantly enhances GOA performance. It accelerates convergence speed and improves solution quality and stability. This mechanism is particularly effective for large-scale optimization problems, providing an efficient solution strategy for complex project scheduling challenges.

Effectiveness analysis of the Gaussian mutation mechanism

The impact of the Gaussian mutation mechanism on optimization performance was evaluated by comparing the traditional Gazelle Optimization Algorithm (GOA) with its improved version (GOAIP), which integrates the Gaussian mutation mechanism. Test cases involving 30, 60, 90, and 120 activities were systematically analyzed with respect to convergence speed, solution stability, and objective value optimization.

• 1. Convergence Performance Analysis

  Improvement in Convergence Speed

  Figure 10 illustrates that GOAIP achieves faster convergence across all activity scales:

  • 30-Activity Case (Fig. 10a) GOAIP reached near-optimal objective values within 30 iterations, while GOA required approximately 50 iterations to achieve comparable results.

  • 120-Activity Case (Fig. 10d) GOAIP demonstrated higher optimization efficiency, significantly reducing the number of iterations required for convergence.

  Fig. 10

  

  Comparison of Gaussian Mutation Effect for Different Case.

  Enhanced Solution Stability

  The convergence curves of GOAIP exhibited reduced fluctuations, becoming significantly more stable during later iterations. For example:

  • 90- and 120-Activity Cases (Fig. 10c, d) GOAIP’s fluctuations were considerably smaller than those of GOA, indicating enhanced stability.

• 2. Quantitative Comparison Analysis

  Table 5 further quantifies the performance improvements resulting from the Gaussian mutation mechanism:

  • Average Objective Value Optimization:

  GOAIP consistently achieved lower average objective values across all cases compared to GOA. For example:

  Table 5 Gaussian Mutation Impact Comparison.

  • 30-Activity Case GOAIP reduced the average objective value to 143.78, a 6.9% improvement over GOA’s value.

  • 120-Activity Case GOAIP achieved a 6.7% reduction in the average objective value.

• Reduction in Standard Deviation:

  GOAIP exhibited lower standard deviations across all scales, indicating more stable optimization results. For example:

  • 60-Activity Case GOAIP’s standard deviation was 3.89, a 27% reduction compared to that of GOA.

• Improved Best and Worst Objective Values:

  GOAIP consistently achieved better best-case and worst-case values than GOA. For example:

  • 90-Activity Case GOAIP’s best objective value was 302.89, significantly outperforming GOA’s 317.33.

Comprehensive Conclusion

The integration of the Gaussian mutation mechanism significantly enhances GOA’s performance. Across all activity scales, GOAIP demonstrates faster convergence, superior solution stability, and better objective values. This improvement highlights the effectiveness of the Gaussian mutation mechanism as a high-performance solution strategy for complex optimization problems.

Performance comparison of seven algorithms across different activity scales

Table 6 and Fig. 11 present independent experiments comparing GOAIP with six other algorithms across varying case scales and resource allocation scenarios. A detailed analysis of the data provides the following insights:

Table 6 Independent Performance Comparison of Multiple Algorithms.

Fig. 11

Comparison of Seven Algorithms Across Different Activity Scales.

• 1. Superior Solution Quality of GOAIP:

GOAIP consistently outperformed the other five algorithms in terms of solution quality across all testing scenarios. This underscores GOAIP’s robustness and effectiveness in handling diverse case scales and varying resource availability scenarios.

• 2. Enhanced Convergence Performance:

The convergence curves in Fig. 11 further demonstrate that GOAIP exhibited superior convergence performance relative to the other six algorithms. GOAIP achieved faster convergence and superior solution stability, further underscoring its suitability for complex optimization tasks.

These findings collectively establish GOAIP as a robust and efficient solution for multi-skill resource-constrained project scheduling problems across various case complexities and resource configurations.

Case analysis

Case introduction

In 2013, the Jiangsu Maternal and Child Health Hospital commenced the construction of a new inpatient building, which stands at a height of 73.5 m, covers a total floor area of 68,033.9 square meters, and required an investment of 630 million RMB. The project was completed in 2018 and officially began operations.

This project, focusing on specific construction processes, was selected as a case study to validate the proposed model. The project consists of 14 specific activities and two virtual activities (1 and 16). Activity dependencies are represented through an Activity-on-Node (AON) network, as illustrated in Fig. 12.

Fig. 12

Project AON Network.

The project requires three primary skills: operating architectural design software, construction and installation, and engineering budget and cost control. Tables 7 and 8 present detailed skill distributions and levels.

Table 7 Project activity information.

Table 8 Personnel and skills information.

The “Weakest Link” quality transmission mechanism was selected for this case study because it effectively models task interdependence, where quality issues in one task can impact subsequent tasks. This mechanism captures the cascading effect, where problems in critical tasks lead to rework in later tasks, closely resembling real-world scenarios in construction, where the overall quality is often determined by the weakest task. By accurately reflecting these dynamics, the Weakest Link mechanism is well-suited for the project, ensuring a realistic representation of quality propagation.

Model linearization

To address the nonlinear constraints in the "shortest plank effect" quality propagation function, Eqs. (18)–(20) were linearized by introducing auxiliary decision variables pill and oil. The reformulated constraints are as follows:

$$\begin{array}{c}{Q}_{i}^{\text{In }}\le {Q}_{j}^{\text{out }},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\,j\in {V}_{i}^{\text{Pre}}\end{array}$$

(39)

$$\begin{array}{c}{Q}_{i}^{\text{out }}\le {Q}_{i}^{\text{Sub }},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

(40)

$$\begin{array}{c}{Q}_{i}^{\text{out }}\le {Q}_{i}^{\text{In }},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\}\end{array}$$

(41)

$$\begin{array}{c}M\left({p}_{il}-1\right)\le {Q}_{i}^{\text{out }}-L{Q}_{il}\le M{p}_{il},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\,l\in L\end{array}$$

(42)

$$\begin{array}{c}M\left({r}_{il}-1\right)\le M{Q}_{il}-{Q}_{i}^{\text{out }}-\frac{1}{M}\le M{r}_{il},\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\,l\in L\end{array}$$

(43)

$$\begin{array}{c}{z}_{il}={p}_{il}+{r}_{il}-1,\,\forall i\in V\setminus \left\{0,\,\left|V\right|+1\right\},\,l\in L\end{array}$$

(44)

The resulting linear integer programming model is:

$$\begin{array}{*{20}l} {Min} & {F^{T} } \\ {s.t.} & {(1) - (13),(21),(22),(24),(25),(39) - (44)} \\ \end{array}$$

To linearize the nonlinear constraints of the "shortest plank effect" quality propagation function (Eqs. 18–20), binary auxiliary variables ${p}_{il}$ and ${r}_{il}$ are introduced. Equations (39)–(41) decompose the original minimum function $\text{min}\{{Q}_{j}^{\text{out }},{Q}_{i}^{\text{Sub }}\}$ into linear inequalities: ${Q}_{i}^{\text{In }}\le {Q}_{j}^{\text{out}}$ upper bounds from predecessor quality), ${Q}_{i}^{\text{out }}\le {Q}_{i}^{\text{Sub}}$ (inherent quality limits), and ${Q}_{i}^{\text{out }}\le {Q}_{i}^{\text{In}}$ (propagation constraints). Equations (42)–(44) employ the big- $M$ method to discretize the piecewise quality intervals $[L{Q}_{il},M{Q}_{il}]$, where ${p}_{il}$ and ${r}_{il}$ indicate whether ${Q}_{i}^{\text{out}}$ falls within interval $l$. The activation of the corresponding quality state is governed by ${z}_{il}={p}_{il}+{r}_{il}-1$. The reformulated model minimizes the total completion time ${F}^{T}$ (Eq. 23) under linearized constraints (1–13, 21–22, 24–25, 39–44), transforming the original nonlinear problem into a tractable mixed-integer linear programming (MILP) formulation, enabling global optimization via commercial solvers.

Computational experiments

To validate the effectiveness of the model, two experimental analyses were performed:

• 1. Comparison with Non-Propagation Models This analysis involved propagation and network reconstruction, assessing the advantages in terms of project duration and rework quantities.

• 2. Sensitivity Analysis Sensitivity analyses were conducted on quality assessment intervals and skill levels to explore their impact on the model’s outputs.

Verifying the advantages of the quality propagation model

Rework quantities and project duration comparison

The model was solved using MATLAB R2023a with the Improved Gazelle Optimization Algorithm (GOAIP), demonstrating significant advantages in optimizing both project duration and rework activity distribution:

• With Quality Propagation:

  • Minimum project duration: 73 days

  • Rework activities: 6 (Fig. 13)

• Without Quality Propagation:

  • Total project duration: 96 days

  • Rework activities: 13

Fig. 13

Comparison of rework levels.

This resulted in a 50% reduction in rework activities and a 24% reduction in project duration.

Critical rework activities (e.g., 7, 12, and 13) were precisely controlled by the quality propagation model, effectively suppressing cascading quality issues. Activity 7, identified as a significant rework node, was contained locally, preventing propagation to subsequent activities (e.g., ${O}_{7}$) . Activities 12 and 13, as intermediate nodes, also limited their rework influence.

In contrast, the non-propagation model exhibited cascading failures originating from activities 2 and 10, triggering a sequence of rework activities (e.g.,${O}_{2}$, ${O}_{3}$, ${O}_{4}$, ${O}_{5}$ and ${O}_{6})$ , which caused resource conflicts and delays.

Resource allocation and scheduling optimization

Table 9 compares resource allocation and quality metrics between the two models, demonstrating that the quality propagation model results in higher sub-quality and total quality (e.g., the total quality of activity 2: 0.93 compared to 0.76). Table 10 illustrates the optimized activity scheduling and highlights effective resource allocation. For example, activity 7 limits its rework scope, preventing propagation to subsequent tasks.

Table 9 Resource Allocation and Quality Comparison.

Table 10 Process Scheduling with Start/End Times and Staffing Assignments.

Figure 14 further visualizes the comparison between the two models, depicting the objective values (minimized project duration) over the course of the iterations. The model incorporating quality propagation (yellow line) exhibits faster convergence and superior results, reducing the project duration to approximately 73 days, compared to 93 days for the rework-only model (blue line). The figure highlights the quality propagation model’s ability to effectively address cascading quality issues, preventing stagnation and enhancing overall scheduling efficiency.

Fig. 14

Comparison of Scheduling Models: Quality Propagation vs. Rework Only.

Key Results:

• Rework activities were reduced by 50%.

• The project duration was reduced to 73 days, reflecting a 24% improvement compared to the non-propagation model.

Multi-algorithm comparison

Figure 15 compares GOAIP with classical algorithms (GA, PSO, GWO, COA, GOA, and COOT) based on the case study.

• 1. Convergence Speed GOAIP achieves rapid optimization within 20 iterations, reducing the project duration to approximately 80 days, thereby outperforming the other algorithms.

• 2. Result Quality GOAIP avoids stagnation and local optima, consistently yielding superior results.

• 3. Robustness GOAIP identifies critical rework activities and optimizes resource allocation, thereby demonstrating superior performance under quality propagation conditions.

Fig. 15

Multi-algorithm convergence curve comparison chart.

Cross-industry case validation

To further validate the applicability of the model in heterogeneous projects, while considering space limitations, this study selects an intelligent manufacturing production line construction project as a case for brief analysis. By comparing the results of two real-world cases, the generalizability of the model can be systematically tested. In this case, the weighted average transmission mechanism is chosen as the quality propagation method for the following reasons:

• 1. Adaptability to Project Characteristics This case involves five parallel assembly units (e.g., precision machining, logistics transportation, etc.), each with significantly different contributions to overall quality. This characteristic aligns well with the dynamic weight allocation in Mechanism 2, effectively capturing the varying impacts of different units on overall quality.

• 2. Methodological Comparability Unlike the construction project case, which is based on the weakest link effect, this case adopts an asymmetric weight configuration. This allows for an assessment of the model’s capability to capture heterogeneous quality contributions, thereby improving its adaptability to weight variations in the quality propagation mechanism.

Through this case study, we can validate the model’s adaptability and effectiveness in handling heterogeneous projects, further demonstrating its broad applicability across different scenarios.

Tables 11 and 12 present detailed information about the project and the personnel skill pool. Next, the project is validated using the GOAIP algorithm, and the results are as follows:

Table 11 Case Data Table.

Table 12 Personnel Skill Pool.

First, the total project duration using the traditional CPM method (without considering quality propagation and with rework) is 69 days. As shown in Fig. 16, the GOAIP-optimized duration, considering rework but excluding quality propagation, is 46 days. However, when both rework and quality propagation mechanisms are incorporated, the optimized duration is reduced to 37 days, representing a 19.6% reduction.

Fig. 16

Comparison Chart of Quality Propagation Before and After.

The core improvements of this optimization can be summarized in three key aspects:

• 1. Rework Control The total number of rework cycles is reduced from 11 to 4, a decrease of 63.6%. Notably, the rework instances for high-priority operations (e.g., precision grinding, where ${\alpha }_{6}$= 0.8) decreased by 2, effectively preventing cascading quality defects.

• 2. Path Optimization By predicting the weights of ${\alpha }_{j}$, the critical path was restructured. This allowed previously serial processes (activities 4–5-6) to be parallelized with the assembly line (activities 7–8), thus saving 9 days of the project timeline.

• 3. Mechanism Advantage The quality propagation mechanism, through dynamic weight allocation, intervened in quality bottlenecks in real time and allocated resources precisely, demonstrating the model’s adaptability in heterogeneous projects.

Sensitivity analysis of parameters

In practical project applications, quality evaluation intervals and employee skill levels are typically based on expert assessments or historical data, which involve inherent uncertainties. Sensitivity analysis was conducted to investigate the impact of these uncertainties on total project duration, following the methodology outlined below:

• 1. The fluctuation range($\pm \Delta$) for quality evaluation intervals and employee skill levels was defined, with $\Delta$ varying from 1 to 10% in 1% increments.

• 2. 25 random experiments were conducted for each fluctuation range, producing 500 datasets for statistical analysis.

Analysis Results:

• Fluctuation in Quality Evaluation Intervals (Left Figure):

When fluctuations exceed 7%, the total project duration exhibits significant variability, indicating that greater uncertainty in quality intervals strongly affects the schedule. However, when the fluctuation is limited to 6% or below, changes in project duration are minimal, demonstrating the model’s robustness.

• Fluctuation in Employee Skill Levels (Right Figure):

A 6% fluctuation introduces a significant probability of considerable variation in project duration. This is primarily due to the fact that changes in skill levels along the critical path directly affect rework times, leading to project delays. In contrast, the total project duration remains stable when fluctuations are limited to 5% or below, demonstrating the model’s adaptability to minor variations in skill levels.

As illustrated in Fig. 17, the proposed model demonstrates robust performance in managing uncertainties in both quality evaluation intervals and employee skill levels. Specifically, when fluctuations in quality intervals are limited to 6% and skill levels to 5%, the predicted project duration aligns closely with baseline parameters, ensuring reliable and stable scheduling solutions.

Fig. 17

Sensitivity Analysis of Quality Assessment Intervals and Skill Level Fluctuations.

Conclusion

This study addresses the Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP) by integrating the effects of quality propagation. A generalized quality propagation model is proposed, along with three specific quality propagation functions. An integer programming model that incorporates the quality propagation mechanism is developed, combined with the Improved Gazelle Optimization Algorithm (GOAIP). The algorithm optimizes the scheduling of workers and skills by utilizing the logical relationships between activities and skill requirements, with the goal of minimizing project duration.

The performance of the proposed algorithm is validated through two experiments:

• 1. Comparison of various algorithms across different test case sizes This analysis demonstrates the superiority and stability of GOAIP.

• 2. Application to real-world project cases In addition to the hospital project case, this study also validates the model with an intelligent manufacturing production line construction project. This project involves multiple parallel assembly units, each contributing significantly differently to the overall quality. By comparing and analyzing the impact of various quality propagation mechanisms, the adaptability and applicability of the model in heterogeneous projects are further validated, enhancing the generalizability of the model and demonstrating its broad applicability across different industries.

The results indicate that, compared to traditional resource-constrained project scheduling methods, incorporating quality propagation into scheduling and resource allocation enhances skill support for critical activities, reduces rework rates, and significantly shortens the overall project duration. Furthermore, sensitivity analysis of quality evaluation intervals and skill level uncertainties reveals that the project duration remains stable when parameter fluctuations are within 5% and 6%, respectively, thus confirming the robustness of the proposed model.

This study demonstrates not only the successful application of the model in a hospital project but also extends its validation to heterogeneous projects such as intelligent manufacturing production lines. Through this cross-industry validation, several generalizable patterns emerge, such as the dynamic adaptability of quality propagation mechanisms across different project types, the importance of quality weight allocation for different tasks, and the criticality of matching workers’ skills to tasks. These findings provide theoretical support for the broader application of the model and further enhance its potential for widespread use across industries.

This research provides valuable insights for project managers, particularly in managing complex projects with high uncertainty and interdependent activities. It improves the efficiency of time and human resource allocation, offering actionable guidance for effective resource management.

Given the potential inaccuracies in assessing worker skill levels in real-world scenarios, future research will focus on project resource scheduling under skill-level uncertainty. It is anticipated that this research will deepen our understanding of how such uncertainties affect resource-constrained project scheduling and contribute to the development of project scheduling theory.