A parameter adaptive EEFO VMD method to mitigate noise and trend interference of blast vibration signals

Abstract

Blasting vibration signals are often contaminated by trend terms and noise, stemming from environments, and instrument errors. This contamination hinders subsequent signal processing and analysis. To obtain a pure blasting vibration signal, a parameter-adaptive variational mode decomposition (VMD) method based on the improved electric eel foraging optimization (EEFO) algorithm is proposed for preprocessing the blasting vibration signal. This method removes high-frequency noise and low-frequency trend components from the signal. Combining the abrupt and related characteristics of blasting vibration signals, a weighted multi-scale permutation entropy is constructed as the fitness function for parameter optimization. The EEFO algorithm, with strong global and local search capabilities, is employed to optimize the VMD decomposition parameters. This approach adaptively determines the optimal combination of decomposition modes K and the secondary penalty factor α. The analysis results of simulated vibration signals with different interference components and actual measured blasting vibration signals using this method show that, compared to traditional VMD, empirical wavelet transform, and empirical mode decomposition methods, EEFO-VMD has superior adaptability and anti-aliasing capabilities. Even in complex interference components, it can adaptively determine the optimal decomposition parameter combination, effectively removing interference components from the vibration signals. This method is suitable for preprocessing blasting vibration signals.

Introduction

Blasting, a prevalent construction technique in engineering, finds widespread application in diverse fields such as tunnel excavation, mining, water conservancy, and hydropower projects^1,2. The blasting process inevitably generates vibrations that can adversely affect the surrounding environment and nearby structures. Accurate analysis of the propagation and attenuation of these vibrations is crucial for effectively mitigating their harmful effects^3,4. However, the measured blasting vibration signal is often contaminated by complex trend components and significant high-frequency noise interference. This contamination arises from factors such as the complex monitoring environment, calibration errors in the monitoring instruments, and deficiencies in the monitoring scheme. These distortions in the signal can hinder subsequent processing and analysis⁵. Therefore, the accurate extraction of real and effective blasting vibration characteristics necessitates the application of appropriate signal preprocessing techniques.

Signal preprocessing is an essential step in the analysis workflow for blasting vibration data, involving the targeted manipulation of the original data. Numerous studies have demonstrated that appropriate preprocessing techniques can significantly enhance data analysis effectiveness and improve model prediction accuracy^6,7. The primary objectives of signal preprocessing⁸ are enhanced robustness and accuracy, improved interpretability, outlier and trend detection and removal, and dimensionality reduction.

Common signal preprocessing steps include denoising, detrending, normalization, dimensionality reduction, outlier, and discrete value removal, etc⁸. However, the specific emphasis and steps of preprocessing vary depending on the signal type and analytical objectives. For instance, ECG signal preprocessing often involves filtering and normalization to detect and identify heartbeat frequency and rhythm⁹. Acoustic emission (AE) signal preprocessing typically involves eliminating abnormal oscillations and jitter to facilitate the extraction of hidden mutation points¹⁰. Preprocessing of Infrared spectroscopy (IR) and Raman spectroscopy (RS) data primarily focuses on feature extraction, dimensionality reduction, and outlier elimination¹¹. Mechanical vibration signal analysis, mainly focused on fault diagnosis and feature information recognition, often involves denoising, smoothing, and detrending¹². Blasting vibration signal analysis emphasizes the identification of time-frequency characteristics and energy distribution, demanding high signal clarity and accuracy. Therefore, blasting vibration signal preprocessing typically involves signal decomposition, denoising, and detrending. Currently, the most prevalent signal decomposition methods include wavelet decomposition^13,14, empirical mode decomposition (EMD)^15,16, and variational mode decomposition (VMD)¹⁷. Wavelet decomposition encompasses discrete wavelet transform and wavelet packet transform. Numerous researchers^18,19,20 have employed wavelet methods for signal processing with notable success. However, discrete wavelet transform and wavelet packet transform have inherent limitations²¹. Decomposition accuracy and level are heavily reliant on the choice of wavelet basis function, leading to significant randomness and limiting the adaptive capabilities of these methods. Consequently, guaranteeing decomposition accuracy remains a challenge. The EMD method, while widely employed due to its good applicability, suffers from drawbacks such as excessive envelope effects, endpoint effects, and modal aliasing^22,23,24, impacting the accuracy of signal decomposition.

Variational mode decomposition (VMD) is a signal processing technique introduced by Dragomiretskiy et al.¹⁷. Unlike recursive mode decomposition methods such as empirical mode decomposition (EMD), VMD simultaneously extracts all intrinsic mode functions (IMFs). By transforming IMFs and center frequencies, the signal is decomposed into a set of IMF ensembles, and signal decomposition is recast as a variational problem solution. This method exhibits strong adaptive characteristics, a robust mathematical foundation, and high noise resistance. Moreover, it effectively mitigates modal aliasing²⁵, making it one of the most widely used decomposition methods in recent years. Li et al.²⁶ proposed an improved VMD method for bearing fault identification and diagnosis. Yang et al. ²⁷ conducted a comparative analysis of VMD and EMD’s feature extraction capabilities in wind turbine condition monitoring. Notably, VMD demonstrated superior anti-noise interference capabilities, enabling effective monitoring of weak sideband features in wind signals. Despite its advantages, VMD has limitations. Specifically, it necessitates presetting the decomposition mode number K and the quadratic penalty factor α prior to decomposition. Previous studies typically rely on prior knowledge to preset these parameters. However, inappropriate parameter selection can lead to substantial decomposition errors, potentially resulting in the loss of feature information or modal aliasing. Consequently, selecting appropriate parameters is a critical aspect of VMD decomposition.

To address this challenge, several researchers have investigated methods for determining optimal VMD decomposition parameters. Liu et al.²⁸ proposed a method combining VMD with Detrended Fluctuation Analysis (DFA), incorporating a screening criterion for modal components to adaptively determine the decomposition level K. Li et al.²⁹ developed a method for identifying the optimal decomposition layer K using similarity principles and kurtosis search. However, this method assumes independence between the two parameters and does not account for the impact of the quadratic penalty factor α on decomposition results. Liang et al.³⁰ proposed an improved variational mode decomposition and multi-eigenvalue extraction method based on the multi-island genetic algorithm (MIGA). This method utilizes MIGA to optimize VMD parameters. However, it employs envelope entropy as the objective function, considering only the envelope characteristics of the IMFs and neglecting the correlation between each IMF and the original signal. This approach can lead to local optima and difficulties in accurately obtaining the optimal parameter combination. Therefore, selecting and constructing an appropriate objective function is paramount for achieving optimal VMD decomposition accuracy and performance.

Noise removal techniques for vibration signals typically encompass filtering denoising and threshold denoising. Filtering denoising employs existing filtering algorithms to process and eliminate high-frequency noise components^31,32. Conversely, threshold denoising relies on assessing the correlation between the decomposed component and the original signal component, or other relevant indicators, to filter noise. Components exhibiting low correlation and high frequencies are typically identified as noise components³⁴. Both methods are widely employed in various fields^34,35,36. Common noise filters include low-pass, high-pass, band-pass, and band-stop filters, designed to remove noise based on distinct signal characteristics and noise characteristics. However, this approach can introduce significant signal distortion. In frequency bands close to or overlapping with the vibration signal frequency band, broadband noise proves difficult to filter out. Consequently, filtering denoising often exhibits limited effectiveness for nonlinear and non-stationary signals³⁷. Compared to filtering denoising, threshold denoising demonstrates superior performance in handling nonlinear and non-stationary signals while effectively preserving the detailed characteristics of the original signal. By adjusting the threshold value, an optimal balance between noise reduction and signal fidelity can be achieved, effectively removing noise components that overlap with the signal frequency band³⁸. These advantages have contributed to the widespread adoption and recognition of threshold denoising in vibration signal processing^39,40.

To address the degradation in signal processing and analysis accuracy caused by environmental noise and trend interference in blasting vibration signals, this study proposes a parameter-adaptive VMD method optimized using an improved EEFO algorithm. By leveraging the strong global and local search capabilities of EEFO, the method adaptively selects key VMD parameters, including the number of decomposition modes K and the quadratic penalty factor α, effectively overcoming the randomness and modal aliasing issues associated with traditional VMD parameter selection. Furthermore, a weighted multiscale permutation entropy is constructed as the fitness function to account for the abrupt and correlated characteristics of blasting vibration signals, enhancing the accuracy and anti-interference capabilities of the signal decomposition. Building on this framework, noise components are filtered using the Hurst exponent and energy ratio method, while trend components are removed via mean normalization, resulting in a complete signal preprocessing framework. Experimental results on both simulated and actual blasting vibration signals demonstrate that, compared to traditional methods such as Empirical Mode Decomposition (EMD) and Empirical Wavelet Transform (EWT), the proposed approach exhibits superior anti-aliasing capabilities and adaptability in complex interference environments, effectively eliminating interference components and significantly improving the accuracy of signal decomposition and subsequent analysis.

Methodology

Brief Introduction of VMD

The Variational Mode Decomposition (VMD) algorithm, introduced by Dragomiretskiy et al.¹⁷, is an adaptive signal decomposition method. The application of VMD for decomposing blasting vibration signals necessitates the pre-selection of two key parameters: the number of decomposition modes K and the penalty factor α. The choice of K directly impacts the completeness of the decomposition. A value of K that is too small will result in an incomplete decomposition, leading to the loss of original signal features. Conversely, a value of K that is too large can lead to over-decomposition and the generation of spurious components. Similarly, the penalty factor α influences the iterative process and decomposition accuracy. A large α value slows down the iteration and convergence speed, while a small α value increases the likelihood of modal aliasing, which can negatively affect decomposition accuracy and subsequent processing. The complexity of measured blast vibration signals is further compounded by factors such as varying propagation media, explosion source characteristics, and geological conditions. These variations make it challenging to determine the optimal values for K and α. Consequently, selecting the optimal parameter combination that aligns with the specific signal being analyzed is crucial for achieving successful VMD decomposition.

Basic principle EEFO VMD algorithm

Weighted multiscale permutation entropy

To effectively optimize VMD parameter selection and mitigate noise contamination during vibration signal monitoring, weighted multiscale permutation entropy (MPE_r) value is proposed as the fitness function for VMD parameter optimization. MPE_r considers not only the mutational characteristics of modal components but also incorporates the correlation between these components and the original signal. This comprehensive approach allows for a more robust representation of multi-dimensional signal characteristics. The weighted multi-scale permutation entropy MPE_r is defined as follows:

Firstly, the autocorrelation function of the original signal is calculated:

$$R_{x} (i) = \frac{1}{N}\sum\limits_{i = 0}^{N - 1} {x(i) \cdot x(i + m)}$$

(1)

Normalization is performed to calculate the multiple correlation coefficient between variables x and y;

$$R_{xy} = \frac{{\sum\limits_{i = 1}^{2N - 1} {R_{x} (i) \cdot R_{y} (i)} }}{{\sqrt {\sum\limits_{i = 1}^{2N - 1} {R_{x}^{2} (i) \cdot \sum\limits_{i = 1}^{2N - 1} {R_{y}^{2} (i)} } } }}$$

(2)

The weighted multi-scale permutation entropy is constructed as the fitness function for VMD parameter optimization:

$$MPE_{r} = H_{p}^{s} \cdot R_{xy}$$

(3)

where MPE_r represents the weighted multiscale permutation entropy value; N denotes the signal length; R_xy indicates the complex correlation coefficient, ranging from 0 to 1, with values closer to 1 indicating stronger correlation. In the EEFO optimization process, a smaller MPE_r value indicates a richer set of characteristic information within the blast vibration signal, suggesting a more effective signal decomposition.

Electric eel foraging optimization

EEFO is a novel meta-heuristic algorithm inspired by the social foraging behaviors of electric eel populations, specifically their interactions, rest, migration, and hunting strategies⁴¹. When tackling optimization problems, EEFO simulates these four social behaviors to facilitate global exploration and local exploitation. The algorithm adaptively transitions between global and local search strategies based on the dynamic changes in the energy factor E(t).

Interaction

Electric eels can interact with randomly selected individuals within their group by leveraging regional information within the search space. This interactive behavior enables eels to explore any position within the search space, promoting global exploration. The mathematical model for this behavior is as follows:

When fit(x_j(t)) < fit(x_i(t)):

$$\left\{ \begin{gathered} v_{i} (t + 1) = x_{j} (t) + C \times (\overline{x} (t) - x_{i} (t))p1 > 0.5 \hfill \\ v_{i} (t + 1) = x_{j} (t) + C \times (x_{r} (t) - x_{i} (t))p1 \le 0.5 \hfill \\ \end{gathered} \right.$$

(4)

When fit(x_j(t)) ≥ fit(x_i(t)):

$$\left\{ \begin{gathered} v_{i} (t + 1) = x_{i} (t) + C \times (\overline{x} (t) - x_{j} (t))p_{2} > 0.5 \hfill \\ v_{i} (t + 1) = x_{i} (t) + C \times (x_{r} (t) - x_{j} (t))p_{2} \le 0.5 \hfill \\ \end{gathered} \right.$$

(5)

where fit(x(t)) represents the fitness of the candidate position of the i-th and j-th electric eel. To randomly select the location of the i-th electric eel from the current population, j-th is chosen randomly from the range [1, n], where n represents population size; r₁ is a random number between 0 and 1.

Resting

To improve search efficiency, electric eels establish resting areas before engaging in resting behavior. Once the resting area is determined, the eel moves to this area and updates its position based on its resting position within the designated area:

$$v_{i} (t + 1) = R_{i} (t + 1) + n_{1} \times (R_{i} (t + 1)round(rand) \times x_{i} (t))$$

(6)

where n₁ is a natural number between 0 and 1.

Hunting

Upon locating prey, electric eels do not directly swarm towards it but instead adopt an encirclement strategy. During the hunting process, each eel can generate a new position within the hunting area:

$$H_{prey} (t + 1) = x_{prey} (t) + \beta \times \left| {\overline{x} (t) - x_{prey} (t)} \right|$$

(7)

$$\beta = 2(e - e^{\frac{t}{T}} ) \times \sin (2\pi r_{2} )$$

(8)

where β denotes the scale of the hunting area. As hunting progresses, β decreases, gradually shrinking the hunting area; r₂ is a random number between 0 and 1. The eel is centered around the prey x_pery and hunts within a hunting area defined by $\beta_{0} \left| {\overline{x} (t) - x_{prey} (t)} \right|$.

Migration

Upon locating prey, electric eels migrate from their resting area towards the hunting area. The following mathematical equations describe this migratory behavior:

$$v_{i} (t + 1) = - r_{3} \times R_{i} (t + 1) + r_{4} \times H_{r} (t + 1) - L \times (H_{r} (t + 1) - x_{i} (t))$$

(9)

$$H_{r} (t + 1) = x_{prey} (t) + \beta \times \left| {\overline{x} (t) - x_{prey} (t)} \right|$$

(10)

where Hr represents any position within the hunting area; r₃ and r₄ are random numbers between 0 and 1; $(H_{r} (t + 1) - x_{i} (t))$ indicates the electric eel’s movement towards the hunting area; L denotes the Levy flight function, which helps prevent the optimization process from becoming trapped in local optima.

Transition from exploration to exploitation

In EEFO, the search behavior is governed by the energy factor E(t), which facilitates the transition from global exploration to local exploitation. The energy factor is defined as:

$$E(t) = 4\sin (1 - \frac{t}{T}) \times \ln \frac{1}{{r_{5} }}$$

(11)

As the iterative process progresses, the energy factor E(t) gradually decreases. When E(t) > 1, the eel engages in global exploration across the entire variable space through interactive behavior. When E(t) ≤ 1, the eel performs a local search within sub-regions that potentially contain the optimal solution or are more conducive to optimization. This local search is facilitated through resting, migration, and predation behaviors. Throughout the optimization process, interactive behavior occurs with the same probability as the other three behaviors, ensuring a balanced exploration of both global and local search spaces.

Screening criteria

Noise component screening

The rescaled range analysis (R/S analysis) method is a classical approach for evaluating the degree of continuous correlation and autocorrelation within time series. Hurst index is mostly used as an index to judge the continuous correlation of time series data because of its good fractal effect⁴².

Accurate evaluation of each order component following decomposition is crucial for improving noise removal effectiveness. While most decomposition methods currently rely solely on correlation coefficients for evaluation, this approach overlooks the inherent characteristics of real signal components. It is well-established that noise components exhibit high frequency, low energy, and strong randomness, often displaying anti-persistent correlation. To more effectively differentiate between order components, this study employs a combined approach using the Hurst index and the instantaneous energy ratio for comprehensive noise component screening. The Hurst index serves as a measure of continuous correlation within a component, while the instantaneous energy ratio assesses its complexity. This combined approach minimizes subjective judgment during component screening.

Trend component screening

The trend term: a linear or time-varying trend error present in a signal, constitutes a baseline component. Its generation is primarily attributed to integral transformations within the testing system and sub-frequency and phase-frequency characteristics of the instrument. This trend term can significantly distort time–frequency analysis and energy identification of vibration signals, ultimately impacting the accuracy of analytical results. Commonly employed methods for identifying trend terms include the mean normalization method, the first derivative method, and the noise median method^43,44,45,46. The first derivative method exhibits sensitivity to noise components and requires complex peak detection and fitting steps. The noise median method, however, lacks a unified criterion for window function selection, leading to variations in discrimination results based on the chosen window function. This inconsistency hinders subsequent analysis. Therefore, the mean normalization method is employed to extract the signal trend term.

Firstly, the mean ratio ξ is calculated by comparing the mean value of the original signal x(t) with the mean value of each modal component. Secondly, starting from l = 1, the cumulative mean ratio S is evaluated. If S is less than 0.95, then l is incremented by 1 and the evaluation is repeated until S exceeds 0.95. At this point, the summation of the modal components from columns l to h represents the extracted trend term d(t).

$$\xi = \frac{{\sum\limits_{i = 1}^{n} {PF(t_{i} )} }}{{\sum\limits_{k = 1}^{L} {x(t_{k} )} }}$$

(12)

$$S = \sum\limits_{l}^{h} {\xi_{l} }$$

(13)

where t_k represents the time corresponding to the k-th sampling point; h denotes the decomposition scale; IMF_l indicates the l-th modal component sequence obtained through VMD decomposition of x(t).

Proposed method for blasting vibration signal preprocessing

This study proposes a novel preprocessing method for blast vibration signals that leverages the EEFO algorithm to optimize the key parameters K and α of VMD decomposition. The weighted multi-scale permutation entropy value serves as the fitness function for EEFO optimization, enabling adaptive decomposition of the blast vibration signal.

$$\left\{ \begin{gathered} \alpha \in \left[ {500,9000} \right] \hfill \\ K = 3,4,...,10 \hfill \\ fitness = \mathop {\min \left\{ {MPE_{r} } \right\}}\limits_{\gamma = (k,\alpha )} \hfill \\ \end{gathered} \right.$$

(14)

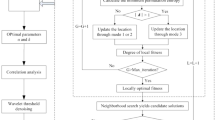
where fitness represents the fitness function, and is defined as the minimum value of MPE_r; γ = (K, α) denotes the parameter group to be optimized; K indicates an integer within the range^3,10; and α ranges from 1000 to 9000. In the EEFO algorithm, the initial electric eel population is set to P = 50, with a maximum number of iterations of N = 20. Figure 1 illustrates the flow chart of this preprocessing method. The specific implementation steps of this preprocessing method are outlined below:

Fig. 1

Flowchart of the EEFO-VMD algorithm.

• Step 1 Initialization. Input the original blasting vibration signal, define the range of VMD parameters to be optimized, and set the initial EEFO parameters, including the fitness function, population size, and maximum number of iterations.

• Step 2 Initial decomposition and fitness calculation. Perform adaptive VMD decomposition using the initial parameters K = 3 and α = 1000. Calculate the fitness for each model component and store the minimum fitness value for each iteration as fitness = min {MPE_r}.

• Step 3 Iterative termination condition. Evaluate the iterative termination condition, i.e., whether the iteration count n has reached the maximum value N. If n ≥ N, stop the iteration. Otherwise, increment n by 1 and continue the iterative process.

• Step 4 EEFO parameter optimization. Perform EEFO parameter optimization. Determine if the energy factor E(t) is greater than 1. If true, execute global search. Otherwise, transition to local search, balancing the three local search behaviors through a random number r between 0 and 1.

• Step 5 Optimal parameter acquisition. Obtain and save the optimized parameters K, α, and the minimum fitness function value.

• Step 6 VMD decomposition and noise removal. Utilize the optimized parameters to execute VMD decomposition of the blast vibration signal. Calculate the Hurst index and instantaneous energy ratio for each order u component. Employ a comprehensive judgment approach to identify and remove high-frequency noise components.

• Step 7 Signal reconstruction and analysis. Perform time–frequency and energy analysis on the remaining u components. Reconstruct the preprocessed blast vibration signal.

Simulation signal analysis

To validate the effectiveness of the proposed EEFO-VMD method, a simulated signal comprising a steady-state sinusoidal signal, an amplitude-modulated frequency-modulated signal, and a segmented harmonic signal is decomposed. A low-frequency trend term and high-frequency noise are introduced to simulate the trend and noise interference commonly observed in field-measured blasting vibration signals. The decomposition results obtained using EEFO-VMD are compared with those achieved using EWT and EMD. The EWT algorithm is improved by incorporating the parameter-free scale method proposed by Gills⁴⁷.

Noise free and trend item free signal

Simulation signal construction

Field-measured blasting vibration signals typically exhibit a frequency range within 200 Hz, with the dominant vibration frequency concentrated in the low-frequency band between 10 and 60 Hz. Therefore, the primary frequency range of the simulated signal is also constrained within 200 Hz. The simulated signal g₁(t) comprises a segmented harmonic signal x₁(t), a low-frequency steady-state sinusoidal signal x₂(t) with a frequency of 30 Hz, and an amplitude-modulated frequency-modulated signal x₃(t) with time-varying frequency and amplitude. The amplitude-modulated frequency-modulated signal is incorporated to simulate the inherent random non-stationary characteristics of blasting vibration signals. The simulated signal has a sampling frequency of 2048 Hz and a sampling time ranging from 0 to 1.5 s. The mathematical expression for the signal is provided in Eq. (15). The waveform and spectrum of the simulation signal g₁(t) are shown in (Fig. 2).

$$\left\{ \begin{gathered} x_{1} (t) = \left\{ \begin{gathered} \sin (60\pi t),\begin{array}{*{20}c} {} & {0 \le t < } \\ \end{array} 0.75 \hfill \\ 0,\begin{array}{*{20}c} {} & {} & {\begin{array}{*{20}c} {} & {0.75 \le t \le 1.5} \\ \end{array} } \\ \end{array} \hfill \\ \end{gathered} \right. \hfill \\ x_{2} (t) = 4sin(60\pi t) \hfill \\ x_{3} (t) = (2sin(40\pi t)) \cdot sin(80\pi t^{2} + 20\pi t) \hfill \\ g_{1} (t) = x_{1} (t) + x_{2} (t) + x_{3} (t) \hfill \\ \end{gathered} \right.$$

(15)

Fig. 2

Simulated signal g₁(t): (a)Time domain waveform, (b) Frequency spectrum.

Simulated signal decomposition

To evaluate the effectiveness of the EEFO-VMD algorithm with optimized parameters in processing vibration signals, the simulated signal g₁(t) is decomposed and compared with the results obtained using traditional VMD, EWT, and EMD algorithms with pre-defined parameters. The calculation of WMPE requires appropriate parameter selection, specifically embedding dimension m, time delay t, and scale factor s. Typically, the value of m, ranges from 3 to 7. In this study, we chose m = 3 to balance computational complexity and modal resolution⁴⁸. The time delay parameter t was set to 1 to avoid random cross effects and maintain computational stability⁴⁸. The scale factor s, which reflects the degree of coarse-graining in the time series, is usually determined based on signal characteristics. Here, we set s = 10 to balance the resolution of multiscale analysis and computational efficiency⁴⁹.

The convergence curve for EEFO is depicted in (Fig. 3). It is observed that the weighted multi-scale permutation entropy converges within a finite number of iterations, demonstrating the algorithm’s computational speed and efficiency. The EEFO algorithm identifies optimal VMD decomposition parameters of K = 3 and α = 4124, corresponding to a minimum weighted multi-scale permutation entropy of 0.0387. In the traditional VMD implementation, K and α are typically set based on prior knowledge or default values. Here, the initial algorithm’s default values are employed, with K = 4 and α = 3000. It is important to note that EWT and EMD methods do not require pre-defined parameter settings.

Fig. 3

Convergence curve of the EEFO algorithm for VMD parameter optimization.

Different methods performance evaluation

To quantitatively assess the anti-aliasing performance of different decomposition methods, the anti-aliasing standard value η, as proposed in reference Lian et al.⁵⁰ is introduced as shown in Eq. (16), A η value of 1 indicates that no mode mixing occurred during decomposition. Conversely, a η value less than 1 suggests the presence of modal aliasing within the decomposition results. The anti-aliasing standard values for each decomposition method are presented in (Table 1).

$$\eta = \frac{{\min (N_{0} ,N_{1} )}}{{\max (N_{0} ,N_{1} )}} \cdot \frac{{\min (N_{0} ,N_{2} )}}{{\max (N_{0} ,N_{2} )}}$$

(16)

where N₀ represents the actual number of modes in the original signal (excluding pure noise components), N₁ denotes the number of modes obtained by a particular signal decomposition method (excluding pure noise components and meaningless spurious components), and N₂ indicates the number of modes containing each dominant frequency.

Table 1 Anti-aliasing performance comparison of EEFO-VMD, VMD, EMD, and EWT based on the η index.

The anti-aliasing indices (η) for the various decomposition methods are 1.00, 0.56, 0.48, and 0.28, respectively. With the exception of EEFO-VMD, all other methods exhibit varying degrees of modal aliasing in their decomposition results. EMD, while capable of adaptive decomposition based on signal characteristics, struggles to differentiate sub-signals with similar waveform structures. In this case, EMD decomposes the simulated signal into six modal components, as illustrated in (Fig. 4d).

Fig. 4

Simulation signal decomposition results: (a) Decomposition of simulated signal g₁(t) using EEFO-VMD (K = 3, α = 4124); (b) Decomposition of simulated signal g₁(t) using conventional fixed-parameter VMD (K = 4, α = 3000); (c) EWT decomposition result; (d) EMD decomposition result.

Notably, Fig. 4d reveals that sub-signals with distinct structures are not effectively separated, and the segmented harmonic signals are distributed across different modal components, leading to noticeable decomposition errors. The frequency band separation of each modal component is inadequate, and significant modal aliasing is evident. These observations align with the calculated anti-aliasing index (η) presented in (Table 1). Moreover, numerous spurious components with unclear significance, such as u₂ to u₅, are generated during the EMD decomposition process. These components significantly deviate from those observed in the g₁(t) waveform diagram of the simulated signal, highlighting the method’s limited effectiveness.

The EWT decomposition results in Fig. 4c reveal the extraction of five modal components. While the modal components of each order exhibit relative clarity, modal aliasing is present in u₃ and u₄, which contain components of the segmented harmonic signal x₁(t). The anti-aliasing index is less than 1, indicating the presence of decomposition errors. However, the reduction of u₂ and the low-frequency steady-state sinusoidal signal x₂(t) is more significant, suggesting that EWT performs best in separating steady-state signals. The VMD decomposition in (Fig. 4b) yields four effective modal components. However, modal aliasing is evident in the mid- and low-frequency bands of u₁ and u₂. Furthermore, u₃ contains both the segmented harmonic and amplitude-modulated frequency-modulated signals, indicating that these components were not successfully separated, leading to an unsatisfactory decomposition outcome. In contrast, Fig. 4a demonstrates that EEFO-VMD and VMD achieve similar decomposition results. The modal components obtained via EEFO-VMD decomposition are clearly organized from high frequency to low frequency, effectively extracting the three signal components. Several components within g₁(t) are successfully separated, closely mirroring the original signal, with a η value of 1, indicating the absence of modal aliasing.

In summary, the proposed EEFO-VMD method adaptively determines the number of decomposition layers and penalty factors based on the characteristics of the signal itself, effectively mitigating the limitations associated with blind parameter selection. The differences observed between EEFO-VMD and conventional VMD decomposition results emphasize the importance of appropriate parameter combinations in achieving successful decomposition. Therefore, compared to the original VMD algorithm, EEFO-VMD exhibits the ability to adaptively determine decomposition parameters and effectively separate multi-component signal components.

Denoising ability analysis

Construction of simulation signal with noise

To demonstrate the robustness of EEFO-VMD against noise, a Gaussian white noise signal x₄(t), with a power of 0.8 is added to the original simulated signal, g₁(t), to generate a noisy signal, g₂(t), as shown in Eq. (17).

$$g_{2} (t) = x_{1} (t) + x_{2} (t) + x_{3} (t) + x_{4} (t)$$

(17)

Figure 5a illustrates the clear vibration signal spectrum without noise and trend interference, exhibiting relatively flat and smooth peaks. The simulated signal spectrum in (Fig. 5b) exhibits significant disturbances after noise addition. Numerous noise spikes and sharp points emerge in the low-frequency region of the time-domain waveform, and deviations in amplitude are observed at the same frequencies compared to the original signal. This noise contamination, particularly the residual high-frequency noise and the masking of low-frequency components, significantly impacts the recognition of waveform features in the original vibration signal. Consequently, practical analysis often necessitates preprocessing to mitigate these effects, increasing both the difficulty and complexity of the analysis.

Fig. 5

Frequency spectra of simulated signals: (a) g₁(t) (noise-free), (b) g₂(t) (with noise).

Decomposition of simulated signal with noise

To further evaluate the proposed method’s capability to handle noisy signals, three methods EEFO-VMD, EWT improved with the parameter-free scale method, and the classical EMD method are employed to decompose the simulated vibration signal g₂(t) with noise interference. It is important to note that an inadequate number of decomposition modes in EEFO-VMD can lead to the intermingling of noise and information components. Conversely, an excessive number of decomposition modes can result in the over-dispersion of information components across the spectrum, leading to insufficient or excessive noise removal.

The VMD parameters are optimized using EEFO, with the iterative convergence curve depicted in (Fig. 6). After 20 iterations, the minimum weighted multi-scale permutation entropy of 0.056 is achieved in the 7th iteration. The corresponding optimal parameters are K = 6 and α = 5637. The aforementioned simulation signals are decomposed using the three methods, with the results illustrated in (Fig. 7). It is worth noting that the EMD decomposition yields a substantial number of redundant and irrelevant components, which are omitted from the figure due to space constraints.

Fig. 6

Convergence curve of the EEFO algorithm for VMD parameter optimization during noise signal decomposition.

Fig. 7

Noise vibration signal decomposition: (a) EEFO-VMD decomposition results; (b) EWT decomposition results.

Signal noise removal

To effectively identify and screen noise components, the Hurst exponent (H) and instantaneous energy ratio are employed as comprehensive evaluation metrics. The Hurst exponent, a measure of long-term memory in time series, quantifies the persistence of trends. Blasting vibration signals, being non-stationary time series, can be analyzed using the Hurst exponent after decomposition. The Hurst exponent typically falls within the range of [0, 1]. A value of H = 0.5 indicates an equal likelihood of positive and negative increments, similar to a random walk. Values of 0 < H < 0.5 suggest anti-persistent behavior, where future trends tend to reverse past trend. Conversely, values of 0.5 < H < 1.0 indicate persistent behavior, where future trends tend to follow past trend. The closer H is to 0.5, the stronger the continuous positive correlation is. Instantaneous energy provides insights into local information within non-stationary time series, offering high resolution and the capability to identify energy mutations. Therefore, instantaneous energy serves as an indicator of the information content within a signal. Higher instantaneous energy signifies richer characteristic information within the component. Given that noise components are characterized by high frequency, low energy, and strong randomness, a combination of the Hurst exponent and the instantaneous energy ratio is utilized for comprehensive component assessment. An embedding dimension m of 6 and a scaling factor σ of 1 are used for Hurst exponent calculation. The component evaluation parameters derived from decomposing the simulated signal using the different methods are presented in (Tables 2 and Table 3).

Table 2 Hurst exponent values for decomposed components using EWT, EMD, and EEFO-VMD.

Table 3 Energy distribution of decomposed components (u-components) for EWT, EMD, and EEFO-VMD.

As per the interpretation of the Hurst exponent, a higher H value for a decomposed component indicates a stronger correlation with the original simulated signal and a closer resemblance in the time domain. In Tables 2 and Table 3, the H values for u₁ and u₂ generated by EEFO-VMD are less than 0.5, signifying a distinct anti-persistent correlation. Moreover, their energy ratios are below 1%, aligning with the characteristics of high frequency, low energy, and strong randomness associated with noise components. Therefore, these components are identified as noise. Following EMD decomposition, the H values for u₆, u₇, and u₈ are greater than 0.5 but close to 1, indicating weak positive persistent correlation and low energy ratios. These components are deemed insignificant artifacts generated during the EMD decomposition process. Similar to EEFO-VMD, EMD also identifies the u₁ and u₂ as noise components. For the EWT decomposition, u₃ exhibits an H value slightly less than 0.5, suggesting weak anti-persistent correlation. However, it possesses an energy ratio exceeding 1% and a correlation coefficient greater than 0.2. Therefore, u₃ is classified as a mixed component, containing both noise and real information. u₁ and u₂ are identified as noise components.

The identified noise components are subsequently removed, and the remaining components are selected for signal reconstruction. Specifically, for EEFO-VMD, components u₃, u₄, and u₅ are utilized; for EMD, components u₃, u₄, and u₅ are used; and for EWT, components u₃, u₄, u₅, and u₆ are employed. The mixed component u₃ is included in the EWT reconstruction to avoid the potential loss of real information. Figure 8 presents the denoised time-domain waveforms reconstructed using EMD, EWT, and EEFO-VMD.

Fig. 8

Time domain waveforms of denoised simulated signals using EMD, EWT, and EEFO-VMD.

While all three methods demonstrate a certain degree of denoising effectiveness in removing high-frequency noise, the EEFO-VMD method exhibits smoother peak points and a more intact overall signal shape, as evident in the enlarged portion of Fig. 8, indicating superior denoising performance in the time domain. However, frequency analysis is also crucial as noise interference can significantly impact signal frequency. Figure 9 presents the spectral comparison of denoised signals obtained using EWT, EMD, and EEFO-VMD.

Fig. 9

Frequency spectrum comparison of denoised simulated signals using EMD, EWT, and EEFO-VMD.

Given that the energy of blasting vibration signal is primarily concentrated in the low-frequency band, while noise predominantly occupies the high-frequency band, Fig. 9 demonstrates that EEFO-VMD achieves superior preservation of vibration characteristic information in the low-frequency range of 0–30 Hz. The peak areas around 30 and 40 Hz represent the dominant energy-containing components of the vibration signal. The amplitude of the reconstructed signal obtained using EEFO-VMD closely aligns with that of the original signal, indicating minimal loss of low-frequency peaks and effective preservation of low-frequency vibration signal energy. In the 100–200 Hz mid-to-high frequency range, where noise is primarily concentrated, the EMD method exhibits significant amplitude fluctuations, suggesting incomplete noise removal. Conversely, the EWT method’s amplitude approaches zero at 90 Hz, implying over-denoising and the inadvertent removal of relevant feature information alongside the noise. The effectiveness of EEFO-VMD in denoising while preserving signal features becomes apparent with increasing frequency, achieving a satisfactory balance between noise reduction and signal fidelity.

Denoising performance evaluation

While analyzing the time-frequency domain characteristics of the signals before and after denoising provides valuable insights, quantitative metrics are crucial for objectively evaluating the denoising performance. Therefore, to quantitatively evaluate the denoising effectiveness of the different methods, three metrics are employed: reconstruction standard deviation r, signal-to-noise ratio SNR, and peak error PE. The definitions of these three indices are as follows:

(1) SNR

$$SNR = 10\lg \left[ {\sum\limits_{n} {\left( {x_{n} } \right)^{2} /\sum\limits_{n} {\left( {x_{n} - x_{n}^{p} } \right)^{2} } } } \right]$$

(18)

(2) r

$$r = \sqrt {\frac{1}{M}\sum\limits_{n}^{M} {(x_{n} - x_{n}^{p} )^{2} } }$$

(19)

where M represents the number of sampling points; x_n denotes the n-th sampling point data of the original signal; $x_{n}^{p}$ indicates the n-th sampling point data of the reconstructed signal.

(3) PE

$$PE = \max \left| {y_{i} - \mathop {y_{i} }\limits^{ \wedge } } \right|$$

(20)

where y_i represents the actual value of the i-th sampling point, $\mathop {y_{i} }\limits^{ \wedge }$ is the expected value of the i-th sampling point, and max denotes the maximum value across all sampling points.

SNR quantifies the ratio of signal power to noise power. A higher SNR indicates better preservation of original signal features and improved denoising effectiveness. The reconstruction standard deviation r reflects the average energy of the residual noise and serves as a measure of similarity between the denoised signal and the original signal. A smaller r value suggests better denoising performance. However, denoising evaluation should not solely rely on objective metrics; subjective requirements must also be considered. Peak error PE addresses this aspect by quantifying the maximum deviation between the original and denoised signals. A smaller PE value indicates higher signal fidelity and a more accurate reconstruction. Table 4 presents the calculated r, SNR, and PE values for both the original and reconstructed signals obtained using each decomposition method.

Table 4 Denoising performance evaluation indices for simulated vibration signal.

A comparison of the metrics presented in Table 4 reveals that EEFO-VMD exhibits superior noise removal performance in this experiment, while EMD demonstrates the least favorable results. Notably, EEFO-VMD outperforms the other methods across all three evaluation indices, particularly in terms of SNR and PE, where it demonstrates significant improvements over both EMD and EWT.

Although the EMD method offers the advantage of self-adaptation and avoids the need for pre-defined parameters, its reliance on local eigenvalues and extreme points for signal decomposition presents limitations. For highly nonlinear and non-stationary signals, EMD can suffer from mode aliasing and endpoint effects, making it difficult to accurately capture all trends and periodic components. Furthermore, when the noise characteristics resemble those of the signal components, EMD struggles to effectively separate noise from information, resulting in suboptimal performance in decomposing complex signals contaminated by noise. EWT, essentially a set of adaptive wavelet filters, achieves a certain degree of noise removal. However, its limitations in accurately determining frequency band boundaries can lead to aliasing between noise and information components, thereby impacting its denoising effectiveness. The choice of decomposition layer K in EEFO-VMD significantly influences the denoising outcome. Once K is determined, the variational method decomposes the signal into modes with specific bandwidths, effectively mitigating mode mixing and enabling the separation of noise from feature information signals. In summary, EEFO-VMD demonstrates superior noise removal performance to both EMD and EWT.

Detrended ability analysis

Construction of simulated signal with trend term

Three primary types of trend components are commonly observed in measured blasting vibration signals: linear, exponential, and polynomial. Due to the complex environments inherent to open-pit mines, collected blasting vibration signals often contain a mixture of these trend types. To accurately represent this real-world complexity, a trend signal, d(t), is constructed, incorporating linear, exponential, and polynomial trend components, as expressed in Eq. (21) and illustrated in (Fig. 10).

$$d(t) = 3\exp ( - 1.4t) - 0.04t^{3} + 3t^{2} + 2t - 5$$

(21)

Fig. 10

The domain representation of the simulated trend term signal.

This trend term signal, d(t), is then added to the noisy vibration signal, g₂(t), to obtain a simulated vibration signal, z(t), containing both trend term and noise components. The waveform and spectrum of z(t) are presented in (Fig. 11).

$$z(t) = g_{2} (t) + d(t)$$

(22)

Fig. 11

Simulation signal z(t) containing noise and trend, (a) Time domain waveform; (b) Frequency spectrum.

As depicted in Fig. 11, the simulated signal exhibits a peak value of 11.723 cm/s, a trough value of − 12.154 cm/s, and a peak-to-peak value is 23.877 cm/s. Additionally, the signal contains noticeable clutter and a singularity with a sharp peak at 0–5 Hz, reaching an amplitude of 2.51, significantly exceeding the dominant frequency peak of the original signal. Furthermore, a distinct baseline drift is observed, indicating a deviation of the signal baseline from the center. This baseline drift can adversely impact the analysis of blasting vibration signals. Field-measured blasting vibration signals are typically recorded over durations of 1 to 5 s, with baseline drift occurring only within specific time intervals. To eliminate any influence of randomly chosen interference time periods on the experimental results, the trend component is applied throughout the entire 1.5-s recording duration in this experiment.

Signal baseline drift correction

Following the EEFO iterations, the optimal parameters obtained are K = 6 and α = 5634, corresponding to a minimum weighted multi-scale permutation entropy of 0.057. The EEFO iterative convergence curve is presented in (Fig. 12). The simulated signal, z(t), is then decomposed using EWT, EMD, and EEFO-VMD. The mean ratio of each decomposed component to the original signal is calculated to assess their contribution to the overall signal. To ensure a comprehensive evaluation and avoid neglecting potentially relevant information, the trend term Res extracted by each method is also considered as a component. Due to space limitations, the complete decomposition results are not presented here. Table 5 presents the calculated mean ratios of each component to the original simulated signal.

Fig. 12

Convergence curve of the EEFO algorithm for VMD parameter optimization.

Table 5 Mean ratio of decomposed components (u-components) to the original signal.

The results in Table 5 show that EMD decomposition obtained eight components, while both EWT and EEFO-VMD produced five components. The mean values for u7 and u8 obtained through EMD decomposition exceed 0.95, suggesting that these components represent the extracted trend. Similarly, u5 from both EWT and EEFO-VMD represents the extracted trend component. Figure 13 illustrates the trend extraction results for the three methods.

Fig. 13

Comparison of trend component extraction using EMD, EWT, and EEFO-VMD for the simulated signal.

A comparison of the extracted trend terms from the complex signal reveals significant fluctuations at the beginning and end of the trends extracted using EMD. This is attributed to EMD’s reliance on local extreme point identification and spline interpolation during decomposition. At the signal endpoints, fewer data points are available for spline differencing, limiting EMD’s trend extraction capability, and leading to a more pronounced endpoint effect. This effect manifests as a physically meaningless amplitude and frequency variations in the EMD-decomposed signal components near the endpoints. In contrast, the EWT method demonstrates superior overall trend extraction compared to EMD, exhibiting closer agreement with the actual trend, d(t), at both the beginning and end sections. This improved performance stems from EWT’s dynamic adjustment of decomposition boundaries, effectively mitigating endpoint effects and modal aliasing. Notably, the trend term extracted by EEFO-VMD exhibits the highest degree of consistency with d(t), indicating its ability to accurately capture the overall trend and dynamic characteristics of the signal. The enlarged inset in (Fig. 13) further highlights the smoothness of the trend extracted using EEFO-VMD. Compared with EMD and EWT, EEFO-VMD better preserves the signal’s transient characteristics, exhibiting fewer fluctuations. This observation also suggests that EEFO-VMD possesses a degree of inherent noise suppression capability. However, minor deviations from d(t) are observed at the beginning and end of the extracted trend. Figure 14 presents the time-domain waveform of the signal after trend removal using EEFO-VMD.

Fig. 14

Baseline corrected blasting vibration signal (EEFO-VMD).

While significant baseline drift is evident in the original signal, the reconstructed waveform following trend extraction using EEFO-VMD effectively eliminates this artifact. This demonstrates the method’s ability to accurately identify and extract low-frequency clutter and trend components from the modal signals, ensuring that the reconstructed signal remains centered around the baseline. Furthermore, the reconstructed signal does not exhibit noticeable distortions or loss of local detail. To further compare the trend removal performance of the different methods, the spectral diagrams are examined (Fig. 15), focusing on the energy-concentrated low-frequency band where trend components have the most significant impact. Figure 15 shows that the original signal exhibits significant fluctuations in the low-frequency region due to trend interference.

Fig. 15

Frequency spectrum comparison: original and trend-corrected signals.

Following trend removal, the EEFO-VMD method effectively preserves the characteristics of the signal’s low-frequency components, closely resembling the original signal in this region. While both EMD and EWT remove the trend, they also result in a noticeable reduction in the amplitude of the low-frequency components, indicating the inadvertent removal of relevant low-frequency information (0–15 Hz) during the trend extraction process. It is crucial to note that the simulated signal used in this experiment includes noise components to assess the robustness and trend extraction capabilities of the different methods under complex interference conditions. Therefore, both the time-domain and frequency-domain representations in Figs. 14 and Fig. 15 contain residual noise that has not been addressed.

In summary, this experiment reinforces the accuracy and effectiveness of EEFO-VMD in extracting trend components under challenging interference conditions. Furthermore, the comparison with EMD and EWT highlights the advantages of EEFO-VMD in processing signals contaminated by complex interference components.

Blasting vibration signal analysis

This section aims to validate the effectiveness and feasibility of the proposed method in processing field-measured blasting vibration signals corrupted by noise and trend term components. This is achieved through the decomposition and analysis of field-measured blasting vibration signals. Furthermore, time-frequency energy analysis is employed to further demonstrate the advantages of the proposed method in processing vibration signals.

Experimental setup

The secondary monitoring experiment is conducted at the Guanbaoshan Iron Mine in Anshan City, Liaoning Province. On-site blasting vibration monitoring is performed using the TC-4850 blasting vibrometer, manufactured by Chengdu Zhongke Measurement and Control Co., Ltd., along with its accompanying velocity sensor. Data is acquired at a sampling frequency of 8000 Hz for a duration of 2 s. Four monitoring points are strategically positioned at distances of 40, 191, 230, and 264 m from the blasting area to effectively capture the blasting vibration velocity. The selection of these monitoring points considers the specific environmental conditions of the site. Figure 16 illustrates the geographical location of the mining area, the geometric configuration of the monitoring points, and the overall layout of the measurement setup.

Fig. 16

Experimental setup at Guanbaoshan Iron Mine: (a) Geographical location (Drawn by the author Zhang Zuofu based on site survey and geographical data); (b) On-site testing environment (Photograph taken by the author Zhang Zuofu at Guanbaoshan Iron Mine, Anshan, Liaoning Province, China); (c) Monitoring point layout.

Experimental results

Analysis of the data reveals that among the vertical, radial, and tangential components of blasting vibration velocity, the peak particle velocity in the vertical direction is the largest. This component is less susceptible to measurement errors and has the most significant impact on surrounding structures⁵⁰. Therefore, the vertical blasting vibration signal is selected as the focus of this study. Figure 17 presents the waveform and spectrum of the vertical vibration velocity measured at the monitoring points. As evident in Fig. 17, the interference characteristics and intensity of the vibration signals differ between the near-field and far-field measurements. The near-field blasting vibration signal exhibits greater volatility, with more pronounced high-frequency noise interference and larger frequency amplitudes. Conversely, the far-field vibration signal is comparatively cleaner, as illustrated in (Fig. 17b). The signal amplitude fluctuations are smaller, and the signal is less susceptible to high-frequency noise. Additionally, no significant baseline drift is observed, and the signal frequency content is primarily concentrated in the low-frequency band. The velocity sensor in the near field can exhibit nonlinear responses to low-frequency vibrations (below 5 Hz) due to the influence of high-frequency noise and low-frequency pulses. This is specifically evident in the spectrum depicted in (Fig. 17a), where the signal displays a singularity with a peak at 2 Hz and an amplitude close to 0.8. Consequently, the signal waveform deviates from the baseline center, making it challenging to differentiate between noise and actual vibration signals. This interference can hinder subsequent time-frequency analysis and feature extraction, necessitating preprocessing steps to mitigate noise and trend effects.

Fig. 17

Comparison of measured velocity time histories: (a) near-field; (b) far-field.

Signal denoising and baseline drift correction

To further validate the superiority of the proposed method in handling disordered and complex field-measured blasting vibration signals, a comparative analysis was conducted with EMD and EWT. The iterative convergence curve of parameter optimization for EEFO-VMD is shown in (Fig. 18). As illustrated in (Fig. 18), the minimum weighted multiscale permutation entropy (MPE_r) value is achieved at the 5th iteration. At this point, the optimal decomposition parameters are determined: the number of decomposition modes K is 9, the mode bandwidth control parameter α is 7113, and the minimum MPE_r value is 0.039. The decomposition results of the three methods are presented in (Fig. 19).

Fig. 18

Convergence curve of EEFO algorithm for VMD parameter optimization during field measurement signal decomposition.

Fig. 19

The measured blasting vibration signal decomposition results: (a) EWT, (b) EMD, (c) EEFO-VMD.

Due to interference from the complex field-testing environment, the measured blasting vibration signals contain high-frequency noise. As shown in Fig. 19, the impact of high-frequency noise on the modal components is evident. For instance, significant noise interference is observed in modes u1 through u6 in (Fig. 19a), u1and u2 in (Fig. 19b), and u1 through u3 in (Fig. 19c), leading to the phenomenon of modal aliasing, where noise is distributed across multiple components.

In Fig. 19a, EWT produces eight modal components, with effective feature information mainly contained in u6 through u9. However, EWT fails to effectively separate trend components, making it challenging to accurately eliminate trend terms using a screening criterion. In Fig. 19b, the decomposition results of EMD exhibit severe modal aliasing, with feature information dispersed across multiple components. Several irrelevant and redundant components, such as u5, u6, and u7, are present, reflecting the low decomposition efficiency of the EMD method.

Using the EEFO-VMD method to preprocess the vibration signals, the iterative convergence curve for parameter optimization is shown in (Fig. 19). As seen in Fig. 19c, the EEFO-VMD decomposition results provide modal components with clear physical significance. The method decomposes the signal into six modal components u1 through u6 and one residual term. While u1 through u3 still contain high-frequency noise, u4 distinctly captures the vibration characteristic information, demonstrating the effectiveness of the proposed approach in extracting meaningful features from noisy signals.

To quantify the anti-modal-aliasing performance of the three methods for field-measured blasting vibration signals, the anti-aliasing index η was adopted to evaluate the decomposed modal components. (The definition of anti-aliasing index is shown in Eq. (16)). When η = 1, it indicates that the decomposed modal components are free from modal aliasing, signifying good decomposition performance. Conversely, when η < 1, modal aliasing is present, with smaller values of η indicating more severe aliasing. The calculated anti-aliasing index η for the three methods is presented in (Table 5).

As shown in Table 6, the EEFO-VMD method achieves an anti-aliasing index of η = 0.75, significantly higher than EWT η = 0.44 and EMD η = 0.27. These results demonstrate the superior anti-aliasing capability of EEFO-VMD. Specifically, the modal number N₁ = 4 extracted by EEFO-VMD and the number of dominant frequencies N₂ = 3 within each mode is closer to the actual modal number N₀ = 3 of the signal. This indicates that EEFO-VMD can more effectively decompose modal components that align with the physical characteristics of the actual signal while avoiding over-decomposition (EMD with N₁ = 10) or modal omission (EWT with N₁ = 3), but with a low η. The superior performance of EEFO-VMD is attributed to the optimization strategies employed in the method, which enhance its decomposition capability for complex field signals. This advantage is particularly evident in scenarios with overlapping frequencies and significant noise interference, where EEFO-VMD excels at restoring the true modal characteristics of the signal.

Table 6 Anti-aliasing evaluation index η of EWT, EMD and EEFO-VMD.

To mitigate the influence of trend and noise on the blasting vibration signal, the signal is decomposed, and the resulting components are preprocessed. Table 7 presents the calculated mean values of each component after mean value normalization. The results in Table 7 indicate that the mean values of components u8 and u9 obtained through EEFO-VMD decomposition exceed 0.95. Consequently, u8 and u9 are identified as the trend components. Figure 20 depicts the reconstructed waveform after extracting the identified trend component.

Table 7 Mean ratio of decomposed components (u-components) to the original signal after trend removal.

Fig. 20

Baseline corrected blasting vibration signal (EEFO-VMD).

As depicted in Fig. 20, the baseline drift present in the measured blasting vibration signal is effectively eliminated, similar to the results observed in the simulated signal analysis. The corrected signal is realigned to the vicinity of the baseline center, exhibiting minimal distortion or loss of local detail. Despite the inherent complexities and potential interferences present in field-acquired blasting vibration signals, the proposed method successfully identifies and eliminates low-frequency trend components. However, the signal remains notably affected by high-frequency noise.

To accurately remove this high-frequency noise contamination, the comprehensive index described in Sect.  2.2 is employed for component evaluation. This approach leverages the characteristics of noise components, specifically their strong anti-persistent correlation, high frequency, low energy, and high degree of randomness. The Hurst exponent, in conjunction with the instantaneous energy ratio, provides a robust and objective assessment for noise component identification. Components u8 and u9, previously identified as low-frequency trend components, are excluded from this analysis. Table 8 presents the calculated comprehensive index values for the remaining components.

Table 8 Hurst index and energy distribution of decomposed components (u-components) for the blasting vibration signal.

The Hurst exponent of each u component reflects the long-term correlation within its respective time series. Given the inherent randomness and volatility of field-measured noise, coupled with its lack of significant long-term correlation, the Hurst exponent for noise components tends towards 0. As evident in Table 7, the H values for components u1 and u2 are less than 0.5 and approach 0, indicating a strong anti-persistent correlation. Furthermore, the energy proportions of u1 and u2 are below 1%, consistent with the characteristics of high frequency, low energy, and strong randomness typically associated with noise components. Consequently, u1 and u2 are classified as noise components. Although component u4 also exhibits an H value less than 0.5, it contains a more substantial portion of vibration energy, suggesting the presence of high-frequency noise contamination and partial modal aliasing within the decomposed signal. To avoid the potential loss of valuable feature information, u4 is retained for further analysis. Following the removal of the noise components u1 and u2, the remaining u components are reconstructed to generate the denoised signal, as depicted in (Fig. 21).

Fig. 21

Denoised blasting vibration signal (EEFO-VMD).

Figure 21 illustrates the enhanced clarity of the denoised signal, within the effective removal of noise-induced spikes and irregularities. The waveform exhibits smoother and flatter peaks. Additionally, the peak particle vibration velocity is reduced from 6.65 cm/s before denoising to 6.45 cm/s, highlighting the significant impact of noise on the signal’s waveform characteristics. This reduction in peak velocity further suggests that external environmental noise interference can lead to an artificial amplification of the perceived peak vibration velocity.

Time frequency energy analysis

To further assess the effectiveness of the preprocessing method, the power spectral density (PSD) curve is employed to analyze the energy distribution across frequencies within the blasting vibration signal. The PSD curve wf of the original signal, the signal after trend term removal, and the signal after both trend and noise removal are presented in (Fig. 22). A logarithmic scale is adopted for enhanced visual clarity. Figure 22a reveals that the signal power progressively diminishes with increasing frequency, with the majority of the blasting vibration energy concentrated in the low-frequency band (0–150 Hz). Similar to the spectrum observed in (Fig. 17a), the original signal exhibits a singular point with a pronounced peak in the 1–10 Hz range, exceeding the amplitude of the main vibration frequency peak. This anomaly arises from the presence of the low-frequency trend term.

Fig. 22

Power spectral density (w_f) comparison of (a) Origin signal, (b) Trend-corrected signal, (c) Denoise and trend-corrected signal.

After removing the low-frequency trend component, the singular points in the 1–10 Hz range are effectively eliminated, resulting in a single peak in the PSD curve. This observation highlights the impact of the low-frequency trend component on the energy characteristics of the blasting vibration signal. Comparing (Fig. 22a,b), it is evident that the removal of the low-frequency trend component accentuates the noise characteristics, leading to multiple random amplitude fluctuations. This noise obscures the dominant vibration frequency peak, resulting in a reduced spectral peak. In Fig. 22c, the reconstructed signal after denoising using the proposed method exhibits a clear and complete spectral profile. The random amplitude fluctuations are mitigated, the spectral peak returns to its expected level, and the signal features are preserved. This outcome closely aligns with the spectral characteristics observed in (Fig. 17a), demonstrating the effectiveness of the proposed method in removing both trend and noise components while preserving signal features.

Discussion

The decomposition results presented in the preceding sections demonstrate that EEFO-VMD and EWT generally outperform EMD, often producing similar decomposition outcomes for simulated signals. This superiority arises from their approach of processing the signal’s spectrum and adaptively decomposing it into distinct, non-overlapping sub-spectra. While EMD also exhibits adaptability, it differs from these methods by operating directly in the time domain. This time-domain approach has been shown to possess certain limitations⁵¹, as it relies on the identification of local extrema points and spline interpolation for signal decomposition. Consequently, EMD is sensitive to sampling frequency and noise, often leading to modal aliasing when dealing with complex interference signals. Despite the fact that both EEFO-VMD and EWT process signals in the frequency domain, their specific operations differ. EWT divides the signal’s spectrum into continuous intervals and constructs a wavelet filter bank for each interval. This approach allows EWT to adaptively select frequency bands and effectively mitigate modal aliasing caused by discontinuities in the time–frequency scale of the signal. However, in scenarios with significant noise interference, EWT can inadvertently process extrema in the noise spectrum, resulting in the introduction of redundant noise components that negatively affect the decomposition outcome⁵².

The analysis of both simulated and field-measured blasting vibration signals revealed the significant impact of trend components and noise on the signal’s amplitude characteristics in both the waveform and spectral domains. For example, the presence of noise components in Figs. 5 and Fig. 22 leads to a degree of amplitude amplification in the simulated and field-measured signals, respectively. This amplified amplitude represents an artifact, interfering with the accurate representation of the signal’s dynamic response. Trend components primarily affect the signal’s low-frequency band. Figures 11b and Fig. 17a demonstrate the presence of singular points with sharp peaks in the low-frequency range (0–10 Hz), which can impede the identification of the peak values associated with the main frequency. As the majority of blasting vibration signal energy is concentrated in the low-frequency band, the presence of trend components can distort the accurate assessment of vibration energy.

While the proposed EEFO-VMD algorithm represents an improvement, it inherently inherits some limitations associated with the VMD algorithm, such as endpoint effects and signal starting point discontinuities. As evident in Figs. 4 and Fig. 13, the signal exhibits noticeable deviations at the endpoint positions. The variation in blasting parameters and the complex geological conditions present in mining areas necessitate adjustments in the signal processing approach for different scenarios. Therefore, future research should focus on addressing the endpoint effects observed during signal processing. Furthermore, greater emphasis should be placed on the selection of instruments, parameter settings, and monitoring point layouts during data acquisition to mitigate baseline drift and suppress environmental noise at the source.

Conclusions

This study proposes a parameter-adaptive variational mode decomposition (VMD) algorithm based on electric eel foraging optimization (EEFO) for preprocessing and time-frequency analysis of field-measured blasting vibration signals. The efficacy and feasibility of this method are validated through the decomposition of simulated signals containing various interference components, followed by the processing and analysis of real-world blasting vibration signals. The key contributions of this work are summarized as follows:

Adaptive WMD parameter optimization

The EEFO algorithm, known for its robust global and local search capabilities, is combined with a weighted multi-scale permutation entropy fitness function to optimize VMD parameters. This fitness function leverages multi-scale permutation entropy and the correlation coefficient, effectively addressing the challenges of VMD parameter selection and enabling a parameter-adaptive VMD algorithm.

Enhanced signal decomposition and denoising

Comparative analysis of EEFO-VMD with traditional VMD, EMD, and EWT (without parameter pre-setting) demonstrates that EEFO-VMD adaptively determines decomposition parameters based on signal characteristics. Compared to EMD and EWT, EEFO-VMD exhibits superior robustness, anti-aliasing capabilities, and a more effective decomposition and denoising performance for complex signals. Furthermore, EEFO-VMD effectively extracts trend components even in the presence of significant high-frequency noise.

Field-measured signal processing

The application of EEFO-VMD to field-measured blasting vibration signals demonstrates its ability to effectively mitigate the detrimental effects of noise and trend components, including the significant baseline drift typically observed in near-field measurements. EEFO-VMD effectively removes high-frequency noise and low-frequency trend components while preserving the complete information related to blasting vibration characteristics.

Time-frequency energy analysis

The study reveals that the energy of blasting vibration signals is primarily concentrated in the low-frequency band. The presence of trend components introduces singular points with high peaks in this band, leading to misinterpretations of the main frequency peaks. Moreover, noise removal accentuates the noise component characteristics, introducing multiple random amplitude fluctuations that can obscure the dominant vibration frequency.