A multimodal model for protein function prediction

Abstract

Protein function, which is determined by sequence, structure, and other characteristics, plays a crucial role in an organism’s performance. Existing protein function prediction methods mainly rely on sequence data and often ignore structural properties that are crucial for accurate prediction. Protein structure provides richer spatial and functional insights, which can significantly improve prediction accuracy. In this work, we propose a multi-modal protein function prediction model (MMPFP) that integrates protein sequence and structure information through the use of GCN, CNN, and Transformer models. We validate the model using the PDBest dataset, demonstrating that MMPFP outperforms traditional single-modal models in the molecular function (MF), biological process (BP), and cellular component (CC) prediction tasks. Specifically, MMPFP achieved AUPR scores of 0.693, 0.355, and 0.478; $F_{max}$ scores of 0.752, 0.629, and 0.691; and $S_{min}$ scores of 0.336, 0.488, and 0.459, showing a 3–5% improvement over single-modal models. Additionally, ablation studies confirm the effectiveness of the Transformer module within the GCN branch, further validating MMPFP’s superior performance over existing methods. This multi-modal approach offers a more accurate and comprehensive framework for protein function prediction, addressing key limitations of current models.

Introduction

The importance of proteins in biological systems is self-evident, as they play crucial roles in the life processes of organisms. Accurately identifying the function of proteins not only contributes to a deeper understanding of biological processes but also promotes advancements in fields such as drug discovery, crop breeding, and biofuel development. Therefore, developing more efficient technologies and methods to improve the accuracy of protein function prediction is of paramount importance.

In recent years, protein function prediction methods have primarily relied on manual feature extraction^1,2 and machine learning or deep learning algorithms^3,4. Deep learning has become a core tool in contemporary scientific research. In 2024, Geoffrey Hinton, the “father” of deep learning, was awarded the Nobel Prize in Physics for his outstanding contributions to the field⁵. In the same year, the Nobel Prize in Chemistry was awarded to David Baker and others for their groundbreaking work in developing the AlphaFold2⁶ model, which revolutionized protein structure prediction. This model has solved a problem that has puzzled the scientific community for over 50 years, enabling the prediction of the structures of approximately 200 million proteins and has been used by over 2 million users.

Currently, the three most commonly used methods for protein function prediction are: prediction based on protein amino acid sequences, prediction based on protein three-dimensional structures, and prediction based on protein-protein interaction networks⁷. These methods have collectively advanced the field of protein function prediction. The earliest protein function prediction methods were based on homology, such as BLAST (Basic Local Alignment Search Tool)⁸. However, these methods have several limitations, such as the fact that proteins with similar sequences do not necessarily have similar functions, and vice versa. Even functionally similar proteins may have different sequences^9,10. These methods fail to fully account for the complexity of protein attributes and their actual functions when calculating similarity, leading to deficiencies in considering related variables. In contrast, machine learning and deep learning-based methods offer advantages in time complexity and higher prediction accuracy because they do not require a pairwise comparison of query sequences with each training sequence.

The amino acid sequence of a protein can be viewed as a set of word vectors, a characteristic that closely resembles tasks in natural language processing. The method proposed by Asgari et al.¹¹ has made significant contributions in this field. Due to the varying lengths of protein sequences, various methods have been developed to encode protein sequences and input them into neural networks for training. For example, Ko et al.¹². used convolutional neural networks for feature extraction, while Ranjan’s ProVecGen¹³ method improved the prediction accuracy of long protein sequences. However, despite these advances, it was shown by Ranjan et al.¹⁴. that relying on a single mechanism or input for prediction is not sufficient to achieve optimal results. The protein sequence alone may fail to capture important structural and functional nuances, which is why a more comprehensive approach is necessary. Therefore, integrating both protein sequence and structure information has the potential to improve prediction accuracy significantly. This multi-modal approach could better capture the intricate relationships between sequence and structure, leading to more robust and precise protein function predictions.

Based on the current research landscape, we propose a multi-modal model for protein function prediction (MMPFP) that takes protein amino acid sequences and structures as fundamental inputs and integrates deep learning methods and artificial neural networks.

Materials and methods

Overview of MMPFP

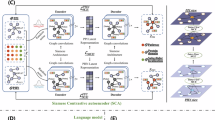
The architecture of our model is shown in Fig. 1, consisting of two modalities and three main modules: the protein sequence encoding module, the multilayer graph convolutional network protein representation module, and the protein convolution module. Each module processes inputs from both the protein sequence and protein structure modalities.

First, the input from the protein sequence modality undergoes encoding through two different embedding methods. The resulting features are then fused with the encoded features from the protein structure modality. Through the complementary information from both modalities and the deep interaction of the three modules, we construct our multi-modal protein function prediction model. After encoding each modality, the inputs are jointly trained within the multi-modal model to fully exploit the complex protein functions.

Next, we will provide a detailed explanation of the input requirements, encoding methods, and structural design for each modality and module in the model.

Fig. 1

The architecture of the MMPFP model consists of two modalities and three distinct modules: (A) represents the protein sequence modality, (B) represents the protein structure modality, and (C) represents the transformer-based feature fusion block, which includes GCN, CNN, and transformer modules.

Protein sequence modality encoding

The left portion of Fig. 1 illustrates two embedding methods for protein sequence data: amino acid embedding and positional embedding, followed by further processing through the Transformer decoder. First, each amino acid in the protein sequence is converted into a dense vector through amino acid embedding. These embedding vectors effectively capture the fundamental characteristics of amino acids, providing an initial representation of the sequence for subsequent processing.

Next, to preserve the positional information of amino acids within the sequence, we use positional encoding. Positional encoding is generated using sine and cosine functions, which assign each amino acid its relative position within the sequence. This helps the model understand the order and structure of the sequence.

The two embedded sequences are then input into the Transformer encoder (shown as the Decoder block in Fig. 1). The Transformer model, utilizing self-attention, learns the global dependencies between amino acids within the sequence and automatically captures the interactions between different positions in the sequence. The output of the encoder generates a high-dimensional representation of the protein sequence, capturing the complex features of the sequence. These representations can then be used for protein function prediction tasks, providing rich contextual information and sequence features, thereby enhancing the accuracy and robustness of predictions.

Amino acid embedding

Amino acid embedding^15,16 maps each amino acid (typically represented by an integer index) to a dense vector space using a lookup table. This dense vector contains the feature information of the amino acid:

$$\begin{aligned} e_{aai} = W_{aa}[a{a_i}] \end{aligned}$$

(1)

Let the embedding vector of the $i-th$ amino acid, and $W_{aa}[a_{a_i}]$ denote the amino acid embedding lookup table. The size of $W_{aa}[a_{a_i}]$ is $V_{aa} \times d$, where $V_{aa}$ represents the size of the amino acid dictionary and d is the dimension of the embedding vector.

Positional encoding

Positional encoding^17,18 is used to capture the positional information of amino acids within the sequence. A commonly used approach is to calculate the positional encoding using sine and cosine functions based on the position of each amino acid. The computation is given by the following formula:

$$\begin{aligned} PE(i,2k) = \sin \left( {\frac{i}{{{{10000}^{2k/d}}}}} \right) \end{aligned}$$

(2)

$$\begin{aligned} PE(i,2k + 1) = \cos \left( {\frac{i}{{{{10000}^{2k/d}}}}} \right) \end{aligned}$$

(3)

PE(i, 2k) and $PE(i,2k + 1)$represent the embedding values of position i in dimension k , where i denotes the position of the amino acid in the sequence, k refers to the dimensional index of the positional embedding, and d represents the dimensionality of the embedding vector. Subsequently, we need to add the amino acid embeddings to the positional embeddings to provide each amino acid with a representation that incorporates both its features and position, preparing the feature for input into the decoder:

$$\begin{aligned} {\mathbf{{e}}_{\mathrm{{input}}_i}} = {\mathbf{{e}}_{\mathrm{{aa}}_i}} + PE(i) \end{aligned}$$

(4)

${\mathbf{{e}}_{\mathrm{{inpu}}{\mathrm{{t}}_i}}}$ represents the final embedding representation of the $i-th$ amino acid, which contains both the feature and positional information of the amino acid, ${\mathbf{{e}}_{\mathrm{{a}}{\mathrm{{a}}_i}}}$ represents the embedding vector of the $i-th$ amino acid, and PE(i) represents the positional information of the $i-th$ amino acid. After combining all the amino acid embeddings and positional embeddings, the representation of the entire protein sequence can be passed as input to the Transformer encoder. Suppose there is a protein sequence of length L , and each amino acid has an embedding dimension of d , then the input to the Transformer can be represented as:

$$\begin{aligned} {L_1} = - \sum \limits _{c = 1}^C {{y_c}} \log ({{\hat{y}}_c}) \end{aligned}$$

(5)

Here, E is a matrix of shape $L \times d$ , representing all amino acids in the protein sequence and their corresponding positional information. Finally, we obtain the loss function as follows:

$$\begin{aligned} \mathbf{{E}} = [{\mathbf{{e}}_{\mathrm{{input}}_1}},{\mathbf{{e}}_{\mathrm{{input}}_2}}, \ldots ,{\mathbf{{e}}_{\mathrm{{input}}_L}}] \in {^{L \times d}} \end{aligned}$$

(6)

Overview of the protein structure modality

The protein structure modality consists of two submodules: the GCN module and the CNN module. The raw input to this modality is the three-dimensional structure of the protein. Given a protein structure, we construct an amino acid contact map as an auxiliary input, which represents the distances between all pairs of amino acid residues within the protein structure. The amino acid contact map and the protein’s amino acid sequence are then fed into the GCN and CNN modules, respectively.

The protein structure information is divided into two components: the first component is the amino acid sequence information, and the second component is the protein contact map. After encoding the amino acid sequence information, it is passed to the CNN module for processing, while the protein contact map, which contains richer spatial structural information, is input into the GCN module. By performing a weighted fusion of the outputs from these two components, we obtain the final protein structure modality output.

This multi-module input and fusion strategy effectively combines the spatial structural features of the protein with the relationships between amino acids, thus enhancing the model’s performance in protein function prediction tasks.

Multi-layer deep convolutional networks in the protein structure modality

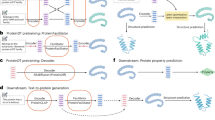
Next, we describe the input and processing steps within the CNN module of this modality. The amino acid sequence information is also encoded. The features of the sequence are composed of two parts: sequence embeddings and label embeddings. Let the set A contain 20 standard amino acids and 5 non-standard amino acids. For a protein sequence $\mathrm{{s}} \in {A^n}$ of length n, we combine a trainable sequence matrix with positional information, using this data to embed each subsequence (patch) composed of feature characters into a h-dimensional space. Additionally, two types of encoding are applied to the sequence: one-hot encoding and Esm encoding. Each amino acid is encoded as a specific number. To further enrich the feature representation, we introduce EMS-1b encoding on top of the one-hot encoding. These two encoding schemes significantly enhance the feature representation of the protein structure modality. The computation flow of the CNN is shown in Fig. 2.

Fig. 2

The workflow within the CNN module is illustrated. In this case, the RepVGG¹⁹ module is employed, which demonstrates improved performance during training while maintaining lower computational overhead during inference. Compared to traditional deep convolutional neural networks such as VGG, RepVGG addresses challenges like overfitting and long training and inference times, offering enhanced scalability.

Graph convolutional network module in protein structural modality

After describing the input and related processes of the Convolutional Neural Network (CNN), we now turn our attention to the processing of protein spatial information such as the protein contact map. Protein contact maps and other structural information carry rich spatial and positional features. In the GCN module, the input first undergoes preliminary feature extraction through a Transformer. The embedding matrix forms theref basis of the Transformer encoder component. Compared to traditional CNNs, Transformers have a distinct advantage in terms of interpretability and capturing long-range dependencies between sequences. In contrast to LSTM, Transformers are more easily parallelized, and the training process is more efficient. Moreover, Transformer-based architectures represent some of the most advanced techniques in the field of deep learning. As shown in the Fig. 3, our GCN component consists of both the Transformer module and the GCN block. Due to experimental limitations, the traditional self-attention mechanism typically uses multi-head attention. However, considering machine performance constraints, we have employed a lightweight single-head self-attention mechanism in this project, as shown in Fig. 3 below.

After passing through the encoder, the output matrix is denoted as $P \in {^{nh}}$, representing the hidden layer dimension. We treat the GO term as the label embedding for the Transformer and embed it into a c-dimensional binary vector ${\gamma _i} \in {\{ 0,1\} ^c}$ , which c represents the total number of GO terms (labels). Next, we need to encode this, similarly to how sequence embeddings are handled, by calculating the dot product between the label matrix ${W_{label}}$ and ${\gamma _i}$ as follows:

$$\begin{aligned} {Q_i} = {\gamma _i} \cdot {W_{label}} \end{aligned}$$

(7)

We then calculate the dot product between P and Q , and pass the result through a softmax layer to compute the similarity M:

$$\begin{aligned} M = \mathrm{{softmax(}}P \cdot {Q^T}\mathrm{{)}} \end{aligned}$$

(8)

After the dot product calculation between the sequence embedding and label embedding to compute the score, the label embedding will be processed by a 1D convolutional feature extraction module. Following pooling, the result is denoted as a. Subsequently, the sequence embedding branch is again subjected to a dot product operation with a to obtain:

$$\begin{aligned} e = {P^T} \cdot a \end{aligned}$$

(9)

This step forms a residual-like structure, and eventually, they will pass through a fully connected layer to output the probability values of the GO terms. Finally, we define the loss of this module using the binary cross-entropy loss function:

$$\begin{aligned} {L_2} = \left[ - {\textstyle {1 \over c}}\sum \limits _{i = 1}^c {{y_i}y_i^* + (1 - {y_i})} (1 - y_i^*)\right] {\lambda _a} \end{aligned}$$

(10)

Where $y_i^*$ represents the model’s output, ${y_i}$ denotes the label values, and ${\lambda _a}$ is a learnable hyper parameter used to adjust the contribution of each modality during the model training.The amino acid contact map and the amino acid one-hot encoding are fed into the network for feature extraction. Here, we reuse the one-hot encoding mentioned earlier. Ultimately, these are combined with the outputs from the three submodules of the GCN, and the final predicted score is obtained (Fig. 3). Taking a single input as an example, our input consists of an adjacency matrix E representing the edges in the protein structure graph, along with a degree matrix D and a weight matrix W . The output, H is computed as:

$$\begin{aligned} H = {D^{ - 0.5}}A{D^{ - 0.5}} \cdot W \end{aligned}$$

(11)

This is the output of one layer. Then, similar to ViT(Vision transformer), it is fed into the softmax layer for output calculation using Q(query matrix) , K(Key matrix) , and V(Value matrix) :

$$\begin{aligned} {\Psi _\mathrm{{i}}} = \mathrm{{softmax}}\frac{{{Q_\mathrm{{i}}}K_i^T}}{{\sqrt{D} }}{V_i} \end{aligned}$$

(12)

Several ${\Psi _\mathrm{{i}}}$ form an output layer:

$$\begin{aligned} A = [{\Psi _1},...,{\Psi _N}] \end{aligned}$$

(13)

The final output is obtained by multiplying ESM and one-hot encoding by a coefficient related to $\alpha$ .

$$\begin{aligned} {A_{final}} = \alpha \cdot {A_{esm}} + (1 - \alpha ) \cdot {A_{one - hot}} \end{aligned}$$

(14)

Finally, after passing through activation functions and basic operations like dropout, the output ${A_{final}}$ is fed into a fully connected layer to obtain the prediction score. Once the prediction score is obtained, we can define the loss function as follows:

$$\begin{aligned} {L_3} = - \left[ \sum \limits _{m = 1}^M {\sum \limits _{n = 1}^C {({y_{mn}}\log ({{{\hat{y}}}_{mn}}) + (1 - {y_{mn}})} \log (1 - {{{\hat{y}}}_{mn}})} \right] {\lambda _b} \end{aligned}$$

(15)

Here, M represents the number of sequences, C represents the number of GO terms, and ${\lambda _b}$ is also a constant coefficient.At this point, we can combine the loss functions of the two modalities and three main modules into the final loss function:

$$\begin{aligned} L = {L_1} + {L_2} + {L_3} \end{aligned}$$

(16)

Fig. 3

The workflow of the GCN module in the protein structure modality is shown in the figure, with the lower section illustrating the calculation process of single-head attention. Compared to multi-head attention, the single-head attention process is more streamlined and practical, making it especially suitable for deployment in environments with limited computational resources.

Experimental results

Model training and evaluation

The datasets used in our experiments are from the PDB database (PDBset) and the AlphaFold protein structure database (AFset). PDBset contains 36,629 protein structures, while AFset includes 42,994 protein structures with GO term annotations. Each protein structure in PDBset includes at least one functional annotation and provides high-resolution PDB chains. We divided both PDBset and AFset datasets into training and testing sets with a 7:3 ratio for model training and evaluation. Specifically, 70% of the data from each dataset was used for training the model, while the remaining 30% was set aside for testing. We ensured a strict separation between the training and testing sets, ensuring no overlap between the two and effectively preventing data leakage.The training set is then fed into the MMPFP multi-modal model, as shown in Fig. 1, for model training and evaluation. We selected these datasets because they are publicly available, easily accessible, and widely used by researchers, making them an ideal choice for benchmarking and evaluating our model.

It is important to emphasize that the testing datasets used are solely from the same division and category, and no proprietary or external datasets were introduced. Additionally, we selected a subset of 10,000 data points from the CAFA dataset for comparison with other baseline models using the MMPFP model. The purpose of this comparison was to mitigate the risk of overfitting on a single or unit dataset, thereby demonstrating the robustness of the model. The detailed comparison results can be found in Table S1 in the Appendix.

Additionally, GO term annotations, including Molecular Function (MF), Biological Process (BP), and Cellular Component (CC), were extracted from studies such as SIFTS²⁰ . Furthermore, we constructed amino acid contact maps, which served as foundational data for this research.

We used several commonly adopted metrics in the academic community to evaluate the performance of our model, including $F_{max}$, $S_{min}$, and AUPR. $F_{max}$ represents the maximum value among all computed predictions, $S_{min}$ indicates the semantic distance between the true and predicted values, and AUPR is used to assess the model’s performance across different prediction thresholds. In our task, higher values of $F_{max}$ and AUPR indicate better model performance, while a smaller value of $S_{min}$ signifies better model performance. We compared our model with several baseline models using these metrics for performance evaluation.

Our model achieved AUPR scores of 0.721, 0.401, and 0.495 for the MF, BP, and CC tasks, respectively. The $F_{max}$ scores were 0.769, 0.632, and 0.695, while the $S_{min}$ scores were 0.320, 0.480, and 0.448. These results, which can be found in Table 1, outperform the current state-of-the-art methods based on single-modal GCN and CNN approaches, demonstrating that our proposed model can more comprehensively learn protein features, including structural information. Additionally, the Transformer module in the GCN effectively captures features of the protein graph through self-attention mechanisms, showing a clear advantage over LSTM-based approaches. These results are presented in Table 2, Figs. 4, and 5. These factors together contribute to the outstanding performance of our model in protein function prediction.

Table 1 Performance of Eight Baseline Models on $F_{max}$, $S_{min}$ and AUPR Scores.

Ablation study

Our model architecture integrates two types of modality inputs and combines CNN, GCN, and Transformer modules. The performance scores of this complete architecture are shown in the table above. To validate the feasibility and effectiveness of the multi-modal model, we designed ablation experiments to evaluate the impact of different modality inputs and the three main modules on the model’s performance. First, we conducted experiments using only a single modality for protein function prediction. Then, we performed ablation studies to evaluate the effectiveness of the Transformer module within the GCN branch. Specifically, in the protein structure modality, we replaced the Transformer component within the GCN module with LSTM as part of the ablation experiment. The choice of LSTM for the ablation module stems from the fact that LSTM is a classical model in deep learning for handling sequential data, and our input can be viewed as a sequence. Consequently, we further conducted ablation experiments with these two modules.

We conducted experiments on the AFset test set, using protein structures predicted by AlphaFold2 for protein function prediction. The experimental results, as shown in Table 2, indicate that models using either the structural modality or the sequence modality alone perform worse in protein function prediction compared to the multi-modal model. This result suggests that the multi-modal protein prediction model is capable of learning a broader range of protein features and better integrating both sequence and structural information, thereby significantly improving the accuracy of function prediction.

Table 2 Performance of Models with Two Independent Modalities and Transformer Replaced by LSTM.

In the MMPFP model, when the Transformer module is used, the model performs better than the one using an LSTM-based encoder (Table 2). However, the performance of the Transformer component under different GO frequencies and sequence identities is also a key focus of our investigation. As shown in Figs. 4 and 5, applying the Transformer component to process structural sequences is not only effective but also essential and practically feasible.

Fig. 4

Comparison of the MMPFP model and the model without using the Transformer across different GO frequency ranges in the Test set. Panels A, B, and C display the distribution of different GO terms, with the subplots showing the relationship between Log(GO frequency) and frequency.

Fig. 5

Comparing the MMPFP model with the model without the Transformer module on proteins with different sequence identities in the test set.

Discussion and conclusion

The importance of protein function prediction and limitations of existing methods

Protein function prediction is crucial in bioinformatics, as it helps reveal the biological roles and functions of proteins. However, existing methods primarily rely on unimodal protein representations (such as sequences or structures)⁷, which have limitations when dealing with the complexity of protein function prediction tasks. To address these challenges, our study proposes the MMPFP model, a multi-modal approach that integrates both protein sequence and structural information. This method effectively overcomes the limitations of unimodal methods, significantly enhancing the accuracy and comprehensiveness of protein function prediction.

Existing approaches and innovations in our method

Traditional protein function prediction methods mainly use unimodal representations, such as one-hot encoding of protein sequences or convolutional neural networks (CNNs) for feature extraction. These methods fail to capture the full spectrum of protein features and thus limit prediction performance. Although advanced single-modality models, such as those employing Transformer architectures^29,30, have shown improvements, they still struggle to outperform multi-modal models. This limitation arises because even with sophisticated sequence modeling, they lack the ability to integrate additional contextual or structural data, which are essential for a more accurate prediction. In contrast, our MMPFP model builds upon previous approaches by integrating protein sequence, structure, and other multi-modal features. The inclusion of a Transformer module within the model enables efficient capture of complex relationships within protein graphs through self-attention mechanisms, providing a significant advantage over LSTM-based models. Experimental results show that MMPFP outperforms traditional unimodal models by 3%-5% in metrics such as $F_{max}$, AUPR, and $S_{min}$ across several public datasets.

Applicability, prospects, and future directions of the new method

The MMPFP model demonstrates strong performance in protein function prediction, particularly in handling complex multi-modal data. Looking ahead, we plan to introduce additional learnable features and explore the fusion of further modalities, such as incorporating protein-protein interaction networks as new modalities within the multi-modal framework, alongside advanced deep learning models. Additionally, we aim to extend the model’s functionality beyond protein function prediction to multitask learning. For example, the model could also be applied to protein structure prediction, creating a unified multitask, multi-modal model. As real-world problems often involve multiple attributes with nonlinear relationships, the development of multi-modal models represents a natural and forward-looking direction for future research. Although multi-modal protein prediction models have been explored by other researchers, the results are not always superior. For instance, experiments in the work by^28,31 suggest that certain multi-modal approaches may even underperform compared to unimodal or feature-fusion models. Therefore, while the integration of multi-modal data in protein prediction is essential, equal attention must be given to the selection and adaptation of advanced modules within these models to maximize their effectiveness.