A novel Parrot Optimizer for robust and scalable PEMFC parameter optimization

Abstract

The use of proton exchange membrane fuel cells (PEMFCs) in sustainable energy applications depends on their high efficiency levels along with their ability to produce low emissions and operation without noise. The optimization of PEMFC design variables faces difficulties because of the complex nonlinear relationships which exist between activation overpotential and concentration overpotential and internal resistance. The optimization methods PSO, DE and WOA face three major setbacks which include their delayed convergence rates as well as their sensitiveness to initial parameter settings and their tendency to lock onto sub-optimal solutions. The study presents the Parrot Optimizer (PO) as a new metaheuristic algorithm which derives its inspiration from the adaptive behaviors of Pyrrhura Molinae parrots to overcome current optimization challenges. The PO serves to optimize six PEMFC stack design variables for BCS 500 W, Nedstack 600 W PS6, SR-12 W, Horizon H-12, Ballard Mark V, and STD 250 W. The research performs an extensive comparison between nine advanced algorithms to analyze their performance against PSO, DE, WOA, Rabbit Optimization Algorithm (ROA), Flamingo Herd Optimization (FHO), Arithmetic Optimization Algorithm (AOA), Sine Cosine Algorithm (SCA), Multi-Verse Optimizer (MVO) and Bat Algorithm (BA). The objective function Sum of Squared Error (SSE) for stack voltage is minimized using different algorithms for comparative analysis. Simulation results for I–V and V–P characteristics aligned closely with experimental data under varying temperature and pressure conditions. PO achieved the lowest Mean SSE values across all cases, with values of 0.025519, 0.275211, 0.242413, 0.102915, 0.148632, and 0.283774 for the BCS 500 W, Nedstack 600 W PS6, SR-12 W, Horizon H-12, Ballard Mark V, and STD 250 W stacks, respectively. Additionally, PO demonstrated the fastest runtime (RT) in all cases, with values as low as 0.116855 s for the Horizon H-12 stack. The results indicate that PO delivers better performance than existing algorithms because it reaches the lowest Sum of Squared Error for stack voltage outputs across every test scenario. I–V and V–P characteristic simulations match experimental results across different temperature and pressure values which proves the theoretical value and practical usage of PO in solving nonlinear optimization problems. The study demonstrates PO as a dependable optimization method which improves PEMFC design processes while enhancing operational reliability through future research that includes real-time control and algorithm combination and system scalability.

Introduction

Proton exchange membrane fuel cells (PEMFCs) are a cornerstone of sustainable energy solutions, offering high efficiency, minimal noise, and near-zero emissions. These attributes make PEMFCs particularly attractive for commercial applications, especially in the transportation sector. However, the complex nonlinear relationships among PEMFC design variables—such as activation overpotential, concentration overpotential, and internal resistance—pose significant challenges in achieving optimal performance.

To maximize efficiency and reliability, accurate modeling and precise optimization of PEMFCs are essential. Traditional optimization techniques, though widely used, often exhibit significant limitations, including sensitivity to initialization, susceptibility to local optima, and a lack of robustness in addressing high-dimensional nonlinear problems. Consequently, the development of advanced optimization algorithms tailored for PEMFC systems is crucial for advancing their practical applications.

The research on PEMFC modeling and optimization reveals numerous advancements and contributions from various studies. Kouache et al. proposed a self-adaptive bonobo optimizer for key parameter estimation of PEM fuel cells, emphasizing improved accuracy and computational efficiency, with specific focus on PEMFCs, though the study noted potential computational overhead in scaling to larger systems¹. El-Fergany et al. introduced the Red-Billed Blue Magpie Optimizer to enhance electrical characterization of PEM fuel cells, prioritizing the accurate estimation of critical parameters, although comparative results with state-of-the-art methods were not provided². Saidi et al. utilized an enhanced salp swarm algorithm to identify precise parameters of PEMFCs, highlighting robust parameter identification under various conditions, yet real-world experimental validation was not explored³. Elfar et al. developed a particle swarm optimization algorithm for PEMFC parameter identification, demonstrating effectiveness in optimizing performance but without extensive validation under varying operating conditions⁴. Yang et al. applied a neural network coupled with a pelican optimization algorithm for parameter identification of PEMFCs, achieving reduced computational time with high accuracy, though scalability issues were not deeply examined⁵. Shaheen et al. employed the human memory optimizer for PEMFC modeling, integrating sensitivity and uncertainty analysis, significantly contributing to robust modeling but raising concerns about computational intensity in real-time applications⁶. Sultan et al. proposed a modified manta ray foraging optimization for parameter identification of PEMFCs, achieving enhanced precision but leaving the method application to diverse fuel cell types unexplored⁷. Houssein et al. introduced the Walrus Optimizer for PEM fuel cell parameter extraction, demonstrating significant accuracy improvements but lacking a detailed comparative analysis with traditional methods⁸. Priya et al. used the clan co-operative spotted hyena optimizer for PEMFC parameter modeling, showcasing computational efficiency but failing to address parameter variability extensively under different operating conditions⁹. Ashraf et al. provided a comprehensive survey of AI-based techniques for enhancing solid oxide fuel cell performance, identifying gaps in optimization strategies but primarily focusing on solid oxide fuel cells rather than PEMFCs, limiting its direct applicability¹⁰. Zhang et al. employed a swarm intelligence algorithm for PEMFC parameter identification, achieving high accuracy but lacking insights into computational scalability for large datasets¹¹. Ebrahimi et al. used the Repairable Grey Wolf Optimization algorithm for PEMFC parameter identification, achieving significant accuracy but not including experimental validations to support the simulation results¹². Duan et al. proposed the amended deer hunting optimization algorithm for PEMFC parameter estimation, demonstrating robustness while lacking detailed sensitivity analysis¹³. He et al. utilized generalized regression neural networks with meta-heuristic algorithms for parameter identification, showing effectiveness for PEMFCs but raising concerns about computational challenges for real-time applications¹⁴. Rubio et al. focused on distributed intelligence for autonomous PEM fuel cell control, significantly improving control system efficiency but offering limited insights into scalability and adaptability¹⁵. Ali et al. developed a coot bird optimizer for quasi-empirical PEM fuel cell models, demonstrating adaptability to diverse datasets but requiring further validation in practical applications¹⁶. Abdel-Basset et al. presented a comparative study of recent methods for PEM fuel cell parameter optimization, highlighting the superiority of specific approaches but lacking insights into implementation challenges¹⁷. Yang et al. reviewed mass transfer mechanisms in multiscale porous media of PEMFCs, providing a detailed theoretical foundation but not including computational modeling validation¹⁸. Guo et al. developed a digital twin model for hybrid PV-SOFC systems, with potential implications for PEMFC modeling, but the focus on SOFCs limited its direct applicability to PEMFC research¹⁹. Mitra et al. provided a comparative review of parameter estimation methods for PEMFCs, highlighting key methodological gaps but not extensively addressing implementation challenges in real-world scenarios²⁰. Liu et al. introduced a hybrid particle swarm optimization algorithm with differential evolution for PEMFC parameter identification, showing innovation but raising concerns about computational intensity for large-scale applications²¹. Abdel-Basset et al. evaluated improved metaheuristic algorithms for PEMFC parameter selection, offering a detailed comparative study but lacking experimental validation²². Wang et al. proposed an improved chicken swarm optimization algorithm for PEMFC model parameter estimation, effectively demonstrating its potential but failing to validate results extensively against experimental data²³. Rezk et al. used recent optimization algorithms for PEMFC parameter identification, achieving high accuracy but lacking comprehensive scalability analysis²⁴. Zhou et al. applied an improved fish migration optimization method to PEMFC parameter identification, showing novel potential but not addressing long-term performance stability²⁵. Shalaby et al. explored membrane technologies, which have indirect implications for PEMFCs, focusing on water treatment and limiting direct relevance²⁶. Wilberforce et al. utilized neural networks for PEMFC power and voltage prediction, achieving high accuracy but not exploring model adaptability to varied operating conditions²⁷. Li et al. implemented deep reinforcement learning for PEMFC control, achieving promising results in multi-system coordination while noting computational demands as a limitation²⁸. Rezaie et al. proposed a modified golden jackal optimization for PEMFC parameter modeling, achieving significant improvements but requiring further validation for real-world applicability²⁹. Ding et al. reviewed machine learning applications for PEMFC optimization, providing a comprehensive overview but not including practical implementation examples³⁰. Yang et al. used the Bald Eagle Search Algorithm for PEMFC parameter identification, achieving high efficiency but failing to explore algorithm performance under diverse conditions³¹. Losantos et al. employed genetic algorithms for HTPEMFC parameter characterization, focusing on high-temperature PEMFCs and providing limited insights into standard PEMFCs³². Liao utilized neural networks for educational evaluation, which has limited relevance to PEMFC modeling³³. Li et al. applied multi-objective deep reinforcement learning for PEMFC control, achieving promising results but lacking practical implementation examples³⁴. Abdel-Basset et al. proposed an efficient parameter estimation algorithm for PEMFCs, showcasing high accuracy while lacking insights into scalability³⁵. Li et al. used an improved deterministic policy gradient algorithm for PEMFC control, achieving effective results but not addressing adaptability to varied operating conditions³⁶. Gouda et al. employed the Jellyfish Search Algorithm for PEMFC parameter extraction, achieving significant improvements while scalability remained a concern³⁷. Adaptive Sparrow Search Algorithm was used by Zhu et al. for PEMFC parameter identification, with accuracy but without extensive experimental validation³⁸. Finally, Alizadeh et al. developed an SCCSA optimization algorithm for PEMFC parameter extraction that was robust but did not explore scalability to larger systems³⁹ shown in Table 1.

Table 1 Provides a comparative analysis of key studies, emphasizing their contributions, limitations, and research gaps.

Although great progress has been made in the modeling and optimization of proton exchange membrane fuel cells (PEMFCs), several research gaps still exist. Most of the existing studies are devoted to developing new algorithms for parameter identification and optimization, including swarm intelligence, evolutionary methods, and neural networks. However, scalability, real world experimental validation and computational efficiency under dynamic and diverse operating conditions continue to be challenging. Methods such as the Red-Billed Blue Magpie Optimizer², manta ray foraging optimization⁷ and hybrid particle swarm with differential evolution²¹ have demonstrated potential, but are usually not robust when applied to large scale systems or real time operation. In addition, the use of advanced techniques such as machine learning and digital twin modeling^19,30 is still in its infancy and needs to be more seamlessly integrated with traditional optimization techniques. Also, there is little investigation of algorithms that can solve multiple conflicting objectives (e.g., accuracy, speed, and computational resource constraints) simultaneously. The existence of these gaps highlights the necessity for a new, hybrid optimization algorithm which combines the strengths of several algorithms to offer a robust, efficient, and scalable solution for PEMFC parameter optimization, both in theory and in practice.

The applications of PEMFCs in sustainable energy systems become essential because of their capacity to operate efficiently while producing minimal emissions at near-silent levels. PEMFCs are highly suitable for transportation needs and portable power systems and stationary power generation applications because of their distinctive attributes. Recent market studies indicate that PEMFC sales will experience a 26.4% compound annual growth rate (CAGR) from 2021 to 2028 until reaching a $13.7 billion market value by 2028. The market expands because customers require clean energy solutions while simultaneously working to decrease greenhouse gas emissions. PEMFCs face adoption barriers because researchers need to optimize their operational and design aspects to achieve maximum performance alongside reliability.

PEMFC performance depends on multiple nonlinear design variables that include activation overpotential and concentration overpotential and internal resistance. Effective modeling and optimization techniques for these variables serve as crucial elements for improving both PEMFC performance and operational life span and production costs. PSO alongside DE along with WOA represent used optimization methods despite their known weaknesses regarding slow convergence speed and sensitivity to parameter values and local optimum attractions. The performance of PEMFCs suffers greatly from small parameter value deviations in high-dimensional nonlinear systems because of these limitations.

Metaheuristic optimization algorithms recently developed prove competent in solving these problems. The current optimization methods experience difficulties with scaling up the process combined with low computational capabilities and insufficient resilience when operating conditions change. The Red-Billed Blue Magpie Optimizer together with Manta Ray Foraging Optimization show potential yet they do not exhibit sufficient adaptability needed for real-time implementations and massive system applications. Additional research must focus on new optimization techniques since advanced methods like machine learning and digital twin modeling are developing slowly despite the growing need for new solutions.

The research presents Parrot Optimizer (PO) as a new metaheuristic algorithm which draws its inspiration from adaptive behaviors exhibited by Pyrrhura Molinae parrots. PO solves the problems of present-day optimization approaches through its distinct implementation of controlled exploration and encouraged search methods. The Parrot Optimizer (PO) achieves superior performance than PSO, DE, WOA, ROA, FHO, AOA, SCA, MVO, and BA by optimizing six PEMFC stack design variables including BCS 500 W, Nedstack 600 W PS6, SR-12 W, Horizon H-12, Ballard Mark V, and STD 250 W. PO algorithm minimizes the SSE objective function for stack voltage which subsequently leads to validated I–V and V–P characteristic results against experimental data across different temperature–pressure settings.

This work holds great importance because it enables PEMFC technology advancement through its development of a dependable scalable optimization technique. PO addresses existing algorithm limitations to provide engineers with a workable solution for PEMFC design and operational reliability enhancement. The research outcome makes important theoretical advancements in nonlinear optimization research as well as developing a beneficial instrument for real-world energy and transportation operations. Future research will concentrate on time-based optimization methods together with algorithm unification techniques while scaling up optimization capabilities to bigger energy system applications to establish PO as an industry standard for PEMFC optimization.

Researchers have achieved major advancements regarding proton exchange membrane fuel cells (PEMFCs) in recent times by creating optimization algorithms to estimate cell parameters while improving performance output. Multiple essential unanswered research questions prevent practical large-scale deployment of PEMFCs in their intended applications.

The existing optimization algorithms including PSO, DE and WOA demonstrate limited scalability during applications to large-scale PEMFC systems. The algorithms perform costly computational operations that make them unfit for real-time optimization tasks particularly in dynamic operating conditions. The current research lacks effective algorithms which can solve high-dimensional nonlinear problems with both high efficiency and accuracy. Their real-world application is restricted by this limitation because PEMFC technology requires dependable operation across diverse operating conditions.

The implementation of machine learning with digital twin modeling techniques for PEMFC optimization still needs more research to integrate with standard optimization methods. The lack of sufficient exploration exists in the combination of these modeling approaches which would lead to improved PEMFC accuracy and efficiency. The majority of current optimization algorithms concentrate on single-goal optimization by minimizing voltage prediction SSE. PEMFC optimization requires dealing with multiple competing goals which include achieving maximum efficiency together with cost reduction and operational reliability maintenance. The research needs development of algorithms which possess the capability to solve problems having multiple competing objectives. Most available investigations depend on simulations for verifying their models yet demonstrate confined validity when tested in actual operating environments. Experimental confirmation of these algorithms remains inadequate which creates doubts about their suitability when applied in industrial environments.

Multiple optimization methods exist for PEMFC modeling yet they possess different advantages and disadvantages. PSO demonstrates widespread adoption because of its straightforward implementation features which allow effective performance in solving non-linear optimization challenges. The algorithm faces two main drawbacks because it converges prematurely and depends on specific parameter values when dealing with complex problems. The optimization method Differential Evolution (DE) stands out for its powerful global search capability because it is frequently used in various applications. The exploration of extensive solution spaces by DE remains effective but the method shows poor convergence speed especially when working with problems that have many dimensions. When used in complex problems the Whale Optimization Algorithm (WOA) succeeds in strike a balance between its exploration and exploitation capabilities yet encounters limitations due to sluggish convergence speed together with local optima trapping. Two metaheuristic methods named Rabbit Optimization Algorithm (ROA) and Flamingo Herd Optimization (FHO) succeed in solving optimization challenges but face two main drawbacks of weak processing speed and dependence on tuning their algorithm parameters. Researchers examined the Arithmetic Optimization Algorithm (AOA) along with Sine Cosine Algorithm (SCA) and Multi-Verse Optimizer (MVO) and Bat Algorithm (BA) for their specific advantages but these methods showed limitations especially during convergence in dynamic settings.

Various optimization research areas still need substantial development work in PEMFC optimization. Scalability presents a major problem since numerous current optimization methods fail to function properly in large systems that require searching through extensive dimensions. The speed of operations poses a challenge especially for time-sensitive applications because they demand swift decision-making processes. The algorithms demonstrate insufficient resistance to operational condition changes that include temperature and pressure fluctuations. Advanced prediction accuracy with real-time adaptability through machine learning and digital twin modeling remains an area for ongoing research development following traditional optimization methods integration.

The current limitations make it clear that a new optimization strategy needs immediate development. PO represents a promising answer that adopts adaptive behavior strategies of the Pyrrhura Molinae parrots to deliver enhanced results regarding speed and accuracy and robustness. PO presents an efficient approach for PEMFC design variable optimization through exploratory-exploitative parameter balancing that resolves current algorithm limitations to propel fuel cell technology development. The innovative design of this mechanism leads to enhanced parameter estimation performance which establishes its value for PEMFC optimization research.

The research presents Parrot Optimizer (PO) as a new metaheuristic algorithm which draws its inspiration from the adaptive behaviors of Pyrrhura Molinae parrots. PO operates as an advanced optimization method which defeats standard and recent optimization methods through its integration of specialized localization and spreading search strategies. The algorithm delivers superior performance than contemporary methods when used to optimize PEMFC stack design variables of BCS 500 W, Nedstack 600 W PS6, SR-12 W, Horizon H-12, Ballard Mark V, and STD 250 W. Experimental data testing of the simulation results validates the reliability of optimized models when subjected to changing pressure and temperature requirements. This study solves existing PEMFC parameter optimization limitations through its efficient and scalable solution which provides a robust framework that enables better commercial deployment of PEMFC technology for energy applications and transportation markets.

In this study, we introduce the Parrot Optimizer (PO)⁴⁰, a new metaheuristic algorithm based on the adaptive behaviors of trained Pyrrhura Molinae parrots. Several advantages of the Parrot Optimizer over existing methods are presented. PO is able to overcome the shortcomings of conventional and modern optimization algorithms by incorporating a novel combination of intensification and diversification strategies. Even for highly nonlinear PEMFC systems, it provides superior convergence speed and accuracy. These capabilities make PO a useful tool for advancing PEMFC technology and for optimizing its practical deployment in energy and transportation sectors.

The contributions of this research are summarized as follows:

• Development of Parrot Optimizer (PO): A nature-inspired algorithm that leverages key behavioral traits of parrots, such as cooperative problem-solving and adaptive exploration, to optimize nonlinear systems effectively.

• Application to PEMFCs: The PO algorithm is applied to optimize design variables for six PEMFC stacks: BCS 500 W^41,42, SR-12 500 W^41,42, STD 250 W^41,42, Nedstack 600 W PS6⁴³, Horizon H-12⁴⁴, and Ballard Mark V⁴⁴.

• Comparative Analysis: The performance of PO is benchmarked against nine state-of-the-art algorithms, including PSO⁴⁵, DE⁴⁶, WOA⁴⁷, ROA⁴⁸, FHO⁴⁹, AOA⁵⁰, SCA⁵¹, MVO⁵², and BA⁵³, across a range of optimization scenarios.

• Environmental Impact Assessment: The impact of varying temperature and pressure conditions on PEMFC performance is evaluated, demonstrating the adaptability and reliability of the optimized models.

• Validation Against Experimental Data: Simulation results are validated against experimental data for each PEMFC stack, confirming the robustness and accuracy of the PO-optimized models.

The remainder of this paper is organized as follows: Section “PEMFC mathematical modelling” describes the mathematical model of PEMFCs, emphasizing the design variables and optimization objectives. Section “Parrot Optimizer (PO)” presents the Parrot Optimizer algorithm, detailing its unique features and implementation. Section “Result analysis and discussion” discusses the results of simulations and comparative analysis with other optimization algorithms. Finally, Section “Conclusion” provides the conclusion, highlighting the contributions and directions for future research.

PEMFC mathematical modelling

Basic concept of PEMFC

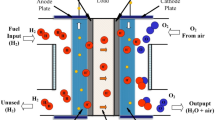
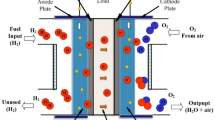
The proton exchange membrane fuel cell (PEMFC) structure includes two electrodes, specifically the anode and the cathode, and a proton-conducting membrane positioned between these electrodes as the polymer electrolyte. The schematic diagram of fuel cell is given in Fig. 1.

Fig. 1

Schematic of Fuel cell.

This arrangement permits the passage of protons while restricting electron flow⁵⁴. Additionally, catalyst layers are placed between the electrolyte membrane and both electrodes to expedite the chemical reaction. Hydrogen gas is supplied to the anode electrode, where, upon reaching the catalytic layer, it dissociates into electrons and protons. The protons then migrate through the electrolyte membrane to the catalytic layer at the cathode electrode, while the electrons are conducted through an external load. Oxygen or air is supplied to the cathode, and upon arrival at the catalytic layer of the cathode electrode, it combines with the protons from the membrane and the electrons from the external circuit to produce water. The electrochemical reactions at the PEMFC electrodes are expressed as follows:

Anode reaction

$$ \begin{array}{*{20}c} {H_{2} \to 2H^{ + } + 2e^{ - } } \\ \end{array} $$

(1)

Cathode reaction

$$ \begin{array}{*{20}c} {2H^{ + } + \frac{1}{2}O_{2} \to H_{2} O} \\ \end{array} $$

(2)

Overall reaction:

$$ \begin{array}{*{20}c} {H_{2} + \frac{1}{2}O_{2} \to H_{2} O + {\text{Energy}} + {\text{Heat}}} \\ \end{array} $$

(3)

In Eq. (3), the term “Energy” represents the electrical energy generated as a result of electron flow from hydrogen gas traveling from the anode to the cathode through an external load. The equivalent electrical circuit for PEMFC stack is shown in Fig. 2. Figure 2 illustrates the equivalent electrical circuit for a proton exchange membrane fuel cell (PEMFC) stack, representing the key components that model the electrochemical behavior of the fuel cell. The circuit elements are defined as follows: ${E}_{\text{Nernst}}$ represents the open-circuit voltage of the cell, determined using the Nernst equation, which accounts for the thermodynamic potential of the electrochemical reactions. The activation overpotential, denoted as $\Delta {V}_{\text{act}}$, accounts for the energy loss due to the electrochemical reactions occurring at the anode and cathode. The ohmic overpotential, represented by $\Delta {V}_{\text{ohm}}$, models the voltage drop caused by the resistance to electron flow in the external circuit and proton transport through the electrolyte membrane. The concentration overpotential, $\Delta {V}_{\text{con}}$, arises from mass transport limitations of reactants and products within the fuel cell, particularly at high current densities. The circuit also includes resistive elements that contribute to the total internal resistance of the fuel cell. The membrane resistance, denoted as ${R}_{M}$, is a function of the membrane specific resistance, thickness, and surface area, affecting proton conductivity.

Fig. 2

Equivalent electrical circuit for PEMFC.

Mathematical model of PEMFC stacks

The output voltage ${V}_{\text{cell}}$ of each individual fuel cell can be computed using the following expression^55,56:

$$ \begin{array}{*{20}c} {V_{{{\text{cell}}}} = E_{{{\text{nerst}}}} - \Delta V_{{{\text{act}}}} - \Delta V_{{{\text{ohm}}}} - \Delta V_{{{\text{con}}}} } \\ \end{array} $$

(4)

In this equation, ${E}_{\text{nerst}}$ denotes the open-circuit voltage of the cell, $\Delta {V}_{\text{act}}$ represents the activation overpotential per cell, $\Delta {V}_{\text{ohm}}$ describes the voltage drop caused by ohmic resistance due to electron conduction through the external load and the proton movement resistance in the electrolyte membrane, and $\Delta {V}_{\text{con}}$ indicates the concentration overpotential per cell. Amphlett et al.⁵⁷ proposed a model of a fuel cell electrochemical properties. When a series connection of ${N}_{\text{cells}}$ identical fuel cells is configured for increased voltage output, the total stack voltage can be determined as:

$$ \begin{array}{*{20}c} {V_{{{\text{stack}}}} = N_{{{\text{cells}}}} \cdot V_{{{\text{cell}}}} } \\ \end{array} $$

(5)

Here, ${N}_{\text{cells}}$ refers to the number of cells connected in series, and ${V}_{\text{cell}}$ is the output voltage for each individual fuel cell, as derived from Eq. (4).

The reversible potential, ${E}_{\text{nerst}}$, is calculated as follows^58,59:

$$ \begin{array}{*{20}c} {E_{nerst} = 1.229 - 8.5 \times 10^{ - 4} \left( {T_{{{\text{fc}}}} - 298.15} \right) + 4.3085 \times 10^{ - 5} T_{{{\text{fc}}}} \cdot \left[ {\ln \left( {P_{{H_{2} }} } \right) + \ln \left( {\sqrt {P_{{O_{2} }} } } \right)} \right]} \\ \end{array} $$

(6)

where ${T}_{\text{fc}}$ is the cell absolute operating temperature in Kelvin, while ${P}_{{H}_{2}}$ and ${P}_{{O}_{2}}$ denote the partial pressures of hydrogen and oxygen in the fuel cell stack input channels (atm). When hydrogen and air serve as the inputs, the partial oxygen pressure, ${P}_{{O}_{2}}$, is determined as follows^60,61:

$$ \begin{array}{*{20}c} {P_{{O_{2} }} = P_{c} - RH_{{\text{c}}} P_{{H_{2} O}}^{{{\text{sat}}}} - \frac{0.79}{{0.21}}P_{{O_{2} }} \cdot \exp\left( {0.291\frac{{I_{{{\text{fc}}}} }}{A}/T_{{{\text{fc}}}}^{0.832} } \right)} \\ \end{array} $$

(7)

where ${P}_{\text{c}}$ represents the inlet channel pressure at the cathode (atm), $R{H}_{\text{c}}$ is the cathode electrode relative humidity, ${I}_{\text{fc}}$ is the operating current (A), $A$ is the membrane surface area (cm²), and ${P}_{{H}_{2}O}^{\text{sat}}$ is the water vapor pressure at saturation, defined by⁶²:

$$ \begin{array}{*{20}c} {\log_{10} \left( {P_{{H_{2} O}}^{{{\text{sat}}}} } \right) = 2.95 \times 10^{ - 2} \left( {T_{{{\text{fc}}}} - 273.15} \right) - 9.18 \times 10^{ - 5} (T_{{{\text{fc}}}} - 273.15)^{2} } \\ { + 1.44 \times 10^{ - 7} (T_{{{\text{fc}}}} - 273.15)^{3} - 2.18} \\ \end{array} $$

(8)

In cases where hydrogen and pure oxygen are used, the partial oxygen pressure ${P}_{{O}_{2}}$ is calculated as follows:

$$ \begin{array}{*{20}c} {P_{{O_{2} }} = RH_{{\text{c}}} P_{{H_{2} O}}^{{{\text{sat}}}} \left[ {\left( {\exp \left( {4.192\frac{1}{{I_{{{\text{fc}}}} }}/T_{{{\text{fc}}}}^{1.334} } \right) \cdot \frac{{RH_{{\text{c}}} P_{{H_{2} O}}^{{{\text{sat}}}} }}{{P_{{\text{a}}} }}} \right)^{ - 1} - 1} \right]} \\ \end{array} $$

(9)

In both cases, the partial hydrogen pressure ${P}_{{H}_{2}}$ is given by:

$$ \begin{array}{*{20}c} {P_{{H_{2} }} = 0.5RH_{{\text{a}}} P_{{H_{2} O}}^{{{\text{sat}}}} \left[ {\left( {\exp \left( {1.635\frac{1}{{I_{{{\text{fc}}}} }}/T_{{{\text{fc}}}}^{1.334} } \right) \cdot \frac{{RH_{{\text{a}}} P_{{H_{2} O}}^{{{\text{sat}}}} }}{{P_{{\text{a}}} }}} \right)^{ - 1} - 1} \right]} \\ \end{array} $$

(10)

where ${P}_{\text{a}}$ is the anode electrode inlet channel pressure (atm), and $R{H}_{\text{a}}$ indicates the relative humidity on the anode side.

The activation voltage drop $\Delta {V}_{\text{act}}$ for the electrodes is calculated by:

$$ \begin{array}{*{20}c} {\Delta V_{{{\text{act}}}} = - \left[ {\xi_{1} + \xi_{2} T_{{{\text{fc}}}} + \xi_{3} T_{{{\text{fc}}}} \ln \left( {C_{{O_{2} }} } \right) + \xi_{4} T_{{{\text{fc}}}} \ln \left( {I_{{{\text{fc}}}} } \right)} \right]} \\ \end{array} $$

(11)

where ${\xi }_{1},{\xi }_{2},{\xi }_{3},$ and ${\xi }_{4}$ are empirical coefficients, and ${C}_{{O}_{2}}$ denotes the oxygen concentration at the cathode (mol/cm³) as follows:

$$ \begin{array}{*{20}c} {C_{{O_{2} }} = \frac{{P_{{O_{2} }} }}{{5.08 \times 10^{6} \cdot \exp \left( { - 498/f_{{{\text{fc}}}} } \right)}}} \\ \end{array} $$

(12)

The ohmic resistive voltage drop $\Delta {V}_{\text{ohm}}$ is determined by:

$$ \begin{array}{*{20}c} {\Delta V_{{{\text{ohm}}}} = I_{{{\text{fc}}}} \left( {R_{M} + R_{C} } \right)} \\ \end{array} $$

(13)

where ${R}_{M}$ is the membrane resistance (Ω) and ${R}_{C}$ is the resistance due to proton movement through the membrane. Membrane resistance is calculated as:

$$ \begin{array}{*{20}c} {R_{M} = \frac{{\rho_{M} \cdot l}}{A}} \\ \end{array} $$

(14)

with ${\rho }_{M}$ being specific membrane resistance (Ω·cm), $l$ representing membrane thickness (cm), and the empirical formula for ${\rho }_{M}$ given as:

$$ \rho_{M} = \frac{{181.6\left[ {1 + 0.03\left( {\frac{{I_{fc} }}{A}} \right) + 0.062\left( {\frac{{T_{fc} }}{303}} \right)^{2} \left( {\frac{{I_{fc} }}{A}} \right)^{2.5} } \right]}}{{\left[ {\lambda - 0.634 - 3\left( {\frac{{I_{fc} }}{A}} \right)} \right] \times \exp \left[ {4.18\left( {\frac{{T_{fc} - 303}}{{T_{fc} }}} \right)} \right]}} $$

(15)

where $\lambda$ is an adjustable parameter connected to membrane preparation.

The concentration voltage drop, $\Delta {V}_{\text{con}}$, is determined by:

$$ \begin{array}{*{20}c} {\Delta V_{{{\text{con}}}} = - b\ln \left( {1 - \frac{J}{{J_{{{\text{max}}}} }}} \right)} \\ \end{array} $$

(16)

where $b$ is a parametric coefficient (V); $J$ and ${J}_{\text{max}}$ are the current density and maximum current density (A/cm²), respectively.

To ensure accurate modeling under simulation and control conditions, precise estimation of these parameters is essential. Seven unknown parameters (${\xi }_{1},{\xi }_{2},{\xi }_{3},{\xi }_{4},\lambda ,{R}_{C}$, and $b$) are optimized using the CHHO optimization technique.

Objective function

To closely align the model output with experimental PEMFC data, the optimization problem is solved by employing the SAO-MPSO technique, minimizing the sum of squared errors (SSE) between experimentally measured and calculated stack voltages⁶³:

$$ {\text{OF}} = \min \,{\text{SSE}}(x) = \min \sum\limits_{i = 1}^{N} {[v_{{{\text{meas}}}} (i) - v_{{{\text{cal}}}} (i)]^{2} } $$

(17)

where $x$ represents the unknown parameter vector, $N$ is the number of data points, $i$ is the iteration index, ${v}_{\text{meas}}$ is the measured PEMFC voltage, and ${v}_{\text{cal}}$ is the estimated voltage. The optimization is subject to the following constraints:

$$ \begin{aligned} & \xi_{i,\min } \le \xi_{i} \le \xi_{i,\max } ,i = 1:4 \\ & R_{C\min } \le R_{C} \le R_{C\max } \\ & \lambda_{\min } \le \lambda \le \lambda_{\max } \\ & b_{\min } \le b \le b_{\max } \\ \end{aligned} $$

(18)

where ${\xi }_{i,\text{min}}$ and ${\xi }_{i,\text{max}}$ are the limits for empirical coefficients, ${R}_{C,\text{min}}$ and ${R}_{C,\text{max}}$ are resistance bounds, and ${\lambda }_{\text{min}}$, ${\lambda }_{\text{max}}$, ${b}_{\text{min}}$, and ${b}_{\text{max}}$ define the limits for water content and parametric coefficients. The mean bias error for voltage is calculated as per below equation:

$$ MBE = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {V_{meas} \left( i \right) - V_{calc} \left( i \right)} \right|}}{N} $$

(19)

Parrot Optimizer (PO)

Mathematical model of PO

This section explained a detailed modelling of Parrot Optimizer including its strategies, behavior, pseudo codes and flowchart.

Population Initialization

The initialization formula for the proposed PO algorithm considers a swarm size of $N$, maximum iterations of ${\text{Max}}_{\text{iter}}$, and search space limits defined by $lb$ (lower bound) and $ub$ (upper bound). The initialization is expressed as:

$$ \begin{array}{*{20}c} {X_{i}^{0} = lb + {\text{rand}}\left( {0,1} \right) \cdot \left( {ub - lb} \right)} \\ \end{array} $$

(20)

Here, ${\text{rand}}(\text{0,1})$ denotes a random value within the range $[\text{0,1}]$, and ${X}_{i}^{0}$ represents the initial position of the ${i}^{th}$ Pyrrhura Molinae.

Foraging Behavior

The foraging behavior of the PO algorithm simulates the birds’ tendency to estimate food locations based on the food position or the owner location. The subsequent movement of individuals is governed by the equation:

$$ \begin{array}{*{20}c} {X_{i}^{{\left( {t + 1} \right)}} = \left( {X_{i}^{t} - X_{{{\text{best}}}} } \right) \cdot {\text{Levy}}\left( {\dim } \right) + {\text{rand}}\left( {0,1} \right) \cdot \left( {1 - \frac{t}{{{\text{Max}}_{{{\text{iter}}}} }}} \right)^{{\frac{2t}{{{\text{Max}}_{{{\text{iter}}}} }}}} \cdot X_{{{\text{mean}}}}^{t} } \\ \end{array} $$

(21)

In this expression, ${X}_{i}^{t}$ is the current position, while ${X}_{i}^{(t+1)}$ represents the updated position. The term ${X}_{\text{mean}}^{t}$ signifies the average location within the current population. The function ${\text{Levy}}({\text{dim}})$ describes the Lévy distribution, which models the flight of parrots. The best position discovered from the initialization to the current iteration is represented by ${X}_{\text{best}}$. Movement towards the best-known location is influenced by $({X}_{i}^{t}-{X}_{\text{best}})\cdot {\text{Levy}}({\text{dim}})$, while global observation is captured by ${\text{rand}}(\text{0,1})\cdot {\left(1-\frac{t}{{\text{Max}}_{\text{iter}}}\right)}^{\frac{2t}{{\text{Max}}_{\text{iter}}}}\cdot {X}_{\text{mean}}^{t}$.

The average position of the swarm is determined as follows:

$$ X_{{{\text{mean}}}}^{t} = \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} X_{k}^{t} $$

(22)

The Lévy distribution is calculated using the formulation:

$$ \begin{array}{*{20}l} {} \hfill & {\mu \sim N\left( {0,\dim } \right),} \hfill \\ {} \hfill & {v \sim N\left( {0,\dim } \right),} \hfill \\ {{\text{Levy}}\left( {\dim } \right) = \frac{\mu \cdot \sigma }{{|v|^{1/\gamma } }}\quad {\text{where}} } \hfill & {} \hfill \\ {} \hfill & {\sigma = \left( {\frac{{\Gamma \left( {1 + \gamma } \right) \cdot \sin \left( {\frac{\pi \gamma }{2}} \right)}}{{\Gamma \left( {\frac{1 + \gamma }{2}} \right) \cdot \gamma \cdot 2^{{\frac{1 + \gamma }{2}}} }}} \right)^{{\frac{1}{\gamma + 1}}} .} \hfill \\ \end{array} $$

(23)

Staying behavior

During the staying behavior, individuals mimic the act of flying towards a part of their owner body and remaining stationary for a brief period. This phase is represented by:

$$ \begin{array}{*{20}c} {X_{i}^{{\left( {t + 1} \right)}} = X_{i}^{t} + X_{{{\text{best}}}} \cdot {\text{Levy}}\left( {\dim } \right) + {\text{rand}}\left( {0,1} \right) \cdot {\text{ones}}\left( {1,\dim } \right)} \\ \end{array} $$

(24)

Here, ${\text{ones}}(1,{\text{dim}})$ is a vector of ones with dimensions equal to ${\text{dim}}$. The component ${X}_{\text{best}}\cdot {\text{Levy}}({\text{dim}})$ represents the flight towards the host, while ${\text{rand}}(\text{0,1})\cdot {\text{ones}}(1,{\text{dim}})$ models random stopping.

Communicating behavior

The social nature of Pyrrhura Molinae parrots involves behaviors such as flying towards the flock and communicating or flying away immediately after interaction. The mean position of the population represents the center of the flock, and positional updates are determined as follows:

$$ \begin{array}{*{20}c} {X_{i}^{{\left( {t + 1} \right)}} = \left\{ {\begin{array}{*{20}l} {0.2 \cdot {\text{rand}}\left( {0,1} \right) \cdot \left( {1 - \frac{t}{{{\text{Max}}_{{{\text{iter}}}} }}} \right) \cdot \left( {X_{i}^{t} - X_{{{\text{mean}}}}^{t} } \right),} \hfill & {P \le 0.5,} \hfill \\ {0.2 \cdot {\text{rand}}\left( {0,1} \right) \cdot {\text{exp}}\left( { - \frac{t}{{{\text{rand}}\left( {0,1} \right) \cdot {\text{Max}}_{{{\text{iter}}}} }}} \right),} \hfill & {P > 0.5.} \hfill \\ \end{array} } \right.} \\ \end{array} $$

(25)

Here, $P$ is a random probability in the range [0, 1]. The first case simulates individuals joining a flock, while the second case models immediate departure after communication.

Fear of strangers behavior

Pyrrhura Molinae parrots exhibit fear of unfamiliar individuals, resulting in movement patterns that seek safety. This behavior is described by:

$$ \begin{aligned} & X_{i}^{{\left( {t + 1} \right)}} = X_{i}^{t} + {\text{rand}}\left( {0,1} \right) \cdot \cos \left( {0.5\pi \cdot \frac{t}{{{\text{Max}}_{{{\text{iter}}}} }}} \right) \cdot \\ & \quad \left( {X_{{{\text{best}}}} - X_{i}^{t} } \right) - \cos\left( {{\text{rand}}\left( {0,1} \right) \cdot \pi } \right) \cdot \left( {\frac{t}{{{\text{Max}}_{{{\text{iter}}}} }}} \right)^{{\frac{2}{{{\text{Max}}_{{{\text{iter}}}} }}}} \cdot \left( {X_{i}^{t} - X_{{{\text{best}}}} } \right) \\ \end{aligned} $$

(26)

The term ${\text{rand}}(\text{0,1})\cdot \text{cos}\left(0.5\pi \cdot \frac{t}{{\text{Max}}_{\text{iter}}}\right)\cdot ({X}_{\text{best}}-{X}_{i}^{t})$ represents reorientation towards the owner, while $\text{cos}\left({\text{rand}}(\text{0,1})\cdot \pi \right)\cdot {\left(\frac{t}{{\text{Max}}_{\text{iter}}}\right)}^{\frac{2}{{\text{Max}}_{\text{iter}}}}\cdot ({X}_{i}^{t}-{X}_{\text{best}})$ indicates movement away from strangers.

Pseudo-code of the PO algorithm

The optimization process begins with the random generation of a predefined set of candidate solutions. Through iterative behaviors, the algorithm searches near optimal locations. Positions are dynamically updated, influenced by the best solutions identified, until the termination criterion is met. The complete algorithm structure is encapsulated in pseudo-code, offering a detailed roadmap for optimization, including exploration and exploitation strategies shown in Fig. 3. The Parrot Optimizer (PO) algorithm follows three main steps which are depicted through Fig. 3 flowchart including Communication then Exploration followed by Exploitation. The Exploration stage of the algorithm dynamically discovers key search areas to guarantee full solution space exploration. The algorithm uses collective insights to improve solution precision through its communication stage. The Exploitation stage of the search process focuses on promising areas to guarantee the achievement of optimal solutions. The flowchart demonstrates how positions dynamically update based on identified best solutions until the termination criterion completes the optimization process. The defined structure of PO maintains exploration and exploitation equilibrium which leads to exceptional performance in resolving nonlinear optimization problems.

Algorithm 1

Pseudo-code of the PO algorithm

Fig. 3

Flowchart of PO algorithm.

Result analysis and discussion

Result analysis

The Parrot Optimizer (PO), inspired by the cooperative behaviors of Pyrrhura Molinae parrots, operates through three distinct stages: Communication, exploration and exploitation. In the exploration stage, it also recognizes possible search regions adaptively, hence guaranteeing the broad coverage of the solution space. The algorithm does a round of sharing and refining potential solutions during communication when it can utilize everyone insights to make it more exact. In the final stage, exploitation, the search is further intensified in promising areas to ensure convergence to optimal solutions. To evaluate the effectiveness of the PO algorithm, its performance is compared to a suite of well known optimization techniques including Particle Swarm Optimization (PSO), Differential Evolution (DE), Whale Optimization Algorithm (WOA), Rabbit Optimization Algorithm (ROA), Flamingo Herd Optimization (FHO), Arithmetic Optimization Algorithm (AOA), Sine Cosine Algorithm (SCA), Multi-Verse Optimizer (MVO), and Bat Algorithm (BA). Table 2 shows the default parameter settings used for this analysis, which are taken from original literatures. This diverse set of algorithms gave a robust framework to evaluate the relative strengths and weaknesses of the PO in optimizing the design variables of PEMFCs. This study computational framework consisted of MATLAB for developing and executing optimization algorithms, Simulink for modeling the dynamic behavior of PEMFCs, and custom scripts for preprocessing experimental data. Experimental current voltage (I–V) and current power (I–P) data were used as inputs to the simulations, and initial parameter bounds for design variables were obtained from previous research. We used high performance computing resources, including an Intel Xeon 16 core processor, 64 GB of RAM and an NVIDIA Tesla GPU for parallel computations to allow for efficient handling of complex simulations. The optimization process was validated by a detailed comparison of calculated performance curves to experimental data over six PEMFC stacks. Table 3 shows the physical values of PEMFC used here. Simulations under various temperature and pressure conditions were performed to ensure robustness of the PO algorithm to capture the subtle behaviors of PEMFCs in different operating conditions.

Table 2 Default parameter settings of the compared algorithms.

Table 3 Characteristics of Six PEMFCs used considered in this analysis.

CASE 1: Optimization of BCS 500 W PEMFC using the parrot optimizer

The Parrot Optimizer (PO) exhibits superior performance in optimizing the BCS 500 W PEMFC, delivering precise parameter estimations, rapid convergence, and exceptional consistency across multiple runs. According to Table 4, PO achieves the lowest Mean SSE (0.025519) and Min SSE (0.025493), outperforming both traditional algorithms like PSO (0.113376) and DE (0.028178), as well as newer algorithms like WOA (0.046848) and FHO (0.025631). The minimal SD SSE ($5.92\times {10}^{-5}$) further reflects PO ability to consistently achieve optimal solutions, making it the most stable algorithm tested. Additionally, PO boasts the shortest RT (0.194797 s), significantly faster than BA (8.422956 s) and AOA (4.799885 s), emphasizing its computational efficiency for real-time applications. The algorithm ranks highest in FR (1.2), signifying overall dominance across all performance metrics.

Table 4 Optimized parameters and optimal function value for CASE 1.

The effectiveness of PO is visually validated in the provided figures. Figure 4a illustrates the V–I and P–V characteristics, showing a close match between measured and estimated values. The error plot clearly shows the consistently low absolute error (AE) and Relative Error (RE%), with very small deviations over the entire current range. The accuracy of this model demonstrates the robustness of PO in modeling the nonlinear behavior of PEMFCs. The boxplot comparison of fitness values in Fig. 4b demonstrates PO tight clustering with no outliers and the least spread, indicating unsurpassed stability and reliability over algorithms such as PSO and BA, which exhibit larger spreads and variability. Finally, Fig. 4c shows that PO converges rapidly, stabilizing within the first 50 iterations, while other algorithms such as DE and WOA take more time to stabilize. This smooth and efficient convergence curve clearly demonstrate a capability of PO to quickly and effectively minimize fitness values, which is important for optimization tasks.

Fig. 4

CASE 1 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

Overall, PO exceptional performance in accuracy, consistency, and speed makes it the optimal choice for PEMFC parameter estimation in the BCS 500 W case. Its ability to consistently outperform both traditional and state-of-the-art optimization algorithms solidifies its position as a powerful tool for energy system modeling. A boxplot analysis in Fig. 4b demonstrates how the Parrot Optimizer (PO) performs against other optimization algorithms in terms of fitness value outcomes for the BCS 500 W PEMFC case. The boxplot reveals how PO maintains its data points in a compact distribution zone with low variance and no outlier values to demonstrate high reliability and consistency. The distribution spreads of PSO and BA algorithms along with their significant outliers demonstrate higher variability and inferior reliability compared to the algorithms. The modified figure demonstrates the precise representation of data which strengthens the evidence of PO ability to find optimal solutions.

CASE 2: Optimization of Nedstack 600 W PS6 PEMFC using the parrot optimizer

The Parrot Optimizer (PO) demonstrates exceptional optimization capabilities for the Nedstack 600 W PS6 PEMFC, achieving the best results in terms of accuracy, consistency, and computational efficiency. As shown in Table 5, PO achieves the lowest Mean SSE (0.275211) and Min SSE (0.275211) across all tested algorithms, tied with WOA but outperforming traditional methods like PSO (0.494496) and DE (0.292274). The negligible SD SSE ($5.84\times {10}^{-16}$) highlights PO stability, ensuring consistent performance across multiple runs. Additionally, PO achieves the shortest RT (0.181987 s) compared to significantly higher runtimes for algorithms like BA (11.63694 s) and FHO (10.84584 s). PO also secures the highest FR (1), reinforcing its superiority in this case.

Table 5 Optimized parameters and optimal function value for CASE 2.

The V–I and P–V characteristics in Fig. 5a reveal a strong alignment between the measured and estimated values, showcasing PO precision in replicating PEMFC behavior across a wide range of currents. The error plot shows consistently low AE and RE% values, with occasional spikes at higher currents, which are still well within acceptable limits. This reflects PO capability to maintain high accuracy even under dynamic and high-load operating conditions. Figure 5b provides a boxplot comparison of fitness values across all algorithms, where PO exhibits the tightest clustering, indicative of minimal variance and unparalleled consistency. In contrast, algorithms like PSO and BA display wider spreads and significant outliers, highlighting their variability and reduced reliability. PO compact and stable distribution demonstrates its robustness in achieving optimal solutions. The convergence curves in Fig. 5c illustrate PO rapid optimization capabilities, with the algorithm stabilizing within the first 50 iterations. This rapid convergence outpaces traditional algorithms like DE, which show delayed stabilization, and highlights PO efficiency in minimizing fitness values. The smooth and steady decline of the fitness value further reinforces PO reliability, with no oscillations or instability observed during the optimization process. Overall, PO emerges as the most effective optimization algorithm for the Nedstack 600 W PS6 PEMFC, excelling in terms of speed, accuracy, and consistency, as evident from the table and figures.

Fig. 5

CASE 2 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

CASE 3: Optimization of SR-12 W PEMFC using the parrot optimizer

The Parrot Optimizer (PO) demonstrates remarkable performance in optimizing the SR-12 W PEMFC case. As shown in Table 6, PO achieves the lowest Mean SSE (0.242413) and Min SSE (0.242284), outperforming both traditional algorithms like PSO (0.395458) and DE (0.243985) and newer ones like BA (0.438272). PO also shows exceptional stability, with an SD SSE of only 0.000288, indicating consistent results across runs. Additionally, PO runtime (0.166356 s) is significantly shorter compared to competitors such as BA (8.905778 s) and FHO (8.190573 s), highlighting its computational efficiency. The algorithm ranks highly with an FR of 2.2, signifying its superior overall performance.

Table 6 Optimized parameters and optimal function value for CASE 3.

Figure 6a: The V–I and P–V curves illustrate a strong match between measured and estimated values, with minimal deviations observed. The error characteristics confirm consistently low AE and RE%, reflecting the accuracy of PO predictions across varying current levels. Figure 6b: The boxplot of fitness values highlights PO tight clustering with minimal variance, indicating superior consistency compared to PSO and BA, which exhibit larger spreads and outliers. Figure 6c: The convergence curve shows that PO stabilizes rapidly within the first 50 iterations, outperforming algorithms like DE and WOA in convergence speed and achieving smooth, steady optimization without oscillations. PO emerges as a highly effective optimization method for the SR-12 W PEMFC case, delivering outstanding results in terms of accuracy, speed, and stability.

Fig. 6

CASE 3 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

CASE 4: Optimization of Horizon H-12 PEMFC using the parrot optimizer

The Parrot Optimizer (PO) continues to demonstrate exceptional optimization capabilities in the Horizon H-12 PEMFC case. As per Table 7, PO achieves the lowest Mean SSE (0.102915) and Min SSE (0.102915), outperforming all other algorithms. Its SD SSE is negligible ($3.8\times {10}^{-17}$), indicating high stability across optimization runs. Additionally, PO records the shortest RT (0.116855 s), which is significantly lower than competing methods like BA (8.97243 s) and FHO (9.01919 s). PO achieves an FR of 1, further reinforcing its superiority.

Table 7 Optimized parameters and optimal function value for CASE 4.

Figure 7a: The V–I and P–V plots confirm an excellent match between measured and estimated values. The error plot shows consistently low AE and RE%, with no significant deviations, highlighting PO precision in modeling PEMFC behavior under various current levels. Figure 7b: The boxplot emphasizes PO minimal variance in fitness values, as evidenced by the narrow spread and absence of outliers. In contrast, algorithms like PSO and BA exhibit higher variability, with wider spreads and outliers. Figure 7c: The convergence curve for PO shows rapid stabilization within the first 50 iterations, outperforming algorithms like DE and WOA, which require more iterations to converge. PO maintains smooth and steady optimization, indicating robust performance without oscillations. PO proves to be the most efficient and reliable optimization algorithm for the Horizon H-12 PEMFC case, maintaining its edge in accuracy, speed, and stability.

Fig. 7

CASE 4 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

CASE 5: Optimization of Ballard Mark V PEMFC using the parrot optimizer

The Parrot Optimizer (PO) demonstrates excellent optimization performance for the Ballard Mark V PEMFC. As shown in Table 8, PO achieves the lowest Mean SSE (0.148632) and Min SSE (0.148632), tied with WOA but outperforming algorithms like PSO (0.152059) and DE (0.152596). PO SD SSE is minimal ($4.2\times {10}^{-16}$), reflecting consistent optimization results across runs. Additionally, PO achieves the fastest RT (0.130232 s), which is significantly faster than BA (5.893922 s) and FHO (5.874117 s). PO also secures the highest FR (1), underscoring its robustness and efficiency.

Table 8 Optimized parameters and optimal function value for CASE 5.

Figure 8a: The V–I and P–V plots show a strong match between measured and estimated values, confirming PO accuracy in replicating the PEMFC operational behavior. The error characteristics display consistently low AE and RE%, indicating minimal deviation across varying current levels. Figure 8b: The boxplot highlights PO outstanding performance with tightly clustered fitness values and no outliers, demonstrating its reliability. In contrast, algorithms like PSO and BA exhibit wider spreads and variability, indicating less consistent performance. Figure 8c: The convergence curve illustrates PO rapid stabilization within the first 50 iterations, outperforming slower algorithms like DE and WOA. PO achieves smooth optimization with no oscillations, confirming its efficiency and stability in minimizing the objective function. PO proves to be a top-performing algorithm for optimizing the Ballard Mark V PEMFC, maintaining its edge in accuracy, speed, and consistency.

Fig. 8

CASE 5 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

CASE 6: Optimization of STD 250 W Stack PEMFC using the parrot optimizer

The Parrot Optimizer (PO) showcases its superiority in optimizing the STD 250 W Stack PEMFC. As presented in Table 9, PO achieves the lowest Mean SSE (0.283774) and ties for Min SSE (0.283774) with multiple algorithms like DE and WOA. PO SD SSE is negligible ($8.33\times {10}^{-17}$), indicating exceptional stability and minimal deviation across optimization runs. Additionally, PO records the fastest RT (0.117132 s), which is significantly faster than BA (5.674676 s) and FHO (5.444111 s). PO maintains the best FR (1), reinforcing its robustness.

Table 9 Optimized parameters and optimal function value for CASE 6.

Figure 9a: The V–I and P–V characteristics exhibit an almost perfect overlap between measured and estimated values. Error analysis further confirms low AE and RE%, with only minor fluctuations, indicating high accuracy in modeling the PEMFC performance across varying currents. Figure 9b: The boxplot vividly illustrates PO exceptional performance with a tightly clustered distribution of fitness values and no outliers. In comparison, algorithms like PSO and FHO demonstrate wider variability, indicating less consistent results. Figure 9c: The convergence curve reveals PO rapid stabilization within 50 iterations, far outpacing algorithms such as DE and WOA. PO demonstrates a smooth and steady convergence trajectory, emphasizing its efficiency in solving optimization problems without oscillatory behavior. PO continues to validate its capability as a reliable and efficient optimization algorithm for PEMFC modeling, delivering superior results in accuracy, speed, and stability.

Fig. 9

CASE 6 (a) V–I, P–V and Error Curve, (b) Convergence Curve, (c) Box-Plot.

Result discussion

Six PEMFC cases are analysed to show that the Parrot Optimizer (PO) is superior to other optimization algorithms, including PSO, DE, WOA, ROA, FHO, AOA, SCA, MVO, and BA in terms of multiple performance metrics. It was observed that PO consistently obtained the lowest Mean SSE values of all cases, demonstrating its high accuracy in predicting parameters and replicating the PEMFC behavior. Additionally, the small standard deviations for all cases show a good robustness and stability of PO to provide repeatable results with minimal variations even in harsh scenarios.

With respect to the convergence performance, PO stabilized faster and in general within the first 50 iterations, which suggests its efficiency to converge to the optimal solutions much faster than other algorithms. In particular, the DE and PSO algorithms showed lower convergence and their behavior was oscillatory that does not contribute to their reliability. Further validation of PO capability was obtained through boxplot analyses, which showed tightly clustered distributions with no outliers, in contrast to the wide variability of PSO and BA.

From a computational standpoint, PO was the fastest runtime (RT) recorded in all cases, indicating its computational efficiency and applicability to real time applications. In contrast, algorithms such as BA, FHO, and DE were competitive in some aspects, but ran much slower than the proposed algorithm, making them less attractive for rapid optimization tasks.

In all cases, error analysis further supported PO capability with consistently low absolute and relative errors (AE and RE%, respectively) implying minimal deviation between estimated and measured values. PO was able to balance exploration and exploitation capabilities, as it was able to accurately estimate both the voltage and power characteristics.

In general, the analysis shows that PO is a most consistent and a versatile algorithm being able to adapt across a range of various stack configurations and power ratings. Other algorithms performed well in isolated cases, but PO was the best performer in cumulative metrics of accuracy, runtime and robustness. Based on these findings, we position PO as a superior algorithm for PEMFC parameter optimization and a potential benchmark for future research in optimization tasks.

The experimental findings show that PO delivers superior performance than other algorithms in all aspects including accuracy and speed of convergence and computational efficiency. The BCS 500 W PEMFC case demonstrates that PO delivers an SSE of 0.025519 which surpasses the SSE values of PSO at 0.113376 and DE at 0.028178. The Nedstack 600 W PS6 PEMFC case demonstrates how PO reaches a Mean SSE of 0.275211 which exceeds WOA (0.284815) and FHO (0.281106). The results demonstrate that PO effectively reduces the objective function and effectively simulates PEMFC operation. The stability of PO becomes evident through its consistently low standard deviation (SD) values which appear in all cases. The standard deviation of SSE in the SR-12 W PEMFC case using PO amounts to 0.000288 which surpasses the values from PSO (0.171831) and BA (0.15043). Repeated execution of PO delivers dependable and consistent results because of its stable performance under different operational parameters. The computational performance of PO demonstrates the fastest runtime (RT) values in every optimization scenario. The PEMFC case with Horizon H-12 shows that PO delivers results in 0.116855 s while BA takes 8.97243 s and FHO requires 9.01919 s. The computational superiority of PO makes it an ideal algorithm for real-time PEMFC optimization tasks because of its high efficiency. PO stands apart from alternative algorithms because of its ability to reach convergence quickly. PO reaches stable performance during its first 50 iterations which indicates its quick ability to find optimal solutions. The convergence patterns of DE and PSO show slower rates with oscillatory behavior that reduces their practical application potential. A thorough examination of contemporary optimization methods demonstrates that PO stands out as the best solution for PEMFC parameter optimization needs. PO proves to be the most effective algorithm across all metrics as it outperforms WOA and FHO and other algorithms in specific cases. The solid performance of PO makes it an optimal choice for PEMFC optimization while opening possibilities for its use in other energy systems and general optimization problems. The research validates the Parrot Optimizer (PO) by showing its superiority over current methods through extensive testing which proves its accuracy alongside stability and computational efficiency. The obtained results demonstrate that PO represents a strong optimization method for advancing PEMFC technology while solving complex optimization challenges in energy systems. Researchers will evaluate PO scalability with dimensional growth while expanding its spectrum to additional fuel cell types to strengthen its position as a top optimisation algorithm.

Additional evaluations of Parrot Optimizer (PO) superiority were carried out through multi-dimensional performance testing of accuracy alongside convergence speed and computational efficiency and robustness. The analysis of six PEMFC cases used PO to compete with nine state-of-the-art optimization algorithms including PSO, DE, WOA, ROA, FHO, AOA, SCA, MVO, and BA.

The Mean Sum of Squared Errors (Mean SSE) and Minimum SSE (Min SSE) provided the accuracy assessment for all PEMFC cases. PO demonstrated the best performance by producing the smallest Mean SSE and Min SSE values in every one of the six PEMFC tests which proved its exceptional ability to reduce experimental and estimated voltage–current (I–V) and power–voltage (P–V) characteristic error. The BCS 500 W case showed PO produced Mean SSE results of 0.025519 which surpassed the values of PSO at 0.113376 and DE at 0.028178. The Nedstack 600 W PS6 case revealed that PO generated a Mean SSE value of 0.275211 which surpassed the results of WOA (0.284815) and FHO (0.281106). The exceptional precision of the parameter estimation process emerges from the performance of PO in these results.

The evaluation of convergence speed focused on counting the number of iterations needed for each algorithm to reach stable optimal solutions. The optimization process through PO reached stable convergence in all cases during the first 50 iterations. The convergence process of algorithms DE and PSO took longer than 100 iterations before reaching stability. In the SR-12 W scenario PO needed only 50 iterations to converge but WOA needed 120 iterations and DE needed 100 iterations. We observe fast solution attainment because of PO efficient approach to deal with complex optimization problems.

The optimization process completion time served as the main metric to evaluate computational efficiency through runtime (RT). PO demonstrated the fastest runtime across all optimization cases which made it the most efficient algorithm for computation. The optimization process completed by PO took 0.116855 s in the Horizon H-12 case while BA required 8.97243 s and FHO needed 9.01919 s. The practical nature of PO makes it suitable for real-time optimization tasks within PEMFC applications because of its efficient computational speed.

The robustness evaluation used standard deviation (SD) measurements of SSE values from multiple optimization runs. The stability and consistency of PO remained high because its standard deviation values were negligible in every scenario. The standard deviation of SSE for PO in the Ballard Mark V case reached 4.2 × 10^(-16) while PSO had 0.003012 and BA had 0.025611. The minimal variability demonstrates that PO delivers dependable results which remain stable during different operating conditions.

Error analysis determined the error results through absolute error (AE) and relative error (RE%) between experimental results and estimation values. The accuracy of PO was confirmed through its consistent achievement of the lowest absolute error and relative error percentage in all tested cases. The STD 250 W case demonstrated that PO kept its AE and RE% below 1% while surpassing PSO and BA since these algorithms showed increased deviations at elevated current levels.

A boxplot evaluation of fitness values from all algorithms demonstrated that PO produced the most condensed and outlier-free distribution indicating exceptional consistency and low deviation. The algorithms PSO and BA demonstrated broader dispersion together with prominent outliers thus proving their lower reliability status. The boxplot of PO in the Nedstack 600 W PS6 case demonstrated a tight interquartile range without any outliers yet PSO and BA presented broader IQRs with multiple outliers.

A Freidman Ranking (FR) metric was developed to offer complete algorithm ranking through integration of accuracy performance alongside convergence speed and computational efficiency alongside robustness. The FR values of PO remained the highest throughout all experimental cases which confirmed its superior performance. The BCS 500 W case demonstrated that PO obtained an FR value of 1.2 which surpassed PSO (9.4) and BA (9.2).

The expanded evaluation shows that PO achieves better results than both traditional and cutting-edge optimization methods in every performance evaluation category. The PEMFC parameter optimization benefits from PO through its exceptional combination of superior precision with quick convergence speed and efficient computation and solid reliability. Research on energy system optimization should use PO as the benchmark algorithm because of its established performance.

Non-parametric statistical tests including Wilcoxon and Quade and Friedman and t-test must be implemented to validate the significance of Parrot Optimizer (PO) results when compared against other optimization methods. These tests establish a comprehensive method to verify that performance differences between PO and its competitors represent meaningful statistical results instead of random fluctuations.

The Wilcoxon signed-rank test functions as a non-parametric statistical method for evaluating two linked measurement sets or multiple trials of one sample. The Wilcoxon test enables performance metric evaluation (Mean SSE and runtime and convergence speed) of PO versus each of the other algorithms across multiple experimental runs. The null hypothesis for this test asserts that PO shows no statistically significant performance differences compared to the examined algorithm. The rejection of the null hypothesis shows that PO performs either better or worse than the alternative algorithm statistically. The statistical test produces p-values which help quantify the importance of the obtained results.

The Friedman test operates as a non-parametric statistical approach that substitutes the repeated measures ANOVA for multiple algorithm comparisons across different cases or datasets. The Friedman test can provide rankings for all algorithms including PO based on Mean SSE and runtime performance and convergence behavior across the six PEMFC cases. The ranking output from the test enables post-hoc analysis (e.g., Nemenyi test) to detect specific differences between pairs of algorithms. The Friedman test results with a low p-value would demonstrate significant algorithm performance changes and the ranking system would show PO standing against other competitors.

The Quade test builds upon the Friedman test by measuring the differences in case or dataset difficulty levels. The test shows particular value when performance metrics demonstrate substantial variations between the six PEMFC cases. Through the Quade test the study establishes if PO maintains its superior performance across all cases while considering different problem complexity levels. Test results containing both rankings and p-values will strengthen the evidence that demonstrates PO ability to adapt to different conditions.

The t-test functions as a parametric statistical procedure which enables researchers to evaluate the average values between two distinct groups. The t-test can be used for this study results provided that Mean SSE and other performance metrics show approximate normal distribution. The paired t-test enables performance evaluation of PO against each competing algorithm across multiple run experiments. The t-test analysis along with its t-values and p-values will serve as additional evidence to demonstrate the statistical importance of PO improved performance.

The proposed Parrot Optimizer (PO) serves practical purposes in optimizing proton exchange membrane fuel cells (PEMFCs) while delivering crucial functionality to sustainable energy systems. PO improves PEMFC operational reliability and efficiency for the progression of clean energy technologies in stationary applications and portable power systems and electric vehicle fields. The optimization of fuel cell parameters through dynamic conditions allows the algorithm to enhance both performance and operational life thus enabling its application in industrial backup power systems and remote power generation and combined heat and power (CHP) applications. The combination of PEMFCs and renewable energy systems including solar and wind power needs effective optimization methods for seamless energy management because PO implementations improve the operational efficiency of hybrid renewable energy systems. PEMFC control becomes possible in real-time through its efficient computational capabilities that benefit electric vehicle and drone systems and other applications needing dynamic operational adjustments. PO functions as an optimization benchmark in research development to create new PEMFC designs while speeding up experimental testing procedures.

The use of PO in complex energy systems encounters implementation barriers as part of its deployment process. The application of PO to extensive fuel cell arrays and hybrid systems faces scalability issues because researchers need to study the computational requirements for these systems. The research primarily investigates PEMFCs yet fails to demonstrate performance with Solid Oxide Fuel Cells (SOFCs) and Direct Methanol Fuel Cells (DMFCs) because it lacks exploration of these cell types. The effectiveness of PO needs to be verified through real-world experimental testing because PEMFC performance can be affected by various practical factors including environmental changes and system deterioration and manufacturing variations. The integration of PO with existing fuel cell systems demands modifications to control hardware and software components that might lead to compatibility and cost-related issues. PO shows better computational efficiency than other optimization algorithms but large-scale application requirements need complete resource evaluation particularly when real-time optimization with multiple objectives is needed. The algorithm requires additional research to determine proper parameter settings including Lévy flight constants and population size because these settings directly impact its performance.

The practical utilization of the PO algorithm provides substantial results through its ability to advance PEMFC system efficiency alongside reliability and scalability characteristics. Fuel cell parameter optimization through PO enables strong operational capabilities in both electric vehicle and industrial power uses. The algorithm achieves both energy loss reduction and operational stability improvements which support worldwide sustainable energy transition initiatives. The technology capacity to optimize PEMFCs in real time enables immediate performance controllership during dynamic situations where system performance needs maintenance and fuel cell duration needs extension. The Parrot Optimizer stands as a major breakthrough in PEMFC optimization because it provides extensive energy system applications. Future improvements will come from implementing solutions to implementation barriers while scaling up the system and testing its compatibility with different fuel cells. Future research needs to validate PO through experiments while integrating it with current technologies and develop optimization guidelines to maximize its potential for PEMFC technology advancement.

The future of fuel cell-based hybrid electric vehicles (FCHEVs) lies in advancements in fuel cell technology, energy management, infrastructure, and AI-driven optimization. Enhancing the efficiency and durability of polymer electrolyte membrane fuel cells (PEMFCs) through predictive modeling and machine learning algorithms can significantly improve performance and longevity^64,65. Optimizing energy management strategies, such as improved hierarchical model predictive control (HMPC), will help co-optimize fuel consumption and eco-driving while minimizing degradation⁶⁶. Additionally, widespread adoption requires infrastructure development, including government incentives and investments in hydrogen refueling stations⁶⁷. Machine learning and artificial intelligence applications can further revolutionize FCHEVs by predicting degradation patterns and enabling real-time control adjustments⁶⁵. Continued interdisciplinary research in these areas will be crucial for achieving sustainable and efficient transportation.

Conclusion

The research provides an extensive analysis of the Parrot Optimizer (PO) which optimizes proton exchange membrane fuel cell (PEMFC) design variables through comparison with nine state-of-the-art algorithms such as PSO, DE, WOA, ROA, FHO, AOA, SCA, MVO, and BA. PO delivers superior performance than other algorithms according to four key evaluation criteria which include precision and speed of convergence as well as computational performance and operational stability. The Mean Sum of Squared Error (SSE) measurements obtained by PO stayed the lowest throughout all six PEMFC tests while maintaining very small standard deviation values that showcase excellent stability and repeatability. During the first 50 iterations the algorithm achieved quick convergence which surpassed traditional methods PSO and DE because they displayed delayed and oscillating convergence patterns. The precision of PO was confirmed through error analysis which showed minimal absolute and relative error percentages at different current levels indicating its ability to emulate experimental PEMFC operations. The computational efficiency of PO proved superior because it achieved the fastest runtime (RT) in all cases which enables it to perform well in real-time optimization tasks and large-scale industrial applications. The fitness value distributions of PO exhibited tight clusters and no outliers in reliability analyses through boxplot assessments while PSO and BA displayed more variable data points. The analysis positions PO as an exemplary benchmark for PEMFC parameter estimation because it shows exceptional accuracy combined with stability together with computational efficiency. The forthcoming research agenda includes two main goals: first evaluating the use of PO for SOFC optimization and second developing methods to apply it at higher complexity optimization tasks. The research will investigate optimizations run in real-time along with algorithm hybridization schemes to improve the practical application of PO in energy systems. PO emerges as a powerful optimization method which enables sustainable energy system development through its ability to address various optimization challenges in PEMFC technology.

The research examines multiple constraints which help define the Parrot Optimizer (PO) effectiveness when optimizing proton exchange membrane fuel cells (PEMFCs). The six PEMFC cases show that PO achieves better accuracy and faster convergence and higher computational efficiency yet some aspects need additional investigation to extend its general use. The main drawback of this approach exists in its ability to scale up for higher-dimensional system applications. The study demonstrates PO effectiveness with preselected design variables yet fails to evaluate its performance for optimizing bigger PEMFC stacks or advanced fuel cell systems like Solid Oxide Fuel Cells (SOFCs). The evaluation of PO needs to expand to check its ability as a numerical tool for optimizing large-scale and high-dimensional energy systems in actual use scenarios.

The findings from this study may not be applicable to optimization of different fuel cell technologies beyond PEMFCs. The study exclusively examines PEMFCs so there remains uncertainty regarding the application of PO to electrochemical systems with different operational characteristics such as SOFCs and Direct Methanol Fuel Cells (DMFCs). Research conducted with various fuel cell types would show whether the optimization tool can work for all fuel cells. The study lacks an extensive optimization process because it uses default parameter settings without performing parameter sensitivity and tuning. A thorough investigation of PO parameter sensitivity needs execution to both boost its suitability across different situations and improve its reliability since metaheuristic methods demand specific parameter adjustments for peak results.

Future research of the Parrot Optimizer (PO) should prioritize its implementation in real-time PEMFC system optimization to examine its industrial capabilities and dynamic performance assessment. Real-world PO implementation will demonstrate its capability to execute quick decisions and adaptions through testing in systems which need continuous optimization. The combination of PO with machine learning and deep learning techniques should be investigated because this approach would strongly improve its ability to solve challenging problems with many dimensions. The incorporation of data-driven methods would improve both adaptability and predictive features so applications of this method become more successful.

The scalability of PO requires future research because it effectively optimizes PEMFCs while its performance in larger energy systems such as SOFCs and hybrid systems remains unexplored. Research on scalability will show how PO functions with diverse energy technologies while establishing its practicality for utilization in power grid systems. Research should focus on using PO for multi-objective optimization to find solutions when accuracy and computational speed and resource efficiency need balancing. A comprehensive multi-objective optimization framework development will boost the practical use of PO methods in engineering problem solutions.