Introduction

Depth information serves as a fundamental component in accurately perceiving scenes, forming the basis for a wide range of computer vision studies1,2. Beyond its traditional applications in autonomous driving, smart homes, robot navigation, and consumer-level AR/VR, depth information also plays an irreplaceable role in 3D reconstruction of indoor scenes, spatial relationship reasoning of objects, and geometric completion of complex occluded areas3,4.

The existing depth information acquisition equipment mainly includes active sensors and passive sensors, among which the active sensors include LiDAR and depth cameras5,6,7,8. Radar technology is relatively mature and widely used in outdoor environments, especially for autonomous driving, but the equipment is expensive9,10. A depth camera uses structured light (e.g., Microsoft Kinect) or time of flight (e.g., Microsoft Kinect Azure) to provide dense depth information. However, the equipment has low accuracy and a short measuring range and is unable to accurately measure black, specular and transparent objects, limiting its applications in various scenes11,12. Researchers have gradually used passive sensors to carry out depth estimation research, such as using binocular cameras to transform depth estimation into image matching13,14. Using the structure-from-motion (SFM) method, multiple images or video sequences can be used to automatically recover camera parameters and the three-dimensional structure of the scene15,16. Considering the development of many modern devices (mobile phones/VR), monocular depth estimation has garnered increasing attention17,18,19.

With advancements in deep learning, convolutional neural networks have become more widely applied in monocular depth estimation than traditional methods. Many methods obtain the dense depth map of a single image through direct prediction18,19. The most widely studied monocular vision depth estimation method, such as the KITTI dataset, is applied to outdoor scenes in the automatic driving field and has achieved good results20. However, they often perform poorly in indoor scenes, such as those in the NYU Depth V2 dataset21 and SUN RGB-D dataset22, mainly because the indoor environment is more challenging. Many researchers have also obtained impressive results in the depth estimation of indoor scenes23,24,25,26,27. However, one of the core issues that still needs to be solved is how to focus on indoor scenes with complex objects, dense depths and weak feature differences.

First, the objects in the indoor scene are very complex, and the correlations between different objects are diverse, as shown in Fig. 1a. ResNet, VGG, and AlexNet were used as baseline networks in the feature extraction stage of the previous depth estimation neural networks28,29,30. However, traditional convolution structures struggle to extract global information from indoor scenes due to their inherent focus on local features, which lack long-range descriptions.

Second, different from the depth estimation research of outdoor scenes, the depth difference of indoor scenes is small, the depth values are very dense, and the continuity is high, as shown in Fig. 1b. This feature leads to weak distinguishability details. Researchers obtain the details and semantic information in the feature map through the connection between the encoding and decoding layers18,25,26,31. However, this structure only enables simple fusion of details and semantic features without selective fusion or attention. It can achieve good results in environments with large depth differences, which is limited in indoor scenes.Finally, existing methods have achieved good results on the NYU Depth V2 and SUN RGB-D datasets19. However, the generalizability and stability of the current method still need to be further improved in indoor environments, as shown in Fig. 1c.

Fig. 1
figure 1

Analysis of indoor image depth characteristics. (a) The objects in the indoor scene are very complex. (b) The depth values are very dense, and the continuity is high. (c) The indoor scene.

Full size image

The motivation of our work is to establish a more accurate neural network architecture to address the challenges of indoor scene depth estimation. The limitations of the traditional convolution layer on the weak ability of global information processing are eliminated, the problem of insufficient attention to key areas is overcome, and the adaptability of the method to various scenarios is improved. This paper proposes an efficient monocular depth estimation method using a detail–semantic collaborative network for indoor scenes. The main contributions of the proposed approach are highlighted as follows:

  1. (1)

    For indoor scenes, this paper proposes a Detail–Semantic Collaborative Network (DSCNet) for monocular depth estimation. Comparisons with 14 existing methods demonstrate the advantages of the proposed approach in both accuracy and efficiency. Furthermore, the method is analyzed from multiple perspectives, including stability, robustness, computational efficiency, and multi-scenario applicability.

  2. (2)

    To address the issue of weak feature distinguishability in indoor depth estimation, we propose a Detail–Semantic Collaborative Module (DSCM). The module utilizes an adaptive selective attention mechanism to extract key details and semantic information from same-scale encoding-decoding features, constructing hybrid features to enhance feature discrimination capability.

  3. (3)

    To address the challenges of object diversity and complex semantic relationships in indoor scenes, we developed a Multi-level Feature Aggregation Module (MFAM) that integrates detailed and semantic information. This module employs a physical combination strategy to aggregate full-scale semantic and detailed features, capturing global-scale inter-object relationships while enhancing prediction accuracy without increasing model parameters.

The remainder of this paper is arranged as follows. The related work is detailed in “Related work” section. “Proposed method” section introduces the proposed method in detail. The dataset and experimental environment are described in “Predataset and hyperparameter settings” section. “Experimental results and discussion” section compares and discusses the proposed method in detail. “Conclusions and future research” presents the conclusion and future research of this paper.

Related work

The calculation of depth information from a monocular image is considered a pathological problem. The reason is that there are infinite 3D scene models corresponding to the same imaging plane. This inherent uncertainty also makes it difficult to estimate accurate depth from a single image28. Early monocular image depth estimation methods mainly rely on the features of the image, such as hidden points32, shadows33, and focusing and defocusing34,35, to construct a mathematical model and establish the mapping between pixel values and depth values. Although these methods have achieved some results, they all need to add additional assumptions to the depth estimation problem, and the accuracy is limited.

According to previous studies, the essence of obtaining depth information from images is to build a model that relates image information and depth information36. To establish such a mapping relationship model, many methods based on machine learning have been used for depth estimation of monocular images. Machine learning enables computers to learn rules from data through training and then to make predictions through different algorithms. Traditional depth estimation methods for monocular images can be divided into parametric learning and nonparametric learning methods. The parametric learning method means that there are unknown parameters in the function, and these unknown parameters need to be calculated during training36,37,38. These methods assume that the relationship between the image and the depth map conforms to a certain model. However, the assumed model cannot represent the mapping relationship between the image and the real three-dimensional space, which also leads to its limited prediction accuracy. The nonparametric learning method infers the similarity of the existing datasets, which does not require the learning of model parameters39,40,41. Although nonparametric methods avoid artificial model assumptions, these methods require a large search database, which is time consuming and computationally expensive. In addition, the correct results cannot be obtained when the corresponding depth map cannot be retrieved from the database, which means that the method cannot be applied to real scenes.

With the rapid development of deep learning technology, neural networks have played an important role in computer vision, natural language processing, speech recognition and other fields due to their strong nonlinear expression ability and feature fitting ability42,43,44,45,46,47,48,49,50. In particular, various attention mechanisms are widely applied in the training of neural network models51,52,53,54. Similarly, these methods are also applied to monocular image depth estimation. The depth estimation of a single image uses the idea of supervised learning to establish a neural network mapping model between image color pixels and real depth25,28.

The neural network depth estimation methods based on supervised learning include the multiscale feature fusion method, the ordinal relationship method, the multiple image information fusion method, and the fusion condition random field method. In the multiscale feature fusion method, a point-to-point mapping relationship is established between the color image and the depth map to form an end-to-end symmetrical structure. Then, the depth of the input monocular image can be estimated by training the network19. The method using the ordinal relationship can be divided into two types, where the first type obtains the relative depth directly by using the pixel relation of the relative position point in the image through the ordinal relation55. The second type is indirect estimation, which uses discrete labels to classify and estimate the global depth and then obtain the depth information29,56,57. The method of combining information from multiple images uses different dimensional information in the image as the auxiliary constraint condition for image depth estimation, such as using the semantic segmentation results as the auxiliary condition23,24,58, neighborhood information59, time information60, and boundary information61. The fusion conditional random field method usually combines the conditional random field (CRF) with the end-to-end network structure because the depth information has continuous characteristics of the image, and the conditional random field has a better effect on the processing of such data25,60,62,63. In addition, from the perspective of hardware, Chang et al. established an end-to-end training structure by introducing optical principles into image depth estimation tasks64.

The difference between the method in this paper and the existing depth estimation methods is that we focus more on indoor scenes. The scene types are diverse and complex, the depth values are more continuous and dense, and the indoor scenes have no significant details or semantic features. After sufficient feature extraction, adaptive weight settings are used for the degree of attention of different regions to achieve the coordination of details and semantic features. In addition, the multilevel feature aggregation module is used to comprehensively express the relationships between indoor objects. The proposed approach is proven to be more applicable to the depth estimation of indoor scenes.

Proposed method

Fig. 2
figure 2

Overview of the proposed DSCNet.

Full size image

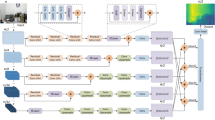
The excellent nonlinear expression ability of the neural network makes it possible to estimate the depth of monocular images. We propose a detail–semantic collaborative network for monocular image depth estimation, as shown in Fig. 2, which is an end-to-end symmetric structure that includes an encoder and decoder. The encoder uses the hierarchical transformer structure for detail and semantic feature extraction in images. Second, a detail and semantic feature extraction module (DSFEM) is established to improve the detail and semantic feature extraction ability of the network through selective fusion. Finally, a multilevel feature aggregation module (MFAM) is established to improve the network’s ability to express features at different scales without increasing network parameters.

Detail and semantic features extraction module

Existing neural network models based on conventional convolutions have achieved remarkable results in various computer vision tasks. However, due to their inherent local characteristics, they lack long-range feature descriptions. To enhance the network’s ability to extract rich detail and semantic information in the task of indoor image depth estimation, we employ a hierarchical Transformer65 as the Detail and Semantic Feature Extraction Module (DSFEM), as illustrated in the encoder in Fig. 2. First, assuming the image size is H × W × 3, the input image is divided into 4 × 4 patches, resulting in 16 distinct image patches, i.e., patch embedding, as shown in Fig. 2. This structure is more conducive to dense prediction tasks. Second, these image patches are fed into the hierarchical Transformer encoder, which includes Block1, Block2, Block3, and Block4, to obtain multi-level features with resolutions of {1/4, 1/8, 1/16, 1/32} of the original image. Each block consists of a self-attention layer (Self Attention), a lightweight multilayer perceptron (MLP-Conv-MLP), and a patch merging layer, where the feature map scales of different Transformer levels are reduced to 1/4, 1/8, 1/16, and 1/32 of the original scale, with dimensions C1, C2, C3, and C4, respectively.

Detail–semantic collaborative module for feature fusion

Continuous downsampling in the encoding stage can transform the features from detailed features to semantic features, while the decoding stage recovers the features from semantic features to detailed features66. In the previous networks, the feature maps in the encoding and decoding processes cannot be fully integrated, which means that the ability to recover detailed features in the decoding process is limited and the focus on the key regions is lacking.

Fig. 3
figure 3

The architecture of the detail–semantic collaborative module and visualization of feature maps at different scales.

Full size image

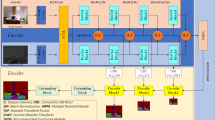
To address the problems of weak distinguishability depth features in indoor scenes, we propose a detail–semantic collaborative module (DSCM) for fusing detailed and semantic features to further improve the network’s ability to extract and discriminate different features, as shown in Fig. 3. The DSCM module consists of three main parts: detail–semantic feature fusion (part A in Fig. 3), extraction of focus regions under self-attention (part B in Fig. 3), and detail–semantic feature collaboration (part C in Fig. 3). In addition, to show the changes in feature maps during the process in detail, we extract two scales of feature maps for visualization and display, and the scales are (8/H, 8/W, C2) and (16/H, 16/W, C3).

  1. (1)

    Detail–semantic feature fusion, as shown in Fig. 3A. The feature maps of the encoding and decoding stages on the same scale are Te (F1 in Fig. 3) and Td (F2 in Fig. 3). The detailed features of the encoding part feature maps under the scale are significant, while the semantic information feature maps of the decoding stage are significant. First, the two feature maps are subjected to an aggregation operation, which allows the initial stitching of the encoding and decoding feature maps so that the later feature selection is based on the fused features. The result contains both detailed and semantic information at the same scale. This mechanism enables the network to capture more discriminative features during depth estimation, effectively enhancing depth prediction performance at the early processing stage, as shown in formula (1). Afterward, a convolution of 1 × 1 is added to change the dimensions of the feature maps.

    $$\:\begin{array}{c}{T}_{de}=\left({\text{f}}_{\left(1\times\:1\right)}\left(\text{C}\text{o}\text{n}\left({\text{T}}_{\text{e}},{\text{T}}_{\text{d}}\right)\right)\right)\end{array}$$
    (1)

    where \(\:{T}_{de}\) is the result of detail–semantic feature fusion. \(\:{T}_{e}\) and \(\:{T}_{d}\) are the feature map outputs of the encoding and decoding stages, respectively, at the same scale. \(\:{f}_{\left(1\times\:1\right)}\) represents the convolution operation with a convolution kernel of 1 × 1, and \(\:Con\) denotes the additive operation.

  2. (2)

    Extraction of the focus regions under self-attention, as shown in Fig. 3B. This part takes the result of detail–semantic feature fusion as the initial input data, which can further trigger the interaction of features according to the spatial location of the input data based on self-attention and can enhance the attention to the key region. This approach effectively enhances the network’s attention to salient regions while suppressing interference from non-critical areas, thereby improving depth estimation performance through optimized feature prioritization. The feature maps in the encoding and decoding stages at the same scale are Te and Td, respectively, and the core parts of the key map (K), query (Q), and value map (V) are defined as K = Q = V = Tde. The computation process can be expressed as formula (2).

    $$\:\text{O}\text{u}\text{t}\text{p}\text{u}\text{t}\_\text{s}\text{e}\text{l}\text{f}=\left({\text{f}}_{\left(1\times\:1\right)}\right(\text{C}\text{o}\text{n}\left({\text{f}}_{\left(\text{k}\times\:\text{k}\right)}\right(\text{K})+\text{M}\text{u}\text{l}(\text{S}\text{i}\text{g}\text{m}\text{o}\text{i}\text{d}\left({\text{f}}_{\left(1\times\:1\right)}\right(\text{C}\text{o}\text{n}\left({\text{f}}_{\left(\text{k}\times\:\text{k}\right)}\right(\text{K}),\text{Q})\left)\right),\text{V}\left)\:\right))$$
    (2)

    where \(\:Mul\) denotes the multiplication operation. \(\:Con\) denotes the additive operation, and \(\:{f}_{\left(1\times\:1\right)}\) represents the convolution operation with a convolution kernel of 1 × 1. \(\:{f}_{\left(k\times\:k\right)}\) is the use of k×k group convolution on all neighboring key spaces in the k×k grid so that each key can be expressed, and the results reflect the contextual relationship between the localities67.

    After the above steps, the results already contained the attention of key areas. However, to extract key areas of the feature map, this attention result needs to be further mapped to the feature map of the encoding and decoding stages at the same scale, as shown in Fig. 3B2. We generate an attention score map through two 3 × 3 convolutional layers and a sigmoid layer to show the degree of attention to different regions. The attention score map at different scales is shown as F3 in Fig. 3.

  1. (3)

    Detail–semantic feature collaboration, as shown in Fig. 3C. The attention score map output from the sigmoid in the previous step represents the degree of emphasis of different regions.First, the feature map is multiplied by each channel in the feature map output in the encoding and decoding stages, which further improves the network’s attention to key areas. Second, the obtained selective features are fused to achieve the collaboration of detailed semantic features, as shown in formula (3).During the depth estimation phase, the synergistic fusion of semantic and detail features produces more discriminative attentional responses to critical regions compared to standalone feature maps, thereby effectively enhancing the network’s depth perception capability through optimized feature-aware representation learning. The attention results at different scales are shown as F4 in Fig. 3. It can be seen from the feature map that the output results aggregate the details and semantic information at the same scale.

    $$\begin{array}{c}Output=Con\left(\text{M}\text{u}\text{l}\left({\text{O}\text{u}\text{t}\text{p}\text{u}\text{t}}_{\text{S}\text{i}\text{g}\text{m}\text{o}\text{i}\text{d}},{\text{T}}_{\text{e}}\right),\text{M}\text{u}\text{l}\left({\text{O}\text{u}\text{t}\text{p}\text{u}\text{t}}_{\text{S}\text{i}\text{g}\text{m}\text{o}\text{i}\text{d}},{\text{T}}_{\text{d}}\right)\right)\end{array}$$
    (3)

    where \(\:Output\) denotes the final selective feature output result. \(\:{Output}_{Sigmoid}\) is the output result of Fig. 3B. \(\:{T}_{e}\) and Td are the feature map outputs of the encoding and decoding stages at the same scale, respectively.

Multilevel feature aggregation module considering detail and semantic information

Fig. 4
figure 4

MFAM architecture.

Full size image

After the fusion of detail–semantic collaboration, different scale feature maps have different differential details and semantic information, as shown in Fig. 4. It can be seen from the figure that the deep structure of the network contains more semantic feature information, such as the feature maps of scales 1/16 and 1/8. The shallow feature maps contain more detailed features, such as a feature map of original size and a scale of 1/4. In general, for networks, only single-level output prediction is performed for the original features. Although some multiscale information can be obtained, the extraction capability is insufficient.

To solve the problem of the diverse and complex relevance of indoor objects, a multilevel feature aggregation module (MFAM) considering detailed and semantic information is constructed. The module further improves the adaptability of the network to complex indoor scenes, Enhances the network’s depth estimation capability for complex indoor scenes, as shown in Fig. 4. First, the feature map scale is restored through continuous upsampling at different scales. The dimension of the feature map at each scale is uniformly set to 64 so that the output dimension is 256, and the features of detail and semantic information obtained at different scales can be fully aggregated. Second, the dimensions are changed via convolution, and the final predicted depth map is obtained via the sigmoid function. This four-layer aggregation operation utilizes all the information from different scales in a separate and integrated manner. Unlike a single multiscale weighted output, this combination aggregates all multiscale features and improves the degree of network optimization. In addition, the module only performs feature output based on the original network without additional computations or time.

Predataset and hyperparameter settings

Data production

  1. (1)

    NYU Depth V2 (NYU dataset). To demonstrate the effectiveness of the method, we tested the method using the existing publicly available depth computation dataset NYU Depth V2, which was acquired by Silberman et al. with a Microsoft Kinect camera21. This dataset includes 1449 pairs of color images and corresponding depth maps, including 464 scenes from three cities. Among them, 249 scenes are used as training data and 215 scenes as testing data, which has become an important benchmark dataset in recent depth estimation research and a key data reference to verify the validity of the method.

    To further improve the robustness of the model and reduce the occurrence of overfitting, more images with different features are generated online via data enhancement based on the original dataset. This approach is also used by many researchers in deep estimation for model training, and the data enhancement methods include scale transformation, rotation, random cropping, blurring, gamma transform, and luminance transform. Finally, the last dataset includes 24,231 training image pairs with a size of 576 × 448 and testing images that remain consistent with the original dataset, for a total of 654 images.

  2. (2)

    SUN RGB-D dataset (SUN dataset). To further validate the robustness of the proposed approach, we selected the SUN RGB-D dataset, which was provided by Song et al. in 201522, to conduct a challenging experiment. This dataset includes a total of 5050 images of different indoor scenes. The experiment uses only the results obtained from training on the NYU dataset without fine-tuning, which increases the robustness of our method.

Hyperparameter configuration

  1. (1)

    Experimental Settings

All experiments in this paper were conducted on a Windows 10 system with an AMD Ryzen 7 5800 × 8-Core Processor 3.80 GHz, Nvidia GeForce RTX 3090 24G, and the deep learning framework used was PyTorch. In the training process, Adam is used for network optimization, and the initial learning rate is set to 0.0001. To balance the GPU memory and CPU read data speed, Batch_size is set to 6, and Epoch is set to 25. In addition, to prevent overfitting and improve the generalization of the model, a dropout function is added after each block in the feature extraction stage, and the parameters in the training process are randomly discarded. The loss function adopts the depth estimation loss proposed by Eigen et al.28, as shown in Eq. (4).

$$\begin{array}{c}Loss=\frac{1}{n}\sum\:_{i}{d}_{i}^{2}-\frac{1}{{2n}^{2}}{\left(\sum\:_{i}{d}_{i}\right)}^{2}\end{array}$$
(4)

where \(\:{d}_{i}\)= \(\:{log}{y}_{i}-log\:{{y}_{i}}^{*}\), \(\:{{y}_{i}}^{*}\) and \(\:{y}_{i}\) represent the i-th pixel corresponding to the predicted result and the true label, respectively, and \(\:n\) represents the total number of pixels.

  1. (2)

    Evaluation Metrics

To compare model performance, four commonly used benchmark evaluation metrics are selected, including the mean relative error (REL) (Eq. (5)), the root mean square error (RMSE) (Eq. (6)), the logarithmic space average error (average log10 error, log10) Eq. (7), and the prediction accuracy (Eq. 8).

$$\:\begin{array}{c}REL=\frac{1}{T}\sum\:_{i}\frac{\left|{{y}_{i}}^{*}-{y}_{i}\right|}{{y}_{i}}\end{array}$$
(5)
$$\:\begin{array}{c}RMSE=\sqrt{\frac{1}{T}\sum\:_{i}{\left({{y}_{i}}^{*}-{y}_{i}\right)}^{2}}\end{array}$$
(6)
$$\:\begin{array}{c}{\text{L}\text{o}\text{g}}_{10}=\frac{1}{T}\sum\:_{i}\left|log\:{{y}_{i}}^{*}-\text{log}{y}_{i}\right|\end{array}$$
(7)
$$\:\begin{array}{c}\text{max}\left(\frac{{{y}_{i}}^{*}}{{y}_{i}},\frac{{y}_{i}}{{{y}_{i}}^{*}}\right)=\delta\end{array}$$
(8)

where \(\:{{y}_{i}}^{*}\) is the model prediction value of pixel I, \(\:{y}_{i}\) is the true value of pixel i, \(\:T\) is the sum of the pixels of the test image, the prediction accuracy is the percentage of the total pixels that satisfy \(\:{\updelta\:}<\text{t}\text{h}\text{r}\text{e}\text{a}\text{d}\text{h}\text{o}\text{l}\text{d}\), and the value of \(\:\text{t}\text{h}\text{r}\text{e}\text{a}\text{d}\text{h}\text{o}\text{l}\text{d}\) is generally set to 1.25, 1.252, and 1.253.

Experimental results and discussion

In this section, several aspects of the proposed method are analyzed in detail. First, the method is qualitatively and quantitatively analyzed with 12 excellent, recent neural networks on the same datasets. Second, the stability, robustness, efficiency, and ablation experiments of the proposed method are discussed in detail. Finally, the use of our method is discussed for real scenes and virtual scenes, and the 3D reconstruction of different types of scenes is carried out according to the depth estimation results to further verify the generality of the proposed approach. Additionally, it should be noted that all experimental results in this paper are derived from test data.

Comparison with SOTA deep learning models

Quantitative analysis

In this section, the proposed method is compared with recent SOTA models. Notably, the accuracy of the above models selected in this paper is the highest according to the published literature; the results are shown in Table 1.

Table 1 Depth estimation result comparison with state-of-the-art models on the NYU dataset.
Full size table

It can be seen from the table that compared with the accuracy of excellent algorithms in recent years, the accuracy of the proposed method has shown a staged improvement. In terms of accuracy, the proposed method surpasses most of the algorithms in the existing research. Even for the latest research of Kim et al., the method is still considerably accurate, and in terms of error, the proposed approach achieves better results. Compared with the accuracy of the best method, the REL is reduced by 0.001, the RMSE is still reduced by 0.002, and the Log10 can be reduced by 0.001. When the error reaches a low level, it is extremely difficult to improve, which further demonstrates the effectiveness of the proposed method.

Qualitative analysis

To intuitively reflect the advantages of different methods in depth estimation, in this section, we select our method and two representative methods for visual analysis, including the methods of Bhat et al. and Kim et al.18,19. We selected six representative regions from the dataset for comparison with the proposed method, as shown in Fig. 5. The first row is the original image, and the second row is the ground truth. The depth map is visualized through different colors corresponding to different depth values, wherein the depth corresponding to dark blue is the smallest, and the depth corresponding to dark red is the largest. The first column and the second column in the figure are indoor office scenes. The scene distribution is simple. Compared with the label, the real depth value can be predicted by all methods. The scenes in the third and fourth columns are more complex, contain more objects and have longer distances, as shown in the box in the figure. Compared with the existing methods, the proposed method has a better effect on both closer and farther objects. In addition to ordinary scenes, we select two groups of images with poor light in the test dataset in the fifth and sixth columns to verify the performance of the method in the case of interference. From the box selection part in the figure, the selected excellent methods all have good performance in the data, but the proposed method is relatively more sophisticated in data processing, especially for the boundary. This is also due to the detail–semantic collaborative module and multilevel feature aggregation module, which further improve the context capture ability of the network and the depth prediction ability of objects at different scales.

Fig. 5
figure 5

Visual analysis of our methods with the SOTA methods for depth estimation on the NYU dataset.

Full size image

Stability analysis

Stability of different types of box plots

To verify the stability of the different models for the different test scenarios, we calculated the accuracy of each test image of the three methods selected and constructed a box plot to analyze the stability of the 654 images. A box plot is used to evaluate the stability of the method according to the distribution of a set of data, including the quartile, maximum, minimum, mean, and outlier data. As shown in Fig. 6, a separate stability analysis was performed for each of the evaluation criteria (the Y-axis represents the evaluation index).

Fig. 6
figure 6

Stability analysis of the depth estimation results of our method and SOTA methods.

Full size image

As shown in the figure, compared with Adabins18, the proposed approach and the GLPN have obvious advantages. In addition, the proposed method has a small advantage over GLPN19. Despite the limited improvement in accuracy, attention should be given to outlier outputs, which are low-accuracy results due to the lack of applicability of the model. The overall number of outliers in the proposed approach is lower, and the accuracy of the outliers generated by the proposed method is better, which also shows that the proposed method can ensure the stability of the model while achieving higher accuracy.

Fig. 7
figure 7

Analysis of poor performance in special scenarios.

Full size image

Based on the above analysis, the method still exhibits some instability in certain special scenarios. To further explore the limitations of the method, this study selected representative challenging scenes from the test set for qualitative analysis. As shown in the black-boxed area in Fig. 7a, the mirror reflection region lacks reliable geometric texture cues, leading to significant deviations in the model’s depth estimation of objects within the mirror, mistakenly identifying the reflected content as actual spatial extension. Additionally, the black boxed area in Fig. 7b shows that the prediction results for complex decorative details (such as fine hollow structures) suffer from edge blurring and structural discontinuities.

Independent Monte Carlo experiment

Fig. 8
figure 8

Average value and standard deviation of Monte Carlo experiments.

Full size image

In addition to the above stability analysis of each testing image, the overall performance of the model is also an important criterion for verifying the stability of the model. Therefore, the stability of the proposed model is further verified through an independent Monte Carlo experiment, specifically by adding a dropout function (probability = 0.5) to the model. The parameters in the training process were randomly discarded, and the changes in each evaluation standard under 20 independent tests were calculated as the average value and standard deviation. As shown in Fig. 8, under 20 independent Monte Carlo experiments, the average accuracy of the proposed method remains high, especially in terms of the standard deviation, and the standard deviation of all the indicators is small. In particular, based on the RMSE data from 20 Monte Carlo experiments (u = 0.342, σ = 0.0009), the 95% confidence interval is [0.3416, 0.3424]. The result indicates that the independent test conducted by the proposed method has a low dispersion, which further confirms the stability of the proposed model.

Robustness analysis

Quantitative analysis

Robustness is a great challenge for the effectiveness of the model, especially with different datasets and scenarios. In addition to the public data of the NYU dataset, to further verify the effectiveness of the proposed method, the module is trained on the NYU dataset and tested on the SUN dataset without fine-tuning.

Since there is no transfer learning, it is a large challenge for the robustness of the method. In addition to the proposed method, we also select three models that perform better on the NYU dataset. The final accuracy results for comparison are shown in Table 2. Compared with the SOTA models, the proposed model achieves the best results in terms of three indicators of error, namely, the REL, RMSE and Log10, and the accuracy can also be maintained at the same level as that of the latest model. This quantitative evaluation demonstrates the good robustness of the proposed approach.

Table 2 Results of models trained on the NYU dataset and tested on the SUN dataset without fine-tuning.
Full size table

Qualitative analysis

To further compare the performances of the different methods, we select representative images of the prediction results for visual analysis, as shown in Fig. 9. The first row is the original image, the second row is the ground truth, and the depth map is visualized through different colors corresponding to different depth values. The selected visual images contain different types of scenes, and the complexity of the objects and scenes also increases. For a simple scene (from the first column to the third column) containing fewer observations, all methods predict the accurate depth, but the proposed method is more sophisticated in dealing with the boundary, as shown in the box selection part of the figure. With increasing scene complexity, the accuracy of various models decreases, but the proposed method is still effective. For example, in the box selection part of the fourth column, the prediction of wall distance by the proposed method is more accurate, and the treatment of the bookshelf boundary and interior in the fifth column is more refined, especially in the sixth column. The long-distance distance predicted by the proposed method has better integrity than that of the other methods. Because the dataset has not been trained and directly predicted on the SUN dataset, it is very difficult to achieve such results, which further shows that the proposed approach has good robustness.

Fig. 9
figure 9

Visual analysis of our methods with the SOTA methods for depth estimation on the SUN dataset.

Full size image

Efficiency analysis

In the process of depth estimation using deep learning, in addition to accuracy, the generalizability of the method is also very important. To verify the usability of the proposed approach, our method is tested in different computing environments, and the results are shown in Table 3.

The first is the training environment in this paper, which has good computing power and can run at a frame rate of 28 FPS. However, such high configuration conditions cannot be achieved in ordinary application scenarios. Therefore, we further test the running speed of our method in a more general computing environment, and the computing power of the second to fourth computing environments gradually decreases. Even so, the efficiency of the proposed method still reaches 21 FPS, 19 FPS and 17 FPS. In particular, in the fourth environment, which has low computing power, it still reaches 17 FPS. When the frame rate of ordinary surveillance video is 20–25 FPS, the proposed approach achieves real-time results.

Table 3 Comparison of the runtime of our method in different computing environments.
Full size table

Ablation experiment

To obtain more accurate depth calculation results for monocular images, the proposed model includes several modules and a more complex connection structure. The main modules include the DSFEM, DSCM, and MFAM. To fully establish the role of each module, three groups of ablation experiments are carried out on the more commonly used public NYU dataset. In addition to the accuracy, we test the parameter changes caused by each module and the impact of the run time.

  1. (1)

    DSFEM. As a comparison, ResNet is also considered an effective feature extraction architecture besides hierarchical Transformer structures. In this experiment, we replaced DSFEM with the most commonly used ResNet101 as the baseline method while keeping other modules unchanged. The experimental results are shown in Table 4: although ResNet101 has advantages in computational efficiency (parameter count of 44.56 M, FPS 45, both superior to the full model’s 61.81 M/28 FPS), its detection accuracy (δ < 1.25 = 0.873) is lower than that of the full model (0.916), and its error rate metrics are comprehensively worse (REL = 0.113 vs. 0.097, RMSE = 0.395 vs. 0.342). This indicates that while ResNet101 reduces computational costs through local convolution operations, its local receptive field characteristics limit global context modeling capabilities, leading to detail loss and semantic ambiguity issues in depth estimation tasks. In contrast, DSFEM, through the global attention mechanism of hierarchical Transformers, achieves key performance improvements at a controllable computational cost (parameter count + 37%, FPS − 37.8%), validating the necessity of balancing accuracy and efficiency in design.

  2. (2)

    DSCM. Feature fusion during the encoding and decoding stages facilitates the recovery of detailed features in the decoding process, but its specific role requires further validation. In this experiment, we replaced DSCM with simple feature concatenation between the encoder and decoder (only fusing feature maps of the same scale), while keeping other structures unchanged. As shown in Table 4, although the simplified model reduced the parameter count by 0.73 M (from 61.81 M to 61.08 M) and increased the frame rate by 1 FPS (from 28 to 29), its accuracy declined (δ < 1.25 dropped from 0.916 to 0.896, REL increased from 0.097 to 0.107, RMSE increased from 0.342 to 0.354). This indicates that while simple feature concatenation reduces computational load, it fails to achieve dynamic complementarity of cross-scale details and semantics: DSCM, through a dual spatial-channel attention mechanism, adaptively fuses multi-scale context with minimal parameter cost (+ 0.73 M, + 1.2%), enabling finer depth recovery at object boundaries (RMSE reduced by 19%) and in low-texture regions (REL reduced by 9.3%), thereby validating the necessity of dynamic feature fusion for depth prediction.

Table 4 Accuracy, parameters, and run time of ablation experiment results with different combinations.
Full size table
  1. (3)

    MFAM. To validate the effectiveness of MFAM, this experiment utilized only the final output layer (single-scale features) for prediction, without aggregating multi-level semantic and detail features. As shown in Table 4, the accuracy of the single-scale model declined (δ < 1.25 = 0.909 vs. the full model’s 0.916, REL = 0.102 vs. 0.097, RMSE = 0.352 vs. 0.342), particularly in occluded regions (e.g., gaps between furniture), where the depth prediction error (RMSE) increased by 2.9%. In contrast, the proposed MFAM adaptively fuses multi-scale features from Block1 to Block4 through hierarchical attention gates and deformable convolution alignment, without additional parameters (increasing from 61.69 M to 61.81 M, a 0.12 M increase) and maintaining an inference speed of 28 FPS. This demonstrates that MFAM enhances depth consistency in complex scenes by reusing encoder features and optimizing cross-scale alignment mechanisms, achieving an efficient balance between multi-scale modeling and real-time performance at a negligible computational cost (parameter increase of 0.2%).

Fig. 10
figure 10

Visual analysis of ablation experiment results with different combinations.

Full size image

In addition to the accuracy, parameters and speed, the differences in the results of each ablation experiment are visualized in detail, as shown in Fig. 10. The first row is the RGB image, and the second row is the ground truth. The third, fourth and fifth columns represent the above three groups of ablation experiments, and the sixth column shows the prediction results of the proposed method. It can be seen from the figure that the proposal of multiple modules and the construction of the network model in this method are very effective, and the results are more refined. This is especially true for boundary processing, as shown in the box selection part of Fig. 10, which effectively captures the context features and refined boundary features.

Availability analysis in uncertain scenarios reconstruction

Fig. 11
figure 11

Visual analysis of depth estimation and scene reconstruction in uncertain scenarios.

Full size image

Unlike the existing testing datasets, the scene for depth estimation or 3D scene reconstruction is uncertain, and whether the method can be applied to the real scene is also a huge challenge. To test the usability of the proposed approach in uncertain scenes, we randomly selected six images with indoor environments in the real and virtual scenes for depth estimation and 3D reconstruction. Since the photos are taken randomly by a simple camera, the real depth cannot be obtained. Therefore, we use the depth information to reconstruct the point cloud and perform a qualitative analysis of the model through the reconstruction results of the point cloud. The depth maps and 3D reconstruction results obtained in different scenes are shown in Fig. 11. It can be seen from the figure that the prediction of the depth map by the proposed method restores the depth information of the original scene. In the real scene, it shows a fine effect. The point cloud reconstruction results of the edges and corners of the table, the wall plane and its convex part, and the ground in the figure further highlights the usability of the method in the real scene. In the virtual scene, the depth prediction results also fully reflect the indoor scene layout and the spatial distribution of different types of objects. Moreover, the description of details also meets the three-dimensional reconstruction goal, which further verifies the usability of the method in uncertain scenes.

Conclusions and future research

This paper addresses the challenges of weak feature discriminability and complex object relationships in indoor scene depth estimation by proposing a neural network model that integrates detail and semantic collaborative reasoning. The method enhances global context awareness through a hierarchical feature extraction structure, optimizes boundary detail reconstruction accuracy with a cross-scale feature interaction mechanism, and improves the modeling of complex spatial relationships with a multi-level fusion strategy. Experiments demonstrate that, compared to existing methods, the model maintains real-time inference efficiency while adapting more stably to varying lighting conditions and scene layout changes providing reliable technical support for 3D perception in indoor environments.

Future research will focus on exploring lightweight deployment solutions and dynamic scene adaptation capabilities, reducing computational resource dependency through algorithm optimization. Additionally, Future work will focus on applying the method to other scenarios, such as outdoor and complex industrial environments, and validating its technical utility in real-world applications.