Reducing power ripple for multi-rotor wind energy systems using FOPDPI controllers

Abstract

Energy systems based on wind energy have now become a necessity due to their many advantages. However, using traditional turbines has several disadvantages, the most notable of which is the low performance and quality of the resulting energy. This work proposes an energy system based on the use of a multi-rotor wind turbine (MRWT) with a double-fed induction generator. In addition, to obtain high-quality power, a new control is used based on the development and modification of direct power control (DPC) based on proportional-integral (PI) controllers. This designed approach has many advantages, such as fast dynamic response, easy adjustment, high robustness, and ease of implementation. In this designed technique, the PI controller is dispensed with, and they are replaced by the designed fractional-order proportional-integral proportional derivative controller. This designed technique is based on power estimation, where the same estimation equations used in the DPC-PI technique are used. Robustness, high competence, and effectiveness in improving power quality are among the most prominent features of the designed technique compared to the DPC-PI approach and some research works. The designed technique was verified using MATLAB, comparing the results obtained in the case of different wind speed profiles with those using the DPC-PI approach. Numerical results demonstrated the efficacy of the designed technique over the DPC-PI approach, as the steady-state error and active power ripples were minimized in the first test by rates estimated at 44.72% and 46.67%, respectively. Also, the reactive power overshoot and ripples were reduced in the fifth test by rates calculated at 81.40% and 42.18%, respectively. On the other hand, the total harmonic distortion of the current was minimized by rates estimated in the five suggested tests at 33.80%, 34.88%, 11.52%, 37.58%, and 33.33%. These percentages show the strength of the performance and effectiveness of the designed technique in enhancing the robustness and efficiency of the MRWT system, making it a promising solution.

Introduction

Global renewable energy (RE) capacity in 2023 reached 3,870 GW, with photovoltaic (PV) power generation accounting for the largest share of the global total. According to the work done in¹, the capacity of the share of PV energy in generating electrical power (EP) reached 1419 gigawatts. Relying on PV energy to generate EP makes the power generation grid system irregular². In addition, to obtain sufficient EP, solar farms with large areas must be used, which creates several problems such as high costs and a shortage of land needed to implement solar energy projects³. Also, the use of a PV system requires the use of an energy storage system to store surplus energy, which increases its costs, degree of complexity, and difficulty of control⁴. To achieve the necessary amount of EP to supply, solar farms with large areas must be used, which is currently impossible and requires advanced technologies. Therefore, the search for improving the performance of EP generation and reducing the costs of producing and consuming EP is one of the most prominent challenges facing the global community, as several scientific researchers have addressed this topic and several solutions have been created that provide the possibility of reducing energy fluctuations and increasing RE acceptance for the grid system^5,6,7. Wind energy (WE) is considered one of the most prominent REs that have been used alongside solar energy to generate EP because it has many positive aspects^8,9. The use of WE allows increasing the energy efficiency of the installed power station^10,11. According to the work done in¹², the Indian electricity market is now more oriented towards renewable energy resources, with the WE industry growing from a marginal activity to a multi-billion dollar business in the power generation sector of India due to its relatively safer and positive environmental features. To meet the growing energy requirements at affordable prices, like other European countries, several WE plants generating electricity have been completed in different geographical locations in India. During the period 2016–2017 to 2019–2020, 14 WE plants were completed in India, which indicates the interest in this type of energy system. These completed plants were operated at a maximum productivity of 14%. As is known, the life of wind turbines (WTs) negatively affects production efficiency. In addition, the altitude of the site has a significant positive effect on the operational efficiency of WE plants.

According to the work done in¹³, to exploit wind energy, WTs are used to generate EP. These WTs are of different shapes and can be classified into vertical-axis WTs¹⁴ and horizontal-axis WTs¹⁵. The difference between these two types lies in structure, yield, performance, efficiency, and cost¹⁶. The use of WTs is of great importance in overcoming energy challenges such as global warming, rising costs, and rising energy demand¹⁷. Compared to a PV system, a single WT with large dimensions can be used to supply the grid with the necessary energy¹⁸. These WTs have negatives that limit their spread, one of the most prominent challenges that hinder these WTs being related to winds generated between turbines in wind farms (which reduces their yield and performance)¹⁹. In the field of WTs, sub-synchronous resonance (SSR) is one of the most prominent problems in turbines. Therefore, it is necessary to reduce the low-frequency torsional oscillations to significantly improve the performance of turbines. In the work²⁰, the Whale optimization algorithm (WOA) is proposed to overcome the SSR problem. This proposed algorithm is used to optimize the controller proposed in the literature to control one of the degrees of freedom, i.e., pitch angle and external resistance connected to the rotor. The effectiveness of the proposed WOA-based controller is examined using a time domain approach based on the dynamic response of different parts of the test system using MATLAB software with a comparison of the results with control strategies proposed in the literature. The simulation results reveal the potential of the proposed WOA-based controller in damping low-frequency torsional oscillations, which is a positive factor that contributes to the spread and use of WTs as an optimal solution in the field of electric power generation. In²¹, to counteract the possible SSR observed by a series of compensated wind farms based on induction generators, STATCOM (Static Synchronous Compensator) is used as a suitable solution. For the control of STATCOM, a controller similar to that used in the literature is used. The controller used in the control scheme of the STATCOM has its gains calculated using the bacterial foraging optimization (BFO) algorithm. The investigation was carried out using a 500 MW IG-based wind farm subjected to a three-phase LLL-G fault near the point of common coupling (PCC) and implemented using MATLAB in both steady and transient cases for three different cases, namely without STATCOM, with the basic STATCOM controller, and in the presence of the proposed STATCOM-based BFO-optimal controller. Simulation results highlight the effectiveness of the proposed STATCOM-tuned BFOA-optimal controller in mitigating the potential SSR. The proposed BFO-based optimal STATCOM controller reduces the settling time by 83.33% and 67.36% without STATCOM and with STATCOM, respectively. Also, the proposed approach improves the overshoot by 87.72% and 92.26% for with STATCOM and without STATCOM, respectively.

To overcome the challenges that hinder the spread of WTs, a new WT technology has been proposed, represented by multi-rotor WTs (MRWTs) that are characterized by high performance and great robustness against strong winds²². The use of MRWTs allows reducing the number of WTs and, thus, reducing the surface of the wind farm and the costs of producing EP²³. So this paper proposes a suitable solution based on MRWT for converting WE into mechanical energy.

Mechanical energy is exploited using several generators, which are converted into EP. The most prominent generators used in WE include both synchronous and asynchronous generators^24,25, as these generators differ in terms of performance, effectiveness, yield, efficiency, cost, maintenance, and ease of control. Asynchronous generators are connected directly to the network without the need for an inverter or any intermediary, which makes their use easy and simple²⁶. However, the use of synchronous generators requires connecting the stator part to a network using inverters, which makes their use expensive and undesirable compared to asynchronous generators^{27,28,29,30,31}. In this work, attention was paid to doubly-fed induction generator (DFIG) type asynchronous generators for generating EP due to their multiple features, as their use allows for greater control of the resulting energy compared to synchronous generators. In addition to its low cost, ease of control, and no need for regular maintenance³². All these features make this generator an effective solution in the field of WE. Among the most famous disadvantages of the energy system based on WTs using DFIG are the decrease in robustness, power quality, current quality, efficiency, complexity, difficulty in achieving control, and decrease in performance^33,34. As is known, the total harmonic distortion (THD) of phase streams and voltages directly affects the life of the electronic device³⁵, so it is necessary to propose a highly effective control that significantly reduces the THD value of the current. Voltage harmonics are caused by non-linear loads and insufficient generated voltage from generators³⁶, so they can be considered an uncontrollable factor for the inverter control system except under weak grid conditions. Therefore, minimizing the THD of phase currents from the specified voltage harmonic state is important while performing active and reactive power (Ps and Qs) control.

Direct power control (DPC) is one of the control methods used to control DFIG powers³⁷. This strategy is very similar in principle and structure to the direct torque control (DTC) strategy, with the difference being only in the controlled quantities. This approach relies on the use of hysteresis comparators (HCs) to control the DFIG power³⁸. The switching table (ST) is also used to control the operation of an inverter, which makes it one of the most prominent strategies: simple, easy to implement, uncomplicated, inexpensive, and with a fast dynamic response³⁹. However, the use of HCs in DPC does not guarantee robustness in case of unknown uncertainty such as parameter variation which leads to high THD value and low power quality⁴⁰. To improve the robust performance of DPC used to control DFIG in the WE system, many effective solutions have been proposed to overcome the disadvantages and problems of low power quality and current. In⁴¹, the simplified super-twisting algorithm (SSTA) was used to overcome the problems and drawbacks of the DPC approach. An SSTA-type controller was used to control the power, and the outputs of these controls are the reference values for the voltage. Also, the space vector modulation (SVM) approach was used to control the operation of the inverter, and the resulting approach is characterized by simplicity, ease of implementation, inexpensive, and high robustness compared to the conventional approach. Simulation results show the high performance of the proposed DPC-SSTA approach in terms of improving the THD value of current, undershoot, and steady-state error (SSE) of power compared to the DPC strategy. These results obtained in⁴¹ using the DPC-DATA approach are similar to those obtained in the work done in⁴². Despite the high performance of the proposed approach, the problem of energy ripples remains, especially in the event of a malfunction in the system. In addition, the proposed approach for power estimation leads to a decrease in power and current quality, which is undesirable. The synergetic control (SC) strategy and fractional-order control (FOC) technique were combined to create a new controller capable of significantly improving the characteristics of the DPC approach⁴³. The fractional-order SC (FOSC) controller was used to control power and DC link voltage, as this controller is characterized by high performance, great robustness, small gain, and ease of operation. In addition to using the FOSC controller, a modified SVM approach was used to generate the pulses needed to operate the T-type inverter. This approach was implemented using MATLAB using several different tests, where simulation results showed the superiority of the DPC-FOSC approach over the conventional approach in terms of ripple reduction, THD, undershoot, and SSE. The negative of this proposed approach lies in the response time, as it provides a longer time than the usual approach, which is not desirable. As is known, time response is of great importance in the field of control. Therefore, it is necessary to look for approaches with a very fast dynamic response, which are also simple and easy to implement.

According to the work done in⁴⁴, the use of a modified sliding mode controller has significantly overcome the problems of the DPC strategy of DFIG. In this work, such a controller characterized by simplicity, high robustness, and ease of implementation is proposed. Also, its use does not require precise knowledge of the mathematical model of the machine, which makes it easy to apply. The pulse width modulation (PWM) approach was used to convert voltage reference values into pulses to operate the machine inverter. A grid inverter using an uncontrolled rectifier was used to simplify the system and reduce its cost. Terminal SC (TSC) strategy is the solution that was proposed in⁴⁵ to overcome the shortcomings of the DPC strategy of DFIG-MRWT, where a control was used to control the power. The TSC-DPC strategy is a development and modification of the DPC approach based on the proportional-integral (PI) controller. This proposed approach was applied to the 1500 kW DFIG inverter only, where the modified SVM strategy was used to operate the machine inverter. Therefore, the proposed approach is characterized by simplicity, inexpensive, ease of implementation, and high robustness. MATLAB was used to verify its performance, comparing the results to the traditional approach based on the PI controller, where two different wind speed (WS) profiles were used to study the behavior of the proposed approach. All tests showed the high performance of the TSC-DPC strategy compared to the PI-DPC strategy and some research work in terms of reducing ripple rates, SSE, and undershoot of DFIG power. Reliance on TSC-DPC strategy on power estimation leads to deterioration of power quality in case of change in DFIG parameters, as demonstrated by robustness testing, which is undesirable.

The backstepping control (BC) strategy is one of the nonlinear approaches that are characterized by high performance and great robustness. This approach was used in the work⁴⁶ to improve the characteristics of the DPC approach of DFIG-MRWT, as it provided satisfactory results in terms of robustness and performance. Using the BC approach led to a significant reduction in power ripples and current THD value compared to the DPC approach. However, its use allows for increasing the complexity of the DPC approach and the difficulty of implementing it. Also, using the BC approach makes the DPC approach related to the parameters of the studied system, which is undesirable, as it increases the impact of the DPC approach and thus reduces the quality of power and current. In work⁴⁷ it was proposed to use a multilevel modified SVM inverter with the BC approach to overcome the problems of the DPC strategy of DFIG-MRWT. In this work, we relied on the seven-level and five-level inverters to improve the THD value of the current and improve the power quality. The proposed strategies are characterized by high efficiency, great robustness, and effectiveness in reducing energy ripples compared to the traditional approach. Simulation results show that the DPC-BC approach based on the seven-level modified SVM technique is more effective in improving power quality and THD of current compared to the DPC-BC strategy based on the five-level modified SVM technique. However, using a multi-level inverter increases the degree of complexity, costs, and difficulty of implementation, which is undesirable. Also, the reliance of the proposed approach on estimating powers increases the degree to which the proposed approach is affected by changes in DFIG parameters, and this is demonstrated by the robustness test. A comparison was made between the BC and SMC approaches in⁴⁸, where these two strategies were used to control the DFIG. In this study, the BC strategy is more complex than the SMC approach. The comparison results showed that the SMC approach has a higher performance than the BC strategy in improving the characteristics of the studied power system. The BC approach provided a larger response time to the speed and flux than the SMC approach. PI controller and SC approach have been combined in⁴⁹ to obtain a powerful and efficient controller. The resulting controller is used to overcome the disadvantages of the DPC strategy of the DFIG-based MRWT system. The SC-PI-DPC strategy is a development and modification approach for the DPC strategy, where the PWM method is used to operate the machine inverter. Simulation results show the higher performance of the SC-PI-DPC strategy compared to the traditional approach and some other approaches in terms of ripple reduction, SSE, and undershoot of DFIG power. The SC-PI-DPC approach has disadvantages that lie in its being affected by changing DFIG parameters, and this appears in the robustness test. Also, the response time to powers is considered a negative of the proposed approach, as it provides a longer time than the traditional approach, which is undesirable. Cascaded fuzzy power control is a modified approach proposed in⁵⁰ to compensate for the use of the DPC technique of DFIG. This approach relies on the use of four fuzzy logic (FL) type controls to replace the traditional HC type control, where two FL controls are used for Ps and the other two FL controls for Qs. In this proposed approach, ST is dispensed with to control the DFIG inverter, as this approach is characterized by high performance and great robustness and this is shown by the numerical results obtained compared to the DPC approach. The proposed strategy reduced in all three tests the THD of the current by approximately 25%, 30.18%, and 47.22% compared to the traditional approach. Also, the response time was reduced compared to the traditional approach by rates estimated at 83.76%, 65.02%, and 91.42% in all completed tests. Despite this high performance, the proposed approach has drawbacks that limit its spread, such as its reliance on estimating powers, the presence of a significant number of gains, and the lack of a rule that facilitates the use of the FL approach, which makes it difficult to apply. The dual super-twisting sliding mode controller (DSTSMC) was used to replace traditional controllers of DPC strategy to control the powers⁵¹, as this controller is characterized by high performance and great robustness. The outputs of DSTSMC controllers are voltage reference values, and the PWM approach was used to convert these reference values into pulses to operate the DFIG inverter. Various tests were used to verify the robustness, performance, and effectiveness of the proposed approach compared to the traditional approach. The simulation results showed high performance, as Ps ripples were reduced in all three tests by rates estimated at 83.33%, 57.14%, and 48.57% compared to the traditional approach. Also, the THD of current was reduced by 72.46%, 50%, and 76.22% in all tests performed. The DSTSMC-DPC strategy has disadvantages that lie in complexity, high costs, and difficulty of implementation compared to the conventional approach. Also, there are a large number of gains which makes dynamic response difficult. In the work⁵², a controller of PI and a proportional derivative (PD) controller were combined in the form of PD(1 + PI) to compensate for using HC in the DPC technique, where two controllers were used to control the characteristic quantities. The PD(1 + PI) control outputs are reference voltage values, as the PWM approach was used to control the operation of the DFIG inverter. The PD(1 + PI)-DPC approach is a modification of the DPC approach, as it uses the same power estimation equations. The simulation results highlight the significant superiority of the PD(1 + PI)-DPC approach in terms of reducing the values of SSE, undershoot, and THD of current compared to the traditional DPC strategy. The PD(1 + PI)-DPC strategy is more complex in terms of implementation than the DPC strategy, which is a negative. Also, in the proposed approach there are a significant number of gains, which makes it difficult to adjust the dynamic response. In the robustness test, it is noted that the PD(1 + PI)-DPC approach is affected by the change in machine parameters and this appears through higher ripple values, THD value, overshoot, and SSE of DFIG power. According to the work done in⁵³, the PI controller gave unsatisfactory results compared to the SMC approach in terms of performance, reference tracking, and robustness. Also, the PI controller gave unsatisfactory results in terms of power ripples and THD of current value compared to the SMC approach. On the other hand, the PI controller gave unsatisfactory results in terms of power ripples for a DFIG-based power system compared to the active disturbance rejection control approach⁵⁴. Given the importance of the PI controller in industrial applications and its numerous advantages, such as simplicity, low-cost, and rapid dynamic response compared to other controllers such as SMCs⁵⁵, it has received significant attention from researchers and students. This interest is reflected in the proposal of appropriate and effective solutions to overcome the problems and shortcomings of the PI controller. The most prominent of these solutions is the use of neural networks⁵⁶, Lyapunov stability theorem⁵⁷, Black Widow optimization algorithm⁵⁸, high-frequency low-pass filter⁵⁹, and dual FL technique⁶⁰. In⁶¹, the author uses a genetic algorithm to improve the performance and efficiency of the PI controller used in the DPC strategy of DFIG. The use of this strategy does not increase the complexity of the PI controller and allows for a significant increase in performance, efficiency, and robustness. This is demonstrated by the results presented compared to the traditional controller and some research work in terms of power fluctuations and THD of current. In⁶², a FL technique-based adaptive PI controller is proposed to replace conventional controllers in the control domain. In this proposed approach, the gains of the PI controller are determined online based on the error signal and its time derivative by a PD-type FLC controller. The method used involves two separate rule bases, one responsible for the gain P and the other for the gain I. According to computer simulations conducted under the same conditions, the results obtained using the proposed method are more promising than those obtained using a conventional fixed-parameter PI controller. However, the proposed controller has a drawback: it lacks mathematical rules that facilitate the selection of the number of FL technique rules to obtain satisfactory results, making it somewhat difficult to obtain good results. Another solution was proposed in⁶³ to overcome the problems and drawbacks of the PI controller to increase performance and efficiency. This proposed solution is the exponential PI (EXP-PI) controller, where high performance, great robustness, and fast dynamic response are the most prominent features of this proposed controller compared to the conventional controller. The gain values ​​of the proposed approach were calculated using the Salp swarm algorithm (SSA). The SSA-tuned EXP-PI controller was implemented using the DSP of TMS320F28335, and the experimental results showed higher performance in reference tracking and torque ripple reduction compared to the conventional approach. In⁶⁴, the exponential PID (EXP-PID) controller is proposed to replace the PI controller in power system control. This controller features a simple design and a nonlinearity characteristic inherited from two adjustable exponential functions placed in front of the PID controller, which affect the error signal and its time derivative individually. The gain values ​​of the EXP-PID controller are calculated using a corrected version of the Snake optimizer (co-SO). This proposed controller has been compared with existing strategies such as PI control, and the results show that co-SO-tuned EXP-PID control, despite its simplicity, offers reliable and promising performance in effectively mitigating the frequency and power biases of the transmission line.

The fuzzy second-order sliding mode approach (FSOSM) is the proposed solution in⁶⁵ to overcome the problems of the DPC strategy of DFIG. FSOSM controller is used to control the powers, where the outputs of these controllers are the reference values ​​of voltage. Besides using the FSOSM controller, the SVM strategy is used to control the operation of the inverter of the DFIG. The proposed approach has high robustness and excellent performance. Simulation results show that using the FSOSM controller is effective in improving the power and current quality compared to the PI controller. The disadvantage of using the FSOSM controller is that it uses the FL technique, as there are no rules that facilitate the selection of the number of rules needed to embody the FL approach. In addition, the use of the SOSM approach is associated with the phenomenon of chattering. This phenomenon creates several undesirable problems.

The FOC approach is one of the strategies that have shown outstanding performance and high robustness in the field of control, as its application leads to a significant improvement of systems⁶⁶. This strategy has been applied in several different energy systems, where it has been used alongside several strategies such as neural networks (NNs)⁶⁷. In this work, a fractional-order NN control is proposed to improve the characteristics of the DPC approach of DFIG-MRWT, where the outputs of this controller are the reference values of the voltage. The PWM approach was used to convert voltage reference values into pulses to operate the DFIG inverter. MATLAB was used to implement the proposed approach, where two different WS profiles were used to test the capabilities of this approach compared to the traditional approach. The results of the completed tests highlight the superiority of the proposed approach over the traditional approach in terms of reducing power ripples, THD value of the current, SSE, and undershoot of DFIG power. However, the proposed approach provided an unsatisfactory capacity time compared to the traditional approach, which is undesirable. In addition, there is no mathematical rule that facilitates the use of NNs, as it mainly depends on the experience of the designer, which requires a large amount of time to determine the best response to the proposed approach. The FOC technique and NN-FL algorithm were combined to improve the characteristics of the DPC approach of DFIG-based MRWT⁶⁸. Using this proposed strategy led to improving the performance and effectiveness of the DPC approach, as this performance appears in improving ripple values, tracking references, robustness, and reducing the THD value of the current. The negative of the DPC-FOC-NN-FL strategy lies in providing a greater response time than the traditional DPC strategy and its reliance on power estimation, which makes it slightly affected by changing DFIG parameters. The effect of this strategy leads to a decrease in the quality of power and current, which creates problems at the network level, which is undesirable. In⁶⁹, a fractional-order fuzzy controller was used to overcome the drawbacks of the DPC approach of the DFIG-based MRWT system. The proposed approach is characterized by high performance, great robustness, and efficiency in reducing power ripples and the THD value of the current compared to the conventional DPC strategy. This approach was applied to the DFIG inverter only, as the PWM approach was used to operate the machine inverter. Two different WS profiles were used to study the behavior of the proposed approach. MATLAB was used to implement it and compare the obtained results with several related research works. Another application of the FOC approach was performed in⁷⁰, where a fractional-order third-order sliding mode controller (FOTOSMC) was used as a suitable solution to overcome the disadvantages of the DPC strategy of the DFIG-based WT system. Two FOTOSMC approaches were used to control the DFIG power, and the outputs of these controllers are the reference values for the voltage. These reference values are converted into pulses using the PWM approach to operate the DFIG inverter. The FOTOSMC approach was implemented in a MATLAB environment using two different WS profiles, comparing the results to the traditional DPC strategy and some scientific works. All completed tests highlight the significant superiority of the FOTOSMC-DPC approach in terms of improving power quality and reducing the THD of current compared to the traditional DPC technique. Using the FOTOSMC-DPC approach has several drawbacks, including the degree of complexity greater than the traditional approach and the presence of a significant number of gains, which make it difficult to adjust the dynamic response. Also, its reliance on estimating powers is affected by changing machine parameters, which is undesirable.

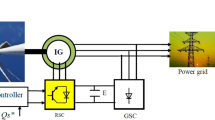
To keep the DPC technique simple and easy to implement with low-cost, increased robustness, and current quality, two fractional-order proportional-derivative proportional-integral (FOPDPI) techniques are proposed here to regulate the DFIG-MRWT power. Therefore, the FOPDPI approach is considered the main contribution of this paper, as it is described by simplicity, ease of realization, and outstanding performance. The second main contribution of the paper lies in relying on an MRWT turbine to convert WE into mechanical energy, which makes the work done new and different from existing work in the literature. The third major contribution of this work is the use of both the PWM strategy and FOPDPI controller to overcome the drawbacks and problems of the DPC strategy of DFIG. The DPC-PDPI-PWM method is completely different from the classical DPC method and several research works^71,72,73 in terms of structure, performance, robustness, and effectiveness in improving power quality and THD value of the current. On the other hand, a FOPDPI controller is used to control the DFIG power. Figure 1 illustrates the proposed technique based on the FOPDPI controller using a schematic diagram. This figure provides a simplified overview of the basic steps involved in implementing this proposed approach.

Fig. 1

Diagram for proposed approach.

The proposed approach is described by high performance, great robustness, and great efficiency in improving the quality of current and power compared to the conventional approach. MATLAB was used to verify the properties and performance of this proposed approach using several different tests. Results were compared in terms of reference tracking, ripple value, response time, SSE, and overshoot of DFIG power. Also, the numerical results of the proposed approach were compared with several related scientific works. Therefore, the objectives achieved by this paper are:

• Overcoming the cons of the DPC approach.

• Improving the current quality by reducing the THD compared to the DPC strategy.

• Significantly increased robustness and effectiveness compared to the DPC strategy.

• Significantly reduced power ripples.

• The SSE value is reduced compared to the DPC strategy.

The work done in this study has been divided into five different main sections. The designed linear regulator to ameliorate the efficiency of the DPC strategy is listed in Section II. In the third section, the DPC-FOPDPI-PWM approach designed to control the RSC of DFIG-MRWT is discussed. Numerical results, comparison with other controls, and graphical results are included in Section IV. Conclusions of the work done are provided in Section V, with future work mentioned as a complement to this work.

Proposed FOPDPI approach

In the field of control, PD and PI controllers have been used in several different applications. In⁷⁴ the use of both PD and PI controllers combined with fractional calculus was proposed as a suitable solution for load frequency control (LFC) of electric power generating systems. The fractional order proportional integral–fractional order proportional derivative (FOPI–FOPD) cascade controller is completely different from the PD and PI controllers in terms of performance and robustness. The gains of the FOPI–FOPD controller were calculated using the dragonfly search algorithm (DSA). Using this algorithm allows obtaining gain values ​​that have the ability to improve the characteristics of the studied system in terms of dynamic response and ripples. The behavior of the FOPI–FOPD controller is compared with the DSA-optimized FOPID controller and recent related works using MATLAB. Different tests are proposed to study the efficiency and effectiveness of the proposed approach. Simulation results show that the proposed DSA-optimized FOPI–FOPD cascade controller contributes significantly to reducing the settling time/decrease/overshoot of frequency and power fluctuations in the interconnection line compared to the FOPID controller. A new controller is proposed in the work⁷⁵ based on the use of the PD and FL approach. This controller is a fuzzy 1 + proportional + derivative-tilt + integral (F1PD-TI) controller. High performance, high robustness, and efficiency are the main features of this proposed controller. The salp swarm algorithm (SSA) is used to calculate the gain values of the F1PD-TI controller. The performance and effectiveness of the proposed approach are verified using MATLAB and compared with the performance of some recent controllers. The obtained results reveal that the proposed approach outperforms other controllers in terms of shorter settling time, lower under/overshoot, and smaller integral squared error values for frequency and offset power deviations. These obtained results and the relatively simpler design of the proposed controller may make it a suitable candidate for other practical applications. The author believes⁷⁶ that the proportional + integral + derivative (PID) controller still forms the backbone of the workload in process control systems. However, these controls have some drawbacks that limit their spread, such as their being affected by changes in the parameters of the system under study. Therefore, a new design methodology of proportional + integral + derivative control with winding protection is introduced, which is combined with a derivative path using a first-order low-pass filter in an innovative way to develop a high-performance controller. The proposed controller is implemented on a DC servo system. The parameters of the proposed controller are calculated using the stochastic fractal search (SFS) algorithm. The effectiveness and efficiency of the algorithm are evaluated using the particle swarm optimization (PSO) algorithm. The proposed approach optimized by SFS is implemented using MATLAB and experimental work, where the results show that the proposed approach optimized by SFS gives a more accurate dynamic speed response compared to the proposed approach tuned by PSO. In⁷⁷, a cascade one proportional derivative incorporating filter (1PDf)-PI controller is proposed as a solution to replace conventional controllers such as PI in the control domain. This proposed controller is used to control the speed of brushless DC motors. Robustness and high performance are the most prominent features of this proposed controller. To improve the performance and efficiency of this controller, a snake optimization algorithm is used to calculate the gain values. Simulations and laboratory experiments were conducted using the DSP of TI TMS320F28335, and the results showed that the proposed approach can greatly improve the reference tracking performance, reduce torque ripples, and significantly increase the robustness of the control system compared to the PI controller. These results, by the observation of this work, confirm that good performance and simplicity are the outstanding advantages of the proposed controller, making it a good alternative to complex controller designs in the future.

To reduce the power fluctuations and THD of the conventional DPC approach, in this section, a new controller is proposed based on the use of PD, PI, and fractional calculus approaches. The proposed controller is used to control powers to overcome problems that hinder the performance, efficiency, efficiency, robustness, and spread of the DPC approach in the field of control. According to scientific works^78,79, PD and PI controllers are characterized by ease of implementation, are inexpensive, easy to implement experimentally, and are characterized by a rapid dynamic response, which makes them an effective solution in several different fields. Also, these controllers have few gains making them easy to adjust. Equations (1) and (2) represent the mathematical form of PD and PI, respectively.

$$u(t) = \mathop K\nolimits_{2} \int {e(t).dt} + \mathop K\nolimits_{1} .e(t)$$

(1)

The PI controller can be expressed by the transfer function represented by Eq. (2).

$${F_{PI}}=\frac{{{K_1}p+{K_2}}}{p}$$

(2)

Where, F_PI is the function transfert of the PI controller.

The model for the PD controller is represented by Eq. (3).

$$w(t) = \mathop K\nolimits_{3} .e(t) + \mathop K\nolimits_{4} \frac{de(t)}{{dt}}$$

(3)

Equation (4) represents the transfer function of the PD controller.

$${F_{PD}}=\frac{{{K_4}p}}{{{K_3}p+1}}$$

(4)

Where, F_PD is the function transfer of the PD controller.

Despite the many advantages of using PD and PI controllers, their use has several drawbacks, as these controllers are affected by changes in the parameters of the studied system. To overcome this problem, it is suggested to use a FOPDPI controller. This controller is a combination of fractional calculus, PI, and PD controllers. To implement the FOPDPI controller, we must first understand the PDPI controller.

A PDPI controller is a combination of two controllers, PD and PI, located in series. This creates a new, high-performance controller, which overcomes the problems of PD and PI controls. Equation (5) represents the mathematical model of a PDPI controller.

$$y\left( t \right)=\left( {{K_3}e\left( t \right)+{K_4}\frac{{de\left( t \right)}}{{dt}}} \right)\left( {{K_1}{e_1}\left( t \right)+{K_2}\smallint {e_1}\left( t \right)dt} \right)$$

(5)

Equation (5) shows that PDPI control differs from the literature in that it is simple, easy to implement, and inexpensive. It is also easy to adjust and does not require knowledge of the mathematical model of the system under study.

The PDPI model can be expressed by the transfer function as shown in Eq. (6).

$${F_{PDPI}}=\frac{{{K_4}p}}{{{K_3}p+1}}\frac{{{K_1}p+{K_2}}}{p}$$

(6)

Where, F_PDPI is the function transfert of the PDPI controller.

The Eq. (6) can be written as follows:

$${F_{PDPI}}=\frac{{{K_4}{K_1}{p^2}+{K_4}{K_2}p}}{{{K_3}{p^2}+p}}$$

(7)

Where, K₁, K₂, K₃, and K₄ are the gains of the PDPI controller. These gains allow for the dynamic response to be modified and adjusted.

Based on Eq. (7) or Eq. (5), the mathematical model of the proposed controller can be extracted. The proposed controller is a combination of the PDPI controller and the fractional calculus strategy. Therefore, the proposed approach is an improvement of the PDPI controller to increase performance and efficiency. This proposed controller uses a type of fractional calculus, is simple, easy to implement and modify, and offers high performance. Using this type of controller does not require precise knowledge of the mathematical model of the system under study, which provides excellent results in the event of a system failure. The FOPDPI controller uses a fractional calculation strategy different from those found in the literature, making the work and proposed controller unique and unparalleled in previous work. This makes the proposed approach significant in the field of control, as the proposed controller plays two roles simultaneously, depending on the value of the fractional calculus.

Based on Eq. (5), the mathematical modeling of the FOPDPI controller is given in Eq. (8). From Eq. (8), the most prominent features of this proposed FOPDPI controller are simplicity, ease of implementation, robustness, high efficiency, and low gain.

$$h\left( t \right)={\left( {\left( {{K_3}e\left( t \right)+{K_4}\frac{{de\left( t \right)}}{{dt}}} \right)\left( {{K_1}{e_1}\left( t \right)+{K_2}\smallint {e_1}\left( t \right)dt} \right)} \right)^\alpha }$$

(8)

Where, h(t) is the output of the proposed controller, α is the gain representing the fractional calculus approach, e and e₁ are the errors, and K₁, K₂, K₃, and K₄ are gains that can take positive or negative values through which the dynamic response is adjusted.

The FOPDPI controller can be expressed by the transfer function as shown in Eq. (9).

$${F_{FOPDPI}}={\left( {\frac{{{K_4}{K_1}{p^2}+{K_4}{K_2}p}}{{{K_3}{p^2}+p}}} \right)^\alpha }$$

(9)

For the proposed controller to be valid, the value of α must not be equal to 0. If the value of α is equal to 1, the proposed FOPDPI controller is a PDPI controller, as shown in Eq. (5). If the value of α is neither 0 nor 1, the proposed approach is a FOPDPI controller. Therefore, to obtain the proposed approach, α must be given a value other than 0 and 1. Therefore, the designed controller plays the role of two different controllers, namely the FOPDPI strategy and the PDPI controller, which gives it an advantage that makes it completely different from the controllers known at present.

Figure 2 represents the internal structure of the proposed approach, where simplicity, ease of realization, few gains, high robustness, and outstanding performance are the most prominent features of this proposed approach. This proposed approach is used in this work to control the power of DFIG-MRWT, where two controllers are used for this purpose.

Fig. 2

Suggested FOPDPI controller.

As shown in Fig. 2, the FOPDPI controller is independent of the mathematical model of the system under study and is not complex. Using this controller does not require complex calculations or extensive memory. Therefore, the FOPDPI controller can be easily used in complex systems. Using the FOPDPI controller requires only knowledge of the error in the quantities to be controlled. Furthermore, the FOPDPI controller can replace traditional control strategies to achieve satisfactory results.

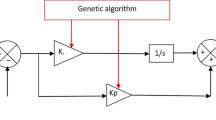
The gain values of the proposed FOPDPI controller are calculated in this work using the simulation and experimentation method. This method is simple and effective in calculating gain values and gives very satisfactory results. Methods that rely on smart strategies can also be used to calculate gain values, such as using a genetic algorithm. However, to use this approach, you need to write complex programs, which are difficult in some cases, especially when the number of gains is large.

The FOPDPI controller is used in this work to overcome the problems of the DPC strategy of DFIG. The next section discusses the DPC strategy based on the FOPDPI controller in detail.

Suggested power control technique

In this section, a new approach for the DPC strategy of the DFIG-based MRWT system is proposed. This new approach relies on the use of a FOPDPI controller and a PWM approach to increase robustness and performance. The proposed approach is a modification and development of the DPC approach, preserving the simplicity and ease of realization that characterize the traditional DPC approach. The traditional controllers (HC) used to control the power for the DPC approach of DFIG are replaced by the proposed controller (FOPDPI), where one controller is used for the Ps and another for the Qs. The outputs of these controllers are reference voltage values ​​and the inputs are power errors. Also, the ST is replaced to control the inverter operation using the PWM strategy, which allows for improved current quality and better control of the inverter operation of the machine. In this way, the drawbacks and problems of the DPC strategy are overcome. Therefore, the DPC-FOPDPI approach with the PWM technique features high performance, high robustness, high efficiency, fast dynamic response, and low cost.

The achievement of the proposed approach for DFIG-MRWT can be summarized in the following steps:

Step 1: Replace conventional controllers with the proposed FOPDPI controller.

Step 2:Replace the switching table with a PWM strategy to control the operation of the machine’s inverter.

Step 3:Extract a three-phase signal from a reference voltage using the Park transform.

Step 4:Find the gain values of the FOPDPI controller. The characteristics of the PWM strategy, such as the frequency of the desired triangular signal, are also determined.

The FOPDPI controller gain values for the proposed approach (DPC-FOPDPI-PWM) can be calculated using intelligent strategies, such as the snake optimization algorithm or grey wolf optimization. Using these strategies requires somewhat complex writing programs. Calculating these gain values does not yield satisfactory results, requiring multiple iterations, which is time-consuming and labor-intensive. The simulation and experimentation method is an easy way to calculate the gain values of the proposed approach, as its use does not require writing any complex programs or a significant amount of time. This method was used to calculate the gain values of the DPC-FOPDPI-PWM strategy, using values that yielded excellent results in terms of power and current quality.

In this proposed approach, the same estimation equations found in the DPC strategy are used. The proposed DPC-FOPDPI-PWM approach was applied to the DFIG inverter only, where the grid inverter was used using an uncontrolled inverter to simplify the system and reduce its cost. Also, to show the extent of the proposed strategy’s ability to improve power quality and the THD of current value without resorting to controlling the grid inverter.

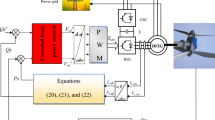
Figure 3 shows the general structure of the proposed approach for DFIG-MRWT power control. Voltage reference values are generated by the proposed FOPDPI controllers to be used later by the PWM strategy in generating the pulses necessary to operate the machine’s inverter. FOPDPI controllers convert power errors into voltage reference values, where each controller used has only one input and output. The proposed approach does not require knowledge of the mathematical model of the studied system, which gives it an advantage if the DFIG parameters change. In this proposed approach, maximum power point tracking (MPPT) is used to generate the Ps reference value. This approach has been discussed in detail in the work^80,81.

On the other hand, Fig. 3 shows that the DPC-FOPDPI-PWM strategy is easy to implement experimentally, as it does not require complex calculations. Furthermore, this strategy makes it easy to adjust the dynamic power response due to the use of a simple and uncomplicated controller. A dSPACE 1104 card can be used to implement this proposed approach experimentally. The proposed approach does not require significant costs to implement experimentally and verify performance and robustness. Furthermore, hardware-in-the-loop testing can be used as an inexpensive method to verify the effectiveness and efficiency of this approach and compare it with other strategies.

Fig. 3

Proposed DPC-FOPDPI approach of DFIG-MRWT.

In this suggested approach, estimation of the DFIG-MRWT power is used, where voltages and supplied currents are measured to calculate the flux. The Qs reference value is set to zero and the reference of the Ps is produced by the MPPT approach.

To calculate the flux, the Eq. (10) can be used⁸².

$$\left\{ {\begin{array}{*{20}c} {\mathop \Psi \nolimits_{r\alpha } = \int\limits_{0}^{t} ( - \mathop R\nolimits_{r} \mathop I\nolimits_{r\alpha } + \mathop V\nolimits_{r\alpha } )dt} \\ {\mathop \Psi \nolimits_{r\beta } = \int\limits_{0}^{t} ( - \mathop R\nolimits_{r} \mathop I\nolimits_{r\beta } + \mathop V\nolimits_{r\beta } )dt} \\ \end{array} } \right.$$

(10)

Where, V_rβ and Vrα are the voltage linkage of β and α-axis.

Ψ_rβ and Ψ_rα are the flux linkage of β and α-axis.

Equation (11) represents the flux of DFIG.

$${\Psi _r}=\sqrt {\Psi _{{r\alpha }}^{2}+\Psi _{{r\beta }}^{2}} .$$

(11)

The Eq. (12) can be used to calculate the flux, as voltage is used for this purpose.

$$\left| {\overline{{\mathop \Psi \nolimits_{r} }} } \right| = \frac{{\left| {\overline{{\mathop V\nolimits_{r} }} } \right|}}{{\mathop w\nolimits_{r} }}$$

(12)

Where, V_r is the rotor voltage.

This proposed approach depends on estimating energies, using the same equations used in^83,84. To estimate powers, Eqs. (13) and (14) can be used for this purpose.

$${P_s}= - \frac{3}{2}\frac{{Lm.Vs.{\psi _{r\beta }}}}{{\sigma .Ls.Lr}}$$

(13)

$${Q_s}= - \frac{3}{2}\left( {\frac{{Vs}}{{\sigma .Ls}} \cdot {\psi _{r\beta }} - \frac{{Vs.Lm.{\psi _{r\alpha }}}}{{\sigma .Ls.Lr}}} \right)$$

(14)

Where, Lm is the mutual inductance.

$$\sigma = 1 - \frac{{\mathop M\nolimits^{2} }}{{\mathop L\nolimits_{r} \mathop L\nolimits_{s} }}$$

(15)

In the DPC-FOPDPI approach, the reference of both direct and quadrature voltages are produced by the Eqs. (16) and (17).

$$V_{{dr}}^{*}={(\left( {{K_3}{e_{Qs}}+{K_4}\frac{{d{e_{Qs}}}}{{dt}}} \right)\left( {{K_1}{e_1}\left( t \right)+{K_2}\smallint {e_1}\left( t \right).dt} \right))^\alpha }$$

(16)

$$V_{{qr}}^{*}={(\left( {{K_3}{e_{Ps}}+{K_4}\frac{{d{e_{Ps}}}}{{dt}}} \right)\left( {{K_1}{e_1}\left( t \right)+{K_2}\smallint {e_1}\left( t \right).dt} \right))^\alpha }$$

(17)

Equations (16) and (17) can be represented by Fig. 4, as this figure shows the controllers used to control DFIG-MRWT power. Therefore, ease of application and simplicity are among the most prominent features of these regulators. The number of gains can be considered a negative for these controllers, as there are four gains for each control, which makes it difficult to adjust the response easily.

Fig. 4

Proposed power controller.

In Table 1, the similarities and differences between the proposed approach and the DPC strategy are given. From this table and the information presented above, the proposed approach is more complex than the DPC approach. However, in terms of robustness and performance, the proposed approach is more efficient than the DPC approach. The proposed approach has similarities to the traditional approach in terms of structure and use of the same estimation equations.

Table 1 Compare the traditional DPC strategy with the proposed approach.

To study the stability of the proposed approach, one can rely on the Lyapunov theorem or use the Bode curve. In the case of using the Lyapunov theorem, calculations such as derivation are required. These calculations are in some cases complicated and lead to incorrect results. However, the Bode curve is a graphical method for studying the stability of control strategies, as it is characterized by ease and high accuracy. The Bode curve does not require complex calculations, as MATLAB is used to extract it. In this work, the Bode curve is relied upon to prove the stability of the DPC-FOPDPI-PWM strategy. The Bode curve is based on extracting the values ​​of both phase (deg) and magnitude (dB). By these values, the stability of the DPC-FOPDPI-PWM approach is proven. Figure 5 represents the Bode curve for the two controls.

Figure 5a represents the Bode curve for the DPC-PI approach. From this curve, it is observed that the values ​​of both phase (deg) and magnitude (dB) change with the change in frequency. The value of phase (deg) changes from 0 to – 180 degrees and the value of magnitude (dB) changes from + 9 to – 80 dB. Therefore, the values ​​of both magnitude (dB) and phase (deg) are negative, which makes the values ​​of both phase margin and margin gain positive. In the case of magnitude (dB) equals 0 dB, the value of phase (deg) is equal to – 81 degrees. Therefore, the value of the phase margin is equal to 99 deg. Thus, the value of the phase margin is positive and thus the DPC-PI technique is stable.

Figure 5b represents the Bode curve of the DPC-FOPDPI-PWM approach. In this figure, the curves of both Magnitude (dB) and phase (deg) are extracted. From these curves, it is observed that the values ​​of both Magnitude (dB) and phase (deg) change with the change of frequency, where the range of variation of Magnitude (dB) is from + 1 to – 150 dB and the range of variation of phase (deg) is from 0 to – 360 degrees. So, both Magnitude (dB) and phase (deg) are negative values, which is good because it makes the values ​​of both phase margin and gain margin positive. It is observed from Fig. 5b that in case the Magnitude (dB) is equal to 0 dB, the value of phase (deg) is approximately equal to – 72 degrees. Therefore, the phase margin value is + 108 degrees. Since the phase margin value is positive, the DPC-FOPDPI-PWM technique is stable.

Fig. 5

Bode curve of both techniques.

Results

In this section, the efficacy of the suggested DPC-FOPDPI-PWM approach is verified in comparison with the DPC-PI approach using MATLAB, in terms of fluctuations value, THD, reference traceability, robustness, and SSE of the DIG-MRWT power. The DFIG parameters used in this work are 50 Hz, 1500 kW, Lm = 13.5 mH, Rs = 12 mΩ, 380/690 V, Rr = 21 mΩ, fr = 0.0024 N.m/s, Lr = 13.6 mH, p = 2, J = 1000 Kg m², Ls = 13.7 mH⁷¹.

Table 2 presents the controller gain values used in this work. These gains were calculated using simulation and experimentation.

Table 2 Controller gain values.

Figure 6 represents a block diagram of the proposed technique in MATLAB. This figure gives a clear picture of the work done. Figure 6a represents the FOPDPI controller implemented in MATLAB without using a transfer function.

Figure 6b represents the mathematical model of the DFIG implemented in MATLAB.

Figure 6c is a MATLAB image of the DPC-FOPDPI strategy using the PWM technique. This figure illustrates all the components of the proposed approach, such as power estimation and Park transform.

Figure 6d is a MATLAB image representing both controls together.

Fig. 6

Block diagram of the proposed technique from MATLAB.

To test the effectiveness and efficiency of the proposed approach compared to the DPC-PI approach, five different tests were proposed. The next test examines the behavior of the proposed approach under variable WSs.

Test 1

This test aims to compare graphical/numerical results with the DPC-PI strategy and investigate the efficiency of the recommended control in tracking references. The results of this test are represented in Figs. 7 and 8. Figure 9 represents the zoom-in results of the first test. Also, the numerical results are listed in Table 3. The WS change profile is listed in Fig. 7a, where the efficiency and performance of the proposed approach were tested using the WS in steps. From Fig. 7b and c, the powers follow the references well, with ripples at the power level. These fluctuations are lower when using the proposed approach compared to the DPC-PI approach (see Fig. 7a and b). Also, it is noted that the Ps changes with a change in WS, and the Qs do not change with a change in WS, as it takes a fixed value equal to 0 VAR.

Figure 7d represents the torque change as a function of time for the two approaches. From this figure, it is noted that the torque has the same form as the change in Ps, as it takes negative values, and this is evidence that the machine generates power. Also, it is noted that the torque has a rapid dynamic response, with ripples at the level of this torque. These undulations are less if the proposed approach is used, and this is evidence of the ability and effectiveness of the proposed approach in improving torque quality compared to the DPC-PI approach (see Fig. 9c).

Figure 7e represents the current for the two approaches. It is noted that the change in current is according to the change in Ps, with the proposed approach having an advantage over the DPC-PI approach in terms of the quality of the current. Also, the current has a sinusoidal shape for both controls. According to Fig. 9d, the current ripples are low in the case of using the proposed approach compared to the DPC-PI approach, which highlights the effectiveness and strength of this approach.

Figure 8 represents the signal amplitude value fundamental signal (50 Hz) and THD of current for both techniques. From this figure, it is noted that the proposed DPC-FOPDPI-PWM strategy provided a better THD value than the DPC-PI approach, which was about 0.47% for the proposed approach and 0.71% for the DPC-PI approach. Therefore, the DPC-FOPDPI-PWM strategy lowered the THD value by an estimated 33.80% compared to the DPC-PI strategy. However, the proposed strategy provided the fundamental signal (50 Hz) amplitude almost equal to that of the DPC-PI approach, where the amplitude value was 462.80 A and 462.70 A for both the DPC-PI technique and the proposed approach, respectively. This drawback can be attributed to the gains of the proposed approach, as smart strategies can be used to overcome this drawback in the future.

Fig. 7

Results of the first test (Step WS profile).

Fig. 8

THD value of the current (Test 1).

Fig. 9

Zoom in the results of the test 1.

Table 3 represents the values and reduction percentages obtained from the first test. From this table, it is noted that the proposed approach provided satisfactory results compared to the DPC-PI approach in terms of ripples, overshoot, and SSE of DFIG power. The DPC-FOPDPI-PWM approach reduced the ripple value of both Qs and Ps compared to conventional DPC-PI by 47.07% and 46.67%, respectively. Also, the proposed approach reduced the SSE value of both Ps and Qs significantly compared to the DPC-PI approach. This reduction was estimated at 44.72% and 46.16% for Ps and Qs, respectively. The designed approach also significantly reduced the overshoot of DFIG energy compared to the DPC-PI approach, as this reduction was estimated at a percentage of 91.84% for Ps compared to the DPC-PI technique. These percentages indicate the high performance and effectiveness of the proposed approach in improving energy quality compared to the DPC-PI approach. However, the proposed approach provided an unsatisfactory turnaround time compared to the DPC-PI approach. Accordingly, the DPC-PI approach reduced the response time for powers by percentages estimated at 40.57% and 59.10% for Ps and Qs, respectively, compared to the proposed approach. Also, the proposed approach gave poor results for the overshoot of Qs compared to the DPC-PI technique. These drawbacks can be attributed to the gain values ​​of the DPC-FOPDPI-PWM technology, and these drawbacks can be overcome in the future by using other methods integrated with the designed approach.

Table 3 The SSE, response time, overshoots, and ripples ratios of the Ps/Qs (First test).

The performance of the proposed approach in the first test, compared to the DPC-PI approach, is verified in the second test. In the subsequent test, the performance of the proposed approach is verified in the event of a change in the machine parameters.

Test 2

In this part, the effectiveness of the DPC-FOPDPI-PWM approach is investigated, and the DFIG parameters were modified to study the effectiveness of the proposed DPC-FOPDPI-PWM compared to the effectiveness of the DPC-PI approach. The parameters were changed by multiplying the resistors by 2 and multiplying the coil values ​​by 0.5. The results of this test are shown in Figs. 10 and 11. Zoom in the second test results are listed in Fig. 12. Also, the numerical results are listed in Table 4. In this test, the same WS profile used in the first test is used.

The powers are represented in Fig. 10a and b. Through these two figures, the powers continue to follow the references despite the change in parameters and the presence of ripples. These ripples increased significantly in the second test compared to the first test, and this is evidence that the power quality is affected by changing the DFIG parameters. These fluctuations are lower when using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach (see Fig. 12a and b). Even though the machine parameters change, the Ps continues to change according to the change in WS, and the Qs remain constant and take a value of 0 VAR.

Figure 10c represents the torque for the two approaches. From the figure, it can be seen that the torque has a fast dynamic response to the two techniques. This torque takes negative values ​​and changes according to the change in Ps. Also, it is noted that there are fluctuations at the torque level, as these fluctuations are larger in the case of using the DPC-PI approach compared to the DPC-FOPDPI-PWM approach (see Fig. 12c).

Figure 10d represents the change in a current as a function of time for the two approaches. This current continues to take the form of a change in Ps despite the change in the DFIG parameters. This current remains sinusoidal, with the DPC-FOPDPI-PWM approach having an advantage in terms of quality compared to the DPC-PI approach. According to Fig. 12d, the current ripples are very low when using the proposed approach compared to the DPC-PI strategy, which highlights the effectiveness and efficiency of this approach in reducing current ripples.

Figure 11 represents the THD value for the two approaches. From this figure, it is noted that the THD value of the stream was 1.29% for the DPC-PI strategy and 0.84% for the DPC-FOPDPI-PWM technique. Through these values, the DPC-FOPDPI-PWM approach gave a better value for THD compared to the DPC-PI approach, as the percentage of THD reduction was estimated at 34.88% compared to the DPC-PI approach. This percentage confirms that the quality of the stream is high despite the change in machine parameters in the case of using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach. Figure 11 also shows that the amplitude value of the fundamental signal (50 Hz) is the same in both control cases. The amplitude value in this test for both controls is estimated to be 474.90 A. Compared with the first test, the amplitude value in this test is significantly affected by the change of DFIG parameters. Therefore, it can be said that the amplitude value is affected by the change in machine parameters.

Fig. 10

Results of the second test.

.

Fig. 11

THD value of the current (Test 2).

Fig. 12

Zoom in the results of the Test 2.

Table 4 represents the reduction ratios and values of ripple, response time, overshoot, and SSE of DFIG power. This table shows that the SSE value for both Qs and Ps is lower when using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach, as this reduction was estimated at 46% and 59.39% for both Ps and Qs, respectively.

The DPC-FOPDPI-PWM approach gave much lower power ripple values ​​than the DPC-PI approach, where the DPC-FOPDPI-PWM approach reduced the ripples by 48.85% and 46.32% compared to DPC-PI for Ps and Qs, respectively. The overshoot value of the Ps is significantly lower when using the proposed approach compared to the DPC-PI approach. The overshoot value of Ps is reduced by 48.09% compared to the DPC-PI strategy. These results indicate the higher performance of the DPC-FOPDPI-PWM strategy compared to the DPC-PI approach, making it a promising solution in many fields in the future.

Despite this high performance of the proposed approach, it provided an unsatisfactory time compared to the DPC-PI approach. The DPC-PI approach provided better time, as the power time was reduced by percentages estimated at 35.75% and 48.78% for both Ps and Qs, respectively, compared to the proposed approach. Also, the proposed approach gave unsatisfactory results for Qs overshoot compared to the DPC-PI strategy. The DPC-PI strategy reduced the Qs overshoot value by 31.69% compared to the DPC-PI strategy. These drawbacks can be attributed to the gains values ​​of the proposed controller used to control the Qs. These drawbacks can be overcome in the future by using the snake optimization algorithm or PSO technique.

Table 4 The SSE, overshoots, response time, and ripples ratios of the Ps/Qs (Second test).

Table 5 represents the change in the values ​​of amplitude of the fundamental signal (50 Hz) and THD for the two controls between the first and second tests. From this table, it is noted that these values ​​increased significantly in the second test compared to the first test, which indicates that these values ​​are affected by changes in the DFIG-MRWT parameters. In the case of the THD value, the difference between the first and second tests was + 0.58% and + 0.37% for both the DPC-PI approach and the DPC-FOPDPI-PWM technique, respectively. Therefore, the DPC-FOPDPI-PWM approach presented less difference than the DPC-PI approach. On the other hand, the amplitude value was increased in the second test compared to the first test for both controls. This increase in amplitude value can be attributed to the influence of the DFIG parameters on the two controls. The difference in fundamental signal (50 Hz) amplitude value between the first and second tests was estimated to be + 12.10 A and + 12.20 A for both DPC-PI and DPC-FOPDPI-PWM approaches, respectively. Thus, the DPC-FOPDPI-PWM approach presented a smaller amplitude difference than the DPC-PI approach, which highlights the effectiveness and robustness of the proposed approach. From this table, it can be concluded that changing the DFIG parameters affects the amplitude and THD of the current. Also, the proposed approach presented a smaller impact than the DPC-PI technique, which makes it a promising solution.

Table 5 Study of the effect of the amplitude value of fundamental signal (50 Hz) and THD value between the first and second tests for the two approaches.

Test 3

This test is different from the tests performed above in terms of the WS profile used. In this test, the effectiveness of the proposed approach is studied in the case of random WS. Numerical results are listed in Table 6 and graphical results are represented in Figs. 13 and 14. The variable WS profile used is represented in Fig. 13a. Zoom the results of the third test for two controls are shown in Fig. 15.

Figure 13b and c represent the change in DFIG power as a function of time. These powers keep track of the references well, with a fast dynamic response when using both approaches. From Fig. 13b, it is noted that the Ps continues to take negative values ​​and the form of its change is the same as the form of the change in WS. Also, it is noted that there are ripples at the Ps level, as these ripples are low when using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach (see Fig. 15a). From Fig. 13c, it is noted that the reflective power is not affected by the change in WS, as it remains equal to the value 0 VAR throughout the simulation period in the presence of fluctuations. These fluctuations are larger if the DPC-PI approach is used compared to the proposed approach (see Fig. 15b). These results highlight the strength of the DPC-FOPDPI-PWM approach in improving the energy quality and characteristics of the studied energy system compared to the DPC-PI approach.

The torque for the two approaches is represented in Fig. 13d. This torque takes negative values and changes according to the change in Ps in the presence of ripples. These fluctuations are lower when using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach (see Fig. 15c).

The current for the two approaches is represented in Fig. 13e, where the current takes a sinusoidal shape. These current changes according to the change in WS with the presence of fluctuations. It is noted that the current fluctuations are lower when using the DPC-FOPDPI-PWM approach compared to the DPC-PI approach (see Fig. 15d).

Figure 14 represents the THD value of the current for both techniques. From this figure, it is noted that the THD value was 2.17% and 1.92% for both the DPC-PI approach and the DPC-FOPDPI-PWM approach, respectively. Therefore, the proposed approach reduces the THD value by an estimated percentage of 11.52% compared to the DPC-PI approach. This percentage indicates that the quality of the current is greater if the DPC-FOPDPI-PWM approach is used. However, the designed approach provided a larger fundamental signal (50 Hz) amplitude than that provided by the DPC-PI approach. This amplitude was equal to 264.30 A and 263.60 A for the proposed approach and the DPC-PI strategy, respectively. These results highlight the effectiveness of the proposed approach, making it a reliable solution for the future.

Fig. 13

Results of the third test.

Fig. 14

Current THD (Test 3).

Fig. 15

Zoom in the third test.

Table 6 represents the values ​​and percentages of reduction for SSE, response time, overshoot, and fluctuations in the third test. From this table, it is noted that the DPC-FOPDPI-PWM approach provided better values ​​for SSE, overshoot, and ripples compared to the DPC-PI approach. The DPC-FOPDPI-PWM approach reduces the values ​​of SSE, overshoot, and ripples Ps by approximately 76.42%, 65.32%, and 50%, respectively, compared to the DPC-PI approach. In the case of Qs, the values ​​of SSE and ripples were minimized by 43.37% and 43.39%, respectively, compared to the DPC-PI approach. Despite these good results, the proposed approach gave an unsatisfactory response time of the power compared to the DPC-PI approach, which is a negative. Also, the proposed approach gave an unsatisfactory overshoot of Qs compared to the DPC-PI technique. Therefore, it can be said that the response time of the power and overshoot of Qs are the negatives of the proposed approach in this test. These drawbacks can be attributed to the values ​​of the control gains used to control the powers, as these drawbacks can be overcome in the future by using grey wolf optimization to adjust the values ​​of these gains.

Table 6 The SSE, response time, overshoots, and ripples ratios of the Ps/Qs (Third test).

Table 7 represents a study of the effect and change of amplitude value of the fundamental signal (50 Hz) and THD value as a function of changing the shape of the WS. From this table, we notice that changing the WS shape affects the values ​​of both capacity and THD significantly, as we notice that the THD value increased significantly in the third test compared to the first test. Therefore, the variable WS affects the THD value significantly compared to the WS in steps. The difference in the THD value between the first and third tests was estimated to be about + 1.45% and + 1.46% for both the DPC-FOPDPI-PWM approach and the DPC-PI approach, respectively. Therefore, the DPC-FOPDPI-PWM approach presented a smaller difference than the DPC-PI technique, highlighting its power in improving the THD value. However, the table shows that the amplitude value in the third test was significantly reduced compared to the first test for the two controls. This difference in amplitude value between the first and second tests was estimated to be -198.40 A and − 199.20 A for the DPC-FOPDPI-PWM approach and the DPC-PI approach, respectively. Therefore, it can be said that the DPC-FOPDPI-PWM approach provided a smaller amplitude difference than the DPC-PI strategy. Thus, the proposed approach has less impact than the DPC-PI technique, which highlights its effectiveness and efficiency in improving the properties of the studied system. These results make the proposed approach of interest in other applications.

Table 7 Study of the effect of the amplitude value of fundamental signal (50 Hz) and THD value between the first and third tests for the two techniques.

Test 4

The fourth test is different from the previous tests. In this test, the same WS as in the third test is used. However, the reference value of the Ps is set to a constant value of 120,000 W. This test aims to study the effectiveness of the proposed approach in case the MPPT strategy is not used to calculate the reference value of the Ps. Also, the effectiveness and robustness of the proposed approach are tested in the case of a constant Ps meadow and a reference Qs equal to 0 VAR.

The results of this test are listed in Figs. 16 and 17. Table 8 lists the numerical values ​​of the fourth test.

According to Fig. 16, the power flow of the references well and is not affected by the change in WS, which proves the effectiveness and robustness of the strategies used. The powers have a fast dynamic response with the presence of undulations.

Figure 16c represents the torque change for the two controllers. This torque takes a constant value for the two controllers. The shape of the torque change is the same as the shape of the Ps change, which is the same observation found in the previous tests. Also, it is noted that the torque has a fast dynamic response with ripples. Figure 16d represents the current for the two controllers. The value of this current is related to the Ps. Also, it is noted that this current takes a sinusoidal shape, with the proposed approach having an advantage over the DPC-PI approach in terms of quality.

Figure 16e and f represent the values ​​of both amplitude and THD of current. From these figures, the THD value was 1.49% and 0.93% for the DPC-PI approach and the proposed approach, respectively. These values ​​highlight the superiority of the proposed approach and its effectiveness in reducing the THD value. Thus, the proposed approach reduced the THD value by 37.58% compared to the DPC-PI strategy. Figure 16e and f show that the amplitude value was almost equal in the case of using the two controls. This amplitude value was estimated to be 210.40 A and 210.30 A for the DPC-PI approach and the proposed approach, respectively. From the presented amplitude values, it can be said that the DPC-PI technique outperforms the proposed approach. This disadvantage can be attributed to the gain values ​​of the proposed controls. In the future, this disadvantage can be overcome by using other strategies such as genetic algorithms.

Fig. 16

Results of the test 4.

Figure 17 represents the Zoom in test results. From this figure, it is observed that the proposed approach reduces the ripples of power, current, and torque significantly compared to the DPC-PI technique. Therefore, the proposed approach improves the quality of current and power to a greater extent compared to the DPC-PI strategy, which highlights its strength and effectiveness. These results make the proposed approach of interest in other applications such as photovoltaic systems.

Fig. 17

Zoom in the results of the test 4.

Table 8 presents the numerical results of the fourth test of the two controllers. In this table, the reduction ratios of SSE, response time, overshoot, and ripples of DFIG power were calculated. From this table, the proposed approach gave satisfactory values ​​for SSE, ripples, and overshoot. However, it gave unsatisfactory results in terms of response time compared to the DPC-PI technique. In the case of Ps, the proposed approach reduces SSE, ripples, and overshoot by 48.79%, 41.18%, and 82.88%, respectively, compared to the DPC-PI technique.

In the case of Qs, the proposed approach reduces the value of SSE and ripples by 41.58% and 43.65% respectively compared to the DPC-PI technique. However, in terms of the overshoot of Qs, the proposed approach gives unsatisfactory results compared to the DPC-PI technique. The DPC-PI approach reduces the value of overshoot of Qs by 95.86% compared to the DPC-PI technique. Therefore, it can be said that the overshoot of Qs and the response time of the powers are the drawbacks of the proposed approach in this test. These drawbacks can be overcome in the future by using neural networks or FL technique.

Table 8 The response time, overshoots, SSE, and ripples ratios of the Ps/Qs (Test 4).

Table 9 represents the study of the extent to which the values ​​of both amplitude (fundamental signal (50 Hz)) and THD of two controls are affected between the third and fourth tests. This table shows that the THD value decreased significantly in the fourth test compared to the third test. Therefore, it can be said that not using the MPPT strategy to obtain the reference value of the Ps affects the THD value. The difference in the THD value between the two tests was estimated to be -0.99% and − 0.68% for the DPC-PI technique and the proposed approach, respectively. Through these values, it is noted that the proposed approach provided a smaller difference in the THD value compared to the DPC-PI technique, which highlights the effectiveness and strength of the proposed approach. Therefore, the effect of the THD value between the two tests in the case of using the proposed approach is much better than in the case of using the DPC-PI technique.

Table 9 shows that the amplitude value (fundamental signal (50 Hz)) of the two controllers decreased in the fourth test compared to the third test. This decrease can be attributed to not using the MPPT strategy in calculating the reference value of Ps. The difference in amplitude value was estimated to be − 54 A and − 53.20 A for the DPC-PI and proposed approaches, respectively. Therefore, this decrease was estimated at 20.43% and 20.18% for both the DPC-PI and proposed approaches, respectively. These percentages show that the proposed approach had a lower impact than the DPC-PI technique, which is a good thing. Therefore, it can be said that the MPPT strategy affects the value of both the amplitude and THD of the current, where not using the MPPT approach leads to a decrease in the value of the amplitude and the value of THD of the current.

Table 9 Study of the effect of the amplitude value of fundamental signal (50 Hz) and THD value between the third and fourth tests for the two techniques.

Test 5

In the fifth test, the proposed approach is studied in terms of not using the MPPT strategy to calculate the reference value of the Ps. In this test, the reference value of the Ps is set in steps. The fifth test differs from the fourth test in terms of the reference value for the Ps used, as in the fourth test a fixed reference value was used, and in this test, a reference value that changes in steps was used. The results of this test are presented in Figs. 18 and 19. The numerical results of this test are presented in Table 10. Figure 18a and b represent the powers of two approaches. These powers follow the reference well with a fast dynamic response. The powers do not change with the change in WS due to not using the MPPT strategy. It is also noted that the Ps remain negative and the Qs remain zero, which are the same observations found in the previous tests. Figure 18c represents the change in torque concerning time for the two controllers. This torque takes negative values ​​with the presence of ripples. The shape of the torque change is the same as the shape of the Ps change.

Figure 18d represents the change in current for the two controls in the case of using the reference value of the Ps variable in steps. From this figure, it is noted that the value of current is related to the change in Ps, which is the same observation found in the previous tests. Also, the current remains in the form of a sinusoid for the two controls, with the proposed approach having an advantage over the DPC-PI technique in terms of quality. Figure 18e and f represent the value of THD of current in the case of using the two controls. The value of THD was equal to 0.21% for the DPC-PI technique and 0.14% for the proposed approach. Thus, the proposed approach significantly reduced the THD value compared to the DPC-PI technique. This reduction in THD value was estimated to be 33.33% compared to the DPC-PI technique. From Fig. 18e and f, it is observed that the amplitude value was estimated to be 1676 A for both approaches. Therefore, both approaches presented the same amplitude value in the fifth test. These obtained results highlight the superiority of the proposed approach and its high capacity, which makes it a promising solution for the future.

Fig. 18

Results of the test 5.

Figure 19 represents the Zoom in the fifth test results of the two controllers. From this figure, it is observed that the ripples of power, current, and torque are higher in the case of using the DPC-PI technique compared to the proposed approach. Therefore, the proposed approach improves the ripple value significantly compared to the DPC-PI technique. These results highlight the effectiveness, efficiency, and robustness of the proposed approach, making it a suitable solution for other industrial applications.

Fig. 19

Zoom in the results of the Test 5.

Table 10 presents the numerical results with the reduction ratios of ripples, response time, overshoot, and SSE of DFIG power in the case of using both controls. In the case of Qs, the proposed approach reduces the values ​​of SSE, overshoot, and ripples by 57.53%, 81.40%, and 42.18% respectively compared to the DPC-PI technique. In the case of Ps, the proposed approach gives very satisfactory values ​​of ripples, SSE, and overshoot compared to the DPC-PI technique. The proposed approach improves the values ​​of ripple and SSE by 92.31% and 46.67%, respectively, compared to the DPC-PI technique. The proposed approach gives the same results as the DPC-PI technique in terms of the overshoot of Ps. However, the DPC-PI technique gave a better response time than the proposed approach. Therefore, the response time of the powers can be considered as the disadvantage of the proposed approach in this test. This disadvantage can be overcome by combining the proposed approach with other strategies such as the SC technique.

Table 10 The response time, overshoots, SSE, and ripples ratios of the Ps/Qs (Test 5).

Table 11 represents a study of the changes in the values ​​of THD of currant and amplitude of the fundamental signal (50 Hz) of both techniques. From this table, it is noted that the THD value decreased in the fifth test of the two controls compared to the fourth test. This decrease is due to the use of the reference value of the Ps in the form of steps. Therefore, it can be said that the reference value of the Ps greatly affects the THD value. The reduction in THD value was estimated at 84.95% and 85.1% for the DPC-PI and proposed approaches, respectively. Therefore, the proposed approach gave a greater reduction in THD value than the DPC-PI strategy, which highlights the power of the proposed approach in reducing THD value and improving current quality. Table 11 shows that using the Ps reference value in steps has a significant advantage in improving the amplitude value compared to using a fixed reference value. The amplitude value increased significantly in the fifth test compared to the fourth test. The difference in the amplitude value was estimated to be + 1465.70 A for the DPC-PI strategy and + 1465.6 A for the proposed approach. The percentage of influence in the amplitude value for the two approaches was estimated to be 87.45%. Therefore, the two approaches presented the same percentage of influence in the amplitude value.

Table 11 Study of the effect of the amplitude value of fundamental signal (50 Hz) and THD value between the fourth and fifth tests for the two techniques.

Finally, the results obtained from the proposed approach are compared with related works. This comparison is necessary, as it proves the effectiveness and efficiency of the proposed approach with other existing strategies. This comparison with related works is listed in Tables 12 and 13. In these tables, a comparison is made in terms of the reduction ratios of power ripples and the SSE of DFIG power. According to Table 12, the proposed approach gave higher SSE reduction ratios than several related works. For example, in work⁴⁶, the SSE reduction ratio was estimated at 35%, while in the proposed approach it was estimated at 76.42% (variable wind speed case). Also, according to Table 13, the proposed approach gave higher power ripple reduction ratios than several related works. The reduction ratio of the reactive power ripples in work⁴⁹ was estimated to be 39.23% while in the proposed approach it was 43.39% (variable wind speed condition). Therefore, it can be said that the proposed approach has an excellent and effective performance compared to many related works, which makes the proposed approach a promising solution in other industrial fields.

Table 12 Comparison table in terms of SSE for Qs and Ps.

Table 13 Comparison in terms of power ripples minimization rates.

Table 14 compares the THD of current with other related works. This table shows that the proposed approach achieved significantly better THD values ​​than several other works in all tests. The THD value in work⁸⁷ was 3.1%, and in work⁸⁸ it was 4.05% and 10.79%. All of these values ​​provided by these works are higher than the value provided by the proposed approach in the third test, for example. This comparison highlights the strength and effectiveness of the proposed approach in improving THD and thus enhancing current quality. Therefore, this comparison is of great importance, as it makes the proposed approach a reliable solution for other industrial applications.

Table 14 Comparison in terms of THD values of current.

Conclusions

In this study, the competence of the DPC-FOPDPI-PWM approach of the DFIG-MRWT is studied. The FOPDPI controller was used to regulate the DFIG power, and its performances were analyzed and investigated compared to the DPC-PI approach. The DPC-FOPDPI-PWM approach has been tested for its properties in terms of overshoot, power fluctuations, SSE value, reference tracking, THD of supplied DFIG streams, and robustness. The designed DPC-FOPDPI-PWM approach was used to command the DFIG-MRWT inverter, where the results showed high efficacy compared to the DPC-PI strategy. As a result, the following points can be used to summarize the study’s findings:

• Verifying the competence and efficacy of the FOPDPI regulator.

• Overcoming the disadvantages of the DPC-PI approach.

• Increasing the current quality by minimizing the THD by 33.80%, 34.88%, 11.52%, 37.58%, and 33.33% in the three suggested tests.

• Reducing the SSE value of Ps compared to the DPC-PI approach by percentages estimated at 44.72%, 46%, 76.42%, 48.79%, and 92.31% in all tests performed. In the case of Qs, the SSE value was reduced in all tests by 46.16%, 59.39%, 43.37%, 41.58%, and 57.53% compared to the DPC-PI approach.

• Reduced Ps ripples compared to the DPC-PI strategy by percentages estimated at 46.67%, 48.85%, 50%, 41.18%, and 46.67% in all tests.

• Reduced Qs ripples compared to the DPC-PI strategy by ratios estimated at 47.07%, 46.32%, 43.3%, 43.65%, and 42.18% in all tests.

The efficiency of the suggested approach can be increased by using intelligent methods such as genetic algorithms to calculate the parameters of the proposed regulator, as this will be future work in addition to implementing this approach experimentally and verifying the extent of performance and results obtained.