TSTA-GCN: trend spatio-temporal traffic flow prediction using adaptive graph convolution network

Abstract

Balancing the need to satisfy both long-term and short-term requirements and comprehensively considering spatial and temporal dependencies are key challenges in metro passenger prediction. A trend spatio-temporal adaptive graph convolution network (TSTA-GCN) model for metro passenger flow prediction is presented in this paper. A trend convolutional self-attention model is designed to learn long-term and short-term trends. Adaptive graph is utilized to capture the complex relationships between stations and an adaptive graph convolutional recurrent unit module is proposed to capture local spatial and dynamic spatio-temporal correlations. In order to simulate the spatio-temporal heterogeneity implied in traffic flow, a spatio-temporal interaction module is used to fuse the heterogeneity in space and time. Extensive experiments are carried out on two metro traffic flow datasets and the experimental results show that the TSTA-GCN model outperforms the state-of-the-art baseline methods and is able to effectively predict long-term and short-term metro passenger flow.

Introduction

In recent years, with the development of artificial intelligence and big data technology, Intelligent Transportation System (ITS)^1,2,3 has been greatly improved in traffic safety and efficiency. As a high-speed, economical and punctual mode of transportation, the subway plays an important role in the modern urban transportation system^4,5. However, at present, the mismatch between people’s travel demands and metro services is becoming increasingly serious. Once high-traffic nodes on the metro network are congested, it will lead to negative travel experiences or even serious consequences. Accurate traffic flow prediction can not only provide convenience for people, but also provide guidance to make transportation decisions.

The prediction of metro passenger flow can be classified into short-term, medium-term and long-term predictions, based on the forecast range. Short-term forecasting can meet the needs of real-time applications, thus avoiding congestion and balancing transportation resources⁶. Medium and long-term predictions are beneficial for subway planning and development. Many studies focus on long-term prediction methods, but they perform poorly in short-term prediction⁷. Therefore, it is increasingly important to study passenger flow forecasting methods that satisfy both short-term and long-term passenger flow demands.

Early traditional statistical models, including statistical models^8,9,10,11 and machine learning models^12,13,14, were rigorously validated by mathematical theory, but they were difficult to learn nonlinear relationships in traffic flow. The methods based on machine learning were able to extract complex non-linear dependencies and performed well on large-scale datasets. Adnan et al.¹⁵ proposed the ELM-IRSA model, which employs the improved reptile search algorithm (IRSA) for ELM parameter optimization, demonstrating excellent performance in river flow prediction. Similarly, an improved relevance vector machine (RVM) model based on the dwarf mongoose optimization algorithm (DMOA), known as RVM-DMOA, has been introduced¹⁶. Compared to a standalone RVM model, the DMOA-optimized relevance vector machine significantly improves accuracy in monthly runoff prediction. However, the effectiveness of these models often relies on tedious feature engineering. In recent years, deep learning methods have made breakthroughs in various fields, such as image classification^17,18, objection detection^19,20, and natural language processing^21,22. The integration of deep learning and optimization algorithms has been widely adopted in time series modeling. For example, Adnan et al.²³ proposed models such as the hybrid adaptive neuro-fuzzy inference system (ANFIS-WCAMFO) and the lstm-based weighted vector optimizer (LSTM-INFO)²⁴. The results indicate that these hybrid deep learning methods exhibit remarkable performance in time series forecasting tasks. However, these models primarily focus on general time series tasks and do not consider the spatio- temporal heterogeneity of subway passenger flow. Deep learning has also made great progress in traffic flow prediction. Recurrent neural networks (RNN)²⁵ are suitable for predicting future traffic flow due to the time sequence of traffic flow. But RNN is prone to gradient vanishing because of its recursive structure, which is difficult to learn because of long-term time dependence. Therefore, many studies have tried to use the transformer framework⁷ to model time series. The transformer framework uses an attention mechanism to dynamically capture temporal correlations, effectively model long-term time, and support parallelization. But it does not perform well in forecasting short-term trends of subway traffic flow.

In addition to temporal dependence, there is also a strong spatial correlation in the flow of subway passengers. As a result, the graph neural network (GNN)¹ that can extract spatial correlation has been applied to predict traffic flow. The GNN framework is capable of effectively capturing spatio-temporal correlations and improving prediction accuracy in the complex evolution process of transportation networks. In terms of spatial modeling, many graph convolutional network (GCN) models use static graphs²⁶ for graph convolution. Static graphs, including the adjacency matrix, the similarity matrix, the origin-destination matrix, etc., are usually constructed based on real transportation networks. The edge weights reflect the distance or similarity relationship between the nodes. Although static graphs can reveal the relationships and mutual influences of nodes to some extent, they have limitations in long-term spatial correlation modeling. To solve the problem, Wu et al.²⁷ proposed the graph wavenet (GWN) model to learn the hidden spatial dependencies through the embedding of nodes. Bai et al.²⁸ presented an adaptive graph convolutional recurrent network (AGCRN) model, which mined different traffic patterns in traffic sequences. Upon combining node embedding, the decomposition of the feature matrix could learn specific parameter spaces for each node. Furthermore, Liu et al.⁴ proposed the physical virtual collaboration graph network (PVCGN) model to construct multiple graphs for spatial feature learning. These methods assigned fixed weights to adjacent nodes during pre-constructing or learning graphs, which is not applicable in traffic tasks with spatio-temporal heterogeneity. Thus, the attention mechanism was used to dynamically determine the weights of nodes and improve prediction accuracy^7,29,30. However, most attention-based methods share feature parameters at all positions and time steps. It means that the correlation between nodes depends only on their ow characteristics, which is inconsistent with actual traffic flow. Nodeown in a traffic network is influenced by its surrounding nodes.

In this paper, a trend spatio-temporal adaptive graph convolution network (TSTA-GCN) model for metro passenger flow prediction is presented. The TSTA-GCN model combines temporal self-attention and causal convolution to capture the time dependencies of long-term and short-term trends. Local spatial correlation and dynamic spatio-temporal correlation are captured by using a graph convolution network and gated recurrent neural network. Based on the temporal and spatial features extracted from the encoder-decoder, the spatio-temporal heterogeneity is modeled by a spatio-temporal interaction module. The encoder-decoder self-attention module of each layer in the decoder is used to reflect the impact of historical traffic flow on future predictions. The main contributions of this paper are as follows:

• 1. A trend spatio-temporal adaptive graph convolution network (TSTA-GCN) model for subway passenger flow prediction is presented to capture the correlation of metro passenger flow and improve prediction performance.

• 2. A trend convolution self-attention module is designed to perceive the contextual information of sequences and extract short-term temporal trends while capturing long-term temporal dependencies.

• 3. A spatial correlation extraction module combining graph convolution and gated recurrent neural network is proposed to capture dynamic spatio-temporal correlations. Spatial and temporal dependencies are entangled to simulate spatio-temporal heterogeneity.

• 4. Extensive experiments on two subway flow datasets are carried out to evaluate the proposed model. The experimental results indicate that the TSTA-GCN model outperforms the state-of-the-art traffic forecasting methods.

Related work

Traffic states prediction

As a classic task in ITS, traffic state prediction has made significant progress in recent years. Early research mainly focused on statistical methods, such as autoregressive integral averaging method⁸, Kalman filtering¹⁰, etc. However, these approaches were unable to learn the nonlinear relationship between traffic data in terms of spatio-temporal correlation. Methods based on machine learning were proposed to solve the problem. For example, Tang et al.^12,31 presented a short-term traffic flow prediction method based on support vector regression (SVR). Zarei et al.¹³ proposed a random forest (RF) method for sensing traffic flow context volatility. Cai et al.¹⁴ proposed a multi-step short-term traffic prediction method based on a k-nearest neighbor. Although these methods can model complex dependencies of traffic data, they rely on high-quality manual feature extraction.

In recent years, deep learning has excelled in feature extraction and representation and has been widely applied in spatio-temporal data modeling^26,32,33. Due to the strong time-dependence of traffic flow, recurrent neural network (RNN) and its variants long short-term memory (LSTM) network²⁵ and gated memory unit (GRU)³⁴ are used to capture temporal correlations. For example, Yao et al.³⁵ proposed a multi-view spatio-temporal network model for taxi demand prediction, which utilized LSTM to learn temporal correlation. Luo et al.³⁶ developed an embedded spatio-temporal network model. Dynamic temporal features were extracted by a sequence encoder composed of GRU networks, and nonlinear features were extracted through a residual network. However, RNN suffers from the problem of gradient vanishing and explosion, which is difficult to learn and store long sequence information^37,38. Convolutional neural networks (CNN) are also widely used to capture temporal correlations. Xu et al.³⁹ combined the advantages of CNN-LSTM in feature extraction and LSTM in time series analysis to capture short-term spatio-temporal dependencies. Compared with RNN, their model could avoid the large-scale computational burden. Huang et al.³⁰ proposed a long short-term graph convolutional network model combining 1D convolution and residual connection to learn longer-term temporal dependencies. However, the receptive field of 1D convolution is difficult to capture long-term temporal correlations, due to its size limitation.

Although CNN and RNN can effectively process Euclidean data, they perform poorly in non-Euclidean structures such as transportation networks. Thus, graph convolutional networks (GCN)¹ are used to process non-Euclidean data. For example, Shang et al.⁴⁰ proposed a discrete graph structure learning model to learn graph structures between multiple time series, which maximized the pairwise interaction between data streams. Li et al.⁴¹ modeled traffic flow as a diffusion process on a directed graph and proposed a diffusion convolutional recurrent neural network (DCRNN) to capture the temporal and spatial dependencies of traffic flow. These models used adjacency matrices for graph convolutional operations, but good results may not be achieved in complex spatial modeling. Therefore, many models have constructed other auxiliary graphs instead of adjacency matrices. Gao et al.⁴² proposed the personalized enhanced GCN (P-GCN). By introducing a learnable diagonal matrix, it adaptively controls the impact of the neighborhood aggregation scheme, thereby improving the accuracy of passenger flow prediction during peak periods. Song et al.⁴³ proposed a spatio-temporal synchronous graph convolutional network. The model combined adjacency matrices within adjacent time steps to extract complex local spatio-temporal correlations. Li et al.⁴⁴ presented a spatial transient fusion graph convolutional network that further integrated data-driven graphs with spatial graph multi-attention. Their model could effectively capture the hidden spatial correlations.

In addition to processing graph structures, GCN-based methods have also been applied to metro passenger flow prediction⁴⁵. Liu et al.⁴ proposed a PVCGN model by combining physical information (station locations, route structures, etc.) and virtual information such as weather. The model could extract multiple features that affect traffic flow by adopting a multi-layer attention mechanism to learn feature weights at different levels. Zeng et al.⁶ presented a split-attention relational graph convolutional networks (SARGCN) model. The model modeled spatial dependency by knowledge graph and relationship graph convolutional network and adaptively learned the importance of nodes and edges by using a split-attention mechanism. However, the use of multiple graphs for spatial modeling may result in higher computational complexity. Recent studies extend graph-based models to aviation traffic prediction. Xu et al.⁴⁶ proposed a bayesian ensemble graph network (BEGAN) for air traffic density, integrating flight plans as domain knowledge, while Xu et al.⁴⁷ developed a physics-informed graph transformer (PIGAT) with fluid dynamics constraints. Although these works share spatiotemporal modeling principles with our TSTA-GCN (e.g., graph attention mechanisms), they focus on aviation-specific challenges (e.g., airspace regulations), whereas TSTA-GCN addresses metro passenger flow dynamics through adaptive station-level graph learning and temporal pattern mining. This highlights the necessity of domain-customized designs in spatiotemporal traffic prediction.

Attention and transformer

At present, the transformer has achieved great success in the fields, such as object detection^19,20, natural language processing^21,22, and time series prediction^48,49, etc. Transformer can dynamically learn the correlations between input features through the attention mechanism, and extract the information that contributes the most to the input. It can better handle the long-distance dependency relationships of input sequences. Due to the parallel mechanism of transformer, the gradient vanishing and exploding can be avoided when modeling long sequences. Thus, the computational efficiency of transformer is higher than that of RNN. Compared with CNN, transformer has a global receptive field and can better model global dependency. As a result, many studies have applied the attention mechanism and transformer to traffic prediction. Guo et al.²⁶ proposed an attention-based spatio-temporal graph convolutional network (ASTGCN) to learn the correlations of traffic data, which demonstrated the superiority of the attention mechanism in modeling the dynamics of traffic data. To model the periodicity of time series, Cai et al.⁵⁰ presented a non-recurrent architecture to extend transformer. Four position embedding strategies were designed to capture temporal correlations, while a GCN module was used to extract spatial dependencies in traffic data. Zheng et al.²⁹ proposed a graph multi-attention network based on the encoder-decoder architecture to capture dynamic spatial correlations through graph attention. Ye et al.⁷ presented a meta graph transformer (MGT) model integrated with a spatio-temporal self-attention mechanism. Multiple static graphs were used to calculate self-attention which were then cascaded to obtain spatio-temporal correlation. However, this model ignores the spatial topology of transportation networks. However, the model ignored spatial the topology structure of the transportation network. These models based on attention mechanism mechanisms have strong global modeling capabilities and perform well in prediction problems. However, attention mechanisms often only focus on the relationships between highly correlated nodes, while neglecting the trend nature of traffic flow.

Most traffic flow prediction methods consider the spatio-temporal correlations of subway passenger flow. Due to the complex nature of traffic data, spatial and temporal dependencies often interact and intertwine. However, existing approaches struggle to effectively capture the implicit spatio-temporal heterogeneity and periodicity in traffic flow. Additionally, these methods face challenges in balancing short-term and long-term prediction accuracy in temporal modeling while also incurring high computational costs in spatial modeling. Therefore, a trend spatio-temporal adaptive graph convolution network (TSTA-GCN) model for metro passenger flow prediction is presented in this paper. TSTA-GCN combines temporal self-attention and causal convolution to capture the temporal dependencies of long-term and short-term trends. In addition, the model uses adaptive graph convolutional recurrent unit (AGCRU) to capture local spatial correlation and dynamic spatio-temporal correlation. To address spatio-temporal heterogeneity, a spatio-temporal interaction module is proposed to effectively entangle spatial and temporal features, enhancing the generalization ability of the model.

Methodology

Overall structure

To learn the temporal and spatial correlations of subway passenger flow data, the TSTA-GCN model adopts an encoder-decoder architecture that stacks several layers in both encoder and decoder, as shown in Fig.1. A trend convolutional self-attention (TCSA) module, an adaptive graph convolutional recurrent unit (AGCRU) module and a spatio-temporal heterogeneity fusion (STHF) module are contained in each layer. The TCSA module learns the temporal dependencies of long-term and short-term trends. The AGCRU module and STHF module are used for spatial modeling and spatio-temporal heterogeneity simulation of subway passenger flow data, respectively. In the decoder, an encoder-decoder self-attention (EDSA) module is proposed to interactively learn the extracted features and the output of the encoder. The association between historical traffic and future traffic flow thereby can be established. Each layer in the encoder and decoder uses a fully connected layer (FNN) to increase the robustness of the network.

Define ${{X}_{t}}=(X_{t}^{1},X_{t}^{2},...,X_{t}^{N})\in {{\mathbb {R}}^{N\times d}}$ as the passenger flow of N stations at time interval t, where d is the status of the flow. Denote $d_{model}$ as the feature size of the model, and L is the number of layers in the encoder and decoder, respectively. For a historical flow sequence $X=({{X}_{t-n+1}},{{X}_{t-n+2}},...,{{X}_{t}})\in {{\mathbb {R}}^{n\times N\times d}}$, where n refers to the length of the sequence, the goal is to forecast the passenger flow $Y=({{\overset{\wedge }{\mathop {X}}\,}_{t+1}},{{\overset{\wedge }{\mathop {X}}\,}_{t+2}},...,{{\overset{\wedge }{\mathop {X}}\,}_{t+m}})\in {{\mathbb {R}}^{m\times N\times d}}$ for the future time interval m. The process of the TSTA-GCN model is described as follows: Firstly, input the historical traffic flow data X into the encoder. Projects X linearly and then activates X by a nonlinear activation function. Add the result with the spatio-temporal embedding to obtain ${{X}^{(0)}}\in {{\mathbb {R}}^{n\times N\times {{d}_{model}}}}$. Secondly, take ${{X}^{(0)}}$ as the input of the encoder. The output of the encoder is obtained after the process of L layers with skip connections. Thirdly, input the ground truth values into the L layers of the decoder through skip connections. In the decoder, the EDSA module takes the output of the encoder and the output of the STHF module together as its input to model the correlation between historical and future flows. In the decoder, the output of the previous layer is considered as the input of the next layer. Finally, a linear layer is stacked to get the final prediction result Y.

Fig. 1

The framework of TSTA-GCN.

Spatio-temporal position embedding

For input that includes periodicity, it is necessary to add temporal embedding to the traffic network flow data to learn the temporal features in the sequence. Denote PE(pos, i) as the temporal embedding of the position pos in the $i^{th}$ dimension ($0\le i\le {{d}_{model}}$), as shown in Eq. (1):

$$\begin{aligned} PE(pos,i) = {\left\{ \begin{array}{ll} \sin \left( {pos}/{10000^{i/d_{model}}}\right) , & \text {if } i \text { is even,} \\ \cos \left( {pos}/{10000^{(i-1)/d_{model}}}\right) , & \text {if } i \text { is odd.} \end{array}\right. } \end{aligned}$$

(1)

Where sin, cos are the sine and cosine functions.

Concatenate the temporal embeddings of nodes at all intervals to obtain the final temporal embedding $TE\in {{\mathbb {R}}^{n\times {{d}_{model}}}}$, as shown in Eq. (2):

$$\begin{aligned} TE=X+PE \end{aligned}$$

(2)

In a transportation network, each node also has static features besides temporal features. These static features are mainly determined by spatial characteristics, including the attributes of nodes and topology structure of network. Thus, spatial embedding for each node is essential.

According to the adjacency matrix of the transportation network, the normalized Laplace matrix is calculated. Then eigendecompose it to obtain eigenvector matrix $U=({{u}_{0}},{{u}_{1}},...,{{u}_{N-1}})$. The spatial embedding of nodes $SE\in {{R}^{{{d}_{model}}}}$ is calculated by linear mapping of feature vector U to dimension ${{d}_{model}}$. Temporal embedding and spatial embedding are concatenated to construct temporal-spatio embedding $TSE\in {{\mathbb {R}}^{n\times N\times {{d}_{model}}}}$.

Denote ${{X}^{(0)}}$ the input of encoder. It is the sum of TSE and historical traffic data, as shown in Eq. (3):

$$\begin{aligned} {{X}^{(0)}}=TSE+Linear(X) \end{aligned}$$

(3)

Where Linear denotes a linear mapping.

Encoder

The encoder consists of several identical layers. Each layer contains TCSA, AGCRU, and STHF modules, as well as a FNN layer.

TCSA module

Multi-head self-attention can obtain richer information through multiple attention heads. Given queries Q ($Q\in {{\mathbb {R}}^{n\times N\times {{d}_{k}}}}$), keys K ($K\in {{\mathbb {R}}^{n\times N\times {{d}_{k}}}}$) and values V ($V\in {{\mathbb {R}}^{n\times N\times {{d}_{k}}}}$), the scaled dot-product attention is computed by Eq. (4):

$$\begin{aligned} Attention(Q,K,V)=Soft\max (\frac{Q{{K}^{T}}}{\sqrt{{{d}_{k}}}})V \end{aligned}$$

(4)

Where ${{d}_{k}}=\frac{{{d}_{model}}}{h}$ is the dimension of Q, K and V.

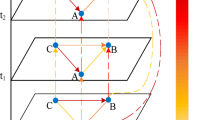
In the traditional multi-head self-attention mechanism, the correlation score of each element in a sequence can be calculated for the aim of long-term modeling by the attention score of the Q, K, V. However, it does not consider the short-term trend hidden in continuous data. As a result, applying it directly to traffic sequence data may lead to mismatching problems. Causal convolution⁵¹ is a one-dimensional convolution operation that considers only past time states, and the output at a given moment depends only on the information from previous moments, as shown in Fig.2(a). Thus, causal convolution can perceive short-term trends over time. A trend convolutional multiple self-attention (TCSA) module considering local contextual information is designed. Causal convolution which can extract the contextual information between sequences is used instead of the linear projection operation in a multi-head self-attention mechanism so that each element in the time sequences depends on the elements in the previous period. As a result, the computed attention scores contain the short-term trendiness in traffic flow. Fig. 2(b) shows the subway flow in three days and A represents the passenger flow at a certain moment (e.g., 18:00). The traditional attention mechanism may match A with the red points (6:00 and 7:00) based on the attention score. Instead, TCSA can match the period in which point A is located (Marked box in blue) according to short-term trendiness, and match it with three time periods with similar trends. Therefore, the TCSA module can not only learn local trends hidden in traffic data series but also adaptively learn long-term temporal correlations through the multi-head self-attention mechanism.

Fig. 2

Causal convolution and its application to traffic flow.

Define $TChea{{d}_{i}}$ as the trend convolutional attention of head i. It is calculated by Eq.(5):

$$\begin{aligned} TChea{{d}_{i}}=Attention(Q\star \Phi _{i}^{Q},K\star \Phi _{i}^{K},V\star \Phi _{i}^{V}),i=1,2,...,h \end{aligned}$$

(5)

Where $\star$ denotes the convolutional operation and $\Phi _{i}^{Q},\Phi _{i}^{K},\Phi _{i}^{V}$ are the parameters of the convolution kernel to be learned.

Concatenate the trend convolutional attention of h heads as the output $Z\in {{R}^{n\times N\times {{d}_{model}}}}$ of the TCSA module, as shown in Eq. (6):

$$\begin{aligned} Z=Concat(TChea{{d}_{1}},...,TChea{{d}_{h}}){{W}^{0}} \end{aligned}$$

(6)

Where ${{W}^{0}}$ is the weight matrix.

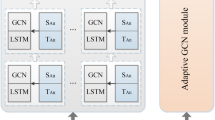
AGCRU module

The AGCRU module is shown in Fig.3. The inputs to the module are spatio-temporal embedding ${{X}^{(0)}}$ and adaptive graph P. The AGCRU module captures the unstructured patterns in the graph by the convolutional operations of GCN, and dynamic spatial correlations by GRU.

Fig. 3

AGCRU.

Graph structures such as adjacency matrix and similarity matrix are generally used for graph convolutional operations. Since these graphs are not able to represent the time-varying characteristics among the nodes of the traffic network due to the constant weights during training, an adaptive graph is used as an input auxiliary graph for the AGCRU module. The adaptive graph $P\in {{\mathbb {R}}^{N\times N}}$ is shown in Eq.(7):

$$\begin{aligned} P=Soft\max (Relu(E{{E}^{T}})) \end{aligned}$$

(7)

Where $E\in {{\mathbb {R}}^{N\times e}}$ is the matrix of transportation network nodes to be learned and Relu is the activation function.

Firstly, graph convolutional operation is performed on the adaptive graph P, as shown in Eq. (8):

$$\begin{aligned} GC(X)=\sigma (\sum \limits _{k=0}^{K}{{{P}^{k}}{{X}_{t}}{{W}_{k}}}) \end{aligned}$$

(8)

Where $GC(\cdot )$ indicates the graph convolutional operation, and ${{W}_{k}}$ is the convolution kernel parameter matrix approximated by K-order Chebyshev polynomials. ${{X}_{t}}\in {{\mathbb {R}}^{N\times {{d}_{model}}}}$ represents the input to the AGCRU module. For the first layer, ${{X}_{t}}$ represents the spatio-temporal embedding ${{X}^{(0)}}$, for other layers, it denotes the output of the previous layer.

Secondly, GRU is used to extract dynamic spatial correlations. Denote ${{H}_{t}}$ as the output of the current layer at time t, and it can be calculated by Eq. (9):

$$\begin{aligned} \left\{ \begin{aligned}&{{u}_{t}}=\sigma (GC[{{X}_{t}},{{H}_{t-1}}]+{{b}_{u}}) \\&{{r}_{t}}=\sigma (GC[{{X}_{t}},{{H}_{t-1}}]+{{b}_{r}}) \\&{{c}_{t}}=\tanh (GC[{{X}_{t}},({{r}_{t}}\odot {{H}_{t-1}})]+{{b}_{r}}) \\&{{H}_{t}}={{u}_{t}}\odot {{H}_{t-1}}+(1-{{u}_{t}})\odot {{c}_{t}} \\ \end{aligned} \right. \end{aligned}$$

(9)

Where ${{u}_{t}}$, ${{r}_{t}}$, ${{c}_{t}}$ are the update gate state, reset gate state, and candidate hidden state at time t, respectively. ${{b}_{u}}$, ${{b}_{r}}$ and ${{b}_{c}}$ are bias coefficients. $\sigma$ and $\tanh$ are activation functions. ${{X}_{t}}$ represents the input at time t.

Finally, denote S as the output of the AGCRU module. It is obtained by concatenating the output of each moment, as shown in Eq. (10):

$$\begin{aligned} S=Concat({{H}_{t-p}},{{H}_{t-p+1}},...,{{H}_{t}}) \end{aligned}$$

(10)

STHF module

TCSA and AGCRU are utilized to learn temporal and spatial correlations, respectively. However, spatial and temporal dependencies often interact and entangle with each other because of the characteristics of traffic data. Therefore, in order to consider this complex spatio-temporal heterogeneity implied in traffic flow, a spatio-temporal heterogeneity fusion (STHF) module is proposed.

Denote as the input of the STHF module. It is calculated by Eq. (11):

$$\begin{aligned} g=\sigma (Z{{W}_{z}}+S{{W}_{s}}+b) \end{aligned}$$

(11)

Where Z and S are the temporal and spatial features extracted by TCSA and AGCRU, respectively. ${W}_{z}\in {{R}^{{{d}_{model}}\times {{d}_{model}}}}$ and ${W}_{s}\in {{R}^{{{d}_{model}}\times {{d}_{model}}}}$ are parameter matrices to be learned, and b is the bias coefficient.

The output $F\in {{\mathbb {R}}^{n\times N\times {{d}_{model}}}}$ of the STHF module is calculated by Eq. (12):

$$\begin{aligned} F=g\odot S+(1-g)\odot Z \end{aligned}$$

(12)

Where $\odot$ denotes the matrix multiplication operation.

At the end of each layer, a FNN layer is used to make the network more robust. The output Y of each layer in the encoder can be defined as Eq. (13):

$$\begin{aligned} Y=LayerNorm(F+{{W}_{2}}Relu({{W}_{1}}F+{{b}_{1}})+{{b}_{2}}) \end{aligned}$$

(13)

Where ${W}_{1}\in {{R}^{{{d}_{model}}\times {{d}_{model}}}}$ and ${W}_{2}\in {{R}^{{{d}_{model}}\times {{d}_{model}}}}$ are parameter matrices to be learned, ${{b}_{1}}$ and ${{b}_{2}}$ are the bias coefficients, and LayerNorm denotes the layer normalization operation.

Decoder

Similar to the structure of the encoder, the decoder contains a projection layer and L decoding layers. Each decoder layer consists of a TCSA, an AGCRU, an STHF, an EDSA, and a FNN layer. Skip connections are used among the decoder layers. AGCRU, STHF, and FFN in the decoder have the same structures as those in the encoder, while a mask is added for each TCSA module after the scaling dot-product to avoid using the sequence information of future time steps. EDSA module, connecting the encoder and decoder, can adaptively learn features from historical data. In EDSA, queries come from the encoder, while keys and values come from the decoder.

In the Decoder, the predict values $({{\overset{\wedge }{\mathop {X}}\,}_{t+1}},{{\overset{\wedge }{\mathop {X}}\,}_{t+2}},...,{{\overset{\wedge }{\mathop {X}}\,}_{t+m-1}})$ are taken as the input. Firstly, the input is processed by projection and spatio-temporal embedding. Secondly, spatio-temporal correlations are extracted through TCSA, AGCRU, and STHF modules, and the relationship between historical traffic and future traffic is learned through the EDSA module. Finally, a linear layer is adopted for prediction.

The final result ${{X}_{t+m}}$ is predicted by stacking multiple decoding layers in the decoder.

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn.

Experiments

Experimental settings

To verify the effectiveness of the TSTA-GCN model, experiments are carried out on two metro datasets with strict temporal consistency in data splitting. The HZMetro dataset is from Hangzhou Metro, China, with the date range from January 1, 2019, to January 25, 2019, and a period from 5:30 to 23:30. Traffic flow for 80 stations is summarized in 15-minute intervals in a single day, with 73 intervals in total. To maintain temporal order, the HZMetro dataset uses the data in the ranges of 1/1-1/18 (chronologically first 18 days), 1/19-1/20 (subsequent 2 days), and 1/21-1/25 (final 5 days) as the training set, validation set, and test set, respectively. The SHMetro dataset from Shanghai Metro, China, covers three months from July 1, 2016, to September 30, 2016. Similar to HZMetro, the period is from 5:30 to 23:30 with a 15-minute interval. The number of stations is 288. Following temporal sequence, the data of the first two months (July-August) is taken as the training set, the first week of September (9/1-9/7) as the validation set, and the remaining data (9/8-9/30) as the test set. This time-respecting partitioning ensures that no future information leaks into the training process, thereby guaranteeing the reliability of model evaluation.

Denote $\text {Y}={{({{Y}_{1}},{{Y}_{2}},...,{{Y}_{N}})}^{T}}$ as the ground truth data, $\overset{\wedge }{\mathop {\text {Y}}}\,={{({{\overset{\wedge }{\mathop {Y}}\,}_{1}},{{\overset{\wedge }{\mathop {Y}}\,}_{2}},...,{{\overset{\wedge }{\mathop {Y}}\,}_{N}})}^{T}}$ as the predicted results. Three metrics, including Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE), are used to measure the performances of different methods, as shown in Eqs. (14)-(16):

$$\begin{aligned} MAE(\text {Y,}\overset{\wedge }{\mathop {\text {Y}}}\,)=\frac{1}{N}\sum \limits _{i=1}^{N}{|{{\text {Y}}_{i}}-\overset{\wedge }{\mathop {{{\text {Y}}_{i}}}}\,|} \end{aligned}$$

(14)

$$\begin{aligned} RMSE(\text {Y,}\overset{\wedge }{\mathop {\text {Y}}}\,)=\sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}{{{\text {(}{{\text {Y}}_{i}}-\overset{\wedge }{\mathop {{{\text {Y}}_{i}}}}\,)}^{2}}}} \end{aligned}$$

(15)

$$\begin{aligned} MAPE(\text {Y,}\overset{\wedge }{\mathop {\text {Y}}}\,) = \frac{1}{N}\sum \limits _{i = 1}^N {\left| {\frac{{{\text {Y}}_{i}}-\overset{\wedge }{\mathop {{{\text {Y}}_{i}}}}}{{{\mathrm{{Y}}_i}}}} \right| \times 100\% } \end{aligned}$$

(16)

Where N is the number of test samples.

The experiments are implemented in the Pytorch framework with NVIDIA GeForce GTX3060 12G GPU. The parameters are set as follows: the feature size ${{d}_{model}}$ is 16, and the number of heads is set to 4. There are 6 layers in both encoder and decoder. The batch size is 8. Adam⁵² is chosen for optimization. The number of epochs is 100 and the initial learning rate is set to 0.001 with a decline rate of 0.1 after 50 epochs. The weight decay is 0.0002.

Baseline methods

To fully evaluate the performance of the TSTA-GCN model, 14 baseline methods were compared in the experiments. These methods can be classified into three categories: statistical models, machine learning methods, and deep learning methods. The results for the competing methods were sourced directly from prior publications. We have relied on the original implementations and reported results from these studies, which are cited accordingly in the manuscript. These results serve as benchmarks for comparison with our approach.

• Historical average (HA)⁵³: This method utilizes the average patronage for each period to predict future values for that period. For example, the future patronage from 5:30 p.m.-7:30 p.m. on a weekday is calculated from the average patronage for the period 5:30 p.m.-7:30 p.m. on past weekdays.

• Random forest (RF)¹³: It is a machine-learning method for regression and classification problems. It predicts results by combining multiple trees, random sampling, and feature selection.

• Multi-layer perception (MLP): It is a feedforward neural network consisting of multiple hidden layers. Two fully connected layers and activation functions are used for prediction.

• Long short-term memory (LSTM)²⁵: This method extracts temporal dependencies through recurrent network structure and combines memory and forget gate units to model long-term temporal dependencies.

• Gated recurrent unit (GRU)³⁴: GRU captures long-term dependencies through update and reset gates. As a variant of LSTM, the same settings as LSTM are used in this model.

• Attention-based spatio-temporal graph convolutional network (ASTGCN)²⁶: The model captures spatial dependencies through the attention mechanism and considers local contextual information by 1D convolution.

• Spatio-temporal graph to sequence (STG2Seq)⁵⁴: This method models spatio-temporal correlations by graph convolution and attention mechanism.

• Diffusion convolutional recurrent neural network (DCRNN)⁴¹: DCRNN models the spatial dependencies by using bidirectional random walks on the graph and captures both spatial and temporal dependencies by graph convolution and diffusion convolution.

• Graph convolutional recurrent neural network (GCRNN)⁴¹: The structure of the model is similar to that of DCRNN. GCRNN replaces the diffusion convolution layer with third order ChebNets¹ based on spectral convolution.

• Graph wavenet (GWN)²⁷: GWN adopts adaptive correlation matrix and temporal convolutional layers to capture spatial dependencies and dynamic temporal correlations, respectively.

• Physical virtual collaboration graph network (PVCGN)⁴: The model constructs a physical-virtual collaborative graph integrating physical, similar, and correlation graphs to learn the integrated spatial correlations of the subway passenger flow.

• Meta graph transformer (MGT)⁷: Similar to PVCGN, the model uses three graphs and extracts temporal and spatial features based on the transformer framework and multi-head self-attention mechanism.

• Split-attention relational graph convolutional network (SARGCN)⁶: The model uses the historical origin-destination matrix to construct a graph and predicts traffic flow combining relational graph convolutional network, split-attention mechanism, and LSTM.

• Adjacency, similarity, correlation, and gated recurrent unit(ASC-GRU)⁵⁵: The model employs a parallel deep learning architecture that integrates multiple graph convolutional networks and gated recurrent units to simultaneously capture spatial and temporal dependencies.

Experimental results and analysis

Comparison on datasets

Tables 1, 2 show the results of TSTA-GCN and baseline methods in the two datasets at all periods. The traditional machine learning models (HA, RF) have good prediction results on both SHMetro and HZMetro datasets. The RNN-based models (LSTM, GRU) have MAPEs of 20.59% and 21.03% in 60-min prediction on the SHMetro dataset, and 16.34% and 17.20% on the HZMetro dataset, respectively. It indicates that the neural networks have better learning capabilities than the machine learning models. In addition, in terms of spatial correlation, GNN-based models (DCRNN, GCRNN, GWN, PVCGN, SARGCN) have higher stability in prediction compared to the HA, RF, MLP, LSTM, and GRU models, which illustrates the importance of spatial correlation. From Tables 1, 2, it can be seen that the RNN-based models (PVCGN, SARGCN) have sub-optimal results with RMSEs of 44.97 and 36.22 for 15-min prediction on SHMetro and HZMetro, respectively. However, they are not the second distances best for 60-min prediction, which is inefficient due to the vanishing gradient problem for long distances in RNNs. A similar problem exists in DCRNN and GCRNN. Although GWN tries to alleviate this problem by 1D convolution and achieves better performance than LSTM and GRU models in 15-min and 30-min predictions, it performs poorly for long-term prediction because the multi-layer stacking used for long-term learning in GWN can’t avoid the problem of gradient vanishing. Both PVCGN and SARGCN use multiple graphs to represent relationships between nodes, and their prediction results are better than DCRNN and ASTGCN models that use static graphs. However, their effects are still not as good as TSTA-GCN since the temporal correlations of traffic flow are ignored. STG2Seq and MGT, based on the Seq2Seq model, can take global correlations into account due to the parallelism of the attention mechanism. It can be found that MGT achieves sub-optimal results for all metrics on the 60-min prediction, indicating the effectiveness of the Seq2Seq model in long-term modeling. However, MGT does not achieve the same results for the 15-min in RMSE, which is because the Seq2Seq model does not consider the temporal periodicity and short-term trend of traffic flow. ASC-GRU underperforms compared to MGT and TSTA-GCN. Despite integrating multi-graph convolutional networks and GRU to model spatiotemporal dependencies in traffic flow, it relies on static graphs for node relationship representation. Additionally, GRU’s vulnerability to the vanishing gradient problem in long-term prediction further hinders its effectiveness. The RMSE and MAE of the TSTA-GCN model in 15min, 30min, and 60min predictions on the SHMetro dataset are better than those of other methods due to the capability of complex spatial and temporal modeling. The MAPE of the TSTA-GCN model on the SHMetro dataset is slightly higher than that of the MGT model, which may result from 0-values in the SHMetro dataset. However, the TSTA-GCN model performs best in RMSE, MAE, and MAPE for the four time-step predictions on the HZMetro dataset. It shows that the trend convolutional self-attention mechanism and adaptive graph proposed in the TSTA-GCN model can effectively predict subway passenger flow while meeting both long-term and short-term prediction needs.

Table 1 Comparison of different methods on the SHMetro dataset.

Table 2 Comparison of different methods on the HZMetro dataset.

Figure 4 shows the results of different methods on the two datasets for multi-step. Compared with other methods, TSTA-GCN shows the best performance at all time steps and especially performs better in short-term trend prediction while balancing long-term prediction performance.

Fig. 4

Multi-step prediction results of different methods on the two datasets.

Comparison on rush hours

In practical applications, accurate prediction for rush hours is very important. The prediction effects of different methods on rush hours (7:30-9:30 and 17:30-19:30) are compared to verify the effectiveness of the TSTA-GCN model, as shown in Table 3 and Table 4. It indicates that the TSTA-GCN model achieves the lowest metrics in all time steps on the two datasets. For 15-min prediction on the SHMetro dataset, the RMSE, MAE, and MAPE of TSTA-GCN are reduced by 7.23%, 3.84%, and 0.54% over the results of MGT, and by 5.16%, 4.09%, and 2.80% for 60-min prediction. As for the HZMetro dataset, TSTA-GCN has reduced by 3.18%, 2.69%, and 2.82% in RMSE, MAE, and MAPE compared to MGT in 15-min prediction, and 0.90%, 0.47%, and 1.53% in 30-min prediction. It is demonstrated that the TSTA-GCN model can effectively and correctly predict traffic flow for rush hours.

Table 3 Comparison of different methods for rush hours on the SHMetro dataset.

Table 4 Comparison of different methods for rush hours on the HZMetro dataset.

Comparison on high-ridership stations

The stations with high passenger flow (the top 1/4 of stations with the highest traffic flow) are selected for experiments to verify the robustness of the TSTA-GCN model. It is shown in Table 5 that the TSTA-GCN has the best performance in RMSE, MAE, and MAPE, which are 69.35, 39.57, and 10.53%, respectively. The MGT model has the second-best results on RMSE and MAE with 74.59 and 41.01, respectively, while PVCGN has the sub-optimal results on MAPE with 10.62%. Compared with MGT, the RMSE, MAE, and MAPE of TSTA-GCN are reduced by 7.02%, 3.41%, and 0.84%, respectively. For 60-min prediction, the RMSE, MAE, and MAPE of PVCGN are 93.59%, 48.02%, and 13.61%, respectively. Compared to its 30-min prediction results, the RMSE, MAE, and MAPE of PVCGN are increased by 17.83%, 11.54%, and 17.02%, respectively. However, the results of TSTA-GCN for 60-min prediction only increased by 9.75%, 7.98%, and 14.45%, respectively compared to the results for 30-min prediction. On the three metrics, the long-term prediction results showed a smaller increase compared to the short-term prediction results, which indicates that the TSTA-GCN model not only has the most accurate prediction results but also has stable performance.

Table 5 Experimental results for the top 1/4 high-ridership stations on the SHMetro dataset.

The prediction results of different methods for high-ridership stations on the HZMetro dataset are listed in Table 6. In 15-min and 60-min predictions, TSTA-GCN achieves the best performance in RMSE, MAE, and MAPE of 56.13, 36.97, 9.84%, and 62.24, 40.04, 12.19%, respectively. Based on the analysis above, it is verified that the TSTA-GCN model is effective and robust in predicting metro passenger flow for high-ridership stations.

Table 6 Experimental results for the top 1/4 high-ridership stations on the HZMetro dataset.

Complexity analysis

Table 7 lists the number of parameters and the average training time for the TSTA-GCN, MGT, PVCGN, and SARGCN methods on the HZMetro dataset. The experimental results are obtained with the same hardware and batch size values. It can be seen that PVCGN has the highest computational cost due to the use of multiple graphs. Although SARGCN has the least number of parameters and the shortest training time, it performs poorly in long-term prediction based on the experimental results discussed in 4.3.1. The number of parameters for TSTA-GCN is much less than that of PVCGN but more than those of MGT and SARGCN methods. TSTA-GCN has more parameters than SARGCN, and MGT due to the GCN and GRU operations on adaptive graphs in the AGCRU module. However, TSTA-GCN has fewer parameters than PVCGN because PVGCN employs multiple graphs while TSTA-GCN only uses adaptive graphs. Due to the use of GRU, the training time of TSTA-GCN is longer than those of PVCGN, SARGCN, and MGT. Although the average training time of TSTA-GCN is relatively long, it reflects the depth and granularity of the model in dealing with complex data and complex relationships. Considering the prediction performance and the number of parameters, the tradeoff in training time for the TSTA-GCN model is acceptable.

Table 7 Computational efficiency comparisons on the Hangzhou metro dataset.

Ablation experiments

Analysis on the effectiveness of module variants

TCSA, AGCRU, and STHF are important components of the TSTA-GCN model. The effectiveness of the three components is assessed through ablation experiments on the HZMetro dataset. To investigate the contribution of each component in terms of temporal and spatial correlation extractions, the following three variants of the model are designed:

• noTCSA: Remove all TCSA modules from TSTA-GCN and replace them with the traditional multi-head self-attention mechanism to investigate the impact of TCSA on temporal correlation modeling. Self-attention in the time dimension.

• noAGCRU: Remove all AGCRU modules from TSTA-GCN. In the noGCRU variant, the TCSA module is directly connected to the FNN layer since the STHF module does not work without AGCRU, to study the impact of AGCRU on spatial correlation modeling.

• noSTHF: Remove all STHF modules from TSTA-GCN and simply sum the outputs of TCSA and AGCRU to investigate the necessity of STHF in modeling spatio-temporal heterogeneity.

Fig. 5

Comparison of different variants of TSTA-GCN on the HZMetro Dataset.

The three variants are experimented with the same settings as TSTA-GCN. Fig. 5 shows the prediction results of the three variants on the HZMetro dataset. It can be seen that noAGCRU has the worst performance, which indicates that it is necessary to consider spatial correlation in the model. The effect of noTCSA is worse than that of TSTA-GCN, which demonstrates that the TCSA module can extract the temporal features of subway passenger flows more efficiently than the multi-head self-attention mechanism. The noSTHF variant, which simulates spatio-temporal heterogeneity only through simple summation, does not perform as well as TSTA-GCN. It suggests that STHF can learn spatio-temporal heterogeneity and is necessary for modeling.

Comparison of graph construction methods

To study the effectiveness of adaptive graphs, the static graph is constructed instead of the adaptive graph in the AGCRU module. The static graph integrates multiple graphs, including the connectivity graph, similarity graph, and origin-destination graph, as the input of the AGCRU module. Fig. 6 shows the prediction accuracy of the TSTA-GCN model on the HZMetro dataset using static graph and adaptive graph, respectively. Except for a slight gap in MAPE for the 60-min prediction, the adaptive graph has better results than the static graph which does not change during the prediction process. It shows that the adaptive graph used in the TSTA-GCN model can better reflect the dynamic changes in spatial correlations.

Fig. 6

Performance comparison of the TSTA-GCN model on the HZMetro dataset using static graph and adaptive graph.

Fig. 7

Comparison of hyperparameters on the HZMetro dataset.

Hyperparameter analysis

Experiments on the HZMetro dataset are conducted to analyze three hyperparameters, including the feature size ${{d}_{model}}$, the number of encoding and decoding layers L, and the number of heads h, on model performance. ${{d}_{model}}$ is set as 8, 16, 24, and 32, respectively. The number of encoding and decoding layers L (${{L}_{en}}={{L}_{de}}=L$) is set as 3, 4, 5, and 6, respectively, and the number of heads h is 1, 2, 4, and 8, respectively. The experimental results under different hyperparameter settings are shown in Fig. 7. It can be seen that the RMSE is maximum when the value of ${{d}_{model}}$ is 8. It does not mean that the larger the value of ${{d}_{model}}$ can lead to better performance, but the value of 16 minimizes the RMSE. For the number of layers L, RMSE, MAE, and MAPE are lowest when L is 6. While the three metrics can be achieved best when the number of heads h is 4. In general, the performance under different hyperparameters does not differ much, which suggests that the TSTA-GCN model is insensitive to hyperparameters.

Error distribution analysis

The error distribution of the predicted values and ground truth values is shown in Fig. 8. It is observed that the slope of the fitted line is close to 1 and ${{R}^{2}}$ is also very close to 1. Although there are still errors, these values are uniformly located on the two sides of the fit line. Moreover, in the high passenger flow range from 200 to 400, the predicted values can well fit the ground truth values. It is proved that the TSTA-GCN model has good prediction effects for subway passenger flow.

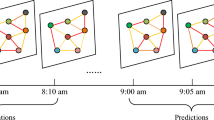
Fig. 9 shows the visualization results of the TSTA-GCN model for predicting traffic flow on the HZMetro dataset. Fig. 9 (a) and Fig. 9(b) show the visualization results of inflow and outflow within five days, respectively, and Fig. 9(c) and Fig. 9(d) show the results of inflow and outflow within one day, respectively. It shows that the TSTA-GCN model can accurately predict subway passenger flow for both five days and one day and respond quickly when the flow changes drastically and complexly, due to its good learning ability.

Fig. 8

Error distribution of the predicted values and ground truth values.

Fig. 9

Visualization results of the TSTA-GCN model on the HZMetro dataset.

Conclusions

A trend spatio-temporal adaptive graph convolution network model for metro passenger flow prediction is presented in this paper. The model captures both temporal dependencies of long-term and short-term trends by using self-attention and causal convolution. For dynamic spatio-temporal correlations, a spatial correlation extraction module based on graph convolution and gated recurrent units is introduced. In addition, a spatio-temporal heterogeneity fusion module is adopted to simulate the complex spatio-temporal heterogeneity of metro passenger flow. Experimental results on SHMetro and HZMetro metro datasets show that the proposed TSTA-GCN model can accurately predict metro passenger flow and have better performance than other baseline methods. Furthermore, the results of the ablation study verify the effectiveness and necessity of each component of the TSTA-GCN model. The optimal hyperparameter settings are analyzed and it is concluded that the TSTA-GCN model is insensitive to hyperparameters.

For the deficiencies of high training time and high computational cost of the model, extraction module based on GRU needs to be further improved in future research. The attention mechanism may be integrated to solve the recursive problem of GRU to design a concise and efficient spatial extraction module. Moreover, the temporal embedding with periodic information will be considered in future due to the periodicity of subway passenger flow.

Real-world implications and future research directions

The proposed method holds substantial potential for applications in Intelligent Transportation Systems (ITS). By improving traffic flow prediction and enabling more accurate route optimization, our approach could play a critical role in reducing urban congestion, enhancing traffic management, and contributing to the development of smarter, more responsive transportation infrastructures. With its ability to process large-scale spatiotemporal data, our model could be integrated into real-time traffic monitoring systems, providing decision-makers with valuable insights for more efficient management.

Furthermore, our work lays the groundwork for future research in the domain of ITS. Key areas for further exploration include the integration of multimodal sensor data, adaptation of the model for real-time traffic conditions, and the application of advanced machine learning techniques to improve the model’s scalability and predictive capabilities. These advancements could enable more accurate, dynamic traffic management systems and enhance the overall user experience in urban mobility.