A simple monocular depth estimation network for balancing complexity and accuracy

Abstract

Monocular depth estimation plays a crucial role in many downstream visual tasks. Although research on monocular depth estimation is relatively mature, it commonly involves strategies that entail increasing both the computational complexity and the number of parameters to achieve superior performance. Particularly in practical applications, enhancing the accuracy of depth prediction while ensuring computational efficiency remains a challenging issue. To tackle this challenge, we propose a novel and simple depth estimation model called SimMDE, which treats monocular depth estimation as an ordinal regression problem. Beginning with a baseline encoder, our model is equipped with a Deformable Cross-Attention Feature Fusion (DCF) decoder with sparse attention. This decoder efficiently integrates multi-scale feature maps, markedly reducing the quadratic complexity of the Transformer model. For the extraction of finer local features, we propose a Local Multi-dimensional Convolutional Attention (LMC) module. Meanwhile, we propose a Wavelet Attention Transformer (WAT) module to achieve pixel-level precise classification of images. Furthermore, we also conduct extensive experiments on two widely recognized depth estimation benchmark datasets: NYU and KITTI. The experimental findings unequivocally demonstrate that our model attains exceptional accuracy in depth estimation while upholding high computational efficiency. Remarkably, our framework SimMDE, extending from AdaBins, demonstrates enhancements, resulting in substantial improvements of 11.7% and 10.3% in the absolute relative error (AbsRel) on the NYU and KITTI datasets, respectively, with fewer parameters.

Introduction

Monocular depth estimation aims to recover depth information for each pixel from a single static image, which is crucial for understanding the three-dimensional world. Many applications, including virtual and reality¹, three-dimensional reconstruction², and robot navigation³, heavily rely on depth estimation. However, with the diversification of application scenarios, the demand for depth estimation is increasing⁴. Not only are high-precision depth estimates required, but real-time processing capabilities and the ability to operate in computationally constrained environments are also expected from the model. Balancing computational burden while ensuring exceptional performance remains a pivotal concern in the realm of depth estimation.

In practical applications, depth estimation encounters a trade-off between complexity and accuracy, such as in autonomous driving and robot navigation. Achieving high accuracy often demands complex algorithms and substantial computational resources, which may not be feasible in resource-constrained embedded systems or real-time scenarios. Current research aims to achieve model lightweight design through various methods^5,6,7,8. These methods enhance computational efficiency, but they often compromise accuracy, which is unacceptable in applications requiring precise depth information. Such one-sided optimization strategies fail to meet the demand for both efficient and accurate depth estimation algorithms.

Nowadays, the core idea of most depth estimation decoders is to expand the multi-scale features generated by the encoder to a specific size and fuse them through convolutional operations⁹. However, this approach may not fully capture all the details in the image, especially in regions with edges or complex textures. Therefore, many studies have started adopting Transformer-based decoders to capture finer-grained features¹⁰. Nevertheless, this approach inevitably introduces the quadratic complexity of the Transformer. To facilitate better integration of multi-scale features and mitigate the quadratic complexity associated with Transformers, we propose the Deformable Cross-Attention Feature Fusion (DCF) Decoder. This decoder reduces computational complexity by incorporating a deformable attention mechanism¹¹ and offers more flexible feature sampling and fusion strategies.

Furthermore, we transform the depth estimation problem into an ordinal regression task¹² and propose SimMDE, a monocular depth estimation network architecture that balances complexity and accuracy. The network architecture comprises two branches: a probability prediction branch and a pixel classification branch.

Fig. 1

Compares the number of trainable parameters against the AbsRel performance on the NYU and KITTI datasets’ test sets. Represented by blue dots are previous models. Our models employ advanced techniques and utilize significantly fewer parameters, achieving remarkable precision.

While dynamic convolution has introduced attention mechanisms to enhance its performance, its design primarily concentrates on the number of convolutional kernels, neglecting the critical dimensions of input and output channel numbers. In essence, existing works have not fully exploit the potential of dynamic convolutional properties, thus leaving considerable room for enhancing model performance. To handle this limitation, we propose the Local Multi-dimensional Convolution Attention (LMC) module to achieve more accurate probability prediction. This module applies attention mechanisms to all convolution kernels across three dimensions: the number of convolution kernels, input channels, and output channels. This dynamic mechanism endows the convolution kernel weights with sample adaptability. LMC facilitates the enhancement of effective channels without increasing the number of model parameters, while suppressing relatively less important channels, thereby significantly enhancing the feature extraction capability of the fundamental operation of convolutional neural networks (CNNs) operation.

To capture global information and accurately classify pixels, we propose the Wave Attention Transformer (WAT) module. While Transformer¹³ architectures have made breakthroughs in various aspects, their self-attention mechanism, which exhibits quadratic complexity in relation to the number of input patches, leads to high computational costs. To tackle this issue, some existing solutions often employ downsampling operations, such as average pooling, on the key and value to reduce computational overhead. However, this aggressive downsampling approach inevitably results in information loss, particularly for high-frequency components in images, such as texture details, as they are crucial for preserving rich image information. To more effectively retain high-frequency information, we introduce a lossless downsampling method using wavelet transforms¹⁴. Compared to traditional downsampling, wavelet transforms preserve high-frequency information in images and avoid the loss of texture details, while also capturing long-range dependencies without increasing computational complexity.

In conclusion, the following are our primary contributions:

• 1. We propose a novel depth estimation model named SimMDE, which effectively balances the relationship between computational complexity and accuracy.

• 2. We propose the Deformable Cross-Attention Feature Fusion (DCF) decoder with sparse attention, which flexibly captures detailed and structural information in images.

• 3. To extract finer local features, we propose Local Multi-dimensional Convolution (LMC) attention to provide more refined feature extraction capabilities.

• 4. We propose Wavelet Attention Transformer (WAT) to achieve precise pixel-level classification of images.

• 5. We demonstrate the effectiveness of our proposed model through extensive experiments on two widely used depth estimation benchmark datasets, NYU and KITTI. The proposed SimMDE model, depicted in Fig. 1, outperforms state-of-the-art methods, achieves performance comparable to existing state-of-the-art methods while maintaining only 30.9M trainable parameters.

Ralated work

Supervised monocular depth estimation

Supervised Monocular Depth Estimation has made significant strides in recent years. Eigen et al.¹⁵ pioneered the use of deep neural networks for monocular depth estimation tasks. They introduced a novel approach employing two depth networks to address depth estimation tasks: one for global prediction and the other for local refinement. TransDepth¹⁶ was the first to incorporate Transformer into monocular depth estimation tasks. It proposed an architecture combining Transformer and convolutional neural networks aimed at tackling continuous pixel-level prediction problems such as monocular depth estimation and surface normal estimation. DORN¹⁷ was the first to introduce the transformation of the depth estimation problem into an ordinal regression task for more effectively handling uncertainty in depth estimation. AdaBins¹² dynamically adjusts the depth range partitioning based on the characteristics of the input image, enabling it to handle depth estimation problems in different scenarios with significant achievements. IEBins¹⁸ introduced the novel Iterative Elastic Bins method, utilizing a classification-regression-based approach to search for high-quality depth. NeWCRFs¹⁹ significantly reduces the enormous computational burden brought by global CRFs by partitioning feature maps into small windows and computing CRFs within local windows, while leveraging shift windows to associate different local windows. LifelongDepth²⁰ introduces an efficient multi-head architecture that facilitates lifelong, cross-domain, and scare-aware monocular depth learning. SADC²¹ proposes a robust depth completion method based on semantic aggregation, which aims to address the challenge of the robustness of the completion model due to variations in the effective pixel density in sparse depth maps. ASNDepth²² proposed a unified scheme to estimate depth and surface normal in the guidance of geometric context. DINOv2²³ is a self-supervised vision transformer that learns rich and generalizable visual representations, enabling strong performance across various downstream tasks, including depth estimation. SQLDepth²⁴ utilizes an innovative Self Query Layer (SQL) to construct a self-cost volume and infer depth from it, rather than inferring depth from feature maps. Depth-Anything²⁵ is a versatile depth estimation model that leverages large-scale pretraining and multi-modal learning to achieve high generalization across diverse scenes and tasks. PatchFusion²⁶ is an end-to-end tile-based framework designed for high-resolution monocular metric depth estimation, which effectively fuses local and global depth cues to achieve accurate and scalable depth predictions. Marigold²⁷ repurposes diffusion-based image generators for monocular depth estimation by leveraging the strong priors learned in generative models to produce high-quality depth predictions from single images. TIE-KD²⁸ achieves efficient knowledge transfer without requiring architectural similarity between teacher and student models by introducing an interpretable Depth Probability Map. Metric3Dv2²⁹ achieves accurate estimation of zero-shot metric depth and surface normals by proposing a canonical camera space transformation and a joint depth-normal optimization module. However, these methods either achieve higher depth estimation accuracy at the cost of increased model complexity or sacrifice accuracy excessively to improve efficiency. In contrast, our proposed method effectively balances depth estimation accuracy and model efficiency by designing a simple encoder-decoder network combined with a convolutional attention module and a wavelet attention Transformer module.

Transformer

Transformer¹³, as a neural network architecture based on self-attention mechanism, has made significant breakthroughs in the field of natural language processing in recent years and has gradually extended to other domains such as computer vision. The introduction of Vision Transformer (ViT)³⁰ marks the successful application of Transformer in the field of computer vision. ViT divides images into multiple small patches and treats them as sequential inputs, utilizing self-attention mechanism to learn feature representations in images, achieving comparable or even superior image classification performance compared to CNNs. Data-efficient Image Transformer (DeiT)³¹ employs a distillation-based training strategy to enhance the performance of small student models by learning knowledge from larger teacher models. Multiscale Visual Transformer (MViT)³² adopts a multi-scale feature hierarchy, enabling it to capture and represent information from high to low resolution more efficiently in videos. Focal Transformer³³ enhances computational efficiency and model performance by focusing more finely on information close to the current position and coarsely on information far from the current position. Pyramid vision transformer (PVT)³⁴ successfully improves the performance of the original ViT on dense prediction tasks by combining pyramid structure, local contiguous features, and flexible position encoding. Swin Transformer³⁵ improves computational efficiency and scalability by introducing sliding window operations to limit the computational range of self-attention. Swin Transformer V2³⁶ enhances the original Swin Transformer³⁵ by introducing scaled cosine attention, log-spaced continuous position bias, and improved training stability, enabling it to handle higher capacity and resolution for various vision tasks. U-DiTs³⁷ introduce a U-shaped architecture for diffusion transformers that strategically downsamples tokens, improving efficiency and scalability while preserving rich hierarchical representations for high-quality image generation and understanding. PIIP³⁸ introduce a novel hierarchical framework that inverts the conventional parameter allocation in image pyramids, enhancing Transformer-based models with improved efficiency and multi-scale feature representation. Current Transformers often employ pooling strategies to reduce the computational burden, inevitably leading to information loss. However, our proposed WAT, through wavelet transform, achieves lossless downsampling without sacrificing crucial information, thus striking a better balance between computational cost and performance.

Fig. 2

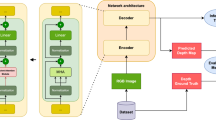
The overview of the proposed SimMDE. The input RGB images are subject to feature extraction and fusion via our innovative encoder-decoder module. Upon the decoder completing feature reconstruction, the resulting feature map is sent to two branches: one for probability prediction incorporating LMC module, and the other for pixel classification utilizing WAT module. By reframing depth estimation as an ordinal regression problem, the final depth estimation is determined using the combined outputs from both branches.

Methodology

In this section, we first outline our proposed depth estimation architecture, SimMDE. Subsequently, we delve into the key components of the architecture, including the Deformable Cross-Attention Feature Fusion (DCF) decoder, the Local Multi-dimensional Convolutional Attention (LMC) module, the Wave Attention Transformer (WAT) module, and the depth estimation module. Finally, we introduce the loss function.

Fig. 3

The proposed encoder-decoder structure. (a) provides an overall view of both the encoder and decoder. (b) delves into the specifics of the decoder, showcasing its intricate details.

Framework overview

The overall network results are depicted in Fig. 2. We utilize the encoder structure from³⁹ to extract multiscale features. For an RGB image of size $H \times W \times C$, we design four depth feature extraction stages: (i) $\frac{H}{4} \times \frac{W}{4} \times {C}_1$, (ii) $\frac{H}{8} \times \frac{W}{8} \times {C}_2$, (iii) $\frac{H}{16} \times \frac{W}{16} \times {C}_3$, (iv) $\frac{H}{32} \times \frac{W}{32} \times {C}_4$, where $C_i$ denotes the number of channels at each stage. The DCF decoder progressively extends multiscale encoder features from $\frac{H}{32} \times \frac{W}{32}$ to $\frac{H}{4} \times \frac{W}{4}$ layer by layer. It utilizes deformable cross-attention to deeply fuse encoder features and decoder features at different levels. After feature reconstruction by the decoder, the output feature map bifurcates into two streams: one is fed into the probability prediction branch, and the other guides the pixel classification branch. (I) Probability Prediction Branch: Initially, LMC is applied to the feature map to enhance the focus on important features and suppress irrelevant information. Subsequently, the feature map is reprocessed through a Softmax function to obtain a probability distribution of N depth intervals. (II) Pixel classification branch: The processing flow for each pixel begins with an embedding layer. Subsequently, the features processed by the embedding layer are transported to our proposed Wave Attention Transformer msodule. The WAT module precisely analyzes the features of each pixel by capturing global information, enabling accurate pixel classification. Ultimately, the results from the probability prediction branch and the pixel classification branch are aggregated by the depth estimation module to generate the final predicted depth map¹².

Deformable cross-attention feature fusion decoder

In current practice, the majority of decoder architectures rely on a fusion approach combining bilinear upsampling and convolution operations⁹. This method aims to recover the intricate details and structural information of images. However, traditional convolution-based methods for feature fusion often struggle to fully capture and reconstruct fine variations in images, especially in complex scenes and with dynamic objects. Despite the existence of many decoders based on standard Transformers¹³, they inevitably suffer from the quadratic complexity of standard Transformers.

To overcome these limitations, we introduce Deformable Attention into feature fusion, constructing our Deformable Cross-Attention Feature Fusion (DCF) Decoder. Unlike standard Transformers, deformable attention¹¹ significantly reduces computational complexity by focusing only on a small subset of key sampling points around reference points. This localized attention strategy avoids the quadratic complexity problem in standard Transformers, empowering our decoder to handle high-resolution images more efficiently. The structure diagram is presented in Fig. 3.

For the outputs from the four different stages of the encoder, we utilize a deformable cross-attention mechanism to deeply integrate them with decoder features at various levels. As an illustration, let’s consider the fusion of outputs from consecutive stages i and $i+1$ in the decoder. Suppose the respective output feature maps are denoted as $X_{i} \in \mathbb {R}^{h \times w \times c_{1}}$ and $X_{i+1} \in \mathbb {R}^{h_{1} \times w_{1} \times c_{2}}$. Initially, a bilinear interpolation operation is applied to $X_{i+1}$ to expand its size, generating a new feature map $Y_{i} \in \mathbb {R}^{h \times w \times c_{2}}$. Subsequently, $X_{i}$ and $Y_{i}$ are fed into the DCF module, which outputs the fused feature map, $Z_{i} \in \mathbb {R}^{h \times w \times c}$.

The deformable attention mechanism focuses on a set of local key sampling points around reference points, regardless of the spatial dimensions of the feature map. By assigning a limited number of key points for each query point, we effectively address the convergence issue of the model and the challenge of feature space resolution. To elaborate, we initially apply $1 \times 1$ convolutional processing to $X_{i}$ and $Y_{i}$ to obtain feature maps $\widehat{X}$, $\widehat{Y} \in \mathbb {R}^{h \times w \times c }$. Subsequently, positional encoding is applied to $\widehat{X}$ to derive $X^{pos} \in \mathbb {R}^{h \times w \times c}$. The resulting $X^{pos}$ is then element-wise added to $\widehat{X}$, yielding the $query \in \mathbb {R}^{h \times w \times c }$. This feature map serves as the query input for computing deformable cross-attention, while $\widehat{Y}$ itself acts as the value input. Given two input feature maps $x \in \mathbb {R}^{h \times w \times c }$ and $y \in \mathbb {R}^{h \times w \times c }$, the mathematical expression for deformable cross-attention is as follows:

$$\begin{aligned} DCF(x,y,c_{q},f_{q}) = {\textstyle \sum _{k=1}^{K}}W_{k}[{\textstyle \sum _{m=1}^{M}}\sigma (W_{mqk}x)\cdot W_{p} y(f_{q}+\bigtriangleup f_{mqk}) ] \end{aligned}$$

(1)

where, K represents the number of attention heads, M represents the number of samples($M<< HW$), $W_k$, $W_{mqk}$, and $W_p$ represent the learnable weights. $\bigtriangleup f_{mqk}$ and $\sigma (W_{mqk}x)$ denote the sampling offset and attention weight of the k-th sampling point in the m-th attention head, respectively. q indexes a characteristic query element of $c_{q}$. $\sigma$ represents the Softmax function.

Fig. 4

Illustration of the LMC’s approach to progressively multiplying three distinct attention types with convolutional kernels. LMC module employs a unique multi-dimensional attention mechanism to simultaneously compute attentions $A_i$, $B_i$, and $C_i$ for $W_i$, each corresponding to a different dimension within the kernel space.

Local multi-dimensional convolutional attention module

Recent research has unveiled the significant enhancement of network processing capabilities through the integration of attention mechanisms within convolutional neural networks^40,41. Following this^42,43, introduced the concept of dynamic convolution. By embedding attention mechanisms, they successfully addressed the inherent limitations of traditional static convolution, which relies on fixed and invariant convolutional kernels for all input signals. Dynamic convolution⁴¹, employing multiple sets of convolutional kernels and their associated weight factors, effectively boosts the network’s adaptability and flexibility in handling input features.

Despite the integration of attention mechanisms to enhance performance, the design of dynamic convolution primarily emphasizes the number of convolutional kernels, neglecting the crucial role of input and output channel dimensions. While replacing conventional convolution with dynamic convolution can enhance processing capacity, it results in an increase in total parameters by a factor of k, where k represents the number of kernel groups. This increase significantly increases model complexity.

Drawing inspiration from^40,41,44, we introduce a module called Local Multi-dimensional Convolutional Attention (LMC). The diagram in Fig. 4 illustrates the structure. This module adaptively learns attention weights across three crucial dimensions: the number of convolutional kernels, input channels, and output channels. This innovative approach aims to amplify the effectiveness of convolutional operations across various facets. Employing a parallel strategy, the LMC module learns attention across these dimensions concurrently. Furthermore, the attention mechanisms applied to these dimensions are mutually reinforcing, collaboratively bolstering the feature extraction capabilities of convolutional neural networks without imposing additional parameters.

Initially, an input feature map $X^{f}$ is fed into a $7 \times 7$ convolutional layer to extract local features efficiently. To minimize computational complexity, depth-wise convolution (DWConv)⁴⁵ and the Gaussian Error Linear Unit (GELU)⁴⁶ are judiciously applied, yielding a further refined feature map $X^{t} \in \mathbb {R}^{h \times w \times C_{in}}$. Subsequently, $X^{t}$ is condensed into a feature vector $X^{c} \in \mathbb {R}^{C_{in} \times 1}$ via average pooling. Following this, its dimensions are reduced to 1/8 of the original size through a fully connected layer (FC) with Rectified Linear Unit (ReLU)⁴⁷. An attention layer is then introduced at the output of the ReLU function. This layer divides the input $X^{c}$ into three branches, each tasked with computing attention across convolutional kernel size, input channel number, and output channel number. After processing through their respective branches, the resulting feature vector dimensions are $n \times 1$, $C_{in} \times 1$, and $C_{out} \times 1$, respectively. The branch for kernel size is subjected to a Softmax layer, while the branches for input and output channel numbers undergo Sigmoid layers to normalize attention weights $A_{i}$, $B_{i}$, and $C_{i}$. Subsequently, the attention weights $B_{i}$ are multiplied by $X^{t}$ and reshaped to create a new feature map $X^{t'}$. Additionally, the attention weights $A_{i}$ are multiplied by learnable parameters $P_{i}$, and after element-wise addition, multiply the result as the convolution kernel $W_{i}$ with $X^{t'}$, and finally multiplied by attention weights $C_{i}$. This result is then combined with shortcut operations to generate the output of the probability branch. For n convolutional kernels, the definition of the LMC module can be articulated as follows:

$$\begin{aligned} x_{out} = x_{t} + {\textstyle \sum _{i=1}^{n}}(B_{i} \odot A_{i} \odot P_{i} \odot C_{i}) \odot x_{t} \end{aligned}$$

(2)

where $A_{i} \in {\mathbb {R} ^ {n \times 1}}$ represents the kernel dimension attention, $P_{i} \in {\mathbb {R} ^ {n \times 1}}$ represents the learnable parameters , $B_{i} \in {\mathbb {R} ^ {C_{in} \times 1}}$ represents the input channel attention, $C_{i} \in {\mathbb {R} ^ {C_{out} \times 1}}$ represents the output channel attention, and $\odot$ represents multiplication operations.

Wave attention transformer module

Fig. 5

Diagrammatic representation of WAT module. Our WAT module utilizes Discrete Wavelet Transform (DWT) and Inverse DWT (IDWT) to implement lossless downsampling.

Given the prevailing use of pooling operations in current Vision Transformer architectures to reduce computational load⁴⁸, this inevitably leads to information loss. Although pooling effectively reduces the number of model parameters and computational complexity, this process is irreversible and sacrifices valuable details and contextual information. On the other hand, avoiding downsampling would drastically increase the computational burden of the model due to the quadratic growth of feature dimensions, rendering it impractical for real-world applications. Inspired by^49,50, we propose the Wave Attention Transformer module, aiming to extract global information from images without loss while controlling computational overhead. By cleverly leveraging the multi-resolution analysis capability of wavelet transformation, the Wave Attention Transformer effectively compresses feature space without sacrificing vital information. With this technique, our model accurately computes the bins-widths of each image. Figure 5 illustrates the architecture of the Wave Attention Transformer.

Initially, the input of the pixel classification branch denoted as $X \in \mathbb {R}^{h \times w \times C_{\text {in}}}$, passes through a linear mapping to obtain $query \in \mathbb {R}^{ \frac{h}{2} \times \frac{w}{2} \times C_{in}}$. Simultaneously, a linear transformation is applied to X by multiplying it with the matrix $W^{d} \in \mathbb {R}^{C_{\text {in}} \times \frac{C_{\text {in}}}{4}}$, resulting in $X^{a}=X W^{d} \in \mathbb {R}^{h \times w \times \frac{C_{\text {in}}}{4}}$. Subsequently, we apply the discrete wavelet transform (DWT)⁵¹ to $X^{a}$, downsampling it and reducing its dimensionality to one-fourth of the original, corresponding to four distinct wavelet subbands. Taking inspiration from⁴⁹, the Discrete Wavelet Transform operation utilizes a high-pass filter $f^{H}= \left( \frac{1}{\sqrt{2}},- \frac{1}{\sqrt{2}}\right)$ and a low-pass filter $f^{L}= \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$. This results in four embedded matrices: $W^{LL}, W^{LH}, W^{HL}, W^{HH} \in \mathbb {R}^{2 \times 2}$. By employing $W^{LL}$, $W^{LH}$, $W^{HL}$, $W^{HH}$, $X^{a}$ is transformed into $X^{LL}$, $X^{LH}$, $X^{HL}$, $X^{HH} \in \mathbb {R}^{\frac{h}{2} \times \frac{w}{2} \times \frac{C_{in}}{4}}$. Where $X^{LL}$ captures the low-frequency information of basic object structures at a coarse level, while $X^{LH}$, $X^{HL}$, and $X^{HH}$ reveal the high-frequency information of object textures preserved at finer levels. Subsequently, they are concatenated to obtain a downsampled result $X^{dwt} \in \mathbb {R}^{ \frac{h}{2} \times \frac{w}{2} \times C_{in}}$ that integrates all details without information loss, effectively covering every detail of the image. When handling $X^{dwt}$, the process follows two pathways. Initially, one pathway performs linear projection on $X^{dwt}$, generating $key, value \in \mathbb {R}^{ \frac{h}{2} \times \frac{w}{2} \times C_{in}}$, which are utilized for subsequent processing.

In the second pathway, the inverse DWT (IDWT) is applied to $X^{dwt}$, to restore it to $X^{idwt} \in \mathbb {R}^{ h \times w \times {\frac{C_{in}}{4}}}$. According to wavelet theory, this process can faithfully reconstruct all detailed information from the original image X without loss. Unlike traditional single $k \times k$ convolutional operations, the integration of DWT, convolution, and IDWT throughout the process effectively extends the model’s perceptual range without introducing additional computational burden or memory requirements.

Ultimately, each head output, containing long-range contextual information, is combined with $X^{idwt}$, which contains local contextual information, integrating contextual information across different scales. Subsequently, a linear transformation is applied to generate the final output of the wavelet transform, facilitating comprehensive extraction and utilization of image insights.

In summary, the formulation for WAT can be expressed as follows:

$$\begin{aligned} \begin{aligned} WAT(X) = MultiHead^k(XW_{q}, XW_{k}, XW_{v}, X^{idwt}), \\ MultiHead(Q, K, V, X^{idwt}) = \\ Concat(head_1, head_2, \ldots , head_n, X^{idwt})W_o, \\ head_j = Attention(Q_j, K_j, V_j) = Softmax\left( \frac{Q_jK_j^{T}}{\sqrt{d_k}}\right) V_j. \end{aligned} \end{aligned}$$

(3)

where $W_{o}$ is the transformation matrix.

Depth esimation module

In this module, we compute the final depth estimation by integrating the outputs from both the probability prediction branch and the pixel classification branch. The output $X^{w} \in \mathbb {R} ^ {N}$ generated by the pixel classification branch provides a probability distribution for each pixel position as the center of N depth intervals. Through the following straightforward steps, we can obtain:

$$\begin{aligned} c(b_{i}) = (d_{max} - d_{min}) \left( { \sum _{j=0}^{i-1}b_{j}} + \frac{b_{i}}{2}\right) + d_{min} \end{aligned}$$

(4)

where $c(b_{i})$ denotes the center depth of the i-th bin, $d_{min}$ and $d_{max}$ represent the minimum and maximum valid depth values in the dataset. The output $X_{w} \in \mathbb {R} ^ {H \times W \times N}$ from the probability prediction branch represents the probability $p_{k}$ for each depth interval. The final depth value is determined by a linear combination of $c(b_{i})$ and $p_{k}$:

$$\begin{aligned} d_{out} = \sum _{i=1}^{N}c(b_{i})p_{i} \end{aligned}$$

(5)

Loss function

We utilize a modified version of the Scale-Invariant (SI) loss¹⁵:

$$\begin{aligned} \mathscr {L} = \alpha \sqrt{\frac{1}{N}\sum (log d^{gt} - log d)^2 - \frac{\lambda }{N^2} \sum (log d - log d^{gt})^2} \end{aligned}$$

(6)

where N represents the count of valid pixels, d stands for the predicted depth, and d indicates the ground truth depth. Drawing from prior research⁵², we opted for $\lambda = 0.85$ and $\alpha = 10$ as hyperparameters for our model.

Fig. 6

Qualitative comparison on the NYU dataset.

Experiments

Datasets

NYU Dataset. The NYU dataset⁵³ consists of 464 indoor scenes, each featuring 120,000 images paired with corresponding depth maps at a resolution of $640 \times 480$. In our methodology, we meticulously adhere to the official data splitting guidelines: 24231 image-depth pairs are designated for training, while 654 images are held out for testing purposes. Depths within the scenes span from 0 to 10 meters.

KITTI Dataset. The KITTI dataset⁵⁴ encompasses a total of 61 scenes, each featuring RGB images with an approximate resolution of $1241 \times 376$ pixels. Our network is trained on a carefully curated subset of around 26000 images captured from the left view, including scenes identified within the 697-image test set specified by¹⁵. Depths within the scenes vary from 0 to 80 meters.

SUN RGB-D Dataset. The SUN RGB-D Dataset⁵⁵ is an indoor dataset comprising approximately 10,000 images capturing a wide range of scenes, obtained from four distinct sensors. Here we use the 5050 test images of the official segmentation.

iBims-1 benchmark. The iBims-1 benchmark⁵⁶ is a high-quality RGB-D dataset captured using a digital single-lens reflex camera and precise laser scanner. We employ 100 images from this dataset for testing purposes.

DIODE Dataset. The DIODE dataset⁵⁷ is a high-resolution dataset containing depth maps obtained from LiDAR sensor measurements. We utilize the complete validation split, comprising 325 indoor samples and 446 outdoor samples.

The main datasets we use to train SimDepth are NYU dataset⁵³ for indoor scenes and KITTI dataset⁵⁴ for outdoor environments.

To illustrate the capacity to generalize, we assess zero-shot performance on several additional datasets: SUN RGB-D⁵⁵, iBims⁵⁶ and DIODE Indoor⁵⁷ for the indoor scenario; DIODE Outdoor⁵⁷ for the outdoor environments.

Table 1 Comparison of performances on the NYU dataset.

Table 2 Comparison of performances on the KITTI dataset.

Training setting and evaluation metrics

Training details. Our models are developed using PyTorch⁶⁴ and trained on an Nvidia GTX 3090 GPU equipped with 24 GB of memory. Training the entire model was conducted with a batch size of 9, employing a learning rate set to $10^{-4}$. We utilized the AdamW⁶⁵ optimizer with a weight decay of $10^{-2}$. Additionally, the learning rate was scheduled using a cosine annealing strategy. For all reported results, the models were trained for 30 epochs.

Evaluation Metrics of Depth Estimation. We conduct a quantitative comparison of our method with state-of-the-art approaches and employ eight standard metrics, as outlined in¹⁵, to evaluate the performance of the predicted depth. These metrics encompass five error metrics and three accuracy metrics. Specifically, we utilize metrics such as relative absolute error (AbsRel), relative squared error (SqRel), root mean squared error (RMSE), root mean squared logarithmic error (RMSElog), log10 error (log10), and threshold accuracy at various deltas ($\delta < 1.25$, $\delta < 1.25^2$, $\delta < 1.25^3$).

Comparison to the state-of-the-art

We conducted a comprehensive comparison of our proposed method with other leading monocular depth estimation models. To meticulously evaluate our approach’s performance, we specifically selected the highly-regarded Adabins¹² as our primary competitor. To ensure fairness and accuracy in the comparison, we replicated the code of Adabins and utilized the pre-trained models provided by the authors to obtain their generated depth images. Additionally, to obtain results from other leading models, we directly ran their official code. Through this series of rigorous comparative experiments, we aim to comprehensively demonstrate the strengths and characteristics of our proposed method. The qualitative comparisons can be observed in Figs. 6 and 7. In a complex environment with many objects, AdaBins¹², NewCRFs¹⁹, and IEbins¹⁸ are inferior to SimMDE in depth prediction. For example, carpets, fallen books, and street lamps.

Fig. 7

Qualitative comparison on the KITTI dataset.

Results on NYU. We compare our SimMDE with previous works on the indoor dataset NYU, and the quantitative results are shown in Table 1. Despite the long-standing saturation of state-of-the-art performance on the NYU dataset, our method has demonstrated remarkable superiority across evaluation metrics. Compared to AdaBins¹², our approach demonstrates a 11.7% improvements in AbsRel, a 9.1% improvements in RMSE, and, a 2.0% improvements in $log_{10}$ error.

Results on KITTI. Table 2 presents the quantitative results for the KITTI outdoor dataset. In comparison to the previous state-of-the-art, our proposed model exhibits clear performance advantages. Additionally, when compared to the monocular depth method that relies on the Swin–Large³⁵ encoder, our model achieves comparable accuracy while boasting reduced parameters and complexity. Specifically, in comparison with¹², our method results in an approximately 10.2% increase in RMSE score, a 10.3% increase in AbsRel score, and a 17.9% increase in SqRel score.

Notice that our model has only 15.2% of the model parameters of Metric3Dv2²⁹, yet achieves nearly identical depth estimation accuracy.

Zero-shot generalization

We evaluate the generalization capability of the proposed method by analyzing its zero-shot performance on three unseen indoor datasets and an outdoor datasets, without any fine-tuning. Comprehensive qualitative results can be found in Table 3.

Table 3 Quantitative results for zero-shot transfer to three unseen indoor datasets and one outdoor dataset.

Even without fine-tuning on additional datasets, our model surpasses the performance of the previous state-of-the-art model. Impressively, it outperforms in the majority of datasets, underscoring its robustness and effectiveness.

Ablation studies

We conducted ablation experiments on the NYU dataset to validate the effectiveness of our method, and the results are presented in Table 4. Initially, we adopted MSCAN³⁹ along with a bilinear upsampling decoder as our baseline architecture. Subsequently, we systematically replaced this architecture with our proposed decoder. Finally, we sequentially incorporated our proposed LMC module and WAT module. While our proposed decoder did not yield significant improvements in the experimental results, it reduced the number of parameters to some extent. The experimental findings indicate that each of the introduced modules contributes to improvements in the experimental outcomes to varying extents.

Table 4 Ablation study on different components of our work on NYU dataset.

Fig. 8

Impact of varying the number of bins (N) on the Absolute Relative Error metric, indicating performance changes.

For fairness and accuracy of the experiments, we maintained consistency in both encoder and decoder architectures, with the only variation being the replacement of the MLP, mViT¹² and MSA (window attention)³⁵ modules by our proposed WAT module. According to the experimental results shown in the Table 5, our proposed WAT module consistently outperforms mViT, MSA, and MLP in various performance metrics. Although the parameter count of our WAT module slightly increases compared to the MSA module, the overall improvement in performance sufficiently demonstrates the effectiveness and superiority of our WAT module design.

Similarly, to verify the effectiveness of our proposed LMC module, we conducted comparative experiments by replacing the LMC module in the same with three different convolutional attention modules: SENet⁶⁷, CABM⁶⁸, and SCConv⁶⁹. As shown in Table 6, although our proposed LMC module does not have the lowest parameter count, it still achieves the best performance across all evaluation metrics. This is because the LMC module learns the attention mechanism from three dimensions, enabling the model to focus more effectively on important regions, thus enhancing the accuracy of probability prediction. These results further validate the rationality and superiority of the LMC module design.

Table 5 Performance Comparison of MLP and other Attention Modules.

Table 6 Performance comparison of different convolutional attention modules.

Table 7 Effect of WAT stacking times on NYU dataset.

Table 8 Comparison with previous works based on the quantity of trainable parameters (Params), Gflops, and FPS.

Table 9 Comparison of time complexity and parameter sizes for different modules.

To delve deeper into the impact of the number of bins (N) on the model’s performance, we systematically trained models using AbsRel as the evaluation metric for different N values (32, 64, 128, 256, 384, 512). As depicted in Fig. 8, it was observed that initially, as N increased, the error decreased, leading to a improvement in AbsRel. However, as N continued to increase, the error also increased, resulting in an increment in AbsRel. Based on a comprehensive analysis of the experimental data, we determined to set $N=256$ in the final model to achieve optimal performance.

In this series of experiments, we meticulously explore the subtle impact of the Wavelet Attention Transformer (WAT) on the efficacy of our network model, we opted to focus on the AbsRel metric for evaluation. Through meticulous experimentation, we systematically trained the model while varying the stacking times of WAT. The detailed experimental results are elaborated in Table 7. Following a thorough analysis and careful consideration of the experimental data, we arrived at the decision to set the stacking times to 2. This choice was made to ensure that the model could attain optimal performance levels, effectively balancing computational efficiency with accuracy.

In Table 8, we present a thorough comparison between our proposed method and Adabins, NeWCRFs, LifelongDepth, IEBins, and Metric3Dv2, focusing on key metrics across both the KITTI and NYU datasets: the number of model parameters, computational complexity (GFLOPs), and frame rate (FPS). To ensure the comparability and objectivity of our experimental results, we consistently utilized the Nvidia GTX 3090 GPU as our testing platform. From the collected data, it is evident that our method achieves a substantial reduction in the number of model parameters, leading to faster inference speeds and a more streamlined and efficient model architecture. In essence, our method demonstrates significant advantages in both performance and efficiency.

Finally, we conducted a detailed comparison of our proposed DCF, LMC, and WAT modules against other mainstream modules in terms of time complexity and parameter count, as shown in Table 9. From the results, it is evident that although our proposed modules do not have the smallest parameter counts, they still achieve a superior balance between performance and computational complexity with a relatively reasonable number of parameters. These findings clearly demonstrate that our proposed modules can effectively enhance model performance while maintaining an excellent trade-off between computational efficiency and accuracy.

Conclusions

We introduce SimMED, a novel monocular depth estimation network that effectively balances complexity and accuracy. Through extensive experimentation and rigorous validation, we have demonstrated the strong performance of our model in achieving high-precision depth estimation while notably reducing computational complexity and resource utilization. At the core of our approach is the Deformable Cross-Attention Feature Fusion (DCF) Decoder, an architecture equipped with sparse attention mechanisms, effectively enhancing model performance while minimizing the number of parameters. Moreover, to further refine accuracy, we introduce two additional modules: the Local Multi-dimensional Convolutional Attention (LMC) module, dedicated to probability prediction, and the Wave Attention Transformer (WAT) module, focusing on pixel-level precise classification. Through comprehensive evaluation on benchmark datasets such as NYU and KITTI, we validate the effectiveness and robustness of our proposed model.

However, in this study, we adopted the bins division method from previous literature, which relies solely on the output from the last decoder layer for depth range prediction. This approach does not effectively integrate multi-scale feature information, resulting in a lack of precision and sophistication in the bins division. Moreover, the use of single-scale features often struggles to adequately handle depth variations in complex scenes, thereby limiting further improvements in prediction accuracy. Therefore, future research will focus on developing a more refined and adaptive bins division strategy capable of effectively integrating multi-scale features to better capture detailed information across different scales, thus further enhancing the depth prediction performance of the model.

In the future, while maintaining a proper balance between complexity and accuracy, our research will expand beyond monocular depth estimation to explore the applicability of our approach in a broader range of computer vision tasks, such as 3D reconstruction, object detection, and semantic segmentation. We aim to validate the versatility and effectiveness of our model across various datasets and real-world scenarios, ensuring its robustness and generalization ability. Additionally, we plan to further optimize the network architecture and training process to enhance performance without compromising the trade-off between complexity and accuracy.