Introduction

Mathematics competencies are essential for understanding other disciplines (Poçan et al. 2022), solving everyday problems, and fostering a country’s economic development (Gravemeijer et al. 2017). Strong mathematics skills also provide future employment opportunities, especially in science, technology, engineering, and mathematics (STEM) fields. However, despite the importance of mathematics, the subject is often perceived by students as being abstract, difficult, and disconnected from real life (Li and Schoenfeld, 2019). This perception is partly driven by the tradition of viewing mathematics as a collection of unrelated facts, rules, and procedures (Bray and Tangney, 2017), teaching practices that focus solely on dispersing knowledge, and beliefs that learning mathematics is difficult, abstract (Li and Schoenfeld, 2019), and burdensome (Hwang and Tu, 2021), resulting in only a few learners being able to master it (Gravemeijer et al. 2017). Traditional teaching methods have contributed to students’ lack of interest in mathematics, many of whom see it as an alien and burdensome domain (Hoyles, 2016). Consequently, Yang and Chen (2024) noted that fostering a positive attitude toward mathematics among students remains a significant challenge, especially given these widely held perceptions.

Educational technology has been proposed as a way to address these challenges in mathematics education (Hwang and Tu, 2021; National Council of Teachers of Mathematics [NCTM], 2014). With the growing availability of digital tools and internet access, technology can transform how mathematics is taught and learned. For instance, dynamic mathematics software enables students to visualize and explore mathematical concepts (Ng et al. 2020) and receive immediate feedback (Demitriadou et al. 2020), which can reduce cognitive overload and make abstract ideas more accessible. Augmented reality has also been used to model complex algebraic expressions, helping students better understand abstract concepts (Poçan et al. 2022). These technologies not only aid in conceptual understanding but also foster active learning and inquiry, which are key to developing advanced thinking skills in mathematics. For example, mobile devices have been used to contextualize complex concepts by supporting outdoor activities, where students take pictures of objects to investigate area, perimeter, symmetry, and angles (Fabian et al. 2018). Similarly, a virtual stock exchange application has provided students with activities related to real life (Çetinkaya, 2019). Moreover, recent research has highlighted the evolving role of digital technologies in mathematics education. According to Drijvers and Sinclair (2024), digital technologies have been shown to not only improve learning outcomes, but also to drive new theoretical developments and design paradigms, emphasizing deeper understanding, equity of access, and innovative learning approaches.

The effectiveness of technology depends on how well it is integrated with key factors such as the content domain (NCTM, 2014) and the role of technology (Ran et al. 2021b). Technologies such as dynamic mathematics software, intelligent tutoring systems, and online assessment platforms have been widely adopted to improve both cognitive and affective outcomes in mathematics classrooms. The COVID-19 pandemic accelerated the adoption of these tools, particularly during prolonged school closures, highlighting the importance of technology in mathematics education (Kaplar et al. 2022). Alabdulaziz (2021) found that mobile technologies, touchscreens, tablets, massive open online courses in mathematics, and computer algebra systems (CAS) played a key role in facilitating communication and collaboration, and in enhancing mathematics education during this time. Engelbrecht and Borba (2024) observed that the digital tools educators adopted for teaching, learning, and assessment during the pandemic were later integrated into post-COVID-19 classrooms, further demonstrating the lasting impact of these technologies.

Technology-enhanced mathematics learning (TEML) refers to the adoption of various types of software, hardware, and the Internet in mathematics instruction to advance learning outcomes through technology-rich environments. In the past decade, at least nine reviews have centered around TEML, as presented in Supplemental Table 1. A wide variety of factors were covered in these reviews: technological attributes (e.g., technology type, role of technology), aspects of mathematics education or education in general (e.g., learning theory, mathematical concept, learning outcome), and methodological features (e.g., duration, intensity, design, sample size, grade level).

Grade level was the most commonly explored influential factor. Interventions were found to be more popular and effective in elementary schools compared to high schools (Cheung and Slavin, 2013; Crompton and Burke, 2015; Ran et al. 2021a; 2021b). However, the meta-analyses did not interpret this result. Another thoroughly explored dimension was classifications of technology, which varied across review studies. In most prior reviews, the classifications combined the type with the role of technology (Benavides-Varela et al. 2020; Bray and Tangney, 2017; Cheung and Slavin, 2013; Crompton and Burke, 2015; Rakes et al. 2020; Ran et al. 2021a; 2021b; Young, 2017). This resulted in difficulty applying the findings, and can be misleading since the same technology can have different roles, while one role can be performed by multiple types of technology. Only Young et al. (2018) examined the role of technology and type of technology separately. However, they simply divided roles into substitution and supplement and failed to explore their interlinkage. Moreover, Roschelle et al. (2016) indicated that the use of educational technology without the fusion of pedagogy can be ineffective and even detrimental to the teaching and learning process. When paired with effective pedagogy, educational technology has the potential to address issues in mathematics education (Hoyles, 2016). Yet, pedagogy was not considered in earlier reviews. To address this oversight, the current review aimed to illuminate the effective coupling of technology type, role, and pedagogy to enable mathematics educators to maximize the potential of technology use in their classes.

The content and process standards describe the mathematical understanding, knowledge, and skills or strategies that students should acquire, and provide a clear guideline for teachers (NCTM, 2014). Yet, among the TEML reviews, only two highlighted content standards, that is, the mathematical knowledge and concepts in mathematic topics such as number and operations, geometry and algebra, which are the key concepts learners must be equipped with. Moreover, none of them referred to the process standards, which suggest the higher-order thinking skills that students need to master, such as problem solving, reasoning and representation. These content and process standards are an integral part of the pedagogical process in mathematical education, ensuring that students develop conceptual understanding and are equipped for real-world mathematics application. Therefore, technology use in mathematics should meet the goals of these mathematical standards. A blueprint which matches the most effective technology to content and learners’ process competencies would be of great benefit to educators in the field. Positive effects of technology-based interventions on mathematics performance have been well-established. However, investigations of other learning outcomes such as affective outcomes (i.e., attitudes, motivation, or enjoyment) are limited (Benavides-Varela et al. 2020).

Learning mathematics is not strictly cognitive; it is also dependent on affective aspects (Grootenboer et al. 2008). The productive failure model (Fries et al. 2021; Kapur, 2008) emphasizes the necessity of sustained cognitive struggle in fostering deep mathematical understanding. In addition to self-concepts such as self-efficacy, affective variables that regulate students’ engagement with effortful and complex problems are central to this process. Mathematics self-efficacy has been identified as a strong positive predictor of mathematics achievement in the PISA framework (Zhang and Cutumisu, 2024; Zhu et al. 2025). Affective variables, including enjoyment and interest, have been found to be significantly influenced by self-efficacy (Mews and Pöge, 2019). Conversely, negative affective responses, such as frustration or math anxiety, are associated with feeling worried, tense, nervous, or helpless when faced with mathematical difficulties or challenging problems (Yuan et al. 2023). Anxiety has been shown to have a strong negative correlation with student interest (Yuan et al. 2023) and is generally a negative predictor of math achievement (Zhu et al. 2025). Rakes et al.’s (2020) is the only review which has paid some attention to affective outcomes. Like achievement outcomes, they found positive effects of technology on affective outcomes, with a small effect size (ES) of 0.11. The most popular affective construct was attitudes or perceptions, which accounted for approximately half of the studies (48.8%, ES = 0.12). The affective constructs with the largest effect sizes were beliefs and interest (ES = 0.74), but each made up less than 1% of the total studies. Nevertheless, the scope of the study excluded the interconnection of these affective outcomes to technological dimensions. This gap is filled by the current review.

Earlier reviews focused on methodological factors (e.g., Ran et al. 2021a; Ran et al. 2021b) in isolation, yielding limited information for stakeholders about effective instructional practices for TEML. Bray and Tangney (2017) attempted to review the interactions between the technological and mathematics aspects of TEML, but used a limited number of dimensions. Technological intervention on its own is not a panacea. Given the importance of educational technology and the well-established positive effect of TEML on student learning, knowing how best to use certain technologies for optimal mathematics experiences is crucial. This calls for a more expansive and comprehensive review of the interconnectedness among the technological attributes such as the role and type of technology and mathematics aspects, including content and process standards, pedagogy, and learning outcomes.

Research questions

Given the gaps in the previous literature, there is a pressing need for a more comprehensive review that not only examines the roles and types of technologies used in mathematics education, but that also investigates how these technologies interact with content and process standards, as well as their effectiveness in terms of producing both cognitive and affective outcomes. By identifying the most effective pairings of technology with specific mathematical content and learning processes, educators can optimize their use of technology in the classroom. This study therefore aimed to address these gaps by answering the following research questions:

  1. 1.

    What are the relationships between the content and process standards and the types of technology used in TEML interventions from 2013 to 2022?

  2. 2.

    What are the relationships among the types and roles of technology used in TEML interventions from 2013 to 2022?

  3. 3.

    How effective were TEML interventions from 2013 to 2022, particularly in terms of both cognitive and affective outcomes?

By investigating these questions, this review seeks to provide a clearer understanding of how different technologies can best support mathematics learning, offering practical guidance for educators, and contributing to the ongoing research in technology-enhanced mathematics education.

Methods

Data collection

We searched the Web of Science database, a reputable journal collection, using the following string of keywords: math* AND learn* OR teach* AND computer OR technolog* OR “e-learning” OR “web-based learn*“ OR “mobile learn*.” The review followed the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA; Moher et al. 2009) guidelines, which consist of four stages, as depicted in Fig. 1. Initially, 722 publications were retrieved and screened according to the following criteria: (a) studies published from 2013 to 2022, (b) articles published under the category of education/educational research, (c) English language articles from peer-reviewed journals, (d) studies focused on technological interventions in mathematics education, and (e) quasi-/experimental designs which compared technological interventions to control conditions (i.e., traditional non-technology instruction), compared two or more technology-enhanced mathematics learning modes, or single experimental technological interventions to allow for inferences regarding the effectiveness of technological interventions. This last criterion provided statistical elements which allowed us to make inferences about the effectiveness of technological interventions (Benavides-Varela et al. 2020). The abstracts of the retrieved articles were examined.

Fig. 1: Selection process following PRISMA.
figure 1

The four-stage process including identification, searching, eligibility, and inclusion to optimize the quality of retrieval and the selection of articles for the review.

Full size image

After examination of the abstracts, it was found that 70 articles were eligible for full-text reading, which resulted in the elimination of 14 articles because the aspect being manipulated was not technology based. In addition, 12 more papers which were not related to mathematics education were deleted, leaving 44 papers for inclusion in the final analysis.

Data distribution

Figure 2 depicts the publication trend of TEML interventions from 2013 to 2022. Only one paper was published in each of the first 2 years. From 2015, that number increased to three papers. Subsequently, the publication numbers remained somewhat steady with a peak in 2020 of eight papers, a fall to three in 2021 and then back up to seven in 2022. The dip in 2021 may be related to the COVID-19 pandemic. Approximately 61% of the studies were published in the second half of the decade, suggesting that TEML has become more popular in recent years, and undoubtedly will continue to expand.

Fig. 2: Distribution status of TEML interventions.
figure 2

The retrieval results between 2013 and 2023.

Full size image

Data analysis and coding scheme

The coding scheme for this study was developed based on the technology-based learning model (Hsu et al. 2012). The model has three dimensions, namely learners, technologies, and environment. The interaction of these variables illuminates six main TEML categories: roles of technologies, types of technologies, learners’ outcomes, pedagogy, content, and process standards (Table 1). To ensure conceptual clarity, particularly regarding the “role,” “type,” and “pedagogy” dimensions, we further defined these constructs based on how they were interpreted across the reviewed studies. The “role” of technology refers to its actual use in mathematics instruction. The “type” of technology is classified according to its core functions, intended educational purpose, and the pedagogical affordances it offers. The “pedagogy” dimension captures the instructional approach or theoretical framework guiding the intervention.

Table 1 Coding scheme for the TEML analysis.
Full size table

To refine the “types of technologies” dimension, particularly for frequently cited categories, we elaborated on four widely used classifications found in the literature: Computer Algebra Systems (CAS), Computer-Assisted Instruction (CAI), Dynamic Mathematics Software (DMS), and Application. These categories vary in pedagogical intent, interactivity, and the types of learning processes they support. CAS tools such as LiveMath (Sevimli, 2016), used in advanced mathematics, facilitate symbolic operations and visualizations (e.g., derivatives, integrals, matrix calculations) through 2D and 3D representations. Given its complex interface, effective implementation requires guidance from instructors with technological-pedagogical expertise. CAI tools such as Tenmarks (Lynch and Kim, 2017) offer structured, self-paced learning with embedded hints and feedback, while SynergyNet (Mercier et al. 2017) supports collaborative problem-solving via multi-touch interaction. DMS tools such as GeoGebra and iLMT (Kaplar et al. 2022) enable learners to manipulate mathematical objects and test conjectures through highly interactive, feedback-driven tasks that foster conceptual understanding. In contrast, Application Software such as Fiete Math (Lassault et al. 2022), designed for early learners, features a simple interface and limited interactivity, offering drag-and-drop tasks to introduce basic arithmetic concepts in gamified, tablet-based environments. Previous reviews have discussed the role and type of technology, but learning outcomes other than cognition, and content standards were underexplored, not to mention the associated pedagogies and process standards.

Since pedagogy and process standards were not always explicitly stated, they had to be inferred from the methodology and the description of the intervention. Due to the high possibility of interventions including more than one category, only the main category was selected to avert double coding. For the other dimensions, “multiple” types of technology, a “combination” of roles of technology, and a “combination” of content standards were coded as separate aspects. For example, Mavrikis et al.’s (2022) intervention included the combined effect of an intelligent tutoring system, Fractions Tutor, and exploratory learning environment, Fractions Lab, and was coded as multiple types of technology. Finally, reviews of technology-enhanced (Wu et al. 2021) and adaptive learning (Xie et al. 2019) have gone beyond cognition and affect to include skills and behaviors to define the effectiveness of the technologies. Therefore, these four aspects of learning outcomes were included in the coding scheme. The coded results for the 44 studies are presented in Supplemental Table 2.

The procedure for intercoder reliability assessment proposed by O’Connor and Joffe (2020) was utilized. First, a preliminary set of codes was created with reference to previous studies, and was discussed by the team. Then, Coder 1 read all the articles to become familiar with the data and to refine the codes accordingly. Next, Coder 1 and Coder 2 coded five of the articles together to clarify any misconceptions prior to formal evaluation of reliability. Finally, the coders independently coded 15 articles. The percentage agreement was calculated by dividing the identical codes by the sum of codes. An inter-coder agreement of 89% was achieved. Guided by Feng (2015), percentage agreement was used because the sample was small and chance agreement was minimal for this well-structured coding task which utilized codes derived from previous TEML reviews.

Results

What are the relationships between the content and process standards and the types of technology used in TEML interventions from 2013 to 2022?

To examine the research trends, the studies published in the earlier 5 years (2013–2017) were compared with those in the later 5 years (2018–2022). Such comparison helps researchers identify shifts in technology adoption and instructional focus over time, as well as highlight evolving research priorities and pedagogical strategies in educational technology. As depicted in Supplemental Fig. 3, application software dominated both time periods (n = 23, 52.27%), followed by CAI (n = 5, 11.36%) and then LMS (n = 4, 9.09%). Computer-aided assessment, dynamic mathematics software, and multiple types of software were each reported in 6.82% (n = 3) of the samples. The other studies utilized ITS (n = 2, 4.54%) and CAS (n = 1, 2.27%). The use of dynamic mathematics software and ITS was reported only in the later period, while CAI use was reported only in the earlier period.

The mathematics topics or domains covered in the 44 TEML articles are illustrated in Supplemental Fig. 2. The most common was number and operations (n = 13, 29.55%), followed by algebra (n = 8, 18.18%) and then geometry (n = 6, 13.64%). Application software was the most popular technology and was connected to all content standards within the K-12 mathematics curricula (n = 23, 52.27%). Furthermore, in situations of TEML where more than one content standard or topic were addressed, application software was typically chosen. Unlike Applications, the sole instance of CAS use was for higher education participants. CAI was the second most frequently used technology, primarily for the delivery of content areas of numbers and operation, data analysis and cases where the content standard was not specified. Nevertheless, its frequency was significantly lower compared to application software (n = 5, 11.33%). Finally, dynamic mathematics software was exclusive to instances in TEML where the strand of geometry was addressed.

Supplemental Fig. 3 depicts the relation between process standards and types of technology. The most frequent mathematical process students were engaged in was problem solving (n = 29, 65.91%), followed by connections (n = 5, 11.36%). All technological software, except DMS and CAS, were connected with problem solving. Similar to content standards, application software dominated the implementation of process standards in TEML (n = 23, 52.27%), and was connected to all five process standards, with problem solving accounting for 65.21% (n = 15) of the total instances. Other technological software was exclusively aligned to certain process standards such as CAI and CAA to problem solving, and CAS to reasoning and proofs. Supplemental Fig. 4 illustrates the widespread use of problem solving across all seven content standards, and especially number and operations (n = 29, 65.61%). Other process standards were less versatile than problem solving. For instance, five articles (11.36%) reported the use of connections aligned with the areas of geometry, number operations, and data analysis and probability, and four interventions (9.09%) each utilized reasoning/proofs and representation connected to several different content standards. Relatively few interventions (n = 2, 4.55%) engaged participants in communication.

What are the relationships among the types and roles of technology used in TEML interventions from 2013 to 2022?

Regarding the role of technology, Supplemental Fig. 5 depicts that most studies used technology in a class activity or as added practice (n = 33, 75%), followed by assessment, combination, and visualization (n = 3, 6.82%, each), and then computation (n = 24, 55%). As can be seen in Supplemental Fig. 6, the most frequently employed pedagogical approach was guided learning (n = 21, 47.72%), followed by game-based learning (n = 11, 25%), collaborative learning (n = 6, 13.64%), inquiry-based learning (n = 5, 11.36%), and problem-based learning (n = 1, 2.27%). None of the studies adapted self-directed learning. The period 2018–2022 saw the inclusion of inquiry-based learning and problem-based learning in TEML. Guided learning was the most popular pedagogical approach for both time periods. It is a process whereby learners advance their knowledge and skills through the support, feedback, and challenges provided by teachers.

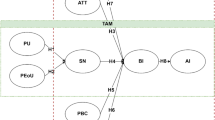
Figure 3 depicts the number of studies and the relationships among the types of technology, roles of technology, and pedagogies used in TEML. Application software was frequently used when the role of technology was instruction, with only one exception for computation. Other technological software was exclusively aligned to certain roles such as LMS, intelligent tutoring systems, and CAI to the role of instruction; CAA to assessment; CAS to computation; and DMS to visualization or modeling. Moreover, more than one type of software was employed only when multiple roles of technology existed.

Fig. 3: Relationships among the type of technology, role of technology, and pedagogy.
figure 3

The network diagram of the links among the types of technology used, the role, and the pedagogy for the 44 papers in this review.

Full size image

How effective were TEML interventions from 2013 to 2022, particularly in terms of both cognitive and affective outcomes?

Figure 4 displays various combinations of outcome variables from TEML interventions. Of the 44 TEML articles, cognition was investigated the most (n = 34, 77.27%), followed by affect (n = 18, 40.91%), learning behaviors (n = 12, 27.27%), and skill (n = 6, 13.64%). Thirteen (29.55%), two (4.55%), and six (13.64%) articles examined a single dimension of cognitive ability, affection, and behaviors, respectively. Most studies examined two or three dimensions, while none addressed all four learning outcomes.

Fig. 4: Four overarching learning outcomes of the 2013 to 2022 TEML studies.
figure 4

A Venn diagram of the frequency of and relations among the learning outcomes captured in the 44 articles in this review.

Full size image

Some of these dimensions were further divided into sub-dimensions, as shown in Table 2. In the cognitive dimension, the most popular learning outcome was achievement (n = 33, 75%). Learning achievement was popular for both periods and was the only cognitive outcome investigated from 2013 to 2017. It is also important to note that moving from the first to the second time period, there was increased interest in higher-order thinking and emphasis on more aspects of the affective domain. The second period saw the emergence of technology acceptance, motivation, and learning experiences. Higher-order thinking was measured in three of the studies (6.82%).

Table 2 Percentage of learning outcomes per dimension in each period.
Full size table

The affective dimension was dominated by motivation, learning experiences, and interest, which made up 11.37% (n = 5) each of the TEML interventions. Attitude and satisfaction were mentioned in four (9.09%) studies each.

Table 3 presents the effects of various technological interventions on mathematics achievement. Most studies presented significant results, and about one third (n = 9, 27.27%) found that the technology did not improve students’ performance. Although LMS (n = 2), DMS (n = 2), and studies using a combination of technologies (n = 1) all resulted in positive results, these studies made up only 15% of the total interventions.

Table 3 Types of technology and the results of intervention on the cognition sub-dimension of achievement (n = 33).
Full size table

Concerning the effectiveness of TEML in the affective dimension, 18 (40.91%) of the studies measured affective variables resulting in 29 instances (Table 4). The instruments used to measure the affective domain in TEML interventions were quite limited and were dominated by self-reports (n = 16, 88.89%).

Table 4 Types of technology and the impact of interventions on affect (n = 18).
Full size table

Discussion

Mathematical standards (content and process) and technology

While various technologies were employed across different content standards, DMS and CAS emerged as a content-specific technology used exclusively for geometry and algebra, respectively, highlighting their specialized application. Application software, on the other hand, was utilized to deliver a wide range of content domains, and was exclusive to instances where multiple mathematical strands were addressed. For example, in the study by Outhwaite et al. (2020), two mathematic applications Maths 3–5 and Maths 4–6 were used for one-on-one early mathematics instruction. These applications focused on topics such as number, shape, space, and measure, providing structured learning activities designed to support young children’s acquisition of basic mathematical skills.

Notably, none of the studies focused specifically on measurement as a standalone topic. Since number and operations are among the first aspects of mathematics that students learn, and form the foundation for more advanced mathematics, it is understandable that a large proportion of interventions in this area made use of application software. The positive outcomes suggest that applications are the best suited technology for this content. Relatively less effort has been put into tackling more abstract topics such as algebra and geometry, indicating a gap in the research that future studies could fill.

In 13.64% (n = 6) of the studies, the topics covered were not specified, which is an improvement on the review by Crompton and Burke (2015) in which 64% of studies failed to specify the topics covered. These six interventions involved multiple schools and long durations; that is, the technology was not confined to one or a few topics. For instance, Roschelle et al. (2016) used an online tool ASSISTments, a CAA, to support students across 42 schools with homework over an entire school year. ASSISTments provides students with timely feedback and hints while they complete their assignments, and gives teachers organized, real-time data on student performance, allowing for more effective monitoring and intervention. Genlott and Grönlund, (2016) utilized Google Apps for education to engage 502 elementary school students in learning mathematics through communication and discussion over 3 years. Supplemental Table 3 provides a summary of the software aligned to some of the content standards.

Application software proved to be very versatile, suitable for all five process standards, and showed a high correlation with problem solving. Unexpectedly, DMS and CAS were the only technologies not aligned with problem solving. The few studies using DMS and CAS focused on other cognitive activities. A computer algebra system (n = 1, 2.27%) has not yet been developed for standards other than reasoning. Dynamic mathematics environments (n = 3, 6.82%) were often used for representations (Ng et al. 2020; constructing physical solids using 3D printing pens), reasoning and proofs (Kaplar et al. 2022; exploring imitative reasoning and creative mathematics reasoning through an interactive learning environment), and connections (Demitriadou et al. 2020; exploring a real-life three-dimensional world). Although no process standard was entirely connected to any specific type of technology, the opposite is the case; that is, most technology tended to align with only a subset of the standards. For example, the functionality of CAS supports higher-order thinking, which can explain its unique alignment with reasoning and proofs. The interactive and analytical nature of CAI and CAA allow for engagement and collaboration; scaffolding and feedback were a great fit for problem solving.

While problem solving was the most common process identified in the reviewed studies, this finding should be interpreted with caution for three reasons. First, studies may have utilized multiple process standards, but only the most prominent one was selected to avoid double coding. Second, there is evidence of the term “problem solving” still being used in the traditional sense, that is, referring to learners applying procedures to solve well-defined problems (e.g., Lai et al. 2015; Roschelle et al. 2016). For instance, university students used an integrated LMS and CAS to complete algebra exercises with an interactive step-by-step solution (Akugizibwe and Ahn, 2020) and an online application to practice procedural vector skills (Mikula and Heckler, 2017). Third, while some authors claimed to have engaged students in problem solving, lower-level, traditional, and inadequate assessment tools such as tests were utilized rather than more authentic assessment tools such as a mathematical problem-solving behaviors scale (Nye et al. 2018) or a rubric for problem-solving ability (Hsiao et al. 2018). Moreover, TEML studies provided limited explanations and examples of both the types of problems solved and the tools used for measuring learning performance.

In TEML, learners are engaged in a variety of processes to facilitate content learning. Problem solving is used for all seven content standards, with a strong link observed between this process and number and operations. Four of the five processes were utilized for number, operations and geometry. However, perhaps due to the abstract nature of algebra, no attempts have been made to develop and evaluate mathematical conjectures, engage students in coherent discussions about algebraic concepts, or relate these concepts to other domains or the real world. TEML may still be limited to tasks that supplement traditional teaching, failing to capitalize on the transformative potential of technology to facilitate tasks that are inconceivable without its use.

Interaction among technology types, role of technology, and pedagogical approaches

Analysis of the reviewed studies (Supplementary Fig. 5) showed that instruction was the most popular role of technology in both periods. This finding is consistent with previous reviews indicating that TEML interventions were mainly used for instructional enhancement, such as by supplementing regular classes (Rakes et al. 2020). For example, Lai et al. (2015) implemented CAI via video- and game-based materials for remedial math outside regular class hours. Similarly, Vanbecelaere et al. (2020) used embedded curriculum-aligned digital games to support early numerical skills development. Both studies demonstrated how technology applied to instruction enabled alternative ways for students to learn and practice mathematics. Echoing Bray and Tangney’s (2017) findings, most technology-enhanced instruction fell under the augmentation level, serving as substitutes for conventional teaching with functional or conceptual enhancements such as feedback or individualized support.

Our research also revealed that the role of computation was used exclusively in the first period, while visualization and modeling emerged in the later stage. This shift may be attributed to two factors. First, wider availability of technological advancements has led to more enriched instruction. For instance, Augmented Reality and Virtual Reality facilitates students’ 3D exploration, outperforming text-based methods for fostering conceptual understanding (Demitriadou et al. 2020). Similarly, the Interactive Learning Materials Triangle enables students to manipulate shapes, thereby deepening their understanding of geometry (Kaplar et al. 2022). Hoyles (2016) emphasized that such technologies extend visualization and modeling beyond conventional approaches, fostering mathematical creativity and innovative thinking. Second, this trend parallels a pedagogical shift from focusing on content delivery to empowering students to model, analyze, and solve real-world problems (Bakker et al. 2021; Santos-Trigo, 2024). Therefore, TEML has expanded beyond improving computation to cultivating higher-order thinking.

Figure 3 illustrates the relationships among types of technology, their roles, and associated pedagogies. As previously noted, instruction dominates TEML research and is mostly delivered through versatile applications, the cross-platform functionality of which stimulates classroom adoption. Our findings also indicate that technology-assisted instruction is prevalent across various pedagogies, implying that teaching tasks are most readily technologized, compared to other roles. Technologies, such as CAI, ITS, and LMS, facilitate instructional delivery, whereas specific tools and technologies, such as CAA, DMS, and CAS, target narrower functions. Studies involving combination roles integrate multiple technologies. Hence, effective TEML relies on matching tools to their intended pedagogical role (Ran et al. 2021a; 2021b).

From the pedagogy perspective, technology plays more diverse roles—beyond instruction, it supports visualization and combination purposes, which, according to the reviewed studies, were not evident in other pedagogies. This may suggest that, while these technology roles are typically used in guided pedagogy to help learners better understand materials, they also contribute to inquiry-based learning. For instance, Dynamic Geometry Environments effectively fostered inquiry-based learning and advanced students’ geometric understanding (Ng et al. 2020). Conversely, collaborative learning and game-based learning primarily rely on application-type tools for instructional delivery. This pattern reflects both the ubiquity of such applications and their interactive nature or game-oriented format. For instance, application software facilitated interactivity in play-based environments, leading to learning gains and promoting collaboration among kindergarteners (Miller, 2018). It also supported social interactions among learners, peers, and teachers, enhancing mathematics performance (Genlott and Grönlund, 2016). This explains the frequent use of applications in collaborative learning and game-based learning to facilitate instruction.

The observed trends regarding the relations among technology, role, and pedagogy substantiate that certain technologies may have specific affordances. Along with Young’s (2017) three didactical functions of technological interventions, we can conclude that CAS and some application software enable “doing mathematics” or computational efficiency; LMS, ITS, computer-based instruction, and application software are best suited for the development of procedural knowledge and practicing mathematics skills, while DMS affords modelling and exploration for the development of conceptual knowledge. Linking these functionalities to pedagogy, our findings indicate that guided, game-based and collaborative learning are more aligned with computational efficiency and procedural knowledge, whereas inquiry-based learning, characterized by granting students autonomy and responsibility, is better suited to developing conceptual knowledge. Building on this, Engelbrecht and Borba (2024) emphasized that the use of effective pedagogical approaches paired with the right technology can ensure conceptual understanding.

TEML outcomes

The interest in cognitive outcomes, particularly achievement, parallels the findings of Bray and Tangney (2017) and Hwang and Tu (2021). This indicates that many TEML interventions are designed primarily to improve students’ performance on standardized measures of mathematical knowledge. While collaboration and communication were considered as means to acquire content in two studies, they were not outcome variables in any study. This absence may be because these studies primarily aimed to assess the impact of technology on specific mathematical knowledge or skills. For example, Wang et al. (2024) reported significant gains in mathematics achievement through features that supported interaction and knowledge co-construction. In many cases, collaboration serves as a pedagogical strategy to facilitate deeper learning and engagement, rather than as an explicit goal of assessment (Demir and Zengin, 2023). Although some studies in the broader computer-supported collaborative learning literature assess social skills (e.g., Bringula and Atienza, 2023), measuring collaborative skills such as communication or collaborative problem solving requires different methodologies, such as observation or interaction analysis. Consistent with Hussein et al. (2022), the limited attention to assessing collaborative competencies highlights a research gap in understanding how collaborative dynamics influence learning outcomes, with subject matter knowledge remaining the dominant focus. Communication and collaborative skills have gained importance in mathematics, as evidenced by their inclusion in the 2015 PISA assessment framework using computer-based assessments in PISA (OECD, 2017). Engelbrecht and Borba (2024) highlighted the growing relevance of student online collaboration in mathematics education via learning environments and social media. Therefore, future TEML studies may consider communication and collaboration as a cognitive learning outcome.

A more in-depth examination of achievement outcomes suggests that further research is needed to confirm the positive effects of TEML interventions. Studies that had mixed effects utilized multiple measures of achievement (Ng et al. 2020; Vanbecelaere et al. 2020) or a delayed test (Ng et al. 2020). This implies that the effects of technology are tied to the specific content and may not last over an extended period. For instance, Vanbecelaere et al. (2020) revealed that elementary school students who played digital games outperformed the control group engaged in non-gaming instruction on number line estimation, but not on number comparison.

Our findings revealed that engagement in TEML was satisfying and provided a positive learning experience for participants. However, results regarding the other affective dimensions such as attitude, self-efficacy, and motivation were less consistent or depended on the affordances for interaction, adaptability, and innovation, yielding varied results. Fabian et al. (2018) noted that the use of tablets and the SnapShot Bingo application was not enough to outweigh traditional daily mathematics activities or to change elementary school students’ attitudes. The increased accessibility and use of application software in and outside classrooms might eliminate the novelty effect, indicating that merely incorporating technology does not automatically enhance student interest in mathematics. Sustained gains emerge only when the digital tools are embedded in well-designed tasks that allow students to connect to meaningful contexts, and are supported by timely teacher scaffolding and feedback.

The assessment of participants’ self-efficacy in CAI and motivation during the use of application software produced inconsistent results. Immediate evaluative feedback in computer-based training utilizing static question sequences resulted in improved self-efficacy (Heckler and Mikula, 2016). At the same time, computer-assisted tutoring sessions held outside of regular school hours to solve routine problems were found to be ineffective (Lai et al. 2015). A game-based application that lacked vivid animations and scenarios had no distinct effect on motivation (Es-Sajjade and Paas, 2020). In contrast, the use of AR applications to support mobile learning in out-of-school learning environments had a positive effect on motivation (Poçan et al. 2022). These findings suggest that certain technological features, such as vivid animations and immediate feedback, may be better suited to particular affective outcomes like motivation and self-efficacy. Finally, relatively few studies incorporated ITS, DMS, and multiple types of software, although those that did all showed significant affective outcomes. This finding suggests that future research should systematically investigate how adaptive tools such as ITS and DMS can be purposefully aligned with pedagogical strategies to cultivate lasting gains in motivation and self-efficacy and identify which specific features deliver the biggest impact across diverse learner populations.

All instances where emotion and technology acceptance were measured reported non-significant differences. Participating in mathematics professional development did not manifest more frequent use of technology (Thurm and Barzel, 2020). Engaging in gameplay to learn number sense did not alter elementary school students’ mathematics anxiety (Vanbecelaere et al. 2020), and providing a free laptop to partake in a computer-assisted online summer mathematics program was not effective in terms of raising enjoyment (Lynch and Kim, 2017). Extensive research has examined the relationship between emotions and mathematical outcomes. A recent longitudinal study reported positive reciprocal relations between emotions and mathematics performance (St Omer et al. 2023). However, only two TEML studies in the past decade evaluated emotions, and both yielded insignificant results. This necessitates an increased examination of the varying emotions students experience as they engage with technology in their mathematics classes.

To make strides in improving and better understanding the affective domain in TEML, researchers should consider including more observational data and mixed methods of data collection (Grootenboer et al. 2008). For instance, Fabian et al. (2018) used interviews and an activity evaluation in addition to questionnaires to obtain comprehensive information about negative attitudes towards mathematics and to explain the insignificant changes in attitudes. While quantitative metrics can capture overall attitudes and improvements in learning, qualitative data from interviews, observations, and artifacts provide deeper insights into students’ perceptions and experiences of the TEML environment, including their sense of autonomy in gamified conditions (Ortiz-Rojas et al. 2025), cognitive processes, and learning strategies (Demir and Zengin, 2023). The triangulation of multiple sources with performance data enhances the validity and credibility of the study findings.

Conclusion

This review study systematically investigated how mathematics technologies have been coupled over time with other instructional elements such as functions of technology, mathematics standards, pedagogies, and learning outcomes. By highlighting exemplary instructional scenarios, it provides a blueprint for future instructional designers and practitioners. For example, the effective attainment of mathematics skills and procedural knowledge is achieved when guided, game-based, or collaborative learning is provided through the use of LMS, computer-based instruction, or ITS. The findings can help in making decisions about how to allocate necessary resources, supply learning models and techniques that allow for the optimal use of TEML, as well as provide future research directions.

First, the trends observed in the relations between types of technology, pedagogy, and role suggest that mathematics teachers understand that technology is most effective when paired with proper technology use and appropriate instructional strategies. However, similar to Bray and Tangney (2017), this review reveals the under-utilization of technology. Technology is often used merely as a direct substitute for traditional methods, foregoing meaningful interactions, visualization, and representations that would be improbable without technological tools. A well-designed educational technology interface has the potential to reduce cognitive demands on learners by storing information and simplifying execution steps (Sweller, 2020). To evaluate the effectiveness of educational technology, the instructional efficiency and cognitive load of TEML should be examined (Mayer, 2024) before it is released, especially for young learners. There is a need to move beyond substitution towards transformation in technology integration.

Second, it is recommended that greater attention be given to collaboration, communication, and higher-order thinking in future TEML research. Ran et al. (2021b) reported that technology integration in mathematics learning was most effective when it was designed to create and support communication and collaboration as well as problem solving. However, few studies have focused on higher-order thinking, perhaps because it requires specific instructional design or the use of specialized software such as GeoGebra. Yohannes and Chen (2021) provided a comprehensive review of this topic. Finally, some studies failed to explicitly state the pedagogy and the mathematical concept covered in the intervention. It is suggested that future TEML articles provide detailed descriptions of interventions to not only facilitate replication but also to assist educators who wish to implement such interventions in their classrooms.

Despite adopting a rigorous methodology in this study, there are two limitations worth mentioning. First, the scope of this systematic review was limited to one of the major academic databases (Web of Science) and to studies adopting quasi-experimental or true experimental design. While the review of peer-reviewed SSCI indexed comparative journal articles ensures the rigor and reliability of the analysis and overall quality, it narrows the breadth of the searched literature. Moreover, it is possible that rigorous studies have been neglected because of insignificant effects, as such studies have a lower chance of being published in SSCI indexed journals. Including additional databases and grey literature in future reviews could provide a more comprehensive understanding of TEML interventions. Second, the findings of the study are confined to aspects of TEML derived from coding schemes of previous studies (e.g., Bano et al. 2018; Rakes et al. 2020; Young, 2017). These coding schemes may need refinement to reflect the advances and the innovative use of technology.