Introduction

Visuomotor learning involves the execution and correction of motor commands to achieve a task goal based on visual feedback, which is underpinned by adaptive interaction between sensorimotor and visual cortices1,2. Thanks to its anatomical location in the dorsal visual stream between sensorimotor and visual cortices, the posterior parietal cortex (PPC) integrates visual and proprioceptive information3,4. Indeed, numerous neuroimaging studies have focused on the PPC as neural substrates of visuomotor learning, either motor sequence learning5,6,7 or motor adaptation3,8. However, the interaction between the sensorimotor and visual cortices has yet to be explored during visuomotor learning, especially among their subregions, such as motor, somatosensory cortices, and early and late visual cortices. To investigate visuomotor interaction, manipulation of visual feedback could be a promising approach as it modulates activities of neural substrates involved in the interaction9,10,11,12,13. For instance, we can manipulate the visibility of the feedback, which provides continuous movement of the end-effector or its position only at the end of movement9,14,15. The visibility could affect the integration of the visual feedback with other sensory feedback, such as proprioception, which is processed by the somatosensory cortices. Additionally, the visibility could distinctively modulate activity in early and late visual cortices and their interaction with sensorimotor cortices.

However, the motor and somatosensory cortices are often coactivated during motor tasks, as reported in previous fMRI studies using a similar manipulation of the visual feedback14,15,16,17. The coactivation would be primarily due to intricate interaction between motor and somatosensory cortices during movement13. The motor and somatosensory cortices are closely interconnected, playing roles in creating motor commands, anticipating sensory outcomes, and processing sensory feedback. The intertwined interaction makes it challenging to determine the extent to which motor versus somatosensory cortices contribute to motor learning13. Previous studies employed simple motor control tasks such as tracking a target14, moving a pendulum15, and hand-grasping tasks16,17, in which they have not investigated neural plastic changes in the sensorimotor network. Moreover, these laboratory-based tasks would be too simple to investigate complicated visuomotor interactions that we experience in everyday life.

Thus, we employed a delicate continuous de novo motor task in fMRI where participants learned an arbitrary visuomotor mapping. Specifically, they used their fingers to control an on-screen cursor while learning a novel hand-to-cursor mapping18,19,20. In contrast to typical motor adaptation and sequence learning tasks with well-defined sensory targets, our task requires exploration in a high-dimensional motor space while learning proprioceptive state, i.e., hand posture, which is mapped to a low-dimensional target space. Furthermore, manipulation of the visibility of the visual feedback allowed us to explore how motor cortices and somatosensory cortices differentially interact with visual cortices during motor learning. We hypothesized that the activity patterns in the visuomotor regions could be dissociated depending on the relative contribution of the afferent proprioceptive state of the hand, which is mediated by the visibility of the visual feedback. We also investigated how the interaction among the subregions of sensorimotor and visual cortices accounts for the performance of de novo motor skill learning. Finally, we discussed the clinical implications of our findings, which provide insight into rehabilitation for patients with visual deficits and sensorimotor impairment by highlighting differential interaction among those subregions and their contribution to visuomotor learning.

Results

Behavioral data analysis

Twenty-four participants completed the experiment. The main task began after the localizer session. The purpose of the localizer session was to define regions related to hand movement. In the main session, participants wore a data glove on their right hand and controlled an on-screen cursor by moving their right fingers. The cursor position was calculated from a predefined hand-to-cursor mapping, which was calibrated for individual participants (see Methods). Their goal in the experiment was to reach a target with a cursor as quickly as possible. Participants performed the task under two different conditions alternately (Fig. 1A, Supplementary Movie 1). In the continuous visual feedback condition (CF), continuous online visual feedback was provided as the position of an on-screen cursor. Additionally, a target appeared red when reached by a cursor. In the other binary visual feedback condition (BF), the online cursor position was not provided. Thus, the target color, which appeared red when reached, was the only feedback available to participants. The hand-to-cursor mapping was identical in both feedback conditions.

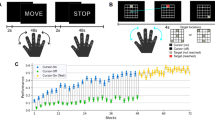
Fig. 1: Overview and behavioral performance of motor learning task across the experimental conditions.
figure 1

A Overview of the de novo motor learning task. Participants learned to control a cursor by moving their right fingers with combinations of adduction, abduction, flexion, and extension. Their goal was to reach a target on a 5 × 5 grid as quickly as possible and stay on the target until the next target was turned on. Two visual feedback conditions, continuous feedback (CF) and binary feedback (BF) conditions, were alternated across blocks, each consisting of 12 trials. Participants could see both cursor movement and a target in the continuous feedback condition, whereas cursor movement was hidden in the binary feedback condition. B Learning curves for CF and BF conditions. The increase in success rate implies that participants reached the targets more quickly and stayed on them longer. Participants performed better with the CF condition. The shaded areas represent the standard error of the mean. C Averaged success rates of the first and the last runs for both conditions. Success rates significantly increased in both conditions, implying they also learned the mapping in the binary feedback condition. The level of significance was represented by asterisks as follows. ***p < 0.001, ****p < 10−4. The error bars in (B) and (C) represent one standard error. Red and blue dots in (B) and (C) represent individual data for corresponding conditions.

Full size image

To quantify how much participants learned a motor skill through the experiment, we formalized success rate as a proportion of time during which a target turned red in a trial. For example, a success rate of 0.1 indicates that participants spent 3.6 seconds to reach a target and stayed in the target for 0.4 seconds. The higher the success rate, the faster the participants reached the target, which implies that the participants had learned hand-to-cursor mapping. During the first run of the experiment, the average success rates of CF and BF were 0.207 and 0.078, respectively, and the difference was statistically significant (t(23) = 7.53, p < 10−4). Then, they gradually learned the task throughout the experiment with significant improvement of the success rate from the first run to the last run both in the continuous feedback condition (t(23) = 13.33, p < 10−4) and in the binary feedback condition (t(23) = 4.49, p < 0.001) (Fig. 1B, C). The improvement of the success rate was 3.27 times higher in the continuous feedback condition than in the binary one (t(23) = 13.97 p < 10−4) (Fig. 1C), confirming that participants learned faster when online cursor feedback was provided. All the participants improved their performance throughout the experiment, as shown in individual learning curves (Supplementary Fig. 1).

Activation in sensorimotor and visual cortices

To understand the distinct roles of sensorimotor cortices in acquiring a novel motor skill with the two visual feedback conditions, we contrasted fMRI activity between the conditions using a conventional GLM analysis. Notably, we defined regions of interest in the sensorimotor cortices on the cortical surface for all the analyses in the present study since the surface-based analysis improves the specificity of fMRI activity across folded cortical regions over the volume-based analysis21. In particular, the surface-based analysis is critical to dissociate fMRI activity between the primary motor (M1) and somatosensory cortices (S1), which are a few millimeters apart in 3D volume space, i.e., Euclidean space. In addition, we focused our analyses on the contralateral (left) hemisphere.

The cortical surface-based GLM analysis revealed that the dorsal premotor cortex (PMd) and higher-order visual cortices in the dorsal and the ventral visual pathways exhibited significantly higher fMRI activity in the continuous feedback condition than in the binary one (Fig. 2A). In contrast, S1 and early visual areas demonstrated significantly higher fMRI activity when the binary feedback was provided. M1 is an intermixed region where the activation levels were similar between the conditions (Fig. 2B, C). Notably, the activity in S1 and part of M1 is contralateral, meaning that we do not observe it on the right hemisphere (Supplementary Fig. 2). In contrast, all the other activation patterns are bilateral. Since the participants used their right hand in the experiment, we focused on the contralateral left hemisphere for subsequent ROI and connectivity analyses (refer to Supplementary Fig. 2 for the GLM results in the right hemisphere).

Fig. 2: GLM result for the continuous vs. binary feedback conditions in sensorimotor regions.
figure 2

A Univariate activation map from the lateral view for the contrast, continuous feedback > binary feedback. B Enlarged map for (A) highlighting sensorimotor regions. C ROI analysis (see Methods) of the mean activation (\(\pm\) standard error of the mean) across the 28 searchlights. The inset shows the sensorimotor ROIs, the intersection of the significant clusters identified from the localizer GLM result, and the Brodmann areas 1, 2, 3, 4, and 6. The t-test results are based on the seven Brodmann areas. Note that the significance level is unusually high in BA4a, despite a small difference with a relatively large standard error of the mean. The significance level of multiple paired t-tests was represented by asterisks as follows. *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 10−4 (Bonferroni-corrected). Red and blue dots in (C) represent individual data for corresponding conditions.

Full size image

To analyze the regional specificity of fMRI activity in the sensorimotor cortices modulated by the visual feedback, we defined seven ROIs across sensorimotor cortices related to finger movement (see Methods and Supplementary Fig. 3 for the localizer GLM result). In the continuous feedback condition, activation was significantly higher in BA6 (PMd) and BA4a (anterior M1), with statistical outcomes of t(23) = 10.32, p < 10−4, and t(23) = 5.83, p < 10−4, respectively. Although the activation is not significantly different between the conditions in BA4p (posterior M1) (t(23) = 0.54, p = 0.56), the activation trends reveal a pivotal shift surrounding this region. In the binary feedback condition, activation became elevated in BA3a, 3b and 1 (S1), as evidenced by t(23) = 6.89, p < 10−4; t(23) = 12.21, p < 10−4; and t(23) = 10.43, p < 10−4, respectively. As activation decreased in both conditions in BA2 (S1), there was no difference between the conditions (t(23) = 0.96, p = 0.35). All p-values reported for statistically significant findings were Bonferroni-corrected for multiple comparisons (Fig. 2C). While the overall fMRI activity in the sensorimotor cortices was comparable (F(2, 46) = 2.30, p = 0.112), there was a significant difference between the feedback conditions (F(1, 23) = 13.25, p < 0.01). Importantly, we found a clear double dissociation of the fMRI activity between the feedback conditions across three representative ROIs, PMd, M1, and S1. The activity was higher in motor cortices (PMd and M1) for the continuous feedback (t(23) = 4.19, p < 0.001) and was higher in somatosensory cortices (S1) for the binary feedback (t(23) = −3.82, p < 0.001), resulting in significant interaction between ROIs and feedback conditions (F(1, 23) = 160.92, p < 10−4).

Interestingly, a similar double dissociation of fMRI activity was also found in the visual cortices (Fig. 3A). While the overall activity across ROIs in the visual cortices (Early visual area, V3AB, and V7; F(1, 23) = 3.45, p > 0.05) was comparable, it was significantly different between the feedback conditions (F(1, 23) = 29.74, p < 0.001). The early visual areas (V1, V2, and V3) were more activated when participants could not see the online cursor movement (t(23) = 2.71, p < 0.05); however, V3AB and V7 showed higher activation for the continuous feedback condition (t(23) = 3.46, p < 0.01; t(23) = 11.98, p < 0.001, respectively) (Fig. 3B), resulting highly significant interaction effect between ROIs and feedback conditions (F(1, 23) = 97.60, p < 0.001). Generally, early visual areas were more activated with the binary feedback, whereas higher-order visual areas were more activated with the continuous feedback.

Fig. 3: GLM result for the continuous vs. binary feedback conditions in visual regions.
figure 3

A Univariate activation map from the caudal view for the contrast, continuous feedback > binary feedback. B ROI analysis of the mean activation over visual areas (\(\pm\) standard error of the mean). The significance level was represented by asterisks as follows. *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 10−4(Bonferroni-corrected). Red and blue dots in (B) and represent individual data for corresponding conditions.

Full size image

In addition, while our main focus is on sensorimotor and visual cortices, we also discovered significant activations in the dorsal attention network (DAN) and the ventral attention network (VAN) during the continuous feedback condition compared to the binary feedback condition (t(23) = 9.30, p < 10−4, and t(23) = 3.69, p < 0.01, respectively; Supplementary Fig. 4). In contrast, no significant differences were observed in the fronto-parietal network (FPN) and the default mode network (DMN) between the two conditions (t(23) = 0.36, p = 0.72, and t(23) = 1.12, p = 0.27).

Connectivity between sensorimotor and visual cortices

Next, we examined whether the brain functional connectivity between sensorimotor and visual networks could explain de novo visuomotor skill learning. As a functional connectivity analysis, we calculated a partial correlation controlling the effect of task-related coactivation22. In this way, we made the connectivity analysis orthogonal to the GLM analysis23.

We hypothesized that the connectivity would decrease as learning hand-to-cursor mapping progressed with the increasing autonomy of each network1. Furthermore, we sought to find which specific sensorimotor or visual regions are involved in de novo skill learning. To define nodes for connectivity analysis, we first chose the top five most significant clusters, which were determined based on the group-level GLM results from the main task session. Then we split the largest motor cluster into two regions: PMd and M1, resulting in three regions for each sensorimotor (PMd, M1, and S1) and visual (dorsal, ventral, early) network (Supplementary Fig. 5). The final six nodes of the networks were defined as circular masks of 3 mm radius around the vertices with the peak intensity in the six regions of interest (Fig. 4A).

Fig. 4: Functional connectivity in the sensorimotor and visual networks and its behavioral correlations.
figure 4

A Six network nodes around the vertices with peak activity of a representative subject used for the connectivity analysis. The white dotted circles are the GLM cluster result of the main task session from which each peak is chosen. B Functional connectivity between the nodes in the sensorimotor network and those in the visual network. The color of the nodes is consistent with the color of the peak vertices in (A). C The relationship between S1-early visual cortices connectivity and the success rate revealed by a linear mixed-effect model. Each participant underwent four fMRI runs, which were indicated by the different shapes of the dots. The shaded region represents a 68% confidence interval.

Full size image

Intriguingly, the connectivity patterns after controlling for task-specific effects were comparable with coactivation patterns under the two alternate conditions shown in Fig. 2 (Fig. 4B). In particular, we found higher connectivity between the motor cortices (PMd and M1) and the late visual regions (dorsal and ventral) than between the motor cortices and the early visual region regardless of conditions or fMRI runs (see Methods; CF and the first run: t(23) = 10.80, p < 10−4; CF and the last run: t(23) = 10.33, p < 10−4; BF and the first run t(23) = 10.89, p < 10−4; BF and the last run: t(23) = 10.11, p < 10−4; all Bonferroni-corrected). In contrast, the connectivity between S1 and the early visual region was higher than between S1 and the late visual regions in the first runs of both conditions (CF and the first run: t(23) = 4.07, p < 0.001; CF and the last run: t(23) = 1.54, p = 0.55; BF and the first run t(23) = 3.93, p < 0.001; BF and the last run: t(23) = 2.54, p = 0.07; all Bonferroni-corrected).

To investigate the relationship between the strength of visuomotor interaction and learning performance, we tested how connectivity between sensorimotor and visual cortices changes over time. Among all the 18 tests for connectivity between three sensorimotor ROIs and three visual ROIs for each feedback condition, only the connectivity between S1 and early visual cortex significantly decreased from the first to the last fMRI run in the continuous feedback condition (t(23) = 5.12, Bonferroni-corrected, p < 0.001) (Fig. 4B). All the other connectivity did not reach significance level of corrected p < 0.05 for multiple tests. Then, we correlated the connectivity reduction with the improvement in learning performance, measured as an averaged success rate during each feedback condition and fMRI run. A linear mixed effect model analysis (fixed effect: connectivity across four fMRI runs, random effect: participants) revealed that the reduction of connectivity between S1 and the early visual region was highly correlated with performance improvement when continuous feedback was provided (coef = −0.36, SE = 0.077, p < 0.001) (Fig. 4C).

Discussion

In this work, we found distinctive involvement of the sensorimotor and visual cortices subregions in learning a motor skill de novo. We found clear double dissociation of fMRI activity in the subregions and their interaction mediated by visual feedback. Motor and late visual cortices were more activated when continuous visual feedback was available than when only binary visual feedback was available. In contrast, somatosensory and early visual cortices exhibited the opposite activation pattern. We also found a significant learning-induced reduction of connectivity between somatosensory and earl visual cortices, which was correlated with improved performance.

It is challenging to separate fMRI activity between closely located motor and somatosensory cortices since efferent motor commands and afferent proprioceptive feedback are processed simultaneously during continuous motor control13. In our experiment, manipulation of visual feedback allowed us to dissociate the fMRI activity by modulating the extent to which participants depended on visual or proprioceptive feedback to perform the task. When visual feedback is limited to binary feedback, participants are more likely to attend to proprioception, i.e., hand posture, leading to higher fMRI activity in somatosensory cortices than in motor cortices. In other words, the extent of visual feedback switches attentional focus on the visual or proprioceptive modality, as suggested in a previous study17. In our experiment of learning an arbitrary hand-to-cursor mapping, this dissociation would be more prominent than in typical motor learning tasks due to considerable uncertainty about the motor and sensory goals of the task13. We also found the boundary of the dissociation in the primary motor cortex. Specifically, the anterior part showed greater activation with the presence of online feedback compared to its absence, while the posterior part exhibited the reverse pattern. Our results are consistent with other studies claiming that the anterior M1 is more involved in motor execution, which is externally triggered, and the posterior M1 is more related to increased sensory attention24,25. Indeed, the anterior and posterior M1 were known to differ not only in their cytoarchitecture and neurochemistry but also in their functions26,27,28. Although our surface-based GLM analysis has the advantage over a volume-based GLM in delineating the boundary with less overlapped fMRI activity between M1 and S125, the spatial resolution would not be enough to dissociate the functional difference. Future studies using 7 T fMRI with superior spatial resolution and signal-to-noise ratio would be necessary to dissociate the roles of sensorimotor subregions more clearly.

The dissociative responses observed in visual cortices could be explained by competition for cognitive resources between early and late visual cortices. In the online feedback condition, we reasonably assumed that participants were visually tracking the cursor to perform the task, although we do not have eye-tracking data to support this assumption. Thus, the late visual cortices, including V5/MT sensitive to visual motion, would be more activated than in early regions. On the other hand, in the binary feedback condition where no online visual feedback is provided, the cognitive resource would be released from the late visual cortices, resulting in higher activation in the early visual cortex16,17. Alternatively, the difference in visual attention and eye movement strategies between the two alternate conditions could influence neural activities. Future research with eye-tracking could elucidate the role of eye movements in visuomotor learning, offering a more nuanced understanding of the neural mechanisms.

A landmark fMRI study revealed that visuomotor interaction in long-term motor sequence learning is more dominant in an earlier stage of learning visuomotor mappings and decreases in the later stage of learning with more automatic performance1. Our study similarly found a significant reduction of visuomotor interaction, specifically between S1 and early visual cortex, during short-term de novo motor skill learning. The more significant contribution of S1 than M1 to learning is potentially due to the complexity of our task with highly uncertain sensory targets, which emphasizes the role of proprioception necessary to estimate sensory states (i.e., hand postures)2,13. The somatosensory cortex could play a more critical role in initial visuomotor learning when a sensory target is highly uncertain2, as in our task learning an arbitrary hand-to-cursor mapping. Our study has a limitation without providing an explanation of the role of S1 in more long-term visuomotor learning.

Additionally, the more significant contribution of the early instead of late visual cortices would be related to higher spatial selectivity of visual fields corresponding to target positions in the early visual cortex29. In contrast, while the interaction between motor cortices and late visual cortices contributed to learning, as shown in more significant connectivity during the CF condition than during the BF condition, there was no significant decrease during learning. This lack of change could be due to the relatively short duration of learning (~40 minutes) for the complicated motor task. It would be intriguing to investigate whether multiple time scales in the interaction3 between M1/S1 and early/late visual cortices contribute to de novo visuomotor learning3 with more extensive practice20.

Finally, our results provide important insight into rehabilitation for patients with visual deficits or sensorimotor impairment. Specifically, research has shown that S1 and early visual areas are functionally connected in early blind individuals, who lost their vision before the age of 16, and thus rely on tactile information that is transferred to V1 to compensate for their loss of vision30. When repetitive transcranial magnetic stimulation (rTMS) was applied over S1 in early-blinded people, V1 showed significantly higher activation, underscoring the robustness of S1-early visual area connection in those individuals31. Our study extends these findings by demonstrating a functional connection between S1 and early visual areas in sighted individuals as well, specifically in the context of proprioceptive tactile information and visual information integrated during motor learning.

Methods

Subjects

Twenty-six healthy adults from the Sungkyunkwan University community participated in this study. According to the Edinburgh Handedness Inventory32, all participants were right-handed. In addition, they had no history of neurological or psychiatric disease and had normal or corrected-to-normal vision. Twenty-four participants (14 females; mean age = 24.9 \(\pm\) 4.7 years, age range = 18-35 years) completed all the experiment sessions. Similar sample sizes were used in recent fMRI experiments with the data gloves20,33,34. Two participants dropped out in the middle of the experiment due to severe fatigue; thus, their data were excluded from the analysis. All participants were provided written consent. All the experimental procedures adhered to the Declaration of Helsinki and were approved by the Institutional Review Board of Sungkyunkwan University, Suwon, Republic of Korea (IRB No. 2018-05-003-032). All ethical regulations relevant to human research participants were followed. Participants underwent two scanning sessions for 1.5 hours at a 3 T fMRI scanner and received monetary rewards for participating after the experiment.

fMRI data collection

The present study acquired fMRI data using a 3-T Siemens Magnetom Prisma scanner equipped with a 64-channel head coil. Functional images were obtained using an echo-planar imaging (EPI) sequence with specific parameters: a total of 300 volumes (with 310 volumes for localizer fMRI), a repetition time (TR) of 2,000 ms, an echo time (TE) of 35.0 ms, a flip angle (FA) of 90°, a field of view (FOV) measuring 200 mm, a matrix size of 101 ×113 × 91 voxels, 72 axial slices, and a slice thickness of 2.0 mm. For anatomical referencing, a T1-weighted anatomical scan of the entire brain was conducted using a magnetization-prepared rapid acquisition with gradient echo MPRAGE sequence. This anatomical scan employed specific parameters, including a TR of 2300 ms, a TE of 2.28 ms, an FA of 8°, an FOV of 256 mm, a matrix size of 204 × 262 × 260 voxels; 192 axial slices, and a slice thickness of 1.00 mm. Before the functional scans, two EPI images were acquired with opposite-phase encoding directions (posterior-to-anterior and anterior-to-posterior) to enable subsequent distortion correction.

Data glove

Participants wore the MR-compatible data glove (5DT Glove 14 Ultra) on their right hand. With the data glove, hand postures recorded by 14 sensors were converted to cursor positions on the 2-dimensional screen. The hand-to-cursor mapping is defined below.

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{ccccc}{a}_{x,1} & {a}_{x,2} & {a}_{x,3} & \cdots & {a}_{x,14}\\ {a}_{y,1} & {a}_{y,2} & {a}_{y,3} & \cdots & {a}_{y,14}\end{array}\right]\times {\left[\begin{array}{ccccc}{s}_{1} & {s}_{2} & {s}_{3} & \cdots & {s}_{14}\end{array}\right]}^{T}+\left[\begin{array}{c}{x}_{0}\\ {y}_{0}\end{array}\right]$$

where \({s}_{k}(k={{\mathrm{1,2}}},\ldots ,14)\) indicates each of the 14 sensor inputs from the data glove, and \(x\) and \(y\) indicate the cursor’s horizontal and vertical position. The time-series data of the 14 sensors was sampled at 60 Hz. The above equation can be rewritten as \({{{\bf{r}}}}={{{\bf{As}}}}+{{{{\bf{r}}}}}_{{{{\bf{0}}}}}\), where the mapping matrix \({{{\bf{A}}}}\) and the offset \({{{{\bf{r}}}}}_{{{{\bf{0}}}}}\) were determined from the calibration and localizer session.

Calibration

Before fMRI scanning, participants had a calibration phase in an MRI scanning control room. After wearing the data glove, participants moved their right hands while they could see a graph of 14 bars moving in real-time based on the 14 sensors. Participants were instructed to try various combinations of hand postures, including adduction, abduction, flexion, and extension of fingers. Next, we conducted a principal component analysis with the covariance matrix derived from the time series collected from the 14 sensors. The first two principal components were employed to create the mapping matrix \({{{\bf{A}}}}\), and the offset \({{{{\bf{r}}}}}_{{{{\bf{0}}}}}\) was calculated to ensure that the average hand posture was aligned with the center of the screen. After that, we ensured that participants could visit all 25 cells of a 5 × 5 grid (Fig. 1A).

Localizer session

After the calibration phase, participants moved to an MRI scanning room. They lay on their back in the scanner, observing the screen via a mirror. Foam pads were applied to all participants to reduce head movement. In addition, they wore the data glove on their right hand and put the hand in a comfortable position. Notably, participants could not see their hands moving during the entire fMRI experiment.

The localizer session aimed to define the brain regions related to finger movement, independently from the main task. When “Move” was displayed on the screen, participants performed natural-speed movements with their right fingers, ceasing their movements upon the appearance of the “Stop” text. Each “Move” or “Stop” condition had a duration of 48 seconds, separated by 2-second intervals, and a total of six sets of “Move” and “Stop” conditions were executed. To ensure it is de novo learning to participants, we recalibrated the mapping matrix \({{{\bf{A}}}}\) and the offset \({{{{\bf{r}}}}}_{{{{\bf{0}}}}}\) using the data acquired from the finger movements in the last two “Move” blocks. We also ensured that all 25 grid cells were reachable by finger movements.

Main task session

Participants were required to move their right fingers to control a cursor and reach a target cell with all combinations of adduction, abduction, flexion, and extension of their fingers. A target cell is a gray cell with a yellow crosshair in its center. If participants reached a target cell, its color changed to red, and they were required to stay in the target cell without moving their fingers until the next one appeared. In other words, the main task was to reach a target as quickly as possible and to stay as long as possible at the target. A target cell appeared for 4 s. Regardless of whether participants reached a target or not, the target was changed to the next one after 4 s. Each block had 12 trials with a sequence of either 13-3-25-21-13-25-3-21-25-13-21-3 (Sequence 1: triangle) or 13-23-5-1-13-5-23-1-5-13-1-23 (Sequence 2: inverted triangle), where the number indicates the grid cell number determined by the formula \(k=5i+j-5\), with \(i\) representing the row index and \(j\) representing the column index. Half of the participants were presented with Sequence 1, and the other half were presented with Sequence 2 for counterbalancing. In total, there were four runs, and each run consisted of 12 blocks. Thus, the duration of each run was about 576 s (144 trials \(\times\) 4 s).

Notably, there were two experimental conditions: continuous visual feedback and binary visual feedback. In the continuous feedback condition, participants could see both cursor movement and targets. On the other hand, in the binary feedback condition, participants could only see targets. However, the cursor was not visible (Fig. 1B). Thus, participants could only guess their cursor position by the color of the targets. The two conditions were applied in separate blocks alternately. During odd-numbered blocks, the cursor position was continuously represented by a white crosshair, whereas it was hidden during even-numbered blocks.

Behavioral data analysis

The proportion of time during which a target turned red was measured as a trial-by-trial success rate. For example, the success rate of one block was defined by the amount of time targets turned red during one block divided by 48 s, a total time of one block. We used a two-sided paired t-test between different feedback conditions, or fMRI runs to see if there was a significant difference. MATLAB (version R2022a, MathWorks), Python (version 3.10.8), and Jupyter Notebook (version 6.4.12) were utilized for all statistical analyses.

fMRI data analysis: preprocessing

MRI data were analyzed with FreeSurfer (version 7.2.0)35. We first followed the FreeSurfer ‘recon-all’ pipeline to preprocess anatomical data. Then, for functional data, we followed the FreeSurfer Functional Analysis Stream (FS-FAST) preprocessing pipeline (https://surfer.nmr.mgh.harvard.edu/fswiki/FsFastTutorialV6.0/FsFastPreProc). Functional data from each subject were registered to the same-subject FreeSurfer anatomical data with motion correction and slice-timing correction. Then, the functional data were resampled to common FreeSurfer space. Note that we did not perform spatial smoothing, which reduces the spatial specificity of the GLM analysis36, since our primary goal of the analysis was to achieve precise brain mapping to distinguish sensorimotor areas. This approach follows the non-smoothing method of previous studies that have successfully distinguished shared voxels37,38. Furthermore, unlike a typical GLM analysis, spatial smoothing should be avoided for a functional connectivity analysis39,40.

fMRI data analysis: GLM

We utilized FS-FAST for the GLM analysis, a FreeSurfer fMRI data analysis tool41. We contrasted fMRI activity between “Move” versus “Stop” conditions and continuous feedback (CF) versus binary feedback (BF), respectively, for the localizer session and the main session. For each session, the regressors of interest were computed by convolving boxcars encoding the contrasting two conditions with the SPM canonical hemodynamic response function (HRF) of zero derivatives. We added nuisance regressors, which are motion parameters created in preprocessing, and third-order polynomial regressors to the design matrix for the GLM analysis. After the first-level analysis, individual results were concatenated into one file with the “isxconcat-sess” function. Then, group GLM was performed with “mri_glmfit .” Multiple comparison correction was done by “mri_glmfit-sim” with cluster-forming threshold (CFT) of p < 10−4 and cluster-wise p-value of p < 0.05. The final full width at half maximum (FWHM) of the inherent smoothness was considered for multiple comparisons correction. A similar analysis was also done on the localizer result with different conditions of “Move” and “Stop” to identify regions responding to hand movement (Supplementary Fig. 3A).

ROI selection and analysis

For regions of interest in (ROIs) the sensorimotor cortices, we identified overlapping regions between significant clusters related to finger movement (the localizer GLM result, Supplementary Fig. 3B) and Brodmann areas provided by FreeSurfer42 (BA6 for PMd; BA4a and 4p for M1; BA1, 2, 3a and 3b for S1; https://surfer.nmr.mgh.harvard.edu/fswiki/BrodmannAreaMaps). These seven ROIs were employed in the univariate activation analysis, where beta estimates obtained from the GLM analysis within the ROIs are averaged and presented in line graphs with their means and standard errors of the means (Figs. 2C and 3B). We reported Bonferroni-corrected p-value for seven statistical tests performed on the ROIs. For visualization purposes only (as shown in Fig. 2C), we defined 28 rectangular searchlights covering the sensorimotor ROIs with regular intervals. The boundaries of these 28 rectangular searchlights were adjusted to align as closely as possible with the Brodmann area boundaries. For ROIs in the visual cortices, we used the surface-based atlas provided by Wang et al.43. They grouped V1d, V1v, V2d, V2v, V3d, and V3v regions, defining the group as an early visual region, and we adhered to their classification.

For connectivity analysis, we chose the five most significant clusters made from the GLM result (Supplementary Fig. 5). On the other hand, based on our hypotheses, we divided the yellow cluster in Figure S4A into PMd and M1 parts based on the Brodmann area. We also used only the posterior part of the scarlet cluster and defined it as a dorsal visual cluster. As a result, we have six clusters of PMd, M1, S1, dorsal, ventral, and early visual regions. Then, we defined individual circular masks of 3 mm radius from each cluster (Fig. 4A). First, we used the “mri_surfcluster” function to identify each vertex number, which serves as the center of a circular mask. This was determined by locating the vertex with the highest absolute beta estimates from the first-level GLM analysis of the main task. After that, the circular masks were drawn around the center with the “mri_volsynth,” “mris_fwhm,” and “mri_binarize” functions.

fMRI data analysis: connectivity

The task-based time-series data were extracted and averaged within the seeds defined in ROIs by “mri_segstats”. For the time-series data of each run, we regressed out the same motion parameters and third-order polynomials as used in the GLM analysis, as well as other nuisance signals, such as a global signal, which is computed as an averaged signal within the whole-brain mask, two signals projected on the top principal component within white matter (WM) and ventricular cerebrospinal fluid (vCSF), respectively from PCA using “fcseed-sess”. To remove task-related components, functional connectivity between two seeds was calculated as a partial correlation controlling the task regressors used in the GLM analysis. The functional connectivity was calculated for nine pairs of sensorimotor ROIs (PMd, M1, and S1) and visual ROIs (early, dorsal, and ventral) for each of the two visual feedback conditions (18 connectivity values).

To check whether there was a significant difference in functional connectivity between the sensorimotor ROIs and the visual ROIs from the first to the last run, we performed 18 separate two-tailed paired t-tests with Bonferroni-corrected p-values for the multiple tests. Given the significant decrease in functional connectivity between S1 and the early visual region, we further conducted the linear mixed effects (LME) model analysis with random intercepts (fixed effect: connectivity across four fMRI runs, random effect: participants). The LME analysis aimed to examine the correlation between the observed changes in functional connectivity and the improvement in behavioral performance.