MolGraph-xLSTM as a graph-based dual-level xLSTM framework for enhanced molecular representation and interpretability

Abstract

Predicting molecular properties is essential for drug discovery, and computational methods can greatly enhance this process. Molecular graphs have become a focus for representation learning, with Graph Neural Networks (GNNs) widely used. However, GNNs often struggle with capturing long-range dependencies. To address this, we propose MolGraph-xLSTM, a novel graph-based xLSTM model that enhances feature extraction and effectively models molecule long-range interactions. Our approach processes molecular graphs at two scales: atom-level and motif-level. For atom-level graphs, a GNN-based xLSTM framework with jumping knowledge extracts local features and aggregates multilayer information to capture both local and global patterns effectively. Motif-level graphs provide complementary structural information for a broader molecular view. Embeddings from both scales are refined via a multi-head mixture of experts (MHMoE), further enhancing expressiveness and performance. We validate MolGraph-xLSTM on 21 datasets from the MoleculeNet and Therapeutics Data Commons (TDC) benchmarks, covering both classification and regression tasks. On the MoleculeNet benchmark, our model achieves an average AUROC improvement of 3.18% for classification tasks and an RMSE reduction of 3.83% for regression tasks compared to baseline methods. On the TDC benchmark, MolGraph-xLSTM improves AUROC by 2.56%, while reducing RMSE by 3.71% on average. These results confirm the effectiveness of our model in learning generalizable molecular representations for drug discovery.

Introduction

Predicting the molecular properties of a compound, particularly its ADMET (Absorption, Distribution, Metabolism, Excretion, and Toxicity) characteristics, is critical during the early stages of drug development^1,2. Leveraging deep learning for molecular representation to predict these properties significantly enhances the efficiency of identifying potential drug candidates^3,4. Molecular graphs retain richer structural information, which is crucial for accurate property prediction. In recent years, Graph Neural Networks (GNNs) built on molecular graph data have been extensively utilized for molecular representation learning to predict a wide range of properties^{5,6,7,8,9,10,11,12,13}.

A key challenge in molecular property prediction lies in capturing long-range dependencies—the influence of distant atoms or substructures within a molecule on a target property. While GNNs leverage neighborhood aggregation as their core mechanism—updating the hidden states of each node by aggregating information from neighboring nodes using operations like sum, max, or mean pooling^14,15—they face significant limitations in capturing these long-range dependencies. Specifically, over-smoothing and over-squashing hinder their performance. Over-smoothing occurs when, as the number of layers increases, node representations become increasingly similar, leading to a loss of distinction between nodes¹⁶. On the other hand, over-squashing refers to the compression of information from distant nodes as it propagates toward the target node, making it challenging for relevant information to be effectively transmitted¹⁷. These issues limit the ability of GNNs to fully exploit global structural information, reducing their effectiveness in complex molecular property prediction tasks.

To address these challenges, we propose the MolGraph-xLSTM model, which integrates the extended Long Short-Term Memory (xLSTM) architecture with molecular graphs. Traditionally, Long Short-Term Memory (LSTM) networks have been widely used in Natural Language Processing (NLP) tasks to capture sequential data representations¹⁸. With its gating mechanisms, LSTM effectively decides which information to retain or discard, enabling it to manage long-range dependencies. Thus, we incorporate LSTM into our model to address the limitations of GNNs in handling long-range information. Recently, an improved version, xLSTM, was introduced¹⁹. xLSTM includes two additional modules, scalar Long Short-Term Memory (sLSTM) and matrix Long Short-Term Memory (mLSTM), which expand the storage capacity of the original LSTM. Experimental results have shown favorable performance compared to two state-of-the-art architectures: Transformer²⁰ and State Space Models²¹. For this reason, we chose this xLSTM model in our framework.

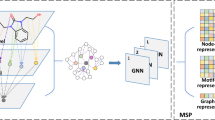
We utilize both atom-level and motif-level molecular graphs in our approach (Fig. 1). In the atom-level graph, each node represents an atom, and each edge represents a bond within the molecule. The motif-level graph, on the other hand, is a partitioned version of the atom-level graph, where each node represents a substructure (such as an aromatic ring) within a molecule. This results in a significantly simplified representation compared to the atom-level graph. Such simplification aids the model in learning features linked to local structures, as similar local motifs, from a functional group perspective, tend to impart similar properties to molecules²². Furthermore, the simplified motif-level graph, by reducing complexity and eliminating cycle structures, becomes closer to sequential data. This structural simplification aligns well with the strengths of xLSTM, which is inherently designed to handle sequential information, making the motif-level graph more suitable for processing with xLSTM.

Fig. 1: Comparison of atom-level and motif-level graph representations.

a Atom-level graph representation, where each atom is represented as a node and each chemical bond as an edge. b Motif-level graph representation, where substructures are represented as single nodes, resulting in a graph that is less complex than the atom-level graph.

However, relying solely on the motif-level graph would not capture all molecular details effectively, and motif partitioning itself demands precise segmentation. Therefore, we incorporate both atom-level and motif-level graphs in our model. For the atom-level representation, we introduce a GNN-based xLSTM with jumping knowledge²³. Here, the GNN collects local information from the atom-level graph, and jumping knowledge aggregates features from multiple GNN layers, producing enriched node representations as inputs to xLSTM. By combining features from both the atom- and motif-level graphs, we constructed a comprehensive molecular representation for accurate property prediction.

Additionally, we integrate the Multi-Head Mixture-of-Experts (MHMoE) module²⁴ to enhance the predictive performance of our model. The sparse mixture-of-experts (SMoE)²⁵ framework has been demonstrated as an effective method for scaling models while maintaining computational efficiency by dynamically assigning inputs to different expert networks. This allows the input features to be processed by multiple experts, enabling diverse perspectives and improving the quality of learned representations. Building upon SMoE, the MHMoE architecture introduces further advancements by enhancing the usage of experts and promoting a more fine-grained understanding of input features. By incorporating the MHMoE module, our model is able to generate more expressive feature representations, which enhances its predictive accuracy.

The contributions of our work are as follows:

• Adaptation of xLSTM to dual-level molecular graph representation: We design a unified architecture that applies the xLSTM to both atom-level and motif-level molecular graphs. At the atom level, xLSTM follows GNN layers to enhance local features with long-range context. At the motif level, the graph is simplified through functional substructure decomposition, resulting in a sequential-like topology that further aligns with xLSTM’s modeling strengths. This dual-level application enables comprehensive capture of fine-grained and high-level structural dependencies, substantially boosting prediction performance across 21 molecular property benchmarks.

• Integration of MHMoE for enhanced prediction: We incorporated the MHMoE module into our framework, which dynamically assigns input features to different expert networks, enabling diverse feature processing and improving predictive accuracy. This architecture refines feature representations through fine-grained expert activation.

• Case study analysis for model interpretability: We conducted a case study to investigate the substructures assigned the highest weights by the network, demonstrating that the atom-level and motif-level information are complementary. By cross-referencing with known literature, we identified strong correlations between the highlighted substructures and specific molecular properties, underscoring the ability of the model to implicitly learn biologically relevant information.

Results

Performance evaluation on MoleculeNet

MolGraph-xLSTM demonstrates improved performance across both classification and regression datasets, highlighting its robustness in handling diverse molecular property prediction tasks. In the classification tasks (Tables 1 and S1), MolGraph-xLSTM achieves particularly strong results on the Sider datasets. For the Sider dataset, MolGraph-xLSTM achieves an area under the receiver operating characteristic curve (AUROC) of 0.697 ± 0.022, representing a 5.45% improvement over the best baseline, FP-GNN (0.661  ± 0.014).

Table 1 Performance evaluation on classification datasets from MoleculeNet

For regression datasets (Table 2 and Table S2), MolGraph-xLSTM delivers competitive performance across multiple benchmarks. On the ESOL dataset, MolGraph-xLSTM achieves a Root Mean Squared Error (RMSE) of 0.527 ± 0.046, reflecting a 7.54% improvement over the best-performing baseline, HiGNN (0.570 ± 0.061). On the FreeSolv dataset, MolGraph-xLSTM achieves the lowest RMSE of 1.024  ± 0.076 and the highest Pearson Correlation Coefficient (PCC) of 0.960 ± 0.006, demonstrating its reliability in regression tasks.

Table 2 Performance evaluation on regression datasets from MoleculeNet

Performance evaluation on TDC benchmarks

MolGraph-xLSTM exhibits consistent performance across both classification and regression tasks in the TDC benchmark, indicating its capacity to generalize across diverse pharmacological endpoints. In classification tasks (Tables 3 and S3), MolGraph-xLSTM achieves the highest average AUROC (0.866) and area under the precision-recall curve (AUPRC) (0.861) across nine classification datasets, slightly outperforming competitive baselines such as DMPNN (AUROC: 0.861, AUPRC: 0.853) and FPGNN (AUROC: 0.859, AUPRC: 0.856).

Table 3 Performance evaluation on classification datasets from TDC

MolGraph-xLSTM achieves noticeable improvement on the Bioavailability dataset, which measures the fraction of an administered drug that reaches systemic circulation. It obtains an AUROC of 0.684 ± 0.118, compared to 0.666 ± 0.035 from the best-performing baseline (FPGNN), and maintains a competitive AUPRC of 0.872 ± 0.057.

In regression tasks (Tables 4 and S4), MolGraph-xLSTM achieves leading or comparable results. It obtains the lowest RMSE on both the Caco2 (0.358 ± 0.015) and PPBR (11.772 ± 0.200) datasets, reflecting 11.17% and 3.81% improvements over the next-best models. Additionally, it achieves the highest PCC of 0.861 ± 0.011 on Caco2 and 0.644 ± 0.019 on PPBR.

Table 4 Performance evaluation on regression datasets from TDC

Interpretability analysis

To evaluate the interpretability of MolGraph-xLSTM, we visualized the motifs and atomic sites with the highest model-assigned weights from the motif-level and atom-level networks. By applying max-pooling to the output of the xLSTM layer, we identified the features with the greatest contributions, providing us insight into the substructures and atomic sites that are most closely related to the properties of a particular molecule.

In Fig. 2, all three molecules highlight the—SO₂NH—(sulfonamide) substructure, a chemical motif known to be strongly linked with adverse reactions such as Type IV hypersensitivity, blurred vision, and other side effects²⁶. These adverse effects correspond to side effects labeled in the Sider dataset, including Eye Disorders, Immune System Disorders, and Skin and Subcutaneous Tissue Disorders, demonstrating an alignment between the highlighted substructure and known biological properties of sulfonamides. Additionally, molecules like Fig. 2e, f emphasize atomic sites beyond the sulfonamide motif. In Fig. 2f, the highlighted N atom resides within the hydrazine group (− NH − N =), which is known to exert toxic effects on multiple organ systems, including neurological, hematological, and pulmonary²⁷. This suggests that the atom-level network captures additional fine-grained features that complement the broader motif-level representations, demonstrating the capacity of the model to integrate complementary information from both atom-level and motif-level networks.

Fig. 2: Visualization of the highest-weighted motifs and atoms identified by the model for molecules from the Sider test set containing the SO₂NH substructure.

a–c Motifs with the highest attention weights from the motif-level branch. d–f Atoms with the highest attention weights from the atom-level branch.

We further conducted an analysis on the BBBP dataset (blood-brain barrier permeability), a crucial property in evaluating the ability of a drug to cross the blood-brain barrier and target Central Nervous System (CNS) disorders. Accurate prediction of this property is essential for developing CNS-targeted therapies. For each molecule in the dataset, the substructure with the highest weight assigned by MolGraph-xLSTM was identified. These substructures were further analyzed using a random forest model²⁸ to determine their relationship with BBBP labels.

Fig. 3 illustrates the importance scores of substructures as determined by the random forest model. Among these, the substructure  − CC(= O)O − , containing a carboxylic group (− C(= O)O −), achieved the highest importance score. This finding is supported by previous studies^29,30, which have highlighted the role of the carboxylic group in influencing BBBP.

Fig. 3: Importance scores of substructures identified by MolGraph-xLSTM on the BBBP dataset.

For each molecule, the substructure with the highest model-assigned weight was analyzed using a random forest model to determine its relationship with BBBP labels. The substructure  − CC( = O)O − , containing a carboxylic group, received the highest importance score (highlighted by the blue dashed box).

Ablation study

Effect of different designed modules

We conducted an ablation study to evaluate the contributions of different components in MolGraph-xLSTM, including the atom-level branch (MolGraph-xLSTM (Atom-Level)), motif-level branch (MolGraph-xLSTM (Motif-Level)), multi-head mixture-of-experts module (MolGraph-xLSTM(w/o MHMoE)), and the GNN component within the atom-level branch (MolGraph-xLSTM (w/o GNN)). The results, presented in Table S5 and Fig. S1, highlight the importance of these components in achieving superior performance.

The full MolGraph-xLSTM model consistently outperformed all ablation variants, highlighting the effectiveness of its integrated architecture. Notably, even with only the atom-level branch, MolGraph-xLSTM achieved competitive performance, outperforming other atom-level graph-based models like DMPNN and DeeperGCN, as well as TransFoxMol, a hybrid model integrating GNN and Transformer. These results validate the design of our hybrid GNN and xLSTM framework as an effective approach for molecular representation learning. For the motif-level branch, it also outperformed other baselines on the Sider dataset, including HiGNN, which also utilizes motif-level graphs, in the classification task. However, its performance on the regression dataset was suboptimal. This suggests that the motif-level initialization features utilized in our model may not sufficiently capture the granularity required for regression tasks, highlighting opportunities for further improvement.

The MHMoE module contributed to the model performance, particularly on the FreeSolv dataset. Removing the MHMoE module resulted in an RMSE increase from 1.024 to 1.158, closely aligning with the performance of the atom-level-only variant, indicating its role in improving regression performance. As shown in Figs. S2 and S3, the activation maps demonstrate that all experts actively contribute to the task, indicating effective load balancing. This balanced activation ensures no single expert is overwhelmed, allowing the network to fully leverage the diverse expertise of all experts.

Among the four components, the GNN had the least impact on the Sider dataset but showed a notable influence on FreeSolv. Overall, the ablation study demonstrates that the atom- and motif-level branches provide complementary insights into molecular representation learning, and their integration enhances the model performance. This highlights the effectiveness of the proposed approach for molecular modeling.

Impact of node input order for molecular graphs on performance

xLSTM is originally designed for sequence data, which inherently has a fixed order. However, graph data does not have this property, as it can start from any node (Fig. 4). In our initial tests, we used the default node order provided by RDKit. In this section, we evaluate the effect of using a randomized starting node during training. Specifically, we generate the node sequence by performing a Depth-First Search (DFS) starting from a randomly selected initial node in the graph for each training instance.

Fig. 4: Examples of different atom input orders for molecular graphs in xLSTM.

a RDKit default order: atoms are ordered as per the default output from RDKit. b DFS order: atoms are ordered based on a DFS traversal of the molecular graph.

Fig. S4 compares the performance of MolGraph-xLSTM trained with the RDKit default node order and the DFS random order on Sider and Freesolv datasets. On the Sider dataset (Fig. S4a), the model trained with the RDKit default order slightly outperformed the DFS random order in both AUROC and AUPRC metrics. Similarly, on the FreeSolv dataset (Fig. S4b), the RMSE and PCC metrics indicate a marginal advantage for the RDKit default order. Despite these differences, the results show that MolGraph-xLSTM achieves competitive performance with both node orderings. This suggests that the model is robust to changes in the input node sequence.

One possible explanation for this robustness is that although the initial node varies, the DFS imposes a relatively consistent traversal pattern across graphs. As a result, the relative positions of most nodes, particularly those within local substructures, tend to be preserved regardless of the starting point. This consistency likely helps maintain the stability of input sequences and contributes to the model’s training stability and reproducibility across runs.

Long-range information retention via gate-based analysis

To provide direct evidence that the proposed xLSTM architecture captures long-range dependencies in the molecular graph, we performed a gate-based memory retention analysis. This analysis is based on the decay matrix D[t, s], which measures how much the hidden state at timestep s contributes to the representation at timestep t through the internal gating mechanism of the model.

Formally, let i_k and f_k denote the input and forget gate activations at timestep k, respectively. The element D[t, s] is defined as:

$$D[t,s]=\left\{\begin{array}{ll}{i}_{s}\cdot \mathop{\prod }\limits_{k=s+1}^{t}{f}_{k},\quad &0\le s\le t,\\ 0,\quad \hfill&s > t,\hfill\end{array}\right.$$

where i_s determines how much new information is introduced at timestep s, and ${\prod }_{k = s+1}^{t}{f}_{k}$ quantifies the proportion of that information retained by the forget gates from s + 1 to t. This formulation can be interpreted as a measure of temporal attention or memory retention within the xLSTM.

As an illustrative case study, we analyzed the molecule C1=C[C@@H]([C@@H]2[C@H]1[C@@]3(C(=C([C@]2(C3(Cl)Cl)Cl)Cl)Cl)Cl)Cl from the FreeSolv dataset. We examined D[22, s], representing the influence of all previous timesteps s ≤ 22 on the final atom. The resulting memory retention plot is shown in Fig. 5.

Fig. 5: Memory retention.

Gate-based memory retention plot at timestep 22 for the molecule C1=C[C@@H]([C@@H]2[C@H]1[C@@]3(C(=C([C@]2(C3(Cl)Cl)Cl)Cl)Cl)Cl)Cl from the FreeSolv dataset.

Interestingly, the retention profile does not decay monotonically with temporal distance. Instead, multiple distant timesteps (e.g., steps 0-15) exhibit substantial influence, in some cases exceeding that of more recent steps. This suggests that xLSTM selectively preserves information from non-adjacent atomic contexts, adapting its retention patterns to the molecular structure and contextual requirements.

These findings provide direct evidence that xLSTM overcomes the short-range dependency bias inherent in standard GNNs, enabling effective modeling of non-local interactions across distant motifs or atoms.

Hyperparameter analysis

Performance of MolGraph-xLSTM with varying numbers of experts and heads in the MHMoE

The heatmaps in Fig. S5 reveal the impact of the number of experts and heads in the MHMoE module on the model’s performance for the Sider and FreeSolv datasets. For both datasets, configurations with two experts generally perform poorly, while increasing the number of experts to 4 or 6 yields better results. Beyond 6 experts, no significant improvements are observed, suggesting that additional experts may become redundant for these datasets, as they do not process substantially different information.

For the Sider dataset, measured by AUROC, an increase in the number of heads consistently enhances performance, indicating that more heads improve the model’s ability to handle classification tasks. In contrast, for the FreeSolv dataset, measured by RMSE, increasing the number of heads beyond 8 leads to a noticeable decline in performance, particularly when the number of heads reaches 16. This decline is likely due to overfitting, as FreeSolv is a relatively small dataset. These observations highlight the need to balance the number of experts and heads based on the task and dataset size, as excessive complexity can negatively affect performance.

Performance of MolGraph-xLSTM with varying number of jump layers

The results in Fig. S6 illustrate the impact of varying the number of jump layers on the performance of MolGraph-xLSTM across the Sider and FreeSolv datasets. On the Sider dataset, the AUROC shows relatively small fluctuations, with the maximum value of 0.697 observed at 4 jump layers and the minimum value of 0.673 at 8 jump layers, representing a difference of 3.4%. In contrast, for the FreeSolv dataset, the impact of jump layers is more pronounced. The RMSE increases significantly from its lowest value of 1.042 at 4 jump layers to its highest value of 1.326 at 8 jump layers, a difference of 27%. The decline in performance at higher numbers of jump layers suggests that the inherent oversmoothing problem in GNNs may lead to the integration of overly smoothed deep features, which can negatively impact the performance of tasks requiring precise regression predictions.

Discussion

In this study, we propose a molecular representation learning framework that leverages xLSTM for both atom-level and motif-level graphs, providing a novel approach to molecular property prediction. Additionally, we incorporate the MHMoE module into our framework, which dynamically assigns input features to diverse expert networks, enhancing predictive accuracy through fine-grained feature activation. The effectiveness of our model is demonstrated across multiple molecular property prediction datasets, as presented in the “Results” section. Additional results for other evaluation metrics are provided in the supplementary material.

Our framework integrates atom-level and motif-level representations, and the ablation study highlights the independent effectiveness of these two levels. Specifically, both the atom-level and motif-level networks achieve competitive results individually in classification tasks (section “Effect of different designed modules”). However, the motif-level network exhibits a noticeable decline in regression performance. This limitation may be due to the initialization features of the motif-level graph, which rely on basic substructure properties, such as the counts of specific atoms (e.g., carbon) or bond types (e.g., single bonds). While these features capture useful information for classification tasks, they may lack the precision required for accurate regression predictions.

Regarding motif decomposition, certain complex molecules, such as polycyclic compounds with fused ring systems, can introduce structural complexity and pose challenges for decomposition. Nevertheless, the adopted decomposition strategy, ReLMole, applies uniform rules across all molecules, ensuring consistent motif representations regardless of topological intricacy. This consistency helps preserve the model’s generalization ability, even when handling multi-ring systems.

We also note some trade-offs between different evaluation metrics. For example, while MolGraph-xLSTM generally achieves strong ranking-based performance across classification datasets, discrete metrics such as F1 or accuracy may be lower on certain datasets, reflecting conservative probability predictions near classification thresholds. Similarly, in regression tasks, RMSE and MAE values may show subtle differences, indicating the model’s ability to control large errors while maintaining a centralized prediction distribution. These observations suggest opportunities for further calibration or representation refinement.

In addition to quantitative results, our interpretability analysis (section “Interpretability analysis”) highlights the strengths of the model. By analyzing the high-weight substructures identified by the model, we observed biologically meaningful correlations between the recognized substructures and specific molecular properties. This demonstrates that the model not only achieves competitive predictive performance but also provides valuable interpretability. Such interpretability is crucial for practical applications, as it can assist in drug design by guiding the identification of key molecular features associated with desired properties.

To further assess the practical utility of our model, we provide a comparison of GPU memory usage, training time, and inference time with FP-GNN in the supplementary material (Table S6). These results indicate that, despite its architectural complexity, our model is computationally efficient in practice and well-suited for large-scale molecular screening tasks.

Methods

Datasets and evaluation

MoleculeNet

MoleculeNet³¹ is a widely used benchmark designed to evaluate machine learning models on molecular property prediction. We selected a subset of MoleculeNet datasets covering both classification and regression tasks.

For dataset splitting, we adopted different strategies based on task type. For single-task classification datasets, we employed scaffold splitting to ensure that molecules with different core scaffolds are separated into training, validation, and test sets. This strategy evaluates model generalization to novel chemical structures. For multi-task classification and regression datasets, we used random splitting to avoid data imbalance due to the relatively small dataset sizes.

Each dataset was split into training, validation, and test sets using an 8:1:1 ratio. The model was trained on the training set and evaluated on the validation set after each epoch. The best-performing model on the validation set was then used to report metrics on the test set. Each experiment was repeated three times, and we report the mean and standard deviation of the results.

Therapeutics data commons (TDC)

We further evaluated our model on benchmark datasets from the TDC³². We adopted the official scaffold-based splits provided by TDC, where each dataset is partitioned into training, validation, and test sets in a 7:1:2 ratio. Each dataset includes five predefined splits. No additional resplitting or preprocessing was applied.

Evaluation metrics

For classification tasks, we used AUROC and AUPRC as evaluation metrics. For regression tasks, we reported RMSE and PCC. Detailed dataset information is summarized in Tables S7 and S8, and training hyperparameters are listed in Tables S9 and S10.

Hyperparameter tuning

For our proposed model, we performed grid search on the validation set to tune the hyperparameters, including the power coefficient (searched over {1, 2, 4}), hidden dimension ({64, 128, 256}), number of experts ({4, 8}), number of attention heads ({4, 8, 16}), and the number of expert layers ({1, 2, 3}). For baseline models, we followed the original implementations and used the reported hyperparameters when available; if not explicitly provided, we adopted values consistent with those used on similar datasets in the literature.

Baselines

We compare our proposed method against seven baseline models: Directed Message Passing Neural Network (DMPNN), Fingerprints and Graph Neural Networks (FPGNN), Hierarchical Informative Graph Neural Networks (HiGNN), Deeper Graph Convolutional Network (DeeperGCN), a transformer-based framework with focused attention (TransFoxMol), a sequence-based BiLSTM model, and an automated machine learning pipeline (AutoML). Each baseline represents a distinct approach to molecular representation learning or model optimization.

• FPGNN¹⁰: combines molecular fingerprints with features derived from graph attention networks, capturing both traditional cheminformatics features and structural insights from graphs.

• DeeperGCN⁷: a pure graph neural network based on GCN, designed for deeper architectures to enhance feature extraction.

• DMPNN⁶: optimizes message passing by centering aggregation on bonds instead of atoms, effectively encoding the chemical structure and avoiding redundant loops.

• HiGNN³³: learns molecular representations at both the atomic level and the level of substructures using hierarchical GNNs.

• TransFoxMol¹²: integrates the power of GNNs and transformers to capture global and local molecular features efficiently.

• BiLSTM³⁴: a sequence-based model that processes SMILES strings using Bidirectional LSTM layers to capture sequential molecular patterns.

• AutoML: a model selection and optimization pipeline based on automated machine learning techniques. It ensembles multiple algorithms and performs hyperparameter tuning automatically. In our experiments, we used H2O AutoML³⁵, which includes tree-based models such as XGBoost, Gradient Boosting Machine (GBM), and stacked ensembles.

xLSTM

A standard LSTM updates its cell state c_t and hidden state h_t through gated mechanisms:

$${{{\bf{c}}}}_{t}={{{\bf{i}}}}_{t}\odot {{{\bf{z}}}}_{t}+{{{\bf{f}}}}_{t}\odot {{{\bf{c}}}}_{t-1},$$

(1)

$${{{\bf{h}}}}_{t}={{{\bf{o}}}}_{t}\odot \tanh ({{{\bf{c}}}}_{t}),$$

(2)

where i_t, f_t, and o_t denote the input, forget, and output gate vectors, respectively, and z_t is the candidate state vector. These gates are parameterized by sigmoid activations, which regulate information flow across time steps.

The xLSTM introduces two enhanced variants, sLSTM and mLSTM. Both replace the sigmoid gating functions in i_t and f_t with exponential gates, improving stability and extending effective memory:

$${{{\bf{i}}}}_{t}=\exp ({{{\bf{w}}}}_{i}^{\top }{{{\bf{x}}}}_{t}+{{{\bf{r}}}}_{i}^{\top }{{{\bf{h}}}}_{t-1}+{b}_{i}),$$

(3)

$${{{\bf{f}}}}_{t}=\exp ({{{\bf{w}}}}_{f}^{\top }{{{\bf{x}}}}_{t}+{{{\bf{r}}}}_{f}^{\top }{{{\bf{h}}}}_{t-1}+{b}_{f}),$$

(4)

where w_i, w_f, r_i, and r_f are weight vectors, and b_i, b_f are bias scalars.

Furthermore, mLSTM extends the memory capacity by upgrading the vector-valued cell state ${{{\bf{c}}}}_{t}\in {{\mathbb{R}}}^{d}$ into a matrix-valued memory ${{{\bf{C}}}}_{t}\in {{\mathbb{R}}}^{d\times d}$, enabling richer storage and interactions:

$${{{\bf{C}}}}_{t}={{{\bf{I}}}}_{t}\odot {{{\bf{Z}}}}_{t}+{{{\bf{F}}}}_{t}\odot {{{\bf{C}}}}_{t-1},$$

(5)

where I_t, F_t, and Z_t are matrix analogs of the input, forget, and candidate states, respectively.

The xLSTM block is formed by stacking alternating sLSTM and mLSTM layers, and multiple blocks are combined to construct the full xLSTM architecture. This design enhances the model’s ability to capture long-range dependencies in sequential data.

Model architecture

Construction of atom- and motif-level molecular graphs

Starting from the SMILES string of a molecule, we convert it into an atom-level molecular graph G_atom = {V_atom, E_atom} using the RDKit tool³⁶, where ${V}_{{{\rm{atom}}}}=\{{v}_{p}^{{{\rm{atom}}}}\}$ represents the set of nodes, and ${E}_{{{\rm{atom}}}}=\{({v}_{p}^{{{\rm{atom}}}},{v}_{q}^{{{\rm{atom}}}})\}$ represents the set of edges. Each node ${v}_{p}^{{{\rm{atom}}}}$ corresponds to an atom and is initialized with 11 atomic features, including atomic number, chirality, and aromaticity (Table S11). Likewise, each edge $({v}_{p}^{{{\rm{atom}}}},{v}_{q}^{{{\rm{atom}}}})$ represents a bond and includes features such as bond type, stereochemistry, and conjugation (Table S12).

Based on the atom-level graph, we then generate a motif-level graph G_motif = {V_motif, E_motif} through ReLMole, as described by ref. ³⁷. In ReLMole, three types of substructures are considered as motifs: rings, non-cyclic functional groups, and carbon-carbon single bonds. In this motif graph, each node represents a motif and is initialized with 12 features, while each edge represents the connection between two motifs. Details of the initial features are provided in Table S13 in the Supplementary Information.

Both node and edge features are embedded into a d-dimensional feature vector. Specifically, we denote the input node feature matrix of the atom-level and motif-level graphs as ${{{\bf{H}}}}_{{{\rm{atom}}}}^{0}\in {{\mathbb{R}}}^{{N}_{{{\rm{atom}}}}\times d}$ and ${{{\bf{H}}}}_{{{\rm{motif}}}}^{0}\in {{\mathbb{R}}}^{{N}_{{{\rm{motif}}}}\times d}$, respectively, where N_atom is the number of atoms and N_motif is the number of motifs. The input feature vector of the edge in the atom-level graph between nodes p and q is ${{{\bf{e}}}}_{pq}\in {{\mathbb{R}}}^{d}$.

Feature extraction on the atom-level graph

Graph neural network

In the GNN component, we employ a simplified message-passing mechanism that incorporates both residual connections⁷ and virtual nodes¹⁴. At each GNN layer, the process starts by applying Layer Normalization (${{\rm{LN}}}$) to the node representations, followed by a ReLU activation. To facilitate the exchange of global information across the graph, we introduce virtual nodes, which aggregate the features of all nodes in the graph. The resulting virtual node information is then added to the individual node representations. The operations can be formally expressed as:

$${{{\bf{h}}}}_{p}^{\,l}={{\rm{ReLU}}}\left({{\rm{LN}}}({{{\bf{h}}}}_{p}^{l})\right)+{{{\bf{v}}}}^{l},$$

(6)

$${{{\bf{v}}}}^{l}=\mathop{\sum }_{k=1}^{{N}_{{{\rm{atom}}}}}{{{\bf{h}}}}_{k}^{l},$$

(7)

where ${{{\bf{h}}}}_{p}^{\,l}\in {{\mathbb{R}}}^{d}$ denotes the hidden state vector of node p at layer l, and v^l represents the virtual node vector.

Next, the message-passing step occurs, where the information from neighboring nodes and the edges connecting them is aggregated. For each edge e_pq, a message is computed as:

$${{{\bf{m}}}}_{pq}={{{\bf{h}}}}_{q}^{\,l}+{{{\bf{e}}}}_{pq}.$$

The messages from all neighboring nodes ${{\mathcal{N}}}(p)$ are summed and used to update the node representation through an MLP:

$${{{\bf{h}}}}_{p}^{\,l+1}={{\rm{MLP}}}\left(\mathop{\sum}\limits_{q\in {{\mathcal{N}}}(p)}{{{\bf{m}}}}_{pq}\right).$$

(8)

Finally, a residual connection is applied, adding the original node representation from layer l to the updated node representation at layer l + 1: ${{{\bf{h}}}}_{p}^{\,l+1}\leftarrow {{{\bf{h}}}}_{p}^{\,l+1}+{{{\bf{h}}}}_{p}^{l}.$

Jumping knowledge

After the GNN, we apply a jumping knowledge mechanism to aggregate information from all GNN layers. This allows each node feature to encapsulate representations from both shallow and deep layers. The operation is defined as:

$${{{\bf{h}}}}_{p}^{{{\rm{GNN}}}}={{\rm{CONCAT}}}\left({{{\bf{h}}}}_{p}^{1}{{{\bf{A}}}}_{1}^{T},{{{\bf{h}}}}_{p}^{2}{{{\bf{A}}}}_{2}^{T},\ldots ,{{{\bf{h}}}}_{p}^{l}{{{\bf{A}}}}_{l}^{T}\right),$$

(9)

where ${{{\bf{h}}}}_{p}^{{{\rm{GNN}}}}\in {{\mathbb{R}}}^{{d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}}}$ represents the aggregated feature vector of node p from the GNN, and ${{{\bf{A}}}}_{l}^{T}\in {{\mathbb{R}}}^{d\times {d}_{{{\rm{skip}}}}}$ is a weight matrix that maps the layer-specific node feature ${{{\bf{h}}}}_{p}^{l}\in {{\mathbb{R}}}^{d}$ to a lower-dimensional space. In our experiments, we evaluate the impact of the number of jumping knowledge layers n_jk on performance.

Using xLSTM to capture long-range information

In this section, we utilize xLSTM to capture long-range dependencies for each node in the graph. We treat the output of the GNN, ${{{\bf{H}}}}^{{{\rm{GNN}}}}\in {{\mathbb{R}}}^{{N}_{{{\rm{atom}}}}\times ({d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}})}$, as a sequence of length N_atom, where each row corresponds to one node. This sequence is then passed through the xLSTM model, producing an output ${{{\bf{H}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}\in {{\mathbb{R}}}^{{N}_{{{\rm{atom}}}}\times ({d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}})}$, as follows:

$${{{\bf{H}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}={{\rm{xLSTM}}}({{{\bf{H}}}}^{{{\rm{GNN}}}}).$$

(10)

Motif-level feature extraction

The motif-level graph is processed directly by the xLSTM model. We first map the input feature ${{{\bf{H}}}}_{{{\rm{motif}}}}^{0}$ to the dimension d_skip × n_jk, matching the output dimension of the atom-level graph. This mapped feature is then passed through the xLSTM model to produce an output ${{{\bf{H}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}\in {{\mathbb{R}}}^{{N}_{{{\rm{motif}}}}\times ({d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}})}$:

$$\begin{array}{r}{{{\bf{H}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}={{\rm{xLSTM}}}({{{\bf{H}}}}_{{{\rm{motif}}}}^{0}).\end{array}$$

(11)

Perform a MHMoE on the features

We first apply a global max-pooling operation to H^GNN, ${{{\bf{H}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$, and ${{{\bf{H}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$ to obtain three graph-level feature vectors: f_GNN, ${{{\bf{f}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$, and ${{{\bf{f}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$. These are summed to produce the final molecular feature f_out. Subsequently, an MHMoE module is applied to enhance representation learning.

For any input feature vector ${{\bf{f}}}\in {{\mathbb{R}}}^{{h}_{{{\rm{moe}}}}\times d}$, we first partition it into h_moe segments ${{{\bf{f}}}}_{1},{{{\bf{f}}}}_{2},\ldots ,{{{\bf{f}}}}_{{h}_{{{\rm{moe}}}}}$, each of dimension d. The output of the MoE layer for a given segment f_s is computed as:

$${{{\bf{f}}}}_{s}^{{{\rm{MoE}}}}=\mathop{\sum}\limits_{i=1}^{n}G{({{{\bf{f}}}}_{s})}_{i}\,{E}_{i}({{{\bf{f}}}}_{s}),$$

(12)

where E_i denotes the i-th expert, implemented as a feedforward network (FFN) with a configurable number of fully connected layers and nonlinear activations. The gating function $G{({{{\bf{f}}}}_{s})}_{i}$ assigns a weight to each expert:

$$G({{{\bf{f}}}}_{s})={{\rm{softmax}}}\left({{\rm{TopK}}}(g({{{\bf{f}}}}_{s})+{{{\bf{D}}}}_{{{\rm{noise}}}},K)\right),$$

(13)

where g(f_s) computes raw expert scores and D_noise introduces stochasticity during training. The TopK function selects the K highest-scoring experts:

$${{\rm{TopK}}}{({{\bf{v}}},K)}_{i}=\left\{\begin{array}{ll}{v}_{i}\quad \hfill&\,{{\rm{if}}}\; {{v}}_{i}\; {{\rm{is}}} \; {{\rm{among}}} \; {{\rm{the}}} \; {{\rm{top}}}\; K\; {{\rm{elements}}} \; {{\rm{of}}}\,{{\bf{v}}},\\ -\infty \quad &\, {{\rm{otherwise.}}}\hfill\end{array}\right.$$

(14)

Finally, the outputs of all segments are concatenated to form the MHMoE output:

$${{{\bf{f}}}}^{{{\rm{MHMoE}}}}={{\rm{CONCAT}}}({{{\bf{f}}}}_{1}^{{{\rm{MoE}}}},{{{\bf{f}}}}_{2}^{{{\rm{MoE}}}},\ldots ,{{{\bf{f}}}}_{{h}_{{{\rm{moe}}}}}^{{{\rm{MoE}}}}).$$

(15)

This design enables each segment of the input to be routed to the top-K most appropriate experts, allowing specialization of different experts for processing distinct types of molecular features.

Overall architecture

The overall architecture is illustrated in Fig. 6. We perform feature extraction on both the atom-level graph and the motif-level graph. For the atom-level graph, we first apply the GNN, followed by a skip connection that aggregates the outputs from all GNN layers, resulting in H^GNN. This aggregated output is then passed through the xLSTM module, producing ${{{\bf{H}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$ (section “Feature extraction on atom-level graph”). Next, global pooling is applied separately to H^GNN and ${{{\bf{H}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$ to obtain graph-level features from the GNN (f_GNN) and from the xLSTM (${{{\bf{f}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$). These two features are then summed to generate ${{{\bf{f}}}}_{{{\rm{atom}}}}\in {{\mathbb{R}}}^{{d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}}}$, representation of the feature of the atom-level graph.

Fig. 6: Architecture of MolGraph-xLSTM.

The architecture consists of four main components: A motif graph construction. The atom-level graph is decomposed into motifs to form a motif-level graph. B Feature extraction on the atom-level graph. A GCN-based xLSTM framework with jumping knowledge extracts features, followed by pooling to generate the atom-level representation ${{{\bf{f}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$. C Feature extraction on the motif-level graph. Using xLSTM blocks and pooling to produce the motif-level representation ${{{\bf{f}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$. D MHMoE and property prediction. Features (${{{\bf{f}}}}_{{{\rm{gcn}}}}$, ${{{\bf{f}}}}_{{{\rm{atom}}}}^{{{\rm{xLSTM}}}}$ and ${{{\bf{f}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$) are combined and refined through the MHMoE module for final property prediction.

The motif-level graph is fed directly into the xLSTM model, yielding ${{{\bf{H}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$ (section “Motif-level feature extraction”). We obtain a graph-level feature ${{{\bf{f}}}}_{{{\rm{motif}}}}\in {{\mathbb{R}}}^{{d}_{{{\rm{skip}}}}\times {n}_{{{\rm{jk}}}}}$ for the motif-level graph by applying global pooling on ${{{\bf{H}}}}_{{{\rm{motif}}}}^{{{\rm{xLSTM}}}}$. Then, f_atom and f_motif are summed to form the final molecular feature, which is passed through the MHMoE module (section “Perform a multi-head mixture-of-experts on the features”) to further enhance the representation. Finally, the resulting feature is passed through an MLP to predict the molecular property:

$${{{\bf{f}}}}_{{{\rm{out}}}}={{\rm{MHMoE}}}({{{\bf{f}}}}_{{{\rm{atom}}}}+{{{\bf{f}}}}_{{{\rm{motif}}}}),$$

(16)

$${{\bf{output}}}={{\rm{MLP}}}({{{\bf{f}}}}_{{{\rm{out}}}}),$$

(17)

where ${{\bf{output}}}\in {{\mathbb{R}}}^{K}$, and K represents the number of tasks.

Loss function

To optimize the model, we applied two loss functions: the task loss ${{{\mathcal{L}}}}_{{{\rm{task}}}}$ and the supervised contrastive loss (SCL) ${{{\mathcal{L}}}}_{{{\rm{SCL}}}}$³⁸. The task loss guides the model to minimize the error between the true label y and the predicted value $\hat{{{\bf{y}}}}$, while the SCL encourages the feature embeddings f_out to have samples with the same label close to each other in the embedding space, and samples with different labels far apart.

Task loss

For classification tasks, we use the cross-entropy loss, which measures the difference between the true label y_i and the predicted probability distribution ${\hat{{{\bf{y}}}}}_{i}$. This loss is formulated as:

$${{{\mathcal{L}}}}_{{{\rm{task}}}}^{{{\rm{classification}}}}=-\mathop{\sum}\limits_{k=1}^{K}{y}_{i,k}\log ({\hat{y}}_{i,k}),$$

(18)

where y_i,k represents the true label for task k, and ${\hat{y}}_{i,k}$ is the predicted probability for task k.

For regression tasks, we adopt the Mean Squared Error (MSE) loss, which captures the discrepancy between the predicted value ${\hat{y}}_{i}$ and the true value y_i. The MSE loss is expressed as:

$${{{\mathcal{L}}}}_{{{\rm{task}}}}^{{{\rm{regression}}}}={({{{\bf{y}}}}_{i}-{\hat{{{\bf{y}}}}}_{i})}^{2}.$$

(19)

SCL for the classification task

We apply the SCL to all features: f_out, f_atom, and f_motif. Here, we illustrate the calculation using f_out. First, we normalize f_out as:

$${{{\bf{f}}}}_{{{\rm{out}}}}^{\,{{\rm{norm}}}}=\frac{{{{\bf{f}}}}_{{{\rm{out}}}}}{\parallel {{{\bf{f}}}}_{{{\rm{out}}}}{\parallel }_{2}+\epsilon },$$

(20)

$$\parallel {{{\bf{f}}}}_{{{\rm{out}}}}{\parallel }_{2}=\sqrt{{\sum }_{d}\,{f}_{{{\rm{out}}},d}^{2}},$$

(21)

where ϵ is a small constant to prevent numerical instability, and d indexes the dimensions of the feature vector.

Next, the SCL ${{{\mathcal{L}}}}_{{{\rm{SCL}}}}$ is computed using the normalized feature:

$${{{\mathcal{L}}}}_{{{\rm{SCL}}}}=\mathop{\sum}\limits_{i\in I}\frac{-1}{| P(i)| }\mathop{\sum}\limits_{p\in P(i)}\log \frac{\exp ({{{\bf{f}}}}_{{{\rm{out}}},i}^{\,{{\rm{norm}}}}\cdot {{{\bf{f}}}}_{{{\rm{out}}},p}^{\,{{\rm{norm}}}}/\tau )}{{\sum }_{a\in A(i)}\exp ({{{\bf{f}}}}_{{{\rm{out}}},i}^{\,{{\rm{norm}}}}\cdot {{{\bf{f}}}}_{{{\rm{out}}},a}^{\,{{\rm{norm}}}}/\tau )},$$

(22)

where i indexes the anchor molecule, P(i) denotes the set of samples sharing the same label as the anchor, A(i) represents the set of all sample indices excluding i, and τ is the temperature parameter.

SCL for the regression task

For regression tasks, positive samples are defined based on the Euclidean distance between labels of all sample pairs in the training set. Let d_med and ${d}_{\max }$ denote the median and maximum distances, respectively. A sample is considered positive for a given anchor if its distance to the anchor is less than d_med. Additionally, weights are assigned to reflect the relative importance of samples: closer positive samples are given higher weight, and farther negative samples are weighted more heavily. The SCL is formulated as:

$${{{\mathcal{L}}}}_{{{\rm{SCL}}}}=\mathop{\sum}\limits_{i\in I}\frac{-1}{| P(i)| }\mathop{\sum}\limits_{p\in P(i)}{w}_{p}\log \frac{\exp ({{{\bf{f}}}}_{{{\rm{out}}},i}^{\,{{\rm{norm}}}}\cdot {{{\bf{f}}}}_{{{\rm{out}}},p}^{\,{{\rm{norm}}}}/\tau )}{{\sum }_{a\in A(i)}{w}_{a}\exp ({{{\bf{f}}}}_{{{\rm{out}}},i}^{\,{{\rm{norm}}}}\cdot {{{\bf{f}}}}_{{{\rm{out}}},a}^{\,{{\rm{norm}}}}/\tau )},$$

(23)

with weights defined as:

$${w}_{p}=\frac{{d}_{{{\rm{med}}}}-{d}_{ip}}{{d}_{{{\rm{med}}}}},$$

(24)

$${w}_{a}=\exp \left(\frac{{d}_{ia}-{d}_{{{\rm{med}}}}}{{d}_{\max }-{d}_{{{\rm{med}}}}}\right),$$

(25)

where d_ip and d_ia are the Euclidean distances between sample i and sample p, and between sample i and sample a, respectively.

Overall loss function

The total loss for training the model is the sum of the task-specific loss and the SCL:

$${{{\mathcal{L}}}}_{{{\rm{total}}}}={{{\mathcal{L}}}}_{{{\rm{task}}}}+{{{\mathcal{L}}}}_{{{\rm{SCL}}}}.$$

(26)