Sliding-attention transformer neural architecture for predicting T cell receptor–antigen–human leucocyte antigen binding

Abstract

Neoantigens are promising targets for immunotherapy by eliciting immune response and removing cancer cells with high specificity, low toxicity and ease of personalization. However, identifying effective neoantigens remains difficult because of the complex interactions among T cell receptors, antigens and human leucocyte antigen sequences. In this study, we integrate important physical and biological priors with the Transformer model and propose the physics-inspired sliding transformer (PISTE). In PISTE, the conventional, data-driven attention mechanism is replaced with physics-driven dynamics that steers the positioning of amino acid residues along the gradient field of their interactions. This allows navigating the intricate landscape of biosequence interactions intelligently, leading to improved accuracy in T cell receptor–antigen–human leucocyte antigen binding prediction and robust generalization to rare sequences. Furthermore, PISTE effectively recovers residue-level contact relationships even in the absence of three-dimensional structure training data. We applied PISTE in a multitude of immunogenic tumour types to pinpoint neoantigens and discern neoantigen-reactive T cells. In a prospective study of prostate cancer, 75% of the patients elicited immune responses through PISTE-predicted neoantigens.

Main

Neoantigen-based cancer immunotherapy has drawn considerable interest and witnessed excellent therapeutic effects in various types of tumour^{1,2,3,4,5,6,7,8,9,10}. Neoantigens are mainly tumour-specific short peptides (epitopes) generated by somatic mutations in cancer^11,12. These antigens are first presented on the surface of tumour cells by binding with human leucocyte antigens (HLA) in the form of a peptide–HLA complex (pHLA), which can then be recognized by T cell receptors (TCRs) to elicit antitumour immune responses^13,14,15,16. Neoantigens exhibit potent immunogenicity as they are absent from normal tissues and they are not subject to thymic selection or host central tolerance. Thus, neoantigens serve as a valuable source of targets for T cell-based cancer immunotherapy¹⁷.

Among the substantial quantity of mutant peptides, only a limited fraction may trigger robust, antitumour immune responses¹⁷, and therefore, the accurate identification of immunogenic neoantigens becomes crucial. It is believed that the binding affinity between antigens and HLAs, and the ‘immunological synapse’ between the pHLA complex and the corresponding TCR are critical determinants of T cell reactivity¹⁸. In the literature, enormous efforts have been devoted towards predictive algorithms to identify such biomolecular interactions^{2,15,19,20,21}. Early methods focused on the binding between intracellular peptides and HLA-I molecules²², including NetMHCpan²³, MHCflurry²⁴, EDGE²⁵, MHCnuggets²⁶ and BigMHC²⁷. However, peptide–HLA binding is only the first step towards tumour-specific immune responses¹⁷. To fulfil the complete process, TCR–antigen binding recognition should be further considered²⁸, for which examples include NetTCR²⁹, IMRex³⁰, ERGO³¹, TEINet³², AEPCAM³³, PanPep³⁴ and TEIM-Res³⁵. In pMTnet³⁶, peptide–HLA binding and TCR–pHLA binding were both considered, leading to state-of-the-art results in TCR–peptide–HLA binding prediction. Recently, Transformers—state-of-the-art deep learning architecture for sequence learning—were applied³⁷ to predict peptide and HLA (that is, pHLA) binding.

Despite these progresses, accurate modelling and prediction of T cell-related immune responses remains challenging for a few reasons. First, except pMTnet³⁶, current methods mainly consider pairwise interactions like peptide–HLA^{23,24,25,26,27} or peptide–TCR binding^{29,30,31,32,33,34,35,38,39}, whereas TCR–antigen–HLA interactions are less studied due to the complex interaction landscape and vast molecular diversities (Supplementary Note 1). Second, advanced artificial intelligence models can be difficult to interpret. Even state-of-the-art sequence models like Transformer⁴⁰ still lack in providing physically consistent estimation of token-level interacting relations (Supplementary Note 2). Although TEIM-Res³⁵ offers valuable insights into TCR–epitope interactions, it faces challenges of scarce three-dimensional (3D) structure training data and high experimental costs. Third, biosequence variability and long-tail distribution make it difficult for artificial intelligence models to accurately predict interactions with new sequences, despite advances in meta-learning and zero-shot learning^34,35.

As summarized in a previous study³⁰, appropriate sequence feature engineering methods and rigorous benchmark standards are crucial to create and validate TCR–epitope predictive models. Therefore, to resolve the multifaceted challenges outlined above, we propose a physics-inspired sliding transformer (PISTE) model, an innovative network that resolves the limitation of Transformers in TCR–antigen–HLA binding prediction under comprehensive evaluation scenarios. PISTE is characterized by the embedding of essential physical and biological priors in Transformer. Specifically, the conventional, data-driven attention is replaced by a physics-driven dynamics that steers the positioning of the residues based on the gradients of their interactions, as if biosequences were ‘sliding’ against each other in search for the most stable binding configuration. Such a dynamic attention allows the effective navigation of the intricate interaction landscape of multiple biosequences at the residue level, simultaneously acquiring physically consistent and interpretable representations for binding prediction.

The PISTE model has several advantages. (1) It improves the performance of TCR–antigen–HLA binding prediction against state-of-the-art models across various benchmark datasets, evaluation metrics and negative sampling schemes. (2) It recovers pairwise residue relations even without any structural training data, thereby being both interpretable and data efficient in biomedical applications. (3) It can be applied to unseen biosequences due to sliding attention that captures intrinsic binding mechanisms. Overall, PISTE demonstrates considerable potential in exploring biosequence interactions for identifying and screening clinically relevant immunotherapeutic responses, including the identification of clonal T cells and tumour neoantigens. In a prospective study of prostate cancer, we observed neoantigen-induced specific T cell responses in 75% of the participants (six out of eight) based on the screening results of PISTE, showing its usefulness in immunological studies (for example, immunogenic neoantigen prediction and prioritization).

Results

Neoantigen screening and prioritization with PISTE

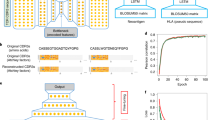
The pipeline of using PISTE for neoantigen screening and prioritization is shown in Fig. 1a. First, the amino acid sequences of all the possible TCR–antigen–HLA triples for an individual are obtained and fed to PISTE, and the binding score (affinity) for each triple is predicted. Then, the predicted scores are used to compute the number of binding TCRs for each peptide as an indicator of the level of immunogenicity, which is used for a personalized ranking of these peptides. Finally, candidate peptides are synthesized and assessed through T cell assays in vitro to verify the immunogenicity of the neoantigen. More details of the pipeline is provided in the Methods.

Fig. 1: PISTE for TCR–antigen–HLA binding prediction and personalized neoantigen screening.

a, Pipeline for peptide selection. First, TCR–antigen–HLA sequence triples of an individual are obtained and fed to a well-trained PISTE model to predict the binding status for each; then, the antigens are prioritized by the number of binding TCRs (as immunogenicity ranking); finally, candidate peptides are synthesized and assessed through T cell assays in vitro to verify the immunogenicity of the neoantigens. b, Neural architecture of PISTE, which has three basic modules: the sequence encoder module extracts subsequence features from the TCR, antigen and HLA sequences; the sliding-attention module recovers their residue-level interactions; the alignment-based pooling module generates a fixed-length representation for all the input sequences to predict their binding status. 1D conv, 1-dimensional convolution. Created with BioRender.com.

Figure 1b illustrates the workflow of PISTE to estimate the molecular interactions at both residue and sequence levels. The network consists of three main modules. First, the sequences of antigen, HLA and TCR are input into the sequence encoder module. Then, the sliding-attention module is used to infer their interactions. Specifically, we first use sliding attention to infer the interaction between the antigen and HLA to obtain the HLA–antigen representation (phase 1), then use sliding attention to characterize the interaction between the HLA–antigen unit and the TCR (phase 2), and then build a global description of the ternary interaction. Finally, all the three sequences are passed to the alignment-based pooling module to convert them to a fixed length (equal to that of the HLA pseudo-sequence) to predict their binding status.

Evaluation of the predictive performance of PISTE

We compared PISTE with eight state-of-the-art computational models for TCR–antigen–HLA binding prediction, including IMRex³⁰, NetTCR²⁹, ERGO-AE³¹, ERGO-LSTM³¹, pMTnet³⁶, PanPep³⁴, TEIM³⁵ and TEINet³². Three evaluation metrics are adopted: area under the receiver operating characteristic curve (AUROC), area under the precision–recall curve (AUPR) and positive predictive value at top-n (PPVn), where n represents the number of true binders in the data²⁶.

Experimental results are reported across different categories. (1) Two external test sets: test set I with 489 binding TCR–peptide–HLA triples³⁶, and test set II with 425 binding triples from peer-reviewed publications (see the ‘Dataset’ section, Supplementary Table 1 and Supplementary Notes 3–5 for details). (2) Two classification scenarios: third-order TCR–peptide–HLA binding (pMTnet and PISTE) and second-order TCR–peptide binding (the remaining seven methods). When comparing PISTE with the numerous second-order models, we transformed its results to the second-order version by following the settings of pMTnet³⁶ (Supplementary Note 6). (3) Three negative sampling schemes for generating negative training/test data: random shuffling, unified peptide and reference TCR (see the ‘Dataset’ section).

Figure 2a shows the results of random-shuffling negative sampling, and Extended Data Fig. 1a,b shows the results for unified peptide and reference-TCR negative sampling schemes, as summarized below. (a) Random shuffling: for third-order classification, PISTE achieved an AUROC of 0.917 on test set I and 0.783 on test set II, which improved over other competing methods by 17–22%. In AUPR, PISTE got 0.362 and 0.252 on the two test sets, which outperformed other competing methods by 11%. For second-order classification, PISTE outperformed all the competing methods under all the metrics by 10–20%. (b) Unified peptide: for third-order classification, PISTE improved over competing methods by 1–13% on both test sets across all the metrics. For second-order classification, PISTE outperformed competing methods by 10–26% across all the metrics on both test sets. (c) Reference TCR: for third-order classification, PISTE improved over competing methods by 8–23% for all the metrics on both test sets; on second-order classification, improvements up to 14% were observed against all the competitors. More results are available in Supplementary Note 8.

Fig. 2: Predictive performance of TCR–antigen–HLA binding based on two external test sets using random-shuffle negative sampling.

a, AUROC, AUPR and PPVn scores for PISTE and competing models using two test sets. The red baseline represents a random classifier. b, The t-SNE embedding for the TCRs of the YLQ pHLA (top), TPR pHLA (middle) and KLG pHLA (bottom) learned by our model, in which PISTE facilitates the segregation of positive and negative TCRs, yielding distinct regions enriched with positive TCRs. All the testing triples whose antigen–HLA pairs were observed in the training data are removed from the test sets.

We also applied PISTE to visualize the distribution of biosequences involved in different binding outcomes. Specifically, we examined the interactions between TCRs and three viral pHLAs: HLA-A02:01/COVID-19 S 269 (YLQPRTFLL)⁴¹, HLA-B07:02/CMV pp65 (TPRVTGGGAM)⁴² and HLA-A03:01/CMV IE1 (KLGGALQAK)⁴³. From PISTE, we extracted the TCR embeddings specific to each pHLA, and visualized them with t-distributed stochastic neighbour embedding (t-SNE) (Fig. 2b). In this figure, the top panel exhibits a notable distinction between YLQ-positive and YLQ-negative TCRs, with three conspicuous enrichments of positive bindings suggesting the presence of cross-reactivity in TCR–pHLA recognition⁴⁴. The middle and bottom panels reveal different distributions for positive/negative TCRs for specific pHLAs.

PISTE uncovers meaningful patterns of residue interaction

Besides predicting the sequence-level binding status accurately, PISTE can also generate physically meaningful attention scores (equation (4)) that shed light on residue-level interactions. The attention matrix can be used to identify interacting residue pairs and study their distributions from various angles like residue type, location and bond type, to obtain useful insights (Supplementary Note 9).

We showed that the PISTE attention matrix aligns well with 3D crystal structures, despite the fact that PISTE did not utilize any structural data during training. Here we collected 86 binding TCR–antigen–HLA triples and their 3D structures from the Protein Data Bank (PDB) dataset⁴⁵ (Supplementary Note 10 and Supplementary Table 5), and specifically examined the TCR–antigen and HLA–antigen contact relations (more details in Supplementary Notes 12 and 13). Both types of matrix were averaged across the 86 binding triples to provide a convenient summary and visualization for assessing their consistency.

Figure 3 reports the ground-truth residue contact matrices alongside the PISTE attention maps. Figure 3a shows the 11 × 34 antigen–HLA residue contact relations revealed by 3D structures (blue) and the PISTE attention map (orange). They have a correlation score of 0.75 (Fig. 3b). Figure 3c shows the real and estimated 11 × 30 TCR–antigen residue interactions, and a correlation score of 0.916 was observed. Supplementary Fig. 10 shows the averaged 30 × 34 attention matrix for TCR–HLA interaction, for which the correlation is 0.758. These evidences substantiated the capacity of PISTE to discern complex patterns of residue interactions (Supplementary Notes 14–16). This is useful in practice considering that no crystal structures were needed for training PISTE, which saved tremendous experimental cost.

Fig. 3: Comparison of the ground-truth residue contact relationships with PISTE predictions, averaged over 86 TCR–antigen–HLA complexes from the PDB dataset.

a, HLA–antigen residue contact relation based on the crystal structures (blue) and PISTE predictions (orange), both averaged over 86 complexes. b, Scatter plot of the true and predicted residue contact scores in which each point corresponds to an HLA–antigen residue pair, both averaged over 86 complexes. The line and shading represent linear regression and 95% confidence intervals, respectively. c, TCR–antigen residue contact relation based on the crystal structures (blue) and PISTE attention (orange). d, Scatter plot of the true and predicted residue contact scores, in which each point corresponds to a TCR–antigen residue pair. The line and shading represent linear regression and 95% confidence intervals, respectively. Note that PISTE did not utilize any 3D structure training data to generate these predictions.

Mutation effects support predicted TCR–pHLA binding

We used PISTE as a tool to unveil the impact of mutations on the binding outcome by virtual mutagenesis of antigens and TCRs. Residue mutations were simulated with zero-vector scanning, by replacing the numerical embedding of the residue at a specified position with a zero vector³⁶.

We performed zero-vector scanning on the CDR3 and antigens of 77 TCR–pHLAs, whose 3D crystal structures were retrieved from the PDB database⁴⁵ and were anticipated to be functional. Subsequently, we quantified the changes in the binding scores predicted by PISTE after sequence mutations. Our statistical analysis revealed that mutations occurring at positions 2, 4, 8 and 9/10 of the peptide exerted a higher impact on the binding score (Fig. 4a). After dividing CDR3 into six equally sized segments, we observed that the mutations of the residues located in the middle segments of CDR3 (segments 3 and 4) induced a greater impact on the predicted binding status compared with the remaining segments (Fig. 4b), the former being more prone to forming close contacts with peptides and HLA (Fig. 4c; t-test, P < 0.0001).

Fig. 4: Mutation analysis using PISTE and zero-vector scanning mutagenesis on 77 TCR–antigen–HLA 3D crystal complexes from the PDB database.

a, Mutant residues at positions 2, 4, 8 and 9/10 of the peptide show a higher impact on the predicted binding scores. b, Mutant residues in the central regions of the six equal-sized segments of CDR3 tend to elicit greater perturbations on the anticipated binding scores. c, Compared with non-contact residues, mutations in the contacting residues of CDR3 (those within a 6 Å distance from the pHLA complex) result in greater changes in the predicted binding scores by the two-sided t-test, with P = 2.09 × 10⁻¹⁰. d, Impact of mutations in different residue types within the peptide. e, Impact of mutations in different residue types within CDR3. The box plots show the medians as centre lines, the 25th and 75th percentiles as lower and upper quartiles, and 1 time the interquartile range as whiskers (outliers are not shown). The number above each box indicates the sample size.

Through residue-type mutation analysis, we found that mutations of arginine (R), tyrosine (Y), proline (P), methionine (M) and aspartic acid (D) on the antigen exhibited higher impact on the binding prediction (Fig. 4d). However, lysine (K), valine (V) and tryptophan (W) residues in the CDR3 loop region led to the biggest perturbations of the predicted binding score after mutation scan (Fig. 4e). These residues typically have elongated or aromatic heterocyclic side chains, which contribute to hydrogen bonding and hydrophobic interactions at the TCR–pHLA binding interface. These interactions are indispensable for maintaining the structural integrity and functional efficacy of the complex. This analysis is only pertinent to the PDB database. A similar mutation scan on the PDB data with pMTnet³⁶ is discussed in Supplementary Note 17.

Applications of PISTE to antigen-based immunological study

To verify the potential clinical utility of PISTE, we performed a series of immunological investigations: (1) analysis of antigen-driven T cell clonal expansion, (2) discovery of immunogenic neoantigens residing within tumour microenvironments and (3) validation of personalized neoantigen-driven T cell immune responses.

Detection of antigen-specific T cell clonality

When TCRs engage with an antigen–HLA (pHLA) complex, a cascade of clonal expansion is initiated to orchestrate the immune response, in which T lymphocytes displaying superior affinity for a specific antigen exhibit an increased predilection for clonal amplification⁴⁶. Here we investigated whether the PISTE model can qualitatively confirm the impact of this interaction on T cell behaviour.

We used the 10x Genomics Chromium single-cell TCR sequencing data of 44 pHLAs from four healthy donors (Supplementary Note 18). We used PISTE to predict the binding affinities (scores) between individual T cells and one or more of the detected pHLAs, and recorded the highest score for each TCR. We then calculated the Spearman correlation between these binding scores and the rate of expansion for T cell clones. As shown in Fig. 5a, a positive correlation is observed between the clone proportion of T cells and the predicted binding scores. This finding aligns with expectations, that is, TCRs exhibiting elevated binding scores are considerably more prone to undergo clonal amplification. Moreover, we demonstrated the enrichment of extended T cell clonotypes with a high binding affinity to pHLA through odds ratio tests (Fig. 5b and Supplementary Note 19; odds ratio > 1 for all the donors).

Fig. 5: Utilizing PISTE for the differentiation of neoantigen-reactive T cells and the evaluation of clinical outcomes in tumour patients.

a, T cell clone proportion shows a positive correlation with their binding scores to pHLAs predicted by PISTE in the 10x Genomics Chromium single-cell immune profiling dataset. The R (correlation coefficient) and P values at the top of each scatter were computed through Spearman correlation tests (two sided). b, Testing the odds ratio for the enrichment of expanded T cell clonotypes with high affinity for HLA–antigens. c, Association of TML, NAL and INAL (predicted by PISTE) with treatment response of the SKCM cohort. We used the irRECIST response variables: progressive disease, partial response and complete response. P value by Jonckheere–Terpstra test (one sided). The sample sizes for the three splittings were 13, 10 and 4. The box plots show the medians as centre lines, outliers as points, the 25th and 75th percentiles as the lower and upper quartiles, and 1.5 times the interquartile range as whiskers. d,e, Association of TML, NAL and INAL with overall survival of SKCM (d) and GBM (e) on immunotherapies. Patients were split by the median of TML/NAL/INAL in each cohort. The P value for the log-rank test (two sided) was also shown.

Identification of immunogenic neoantigens within tumours

Incorporating genome sequencing analysis technology, we applied PISTE to cancer cohorts of skin cutaneous melanoma (SKCM)⁴⁷ and glioblastoma (GBM)⁴⁸ (Supplementary Tables 6 and 7) to confirm the usefulness of PISTE in characterizing immunogenic neoantigens in the tumour microenvironment and determining the clinical efficacy in tumour patients.

We investigated the disparities in TCR–peptide–HLA binding characteristics between neoantigens from mutated proteins and their wild-type counterparts. On the basis of the predicted HLA–antigen–TCR binding scores from PISTE, we found that neoantigens showed greater immunogenicity than wild-type antigens in patients with SKCM and GBM (Supplementary Note 21 and Supplementary Fig. 15b–d).

A comprehensive understanding of tumour neoantigens is vital for assessing the efficacy of immune therapy in patients. Prior research has recognized tumour mutation load (TML) and neoantigen load (NAL) as predictive biomarkers for clinical advantages in solid tumour patients^49,50,51,52. Here we explored the potential of the immunogenic NAL (INAL) predicted by PISTE as a biomarker on the SKCM and GBM cohorts. INAL is delineated as the number of antigens capable of binding with TCR(s), whereas the corresponding wild-type antigens do not induce any TCR interaction; we used the PISTE model to determine the HLA–antigen–TCR binding events. As presented in Fig. 5c–e, INAL is correlated with both immunotherapeutic response and the overall survival rate in SKCM and GBM patients (response for SKCM, P = 0.031; survival rate for SKCM, P = 0.00037; survival rate for GBM, P = 0.11). In contrast, if we only considered the TML or NAL, the predictions of the immune response and the survival rate probability became worse (Fig. 5c–e, two left columns). These results demonstrated the prognostic value of PISTE-predicted immunogenic neoantigen burden compared with tumour mutation burden and neoantigen burden as biomarkers. Nonetheless, the limited sample size of the GBM cohort impedes the attainment of a statistically significant correlation. Further validation should be conducted with a larger cohort.

Validation of individualized neoantigen-induced T cell immunity

Identifying individualized immunogenic neoepitopes is the primary hurdle in translating clinical studies into neoantigen-based cancer immunotherapy⁵³. In this study, we showed how PISTE could be used to identify personalized neoantigens in prostate cancer patients. We also validated the immune response elicited by these neoantigens through cellular-level experiments (Fig. 6).

Fig. 6: Validation of neoantigen-stimulated T cell responses from prostate cancer patients.

a, Schematic of the validation experiment. Somatic mutations were identified by the WES of surgically resected prostate tissues and matched normal cells (PBMCs), and their expression was confirmed by tumour RNA-seq. Candidate immunogenic peptides were selected and validated based on the statistics of binding prediction by PISTE. b, In vitro detection of T cell responses for PBMCs stimulated with individual neoantigens by IFN-γ ELISA. c, IFN-γ production on CD8⁺ T cells against selected peptides was detected by flow cytometry for patient PCA03 and patient PCA06. Percentages shown in the density plots are frequencies of reactive IFN-γ⁺ cells as a proportion of all the CD8⁺ T cells. P value was determined via one-way analysis of variance with Dunnett’s multiple comparisons test. n = 3 repeated technical measurements; error bars show the standard error of the mean. The dashed line indicates the baseline for the identification of positive reactions (Methods). SSC-H, side scatter height. Panel a created with BioRender.com.

We assembled and uniformly analysed the sequencing data from eight prostate cancer patients undergoing surgical therapy (see the ‘Sequencing data processing and immunogenic neoantigen selection’ section). Patient characteristics are shown in Supplementary Table 8. Then, we utilized PISTE to predict the TCR–neoantigen–HLA binding and subsequently used the binding results to prioritize neoantigens. For each patient, we synthesized the top three to four neoantigens in the personalized ranking list and evaluated the T cell immune response (Methods and Supplementary Table 9 list the detailed processing information).

The in vitro identification results revealed that 6 out of 8 (75%) patients exhibited responses inducing IFN-γ secretion of T cells with regard to at least one neoantigen peptide as selected by the PISTE model (Fig. 6b). The cells from the remaining two patients (PCA01 and PCA02) exhibited no discernible reactivity towards the individual peptide. Raw data are shown in Supplementary Table 10. In addition to assessing the immune response by enzyme-linked immunoassay (ELISA), we further explored the recognition of positive peptides by CD8⁺ T cell subsets using flow cytometry. Testing was carried out on patients PCA03 and PCA06, both having sufficient peripheral blood mononuclear cells (PBMCs). The results revealed that peptide (A0301, A0302, A0602 and A0604) stimulation led to the activation of specific CD8⁺ T cells, and CD8⁺ T cells exhibited reactive amplification (Supplementary Fig. 16b–c). Meanwhile, we observed that all four peptides (A0301, A0302, A0602 and A0604) stimulated CD8⁺ T cells to produce IFN-γ (Fig. 6c). This also proved that the peptides screened in ELISA experiments have high reliability.

In general, the overall success rate of our antigen identification showed a slight improvement compared with the previous best practices^21,25. The results demonstrated that PISTE is a useful predictive tool to facilitate the identification and screening of cancer neoantigens. It is important to note that cell-level biology experiments were primarily used to provide the evidence of immunogenicity of selected peptides, rather than to claim that these peptides are definitive candidates for cancer vaccines or immunotherapies (Supplementary Note 22).

Discussion

The PISTE model integrates important physical and biological priors to refine the attention mechanism of Transformers. This includes dynamically updating the positional encoding to simulate residues moving along the gradient of their interactions, and considering residue type, position and bond type when inferring their interactions. Therefore, PISTE inherits the flexibility of conventional data-driven attention mechanisms and the regularity derived from physical principles. However, PISTE does not integrate physical laws to the same extent as physics-inspired neural networks—universal function approximators capable of incorporating any physical law represented by partial differential equations into the learning process (Supplementary Note 23)⁵⁴.

PISTE showed promising results in TCR–antigen–HLA binding prediction, a key step to identify immunogenic neoantigens. It is data efficient and can faithfully recover residue-level interactions even without using structural training data. Besides, sliding attention captures intrinsic binding mechanisms and therefore allows an accurate prediction to be extended to innovative sequences, which is particularly useful to neoantigen identification. Antigen-based immunological studies showed that PISTE can effectively discern clonal T cells and identify immunogenic neoantigens, making it a valuable tool for personalized antigen screening.

There are several directions for our future research. (1) Integrating sequence-specific evolutionary information with state-of-the-art language models for sequence representation learning. (2) Enhancing PISTE to predict the binding of antigens presented by HLA class II to TCRs. (3) Validating the predicted neoantigens in immunotherapy across an expanded panorama of cancer types and patient cohorts with the synergistic utilization of PISTE and genomic technologies.

Methods

Dataset

The limitation of positive TCR–pHLA binding data often motivates data aggregation from multiple sources to build a more substantial dataset for training and evaluation^36,55. We collected positive binding triples for training from three publicly available datasets: McPAS-TCR⁵⁶, VDJdb⁵⁷ and pMTnet³⁶ (Supplementary Table 1). Through data curation, we retained only those triples specific to Homo sapiens, HLA class I and TCRs that feature only the CDR3 β-chain, as these are critical for determining antigen binding specificity. We also excluded records in VDJdb⁵⁷ with 0 confidence score. After data preprocessing (Supplementary Note 5), 32,508 unique TCR–antigen–HLA binding triples were obtained for 607 antigens presented by 65 HLA-I molecules and 29,687 TCRs.

We acquired two independent external data for testing with strict quality control and standardized preprocessing: (1) 489 experimentally validated TCR–antigen–HLA binding triples from pMTnet³⁶, collected from 25 published works subject to systematic validation by those prior studies (Supplementary Table 1); (2) 425 binding triples from a series of studies of melanoma, lung cancer, head and neck squamous cell cancer, lymphoma and GBM (Supplementary Table 1). These sources detected T cell activation via specific pHLA^58,59. Among them, 72% were based on peptide–HLA multimers, 8% were obtained through surface plasmon resonance and the remaining 20% were based on in vitro functional assays (CD137/4-1BB flow cytometry, IFN-γ ELISpot and IFN-γ ELISA). All the CDR3β sequences were acquired through a TCR sequencing assay. The data were subject to strict quality control by unifying the naming conventions and eliminating sequences that are incomplete or contain non-standard amino acids (Supplementary Note 5).

To rigorously evaluate the generalization capacity of different models on new sequences, we excluded all the test triples whose antigen–HLA pairs were previously encountered in the training dataset. Additionally, we explored several negative sampling schemes recommended in systematic studies^28,30,32,60, including the following. (1) Randomly shuffled sequence triples in the positive data as negative samples^31,33,35,36. (2) Unified epitope negative sampling in which the epitopes are sampled by their frequency distributions in the positive dataset³². (3) Reference TCR negative sampling in which each epitope is combined with TCRs sampled uniformly from a reference TCR dataset collected from healthy donors^61,62 in which all the TCRs were exposed to all the tested pHLA multimers and no binding signals were detected^34,63. In our experiments, we generated negative samples that are ten times larger than the positive ones.

PISTE

In the Transformer model⁴⁰, the combination of positional encoding and semantic embedding leads to attention scores that no longer provide meaningful estimations of token relationships⁶⁴, particularly when dealing with two or more interacting sequences (Supplementary Note 2).

To solve this problem, we propose PISTE. Our intuition is that residues typically move along the cumulative forces acting on them due to their interactions before reaching a stable conformation. Leveraging this insight, we use the attention map in a Transformer as a conceptually appealing alternative to quantify pairwise residue interactions, which then serves as the driving force to update residue positions in an iterative and coherent manner. This strategy combines the flexibility of the Transformer with the consistency of physical priors, leading to useful features for predicting biosequence interaction.

The network is shown in Fig. 1 and the three basic building blocks are discussed below.

Sequence encoder module

We use one-dimensional (1D) convolution to encode the local and shift-invariant features from TCR, peptide and HLA sequences to capture useful and transferable sequence information from short amino acid segments. Three convolutional layers are adopted with a kernel size of 1 × 3, a stride of 1 and skip connections. Using PyTorch’s nn.embedding function, we randomly initialized 64-dimensional vectors to represent 21 amino acid types. These embeddings are updated through backpropagation during training.

Sliding-attention module

Sliding attention is a physics-inspired dynamic process that steers the positioning of the residues along the gradient field of their interactions. In this process, the attention (or interaction) between two residues takes into account both their spatial proximity and featural correlations. Then, a series of mode-seeking iterations are used to iteratively ‘drag’ the residues in one sequence towards those of another sequence based on the magnitude of residue interactions (attention). This process allows two or more sequences to virtually ‘slide’ against each other in search of potentially the most stable binding configuration.

Sliding attention is defined for two sequences U = {u₁, u₂…u_m} and V = {v₁, v₂…v_n}, where u_i is the ith residue in U and v_j the jth residue in V. We treat V as the reference sequence and U as the sliding sequence. Two concurrent attention views for U and V are computed as follows.

Spatial attention. We use an m × n proximity matrix S whose ijth entry signifies the spatial closeness between u_i and v_j. Here S_ij is parameterized by the relative distance between residues u_i and v_j. For the reference sequence V, its residue positions Q_V = [q₁ q₂…q_n] are constant integers from 1 to n to signify the linear chain structure of the sequence. For the sliding sequence U, its residue positions are a series of real variables P_U = [p₁ p₂…p_m] that are fully optimizable to recover the spatial relations between the residues in U and V. A Gaussian function ${\mathbb{g}}$ is used to estimate S_ij as

$${S}_{ij}={\mathbb{g}}({p}_{i},{q}_{j})=\exp \left(\frac{-| {p}_{i}-{q}_{j}{| }^{2}}{2{h}^{2}}\right).$$

(1)

Featural attention. We adopt an m × n affinity matrix A whose ijth entry reflects the tendency of two residues u_i and v_j to interact based on their respective embedding vectors by a function ${\mathbb{f}}$:

$${A}_{ij}={\mathbb{f}}({\bf{x}}({u}_{i}),{\bf{x}}({v}_{j}))=\exp \left(\frac{{[{E}_{{\rm{S}}}{\bf{x}}({u}_{i})]}^{\top }[{E}_{{\rm{R}}}{\bf{x}}({v}_{j})]}{\sqrt{d}}\right).$$

(2)

Here x(⋅) is a function that converts a discrete residue type to a d-dimensional vector. The exponentiated inner product is used to estimate the non-negative affinity between two residues, where E_S and E_R represent the learnable transform matrices for the sliding sequence and reference sequence, respectively.

We combine the two attention views and use the non-negative, multiplicative term W_ij = A_ij ⋅ S_ij as a comprehensive indicator of whether residue u_i and v_j are likely to interact, that is, they have to be both spatially close and exhibit a high affinity to form a strong contact. We further use a 1/0 mask function ${\mathbb{M}}$ to refine A_ij values by ${\mathbb{M}}({A}_{ij})={M}_{ij}\cdot {A}_{ij}$ to emphasize the residue pairs forming hydrogen bonds, ionic bonds or hydrophobic interactions (Supplementary Note 11).

Using these definitions, we can establish an iterative process to systematically update the positioning of residues (u_i) in the sliding sequence U based on their interactions with the reference sequence V. The residue u_i location (p_i, for i = 1, 2…m) are updated as follows:

$$\begin{array}{l}{p}_{i}^{(t+1)}=\frac{\mathop{\sum }\nolimits_{j = 1}^{n}{\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)\cdot {q}_{j}}{\mathop{\sum }\nolimits_{j = 1}^{n}{\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)},\\ \,\text{s.t.}\,\,\,\,{S}_{ij}^{(t)}=\exp \left(\frac{-| {p}_{i}^{(t)}-{q}_{j}{| }^{2}}{2{h}^{2}}\right).\end{array}$$

(3)

Here the superscript t is the number of iterations. Considering that A_ij is only dependent of the semantic embedding of the residues and is a constant with respect to the residue locations ${p}_{i}^{(t)}$, and that ${S}_{ij}^{(t)}$ is a Gaussian kernel evaluated on the distance between a pair of residues, equation (3) is very similar to the mean shift mode seeking⁶⁵, for which it has been shown that one such iteration is actually a move (of the residue location ${p}_{i}^{(t)}$) along the gradient of an underlying density function ${\mathbb{D}}(\cdot )$ with adaptive step size. In our context, this ‘density function’ is the accumulated magnitude of the interactions that the residue u_i receives when it is located at position ${p}_{i}^{(t)}$, as ${\mathbb{D}}(\,{p}_{i}^{(t)})=\mathop{\sum }\nolimits_{j = 1}^{n}{\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)$.

It is noteworthy that the positional shift in residue u_i due to equation (3) is along the direction of accumulated attractions that residue u_i receives at location ${p}_{i}^{(t)}$, by noting ${p}_{i}^{(t+1)}-{p}_{i}^{(t)}=\frac{\mathop{\sum }\nolimits_{j = 1}^{n}{\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)\cdot \left({q}_{j}-{p}_{i}^{(t)}\right)}{\mathop{\sum }\nolimits_{j = 1}^{n}{\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)}$; here ${\mathbb{M}}\left({A}_{ij}\cdot {S}_{ij}^{(t)}\right)$ conceptually signifies the magnitude of attraction between residue u_i and v_j at step t, and $\left({q}_{j}-{p}_{i}^{(t)}\right)$ signifies the direction of attraction pointing from u_i to v_j at step t. The bandwidth h in equation (1) controls the size of the receptive field: a larger h allows u_i to be attracted to more distant residues in the reference sequence V.

As the iteration continues, residue u_i moves along the reference sequence V until reaching a local maximum of the interaction density or moves for a pre-defined number of steps (two–five steps). The mode-seeking iteration in equation (3) allows injecting useful physical prior by incrementally adjusting a residue’s position to increase its interaction, or attention, with residues from a counterpart sequence. Compared with learnable positional vectors⁴⁰ that are merely updated thorough gradient, our positional variables are structurally constrained and physically more interpretable.

At the end of the sliding process, the m × n hybrid attention matrix

$$W={\mathbb{M}}\left(A\odot S\right),$$

(4)

will serve as a comprehensive estimation of residue-level interactions. Note that W is unnormalized. Depending on whether it is normalized by rows or columns, we can update the representations for both U and V in the form of cross-attention as

$${\tilde{{\bf{X}}}}_{U}\leftarrow {D}_{W}^{-1}W{\,{\bf{X}}}_{V}{E}_{V}+{{\bf{X}}}_{U},$$

(5)

$${\tilde{{\bf{X}}}}_{V}\leftarrow {D}_{{W}^{\top }}^{-1}{W}^{\top }{{\bf{X}}}_{U}{E}_{U}+{{\bf{X}}}_{V}.$$

(6)

Here D_W and ${D}_{{W}^{\top }}$ are row-wise and column-wise degree matrices for normalization, X_U = [x(u₁) x(u₂)…x(u_m)] and X_V = [x(v₁) x(v₂)…x(v_n)] are residue embedding matrices for U and V, and E_V and E_U are linear matrices to turn X_V and X_U into ‘values’, respectively. In equation (5), U is the query and sequence V is the key; in equation (6), V is the query and U is the key. One can also use the additive version of W in equation (4) as $W={\mathbb{M}}\left(A+S\right)$, which gives a denser attention matrix than the Hadamard product. Finally, no self-attention is used within each sequence before cross-attention.

The sliding attention for two sequences is summarized in Algorithm 1 and illustrated in Supplementary Fig. 2b. A comparison with standard cross-attention is shown in Supplementary Fig. 3.

Algorithm 1

Sliding attention for two sequences.

Input: Sliding sequence U: embedding X_U, position P_U;

  Reference sequence V: embedding X_V, position Q_V;

  Learnable parameters: ${E}_{S},{E}_{R},{E}_{U},{E}_{V}\in {{\mathbb{R}}}^{d\times d}$;

  Hyper-parameters: mask ${\mathbb{M}}$, bandwidth h, steps T.

Output: updated residue embedding ${\tilde{{\bf{X}}}}_{U}$, ${\tilde{{\bf{X}}}}_{V}$.

  // initialize variables

1: Initialize X_U and X_V by random vectors.

2: Set Q_V as consecutive integers from 1 to n.

3: Initialize P_U by m evenly spaced numbers in [1:n].

  // compute featural attention A

4: $A\leftarrow \exp \left({{\bf{X}}}_{U}^{\top }{E}_{S}^{\top }{E}_{R}{{\bf{X}}}_{V}/\sqrt{d}\right)$—equation (2).

  // update spatial attention S, residue position P_U

5: for t = 1 to T do

6:  $S\leftarrow \,\text{Gaussian}\,\left({P}_{U},{Q}_{V},h\right)$—equation (1)

7:  $W\leftarrow {\mathbb{M}}\left(S\odot A\right)$—equation (4).

8:  ${P}_{U}\leftarrow {D}_{W}^{-1}W{Q}_{V}$—equation (3)

9: end for

  // converged attention matrix W

10: S ← Gaussian(P_U, Q_V, h)—equation (1).

11: $W\leftarrow {\mathbb{M}}\left(S\odot A\right)$—equation (4).

  // update representations of U and V

12: ${\tilde{{\bf{X}}}}_{U}\leftarrow {D}_{W}^{-1}W{{\bf{X}}}_{V}{E}_{V}+{{\bf{X}}}_{U}$—equation (5).

13: ${\tilde{{\bf{X}}}}_{V}\leftarrow {({D}_{{W}^{\top }})}^{-1}{W}^{\top }{{\bf{X}}}_{U}{E}_{U}+{{\bf{X}}}_{V}$—equation (6).

14: return ${\tilde{{\bf{X}}}}_{U},{\tilde{{\bf{X}}}}_{V}$.

The attention matrix in equation (4) (or its additive version) can be naturally used to approximate residue-level contact relations between U and V. The nonlinear nature of W allows capturing complex patterns of residue sequences that may curl up in three dimensions, despite the 1D positional variables in sliding attention. We can further augment the sliding attention by extending the 1D positional variables to higher dimensions, enforcing a smoothness constraint to the shift of neighbouring residues, and considering intrasequence residue interactions. These will be studied in our future research.

Alignment-based pooling module

We propose a systematic way to turn variable-sized biosequences into fixed-length representations, to avoid arbitrary token shift in sequence cutting or padding. Here we exploit a biological prior that HLA sequences have a stable 3D substructure⁶⁶. In particular, the α-1 and α-2 domains in the α chain of an HLA molecule are connected by a short peptide in the shape of a β sheet, forming a groove that is the key to antigen binding. This allows defining the HLA pseudo-sequence, that is, the part of HLA sequence that is in close contact with the peptide (within 4.0 Å of the peptide), which consists of 34 amino acid residues or positions along the entire HLA molecule²³.

The HLA pseudo-sequence was used in several studies of HLA–peptide and pHLA–TCR interactions^36,37,67. Since the pseudo-sequence has a fixed length, we use it as a skeleton so that both TCRs and antigens can be projected onto it to convert to fixed-length sequences. The alignment is based on the attention matrix in equation (4), which precisely specifies the residue interactions between the two sequences.

To project the representation matrix X of a sequence onto a skeleton sequence X₀ (HLA pseudo-sequence), we use the attention matrix W between X₀ and X as a bridge and left multiply it with X:

$${\tilde{{\bf{X}}}}_{\to {{\bf{X}}}_{0}}={D}_{W}^{-1}\cdot W\cdot {\bf{X}}.$$

(7)

Here W is the attention matrix (4) by treating X₀ as the reference sequence and X as the sliding sequence, and D_W is the row-wise degree matrix of W. The normalized attention matrix ${D}_{W}^{-1}W$ serves as a probabilistic alignment matrix that maps residues from X to those of X₀, effectively reshaping X to the same size of the skeleton sequence X₀ based on their residue interactions specified by W.

Loss function for imbalanced classification

Predicting TCR–antigen–HLA binding requires identifying a small number of truly binding triples from a large repertoire, that is, the positive and negative classes are highly imbalanced. Therefore, we used the following focal loss⁶⁸:

$${\mathscr{L}}(\,{p}_{i})=\left\{\begin{array}{ll}-\alpha {(1-{p}_{i})}^{\gamma }\log (\,{p}_{i})\quad &{\rm{if}}\,\,{y}_{i}=1\\ -(1-\alpha ){p}_{i}^{\gamma }\log (1-{p}_{i})\quad &{\rm{otherwise}}.\end{array}\right.$$

(8)

Here i is the sample index, y_i is the class label and p_i is the estimated probability for the ith sample to be positive.

Sliding transformer for TCR–antigen–HLA binding prediction

The workflow of PISTE for TCR–antigen–HLA binding prediction is as follows (Supplementary Fig. 2a).

• 1. Use HLA as the reference, and let peptide slide against it through the sliding-attention module. This allows updating the HLA and peptide representations (pHLA).

• 2. Use the pHLA complex as the reference, and let TCR slide along it through the sliding-attention module. This allows simultaneously updating the representations for the TCR and pHLA complex.

• 3. Project TCR and peptide representations onto HLA pseudo-sequence by alignment-based pooling.

• 4. The representations of TCR, HLA and peptide are passed to a feed-forward layer to make predictions.

These four steps are connected in an end-to-end framework to allow for simultaneous variable optimization. The order of the four steps is biologically meaningful, that is, the peptide–HLA interaction is modelled first before the interaction between the pHLA complex and TCRs. PISTE predicts ternary TCR–antigen–HLA binding, rather than binary (peptide–HLA or peptide–TCR), by using only ternary binding status as the labels. However, if the peptide–HLA binding status was also known, it could be incorporated in training as well.

Performance evaluation metrics

The performance was evaluated by AUROC, AUPR and PPVn.

In AUROC (TPR versus FPR for a series of threshold values), the true-positive rate (TPR) and false-positive rate (FPR) are computed as

$${\rm{TPR}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FN}}},\,\,\,\,\,\,{\rm{FPR}}=\frac{{\rm{FP}}}{{\rm{TN}}+{\rm{FP}}}.$$

Here TP denotes true positive; FN, false negative; TN, true negative; and FP, false positive.

In AUPR, the precision and recall are computed by

$${\rm{Precision}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FP}}},\,\,\,\,\,\,{\rm{Recall}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FN}}}.$$

PPVn is the fraction of the top-ranked n prediction triples that are true positives, defined as

$${\rm{PPVn}}=\frac{{\rm{TP}}_{n}}{{\rm{TP}}_{n}+{\rm{FP}}_{n}}.$$

PPVn is widely used in immunogenicity prediction studies^23,24,27. Here n is chosen as the number of true binders in the data, as per ref. ²⁶.

Experiment settings

In training the PISTE, we used the ADAM optimizer with a mini-batch size of 1,024 sequences (triples) and a learning rate of 0.001 with 200 epochs. Each residue type has a dimension d = 64 and is randomly initialized. In the loss function in equation (8), α = 0.75 and γ = 2. Hyper-parameters were chosen as follows. The bandwidth h in equation (1) was fixed as h = 1. The number of iterations t for sliding attention was chosen from {2, 3, 4, 5}, and the best t was determined as the one that leads to the highest evaluation metric (average of AUROC and AUPR) on the validation set, which was chosen as 20% of the training data (the remaining 80% was used for training the model). The codes were written with PyTorch 1.7 and run on a PC with NVIDIA RTX A6000 GPU and 3.70 GHz CPU.

Patient specimen collection

This study was reviewed and approved by the Institutional Review Board of Shanghai Sixth People’s Hospital (declaration 2023-KY-155K). Informed consent was obtained from all the patients and the study strictly adhered to all the institutional ethical regulations. The tumour tissues and peripheral blood samples from eight patients with primary prostate cancer were attained following surgery at the Shanghai Sixth People’s Hospital (see the detailed clinical characteristics listed in Supplementary Table 8). No patients had undergone immunotherapy treatment before surgery. Samples were snap frozen by immediate immersion in liquid nitrogen and stored at –80 °C for next-generation sequencing by the Shanghai Applied Protein Technology. PBMCs were prepared from fresh whole blood by Ficoll–Paque density gradient centrifugation and in 90% foetal bovine serum + 10% dimethyl sulfoxide (DMSO).

WES and RNA-seq

DNA extraction was executed from both peripheral blood and tumour tissue samples using the QIAamp DNA MiniKit (Qiagen). Quantification of DNA concentrations was carried out using the Qubit 2.0 fluorometer (Invitrogen). The DNA underwent fragmentation into segments measuring 180–280 bp in length, using a Covaris instrument. The preparation of the sequencing libraries and capture of exons were conducted in strict accordance with the manufacturer’s protocol, utilizing the Agilent SureSelect Human All Exon V5/V6 Kit. The captured exons were amplified linearly by polymerase chain reaction and then checked by quantitative polymerase chain reaction. The sequencing procedure was executed on two lanes of the Illumina HiSeq 4000 v. 2 (Pair End 150 bp) platform, strictly adhering to the manufacturer’s guidelines and recommendations set forth by Illumina.

The extraction of RNA from fresh tissues was carried out by utilizing a combination of TRIzol reagent and the RNeasy MinElute Cleanup Kit (Invitrogen). The assessment of RNA quality was conducted using a fragment analyser (Agilent Technologies). The TruSeq Stranded Total RNA kit (Illumina) was used for the preparation of sequencing libraries, which were subsequently subjected to 150 bp paired-end sequencing on a HiSeq 4000 sequencer (Illumina).

Finally, we obtained whole-exome sequencing (WES) and transcriptome sequencing data of the tumour tissue and exome sequencing data of match normal sample for each patient.

Sequencing data processing and immunogenic neoantigen selection

WES information processing. On successful completion of sample sequencing, we leveraged OptiType v. 1.3.5 (ref. ⁶⁹) to determine the genotypes of patients’ HLA alleles. Meanwhile, we utilized a general mutation calling pipeline to detect somatic variations in the genome⁷⁰. Trimmomatic v. 0.39 (ref. ⁷¹) was used for the WES data quality control. The processed WES data of the tumour and matched blood (as a source of normal germ-line DNA) from each patient were aligned to the reference human genome (hg38) utilizing the Burrows–Wheeler alignment tool v. 0.7.17 (ref. ⁷²). Preprocessing was carried out following the GATK (v. 4.2.0) Best Practices Workflow⁷³ before variant calling. To perform single-nucleotide variant and insertion/deletion mutation calls, MuTect2 (GATK v. 4.2.0)⁷⁴, VarScan v. 2.3 (ref. ⁷⁵) and Strelka2 v. 2.9.2 (ref. ⁷⁶) were utilized. To eliminate false-positive mutations, all the mutations detected with allelic fractions of less than 0.05 or coverage of less than 10× were excluded. Then, all the mutations were annotated by leveraging Ensembl Variant Effect Predictor⁷⁷. The Quantitative Biomedical Research Center (QBRC) neoantigen calling pipeline was subsequently used to retrieve HLA-I-binding neoantigens of 8–11-mer length from the mutation data⁷⁰, and the corresponding wild-type sequences of neoantigens were also recorded. A median of 2,617 HLA–peptide complexes per sample were used to combine with TCRs into TCR–antigen–HLA triples and then run through PISTE.

RNA information processing. RNA sequencing (RNA-seq) data were aligned to the reference transcriptome (hg38) using Kallisto v. 0.46.0 (ref. ⁷⁸) to determine the abundance of gene expression levels, quantified as transcripts per kilobase million (TPM).

TCR repertoire data. To enhance the diversity and coverage of the patient TCR repertoire, the TCR data for each patient were sourced from two distinct origins. One portion comprised TCR sequences acquired through the analysis of the patient’s WES and RNA-seq data using the MiXCR v. 3.0.13 algorithm⁷⁹. The other segment was drawn from publicly accessible TCR sequencing data documented in the literature pertaining to prostate cancer patients⁸⁰.

Input to PISTE. The pHLA (with mutant neoantigen or wild-type antigen) and TCR sequences obtained from each patient were then combined to generate all the possible TCR–antigen–HLA triples. These triples were fed into the PISTE model for predicting the binding status for each triple.

Peptides ranking. Meticulous screening procedures were taken to select candidates from among thousands of neoantigens. First, we categorized all the predicted binding TCR–antigen–HLA triples from our model by antigen. This categorization allowed us to assess the potential immunogenicity level of each antigen by counting the number of TCRs binding to it. Here we focused on mutated neoantigens that bind with at least 100 TCRs and whose wild-type counterparts do not bind with any TCR. Additionally, considering that a single gene mutation could produce multiple antigens, we excluded those genes (and thus all the mutated neoantigens they produced) whose expression levels were under 5 TPM (ref. ⁸¹). After refining our candidate list, we ranked the genes by their expression levels and assessed each gene sequentially from the top of this list. For each gene, we selected the neoantigen with the highest number of binding TCRs as the ‘optimal peptide’. We continued this process until we had selected three to four optimal peptides for a patient, typically requiring probing of two to four highly expressed genes per patient.

Peptide synthesis

Lyophilized peptides for neoantigens were manufactured at ≥95% purity from GenScript. The peptides were verified by high-performance liquid chromatography and stored at –80 °C for testing the T cell reactivity.

Expansion of T cells specific to neoantigens

PBMCs obtained from patients were used to assess the T cell response to candidate neoantigens in an ex vivo setting. For in vitro pre-stimulation of antigen-specific T cells, PBMCs were thawed and cultured in RPMI 1640 medium (Thermo Fisher, cat. no. A1049101-01) supplemented with 10% foetal bovine serum and 1% penicillin–streptomycin (Thermo Fisher). The cells were stimulated in 96-well cell culture plates at 1.5 × 10⁵ cells per well pulsed with individual neoantigen (2.5 μg ml^–1) in the presence of interleukin-2 (20 U ml^–1; T&L Biotechnology). Interleukin-2 and peptide were added on days 3, 6 and 8, with the same concentration as before. Here phytohemagglutinin (PHA; 10 μg ml^–1) was used as the positive control and DMSO and unrelated peptide as negative controls. Cells were harvested after 10 days post-stimulation; quantification of peptide-specific T cell immune response intensity was conducted with the IFN-γ ELISA and flow cytometry assay.

T cell response analysis by IFN-γ ELISA assay

IFN-γ secretion of T cells was measured by ELISA using human IFN-γ ELISA kit (Multi Sciences, cat. no. EK180-96). Briefly, 5 × 10⁴ pre-stimulated PBMCs in RPMI 1640 containing 10% foetal bovine serum and 1% penicillin–streptomycin were added to each well of a 96-well plate with a total volume of 150 μl. The cells were subjected to re-stimulation using a peptide concentration of 2.5 μg ml^–1 at 37 °C with 5% CO₂ for a duration of 24 h; PHA (10 μg ml^–1) was used as a positive control and DMSO and unrelated peptide as the negative controls. The concentration of IFN-γ secretion was measured with the EnVision plate reader (PerkinElmer). A positive response was determined when the secretion of IFN-γ greater than 15.63 pg ml^–1 and greater than twice the negative control (DMSO and unrelated peptide), according to standard criteria^8,82.

T cell response analysis by flow cytometry

For ex vivo intracellular cytokine detection, PBMCs were re-stimulated with 5 μg ml^–1 peptide or 50 ng ml^–1 PMA (YEASEN) and 1 μg ml^–1 ionomycin (YEASEN) in complete RPMI 1640 (Thermo Fisher, cat. no. A1049101-01) with 10 μg ml^–1 brefeldin A (MKBio) at 37 °C overnight. Subsequently, cells were harvested and resuspended in phosphate-buffered saline (Gibco). After treatment, cells were stained for 30 min at room temperature with a Zombie Aqua Fixable Viability kit (BioLegend, cat. no. 423101), anti-CD3 (clone HIT3a, PerCP, BioLegend, cat. no. 300325) and anti-CD8 (clone SK1, APC, BioLegend, cat. no. 344721). After washing, cells were fixed and permeabilized (Foxp3/Transcription Factor Staining Buffer Set, Thermo Fisher, cat. no. 00-5523-00). Intracellular cytokines were stained with anti-IFN-γ (clone 4S.B3, PE, BioLegend, cat. no. 502508) for 30 min at room temperature. Cells were washed with the fluorescence-activated cell sorting buffer and collected using a ACEA NovoCyte flow cytometer.

To assess the formation of specific CD8⁺ T cells following antigen peptide stimulation, we conducted activation induction markers experiment. Cells were collected after 10 days of pre-stimulation, and then re-stimulated with antigen peptides. Following overnight incubation, cells were harvested and stained with the Zombie Aqua Fixable Viability kit at room temperature for 30 min. Subsequently, the cells were stained with anti-CD3 (PerCP, clone HIT3a, PerCP, BioLegend, cat. no. 300325), anti-CD8 (clone SK1, FITC, BioLegend, cat. no. 344703), anti-CD137 (clone 4B4-1, APC, BioLegend, cat. no. 309809) and anti-CD69 (clone FN50, PE, BioLegend, cat. no. 310905) antibodies. The dilution of all the antibodies was 1:100. After incubation at room temperature for 30 min, cells were resuspended in the fluorescence-activated cell sorting buffer and analysed using ACEA NovoCyte flow cytometer.

The gating strategy is shown in Supplementary Fig. 16a. Density maps were drawn for each cell group using ACEA NovoExpress v. 1.6. CD8⁺ T cell activation is identified when the proliferation percentage of the IFN-γ⁺ CD8⁺ population (or the double-positive rate of CD69 and CD137) following antigen peptide stimulation is 20% higher than that of the control group (DMSO). Meanwhile, we also quantified the proportion of CD8⁺ T cells in CD3⁺ T cells after antigen peptide stimulation.

Graphical and statistical analyses

Plots and analyses were generated using matplotlib and seaborn package in Python v. 3.8; survival package and survminer package in R v. 4.2.2; and GraphPad Prism software v. 8. A two-sided t-test was used to compare the continuous variables between two groups. To accommodate multiple comparisons, a standard one-way analysis of variance with Dunnett’s test was used. To investigate the existence of a positive ordinal association between the INAL and efficacy of immune therapy, we utilized the Jonckheere–Terpstra test. Survival curves were generated through the Kaplan–Meier method, whereas the log-rank test was used to assess the presence of significant differences between two survival curves. P values of <0.05 were considered to be statistically significant.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.