Introduction

As a significant material cultural heritage of Chinese civilization, the Terracotta Warriors possess considerable academic value and social significance for an in-depth understanding of China’s extensive history and culture. However, due to long-term natural erosion and human activities, most of the Terracotta Warriors have been unearthed as fragments, posing substantial challenges to their protection and restoration1. Traditional manual restoration methods are cumbersome and time-consuming, making it difficult to meet the demands of large-scale restoration projects. In recent years, the rapid development of 3D laser scanning technology has significantly advanced virtual restoration techniques, offering new possibilities for the digital preservation and restoration of the Terracotta Warriors2. Within the virtual restoration process, the classification and segmentation of Terracotta fragments are crucial steps. Accurate fragment classification directly impacts the effectiveness of subsequent matching and assembly, while precise segmentation not only addresses the issue of insufficient calibration data but also enables semantic annotation of the Terracotta Warriors, facilitating an in-depth analysis of the relics’ structure and features. Thus, obtaining an effective feature representation is essential for improving the accuracy of downstream classification and segmentation tasks, thereby enhancing the overall restoration efficiency.

Traditional heritage feature extraction methods primarily rely on expert-designed feature descriptors. Rasheed et al.3 proposed a method to extract texture features based on RGB color features and the gray-level co-occurrence matrix. Lin et al.4 proposed a multi-scan point cloud hierarchical registration method for the 3D reconstruction of ancient buildings, which effectively solved the problem of digitally reconstructing complete and real models of complex architectural structures without damage. Although effective, these methods often depend on expert prior knowledge, and the expressive power of hand-designed feature extraction techniques is limited, which constrains the generalization performance of classification models. With the rapid advancement of deep learning technology and the proliferation of 3D data acquisition devices, point cloud-based representation learning algorithms, such as PointNet5, PointNet + +6, and DGCNN7, have been proposed, providing novel approaches for feature extraction from cultural relic fragments. Zhou et al.8 introduced the Multi-scale Local Geometric Transformer-Mamba (MLGTM) method to improve the accuracy and robustness of Terracotta Warriors point cloud classification tasks by effectively capturing complex local morphology and handling data sparsity and irregularity. Zhu et al.9 developed a transfer learning-based method to recover the three-dimensional shape of cultural relics faces from a single old photo, effectively addressing the issue of limited cultural relic samples. However, these methods typically require labeled data, posing challenges for their application in the field of cultural heritage. Self-supervised representation learning (SSRL), which has shown promise in fields like computer vision and natural language processing (NLP), may provide new solutions to these challenges10.

SSRL seeks to enhance the performance of various downstream tasks by learning general and robust feature representations from unlabeled data11. Recent research in the field of image processing has shown that representations obtained through SSDL can be as effective as those achieved through supervised learning methods12. However, the learned embedded features often contain redundant information, leading to a decrease in semantic representation ability and impacting downstream task performance. To address these challenges, innovative approaches such as Barlow Twins13 and HOME14 have been proposed. These methods focus on feature redundancy to of SSDL in image-processing tasks. In recent years, several algorithms also have been developed for self-resolve the aforementioned issues, enhancing the overall efficacy supervised learning with point clouds, including self-reconstruction, adversarial generation, and completion15,16. However, methods like Latent GAN17, FoldingNet18, and OcCo19 require significant computing resources and time, and all these algorithms are highly sensitive to rotational and translational variations. Contrastive learning, successful in video and image domains, is increasingly being applied to point cloud understanding20. For instance, PointContrast uses contrastive learning to achieve viewpoint-invariant point cloud representations, facilitating high-level scene understanding21. CrossPoint enhances this by leveraging multiple modalities for contrastive learning, extracting richer signals22. These methods involve pre-training with a pretext task designed to bring similar samples closer and push dissimilar ones further apart in the feature space. Yet, these methods commonly face model collapse, where the learned representation vector shrinks to a constant or low-dimensional subspace, underutilizing the full representational capacity. Existing contrast-based learning methods often mitigate this by using complex mechanisms, such as memory banks23 or asymmetric networks with gradient stopping, predictor networks, and momentum update strategies24. Notably, in the field of cultural heritage protection, particularly in the digital preservation of Terracotta Warriors, significant strides have been made. Wang et al.25 proposed a transformer-based method to enhance point cloud registration, effectively improving the accuracy of point cloud alignment in Terracotta Warriors preservation. Additionally, Xu et al.26 developed CPDC-MFNet, a conditional point diffusion completion network with multi-scale feedback refinement for repairing damaged 3D models of Terracotta Warriors, which improves generation speed while maintaining diverse outputs. Despite these advancements in the preservation of Terracotta Warriors, the open challenge of preventing model collapse without relying on complex designs still remains, underscoring the need for further research in this area.

Motivated by the above analysis and inspiration from14, we introduce a self-supervised contrastive learning method for terracotta fragment classification and segmentation that leverages high-order mixed moments. This approach effectively prevents model collapse by minimizing redundancy among feature variables without relying on complex mechanisms. Specifically, we utilize high-order mixed moments to minimize redundancy among arbitrary feature variables, aiming to learn meaningful point cloud representations. It is known that pairwise independence of each variable does not guarantee their mutual independence, and that the total correlation among all variables is minimized only if multiple variables are independent. This implies that the mixed moment of multiple features can be decomposed into the product of their individual moments. Drawing from statistical theory and the contrastive learning paradigm, we design a loss function based on high-order mixed moments. This function reduces redundancy among multiple variables, allowing the high-dimensional features learned through self-supervised learning to be rich in information and independent. It also ensures maximum consistency in representation across different augmented point clouds. Our extensive experiments on various datasets show that our method achieves state-of-the-art accuracy.

The main contributions of this paper are as follows:

  • We propose a self-supervised learning method for point clouds using high-order mixed moments. Our approach reduces feature redundancy, enhancing representational capability while inherently avoiding model collapse without additional techniques. We also successfully applied it to Terracotta warrior analysis.

  • Our approach offers a plug-and-play solution with symmetric network architecture, enabling flexible integration with various point cloud processing methods.

  • We evaluated our approach on object classification and segmentation tasks. PointMoment significantly outperformed existing unsupervised learning methods. Notably, its application to the Terracotta Warriors dataset yielded exceptional results, further validating our method’s effectiveness and superiority in point cloud analysis.

Related work

In this section, we provide a brief overview of recent advancements in two pertinent areas: supervised and self-supervised representation learning for point clouds.

Supervised representation learning on point cloud

We can divide supervised representation learning methods for point clouds into two main categories: structure-based and point-based. Structure-based methods often transform point clouds into 2D images or regular structured data like voxels for feature extraction. MVCNN27 uses 2D convolutional networks with max-pooling to create global shape descriptors from multi-view features. However, it may result in information loss and overlooks view relationships. To address this, View-GCN28 employs a Graph Convolutional Network (GCN) on the view graph for hierarchical feature aggregation. VoxNet29 uses 3D convolutional networks to extract features from voxel grids but can be computationally intensive and memory-demanding with dense 3D data, which grows cubically with resolution. Overall, these methods may struggle to capture fine-grained geometric details and can be memory-intensive.

Point-based methods utilize raw data without conversion to other formats and can be divided into four types: MLP-based, Transformer-based, Graph-based, and CNN-based. MLP-based methods, such as the pioneering PointNet5, as a pioneering work, has inspired many subsequent methods, such as PointWeb30. PointNet + +6 improves upon PointNet by using set abstraction to capture local features and generate global representations. CNN-based methods use specially designed convolution kernels for point cloud feature extraction. PointCNN31 introduces the X-Conv operator for direct processing of point clouds, while SpiderCNN32 employs step functions and Taylor expansions to capture complex local geometries. Graph-based methods treat each point as a graph vertex and construct edges to reflect relationships with neighbors. DGCNN7 reconstructs local graphs and uses EdgeConv for local feature extraction but may not fully capture edge features. Recently, Transformer-based methods, leveraging self-attention mechanisms successful in image analysis and NLP, have been explored for point cloud data, as seen in PCT33 and PointTransformer34. However, the primary challenge for these supervised methods is the scarcity of large annotated datasets.

Self-supervised representation learning on point cloud

Self-supervised representation learning is a prominent research area in point cloud analysis, adept at extracting effective features without labeled data. It can be divided into two main types: contrastive and generative.

Generative methods use models to approximate the underlying data or feature distribution, revealing intrinsic point cloud characteristics. Common models include variational autoencoders and generative adversarial networks (GANs). Latent-GAN17 is a pioneering model that applies GAN to raw point cloud data and embedded features to generate high-quality samples. Yang et al.18 developed a decoder based on the concept that 3D object surfaces can be folded from 2D planes, enhancing 3D reconstruction quality. As transformers gain popularity in image and NLP fields, transformer-based generative methods like Point-BERT35 and Point-MAE36 are emerging, with Point-MAE extending Point-BERT. OcCo19, introduced by Wang et al. is a novel approach to point cloud completion that learns representations by reconstructing missing data. However, these methods can struggle with accurate reconstruction and are computationally demanding.

Contrastive learning methods train a feature encoder to learn representations that are similar to positive examples and dissimilar to negatives. Info3D23 merges mutual information with contrastive learning to enhance 3D object representation by optimizing the mutual information between local structures and the global shape. PointGLR20 integrates normal estimation, self-reconstruction, and contrastive learning into a single framework for bidirectional inference between global and local 3D object features, in an unsupervised manner. PointContrast21 unifies the contrastive learning paradigm for 3D point clouds to promote high-level scene understanding through multi-view learning. DepthContrast37 introduces a joint strategy for voxel and point cloud contrastive learning to improve downstream task performance. STRL24 adapts BYOL10 for point cloud representation learning, while CrossPoint22 uses 2D images to enhance 3D point cloud understanding with a cross-modal contrastive method, however, obtaining 2D-rendered images can be challenging.

Unlike methods that rely on complex strategies to prevent model collapse, such as memory banks or asymmetric networks, we propose a versatile contrastive learning framework with a novel loss function for ideal point cloud representation.

Methodology

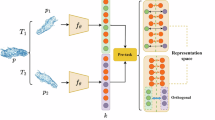
In this section, we introduce PointMoment, a self-supervised approach for learning meaningful point cloud representations using high-order mixed moments. We first explain the concept of high-order mixed moments (section High-order mixed-moment). Then, we present a loss function (section Formulation of high-order mixed-moment as a loss) designed to pre-train the feature extractor \({{\rm{f}}}_{{\rm{\theta }}}({\rm{\cdot }})\) in a self-supervised manner. Figure 1 shows the network framework of our approach. Finally, we detail an application of our approach to third-order mixed moment-based self-supervised representation learning (section Instantiating three-order mixed-moment for contrastive learning), as depicted in Fig. 2.

Fig. 1: The overall architecture of our approach PointMoment.
figure 1

The loss is composed of two important parts, one is the loss based on invariance, and the other is the loss based on redundancy reduction. The latter involves constraints of order two or higher.

Full size image
Fig. 2: Self-supervised representation learning based on third-order mixed moment.
figure 2

a Indicates that mixed moment are calculated for the output of each branch, and b indicates that mixed moment are calculated for the output of a particular branch, where the dashed line indicates that the corresponding output is not constrained by the mixed moment. c Visualization shows the specific meaning of each curve, and the red square part does not take into account the calculation of the mixed moment.

Full size image

High-order mixed-moment

Moments are numerical characteristics used in probability theory and statistics to describe the distribution of random variables. The most common moments are the first-order moment (mean) and the second-order central moment (variance), which measure the average and dispersion of a single random variable, respectively. For a more comprehensive assessment of multiple random variables, mixed moments are utilized.

Mixed moments are statistical measures that describe the fundamental characteristics of a multivariate random variable’s distribution. They are typically defined as follows:

For any positive integer \({{\rm{k}}}_{{\rm{i}}}\), the mathematical expectation \({\rm{E}}[{{\rm{X}}}_{1}^{{{\rm{k}}}_{1}}...{{\rm{X}}}_{{\rm{n}}}^{{{\rm{k}}}_{{\rm{n}}}}]\) of multiple random variables is called the k-order mixed moment, where \({{\rm{k}}={\rm{k}}}_{1}+...{+{\rm{k}}}_{{\rm{n}}}\). \({\rm{E}}[({{{\rm{X}}}_{1}-{\rm{E}}[{{\rm{X}}}_{1}])}^{{{\rm{k}}}_{1}}...({{{\rm{X}}}_{{\rm{n}}}-{\rm{E}}[{{\rm{X}}}_{{\rm{n}}}])}^{{{\rm{k}}}_{{\rm{n}}}}]\) is then called the k-order central mixed moment. If there are only two random variables and both \({{\rm{k}}}_{{\rm{i}}}\) are 1, then the mixed moment \({\rm{E}}[({{\rm{X}}}_{1}-{\rm{E}}[{{\rm{X}}}_{1}]){({\rm{X}}}_{2}-{\rm{E}}[{{\rm{X}}}_{2}])]\) is called the covariance, which describes the degree of correlation between the two random variables13. just start from the perspective of covariance and reduce the feature redundancy by reducing the correlation between any two feature variables.

After introducing mixed moments, we’ll explain their utility. In high-dimensional feature spaces, redundant information within embedded features can impair their utility. To mitigate this, we apply mutual information to measure the interdependence among random variables. Let \({{\rm{X}}}_{1},{{\rm{X}}}_{2},...,{{\rm{X}}}_{{\rm{d}}}\) be the random variables representing each dimension (denoted as d) of the embedding feature. We can use the mutual information (MI) formula to measure the shared information between variables:

$${\rm{I}}({{\rm{X}}}_{1},{{\rm{X}}}_{2},...,{{\rm{X}}}_{{\rm{d}}})=\mathop{\int }\limits_{{{\rm{X}}}_{1}}\mathop{\int }\limits_{{{\rm{X}}}_{2}}...\mathop{\int }\limits_{{{\rm{X}}}_{{\rm{d}}}}{\rm{p}}({{\rm{x}}}_{1},{{\rm{x}}}_{2},...,{{\rm{x}}}_{{\rm{d}}})\log \frac{{\rm{p}}({{\rm{x}}}_{1},{{\rm{x}}}_{2},...,{{\rm{x}}}_{{\rm{d}}})}{{\rm{p}}({{\rm{x}}}_{1}){\rm{p}}({{\rm{x}}}_{2})...{\rm{p}}({{\rm{x}}}_{{\rm{d}}})}{\rm{d}}{{\rm{x}}}_{1}{\rm{d}}{{\rm{x}}}_{2}...{\rm{d}}{{\rm{x}}}_{{\rm{d}}}$$
(1)

where \({\rm{p}}({{\rm{x}}}_{1},{{\rm{x}}}_{2},...,{{\rm{x}}}_{{\rm{d}}})\) is the joint density function of \({{\rm{X}}}_{1},{{\rm{X}}}_{2},....{{\rm{X}}}_{{\rm{d}}}\) and \({\rm{p}}\left({{\rm{x}}}_{1}\right),{\rm{p}}\left({{\rm{x}}}_{2}\right),...,{\rm{p}}({{\rm{x}}}_{{\rm{d}}})\) is the marginal probability density function of \({{\rm{X}}}_{1},{{\rm{X}}}_{2},....{{\rm{X}}}_{{\rm{d}}}\) respectively.

To make the information contained in the embedding features rich and compact, we need to minimize Eq.1 to reduce the redundant information between feature variables. According to statistics, Eq.1 can be minimized when \({{\rm{X}}}_{1},\,{{\rm{X}}}_{2},...{{\rm{X}}}_{{\rm{d}}}\) are independent of each other, that is, \({\rm{p}}({{\rm{x}}}_{1},{{\rm{x}}}_{2},...,{{\rm{x}}}_{{\rm{d}}})={\rm{p}}({{\rm{x}}}_{1}){\rm{p}}({{\rm{x}}}_{2})...{\rm{p}}({{\rm{x}}}_{{\rm{d}}})\). However, this minimization process faces two key challenges. One challenge is that pairwise independence of random variables does not necessarily ensure that the total redundancy of all variables is minimized, unless \({\rm{p}}({{\rm{x}}}_{1},{{\rm{x}}}_{2},...,{{\rm{x}}}_{{\rm{d}}})\) follows a multivariate normal distribution, which is often hard to satisfy in practice. Another challenge is that directly modelling the probability distribution of continuous variables can be difficult. Therefore, a common approach is to use statistical moment to model the probability distribution. We introduce high-order mixed moment. We exploit the fact that all random variables are independent of each other if and only if the expectation of all random variables is equal to the product of their individual expectations, which can be mathematically expressed as follows:

$${\rm{E}}[\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{{\rm{X}}}_{{\rm{d}}}]=\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{\rm{E}}[{{\rm{X}}}_{{\rm{d}}}]$$
(2)

where \({\rm{E}}[\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{{\rm{X}}}_{{\rm{d}}}]\) is the mixed moment of order D. We can minimize Eq.1 by modelling and enforcing the random variables to satisfy the condition of Eq.2, which induces more independence among them.

Formulation of high-order mixed-moment as a loss

Preliminary

Given a batch of randomly selected point clouds \({\rm{B}}=\,{\{{{\rm{p}}}_{{\rm{i}}}\}}_{{\rm{i}}=1}^{{\rm{|B|}}}\), where \({{\rm{p}}}_{{\rm{i}}}\in {{\rm{R}}}^{{\rm{N}}\times 3}\), \({\rm{|B|}}\) denotes batch size and N denotes the total number of points in each point cloud. We apply random data augmentation techniques such as rotation, jittering and scaling to each point cloud \({{\rm{p}}}_{{\rm{i}}}\), generating two distinct enhanced versions of the original data, \({{\rm{p}}}_{{\rm{i}}}^{{{\rm{t}}}_{1}}\) and \({{\rm{p}}}_{{\rm{i}}}^{{{\rm{t}}}_{2}}\). Next, we feed both enhanced datasets into a network architecture. Specifically, the feature extractor \({{\rm{f}}}_{{\rm{\theta }}}\) maps \({{\rm{p}}}_{{\rm{i}}}^{{{\rm{t}}}_{1}}\) and \({{\rm{p}}}_{{\rm{i}}}^{{{\rm{t}}}_{2}}\) into a feature representation space, followed by a projection head \({{\rm{g}}}_{{\rm{\varphi }}}\), which projects resulting feature vectors onto an embedding feature space. We denote the final embedding vectors produced from this process as \({{\rm{z}}}_{{\rm{i}}}^{{{\rm{t}}}_{1}}\) and \({{\rm{z}}}_{{\rm{i}}}^{{{\rm{t}}}_{2}}\), respectively, where \({{\rm{z}}}_{{\rm{i}}}^{{\rm{t}}}={{\rm{g}}}_{{\rm{\varphi }}}({\rm{f}}({{\rm{p}}}_{{\rm{i}}}^{{\rm{t}}};{{\rm{\theta }}}_{{\rm{f}}});{{\rm{\varphi }}}_{{\rm{g}}})\) and \({{\rm{z}}}_{{\rm{i}}}^{{\rm{t}}}\in {{\rm{R}}}^{{\rm{D}}}\), \({{\rm{\theta }}}_{{\rm{f}}}\) and \({{\rm{\varphi }}}_{{\rm{g}}}\) denote the trainable parameters of the encoder and projector, respectively, and D denotes the dimension of the embedding vector. Our goal is to learn compact, meaningful feature vectors without the need for complex network architectures or optimization processes. Furthermore, our loss function can be used in combination with a range of other network frameworks. Figure 1 provides a general representation of our self-supervised learning approach for point clouds.

Loss based on high-order mixed-moment

We argue that an ideal embedding feature should possess two key attributes: invariance to random augmentations of samples and minimal total correlation among the vector’s variables. To achieve these, we’ve crafted distinct loss functions for each property.

Redundancy reduction based on high-order mixed-moment: Minimizing redundancy prompts the network to learn a compact embedding where each variable conveys unique semantic information. As outlined in Section “High-order mixed-moment,” we enforce Eq. 2 to reduce total correlation among variables to a certain extent. We apply the Law of Large Numbers to estimate a variable’s expectation using sample moments, which are then used to calculate the expectation in Eq. 2. For ease, we standardize each feature variable z across the batch dimension to have a mean of zero and a variance of one, as follows:

$${\hat{{\rm{z}}}}_{{\rm{b}},{\rm{d}}}^{{\rm{t}}}=\frac{{{\rm{z}}}_{{\rm{b}},{\rm{d}}}^{{\rm{t}}}-\frac{1}{{\rm{B}}}{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{{\rm{z}}}_{{\rm{b}},{\rm{d}}}^{{\rm{t}}}}{\sqrt{{\sum }_{{\rm{b}}=1}^{{\rm{B}}}({{\rm{z}}}_{{\rm{b}},{\rm{d}}}^{{\rm{t}}}-\frac{1}{{\rm{B}}}{{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{{\rm{z}}}_{{\rm{b}},{\rm{d}}}^{{\rm{t}}})}^{2}/{\rm{B}}}}$$
(3)

Now for each dimension satisfies \({\rm{E}}[{\hat{{\rm{Z}}}}_{{\rm{d}}}]=0\), so we only need to set \({\rm{E}}[\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{\hat{{\rm{Z}}}}_{{\rm{d}}}]=0\) to make Eq.2 hold, that is, \({\rm{E}}[\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{\hat{{\rm{Z}}}}_{{\rm{d}}}]=\mathop{\prod }\limits_{{\rm{d}}=1}^{{\rm{D}}}{\rm{E}}[{\hat{{\rm{Z}}}}_{{\rm{d}}}]=0\). Therefore, we propose the redundancy reduction loss based on the high-order mixed moment as follows:

$${{\mathscr{L}}}_{{\rm{RR}}}=\frac{1}{{\rm{T}}}\mathop{\sum }\limits_{{\rm{t}}=1}^{{\rm{T}}}\left[\frac{1}{2{\rm{M}}}\mathop{\sum }\limits_{{\rm{K}}=2}^{{\rm{D}}}\left(\mathop{\sum }\limits_{{{\rm{d}}}_{1}}^{{\rm{D}}}\mathop{\sum }\limits_{{{\rm{d}}}_{2}\ne {{\rm{d}}}_{1}}^{{\rm{D}}}{\rm{\cdot \cdot \cdot }}\mathop{\sum }\limits_{{{\rm{d}}}_{{\rm{K}}}\ne {\rm{\cdot \cdot \cdot }}\ne {{\rm{d}}}_{2}\ne {{\rm{d}}}_{1}}^{{\rm{D}}}{\left({{\rm{E}}}_{{{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{K}}}}\right)}^{2}\right)\right]$$
(4)

where K denotes the order of the mixed moment and M denotes the total number of combinations of mixed moment of all orders, i.e. \({\rm{M}}={\sum }_{{\rm{K}}=2}^{{\rm{D}}}\frac{{\rm{D}}!}{({\rm{D}}-{\rm{K}})!{\rm{K}}!}\). \({{\rm{E}}}_{{{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{k}}}}\) is the matrix of mixed moment of order K calculated along the batch dimension:

$${{\rm{E}}}_{{{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{K}}}}=\frac{1}{{\rm{B}}}\mathop{\sum }\limits_{{\rm{b}}=1}^{{\rm{B}}}{\prod }_{{\rm{i}}=1}^{{\rm{K}}}{\hat{{\rm{z}}}}_{{\rm{b}},{{\rm{d}}}_{{\rm{i}}}}^{{\rm{t}}}$$
(5)

where \({{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{K}}}\) etc. denote the index of the dimension of the embedding vector, respectively, for any K variables with \({\rm{K}}\le {\rm{D}}\) and with \(1\le {{\rm{d}}}_{{\rm{K}}}\le\)D for any \({{\rm{d}}}_{{\rm{K}}}\). \({{\rm{E}}}_{{{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{k}}}}\) denotes the value of the K-order mixed moment of the random variables with index value \({{\rm{d}}}_{1},{{\rm{d}}}_{2},{\rm{\cdot \cdot \cdot }},{{\rm{d}}}_{{\rm{k}}}\), respectively.

Transformation invariance based on co-correlation: Invariance is the property that ensures semantically similar point cloud data are mapped to close regions in the embedding feature space. While many methods calculate cosine similarity between different augmented point cloud versions and build contrastive losses around it, we utilize the co-correlation matrix from13 to bolster invariance, proposing the following loss function:

$${{\mathcal{L}}}_{{\rm{TI}}}=\frac{1}{{\rm{D}}}\mathop{\sum }\limits_{{\rm{d}}=1}^{{\rm{D}}}{\left({1-{\rm{C}}}_{{\rm{dd}}}\right)}^{2}$$
(6)

where \({\rm{C}}\) is the co-correlation matrix, calculated from the outputs of two identical networks along the batch dimension:

$${{\rm{C}}}_{{\rm{i}},{\rm{j}}}=\frac{{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{\hat{{\rm{z}}}}_{{\rm{b}},{\rm{i}}}^{{{\rm{t}}}_{1}}{\hat{{\rm{z}}}}_{{\rm{b}},{\rm{j}}}^{{{\rm{t}}}_{2}}}{\sqrt{{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{\left({\hat{{\rm{z}}}}_{{\rm{b}},{\rm{i}}}^{{{\rm{t}}}_{1}}\right)}^{2}}\sqrt{{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{\left({\hat{{\rm{z}}}}_{{\rm{b}},{\rm{j}}}^{{{\rm{t}}}_{2}}\right)}^{2}}}=\frac{1}{{\rm{B}}}{\sum }_{{\rm{b}}=1}^{{\rm{B}}}{\hat{{\rm{z}}}}_{{\rm{b}},{\rm{i}}}^{{{\rm{t}}}_{1}}{\hat{{\rm{z}}}}_{{\rm{b}},{\rm{j}}}^{{{\rm{t}}}_{2}}$$
(7)

where i and j denote the dimensional index of the embedding vector, C is a square matrix of size D and \({-1\le {\rm{C}}}_{{\rm{i}},{\rm{j}}}\le 1\), -1 denotes negative correlation and 1 denotes positive correlation. It is analytically easy to see that Eq.7 can eventually be reduced to the same expression as Eq.5, which essentially satisfies the same underlying logic. Equation 6 maximizes the correlation of the different augmented embedding features by forcing the diagonal elements of the co-correlation matrix to be 1, thus satisfying the transformation invariance.

Based on the above analysis, we give the final loss:

$${{\mathscr{L}}}_{{\rm{total}}}={{\mathscr{L}}}_{{\rm{TI}}}+{\rm{\lambda }}{{\mathscr{L}}}_{{\rm{RR}}}$$
(8)

where \({\rm{\lambda }}\) is a parameter used to trade off the first and second terms.

Instantiating three-order mixed-moment for contrastive learning

Following the discussions in sections “High-order mixed-moment” and “Formulation of high-order mixed-moment as a loss,” we introduce a self-supervised representation learning approach for point clouds that utilizes third-order mixed moments, as depicted in Fig. 2a. Additionally, we present a more computationally efficient version shown in Fig. 2b, which alleviates the requirement for all network branches to be active. It randomly selects a branch to achieve the desired outcome, thereby reducing computational demands. The experimental results validating this approach are detailed in the subsequent section. The subsequent experiments are all based on k = 3, that is, the third-order mixing moment.

Figure 2 illustrates our approach utilizing third-order mixed moments to compute the total loss \({{\mathscr{L}}}_{{\rm{total}}}\) for K = {2,3}. The green curve represents the second-order mixed moment calculated for the embedding features of the branch output. Similarly, the blue curve represents the third-order mixed moment computed for the branch output. These two constraints are combined, i.e. \({{\mathscr{L}}}_{{\rm{RR}}}\), to eliminate redundancy in the embedding features. Finally, the red curve signifies the consistency of data after undergoing two transformations, i.e. \({{\mathscr{L}}}_{{\rm{TI}}}\), which completes the transformation invariance constraint.

Experiments

This section presents a comprehensive evaluation of our proposed method. First, we elucidate our pre-training strategy and describe the datasets employed. Second, we assess the transferability of our approach through two prevalent downstream tasks: object classification and segmentation. Third, to validate the efficacy of our loss function and parameter selection, we conduct thorough ablation studies. Finally, we demonstrate the practical utility of our method by applying it to the Terracotta Warriors dataset, showcasing its performance in a real-world scenario.

Pre-training

Dataset. For pre-training, we utilized the ShapeNet38 dataset, a comprehensive repository of synthetic 3D shapes comprising over 50,000 unique models across 55 common object categories. To ensure comparability, we adhered to the training protocol established by STRL24. This procedure involved randomly sampling 2048 points from each model in the dataset. Subsequently, we applied a series of data augmentation techniques, including random rotation, translation, scaling, clipping, and jittering, followed by normalization. These augmented samples were then fed into the network for pre-training, maintaining consistency with established methodologies in the field.

Pre-training Detail. For a fair comparison with existing methods, we adopt the same method as STRL24, OCCO19, etc., using PointNet5 and DGCNN7 as feature extractors for point clouds and a two-layer multilayer perceptron as the projection head to map feature vectors into a 512-dimensional embedding space. We train the model in an end-to-end manner for 200 rounds using an Adam optimizer with a weight decay of 1×10-6 and an initial learning rate of 1 × 10-3. Additionally, we also adjust the learning rate by implementing a decay strategy based on cosine annealing. The batch size is 16. After pre-training, we discarded the projection head \({{\rm{g}}}_{{\rm{\phi }}}({\rm{\cdot }})\) and retained \({{\rm{f}}}_{{\rm{\theta }}}({\rm{\cdot }})\) for the following downstream task.

Downstream tasks

3D Object classification

The 3D object classification task involves categorizing point cloud data to identify the specific class of each point cloud. We assess the shape understanding and generalization of pre-trained models using two benchmark datasets: ScanObjectNN39 and ModelNet4040. ScanObjectNN, a challenging dataset of real-world 3D point clouds from indoor scenes, contains 15 categories with 2880 objects, Among these, 2304 for training and 576 for testing. ModelNet40, featuring synthetic objects, includes 12,311 CAD models across 40 categories, and 2468 for testing and 9843 for training, allowing us to evaluate classification performance on synthetic data.

Linear classification is a common method to evaluate the migration and generalization ability of self-supervised models in classification tasks. We follow the standard protocols of ref. 24 and ref. 19 to test the accuracy of our network model in object classification. On the classification data set, a linear Support Vector Machine (SVM) classifier is employed. This classifier is trained on features extracted from the training set using a pre-trained feature extractor, whose parameters remain fixed during this process. Subsequently, the trained SVM is applied to predict classifications based on the 3D features extracted from the test set. This methodology is widely adopted in the field for assessing the effectiveness of learned feature representations in downstream classification tasks. For our experiments, we employ two commonly used backbone networks, PointNet and DGCNN, as feature extractors.

Table 1 presents the accuracy of PointMoment for linear classification on ModelNet40. To conserve computational resources, we randomly chose one network branch for the high-order mixed moment constraint, achieving comparable results to using all branches, and adopted this single-branch constraint for subsequent experiments. Our method surpasses other state-of-the-art (SOTA) unsupervised and self-supervised algorithms when employing PointNet or DGCNN as the backbone network. Notably, our approach uses a basic network architecture without the complex features of STRL, such as asymmetric networks or gradient stopping. Specifically, our method outperforms STRL by 0.5% and 0.1% when using PointNet and DGCNN, respectively, highlighting the effectiveness of our approach. We assessed the generalizability of PointMoment in real-world scenarios by testing on ScanObjectNN with an SVM classifier.

Table 1 Comparison of the linear SVM classification on ModelNet40
Full size table

Table 2 compares the linear classification accuracy of other self-supervised methods on ScanObjectNN. Our method outperformed the previous SOTA approaches by 4.8% and 2.6% when using PointNet and DGCNN as feature extractors, respectively. This result underscores the generalizability of representations learned from synthetic data, confirming the effectiveness of our approach.

Table 2 Comparison of classification on ScanObjectNN
Full size table

3D Object part segmentation

Object part segmentation, a complex and crucial task in 3D recognition, involves categorizing each point of an object into specific part classes, such as a table’s leg or a car’s tire. We conducted experiments using the ShapeNetPart41 dataset, which includes 16,991 objects across 16 categories with 50 distinct parts, ranging from 2 to 6 parts per object. As a benchmark, ShapeNetPart effectively measures object part segmentation performance. Following the approach of previous studies24 and19, we pre-trained our model using DGCNN as the backbone network, followed by fine-tuning to enhance performance. Specifically, we conducted fine-tuning experiments on the ShapeNetPart dataset in an end-to-end manner. For the fine-tuning process, we employed SGD as the optimizer, with an initial learning rate of 0.1 and weight decay of 1 × 10−4. The momentum was set to 0.9, with a batch size of 8. The model was trained for 300 epochs. We selected mean Intersection over Union (mIoU) as the evaluation metric, given its precision and widespread use in the field.

Table 3 compares segmentation outcomes for supervised learning methods and various self-supervised approaches on ShapeNetPart. Our pre-training approach offered better initial weights for DGCNN than those from random initialization by supervised learning, increasing mIoU by 0.3%. Additionally, our model outperformed the current SOTA self-supervised method by 0.3% in mIoU, indicating that our use of high-order mixed moments yields more discriminative and less redundant features. The visualization results are presented in Fig. 3 Our segmentation outcomes demonstrate a high degree of similarity to the ground truth, indicating that our method effectively captures fine-grained information within the point cloud. This close correspondence between our results and the actual segmentation underscores the capability of our approach to discern and represent detailed structural features in point cloud data.

Table 3 Part segmentation results on ShapeNetPart dataset
Full size table
Fig. 3: The visualization of part segmentation results on ShapeNetPart.
figure 3

The first row is the ground truth, and the second row is our method.

Full size image

3D semantic segmentation

Semantic segmentation is a challenging task that aims to assign a semantic label to each point in a point cloud, enabling the grouping of regions with meaningful significance. This task is particularly important in complex indoor and outdoor scenes, which are often characterized by substantial background noise. To evaluate the representational capacity and generalization capability of our model, we conducted semantic segmentation experiments on the Stanford Large-Scale 3D Indoor Spaces (S3DIS) dataset. S3DIS is a widely used 3D indoor scene dataset that comprises scanned data from 272 rooms across 6 zones, covering a total area of approximately 6000 square meters. The dataset defines 13 semantic categories and provides fine-grained, point-wise semantic labels, where each point is annotated with comprehensive 9-dimensional feature information, including spatial coordinates (XYZ), color attributes (RGB), and normalized positional coordinates.

In our experiments, we fine-tuned the pre-trained model on all areas except Area 5 (the largest region in the dataset) and evaluated it on Area 5. The backbone network of our model is PointNet. To ensure experimental fairness, we strictly adhered to the experimental protocol proposed by Qi et al.5 and Wang et al.7 Specifically, we divided each room into small blocks of 1 m × 1 m and randomly sampled 4096 points from each block as inputs to the model, using only geometric features (XYZ coordinates) for each point.

The experimental results are summarized in Table 4. Our method demonstrates significant performance improvements compared to existing supervised and self-supervised learning approaches. Specifically, our method achieves a mIoU (mean Intersection-over-Union) improvement of 0.2 over the Multi-view rendering method. Furthermore, by applying self-supervised pre-training on PointNet, our approach achieves a 1.5-point gain in mIoU compared to PointNet trained from scratch. These results clearly highlight the effectiveness of self-supervised pre-training in learning robust and transferable features, particularly in scenarios with limited labeled data.

Table 4 Semantic segmentation results on S3DIS dataset, evaluated on Area 5
Full size table

Ablations and analysis

Impact of high-order mixed moment

To assess the impact of high-order mixed moments, we conducted ablation studies with three loss functions: i) an invariance-based loss as a baseline; ii) the baseline plus a second-order mixed moment loss to evaluate its effectiveness; iii) the second-order loss plus a third-order mixed moment loss to understand the third-order’s impact. Table 5 presents the comparative results. Relying only on the invariance-based loss led to an uneven feature distribution and reduced classification accuracy. Adding the second-order mixed moment mitigated model collapse and redundancy, significantly improving the model’s representational power for both PointNet and DGCNN across datasets. The third-order mixed moment further minimized redundancy. It increased classification accuracy by 0.8% for PointNet and 1.7% for DGCNN on ModelNet40 compared to using only the second-order moment. These findings underscore the importance of incorporating higher-order mixed moments.

Table 5 The accuracy of linear SVM classification using retrained embedding on ModelNet40 and ScanObjectNN for PointMoment
Full size table

Figure 4 visualizes features from the ModelNet1040 test set using t-SNE, extracted with the pre-trained PointNet. Incorporating second- and third-order mixed moments improved the separability of different classes. Notably, the addition of the third-order mixed moment allowed for clearer differentiation of objects with less distinct boundaries, including sofas, beds, and bathtubs.

Fig. 4: The T-SNE feature visualization on the ModelNet10 test set, post the training of PointNet as the self-supervised backbone network.
figure 4

The feature learned by three-order mixed moment(right) provides better discrimination of classes (e.g., sofas, beds and bathtubs) than using only invariance(left) or two-order mixed moment(middle).

Full size image

Sensitivity analysis of \({\rm{\lambda }}\)

Intuitively, the parameter \({\rm{\lambda }}\) significantly influences pre-training and, consequently, the performance on downstream tasks. Our study examines how varying \({\rm{\lambda }}\) affects classification performance. We tested \({\rm{\lambda }}\) values from 0.001 to 5, using PointNet as the backbone network for pre-training, and conducted linear classification on both ScanObjectNN and ModelNet40 datasets. As Table 6 shows, an optimal classification performance on both datasets was achieved when \({\rm{\lambda }}\) was set to 0.5.

Table 6 Linear classification results for different \({\boldsymbol{\lambda }}\) parameters on ModelNet40 and ScanObjectNN datasets after pre-training using PointNet
Full size table

Application on the Terracotta Warrior Dataset

Terracotta Warriors Dataset

The Terracotta Warriors, renowned as one of the Seven Wonders of the World, represent a significant ceramic cultural relic in China. Their virtual restoration holds great importance for cultural heritage preservation and transmission. This study focuses on the 3D digitization and processing of Terracotta Warrior fragments for neural network analysis. Our dataset was acquired using a Creaform VIU 718 handheld 3D scanner in the Visualization Laboratory. Due to the high resolution of the resulting point clouds, which poses challenges for direct neural network input, we employed a preprocessing step. The Clustering Decimation method, available in the Meshlab tool, was utilized to downsample the point cloud data. This approach effectively preserves structural information while reducing each fragment to a uniform 2048 points. The dataset was categorized according to the anatomical parts of the Terracotta Warriors: arms, heads, legs, and bodies (as illustrated in Fig. 5). The sample distribution across these categories is presented in Table 7. For our experimental protocol, we adopted an 80–20 split, allocating 80% of the data for training and the remaining 20% for testing.

Fig. 5
figure 5

Illustration of the Terracotta Warriors fragments.

Full size image
Table 7 Number of fragments for each class in the Terracotta Warriors fragments dataset
Full size table

Classification of Terracotta Warrior Dataset

To validate the efficacy of our method on real-world 3D Terracotta Warrior fragments, we conducted classification experiments using our dataset. We fine-tuned a pre-trained DGCNN model on the Terracotta Warrior dataset, with the results presented in Table 8. It’s worth noting that research on self-supervised representation learning methods based on Terracotta Warrior point cloud data is scarce. Consequently, our comparisons primarily involve traditional and supervised methods. The highest accuracy achieved by existing traditional methods is 87.64%. Our approach significantly outperforms this benchmark, demonstrating an improvement of 4.46%. Moreover, our method yields competitive results when compared to supervised learning approaches. These experimental outcomes indicate that our technique effectively bridges the gap between supervised and self-supervised learning. It provides a robust set of initial model parameters for the task of Terracotta Warrior fragment classification, thus contributing a valuable research methodology for the virtual restoration of these artifacts. These results not only demonstrate the potential of our method for the specific task of Terracotta Warrior restoration but also suggest its applicability to broader cultural heritage preservation efforts involving 3D artifact reconstruction.

Table 8 Compared with other methods on the 3D Terracotta Warrior fragment datasets
Full size table

Segmentation of Terracotta Warrior Dataset

Segmentation of Terracotta Warriors plays a crucial role in the effective and accurate restoration of cultural relics, particularly in the virtual reconstruction of ceramic artifacts. Unlike the Terracotta fragment classification task, our segmentation study utilizes complete Terracotta Warrior models. We compiled a dataset of 150 complete Terracotta models using 3D scanners and data augmentation techniques, and all terracotta warriors models are uniformly downsampled into 4096 point clouds. Traditionally, the three-dimensional model of a Terracotta Warrior is divided into six parts: head, body, left arm, right arm, left leg, and right leg. However, to enhance the restoration process and rigorously evaluate our method’s performance, we manually annotated the original Terracotta models into eight distinct segments: head, body, left hand, left arm, right hand, right arm, left leg, and right leg. We employed an 8-2 split for our dataset, allocating 80% for training and 20% for testing. To validate the effectiveness of our approach in segmenting Terracotta Warriors, we fine-tuned a pre-trained Dynamic Graph CNN (DGCNN) on our Terracotta Warriors dataset. The segmentation results are presented in Table 9. The empirical evidence demonstrates that our approach significantly outperforms existing unsupervised segmentation methods for Terra-cotta warriors. Specifically, our method achieves improvements of 6.8% and 3.8% in segmentation accuracy compared to SRG(DGCNN) and EGG(DGCNN), respectively. The resulting segmentation outcomes are illustrated in Fig. 6. The visual results demonstrate that our method achieves high-quality segmentation, effectively distinguishing between the eight predefined parts of the Terracotta Warriors. These results not only showcase the capability of our method in accurately segmenting Terracotta Warrior models but also highlight its potential in facilitating more precise virtual restoration processes. The improved granularity of segmentation (eight parts instead of six) allows for more detailed analysis and reconstruction, potentially leading to more accurate and comprehensive restoration outcomes.

Table 9 Comparison of different methods on Terracotta Warrior dataset
Full size table
Fig. 6
figure 6

PointMoment segmentation results on Terracotta Warrior Datasets.

Full size image

Conclusion

The digital preservation of cultural heritage has become increasingly crucial in our technologically advancing world. This paper has explored the application of point cloud self-supervised learning technology to the Terracotta Warriors, introducing high-order mixed moments as an innovative approach to enhance feature characterization while reducing redundant information in high-dimensional embedded features. Firstly, our research demonstrates the significant potential of high-order mixed moments in feature redundancy reduction. By effectively minimizing redundant information in high-dimensional embedded features, we have developed a feature extractor with superior representational capabilities. This approach results in more independent and compact representational information, which is crucial for accurate analysis and restoration of complex artifacts like the Terracotta Warriors. Secondly, a key advantage of our method is its ability to address the model collapse problem inherent in self-supervised learning without resorting to complex techniques such as asymmetric network frameworks. This simplification in implementation, while maintaining robust performance, represents a significant step forward in the field of self-supervised learning for 3D data. Furthermore, extensive testing on multiple downstream tasks using existing public datasets has validated the versatility and effectiveness of our technique. The competitive results achieved across various applications underscore the broad applicability of our approach beyond the specific context of cultural heritage preservation. Notably, when applied to the Terracotta Warriors dataset, our method has shown remarkable performance, outperforming existing approaches in both fragment classification accuracy and segmentation precision. These results are particularly significant given the complexity and historical importance of the Terracotta Warriors. The improved accuracy in classification and segmentation can potentially lead to more precise virtual restorations and deeper insights into the manufacturing techniques and artistic styles of ancient China. Looking ahead, we recognize that the computational complexity of calculating high-order mixed moments is a challenge that requires further improvement. To address this, we plan to explore more efficient algorithms to approximate or estimate high-order mixed moments. Our initial idea is to utilize feature decomposition techniques to decompose high-order mixed moments into combinations of lower-order moments, thereby reducing computational complexity. Additionally, we can employ block processing techniques to divide large-scale data into smaller chunks, compute each separately, and then combine the results. This approach would reduce memory usage and improve computational efficiency. Furthermore, we intend to perform random sampling on the final result matrix based on existing high-order mixed-moment algorithms. By avoiding the inclusion of all matrix elements in the loss calculation, we can significantly reduce computational complexity. Specifically, we plan to adopt Monte Carlo sampling techniques to randomly select a subset of matrix elements for estimation, approximating the true values. We will then apply weighted sampling according to the importance of feature variables to ensure that the impact of key features is fully considered. Finally, during backpropagation, we will compute gradients only for the important sampled points, further reducing computational load. This continued research aims to optimize the performance of our methods and push the boundaries of what’s possible in digital cultural heritage preservation. Additionally, we anticipate that our approach could be extended to other types of 3D cultural artifacts, potentially opening up new possibilities in the field of virtual museums and digital archiving. In conclusion, our work not only presents a novel technical approach but also demonstrates the transformative potential of interdisciplinary research combining computer science and archaeology. As we continue to refine and expand these techniques, we move closer to a future where our cultural heritage is not only preserved but also made more accessible and understandable through advanced digital technologies. The success of our method in both general point cloud tasks and specific Terracotta Warrior applications underscores the potential of high-order mixed moments as a powerful technique for point cloud representation learning, opening up new avenues for research in self-supervised learning for 3D data across various domains.