Dual-stream multi-layer cross encoding network for texture analysis of architectural heritage elements

Abstract

Texture provides valuable insights into building materials, structure, style, and historical context. However, traditional deep learning features struggle to address architectural textures due to complex inter-class similarities and intra-class variations. To overcome these challenges, this paper proposes a Dual-stream Multi-layer Cross Encoding Network (DMCE-Net). DMCE-Net treats deep feature maps from different layers as experts, each focusing on specific texture attributes. It includes two complementary encoding streams: the intra-layer encoding stream efficiently captures diverse texture perspectives from individual layers through multi-attribute joint encoding, while the inter-layer encoding stream facilitates mutual interaction and knowledge integration across layers using a cross-layer binary encoding mechanism. By leveraging collaborative interactions between both streams, DMCE-Net effectively models and represents complex texture attributes of architectural heritage elements. Extensive experimental evaluations on architectural heritage datasets and three texture databases demonstrate that DMCE-Net achieves superior performance compared to existing deep learning methods and handcrafted features, providing reliable texture representations.

Introduction

Architectural heritage¹ is a vital component of human culture and history, and its preservation, particularly through digital means, is of utmost importance. These structures embody profound cultural, historical, and artistic values. By applying texture analysis to architectural images, we can not only provide quantitative support for academic research but also offer the public a deeper and more nuanced understanding of their historical significance². Texture³ is a crucial visual feature of building surfaces, offering key insights into a structure’s materials, design, style, and even its historical context. For instance, surface features such as bricks, stone, wood, and carvings—commonly found in ancient buildings—reflect distinct craftsmanship and techniques. Texture⁴ analysis not only aids in extracting detailed surface information but also helps in identifying various architectural elements and their stylistic characteristics. Moreover, this process contributes to the intelligent processing of large-scale datasets. Related intelligent applications^5,6, such as visual question-answering systems^7,8 and cross-modal fusion⁹ can assist non-experts in accurately classifying and recognizing architectural heritage. Ultimately, these technologies provide more refined and effective tools for the preservation of cultural heritage.

As illustrated in Fig. 1, visual texture¹⁰ refers to the structured patterns on an object’s surface, which may appear either regular or random. These patterns result from the complex interplay of surface details, inherent structures, lighting conditions, and material properties, conveying vital information about the object’s composition, shape, and structural characteristics. The surfaces of architectural heritage structures are particularly rich in intricate texture details. Robust texture analysis methods are crucial for effectively addressing the fundamental challenges posed by inter-class similarity and intra-class variability in the classification of architectural heritage elements (AHE). However, designing effective texture features remains a significant challenge in image analysis, as texture images often exhibit a wide variety of complex, both regular and irregular, patterns. Moreover, these textures are highly sensitive to changes in imaging conditions, including illumination, scale, rotation, viewpoint, and blur. To tackle these issues, a wide range of texture recognition methods have been proposed and applied across diverse domains in recent years. Broadly, these methods can be divided into two main categories: those based on handcrafted features, developed with deep expertise from domain specialists, and those that utilize deep features learned automatically by deep neural networks.

Fig. 1: Texture images of architectural heritage elements.

This figure presents representative texture image samples, illustrating the visual diversity and material complexity of architectural heritage elements.

The binary pattern method^11,12 captures local texture features by analysing the difference between neighboring pixels and the central pixel. As one of the most successful handcrafted texture descriptors, it offers several advantages, including a simple theoretical implementation, low feature dimensionality, and robustness to monotonic illumination changes. In recent years, deep neural networks have exhibited remarkable performance advantages in image classification. Consequently, researchers have increasingly explored their applications in texture attribute analysis within the domain of texture classification. Specifically, Zhai et al.¹³ proposed a deep structure-revealed network (DSR-Net) which leveraged the spatial dependencies captured by the deep network as a structural representation for texture recognition. Khwaja et al.¹⁴ proposed a LM trained multi-layer perceptron neural network structure optimization algorithms for defective texture classification. A multi-scale boosting feature encoding network¹⁵ was proposed to address the challenge of scale variation and improve texture recognition accuracy. Literature¹⁶ analysed the impact of global pooling measurements and developed RANKGP-CNN, demonstrating that layers at different depths could provide high-quality texture information. Wu et al.¹⁷ designed a trimmed texture convolutional neural network for automatic texture exemplar extraction across a variety of texture objects, scales, and regularities under diverse conditions.

Recently, researchers have started integrating the strengths of handcrafted features into neural networks, leading to the development of a series of advanced hybrid frameworks. Lee et al.¹⁸ combined the advantages of hand-crafted feature preprocessing and shallow neural networks to develop ILBPSDNet for real-time character recognition. Reference¹⁹ analysed deep convolutional neural networks to extract precise and robust latent features based on entropy for texture representation and plant species identification. Florindo et al.²⁰ proposed ELMP-Net, which constructs a two-layer mapping and uses the learned parameters to transform the original image, achieving competitive performance compared to state-of-the-art approaches. The author also designed fractal pooling²¹, which uses fractal dimension of the feature map to capture more complex, multiscale, and non-linear relationships. In addition, the tailored design of modules for texture attributes has further broadened the potential applications of deep networks in texture analysis. Chen et al.²² proposed deep tracing patterns that trace features generated along the convolutional layers, achieving a highly discriminative and robust global feature representation for texture descriptors. Lyra et al.²³ employed a hierarchical application of deep filter bank modules combined with Fisher vector pooling, proposing a multilevel pooling scheme for texture classification and Brazilian plant species identification. Pavlopoulos et al.²⁴ designed a fuzzy neural network classifier that enhances the effectiveness of texture feature analysis in ultrasonic liver images. Saihood et al.²⁵ proposed a guided attention-based fusion method for lung nodule classification by leveraging multi-orientation local texture features, enabling the extraction of more fine-grained discriminative information within the nodule volume. This approach not only improves classification performance but also provides strong support for the practical needs of medical experts. Reference²⁶ proposed a coarse-to-fine contrastive self-supervised learning framework for pixel-level texture analysis of low-resolution remote sensing images. Reference²⁷ proposed a dual-branch hybrid encoding embedded network to extract diverse pathological texture features, enabling efficient classification of histopathological images. Moinuddin et al.²⁸ designed a texture-compensated multi-resolution convolutional neural network to prevent over-smoothing and preserve both structural and textural information. Reference²⁹ proposed a structure-aware infrared and visible image fusion network, which effectively mitigates the loss of texture details in the fused images. It is evident that deep network frameworks demonstrate remarkable performance advantages in the field of texture analysis, thereby offering a solid theoretical foundation for their application in related domains.

In recent years, the application of texture feature analysis^30,31,32 has become increasingly widespread in the study of ancient relics. Andreetto et al.³³ proposed an automatic 3D modeling approach for textured cultural heritage objects to address the cost challenges associated with cultural heritage modeling. Reference³⁴ developed deterioration identification models for stone cultural heritage based on hyperspectral image texture features to distinguish between various types of deterioration. Earl et al.³⁵ presented the archaeological applications of polynomial texture mapping, a technique that allows for the recording and representation of subtle surface details. Reference³⁶ trained convolutional neural network (CNN) on Cypriot-built heritage to classify the architectural style of built heritage in 3D. Fan et al.³⁷ proposed to combine attached textual descriptions to perform intangible cultural heritage image classification. Li et al.³⁸ proposed LBCapsNet to extract features from images of porcelain artifact fragments, effectively handling unique textures and providing technical support for the digital preservation and restoration of cultural heritage. Clearly, texture analysis holds substantial potential in the classification of AHE. With the rapid advancements in image processing technology and deep learning, researchers can gain deeper insights into the evolution, structural characteristics, and possible damage of buildings by classifying and analysing images of architectural heritage, thereby offering a scientific foundation for conservation and restoration efforts.

This paper presents the design of a deep network framework aimed at capturing multi-view texture attribute information to address the challenges of subtle inter-class differences and significant intra-class variations in texture analysis. The proposed framework is applied to the classification of AHE. Specifically, we introduce the Dual-stream Multi-layer Cross Encoding Network (DMCE-Net), with the following key contributions:

• 1. To effectively address the inherent challenges of high inter-class similarity and significant intra-class variability in AHE, the proposed DMCE-Net introduces two complementary feature encoding streams: an intra-layer encoding stream and an inter-layer encoding stream.

• 2. The intra-layer encoding stream is dedicated to capturing multi-level texture information from the perspective of individual expert layers and achieves efficient fusion of diverse texture representations through a novel multi-attribute joint encoding strategy.

• 3. The inter-layer encoding stream focuses on facilitating mutual learning among texture cues across different expert layers and introduces a cross-layer binary encoding mechanism to enable effective integration of multi-level texture perspectives

• 4. Extensive experiments on AHE dataset and three challenging texture databases demonstrate that the proposed MCBE-Net achieves a compact and highly discriminative texture representation. Furthermore, it surpasses state-of-the-art methods in classification performance, exhibiting particularly remarkable advantages in AHE dataset.

The remainder of the paper is organized as follows: Section “Methods” introduces the related methods, including the basics of CNN, the architecture and strategy of the proposed DMCE-Net. Results are given in Section “Results”. The discussion is drawn in Section “Discussion”.

Methods

Review of CNN

Classical deep neural networks tackle complex problems by alternately connecting convolutional and pooling layers followed by one or more fully connected layers at the end. They learn features by training network parameters on large datasets. The core concept is to extract local features from the image using convolution operations and progressively capture higher-level, more abstract features through the cascade of multiple convolutional layers, thereby enabling effective image understanding and classification.

The convolutional layer is the core building block of a neural network. It extracts local features from the input image using convolutional kernels, followed by element-wise nonlinear activation. The activation of the ith feature map in the lth layer can be expressed as:

$${F}_{i}^{l}=\mathop{\sum }\limits_{j}g({w}_{i,j}^{l}\ast {F}_{j}^{l-1}+{b}_{i}^{l})$$

(1)

where $\ast$ is the convolutional operation. ${F}_{j}^{l-1}\in {{\mathbb{R}}}^{p\times q}$ is the output of ${(l-1)}^{th}$ layer, and it is also the input to the ${l}^{th}$ layer. ${w}_{i,j}^{l}$ is the ${i}^{th}$ convolutional kernel of the ${l}^{th}$ layer. ${b}_{i}^{l}$ is the corresponding bias. $g(g)$ is nonlinear activation function.

Then the feature map vector of the lth layer is represented as:

$${{\bf{F}}}^{l}=g({{\bf{w}}}^{l}\ast {{\bf{F}}}^{l-1}+{{\bf{b}}}^{l})$$

(2)

where ${{\bf{w}}}^{l}$ is a set of convolutional kernels in the ${l}^{th}$ layer. ${{\bf{F}}}^{l-1}$ is the feature map vector of the ${(l-1)}^{th}$ layer, and ${{\bf{b}}}^{l}$ is the corresponding bias vector of the ${l}^{th}$ layer.

Typically, a pooling layer is applied after the convolutional layer. Pooling operations are a crucial local mechanism in neural networks, helping to reduce overfitting and enhance generalization. By effectively aggregating local information, they preserve the invariance of deep features to translation and slight local distortions. The pooling operation is represented as:

$${Z}_{i}^{l}={P}_{p}({F}_{i}^{l})$$

(3)

where ${Z}_{i}^{l}$ is the ${i}^{th}$ pooling feature map of the ${l}^{th}$ layer. ${P}_{p}(g)$ is the type of pooling operation, such as max, average, and spatial pyramid pooling.

As illustrated in Fig. 2, CNNs extract deep features of an image in a hierarchical, layer-by-layer manner. The convolutional operations in the lower layers capture relatively simple, low-level features, while deeper layers progressively capture more abstract and semantic information. Unlike general images, texture images have distinct characteristics. On one hand, most of the recognizable features in texture images are low-level features derived from basic pixel information. On the other hand, textures, as crucial elements reflecting the local structure and surface patterns of an image, often display contradictory properties, such as both regularity and randomness, making their underlying attributes difficult to capture. This creates challenges for neural networks designed for general image processing when tasked with texture analysis.

Fig. 2: Typical architecture of CNN.

This figure illustrates the standard architecture of a convolutional neural network (CNN), widely adopted for image classification. The model consists of an input layer, a sequence of convolutional and pooling layers, and one or more fully connected layers leading to the final classification output.

Considering the unique nature of texture images, this paper proposes a deep network framework with adaptability to texture attributes, motivated by the following key factors:

• 1. In neural networks, lower-layer convolutional kernels typically capture relatively simple image attributes, and these basic low-level features are essential for texture recognition. Traditional networks that rely solely on deep features are not well-suited for texture analysis. Therefore, designing effective methods to properly harness the key texture information contained in shallow feature maps is crucial for the texture recognition tasks.

• 2. Although classical pooling schemes are effective local operations, they are not well-suited for texture attributes that depend on pixel-level information. The traditional Local Binary Pattern (LBP) approach offers an efficient technique for capturing texture features. Therefore, integrating the concept of binary patterns into the information processing of deep feature maps is crucial for effectively capturing texture attributes within deep learning frameworks.

• 3. The neural network framework is capable of extracting texture features at various levels. Convolution operations in the lower layers capture relatively simple texture features, while deeper layers use higher-level convolutional kernels to combine and abstract more complex texture patterns. In recent years, the concepts of dual-stream and cross-layer encoding have attracted widespread attention in computer vision fields such as object tracking^39,40 due to their powerful capability of representing multi-level abstract features. However, these approaches have been scarcely explored in the field of texture analysis. Texture is both a local perceptual feature and a global property. Therefore, achieving dual-stream feature learning across different regions and levels, while considering both the fine details and overall patterns of textures, is crucial for improving the recognition of complex textures.

Intra-layer encoding stream

In deep neural networks, convolutional kernels at different depths capture feature attributes at progressively higher levels of abstraction. Shallow feature maps primarily represent simple low-level features, while deeper feature maps extract increasingly abstract and intricate texture patterns.

To preserve feature attributes as comprehensively as possible, this paper extracts $K$ layers of feature map tensors from the deep network framework (e.g., AlexNet⁴¹, VGGNet⁴²), each denoted as ${{\bf{F}}}^{k}$.$k=1,2,\cdots ,K$ is the index of the mapping layer. Here, we treat the deep feature maps from different layers as domain experts, each possessing unique preferences for specific feature perspectives and contributing discriminative texture cues from various depth levels. Taking VGG19 as an example, we extract feature maps from $K=4$ layers of VGG-VD19 (i.e., “conv2-2”, “conv3-4”, “conv4-4”, and “conv5-4”), denoted as follows: ${{\bf{F}}}^{1}\in {{\mathbb{R}}}^{112\times 112\times 128}$ ${{\bf{F}}}^{2}\in {{\mathbb{R}}}^{56\times 56\times 512}$ ${{\bf{F}}}^{3}\in {{\mathbb{R}}}^{28\times 28\times 512}$ and ${{\bf{F}}}^{4}\in {{\mathbb{R}}}^{14\times 14\times 512}$. It is evident that the spatial dimensions of different convolutional layers vary, which presents a challenge for the encoding mechanisms proposed in this paper.

To address this, bilinear interpolation is applied for down-sampling, ensuring that feature maps from different layers are unified to a consistent spatial resolution, denoted as s×s. For VGG19, s is set to 14. Furthermore, to reduce both computational complexity and feature dimensionality, an expert-level average reduction strategy is employed, as shown in Fig. 3. Following this operation, the number of feature maps for each layer is reduced and denoted as N. This reduction is applied to the feature maps corresponding to each expert perspective. The resulting processed feature maps can be expressed as: ${\widehat{{\bf{F}}}}^{1}\in {{\mathbb{R}}}^{s\times s\times N}$,${\widehat{{\bf{F}}}}^{2}\in {{\mathbb{R}}}^{s\times s\times N}$,${\widehat{{\bf{F}}}}^{3}\in {{\mathbb{R}}}^{s\times s\times N}$ and ${\widehat{{\bf{F}}}}^{4}\in \in {{\mathbb{R}}}^{s\times s\times N}$.

Fig. 3: The illustration of Expert Perspective Feature Mapping Layer.

This figure illustrates the basic structure of the Expert Perspective Feature Mapping Layer. The gray blocks represent Convolution followed by ReLU activation, the orange blocks indicate Pooling operations, the light blue blocks denote Fully Connected layers followed by ReLU, the green block corresponds to the Softmax layer, and the dark blue blocks represent the resulting Expert Perspective Feature Mappings.

To ensure that the network effectively captures the texture cues perceived by each expert perspective layer, this paper introduces the intra-layer encoding stream. In this stream, each layer’s feature map undergoes independent intra-layer binary encoding strategy based on the local mean, allowing for the extraction of local texture attributes. Notably, this proposed strategy offers a simple yet efficient means of representing local texture information. It is applied to each local feature map ${\widehat{F}}_{i}^{k}$ in layer$k,k=1,2,3,4$, and get the intra-layer sign binary mapping $Intra\_S{M}_{i}^{k}$, formulated as follows:

$$Intra\_S{M}_{i}^{k}=\text{sign}({\widehat{F}}_{i}^{k}-mean({\widehat{F}}_{i}^{k}))$$

(4)

where $mean(g)$ is the adaptive encoding threshold, is equal to the mean of all points in the local feature map ${\widehat{F}}_{i}^{k}$. It is worth noting that in this study, the mean value is consistently used as the threshold for binary encoding. The main reason lies in its statistical significance - the mean serves as a global measure of central tendency, making it a suitable reference for partitioning when the distribution of texture attributes is approximately symmetrical. This choice also offers the advantages of simplicity in implementation and computational efficiency. And $\text{sign}(g)$ is the sign function, defined as

$$\text{sign}(x)=\left\{\begin{array}{l}1,x > 0\\ 0,otherwise\end{array}\right.$$

(5)

Then for the layer $k,k=1,2,\cdots ,K$, we can get four independent intra expert perspectives sign mapping tensor, denoted as ${\bf{I}}{\bf{n}}{\bf{t}}{\bf{r}}{\bf{a}}{\boldsymbol{\_}}{\bf{S}}{{\bf{M}}}^{k},k=1,2,\cdots ,K$. To enable the effective fusion of multiple independent sign mappings, this paper proposes a novel multi-attribute joint encoding strategy, as illustrated in Fig. 4. This strategy re-encodes the sign mappings derived from different expert layers into a unified, integrated sign pattern code. To facilitate histogram-based feature statistics, the resulting sign pattern code is further converted into its decimal form, computed as follows:

$$\begin{array}{lll}Intra\_SM{P}_{i}&=&\mathop{\sum }\limits_{k=1}^{K}{2}^{k-1}gIntra\_S{M}_{i}^{k}\\ &=&{2}^{0}gIntra\_S{M}_{i}^{1}+{2}^{1}gIntra\_S{M}_{i}^{2}+\cdots +{2}^{K-1}gIntra\_S{M}_{i}^{K}\end{array}$$

(6)

Fig. 4: The illustration of Intra-layer Encoding Stream.

This figure presents the core structure of the Intra-layer Encoding Stream. First, each convolutional layer’s feature map is independently processed using an intra-layer binary encoding strategy based on local mean values, aiming to capture fine-grained local texture patterns. Second, this process yields four independent intra expert perspectives sign and magnitude mapping tensors. Last, we concatenate the intra-layer sign and magnitude encoding feature vectors to obtain the final feature vector.

It is worth noting that, for histogram representation, formula (6) converts the binary-coded $Intra\_SM$ into its decimal form$Intra\_SMP$, where the weight ${2}^{k-1}$ is primarily used to facilitate the conversion from binary code to decimal value.

Furthermore, we utilize the histogram of $Intra\_SM{P}_{i}$ to construct feature histograms $H(Intra\_SM{P}_{i})$ and concatenate the histograms of I channels to form the intra-layer sign encoding feature vector, represented as:

$$HS\_Intra=[H(Intra\_SM{P}_{1}),H(Intra\_SM{P}_{2}),\mathrm{..}.,H(Intra\_SM{P}_{I})]$$

(7)

Inspired by Completed Local Binary Pattern (CLBP)¹², in addition to the intra-expert perspectives sign mapping tensor, we also design an intra-expert perspectives magnitude mapping tensor to provide complementary local texture information. Specifically, the intra-layer magnitude difference mapping $Intra\_M{D}_{i}^{k}$ is defined as follows:

$$Intra\_M{D}_{i}^{k}=abs({\widehat{F}}_{i}^{k}-mean({\widehat{F}}_{i}^{k}))$$

(8)

where $abs(g)$ is the absolute value operation.

Furthermore, to obtain the binary encoding, the mean of $Intra\_M{D}_{i}^{k}$ is used as the encoding threshold for$Intra\_M{D}_{i}^{k}$, which is defined as follows:

$$Intra\_M{M}_{i}^{k}=t(Intra\_M{D}_{i}^{k}-mean(Intra\_M{D}_{i}^{k}))$$

(9)

where $t(g)$ is the binarization threshold function, defined as $t(x-c)=\left\{\begin{array}{l}1,x > c\\ 0,otherwise\end{array}\right.$.

Similar to the previous step, the resulting magnitude pattern code is also converted into its decimal form, which is computed as follows:

$$\begin{array}{lll}Intra\_MM{P}_{i}&=&\mathop{\sum }\limits_{k=1}^{K}{2}^{k-1}gIntra\_M{M}_{i}^{k}\\ &=&{2}^{0}gIntra\_M{M}_{i}^{1}+{2}^{1}gIntra\_M{M}_{i}^{2}+\cdots +{2}^{K-1}gIntra\_M{M}_{i}^{K}\end{array}$$

(10)

Furthermore, we compute the histogram of $Intra\_MM{P}_{i}$ to construct feature histograms $H(Intra\_MM{P}_{i})$, and concatenate the histograms across I channels to form the intra-layer magnitude encoding feature vector, denoted as:

$$HM\_Intra=[H(Intra\_MM{P}_{1}),H(Intra\_MM{P}_{2}),\mathrm{..}.,H(Intra\_MM{P}_{I})]$$

(11)

It is noteworthy that histogram fusion is adopted for feature vector construction due to its statistical integration capability at the distribution level. By aggregating histograms obtained from multiple binary encoding patterns, the fusion process effectively balances local variations and mitigates the bias associated with any single encoding scheme. Consequently, the resulting feature distribution becomes more representative and robust, reducing the impact of sample-specific randomness and enhancing the discriminative power across diverse samples.

As shown in Fig. 4, we concatenate the intra-layer sign and magnitude encoding feature vectors to obtain the final feature vector, denoted as:

$$H\_Intra=[HS\_Intra,HM\_Intra]$$

(12)

Intra-layer encoding stream

To facilitate mutual learning and interaction of key texture attributes across different expert layers, this paper introduces the inter-layer encoding stream. In contrast to the intra-layer encoding stream, it effectively captures hierarchical representations and models cross-layer dependencies within deep feature mappings. Specifically, the inter-layer encoding stream incorporates a cross-layer binary encoding mechanism, which leverages binary mutual encoding between different expert layers to extract inter-layer binary mappings.

We begin by defining the interaction differences between adjacent expert view layers, denoted as ${D}_{i}^{k}={\widehat{F}}_{i}^{k}-{\widehat{F}}_{i}^{k+1}$. Based on the sign of these interaction differences, a binary mutual sign encoding is then constructed, as formulated below:

$$Inter\_S{M}_{i}^{k}=\text{sign}({D}_{i}^{k})=\text{sign}({\widehat{F}}_{i}^{k}-{\widehat{F}}_{i}^{k+1})$$

(13)

where $k,k=1,2,\cdots ,K$, ${\widehat{F}}_{i}^{k}$ and ${\widehat{F}}_{i}^{k+1}$ are the adjacent different expert mapping layers. $\text{sign}(g)$ is the sign function, defined in formula (5). $Inter\_S{M}_{i}^{k}$ is the resulting inter-layer binary mapping.

As shown in Fig. 5, if four layers of deep feature mappings ${\widehat{F}}_{i}^{k},k=1,2,3,4$ are selected, they will yield three inter-layer binary mapping ${\bf{I}}{\bf{n}}{\bf{t}}{\bf{e}}{\bf{r}}{\boldsymbol{\_}}{\bf{B}}{{\bf{M}}}^{k},k=1,2,3$. To achieve more compact and effective cross-layer feature dependencies, the cross-layer binary encoding mechanism re-encodes the generated inter-layer sign binary mappings into a multi-bit binary code, denoted as

$$\begin{array}{lll}Inter\_SM{P}_{i}&=& \mathop{\sum }\limits_{k=1}^{K-1}{2}^{k-2}\bullet Inter\_S{M}_{i}^{k-1}\\ &=& {2}^{0}\bullet Inter\_S{M}_{i}^{1}+{2}^{1}\bullet Inter\_S{M}_{i}^{2}+\cdots +{2}^{K-2}\bullet Inter\_S{M}_{i}^{K-1}\end{array}$$

(14)

Fig. 5: The illustration of inter-layer encoding stream.

This figure presents the core structure of the inter-layer encoding stream. First, the interaction differences between adjacent expert perspective layers are computed to capture cross-layer feature variations. Then, a cross-layer binary encoding mechanism is applied to generate the corresponding inter-layer sign and magnitude pattern codes, which are used to construct the inter-layer sign and magnitude encoding feature vectors. Finally, these feature vectors are concatenated to form the final inter-layer feature representation.

Furthermore, similar to intra-layer encoding stream, we employ the histogram of $Inter\_SM{P}_{i}$ to build feature histograms $H(Inter\_SM{P}_{i})$ and concatenate the histograms across I channels to construct the inter-layer sign encoding feature vector, described as:

$$HS\_Inter=[H(Inter\_SM{P}_{1}),H(Inter\_SM{P}_{2}),\mathrm{..}.,H(Inter\_SM{P}_{I})]$$

(15)

Analogous to the intra-layer encoding stream, a binary mutual magnitude encoding is devised to capture complementary information derived from the magnitude differences between adjacent layers. Specifically, the inter-layer magnitude difference mapping is defined as follows

$$Inter\_M{D}_{i}^{k}=abs({\widehat{F}}_{i}^{k}-{\widehat{F}}_{i}^{k+1})$$

(16)

Then the inter-layer magnitude difference mapping is defined as:

$$Inter\_M{M}_{i}^{k}=t(Inter\_M{D}_{i}^{k}-mean(Inter\_M{D}_{i}^{k}))$$

(17)

where $t(g)$ is the binarization threshold function. Similar to the previous step, the corresponding inter magnitude pattern code is also converted into its decimal form, computed as:

$$\begin{array}{lll}Inter\_MM{P}_{i}&=&\mathop{\sum }\limits_{k=1}^{K}{2}^{k-1}\bullet Inter\_M{M}_{i}^{k}\\ &=& {2}^{0}gInter\_M{M}_{i}^{1}+{2}^{1}gInter\_M{M}_{i}^{2}+\cdots +{2}^{K-1}gInter\_M{M}_{i}^{K}\end{array}$$

(18)

Furthermore, we compute the histogram of $Inter\_MM{P}_{i}$ to construct feature histograms $H(Inter\_MM{P}_{i})$, and concatenate the histograms across I channels to form the inter-layer magnitude encoding feature vector, denoted as:

$$HM\_Inter=[H(Inter\_MM{P}_{1}),H(Inter\_MM{P}_{2}),\mathrm{..}.,H(Inter\_MM{P}_{I})]$$

(19)

As shown in Fig. 5, we concatenate the inter-layer sign and magnitude encoding feature vectors to obtain the final feature vector, denoted as:

$$H\_Inter=[HS\_Inter,HM\_Inter]$$

(20)

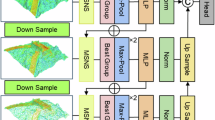
Dual-stream multi-layer cross encoding network

To capture reliable texture cues and distinguish between inter-class similarity and intra-class diversity, this paper proposes a DMCE-Net. It treats feature maps from different layers as expert representations, where the intra-layer stream extracts texture attributes from individual experts, and the inter-layer stream captures joint features through cross-layer interaction. This framework enhances both the discriminative power and interpretability of deep texture representations in complex visual scenes.

Our architecture systematically integrates complementary feature representations through hierarchical feature integration. Specifically, we construct a comprehensive final feature vector $FH$ by concatenating the intra-layer encoding feature vector $H\_Intra$ and the inter-layer encoding feature vector $H\_Inter$, formulated as:

$$FH=[H\_Intra,H\_Inter]$$

(21)

As shown in Fig. 4, for $K=4$, the intra-layer encoding stream generates 4-bit binary codes using a multi-attribute joint encoding strategy, resulting in an intra-layer encoding feature vector with a dimensionality of $32N$. Meanwhile, as shown in Fig. 5, the inter-layer encoding stream produces 3-bit binary codes via a cross-layer binary encoding mechanism, yielding an inter-layer encoding feature vector with a dimensionality of $16N$. Therefore, the final feature vector has a total dimensionality of $48N$. This clearly indicates that the system parameter N, determined by the expert-level average reduction strategy, directly influences the output feature dimensionality of DMCE-Net. A detailed analysis of N is provided in Section “Effect of parameters setting” of this paper.

The technical advantages of the proposed DMCE-Net can be outlined as follows:

• 1. The proposed DMCE-Net regards feature maps from different layers of a deep network as domain experts, each offering a distinct specialized perspective. The dual-stream framework is designed to not only preserve the independence of expert-specific features but also promote mutual learning and interaction of texture attributes across hierarchical levels. This design effectively addresses the challenges posed by inter-class similarity and intra-class variability in texture representation.

• 2. In the intra-layer encoding stream, the proposed intra-layer binary encoding strategy effectively harnesses the advantages of binary encoding to capture fine-grained local texture attributes. Moreover, the multi-attribute joint encoding strategy enables efficient fusion of features from diverse expert perspectives, thereby enhancing the overall expressiveness and robustness of texture representation.

• 3. In the inter-layer encoding stream, the proposed cross-layer binary encoding mechanism cleverly facilitates mutual learning and interaction of texture attributes across different expert perspective layers, offering robust technical support for the unified representation of cross-layer features.

In conclusion, the dual-stream mechanism of DMCE-Net facilitates dual-stream learning across regions and layers, striking a balance between fine details and overall patterns, and ensuring the collaborative optimization of multi-level texture features. This offers a reliable technical approach for the representation and recognition of complex textures.

Results

Experimental setup and database

In our experiments, we employ three widely-used CNN pre-trained frameworks—AlexNet⁴¹, VGG-VD16⁴², and VGG-VD19⁴²—to extract deep feature maps. For AlexNet, feature maps are obtained from three convolutional layers: conv3, conv4, and conv5, with the input images resized to 227 × 227 × 3. For VGG-VD16, we utilize intermediate convolutional layers conv2-2, conv3-3, conv4-3, and conv5-3 to capture deep features. Similarly, for VGG-VD19, feature maps are extracted from four layers: conv2-2, conv3-4, conv4-4, and conv5-4. The input images for both VGG-VD16 and VGG-VD19 are resized to 224 × 224 × 3. All experiments are conducted on a desktop running MATLAB 2024, equipped with a 2.6 GHz CPU and 64 GB of RAM, without GPU acceleration. All experiments in this study employ an SVM classifier. Specifically, we use a linear-kernel SVM based on the LIBSVM⁴³ library with default parameter settings.

As shown in Fig. 6, the experiments in this section involve one challenging AHE dataset and three competitive texture classification datasets: AHE⁴⁴, UIUC⁴⁵, UMD⁴⁶, and CUReT⁴⁷ database.

Fig. 6: The texture samples of four databases.

This figure presents representative texture image samples from the four datasets employed in this study. a It shows samples from the AHE database, containing diverse architectural heritage textures with varying material properties and surface patterns. b It displays samples from the UIUC database, which includes textures captured under uncontrolled imaging conditions with significant variations in scale and orientation. c It presents samples from the UMD database, characterized by complex environmental conditions. d It shows samples from the CUReT database, featuring textures affected by specular reflections and self-shadowing.

The AHE dataset⁴⁴ is a specialized collection designed for the recognition and classification of architectural components found in cultural heritage sites. It contains high-resolution images of various elements—such as columns, arches, windows, cornices, and decorative motifs—captured from a wide range of historical buildings. The dataset poses significant challenges due to variations in scale, viewpoint, illumination, occlusion, weathering, and stylistic diversity across different architectural periods and regions. AHE provides a valuable benchmark for developing and evaluating computer vision algorithms aimed at the visual understanding and preservation of historical structures. The UIUC database⁴⁵ is a widely adopted benchmark for evaluating texture classification algorithms. It comprises 25 texture categories, each containing 40 grayscale images with a resolution of 640 × 480 pixels. The images exhibit considerable variations in scale, viewpoint, illumination, and minor deformations, making the dataset well-suited for assessing the robustness and generalization capability of texture analysis methods. The UMD texture dataset⁴⁶ comprises 25 texture categories, each containing 40 high-resolution images of 1280 × 960 pixels captured under diverse viewpoints, scales, and lighting conditions. The textures feature pronounced 3D structures, non-uniform patterns, and natural appearances, making the dataset particularly well-suited for evaluating the performance of algorithms in real-world texture recognition tasks. The CUReT database⁴⁷ comprises images from 61 texture categories, each containing 92 samples of size 200 × 200 pixels, captured under diverse combinations of illumination directions and viewing angles. The textures span a wide range of real-world materials—including fabric, metal, wood, and stone—and exhibit substantial variations in reflectance properties and surface geometry.

In our experiments, 80% of the samples were randomly selected for training, and the remaining 20% were used for testing. The final classification accuracy was computed as the average over 50 independently randomized dataset splits. Notably, the proposed method leverages pre-trained deep backbone networks without the need for parameter fine-tuning or GPU acceleration. This characteristic results in low computational overhead, thereby enhancing the method’s applicability, scalability, and ease of deployment in resource-constrained environments.

Effect of parameters setting

Before performing the intra-layer and inter-layer encoding stream, the proposed DMCE-Net normalizes feature maps from different depth levels to a unified size of $s\times s\times N$ through down-sampling and an expert-level average reduction strategy. For AlexNet, $s=13$; for VGG-VD16 and VGG-VD19, $s=14$. The parameter N is empirically determined through preliminary experiments. Taking VGG-VD19 as an example, Fig. 8 illustrates the impact of N on the classification performance of DMCE-Net on the AHE database.

As shown in Fig. 7, the classification accuracy increases significantly as the value of N rises from 100 to 190. When N exceeds 190, the performance improvement gradually becomes marginal, reaching its peak at $N=230$. Since the value of N directly determines the final feature dimensionality, we fix N at 230 in this study, considering both classification performance and computational cost. Taking VGG-VD19 as an example, the feature dimension of intra-layer and inter-layer encoding feature vector are $32N=7360$ and $16N=3680$, respectively. Consequently, the final feature vector of DMCE-Net has a total dimensionality of 11040.

Fig. 7: The impact of N on the classification performance of DMCE-Net on the AHE database.

This figure illustrates how varying the number of aggregated channels (N) influences the classification accuracy of DMCE-Net on the AHE database.

Ablation study on AHE database

To validate the effectiveness of the proposed DMCE-Net, as well as its two individual encoding streams—the Intra-layer and inter-layer encoding streams—this section evaluates both the overall classification performance and the per-category results across various AHE types on the AHE database, using three deep backbone networks: VGG-VD19, VGG-VD16, and AlexNet.

Table 1 summarizes the overall classification accuracy of DMCE-Net and its two individual encoding streams employing different backbone networks on the AHE database. For each class, 80% of the sample images were used for training, with the remaining 20% reserved for testing. The reported results represent the mean classification accuracy and variance computed over 50 random dataset splits. As shown in Table 1, DMCE-Net achieves significantly higher classification accuracy compared to its two individual encoding streams. Moreover, the intra-layer encoding stream outperforms the inter-layer encoding stream by a notable margin. For instance, when using VGG-VD19 as the backbone network, DMCE-Net achieves a classification accuracy of 95.27%, which is 0.22% and 2.34% higher than that of the intra-layer and inter-layer encoding streams, respectively.

Table 1 The overall classification accuracy (%) on the AHE database using different backbone network

Figure 8 illustrates the classification accuracy of DMCE-Net and its two individual encoding streams for each category in the AHE database, using VGG-VD19 as the backbone network. As shown, DMCE-Net shows generally higher classification accuracy across most AHE types. Specifically, for category 10 (stained glass), DMCE-Net achieves the highest classification accuracy of 98.87%, outperforming both the intra-layer and inter-layer encoding streams by 0.43%. For the most challenging category, category 7 (flying buttress), DMCE-Net surpasses the intra-layer and inter-layer encoding streams by 1.43% and 6.07%, respectively. Figure 9 illustrates representative visual classification results for samples from distinct categories. It can be observed that DMCE-Net tends to outperform the individual intra-layer and inter-layer encoding streams, particularly in handling complex architectural textures. For example, in Class 8 (gargoyle), the second and fourth samples exhibit pronounced variations in illumination and viewpoint. In these challenging scenarios, relying solely on either the intra-layer encoding stream or the inter-layer encoding stream result in less reliable feature discrimination. By contrast, DMCE-Net, leveraging the complementary strengths of both encoding strategies, achieves correct classification. Notably, for the fourth sample in Class 8 (gargoyle), which contains only a minimal region of discriminative texture features and a large proportion of irrelevant background, none of the three methods yields correct classification. This result highlights a limitation of DMCE-Net when confronted with samples characterized by extensive background interference and extremely sparse target features.

Fig. 8: Category-wise classification results on the AHE database using VGG-VD19 as the backbone network.

This figure presents the classification accuracy for each texture category in the AHE database, obtained using DMCE-Net with VGG-VD19 as the backbone network. Red, green, and blue bar represent the classification results of DMCE-Net, the intra-layer encoding stream, and the inter-layer encoding stream, respectively.

Fig. 9: The classification results of representation images on the AHE database using VGG-VD19 as the backbone network.

This figure presents the classification results of representative samples. The red text in the figure indicates misclassified results, while the black text represents correctly classified results.

To further investigate the classification performance of the proposed model, Fig. 10 presents the confusion matrix obtained by averaging the results of 50 random experiments on the AHE dataset. Overall, the distribution of the confusion matrix exhibits generally good classification performance across most categories, as indicated by the dominance of diagonal elements. This suggests that the model is able to capture and distinguish discriminative features among different classes. However, certain categories exhibit notable confusion, particularly Category 2 (87.47%) and Category 7 (83.75%), whose classification performance is slightly inferior compared to other categories. On one hand, the misclassification rates of Category 2 and Category 7 are relatively high. Specifically, 6.08% of the Category 2 samples were misclassified as Category 3, and 3.03% as Category 7. Similarly, Category 7 showed 3.88% misclassification into Category 2, and 4.57% into Category 3. These results indicate that the model encounters challenges in discriminating between these categories. Further, among all samples predicted as Category 7, 3.02% actually belong to Category 2. This bilateral misclassification highlights the overlap in feature distributions between Category 2 and Category 7, which may lead to ambiguous decision boundaries and increased risk of cross-category errors.

Fig. 10: The confusion matrix of DMCE-Net with VGG-VD19 on the AHE database.

This figure presents the confusion matrix of the proposed DMCE-Net using VGG-VD19 as the backbone network on the AHE database. The results are averaged over 50 random splits to ensure statistical stability and robustness. The matrix illustrates the model’s classification accuracy across all categories, where diagonal elements represent correct predictions and off-diagonal elements indicate misclassifications.

Figure 11 compares the classification performance of the proposed DMCE-Net with its original backbone networks on the AHE dataset. As observed, DMCE-Net shows consistent performance gains over its backbone counterparts. Specifically, DMCE-Net with VGG-VD19 outperforms VGG-VD19 by 2.10%, while DMCE-Net with VGG-VD16 and AlexNet show gains of 1.57% and 8.29%, respectively. These results demonstrate the effectiveness of the proposed DMCE framework leverages texture cues from different expert view layers via the Intra-layer and Inter-layer encoding streams. Furthermore, the integration of the multi-attribute joint encoding strategy and the cross-layer binary encoding mechanism offers a robust approach for enhancing the representation and utilization of deep texture features.

Fig. 11: Comparative analysis of the proposed DMCE-Net and its backbone counterparts on the AHE database.

This figure presents a comparative analysis between the proposed DMCE-Net and its corresponding backbone networks on the AHE database. DMCE-Net consistently outperforms the baseline networks, demonstrating its enhanced capability in capturing fine-grained texture attributes and improving overall classification accuracy.

To further investigate the impact of different feature components on classification performance, Table 2 presents the results of ablation experiments based on various encoding streams. As shown in the table, DMCE-Net achieves the highest average classification accuracy of 95.27% across all categories, achieving higher accuracy than each individual encoding stream or feature component. This result suggests that the dual-stream mechanism and multi-feature representation contribute to enhancing the overall model performance.

Table 2 Classification results of different feature components DMCE-Net with VGG on the AHE Dataset

The Intra-layer Sign encoding stream and Magnitude encoding stream yield classification accuracies of 93.02% and 93.53%, respectively, both lower than that of the full Intra-layer encoding stream. Similarly, the Inter-layer Sign encoding stream and Inter-layer Magnitude encoding stream achieve 90.08% and 92.30%, respectively, which are also relatively lower than the inter-layer encoding stream. These findings suggest that using Sign or Magnitude features independently may lead to incomplete feature representations, while their joint encoding is more effective in capturing discriminative information. Furthermore, the inter-layer encoding stream achieves an average accuracy of 92.93%, slightly lower than the Intra-layer encoding stream, indicating that the cross-layer encoding serves as a complementary feature extractor but may have limited standalone effectiveness.

In summary, the complete DMCE-Net model, by jointly leveraging Intra-layer and inter-layer encoding streams as well as integrating both Sign and Magnitude features, achieves the highest classification accuracy among the tested configurations. The ablation results demonstrate that individual feature branches generally underperform compared to the combined encoding strategy, particularly, the performance degradation is more pronounced when using Sign or Magnitude features alone, emphasizing the critical role of comprehensive multi-feature integration and the cooperative advantage brought by the dual-stream design.

To investigate the impact of the number of encoding layers on classification performance, Table 3 reports results on the AHE dataset using different sets of convolutional layers as feature encoding sources: k = 1,2,3,4；k = 1,2,3 and k = 2,3. The full configuration incorporating four layers achieves the highest average accuracy of 95.27%, showing improved performance over the three-layer (93.04%) and two-layer (89.20%) variants. This clearly underscores the benefit of multi-layer encoding feature integration, where the combination of both shallow and deep representations contributes to improved discriminative power. A class-wise analysis reveals a general decline in accuracy as fewer layers are included in the encoding, with Categories 2, 3, 6, and 7 exhibiting particularly notable drops. For example, the accuracy for Category 3 decreases from 90.45% (four-layer) to 86.65% (three-layer), and further to 76.62% (two-layer). A more severe drop is observed for Category 7, which falls from 83.75% to 70.05%, suggesting that deeper-layer features are especially critical for classes characterized by high intra-class variability or inter-class similarity.

Table 3 Classification results of DMCE-Net with different number of layers on the AHE Dataset

In summary, these results provide evidence for the effectiveness of the complete four-layer DMCE-Net configuration, which enables more comprehensive capture of hierarchical texture attributes ranging from fine-grained local patterns to high-level semantic abstractions. Such multi-level encoding is shown to be essential for achieving robust and accurate classification across diverse texture categories.

Performance comparison on different texture datasets

The UIUC dataset poses significant challenges for texture classification due to its uncontrolled acquisition conditions. Each class exhibits considerable variations in scale, orientation, illumination, and viewpoint, while inter-class similarity in visual patterns and structural appearance leads to limited discriminative cues. Table 4 reports the classification results of DMCE-Net using different backbone networks on the UIUC dataset, averaged over 50 random splits.

Table 4 Category-wise classification accuracy (%) of DMCE-Net with different backbone networks on the UIUC dataset

As shown, DMCE-Net with AlexNet performs slightly below its VGG-VD16 and VGG-VD19 counterparts. Specifically, the DMCE-Net with AlexNet achieves perfect classification on three classes (Classes 7, 16, and 19), while the DMCE-Net with VGG-VD16 and VGG-VD19 correctly classify 16 and 14 classes, respectively. The poorest performance for DMCE-Net with AlexNet is observed on Classes 3 and 14. In contrast, DMCE-Net with VGG-VD16 and VGG-VD19 achieves 100% and 99.50% accuracy on Category 3, respectively. For Category 14, the DMCE-Net with VGG-VD16 and VGG-VD19 outperform the DMCE-Net with AlexNet by 3.25% and 6.00%, respectively. Similar trends are observed across other categories in the dataset. The primary advantage stems from the architectural depth of VGG-VD16 and VGG-VD19, which contain 16 and 19 weight layers, respectively—substantially deeper than the 8-layer structure of AlexNet. This increased depth facilitates the extraction of more complex and abstract hierarchical features, which is essential for capturing fine-grained texture patterns. Moreover, in contrast to AlexNet’s use of large convolutional kernels (e.g., 11 × 11 and 5 × 5), the VGG networks adopt uniform 3 × 3 kernels throughout. This design enables finer localization of texture details and better preservation of discriminative micro-patterns, thereby improving overall texture classification performance.

Figure 12 illustrates the classification performance comparison between the proposed DMCE-Net and state-of-the-art methods (including VisGraphNet⁴⁸, ELMP-Net²⁰, Deep Fractal Interpolation⁴⁹, DSTNet⁵⁰, DeCAF⁵¹ and FC-CNN⁵² with VGGM and AlexNet) on the UIUC dataset. As illustrated in Fig. 10, the proposed DMCE-Net with VGG-VD19 achieves the highest classification accuracy among the compared methods at 99.50%, exceeding the versions based on VGG-VD16 and AlexNet by 0.03% and 2.56%, respectively. Compared to FC-CNN with AlexNet, DMCE-Net with AlexNet achieves an improvement of 5.84%. Moreover, DMCE-Net generally outperforms several recently proposed deep networks for texture classification. Specifically, DMCE-Net with VGG-VD19 surpasses VisGrapNet, ELMP-Net, DSTNet, and DeCAF by 1.50%, 3.20%, 5.90%, and 5.30%, respectively. These results clearly demonstrate the effectiveness of the proposed DMCE-Net in capturing discriminative texture features, attributed to its dual-stream design incorporating intra-layer and inter-layer encoding streams.

Fig. 12: Comparison between DMCE-Net with various backbones and state-of-the-art methods on the UIUC dataset.

This figure compares the classification performance of the proposed DMCE-Net, implemented with different backbone networks, against several state-of-the-art texture classification methods on the UIUC dataset.

The UMD texture classification dataset comprises texture images captured under complex real-world imaging conditions, and is specifically designed to comprehensively evaluate the robustness of texture classification methods with respect to sampling environments, as well as their scale, viewpoint, and illumination invariance. Table 5 summarizes the classification performance of the proposed DMCE-Net using different backbone networks across 25 texture categories in the UMD dataset. As observed, DMCE-Net with AlexNet successfully classified 16 categories, with its lowest accuracy recorded at 97.50% in Category 1. In comparison, DMCE-Net with VGG-VD16 and DMCE-Net with VGG-VD19 both achieved 100% classification accuracy in Category 1. Moreover, DMCE-Net with VGG-VD16 correctly classified 21 categories, whereas DMCE-Net with VGG-VD19 failed to achieve perfect classification in only Category 3 (96.75%) and Category 10 (98.50%). These results clearly indicate that DMCE-Net with VGG-VD19 and VGG-VD16 delivers superior classification performance on the UMD dataset compared to its counterpart based on AlexNet.

Table 5 Category-wise classification accuracy (%) of DMCE-Net with different backbone networks on the UMD dataset

Figure 13 compares the classification performance of the proposed DMCE-Net with state-of-the-art methods reported in the literature. As illustrated in Fig. 13, DMCE-Net with VGG-VD16 achieved the best classification accuracy among the compared methods at 99.89%, slightly outperforming DMCE-Net with VGG-VD19, and surpassing DMCE-Net with AlexNet by 0.52%. Moreover, DMCE-Net with AlexNet improved upon FC-CNN with AlexNet by 3.47% in classification accuracy. Compared to several recently proposed deep learning methods for texture image classification, the proposed DMCE-Net shows a measurable performance advantage. For instance, DMCE-Net with VGG-VD16 outperforms VisGraphNet, ELMP-Net, DSTNet, and DeCAF by 1.49%, 0.69%, 1.39%, and 3.49%, respectively. These results clearly indicate that the proposed DMCE-Net effectively handles the complex imaging condition variations present in the UMD dataset and generally outperforms several state-of-the-art deep learning approaches in terms of classification accuracy. This can be primarily attributed to the Dual-stream architecture of the proposed DMCE-Net, which not only maintains the independence of expert-specific features but also fosters mutual learning and interaction of texture attributes across different hierarchical levels. This design effectively addresses the complex imaging challenges posed by inter-class similarity and intra-class variability in texture representation.

Fig. 13: Comparison between DMCE-Net with various backbones and state-of-the-art methods on the UMD dataset.

This figure presents a comparative evaluation of the proposed DMCE-Net with different backbone networks against several state-of-the-art texture classification methods on the UMD dataset.

To further evaluate the effectiveness of the proposed DMCE-Net in handling complex texture classification tasks, comprehensive experiments were conducted on the CUReT dataset. In addition to its diverse and challenging imaging conditions, CUReT includes a substantial number of images affected by specular reflections and self-shadowing, which introduce additional complexity and serve as rigorous benchmarks for assessing the robustness of texture analysis approaches.

Figure 14 presents the confusion matrix of DMCE-Net with different backbone networks on the CUReT dataset. As illustrated in the figure, DMCE-Net shows generally good classification performance across the majority of texture categories in the CUReT dataset. Even for samples exhibiting high inter-class similarity, the model achieves superior classification accuracy. In particular, for Category 12, DMCE-Net with all three backbone networks (i.e., AlexNet, VGG-VD16, and VGG-VD19) achieves a classification accuracy of up to 99%. However, each of them misclassifies 1% of the samples as Category 31. Similarly, the classification accuracies for Category 31 are 98%, 99%, and 98% for DMCE-Net with AlexNet, VGG-VD16, and VGG-VD19, respectively, with 2%, 1%, and 2% of the samples being incorrectly classified as Category 12. Figure 15 presents example samples from both Category 12 and Category 31, which visually exhibit extremely high inter-class similarity. A similar observation can be made for Category 61 and Category 44. These findings highlight the substantial challenge posed by the extreme inter-class similarity and intra-class variability inherent in texture image classification. The proposed DMCE-Net appears to mitigate this issue by leveraging complementary information derived from expert-specific feature mappings at different depths through intra-layer and inter-layer encoding streams. This design enables more efficient capture of local texture details and allows the model to maintain robust classification performance even under conditions of high inter-class similarity and intra-class variation.

Fig. 14: Confusion matrix of DMCE-Net with different backbones on the CUReT dataset.

This figure shows the confusion matrices of the proposed DMCE-Net using three different backbone networks on the CUReT dataset. a It corresponds to DMCE-Net with AlexNet, b shows the results with VGG-VD16, and c presents the results with VGG-VD19.

Fig. 15: Some sample instances from Category 12 and Category 31 of the CUReT dataset.

This figure displays representative image samples from Category 12 and Category 31 of the CUReT dataset. These two categories are selected to illustrate the visual similarity that often leads to misclassification.

Figure 16 presents a comparison between the highest classification accuracy previously reported in the literature on the CUReT dataset (including MWSN⁵³, SSR⁵⁴, WMACapsNet⁵⁵, FC-VGGVD⁵², FC-VGGM⁵², FC-AlexNet⁵² and Vision Transformer⁵⁶) and the accuracy achieved by the proposed DMCE-Net. As shown in Fig. 16, DMCE-Net with AlexNet achieves the highest classification accuracy among the compared methods on the CUReT dataset, reaching 99.82%, which constitutes a 2.02% improvement over the baseline AlexNet. Similarly, DMCE-Net with VGG-16 outperforms the original VGG-VD16 by 2.59%, while DMCE-Net with VGG-VD19 delivers a 3.47% performance gain compared to its corresponding backbone. These results demonstrate that the proposed DMCE-Net provides an enhancement in texture representation by leveraging mutual learning and cross-encoding mechanisms among expert-level feature mappings at different network depths. In addition to improvements over its own backbones, DMCE-Net also exhibits clear performance advantages compared with other state-of-the-art deep learning methods. For instance, the classification accuracy of DMCE-Net with AlexNet surpasses that of the Vision Transformer by 32.24%. This performance gap is primarily due to the fact that Vision Transformers are better suited for modeling global relationships, whereas texture recognition typically relies on strong local structural awareness. This underscores our choice of convolutional neural networks as the foundational backbone in the proposed framework. The proposed DMCE-Net with AlexNet also surpasses FC-AlexNet by 6.75% in classification accuracy. Moreover, it outperforms MWSN, SSR, and WMACapsNet by 2.48%, 1.20%, and 0.92%, respectively. These experimental provide additional evidence supporting the effectiveness of DMCE-Net’s architectural design. Through the integration of intra-layer and inter-layer encoding streams, the model facilitates mutual learning and joint representation across deep expert mappings. By incorporating the intra-layer binary encoding strategy, multi-attribute joint encoding strategy, and cross-layer binary encoding mechanism, DMCE-Net enables comprehensive and fine-grained learning of diverse texture attributes. Consequently, it contributes to improved discriminative capacity, indicating that it can serve as a promising framework for texture analysis and related applications.

Fig. 16: Comparison between DMCE-Net with various backbones and state-of-the-art methods on the CUReT dataset.

This figure presents a comparative analysis of the proposed DMCE-Net, implemented with different backbone networks, against several state-of-the-art texture classification methods on the CUReT dataset.

Table 6 presents a comparison of the classification accuracy and average running time between representative binary pattern–based methods (including LBP⁵⁷, CLBP¹², SWOBP⁵⁸, and MCLBP+M⁵⁹) and deep learning–based approaches. As observed, the proposed DMCE-Net consistently achieves higher classification accuracy than both categories of methods. In terms of computational efficiency, the feature extraction time of DMCE-Net depends on the choice of backbone network. When employing the lightweight AlexNet backbone, DMCE-Net achieves shorter running time than all binary pattern–based methods, while remaining slightly slower than FC-AlexNet, FC-VGGM, and FC-VGGVD. These results indicate that DMCE-Net is capable of delivering competitive computational efficiency while maintaining superior classification performance.

Table 6 Classification accuracy (%) and average running time (s) on the CUReT dataset

Discussion

To address the challenges of complex inter-class similarity and intra-class variability commonly encountered in architectural textures, this paper proposes a DMCE-Net. The proposed framework treats different feature mapping layers within the deep backbone as expert modules, each capturing distinct domain-specific representations. A dual-stream architecture is introduced, wherein the intra-layer encoding stream facilitates the joint representation of independently learned expert knowledge, while the inter-layer encoding stream enables mutual learning and integration across these expert modules. Comprehensive experiments conducted on the AHE dataset demonstrate that DMCE-Net effectively addresses the intricate texture classification tasks associated with architectural relic surfaces. In addition, evaluation on three benchmark texture classification datasets further validates the robustness of DMCE-Net in handling significant inter-class similarity and intra-class variation across diverse texture scenarios. The integration of a dual-stream architecture, multi-attribute joint encoding strategy, and cross-layer binary encoding mechanism provides a strong theoretical foundation for the effective capture of deep texture attributes. However, this result also highlights a limitation of DMCE-Net when confronted with samples characterized by extensive background interference and extremely sparse target features, which may lead to reduced discriminative power. The demonstrated capability of DMCE-Net in texture analysis has the potential to significantly advance various texture classification applications. Future work will focus on extending this framework to broader domains, such as remote sensing and fine-grained visual recognition.