E(n)-Equivariant cartesian tensor message passing interatomic potential

Abstract

Machine learning potential (MLP) has been a popular topic in recent years for its capability to replace expensive first-principles calculations in some large systems. Meanwhile, message passing networks have gained significant attention due to their remarkable accuracy, and a wave of message passing networks based on Cartesian coordinates has emerged. However, the information of the node in these models is usually limited to scalars, and vectors. In this work, we propose High-order Tensor message Passing interatomic Potential (HotPP), an E(n) equivariant message passing neural network that extends the node embedding and message to an arbitrary order tensor. By performing some basic equivariant operations, high order tensors can be coupled very simply and thus the model can make direct predictions of high-order tensors such as dipole moments and polarizabilities without any modifications. The tests in several datasets show that HotPP not only achieves high accuracy in predicting target properties, but also successfully performs tasks such as calculating phonon spectra, infrared spectra, and Raman spectra, demonstrating its potential as a tool for future research.

Introduction

Molecular dynamics (MD) is a powerful computational technique allowing for the exploration of various physical and chemical phenomena at the atomic level and the study of the behavior of molecules and materials over time. It bridges the gap between theoretical predictions and experimental observations, enabling researchers to gain a comprehensive understanding of the behavior, properties, and interactions of molecules and materials. With sufficient computational resources, first principles calculations based on Density Functional Theory (DFT)¹ can simulate systems with hundreds or even thousands of atoms. However, it struggles when it comes to larger systems. Another approach to computing atomic interactions is empirical force fields, providing much quicker calculations and the ability to handle significantly larger systems. Nevertheless, many of these force fields rely on empirical observations, limiting their applicability to specific ranges and lacking universality and transferability. The machine learning potential (MLP)^{2,3,4,5,6,7,8}, which aim to accurately describe the potential energy surface of atomic configurations, combines the advantages of both DFT and empirical force fields. A well-trained machine learning force field can achieve accuracy close to DFT and even beyond DFT^9,10, and perform very large-scale, long-time simulations, offering a glimpse into the future of research in studying complex dynamical problems.

Most existing machine learning potentials are based on the framework proposed by Behler², which fits the total energy as a sum of atomic energies $E=\sum {E}_{i}$, and the atomic energies are determined by the atomic environment within a certain cutoff radius. This format ensures the scalability of the potential, allowing the network to be trained on small systems and extrapolated to larger systems. The quality of such a model is highly dependent on the choice of descriptors that describe the atomic environments¹¹. A reasonable descriptor should first possess invariance to rotations, translations, and atom permutation; thus, the same atomic environment yields the same atomic energy. A common approach is to construct a series of symmetric functions based on interatomic distances and angles between atoms since these two quantities are naturally invariant under rotations and translations. Depending on the number of atoms involved, a series of so-called two-body and three-body descriptors can be obtained, such as atom-centered symmetry functions (ACSF)^2,12,13, the NEP descriptor^7,14,15,16, the smooth overlap of atomic positions (SOAP)¹⁷, the DeePMD descriptor^5,18. However, these descriptors are not complete¹⁹, as different atomic environments can yield the same descriptor. Atomic cluster expansion (ACE)^6,20 and Moment Tensor Potential (MTP)^4,21 have proposed complete descriptors that can account for interactions of arbitrary order, but the number of descriptors can easily grow to tens of thousands as the order increases. Another issue is that such descriptors are only dependent on the coordinate information within the cutoff radius. When dealing with long-range interactions, simply increasing the cutoff radius would significantly raise computational complexity since the number of atoms is proportional to the cube of cutoff radius.

Message passing network (MPN)²² can help address both of these issues. In the context of MLP, MPN is used to represent molecule or crystal structures as graphs, where atoms are nodes and bonds are edges. The key idea behind MPN is the iterative passing of messages between nodes, allowing information to be exchanged and aggregated. Such message passing processes can, on one hand, lead to the emergence of multiple atoms in the final descriptor (thus, resulting in n-body symmetric functions). On the other hand, it allows information from atoms beyond the cutoff radius to be transmitted to the current atom. As a result, many machine learning potentials based on message passing networks have achieved high levels of accuracy^{8,23,24,25,26,27,28,29,30,31}. It is worth noting that as long as the energy (or other properties) obtained at the end satisfies the symmetry requirements, the messages used in the network do not necessarily have to be scalars^24,32. For example, NequIP⁸, BotNet³⁰, and MACE³¹ utilize high-order tensors based on spherical harmonics in the message passing, coupling them through Clebsch-Gordon (CG) coefficients to construct equivariant networks. These methods have shown significant improvements in accuracy compared to approaches that only use scalar messages. Another category of methods, including PaiNN²⁶ and torchMD-Net²⁸, directly utilize vectors in Cartesian space as messages and obtain equivariant results through a series of designed layers. This approach does not require coupling through CG coefficients, but the vectors are only equivalent to l = 1 tensors in the spherical harmonics method. TeaNet³³ can pass matrices information equivalent to l = 2 tensors, but this introduces a multitude of artificially designed duplications, resulting in a highly intricate network structure that becomes challenging to extend to higher order tensors. Machine learning potential that use tensors of arbitrary orders as messages based on Cartesian coordinates have not been proposed.

In this work, we propose High-order Tensor Passing Potential (HotPP), which can utilize arbitrary order Cartesian tensors as messages. By combining some basic equivariant operations between tensors, all the high-order tensors used in the network are E(n)-equivariant, thus the output is consistent with the rotation of coordinates. In other words, if the output is a scalar, it remains invariant under rotations, while the vector output will rotate in accordance with the rotation of the coordinates, and the matrix output will transform as ${M}^{{\prime} }={RM}{R}^{T}$. Therefore, the method can directly predict high-order tensors such as dipole moments and polarizability tensors without any modifications. We validate HotPP in three prediction tasks: the energies and forces of molecular dynamics trajectory of small molecule; the energies, forces, and stresses of carbon with periodic boundary conditions; and the dipole moments and polarizability tensors of small molecules with coupled cluster singles and doubles (CCSD) accuracy. In these tests, our model achieves good performance with fewer parameters comparable to other high-order models, which provide a frame of equivariant network based on Cartesian coordinates.

Results

Equivariant functions of Cartesian tensors

Cartesian tensors are the tensors that transform under rotations in Euclidean space in a simple way. In other words, a Cartesian tensor is a tensor whose components transform as a product of vectors and covectors under rotations, without any additional factors that depend on the rotation matrix itself. Specifically, a n-th rank tensor transforms under rotation as:

$${{{\boldsymbol{T}}}}_{{i}_{1}{i}_{2}\cdots {i}_{n}}{\to }^{{{\boldsymbol{R}}}}{{{{\boldsymbol{T}}}}^{{\prime} }}_{{i}_{1}{i}_{2}\cdots {i}_{n}}=\left({{{\boldsymbol{R}}}}_{{i}_{1}{j}_{1}}\right)\left({{{\boldsymbol{R}}}}_{{i}_{2}{j}_{2}}\right)\cdots \left({{{\boldsymbol{R}}}}_{{i}_{n}{j}_{n}}\right){{{\boldsymbol{T}}}}_{{j}_{1}{j}_{2}\cdots {j}_{n}}$$

(1)

where R is an orthogonal matrix. Under this definition, it is easy to find that since ${{{\bf{v}}}}_{i}\to {{{\bf{v}}}}_{i}^{{\prime} }={{{\boldsymbol{R}}}}_{{ij}}{{{\bf{v}}}}_{j}$, the vectors are first-order tensors, and the dyadic product of two vectors is a second-order tensor since ${({{\bf{u}}}{{\bf{v}}})}_{{i}_{1}{i}_{2}}{\longrightarrow }^{{{\boldsymbol{R}}}}{({{\bf{u}}}{{\bf{v}}})}_{{i}_{1}{i}_{2}}^{{\prime} }=({{{\boldsymbol{R}}}}_{{i}_{1}{j}_{1}})({{{\boldsymbol{R}}}}_{{i}_{2}{j}_{2}}){({{\bf{u}}}{{\bf{v}}})}_{{j}_{1} \, {j}_{2}}$.

And equivariance is a property of functions or transformations between two spaces, where the transformation preserves the relationships between the elements of those spaces. More formally, a function ${{\rm{\phi }}}:{{\bf{X}}}\to {{\bf{Y}}}$ is said to be equivariant with respect to a group G acting on two sets X and Y if for all $g\in {{\bf{G}}}$ and $x\in {{\bf{X}}}$, we have:

$${{\rm{\phi }}}\left(g^{\circ} \, x\right)=g^{\circ} \, {{\rm{\phi }}}\left(x\right)$$

(2)

This means that applying a function ϕ to an object x and then applying a group element g to the resulting object should give the same result as first applying the group element to the object and then applying the function. And the composition of equivariant maps is also equivariant:

$${{\rm{\psi }}}\left({{\rm{\phi }}}\left(g\circ x\right)\right)={{\rm{\psi }}}\left(g\circ {{\rm{\phi }}}\left(x\right)\right)=g\circ {{\rm{\psi }}}\left({{\rm{\phi }}}\left(x\right)\right)$$

(3)

Therefore, by providing some basic equivariant functions between Cartesian tensors and combining them, we can obtain an equivariant neural network. Here, we use the following three equivariant operations, whose equivariances are proven in the Supplementary Note 1:

• 1. Linear combinations of tensors with the same order: $f\left({T}_{1},{T}_{2},\cdots,{T}_{m}\right)=\sum {c}_{i}{T}_{i}$.

• 2. Contraction of two tensors.

The contraction of tensors is a mathematical operation that reduces the rank of tensors by summing over one or more pairs of indices. For example, consider a 3-order tensor A and a 2-order tensor B, the contraction of them can be ${{{\boldsymbol{C}}}}_{{ijk}}={{{\boldsymbol{A}}}}_{{ijl}}{{{\boldsymbol{B}}}}_{{kl}}$, this will reduce the rank of tensors by 2. More generally, if we sum over more than one pair of indices between an x-order tensor T₁ and a y-order tensor T₂ such as:

$${{{\rm{\phi }}}}_{z}{\left({{{\boldsymbol{T}}}}_{1},{{{\boldsymbol{T}}}}_{2}\right)}_{{a}_{1}\cdots {a}_{x-z}{b}_{1}\cdots {b}_{y-z}}={{{{\boldsymbol{T}}}}_{1}}_{{a}_{1}\cdots {a}_{x-z}{c}_{1}\cdots {c}_{z}}\cdot {{{{\boldsymbol{T}}}}_{2}}_{{b}_{1}\cdots {b}_{y-z}{c}_{1}\cdots {c}_{z}}$$

(4)

We can get a new tensor with $x+y-2z$ order, where $0\le z\le \min (x,y)$. When z = 0, none of the indices are contracted and the Eq. (4) becomes tensor product ${{{\boldsymbol{T}}}}_{{a}_{1}\cdots {a}_{x}{b}_{1}\cdots {b}_{y}}={{{{\boldsymbol{T}}}}_{1}}_{{a}_{1}\cdots {a}_{x}}\cdot {{{{\boldsymbol{T}}}}_{2}}_{{b}_{1}\cdots {b}_{y}}$.

3. Partial derivative with respect to another Cartesian tensor: $\frac{\partial }{\partial {{{\boldsymbol{T}}}}_{{j}_{1}{j}_{2}\cdots {j}_{n}}}$.

By the combination of these operations, we can get many equivariant functions. Many common operations frequently used in other equivariant neural networks that operate on vectors, such as scaling of vectors: ${{\rm{s}}}\cdot \vec{{{\rm{v}}}}$, scalar products $\left\langle \vec{{v}_{1}},\,\vec{{v}_{2}}\right\rangle$, vector products $\vec{{v}_{1}}\times \vec{{v}_{2}}$ (the upper triangle part of $\vec{{v}_{1}}\otimes \vec{{v}_{2}}-\vec{{v}_{2}}\otimes \vec{{v}_{1}}$) can all be viewed as special cases of these three operations. Some other more complex descriptors, such as MTP descriptors^4,21, can also be obtained through combinations of these operations as shown in the Supplementary Note 3.

Equivariant message passing neural network

To obtain an end-to-end machine learning model for predicting material properties, the input should be the positions $\{{{{\bf{r}}}}_{i}\}$ and chemical elements $\{{Z}_{i}\}$ of all atoms, and for periodic crystals, the lattice parameters should also be considered. To apply graph neural networks, we first transform the crystal structure into a graph $\{{n}_{i},{e}_{{ij}}\}$, where each node ${n}_{i}$ corresponds to an atom i in the unit cell, and all atoms j within a given cutoff distance r_cut are considered connected to ${n}_{i}$ labeled with their relative positions r_ij. For periodic structures, since atom j and its equivalent atom j’ may both lie within the cutoff distance of atom i, ${n}_{i}$ may have more than one edge connected to ${n}_{j}$. To extract the information of the nodes, we use the scheme of MPN. A normal MPN can be described as:

$${m}_{i}^{t+1}={\oplus }_{j\in N(i)}{{{\rm{M}}}}_{t}\left({h}_{i}^{t},{h}_{j}^{t},{e}_{{ij}}\right)$$

(5)

$${h}_{i}^{t+1}={{{\rm{U}}}}_{t}\left({h}_{i}^{t},{m}_{i}^{t+1}\right)$$

(6)

where ${h}_{i}^{t}$ is the hidden feature of ${n}_{i}$ at layer t that captures its local information, messages are then passed between nodes along edges, with the message at each edge ${e}_{{ij}}$ being a function ${{{\rm{M}}}}_{t}$ of the features of the nodes connected by that edge. The ⨁ is a differentiable and permutation invariant function such as sum, mean or max to aggregate the message at each node together to produce an updated message ${m}_{i}^{t+1}$ for that node, which in turn is used to update the hidden feature with the function ${{{\rm{U}}}}_{t}$ for the next iteration.

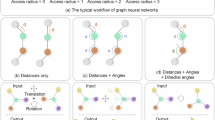
A concrete example illustrating the principles of MPN is presented in Fig. 1. We first determine the connectivity of a structure based on a given cutoff radius and convert it into a graph (quotient graph for periodic structures). Then the messages on the nodes can be passed through the edges by a two-body interaction. As the process of message passing, the information from atoms beyond the cutoff radius can also be conveyed to the central atom. As illustrated in Fig. 1b, the blue arrows represent the first time of message passing, while the yellow arrows denote the second. To be noticed, each layer of message passing is performed simultaneously on all atoms; here, we focus on a specific atom in each layer for ease of analysis. During the initial time of message passing, information of atom 1 is encoded into the hidden information of atom 2. Subsequently, in the second time of message passing, the information of atom 2 including some information of atom 1 is collectively transmitted to atom 3, thereby achieving non-local effects from atom 1 to atom 3. On the other hand, due to the interaction between atom 4 and atom 2 in the second time of message passing also containing the information from atom 1, the effective interaction is elevated from a two-body interaction to a three-body interaction. This indeed encapsulates the two advantages of the message-passing architecture.

Fig. 1: The schematic diagram of message-passing networks.

a the origin structure; b the graph corresponding (a). The blue arrows represent the first time of message passing of the atom 2, while the yellow arrows denote the second time of the atom 3.

However, the scalar hidden feature, message, and edge information (always relatively distance between two atoms) here will limit the expressive capacity and may cause the incompleteness of atomic structure representations. As shown in Fig. 2a and d, if we only use scalar information ${h}_{i}$, ${h}_{j}$, and ${d}_{{ij}}$ to pass the message in Eq. (5) and update the feature in Eq. (6), all nodes will always produce the same embedding information. As a result, the network will be unable to distinguish between these two structures and give the same total energy. Even if the 3-body message includes angles ${\alpha }_{{ijk}}$ are taken into consideration, some structures with only 4 atoms cannot be distinguished²⁶, as shown in Fig. 2b and e. Due to the identical atomic environments within the truncation radius, no matter how many message passing iterations are performed, these two different structures will only yield the same result. To alleviate this problem, a series of models that use high-order geometric tensors during the message passing have been proposed. For example, allowing vectors in the message passing process can differentiate Fig. 2b and e, but in the case of Fig. 2c and f which have different α, the summation in Eq. (5) would cause the network to confuse these two structures (a more detailed explanation can be seen in the Supplementary Note 5). It can be anticipated that increasing the order of tensors in message passing would enhance the expressive power of the network. Previously, the order of high-order tensor networks based on Cartesian space was typically limited to 2^33,34, while our method can work with any order Cartesian tensors. In the following, we use ${\scriptstyle{l}\atop}\!{{\boldsymbol{h}}}_{i}^{t}$ to represent the l-order Cartesian tensor features of node i in the t-th layer, and ${{{\bf{r}}}}^{\otimes n}$ to represent tensor product of a vector r for n times: r⊗r⊗⋯⊗r. In particular, for n = 0 we define this to a learnable function of ${||}{{\bf{r}}}{||}:\,{{{\bf{r}}}}^{\otimes 0}={{\rm{f}}}({||}{{\bf{r}}}{||})$.

Fig. 2: Some structures that cannot be distinguished by message passing networks that do not utilize high-order tensor information.

a, d cannot be distinguished by using two-body scalar information; b, e cannot be distinguished by using three-body scalar information²⁶; and c, f cannot be distinguished by using two-body vector information. c, f have different α and β, so they have the same center of mass but different moment of inertia.

Initialize of node features

The scalar features in the first layer ${\scriptstyle0\atop}\!h_{i}^{0}$ should be invariant to rotation, translation, and permutation of the atoms with the same chemical species. This is also the requirement for most descriptors used in machine learning potentials, so these descriptors such as ACSF, SOAP, ACE, MTP, etc., can be used directly to expedite the process of feature extraction. Here, we used the trainable chemical embedding similar to SchNet²³ to minimize human-designed elements as much as possible. Specifically, the atomic numbers are first encoded by one-hot and then multiplied by a learnable weight matrix, resulting in a learnable embedding for each element Z_i. For high-order features ${\scriptstyle{l}\atop}\!{{\boldsymbol{h}}}_{i}^{0}$ with l > 0, we set them all to 0 at the beginning.

Message and aggregate

To combine the information of neighboring nodes, we need to design a message passing function ${{{\rm{M}}}}_{t}$ in Eq. (5). Considering that the hidden feature ${\scriptstyle{l}_{i}\atop}\!{{\boldsymbol{h}}}_{i}^{t}$, ${\scriptstyle{l}_{j}\atop}\!{{\boldsymbol{h}}}_{j}^{t}$, the bond info ${e}_{{ij}}$, and the target message ${\scriptstyle{l}_{{{\rm{out}}}}\atop}\!{{\boldsymbol{m}}}_{{ij}}^{t+1}$ can be tensors of arbitrary order. Therefore, we need to find an equivariant way to compose the two tensors to a new tensor with different order, and Eq. (4) is such an operation. In our model, we write ${{{\rm{M}}}}_{t}$ in Eq. (5) as:

$${\atop{\scriptstyle{l}_{i},{l}_{r}\!}}{\!\scriptstyle{l}_{o}\atop}{\!{\boldsymbol{\!m}}}_{{ij}}^{t}={{{\rm{M}}}}_{t}\left({{{\boldsymbol{h}}}}_{i}^{t},{{{\boldsymbol{h}}}}_{j}^{t},{{{\boldsymbol{e}}}}_{{ij}}\right)={{{\rm{f}}}}_{l_r}^{t}\left({d}_{{ij}}\right){{\cdot }}{\scriptstyle{l}_{i}\atop}{\!{{\boldsymbol{h}}}}_{j_{a_{1}\cdots {a}_{{l}_{i}{-}{l}_{c}}{c}_{1}\cdots {c}_{{l}_{c}}}}^{t}{{\cdot }}{\left({{{\bf{u}}}}_{{ij}}^{\bigotimes {l}_{r}}\right)}_{{c}_{1}\cdots {c}_{{l}_{c}}{b}_{1}\cdots {b}_{{l}_{r}{-}{l}_{c}}}$$

(7)

Where ${d}_{{ij}}={||}{r}_{{ij}}{||}$ is the relative distance between atom i and atom j, ${{{\bf{u}}}}_{{ij}}=\frac{{{{\bf{r}}}}_{{ij}}}{{d}_{{ij}}}$ is the direction vector, $0\le {l}_{c}\le \min ({l}_{i},{l}_{r})$ is the number of the indices summing up during the contraction. ${{{\rm{f}}}}_{{l}_{r}}^{t}\left({d}_{{ij}}\right)$ is the radial function, which is a learnable multi-layer perceptron of radial basis functions such as Bessel basis and Chebyshev basis. The result is a Cartesian tensor with order ${l}_{o}=|{l}_{i}+{l}_{r}-2{l}_{c}|$, which is between $|{l}_{i}-{l}_{r}|$ and ${l}_{i}+{l}_{r}$. Since ${l}_{r}$ can be chosen arbitrarily, we can obtain an equivariant tensor of order from 0 to any arbitrary order.

We use a summation operation as the aggregation function for the messages in Eq. (5), that is, directly adding all the messages obtained from neighboring nodes. For tensors of the same order obtained from different $({l}_{i},{l}_{r})$, we add them together with different coefficients. Due to the arbitrariness of ${l}_{o}$ and ${l}_{r}$, we need to specify their maximum values. With given ${l}_{{{\rm{omax}}}}^{t}$, ${l}_{{{\rm{rmax}}}}^{{{\rm{t}}}}$, we sum up all possible $({l}_{i},{l}_{r})$:

$${\scriptstyle{l}_{o}\atop}{\!{\boldsymbol{m}}}_{i}^{t+1}={\sum}_{{l}_{r}\le {l}_{{{\rm{rmax}}}}^{t}}{\sum}_{{l}_{i}}{c}_{{l}_{o},{l}_{r},{l}_{i}}{\sum}_{j\in N\left(i\right)}{{{\rm{f}}}}_{{l}_{r}}\left({d}_{{ij}}\right)\cdot {\scriptstyle{l}_{i}\atop}{\!{{\boldsymbol{h}}}}_{j_{{a}_{1}\cdots {a}_{{l}_{i}-{l}_{c}}{c}_{1}\cdots {c}_{{l}_{c}}}}^{t}\cdot {\left({{{\bf{u}}}}_{{ij}}^{\bigotimes {l}_{r}}\right)}_{{c}_{1}\cdots {c}_{{l}_{c}}{b}_{1}\cdots {b}_{{l}_{r}-{l}_{c}}}$$

(8)

Update

For scalar message ${\scriptstyle0\atop}\!m_{i}^{t+1}$, we feed it to a fully connected layer followed by a non-linear activation function to extract the information, and update the hidden feature with residual neural networks:

$${{\scriptstyle0}\atop}\!h_{i}^{t+1}={\scriptstyle0\atop}\!h_{i}^{t}+{{\upsigma }}\left({\scriptstyle0\atop}\!{{\rm{W}}}^{t}({\scriptstyle0\atop}\!m_{i}^{t+1})\right)$$

(9)

Where σ is the nonlinear activation function, ${\scriptstyle0\atop}\!{{\rm{W}}}^{t}$ is a linear layer with bias in the t layer for the scalar message. However, for the tensors above 0 order, both the bias and the activation function will break the equivariance (Supplementary Note 2). Therefore, we only apply bias when l = 0.

For the high-order activation function, as shown in Eq. (3), tensor multiplication by a scalar is equivariant. Hence, we need to find a mapping from an n-order tensor to a scalar. One simple idea is to use the squared norm of the tensor ${{||}{{\boldsymbol{T}}}{||}}^{2}={\sum }_{{i}_{1}\cdots {i}_{l}}{{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}^{2}$ since it is invariant by definition. Therefore, for $l \, > \, 0$, we write the element-wise non-linear function as:

$${\scriptstyle{l}\atop}{\!{\upsigma }}{\left({{\boldsymbol{T}}}\right)}_{{i}_{1}\cdots {i}_{l}}={{{\upsigma }}}^{{\prime} }\left({\scriptstyle{l}\atop}\!{{\rm{W}}}({{||}{{\boldsymbol{T}}}{||}}^{2})\right)\cdot {{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}$$

(10)

It should be noted that different notations σ and σ' were used for the activation function in Eqs. (9) and (10), as the choice of activation function may vary for scalar and high-order tensors. Take the SiLU function ${{\rm{\sigma }}}\left(x\right)=x\cdot {{\rm{sigmoid}}}(x)$ for example and suppose ${\scriptstyle{l}\atop}\!{{\rm{W}}}$ is the identity function. For scalar, SiLU maps x to x itself when $x\gg 0$. However, for higher-order tensors, Eq. (10) will map ${{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}$ to ${{||}{{\boldsymbol{T}}}{||}}^{2}\cdot {{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}$ instead of ${{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}$ when ${{{\boldsymbol{T}}}}_{{i}_{1}\cdots {i}_{l}}\gg 0$. This is because if we apply the formula for higher-order tensors to a scalar, which is ${y}_{i}=\sigma \left({{\rm{W}}}({x}_{i})\right)\cdot {x}_{i}$, an extra ${x}_{i}$ is multiplied. Therefore, if we use SiLU function for ${{\rm{\sigma }}}$, we should use Sigmoid function for ${{\rm{\sigma }}}^{\prime}$. Other activation functions can be handled using a similar approach, and hence the update function for high-order tensors is:

$${\scriptstyle{l}\atop}{\!{\boldsymbol{h}}}_{i}^{t+1}={\scriptstyle{l}\atop}{\!{\boldsymbol{h}}}_{i}^{t}+{\scriptstyle{l}\atop}{\!{\upsigma }}\left({\scriptstyle{l}\atop}\!{{\rm{W}}}^{t}({\scriptstyle{l}\atop}\!{{\boldsymbol{m}}}_{i}^{t + 1})\right)$$

(11)

Readout

For a target n-order property, we utilize a two-layer nonlinear MLP to operate on the n-order tensor at the last hidden layer. For the same reason, bias and element-wise nonlinear functions cannot be used in the high-order tensor.

$${\scriptstyle{l}\atop}\!{{\boldsymbol{o}}}_{i}={\scriptstyle{l}\atop}\!{{\rm{W}}}_{2}\left({\scriptstyle{l}\atop}\right.{{\upsigma }}\left({\scriptstyle{l}\atop}\!{{\rm{W}}}_{1}({\scriptstyle{l}\atop}\!{{\boldsymbol{h}}}_{i}^{t})\right)$$

(12)

Performance of HotPP

We validate the accuracy of our method on a diverse range of systems, including small organic molecules, periodic structures, and predictions of dipole moments and polarizability tensors. For each system, we trained the HotPP model on the commonly used dataset and compared the results with other models. To demonstrate the robustness of our model, most models were trained using the same network architecture shown in Fig. 3 and similar hyperparameters. More training details can be seen in Methods section.

Fig. 3: The architecture of HotPP.

After embedding atomic information into scalars, vectors, and tensors, 4 propagation layers are used to further extract information and outputs the target properties. For higher-order tensors or additional propagation layers, the frame remains similar. The inputs to the network are the atomic numbers Z_i and relative displacements between atoms r_ij. After Embedding layer, the scalar node embedding ${\scriptstyle0\atop}\!h^{0}$ are initialized based on Z_i and the higher order embeddings are set to zero. In each Propagate layer, the inputs are the node embeddings ${\scriptstyle{l}_{{in}}\atop}\!h$ and the filter tensors ${\scriptstyle{l}_{r}\atop}\!f_{{ij}}$ obtained by the Filter layer as ${f}_{{l}_{r}}\left({d}_{{{\rm{ij}}}}\right)\cdot {{{\bf{u}}}}_{{ij}}^{\otimes {l}_{r}}$, where ${d}_{{{\rm{ij}}}}$ is the relative distance and u_ij is the unit vector of r_ij. The output messages ${\scriptstyle{l}_{{out}}\atop}\!m_{i}$ are transformed through a linear layer and activated by the nonlinear function $\sigma$ or $\sigma {\prime}$, dependent on the order of the message tensors. In the Readout layer, the node embeddings are transformed and summed up to get the target properties ${\scriptstyle{l}\atop}\!o$, such as ${\scriptstyle0\atop}\!o$ for energy, and ${}^{1}o$ for dipole.

Small organic molecule

We first test our model on molecular dynamics trajectories of small organic molecules. The ANI-1x dataset^35,36 contains DFT calculations for approximately five million diverse molecular conformations obtained through an active learning algorithm. To evaluate the extrapolation capability of HotPP, we train our model with 70% data from the ANI-1x dataset and test on the COmprehensive Machine-learning Potential (COMP6) benchmark³⁵, which samples the chemical space of molecules larger than those included in the training set. The results are shown in Table 1. Compared to ani-1x, our model has demonstrated superior performance across the majority of prediction tasks.

Table 1 Test results on COMP6 dataset

Periodic systems

After testing HotPP on small molecule datasets without periodicity, we evaluated its performance on periodic systems. We selected the carbon system with various phases as the example³⁷. It is a complicated dataset with a wide range of structures containing structural snapshots from ab initio MD and iteratively extended from GAP-driven simulations, and randomly distorted unit cells of the crystalline allotropes, diamond, and graphite. We show the results in Table 2. Clearly, our model with about 150k parameters demonstrates advantages in predicting forces and virials compared to most models and can achieve accuracy close to l = 3 NequIP model with around 2 million parameters. And when the parameters are expanded to 600k, HotPP achieves the best results on this dataset.

Table 2 Test results on Carbon

Next, we verify the accuracy of our potential in calculating phonon dispersions of diamond, which was not well-predicted in some of the previous models for carbon³⁸. We can obtain the force constant matrix of the structure directly through automatic differentiation $\frac{{\partial }^{2}E}{\partial {r}_{i\alpha }\partial {r}_{j\beta }}$. We used Phonopy Python package^39,40 to calculate the phonon spectrum of diamond and compared it with the results from DFT in Fig. 4. The results show that HotPP can describe the vibrational behavior well. Although there are relatively large errors in the high-frequency part at the gamma point, this could be attributed to the inaccuracy of the DFT calculations within the training dataset. We retrained the model using a more accurate dataset³⁸, and the newly calculated phonon spectrum almost perfectly matches the results from DFT, which demonstrates the reliability of our model.

Fig. 4: Phonon spectrum of diamond.

Phonon dispersion relation for diamond as predicted by HotPP1 (blue dotted) and HotPP2 (red dotted) with comparison to DFT reference data (black solid). The HotPP1 was trained with the dataset GAP2017³⁷, and the HotPP2 was trained with GAP2020³⁸. Source data are provided as a Source Data file.

Dipole moment and polarizability tensor

Since our model can directly output vectors and matrices, we attempted to directly predict the dipole moments and polarizability tensors of structures in the final section. We consider the water systems including water monomer, water dimer, Zundel cation, and liquid water bulk⁴¹. The dipole and polarizability of the aperiodic systems were calculated by CCSD theory and those of liquid water were calculated by DFT. Each system contains 1000 structures and we use 70% of them as a training set and the rest as a testing set. We calculate the RMSEs relative to the standard deviation of the testing samples to compare with previous results obtained by other models^41,42,43 as shown in Table 3 In most cases, HotPP gets the best results except for the polarizability tensor of the water monomer. Compared to T-EANN⁴² and REANN⁴³, HotPP performs particularly well in the case of the dipole moment of liquid water. This may be because they fit the dipole moment by learning ${q}_{i}$ and calculating ${{\boldsymbol{\mu }}}={\sum }_{i=1}^{N}{q}_{i}{{{\bf{r}}}}_{i}$, which is inappropriate for periodic systems. In contrast, the output results of our model are all obtained through relative coordinates and thus we can get rid of the selecting of reference point.

Table 3 Comparison the results obtained by SA-GPR, T-EANN, REANN and HotPP in different water systems

Since now we can obtain the dipole moment and polarizability by HotPP, we can calculate the infrared (IR) absorption spectrum and Raman spectrum for liquid water. We separately trained a machine learning potential to learn the energy, forces, and stresses of liquid water to assist us in conducting dynamic simulations. With this potential, we perform a classical MD simulation under ambient conditions (300 K, 1 bar) for 100 ps and calculate the dipole moment and the polarizability tensor every 1 fs. Then we compute the IR and Raman spectra by Fourier transforming the autocorrelation function (ACF) of them and the results are compared to the experiment data^44,45 as shown in Fig. 5. We can observe that both HotPP model and DeePMD model^46,47 can closely approximate the experimental IR spectra. Our results accurately fit the first three peaks, corresponding to the hindered translation, libration, and H-O-H bending respectively, but there is a long tail in comparison to the experimental data for the O-H stretching mode. This discrepancy may arise from not accounting for quantum effects in our classical molecule dynamic simulation. And for Raman spectra, our model also gives the result in agreement with experimental data.

Fig. 5: Experimental and simulated infrared absorption spectrum and reduced anisotorpic Raman spectra of liquid water under ambient condition.

a The comparasion of the infrared abosption spectrum b The comparasion of the reduced anisotropic Raman spectra. The black circles are the experimental data^44,45, and the lines are calculated with molecular dynamics trajectories performed by HotPP, MB-pol⁵⁶, DeePMD^46,47, and T-EANN⁴². Source data are provided as a Source Data file.

Discussion

In this work, we introduce HotPP, an E(n) equivariant high-order tensor message passing network based directly on Cartesian space. Compared to other Cartesian-space based high-order tensor networks, HotPP can utilize tensors of arbitrary order, providing enhanced expressive power. In contrast to high-order tensor networks based on spherical harmonics and coupled with CG coefficients, HotPP employs simple tensor contraction operations, resulting in a reduced number of parameters and better computational efficiency for small l (Supplementary Note 6). Moreover, the network’s output can be any-order tensor, enabling convenient prediction of vector or tensor properties. With its ability to achieve high accuracy while saving substantial computational time compared to first-principles calculations, HotPP holds great promise in scenarios such as molecular dynamics simulations and structure optimizations, where exploration of potential energy landscapes is essential. In future work, we would investigate approaches to eliminate redundancies in high-order Cartesian tensors to further enhance accuracy. Additionally, due to its E(n) equivariance (rather than E(3)), HotPP can be explored for high-dimensional structure optimization⁴⁸ to expedite potential energy surface exploration. It can also serve as a foundation for generating models to directly generate structures or predict wave functions. Overall, HotPP is a promising neural network that we believe can facilitate further explorations in physical chemistry, biology, and related fields.

Methods

Software

All experiments were run with the HotPP software available at https://gitlab.com/bigd4/hotpp, git commit be36dae6c2b35148ba214d5626f9960a8eaf5a07. In addition, the Pytorch version was 2.0.1+cu117, PyTorch Lightning under version 2.0.7, and Python under version 3.9.17.

Datasets

Ani-1x: The ANI-1x dataset^35,36 contains approximately five million diverse molecular conformations obtained through an active learning algorithm. We use 70% data of ani1x.h5 dataset downloaded from https://doi.org/10.6084/m9.figshare.c.4712477.v1 to train the model, and then test on the COmprehensive Machine-learning Potential (COMP6) benchmark³⁴. The reference energies are extracted from “wb97x_dz.energy” label, and forces from “wb97x_dz.forces” label.

Carbon: The GAP-17 dataset³⁷ consists of a training set comprising 4080 structures and a test set comprising 450 structures. The reference data are got by single-point DFT-LDA computations with dense reciprocal-space meshes. The GAP-20 dataset³⁸ contains 6088 structures and are calculated with the optB88-vdW dispersion inclusive exchange–correlation functional. We use 70% of the data as the training set.

Water: This dataset includes water monomer, water dimer, Zundel cation, and liquid water bulk⁴¹, each systems contains 1000 configurations, 70% of which are used for training. The water monomer, water dimer, and Zundel cation are calculated at (CCSD)/d-aug-cc-pVTZ level, and the liquid water bulk at the DFT/PBE-USPP level.

Training details

The tensor of the out layer ${l}_{{{\rm{omax}}}}^{t}$ and the tensor product of the relative coordinates ${{{\rm{l}}}}_{{{\rm{rmax}}}}^{{{\rm{t}}}}$ in the models are both set to 2 and a discussion about the effect of these values can be seen in the Supplementary Note 4. The number of chemical embedding channels and features of node messages is 64. The radial function is a 3 layer MLP of dimensions [64, 64, 64] with SiLU nonlinearity and the basis function is 8 trainable Bessel functions similar to NequIP⁸. The readout layer is a 2 layer MLP of dimensions [64, 64] and SiLU nonlinearity. The models were trained with the Adam optimizer⁴⁹ in PyTorch with default parameters. We used a learning rate of 0.01 and the learning rate was reduced using an on-plateau scheduler based on the validation loss with a decayfactor of 0.8.

Ani-1x: We used 5 propagation layers, a radial cutoff of 4.5 Å, a batchsize of 128, and the following loss function with ${\lambda }_{E}$ = 0.1 and ${\lambda }_{f}=1$:

$$L=\frac{{\lambda }_{E}}{N}{\left|\left|\hat{E}-{E}\right|\right|}^{2}+\frac{{\lambda }_{f}}{3N}{\sum }_{i=1}^{N}{\sum }_{\alpha=1}^{3}{\left|\left|-\frac{\partial \widehat{E}}{\partial {{{\bf{r}}}}_{i\alpha }}-{{{\bf{F}}}}_{i\alpha }\right|\right|}^{2}$$

Where N, $E$, $\hat{E}$, ${{{\bf{F}}}}_{i\alpha }$ denote the number of atoms, target energies, predicted energies, and the force of atom i on direction $\alpha$.

Carbon: The cell is multiplied by a unit matrix S before calculations. We used 5 propagation layers, the difference between the models with different parameters is that, for the model with more parameters, we updated both node information and edge information in the propagation layers. We used a radial cutoff of 3 Å, a batchsize of 16, and the following loss function with ${\lambda }_{E}$ = 0.5, ${\lambda }_{f}=1$, and ${\lambda }_{v}=0.2$:

$$L=\frac{{\lambda }_{E}}{N}{\left|\left|\hat{E}-E\right|\right|}^{2}+\frac{{\lambda }_{f}}{3N}{\sum }_{i=1}^{N}{\sum }_{\alpha=1}^{3}{\left|\left|\frac{\partial \hat{E}}{\partial {r}_{i\alpha }}-{{{\bf{F}}}}_{i\alpha }\right|\right|}^{2}+\frac{{\lambda }_{v}}{9}{\sum}_{\alpha,\beta }{\left|\left|-\frac{\partial \widehat{E}}{\partial {{{\boldsymbol{s}}}}_{\alpha \beta }}-{{{\bf{V}}}}_{\alpha \beta }\right|\right|}^{2}$$

Where ${{{\boldsymbol{V}}}}_{\alpha \beta }$, ${{{\boldsymbol{s}}}}_{\alpha \beta }$ denotes the $\alpha,\,\beta$ component of the virial and the unit matrix S.

The NequIP model was trained on the same dataset with NVIDIA GeForce RTX 4090 24GB. We used 4 layers with 64 channels for even and odd parity for both l = 1, l = 2, and l = 3. Radial features are generated using 8 trainable Bessel basis functions and a polynomial envelope for the cutoff with p = 6, the numbers of invariant layers and neurons were set to 2 and 64. Such hyperparameter settings result in model parameter quantities of 389k, 971k, and 1,970k respectively. Models were trained with Adam optimizer with default parameters. We initialized the learning rate to 0.01 and used an on-plateau scheduler based on the validation loss with a patience of 100 and a decay factor of 0.8. We used an exponential moving average with weight 0.99.

Water: We used 4 propagation layers, a radial cutoff of 4 Å, a batchsize of 4, and the following loss functions:

$$L={\left|\left|\widehat{{{\bf{P}}}}-{{\bf{P}}}\right|\right|}^{2}$$

$$L={\left|\left|\widehat{{{\boldsymbol{\alpha }}}}-{{\boldsymbol{\alpha }}}\right|\right|}^{2}$$

Where ${{\bf{P}}}{{\boldsymbol{,}}}\,\hat{{{\bf{P}}}}{{\boldsymbol{,}}}\,{{\boldsymbol{\alpha }}}{{\boldsymbol{,}}}\,\hat{{{\boldsymbol{\alpha }}}}$ are target dipoles, predicted dipoles, target polarizations, predicted polarizations.

Molecluar dynamics simulations

We constructed the PES of liquid water using HotPP with the dataset provided by DeePMD⁵⁰, including 1888 structures computed with the strongly constrained and appropriately normed (SCAN) functional⁵¹. Our model gives the RMSE of 2 meV/atom for the per atom energy, 49 meV/ Å for forces, and 11 meV/atom for per atom virials.

Next we used LAMMPS⁵² to perform the MLMD with the system of 512 water molecules in a cubic≈24.8 Å supercell to make sure the density close to 1 ${{\rm{g\; c}}}{{{\rm{m}}}}^{-3}$. The system was equilibrated at ambient conditions using Nosé-Hoover chain thermostat^53,54 for 200 ps. 10 statistically independent initial conditions were then sampled from the last 100 ps simulation to initialize NVE trajectories of 200 ps length using a time step of 0.5 fs. The initial and final configurations of these 10 simulations can be found in Supplementary Data 1. The dipole moment and polarizability tensor were calculated every 1 fs.

Calculation of infrared absorption spectrum and Raman spectrum

We can get different types of vibrational spectra by Fourier transforming the time autocorrelation functions (ACF) of different physical properties with a trajectory sampled by molecule dynamics. For IR absorption, it can be computed by the ACF of the dipole moment as:

$$I(\omega )\propto {\omega }^{2}{\int }_{\!\!\!\!-{\infty }}^{+{\infty }}{e}^{-i\omega t}\left\langle \mu \left(0\right)\cdot \mu \left(t\right)\right\rangle {dt}$$

Where $\mu$ is dipole moment, $\omega$ is the vibrational frequency, and the bracket is the average over the time origin.

And for Raman spectrum, the isotropic components can be calculated by:

$${R}_{{iso}}(\omega )\propto \omega \tanh (\frac{{{\hslash }}\omega }{2{kT}}){\int }_{\!\!\!\!-{\infty }}^{+{\infty }}{e}^{-i\omega t}\left\langle {\alpha }_{{iso}}\left(0\right)\cdot {\alpha }_{{iso}}\left(t\right)\right\rangle {dt}$$

Where ${\alpha }_{{iso}}\equiv {Tr}(\alpha )/3$ is the isotropic components of the polarizability tensor. And,

$${R}_{{aniso}}(\omega )\propto \omega \tanh (\frac{{{\hslash }}\omega }{2{kT}}){\int }_{\!\!\!\!-{\infty }}^{+{\infty }}{e}^{-i\omega t}{Tr}\left\langle \beta \left(0\right)\cdot \beta \left(t\right)\right\rangle {dt}$$

Where $\beta$ is the anisotropic traceless tensor $\beta=\alpha -{\alpha }_{{iso}}I$.

The IR spectrum and Raman spectrum are scaled to make the maximum values consistent with the experimental data.