Introduction

Nonlinear photonics is a fascinating and advanced branch of modern optics that delves into the study and manipulation of light/photons in media where the response to light intensity is not linear1,2. The relentless pursuit of efficient and versatile nonlinear optical materials that can on-demand manipulate various degrees of freedom of photons (e.g., frequency, amplitude, phase, spin and orbital angular momenta)3,4,5,6 lies in the heart of nonlinear optics and has considerably boosted the development of materials science, quantum computing, biomedical engineering, and information technology7,8,9,10,11,12. So far, numerous novel physical effects and functionalities, including nonlinearity phase control5, nonlinear wavefront shaping13, nonlinear generation of Airy beams14, vectorial meta-holography15, three-dimensional lithium niobate nanodomain writing16, giant second-harmonic generation (SHG)17, ultrathin multiphoton quantum light source18,19, and full-wavelength phase-matching20, have been reported with emerging nonlinear optical materials (e.g., two-dimensional ferroelectrics family, photonic crystals, organic salts, metamaterials and metasurfaces). However, difficulties still persist in their processability and tunability. For instance, the growth and poling of lithium niobate usually require thousands of degrees Celsius temperature, kilovolt voltage, or femtosecond laser writing with high power density, leading to complicated fabrication process, high cost, and large energy consumption. Furthermore, due to the intrinsic symmetry constraint of ferroelectric crystals, the electric polarization is restricted to being oriented in a binary manner and this property finally limits the tunability of the generated nonlinear optical waves.

A possible solution to these challenges would be soft materials21,22, especially liquid crystals (LCs), due to their unique anisotropic optical properties, self-assembly characteristics, flexible domain tailoring, as well as dynamic tunability. These features have made them ideal for light manipulation in the regimes of both linear (e.g., optical vortex generator, holography, and topological beam steering)23,24,25,26,27 and nonlinear optics (e.g., self-phase modulation, self-focusing, and self-diffraction)28,29,30. However, second-order nonlinear optical response in soft materials has garnered limited attention. This paradigm has been changed recently due to the advent of ferroelectric nematic liquid crystals (FNLCs). Such fluids were first predicted by M. Born in 1916 that if LC molecules were properly designed, their molecules would self-assemble into polar arrangements31. After a century, FNLCs were experimentally validated32,33,34 with inherent macroscopic spontaneous polarization that couples the local electric polarity and the orientational ordering35. Large dielectric permittivity and strong nonlinear optical properties have been studied36. To date, although much effort has been dedicated to developing high-performance materials, unveiling attractive electro-optic properties, and achieving high-resolution polar ordering characterizations37,38,39,40,41, the ferroelectric nematic fluid for programmable, dynamic, structured light field manipulation in the realm of nonlinear optics has not yet been explored, mainly due to the difficulties in nonlinear polarization manipulation.

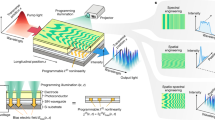
Here, we find that the second-order nonlinear polarization of ferroelectric nematic LC (Figs. 1a and 1b) carries distinct nonlinear geometric phase for the left- and right-handed circular polarization components of the SH signal. Continuous control of these nonlinearity phase for nonlinear wavefront shaping can be further achieved through spatially-variant engineering of the ferroelectric nematic fluid. In the proof-of-concept experiment, we study the nonlinear optical spin-orbit interaction process in a nonlinear geometric-phase coded topological FNLC q-plate. As illustrated in Fig. 1c, the polar orientations of FNLCs exhibit a radial distribution, which is achieved via photopatterning a continuously varied alignment configuration with a topological charge of q = 1. When a fundamental wave (FW) with angular momentum state of (σ, ℓ0)ω is incident upon the ferroelectric nematic q-structure, where σ (σ = ±1) and ℓ denote the spin and orbital angular momentum states, respectively, the cascaded spin-orbit interaction enables two spin-orbit locked SH optical vortices, specifically (σ, 2ℓ0 + σq)2ω and (−σ, 2ℓ0 + 3σq)2ω, in addition to the two fundamental optical vortices, namely (−σ, ℓ0 + 2σq)ω and (σ, ℓ0)ω. Moreover, we present thermally and electrically switchable, as well as twist-elastic-force controlled, FNLC q-superstructures, which enable the generating and tuning of SH optical vortices. This study introduces a soft-matter platform for nonlinear manipulation of light, offering a great promise for applications in optical communications, high-resolution imaging, high-density data storage, and high-dimensional optical information processing.

Fig. 1: Ferroelectric nematic liquid crystal for nonlinear soft-matter photonics.
figure 1

a Chemical structure of the FNLC RM734 material. b SHWs from the polar RM734 material under the pumping of the linearly polarized FW. The nonlinear polarization is along the polar direction of LC. c Generation of SHWs with multiple spin-orbit angular momentum states with a nonlinear LC q-plate. For the incident FW with an angular momentum state of (σ, ℓ0)ω, the SHWs have specific angular momentum states due to the spin-orbit interactions of both FW and SHWs. σ = ±1 stands for the circular polarization state of light.

Full size image

Results

Nonlinear polarization of the ferroelectric nematic LC

As shown in Fig. 1a, the molecular structure of the ferroelectric nematic fluid RM734 used in this work possesses a onefold in-plane rotational symmetry (LC director n ≠ −n). The long π-bridged donor-acceptor groups are along the spontaneous polarization of the RM734 molecule, leading to a strong nonlinear optical response with non-zero second-order susceptibilities \({\chi }_{{{{\rm{aaa}}}}}^{(2)}=11.2{{{\rm{pm}}}}\cdot {{{{\rm{V}}}}}^{-1}\) and \({\chi }_{{{{\rm{abb}}}}}^{(2)}={\chi }_{{{{\rm{bab}}}}}^{(2)}={\chi }_{{{{\rm{bba}}}}}^{(2)}=1.2{{{\rm{pm}}}}\cdot {{{{\rm{V}}}}}^{-1}\) at 1064 nm42, where a- and b-axes are parallel and perpendicular to the polar direction, respectively.

We start with the theory of nonlinear polarization occurring in the FNLCs using a linearly polarized FW with the electric field of \({{{{\bf{E}}}}}^{{{{\rm{\omega }}}}}={{{{\rm{A}}}}}_{0}(\cos \phi {\hat{{{{\bf{e}}}}}}_{x}+\,\sin \phi {\hat{{{{\bf{e}}}}}}_{y})\) for incidence, where A0 and ω are the amplitude and angular frequency of the FW, ϕ is the polarization angle relative to the x-axis, and \({\hat{{{{\bf{e}}}}}}_{x}\) (\({\hat{{{{\bf{e}}}}}}_{y}\)) represents the unit vector of the x (y)-axis. As the values of \({\chi }_{{{{\rm{abb}}}}}^{(2)}\), \({\chi }_{{{{\rm{bab}}}}}^{(2)}\), and \({\chi }_{{{{\rm{bba}}}}}^{(2)}\) are about one tenth that of \({\chi }_{{{{\rm{aaa}}}}}^{(2)}\), only \({\chi }_{{{{\rm{aaa}}}}}^{(2)}\) is taken into account in our theoretical model. If the polar direction of FNLC is rotated by an orientation angle of α relative to the x-axis, the second-order nonlinear polarization can be analytically expressed as

$${{{{\bf{P}}}}}^{2{\rm{\omega}}}=\, {\varepsilon }_{0}{{{{\rm{A}}}}}_{0}^{2}{\chi }_{{{{\rm{aaa}}}}}^{(2)}{\cos }^{2}(\phi -\alpha )(\cos \alpha {\hat{{{{\bf{e}}}}}}_{x}+\,\sin \alpha {\hat{{{{\bf{e}}}}}}_{y})\\=\, {\varepsilon }_{0}{{{{\rm{A}}}}}_{0}^{2}{\chi }_{{{{\rm{aaa}}}}}^{(2)}{\cos }^{2}(\phi -\alpha ){\hat{{{{\bf{e}}}}}}_{a}$$
(1)

where \({\hat{{{{\bf{e}}}}}}_{a}\) represents the unit vector of the a-axis, ε0 is the vacuum permittivity, \(2{{{\rm{\omega }}}}\) is the angular frequency of the SH wave (SHW). Detailed formula derivation is provided in Supplementary Section 1. Equation (1) reveals the unique SH optical response (Fig. 1b). Specifically, the excited nonlinear polarization is linearly polarized along the a-axis, i.e., the polar direction of FNLC. It can be found that the magnitude of excited nonlinear polarization is primarily modulated by the cos2 term. The maximum and minimum SHG intensities occur at ϕ – α = 0° and ϕ – α = 90°, respectively. This means the nonlinear optical response is polarization-dependent and the largest SH intensity can be achieved when the polarization of FW is parallel to the FNLC.

Then, we experimentally demonstrate the SH optical response in a homogeneously photoaligned FNLC device. Such a device comprises two glass substrates coated with ITO electrodes and photoalignment layers. After unidirectionally photoaligned and infiltrated with FNLC, the device is encapsulated and undergoes a thermal annealing treatment (see Methods for more details) to achieve a uniform spontaneous polarization distribution. Figure 2a exhibits the polarized optical microscopic textures of the nonlinear LC device in its nematic phase (140 °C, featureless) and polar ferroelectric nematic phase (120 °C, with distinctive lens-shaped polar domains). The polar orientation within the lens-shaped domain demonstrates an inverse direction relative to the surrounding region34. The elongated direction of the polar domains is parallel to the photoalignment direction. The high-quality alignment of FNLC enables the observation of a strong emission of the SHW with a Gaussian beam profile when a circularly polarized femtosecond laser (FW) passes through the device, as depicted in Fig. 2b and Supplementary Fig. 1. The measured spectra of power-dependent SHG signals are summarized in Fig. 2c. The central wavelength of the SHWs is at 650 nm, corresponding to the half wavelength of incident FW at 1300 nm. Figure 2d displays the log-log relationship between the pumping power and the maximum SH intensity, confirming the quadratic nonlinear optical process. When a linearly polarized FW passes through the device, and the polarization (ϕ) of FW is continuously rotated, the intensity of SHW generated from the FNLC (α = 0°) shows a dumbbell-shaped polar diagram (Fig. 2e). This validates the polarization-dependent nonlinear optical response of the FNLC. The highest value is observed at ϕ = 0°, i.e., when the incident polarization is parallel to FNLC, and the lowest value is at ϕ = 90°. The polarization state of SHW is further characterized using an analyzer (Fig. 2f). Regardless of the incident polarization state (circular or linear polarization), the analyzed SHG signals show a maximum intensity at 0° and a minimum intensity at ±90°, which is consistent with Malus’s law. This behavior verifies the generated linear polarization of the SHW, which is parallel to the polar orientation of FNLC and agrees well with the theoretical prediction by Eq. (1).

Fig. 2: Nonlinear polarization excited in a homogeneously aligned FNLC device.
figure 2

a Polarized optical microscopic textures of the homogeneous FNLCs in the nematic phase (left panel) and ferroelectric nematic phase (right panel). The magenta bars denote the direction of photoalignment. N: nematic phase. FN: ferroelectric nematic phase. Scale bar: 100 μm. b Normalized profile of the SHG beam, λSH = 650 nm. c Normalized SHG spectra of the homogeneous FNLCs under different pumping powers. The central wavelength of the SHG spectra is 650 nm, corresponding to the fundamental wavelength at 1300 nm. d Normalized power-dependent SHG intensity. The linearly fitted slope value is 2.03 (inset), confirming the quadratic nature of the SHG process. e Polarization-dependent SHG signals from the homogeneously photoaligned FNLC device. α = 0°, i.e., the orientation angle of FNLC with respect to the x-axis is 0°. f, Relationship between the SHG intensity and the angle of the analyzer. The SHG intensities are normalized for the linear polarization incidence and circular polarization incidence, respectively. Source data are provided as a Source Data file.

Full size image

Cascaded spin-orbit interaction in the nonlinear LC q-plate

By leveraging the programmable photopatterning of LCs, the nonlinear polarization can be further engineered. Assuming that the FW possesses an angular momentum state of (σ, ℓ0)ω (σ = ±1) and the LC device is photopatterned with a specific spatially-variant LC configuration, the FW will undergo an optical spin-orbit interaction within the context of linear optics, resulting in transformation into a new angular momentum state of (−σ, ℓ0 + 2σ)ω. Concurrently, distinctive angular momentum states within the framework of nonlinear optics will be generated, which are determined by both the FW states and the geometric phase encoded FNLC structure (Fig. 1c).

A particular class of wavefront engineering that has garnered substantial attention over the past decade is the generation of beams carrying orbital angular momentum. Here, in the proof-of-concept experiment, we photopattern a topological q-plate structure with the polar FNLC material to demonstrate the intriguing spin-orbit interactions in the SHG process (for more details of photopatterning, see Methods and Supplementary Section 2).

Firstly, we study the optical properties of the SHW when a linearly polarized femtosecond laser passes through the device (Figs. 3a and 3b). The spatially variant LC director distribution follows the equation of \(\alpha (\varphi )=q\varphi\), where φ is the azimuthal angle and q is the topological charge set to 1. Typical textures of the device are shown in Fig. 3c and Supplementary Fig. 2. A Maltese cross, where the polar LC orientation is either parallel or perpendicular to the crossed polarizers, is clearly observed. To deduce the inherent spontaneous polarization distribution, we apply an in-plane electric field (DC, ±0.2 mV⋅μm−1) to the device. When a negative electric field is applied, the spontaneous polarization that does not align with the electric field undergoes reorientation, leading to the deformation of the Maltese cross pattern (Fig. 3d). When the electric field direction is inversed, the Maltese cross deforms in the opposite direction, with horizontal extinction brushes shifting contrary to the direction of the electric field (Fig. 3e). These phenomena indicate a radially outward polarization distribution in the FNLC q-plate (Fig. 3b). Furthermore, such polarization distribution satisfies the flexoelectric coupling39 with minimized excluded volume of wedge-shaped LC molecules, which facilitates the stable polar ordering formation. A whirl-like director distribution is also observed close to the singularity point, which prevents the large accumulation of charges at the singularity point, thereby reducing the free energy of the entire system.

Fig. 3: SH vector vortex beam generated by FNLC q-plate.
figure 3

a Schematic illustration of the SH optical response of an FNLC director for the incident FW with linear polarization. The LC director is counterclockwise rotated by an angle α around the z-axis (facing the direction of light propagation). b Illustration of the light-matter interaction geometry between the linearly polarized FW and the nonlinear LC q-plate. LP: linear polarization. c Polarized optical microscopic texture of the LC q-plate with the topological charge of 1. d, e Polarized optical microscopic textures of the LC q-plate under an in-plane electric field. Scale bar: 50 μm. f–j Intensity distributions of the FW and SH vector vortex beams. Analyzed SH vector vortex beams are in the second and third panels of (g) with the fast axes of the polarizer and analyzer denoted by black and blue arrows, respectively. White dotted lines in (g) indicate the extinction regions. White single-sided arrows in (f) indicate the polarization distribution of output FW. White double-sided arrows represent the incident polarization of FW (ϕ = 0°, 0°, 45°, 90°, and 135°). Yellow arrows in (g–j) indicate the polarization distribution of the SHWs.

Full size image

Upon a linearly polarized FW incidence, a vector vortex beam in the realm of linear optics (|ℓ| = 2) is generated due to the imprinted linear geometric phase26 (Fig. 3f). Simultaneously, an SH vector vortex beam with a two-lobe intensity profile is also observed (Fig. 3g), of which the strongest intensity occurs in the direction that is parallel to the incident polarization. When rotating the incident polarization, the SH light field follows its rotation, as shown in Fig. 3h–j. Moreover, the vector nature of the SH beam for the linear polarization incidence (ϕ = 0°) is further characterized by using an analyzer behind the device. Extinction regions occur where the polarization is perpendicular to the analyzer. Thus, by analyzing the extinction pattern (the second and third panels in Fig. 3g), the SHW with a radial polarization distribution and a singularity point is confirmed. These results agree well with the nonlinear polarization model described in the previous section.

Then, we use a circularly polarized FW for incidence to systematically investigate the nonlinear spin-orbit interaction of light occurring in the LC q-plate. Nontrivial nonlinear geometric phase5,43 is disclosed to describe the nonlinear optical response of an FNLC director, of which the magnitudes are closely related to the geometric rotation of the LC director and the spin states of the SHWs. As depicted in Fig. 4a, when the LC director undergoes a counterclockwise rotation by an angle α with respect to the z-axis, the generated SHWs with co- (σ) and cross- (−σ) circular polarization to that of the FW carry the nonlinear geometric phase of σα and 3σα, respectively. This can be explained as follows. In the local coordinate of the unidirectionally aligned FNLC, a Gaussian FW with the spin state of σ acquires a linear geometric phase owing to the spin coupling effect, i.e., \({{{{\bf{E}}}}}_{{{{\rm{Local}}}}}^{{{{\rm{\omega }}}}}={{{{\bf{E}}}}}_{{{{\rm{Lab}}}}}^{{{{\rm{\omega }}}}}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\sigma \alpha }\), where the indices “Local” and “Lab” denote the local and laboratory coordinate frames, respectively. Assuming that the second-order nonlinear susceptibility in the local frame is \({\overleftrightarrow{{{{\boldsymbol{\chi }}}}}}^{\,({{{\rm{2}}}})}(0)={{\overleftrightarrow{{{{\boldsymbol{\chi }}}}}}^{\,({{{\rm{2}}}})}(\alpha )|}_{\alpha=0}\), the nonlinear polarization in the local frame is given by \({{{{\bf{P}}}}}^{2{{{\rm{\omega }}}}}={\varepsilon }_{0}{\overleftrightarrow{{{{\boldsymbol{\chi }}}}}}^{\,({{{\rm{2}}}})}(\alpha=0){({{{{\bf{E}}}}}_{{{{\rm{Local}}}}}^{{{{\rm{\omega }}}}})}^{2}={\varepsilon }_{0}{\chi }_{{{{\rm{aaa}}}}}^{(2)}{({{{{\bf{E}}}}}_{{{{\rm{Lab}}}}}^{{{{\rm{\omega }}}}})}^{2}{{{{\rm{e}}}}}^{{{{\rm{2i}}}}\sigma \alpha }\). After transforming back to the laboratory frame, the nonlinear polarizations with co- and cross-circular polarization to that of the FW are derived (details in Supplementary Section 3):

$$\begin{array}{c}{{{{\bf{P}}}}}_{\sigma }^{2{{{\rm{\omega }}}}}={\varepsilon }_{0}{\chi }_{{{{\rm{aaa}}}}}^{(2)}{({{{{\bf{E}}}}}_{{{{\rm{Lab}}}}}^{{{{\rm{\omega }}}}})}^{2}{{{{\rm{e}}}}}^{{{{\rm{2i}}}}\sigma \alpha }{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\sigma \alpha }\propto {{{{\rm{e}}}}}^{{{{\rm{i}}}}\sigma \alpha }\\ {{{{\bf{P}}}}}_{-\sigma }^{2{{{\rm{\omega }}}}}={\varepsilon }_{0}{\chi }_{{{{\rm{aaa}}}}}^{(2)}{({{{{\bf{E}}}}}_{{{{\rm{Lab}}}}}^{{{{\rm{\omega }}}}})}^{2}{{{{\rm{e}}}}}^{{{{\rm{2i}}}}\sigma \alpha }{{{{\rm{e}}}}}^{{{{\rm{i}}}}\sigma \alpha }\propto {{{{\rm{e}}}}}^{{{{\rm{3i}}}}\sigma \alpha }\end{array}$$
(2)

The acquired nonlinear geometric phase shows a linear relation of one and three times of α (Supplementary Fig. 3).

Fig. 4: Geometric phase coded nonlinear optical spin-orbit interaction and the generation of SH optical vortices with the FNLC q-plate.
figure 4

a Generation of the SHWs with spin-locked nonlinear geometric phase. b Illustration of the spin-orbit coupling and the light-matter interaction geometry between the circularly polarized FW and the nonlinear LC q-plate. LSOI: linear spin-orbit interaction. NSOI: nonlinear spin-orbit interaction. c, d Linear and nonlinear geometric phase associated optical vortex generation in the FNLC q-plate. The angular momentum state of the incident FW is (+1, 0)ω. The abbreviation “Exp.” represents the experimental results. e, f Linear and nonlinear geometric phase associated optical vortex generation in the LC q-plate. The angular momentum state of the incident FW is (+1, +1)ω.

Full size image

For the incident FW with an arbitrary spin and orbital angular momentum state (σ, ℓ0)ω, it will experience a linear spin-orbit interaction in the ferroelectric nematic q-plate. After passing through the FNLC film with a certain thickness L, the electric field of the FW contains two components: unconverted \({{{{\bf{E}}}}}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}}\propto {{{{\rm{e}}}}}^{{{{\rm{i}}}}{\ell }_{0}\varphi }{E}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}}{\hat{{{{\bf{e}}}}}}_{\sigma }\) and modulated \({{{{\bf{E}}}}}_{{{{\rm{Lab}}}},-\sigma }^{{{{\rm{\omega }}}}}\propto {{{{\rm{e}}}}}^{{{{\rm{2i}}}}\sigma q\varphi }{{{{\rm{e}}}}}^{{{{\rm{i}}}}{\ell }_{0}\varphi }{E}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}}{\hat{{{{\bf{e}}}}}}_{-\sigma }\). The light with \({{{{\bf{E}}}}}_{{{{\rm{Lab}}}},-\sigma }^{{{{\rm{\omega }}}}}\) component acquires an additional orbital angular momentum with Δℓ = 2σq.

The nonlinear polarizations generated by each component of FW are presented as follows. For an ultrathin layer of the FNLC q-plate, the nonlinear polarizations for \({{{{\bf{E}}}}}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}}\) can be described as:

$${{{{\bf{P}}}}}_{\sigma }^{2{{{\rm{\omega }}}}} \propto {{{{\rm{e}}}}}^{{{{\rm{i}}}}(2{\ell }_{0}\varphi+\sigma q\varphi )}{({E}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}})}^{2}{\hat{{{{\bf{e}}}}}}_{\sigma }\\ {{{{\bf{P}}}}}_{-\sigma }^{2{{{\rm{\omega }}}}} \propto {{{{\rm{e}}}}}^{{{{\rm{i}}}}(2{\ell }_{0}\varphi+3\sigma q\varphi )}{({E}_{{{{\rm{Lab}}}},\sigma }^{{{{\rm{\omega }}}}})}^{2}{\hat{{{{\bf{e}}}}}}_{-\sigma }$$
(3)

Remarkably, the co- and cross-circularly polarized nonlinear polarizations generated in the FNLC q-plate carry distinct phase factors of 2ℓ0φ + σqφ and 2ℓ0φ + 3σqφ, respectively. The first item of each phase factor 2ℓ0φ, which is contributed by the FW, represents the conventional conservation law of orbital angular momentum in nonlinear optics. The second items σqφ and 3σqφ come from the nonlinear geometric phase generated from the FNLC molecules, which are locked to the co- and cross-spin states of the FW, respectively. We thus call them spin-locked nonlinear geometric phase. Therefore, the SH beams acquire additional orbital angular momenta of σq and 3σq. Finally, the angular momentum states of the SHWs become (σ, 2ℓ0 + σq)2ω and (−σ, 2ℓ0 + 3σq)2ω. Notably, the angular momentum states of the SHWs generated by the \({{{{\bf{E}}}}}_{{{{\rm{Lab}}}},-\sigma }^{{{{\rm{\omega }}}}}\) component of the FW are the same as that in Eq. (3) (details in Supplementary Section 3, Eq. (S15), Supplementary Fig. 4), further demonstrating the spin locking effect. It is also interesting to note that for the linear spin-orbit interaction during the propagation of SHWs towards the exit plane, the angular momentum states are spin-locked as well (Fig. 4b and Supplementary Fig. 4).

In order to experimentally verify the nonlinear geometric phases, we employ a circularly polarized FW to pump the LC q-plate (Fig. 4b). As shown in Figs. 4c and 4d, for the FW with angular momentum state of (+1, 0)ω, the measured states of modulated FW and generated SHW include (+1, 0)ω, (−1, +2)ω, (+1, +1)2ω, and (−1, +3)2ω. The existence of the unconverted FW ( + 1, 0)ω is mainly due to the LC film thickness, which is not optimized to make the phase retardation satisfy the half-wave condition Γ = (2m + 1)π (m is a natural number)26. Notably, the total SHG signal reaches 20 μW at the pumping power of 124 mW, corresponding to a SHG conversion efficiency of 1.6 × 10−4 (see Supplementary Section 4). To our knowledge, this represents the highest efficiency ever reported in FNLCs. The intensities of the co- and cross-circular polarization components of the SHW are almost evenly distributed. The measured intensity ratio is approximately 46:54, which is very close to the theoretical prediction (see Supplementary Section 3). The minor discrepancy may be attributed to the imperfections of the polarizer and quarter-wave plate. It is well known that the linear geometric phase effect relies on the conversion of the incident circular polarization light into the opposite spin state with imprinted geometric phases e±i2α. In this case, the energy allocation of co- and cross-circularly polarized light components is determined by the thickness of the FNLC film. In contrast, the nonlinear geometric phase encoded co- and cross-circular polarization SH vortices have an equal energy distribution regardless of the thickness of the LC film. This feature enables a remarkable wavelength tolerance of LC device in the SHG process, as evidenced by the generation of paired nonlinear optical vortices with equivalent energies at various wavelengths (see Supplementary Fig. 5). Furthermore, we conducted the experiments on an alternative device featuring an LC film thickness of 1.8 μm. The results are provided in Supplementary Fig. 6, further validating our theory and showing the scalability of the spin-locked nonlinear geometric phase with cascaded spin-orbit interactions.

Additionally, the results for incident FW state (−1, 0)ω are presented in Supplementary Fig. 7. We also investigate the high-order nonlinear spin-orbit interaction using the FWs with angular momentum states of (+1, +1)ω and (−1, +1)ω (Figs. 4e, 4f, and Supplementary Fig. 8). The FWs with these angular momentum states are obtained by using home-made nematic LC q-plates with the topological charges of −0.5 and +0.5, respectively. It is noteworthy that all the SH vortices are in accordance with our theoretical predictions.

Dynamically switchable nonlinear optical response of LC q-plate

Thanks to the high sensitivity to various external stimuli, LCs have received significant attention in developing compact and intelligent optoelectronic devices. Here, we show the thermally and electrically switchable nonlinear optical responses of the ferroelectric nematic LC q-plate. The differential scanning calorimetry thermogram illustrates the sequential presence of different LC phases, including the isotropic phase (> 182 °C), nematic phase (128 °C ~ 182 °C), and ferroelectric nematic phase (40 °C ~ 128 °C) (Supplementary Fig. 9). The FNLC material crystallizes around 40 °C, a temperature that can vary depending on the cooling rate39. This suggests the potential for thermal control of the linear optical anisotropy and nonlinear polarization. For a circularly polarized FW with a Gaussian-type distribution (+1, 0)ω, the SHG intensity as a function of temperature is shown in Fig. 5a. When the LC device is in the isotropic phase, no SHG signal is obtained, and no spin-orbit interaction occurs due to the disappearing of linear optical anisotropy, thus the output light field is the same as incident FW. After entering the nematic phase (temperature decreases below 182 °C), the linear spin-orbit interaction of the FW leads to a modulated FW. Thus, two optical states of FW are captured at this stage. As the temperature decreases from 128 °C to 40 °C, the intensity of the SHW increases rapidly at the beginning, then shows slow growth property, and ultimately reaches saturation. The Gaussian-type FW experiences both linear and nonlinear spin-orbit interactions, thus four optical states including two FW states and two SH vortices are experimentally observed.

Fig. 5: Dynamically switchable SH optical response of the nonlinear LC q-plate.
figure 5

a Thermally switchable FW and SH vortices. FN: ferroelectric nematic phase. N: nematic phase. Iso: isotropic phase. b Schematic illustration of the electrically switchable nonlinear LC q-plate. c Periodic switching of the intensity of the SH vortices by electrically tuning the spontaneous polarization of ferroelectric nematic q-plate from the transverse direction to the longitudinal direction. Source data are provided as a Source Data file.

Full size image

In addition, we demonstrate the electrical switching36,44 of the SH optical vortices. In the experiment, a triangular-wave electric field (0.5 Hz, AC voltage 0.12 V⋅μm−1, Supplementary Fig. 10) is vertically applied to the LC device. As depicted in Fig. 5b, the spontaneous polarization of FNLC undergoes electrical realignment, leading to the change of nonlinear susceptibility from a transverse tensor element \({\chi }_{{{{\rm{aaa}}}}}^{(2)}\) to a longitudinal one \({\chi }_{{{{\rm{bbb}}}}}^{(2)}\). Therefore, for the FW with angular momentum state (+1, 0)ω, the second-order nonlinear polarizations are \({P}_{\sigma }^{2{{{\rm{\omega }}}}}=0\) and \({P}_{-\sigma }^{2{{{\rm{\omega }}}}}=0\). Figure 5c demonstrates the periodic switching of the intensity of SH vortices, with the modulation frequency of 1.0 Hz (see Supplementary Section 5, Supplementary Fig. 11, and Supplementary Video 1). The intensity of FW is also electrically switched between the converted vortex and unconverted Gaussian beam.

Spin-selective nonlinear optical response of chiral LC q-superstructure

By utilizing the three-dimensional controllable architecture of FNLCs, we further demonstrate a notable spin-selective SH optical response. In addition to the successful photopatterning of FNLCs in the x-y plane, a right-handed chiral agent (R811, 1.0 wt%) is introduced to further engineer the rotational arrangement of LC molecules along the propagation (z) direction. Consequently, a three-dimensional, space-variant chiral q-superstructure with right-handedness is achieved, as illustrated in the left panel of Fig. 6a. For the sake of simplicity, one can assume that the variation of the LC director follows a linear distribution as described by the equation \(\alpha (\varphi,z)=q\varphi+2{{{\rm{\pi }}}}z/p\), where p represents the helical pitch, and z is the position of each LC layer. It is worth noting that p is calculated to be ~ 8.2 μm, and there is no spectral feature associated with Bragg reflection. In this particular scenario, the SHWs generated from the right-handed chiral q-superstructure carry both spin-dependent nonlinear geometric phases and spin-independent dynamic phases, which gives rise to a strong circular dichroism of the generated SH vortices (Fig. 6a, right panel). The nonlinear circular dichroism is defined as \(C{D}_{{{{\rm{SHG}}}}}=({I}_{{{{\rm{LCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}}-{I}_{{{{\rm{RCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}})/({I}_{{{{\rm{LCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}}+{I}_{{{{\rm{RCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}})\), where \({I}_{{{{\rm{LCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}}\) and \({I}_{{{{\rm{RCP}}}}-{{{\rm{FW}}}}}^{2{{{\rm{\omega }}}}}\) represent the SH intensities under the incidence of FWs with left-handed and right-handed circular polarization, respectively.

Fig. 6: Elastic force-driven spin-selective SH optical response of the chiral LC q-superstructure.
figure 6

a Schematic illustration of the three-dimensional chiral LC q-superstructure and the spin-selective generation of the SH optical vortex beams. b, c Calculated and measured intensity distributions of spin-selective SH vortices under the pumping of FWs with left-handed circular polarization (LCP) and right-handed circular polarization (RCP) states. The abbreviation “Exp.” represents the experimental results.

Full size image

The mechanism of the nonlinear circular dichroism in the three-dimensional chiral q-superstructure is theoretically explored. Firstly, we divide the q-superstructure into a stack of L/∆z layers with an equal thickness of ∆z. The electric field of the FW, after propagating through N (N = 1, 2, 3, …, L/∆z) layers, can be derived using the Jones matrices \({{{{\bf{M}}}}}_{N}^{{{{\rm{\omega }}}}}\cdots {{{{\bf{M}}}}}_{1}^{{{{\rm{\omega }}}}}\) (details in Supplementary Section 6). Then, the nonlinear polarization is described as \({{{{\bf{P}}}}}^{2{{{\rm{\omega }}}}}(z=N\varDelta z)={\varepsilon }_{0}{\overleftrightarrow{{{{\boldsymbol{\chi }}}}}}^{(2)}{[{{{{\bf{M}}}}}_{N}^{{{{\rm{\omega }}}}}\cdots {{{{\bf{M}}}}}_{1}^{{{{\rm{\omega }}}}}{{{{\bf{E}}}}}_{{\mbox{in}}}^{{{{\rm{\omega }}}}}(z=0)]}^{2}\), where \({{{{\bf{E}}}}}_{{\mbox{in}}}^{{{{\rm{\omega }}}}}(z=0)\) is the incident FW at z = 0. Subsequently, we calculate the SHWs from each LC layer propagating towards the exit plane at z = L. All these coherent SHWs are accumulated to obtain the total nonlinear polarization. This process takes into account the complex amplitudes of the SHWs generated at each layer, as well as their interference effects at the exit plane. The intensity of the SHW is then calculated by \({I}_{{{{\rm{total}}}}}^{2{{{\rm{\omega }}}}}\propto {|{P}_{\sigma,{{{\rm{sum}}}}}^{2{{{\rm{\omega }}}}}(z={{{\rm{L}}}})|}^{2}+{|{P}_{-\sigma,{{{\rm{sum}}}}}^{2{{{\rm{\omega }}}}}(z={{{\rm{L}}}})|}^{2}\). In this case, both the dynamic phase that evolves with the propagation and the geometric phase originated from \(\alpha (\varphi,z)\) lead to the distinct nonlinear susceptibilities for different circular polarization incidence, thus resulting in the emergence of the strong nonlinear circular dichroism. In this context, the helical twisted elastic force with a specific chirality plays a crucial role in the switching of the SH signal.

The theoretical and experimental results of the SH vortex beams are presented in Figs. 6b and 6c. The measured SHG intensity under the incidence of left-handed circularly polarized FW (opposite handedness to the chirality of the q-superstructure) is about 26 times stronger than that for the right-handed circular polarization incidence. Thus, the measured nonlinear circular dichroism value is ~ 0.93, which is consistent with the calculated circular dichroism value of 0.96 (see Supplementary Section 6).

Discussion

To summarize, we demonstrate the geometric phase associated nonlinear optical responses in the ferroelectric nematic LC q-plate, which allows for a series of cascade spin-orbit interactions enabling the simultaneous manipulation of various degrees of freedom of light, including amplitude, phase, polarization, orbital angular momentum, and frequency conversion. The unique structured vector vortex beams and spin-orbit locked optical vortices with different topological charges are systematically investigated in the SHG process. By taking advantage of the high-precision and arbitrary photopatterning technique, we are able to achieve more functional nonlinear geometric phase encoded LC architectures for desired nonlinear optical applications. Remarkably, we explore the thermal, electrical, and elastic force switching of the spin-orbit optical vortices with the planar q-plates and chiral q-superstructure, demonstrating the capability of dynamic wavefront engineering. The measured SH conversion efficiency of the FNLC superstructure is up to ~ 10−4, and we expect that it can be further improved by introducing the phase-matching condition38,45. The proposed soft-matter platform and the concept of nonlinear geometric phase in the FNLCs not only broaden the fundamental understanding of dynamic light-matter interactions in the framework of nonlinear optics, but also open new avenues for developing reconfigurable nonlinear photonic devices. More applications, ranging from nonlinear vortex source46, super-resolution imaging, to quantum information processing, are expected to be developed based on the proposed nonlinear soft-matter platform.

Methods

Sample fabrications

UV-Ozone cleaned indium-tin-oxide glass substrates were spin-coated with a photoalignment agent SD1 (Supplementary Fig. 12) by 800 rpm for 8 s and then 3000 rpm for 40 s. After curing at 100 °C for 10 minutes, two pieces of glass substrates were assembled to form a cell using UV curing adhesive. The cell gap of 4.1 μm was measured using the interferometry method. To achieve spatially variant alignment, a multistep partially overlapping exposure process47 was conducted using a digital micromirror device-based dynamic microlithography system with optimized exposure parameters (intensity, time, and sequence) (Supplementary Section 2). After a total exposure dose of ~ 5 J⋅cm−2, the desired alignment pattern of SD1 would be achieved. The photoalignment layer demonstrated exceptional thermal stability48, which remained stable throughout our tests. Ultraviolet light illumination and high humidity environment should be avoided to prevent potential degradation of the photoalignment quality. Following the infiltration of RM734 material into the cell at 190 °C, a three-step thermal annealing treatment was performed to facilitate the self-assembly of FNLC atop the SD1 layer. In step (1), the device was rapidly cooled down from 190 °C to 132 °C at a rate of 5 °C⋅min−1; in step (2), the device was gradually cooled from 132 °C to 126 °C at a rate of 0.5 °C⋅min−1 to facilitate the flexoelectric coupling relaxation during the nematic to ferroelectric nematic phase transition; step (3), the device was cooled from 126 °C to 120 °C at a rate of 1 °C⋅min−1 to prevent crystallization. It is important to set a slow cooling rate during the phase transition to prevent the formation of defective ferroelectric nematic structures. Polarized optical microscopic textures resulting from rapid cooling rates of 5 °C⋅min−1 and 20 °C⋅min−1 were provided in Supplementary Fig. 13 for contrast. Finally, the arrangement of ferroelectric nematic q-plate was guided by the photopatterned alignment layer combined with the flexoelectric coupling of FNLC. The obtained FNLC device was then observed using a crossed polarized optical microscope (DM2700P, Leica). For the right-handed FNLC q-superstructures, the photoaligned cell was filled with RM734 material mixed with a right-handed chiral dopant R811 at a concentration of 1.0 wt%.

Optical characterizations

In the nonlinear optical experiment, a Ti:sapphire femtosecond laser (Revolution, Coherent Inc.) was used to pump an optical parametric amplifier (Light Conversion). The optical parametric amplifier has a pulse duration of approximately 40 fs, a repetition rate of 1 kHz, enabling a tuned output wavelength ranging from 900 nm to 1300 nm. The collimated laser beam was focused onto the FNLC device by a spherical lens (f = 150 mm). Subsequently, the generated SHWs were re-collimated using an objective lens with the numerical aperture NA = 0.25. The non-zero orbital angular momentum states of incident FW were produced using nematic LC q-plates with q values of ±1/2. The experimental setup was depicted in Supplementary Fig. 14. The co- and cross-circularly polarized SHWs were sorted using a quarter-wave plate and a linear polarizer. The topological charges of generated orbital angular momentum states were characterized by a cylindrical lens49. The laser power was measured using a thermal power meter (S401C, Thorlabs).

Numerical modeling

The modulated FWs and the generated SHWs in the FNLC were calculated by the commercial software MATLAB R2022a, with the Jones matrix formalism and nonlinear susceptibility tensor calculation (second-order nonlinear polarization: \({P}_{i}^{2{{{\rm{\omega }}}}}={\varepsilon }_{0}{\sum}_{jk}{\chi }_{ijk}^{(2)}{E}_{j}^{{{{\rm{\omega }}}}}{E}_{k}^{{{{\rm{\omega }}}}}\)). Initially, the propagation behaviour of linearly or circularly polarized FW within the FNLC was calculated. Subsequently, the SHWs within the FNLC were derived by multiplying the second-order nonlinear susceptibility tensor with the distribution of the FW at each LC layer. Finally, the SHWs produced by each LC layer propagated toward the exit plane in the framework of linear optics, where they were accumulated. The far-field intensity profiles of SH vortices were then obtained using the Fourier transformation method50.