Introduction

Terrestrial ecosystems are profoundly influenced by various human-driven environmental changes1, such as climate warming, elevated CO2 concentrations, increased atmospheric nitrogen (N) deposition, and altered precipitation patterns. These global change factors (GCFs) not only alter the abiotic environment but also impact ecosystem structures and functions2. These impacts are largely dependent on the above- and below-ground organism components. Aboveground plants provide essential resources such as organic carbon, which is vital for the functioning of belowground decomposer organisms and root-associated organisms3. Decomposers, in turn, break down dead plant material, influencing nutrient availability, plant growth, and community composition4,5. Root-associated organisms, including herbivores, pathogens, and mutualistic symbionts, directly impact plant health and nutrient uptake6. This interdependence underscores the significance of aboveground - belowground (AG-BG) coupling for key ecosystem processes7. The interactions between above- and belowground organisms influence the quality, direction, and flow of energy and nutrients8,9. Any disruption or decoupling in these linkages can lead to imbalances in nutrient cycling10, and thus affect the overall functioning11,12 and stability of the terrestrial ecosystems13,14. Many global change experiments have been conducted worldwide in the last decades to simulate and better predict the impacts of climate change on terrestrial ecosystems15. While these experiments have revealed significant effects of GCFs on either above- or below-ground compartments16,17, the combined effects on both above- and below-ground ecosystem compartments have been largely overlooked7. Therefore, there is an urgent need to integrate above- and below-ground ecosystem sensitivities to GCFs to accurately predict future consequences of global environmental change.

Global change generally affects the composition and structure of plant communities18. For example, plant biomass is often promoted by elevated CO219, increased N deposition20, climate warming21, and increased precipitation22, while it is reduced by drought23. However, given the complexity of soil biota (e.g., microbes, protozoa, nematodes, and collembola), a distinct pattern is now emerging belowground. For instance, warming24, elevated CO225, and higher N deposition24 often negatively impact microbial biomass. Responses of soil microbes to GCFs depend on environmental conditions like ecosystem type and soil pH17. A meta-analysis showed that increased precipitation promoted the abundance of soil fauna, while warming and CO2 did not have a significant effect on the abundance of soil fauna26. Multiple meta-analyses have addressed the effects of global change on terrestrial ecosystems15,23, but none of them focused on the interactions between above- and belowground components whose interactions regulate fundamental functions of terrestrial ecosystems. Evidence from unique experiments suggests that aboveground and belowground components may decouple in response to global change. For example, increased N deposition weakened plant-microbe interactions in grassland ecosystems27. Positive correlations between aboveground plant biomass and microbial biomass were observed under elevated precipitation28, while this relationship disappeared under drought29. These varied relationships may arise from the distinct sensitivities exhibited in specific aboveground and belowground biota towards GCFs. In other words, different above- and belowground biota may respond differently to GCFs, leading to variations in their interactions and dynamics. Collectively, there is a major gap in understanding whether the current balance of above- and below-ground linkages will shift under future environmental change. This knowledge gap fundamentally constrains our ability to forecast the consequences of global change on terrestrial ecosystems.

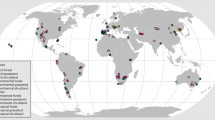
Here, we perform a global meta-analysis of 13,209 GCF experimental observations from 1166 publications across the world’s land ecosystems to quantify plant (biomass and diversity) and soil biota (biomass, diversity, and abundances) responses to GCFs in different biomes (Fig. 1). Soil biota includes soil microbes (bacteria and fungi), protozoa, nematodes, collembola, and other arthropods. The GCFs studied here include elevated CO2 (CO2), warming (W), precipitation reduction (PRE-), precipitation addition (PRE + ), nitrogen fertilization (N), phosphorus fertilization (P), and nitrogen and phosphorus fertilization (N + P). Further, we use 3223 paired data of plants and soil biota to examine above- and below-ground alignment and asynchrony of the responses. We hypothesize that the differential responses to GCFs may decouple above- and belowground processes, thus threatening the overall functioning of terrestrial ecosystems. In particular, the response of soil biota may be more sensitive relative to aboveground plants because of the inherent complexity of soil biota and a lack of consistent experimental methods used in the studies.

Fig. 1: Conceptual framework of this study showing the relationship between plants and belowground soil organisms in response to GCFs across global forests, grasslands, and croplands.
figure 1

The diagram in the upper right corner shows the distribution of the study sites in the Whittaker biomes78 mapped based on mean annual temperature and mean annual precipitation. The numbers in parentheses show sample sizes of plants and soil biota, respectively. Lines in different colors show the hypothetical relationships between the plant and soil-biota responses under GCFs; the dark blue line indicates a positive correlation between plant and soil-biota responses, the yellow line shows a negative correlation, and the gray line shows no significant relationship. CO2, elevated CO2; W, increased temperature; PRE-, precipitation reduction; PRE +, precipitation addition; N, nitrogen fertilization; P, phosphorus fertilization; N + P, nitrogen plus phosphorus fertilization. Symbols of global change factors, plants, soil microbes, and fauna were created by Qingshui Yu and Chenqi He.

Full size image

Results and discussion

Contrasting responses between plants and soil biota to GCFs

In general, except for PRE- causing a reduction in both aboveground plant biomass (AGB) and belowground plant biomass (BGB), all other GCFs were found to promote increases in both AGB and BGB (Fig. 2a, all P < 0.05). Specifically, CO2, W, PRE +, N, P and N + P increased AGB by 17.8% (95% confidence interval, 13.1–22.7%), 8.6% (4.1–13.4%), 22.3% (16.8–28.1%), 36.7% (32.0–41.5%), 29.0% (23.1–35.1%) and 65.5% (57.6–74.0%), respectively (Supplementary Table 3). BGB was increased by 8.0% (1.1–15.3%), 11.5% (4.4–19.2%), 9.5% (2.3–17.1%), 10.8% (5.5–16.5%), 20.8% (10.0–32.8%) and 15.0% (0.8–31.2%) under CO2, W, PRE +, N, P and N + P, respectively. PRE-alone decreased AGB by 19.7% (15.9–23.3%), consistent with earlier studies15,30. This suggests that plants will store more carbon in their biomass under most global change conditions except drought. AGB showed consistent trends in response to GCFs in forests, grasslands, and croplands (Fig. 2b), while BGB showed greater variability across ecosystems (Fig. 2c). For example, both PRE + and N addition increased BGB only in grasslands, and P addition decreased BGB only in forests. This indicates that GCFs may affect the pattern of biomass allocation between shoots and roots, allocating more biomass to the aboveground organs to maximize efficiency in the utilization of resources and increase chances of survival31. The reasons for the differences in the response of BGB to GCFs in different ecosystems may arise from the varying growth forms of plants, such as woody and herbaceous species, which exhibit distinct root responses to GCFs, probably owing to differences in xylem structural investment32.

Fig. 2: Responses of attributes of plant and soil biota to GCFs among global forests, grasslands, and croplands.
figure 2

a Mean effect sizes of plant and soil biota attributes under GCFs across all (combined forests, grasslands, and croplands) ecosystems. Green shapes indicate plant attributes, and yellow are soil biota attributes. Circles, regular triangles, squares, and inverted triangles denote plant aboveground biomass or soil biota biomass, plant belowground biomass, diversity, and abundance, respectively. b–d Effect sizes on plant aboveground biomass, plant belowground biomass, and plant diversity under GCFs among global forests, grasslands, and croplands. Different colored circles indicate various biomes. e–g Effect sizes of biomass, diversity, and abundance of soil biota under GCFs among global forests, grasslands, and croplands. Closed shapes are statistically significant and open shapes are not significant. Weighted means and their 95% confidence intervals of effect sizes are given. Numbers are sample sizes for each global change factor.

Full size image

While it may be expected that the magnitude of global change to have linear impacts on plants, our results showed that plant biomass was not linearly related to the duration nor intensity of GCFs. Specifically, the effect sizes of aboveground plant biomass responses generally exhibit an unimodal pattern (Supplementary Figs. 5a–10a), initially increasing and then declining or leveling off. These response trends indicate that plant growth may be inhibited if future global change surpasses a certain threshold. This aligns with observations from continental-scale forest monitoring plots showing that N deposition generally increases tree biomass until reaching a threshold value at which it becomes harmful33.

Along with the promotion of aboveground plant biomass, the response of plant species diversity generally decreased in response to GCFs, in spite of large variation (Fig. 2a, all P < 0.05). Under W, PRE-, N, P, and N + P, plant species diversity decreased by 5.4% (0.8–9.8%), 13.0% (9.3–16.5%), 15.7% (12.6–18.6%), 5.4% (0.8–9.7%), and 15.1% (11.1–18.9%), respectively (Supplementary Table 3). In comparison, PRE+ alone increased plant diversity in grasslands by 5.7% (1.2–10.3%) (Fig. 2d and Supplementary Table 4). Numerous individual studies demonstrate that GCFs lead to a loss of species richness by exacerbating environmental stresses that affect particularly sensitive species. For example, soil acidification due to elevated N deposition34,35, temperature extremes36, and severe drought37 can all reduce plant diversity, in line with our findings. We show that nutrient additions had the strongest negative effects on plant diversity among all GCFs considered in our study. This may be due to the greater dominance of a few individual taxa and the loss of sensitive species38,39 since nutrient additions change plant competitive interactions. In addition, effect sizes for plant diversity exhibited initially decreasing and subsequently increasing trends with duration and intensity in forests under the PRE- and N (Supplementary Figs. 5c, 6c) and in grasslands under W, N, and N + P (Supplementary Figs. 7c, 8c). We attribute this to plant acclimation to GCFs in non-managed ecosystems with longer-lived perennials and/or opportunities for new species colonization and establishment40.

Compared to the generalized plant aboveground responses, responses of soil biota to most GCFs were highly variable (Fig. 2a). Fewer GCFs exerted generally positive or negative effects on soil biota attributes, though there were some clear directional responses. The addition of CO2, P, and N + P resulted in increased soil biota biomass by 7.8% (2.0–13.8%), 7.0% (1.2–13.0%), and 8.8% (2.4–15.6%), respectively, whereas a decrease of 5.7% (2.0–9.4%) was observed under N addition (Supplementary Table 3). Addition of N alone caused a decline of 2.8% (1.0–4.6%) in soil biota diversity. PRE- led to a reduction of 22.2% (14.8–28.9%) in soil biota abundance. Conversely, PRE +, P, and N + P resulted in increases of 15.8% (4.4–28.4%), 17.4% (6.7–29.3%), and 43.2% (27.9–60.3%) in soil biota abundance, respectively. Across ecosystems, the biomass of soil biota increased in croplands under CO2 and N + P (Fig. 2e and Supplementary Table 4, all P < 0.05). Reductions in the diversity of soil biota were observed in croplands under PRE- and in forests under N (all P < 0.05) (Fig. 2f). PRE- reduced the abundance of soil biota in forests and in croplands (Fig. 2g, all P < 0.05). In contrast, the abundance of soil biota was enhanced under P in grasslands and croplands and under N + P in grasslands (all P < 0.05).

Responses of individual soil organism groups to GCFs showed various patterns for each ecosystem type (forest, grassland, and cropland; Supplementary Fig. 3). In forests, CO2 enrichment led to an increase in fungal and total microbial biomass, but N addition reduced their biomass (Supplementary Fig. 3a). The N Addition reduced bacterial and fungal diversity, and PRE- resulted in a reduction in the diversity and abundance of collembola and oribatida (Supplementary Fig. 3d, g). In grasslands, W, N, and N + P reduced the diversity of nematodes, but PRE + increased their diversity (Supplementary Fig. 3e). In croplands, CO2 enrichment increased the biomass of microorganisms and nematodes (Supplementary Fig. 3c); PRE- resulted in a reduced abundance of bacteria and nematodes (Supplementary Fig. 3i), whereas PRE + increased their abundance. Overall, these results demonstrate the distinct GCF responses in different taxa in different ecosystems, highlighting the complexity and variability of soil biota dynamics under various environmental factors and management practices.

Soil communities have been long considered the mysterious “black box” for several decades41. For instance, a number of drought experiments report profound shifts in soil microbial community composition and diversity42,43, while others observed unexpectedly high resistance44,45. Our synthesis reveals that this variation is typical of most GCFs, including drought. We also found that soil fauna, e.g., soil nematodes collembola, exhibited a higher sensitivity to precipitation changes, which may be because water availability can directly affect the metabolic functions of soil fauna46,47. What mechanisms underpin differential responses to GCFs by particular soil groups and ecosystems remains an open question. However, as for the plant responses, we find that the responses of soil biota are quadratically related to the duration and intensity of GCFs (Supplementary Figs. 5–10). In forests, biomass responses of soil biota first decreased and then began to flatten at the highest level of the GCF duration (Supplementary Fig. 5d) and intensity (Supplementary Fig. 6d) under N. However, opposite patterns were found for soil biota abundances with duration (Supplementary Fig. 5e) and intensity (Supplementary Fig. 6e) under PRE +. Traditionally, it was assumed that increased precipitation could lead to an overall increase in soil biota abundances26. The opposite patterns suggest that the response of soil biota to increased precipitation is not universally positive but can be more intricate. In croplands, experimental duration first decreased and then increased soil biota biomass (Supplementary Fig. 9b) and abundance (Supplementary Fig. 9d) under PRE- conditions. This can be interpreted as an adaptation of soil organisms to long-term drought stresses48. When we considered different soil organismal groups separately, their responses to specific GCFs were also generally non-linear with respect to duration (Supplementary Figs. 11, 12) and intensity (Supplementary Figs. 13, 14). This is consistent with some other studies that reported non-linear responses of soil organisms to GCFs49,50. Because these non-linear belowground responses show opposite directions to those of aboveground responses, they further documented uncoupled changes in some aboveground and belowground processes under future global environmental changes.

Plant and soil-biota responses to GCFs are usually uncoupled but not always

Based on paired observations of above- and belowground data, we found a significant positive correlation between the responses of aboveground and belowground biota to CO2 and PRE + (Fig. 3). In addition, the coupling coefficients of above- and belowground responses did not change with treatment duration and intensity, except for a positive trend under CO2 (Fig. 3a) and a negative trend under W (Fig. 3b). We also separately examined pair-wise relationships across ecosystem types to test whether these global trends are driven by strong responses within particular ecosystem-GCFs scenarios (Table 1, Supplementary Fig. 15 and Supplementary Table 10). Positive correlations between these response variables of plants and soil biota were observed in forests under CO2 (Fig. 4a), N (Supplementary Fig. 15l), and P (Supplementary Fig. 15o), in grasslands (Fig. 4b) and croplands under PRE + (Supplementary Fig. 15k) (all P < 0.05). We observed similar trends when testing separately different soil organismal groups (Supplementary Figs. 16, 17). Overall, we show little support for coupled responses to global change by pairing above- and below-ground data across various ecosystem types and groups of soil biota. Adair et al.51 found that plant diversity readily responded to N additions, while shifts in soil microbial communities were primarily driven by warming in the four-year GCF experiment, suggesting generally uncoupled above- and below-ground responses. This is consistent with our primary hypothesis, and it is expected from our individual above and belowground analyses since plants generally responded in a more concerted direction to GCFs than soil organisms.

Fig. 3: Overall relationships between the responses of plant and belowground soil biota under GCFs.
figure 3

Overall relationships between the responses of plant and belowground soil biota for seven GCFs (a–g) at the left panel, and the effect of experimental treatments (duration and intensity) on the coupling coefficients of the relationships for each GCF at the right of the panel. The aboveground and belowground responses represent the relative changes of biomass, diversity, and abundance in plants and soil biota to different GCFs based on paired data. Relative changes were calculated as the logarithm of the ratio of the variable within each treatment plot divided by the same variable in the control plot. Point size indicates the weight of the sample size. P-values represent the statistical significance of coefficients by the two-sided z-test, and n represents study observations, respectively. Different lines indicate fitted relationships for each treatment based on the “REML” method in mixed-effects meta-regression. The solid lines indicate a significant difference (P < 0.05) from zero for the coupling coefficient, and the dashed lines indicate non-significance.

Full size image
Table 1 Statistics on relationships between plant and soil biota responses to GCFs across forests, grasslands, and croplands in mixed-effects meta-regression models
Full size table
Fig. 4: Significant linkages between the responses of plant and belowground soil biota under specific GCFs and relationship types.
figure 4

a Positive relationships between the responses of the plants and soil biota under CO2 in forests and (b) under PRE+ in grasslands. Point size indicates the weight of the sample size. P values represent the statistical significance of coefficients by the two-sided z-test, and n represents study observations, respectively. The solid lines indicate a significant difference (P < 0.05) from zero for the coupling coefficient, and the dashed lines indicate non-significance. Black lines show overall relationships between the responses of the aboveground and belowground compartments, the shades represent 95% confidence intervals. Other colored lines show different relationship types between corresponding variables of plants and soil biota. The posterior distribution of the coefficient is based on the Bayesian hierarchical meta-regression. The gray distribution indicates the posterior coefficient distribution of the overall relationship. c Different colored posterior distributions represent corresponding relationship types between plant aboveground biomass (AGB), plant belowground biomass (BGB), plant diversity (AGD) and soil biota diversity (SBD), soil biota abundance (SBA), soil biota biomass (SBB). Points indicate the mean of coefficients, and thick and thin bars represent 95% and 90% confidence intervals, respectively.

Full size image

Why would plants and soil organisms respond differently to global change? There are three main explanations for our observations. First, it is possible that GCFs disrupted an originally balanced nutrient cycling between above- and below-ground organisms52. Interactions like mycorrhizal symbiosis, which feedback to influence both above- and below-ground diversity, break down under certain GCFs if plants no longer rely on fungi for nutrients53, or if compatible partners become less available54. Second, drivers of above- and belowground biomass and biodiversity are also inherently different. Belowground biota is more likely driven by water availability42, whereas the plant biodiversity showed greater sensitivity to climate warming55. Changes to one of these factors due to global change can, therefore, more strongly impact either above- or below-ground communities. Third, there may be a time lag before changes in the plant community affect belowground communities (and vice versa) due to differences in growth rates between macro- and microorganisms. For example, Liu, et al.56 and Wilcox, et al.57 observed phenological mismatches between above- and below-ground plant parts in response to climate warming. Changes in belowground plant biomass often follow aboveground changes58, which implies that the impacts of lagged changes in carbon and biomass allocation could lead to asynchronous responses of soil biota and plant communities. The decoupling of root biomass and soil biota responses suggests substantial differences between aboveground and belowground systems. Aboveground decoupling with soil biota may primarily reflect changes in light availability and plant competition, influencing litter quality and microbial activity in the soil59,60. In contrast, below-ground decoupling with soil biota often relates to root exudate dynamics and nutrient uptake61,62, which can be less responsive to immediate environmental changes. This difference implies that the interactions between plants and soil biota are mediated by different mechanisms, affecting ecosystem processes such as nutrient cycling and plant health. It is likely that all three of the above together explain the de-coupling of above- and below-ground responses to GCFs. However, we also note that aboveground plant indicators were measured in a relatively uniform way, while the experimental methods for belowground biological indicators were more varied and complex63, potentially biasing our findings of uncoupled aboveground-belowground relationships.

Despite the generally uncoupled above- and belowground responses to GCFs, we did find positive correlations between the responses of plants and soil biota in forests under CO2, N, and P, and in grassland under PRE +. This is particularly important given the projected increases in forest tree growth in response to elevated CO2. For example, our results suggest that elevated CO2 generally promotes plant and soil microbial biomass in forests, which should ultimately increase ecosystem both above and belowground C storage64. We find the same patterns with increased precipitation in grasslands, i.e., coupled increases in plant and microbial biomass under irrigation. While the effects of GCFs are obviously complicated when we consider both above- and below-ground responses, these findings help us predict the effects of different types of GCFs in forest vs. grassland ecosystems. Additionally, the uncoupling effects were observed under W and PRE-, as well as N + P treatments. Consequently, future climate change research should place an emphasis on investigating the impacts of temperature increases, drought, and fertilization. This will enhance our understanding of how these factors influence ecosystem dynamics and interactions between aboveground and belowground components.

Clarifying above- and belowground ecological responses and their relationships in ecosystems under global change is essential for maintaining, conserving, restoring, and predicting ecosystem functioning in the future65,66,67. Our study shows that aboveground and belowground communities do not respond synchronously to global change and, therefore, whole-ecosystem responses cannot be predicted by looking only at one subsystem in isolation. In particular, attempts to use relatively well-understood aboveground ecosystem compartments to understand and predict what will happen belowground and in the total ecosystem can be erroneous, even though observing what happens aboveground across scales using satellite imagery is increasingly considered a standard for whole-ecosystem monitoring. Our study underscores the need to deepen our understanding of below-ground responses to GCFs, as our results reveal significant variability in the strength and direction of below-ground responses to global environmental change. Joint considerations of aboveground and belowground responses are critical for informing conservation and climate change mitigation strategies.

Methods

Data collection and processing

We used meta-analysis to assess the effects of global change factors (GCFs) on aboveground plant and belowground soil biota across global ecosystems. A comprehensive literature survey was conducted according to specific search criteria (Supplementary Table 1) in the Web of Science and the China National Knowledge Infrastructure (CNKI), with the final search occurring in April 2024. All publications were screened according to the following criteria: (1) GCF experiments were conducted in terrestrial ecosystems; (2) the GCFs included at least one out of seven treatments of elevated CO2 concentrations (hereafter: CO2), increased temperatures (W), precipitation reduction (PRE-) or precipitation addition (PRE + ), nitrogen fertilization (N), phosphorus fertilization (P), nitrogen and phosphorus fertilization (N + P); (3) each publication included at least one of the indicators of the plant (aboveground or belowground biomass, diversity) and soil biota (biomass, diversity and abundances); and (4) for pairwise data, each publication includes at least one indicator of biomass, diversity, and/or abundances of both plants and soil biota. The screened data included different indicators of plant and soil attributes that allow us to identify how both biodiversity and abundance shifted with GCFs (Supplementary Table 2). Plant attribute data included plant aboveground biomass and diversity (i.e., species richness or Shannon index). Phospholipid fatty acid (PLFA) or microbial biomass carbon were used as indicators of the biomass of bacteria, fungi, and total microbes, which are two metrics of microbial biomass that are strongly correlated68. The biomass of soil fauna was defined as g mass per m2. We used operational taxonomic units (OTU), the most reported molecular species concept for microbes, to calculate soil biota diversity (i.e., OTU richness or Shannon index). Gene copies per ng DNA were used to characterize the abundance of bacteria and fungi, and the number of individuals was used to quantify the abundance of soil fauna. We identified a total of 13,209 observations from 1166 publications matching our selection procedures (Supplementary Fig. 1). These study sites were located along an extensive range of climatic zones (see Whittaker biomes in Fig. 1). From this set of observations, 3223 pairwise observations of plants and soil biota from 241 publications were extracted (Supplementary Fig. 2). We also extracted data on location (latitude, and longitude), mean annual temperature (MAT), mean annual precipitation (MAP), type, intensity, and duration of the GCF treatments, vegetation type, and taxa of soil biota. GetData Graph Digitizer 2.25 (https://getdata-graph-digitizer.com/) was used to extract data from figures if individual datasets were not available. We supplemented missing standard deviation (SD) data by establishing a linear regression between the log SD and the log of the mean value69 under separate GCFs. There were a total of 143 missing SDs. We computed the SD missing values using the impute_SD () function of the “Metagear” package in R language. MAT and MAP were taken directly from the original study or from papers cited in that study. If the MAP and MAT were not reported in the publication, we extracted them from the WorldClim database (www.worldclim.com)70.

The publication screening process was demonstrated in Supplementary Fig. 1. The screened data included different indicators of biomass, diversity, and abundance of plants and soil biota. We classified plants into three ecosystem types: forests, grasslands, and croplands. Belowground soil biota was divided into four groups: bacteria, fungi, total microbes, and fauna. The collected publications encompassed studies that conducted one or more than one of seven single-factor experiments, including elevated CO2 concentrations (CO2, ppm), increased temperature (W, °C), precipitation reduction (PRE-, %), precipitation addition (PRE +, %), nitrogen addition (N, Kg/ha), phosphorus addition (P, Kg/ha), nitrogen and phosphorus addition (N + P, Kg/ha). We recorded the experiment information, including the duration and intensity of the treatments, and considered their impacts on the change of response variables. Description of the intensities of GCFs is as follows: CO2, the concentration of anthropogenic inputs of CO2 (ppm) in treatment plots; W, air or soil temperature increase (°C) in treatment plots over control plots; PRE-, reduced precipitation or soil moisture (%) in treatment plots compared with controlled plots; PRE +, increase precipitation or soil moisture (%) in treatment plots compared with controlled plots; N, amount of nitrogen fertilizer applied in treatment plots; P, amount of phosphorus fertilizer applied in treatment plots; N + P, amount of combined nitrogen and phosphorus fertilizer applied in treatment plots. The units of each treatment were unified between different sites. Unifying the scaling of duration time (yr) between different GCF experiments was simple, however the units of treatment intensity were various. We used the deviation standardization method to scale the intensity of specific GCF treatment (\({x}_{T,i}\)) into [0,1]:

$${{x}_{T,i}}{*}=\frac{{{x}_{T,i}}^{-}{\min}_{1\le j\le n}\left\{{x}_{T,j}\right\}}{{{\max}_{1\le j\le n}}{\left\{{x}_{T,j}\right\}-}{{\min}_{1\le j\le n}}{\left\{{x}_{T,j}\right\}}}$$
(1)

Where \({{x}_{T,i}}^{*}\) was the treatment (T) intensity of observation i after unifying scaling into \(\left[{{\mathrm{0,1}}}\right]\). \({\max }_{1\le j\le n}\{{x}_{T,j}\}\) or \({\min }_{1\le j\le n}\{{x}_{T,j}\}\) indicates the maximum and minimum of treatment (T) intensity among n observations.

The effect size of GCF on any individual response variable was estimated for each observation and calculated as the natural logarithm-transformed (ln) of the response ratio (RR):

$${{{\rm{RR}}}}=\,{{{\mathrm{ln}}}}\left(\frac{{\bar{Y}}_{T}}{{\bar{Y}}_{C}}\right)$$
(2)

Where \({\bar{Y}}_{T}\) and \({\bar{Y}}_{C}\) are the mean of response variables in the treatment and control plots, respectively. For observations that only included the standard error (SE), the standard deviation (SD) was estimated with the following formula:

$${{{\rm{SD}}}}={{{\rm{SE}}}}\sqrt{n}$$
(3)

Where n is the sample size of each treatment. The variance of each RR was calculated as:

$$v=\frac{{{{{{\rm{SD}}}}}_{T}}^{2}}{{n}_{T}{{\bar{Y}}_{T}}^{2}}+\frac{{{{{{\rm{SD}}}}}_{C}}^{2}}{{n}_{C}{{\bar{Y}}_{C}}^{2}}$$
(4)

Where the \({n}_{T}\) and \({n}_{C}\) are the sample sizes of the response variables in the treatment and control plots; \({{SD}}_{T}\) and \({{SD}}_{C}\) are the standard deviation of the variables in the treatment and control plots, respectively.

Analysis of plant and soil-biota responses to GCFs

We analyzed 13,209 observations from 1166 publications to assess plant and soil biota responses to GCFs across forests, grasslands, and croplands. The response ratio was quantified separately for plants and soil biota:

$${{{{\rm{RR}}}}}_{plant}={{{\rm{In}}}}\left(\frac{{\bar{Y}}_{{T}_{plant}}}{{\bar{Y}}_{{c}_{plant}}}\right)$$
(5)
$${{{{\rm{RR}}}}}_{soil}={{{\rm{In}}}}\left(\frac{{\bar{Y}}_{{T}_{soil}}}{{Y}_{{c}_{soil}}}\right)$$
(6)

Where \({{RR}}_{{plant}}\) and \({{RR}}_{{soil}}\) represent the response ratios of single plant and soil biota observation, respectively. For each observation, \({\bar{Y}}_{{T}_{plant}}\) and \({\bar{Y}}_{{C}_{plant}}\) are the mean response variables of plants in the treatment and control plots; \({\bar{Y}}_{{T}_{soil}}\) and \({\bar{Y}}_{{C}_{soil}}\) are the mean response variables of soil biota in the treatment and control plots. To minimize the influence of outliers, all response ratios and their variance between the 2.5 % and 97.5% quantiles were selected for further analysis. For plants, we analyzed biomass and diversity. Soil biota attributes included biomass, diversity, and abundance, categorized into four groups: bacteria, fungi, total microbes, and fauna.

Models of GCF treatment effects

Independence between samples is crucial for pooling effect sizes and conducting meta-regression analyses71. Due to the multilevel structure of our data and the potential non-independence of some samples, we used a hierarchical mixed-effect model72 without the intercept to evaluate the effects of GCF treatments on plants and soil biota:

$${{{{\rm{RR}}}}}_{{plant},{ijlmn}}={\beta }_{T}T+{\mu }_{i}+{\mu }_{{ij}}+{\mu }_{l}+{\mu }_{{lm}}+{e}_{{lmn}}$$
(7)
$${{{{\rm{RR}}}}}_{soil,ijklmn}={\beta }_{T}T+{\mu }_{i}+{\mu }_{ij}+{\mu }_{k}+{\mu }_{l}+{\mu }_{lm}+{e}_{lmn}$$
(8)
$${\beta }_{p,T}=(\exp ({\beta }_{T})-1)\times 100\%$$
(9)

In our model, \(T\) is a categorical variable representing the fixed effects of seven GCF treatments.\(\,{\beta }_{T}\) indicates the estimated mean effect size of each GCF treatment. The random effects include both crossed and nested structures: \({\mu }_{i}\) is the between-site heterogeneity based on latitude and longitude. \({\mu }_{{ij}}\) is the between-publication heterogeneity and nested within-site heterogeneity, accounting for different studies conducted at the same site. \({\mu }_{l}\) is the heterogeneity of ecosystems (forest, grassland, and cropland), and it is crossed with other random effects because, generally there is only a single ecosystem being studied at a site. \({\mu }_{{lm}}\) is the between-experiment heterogeneity, including the duration and intensity of experiments, and it is nested within the ecosystem as there are multiple experimental conditions setup for the ecosystem. \({e}_{{lmn}}\) is the sampling level residual, and it is nested within the experiment heterogeneity to account for sampling errors. Equation (7) shows the effect of GCF treatments on plants, while Eq. (8) presents this for belowground observations, incorporating soil biota into a crossed random effect (\({\mu }_{k}\)), divided into bacteria, fungi, total microbes, and fauna, because the soil biota group varied across all sites and ecosystems in our dataset. For clarity, we converted \({\beta }_{T}\) to a percentage change (\({\beta }_{T}\)) for an intuitive interpretation of the results (Eq. 9).

Models of ecosystem effects

Given that forests, grasslands, and croplands may respond differently to GCF treatments, we analyzed the effects of these treatments for different ecosystems:

$${{{{\rm{RR}}}}}_{T,ijkmn}={\beta }_{E}E+{\mu }_{i}+{\mu }_{ij}+{\mu }_{k}+{\mu }_{m}+{e}_{mn}$$
(10)

Where \({{RR}}_{T,{ijklm}}\) represents the response ratio for an observation under a specific GCF treatment (\(T\)). The ecosystem (\(E\)) is a categorical variable and acts as the fixed effect, \({\beta }_{E}\) denoting the estimated mean effect size for each ecosystem. Most of the random effect structures are unchanged. \({\mu }_{i}\) is the between-site heterogeneity. \({\mu }_{{ij}}\) is the between-publication heterogeneity and nested within between-site heterogeneity. \({\mu }_{m}\) is the between-experiment heterogeneity. \({e}_{{mn}}\) is the sampling level residual. For below-ground analysis, a crossed random effect for soil biota (\({\mu }_{k}\)) is included. We also converted \({\beta }_{E}\) to a percentage change for easier interpretation (Eq. 9).

Sensitivity test

Since the soil biota contains various microorganism and invertebrate groups, to evaluate the response of various soil organism groups to GCF treatments, we used the following model:

$${{{{\rm{RR}}}}}_{T,ijmn}={\beta }_{S}S+{\mu }_{i}+{\mu }_{ij}+{\mu }_{m}+{e}_{mn}$$
(11)

Where \({{RR}}_{T,{ijmn}}\) represents the response ratio of soil biota to a specific GCF treatment (\(T\)). The soil organism group (\(S\)) is a categorical variable acting as the fixed effect, including eight major groups: bacteria, fungi, microbes, arthropods, collembola, oribatida, nematode, and protozoan. \({\beta }_{S}\) denotes the estimated mean effect size for each group. We compared the propensity of mean effect size (\({\beta }_{S}\)) of different soil organism groups with those in specific ecosystems (\({\beta }_{E}\)) to assess their sensitivity to GCF treatments (Supplementary Fig. 3).

In addition, we considered metric units as fixed effects to evaluate the sensitivity of mean effect sizes to different metrics of biomass, diversity, and abundance for plants and soil biota. Results showed consistent responses across different metrics (Supplementary Fig. 4).

We also analyzed the effects of treatment duration and intensity on plant and soil biota responses to GCFs using linear and quadratic meta-regression models without intercepts. Duration and intensity were continuous variables chosen as fixed effects, while other random effect structures remained unchanged. We compared the AIC and BIC indices between linear and quadratic models and tested the significance of the estimated coefficients of fixed effects (Supplementary Tables 5, 6). The quadratic model was ultimately selected due to the parabolic distribution of the data (Supplementary Figs. 5–14). All mixed-effect model construction and analyses were conducted in R 4.0.5 using the “metafor” package73,74.

Relationships between plants and soil biota responses to GCFs

We analyzed 3223 paired observations from 241 publications to examine the relationships between plant and soil biota responses to GCFs. A hierarchical mixed-effects model was developed to investigate these relationships:

$${{{{\rm{RR}}}}}_{plant,T}={\beta }_{0}+{\beta }_{1}{{{{\rm{RR}}}}}_{soil,T}+{\mu }_{i}+{\mu }_{ij}+{\mu }_{k}+{\mu }_{r}+{\mu }_{l}+{\mu }_{lm}+{e}_{lmn}$$
(12)

Where, \({{RR}}_{{plant},T}\) and \({{RR}}_{{soil},T}\) are the response ratios of plant and soil biota observations under specific GCF treatments (\(T\)). \({\beta }_{0}\) is the intercept, and \({\beta }_{1}\) is the estimated correlation coefficient between plant and soil biota responses. The random effect structures are similar to previous models. Specifically, we considered relationship types (\({\mu }_{r}\)) as a crossed effect in the random effect structure due to their variation across ecosystems and soil biota. We examined nine relationship types: plants diversity – soil biota diversity; plants diversity – soil biota abundance; plants diversity – soil biota biomass; plants aboveground biomass – soil biota diversity; plants aboveground biomass – soil biota abundance; plants aboveground biomass – soil biota biomass; plants belowground biomass – soil biota diversity; plants belowground biomass – soil biota abundance; plants belowground biomass – soil biota biomass. In addition, the coupling responses of plants and soil biota to GCFs across three ecosystems and the nine relationship types were examined separately (Supplementary Fig. 15). We summarized the P-value of \({\beta }_{1}\) to infer the significance of these relationships (α = 0.05) via the restricted maximum-likelihood method in mixed-effects meta-regression. For forests and grasslands showing significant relationships between plant and soil biota responses under specific GCF treatments, results were presented individually for better interpretation.

Bayesian regression models

To obtain more reliable confidence intervals for the estimated correlation coefficient (\({\beta }_{1}\)) and solidify our model results, we employed a Bayesian regression approach. This method allowed us to infer the posterior distributions of coefficients and evaluate if their bounds contain zero (α = 0.05). The posterior distributions were estimated using Bayesian inference with MCMC samplers via the “brms” package75. All Bayesian regression models were fitted with four chains, 8000 iterations, and 4000 warm-up iterations, with a thinning rate of 10. Uninformative priors were assigned to the intercept and coefficients (normal distribution with mean 0 and standard deviation 2) and to the standard deviations (Half-Cauchy distribution with mean 0 and standard deviation 1). The maximum tree depth was set to 15, and the adapt delta was adjusted to no more than 0.999 to prevent divergent transitions and ensure reliable inference. Convergence was confirmed by R-hat values being less than 1.01 and bulk-ESS greater than 400.

Sensitivity test

We assessed how treatment duration and intensity affect the correlation between plant and soil biota responses. Two interaction terms were added to the model, with the random effects structure similar to Eq. (12):

$${{{{\rm{RR}}}}}_{plant,T}={\beta }_{0}+{\beta }_{1}{{{{\rm{RR}}}}}_{soil,T}+{\beta }_{2}{{{\rm{Duration}}}}\times {{{{\rm{RR}}}}}_{soil,T}\\+{\beta }_{3}{{{\rm{Intensity}}}}\times {{{{\rm{RR}}}}}_{soil,T}+{\mu }_{i}+{\mu }_{ij}+{\mu }_{k}+{\mu }_{r}+{\mu }_{l}+{\mu }_{lm}+{e}_{lmn}$$
(13)

Where, \({\beta }_{2}\) is the estimated correlation coefficient for the interaction between the soil biota response ratio (\({{RR}}_{{soil},{T}}\)) and treatment duration. \({\beta }_{3}\) is the correlation coefficient for the interaction between the soil biota response ratio and treatment intensity under specific GCF treatments (\(T\)). We summarized the P value of the correlation coefficients to infer the significance of these relationships (α = 0.05). A significant difference (P < 0.05) from zero indicates that the relationships of responses change with experimental treatments.

In addition, we analyzed the sensitivity of relationships for different soil biota groups. We modeled the aboveground and belowground relationships for bacteria, fungi, microbes, and fauna. Moreover, we also focused on five soil fauna groups with abundant observation data: arthropod, collembola, oribatid, nematode, and protozoan. We analyzed these soil groups separately and estimated the correlation coefficients for each soil fauna group (Supplementary Figs. 16, 17). We summarized the P value of the coefficient to infer the significance of these relationships (α = 0.05).

Publication bias analysis

Publication bias refers to the fact that findings with statistically significant research are more likely to be reported and published than findings that are not significant and invalid. We conducted a publication bias analysis using Egger’s coefficient and applied the trim and fill method to calculate corrected effect sizes if bias was identified76,77. Although we detected marginal publication bias in some variables (Supplementary Tables 7–9), most of the corrected effect sizes were close to original values and maintained the same sign, indicating that our results were robust against marginal publication biases.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.