Introduction

Quantum information processing requires qubits with long coherence time enabling high-fidelity quantum gates. Over the past two decades, superconducting circuits have led to the realization of quantum processors of ever-growing size made of qubits with steadily improving fidelities1. This way, superconducting qubits have become one of the most advanced physical platforms for quantum computing. Progress has been driven by material engineering and optimization, as well as by the development of new device concepts capable of providing a growing level of protection against noise sources in the environment2,3,4. Qubit protection against relaxation and dephasing processes can be granted from the symmetry properties of the qubit Hamiltonian. In this direction, a variety of possible solutions have been proposed and only partly explored5,6,7,8,9,10,11. One of the leading ideas is to create superconducting qubits whose two lowest energy states are associated with odd and even numbers of Cooper pairs in a superconducting island, respectively. Due to the different parity, these states are orthogonal to each other in both charge and phase space12,13,14,15,16,17,18,19. This type of parity-protected qubit requires a parity-preserving Josephson element that only allows the coherent transfer of correlated pairs of Cooper pairs, which translates into devising a Josephson circuit with a π-periodic, \(\sin (2\varphi )\) current phase relation (CPR).

Some proposals to engineer such a \(\sin (2\varphi )\) qubits rely on conventional \(\sin (\varphi )\) Josephson junctions, either arranged into large arrays14 or embedded in a superconducting quantum interference device (SQUID) together with extremely large inductances15. The practical realization of these ideas is technologically challenging and some significant experimental progress was reported only recently19. Another approach is to leverage the multi-harmonic CPR and the gate tunability of superconductor(S)–semiconductor(Sm) Josephson field-effect transistors (JoFETs)20,21,22,23,24,25,26,27,28,29. Various signatures of \(\sin (2\varphi )\) Josephson elements were recently reported30,31,32,33,34,35 and harnessed to demonstrate some first experimental evidence of parity protection16. However, a direct measurement of a \(\sin (2\varphi )\) CPR, a precise quantitative evaluation of its harmonic purity including the flux and gate tunability and the influence of the SQUID arm inductance, have been missing so far. These important aspects are addressed in the present work.

Our experimental study takes advantage of a recently developed S–Sm platform based on SiGe/Ge/SiGe quantum-well heterostructures36. Notably, these heterostructures embed a high-mobility two-dimensional hole gas enabling the reproducible top-down fabrication of multi-harmonic, gate-tunable Josephson junctions. We investigate the CPR of a SQUID incorporating two of such junctions, in short a G-SQUID. We demonstrate ample gate and magnetic-flux control of the Josephson harmonic content. By a quantitative analysis based on a fully comprehensive model of our circuit, we show that half a flux quantum through the SQUID results in an unprecedented suppression of the first junction harmonic, which is reduced by two orders of magnitude. Under these conditions, the desired \(\sin (2\varphi )\) (i.e., charge-4e) contribution to the supercurrent flow reaches up to 95.2% of the total supercurrent. This achievement is a significant step forward in the development and optimization of a semiconductor-based parity-protected qubit.

Results

Device and measurement setup

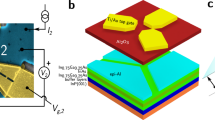
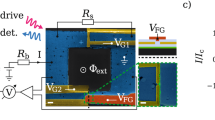
The G-SQUID (shown in Fig. 1a) consists of an aluminum superconducting loop with nearly symmetric arms embedding two nominally identical JoFETs fabricated out of a SiGe/Ge/SiGe quantum-well heterostructure. The compressively strained Ge quantum well lies 22 nm beneath the semiconductor surface and hosts a two-dimensional hole gas exhibiting mobility of 105 cm2/Vs measured at a carrier density of 6 × 1011 cm−2. The two JoFETs, JN1 and JN2, have a 1 μm-wide and a 300 nm-long Ge channel, short enough to be considered as quasi-ballistic junctions (for more details on the JoFETs see Supplementary Note 1). The G-SQUID is embedded in a second larger loop together with a wider reference JoFET, JW, (10 μm-wide and 300 nm-long Ge channel), enabling a direct CPR measurement20,22,37,38,39,40,41,42. To this purpose, JW is designed to have a critical current much larger than those of JN1 and JN2. The small and large superconducting loops are locally flux-biased by means of two 10 μm-wide and 50 nm-thick Al lines whose cross-talks have been calibrated in situ and then implicitly compensated throughout the rest of the paper (see Supplementary Note 6).

Fig. 1: Double SQUID device and single-JoFET characteristics.
figure 1

a Schematic and scanning electron micrograph of the device. A Ge-based SQUID (G-SQUID), embedding JoFETs JN1 and JN2, is connected in parallel to a wider JoFET (JW) used as a reference Josephson junction for current-phase-relation (CPR) measurements. The aluminum arms are modeled by three inductances: L1, L2 and LW. b–d Current-biased measurements of the JoFET characteristics for JW, JN1, and JN2, respectively. In each panel, the measured source-drain voltage is plotted as a function of gate voltage, \({V}_{{{{\rm{G}}}}}^{i}\) (i = W, N1, N2), and source-drain current bias IDC. e (resp. f), Left: critical current, IC, as a function of magnetic flux Φ1 through the large loop in (a). The reference JoFET JW is biased to strong accumulation (\({V}_{{{{\rm{G}}}}}^{W}=-\!1.5\,{{{\rm{V}}}}\)), JN2 (resp. JN1) is pinched off and \({V}_{{{{\rm{G}}}}}^{{{{\rm{N1}}}}}=-\!0.6\,{{{\rm{V}}}}\) (resp. \({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=-\!1.5\,{{{\rm{V}}}}\)). The IC oscillations are a direct measurement of JN2 (resp. JN1) CPR. Right: Fast Fourier transform (FFT) of the CPR on the left, calculated over 15 Φ0. Black dashed line: calculated CPR and FFT based on the circuit model in a with parameters obtained from a fit of the data in Fig. 2a.

Full size image

Furthermore, we stress that the Al arms have small but non-negligible inductances, mostly of kinetic origin, that we label as L1, L2, and LW. As our later analysis will reveal, properly extracting the intrinsic harmonic content of the JoFET CPRs from the measurements requires taking these inductances into account. In the rest of the paper, all of the calculated curves are obtained using the circuit model shown in Fig. 1a (see Supplementary Note 2 for more details).

All measurements were performed in a dilution refrigerator at a base temperature of 38 mK, see Supplementary Note 8. A detailed description of the fabrication process and the measurement methods was provided in our previous publications32,43.

Characterization of the individual JOFETs

To access the individual DC transport characteristic of a given JoFET in such a parallel configuration, we purposely apply large positive gate voltages (≈1.5 V) to the other JoFETs, thereby suppressing current flow through their respective arms. The resulting individual characteristics of JW, JN1, and JN2 as a function of their respective gate voltages are shown on the color scale in Fig. 1b–d, with the corresponding circuit measurement schematics displayed in the insets.

For all the JoFETs, the current at which the device switches from superconducting to normal state, close to the critical current IC, is clearly visible as an abrupt change of the measured source-drain voltage drop from 0 to a finite value. The three JoFETs exhibit a similar behavior denoting consistent properties of the Ge channel and the superconducting contacts. In particular, we note that the two narrow JoFETs, designed to be identical, have very similar \({I}_{C}^{{{{\rm{Ni}}}}}({V}_{{{{\rm{G}}}}}^{{{{\rm{Ni}}}}})\) characteristics.

By varying the magnetic flux, Φ1, through the larger loop we can sequentially measure the CPR of each JoFET in the G-SQUID. To this aim, the reference JoFET, JW, is biased at full accumulation (\({V}_{{{{\rm{G}}}}}^{{{{\rm{W}}}}}=-1.5\,{{{\rm{V}}}}\)) such that the necessary condition \({I}_{C}^{{{{\rm{W}}}}}\, \gg \,{I}_{C}^{{{{{\rm{N}}}}}_{{{{\rm{1}}}}}},{I}_{C}^{{{{{\rm{N}}}}}_{{{{\rm{2}}}}}}\) is fulfilled37,44. To measure the \({J}_{{N}_{1}}\) (\({J}_{{N}_{2}}\)) CPR, we apply \({V}_{{{{\rm{G}}}}}^{{{{{\rm{N}}}}}_{{{{\rm{1}}}}}}=-0.6\,{{{\rm{V}}}}\) (\({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=-1.5\,{{{\rm{V}}}}\)) while \({J}_{{N}_{2}}\) (\({J}_{{N}_{1}}\)) is pinched off by setting \({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=1.5\,{{{\rm{V}}}}\) (\({V}_{{{{\rm{G}}}}}^{{{{\rm{N1}}}}}=1.5\,{{{\rm{V}}}}\)). The on-state voltages \({V}_{{{{\rm{G}}}}}^{{{{\rm{N1}}}}}=-0.6\,{{{\rm{V}}}}\) and \({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=-1.5\,{{{\rm{V}}}}\) are chosen to obtain equal amplitudes of the first CPR harmonic. As we shall see below, operating the G-SQUID at these gate voltages enables the suppression of the first harmonic by flux-induced destructive interference, hence leaving a dominant sin(2φ) component.

The measured CPRs are shown in Fig. 1e, f together with the respective Fourier transforms. A total of 15 flux periods were measured in order to ensure sufficient resolution of the harmonics in Fourier space. Each reported IC data point represents the median value obtained from 10 measurements, with the light green area indicating  ±1 standard deviation. Both CPRs are clearly skewed and we distinguish up to five harmonics. This multi-harmonicity indicates a high transparency of the superconducting contacts, which is consistent with earlier observations with similar devices30,32. Yet, as we shall discuss below, the higher harmonics, especially the fourth and fifth ones, have largely enhanced amplitudes due to the finite inductance of the aluminum arms.

sin(2φ) Josephson element

With the two JoFETs JN1 and JN2 independently characterized, we now turn to the study of the G-SQUID CPR, once again using JW as a reference (\({V}_{{{{\rm{G}}}}}^{{{{\rm{W}}}}}=-1.5\,{{{\rm{V}}}}\)). With the ultimate goal to engineer a sin(2φ) Josephson element, we symmetrize the G-SQUID by applying \({V}_{{{{\rm{G}}}}}^{{{{\rm{N1}}}}}=-0.6\,{{{\rm{V}}}}\) and \({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=-1.5\,{{{\rm{V}}}}\). These two values have been chosen such that the critical current amplitudes of the two junctions are equal. As it will be shown later, it also implies very similar harmonic contents, corroborating the reproducible electronic properties of our junctions.

Figure 2a shows a measurement of the G-SQUID critical current as a function of Φ1 and Φ2, the latter being the magnetic flux through the G-SQUID loop. This is the most important data set.

Fig. 2: Frequency doubling of the G-SQUID CPR.
figure 2

The G-SQUID is symmetrized by setting \({V}_{{{{\rm{G}}}}}^{{{{\rm{N1}}}}}=-1.5\,{{{\rm{V}}}}\) and \({V}_{{{{\rm{G}}}}}^{{{{\rm{N2}}}}}=-0.6\,{{{\rm{V}}}}\), which equalizes the amplitudes of the first harmonics in JN1 and JN2. JW is kept in strong accumulation (\({V}_{{{{\rm{G}}}}}^{{{{\rm{W}}}}}=-1.5\,{{{\rm{V}}}}\)). a Critical current as a function of the two compensated magnetic fluxes, Φ1 and Φ2, threading the large superconducting loop and the G-SQUID, respectively. b–d G-SQUID CPR (IC vs Φ1) for Φ2 = 0,  −Φ0/4, and  −Φ0/2, i.e., at the line cuts denoted by green lines in (a). e–g The FFTs obtained from the CPRs in (b–d), respectively, are calculated over 15 Φ0. Black dashed lines in b–g are calculated CPRs (FFTs) based on the circuit model in Fig. 1a with parameters obtained from a fit of the data in a. In d, following a suppression of the odd harmonics (clearly shown in d), we observe the doubling of the CPR frequency as expected for a \(\sin (2\varphi )\) Josephson element.

Full size image

We fit the entire two-dimensional plot to the circuit model shown in Fig. 1a, with fixed inductances of the Al arms (see Supplementary Note 1) and 12 free parameters accounting for the amplitudes of the first four harmonics of the three JoFETs (see Supplementary Note 2 for details). Interestingly, the fit yields negligible amplitudes for all the fourth-order harmonics, implying that only three harmonics per JoFET are sufficient to reproduce the data. This outcome apparently contrasts with the experimental data in Fig. 1e, f, where up to five harmonics can be distinguished for both JN1 and JN2. The presence of higher harmonics arises from the finite inductances of the Al arms42,45. We estimate L1 ≈ L2 ≈ 50 pH (i.e., 20 times smaller than the inductances of JN1 and JN2) and LW ≈ 210 pH. Even such relatively small inductances can significantly enhance the harmonic amplitudes. The enhancement becomes proportionally larger as the harmonic order increases42,45. This aspect is fully captured by our circuit model. Indeed, the black dashed lines in Fig. 1e, f are calculated using the parameters extracted from the fit of Fig. 2a. The experimental data are accurately reproduced despite the fact that only three harmonics effectively contribute to the CPR of each JoFET.

In Fig. 1e, f the arm inductances amplify the 1st, 2nd, and 3rd harmonics of JN1 (JN2) by 7(6)%, 22(30)%, and 250(244)%, respectively, and lead to the emergence of a 4th and a 5th harmonic46. Hence our analysis reveals the importance of including even small contributions of arm inductances in order to avoid a crude overestimation of the harmonic amplitudes. Finally, we remark that arm inductances can also induce a phase shift in the CPR45.

Moreover, we notice that the harmonic content of the two junctions obtained from our analysis is very similar (Supplementary Tab. 1) despite the different gate-voltage dependence of their critical current (Supplementary Fig. 10). This high level of symmetry indicates a good reproducibility of the fabrication process. In addition, we argue that the very large number of channels in our junctions should make the CPR less sensitive to the distribution of transmission coefficients. This can be a clear advantage over junctions based on one-dimensional semiconductor nanowires.

The magnetic-flux dependence of the G-SQUID CPR for three values of Φ2 is shown in Fig. 2 together with the Fourier decomposition. At Φ2 = 0 (Fig. 2b, e), we expect the G-SQUID CPR to be the sum of the JN1 and JN2 CPRs shown in Fig. 1e, f. Instead, we observe a CPR containing about ten harmonics. Moreover, all harmonics beyond the first one exhibit amplitudes clearly larger than expected from a simple addition. Fully captured by our circuit model (see dashed lines in Fig. 2b, e), this finding is mostly a consequence of the moderate ratio between the critical current of the reference junction JW and the one of the G-SQUID44, i.e., \({I}_{{{{\rm{C}}}}}^{{{{\rm{W}}}}}/{I}_{{{{\rm{C}}}}}^{{{{\rm{G-SQUID}}}}}\approx 5\) at Φ2 = 0.

At Φ2 = −Φ0/4 (Fig. 2c, f), JN1 and JN2 are dephased by π/2, resulting in a destructive interference between even harmonics. The 2nd and 4th harmonics are consequently suppressed while the 1st and 3rd preserve the same amplitude. The resulting CPR is clearly less skewed than at Φ2 = 0. From our model, we conclude that the residual 2nd and 4th harmonics are again due to a moderate ratio \({I}_{{{{\rm{C}}}}}^{{{{\rm{W}}}}}/{I}_{{{{\rm{C}}}}}^{{{{\rm{SQUID}}}}}\). Increasing the JW critical current by a factor of ten would further suppress the 2nd harmonic by the same factor.

At Φ2 = −Φ0/2 (Fig. 2d, g), a π phase shift induces a destructive interference between the odd harmonics of JN1 and JN2 with a reduction of the G-SQUID critical current. Following the suppression of the 1st and 3rd harmonics, the 2nd harmonic becomes the dominant one resulting in the emergence of a Φ0/2 flux periodicity in the CPR. In conclusion, at half flux quantum, the G-SQUID behaves as a \(\sin (2\varphi )\) Josephson element.

Harmonic tuning and sin(2φ) purity

Magnetic flux tunability

Figure 2a shows how, in a symmetrized configuration with balanced Josephson junctions, the magnetic flux Φ2 can profoundly change the harmonic composition of the G-SQUID CPR with singularities at Φ2 = ±Φ0/4 and Φ2 = ±Φ0/2. In order to gain more insight into this magnetic-flux control and to quantify the level of harmonic “distillation” at the singularity points, we show in Fig. 3a the complete Φ2 dependence of the first four harmonics. The plotted amplitudes of these harmonics (colored dots) are extracted from Fig. 2a by performing a Fourier transform of the measured IC(Φ1) at every Φ2 value. The corresponding uncertainties are represented by  ±1σ-wide colored bands. These uncertainties are significant and visible only when the harmonic amplitudes are below  ~1 nA, which is always the case for the fourth harmonic.

Fig. 3: Flux modulation of the G-SQUID harmonics.
figure 3

a Amplitudes of the first four harmonics in the G-SQUID CPR as a function of Φ2. The first harmonic vanishes at Φ0/2, while the second one vanishes at Φ0/4. b Flux dependence of \(\sin (2\varphi )\) purity, which is defined as the ratio between the amplitude of the second harmonic, A2φ, and the sum of all four harmonic amplitudes, ΣnAnφ. The \(\sin (2\varphi )\) purity has a sharp maximum at Φ0/2 where it reaches 95.2(2.4)%. Inset: close-up around the maximum. Colored bands in a and b represent the  ± σ standard deviation originating from the experimental uncertainty on the CPR data points. Black dashed lines in a and b represent the harmonic amplitudes calculated from our circuit model using the fit parameters from Fig. 2a.

Full size image

The overlaid black dashed lines represent the amplitudes of the first four harmonics calculated using the circuit model of Fig. 1a with model parameters obtained from the fitting of the data in Fig. 2a as previously discussed. The remarkable quantitative agreement over four orders of magnitude confirms the validity of our circuit model.

At Φ2 = ±Φ0/2, the first and third harmonics exhibit cusp-like dips where their amplitude is suppressed by two orders of magnitude, while the second and fourth harmonics simultaneously attain local maxima. In particular, the amplitude of the second harmonic at Φ2 = ±Φ0/2 is almost identical to the one at Φ2 = 0. We can define a “purity” level of the \(\sin (2\varphi )\) CPR as the ratio between the second harmonic amplitude, A2φ, and the sum of the four harmonic amplitudes, ΣnAnφ. Its flux dependence is displayed in Fig. 3b. At Φ2 = ± Φ0/2, we reach a second-harmonic purity of 95.2(2.4)%, largely exceeding the state-of-the-art33,35. We note that such a high purity level was reached owing to the very close electronic properties of the two S–Sm SiGe/Ge junctions in the G-SQUID. We also argue that, with these very same junctions, further circuit optimization should have resulted in an even higher value of the measured purity level. In fact, based on the circuit model of Fig. 1a, our measurement underestimates the purity value due to the relatively small \({I}_{{{{\rm{C}}}}}^{{{{\rm{W}}}}}/{I}_{{{{\rm{C}}}}}^{{{{\rm{G-SQUID}}}}}\) ratio. With a wider reference junction yielding a ten times larger \({I}_{{{{\rm{C}}}}}^{{{{\rm{W}}}}}/{I}_{{{{\rm{C}}}}}^{{{{\rm{G-SQUID}}}}}\) ratio, the same measurement should have given a purity level of 96.3%, much closer to the intrinsic value expected for exactly the same G-SQUID. Additionally, the intrinsic purity level could be increased by acting on other circuit parameters.

To illustrate that, we begin by noting that our fit of Fig. 2a reveals a slightly imperfect symmetry of the G-SQUID, quantified by a 0.7% discrepancy between the amplitudes of the first harmonics of JN1 and JN2 (see Supplementary Note 2). Reducing this discrepancy to less than 0.14% is, in principle, possible through a fine adjustment of the gate voltages. This would increase the weight of the even harmonics to more than 99%, with the fourth harmonic accounting for a few percent of the total weight. We note that both the second and the fourth harmonics contribute to parity protection since they reflect the simultaneous transport of even numbers of Cooper pairs. As discussed before, the fourth harmonic is essentially absent in the CPR of the individual JoFETs, and it originates from the non-negligible inductance for G-SQUID arms. Based on our circuit model, we estimate that in a properly symmetrized G-SQUID, reducing the arm inductances L1 and L2 from 51 to 46 would largely suppress the fourth harmonic resulting in \(\sin (2\varphi )\) purity above 99%.

Finally, at Φ2 = ±Φ0/4 the contribution of the second harmonic goes down to 2.6(0.1)%. This suppression of the second harmonic could be further pushed below 1% by changing the gate configuration (see Supplementary Note 5).

Gate voltage tunability

So far, we have demonstrated the flux dependence of the harmonic content in the CPR of the symmetrized G-SQUID. We will now address its gate voltage tunability while keeping the flux Φ1 fixed at Φ0/2.

In this experiment, the gate voltage of JN2 is fixed at \({V}_{G}^{N2}=-1.5\,{{{\rm{V}}}}\), while the gate voltage of JN1 is swept. The amplitude of the first harmonic exhibits a strong suppression around \({V}_{G}^{N1}=-0.7\,{{{\rm{V}}}}\) (see Fig. 4a), which corresponds to the symmetric condition. (In comparison to Fig. 3, here, this condition is achieved for a slightly different gate-voltage setting, due to a small electrostatic charge reconfiguration that occurred between the two measurement runs, which were taken several weeks apart.) Since the second-harmonic shows only a weak dependence on \({V}_{G}^{N1}\), the \(\sin (2\varphi )\) purity attains its maximum at \({V}_{G}^{N1}=-0.7\,{{{\rm{V}}}}\), as shown in Fig. 4b. The maximal purity level is robust against \({V}_{G}^{N1}\) deviations of up to 50 mV from the symmetry point. This robustness is largely reduced when operating the JoFETs JN1 and JN2 in a regime of moderate accumulation where their critical current is more sensitive to gate voltage variations (see Supplementary Note 4).

Fig. 4: Gate modulation of the G-SQUID harmonics.
figure 4

a Amplitudes of the first four harmonics in the G-SQUID CPR as a function of \({V}_{G}^{N1}\), while \({V}_{G}^{N2}\) is fixed at −1.5 V and Φ1 is set to Φ0/2. The symmetric SQUID regime is reached when \({V}_{G}^{N2}\) approaches −0.7 V, coinciding with the maximum suppression of the first harmonic. b Gate dependence of the \(\sin (2\varphi )\) purity, defined as the ratio of the second harmonic amplitude, A2φ, to the sum of the amplitudes of all four harmonics, ΣnAnφ. The \(\sin (2\varphi )\) purity reaches its maximum near \({V}_{G}^{N2}=-0.7\,{{{\rm{V}}}}\), as shown in the inset. Colored bands in a and b represent the  ±σ standard deviation originating from the experimental uncertainty on the CPR data points.

Full size image

Discussion

Our study provides important insight to devise practical realizations of parity-protected superconducting qubits based on the demonstrated \(\sin (2\varphi )\) Josephson element16,17. By leveraging a recently developed S–Sm platform based on SiGe/Ge/SiGe heterostructures, we obtained highly symmetric, multi-harmonic Josephson junctions leading to an unprecedented second-harmonic purity as high as 95%. Such a high purity should allow for enhanced protection against charge relaxation protection. We expect an improvement of two orders of magnitudes with respect to the nanowire-based \(\cos (2\varphi )\) qubit reported by Larsen et al.16 or to typical Transmon7 and Fluxonium8 qubits (see Supplementary Note 9).

In principle, parity protection enhances the qubit lifetime at the cost of rendering the qubit resilient to external control pulses. Therefore, qubit operation would require temporarily exiting the protected regime, e.g., by controlling the ratio between the second and first harmonics. We show here that this ratio can be tuned by a magnetic flux or a gate voltage. A flux shift δΦ2 = 0.025Φ0 from Φ2 = Φ0/2 lowers the second-harmonic content from 95% to 60%. In Fig. 4, we show that starting from a symmetric biasing of the G-SQUID, a gate voltage shift δVG = 100 mV in one of the two JoFETs lowers the \(\sin (2\varphi )\) purity by about 20%. An even smaller swing, δVG = 20 mV, would result in a similar purity reduction in a regime of moderate hole accumulation (see Supplementary Fig. 6e). Such flux and gate-voltage shifts are experimentally accessible with electrical control pulses on the typical time scale (~10 ns) of single-qubit operations.

Building on the S–Sm platform based on the SiGe/Ge/SiGe heterostructure presented in this report, future experimental efforts should integrate the \(\sin (2\varphi )\) element into a circuit quantum electrodynamics (cQED) architecture to investigate its potential parity protection. To achieve this, the challenge posed by the relatively large dielectric losses in the SiGe substrate47,48 could be addressed by fabricating the superconducting microwave circuitry on a separate low-loss chip and subsequently employing flip-chip assembly to connect it with the semiconductor-based Josephson elements49.

In conclusion, we have reported an experimental realization of a \(\sin (2\varphi )\) Josephson element leveraging the intrinsic multi-harmonicity and gate tunability of SiGe-based JoFETs. The CPRs of these JoFETs can be accurately described by the sum of only three harmonics albeit higher harmonics are measured due to the relatively modest ratio between \({I}_{{{{\rm{C}}}}}^{{{{\rm{ref}}}}}\) and \({I}_{{{{\rm{C}}}}}^{{{{\rm{W}}}}}\). The almost complete suppression of the odd harmonics at half a flux quantum leaves a \(\sin (2\varphi )\) CPR with a remarkably high purity level exceeding 95%. We argued that even higher values beyond 99% could be reached through further circuit optimization. All data analysis was based on a relatively simple but accurate circuit model taking into account the non-sinusoidal CPRs of the JoFETs as well as the inductances of the superconducting arms.