Sub-cellular population imaging tools reveal stable apical dendrites in hippocampal area CA3

Moore, Jason J.; Rashid, Shannon K.; Bicker, Emmett; Johnson, Cara D.; Codrington, Naomi; Chklovskii, Dmitri B.; Basu, Jayeeta

doi:10.1038/s41467-025-56289-9

Download PDF

Article
Open access
Published: 28 January 2025

Sub-cellular population imaging tools reveal stable apical dendrites in hippocampal area CA3

Nature Communications volume 16, Article number: 1119 (2025) Cite this article

6967 Accesses
2 Citations
4 Altmetric
Metrics details

Subjects

Abstract

Apical and basal dendrites of pyramidal neurons receive anatomically and functionally distinct inputs, implying compartment-level functional diversity during behavior. To test this, we imaged in vivo calcium signals from soma, apical dendrites, and basal dendrites in mouse hippocampal CA3 pyramidal neurons during head-fixed navigation. To capture compartment-specific population dynamics, we developed computational tools to automatically segment dendrites and extract accurate fluorescence traces from densely labeled neurons. We validated the method on sparsely labeled preparations and synthetic data, predicting an optimal labeling density for high experimental throughput and analytical accuracy. Our method detected rapid, local dendritic activity. Dendrites showed robust spatial tuning, similar to soma but with higher activity rates. Across days, apical dendrites remained more stable and outperformed in decoding of the animal’s position. Thus, population-level apical and basal dendritic differences may reflect distinct compartment-specific input-output functions and computations in CA3. These tools will facilitate future studies mapping sub-cellular activity and their relation to behavior.

Functional architecture of intracellular oscillations in hippocampal dendrites

Article Open access 26 July 2024

Activity-dependent compartmentalization of dendritic mitochondria morphology through local regulation of fusion-fission balance in neurons in vivo

Article Open access 08 March 2024

Responses of pyramidal cell somata and apical dendrites in mouse visual cortex over multiple days

Article Open access 17 May 2023

Introduction

Neurons receive inputs arranged in a stratified manner, in which synapses from specific afferent brain areas arrive onto different apical and basal dendritic compartments. Beyond differences in the inputs they receive, apical and basal dendrites may differ in their molecular composition, structural and biophysical properties, and function¹. Dendritic activity in the form of dendritic spikes^{2,3,4,5,6,7,8} and other ionic conductances^9,10 can tremendously enhance the computational capacity of individual neurons^{11,12,13,14,15,16,17,18}. However, these have primarily been studied using single neuron recordings in brain slices or with calcium imaging^19,20 in sparsely labeled in vivo preparations^{21,22,23,24,25}. While such single-neuron approaches allow faithful tracking of the activity of individual dendrites, they limit experimental throughput, are often confined to only one dendritic compartment (apical or basal), and provide limited insight into the population dynamics of large numbers of dendrites. In vivo two-photon calcium imaging from densely labeled preparations allows simultaneous recording of large populations of neurons, which enables population vector decoding of behavior^26,27, and can yield insights into network properties and circuit-level function. Though calcium imaging provides subcellular resolution, thus far studies have not fully utilized the ability to track large populations of sub-cellular processes like dendrites over time.

A major limiting factor in understanding dendritic function in vivo is technical, particularly when recording from dense populations. Manually identifying regions of interest (ROIs) belonging to individual neurons or dendrites can be tedious and time-consuming. While several software suites have been developed to automate this process when recording from fields of view composed of cell bodies^28,29,30,31, dendrites’ diverse shapes make morphology-based methods of dendritic ROI detection less reliable. A proper estimate of the time-varying fluorescence values from each ROI is also complicated by the highly overlapping nature of dendrites and the smaller number of pixels per ROI. Human screening of detected calcium transients can address these problems, but the amount of manual labor and time needed makes manual checking of dense datasets infeasible. Overcoming such difficulties will tremendously expand the field’s ability to investigate sub-compartment level population activity and behaviorally relevant functional properties.

To address the segmentation and demixing problems inherent to processing densely labeled dendritic populations, we developed an automated detection algorithm flexible enough to identify dendritic and somatic ROIs in dense datasets. The algorithm identifies initial ROI estimates using minimal morphological assumptions and refines them using constrained non-negative matrix factorization (CNMF)^28,32. It then screens putative calcium transients with an additional fitness measure to eliminate spurious activity from undetected ROIs. To demonstrate the efficacy and utility of this approach, we applied it to several sets of data recorded from area CA3 of the mouse hippocampus⁸, an area containing place cells important for spatial navigation. Using this preparation, we characterized the spatial tuning properties of soma, apical dendrites, and basal dendrites during a simple navigation task. We find that apical and basal dendrites show higher calcium event rates compared to soma with faster kinetics. While all compartments show similar spatial selectivity within a single day, apical dendrites have higher stability across days in a familiar environment compared to basal dendrites. This results in CA3 apical dendrites having a better population decoding accuracy of position across days, indicating a functional divergence between sub-cellular compartments of hippocampal pyramidal neurons for long-term spatial representation.

Results

Dense dendritic fields of view are highly overlapping

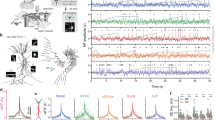
To generate dendritic imaging data sets for developing and testing our algorithm, we expressed GCaMP6f or 7b in hippocampal area CA3a/b in mice using a range of virus titers to control the labeling density (Fig. 1, Supplementary Fig. 1, Supplementary Table 1, see Methods)^{8,19,21,33,34}. At low titers, single neurons in a given field of view (FOV) were labeled (Fig. 1d). To quantify the degree of overlap, human experts manually labeled these datasets, identifying groups of contiguous pixels with coordinated activity (Fig. 1e, see Methods). At higher titers, neurons and dendrites were labeled so densely that most ROIs overlapped with at least one other ROI, and most pixels were covered by more than one ROI. Despite the highly overlapping nature of dendrites in the more densely labeled samples, manual segmentation was possible because the neurons were sparsely active in time, such that only a few neurons were active on any given frame (Fig. 1e, Supplementary Movie 1), reducing the dense segmentation problem into a series of sparse segmentation problems. In the eight mice with the highest titer virus injected, a mean of 47% of the field of view was covered with ROIs (Fig. 1f). Manual labeling of these datasets took approximately 50 hours per field of view. Any given ROI at least partially overlapped with a mean of 5 other ROIs, and a mean of 22% of pixels belonged to a single ROI, demonstrating a high degree of spatial overlap.

**Fig. 1: Sparse and dense GCaMP expression in hippocampal area CA3.**

Dendritic NMF algorithm enables efficient ROI extraction

The effort required to manually curate densely labeled neuronal datasets is massive, and the large amount of spatial overlap complicates efforts to accurately estimate activity. Hence, we sought a method to identify ROIs in an automated and unbiased way. CNMF^28,32 has previously been used to identify ROIs and activities from partially overlapping neurons, so we used it as a starting point for dendritic segmentation. The goal of non-negative matrix factorization (NMF) is to identify ROIs and corresponding fluorescence traces that best approximate the original image stack. The objective function is the following:

$${{{\rm{argmin}}}}_{{{\rm{A}}},{{\rm{C}}}}{{||}{{\bf{Y}}}-{{\bf{AC}}}{||}}_{{{\rm{F}}}}^{2}+\eta {{||}{{\bf{C}}}{||}}_{{{\rm{F}}}}^{2}+\beta {{||}{{\rm{sum}}}\left({{\bf{A}}}\right){||}}^{2};{{\rm{A}}}\ge 0,{{\rm{C}}}\ge 0$$

(1)

Here, Y represents the raw calcium imaging sequence, A represents the spatial footprints (ROIs), and C represents the fluorescence traces for each ROI. Background fluorescence from out-of-plane neuropil is accounted for by additional columns and rows in A and C, respectively. The η and β terms are penalties to encourage sparsity in the fluorescence traces and ROIs, respectively. This equation is solved by iteratively solving for A and C, fixing one while optimizing the other (see Methods). This process can identify large neural populations but has not been systematically applied to densely-labeled dendritic preparations.

We developed a pipeline of unique initialization and refinement steps to be amenable to detecting soma and dendrites, which we call dendritic-NMF, or d-NMF (Fig. 2). The algorithm consists of four broad stages or steps: Initialization, Refinement, Merging, and Screening.

The Initialization stage is an important step for these types of matrix factorization problems, as NMF is a non-convex problem with many local minima³⁵. ROI initialization was performed by identifying contiguous regions of pixels active above a threshold (see Methods, Supplementary Table 2a). Such guided initialization techniques can improve performance and avoid the need to specify the number of components to be identified, but can also be influenced by poor signal-to-noise ratio (SNR) data. To address SNR issues, one can denoise data by temporal smoothing, spatial smoothing, temporal downsampling, or any combination of the three for the initialization step, tailored to the dataset and scientific question at hand. While this is not a requirement of the Initialization stage, d-NMF allows users to choose these options at their discretion. In the results presented here, we chose to temporally downsample the data from 30 Hz to 1.5 Hz for the initialization step. d-NMF operates on the image sequence in patches to reduce the memory and time requirements of the algorithm to enable processing on standard desktop computers (Fig. 2a, see Methods). Processing the image in patches had the added benefit of incorporating multiple background sources for each image patch, to better capture regional differences in neuropil signal.

The Refinement step can be performed on the original raw data or downsampled and/or otherwise filtered data. Spatial footprints and temporal traces were estimated by iterating through NMF until convergence (Fig. 2b, Supplementary Table 2b) with no explicit constraint on component size. In the final refinement step, ROIs were thresholded and split into connected components (see Methods). These final morphological operations ensured that all identified ROIs were relatively compact and easily interpretable as neuronal structures. The resulting ROIs also had the property that their activity was homogenous within an ROI. Any dendritic branch or portion of a large ROI that had independent activity was identified as a separate ROI. (Supplementary Fig. 2).

In the Merging step, we combine ROIs (Supplementary Table 2c) that are likely to correspond to the same functional unit. Long dendritic branches may span multiple image patches (Fig. 2a) or may be represented by multiple ROIs due to local variations in activity. The algorithm offers users the ability to set a threshold correlation with which to merge ROIs. A high threshold can result in a fine parcellation of dendritic structure, preserving local differences in activity, while a low threshold will merge ROIs with broadly the same activity. We observed that a general rule on the lower bound of the merging threshold is to identify when ROIs not belonging to the same neuron become linked together. This is indicated by a sudden drop in minimum within-group correlations (Supplementary Fig. 3, see Methods). Even if users decide not to merge ROIs, correlation-based linkage information can aid in scientific interpretations at later stages.

The Screening step provides a final stage to include or exclude ROIs. The raw output of d-NMF contains any set of contiguous pixels that had simultaneously high activity at least once, which can result in false positives. In many brain regions, including the hippocampus, excitatory neural activity is characterized by long periods of quiescence punctuated by short periods of activity, resulting in positive skewness values. Hence, we used the skewness of the extracted calcium traces for each ROI (Fig. 2c), to classify valid and invalid ROIs, trained on manually-labeled data (see Methods). Skewness was a very effective separator of valid and invalid ROIs (Fig. 2c), yielding comparable outcomes as signal-to-noise ratio (Supplementary Fig. 4). The optimal skewness value was relatively close across the population of fields of view, at 3.8, [3.2, 3.9]. Note that this cutoff value may vary across brain regions, cell types, or fluorescent indicators. This process yields interpretable ROIs (Supplementary Fig. 2) of varying shapes without random initialization or needing to specify the number of components to be detected beforehand. A comparison of the algorithm design choices in various methods is summarized in Supplementary Table 3.

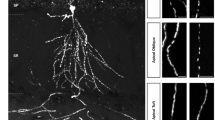
To further validate the accuracy of d-NMF, we constructed synthetic dense datasets using one of the sparsely labeled datasets (Fig. 3). This sparse dataset had known ROI boundaries and temporal traces, serving as a ground truth. By copying, rotating, and shifting the original movie, we constructed synthetic dense datasets with up to 200 neurons with a high degree of overlap between dendrites (see Methods). We found that as we added more duplicates, the quality of signals decreased, due to the addition of more background from other ROIs and additional neuropil (Fig. 3c). This had the result that adding additional neurons beyond a certain point no longer yielded additional detectable ROIs or even decreased the amount of ROIs with a high-quality signal (Fig. 3d,e). Nevertheless, for ROIs with a signal quality above 2 standard deviations, d-NMF maintained an F1 score (Supplementary Fig. 5a, see Methods) of 0.8 out of 1, outperforming the output of suite2p, another open-source analysis package²⁹ (Fig. 3f). This serves as evidence that our method is sound and accurate at detecting ROIs from dense fields of view.

**Fig. 3: Synthetic data demonstrates that d-NMF remains accurate at high density.**

d-NMF matches manual labeling and exceeds existing methods

To demonstrate the accuracy and utility of d-NMF in detecting ROIs, we evaluated its performance with human-labeled ROIs used as ground truth. At a wide range of imaging densities, d-NMF closely matched manually-labeled ROIs (Fig. 4). Segmentation similarity between algorithmic ROIs and manual ROIs was measured both based on a morphology and overall pixel-by-pixel coverage (Supplementary Fig. 5, see Methods).

**Fig. 4: d-NMF accurately labels ROIS with highest coverage.**

We compared performance against CNMF, implemented with the CaImAn software package²⁸, as well as suite2p²⁹, (see Methods). The median F1 score using d-NMF was 0.45, exceeding that of CNMF (0.32) and suite2p (0.42) (Fig. 4b, Left). Similarly, the True Positive Rate of d-NMF (0.45) exceeded CNMF (0.21) and suite2p (0.31) (Fig. 4c). The percentage of the FOV covered by ROIs (coverage) using d-NMF (27%) was also higher than CNMF (14%), but not suite2p (28%) (Fig. 4d, Right). In particular, CaImAn did not identify ROIs in particularly dense regions of the FOV. While suite2p performed comparably with d-NMF in sparse preparations (Fig. 4a, Left), dense preparations were more completely labeled using d-NMF (Fig. 4a, Right). d-NMF performed well on both sparse and dense datasets with a single set of parameters, whereas other methods may need careful parameter tuning depending on the density of the preparation. The success of d-NMF compared to other methods is not due to systematic detection of a higher number of smaller ROIs; ROI size was largely comparable across methods, with several instances of ROIs identified spanning well over 100 μm (Supplementary Fig. 6). Changes in parameter settings for CNMF and suite2p led to small improvements in performance (Supplementary Fig. 7, see Methods), so we compare to the highest performing version of each in Fig. 4. d-NMF also matched or outperformed other methods when applied to other types of independently imaged data, including dendrites from motor cortex in macaque monkeys³⁶, and entorhinal cortex axons in mouse CA1 (Supplementary Fig. 8).

Of great interest to the dendritic field is investigating localized activity, generally represented by calcium transients with rapid kinetics that remain confined to a small dendritic segment. We validated that d-NMF was able to detect localized activity from two previously published datasets, using calcium imaging in mouse hippocampal area CA1²¹ and voltage imaging in the visual cortex³⁷, respectively. We also identified local activity in a putative dendritic spine in our own data (Supplementary Figs. 9, 10). To explore the bounds of activity in which d-NMF could detect localized activity, we prepared synthetic datasets by injecting calcium transient waveforms of different amplitude, duration, and number into localized dendritic regions of interest with known baseline activity. This analysis demonstrated that by analyzing non-downsampled, 30 Hz data, localized transients as brief as 100 ms in width³³ were sufficient to identify independent ROIs, provided the transients were of sufficient amplitude to rise above the noise level (Supplementary Fig. 11, Supplementary Table 4).

Higher sampling rates are generally required to detect rapid events. However, a higher sampling rate comes at the cost of noisier data, which may adversely impact ROI detection and refinement. Indeed, in our hippocampal data, performing the Refinement step on 30 Hz data resulted in slightly lower coverage, though the overall performance against manually-labeled data was relatively similar (Supplementary Fig. 12) to temporally downsampled data. Additionally, processing raw data increases both the size of files in memory and computation time. Depending on the expected kinetics and spatial extents of activity as well as the computing power available, users may choose to downsample or filter in time, space, or both. Because we are investigating dendritic activity, which may be rapid, all following analyses are done on data extracted from non-downsampled, 30 Hz files.

A fitness trace to refine activity estimates and eliminate cross-contamination

Densely labeled datasets present added difficulties in estimating the fluorescence activity of each ROI due to overlapping sources. Given a complete set of ROIs, NMF accurately de-mixes these signals and properly assigns activity to each ROI. However, despite the best efforts of manual labeling or automated labeling, some processes may go unlabeled. This will lead to contamination of signals from identified ROIs by unidentified ones. Such contamination can affect estimates of activity rates, tuning properties, stability, or correlation with related ROIs. While simply setting a high threshold for transient detection may reliably screen out false transients, this runs the risk of excluding low-amplitude calcium transients, which may represent different firing modes such as localized events versus back-propagating action potentials (bAPs), or single spikes versus bursts.

To both evaluate the degree of contamination and to provide an additional tool to correct this, we developed the concept of a Fitness Trace for each ROI (Fig. 5a), defined as the frame-by-frame correlation between the spatial footprint of that ROI with the fluorescence activity from the video (see Methods). The intuition behind this trace is that true activity in a given ROI occurs when all pixels show elevated activity, not just some. Significant calcium transients were detected by thresholding the Fitness trace along with the original calcium trace (Fig. 5b). Overall classifier performance was evaluated by computing the Jaccard index (the size of the intersection divided by the size of the union)³⁸ between detected events and manually-labeled true events (see Methods). Across 9 different FOVs there was a relatively consistent optimal parameter range, at a ΔF/F threshold of 3.9z and a Fitness threshold of 0.2.

**Fig. 5: Fitness trace screens out false activity.**

An implicit requirement of the Fitness Trace is that the entire ROI must be active for a calcium transient to be detected, which could potentially discard localized dendritic activity and bias estimates. If ROIs are too broadly defined, such that they span multiple branches containing independent activity, this would lead to a bias to exclude branch-independent transients. However, the d-NMF algorithm identifies ROIs precisely as groups of pixels with synchronous activity. Dendritic branches that show independent activity are automatically split off from other branches and analyzed as a separate ROI (Supplementary Fig. 2). In this way, accurate ROI identification assists in accurate transient detection.

We compared detection accuracy and the rate of detected transients from our optimized Fitness method to those of other event detection methods (Fig. 5c). A widely used approach is to set a threshold of 2 standard deviations above the mean on the raw ΔF/F traces, with no de-mixing (with an additional false positive rejection criterion, see Methods). We call this method 2z. We call our method using optimal values for the ΔF/F threshold and Fitness threshold D_Fit. Event classification performance was significantly higher using D_Fit (0.63) compared to 2z (0.31). Other detection methods incorporating different elements of these two approaches achieved intermediate results (Supplementary Fig. 13, Supplementary Table 5, 6). The use of the Fitness Trace also was comparable to or outperformed other related measures³⁹ (Supplementary Fig. 13e-h, Supplementary Table 5, 6). More striking, the estimated calcium transient rate using 2z was overestimated by more than a factor of 3, while D_Fit closely matched the manually identified transient rate (Fig. 5c). This demonstrates that accurate event detection and screening is a vital step in processing data from densely labeled FOVs. Detected calcium transients spanned a wide range of durations, with half-widths from 100 ms up to 10 seconds. Transients in apical and basal dendrites were more rapid than those in the soma (an average of 500 ms in apical and basal dendrites, compared to an average of 850 ms in soma), with transients as fast as 100 ms in dendrites, which may be missed or severely reduced in amplitude due to averaging when imaged at slower frame rates.

Spatial coding properties of dendrites in CA3

To demonstrate the utility of d-NMF, we analyzed the activity of detected ROIs in relation to behavior as mice performed a random foraging task on a textured treadmill belt (Fig. 6, see Methods). Somata of pyramidal cells in area CA3 demonstrate place coding, where they have reliable elevated activity levels in restricted regions of space. Using d-NMF, across 8 mice we identified 709 total somatic ROIs, 3139 apical dendritic ROIs, and 3999 basal dendritic ROIs. This allowed us to examine and compare the activity and spatial tuning properties of populations of apical and basal dendrites.

**Fig. 6: CA3 dendritic spatial coding properties.**

While spatial tuning in CA3 PN somata has been well described through electrophysiology approaches^40,41,42 and more recently with Ca²⁺ imaging^43,44, we know little about how reliably CA3 dendrites encode place and their spatial tuning properties. Using our automated approaches, we identified spatially tuned CA3 dendrites (place dendrites) both in the apical and basal compartments (Fig. 6a-e). Dendritic and somatic compartments had similar spatial tuning properties in terms of the proportion of tuned ROIs (16-20%) and place field width ( ~ 25 cm) (Fig. 6e, Supplementary Table 7). Despite these similarities, dendrites showed a number of differences from soma. Apical and basal dendrites had higher activity rates than soma (0.7 events/minute (apical) and 0.6 events/minute (basal) compared to 0.5 events/minute in the soma, Fig. 6f, Supplementary Table 7), with faster kinetics (Fig. 6g). Spatial information content was lower in dendrites (1.9 bits/event) compared to soma (2.1 bits/event), possibly related to the differences in activity rates (Fig. 6h). Apical dendrites, but not basal, exhibited increasing event rates, thinner transients, lower spatial selectivity, and a higher number of place fields as a function of distance from the cell body layer (Fig. 6f-h, Supplementary Table 7, see Methods).

Basic spatial tuning characteristics were not systematically related to the ROI size or the number of overlapping ROIs (Supplementary Fig. 14, Supplementary Table 8). Additionally, these results were not biased by over splitting of dendrites into multiple compartments, as all comparisons were similar when we merged ROIs with highly correlated activity (see Methods, Supplementary Fig. 15, Supplementary Table 9).

To provide support that these findings were not influenced by the dense recording preparation or our analytical approaches, we analyzed a subset of the data with neurons labeled sparsely with GCaMP, manually identifying ROIs and calcium transients (Supplementary Fig. 16). We found corroborating evidence of higher activity rate in the apical and basal dendrites compared to soma as well as more rapid calcium kinetics at farther distance from the soma. The similar findings in dense and sparse data validate that we can accurately detect calcium transients in the dense data.

Apical dendrites are more stable across days and provide better place decoding

An advantage of optical recording techniques is the ability to track the same ROIs across long timespans. Thus, we quantified the short-term (within-day) and long-term (across-day) stability of apical dendrites, soma, and basal dendrites in a familiar environment (Fig. 7, Supplementary Table 10, see Methods). Within-day stability was not significantly different across compartments when quantified using Tuning Curve (TC) correlation (which quantifies stability per ROI), but apical dendrites showed higher within-day stability than basal dendrites when quantified using Population Vector (PV) correlation (which quantifies stability of the overall spatial representation, see Methods). More strikingly, apical dendrites were more stable across days compared to basal dendrites using TC or PV correlation. We were not able to extend these analyses to the sparse data due to the limitation of the small amount of tuned neurons in that dataset. The differences in across-day stability were not due to fields of view distorting across days (Supplementary Fig. 17), or differences in ROI size or overlap (Supplementary Fig. 18).

**Fig. 7: Stability measures across compartments show apical dendrites are more stable across days.**

Because apical dendrites showed better across-day stability compared to basal dendrites, we predicted that apical dendrites would also outperform basal dendrites in population vector decoding. Thus, we constructed population vector decoders using only apical dendrites, soma, or basal dendrites, and tested their ability to decode position within a session (Fig. 8a) or across sessions (Fig. 8b). There was no significant difference between decoding accuracy within-day. However, apical dendrites had significantly lower decoding error compared to basal dendrites across days (Fig. 8c). Population vector decoding accuracy is highly dependent on the number of sources used to train the model, so we repeated the analysis using random subsets of data. Consistently, we found no differences across groups for within-day decoding (Fig. 8d), but a significant interaction effect of compartment group and number of ROIs on across-day decoding, with apical dendrites and soma showing significantly better decoding accuracy compared to basal dendrites (Fig. 8e).

**Fig. 8: Population vector decoding for apical dendrites outperforms basal dendrites.**

Discussion

In summary, we developed a versatile algorithm and toolkit that facilitates analysis of densely labeled fields of view containing both apical and basal dendrites and cell bodies (Fig. 1), enabling large-throughput in vivo investigation of dendritic activity. The algorithm utilizes the well-validated mathematical framework of CNMF while providing automated initialization flexible enough to identify neural processes of varied shape and size in sparsely- and densely-labeled preparations (Figs. 2, 3, 4). The addition of the Fitness Trace post-hoc helps screen out false calcium transients to more accurately estimate dendritic event rates and tuning properties (Fig. 5). Using these tools, we demonstrate spatial tuning in apical and basal dendrites of pyramidal neurons in CA3 (Fig. 6). While the proportion of tuned ROIs and within-day tuning properties were largely comparable across all compartments, basal and apical dendrites showed higher event rates than soma. Dendritic event widths were noticeably thinner than soma, on a population (dense data) as well as on an individual neuron level (sparse data). By comparing longer-term population dynamics across days, we demonstrate that apical dendrites are more stable than basal dendrites (Fig. 7). This leads to better accuracy when constructing a population vector decoder to predict the animal’s position (Fig. 8). These population-level analyses would not be possible with sparsely labeled preparations, and we were only able to take advantage of our densely labeled preparations using the analytical tools we have developed.

Densely labeled dendritic fields of view present a number of challenges for existing automated detection methods, particularly the initialization step. Initialization is often based on morphology, with parameters to be set for the expected diameter of an ROI. This assumes a uniform size of circular ROIs throughout the FOV, which is not the case for dendrites. Seed pixels for initialization can be chosen from the peaks of the correlation map, constructed by computing the average correlation of a pixel with its neighbors⁴⁵. However, thin dendritic segments a few pixels wide may skew towards low correlation values and be systematically missed compared to wider somatic ROIs. Furthermore, overlapping dendrites result in pixels containing activity from a combination of sources, which may obscure correlations within individual branches. Random initialization does not suffer from the drawbacks of morphology-based approaches, but there is no guarantee of complete labeling or consistent labeling across iterations. Additionally, the number of components must be specified for initialization, which may vary over the field of view. One approach is to over-specify the model and then discard unusable ROIs afterwards³², but this comes at a higher computational cost. Additionally, unusable ROIs may distort the spatial or temporal aspects of remaining, valid ROIs, so a proper estimate of the number of components is important, which we solve in a data-driven manner.

Though our approach utilizes NMF as the core extraction algorithm, there are notable differences between our approach and other published methods. Our initialization method is based on localized coactivity, and the number of components within a patch is discovered from the data, rather than prespecified. This approach works in our densely labeled datasets because soma and dendrites tended to be sparsely active in time, such that only a few ROIs are active on any given frame. This mimics the method by which manual segmentation is done, and allows the identification of ROIs that may overlap with many others (Fig. 4). We also enforce ROIs to consist of contiguous pixels, in contrast to CNMF, which imposes no spatial constraints on the ROIs. CNMF additionally constrains the temporal component by an autoregressive fit, while d-NMF has no constraint on the temporal components. This allows for the possibility of calcium transients with different dynamics to exist within a single ROI.

Different aspects of d-NMF could be used in conjunction with pre-existing methods. Other segmentation software could be initialized with the initial ROI cores or the final ROIs obtained after de-mixing. The Fitness Trace (Fig. 5) could be used to screen any activity trace regardless of the method used to obtain it⁴⁶, though it would be crucial to verify that the underlying ROIs should not be further split into independent units. Ultimately, different tools may be better suited to different data sets, so it is worthwhile for investigators to be able to combine the strengths of all available approaches.

As with any data analysis pipeline, the user takes on the responsibility of curating the output of d-NMF to ensure the interpretability and robustness of their results. For instance, depending on the threshold specified for merging ROIs with similar activity, d-NMF can give a very fine or coarse parcellation of the dendritic tree (Supplementary Fig. 10). For those wanting to investigate changes in activity along the dendrite, a high merging threshold would be best, but for those wanting to capture the main global activity across an entire branch, a more permissive merging threshold would be appropriate. Furthermore, the specific optimal threshold may vary across fluorescent indicators, brain region, behavioral state, or species. Additionally, if a dendritic branch is split into multiple ROIs, these will not have independent activity, violating the assumptions of some statistical tests. This can be addressed by calculating summary statistics across ROIs for an entire FOV, or to merge or subsample ROIs with similar activity and verifying that scientific results still hold. We encourage such control analyses to be standard practice when performing population imaging.

Large population recordings allow the use of fewer animals to record from a given number of neurons, saving on time and resources. For characterizing single dendrite properties, this is particularly advantageous if a relatively small percentage of units show tuning to a given stimulus or behavioral feature. This is the case in CA3, where only ~20% of dendrites or soma show spatial selectivity (Fig. 6). Methods of inducing selectivity through artificial means^47,48 can somewhat circumvent this, but the effects of these manipulations may be limited or constrained⁴⁹. Larger population data not only add more power to the analysis but also provide insights into functional heterogeneity and dynamics^50,51,52. Simultaneous longitudinal recording of multiple dendrites in the same animal provides within-subject control on the effect of behavior on dendritic activity, and large enough population recording enables analysis of population-level stability (Fig. 7) and decoding of behavior (Fig. 8)^26,27,53. It is important to note, however, that increased density does not come for free. When we constructed our synthetic datasets by duplicating and shifting a field of view with a single neuron, the overall signal quality decreased as more neurons were added. This indicates that, for a given expected morphology and distribution of cells, a sweet spot of labeling density may exist which maximizes the number of usable neurons while minimizing the number of animals needed.

Our results demonstrate that both apical and basal dendrites show spatial selectivity on par with nearby soma (Fig. 6), and the apical dendritic signal is more stable than the basal dendritic signal (Fig. 7). Long-term recordings of large populations of neurons have revealed changing neural representations over time, a phenomenon termed representational drift^54,55. This has been documented in the hippocampus⁵⁶ as well as several other brain areas^{57,58,59,60,61,62}. Previous studies have shown that population responses of areas CA1 and CA3 of the hippocampus are particularly unstable across several days^44,56, though other regions of the hippocampal circuit are more stable, including the dentate gyrus⁴⁴ and entorhinal cortex⁶³. Different levels of stability in apical and basal dendrites (Figs. 7, 8) suggest that representational drift may not be homogenous across compartments of individual neurons. This may be related to the segregated inputs received and the varying functionality of CA3 as performing pattern completion or pattern separation^{64,65,66,67,68} by biasing propagation of inputs from apical or basal dendrites. Different compartments are likely subject to differential gating by target selective GABAergic circuits or gradient distributions of channel conductances. A similar mechanism may be at work in the neocortex, where anatomy^69,70,71 and theory^72,73,74 suggest that bottom-up input arrives onto the basal dendrites while top-down input arrives on to the apical dendrites, providing a spatial segregation matching the functional segregation. Apical dendrites may also be more stable due to integrating signals from several different inputs. The conjunctive activity of entorhinal cortex, dentate gyrus, and recurrent collaterals may act to trigger supra-linear dendritic spikes^7,18, triggering long-term synaptic plasticity^{16,18,47,75,76} which could contribute to increased stability²¹. Differences in task demands also affect the representational stability of soma in CA1⁵³, so the stability of dendritic compartments under different behavioral tasks should be explored in the future.

It is also important to consider the contribution of forward-propagating versus back-propagating signals in defining dendritic activity. Proximal dendrites that are electrotonically close to the soma are likely to be dominated by back-propagated activity. However, the higher transient rates in apical and basal dendrites indicate a mixture of localized and back-propagated activity. Distal dendrites may enjoy a larger degree of independence because back-propagating action potentials often decay with distance⁷⁷. Localized spikes likely do exist in hippocampal CA3 and CA1, supported by previous slice studies^8,18,46,78. Using calcium signals as an indicator of across-compartment correlation should be done with caution though, as calcium signals may reflect large bursts of activity more robustly than single action potentials¹⁹. Future studies using voltage-sensitive indicators or more sensitive calcium indicators in large populations should provide higher temporal resolution into these questions. Due to these considerations, d-NMF does not identify different event types but rather provides the time-varying concentration of calcium in a given ROI, de-mixed from the activity of overlapping ROIs. This is a critical starting point before the identification of different event types can be done. We have demonstrated using voltage imaging and synthetic data that d-NMF can detect localized, thin transients if they are present. Knowledge of the activity of neighboring, connected ROIs is necessary to identify activity as local or more widespread.

Many valuable insights about dendritic function have been gleaned without explicitly delineating local dendritic events from back-propagating events, across different brain areas such as motor cortex^22,25,79, visual cortex^1,23,80,81, hippocampal CA1^21,33,82, and lateral amygdala⁸³. Definitively resolving back-propagating action potentials from local dendritic activity requires deliberate experimental design involving technically challenging approaches^37,84. For accurately dissociating the source of dendritic activity (forward vs. back-propagating) one needs to establish ground truth with simultaneous dendritic and somatic electrophysiology and imaging coupled with well-defined stimulation protocols^85,86. Given the slower kinetics and lower single spike resolution of Ca²⁺ indicators, resolving bAPs requires further tool development such as in vivo optimized high signal-to-noise ratio voltage imaging sensors⁸⁷. The analysis tools presented here will synergize with future developments in these experimental areas to enable principled investigation into dendritic signaling.

This study examined the activity of ensembles of apical dendrites, soma, and basal dendrites separately. In our dense datasets, we already merge together ROIs of neighboring dendrites and soma which have substantial spatial overlap and highly correlated activity. Such ROIs obtained from merging the soma and dendrites indicate a high degree of coupling between the soma and its proximal dendritic branches, as would be expected from the diffusion of calcium over short distances. But the possibility of dendrites exhibiting semi-independent activity^6,22,25,84 from their cell bodies poses a challenge in linking ROIs based on correlations alone. Additional structural markers would likely help in linking connected dendrites and soma. Furthermore, many distal dendrites are connected to soma that are not in the focal plane. This could be resolved with multi-planar imaging in future studies. A more in-depth investigation of input-output transformations at a sub-cellular level would require simultaneous measurement of connected dendrites and soma, as we provided in our sparely labeled datasets (Supplementary Fig. 16). By comparing the tuning properties of the apical dendrite, soma, and basal dendrite of the same neuron within densely labeled fields of view, one could learn about branch-specific^6,22,25,84 versus branch prevalent activity^21,23,81 and soma-dendrite coupling dynamics while sampling large populations. Such information has so far been limited to very sparse preparations, which may overlook cellular heterogeneity within regions^50,51,52.

The methods presented here were primarily tested on the calcium activity of dendrites and soma measured with GCaMP6f in hippocampal area CA3. But the approaches are broadly applicable to any cell or cellular process exhibiting dynamic fluorescence activity, including axons^18,88,89 and astrocytes^90,91 recorded with a range of different genetically encoded calcium indicators⁹² or voltage indicators^93,94. These different indicators have varying signal-to-noise ratios and kinetics, so a reasonable parameter search may be necessary to obtain the optimal performance of our tools. The rapid kinetics of voltage indicators with respect to the speed of propagation within dendrites may also result in the identification of finer-grained ROIs, as an assumption of our mathematical model is that the signal in a given ROI is uniform. Hippocampal area CA3 provides the geometrical advantage of imaging large dendritic trees in a single focal plane, but our approach would easily extend to brain areas such as retrosplenial cortex with similar affordances, or those accessible with microprism approaches⁹⁵. Our method can also be utilized in more traditional tuft dendrite or basal dendrite imaging, and could facilitate analysis of sparsely labeled preparations as well. Clever intersectional genetic approaches should be able to provide access to axonal input, dendritic processing, and somatic output in a single preparation, and our tools will facilitate the rigorous analysis of such datasets.

Methods

Animals

All experiments were conducted in accordance with the National Institute of Health guidelines and with the approval of the New York University Grossman School of Medicine Institutional Animal Care and Use Committee (IACUC). Imaging experiments used mice on a C57BL/6 J background, from both sexes, 15–25 weeks old, housed on a reversed light cycle.

Cranial window surgery

Surgery procedures were similar as described previously⁸. Mice were anesthetized using isoflurane (1.5–2.5%), a 0.5 mm hole was drilled in the skull above dorsal area CA3 of hippocampus (1.6 mm lateral, and 1.4 mm caudal of Bregma) and AAV virus was injected. For densely expressing preparations, AAV1.CamKII. GCaMP6f.WPRE.SV40 (Penn Vector Core, titer: 2.76x10¹³ GC/ml, 23 nL per site) was injected at two sites (1.5 mm ML, 1.3 mm AP; 1.7 mm ML, 1.5 mm AP relative to Bregma; 1.8 and 2 mm Z depths below the dural surface, covering areas CA3a/b). For sparser expression, we used a mixture of AAV1.CamKII-Cre (diluted with ACSF) and AAV1.Syn.Flex.GCaMP6f.WPRE.SV40 or AAV1.Syn.Flex.jGCaMP7b.WPRE at 23 nL per site, at different ratios⁸ (see Supplementary Fig. 1 for specific titers). After injection, a 3 mm glass coverslip cranial window attached to a 1.7 mm deep stainless steel cannula was implanted by performing a craniotomy centered around the injection site and aspiration of the overlying cortex and external capsule. The window was sealed to the skull using Vetbond, and a custom-designed 3D-printed plastic head post was cemented over the skull.

Immunohistochemistry

To verify our imaging was in area CA3 and not neighboring CA2, we tested for localization of GCaMP6f and the CA2 marker PCP4⁹⁶ (Supplementary Fig. 1b) using immunohistochemistry of 50 µm PFA fixed horizontal slices in TBS. GCaMP-labeled neurons and were stained using a chicken polyclonal anti-GFP primary antibody (1:1000; Invitrogen) with a donkey anti-chicken Alexa Fluor 488 dye-conjugated IgG antibody (1:1000; Invitrogen). PCP4-positive neurons were stained using a rabbit polyclonal anti-PCP4 primary antibody (1:200; Invitrogen) with a goat polyclonal anti-rabbit Alexa Fluor 633 dye-conjugated IgG antibody (1:400; Invitrogen).

Two-photon imaging

In vivo imaging was performed on head-fixed running mice as described previously^8,53,97,98 using a dual resonant galvanometric laser scanning two-photon microscope (Ultima, Bruker). The microscope was coupled to a tunable Ti:Sapphire laser (MaiTai eHP DeepSee, Spectraphysics) at 80 MHz pulse repetition rates and <70 fs pulse width with dispersion compensation, to excite GCaMP and tdTomato fluorophores at 920 nm. Images were acquired at scan speeds of 30 fps, using 512x512 frame size (1.085 mm/pixel resolution) with a resonant scanning galvanometer system mounted on a movable objective Ultima microscope, with an orbital nosepiece coupled to a 16X, 0.8NA, 3 mm water immersion objective (Nikon). The fluorescence signal was detected using high-sensitivity GaAsP photomultiplier tubes (model 7422PA-40 PMTs, Hamamatsu). Recording sessions were ~10 minutes long, yielding datasets of ~10 GB.

Head-fixed spatial navigation

Mice were trained to perform a random foraging task by running head-fixed on a 2-meter linear treadmill belt^18,53 to lick for randomly located but uniformly distributed sugar-water (5% sucrose) rewards along the track. The position of the mouse, and lap onset were measured using an optical rotary encoder (S5-720, US Digital) and reading RFID tags and reader (ID-20LA, SparkFun Electronics). Behavioral programs were controlled with an Arduino Mega 2560 microcontroller. Behavior data was acquired at a sampling rate of 10 kHz synchronized to the two-photon imaging. Mice ran head-fixed on the same treadmill belt for 3 days to become acclimated to the textures and cues. The following days (Days 4-7) were designated as familiar days for the purposes of stability analysis. We always compared activity across consecutive familiar days for each animal, either days 4&5, 5&6, or 6&7, taking data recording and template matching artifacts into account.

Statistics

Unless otherwise stated, all data are reported as the median (M) and its 95% confidence interval [Lower, L and Upper, U bounds], calculated through a resampling procedure previously described⁶. All statistical comparisons were done using a two-sided Wilcoxon signed-rank (for paired data) or rank-sum (for unpaired data) unless otherwise specified (See section Subsampled Decoder).

All analyses were performed using custom-written codes in MATLAB R2021a (MathWorks).

d-NMF

Initialization

Pre-processsing

Image stacks were motion-corrected for XY-motion using NoRMCorre⁹⁹. For temporal downsampling, each downsampled frame was computed as the mean of the surrounding frames, rounded, and stored as unsigned 16-bit integers.

Division into Patches

Image stacks were divided into 81 patches of 64x64 pixel size, with an 8-pixel overlap.

ROI Core Detection

Within each patch, the image sequence was first de-trended and transformed into ΔF/F values by subtracting and dividing by the minimum value in a rolling 30-second window. The activity threshold was set to 3 times the median ΔF/F for each pixel and optionally passed through a temporal median filter. Connected components of active pixels were then detected in the resulting 3-dimensional (X-Y-Time) image stack. Components with membership ≥ 30 pixels were projected into 2 (X-Y) dimensions. See Supplementary Table 2a.

We merged components based on the Jaccard index (size of the intersection divided by the size of the union) between components, using a 0.5 merge threshold. This step merges ROIs that are active in distinct time spans and are detected multiple times in the previous step. Pixel values of each component are then normalized to sum to 1. Two extra ROIs were included, one composed of all pixels not belonging to any other ROI and the other composed of all pixels in the area being considered, to model background neuropil fluorescence.

Refinement

Iteration and Activity Extraction

The following steps are the standard fitting procedure for constrained non-negative matrix factorization^28,32 (See Supplementary Table 2b) and are performed on the original image sequence patch, without de-trending or ΔF/F transformation. An image patch with t time steps and d x d pixel size is stored as a matrix Y $\in {R}^{d\times d\times t}$. This is reshaped into the matrix Y^* $\in {R}^{{d}^{2}\times t}$. The objective function is the following:

$${{{\rm{argmin}}}}_{{{\rm{A}}},{{\rm{C}}}}{{||}{{{\bf{Y}}}}^{{{\boldsymbol{*}}}}-{{\bf{AC}}}{||}}_{{{\rm{F}}}}^{2}+\eta {{||}{{\bf{C}}}{||}}_{{{\rm{F}}}}^{2}+\beta {{||}{{\rm{sum}}}({{\bf{A}}}){||}}^{2};{{\rm{A}}}\ge 0,{{\rm{C}}}\ge 0$$

where ‖∙‖_F denotes the Frobenius norm. For k components, A $\in {R}^{{d}^{2}\times k}$ represents the spatial footprints (ROIs), and C $\in {R}^{k\times t}$ represents the time-varying activity for each ROI. η and β are regularization terms to enforce sparsity of the temporal components (C) and spatial components (A), respectively.

The algorithm then iterates over solving for C and A while enforcing non-negativity. The optimal solutions for C and A are as follows:

$${{{\bf{C}}}}^{\ast }=\,\max \left(({{{\bf{A}}}}^{{{\rm{T}}}}{{\bf{A}}}+\eta {{\bf{I}}}){({{{\bf{Y}}}}^{{{\rm{T}}}}{{\bf{A}}})}^{{\dagger} }0\right)$$

(2)

$${{{\bf{A}}}}^{\ast }=\,\max \left({{\bf{Y}}}{{{\bf{C}}}}^{{{\rm{T}}}}{({{\bf{C}}}{{{\bf{C}}}}^{{{\rm{T}}}}+\beta {{\bf{1}}})}^{{\dagger} },0\right)$$

(3)

Where I represents the identify matrix, and 1 represents a matrix with each element equal to 1.

At each iteration n, C and A are then updated from their current values with a learning rate of α (here, 0.5):

$${{{\bf{C}}}}_{{{\rm{n}}}+1}+1=(1-\alpha ){{{\bf{C}}}}_{{{\rm{n}}}}+{{{\rm{\alpha }}}{{\bf{C}}}}^{*}$$

(4)

$${{{\bf{A}}}}_{{{\rm{n}}}+1}=(1-\alpha ){{{\bf{A}}}}_{{{\rm{n}}}}+\alpha {{{\bf{A}}}}^{\ast }$$

(5)

After convergence, the resulting ROIs are passed through a 2-dimensional median filter of size 3x3, and the top 10% of pixel values are kept. Resulting ROIs are split into contiguous components, and final time courses are calculated by updating C from the final ROIs with a learning rate of α = 1. Only ROIs ≥ 30 pixels are included.

Merging

Combining Results from Patches

After all image patches are processed, the resulting ROIs are evaluated to be merged. The temporal traces are detrended by subtracting the minimal value in a rolling 30 second window. In data presented here, ROIs were merged if their temporal components had a correlation coefficient above 0.8, and they shared at least 1 pixel in membership. The spatial and temporal components of merged ROIs are then updated according to the algorithm in Supplementary Table 2c.

Merging Threshold Analysis

We present a method to estimate a lower bound of a useful merging threshold in Supplementary Fig. 3. This lower bound allows users to avoid linking ROIs from different neurons. Above this lower bound, the choice of merging threshold is up to the user, depending on the scientific question. For a given FOV, all pairwise correlations between the detrended activity traces of ROIs were computed. Then, for a range of threshold values from 1 to 0 (in steps of 0.01), we merged ROIs with correlations above that value. To estimate how well the clustering worked, we identified the cluster with the largest number of member ROIs. We defined the minimum correlation as the lowest correlation value between ROIs in that cluster. This approach is similar to complete-linkage hierarchical clustering¹⁰⁰, with distance inversely proportional to correlation. We observed that all FOVs had a critical value below which the minimum correlation substantially decreased. This corresponded to ROIs from different neurons becoming linked. We estimate this as the lower bound on an interpretable merging threshold for that FOV.

Screening

Skewness Classification

The d-NMF output contains a mixture of valid and invalid ROIs. To automatically classify ROIs as valid or invalid, we computed the skewness of the extracted temporal traces after de-trending with a rolling 30-second window. For ground truth, human labelers manually screened all extracted ROIs and labeled them as ‘valid’ or ‘invalid’ based on morphology. Using skewness as a threshold value, we quantified the performance of the classifier using two metrics: the area under the ROC curve plotting the True Positive Rate versus the False Positive Rate, and the Jaccard Index, computed as TP/(TP + FP + FN), where TP is the count of True Positives, FP is the count of False Positives, and FN is the count of False Negatives (Fig. 2c).

Signal-to-noise ratio

We also tested the efficacy of the signal-to-noise ratio as a classifier threshold (Supplementary Fig. 4). For a de-trended calcium trace, the signal-to-noise ratio was defined as SNR = P/M, where P is the 99.9^th percentile of the trace, and M is the median absolute deviation of the trace (median( | x – median(x)|)).

ROI Comparisons

Manual Labeling

Human experts manually labeled ROIs using FIJI software¹⁰¹ on 20X temporally downsampled image stacks to generate ground truth labeling data. Image stacks were inspected frame-by-frame for neural segments showing synchronous activity. Dendritic branches were split up into multiple ROIs at branch points. Additionally, labelers were instructed to break up long dendritic branches into smaller ROIs about the length of the soma (approximately 33 µm).

CaImAn Parameters

The python implementation of CaImAn²⁸ was run on the motion-corrected, downsampled image stacks using default parameters using the sparse_nmf initialization procedure. Patch sizes and overlaps were chosen to be 64 x 64 and 8 pixels to match those used by d-NMF. Only those ROIs labeled as valid were used for analyses (Fig. 4). K = 15 or 30 components per patch (number of clusters parameter) were chosen to be estimated, giving results for CNMF-15 and CNMF-30, respectively, in Supplementary Fig. 7. We compared against the higher-performing CNMF-30 in Fig. 4.

suite2p Parameters

Suite2p was run on the motion-corrected, downsampled image stacks using pre-configured parameters for dendrites and axons. All labeled ROIs were used for analysis (Fig. 4). Three settings of suite2p were run, with different values for the threshold parameter: 1, 0.75, and 0.5, giving results for s2p-1, s2p-0.75, and s2p-0.5, respectively, in Supplementary Fig. 7. We compared against the higher-performing s2p-0.75 in Fig. 4.

F1 score for model comparison

The output of d-NMF, CNMF, and suite2p were compared to manually labeled data in a pixel-wise fashion. The metric used was the F1 score, calculated as

$$F1=2*\frac{{Precision}*{Recall}}{{Precision}+{Recall}}$$

(6)

This measure is a combination of recall (True Positive Rate, TP/(TP + FN)) and precision (Positive Predictive Value, TP/(TP + FP)), as human-labeled datasets may have incomplete labeling, which would yield poor estimates of false positives. The True Positive Rate and F1 score computed pixel-wise are denoted TPR_px and F1_px, respectively.

The pixel-wise metric defined above has advantages in its flexibility. It is agnostic to how a neuron may be parceled up, and quantifies completeness of labeling and accuracy of the placement of ROIs. It is most interpretable for sparsely labeled datasets, but has drawbacks when applied to densely labeled datasets. Namely, a single ROI covering all pixels of all neurons in the field of view will achieve the same score as a set of individual ROIs for each dendritic branch. Hence, we defined a second metric based entirely on ROI morphology.

Algorithmically defined ROIs can often span multiple dendritic branches or encompass soma and proximal branches (Supplementary Fig. 6). To define ROIs in a systematic manner, we performed a morphological split operation on all ROIs (Supplementary Fig. 5), drawing boundaries at branch points and separating putative somatic regions, defined by connected groups of pixels with a radius of at least 10 pixels (11 μm). Resulting ROIs with a size less than 30 pixels were discarded.

Manually-drawn ROIs that sub-segmented a dendritic branch were first merged together and then put through the same morphological split operation. This ensured that manually drawn ROIs followed the same well-defined guidelines across labelers. For each ROI in set A, we found the ROI in set B that had the highest spatial correspondence, as computed by the Jaccard index (size of the intersection divided by size of the union). We then define a pixel in an ROI as “covered” if it intersects with the matching ROI.

If A is the manually-drawn ground truth and B is a test set, define:

True Positive (TP) as the number of pixels that are covered in ROIs in set A

False Negative (FN) as the number of pixels that are not covered in ROIs in set A

False Positive (FP) as the number of pixels that are not covered in ROIs in set B

The True Positive Rate (TPR) and F1 score are then computed accordingly. These measures computed ROI-wise are denoted TPR_roi and F1_roi, respectively.

Construction of Synthetic Data

Movie Generation

To validate the accuracy of d-NMF, we constructed a series of synthetic datasets using one of our sparse FOVs (Fig. 3). To define ground truth, we took FOV2 (Supplementary Fig. 1), manually drew ROIs, and computed the activity of those ROIs by averaging over member pixels. A template movie was constructed by shifting the movie by -100 pixels in the Y dimension and -40 pixels in the X dimension, to center the visible neuron. This template was then modified by shifting the X-dimension of the entire movie by a random amount -50 to 50 μm, shifting the Y-dimension by -50 to -50 μm, then rotating by a random angle between 0 and 360 degrees. The altered template was then shifted in time by a random amount between -250 and 250 seconds. The ground truth ROIs and activity traces were modified accordingly. ROIs that fell outside of the original 512x512 pixel frame after shifting and rotating were discarded. The frames from this new movie were then added to the original template. This process was repeated 200 times, to generate synthetic movies with 1 to 201 neurons.

ROI Signal Quality

The overlaying of movie replicates increased the noise present in each pixel, which had the potential to degrade overall signal quality of the known ROIs. To quantify this degradation, we computed the signal quality of each ROI in our synthetic datasets (Fig. 3c-e). For a given ROI, the frame of maximum activity was identified from its ground truth activity trace. From the z-scored movie, the mean value of pixels within that ROI at that frame was computed to define the ROI signal quality. This value gets smaller as more neurons are added to the synthetic data, an unavoidable consequence of adding uncorrelated variables.

Evaluating Performance

Because different methods or experimenters may segment dendrites into more fine or coarse-grained ROIs, we defined an approach to compute the similarity between ground truth ROIs and ROIs obtained through automated methods. To do this, we introduce the concept of Coverage.

Define 2 sets of ROIs, set A and B and their corresponding activity traces. For any ROI_i in set A, identify all ROIs in set B that 1) Spatially overlap ROI_i; and 2) Are correlated in time above a value of 0.5. This excludes contributions from unrelated crossing ROIs. Take the union of these ROIs, and quantify the pixels covered by that union. Repeat this process by covering B with A. Define classification accuracy in a similar fashion as above:

If A is the ground truth and B is a test set, define:

True Positive (TP) as the number of pixels that are covered in ROIs in set A

False Negative (FN) as the number of pixels that are not covered in ROIs in set A

False Positive (FP) as the number of pixels that are not covered in ROIs in set B

The True Positive Rate and F1 score (Fig. 3e) are then computed accordingly, denoted as TPR_cov and F1_cov, respectively.

Note this measure differs from the ROI-based measure above because we know the ground truth activity to use to link together ROIs and thus are not restricted to choosing a single ROI with the highest overlap.

In Fig. 3f, these values were only computed for ROIs with a minimum Signal Quality of 2.

Temporal Fidelity Testing Using Synthetic Data

To test the limits of d-NMF in detecting localized activity, we generated synthetic data in two ways. For Supplementary Fig. 11a-b, entirely synthetic data was simulated in a dendritic segment 6 pixels in width by 90 pixels long, diagonally embedded in a 64 x 64-pixel space. Background fluorescence was generated independently for each pixel by drawing from an exponential distribution with mean 7, raised to the power of 1.8, to match the statistics of noise observed in our data.

Calcium transients were simulated by a difference of exponentials of the form

$${A}({e}^{-t/\tau }-{e}^{-4t/\tau })/B$$

(7)

Where B is chosen to normalize values such that the peak of the waveform has amplitude A. When simulated at 30 Hz, a transient characterized by the time constant τ has a full width at half max of approximately τ/10 seconds.

3 transients with τ = 24 (2.4-second half-width), A = 700 were generated across the entire synthetic dendrite to provide global activity. A variable number N of additional transients with variable values of A and τ were present in a portion of the dendrite with variable length L. The full array of parameters is listed in Supplementary Table 4.

Each parameter combination was simulated 5 times, resulting in 5200 simulations to generate Supplementary Fig. 11b.

Data for Supplementary Fig. 11d was generated in a similar fashion. A patch of dendrite from FOV 2 (Supplementary Fig. 1) was taken as background activity, and calcium transients were added to the movie only for pixels belonging to a small branch. The array of parameters is listed in Supplementary Table 4.

Each parameter combination was simulated 5 times, resulting in 3600 simulations to generate Supplementary Fig. 11d.

Spatial accuracy was computed as the maximum correlation coefficient between any detected ROI and the target ROI. Temporal accuracy was computed as the proportion of injected transients that were detected in the ROI with the highest spatial correlation with the target ROI. Total accuracy was calculated as the product of these two measures.

Fitness Trace

To generate ground truth data to evaluate the Fitness Trace (Fig. 5), 90 ROIs generated from d-NMF (30 apical dendrites, 30 soma, and 30 basal dendrites, when possible) were chosen at random from 9 FOVs. Their activity traces were re-estimated by taking a weighted average across the ROI, which was then de-trended using a rolling minimum of 30-second frames, then z-scored. Putative transients were identified as contiguous time bins where the z-scored trace exceeded 1 standard deviation. These event detection criteria were meant to be permissive, to include examples of valid and invalid transients. Transients were then manually reviewed and classified as valid or invalid using a previously published graphical user interface³⁹.

The image stack was de-trended and transformed into ΔF/F values, then z-scored across time. For a given ROI, a rectangular bounding box was defined around all non-zero values with a padding of 3 pixels in each dimension. The Fitness Trace for a given ROI at time t was defined as the correlation coefficient between the z-scored image stack at time t and the ROI, calculated only using the pixels in that bounding box.

Transient Detection Methods

To describe the different detection methods (Fig. 5, Supplementary Fig. 13), it is useful to define two types of activity traces. The first is the activity trace arrived at through d-NMF, that is, a signal de-mixed from overlapping sources; we denote this as De-mixed ΔF/F. The second is a simple signal obtained through taking a weighted average across all of the pixels of an ROI. We denote this as Simple ΔF/F. Detection method differences are summarized in Supplementary Table 5. Unless otherwise noted, activity traces are all de-trended by subtracting the rolling minimum across 30 seconds, then z-scored.

Sparse Data Processing

In addition to expressing GCaMP, animals used for the Sparse Data analyses (Supplementary Fig. 16) expressed a Cre-dependent tdTomato. ROIs were manually drawn and the time-varying activity in the green (G) and red (R) channels was computed by a simple average and temporally smoothed by convolving with a Gaussian kernel with σ = 33 ms. The activity of a given ROI (S) was then defined as the ratio of the calcium-dependent green fluorescence versus the calcium-independent red fluorescence (G/R)⁸⁶. This step was critical to correct for motion in the Z plane. Calcium transients were manually identified and verified with the original image stacks for each ROI in the Sparse Data.

Spatial Tuning Properties

Single session analyses (Fig. 6, Supplementary Figs. 11-12) were performed on data from Familiar Day 1. Behavioral data was first downsampled to match the frame rate of imaging. Only data during movement (speed > 2 cm/s) was used for all spatial analyses. To construct firing rate maps, the track was divided into 40 equally spaced bins of width 5 cm. Occupancy and transient event count were computed, circularly smoothed with a Gaussian smoothing kernel of width 5 cm, and then divided to compute the rate.

ROIs were manually classified as apical dendrites, soma, or basal dendrites based on position in the field of view. ROIs encompassing both a soma and one or more dendritic branches were classified as soma. In all other instances we treat apical dendrites, soma, and basal dendrites as independent populations, without assigning parent soma to individual dendrites. Thus, when we refer to apical dendrites or basal dendrites, we are referring to dendrites, which are some distance from their parent cell body, which is often not visible in the same field of view.

We used two measures to quantify the degree of tuning of each rate map. Maps were divided into 40 bins as described above. Spatial information content¹⁰² was computed as

$${{\rm{Info\; Content}}}={\sum }_{i=1}^{N}{P}_{i}{R}_{i}\,{\log }\,_{2}{R}_{i}$$

(8)

Where P_i is the normalized occupancy in the ith bin, such that the sum across all P_i = 1, and R_i is the normalized value of the rate map in the ith bin, such that the sum across all R_i = 1.

Sparsity was computed as

$${{\rm{Sparsity}}}=1-\frac{{\left(\mathop{\sum} _{i=1}^{N}{R}_{i}\right)}^{2}}{N\mathop{\sum }_{i=1}^{N}{R}_{i}^{2}}$$

(9)

Where R_i is the value of the rate map in the ith bin.

Each ROI served as its own control to determine the statistical significance of spatial tuning. For each ROI, the transient times were shifted between -166 and 166 seconds (500 total shifts per ROI). The information content at a shift of 0 was then normalized to the 99^th percentile of information content at non-0 shift. A normalized information content value greater than 1 indicated significant tuning. Additionally, a minimum of 4 transients must have been detected for an ROI to be called significantly tuned.

Tuning Parametrization

Tuning curves were parametrized as a mixture of Von Mises functions, as described previously¹⁰³. Rate maps were circularly smoothed with a sigma of 15 cm (3 bins), and the curve was fit by increasing the number of Von Mises functions until the residuals were below 25% of the maximum value of the original rate map. Place field width was defined as the width of a fitted component at 50% of the component’s amplitude (i.e. full width at half max). For ROIs with multiple place fields, their width was defined as the mean width of all place fields.

Merging ROIs to Address Oversplitting

It is likely that extended dendrites could be split into multiple ROIs, especially if a portion of the dendrite dives out of the focal plane or if it is obscured by another neuron. This could lead to a problem of oversplitting, where multiple dendrites from the same neuron with highly correlated signals contribute multiple times to statistical estimates. To investigate if this biased our results, we merged dendritic ROIs with highly correlated activity into single ROIs (Supplementary Fig. 15, Supplementary Table 9). Correlation was calculated on a smoothed binary activity vector. This avoids issues of correlation being affected by different decay time constants or contaminated activity from overlapping dendrites. Dendrites of the same type (apical or basal) were merged if their activity was correlated above a value of 0.7. When 2 or more ROIs were merged, the statistics (activity rate, information content, rate map, etc.) were computed as the median value of the statistics of the ROIs being merged.

Quantifying Overlap

We defined two ROIs as overlapping if they shared at least 8 pixels and had a correlation coefficient between their activity traces less than 0.75. This avoids inflating the overlap amount from ROIs that are part of the same dendritic tree.

Distance Dependence

Distance dependence in the sparse dataset was defined as the path distance from the center of a neuron’s soma to the center of an ROI, only traversing ROIs that belong to that neuron.

To quantify distance-dependence in the dense dataset, a line was fit to the center of all somatic ROIs to define the cell body layer. Distance to any dendritic ROI was defined as the tangential distance to the cell body layer, as not all dendritic ROIs could be directly traced back to their parent soma.

Stability

Within-day stability (Fig. 7) was assessed by splitting the data from Familiar Day 1 in half. Rate maps were re-estimated for each ROI using only the data in each session half. The tuning curve (TC) correlation was defined as the correlation coefficient between the tuning curves for each half. This measure was computed for each ROI and then averaged to obtain a single value for the session. To be included in the calculation for TC correlation, an ROI must have had a minimum of 4 calcium transients and be significantly tuned across the entire session. Population vector (PV) correlation was computed by constructing the rate estimates of all ROIs for a given position bin in the first half and taking the correlation coefficient between that vector and the corresponding vector in the second half. This yields a value for each position bin, which was then averaged to obtain a single value for a session. To be included in the calculation for PV correlation, an ROI must have had a minimum of 4 calcium transients, with no criteria for significant tuning.

To quantify across-day stability (Fig. 7, Supplementary Figs. 14-15), image stacks from Familiar Days 1 and 2 were stitched into a single image stack and motion-corrected together. d-NMF was then run on the combined image stack to obtain ROIs that spanned both sessions. Stability analysis was then performed as for within-day estimates. To be included in across-day stability analyses, an ROI must have had at least 4 detected calcium transients in both days and significantly tuned in at least one day. The activity criterion ensured that correlation estimates were not skewed by ROIs that were not visible on one of the recording days.

Structural Stability

To verify that differences in tuning stability were not due to the inability to track ROIs across days, we additionally quantified the structural stability of ROIs (Supplementary Fig. 17). For each ROI we took the average of frames at which significant calcium transients were detected for Familiar Days 1 and 2. The structural stability was defined as the correlation coefficient between these averages, using only data within the modified boundary of the ROI. The modified boundary of an ROI was defined by first thresholding the ROI above 20% of its maximum pixel intensity, then dilating the resulting mask by one pixel.

Population Vector Decoding

To test the impact of increased across-day stability in apical dendrites, we performed population vector decoding in a manner similar to that described previously⁵³ (Fig. 8). A separate decoder was constructed for each FOV for each of apical dendrites, soma, and basal dendrites. Template tuning curves for each ROI were constructed as above. For within-day decoding, data from the first half of Familiar Day 1 was used to define the template. For across-day decoding, all data from Familiar Day 1 was used to define the template. As above for defining Population Vector correlations, only ROIs that were active in both days and significantly tuned in at least one day were included for decoding.

Time-varying rate vectors for each ROI were constructed using data from either the second half of Familiar Day 1 (within-day decoding) or all data from Familiar Day 2 (across-day decoding), using 33 ms bins smoothed with a Gaussian smoothing kernel with σ = 667 ms. For each time point in the decoded portion of the data, the decoded position was the position corresponding to the highest correlation with the template matrix. Any time points with zero activity across all relevant ROIs had an undefined correlation with any position. The most recently decoded position was copied in to those undefined frames.

Decoding error was defined as the median absolute error between decoded position and actual position, defined circularly so the beginning of the track (position 0 cm) and the end of the track (position 200 cm) were 0 cm away.

Subsampled decoder

The performance of a population vector decoder is highly dependent on the number of units used to construct it⁵³. To control for variation in the number of ROIs across compartments, we constructed additional population vector decoders using subsets of eligible ROIs (Fig. 8d,e). For each session and compartment type (apical, soma, basal), we randomly selected (without replacement) 5, 15, 25, 35, 45, 55, or 65 ROIs if available to decode position and record decoding error. This process was repeated 100 times and the median value across the 100 iterations was used as the decoding error of the subsampled classifier.

The statistical significance of decoding for subsampled decoders was assessed using a two-way ANOVA with the number of ROIs as a continuous predictor, the ROI type (Apical, Soma, or Basal) as a categorical predictor, and the decoding error as the dependent variable. The p-values reported in Fig. 8 are the p-values for an interaction effect between the number of ROIs and the ROI type, performed in a pairwise manner (Apical vs Soma, Apical vs Basal, Soma vs Basal).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

Downsampled (1.5 Hz) imaging data and intermediate data analysis files generated in this study have been deposited in the Zenodo database: https://doi.org/10.5281/zenodo.14207307 and https://doi.org/10.5281/zenodo.14207412. The raw, 30 Hz imaging data are available under restricted access due to large file sizes, and access can be obtained by request to the corresponding authors, with an expected timeframe of two weeks for response.

Code availability

Code and data needed to generate the figures in this study can be downloaded from Zenodo: https://doi.org/10.5281/zenodo.14207307 and https://doi.org/10.5281/zenodo.14207412. The most updated version of the d-NMF code is available at https://github.com/basulab-nyu/d-NMF.

References

Park, J. et al. Contribution of apical and basal dendrites to orientation encoding in mouse V1 L2/3 pyramidal neurons. Nat. Commun. 10, 1–11 (2019).
Article ADS Google Scholar
Amitai, Y., Friedman, A., Gutnick, M. J. & Connors, B. W. Regenerative activity in apical dendrites of pyramidal cells in neocortex. Cereb. Cortex 3, 26–38 (1993).
Article PubMed CAS Google Scholar
Kim, H. G. & Connors, B. W. Apical Dendrites of the Neocortex: Correlation between Sodium- and Calcium-dependent Spiking and Pyramidal Cell Morphology. J. Neurosci. 13, 5301–5311 (1993).
Article PubMed PubMed Central MATH CAS Google Scholar
Larkum, M. E., Zhu, J. J. & Sakmann, B. Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J. Physiol. 533, 447–466 (2001).
Article PubMed PubMed Central MATH CAS Google Scholar
Schiller, J., Major, G., Koester, H. J. & Schiller, Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404, 285–289 (2000).
Article ADS PubMed MATH CAS Google Scholar
Moore, J. J. et al. Dynamics of cortical dendritic membrane potential and spikes in freely behaving rats. Science 355, (2017).
Bilash, O. M., Chavlis, S., Johnson, C. D., Poirazi, P. & Basu, J. Lateral entorhinal cortex inputs modulate hippocampal dendritic excitability by recruiting a local disinhibitory microcircuit. Cell Rep 42, 111962 (2023).
Article PubMed PubMed Central CAS Google Scholar
Moore, J. J., Robert, V., Rashid, S. K. & Basu, J. Assessing Local and Branch-specific Activity in Dendrites. Neuroscience 489, 143–164 (2022).
Article PubMed CAS Google Scholar
Kupferman, J. V. et al. Reelin signaling specifies the molecular identity of the pyramidal neuron distal dendritic compartment. Cell 158, 1335–1347 (2014).
Article PubMed PubMed Central MATH CAS Google Scholar
Tran-Van-Minh, A. et al. Contribution of sublinear and supralinear dendritic integration to neuronal computations. Front. Cell. Neurosci. 9, 1–15 (2015).
Article MATH Google Scholar
Mel, B. W. Synaptic integration in an excitable dendritic tree. J. Neurophysiol. 70, 1086–1101 (1993).
Article PubMed MATH CAS Google Scholar
Poirazi, P., Brannon, T. & Mel, B. W. Pyramidal neuron as two-layer neural network. Neuron 37, 989–999 (2003).
Article PubMed CAS Google Scholar
Mehta, M. R. Cooperative LTP can map memory sequences on dendritic branches. Trends Neurosci 27, 69–72 (2004).
Article PubMed MATH CAS Google Scholar
London, M. & Häusser, M. Dendritic computation. Annu. Rev. Neurosci. 28, 503–532 (2005).
Article PubMed MATH CAS Google Scholar
Johnston, D. & Narayanan, R. Active dendrites: colorful wings of the mysterious butterflies. Trends Neurosci 31, 309–316 (2008).
Article PubMed MATH CAS Google Scholar
Golding, N. L., Staff, N. P. & Spruston, N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331 (2002).
Article ADS PubMed CAS Google Scholar
Gambino, F. et al. Sensory-evoked LTP driven by dendritic plateau potentials in vivo. Nature 515, 116–119 (2014).
Article ADS PubMed MATH CAS Google Scholar
Basu, J. et al. Gating of hippocampal activity, plasticity, and memory by entorhinal cortex long-range inhibition. Sciene (80-.). 351, aaa5694 (2016).
Article MATH Google Scholar
Chen, T. W. et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013).
Article ADS PubMed PubMed Central MATH CAS Google Scholar
Dana, H. et al. High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat. Methods 16, 649–657 (2019).
Article PubMed MATH CAS Google Scholar
Sheffield, M. E. J. & Dombeck, D. A. Calcium transient prevalence across the dendritic arbour predicts place field properties. Nature 517, 200–204 (2015).
Article ADS PubMed CAS Google Scholar
Cichon, J. & Gan, W. B. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature 520, 180–185 (2015).
Article ADS PubMed PubMed Central CAS Google Scholar
Francioni, V., Padamsey, Z. & Rochefort, N. L. High and asymmetric somato-dendritic coupling of V1 layer 5 neurons independent of visual stimulation and locomotion. Elife 8, 1–25 (2019).
Article Google Scholar
Kerlin, A. et al. Functional clustering of dendritic activity during decision-making. Elife 8, 1–32 (2019).
Article MATH Google Scholar
Otor, Y. et al. Dynamic compartmental computations in tuft dendrites of layer 5 neurons during motor behavior. Science (80-.). 376, 267–275 (2022).
Article ADS MATH CAS Google Scholar
Huber, D. et al. Multiple dynamic representations in the motor cortex during sensorimotor learning. Nature 484, 473–478 (2012).
Article ADS PubMed PubMed Central MATH CAS Google Scholar
Mau, W. et al. The Same Hippocampal CA1 Population Simultaneously Codes Temporal Information over Multiple Timescales. Curr. Biol. 28, 1499–1508.e4 (2018).
Article PubMed PubMed Central MATH CAS Google Scholar
Giovannucci, A. et al. CaImAn an open source tool for scalable calcium imaging data analysis. Elife 8, 1–45 (2019).
Article MATH Google Scholar
Pachitariu, M. et al. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv 061507 https://doi.org/10.1101/061507 (2016).
Mukamel, E. A., Nimmerjahn, A. & Schnitzer, M. J. Automated Analysis of Cellular Signals from Large-Scale Calcium Imaging Data. Neuron 63, 747–760 (2009).
Article PubMed PubMed Central CAS Google Scholar
Kaifosh, P., Zaremba, J. D., Danielson, N. B. & Losonczy, A. SIMA: Python software for analysis of dynamic fluorescence imaging data. Front. Neuroinform. 8, 1–10 (2014).
Article Google Scholar
Pnevmatikakis, E. A. et al. Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron 89, 285 (2016).
Article PubMed PubMed Central MATH CAS Google Scholar
Sheffield, M. E. J., Adoff, M. D. & Dombeck, D. A. Increased Prevalence of Calcium Transients across the Dendritic Arbor during Place Field Formation. Neuron 96, 490–504.e5 (2017).
Article PubMed PubMed Central CAS Google Scholar
Rajasethupathy, P. et al. Projections from neocortex mediate top-down control of memory retrieval. Nature 526, 653–659 (2015).
Article ADS PubMed PubMed Central MATH CAS Google Scholar
Lee, D. D. & Seung, H. S. Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791 (1999).
Article ADS PubMed MATH CAS Google Scholar
Trautmann, E. M. et al. Dendritic calcium signals in rhesus macaque motor cortex drive an optical brain-computer interface. Nat. Commun. 12, (2021).
Cornejo, V. H., Ofer, N. & Yuste, R. Voltage compartmentalization in dendritic spines in vivo. Science (80-.) 375, 82–86 (2022).
Article ADS MATH CAS Google Scholar
Jaccard, P. The Distribution of the Flora in the Alpine Zone. New Phytol 11, 37–50 (1912).
Article MATH Google Scholar
Gauthier, J. L. et al. Detecting and correcting false transients in calcium imaging. Nat. Methods https://doi.org/10.1038/s41592-022-01422-5 (2022).
Article PubMed PubMed Central MATH Google Scholar
Leutgeb, S., Leutgeb, J. K., Treves, A., Moser, M. B. & Moser, E. I. Distinct ensemble codes in hippocampal areas CA3 and CA1. Science (80-.). 305, 1295–1298 (2004).
Article ADS MATH CAS Google Scholar
Muller, R. U., Kubie, J. L. & Ranck, J. B. Spatial firing patterns of hippocampal complex-spike cells in a fixed environment. J. Neurosci. 7, 1935–1950 (1987).
Article PubMed PubMed Central MATH CAS Google Scholar
Barnes, C. A., McNaughton, B. L., Mizumori, S. J. Y., Leonard, B. W. & Lin, L.-H. Comparison of spatial and temporal characteristics of neuronal activity in sequential stages of hippocampal processing. Prog. Brain Res. 83, 287–300 (1990).
Article PubMed CAS Google Scholar
Dong, C., Madar, A. D. & Sheffield, M. E. J. Distinct place cell dynamics in CA1 and CA3 encode experience in new environments. Nat. Commun. 12, 1–13 (2021).
Article MATH Google Scholar
Hainmueller, T. & Bartos, M. Parallel emergence of stable and dynamic memory engrams in the hippocampus. Nature 558, 292–296 (2018).
Article ADS PubMed PubMed Central MATH CAS Google Scholar
Zhou, P. et al. Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data. Elife 7, 1–37 (2018).
Article MATH CAS Google Scholar
Robert, V. et al. Entorhinal cortex glutamatergic and GABAergic projections bidirectionally control discrimination and generalization of hippocampal representations. bioRxiv (2023).
Bittner, K. C. et al. Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat. Neurosci. 18, 1133–1142 (2015).
Article PubMed PubMed Central MATH CAS Google Scholar
Bittner, K. C., Milstein, A. D., Grienberger, C., Romani, S. & Magee, J. C. Behavioral time scale synaptic plasticity underlies CA1 place fields. Science (80-.). 357, 1033–1036 (2017).
Article ADS CAS Google Scholar
McKenzie, S. et al. Preexisting hippocampal network dynamics constrain optogenetically induced place fields. Neuron 109, 1040–1054.e7 (2021).
Article PubMed PubMed Central MATH CAS Google Scholar
Sun, Q. et al. Proximodistal Heterogeneity of Hippocampal CA3 Pyramidal Neuron Intrinsic Properties, Connectivity, and Reactivation during Memory Recall. Neuron 95, 656–672.e3 (2017).
Article PubMed PubMed Central MATH CAS Google Scholar
Hunt, D. L., Linaro, D., Si, B., Romani, S. & Spruston, N. A novel pyramidal cell type promotes sharp-wave synchronization in the hippocampus. Nat. Neurosci. 21, 985–995 (2018).
Article PubMed CAS Google Scholar
Soltesz, I. & Losonczy, A. CA1 pyramidal cell diversity enabling parallel information processing in the hippocampus. Nat. Neurosci. 21, 484–493 (2018).
Article PubMed PubMed Central MATH CAS Google Scholar
Zemla, R., Moore, J. J., Hopkins, M. D. & Basu, J. Task-selective place cells show behaviorally driven dynamics during learning and stability during memory recall. Cell Rep 41, 111700 (2022).
Article PubMed PubMed Central CAS Google Scholar
Mau, W., Hasselmo, M. E. & Cai, D. J. The brain in motion: How ensemble fluidity drives memory-updating and flexibility. Elife 9, 1–24 (2020).
Article MATH Google Scholar
Qin, S. et al. Coordinated drift of receptive fields in Hebbian/anti-Hebbian network models during noisy representation learning. Nat. Neurosci 26, 339–349 (2023).
Article PubMed MATH CAS Google Scholar
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
Article PubMed PubMed Central MATH CAS Google Scholar
Schoonover, C. E., Ohashi, S. N., Axel, R. & Fink, A. J. P. Representational drift in primary olfactory cortex. Nature 594, 541–546 (2021).
Article ADS PubMed CAS Google Scholar
Deitch, D., Rubin, A. & Ziv, Y. Representational drift in the mouse visual cortex. Curr. Biol. 31, 4327–4339.e6 (2021).
Article PubMed MATH CAS Google Scholar
Marks, T. D. & Goard, M. J. Stimulus-dependent representational drift in primary visual cortex. Nat. Commun. 12, 1–16 (2021).
ADS MATH Google Scholar
Rokni, U., Richardson, A. G., Bizzi, E. & Seung, H. S. Motor Learning with Unstable Neural Representations. Neuron 54, 653–666 (2007).
Article PubMed CAS Google Scholar
Driscoll, L. N., Pettit, N. L., Minderer, M., Chettih, S. N. & Harvey, C. D. Dynamic Reorganization of Neuronal Activity Patterns in Parietal Cortex. Cell 170, 986–999.e16 (2017).
Article PubMed PubMed Central CAS Google Scholar
Lecoq, J. et al. Visualizing mammalian brain area interactions by dual-axis two-photon calcium imaging. Nat. Neurosci. 17, 1825–1829 (2014).
Article PubMed PubMed Central MATH CAS Google Scholar
Diehl, G. W., Hon, O. J., Leutgeb, S. & Leutgeb, J. K. Stability of medial entorhinal cortex representations over time. Hippocampus 29, 284–302 (2019).
Article PubMed MATH Google Scholar
Rolls, E. T. The mechanisms for pattern completion and pattern separation in the hippocampus. 7, 1–21 (2013).
Yassa, M. A. & Stark, C. E. L. Pattern separation in the hippocampus. Trends Neurosci 34, 515–525 (2011).
Article PubMed PubMed Central MATH CAS Google Scholar
Guzman, S. J., Schlögl, A., Frotscher, M. & Jonas, P. Synaptic mechanisms of pattern completion in the hippocampal CA3 network. Science (80-.). 353, 1117–1123 (2016).
Article ADS CAS Google Scholar
Leutgeb, J. K., Leutgeb, S., Moser, M. B. & Moser, E. I. Pattern separation in the dentate gyrus and CA3 of the hippocampus. Science (80-.). 315, 961–966 (2007).
Article ADS MATH CAS Google Scholar
Neunuebel, J. P. & Knierim, J. J. CA3 retrieves coherent representations from degraded input: Direct evidence for CA3 pattern completion and dentate gyrus pattern separation. Neuron 81, 416–427 (2014).
Article PubMed PubMed Central CAS Google Scholar
Callaway, E. M. Feedforward, feedback and inhibitory connections in primate visual cortex. Neural Networks 17, 625–632 (2004).
Article PubMed MATH Google Scholar
Spruston, N. Pyramidal neurons: Dendritic structure and synaptic integration. Nat. Rev. Neurosci. 9, 206–221 (2008).
Article PubMed CAS Google Scholar
Larkum, M. A cellular mechanism for cortical associations: An organizing principle for the cerebral cortex. Trends Neurosci 36, 141–151 (2013).
Article PubMed MATH CAS Google Scholar
Sacramento, J., Bengio, Y., Costa, R. P. & Senn, W. Dendritic cortical microcircuits approximate the backpropagation algorithm. (2018).
Golkar, S., Tesileanu, T., Bahroun, Y., Sengupta, A. M. & Chklovskii, D. B. Constrained Predictive Coding as a Biologically Plausible Model of the Cortical Hierarchy. 1–24 (2022).
Siegel, M., Körding, K. P. & König, P. Integrating Top-Down and Bottom-Up Sensory Processing by Somato-Dendritic Interactions. 173, 161–173 (2000).
Losonczy, A., Makara, J. K. & Magee, J. C. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature 452, 436–441 (2008).
Article ADS PubMed MATH CAS Google Scholar
Brandalise, F., Carta, S., Helmchen, F., Lisman, J. & Gerber, U. Dendritic NMDA spikes are necessary for timing-dependent associative LTP in CA3 pyramidal cells. Nat. Commun. 7, 1–9 (2016).
Article Google Scholar
Golding, N. L., Kath, W. L. & Spruston, N. Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites. J. Neurophysiol. 86, 2998–3010 (2001).
Article PubMed MATH CAS Google Scholar
Kim, S., Guzman, S. J., Hu, H. & Jonas, P. Active dendrites support efficient initiation of dendritic spikes in hippocampal CA3 pyramidal neurons. Nat. Neurosci. 15, 600–606 (2012).
Article PubMed PubMed Central CAS Google Scholar
Kerlin, A. et al. Functional clustering of dendritic activity during decision-making. Elife 8, 1–33 (2019).
Article MATH Google Scholar
Smith, S. L., Smith, I. T., Branco, T. & Häusser, M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature 503, 115–120 (2013).
Article ADS PubMed PubMed Central MATH CAS Google Scholar
Beaulieu-Laroche, L., Toloza, E. H. S., Brown, N. J. & Harnett, M. T. Widespread and Highly Correlated Somato-dendritic Activity in Cortical Layer 5 Neurons. Neuron 103, 235–241.e4 (2019).
Article PubMed PubMed Central CAS Google Scholar
O’Hare, J. K. et al. Compartment-specific tuning of dendritic feature selectivity by intracellular Ca2+ release. Science (80-.). 375, eabm1670 (2022).
Article PubMed Central MATH Google Scholar
d’Aquin, S. et al. Compartmentalized dendritic plasticity during associative learning. Science (80-.). 376, eabf7052 (2022).
Article Google Scholar
Jia, H., Rochefort, N. L., Chen, X. & Konnerth, A. Dendritic organization of sensory input to cortical neurons in vivo. Nature 464, 1307–1312 (2010).
Article ADS PubMed MATH CAS Google Scholar
Branco, T., Clark, B. A. & Häusser, M. Dendritic Discrimination of Temporal Input Sequences in Cortical Neurons. Science (80-.). 329, 1671–1675 (2010).
Article ADS MATH CAS Google Scholar
Tsay, D., Dudman, J. T. & Siegelbaum, S. A. HCN1 Channels Constrain Synaptically Evoked Ca2+ Spikes in Distal Dendrites of CA1 Pyramidal Neurons. Neuron 56, 1076–1089 (2007).
Article PubMed PubMed Central CAS Google Scholar
Popovic, M. A., Carnevale, N., Rozsa, B. & Zecevic, D. Electrical behaviour of dendritic spines as revealed by voltage imaging. Nat. Commun. 6, (2015).
Kaifosh, P., Lovett-Barron, M., Turi, G. F., Reardon, T. R. & Losonczy, A. Septo-hippocampal GABAergic signaling across multiple modalities in awake mice. Nat. Neurosci. 16, 1182–1184 (2013).
Article PubMed CAS Google Scholar
Lovett-Barron, M. et al. Dendritic Inhibition in the Hippocampus Supports Fear Learning. Science (80-.). 343, 857–864 (2014).
Article ADS MATH CAS Google Scholar
Srinivasan, R. et al. New Transgenic Mouse Lines for Selectively Targeting Astrocytes and Studying Calcium Signals in Astrocyte Processes In Situ and In Vivo. Neuron 92, 1181–1195 (2016).
Article PubMed PubMed Central MATH CAS Google Scholar
Bindocci, E. et al. Three-dimensional Ca2+ imaging advances understanding of astrocyte biology. Science (80-.). 356, eaai8185 (2017).
Article Google Scholar
Zhang, Y. et al. Fast and sensitive GCaMP calcium indicators for imaging neural populations. bioRxiv 2021.11.08.467793 https://doi.org/10.1101/2021.11.08.467793 (2021).
Piatkevich, K. D. et al. A robotic multidimensional directed evolution approach applied to fluorescent voltage reporters article. Nat. Chem. Biol. 14, 352–360 (2018).
Article PubMed PubMed Central CAS Google Scholar
Abdelfattah, A. S. et al. Bright and photostable chemigenetic indicators for extended in vivo voltage imaging. Science (80-.) 364, 699–704 (2019).
Article ADS MATH Google Scholar
Andermann, M. L. et al. Chronic cellular imaging on entire cortical columns in awake mice using microprisms. Neuron 80, 900–913 (2013).
Article PubMed MATH CAS Google Scholar
Kohara, K. et al. Cell type-specific genetic and optogenetic tools reveal hippocampal CA2 circuits. Nat. Neurosci. 17, 269–279 (2014).
Article PubMed MATH CAS Google Scholar
Danielson, N. B. et al. Distinct Contribution of Adult-Born Hippocampal Granule Cells to Context Encoding. Neuron 90, 101–112 (2016).
Article PubMed PubMed Central MATH CAS Google Scholar
Magnus, C. J. et al. Ultrapotent chemogenetics for research and potential clinical applications. Science (80-.). 364, (2019).
Pnevmatikakis, E. A. & Giovannucci, A. NoRMCorre: An online algorithm for piecewise rigid motion correction of calcium imaging data. J. Neurosci. Methods 291, 83–94 (2017).
Article PubMed CAS Google Scholar
Everitt, B., Landau, S., Leese, M. & Stahl, D. Cluster analysis. In Cluster Analysis 62–64 (Arnold, 2001). https://doi.org/10.1007/BF00154794.
Schindelin, J. et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).
Article PubMed MATH CAS Google Scholar
Skaggs, W. E., McNaughton, B. L., Gothard, K. M. & Markus, E. J. An Information-Theoretic Approach to Deciphering the Hippocampal Code. Adv. neural Inf. Process. 5, 1030–1037 (1993).
Google Scholar
Moore, J. J., Cushman, J. D., Acharya, L., Popeney, B. & Mehta, M. R. Linking hippocampal multiplexed tuning, Hebbian plasticity and navigation. Nature https://doi.org/10.1038/s41586-021-03989-z (2021).
Article PubMed PubMed Central Google Scholar

Download references

Acknowledgements

This work was supported by funding to J.B. from the NIH NINDS BRAIN INITIATIVE grant 1R01NS109994, NINDS 1R01NS109362, NINDS 1RM1NS132981, NIH NIMH 5R01MH122391, Mathers Charitable Foundation Investigator Award, McKnight Scholar Award in Neuroscience, Klingenstein-Simons Fellowship Award in Neuroscience, Alzheimer’s Association Research Grant to Promote Diversity – New to the Field (AARG-D-NTF), Alfred P. Sloan Research Fellowship, Whitehall Research Grant, American Epilepsy Society Junior Investigator Award, Blas Frangione Young Investigator Research Grant, New York University Whitehead Fellowship for Junior Faculty in Biomedical and Biological Sciences, and Leon Levy Foundation; and funding to D.B.C. from the Flatiron Institute, Center for Computational Neuroscience. J.J.M. was supported by an HHMI extension grant to D.B.C., a T32AG052909 grant (Wisniewski, Scharfman), and the Emerald Foundation. S.K.R was supported by a NIH T32GM007308. N.C. was supported by a McKnight Endowment Fund for Neuroscience Mathew Pecot URM Award. We thank Martial Dufour for early development of the experimental preparation and Roland Zemla for his contribution in developing the hardware and software for the custom treadmill and behavioral tracking system. We are indebted to Andrea Giovannucci, Eric Thomson, Pat Gunn, and Johannes Friedrich for their expertise and support in modifying CNMF and CaImAn parameters. NYU High Performance Computing resources were used for data analysis. We thank Tanvi Butola for generously providing axonal calcium imaging data (Data reused from Butola et al., Nature Neuroscience 2025 in Press, NN-A80353B manuscript with permission from Nature Neuroscience); Rafael Yuste and Victor Cornejo for generously providing dendritic voltage imaging data (Data reused with permission from 37); and Daniel Dombeck and Mark Sheffield for generously providing dendritic calcium imaging data (Data reused with permission from 21). We thank Pauline Rahal and Buyong Kim for help with data curation. We thank Vincent Robert, Keelin O'Neil and Tanvi Butola for valuable discussions and critical review of previous versions of the manuscript.

Author information

Authors and Affiliations

Neuroscience Institute, New York University Langone Health, New York, NY, 10016, USA
Jason J. Moore, Shannon K. Rashid, Emmett Bicker, Cara D. Johnson, Naomi Codrington, Dmitri B. Chklovskii & Jayeeta Basu
Center for Computational Neuroscience, Flatiron Institute, Simons Foundation, New York, NY, 10010, USA
Jason J. Moore & Dmitri B. Chklovskii
Department of Neuroscience and Physiology, New York University Grossman School of Medicine, New York, NY, 10016, USA
Jayeeta Basu
Department of Psychiatry, New York University Grossman School of Medicine, New York, NY, 10016, USA
Jayeeta Basu
Center for Neural Science, New York University, New York, NY, 10003, USA
Jayeeta Basu

Authors

Jason J. Moore
View author publications
Search author on:PubMed Google Scholar
Shannon K. Rashid
View author publications
Search author on:PubMed Google Scholar
Emmett Bicker
View author publications
Search author on:PubMed Google Scholar
Cara D. Johnson
View author publications
Search author on:PubMed Google Scholar
Naomi Codrington
View author publications
Search author on:PubMed Google Scholar
Dmitri B. Chklovskii
View author publications
Search author on:PubMed Google Scholar
Jayeeta Basu
View author publications
Search author on:PubMed Google Scholar

Contributions

J.J.M. and J.B. conceived the project and designed experiments. S.K.R. and J.J.M. performed surgeries and recorded data. J.J.M. developed all software code and performed all analyses with guidance and supervision from J.B. and D.B.C. J.J.M. and E.B. wrote software. J.J.M., S.K.R., E.B., C.D.J., and N.C. performed manual curation of data. J.J.M. and J.B. wrote the manuscript.

Corresponding authors

Correspondence to Jason J. Moore or Jayeeta Basu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Movie 1

Reporting Summary

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Moore, J.J., Rashid, S.K., Bicker, E. et al. Sub-cellular population imaging tools reveal stable apical dendrites in hippocampal area CA3. Nat Commun 16, 1119 (2025). https://doi.org/10.1038/s41467-025-56289-9

Download citation

Received: 14 April 2023
Accepted: 15 January 2025
Published: 28 January 2025
Version of record: 28 January 2025
DOI: https://doi.org/10.1038/s41467-025-56289-9

This article is cited by

Hippocampus shapes entorhinal cortical output through a direct feedback circuit
- Tanvi Butola
- Melissa Hernández-Frausto
- Jayeeta Basu
Nature Neuroscience (2025)