Introduction

The exploration of novel chemical materials is a pivotal scientific endeavor with the potential to significantly advance both the economy and society1,2,3,4. Historically, the discovery of innovative molecules has led to major breakthroughs in various fields, including the development of enhanced medical therapies5, innovative catalysts for chemical reactions6, and more efficient carbon capture technologies7. These discoveries have traditionally resulted from labor-intensive experimental processes characterized by extensive trial and error.

In response to the limitations of these traditional experimental approaches, computational-aided molecular design (CAMD) has emerged as a crucial innovation. By conceptualizing material design as an optimization problem, where molecular structures and their properties are treated as variables and objectives, CAMD harnesses computational power to efficiently predict and identify promising materials. The advent of sophisticated machine learning algorithms has marked a paradigm shift from conventional knowledge-based methods, such as the group contribution method8,9,10, to advanced learning-based strategies11. Among these, deep learning has demonstrated exceptional accuracy and flexibility, modeling complex interrelations between chemical structures and properties that challenge traditional theoretical approaches12. For example, graph neural networks (GNNs) have emerged as powerful tools for representing molecular structures13. Unlike traditional models that rely on fixed molecular descriptors, GNNs operate directly on molecular graphs, capturing detailed connectivity and spatial relationships between atoms. This graph-based approach enables GNNs to model molecular interactions with high fidelity14,15, making them particularly well-suited for applications in molecular design, where accurate structural representation is critical. Furthermore, GNNs offer scalability16, enabling efficient processing of large datasets, which is essential for exploring the expansive chemical spaces required in CAMD.

As CAMD has evolved, it has incorporated various generative models and sophisticated optimization strategies that employ surrogate models as objective functions to enhance molecular design. For example, variational autoencoders (VAEs) have been widely used for molecular generation by encoding molecules into a latent space where new structures can be sampled and decoded, facilitating exploration of chemical space17,18. These VAEs are often coordinated with optimization techniques, such as evolutionary algorithms19,20,21, Bayesian optimization (BO)18,22, or Monte Carlo tree search (MCTS)23 to guide the search toward novel molecules with desired properties. Similarly, SMILES-based recurrent neural networks (RNNs) have been employed to generate molecular structures24,25,26. After a pretraining phase, RNNs are often fine-tuned using reinforcement learning, enhancing the model’s ability to achieve goal-directed optimization. However, a significant challenge for generative models can be ensuring diversity in the generated molecules, especially if training data is limited or narrowly focused, which may limit their utility for exploring diverse chemical spaces27. Beyond generative models, some approaches apply optimization algorithms directly to molecular representations without requiring latent spaces. For instance, genetic algorithms (GAs) operate on molecular graphs28,29 or SMILES strings30,31, iteratively generating improved candidates through mutation and crossover operations. This approach bypasses the need for a pretrained generative model, making GAs adaptable and accessible for a variety of CAMD tasks. Compared with generative models, GAs can work well even with smaller datasets and may have lower initial computational demands, which can be beneficial for direct exploration and optimization of molecular properties. Additionally, their evolutionary principles naturally maintain diversity, supporting a broad exploration of chemical space and adaptability to specific property objectives32.

Despite the promise of these optimization approaches, a major challenge with data-driven models in CAMD is their tendency to fail in accurately predicting properties for molecules outside their training scope. This limitation underscores the importance of integrating uncertainty quantification (UQ) into CAMD to assess prediction reliability. Previous studies have commonly addressed this challenge through BO frameworks, often using Gaussian process regression (GPR), including Kriging models33. These non-parametric models make predictions with uncertainty estimates based on the posterior distribution, leveraging a kernel function to define the covariance between training data points. However, the matrix inversion required for non-parametric methods can become time-consuming, particularly for large datasets, as the computational complexity scales \({\mbox{O}}\left({n}^{3}\right)\) with the number of training data and \({\mbox{O}}\left(n\right)\) with the dimension of molecular features34,35. As a result, GPR models are typically constrained to smaller training datasets36, limiting the chemical space that can be explored in CAMD37. To alleviate this computational bottleneck and enable the use of larger datasets, several approximation strategies have been proposed for GPR38. Low-rank or sparse methods (e.g., inducing-point approaches) address the \({\mbox{O}}({n}^{3})\) scaling by selecting a small subset of points (inducing points), reducing the effective size of the Gram matrix, and leading to a more manageable \({\mbox{O}}({{nm}}^{2})\) complexity. Random feature expansions—such as random Fourier features—approximate the kernel function by mapping data into a lower-dimensional feature space, converting GPR into an approximately linear model that can be trained in \({\mbox{O}}\left({nD}\right)\) or \({\mbox{O}}({{nD}}^{2})\), where \(D \, \ll \, n\). Distributed or parallel GPs divide the dataset across multiple machines or computational nodes, combining local posteriors to maintain predictive accuracy while managing larger data volumes. These techniques collectively address the high computational burden of Gaussian process models and may expand the applicability of BO-driven CAMD to larger chemical search spaces.

In contrast, parametric models like GNNs offer a scalable alternative, as they maintain a fixed number of parameters regardless of dataset size, allowing efficient handling of larger datasets. UQ has been successfully integrated with parametric models for active learning and virtual screening, enhancing workflow efficiency39,40. However, optimizing over expansive chemical spaces presents distinct challenges, as accurate UQ under domain shifts remains notoriously difficult41,42. To the best of our knowledge, whether UQ integration within parametric models can enable effective optimization across broad, open-ended chemical spaces—and how best to implement this—remains an open question. Such an approach is particularly valuable for CAMD, as it enables exploration across vast and less-characterized chemical spaces essential for discovering novel compounds.

In this work, we address this issue by combining GNNs with GAs for molecular optimization, allowing direct exploration of chemical space without reliance on predefined libraries or generative models. To mitigate errors associated with surrogate model predictions in extrapolated regions, we integrate UQ into our GNN framework43,44,45. Inspired by acquisition functions used in BO46, we systematically investigate different ways to incorporate UQ into CAMD, including probabilistic improvement and expected improvement methods. Our experiments show that the probabilistic improvement optimization (PIO) approach, which uses probabilistic assessments to guide the optimization process, is particularly effective in facilitating exploration of chemical space with GNNs. Given that practical applications often require molecular properties to meet specific thresholds rather than extreme values47,48, the PIO method quantifies the likelihood that a candidate molecule will exceed predefined property thresholds, reducing the selection of molecules outside the model’s reliable range and promoting candidates with superior properties.

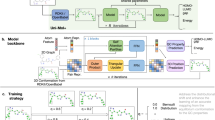
Our study includes a comprehensive evaluation of uncertainty-agnostic and uncertainty-aware optimization approaches using the Tartarus49 and GuacaMol48 platforms, both open-source molecular design tools addressing a range of design challenges. Tartarus utilizes physical modeling across various software packages to estimate target properties, effectively simulating the experimental evaluations required in molecular design processes, while GuacaMol focuses on drug discovery tasks such as similarity searches and physicochemical property optimization. The benchmarking workflow, illustrated in Fig. 1, starts with datasets from these platforms to develop GNN-based surrogate models using the directed message passing neural network (D-MPNN) implemented in Chemprop50. These models predict molecular properties and their uncertainties, which, when coupled with a GA, optimize molecular structures based on the PIO and other selected fitness functions. Our results indicate that the PIO method substantially improves the likelihood of meeting threshold requirements, especially in multi-objective optimization tasks.

Fig. 1: Workflow and methodology for illustrating probabilistic improvement optimization (PIO) strategy.
figure 1

a Schematic diagram illustrating the overall workflow used in this study to evaluate the optimization strategy. b Description of the benchmark tasks comprising three molecular design challenges from the Tartarus suite, which utilize physical modeling across different software packages to estimate target properties, circumventing the need for actual experimental assessments. Seven additional drug discovery tasks were selected from GuacaMol, using similarity metrics and physicochemical descriptor calculations as oracle functions to evaluate molecular properties. c Schematic representation of the genetic algorithm (GA), where the mutation operator randomly modifies molecular structures, and crossover operations generate new molecular structures through recombination. d Construction of a machine learning (ML) surrogate model employing the directed message passing neural network (D-MPNN) architecture, designed to predict molecular properties and their associated uncertainties via either the evidential method or the ensemble with mean-variance estimation (MVE) method. e The PIO fitness function, calculated using probability improvement, generally enhances the likelihood of meeting threshold requirements. TS transition state, logP octanol-water partition coefficient, TPSA topological polar surface area.

Full size image

In summary, this integration of UQ with GNNs for CAMD represents a pioneering approach, offering a more reliable and scalable strategy for discovering novel chemical materials. Through extensive benchmarking and validation, our work demonstrates the potential of uncertainty-aware GNN algorithms in molecular design, with promising applications across domains such as organic electronics, biochemistry, and materials science.

Results

Molecular design benchmarks

To effectively evaluate molecular design strategies, tasks must be complex enough to reflect the challenges encountered in real-world applications. Our study provides a comprehensive assessment of different optimization approaches across 19 molecular property datasets, encompassing 10 single-objective and 6 multi-objective tasks (Table 1), derived from the Tartarus49 and GuacaMol48 platforms.

Table 1 Summary of the molecular design tasks investigated in this study
Full size table

The first platform, Tartarus49, offers a sophisticated suite of benchmark tasks tailored to address practical molecular design challenges within the realms of materials science, pharmaceuticals, and chemical reactions. Utilizing well-established computational chemistry techniques, including force fields and density functional theory (DFT), Tartarus models complex molecular systems with high computational efficiency. The benchmarks encompass a wide array of applications, ranging from optimizing organic photovoltaics and discovering novel organic light-emitting diodes (OLEDs) to designing protein ligands and pioneering new chemical reactions. This breadth enables a comprehensive evaluation of various molecular design algorithms across multiple real-world simulation scenarios.

Three molecular design categories from Tartarus, comprising seven single-objective and two multi-objective tasks, are listed in Table 1. Each task employs specific computational methods: organic emitter design involves conformer sampling51, semi-empirical quantum mechanical methods for geometry optimization52,53, and time-dependent DFT for single-point energy calculations54. Protein ligand design utilizes docking pose searches to determine stable binding energies55, supplemented by empirical functions for final score calculations56. Reaction substrate design tasks employ force fields for optimizing reactant and product structures57, with transition state structures further refined using the SEAM method58. These methods include stochastic elements such as conformer search and docking site sampling, introducing variability in simulation outcomes due to the inherent randomness of geometry optimization. For multi-objective tasks, a typical approach might involve aggregating multiple objectives into a single composite score. However, this can lead to suboptimal compromises where certain objectives are sacrificed to maximize the overall score. In practical applications, molecules often need to satisfy multiple objectives simultaneously, which can be particularly challenging when these objectives are mutually constraining. To evaluate the efficacy of molecular design strategies under these conditions, we analyzed each objective within multi-objective tasks, choosing scenarios where objectives could potentially conflict. For example, the task of simultaneously minimizing both activation energy and reaction energy was excluded due to their positive correlation, as explained by the Bell–Evans–Polanyi principle59,60. Conversely, we included the task of simultaneously maximizing activation energy while minimizing reaction energy, as it poses a significant challenge by deviating from conventional expectations and thus aligns more closely with the aims of our study. These choices are detailed in Table 1, illustrating the structured approach to assessing molecular design algorithms against complex, real-world criteria.

The second molecular design platform, GuacaMol48, serves as a widely recognized benchmark in drug discovery and is extensively utilized in various molecular optimization studies. The design tasks include marketed drug rediscovery, similarity assessment, median molecule generation, and isomer generation. From these, we selected tasks suitable for molecular property optimization, comprising three single-objective tasks aimed at identifying structures similar to a specific drug and four multi-objective tasks focused on finding median molecules between two drugs or achieving multi-property optimization (MPO), as detailed in Table 1. Unlike the physical simulations in Tartarus, GuacaMol uses deterministic functions implemented in RDKit to compute property values, thereby eliminating data randomness. To simulate real-world scenarios where machine learning (ML) surrogate models are rarely perfect, we downsample the GuacaMol dataset to build ML surrogate models for fitness prediction during the GA process. In this setup, the molecular design process initially relies on a potentially imperfect surrogate model to propose molecular structures, which are subsequently validated using the RDKit-based oracle functions.

Uncertainty-aware and uncertainty-agnostic fitness functions

In conventional molecular design, the typical single-objective optimization approach focuses on maximizing a specific fitness function \({F}_{{{{\rm{DOM}}}}}\left(m\right)\) without consideration of uncertainty. This naïve approach, referred to as the direct objective maximization (DOM), or greedy method61, is defined as

$${F}_{{{{\rm{DOM}}}}}\left(m\right)=\eta \mu \left(m\right)$$
(1)

where \(\mu \left(m\right)\) represents the predicted property value of molecule \(m\) by the surrogate model, and \(\eta\) is the sign factor taking the values of +1 or -1. This factor is assigned a value of +1 when a higher \(\mu\) is desired, and −1 when a lower \(\mu\) is preferred. However, practical applications often do not necessitate driving the property values to their extremes. Instead, it is usually sufficient for the property to meet a certain threshold \(\delta\) that is deemed acceptable for a given application47,48.

In such scenarios, the goal should shift from merely optimizing the property value to ensuring that the property of the molecule \(m\) exceeds this threshold \(\delta\). Assuming the property predicted by the surrogate model follows a Gaussian distribution with mean \(\mu \left(m\right)\) and variance \({\sigma }^{2}\left(m\right)\), the PIO fitness function can be defined as

$${F}_{{{{\rm{PIO}}}}}\left({m;}\delta \right)=\eta {\int }_{\delta }^{\eta \infty }\frac{1}{\sigma \left(m\right)\sqrt{2{{\pi }}}}\exp \left(-\frac{1}{2}{\left(\frac{x-\mu \left(m\right)}{\sigma \left(m\right)}\right)}^{2}\right){{{\rm{d}}}}x$$
(2)

where \({F}_{{{{\rm{PIO}}}}}\left({m};\delta \right)\) ranges between 0 and 1. In this expression, \({F}_{{{{\rm{PIO}}}}}\left({m};\delta \right)\) quantifies the probability that the property value of molecule \(m\) will exceed the threshold \(\delta\). The PIO approach inherently incorporates the uncertainty (variance) of the prediction and mitigates the risk of extrapolating the surrogate model beyond its reliable range and has been recently adopted in other works utilizing active learning for drug discovery61, co-cured polycyanurates62, organic semiconductors63 and boron–carbon–nitrogen crystal structure design64. By establishing a realistic threshold \(\delta\), this method significantly enhances the practicality and applicability of molecular design optimization in real-world settings.

An alternative approach to incorporating uncertainty into the fitness function is the expected improvement (EI) method, which evaluates the expected magnitude of the improvement46. Assuming the property predicted by the surrogate model follows a Gaussian distribution with mean \(\mu \left(m\right)\) and variance \({\sigma }^{2}\left(m\right)\), the fitness function for EI can be defined as

$${F}_{{{{\rm{EI}}}}}\left({m;}\delta \right)=\eta {\int }_{\delta }^{\eta \infty }\frac{x-\delta}{\sigma \left(m\right)\sqrt{2{{\pi }}}}\exp \left(-\frac{1}{2}{\left(\frac{x-\mu \left(m\right)}{\sigma \left(m\right)}\right)}^{2}\right){{{\rm{d}}}}x$$
(3)

The primary difference between PIO (Eq. 2) and EI (Eq. 3) lies in whether the integration over possible improvements at a given \(x\) is considered. The PIO method focuses solely on the likelihood of improvement at a specific threshold, making it a unitless probability value, whereas the EI method considers both the probability and magnitude of potential gains, yielding a value with the same unit as the target variable. Both approaches are commonly used as acquisition functions in BO46. In this work, we compare the performance of DOM with both PIO and EI for single-objective optimization tasks. This comparative analysis aims to highlight the advantages of incorporating UQ with GNN in molecular design and to determine the most effective optimization strategy for various practical applications.

When considering multiple properties in molecular design, a common method, known as scalarization, aggregates all objectives into a single value using their corresponding weights. The weights should be carefully chosen to balance the contributions of each property in the objective function. One approach is to use the reciprocal of the standard deviation \(\widetilde{\sigma }\) of each target’s distribution in the dataset as weights65, scaling the contribution of each property according to the potential variability of its values:

$${F}_{{{{\rm{WS}}}}}^{{{{\rm{multi}}}}}\left(m\right)={\sum }_{i=1}^{k}\frac{{F}_{{{{\rm{DOM}}}}}^{i}\left(m\right)}{{\widetilde{\sigma }}_{i}}$$
(4)

where \(k\) is the number of properties considered. However, this weighted sum (WS) approach can still lead to suboptimal compromises where certain objectives are sacrificed to enhance the overall score65. In practical scenarios, molecules often need to meet multiple objectives simultaneously, typically represented by thresholds. To address this, we propose calculating the product of individual probabilities that each property surpasses its respective threshold, representing the overall probability of meeting all specified targets:

$${F}_{{{{\rm{PIO}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right)={\prod }_{i=1}^{k}{F}_{{{{\rm{PIO}}}}}^{i}\left(m;{\delta }_{i}\right)$$
(5)

If any single probability approaches zero, the overall fitness score will also approach zero, regardless of high scores in other targets. This method emphasizes balancing trade-offs and aligns more closely with the complex demands of real-world applications66,67,68.

One limitation of the WS method in Eq. 4 is that it does not account for specific optimization thresholds, which may lead to unbalanced solutions in multi-objective optimization. Inspired by the \(\varepsilon\)-constraint method69, which reformulates additional objectives as constraints with threshold values to ensure feasible trade-offs, this study explores alternative formulations, such as the normalized Manhattan distance (NMD) to the ideal threshold values \(\left({\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right)\) as the objective function70. This approach treats objective values that meet or exceed the thresholds as equally favorable, potentially reducing the risk of overemphasizing certain properties at the expense of others

$${F}_{{{{\rm{NMD}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right)={\sum }_{i=1}^{k}\frac{\min \left({\eta }_{i}\left(\mu \left(m\right){-\delta }_{i}\right),0\right)}{{\widetilde{\sigma }}_{i}}$$
(6)

where \({F}_{{{{\rm{NMD}}}}\,}^{{{{\rm{multi}}}}}\le 0\). Both the NMD and \(\varepsilon\)-constraint methods aim to achieve balanced solutions by incorporating objective-specific limits. However, while NMD minimizes cumulative deviations to treat all objectives meeting thresholds as equally favorable, the \(\varepsilon\)-constraint method enforces strict feasibility by converting secondary objectives into constraints, resulting in a more rigid adherence to specified bounds. A key limitation of NMD, though, is that it restricts further optimization once all thresholds are met. To overcome this, we propose a hybrid fitness function that combines the NMD and the simple WS approach, transitioning form \({F}_{{{{\rm{NMD}}}}\,}^{{{{\rm{multi}}}}}\) to \({F}_{{{{\rm{WS}}}}}^{{{{\rm{multi}}}}}\) once all property values meet their respective thresholds

$${F}_{{{{\rm{NMD}}}}-{{{\rm{WS}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right)=\left\{\begin{array}{c}{F}_{{{{\rm{NMD}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right),{{{\rm{if}}}}{F}_{{{{\rm{NMD}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right) \, { < } \, 0\\ {F}_{{{{\rm{WS}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right),{{{\rm{if}}}}{F}_{{{{\rm{NMD}}}}}^{{{{\rm{multi}}}}}\left({m};{\delta }_{1},{\delta }_{2},\ldots,{\delta }_{k}\right) \,=\, 0\end{array}\right.$$
(7)

This hybrid approach (NMD-WS), similar to methods combining \(\varepsilon\)-constraint and weighted sum techniques69, aims to combine the strengths of both methods, achieving a balanced optimization that respects the thresholds while allowing further improvements once the initial conditions are met.

Surrogate model and UQ performance

For effective CAMD, it is crucial that the surrogate model accurately represents the molecular properties of interest. To this end, we first assessed the performance of the D-MPNN model along with two UQ methods—deep ensemble combined with mean-variance estimation (MVE)71 and evidential learning72—on the target properties of the design tasks specified in Table 1. Our evaluations revealed that neither UQ method delivered consistent performance across all datasets. Notably, the MVE loss function exhibited a tendency to diverge when training models on the reactivity dataset, which occasionally led to the premature termination of training sessions. In contrast, the evidential loss function faced convergence issues during the training of models for the organic emitter dataset, resulting in reduced accuracy. These challenges in model training may be partly attributed to data noise inherent in the property values, a consequence of the non-deterministic computational procedures used to generate these data, as detailed in the method section and illustrated in Supplementary Figs. S1, S2, and S3. These observations highlight the critical need for further development and refinement of these UQ methods to enhance their robustness. In response to these findings, we selected the deep ensemble and MVE approach for the organic emitter dataset, while applying evidential regression for the other datasets in our molecular design experiments. The efficacy of these approaches was visually assessed using parity plots and confidence-based calibration curves, displayed in Figs. 2 and 3, respectively. These figures show that the D-MPNN effectively captures the trends in property values, with the estimated uncertainties generally well-calibrated against the test set.

Fig. 2: Parity plots comparing reference values with predictions from the directed message passing neural network (D-MPNN) surrogate models on the test set.
figure 2

The color coding of the data points indicates the level of total uncertainty (\({\sigma }_{{{{\rm{total}}}}}^{2}\)) in the model predictions. Uncertainty quantification (UQ) across the panels varies: a–c ensemble and mean-variance estimation (MVE) methods were utilized; d–s the evidential method was applied in panels. The molecular structure similarity is calculated using the Tanimoto similarity metric. Abs. diff. of VEE absolute difference of vertical excitation energy, \({{{{\rm{R}}}}}^{2}\) (coefficient of determination), logP octanol-water partition coefficient, TPSA topological polar surface area. Source data is provided as a Source Data file.

Full size image
Fig. 3: Confidence-based calibration curves (orange) for various models assessed using testing data.
figure 3

The area under the calibration error curve (AUCE), or miscalibration area106 (gray area in this figure), is calculated, with perfect calibration indicated by an AUCE of 0. Uncertainty quantification (UQ) across the panels varies: a–c ensemble and mean-variance estimation (MVE) methods were utilized; d–s the evidential method was applied. The molecular structure similarity is calculated using the Tanimoto similarity metric. Abs. diff. of VEE absolute difference of vertical excitation energy, logP octanol-water partition coefficient, TPSA topological polar surface area. Source data is provided as a Source Data file.

Full size image

It is important to recognize that prediction uncertainties may arise from multiple sources, such as data noise and model uncertainty, meaning that the residuals between predicted and reference values may not always follow a Gaussian distribution. Therefore, we validated the Gaussian distribution assumption by examining the actual distribution of residuals. This was achieved by using confidence-based calibration curves (Fig. 3)73,74. These curves assess the proportion of test data points that fall within a confidence interval around their predicted values. The intervals are calculated based on predicted variance under the Gaussian assumption, and the observed proportions are then compared to the expected confidence levels. Ideally, a perfect calibration curve would follow a diagonal line, where predicted probabilities align with observed proportions across various confidence levels. To quantify deviations from this ideal calibration, we calculated the area under the calibration error curve (AUCE), with higher AUCE values reflecting greater deviations from perfect calibration. As shown in Fig. 3, the calibration curves closely follow the diagonal line across all test sets, with AUCE values remaining below 0.1, suggesting that the residual distribution for the test data does not significantly deviate from Gaussian assumptions and aligns well with estimated variance. Nonetheless, further improvement in uncertainty estimation may be achieved through additional recalibration steps75,76 or by employing alternative UQ methods77,78 that do not rely on strong distributional assumptions. Incorporating these enhanced UQ methods with uncertainty-aware optimization presents a promising direction for future research.

Optimization results of single-objective task

This section evaluates the optimization results obtained using DOM (Eq. 1), PIO (Eq. 2), and EI (Eq. 3) fitness functions across ten single-objective tasks, focusing on the hit rate of molecules—i.e., their ability to exceed predetermined threshold values. This metric assesses whether the integration of uncertainty into the fitness function could improve the success rate of generating molecules that surpass these thresholds. As shown in Table 2, the PIO method consistently achieved the highest hit rates for most tasks. Additionally, Fig. 4 illustrates that, under the PIO approach, the top-100 molecules for these tasks exhibit a greater proportion of candidates meeting or exceeding the threshold, compared to those generated by DOM, further demonstrating the benefit of incorporating uncertainty in the optimization process. However, despite integrating uncertainty, the EI method does not consistently outperform the uncertainty-agnostic DOM method.

Table 2 Comparison of top-k hit rates for single-objective optimization results across various methods
Full size table
Fig. 4: Comparative distribution of true property values for the top-100 molecules generated by different methods.
figure 4

a–j These plots show direct objective maximization (DOM, brown), expected improvement (EI, purple), and probabilistic improvement optimization (PIO, green) results. The black dotted line represents the cutoff values, while orange arrows illustrate the desired optimization direction. For the final three similarity optimization tasks, the structures of the target molecules are displayed within their respective figures. The molecular structure similarity is calculated using the Tanimoto similarity metric. Source data are provided as a Source Data file.

Full size image

To understand why only the PIO method outperformed its uncertainty-agnostic counterpart while the EI method did not, we generated parity plots of the molecules optimized by each method (Fig. 5). These plots show that the leading molecules selected by EI tend to exhibit the highest uncertainties in the surrogate model compared to those identified by DOM and PIO. Conversely, DOM-selected molecules often display extreme predicted mean values—either lowest or highest for minimization or maximization tasks, respectively. This outcome is expected, as DOM focuses solely on optimizing the predicted mean without considering uncertainty, often pushing optimization toward extrapolative regions where predictions are less reliable. While EI does incorporate uncertainty, its performance in most single-objective optimization tasks was not particularly robust. This outcome likely stems from EI’s tendency to favor candidates with high uncertainty when their predicted mean values are similar, as it calculates expected improvements as the fitness function. Such a preference can lead to the selection of molecules with significant prediction uncertainties, which often causes discrepancies between predicted and actual properties, contributing to EI’s relatively unstable performance across tasks. It is worth noting that EI is widely used as an acquisition function in BO with Gaussian processes79,80,81,82,83, where it effectively identifies optimal solutions within smaller, more confined search spaces over fewer iterations. However, molecular design requires navigating a much larger chemical space, where D-MPNN surrogate models can assign considerable uncertainty to numerous candidate structures, inflating expected improvements and diminishing EI’s effectiveness in our test cases. In contrast, PIO focuses exclusively on the probability of improvement, yielding a bounded fitness value between 0 and 1, which makes it less susceptible to the issues of extreme variance. By emphasizing candidates with a higher probability of exceeding the threshold without overemphasizing uncertain regions, PIO achieves more stable and reliable performance. This balance enables PIO to identify candidates that meet cutoff criteria while maintaining lower uncertainties, leading to more reliable predictions.

Fig. 5: Parity plots comparing reference values with predictions as well as uncertainties from the directed message passing neural network (D-MPNN) models.
figure 5

a–j These plots show top-50 candidate molecules generated based on the fitness values from direct objective maximization (DOM, brown), expected improvement (EI, purple), and probabilistic improvement optimization (PIO, green). Predictions are presented as means with standard deviations (error bars), capturing both aleatoric and epistemic uncertainty, as estimated by the D-MPNN model. The black dotted line represents the cutoffs, while the orange arrows illustrate the desired direction for optimization. The molecular structure similarity is calculated using the Tanimoto similarity metric. Source data is provided as a Source Data file.

Full size image

However, certain challenging tasks reveal limitations across all methods—DOM, EI, and PIO—in identifying candidates that surpass thresholds. For example, tasks involving singlet-triplet gap, 1SYH score, and similarity to mestranol demonstrate cases where all of these approaches struggle to find candidates meeting the set criteria, highlighting areas for further improvement. The first limitation arises from the dependency of both PIO and EI on threshold-based guidance during the search process. When thresholds are set too stringently, far beyond the performance range of the current population, the fitness score remains zero regardless of optimization direction, which can impede the search for high-performing molecules. In our study, most thresholds were set near the performance of top molecules within each task’s original dataset (as shown in Supplementary Table S5). Consequently, the difficulty of exceeding these thresholds varies depending on the structural diversity in each dataset. The second limitation involves decreased model accuracy in predicting property mean and variance in extrapolated regions. This issue is evident in the mestranol similarity task, where the objective is to identify molecules resembling mestranol’s complex polycyclic structure, featuring four fused rings (Fig. 4j). Accurately capturing these complex ring structures remains challenging for D-MPNN, which would benefit from additional structural features—such as ring size indicators—to improve prediction accuracy for complex species in highly extrapolated regions84. Therefore, although D-MPNN performed reasonably well on the test set for this task (Fig. 2k), it struggled to identify similar molecules within the broader chemical space, consistently yielding similarity predictions for recommended candidates that deviated significantly from the true reference values (Fig. 5j). An additional concern is that these predictions frequently showed small uncertainty estimates, suggesting that D-MPNN may have inaccurately assessed uncertainty in these cases. This finding underscores a critical limitation: even well-calibrated models may struggle to generalize accurately during molecular optimization over an extensive chemical space, leading to unreliable predictions not only for mean values but also for variance estimates with current UQ methods. One approach to address these challenges is adaptive modeling, which iteratively incorporates newly validated molecules to refine predictions and improve uncertainty estimates. However, improving the reliability of UQ methods is essential to address these challenges and strengthen the robustness of molecular design workflows.

Optimization results of multi-objective tasks

In this subsection, we evaluate the impact of various fitness function designs on the performance of molecule generation for multi-objective tasks. These designs included uncertainty-agnostic methods such as the WS (Eq. 4), NMD (Eq. 6), and the hybrid approach NMD-WS (Eq. 7), as well as the uncertainty-aware PIO method (Eq. 5), which calculates the product of single-objective probabilities where each indicator exceeds its corresponding cutoff. A molecule was considered a hit in multi-objective tasks if it met all specified property cutoffs.

As detailed in Table 3, the PIO approach emerged as the most effective in identifying molecules that satisfied criteria for multi-objective criteria, achieving the highest hit rates for most tasks. Among the uncertainty-agnostic methods, no single approach demonstrated consistent superiority across all tasks. The NMD method showed higher success rates in generating viable molecules for organic emitter designs and the fexofenadine MPO task, while the hybrid NMD-WS method outperformed other uncertainty-agnostic approaches in the remaining multi-objective tasks. In contrast, the WS method consistently struggled, failing to identify molecules that met all required thresholds in any multi-objective task.

Table 3 Comparison of top-k hit rates for multi-objective optimization results across various methods
Full size table

A primary challenge in multi-objective tasks, as opposed to single-objective tasks, lies in balancing the contributions of different properties. For instance, in the organic emitter design task, there is a moderate positive correlation between the singlet-triplet gap and oscillator strength (Supplementary Fig. S24), complicating the task, which demands minimizing the singlet-triplet gap while maximizing oscillator strength, thereby creating conflicting optimization directions. This complexity was exacerbated by the disproportionate emphasis on oscillator strength, whose unbounded maximum value could lead the WS method to overly prioritize this trait, neglecting the other (Fig. 6). Similar challenges were observed in the fexofenadine and ranolazine MPO tasks, which involve maximizing similarity to target molecules while optimizing octanol-water partition coefficient (logP) and topological polar surface area (TPSA). Here, the WS method tended to prioritize logP and TPSA optimization at the expense of similarity scores (Fig. 6). This observation aligns with previous research85, emphasizing the challenge of balancing each target’s contribution in the fitness function to prevent bias in multi-objective optimization scenarios. Methods such as NMD and NMD-WS, which incorporate cutoff values into fitness functions, better address this balancing challenge. However, these uncertainty-agnostic methods can still lead to over-optimization in regions beyond the model’s predictive range, potentially resulting in discrepancies between predicted and actual outcomes. Consequently, the PIO method generally demonstrates a higher hit rate by incorporating uncertainty information and thus achieving a better balance across all targets.

Fig. 6: Parallel coordinate plots illustrating the true property values for the top-50 molecules derived from various optimization methods in multi-objective design tasks.
figure 6

Each subplot displays molecules generated by the methods: a weighted sum (WS), b normalized Manhattan distance (NMD), c hybrid approach (NMD-WS), and d probabilistic improvement optimization (PIO), organized into six sections arranged from left to right, corresponding to the design tasks for organic emitters, reaction substrates, median molecules 1, median molecules 2, fexofenadine multi-property optimization (MPO), and ranolazine MPO. Blue lines represent molecules that failed to meet all established cutoffs, while orange lines signify those that met all criteria. Black dotted lines across the plots denote the cutoffs. Orange arrows indicate the desired direction for optimization. The molecular structure similarity is calculated using the Tanimoto similarity metric. Abs. diff. of VEE absolute difference of vertical excitation energy, \({{{{\rm{R}}}}}^{2}\) (coefficient of determination) logP octanol-water partition coefficient, TPSA topological polar surface area. Source data is provided as a Source Data file.

Full size image

Despite the overall success of the PIO method, one task presented challenges for all optimizers: the median molecules 2 task, which aimed to find molecules similar to both camphor and menthol. In this case, none of the optimization methods succeeded in identifying molecules with similarity scores exceeding the cutoff of 0.2. This difficulty is likely due to the low similarity scores in the original dataset, where the majority of scores fall below 0.1 for these target molecules (Supplementary Figs. S17 and S18). This task proved more challenging compared to the median molecules 1 task, where similarity scores with the target molecules (tadalafil and sildenafil) in the original data generally ranged between 0.1 and 0.2, closer to the target value of 0.2 (Supplementary Figs. S15 and S16).

Multi-objective optimization problems are prevalent in fields such as chemical, drug, and material design, where property cutoffs are often required to meet specific commercial objectives. The PIO method achieves the highest hit rates across most multi-objective tasks by integrating uncertainty information and balancing optimization across all targets. In the PIO fitness function (Eq. 5), any molecule deviating significantly from a target threshold receives a lower overall score, guiding the optimization process to consider all objectives equally. When certain objectives are of lower priority, cutoff values for these properties can be relaxed to minimum acceptable levels, reducing their impact on the overall fitness score as long as the values remain within acceptable ranges. Conversely, if a property approaches its minimum acceptable threshold, it appropriately impacts the fitness score, signaling the need for further optimization in that direction.

Discussions

This study addresses a central challenge in molecular design: optimizing across expansive chemical spaces, where maintaining predictive accuracy is difficult, especially under domain shifts. The PIO method introduced here integrates UQ within molecular optimization frameworks, combining D-MPNNs with GAs to enhance reliability in exploring broad chemical spaces. Our systematic analysis evaluates the strengths and limitations of PIO in comparison to another UQ-integrated method, EI, providing insights into each method’s ability to adapt to domain shifts and effectively guide exploration. Previous research has indicated that in virtual screening settings, uncertainty-agnostic acquisition functions can exhibit surprisingly equivalent or even superior performance compared to uncertainty-aware active learning approaches39,86, suggesting that purely exploitative methods can be highly efficient in the well-defined chemical library. In contrast, our experimental setup explores an open-ended chemical space and continuously updates the optimization trajectory using fitness values. Under these conditions, PIO outperforms uncertainty-agnostic methods in most instances, whereas the EI approach proves less effective.

Benchmarking results on the Tartarus and GuacaMol platforms indicate that PIO generally improves optimization success compared to traditional uncertainty-agnostic methods. In single-objective tasks, PIO balances the search between well-understood regions and less-explored areas, reducing the risk of selecting candidates where predictions may be unreliable. This approach contrasts with EI, which often focuses on high-variance areas, leading to inconsistent performance. However, it is important to note that PIO’s performance may diminish in tasks where the required properties differ significantly from those represented in the available data. This highlights an area for further methodological improvement.

In multi-objective optimization scenarios, PIO consistently proves advantageous, balancing competing objectives more effectively than weighted scalarization methods, which can skew optimization toward particular properties at the expense of others. By incorporating UQ directly into the fitness function, PIO supports a more balanced approach, generally achieving higher hit rates across multiple objectives. This is particularly relevant in CAMD, where real-world applications often require that multiple property thresholds be met concurrently. The ability of PIO to adapt to varying objectives without overemphasizing any single goal enhances its practical utility in discovering compounds suitable for complex applications.

This study’s comparative analysis of UQ-integrated methods also reveals the critical role of UQ calibration in determining optimization outcomes. Our results show that robust UQ calibration is fundamental to the success of UQ-driven methods. When UQ calibration is poor, PIO’s advantages are reduced, underscoring the need for more accurate and robust UQ techniques in molecular optimization. This finding suggests a direction for future research, where advancements in UQ methodologies, such as those that dynamically adapt to domain shifts, could further enhance the reliability of PIO and similar approaches in broad chemical spaces. In conclusion, this research provides valuable insights into the role of UQ in optimizing molecular design across diverse chemical spaces, demonstrating that the integration of UQ can mitigate some of the limitations posed by domain shifts. The PIO method presents a promising pathway for exploring large chemical spaces with enhanced reliability, paving the way for uncertainty-informed optimization strategies in CAMD.

Methods

Surrogate models and uncertainty quantification

The choice of surrogate method is crucial in molecular design, as it directly impacts predictive accuracy and computational efficiency. For this study, we selected D-MPNN, a type of GNN architecture, due to its scalability, computational efficiency, and established performance in predicting both mean properties and associated uncertainties in molecular datasets. Although Bayesian inference-based87 methods offer theoretical advantages, their adoption in molecular property prediction has been limited by challenges such as computational costs, intractability in deep neural networks, and complex implementation requirements41. This has restricted their scalability in large datasets, which is a key requirement for molecular design. To assess the effectiveness of molecular design strategies, we utilized the D-MPNN model, as implemented in Chemprop50, which facilitates the automatic extraction and learning of significant structural features of molecules by leveraging atom and bond information. It updates hidden atom states based on molecular connectivity, ultimately deriving a molecular fingerprint from the summation or averaging of all hidden atomic vectors88. This fingerprint is then utilized as input for subsequent feed-forward neural networks. The D-MPNN model has demonstrated robust performance in various studies focused on the prediction of chemical properties89,90,91.

Various methods have been proposed to quantify uncertainty, such as Bayesian neural networks92, Monte Carlo dropout93, ensemble learning94, MVE71, and evidential learning72,95. Chemprop also incorporates techniques to quantify uncertainty from various sources, categorizing it into aleatoric and epistemic types96. Aleatoric uncertainty, arising from inherent data randomness due to experimental or computational errors, poses challenges for mitigation as it requires enhancements in data accuracy. Conversely, epistemic uncertainty, stemming from model ignorance, can be addressed by enriching the training dataset or improving molecular feature encoding.

One of the UQ methods implemented in Chemprop is the combination of deep ensemble and MVE71. The deep ensemble method estimates epistemic uncertainty, \({\sigma }_{{{{\rm{e}}}}}^{2}\), by training multiple models and evaluating the variance among their predictions94. Specifically, for \(M\) models within Chemprop, with each model’s prediction denoted as \(\hat{y}_{i}\), the final prediction \(\widetilde{y}\) is the average of these individual predictions, and the epistemic uncertainty is calculated as:

$${\sigma }_{{{{\rm{e}}}}}^{2}=\frac{1}{M}{\sum }_{i}^{M}{\left(\widetilde{y}-\hat{y}_{i}\right)}^{2}$$
(8)

In this study, we prepared ten models with different initialization seeds to form the deep ensemble. On the other hand, MVE is used to calculate aleatoric uncertainty, \({\sigma }_{{{{\rm{a}}}}}^{2}\), by introducing an additional output neuron that predicts the data-dependent uncertainty, ensuring positivity via the softplus activation. In MVE, the residuals between the predicted value and the reference value are assumed to follow a Gaussian distribution with mean 0 and variance \({\sigma }_{{{{\rm{a}}}}}^{2}\). This assumption justifies the use of the negative log likelihood (NLL) of a Gaussian distribution as the loss function:

$${{{\rm{NLL}}}}\left(y,\hat{y}_{i},{\sigma }_{{{{\rm{a}}}}}^{2}\right)=\frac{1}{2}{{\mathrm{ln}}}\left(2{{{\rm{\pi }}}}\right)+\frac{1}{2}{{\mathrm{ln}}}\left({\sigma }_{{{{\rm{a}}}}}^{2}\right)+\frac{{\left(y-\hat{y}_{i}\right)}^{2}}{2{\sigma }_{{{{\rm{a}}}}}^{2}}$$
(9)

where \(y{\mathbb{\in }}{\mathbb{R}}\) is the reference property value. When using the ensemble approach, the aleatoric uncertainties of each model are averaged to derive a composite aleatoric uncertainty value, with each model trained using the NLL as the loss function44.

Additionally, evidential learning, another UQ method in Chemprop, avoids the need for multiple model training by directly predicting the parameters of an evidential distribution72. This approach involves imposing a prior Gaussian distribution on the unknown mean \(\mu \sim {{{\mathcal{N}}}}\left(\gamma,\frac{{\sigma }^{2}}{v}\right)\) and an inverse-Gamma prior on the unknown variance \({\sigma }^{2}\sim {\Gamma }^{-1}\left(\alpha,\beta \right)\). The joint posterior distribution \(p\left(\mu,\,{\sigma }^{2}\right)=p\left(\left.\mu \right|{\sigma }^{2}\right)p\left({\sigma }^{2}\right)\) takes the form of Normal Inverse-Gamma (NIG) distribution:

$$p\left(\mu,\left.{\sigma }^{2}\right|\gamma,v,\alpha,\beta \right) \,= \, p\left(\left.\mu \right|{\sigma }^{2},\gamma,v\right)\cdot p\left(\left.{\sigma }^{2}\right|\alpha,\beta \right)\\= \frac{\sqrt{v}}{\sqrt{2{{{\rm{\pi }}}}{\sigma }^{2}}}\exp \left(-\frac{v{\left(\gamma -\mu \right)}^{2}}{2{\sigma }^{2}}\right)\cdot \frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}{\left(\frac{1}{{\sigma }^{2}}\right)}^{\alpha+1}\exp \left(-\frac{\beta }{{\sigma }^{2}}\right)\\= \frac{\beta \root \alpha \of {v}}{\Gamma \left(\alpha \right)\sqrt{2{{{\rm{\pi }}}}{\sigma }^{2}}}{\left(\frac{1}{{\sigma }^{2}}\right)}^{\alpha+1}\exp \left(-\frac{2\beta+v{\left(\gamma -\mu \right)}^{2}}{2{\sigma }^{2}}\right)$$
(10)

where \(\Gamma \left(\cdot \right)\) represents the gamma function, and the NIG parameters \(\gamma {\mathbb{\in }}{\mathbb{R}}\), \(v \, > \, 0\), \(\alpha \, > \, 1\), \(\beta \, > \, 0\) determine the mean (\({\mathbb{E}}\left[\mu \right]=\gamma\)) and uncertainty associated with the likelihood function. In Chemprop, four neuron outputs are used to predict the NIG parameters. The softplus activation function is applied to \(v\), \(\alpha\) and \(\beta\), ensuring their outputs are always greater than zero. The aleatoric uncertainty and epistemic uncertainty can be separately derived by:

$${\sigma }_{{{{\rm{a}}}}}^{2}={\mathbb{E}}\left[{\sigma }^{2}\right]=\frac{\beta }{\alpha -1}$$
(11)
$${\sigma }_{{{{\rm{e}}}}}^{2}={{{\rm{Var}}}}\left[\mu \right]=\frac{\beta }{v\left(\alpha -1\right)}$$
(12)

Ultimately, both deep ensemble with MVE and evidential learning can estimate total uncertainties by combining aleatoric and epistemic uncertainties: \({{\sigma }_{{{{\rm{a}}}}}^{2}+\sigma }_{{{{\rm{e}}}}}^{2}={\sigma }_{{{{\rm{total}}}}}^{2}\)41. The PIO and EI algorithm for molecular design then both use total uncertainty to calculate the probability that a molecule’s properties will meet the specified cutoff.

Genetic algorithm for molecular optimization

In this study, we employed the GA for molecular optimization. GA is a population-based metaheuristic designed to iteratively refine a pool of candidate solutions, aiming to discover the optimal configuration for complex problems characterized by large search spaces97. Our method utilizes an advanced version of GA, known as Janus98, which specifically manipulates SELFIES99 representations of molecular structures. In contrast to traditional SMILES100 representations, which are limited by stringent syntax rules101, SELFIES ensures that any textual modifications maintain chemical validity, thus preserving the structural integrity of molecules even after random modifications. For further insights into the operational principles and efficiency of the Janus algorithm, readers are encouraged to refer to the foundational work by Nigam et al.98. Within our experiments, all hyperparameters were set according to the default specifications of the Janus package unless otherwise noted.

Computational details

The data volumes used to develop the D-MPNN model for each prediction task are summarized in Table 1. For the Tartarus dataset, each of the three design tasks was divided into training, validation, and testing subsets using an 8:1:1 random split. Within each task, a multi-task learning strategy was employed, enabling the model to predict all designated targets simultaneously for the given dataset. In the case of GuacaMol, all design tasks utilized the same training, validation, and testing subsets, consisting of 10,000, 2000, and 10,000 data points, respectively. These subsets were randomly downsampled from the platform’s original dataset. The distribution of molecular properties for each dataset is illustrated in Supplementary Figs.  S4–S22.

In this study, we systematically examine the performance of each fitness function formulation for single (Eqs. 1–3) and multi-objective (Eqs. 4–7) optimization tasks in molecular design. Each design task incorporates a penalty term \(P\left(m\right)\) to ensure that the molecules adhere to specific structural constraints required for each task. The specific definitions of these penalty terms can be found in Supplementary Tables S1–S4, and closely align with the original definitions used in the Tartarus and GuacaMol platforms. In the EI method, \(\sigma \left(m\right)\) is capped at 100 to avoid the situation where a very large uncertainty value could make the EI fitness value infinite. For the median molecules tasks in the GuacaMol dataset, the objective is to identify molecules with high similarity scores to two target molecules simultaneously. Because similarity scores range from 0 to 1 and there is minimal variation across the training dataset, no additional weighting was applied between indicators in the WS, NMD, and NMD-WS methods for these tasks. Specific thresholds for each design task are listed in Supplementary Table S5.

For each molecular optimization experiment, we initiated with a pool of the top 10,000 molecules from the datasets, selected based on their performance under DOM or WS fitness functions (Eqs. 1 and 4). This pool underwent 15 independent optimization runs using the GA and the D-MPNN surrogate model, with hyperparameters detailed in the Supplementary Table S6. Each optimization run was structured to update the candidate pool across 10 iterations, introducing 500 new molecules per iteration through mutation and crossover processes. The final candidate molecules from these runs were then amalgamated to minimize variability inherent in the stochastic nature of the GA102. The consolidated list of molecules was subsequently ranked based on their fitness scores.

This procedure was carried out for each fitness function formulation. The top-performing molecules, derived using each fitness function, were then subjected to validation simulations within the Tartarus or GuacaMol frameworks to verify their actual properties. Our primary metric for evaluation was the hit rate of these molecules, particularly their ability to exceed the predefined threshold values. This analysis provides key insights into the optimization strategies that best improve success rates in generating molecules meeting targeted criteria.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.