Delayed leaf green-up is associated with fine particulate air pollution in China

Abstract

Climate warming has led to earlier leaf green-up dates (GUD) with a greening trend of land surfaces in spring, yet the influence of multi-source particle pollution is not well understood. Using ground records and satellite observations of green-up date and fine particulate matter below 2.5 μm (PM_2.5) over the last two decades in China, here we show that PM_2.5 pollution is associated with reduced plant carbon uptake and delayed green-up dates. These effects offset climate-driven spring greening and reduce subsequent photosynthesis in China. We find that pollution-associated delays in green-up date are primarily linked to increased chilling demands and higher heat requirements. PM_2.5-associated decreases in photosynthetically active radiation and maximum rate of carboxylation could also weaken plant photosynthetic capacity. Finally, when we incorporate a PM_2.5 effect, phenological models predict up to a one-week delay in green-up date by the year 2060 compared to previous predictions. Negative feedbacks between anthropogenic pollution and terrestrial carbon uptake suggest unexpected uncertainty of China’s carbon neutral targets resulting from air pollution, with far-reaching implications for both ecosystem health and policy-making.

Introduction

With a 12% increase in global atmospheric CO₂ concentration since 2000¹, understanding the effects of climate change on photosynthetic processes is essential for comprehending and forecasting the upcoming carbon cycle. The carbon uptake of terrestrial ecosystems has increased due to elevated CO₂ levels, climate warming^2,3,4, land-use management practices^5,6, and climate-driven advances in spring leaf green-up dates (GUD) across local, regional, and continental scales^7,8,9,10,11. However, certain complex mechanisms, which are not yet fully comprehended, have the potential to negate the advanced GUD and enhanced plant photosynthesis, including factors like air pollution. This complexity presents considerable difficulties when attempting to predict the future potential of carbon uptake.

China has played a significant role in the global effort to conserve and restore forests, contributing to a greening of the terrestrial surface⁵. Together with natural greening processes due to climate change^2,3, these initiatives have led to an increase in the carbon sink of China’s terrestrial ecosystems, aiding in reducing atmospheric CO₂ levels. However, China is also facing a major challenge with air pollution, particularly in its rapidly growing cities, where emissions of fine particulate matter (PM_2.5) are of high record¹². This pollution negatively impacts human health^13,14,15, however, its effects on GUD and carbon uptake remain poorly understood.

Although the considerable influence of human activities on ecosystem functions is widely acknowledged¹⁶, the effects of PM_2.5 pollution in China over the past 20 years on plant activity have not yet been determined. PM_2.5 pollution could change the transmission of visible light and substantially decrease atmospheric clarity¹⁷, potentially regulating spring vegetation growth by altering microclimate (temperature and radiation)¹⁸ and plant activities (leaf gas exchange and photosynthesis)^19,20,21. For example, particulate pollution on weekdays could inhibit satellite-detected photosynthesis by reducing light availability in Europe, suggesting the regulation of human activities on ecosystem carbon dynamics²². Aiming at a broader view of PM_2.5 pollution impacts on GUD and carbon uptake, we utilized satellite-driven PM_2.5 data records²³, together with a ground monitoring network of GUD with 1030 site-species time series²⁴ (Supplementary Fig. 1), and satellite-derived GUD²⁵ and solar-induced fluorescence (SIF, a proxy of plant photosynthesis)²⁶ since the 2000s for terrestrial ecosystems in China (Supplementary Table 1). We investigated the responses of spring GUD and SIF to PM_2.5 pollution from site to regional scales. We also explored potential biogeochemical and biogeophysical mechanisms under the PM_2.5-GUD relationship, considering the pollution-driven alterations in winter chilling accumulation (CA), heat requirement (HR), and photosynthetic rate. As a last step, we incorporated PM_2.5 pollution into phenological models and predicted future projections of spring GUD under different emission scenarios that are central to China’s efforts to realize carbon-neutral targets.

Results

Earlier GUD is associated with alleviated PM_2.5 pollution

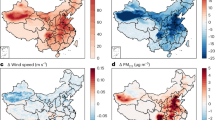
Through a comprehensive evaluation of GUD from both ground and satellite observations, we explored the impacts of PM_2.5 pollution and climate on GUD and SIF (Methods). We found highly consistent temporal patterns between variations of the anomaly of spring PM_2.5 (March-May) and ground GUD from 2003 to 2018 for each site and each species (site-species-independent time series, n = 1030) (Fig. 1A). A further partial correlation analysis, excluding effects of temperature, precipitation, and radiation, showed that spring GUD delayed significantly with increased PM_2.5. The proportions of significant positive (delaying effects) and negative (advancing effects) GUD-PM_2.5 correlations were 11.8% and 5.0, respectively (p < 0.05) (Fig. 1B). Further analysis of sensitivity, using ridge regression to mitigate potential multicollinearity between PM_2.5 and climatic factors (Methods), revealed that the advancement of GUD due to spring temperature was significantly offset by PM_2.5 pollution. For example, ground GUD had a sensitivity of –0.47 (advanced GUD, unitless) for temperature, but PM_2.5 delayed GUD with a sensitivity of 0.11 (unitless). Using satellite GUD provides similar results, only differing in the magnitudes. The sensitivities of GUD and SIF to PM_2.5 were much stronger than those to precipitation and radiation. Grouping PM_2.5 sensitivities into different plant species (Supplementary Fig. 2) and vegetation types (Supplementary Fig. 3) confirms the widespread adverse effects of PM_2.5 on spring vegetation activities. The spatial analysis of nine regions across China showed consistent impacts of PM_2.5 pollution on spring GUD and SIF (Fig. 1D–L). Specifically, higher PM_2.5 pollution consistently led to delays in GUD (Supplementary Fig. 4), especially for relatively dry and cold regions (Supplementary Fig. 5). These findings reveal that PM_2.5 pollution offsets the ongoing earlier trends in spring phenology in China.

Fig. 1: The effects of PM_2.5 pollution on spring green-up date (GUD) and solar-induced fluorescence (SIF).

A Variations of the anomaly of spring PM_2.5 (March-May) and ground GUD from 2003 to 2018. The bold lines represent the trends of yearly mean values of the anomaly of spring PM_2.5 and GUD across all sites and species smoothed by an adjacent averaging method. B The distribution of partial correlation coefficient (R) between PM_2.5 and ground GUD. The effects of climatic factors (i.e., temperature, precipitation, and radiation) were removed for partial correlation analysis. The values in brackets represent frequencies of sites with significantly positive and negative partial correlations, respectively (p < 0.05). A two-sided t-test was used to assess the significance of the partial correlation analysis. C Sensitivities of GUD and SIF to PM_2.5 pollution and climatic factors for ground- and satellite-based analyses using ridge regression (unitless). D–L Regional results for northeastern China, Inner Mongolia, northwestern China, northern China, central China, the Tibetan Plateau, southeastern China, southern China, and southwestern China, respectively. Data are presented as mean values ± 95% CIs of sensitivities for C–L. The numbers in brackets represent the number of sites or pixels in the corresponding region. Source data are provided as a Source Data file.

Potential mechanisms under PM_2.5-GUD relationships

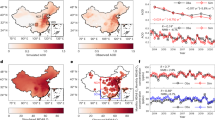
Mechanisms through both biogeophysical and biogeochemical paths may underlay the response of spring GUD to PM_2.5 pollution. First, we investigated the impacts of PM_2.5 pollution on the chilling accumulation (CA, the chilling demand for plants during endodormancy) and the heat requirement (HR, the accumulated forcing temperature required for a phenological event), simulated by 11 CA models and five HR models (see “Methods”). We found that higher PM_2.5 caused a significant increase in CA after removing the effects of temperature variations during CA periods (Fig. 2A). Because CA and GUD were also positively correlated, increased PM_2.5 led to delayed GUD. In addition, higher PM_2.5 also slightly increased HR, as evidenced by positive partial correlations between PM_2.5 and HR, after excluding the effects of preceding CA and temperature variations during HR periods. PM_2.5-induced increases in HR contributed to a later GUD accordingly, with strong and positive partial correlations between HR and GUD (Fig. 2B). Analyses on ground GUD were consistent for these correlations (Fig. 2C). Biogeochemically, an increase in PM_2.5 significantly decreased the maximum rate of carboxylation (VC_max), an indicator of leaf photosynthetic capacity, with 26.9% (out of 84.4%) negative correlations compared with only 0.7% (out of 15.6%) of positive correlations (p < 0.05) (Fig. 2D). Since VC_max positively correlated with SIF, higher PM_2.5 negated spring plant growth consequently (Fig. 2E). A negative correlation between PM_2.5 pollution and photosynthetically active radiation (PAR) confirmed the PM_2.5-induced decreases in light availability (Fig. 2F). Lower PAR greatly reduced the rate of photosynthesis, declining the potential of spring greening under climate change. PM_2.5-induced increase in diffuse PAR was limited, showing minor effects on plant productivity (Supplementary Fig. 6). Structural equation modeling (SEM) generally supported our hypothesis that PM_2.5 increased chilling accumulation, decreased VC_max, and delayed GUD accordingly, further regulating spring SIF (Fig. 2G).

Fig. 2: Potential mechanisms underlying the correlation between spring greening and PM_2.5 pollution.

A–C The effects of PM_2.5 on chilling accumulation (CA), heat requirement (HR), and green-up date (GUD). The CA and HR were simulated by 11 CA models and five HR models (Methods). A, B represent PM_2.5-CA-GUD and PM_2.5-HR-GUD associations for satellite-based analyses. Data are presented as mean values + SDs of correlation coefficients (R). The numbers in brackets represent the number of pixels (n). C Represents associations for ground-based analyses. The correlations were determined by partial correlation analyses. Box plots display medians (horizontal lines), the 25th and 75th percentiles (box edges), and minimum and maximum values (whiskers). The numbers in brackets represent the number of models (n). The patterns of partial correlations: PM_2.5 versus the maximum rate of carboxylation (VC_max) (D), VC_max versus solar-induced fluorescence (SIF) (E), and PM_2.5 versus photosynthetically active radiation (PAR) (F). P and N indicate positive and negative correlations, respectively. The values in the brackets represent the frequency of pixels with significant correlations (p < 0.05). G Structural equation model (SEM) describing the biogeophysical and biogeochemical relationships between PM_2.5 pollution and spring greening. Red and blue values indicate positive and negative correlations, respectively; numbers represent the means ± 95% CIs of standardized direct path coefficients under two-sided Wald test. The Chi-square test for model fit was one-sided. The arrow widths reflect the strength of the relationships. The criteria for evaluating SEM can be seen in “Methods”. Source data are provided as a Source Data file.

GUD model improvements and future projections

We developed a series of new spring GUD models by incorporating the effects of PM_2.5 using several algorithms, including one-phase algorithms (growing degree days and spring warming) and two-phase algorithms (sequential model and parallel model). Our findings revealed that models incorporating PM_2.5 resulted in significantly better estimates of GUD, as evidenced by the higher percentages of pixels with significant correlations between model estimates and satellite observations, a higher average correlation coefficient (R), a lower average root mean square error, and a higher Kling-Gupta efficiency (Fig. 3). Besides, two-phase (chilling and forcing) algorithms showed better performances when PM_2.5 adjusted both phases. Using ground GUD, we confirmed the improvement of GUD models by incorporating PM_2.5 effects (Supplementary Fig. 7).

Fig. 3: Comparison of modeling of spring green-up date (GUD) before and after considering PM_2.5 pollution effects.

A–D Results represent the percentages of pixels with significant correlations between model estimates and satellite observations of GUD (A), the average correlation coefficient (R) (B), the average root mean square error (RMSE) (C), and the Kling-Gupta efficiency (KGE) (D), respectively, using the growing degree days (GDD), spring warming (SW), the sequential model (SM) and the parallel model (PM) and corresponding revised model with PM_2.5 effects in chilling, forcing, and both phases. Significance was set as p < 0.05. A two-sided t-test was used to assess the significance of the correlation analysis. Data are presented as mean values ± SDs for (B–D). The legend in (D) applies to all panels. The number in bracket represents the number of pixels (n). Source data are provided as a Source Data file.

Among these GUD models, the sequential model incorporating PM_2.5 effects into chilling and forcing phases performed the best in modeling GUD with the lowest RMSE and highest KGE. Hence, we employed this model to predict GUD for China and compared its estimates with current temperature-driven sequential model under three future emission scenarios based on the Dynamic Projection Model for Emissions in China (DPEC v1.1): a best-health-effect scenario (SSP1-Neutrality-BHE), an enhanced-control-policy scenario (SSP2-45-ECP), and a business-as-usual scenario (SSP4-60-BAU) (Methods, Fig. 4). The difference in GUDs modeled with and without accounting for PM_2.5 using the sequential model was more pronounced in scenarios predicting higher pollution levels. Notably, the greatest GUD difference occurred under the high-emission SSP4 scenario. However, this difference is expected to decrease over time, as PM_2.5 pollution is projected to decline across all scenarios. We also tested for spatial differences in GUD projections with different levels of PM_2.5 and found that GUD was typically more delayed in areas with high PM_2.5 pollution, such as northern China and central China, especially under the high-emission scenario (Fig. 4B, C). The one-phase GUD model (i.e., spring warming) projections also supported these results for all emission scenarios (Supplementary Fig. 8).

Fig. 4: Projections of spring green-up dates (GUD) under future emission and climate scenarios.

A Variations of the differences of the projected GUD using PM_2.5-weighted sequential model (SM_PM) and original sequential model (SM) under different emission scenarios over 2025–2060. SSP1-Neutrality-BHE, SSP2-45-ECP, and SSP4-60-BAU represent scenarios of the neutral (the lowest), the current goal (middle), and a baseline goal (the highest) of PM_2.5 pollution, respectively. B Multi-year mean differences of the projected GUD (SM_PM minus SM) and multi-year mean spring PM_2.5 under different scenarios for the nine main regions in China. C The left map shows the spatial pattern of multi-year averaged PM_2.5 for winter and spring under the SSP4-60-BAU scenario. The right trends indicate the differences in projected GUD (SM_PM minus SM) across various emission scenarios from 2025 to 2060 for nine major regions in China. The legend in (A) applies to (C). Data are presented as mean values (bold lines) ± 95% CIs (error bands) for (A, C). Source data are provided as a Source Data file.

Discussion

Using multiple ground and satellite observations, we found that ambient PM_2.5 pollution in China has reduced carbon uptake mainly by offsetting climate-induced earlier GUD. These results enhance our understanding of how human activities, including economic and social development, influence regional ecosystem functioning and contribute to climate change. Given the strong association between high PM_2.5 pollution, industrialization, and urbanization¹³, these results hold key environmental implications for the disparities across population and income groups²⁷. They also underscore the urgent need to reduce air pollution to mitigate the environmental consequences of human activity.

We identified specific mechanisms that explain how PM_2.5 contamination leads to a later spring GUD. High concentrations of PM_2.5 significantly increase chilling demands in winter and early spring, which may cause insufficient chilling for spring leaf unfolding²⁸. Insufficient chilling causes a higher heat requirement for spring leaf unfolding, resulting in delayed GUD²⁹. Such results were supported by the SEM analysis, which shows that the regulation of chilling accumulation appears to have much larger path effects than other paths. Of comparable importance to CA, the adverse effects of PM_2.5 on VC_max, which is one of the most important drivers of leaf photosynthetic capacity, explains the decline in spring SIF under high PM_2.5 pollution.

The Chinese government’s Air Pollution Prevention and Control Action Plan (APPCAP) from 2013-2017 represents the most significant effort to combat air pollution in China to date, as it covers more than 300 cities and involves multiple sectors, including energy, industry, transport, legal, and regulatory sectors³⁰. Our study predicts that earlier spring GUD will be hindered in the future if PM_2.5 pollution is not properly addressed, resulting in a less green China than current expectations. This finding is particularly important as China, the largest emitter of CO₂ in the world, has set ambitious goals to achieve peak CO₂ emissions by 2030 and carbon neutrality by 2060^31,32. The success of these goals will be supported by an alleviated offset in spring greening due to air pollution control, which is crucial for reducing CO₂ emissions via photosynthesis processes. Our findings have far-reaching implications for policy design and implementation, emphasizing the synergies and trade-offs among multiple policies aimed at achieving sustainable development amid social and climate change. Beyond this, this study underscores the regulation of PM_2.5 on C cycling, highlighting the potential uncertainties of future climate projections^33,34. In conclusion, our findings are of significant value as they identify the crucial role of atmospheric pollution on spring GUD and productivity, providing essential insights for promoting comprehensive and sustainable development in China and the world.

Methods

In situ GUD records

We gathered and utilized all available in situ records for ground GUD (also known as leaf unfolding date) in China from the Chinese Phenological Observation Network (CPON)²⁴, which has compiled phenological data since 1963 for 112 plant species across 145 sites nationwide. In CPON, spring GUD is defined as the date when leaves begin to unfold.

To detect and eliminate possible outliers of ground GUD, we applied the median absolute deviation (MAD) method, which is more resilient to outliers in a data set than the standard deviation. For each site and species, MAD of GUD dataset (GUD₁, GUD₂,…, GUD_i) can be expressed as:

$${\rm{MAD}}\,=\,{\rm{median}}(|{{\rm{GUD}}}_{{{i}}}\,-\,{\rm{median}}({\rm{GUD}})|)$$

(1)

For each site and species, any data record with more than 2.5 times MAD was removed as an outlier¹⁰. We also excluded all GUD records that were shorter than 15 years to make temporal analyses more reliable. In this way, we used a total of 1030 time series from 35 sites and 505 species for 2003-2018. The distribution and descriptions of the in situ data are detailed in Supplementary Fig. 1 and Table 2.

Satellite-derived GUD observations

We applied satellite-derived spring GUD from 2001 to 2021, obtained from the Terra and Aqua combined Moderate Resolution Imaging Spectroradiometer (MODIS) Land Cover Dynamics (MCD12Q2) Version 6.1 data product²⁵ (Supplementary Table 1). This product uses the two-band Enhanced Vegetation Index (EVI2) to provide yearly metrics of global terrestrial surface phenology with an initial spatial resolution of 500 × 500 m. For each pixel, satellite GUD was defined as the date when EVI2 first crossed 15% of the segment EVI2 amplitude. We implemented quality control measures to reduce uncertainties, and we removed GUD dates before 1 February or later than 30 June³⁵. We downloaded, processed, and resampled the satellite GUD data into 0.05 × 0.05 degree at the Google Earth Engine platform.

Satellite-derived SIF observations

We used the long-term contiguous SIF (LCSIF) dataset (2001–2021)²⁶. The dataset is accessible at a bi-monthly temporal resolution, accompanied by a spatial resolution of 0.05 × 0.05 degree (Supplementary Table 1). The LCSIF showed strong correlations with satellite-based SIF observations from the Orbiting Carbon Observatory-2 (OCO-2) and ground-based estimates of gross primary productivity across different vegetation types, demonstrating its ability to accurately represent terrestrial photosynthesis. To examine PM_2.5-induced SIF signal attenuation, we calculated relative SIF, which refers to SIF normalized by the continuum-level NIR-reflected radiance, to check the response of SIF to PM_2.5 pollution. We found overall consistent patterns of both PM_2.5 and temperature sensitivities of SIF and relative SIF (Supplementary Fig. 9). These results indicated that the widespread decreases in spring SIF under PM_2.5 pollution are primarily attributed to the biophysical effects of PM_2.5 pollution rather than being influenced by signal attenuation²².

Satellite-driven PM_2.5 data and evaluation

Daily and monthly satellite-driven PM_2.5 data was obtained from the China High Air Pollutants (CHAP, version 4) dataset, covering the period 2001 to 2021, with a spatial resolution of 1 × 1 km²³. The CHAP data was derived by combining the MODIS Collection 6 MAIAC AOD product (MCD19A2) with information on meteorology, surface conditions, pollutant emission, and population distribution using the Space-Time Extra-Trees model. To evaluate the satellite-driven PM_2.5 data, we used a ground monitoring network of PM_2.5 observations with 1599 sites (at least 5-year records) in China from 2013 to 2021 (Supplementary Fig. 1). We evaluated the satellite-based spring and winter averaged PM_2.5 concentrations using all collected site monitoring data, with R² of 0.85 and 0.82 and RMSE of 6.89 and 11.74 μg m⁻³ for spring and winter, respectively (Supplementary Fig. 10). The high accuracy of satellite-based PM_2.5 data allows us to examine the response of spring vegetation activity to PM_2.5 pollution. To match the spatial resolution of satellite GUD and SIF, we resampled satellite-driven PM_2.5 data into 0.05 × 0.05 degree.

Future PM_2.5 simulations

We simulated future PM_2.5 data from 2025 to 2060 at 5-year intervals under three emission scenarios: SSP1-Neutrality-BHE (best-health-effect scenario), SSP2-45-ECP (enhanced-control-policy scenario), and SSP4-60-BAU (business-as-usual scenario), using the Nested Air Quality Prediction Modeling System (NAQPMS)³⁶ (Supplementary Fig. 11). The PM_2.5 output has a horizontal resolution of 45 km and a temporal resolution of 6 h. Future emission inventories under the three scenarios were obtained from the Dynamic Projection Model for Emissions in China (DPEC v1.0, http://meicmodel.org/)³⁷. Meteorological fields were provided by the Weather Research and Forecasting Model (WRF, version 3.6.1, available at https://www.mmm.ucar.edu/weather-research-and-forecasting-model). Initial and boundary conditions for four future climate scenarios (SSP1-19, SSP1-26, RCP4.5, and RCP6.0) were provided by Phases 5 and 6 of the Coupled Model Intercomparison Project (CMIP5 and CMIP6). A summary of the future emissions and climate scenarios is provided in Supplementary Table 3.

Climatic data and ancillary data

Monthly meteorological data at a 1/24 degree resolution, including mean temperature and total precipitation, were obtained from TerraClimate³⁸ for 2001-2021. Since spring vegetation activity could be positively regulated by solar radiation and PM_2.5 could directly reduce the radiation, here we used cloudiness (0–100%) data derived from the Climate Research Unit (CRU TS v4.07) to represent the level of radiation (Supplementary Table 1)³⁹. In our analyses, we negated the value of cloudiness sensitivity as radiation sensitivity (multiplied by −1) to make it more understandable. We obtained CN05.1 gridded daily mean temperature with a spatial resolution of 0.25°, derived from the National Meteorological Information Center of China, to calculate CA and HR, and to build and improve GUD models⁴⁰. To exclude the impact of human activity on agricultural ecosystems, we removed all cropland areas using the MCD12Q1 MODIS land-cover product (collection 6) (Supplementary Fig. 1).

Chilling models and forcing models

We used 11 chilling models (C₁–C₁₁) and five forcing models (F₁–F₅) to quantify CA and HR, respectively²⁶. Models C₁–C₆ were developed based on various combinations of the upper and lower temperature limits. The equations for Models C₁–C₆ are as follows:

$${{\rm{CU}}}_{1}=\left\{\begin{array}{cc}1 & T\le 5\\ 0 & T \, > \, 5\end{array}\right.$$

(2)

$${{\rm{CU}}}_{2}=\left\{\begin{array}{cc}1 & -10\,\le \,T\,\le \,5\\ 0 & \,{\rm{T}}\, > \,5\,{\rm{or}}\,T \, < \, -10\end{array}\right.$$

(3)

$${{\rm{CU}}}_{3}=\left\{\begin{array}{cc}1 & 0\le T\le 5\\ 0 & \,T \, > \, {\rm{5}} \, {\rm{or}} \, T \, < \, 0\end{array}\right.$$

(4)

$${{\rm{CU}}}_{4}=\left\{\begin{array}{cc}1 & T\le 7\\ 0 & T \, > \, 7\end{array}\right.$$

(5)

$${{\rm{CU}}}_{5}=\left\{\begin{array}{cc}1 & -10\le T\le 7\\ 0 & \,{\rm{T}} \, > \, 7\,{\rm{or}}\,T \, < \, -10\end{array}\right.$$

(6)

$${{\rm{CU}}}_{6}=\left\{\begin{array}{cc}1 & 0\le T\le 7\\ 0 & \,T \, > \, 7\,{\rm{or}}\,T \, < \, 0\end{array}\right.$$

(7)

where CU_i is the rate of chilling for Model C_i, and T is the daily mean temperature (°C).

Models C₇ and C₈ were designed by assigning different weights to different ranges of temperatures⁴¹. Models C₉–C₁₁ have triangular forms designed for multiple plant species⁴². The equations for Models C₇–C₁₁ are as follows:

$${{\rm{CU}}}_{7}=\left\{\begin{array}{cc}0 & T\le 1.4\\ 0.5 & 1.4 \, \, < \, T\le 2.4\\ 1 & 2.4 \, < \, T\le 9.1\\ 0.5 & 9.1 \, < \, T\le 12.4\\ 0 & 12.4 \, < \, T\le 15.9\\ -0.5 & 15.9 \, < \, T\le 18\\ -1 & T \, > \, 18\end{array}\right.$$

(8)

$${{\rm{CU}}}_{8}=\left\{\begin{array}{cc}0 & T\le 1.4\\ 0.5 & 1.4\, \, < \, \,T\le 2.4\\ 1 & 2.4 \, < \, T\le 9.1\\ 0.5 & 9.1 \, < \, T\le 12.4\\ 0 & T \, > \, 12.4\end{array}\right.$$

(9)

$${{\rm{CU}}}_{9}=\left\{\begin{array}{cc}1 & 2.5 \, < \, T \, < \, 7.4\\ 0 & T \, < \, -4.7\,{\rm{or}}\,T\, \, > \, \,16\\ 3.13\times (\frac{T+4.66}{10.93})^{2.10}{\times {\rm{e}}}^{-(\frac{T+4.66}{10.93})^{3.10}} & {\rm{else}}\end{array}\right.$$

(10)

$${{\rm{CU}}}_{10}=\left\{\begin{array}{cc}0 & T\le -3.4\,{\rm{or}}\,T\ge 10.4\\ \frac{T+3.4}{5+3.4} & -3.4 \, < \, T \, < \, 5\\ \frac{T-10.4}{5-10.4} & \,5 \, < \, T \, < \, 10.4\end{array}\right.$$

(11)

$${{\rm{CU}}}_{11}=\left\{\begin{array}{cc}0 & T\le -6.5\,{\rm{or}}\,T\ge 6.9\\ \frac{T+6.5}{6.9-0.2} & -6.5 \, < \, T\,\le \,0.2\\ \frac{6.9-T}{6.9-0.2} & 0.2 \, < \, T \, < \, 6.9\end{array}\right.$$

(12)

where CU_i is the rate of chilling for Model C_i, anT is the daily mean temperature (°C).

We used five widely used forcing models to measure the HR of GUD^29,42. The growing degree days (GDD) model is the most commonly used forcing model, which assumes that the rate of forcing is linearly correlated with temperature if the temperature is above a particular threshold. The equations for models F₁-F₅ are as follows:

$${{\rm{FU}}}_{1}=\,{\max }(T,\,0)$$

(13)

$${{\rm{FU}}}_{2}=\,{\max }({\rm{T}}-5,\,0)$$

(14)

$${{\rm{FU}}}_{3}=\left\{\begin{array}{cc}\frac{28.4}{{1+{\rm{e}}}^{-0.185\times (T-18.5)}} & T \, > \, 0\\ 0 & {\rm{else}}\end{array}\right.$$

(15)

$${{\rm{FU}}}_{4}=\frac{1}{{1+{\rm{e}}}^{-0.47\times T+6.49}}$$

(16)

$${{\rm{FU}}}_{5}=\left\{\begin{array}{cc}0 & T \, < \, {T}_{L}\,{\rm{or}}\,T \, > \, {T}_{c}\\ \frac{{T}_{u}-{T}_{L}}{2}\times (1+\,\cos ({\rm{\pi }}+{\rm{\pi }}\times \frac{T-{T}_{{\rm{L}}}}{{T}_{{\rm{u}}}-{T}_{{\rm{L}}}})) & {T}_{L}\ge T\ge {T}_{u}\\ ({T}_{u}-{T}_{L})\times (1+\,\cos (\frac{{\rm{\pi }}}{2}+\frac{{\rm{\pi }}}{2}\times \frac{T-{T}_{u}}{{T}_{c}-{T}_{u}})) & {T}_{u} \, < \, T\le {T}_{c}\end{array}\right.$$

(17)

where FU_i is the rate of forcing for Model F_i, and T is the daily mean temperature (°C). T_L = 4, T_u = 25, and T_c = 36.

Spring phenological models

In this study, we used four spring phenological models: the GDD and spring warming (SW) models (one-phase models), and the sequential model (SM) and parallel model (PM) (two-phase models)⁴³. In all models, GUD was simulated as the date when the state of forcing (S_f) reached its critical value (F_crit). The primary differences among the models lay in the calculation of the daily rate of forcing (R_f) and the conditions required for the accumulation to start.

$${{\rm{S}}}_{f}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{f}$$

(18)

$${\rm{GUD}}=t,\,{\rm{if}}\,{S}_{f}\ge \, {F}_{crit}$$

(19)

The one-phase models solely accounted for the influence of forcing and calculated R_f starting from 1 January of the current year (t₀) (Eq. 18). The date when S_f exceeds F_crit is regarded as the GUD.

The GDD model begins to accumulate R_f when the temperature reaches a baseline threshold (T_baseline):

$${{\rm{R}}}_{{\rm{f}}}=\left\{\begin{array}{cc}0 & T\le {T}_{{\rm{baseline}}}\\ T & T \, > \, {T}_{{\rm{baseline}}}\end{array}\right.$$

(20)

The SW model calculates the R_f based on a logistic function:

$${{\rm{R}}}_{f}=\frac{{A}_{f}}{{1+{\rm{e}}}^{{\rm{alpha}}(T-{\rm{beta}})}}$$

(21)

where A_f, alpha and beta are process-specific parameters to be determined.

The two-phase SM and PM, in contrast to the one-phase models, assume that the accumulation of forcing cannot begin until a critical threshold (C_crit) of the chilling state (S_c, a daily sum of chilling rates) is reached. A triangle function (Eq. 22) was used to describe the daily rate of chilling (R_c), and S_c began to accumulate after 1 September of the preceding year (t_c) (Eq. 23):

$${{\rm{R}}}_{{\rm{c}}}=\left\{\begin{array}{cc}0,& T\le {T}_{a}\\ \frac{T-{T}_{a}}{{T}_{b}-{T}_{a}},& {T}_{a} \, < \, T\le {T}_{b}\\ \frac{T-{T}_{c}}{{T}_{b}-{T}_{c}},& {T}_{b} \, < \, T \, < \, {T}_{c}\\ 0,& T\ge {T}_{c}\end{array}\right.$$

(22)

$${S}_{c}=\mathop{\sum }\limits_{{t}_{c}}^{t}{R}_{c}$$

(23)

where T_a, T_b and T_c are the threshold temperatures at which the state of R_c changes during the chilling accumulation process.

The forcing phase of the SM was similar to that of the SW model using R_f, but with an adjustment factor, K, to ensure that the accumulation of forcing occurs after the chilling state (C_crit) is fulfilled (Eq. 24). Like the GDD model, the SM also uses a temperature threshold (T_d) to establish the requirement for beginning the accumulation of forcing (Eq. 8) and meeting C_crit.

$${\rm{K}}=\left\{\begin{array}{cc}0 & {S}_{c} \, < \, {C}_{crit}\\ 1 & {S}_{c}\ge {C}_{crit}\end{array}\right.$$

(24)

$${R}_{f}=\left\{\begin{array}{cc}0 & T\le {T}_{d}\\ {\rm{K}}\times \frac{Af}{{1+{\rm{e}}}^{{\rm{alpha}}\times (T-{\rm{beta}})}} & T \, > \, {T}_{d}\end{array}\right.$$

(25)

The PM is a modified version of the SM that assumes that the accumulation of forcing is not strictly zero before C_crit is achieved. The only difference between the parameters of the SM and the PM is how K is calculated (Eq. 26). The PM adds a new parameter (K_min), which calculates the minimal potential of a bud that has not been chilled to react to the forcing temperature^39,40.

$${\rm{K}}=\left\{\begin{array}{cc}{K}_{{\min }}+\frac{1-{K}_{{\min }}}{{C}_{crit}}\times {S}_{c} & {S}_{c} \, < \, {C}_{crit}\\ 1 & {S}_{c}\ge \, {C}_{crit}\end{array}\right.$$

(26)

The improved models were developed by incorporating the daily PM_2.5 data into the above models, i.e., GDD, SW, SM, and PM. We added two new parameters (K_chiling, K_forcing), together with the normalized difference of daily PM_2.5 concentration (NDPM, Eq. 27), to these new models to modify the R_c and R_f using an exponential function (Eqs. 28, 29), accounting for the processes of how PM_2.5 regulates CA and HR before the leaf green-up. For one-phase models (i.e., GDD and SW), we modified the daily rate of forcing. For two-phase models (i.e., SM and PM), we modified rates of chilling and forcing.

$${{\rm{NDPM}}}_{{{\rm{t}}}_{{\rm{i}}}}=\frac{PM{25}_{{t}_{i}}-\,{\min }(PM25)}{{\max }(PM25)-\,{\min }(PM25)}$$

(27)

$${S}_{PM25-c}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{PM25-c}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{c}\times {F}_{PM25-c}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{c}\times {e}^{{K}_{chilling}\times {{\rm{NDPM}}}_{{\rm{t}}}}$$

(28)

$${S}_{PM25-f}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{PM25-f}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{f}\times {F}_{PM25-f}=\mathop{\sum }\limits_{{t}_{0}}^{t}{R}_{f}{\times {\rm{e}}}^{{K}_{forcing}\times {{\rm{NDPM}}}_{{\rm{t}}}}$$

(29)

where PM25 represents daily PM_2.5 concentration, ${{\rm{NDPM}}}_{{{\rm{t}}}_{{\rm{i}}}}$ represents the normalized difference of daily PM_2.5 concentration of t_i. ${S}_{PM-c}$ and ${S}_{PM-f}$ represent the PM_2.5-adjusted ${S}_{c}$ and ${S}_{f}$, respectively. t₀ and t represent the start and end days of chilling (Eq. 28) and forcing (Eq. 29), respectively.

We implemented the Particle Swarm Optimization (PSO) algorithm at each pixel or site to iteratively calculate a set of optimal model parameters for each spring phenology model, using satellite and ground GUD data and daily air temperature. The nature-based PSO algorithm is one of the most widely used swarm intelligence algorithms, in which individuals are referred to as particles and seek the search space for the global optimal position that minimizes (or maximizes) a given problem^44,45. The set of optimal parameters was selected when RMSE between the modeled and observed GUD was lowest⁴³. We further checked the patterns of PM_2.5-weighted parameters (K_chilling and K_forcing). We found that K_chilling was positive at 54.6% of the area, nearly five times the negative value (Supplementary Fig. 12), confirming that PM_2.5 pollution reduced the efficiency of CA.

To evaluate the GUD models, we calculated the frequency of pixels with significant correlations between model estimates and observations, the correlation coefficient (R), the root mean square error (RMSE), and the Kling-Gupta efficiency (KGE) using both ground and satellite GUD.

Analyses

Response of spring GUD and SIF to PM_2.5 pollution

We conducted site-level and grid-level analyses for ground and satellite observations. For site-level analyses, we used ground GUD derived from the CPON and PM_2.5 and climatic data for the same location extracted from gridded products. We also extracted satellite SIF for all GUD sites to determine site-level climatic and PM_2.5 sensitivities. For grid-level analyses, we used satellite GUD, SIF, and gridded climatic and PM_2.5 data with a consistent spatial resolution (0.05 × 0.05 degree) resampled by the bilinear interpolation method. We applied the Theil-Sen slope estimator to analyze the temporal patterns of spring GUD, SIF, and PM_2.5, evaluated by the Mann–Kendall trend test at a significance level of 0.05. We found overall advancing trends of GUD, increasing trends of SIF, and decreasing trends of PM_2.5 concentration (Supplementary Fig. 13) for 2001-2021, indicating the synergistic changes in PM_2.5 pollution and spring vegetation activities and their potential interplays.

To avoid potential multicollinearity between climatic factors and PM_2.5 concentration, we applied ridge regression, which incorporates a penalty parameter to reduce the variance of regression coefficients. This approach was used to determine the sensitivities of GUD and SIF to PM_2.5 pollution and climatic factors (i.e., temperature, precipitation, and radiation). To isolate the effects of PM_2.5 and climatic factors on GUD, we first conducted partial correlation analyses to calculate the optimal length of preseason of each factor for each site or pixel. For each factor, the optimal preseason was defined as the period before the GUD with the highest absolute partial correlation coefficient between GUD and corresponding factors. We then calculated the PM_2.5 and climatic sensitivities as the coefficients of the ridge regression between the GUD and the averaged PM_2.5, temperature, radiation, and accumulated precipitation during the preseason periods for corresponding driving factors¹⁰. It should be noted that ridge-regression-based sensitivities are unitless since we used normalized anomalies of all variables mentioned above. Positive sensitivities indicate delayed GUD, while negative sensitivities suggest advanced GUD.

To determine the environmental responses of spring SIF, we applied the ridge regression method, with spring mean SIF as the response variable and spring averaged PM_2.5, temperature, radiation, and accumulated precipitation as predictors. It should be noted that cloudiness (the proxy of radiation) could be potentially impacted by heavy PM_2.5 pollution due to aerosol-cloud interactions⁴⁶, further influencing precipitation and even temperature. We used partial correlation analyses and ridge regression methods to minimize the potential multicollinearity between climatic factors and PM_2.5 concentration and to focus on the PM_2.5 effects on spring vegetation activity. Future investigations on the interactive effects of climate change and PM_2.5 pollution are potentially needed. Here, we also examined the impact of PM_2.5 on near-surface temperature using weather station records from 633 sites (Supplementary Table 1). We found that PM_2.5 had varying impacts on daily mean, maximum, and minimum temperatures in spring: while it slightly increased daily mean and maximum temperatures, it did not affect daily minimum temperature (Supplementary Fig. 14). These results indicate a limited regulatory role of PM_2.5 on temperature.

Potential mechanisms under PM_2.5 effects

We investigated the biogeochemical and biogeophysical mechanisms underlying the effects of PM_2.5. We first checked the impacts of PM_2.5 on the CA derived from 11 models and HR derived from five models. Given that CA may be influenced by temperature variations, we conducted partial correlation analyses to examine the relationship between PM_2.5 and CA while controlling for temperature effects during CA periods. Previous studies have shown a negative correlation between CA and HR^28,47, which aligns with our SEM analysis results (Fig. 2G). To assess the impact of PM_2.5 on HR, we also performed partial correlation analyses, controlling for temperature effects during HR periods and preceding CA. Since CA and HR jointly and interactively influence GUD, we used partial correlation analyses to explore the CA-GUD and HR-GUD relationships, excluding the effects of HR and CA, respectively.

We introduced PAR⁴⁸ and VC_max⁴⁹, together with GUD, to explain PM_2.5’s effects on SIF. We used partial correlation analyses to examine associations between PM_2.5 and PAR and VC_max, as well as between VC_max and SIF (Fig. 2D–F). The data description of PAR and VC_max can be seen in Supplementary Table 1. We also considered PM_2.5 effects on diffuse PAR⁴⁸, and its association with SIF (Supplementary Fig. 6). It should be noted that the modeled VC_max we used has been evaluated using measurements of leaf chlorophyll and VC_max across different species and vegetation types^50,51. In the last step, we applied Structural Equation Models (SEM) to investigate the biogeophysical (through CA and HR) and biogeochemical (through VC_max and PAR) effects of PM_2.5 pollution on spring GUD and SIF (Fig. 3C–H). The SEM allows us to quantify both direct and indirect causal relationships among multiple driving factors. Utilizing multiple gridded variables, our SEM elucidated the mechanisms of distinct negative influences of PM_2.5 pollution on spring greening. All variables were standardized before analyses, and maximum-likelihood estimation was used to calculate the path coefficients. We used the standard criteria to assess the validity of our SEM, including the χ2 test (p > 0.05), the comparative fit index (CFI > 0.9), the Standardized Root Mean Square Residual (SRMR < 0.08), the goodness of fit index (GFI > 0.95), and the Root Mean Square Error of Approximation (RMSEA < 0.08). We conducted SEM for each pixel, and the SEM was considered valid if at least three out of five criteria were met⁵². SEMs were constructed using the “lavaan” package in R⁵³. To better disentangle the effects of PM_2.5 and understand the underlying mechanisms, future investigations, especially simulation experiments that measure plant physiology and hormones under different levels of PM_2.5 pollution, are essential.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.