Introduction

Materials with a honeycomb lattice and heavy elements can sustain anisotropic Kitaev interactions that favor a quantum spin liquid (QSL) ground state1,2,3. The same materials also host isotropic Heisenberg interactions that favor a long-range magnetic order (LRO)4,5. Theoretically, the QSL ground state could be established by tuning the competition between the Kitaev and Heisenberg interactions in favor of the former6,7. One approach to this problem would be to chemically design new materials with a large Kitaev to Heisenberg coupling ratio ∣K/J∣. Unfortunately, this is proven to be an extremely challenging task8,9,10,11,12. An alternative approach would be to use external parameters such as magnetic field strength13 or angle14 to tune an existing material away from the Heisenberg limit and toward the Kitaev limit. In this work, we present a successful case of such tuning by applying hydrostatic pressure, instead of a magnetic field, on the honeycomb lattice of Ag3LiRh2O6. Unlike all prior Kitaev materials, Ag3LiRh2O6 avoids a structural dimerization at low pressures, providing a hitherto unavailable opportunity to investigate competing exchange interactions under pressure in a spin-1/2 honeycomb system.

Ag3LiRh2O6 is synthesized from the parent compound Li2RhO3 by replacing the small interlayer Li atoms with large Ag atoms in a topochemical exchange reaction (Fig. 1a)15. Changing the interlayer atoms induces a trigonal distortion in RhO6 octahedra, which enhances the Ising-like anisotropy of the pseudospin-1/2 states15. As a result, a robust antiferromagnetic (AFM) order is established in Ag3LiRh2O6 at TN  =  100 K, in stark contrast to the glassy transition at 6 K in Li2RhO3. The large TN in Ag3LiRh2O6 indicates a dominant Heisenberg interaction, i.e., a small ∣K/J∣ ratio. We decided to study this material under pressure based on quantum chemistry calculations that predict the ∣K/J∣ ratio could be increased by modifying the ∠Rh-O-Rh bond angles within the honeycomb layers (Fig. 1b)16. 4d transition metal systems such as Li2RhO3 and Ag3LiRh2O6 are particularly sensitive to changes of bond angles, since they have comparable spin–orbit coupling and crystal field energy scales17.

Fig. 1: Magnetization data.
figure 1

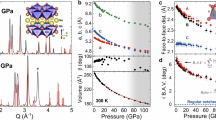
a Unit cell of Ag3LiRh2O6 in the monoclinic space group C2/m with Ag atoms between the [LiRh2O6] honeycomb layers. b ∠Rh-O-Rh bond angles within a honeycomb layer. c Suppression of TN with increasing pressure. d TN is identified by the peak in χ(T) at different pressures. e Both TN and ΘCW decrease in parallel with pressure while μeff remains nearly unchanged. All data in this panel are from run No. 4. f The peak in susceptibility data (TN) disappears at P  >  4 GPa.

Full size image

Our multiprobe investigations reveal three pieces of evidence for a shift in the balance between the Heisenberg and Kitaev interactions with increasing pressure in Ag3LiRh2O6. (i) Magnetization measurements show a rapid suppression of TN under pressure up to 3 GPa, beyond which, the AFM order disappears. (ii) X-ray diffraction (XRD) confirms the absence of structural transitions up to 5 GPa, beyond which, the honeycomb lattice undergoes a dimerization transition. (iii) μSR experiments reveal a long-range order below TN at low pressures but a short-range order at high pressures, which becomes long-range only when T  < TN/2. Thus, the μSR data indicate an extended temperature regime of fluctuating short-range magnetism. Details of the magnetization, XRD, and μSR data are presented below.

Magnetization

We started the high-pressure investigations of Ag3LiRh2O6 by measuring the DC magnetic susceptibility of a polycrystalline sample inside a ceramic anvil pressure cell. To reach the maximum pressure of about 5.5 GPa, we used a pair of anvils with small culets in runs 1, 2 and 3 (Methods). To obtain higher quality data for the Curie–Weiss (CW) analysis, we used another pair of anvils with larger culets which limited the pressure to 2 GPa in run 4.

The first observation in Fig. 1c is a rapid suppression of TN with pressure at a rate of  − 20 K/GPa up to about 3 GPa. At each pressure, TN was obtained from the peak in the χ(T) curve as seen in Fig. 1d for run 4. The high quality of these data enabled us to perform Curie–Weiss (CW) fits to extract the CW temperature (ΘCW) and effective magnetic moment (μeff). Plotting TN, ΘCW, and μeff as a function of pressure in Fig. 1e reveals a parallel suppression of TN and ΘCW with pressure, while μeff remains nearly unchanged. Since ΘCW is proportional to the Heisenberg coupling J, the parallel suppression of ΘCW and TN indicates a weakening of the average J under pressure. The value of μeff ≈ 1.9 μB, which is unaffected by pressures, is close to the expected moment for a pseudospin-1/2 state. In the supplementary information, we also provide DFT results that confirm the robustness of the pseudospin-1/2 state up to 5 GPa. These observations suggest that while the pseudospin-1/2 state in Ag3LiRh2O6 remains unchanged under pressure, the Heisenberg interactions weaken with increasing pressure, resulting in a rapid suppression of TN.

Switching to anvils with smaller culet sizes, we extended measurements of χ(T) to higher pressures in runs 1, 2, and 3 (Fig. 1f and the supplementary Fig. S1). The χ(T) curves qualitatively changed at P  >  3 GPa, where the AFM peak became smaller in magnitude and nearly disappeared at P  > 4 GPa (Fig. 1f). The disappearance of the AFM peak at high pressures suggests that the Kitaev coupling K is suppressed at a slower rate than Heisenberg coupling J, hence the ratio ∣K/J∣ is enhanced with increasing pressure.

X-ray diffraction

We performed XRD measurements under pressure with two goals in mind. First, to confirm that the suppression of the AFM order was not due to a structural transition, and second, to correlate the TN suppression with a change of ∠Rh-O-Rh bond angle.

Our search for a pressure-induced structural transition was motivated by previous studies on the hyper-honeycomb system β-Li2IrO3, which similar to Ag3LiRh2O6, has a high TN of 38 K at ambient pressure and loses its AFM order under pressure18,19,20,21. However, unlike in Ag3LiRh2O6, TN remains nearly independent of pressure in β-Li2IrO3 until the AFM order disappears abruptly at Pc  =  1.4 GPa20,21. The sudden loss of the AFM order in β-Li2IrO3 is unrelated to competing interactions. Instead, it originates form the loss of local moments due to the formation of Ir2 dimers under pressure19,20,21. Measurements of x-ray magnetic circular dichroism (XMCD)19 revealed a quenching of both spin and orbital moments due to this dimerization at Pc  =  1.4 GPa. Thus, we performed high-pressure x-ray diffraction on Ag3LiRh2O6 to distinguish between two mechanisms for the loss of AFM order: (i) structural dimerization, and (ii) competing interactions.

The XRD patterns in Fig. 2a show that the monoclinic C2/m structure is preserved in Ag3LiRh2O6 from 0 to 5 GPa at both 293 and 85 K. The Bragg peaks are slightly broadened with increasing pressure due to the loss of hydrostatic conditions. However, the amount of stacking faults is not changed considerably as evidenced by a nearly unchanged Warren line shape22 between 5 and 6 degrees (see the supplementary Fig. S3). In similar compounds such as Li2RhO3 and Cu2IrO3, the stacking faults are in fact reduced under pressure23,24. Thus, increasing stacking faults is not responsible for the TN suppression in Ag3LiRh2O6.

Fig. 2: X-ray diffraction.
figure 2

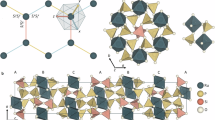
a Pressure-dependent diffraction patterns at 293 K (black) and 83 K (red). The *, +, and . symbols indicate, respectively, the Re peaks (gasket), Au peaks (manometer), and boron carbide seat. Red vertical bars in the bottom panel indicate calculated Bragg peak intensities at 1.9 GPa (293 K) and 2.7 GPa (83 K). b Monoclinic unit cell parameters, angle β, and volume plotted as a function of pressure. The P-V data are fitted (solid lines) using both second-order Vinet and second-order Birch–Murnaghan equations of state, rendering comparable values for the bulk modulus (B0) and ambient pressure volume (V0). c The bifurcation of the 9.5° Bragg peak at Pc  =  6.6 GPa indicates a dimerization transition (see also Fig. S2). d The linear and quadratic dependence of K and J on ∠Rh-O-Rh are reproduced from ref. 16. Dashed lines indicate the average bond angle at different pressures.

Full size image

Using Le Bail fits to these data, we trace the evolution of the unit cell parameters with pressure in Fig. 2b. All lattice parameters are smoothly decreasing with increasing pressure, and the monoclinic angle β fluctuates around 74.6(1) degrees. The absence of a structural transition up to 5 GPa in Figs. 2a, b rules out the dimerization of Rh2 units as the mechanism of TN suppression. This is consistent with the pressure independent μeffin Fig. 1e, since the formation of Rh2 dimers would have quenched the local moments.

Figure 2c shows that a structural transition finally occurs at Pc  =  6.6(5) GPa, well above the pressure range of TN suppression in Fig. 1c. The structural transition is signaled by a bifurcation of the Bragg peak at 9.5° in Fig. 2c (see also supplementary Fig. S2). A similar dimerization transition has been reported in Li2RhO3 at nearly the same critical pressure23.

The known presence of stacking faults in Ag3LiRh2O615 and the limited angular range of the high-pressure XRD data made Rietveld refinements of atomic positions challenging. Instead, we used the lattice parameters from XRD as input to a density functional theory (DFT) code and found the atomic positions that minimized the free energy (supplementary information). Using the atomic coordinates from DFT, we evaluated the ∠Rh-O-Rh bond angles at high pressures. The three dashed lines in Fig. 2d indicate the average values of ∠Rh-O-Rh at different pressures, overlaid on a plot of J and K couplings versus ∠Rh-O-Rh according to quantum chemistry calculations in Li2RhO316. The key observation is that ∣K/J∣ ratio increases rapidly with increasing pressure as the bond angles approach the critical value of 96° where J → 0. Note that J changes quadratically with bond angle while ∣K∣ changes linearly. This leads to the rapid increase of ∣K/J∣ from 1.6 to 2.6 and 3.6 as the pressure increases from 0 to 2.8 and 5.1 GPa, respectively. Such enhancement of the ∣K/J∣ ratio in the absence of a structural transition before 5.5 GPa suggests that competing interactions are responsible for the TN suppression and disappearance of the AFM peak in Fig. 1.

We used the calculated J and K curves for Li2RhO3 in Fig. 2d, because such calculations do not exist for Ag3LiRh2O6 at present. However, the 2D layers of Ag3LiRh2O6are similar to Li2RhO3, justifying our approach. Future material-specific calculations will be necessary for a quantitative analysis. Nevertheless, the analysis in Fig. 2d demonstrates how competing Kitaev and Heisenberg interactions could lead to the suppression of the AFM order.

Muon spin relaxation

In μSR, positively charged spin-polarized muons are implanted in a sample to probe the local magnetic field at some preferred crystallographic stopping site(s). The average time evolution of the muon polarization G(t) is monitored by detection of positrons which are preferentially emitted along the muon polarization direction upon its decay (lifetime τ  =  2.2 μs). Long-range magnetic order is signaled by the onset of oscillations in G(t) in zero magnetic field, and decay of G(t) (depolarization) can be caused by either magnetic disorder or dynamical fluctuations. The polarization curves in Fig. 3 are labeled Gmag(t) to indicate the removal of background signal from the pressure cell25 and a small non-magnetic signal from silver inclusions in the sample from the total polarization signal G(t). Details of background subtraction are given in the supplementary information (Fig. S4).

Fig. 3: μSR data.
figure 3

a Muon polarization at a low pressure showing oscillations immediately below TN. b At high pressure, oscillations do not appear until TN/2. c Comparing the low-T polarization curves at low-pressure (0 and 0.6 GPa) and high-pressure (2.3 GPa). d Comparing the Fourier transforms of polarization curves. e Visualizing the muon stopping sites (black circles near each oxygen site) in the lattice structure. f Phase diagram of the magnetic (TN) and structural (TS) transitions shown by circles and stars, respectively. The red and blue shades correspond to the disappearance of the magnetic order and the appearance of the structural dimerization.

Full size image

Before presenting any quantitative analysis, we reveal a qualitative difference between Gmag(t) curves obtained at low-pressure (P  <  2 GPa) and high-pressure (P  >  2 GPa) in Figs. 3a, b. Whereas the oscillations appear immediately below TN  =  95 K at P  =  0 (Fig. 3a), they do not appear until the temperature is decreased to half the TN  =  43 K at P  =  2.3 GPa (Fig. 3b). The observation of spontaneous oscillations below TN at low pressures (Fig. 3a) indicates the onset of long-range ordering. This is a typical behavior in a sample without magnetic disorder. The surprising result is that at high pressures (Fig. 3b), oscillations associated with a long-range order do not appear until temperatures below 20 K, which is half the TN  =  42 K at 2.3 GPa (Fig. 1c). In the intermediate range \(\frac{{T}_{{{{\rm{N}}}}}}{2} < T < {T}_{{{{\rm{N}}}}}\), oscillations are replaced with a fast depolarization, suggesting short-range magnetic ordering. A similar behavior has been reported at ambient pressure in Li2RhO3 and α-Li2IrO3, which are proximate Kitaev spin liquid materials16,26,27. Thus, pressure tunes the long-range AFM order in Ag3LiRh2O6 toward the short-range order observed in its parent compound Li2RhO3.

In addition to the qualitative differences between low-pressure and high-pressure polarization curves at \(\frac{{T}_{{{{\rm{N}}}}}}{2} < T < {T}_{{{{\rm{N}}}}}\), we also find quantitative differences at T ≪ TN. Figures 3c, d show Gmag(t) spectra and their Fourier transforms at ambient pressure, 0.6 GPa, and 2.3 GPa for T ≤ 10 K. We fit the magnetic polarization curves to the following expression

$${G}_{{{{\rm{mag}}}}}(t)= {f}_{{{{\rm{osc}}}}}\left[{f}_{1}{J}_{0}({\gamma }_{\mu }\Delta {B}_{1}t)\cos ({\gamma }_{\mu }{B}_{1,{{{\rm{avg}}}}}t)\exp (-{\Lambda }_{1}t)\right.\\ \left.+{f}_{2}{J}_{0}({\gamma }_{\mu }\Delta {B}_{2}t)\cos ({\gamma }_{\mu }{B}_{2,{{{\rm{avg}}}}}t)\exp (-{\Lambda }_{2}t)\right]\\ +\left(1-{f}_{{{{\rm{osc}}}}}\right)\exp (-{\lambda }_{L}t)$$
(1)

which consists of two oscillatory terms, indicating two inequivalent muon stopping sites. The two stopping sites were calculated by minimizing electrostatic potential near each crystallographically distinct oxygen site (O1 and O2) in the unit cell (Fig. 3e). Each term in Eq. (1) has a fractional contribution (f1 and f2) to the total oscillatory component fosc constrained by f1  + f2  = 1; fosc was found to be 0.59(1) at low temperature and ambient pressure and fixed at that value in all subsequent fits. f1 and f2 were 0.6 and 0.4, respectively, at low temperatures. The two oscillatory terms are known as the Overhauser approximation28 for incommensurate magnetic ordering (consistent with neutron scattering data in the SI) with a field distribution experienced by the muon which is symmetric about some non-zero average field in the range \({B}_{i,\min }\le {B}_{i}\le {B}_{i,\max }\), with

$${B}_{i,{{{\rm{avg}}}}}=\frac{{B}_{i,\max }+{B}_{i,\min }}{2},\quad \Delta {B}_{i}=\frac{{B}_{i,\max }-{B}_{i,\min }}{2}$$
(2)

and J0 being the zeroth-order Bessel function of the first kind. Each term in Eq. (1) is damped at a respective rate Λi. A long-time exponential decay with the rate λL constitutes the remaining fraction of the Ag3LiRh2O6 response from the muons that experience a local field parallel to the initial muon spin orientation (on average 1/3 of the muons in an isotropic polycrystalline sample). For ease of fitting, we only used a single λL for both muon stopping sites. The fit parameters at low- and high-pressure regimes are listed in Table 1. We note that fosc is somewhat less than 0.67 expected for an isotropic polycrystalline sample, suggesting a small degree of preferred orientation in the pressed polycrystalline pellet. Also, beamline optimization between measurements at different pressures could lead to slightly lower fosc at 2.3 GPa. Such optimizations are necessary as the sample volume and its precise location in the cryostat change between different pressure runs.

Table 1 Fit parameters from Eq. (1) at ambient, low, and high pressures for T ≪ TN
Full size table

While TN is substantially reduced by the application of 2.3 GPa, consistent with the magnetization data, we find small changes in the local field parameters \({B}_{1,\max }\) and \({B}_{2,\max }\). Such modest changes of the upper limits on the local field (less than 20%) could be accounted for by small changes of lattice parameters with pressure (Fig. 2b), which change the local field experienced by muons at the stopping sites (Fig. 3e). The small change of local fields in μSR is consistent with the nearly unchanged magnetic moment under pressure in the Curie–Weiss analysis (Fig. 1e). These observations show the presence of robust local moments despite weakening of the magnetic order at high pressures, consistent with increasing ∣K/J∣ ratio.

Discussion

In previous studies,13,14 magnetic field has been used to melt the long-range order into a fluctuating regime in honeycomb lattices such as α-RuCl3. Instead of changing the strength of J or K couplings, the magnetic field enters the Hamiltonian as an external parameter (Zeeman term)29,30. In contrast, pressure tunes the relative strength of competing interactions directly, by changing orbital overlaps. Despite theoretical proposals about using pressure as a powerful tuning parameter in Kitaev systems31,32, an experimental verification has not been possible until now, because a small pressure is enough to induce a dimerization transition in both 4d systems (Ru2 dimerization at 0.2 GPa in α-RuCl3 and at 0.5 GPa in Ag3LiRu2O6)33,34,35,36 and 5d systems (Ir2 dimerization at 1.4 GPa in β-Li2IrO3)19. Remarkably, such a structural transition does not appear in Ag3LiRh2O6 until 5 GPa, leaving a gap between the AFM (red) and dimerized (blue) phases in the phase diagram of Fig. 3f.

This work introduces Ag3LiRh2O6 as a unique Kitaev material that avoids structural dimerization under pressure while the magnetic correlations change from long-range to short-range. It opens the possibility of tuning Kitaev and Heisenberg interactions as demonstrated in Fig. 2d. Such a possibility was not offered by other Kitaev materials so far, as they all dimerized at low pressures. Moving forward, it will be helpful to get spectroscopic information from inelastic x-ray scattering and Raman scattering about the pressure-induced quantum critical regime near 4 GPa, and to search for evidence of quantum critical behavior by measuring temperature dependence of specific heat or NMR at low temperatures (T <  2 K) near 4 GPa. Material specific calculations will be necessary to carefully investigate the tuning of Kitaev, Heisenberg, and off-diagonal exchange (Γ) interactions under pressure. The combination of such experimental and theoretical studies could reveal the nature of the low-lying excitations in the gap between the red and blue regimes in Fig. 3f.

Methods

Material synthesis

Polycrystalline samples of Ag3LiRh2O6 were synthesized using a topochemical cation-exchange reaction from the parent compound Li2RhO3 following a previous publication15. The structural and compositional quality of all samples were characterized at ambient conditions with powder X-ray diffraction and energy dispersive X-ray spectroscopy. The only impurity found was about 5% silver inclusions.

Magnetization measurements

Magnetization of the powder sample was measured in a Quantum Design MPMS3 using a composite ceramic anvil cell37 with Daphne oil 7373 as the pressure-transmitting medium. Pressure was determined from the superconducting transition of a lead manometer. To achieve the maximum pressure of about 5.5 GPa, a pair of anvils with small culet sizes (1 mm) were used in runs 1, 2, and 3. A small sample chamber with both diameter and thickness of 0.5 mm was drilled into the Be-Cu gasket. To obtain data with higher quality for the CW fits, another pair of anvils with larger culets (1.8 mm) were used in run 4. This time, the maximum pressure was about 2 GPa due to the larger sample chamber with both diameter and thickness of 0.9 mm. In each run, the magnetization of the empty cell was measured first as the background and subtracted from the total signal. The small jumps near zero magnetization in Fig. 1f and Fig. S1a, b are due to this subtraction.

Muon spin relaxation (μSR)

The μSR experiments were performed at the Paul Scherrer Institute using the General Purpose Surface-Muon (GPS) and General Purpose Decay-Channel (GPD) spectrometers on the “πM3” and “μE1” beamlines, respectively. Measurements on a pressed disk (12-mm diameter, 1-mm thickness) were made on GPS at ambient pressure using a gas flow cryostat between 110 and 6.5 K. Measurements in GPD at pressures of 0.57 and 2.29 GPa (as determined by an indium manometer) were made in a He-flow cryostat using a piston-cylinder pressure cell25 with Daphne oil 7373 as the pressure-transmitting medium. Data were analyzed using the MUSRFIT program38.

X-ray diffraction

X-ray diffraction (XRD) data were collected at the High Pressure Collaborative Access Team (HPCAT) beamline 16-BM-D of the Advanced Photon Source using diamond anvil cells (DAC) with a combination of full and partially perforated anvils to reduce x-ray attenuation. Anvil culet diameter was 300 μm. Rhenium gaskets were pre-indented to a thickness of 50 μm, and a 180-μm-diameter sample chamber was laser drilled at the center of the indentation. Fine powder (5 μm) of Ag3LiRh2O6, together with ruby and gold manometers, were loaded into the sample chamber filled with Ne pressure medium. The entire sample chamber was rastered over the 25  × 25 μm2 area of the 30 keV X-ray beam to improve powder averaging on the CCD detector. Measurements were carried out at both ambient and low temperature (83 K). 2D XRD images were integrated over 2π using Dioptas software39 and the integrated diffractograms were Le Bail fitted using Jana202040. Pressure-dependent lattice parameters were extracted and second-order Vinet and Birch–Murnagham equations of state were both fitted using EoSFit41.

DFT calculations

Structural optimization and electronic structure calculations at high pressures were performed using the QUANTUM ESPRESSO and Wannier90 codes42,43,44 with the experimental crystallographic information as the input. To evaluate the wavefunctions in the supplementary information (Table S1), we first used Quantum ESPRESSO and Wannier90 codes to compute the electronic structure using experimental lattice parameters from our XRD measurements under pressure. Then, a tight-binding model was constructed for an individual RhO6 cluster, defined by real-space hopping parameters extracted from DFT. The orbital information were calculated from a Hartree–Fock mean-field model.

Neutron diffraction

Neutron powder diffraction (NPD) was performed on 2 g of polycrystalline Ag3LiRh2O6 using the HB-2A powder diffractometer and the HB-1A45 triple-axis spectrometer (VERITAS) at the high flux isotope reactor (HFIR) at Oak Ridge National Laboratory (ORNL). On HB-2A, the sample was loaded into a 5-mm diameter Al can to give an overall neutron transmission of 77.67%. We used collimations of open-21’-12’ with a wavelength of 2.41 Å. On HB-1A, the sample was loaded into an annular can with a 1-mm annulus and resulting neutron transmission of 90.38%. We used collimations of 40’-40’-40’-80’ with a fixed incident energy of 14.5 meV. FULLPROF46 was used for Rietveld refinements of crystal structures and computing predicted magnetic diffraction patterns to compare with experimental data.