Transforming jet flavour tagging at ATLAS

doi:10.1038/s41467-025-65059-6

Download PDF

Article
Open access
Published: 14 January 2026

Transforming jet flavour tagging at ATLAS

The ATLAS Collaboration

Nature Communications volume 17, Article number: 541 (2026) Cite this article

2494 Accesses
1 Citations
119 Altmetric
Metrics details

Subjects

Abstract

Jet flavour tagging enables the identification of jets originating from heavy-flavour quarks in proton–proton collisions at the Large Hadron Collider, playing a critical role in its physics programmes. This paper presents GN2, a transformer-based flavour tagging algorithm deployed by the ATLAS Collaboration that represents a different methodology compared to previous approaches. Designed to classify jets based on the flavour of their constituent particles, GN2 processes low-level tracking information in an end-to-end architecture and incorporates physics-informed auxiliary training objectives to enhance both interpretability and performance. Its performance is validated in both simulation and collision data. The measured c-jet (light-jet) rejection in data is improved by a factor of 3.5 (1.8) for a 70% b-jet tagging efficiency, compared to the previous algorithm. GN2 provides substantial benefits for physics analyses involving heavy-flavour jets, such as measurements of Higgs boson pair production and the couplings of bottom and charm quarks to the Higgs boson, and demonstrates the impact of advanced machine learning methods in experimental particle physics.

Reconstruction of unstable heavy particles using deep symmetry-preserving attention networks

Article Open access 30 April 2024

Quantum-inspired machine learning on high-energy physics data

Article Open access 15 July 2021

Implementation and analysis of quantum computing application to Higgs boson reconstruction at the large Hadron Collider

Article Open access 24 November 2021

Introduction

The Large Hadron Collider (LHC)¹ is the world’s most powerful particle collider. It is used to extend the boundaries of our understanding of fundamental particles and their interactions. It offers a unique opportunity to test the Standard Model (SM) of particle physics, as well as search for new phenomena beyond the Standard Model (BSM). The demanding experimental conditions at the LHC necessitate continuous innovation by the main experiments, pushing them to apply cutting-edge technologies to efficiently identify physics processes of interest within the largest proton–proton (pp) collision dataset ever recorded. Hadronic jets, collimated streams of particles initialised by quarks or gluons, are the most abundant physics objects in pp collision events, and their characteristics are widely utilised in data analyses.

The flavour of a hadronic jet is determined by the types of hadrons or leptons it contains. Flavour tagging concerns the classification of hadronic jets into those containing b-hadrons (b-jets), c-hadrons (c-jets), hadronic τ-lepton decays (τ-jets), and none of the above (light-jets), using algorithms sensitive to the distinctive properties of the respective classes. Since the beginning of Run 1 of the LHC (2009–2013), the ATLAS experiment^2,3 has achieved continuous improvement in the performance of these algorithms. The progress has mostly been driven by the integration of machine-learning techniques, including boosted decision trees and neural networks. The state-of-the-art algorithms used thus far to analyse the data at $\sqrt{s}=13\,{{\rm{TeV}}}$ from Run 2 of the LHC (2015–2018)^4,5 led to very impactful physics results such as the observations of the Higgs boson decaying to bottom quarks⁶ and its production in association with a pair of top quarks⁷. Flavour tagging plays an essential role in the comprehensive research programme of ATLAS, which includes precision measurements of the Higgs boson⁸, top quark⁹ and other SM processes¹⁰, as well as the searches for supersymmetry¹¹ and other BSM phenomena¹². This work describes a flavour tagging algorithm developed by the ATLAS Collaboration for the analysis of data from pp collisions recorded during Run 2 (2015–2018) and Run 3 (2022–2026) of the LHC at centre-of-mass energies of $\sqrt{s}=13\,{{\rm{TeV}}}$ and $\sqrt{s}=13.6\,{{\rm{TeV}}}$, respectively.

Flavour-tagging techniques rely on the long lifetime, high mass, high decay multiplicity and characteristic decay modes of b- and c-hadrons, and the properties of heavy-quark fragmentation¹³. The typical lifetime of the order of τ ≈ 1.5 ps^13,14,15 for b-hadrons in jets with transverse momenta in the range from tens to hundreds of GeV results in them travelling a mean flight length 〈l〉 = βγcτ in the range from few millimetres to centimetres before decaying, which often leads to a secondary vertex significantly displaced from the collision point. Displaced vertices can also be produced by c-hadrons, which have lifetimes of τ ≈ 0.2–1.0 ps, depending on the species^16,17,18, and τ-leptons, which have a lifetime of τ ≈ 0.29 ps but a much lower decay multiplicity^18,19. The majority of b-jets also contain a tertiary vertex from the decay of the c-hadron produced in the b-hadron decay.

The traditional flavour-tagging algorithms developed by the ATLAS Collaboration are based on a two-stage approach^4,5,20. In the first step, specialised low-level algorithms employ complementary approaches to extract information from the trajectories of the charged-particle constituents (‘tracks’) associated with the jet. These specialised algorithms either rely on the properties of individual tracks or leverage their correlations with properties of other tracks to explicitly reconstruct displaced vertices. In the second step, the outputs of low-level algorithms are subsequently combined in a high-level multivariate classifier to maximise performance. The most recent algorithm employed by the ATLAS Collaboration, following this paradigm, is a deep neural network (DL1d) that leverages a low-level track-based algorithm (DIPS)²¹ based on Deep Sets²². DL1d has already improved the performance by a factor of 1.3 relative to the most advanced algorithm used in published Run-2 physics analyses⁵.

The introduction of graph neural networks for object reconstruction in particle physics experiments²³ prompted a shift in the design strategy of the ATLAS Collaboration. This led to the development of the General Network (GN) series of flavour-tagging algorithms, which directly process track and jet information and are trained using target labels extracted from Monte Carlo (MC) simulation. In parallel, the CMS Collaboration followed a similar trajectory, evolving from two-stage approaches^24,25 to unified, end-to-end network architectures^26,27,28.

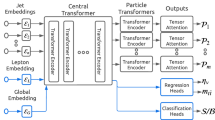
The ATLAS GN tagger uses jet flavour prediction as its primary training target and introduces auxiliary training objectives to reconstruct the internal structure of a jet by grouping tracks originating from a common vertex and by predicting the underlying physics process from which each track originated. Such physics domain knowledge is embedded in a combined loss function that enables a simultaneous optimisation, instead of relying on manually optimised low-level algorithms. This flexible structure allows the swift re-tuning of the algorithms to suit alternative experimental conditions or physics goals. A demonstrator version, GN1, achieves the above design goals using a graph-neural-network²⁹, while the deployment version, GN2, applies a single transformer model³⁰, illustrated in Fig. 1. Details of the algorithm architectures are summarised in the ‘Methods’ section, together with descriptions of the ATLAS detector, simulation samples, physics objects, and analysis strategies.

Fig. 1: Illustration of the GN2 algorithm with jet and track input variables, discriminating between jet flavours by exploiting secondary vertices and other properties stemming from the displaced decays of b-hadrons, in the transverse plane.

GN2 achieves a remarkable performance boost compared with the DL1d algorithm, with improvements by a factor of 1.5-4 observed in its major experimental applications. The deployment of GN2 should greatly enhance the physics reach of ATLAS in flagship analyses, such as the search for Higgs pair production and the c-quark Yukawa coupling measurement, for which the projected sensitivity at the High Luminosity LHC is improved by up to 30%³¹. These improvements do not come with a strong dependence on the choice and configuration of the MC event generator, and are confirmed by measured performance in recorded collisions. The innovative auxiliary training objectives bring excellent interpretability and opens up new avenues for future applications.

To facilitate future developments and strengthen the connections between collider experiments and the broader scientific research community, a subset of the training sample with all the required information to train GN2 can be acquired via the CERN Open Data Portal^32,33.

Results

Algorithm performance in simulation

The performance of a b-tagging algorithm is evaluated based on its ability to reject c-, τ- and light-jets while maintaining a desired b-jet tagging efficiency. Similarly, the c-tagging performance is assessed by its capability to distinguish c-jets from the other jet flavours. The data samples used for training and evaluation of the model must contain jets from all flavour classes. This is achieved using jets sampled from a mixture of simulated top quark pair ($t\overline{t}$) and ${Z}^{{\prime} }$ events, where the latter sample considers a hypothetical heavy BSM particle, ${Z}^{{\prime} }$³⁴, which can decay into pairs of b-quarks, c-quarks, τ-leptons or light quarks, to populate jets in the TeV regime. The samples are simulated with MC event generators at centre-of-mass energies of both $\sqrt{s}=13\,{{\rm{TeV}}}$ and $\sqrt{s}=13.6\,{{\rm{TeV}}}$. All simulated events are processed through the ATLAS detector simulation³⁵ based on GEANT4^36,37,38. Further details on the simulation samples and the jet flavour labelling are discussed in the ‘Methods’ section. A mixture of samples generated at $\sqrt{s}=13.6\,{{\rm{TeV}}}$ and $\sqrt{s}=13\,{{\rm{TeV}}}$ is used in the training, to achieve similar performance in both conditions. In this section, the performance evaluated with Run-3 samples at $\sqrt{s}=13.6\,{{\rm{TeV}}}$ is presented. Jets are classified for b-tagging using a single discriminant D_b, which combines the algorithm’s jet flavour prediction output probabilities of a jet being a b-jet (p_b), a c-jet (p_c), a τ-jet (p_τ) or a light-jet (p_u) and is defined as:

$${D}_{b}=\log \left(\frac{{p}_{b}}{{f}_{c}{p}_{c}+{f}_{\tau }{p}_{\tau }+\left(1-{f}_{c}-{f}_{\tau }\right){p}_{u}}\right).$$

(1)

A jet is considered b-tagged if it has a D_b score larger than a given value. A selection on D_b defines an operating point (OP) associated with a certain inclusive b-jet tagging efficiency, calculated as the fraction of b-jets that are b-tagged. The mis-tagging rate for c-, τ- and light-jets is determined by the fraction of jets that are mistakenly b-tagged, for that given jet flavour, and the rejection is the reciprocal of the mis-tagging rate. The ATLAS Collaboration uses a sample of simulated $t\bar{t}$ events, where most jets have a p_T below 250 GeV, to derive the OPs. The free parameters f_c(τ) determine the relative weighting between p_c(τ) and p_u in the discriminant D_b. The specific value of f_c is determined through an optimisation procedure aimed at obtaining a certain balance between rejections of c-jets and light-jets in simulated $t\overline{t}$ events. The value of f_τ is optimised to maximise the τ-jet rejection, while ensuring a negligible impact upon the c-jet and light-jet rejection. In the case of GN2, f_c(τ) is set to 0.2 (0.05), while for DL1d, which does not have a τ-jet output in the model, f_c is set to 0.018. For GN2, f_c is tuned to reach a much higher c-jet rejection, while still achieving a better light-jet rejection, compared with DL1d.

Figure 2 illustrates the tagger performance in terms of the c-jet, light-jet and τ-jet rejection as a function of the b-jet tagging efficiency. In both the $t\overline{t}$ and ${Z}^{{\prime} }$ samples, GN2 exhibits significantly better background rejection compared with DL1d across the entire range of b-jet tagging efficiencies. The degree of improvement depends on the b-jet tagging efficiency. In the $t\overline{t}$ sample, the c-jet (light-jet) rejection of GN2 improves by more than a factor of 3 (1.6), compared with DL1d, for the most commonly used 70% OP. The performance of both algorithms starts degrading once the jet p_T reaches around 200 GeV, due to several confounding factors, including suboptimal tracking performance in dense environments where the spatial separation between tracks becomes smaller³⁹. In the ${Z}^{{\prime} }$ sample, applying the 70% OP selection on D_b yields a b-jet tagging efficiency of 30%, and the c-jet (light-jet) rejection of GN2 improves by more than a factor of 3 (4), compared with DL1d. The inclusion of a τ-jet output node in GN2 leads to an even greater enhancement in the τ-jet rejection, by up to a factor of 8 (9) for jets in the $t\overline{t}$ (${Z}^{{\prime} }$) sample, without significantly degrading the c-jet and light-jet rejection.

**Fig. 2: $b$-tagging performance of GN2 and DL1d evaluated in MC simulations.**

The performance of a c-tagging algorithm is evaluated based on its ability to reject b-, τ- and light-jets while maintaining a desired c-jet tagging efficiency. Due to the end-to-end architecture that does not rely on low-level tagger inputs, GN2 can seamlessly be adapted as a c-tagging algorithm without re-training any lower level algorithms. Similar to b-tagging, a discriminant, D_c, is constructed as:

$${D}_{c}=\log \left(\frac{{p}_{c}}{{f}_{b}{p}_{b}+{f}_{\tau }{p}_{\tau }+\left(1-{f}_{b}-{f}_{\tau }\right){p}_{u}}\right),$$

(2)

where f_b(τ) is the free parameter that controls the flavour composition of the background in the background hypothesis. The value chosen for f_b(τ) is 0.3 (0.01) for GN2, while for DL1d, f_b is 0.1, following a similar optimisation procedure as for D_b.

The c-tagging performance of DL1d and GN2 are compared in Fig. 3, which shows a significant improvement in performance across all c-jet tagging efficiencies. The b-jet (light-jet) rejection is enhanced by a factor of approximately 1.8 (2.2) in the $t\overline{t}$ sample at a 30% c-jet tagging efficiency, which is a typical choice in measurements of the c-quark Yukawa coupling⁴⁰. The b-jet (light-jet) rejection is increased by a factor of approximately 2.7 (4.7) in the ${Z}^{{\prime} }$ sample at a corresponding efficiency of 10%. The τ-jet rejection is improved by a factor of approximately 15 (40) in the $t\overline{t}$ (${Z}^{{\prime} }$) sample.

**Fig. 3: $c$-tagging performance of GN2 and DL1d evaluated in MC simulations.**

Algorithm performance in collision data

Due to imperfections in the physics modelling of the MC generator and in the simulated detector response, the distribution of the input variables to the algorithms and their correlations differ between collision data and simulation, resulting in a performance difference. It is not practical to correct each individual mis-modelled variable, so dedicated calibration analyses are employed to measure the tagging efficiency of b-jets, c-jets and light-jets for pre-defined OPs directly^4,41,42. In the case of the GN2 algorithm, five OPs are defined corresponding to inclusive b-jet tagging efficiencies of 65%, 70%, 77%, 85% and 90% while for DL1d four OPs are constructed corresponding to inclusive b-jet tagging efficiencies of 60%, 70%, 77% and 85%. The results presented in this paper are derived using pp collision data recorded during Run 2 of the LHC at $\sqrt{s}$ = 13 TeV, corresponding to an integrated luminosity of 140 fb⁻¹. The tagging performance in data for b-jets, c-jets, and light-jets is measured, in order to obtain jet-flavour-dependent simulation-to-data correction factors, binned in jet p_T. They are applied to MC-simulated jets to rescale their tagging efficiencies and mis-tagging rates to match those measured in collision data. The calibration of b-jets and c-jets is done with $t\bar{t}$ events^4,41, while the calibration of light-jets is performed using jets produced in association with a Z boson⁴². Details of the calibration analyses are provided in the ‘Methods’ section.

Figure 4 presents the calibrated tagging efficiencies and rejections of GN2 and DL1d, along with their associated uncertainties, for each OP. The inclusive efficiencies and rejections are obtained by averaging over the events in a simulated $t\overline{t}$ sample after requiring the presence of one reconstructed electron or muon. The original efficiencies from the simulated sample are included as references, enabling a direct comparison that shows similar agreement between data and simulation for both GN2 and DL1d. The GN2 tagger demonstrates clear improvements over DL1d in collision data. For instance, the measured c-jet (light-jet) rejection in data is increased by a factor of 3.5 (1.8) for the 70% OP. The measurements in data provide conclusive evidence of the enhanced performance enabled by advanced machine-learning algorithms in identifying heavy-flavour jets at the LHC.

**Fig. 4: $b$-tagging performance of GN2 and DL1d measured in data and MC simulations.**

Discussion

Key challenges with machine-learning algorithms based on low-level inputs, such as GN2, include the potential loss of interpretability and the need to ensure consistent performance across different MC simulation methods. Robustness against these potential shortcomings is critical to prevent the algorithm from relying on unphysical features of the training sample. In this section, these aspects are discussed further.

Physics inspiration and the auxiliary training objectives

A key strength of the GN2 model lies in its physics-inspired constraints, which aid the main task of jet classification while also improving the interpretability of the model. This is accomplished by incorporating two additional training objectives: predicting the origin of tracks associated with the jet and determining which tracks originate from common vertices. These objectives are not strictly necessary for the jet classification task and are therefore referred to as auxiliary training objectives. The technical implementation details are provided in the ‘Methods’ section.

The track classification auxiliary training objective aims to estimate the probability that a track originates from one of the following physical processes: a pile-up interaction⁴³; the primary hard-scatter interaction; the decay of a b-hadron; the decay of a c-hadron produced by a b-hadron; the decay of a c-hadron; the decay of a τ-lepton; or any other secondary source. Class-weighted losses are applied during training to mitigate the class imbalance, and tracks are classified by the highest-probability category during evaluation. The class weights are fixed and based on the inverse class frequencies in the training dataset.

The classification efficiency refers to the probability for the track’s origin to be correctly predicted, in a group of tracks with certain target origins, while the purity corresponds to the fraction of correctly predicted tracks, within a group of tracks with specific predicted origins. When combining the two categories involving a b-hadron, GN2 achieves an efficiency (purity) of 84% (84%). For tracks that are not of heavy-flavour (HF) origin, the efficiency (purity) is 85% (96%). The above performance is evaluated in Run-3 samples at $\sqrt{s}=13.6\,{{\rm{TeV}}}$.

The vertex finding auxiliary training objective aims to identify groups of tracks that originate from a common spatial point. Each pair of tracks in the jet is classified to determine whether they share the same vertex. Using these pair-wise compatibility scores, track groups (vertices) are formed via a union-find algorithm⁴⁴. SV1, an existing secondary vertex reconstruction algorithm detailed in ref. ⁵, serves as a reference algorithm. SV1 reconstructs a single inclusive vertex, whereas GN2 can identify multiple vertices of various types within a jet. Therefore, an aggregation procedure is applied to the output of GN2 to enable a direct comparison with the single inclusive vertex produced by SV1. To study the vertex properties of b-jets, the identified vertex containing the most tracks that have a predicted primary origin is removed, as this is likely to be the vertex associated with the primary hard-scatter interaction. Next, the remaining GN2 vertices that include at least one track predicted to have a HF origin are consolidated into a single inclusive vertex.

An inclusive reference vertex is constructed in simulated events, by combining all tracks from simulation-level secondary vertices within the jet that consist solely of HF tracks. A Billoir fit⁴⁵ is performed on the tracks selected by the GN2 and SV1 vertex finding algorithms to obtain the transverse displacement of the vertex, L_xy. Figure 5 presents the L_xy distribution for vertices obtained with GN2 and DL1d in b-jets from a simulated $t\overline{t}$ sample, compared to the expected distribution derived from the inclusive reference vertex. GN2 consistently achieves higher vertex-finding efficiency than SV1 across the entire distribution of L_xy. The mass of the secondary vertex can also be calculated using the momenta of tracks selected by the vertex finding algorithms. The distribution of the secondary vertex mass normalised to unity is also shown in Fig. 5. Remarkably, the mass of the secondary vertices reconstructed by GN2 exhibits good agreement with the mass of the inclusive reference vertex, despite the vertex mass not being explicitly targeted during training. Unlike SV1, GN2 does not impose explicit selections on track properties such as impact parameters. This leads to a higher efficiency, albeit with a small contamination from non-HF tracks, which results in a slightly larger secondary vertex mass.

**Fig. 5: Secondary vertex properties reconstructed using tracks grouped by the GN2 and SV1 algorithms.**

GN2 identifies all types of vertices including those from material interactions, photon conversions, and in-flight decays of light hadrons. Consequently, the rate of vertices reconstructed in light-jets, defined as the fraction of light-jets containing a GN2 inclusive vertex, is expected to be much higher compared to SV1 if no selections are applied in the aggregation procedure described above. Figure 6 confirms this with light-jets in the simulated $t\overline{t}$ sample and shows that once requiring the GN2 inclusive vertex to contain at least one track with predicted HF origin, the vertexing rate is dramatically reduced, down to the same level as SV1.

Fig. 6: The rate of inclusive vertices reconstructed by the GN2 algorithm in light-jets as a function of the jet p_T, without any selections (dotted-dashed) and with the requirement of the vertex containing at least one track with predicted HF origin (solid).

To test the impact of the auxiliary objectives on the performance of the main jet classification task, various GN2 configurations are trained and tested. The resulting c-jet and light-jet rejections are reduced by up to 30% in both the $t\overline{t}$ and ${Z}^{{\prime} }$ samples, if both auxiliary objectives are disabled. Disabling only one of them is sufficient to recover most of the performance loss, indicating that the two tasks are highly correlated in their contributions to the main jet flavour tagging objective.

Although the outputs from the auxiliary tasks described above mainly serve as a way to improve HF jet identification, with future development, their direct usage in physics analyses remains a promising possibility.

Robustness against generator modelling variations

Flavour-tagging algorithms are sensitive to the modelling of parton showering, hadronisation, the underlying event and the properties of heavy-hadron decays⁴⁶. To evaluate the robustness of the algorithm against modelling variations, a comparative study of the GN2 performance in the nominal simulated $t\overline{t}$ sample used during training and samples produced with alternative generator settings, both with Run-2 conditions at $\sqrt{s}=13\,{{\rm{TeV}}}$, is performed.

The event and showering generators adopted for the nominal sample are Powhegbox^47,48,49,50 and Pythia⁵¹, respectively. The alternative samples include the use of a different showering generator (Herwig^52,53,54), whilst keeping the same event generator, and the use of Sherpa⁵⁵, which applies a different approach to all parts of the event generation model. The ratio between the efficiency obtained with an alternative generator setup and with the nominal setup is used to quantify the generator dependence of the algorithms.

Table 1 shows these ratios for b-jets, c-jets, and light-jets at the 70% and 85% OPs. Across the tested generators, the GN2 performance for b-jets agrees to within 1–2%, for c-jets the agreement is within 10%, and for light-jets the agreement is within 4%. Similar agreement is also observed for other OPs. The level of relative disagreement between DL1d and GN2 is close to unity, suggesting that despite the GN2 model being significantly more complex, it does not induce additional generator dependence.

Table 1 Ratios of the efficiencies obtained with samples using alternative MC generators, relative to those in the nominal Powhegbox + Pythia sample used during training of the algorithm

Full size table

Methods

The ATLAS detector

The ATLAS experiment^2,3 at the LHC is a multipurpose particle detector with a forward-backward symmetric cylindrical geometry and a solid-angle coverage of almost 4π. It is used to record particles produced in pp collisions at the LHC through a combination of particle position and energy measurements. It includes an inner-tracking detector (ID) surrounded by a thin superconducting solenoid providing a 2 T axial magnetic field, electromagnetic and hadronic calorimeters, and a muon spectrometer. The ID consists of silicon pixel, silicon microstrip, and transition radiation tracking detectors. The muon spectrometer surrounds the calorimeters and is based on three large superconducting air-core toroidal magnets with eight coils each providing a field integral of between 2 T m and 6 T m across the detector.

An extensive software suite⁵⁶ is used in data simulation, the reconstruction and analysis of real and simulated data, detector operations, and the trigger and data acquisition systems of the experiment.

Monte Carlo simulation samples

The $t\overline{t}$ events at $\sqrt{s}=13\,{{\rm{TeV}}}$ are modelled using the Powhegbox[v2]^47,48,49,50 event generator at next-to-leading-order (NLO) in the strong coupling constant α_s with the NNPDF3.0 NLO⁵⁷ parton distribution function (PDF) set and the first-gluon-emission cut-off scale parameter h_damp set to 1.5m_t, with a top-quark mass of m_t = 172.5 GeV. Parton shower, hadronisation, and the underlying event are modelled by interfacing Powhegbox[v2] to Pythia 8.230⁵¹, using the A14 set of tuned parameters⁵⁸ and the NNPDF2.3LO PDF set⁵⁹. The decays of b- and c-hadrons are performed by Evtgen 1.6.0⁶⁰.

The ${Z}^{{\prime} }$ events at $\sqrt{s}=13\,{{\rm{TeV}}}$ used to enrich the dataset with high-p_T jets are generated using Pythia 8.243 with the A14 set of tuned parameters for the underlying event and the leading-order (LO) Nnpdf 2.3LO PDF set. A broad jet p_T spectrum with an almost uniform distribution between 250 GeV and 1.5 TeV and a tail expanding to 6 TeV is obtained by applying a weighting factor that modifies the original cross-section of the ${Z}^{{\prime} }$ resonance. The decays to $b\bar{b}$, $c\bar{c}$, and light-flavour quark pairs are set to have equal branching ratios, while the branching ratio to $\tau \bar{\tau }$ is set to 5%. The decays of b- and c-hadrons are performed by Evtgen 1.7.0.

The $t\overline{t}$ and ${Z}^{{\prime} }$ events at $\sqrt{s}=13.6\,{{\rm{TeV}}}$ are produced using the same setups, but with newer versions of Pythia (8.308) and Evtgen (2.1.1).

The impact of using different generators and models for parton shower and hadronisation is studied with simulated $t\overline{t}$ events from alternative generator setups. Two scenarios are considered, where either only the showering algorithm is varied, or the entire chain is changed. The former is achieved by interfacing the Powhegbox[v2] generator with the Herwig[7.2.1]^52,53,54 showering algorithm using the Herwig[7.1] default set of tuned parameters, with the Nnpdf 3.0 NLO set of PDFs. The latter is realised with the Sherpa[2.2.12]⁵⁵ generator, using NLO-accurate matrix elements for up to one additional parton, and LO-accurate matrix elements for up to four additional partons, calculated with the COMIX⁶¹ and Openloops^62,63,64 libraries. The Sherpa parton shower^65,66 is applied using the Meps@nlo prescription^67,68,69,70 and the set of tuned parameters developed by the Sherpa authors to match the Nnpdf 3.0 NNLO set of PDFs.

Objects for flavour tagging

ATLAS uses a right-handed coordinate system with its origin at the nominal interaction point in the centre of the detector and the z-axis along the beam pipe. The x-axis points from the nominal interaction point to the centre of the LHC ring, and the y-axis points upwards. Cylindrical coordinates (r, ϕ) are used in the transverse plane, ϕ being the azimuthal angle around the z-axis. The pseudorapidity is defined in terms of the polar angle θ as $\eta=-\ln \tan (\theta /2)$. Angular distance is measured in units of $\Delta R\equiv \sqrt{{(\Delta \eta)}^{2}+{(\Delta \phi)}^{2}}$.

The fundamental objects for flavour tagging are jets, tracks, and vertices. A concise description of these objects is provided below, while a detailed description is available in ref. ⁵.

Tracks are reconstructed from ID information^39,71. To be considered for jet flavour tagging they are required to be within ∣η∣ < 2.5, have p_T > 0.5 GeV and satisfy criteria designed to reject fake and poorly measured tracks⁷².

Primary vertices (PVs) are reconstructed from tracks in the luminous region of the colliding LHC beams using an adaptive multi-vertex filter^73,74. The PV with the highest sum of squared transverse momenta p_T of contributing tracks is selected as the primary interaction point (IP) and provides the reference point in an event. The distance of closest approach of a track to the IP, the ‘perigee’, is indicated in the transverse plane by the transverse impact parameter d₀. The longitudinal separation between the IP and the point on the track where d₀ is measured, is indicated by the longitudinal impact parameter z₀. Tracks with large impact parameters can indicate the presence of displaced decays, providing vital information to the flavour tagging algorithms.

The DIPS and GN2 algorithms require tracks to be reconstructed from at least 8 hits in the silicon detector, at most one of which contributes to two tracks, at most two ‘holes’ in the silicon detector, and at most one hole in the pixel detector, where hole denotes a hit missing where one is expected from the track trajectory. Further, requirements on the track impact parameters, ∣d₀∣ < 3.5 mm and $| {z}_{0}\sin \theta | < 5\,{{\rm{mm}}}$, retain charged particle tracks originating from HF hadron decays while suppressing tracks from other sources.

Jets are reconstructed using the anti-k_t algorithm⁷⁵ with radius parameter R = 0.4 using the ‘fastjet’ package⁷⁶. The input constituents are ‘particle-flow’ objects⁷⁷ which combine signals in the ATLAS calorimeters and ID to exploit precision tracking information for low-p_T charged hadrons spatially matched with calorimeter energy deposits. The jet p_T is corrected to the corresponding particle-level jet p_T using calibration techniques described in ref. ⁷⁸. The jets are required to have p_T > 20 GeV (to be within the valid calibration range) and ∣η∣ < 2.5 (to be within the tracking fiducial volume set by the ID acceptance) to be considered for flavour tagging. Additionally, jets from pile-up interactions are suppressed by the ‘jet vertex tagger’ (JVT) algorithm⁷⁹, which uses the ID tracks associated with the jet to form a multivariate discriminant. The JVT efficiency for jets originating from the IP is 92% in the simulation. The jet axis, derived from the sum of the momenta of the jet constituents, is used when associating tracks with the jet and when assigning a lifetime sign to the tracks’ impact parameters. Tracks are associated with a given jet by setting a maximum allowed angular separation ΔR between the track momenta, defined at the perigee, and the jet axis. The ΔR requirement varies as a function of the jet p_T to account for decay products from b-hadrons with larger p_T being more collimated, ranging from 0.45 for jet p_T = 20 GeV to 0.26 for jet p_T > 150 GeV. If a track can be associated with multiple jets, it is assigned to the jet closest in ΔR. The sign convention for the lifetime-signed impact parameters assigns a positive sign if the track intersects the jet axis in the transverse plane in front of the IP, and a negative sign if the intersection lies behind the IP²⁰. The flavour labels of jets in simulation are assigned depending on the hadrons associated with the jet. The set of weakly decaying hadrons and hadronically decaying τ-leptons with p_T > 5 GeV within a ΔR < 0.3 cone around the jet axis determines the jet flavour following a sequential labelling decision tree. A jet is labelled a b-jet if it contains at least one b-hadron with p_T > 5 GeV, a c-jet (τ-jet) if it contains at least one c-hadron (hadronic τ-lepton decay) and no b-hadron, and otherwise it is called a light-jet, where the latter is an inclusive label for the jets originating from a light quark or gluon. These labels are used both for training the algorithms, and for evaluating their performance.

Targets for the auxiliary training objectives are obtained from the simulation-level event record. Tracks are matched with simulation-level particles using the approach in ref. ³⁹. Track-origin labels are obtained by analysing the decay history of the matched particles, while track-pair-compatibility labels are obtained by considering the production vertices of the matched particles. Production vertices within 0.1 mm in 3D space are merged to account for the finite resolution of the detector, and the matched track-pairs are assigned the same label.

The algorithm architecture

The primary flavour tagging algorithm presented is GN2, which directly learns from the charged particle tracks via a transformer-based model. Another algorithm, DL1d, which follows previous approaches of combining inputs from several low-level taggers in a multivariate technique, is also discussed as a baseline reference.

Both algorithms are trained on a dataset created from combining the simulated $t\overline{t}$ and ${Z}^{{\prime} }$ samples described earlier in this section. Jets with 20 GeV < p_T < 250 GeV are taken from the $t\overline{t}$ sample and those with 250 GeV < p_T < 6 TeV from the ${Z}^{{\prime} }$ sample. The b-jets, light-jets and τ-jets are re-sampled in p_T and η to match the corresponding c-jet distributions, thereby preventing the models from discriminating between jet flavours based on relative kinematic differences. All input variables to the algorithm training are normalised to have zero mean and unit variance. A coarse optimisation of hyperparameters, such as the number of layers, is carried out for both algorithms, and the AdamW⁸⁰ (Adam⁸¹) optimiser is used for training GN2 (DL1d) with the learning rate and optimisation schedule defined below.

The GN2 algorithm is an end-to-end architecture without any intermediate taggers involved, as illustrated in Fig. 1. It is based on the GN1²⁹ demonstrator version of the algorithm, replacing the Graph Attention Network⁸² with a Transformer³⁰ along with other architecture optimisations. GN2 directly accepts information about the jet and associated tracks that are provided by the standard event reconstruction. This results in a simpler and more flexible algorithm which can be easily reoptimised for different physics objectives, such as the identification of highly energetic Higgs bosons decaying into b- or c-quark pairs⁸³, jet energy regression⁸⁴, exotic jet tagging⁸⁵, and jet flavour tagging in the ATLAS high-level trigger⁸⁶. Additionally, when compared with DL1d, GN2 is trained to recognise an additional class of jets that originate from hadronic τ-lepton decays.

First, the jet features are concatenated with a fixed-size array of 40 track feature vectors, with unused elements masked when fewer than 40 tracks are available, allowing it to handle variable track multiplicity without zero-padding. Tracks with smaller absolute track impact parameter significance⁵ are dropped if there are more than 40 tracks. The same inputs as for GN1²⁹ are used, except the variables related to holes in the silicon tracker, which were found to have no impact on performance. A complementary interpretability analysis using integrated gradients shows that the impact parameter significances and angular variables emerge as particularly influential⁸⁷. The combined vectors are then fed into a per-track initialisation network, which is composed of a single hidden layer and an output layer of size 256. Next, a four layer transformer encoder with eight attention heads is used to produce track representations that incorporate information from other tracks inside the jet. The transformer has an embedding size of 256 and a feed-forward dimension of 512, and uses pre-LayerNorm⁸⁸. After the transformer encoder, the output track representations are projected down to dimension 128, and a global representation of the jet is produced using attention pooling⁸⁹. The pooled jet representation and output track embeddings are provided as inputs to the three task-specific networks. The primary objective, jet classification, uses only the pooled jet representation and has an output layer of size 4, providing p_b, p_c, p_u and p_τ for the final discriminant definition. The two auxiliary objectives introduced in the Discussion section take advantage of the track embeddings, in addition to the global jet representation. The track origin classification task uses individual track embeddings and has 7 output categories, while the track-pair compatibility task employs a binary output layer, using the embeddings of each pair of tracks. Each task-specific network consists of three hidden layers with size 128, 64 and 32, respectively. ReLU activation⁹⁰ is used throughout the model. Cross-entropy loss is used by all three task-specific networks, which is combined with tunable weights to form the final loss function, enabling a simultaneous optimisation of the entire algorithm. GN2 applies the same auxiliary network structures and loss weights as GN1²⁹.

GN2 is trained using a 4-fold strategy to prevent memorisation of the training samples, given their possible use in ATLAS physics analyses. Jets are assigned to one of the four folds pseudo-randomly, with a number seeded by the event number and discrete jet properties. Four classifiers are then trained, each excluding one of the four folds from the training dataset. In physics analysis, each jet is tagged using the classifier it was excluded from during training. Each of the four networks has approximately 2.3M trainable parameters and is trained using approximately 45M (18M) b-jets, 45M (18M) c-jets, 90M (36M) light-jets and 6.25M (2.5M) τ-jets from the $t\overline{t}$ (${Z}^{{\prime} }$) sample, simulated at both $\sqrt{s}=13\,{{\rm{TeV}}}$ and $\sqrt{s}=13.6\,{{\rm{TeV}}}$, with a mixing ratio of 2:1. A learning rate scheduler with cosine annealing⁹¹ is used with the initial learning rate set to 1 × 10⁻⁷, which is increased to 5 × 10⁻⁴ after the first 1% of training steps have been completed. It reduces to 1 × 10⁻⁵ over the remainder of the training run. A weight decay of 1 × 10⁻⁵ is also added. A batch size of 12,000 is adopted. The different folds have compatible performance within statistical uncertainty. The training data is translated from a standard ATLAS format⁵⁶ to HDF5⁹². The network is trained with PYTORCH LIGHTNING^93,94,95, consuming roughly 300 GPU hours on an NVIDIA A100 card. It is deployed in ATLAS software with ONNXRUNTIME⁹⁶, adding negligible CPU time. With the updated architecture and training setup, the c-jet (light-jet) rejection is improved by a factor of 1.5 (1.7) for a 70% b-jet tagging efficiency, in the $t\overline{t}$ sample, and by a factor of 1.3 (1.4) for the corresponding 30% b-jet tagging efficiency, in the ${Z}^{{\prime} }$ sample.

The DL1d algorithm inherits the architecture from its predecessor DL1r, described in Ref. ⁵, but processes track impact parameters with the DIPS algorithm based on DeepSets^21,22 instead of a recurrent neural network⁹⁷. Overall, 44 input features are fed into DL1d, including the jet p_T and η. The architecture of DL1d includes eight hidden layers of size 256, 128, 60, 48, 36, 24, 12, and 6, each followed with ReLU activation and batch normalisation. The training was performed with a learning rate of 1 × 10⁻³ and training batch size of 15,000. The training data pipeline is similar to GN2, with the exception that training is done with KERAS and TENSORFLOW⁹⁸ via UMAMI, a dedicated Python toolkit⁹⁹, and deployed in the ATLAS software with LWTNN¹⁰⁰.

Performance measurement strategies in collision data

The measurement of the b-jet tagging efficiency in collision data is carried out in a roughly 90% pure sample of $t\bar{t}$ events where both top quarks decay leptonically into a lepton, a neutrino and a b-quark. The events are required to contain exactly one electron and one muon of opposite charge, in addition to two jets. The invariant masses of the two lepton-jet pairs are used to define one region enriched in b-jets and three control regions (CRs). The b-jet-enriched region is determined by requiring that both lepton-jet pairs have invariant masses compatible with an on-shell top quark decay. The CRs are used in a likelihood fit to constrain the predicted jet flavour composition. They are constructed to have increased fractions of non-b-jets by requiring that at least one or both of the lepton-jet pairs do not originate from the same top-quark decay. The analysis employs a statistical model based on a likelihood function that extracts the efficiency in collision data binned in p_T for all the b-jets in the sample. The dominant systematic uncertainty comes from the modelling of $t\bar{t}$ events. Additional details on the b-jet calibration procedure are available in ref. ⁴.

The calibration measurement of the c-jet mis-tagging rate is performed in $t\bar{t}$ events where one top quark decays leptonically while the other top quark decays hadronically. A sample of c-jets is obtained through the ${W}^{\pm }\to c\bar{s}(\bar{c}s)$ decay from the hadronically decaying top quark. A likelihood-based kinematic reconstruction is employed to find, among the four jets in the event, two jets associated with the hadronically decaying W-boson and two jets stemming from the b-quarks produced in the top quark decays. The mis-tagging rate of c-jets is determined by minimising a χ² function computed in bins of the jet p_T of the two jets from the W-boson decay. Additional terms that correct for the potential mis-modelling of the total number of events in each jet p_T bin are estimated simultaneously from the fit to collision data, while the contribution of background events, in which no c-jets are associated with the W-boson decay, is estimated from simulations. The mis-tagging rate of light-jets in this sample is corrected using the method described below. As with the b-jets calibration analysis, the leading source of systematic uncertainties is the modelling of $t\bar{t}$ events. The c-jet mis-tagging rate calibration procedure is detailed in ref. ⁴¹.

The mis-tagging rate for light-jets is determined using jets produced in association with a Z boson, where the Z boson decays into muon or electron pairs. The key challenge in this calibration is to develop a method capable of extracting a light-jet mis-tagging rate in data despite the high rejection of the taggers. The method used in this work involves exploiting transformed track variables in alternate taggers that provide reduced b(c)-jet tagging efficiency and almost unchanged light-jet rejection. The mis-tagging rate of this modified tagger is measured from a fit to the flavour-sensitive secondary vertex mass distribution in collision data, and dedicated uncertainties are introduced so that it can be extrapolated to that of the nominal tagger. These extrapolation uncertainties are a leading source of systematic uncertainty. A detailed description of the procedure is provided in ref. ⁴².

Data availability

Raw data were generated by the ATLAS experiment. Derived data supporting the findings of this study are available from the ATLAS Collaboration upon request. A subset of the training sample and instructions to train GN2 can be acquired via the CERN Open Data Portal^32,33.

Code availability

The ATLAS data reduction software is available at Zenodo (https://doi.org/10.5281/zenodo.4772550)¹⁰². The GN2 training software suite can be found at JOSS (https://joss.theoj.org/papers/10.21105/joss.07217)⁹⁵, and the DL1d training software stack is available at JOSS (https://joss.theoj.org/papers/10.21105/joss.05833)⁹⁹.

References

Evans, L. & Bryant, P. LHC machine. J. Instrum. 3, S08001 (2008).
Article Google Scholar
ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider. J. Instrum. 3, S08003 (2008).
Google Scholar
ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider: a description of the detector configuration for Run 3. J. Instrum. 19, P05063 (2024).
Article Google Scholar
ATLAS Collaboration. ATLAS b-jet identification performance and efficiency measurement with $t\bar{t}$ events in pp collisions at $t\bar{t}$. Eur. Phys. J. C 79, 970 (2019).
Article ADS Google Scholar
ATLAS Collaboration. ATLAS flavour-tagging algorithms for the LHC Run 2 pp collision dataset. Eur. Phys. J. C 83, 681 (2023).
Article ADS Google Scholar
ATLAS collaboration. Observation of $H\to b\bar{b}$ decays and VH production with the ATLAS detector. Phys. Lett. B 786, 59 (2018).
Article ADS Google Scholar
ATLAS collaboration. Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector. Phys. Lett. B 784, 173 (2018).
Article ADS Google Scholar
ATLAS collaboration. Characterising the Higgs boson with ATLAS data from the LHC Run-2. Phys. Rep. 1116, 4 (2025).
Article Google Scholar
ATLAS collaboration. Climbing to the top of the ATLAS 13 TeV data. Phys. Rep. 1116, 127 (2025).
Article Google Scholar
ATLAS collaboration. Electroweak, QCD and flavour physics studies with ATLAS data from Run 2 of the LHC. Phys. Rep. 1116, 57 (2025).
Article Google Scholar
ATLAS collaboration. The quest to discover supersymmetry at the ATLAS experiment. Phys. Rep. 1116, 261 (2025).
Article Google Scholar
ATLAS collaboration. Exploration at the high-energy frontier: ATLAS Run 2 searches investigating the exotic jungle beyond the Standard Model. Phys. Rep. 1116, 301 (2025).
Article Google Scholar
HFLAV collaboration. Averages of b-hadron, c-hadron, and τ-lepton properties as of 2021. Phys. Rev. D 107, 052008 (2023).
Article ADS Google Scholar
BABAR collaboration. Measurement of the B⁰ and B⁺ meson lifetimes with fully reconstructed hadronic final states. Phys. Rev. Lett. 87, 201803 (2001).
Article Google Scholar
ATLAS collaboration. Precision measurement of the B⁰ meson lifetime using B⁰ → J/ψK^*0 decays with the ATLAS detector. Eur. Phys. J. C 85, 736 (2025).
Article ADS CAS Google Scholar
Belle-II collaboration. Precise measurement of the D⁰ and D⁺ lifetimes at Belle II. Phys. Rev. Lett. 127, 211801 (2021).
Article ADS Google Scholar
Belle-II Collaboration. Measurement of the Λc+ Lifetime. Phys. Rev. Lett. 130, 071802 (2023).
Article ADS Google Scholar
Particle Data Group collaboration. Review of particle physics PTEP 083C01 (2020).
Belle Collaboration. Measurement of the τ-lepton lifetime at Belle. Phys. Rev. Lett. 112, 031801 (2014).
Article ADS Google Scholar
ATLAS collaboration. Performance of b-jet identification in the ATLAS Experiment. J. Instrum. 11, P04008 (2016).
Article Google Scholar
ATLAS Collaboration. “Deep Sets based Neural Networks for Impact Parameter Flavour Tagging in ATLAS.” ATL-PHYS-PUB-2020-014 (2020).
Komiske, P. T., Metodiev, E. M. & Thaler, J. Energy flow networks: deep sets for particle jets. J. High Energy Phys. 1, 121 (2019).
Article ADS Google Scholar
Shlomi, J., Battaglia, P. & Vlimant, J.-R. Graph neural networks in particle physics. 7, https://doi.org/10.1088/2632-2153/abbf9a (2020).
CMS Collaboration. Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV. J. Instrum. 13, P05011 (2018).
Article Google Scholar
Bols, E., Kieseler, J., Verzetti, M., Stoye, M. & Stakia, A. Jet flavour classification using DeepJet. J. Instrum. 15, P12012 (2020).
Article CAS Google Scholar
Qu, H. & Gouskos, L. ParticleNet: jet tagging via particle clouds. Phys. Rev. D 101, 056019 (2020).
Article ADS CAS Google Scholar
CMS Collaboration. “A unified approach for jet tagging in Run 3 at $\sqrt{s}=13.6 \,\, {\mbox{TeV}}$ in CMS.” CMS DP 2024 066, (2024).
CMS Collaboration. “Performance of heavy-flavour jet identification in boosted topologies in proton-proton collisions at $\sqrt{s}=13 \,\, {\mbox{TeV}}$.” CMS-PAS-BTV-22-001 (2023).
ATLAS Collaboration. “Graph Neural Network Jet Flavour Tagging with the ATLAS Detector.” ATL-PHYS-PUB-2022-027 (2022).
Vaswani, A. et al. Attention Is All You Need. Preprint at https://doi.org/10.48550/arXiv.1706.03762 (2017).
ATLAS and CMS Collaborations, “Highlights of the HL-LHC physics projections by ATLAS and CMS.” ATL-PHYS-PUB-2025-018 CMS-HIG-25-002, 4 (2025).
ATLAS Collaboration, ATLAS t$\overline{t}$ simulation for ML-based jet flavour tagging (JetSet), CERN Open Data Portal (2025).
The JetSet Developers. “Transforming Jet Flavor.”
Langacker, P. The Physics of Heavy ${Z}^{{\prime} }$ Gauge Bosons. Rev. Mod. Phys. 81, 1199 (2009).
Article ADS CAS Google Scholar
ATLAS Collaboration. The ATLAS Simulation Infrastructure. Eur. Phys. J. C 70, 823 (2010).
Article ADS Google Scholar
Agostinelli, S. et al. GEANT4 – a simulation toolkit. Nucl. Instrum. Meth. A 506, 250 (2003).
Article ADS CAS Google Scholar
Allison, J. et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006).
Article ADS Google Scholar
Allison, J. et al. Recent developments in Geant4. Nucl. Instrum. Meth. A 835, 186 (2016).
Article ADS CAS Google Scholar
ATLAS collaboration. Performance of the ATLAS track reconstruction algorithms in dense environments in LHC Run 2. Eur. Phys. J. C 77, 673 (2017).
Article ADS Google Scholar
ATLAS Collaboration. Measurements of WH and ZH production with Higgs boson decays into bottom quarks and direct constraints on the charm Yukawa coupling in 13 TeV pp collisions with the ATLAS detector. J. High Energy Phys. 4, 75 (2025).
Article Google Scholar
ATLAS Collaboration. Measurement of the c-jet mistagging efficiency in $t\bar{t}$ events using pp collision data at $t\bar{t}$ collected with the ATLAS detector. Eur. Phys. J. C 82, 95 (2022).
Article ADS Google Scholar
ATLAS Collaboration. Calibration of the light-flavour jet mistagging efficiency of the b-tagging algorithms with Z+jets events using 139 fb⁻¹ of ATLAS proton–proton collision data at $\sqrt{s}=13 \,\, {\mbox{TeV}}$. Eur. Phys. J. C 83, 728 (2023).
Article ADS Google Scholar
Soyez, G. Pileup mitigation at the LHC: a theorist’s view. Phys. Rep. 803, 1 (2019).
Article ADS MathSciNet CAS Google Scholar
Kozen, D.C. Union-find. in The Design and Analysis of Algorithms 48–51. https://doi.org/10.1007/978-1-4612-4400-4_10 (Springer New York, 1992).
Billoir, P. & Qian, S. Fast vertex fitting with a local parametrization of tracks. Nucl. Instrum. Meth. A 311, 139 (1992).
Article ADS Google Scholar
Buckley, A. et al. General-purpose event generators for LHC physics. Phys. Rep. 504, 145 (2011).
Article ADS CAS Google Scholar
Frixione, S., Ridolfi, G. & Nason, P. A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction. J. High Energy Phys. 9, 126 (2007).
Article ADS Google Scholar
Nason, P. A new method for combining NLO QCD with shower Monte Carlo algorithms. J. High Energy Phys. 11, 40 (2004).
Article ADS Google Scholar
Frixione, S., Nason, P. & Oleari, C. Matching NLO QCD computations with parton shower simulations: the POWHEG method. J. High Energy Phys. 11, 70 (2007).
Article ADS Google Scholar
Alioli, S., Nason, P., Oleari, C. & Re, E. A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. J. High Energy Phys. 6, 43 (2010).
Article ADS Google Scholar
Sjöstrand, T. et al. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159 (2015).
Article ADS Google Scholar
Bähr, M. et al. Herwig++ physics and manual. Eur. Phys. J. C 58, 639 (2008).
Article ADS Google Scholar
Bellm, J. et al. Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76, 196 (2016).
Article ADS Google Scholar
Bellm, J. et al. Herwig 7.2 release note. Eur. Phys. J. C 80, 452 (2020).
Article ADS CAS Google Scholar
Bothmann, E. et al. Event generation with Sherpa 2.2. SciPost Phys. 7, 034 (2019).
Article ADS CAS Google Scholar
ATLAS Collaboration. Software and computing for Run 3 of the ATLAS experiment at the LHC. Eur. Phys. J. C 85, 234 (2025).
Article ADS CAS Google Scholar
NNPDF Collaboration. Parton distributions for the LHC run II. J. High Energy Phys. 4, 040 (2015).
Google Scholar
ATLAS Collaboration. “ATLAS Pythia 8 tunes to 7TeV data.” ATL-PHYS-PUB-2014-021 (2014).
NNPDF Collaboration. Parton distributions with LHC data. Nucl. Phys. B 867, 244 (2013).
Article ADS Google Scholar
Lange, D. J. The EvtGen particle decay simulation package. Nucl. Instrum. Meth. A 462, 152 (2001).
Article ADS CAS Google Scholar
Gleisberg, T. & Höche, S. Comix, a new matrix element generator. J. High Energy Phys. 12, 039 (2008).
Article ADS Google Scholar
Buccioni, F. et al. OpenLoops 2. Eur. Phys. J. C 79, 866 (2019).
Article ADS Google Scholar
Cascioli, F., Maierhöfer, P. & Pozzorini, S. Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012).
Article ADS CAS PubMed Google Scholar
Denner, A., Dittmaier, S. & Hofer, L. COLLIER: A FORTRAN-based complex one-loop library in extended regularizations. Comput. Phys. Commun. 212, 220 (2017).
Article ADS CAS Google Scholar
Gleisberg, T. et al. Event generation with SHERPA 1.1. J. High Energy Phys. 2, 7 (2009).
Article ADS Google Scholar
Schumann, S. & Krauss, F. A parton shower algorithm based on Catani–Seymour dipole factorisation. J. High Energy Phys. 3, 38 (2008).
Article ADS Google Scholar
Höche, S., Krauss, F., Schönherr, M. & Siegert, F. A critical appraisal of NLO+PS matching methods. J. High Energy Phys. 9, 49 (2012).
Article ADS Google Scholar
Höche, S., Krauss, F., Schönherr, M. & Siegert, F. QCD matrix elements + parton showers. The NLO case. J. High Energy Phys. 4, 27 (2013).
Article ADS Google Scholar
Catani, S., Krauss, F., Webber, B. R. & Kuhn, R. QCD Matrix Elements + Parton Showers. J. High Energy Phys. 11, 63 (2001).
Article ADS Google Scholar
Höche, S., Krauss, F., Schumann, S. & Siegert, F. QCD matrix elements and truncated showers. J. High Energy Phys. 5, 53 (2009).
Article ADS Google Scholar
ATLAS Collaboration. Software performance of the ATLAS track reconstruction for LHC Run 3. Comput. Softw. Big Sci. 8, 9 (2024).
Article ADS Google Scholar
ATLAS Collaboration. “Performance of ATLAS Pixel Detector and Track Reconstruction at the start of Run 3 in LHC Collisions at $\sqrt{s}=900 \,\, {\mbox{GeV}}$.” ATL-PHYS-PUB-2022-033 (2022).
ATLAS Collaboration. Reconstruction of primary vertices at the ATLAS experiment in Run 1 proton–proton collisions at the LHC. Eur. Phys. J. C 77, 332 (2017).
Article ADS Google Scholar
ATLAS Collaboration. “Vertex Reconstruction Performance of the ATLAS Detector at $\sqrt{s}=13 \,\, {\mbox{TeV}}$.” ATL-PHYS-PUB-2015-026 (2015).
Cacciari, M., Salam, G. P. & Soyez, G. The anti-k_t jet clustering algorithm. J. High Energy Phys. 04, 063 (2008).
Article ADS Google Scholar
Cacciari, M., Salam, G. P. & Soyez, G. FastJet user manual. Eur. Phys. J. C 72, 1896 (2012).
Article ADS CAS Google Scholar
ATLAS Collaboration. Jet reconstruction and performance using particle flow with the ATLAS Detector. Eur. Phys. J. C 77, 466 (2017).
Article ADS Google Scholar
ATLAS Collaboration. Jet energy scale and resolution measured in proton–proton collisions at $\sqrt{s}=13 \,\, {\mbox{TeV}}$ with the ATLAS detector. Eur. Phys. J. C 81, 689 (2021).
Article ADS Google Scholar
ATLAS Collaboration. “Tagging and suppression of pileup jets with the ATLAS detector.” ATLAS-CONF-2014-018 (2014).
Loshchilov, I. & Hutter, F. Fixing weight decay regularization in Adam. Proc. Int. Conf. Learn. Represent. (ICLR 2018).
Kingma, D.P. & Ba, J. Adam: A method for stochastic optimization. Preprint at https://doi.org/10.48550/arXiv.1412.6980 (2017).
Brody, S., Alon, U. & Yahav, E. How attentive are graph attention networks? Preprint at https://doi.org/10.48550/arXiv.2105.14491 (2021).
ATLAS Collaboration. “Transformer Neural Networks for Identifying Boosted Higgs Bosons decaying into $b\bar{b}$ and $c\bar{c}$ in ATLAS.” ATL-PHYS-PUB-2023-021 (2023).
ATLAS Collaboration. “Transformer networks for constituent-based b-jet calibration with the ATLAS detector.” ATL-PHYS-PUB-2025-012 (2024).
ATLAS Collaboration. Search for emerging jets in pp collisions at $\sqrt{s}=13.6$ TeV with the ATLAS experiment. Rep. Prog. Phys. 88, 097801 (2025).
Article ADS Google Scholar
ATLAS Collaboration. Configuration, performance, and commissioning of the ATLAS b-jet triggers for the 2022 and 2023 LHC data-taking periods. J. Instrum. 20, P03002 (2025).
Article Google Scholar
ATLAS Collaboration. “Explaining the ATLAS GN2 flavour tagging algorithm with integrated gradients.” ATL-PHYS-PUB-2025-029 (2025).
Xiong, R. et al. On layer normalization in the transformer architecture. Preprint at https://doi.org/10.48550/arXiv.2002.04745 (2020).
Li, Y., Tarlow, D., Brockschmidt, M. & Zemel, R. Gated graph sequence neural networks. Preprint at https://doi.org/10.48550/arXiv.1511.05493 (2015).
Fukushima, K. Cognitron: a self-organizing multilayered neural network. Biol. Cybern. 20, 121 (1975).
Article CAS PubMed Google Scholar
Loshchilov, I. & Hutter, F. SGDR: stochastic gradient descent with warm restarts. Preprint at https://doi.org/10.48550/arXiv.1608.03983 (2016).
The HDF Group. “Hierarchical Data Format, version 5”. https://github.com/HDFGroup/hdf5
Ansel, J. et al. Pytorch 2: faster machine learning through dynamic Python bytecode transformation and graph compilation. In Proc. 29th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Volume 2 (ASPLOS ’24) https://doi.org/10.1145/3620665.3640366 (ACM, 2024).
William, F. et al. PyTorch Lightning. https://doi.org/10.5281/zenodo.3828935 (2019).
Barr, J. et al. Salt: multimodal multitask machine learning for high energy physics. J. Open Source Softw. 10, 7217 (2025).
Article ADS Google Scholar
ONNX Runtime developers. “Onnx runtime.” https://onnxruntime.ai/ (2021).
ATLAS Collaboration. “Identification of Jets Containing b-Hadrons with Recurrent Neural Networks at the ATLAS Experiment.” ATL-PHYS-PUB-2017-003 (2017).
TensorFlow Developers. Tensorflow. https://doi.org/10.5281/zenodo.4724125 (2022).
Barr, J. et al. Umami: a Python toolkit for jet flavour tagging. J. Open Source Softw. 9, 5833 (2024).
Article ADS Google Scholar
Guest, D.H. et al. lwtnn/lwtnn: v2.14.1. https://doi.org/10.5281/zenodo.14276439 (2024).
ATLAS Collaboration. “ATLAS Computing Acknowledgments.” ATL-SOFT-PUB-2025-001 (2025).
ATLAS Collaboration. Athena. https://doi.org/10.5281/zenodo.4772550 (2021).

Download references

Acknowledgements

The authors thank CERN for the very successful operation of the LHC and its injectors, as well as the support staff at CERN and at their institutions worldwide without whom ATLAS could not be operated efficiently. The crucial computing support from all WLCG partners is acknowledged gratefully, in particular from CERN, the ATLAS Tier-1 facilities at TRIUMF/SFU (Canada), NDGF (Denmark, Norway, Sweden), CC-IN2P3 (France), KIT/GridKA (Germany), INFN-CNAF (Italy), NL-T1 (Netherlands), PIC (Spain), RAL (UK) and BNL (USA), the Tier-2 facilities worldwide and large non-WLCG resource providers. Major contributors of computing resources are listed in ref. ¹⁰¹. The authors gratefully acknowledge the support of ANPCyT, Argentina; YerPhI, Armenia; ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbaijan; CNPq and FAPESP, Brazil; NSERC, NRC and CFI, Canada; CERN; ANID, Chile; CAS, MOST and NSFC, China; Minciencias, Colombia; MEYS CR, Czech Republic; DNRF and DNSRC, Denmark; IN2P3-CNRS and CEA-DRF/IRFU, France; SRNSFG, Georgia; BMFTR, HGF and MPG, Germany; GSRI, Greece; RGC and Hong Kong SAR, China; ICHEP and Academy of Sciences and Humanities, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Morocco; NWO, Netherlands; RCN, Norway; MNiSW, Poland; FCT, Portugal; MNE/IFA, Romania; MSTDI, Serbia; MSSR, Slovakia; ARIS and MVZI, Slovenia; DSI/NRF, South Africa; MICIU/AEI, Spain; SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons of Bern and Geneva, Switzerland; NSTC, Taipei; TENMAK, Türkiye; STFC/UKRI, United Kingdom; DOE and NSF, United States of America. Individual groups and members have received support from BCKDF, CANARIE, CRC and DRAC, Canada; CERN-CZ, FORTE and PRIMUS, Czech Republic; COST, ERC, ERDF, Horizon 2020, ICSC-NextGenerationEU and Marie Skłodowska-Curie Actions, European Union; Investissements d’Avenir Labex, Investissements d’Avenir Idex and ANR, France; DFG and AvH Foundation, Germany; Herakleitos, Thales and Aristeia programmes co-financed by EU-ESF and the Greek NSRF, Greece; BSF-NSF and MINERVA, Israel; NCN and NAWA, Poland; La Caixa Banking Foundation, CERCA Programme Generalitat de Catalunya and PROMETEO and GenT Programmes Generalitat Valenciana, Spain; Göran Gustafssons Stiftelse, Sweden; The Royal Society and Leverhulme Trust, United Kingdom. In addition, individual members wish to acknowledge support from Armenia: Yerevan Physics Institute (FAPERJ); CERN: European Organization for Nuclear Research (CERN DOCT); Chile: Agencia Nacional de Investigación y Desarrollo (FONDECYT 1230812, FONDECYT 1240864); China: Chinese Ministry of Science and Technology (MOST-2023YFA1605700, MOST-2023YFA1609300), National Natural Science Foundation of China (NSFC - 12175119, NSFC 12275265); Czech Republic: Czech Science Foundation (GACR - 24-11373S), Ministry of Education Youth and Sports (ERC-CZ-LL2327, FORTE CZ.02.01.01/00/22_008/0004632), PRIMUS Research Programme (PRIMUS/21/SCI/017); EU: H2020 European Research Council (ERC - 101002463); European Union: European Research Council (BARD No. 101116429, ERC - 948254, ERC 101089007), European Regional Development Fund (SMASH COFUND 101081355, SLO ERDF), Horizon 2020 Framework Programme (MUCCA - CHIST-ERA-19-XAI-00), European Union, Future Artificial Intelligence Research (FAIR-NextGenerationEU PE00000013), Italian Center for High Performance Computing, Big Data and Quantum Computing (ICSC, NextGenerationEU); France: Agence Nationale de la Recherche (ANR-21-CE31-0022, ANR-22-EDIR-0002); Germany: Baden-Württemberg Stiftung (BW Stiftung-Postdoc Eliteprogramme), Deutsche Forschungsgemeinschaft (DFG - 469666862, DFG - CR 312/5-2); China: Research Grants Council (GRF); Italy: Istituto Nazionale di Fisica Nucleare (ICSC, NextGenerationEU), Ministero dell’Università e della Ricerca (NextGenEU 153D23001490006 M4C2.1.1, NextGenEU I53D23000820006 M4C2.1.1, NextGenEU I53D23001490006 M4C2.1.1, SOE2024_0000023); Japan: Japan Society for the Promotion of Science (JSPS KAKENHI JP22H01227, JSPS KAKENHI JP22H04944, JSPS KAKENHI JP22KK0227, JSPS KAKENHI JP23KK0245, JSPS KAKENHI JP24K23939); Norway: Research Council of Norway (RCN-314472); Poland: Ministry of Science and Higher Education (IDUB AGH, POB8, D4 no 9722), Polish National Science Centre (NCN 2021/42/E/ST2/00350, NCN OPUS 2023/51/B/ST2/02507, NCN OPUS nr 2022/47/B/ST2/03059, NCN UMO-2019/34/E/ST2/00393, UMO-2022/47/O/ST2/00148, UMO-2023/49/B/ST2/04085, UMO-2023/51/B/ST2/00920, UMO-2024/53/N/ST2/00869); Portugal: Foundation for Science and Technology (FCT); Spain: Ministry of Science and Innovation (MCIN & NextGenEU PCI2022-135018-2, MICIN & FEDER PID2021-125273NB, RYC2019-028510-I, RYC2020-030254-I, RYC2021-031273-I, RYC2022-038164-I); Sweden: Carl Trygger Foundation (Carl Trygger Foundation CTS 22:2312), Swedish Research Council (Swedish Research Council 2023-04654, VR 2021-03651, VR 2022-03845, VR 2022-04683, VR 2023-03403, VR 2024-05451), Knut and Alice Wallenberg Foundation (KAW 2018.0458, KAW 2022.0358, KAW 2023.0366); Switzerland: Swiss National Science Foundation (SNSF - PCEFP2_194658); United Kingdom: Leverhulme Trust (Leverhulme Trust RPG-2020-004), Royal Society (NIF-R1-231091); United States of America: U.S. Department of Energy (ECA DE-AC02-76SF00515), Neubauer Family Foundation.

Author information

B. S. Acharya
Present address: Department of Physics, King’s College London, London, UK
F. Ahmadov
Present address: Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
H. M. J. Ali
Present address: Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia
K. Bachas
Present address: Department of Physics, University of Thessaly, Volos, Greece
A. Bassalat
Present address: An-Najah National University, Nablus, Palestine
H. P. Beck
Present address: Department of Physics, University of Fribourg, Fribourg, Switzerland
B. T. Carlson
Present address: Department of Physics, Westmont College, Santa Barbara, CA, USA
M. P. Casado
Present address: Departament de Fisica de la Universitat Autonoma de Barcelona, Barcelona, Spain
A. Cerri
Present address: University of Siena, Siena, Italy
G. A. Chelkov, O. L. Fedin, A. G. Myagkov, V. Nikolaenko & L. N. Smirnova
Present address: Affiliated with an institute formerly covered by a cooperation agreement with CERN, Geneva, Switzerland
X. Chen
Present address: The Collaborative Innovation Center of Quantum Matter (CICQM), Beijing, China
M. V. Chizhov
Present address: Faculty of Physics, Sofia University ‘St. Kliment Ohridski’, Sofia, Bulgaria
F. Conventi
Present address: Università di Napoli Parthenope, Naples, Italy
F. Corriveau, R. A. McPherson, R. Sobie & R. J. Teuscher
Present address: Institute of Particle Physics (IPP), Ottawa, ON, Canada
H. Denizli
Present address: Department of Physics, Bolu Abant Izzet Baysal University, Bolu, Türkiye
M. S. Filip
Present address: Faculty of Physics, University of Bucharest, Bucharest, Romania
M. C. N. Fiolhais
Present address: Borough of Manhattan Community College, City University of New York, New York, NY, USA
M. Flores
Present address: National Institute of Physics, University of the Philippines Diliman (Philippines), Quezon City, Philippines
L. Fountas & I. Gkialas
Present address: Department of Financial and Management Engineering, University of the Aegean, Chios, Greece
D. M. Gingrich, P. Savard & M. C. Vetterli
Present address: TRIUMF, Vancouver, BC, Canada
S. Grinstein, A. Juste Rozas & M. Martinez
Present address: Institucio Catalana de Recerca i Estudis Avancats, ICREA, Barcelona, Spain
L. Guo
Present address: Henan University, Kaifeng, China
S. Istin
Present address: Physics Department, Yeditepe University, Istanbul, Türkiye
J. Jejelava
Present address: Institute of Theoretical Physics, Ilia State University, Tbilisi, Georgia
P. Jenni
Present address: CERN, Geneva, Switzerland
K. Kordas, C. Lampoudis, C. Petridou, D. Sampsonidis & S. Tzamarias
Present address: Center for Interdisciplinary Research and Innovation (CIRI-AUTH), Thessaloniki, Greece
A. Leisos & A. Tsirigotis
Present address: Hellenic Open University, Patras, Greece
Z. Liu
Present address: Department of Modern Physics and State Key Laboratory of Particle Detection and Electronics, University of Science and Technology of China, Hefei, China
P. T. Mafa
Present address: Department of Mathematical Sciences, University of South Africa, Johannesburg, South Africa
F. Malek
Present address: Department of Physics, Stellenbosch University, Stellenbosch, South Africa
J. L. Nagle & D. V. Perepelitsa
Present address: Department of Physics, University of Colorado Boulder, Boulder, CO, USA
M. Nessi
Present address: Département de Physique Nucléaire et Corpusculaire, Université de Genève, Geneva, Switzerland
S. Oerdek & K. Tackmann
Present address: Institut für Experimentalphysik, Universität Hamburg, Hamburg, Germany
A. Onofre
Present address: Centre of Physics of the Universities of Minho and Porto (CF-UM-UP), Porto, Portugal
M. Shiyakova
Present address: Institute for Nuclear Research and Nuclear Energy (INRNE) of the Bulgarian Academy of Sciences, Sofia, Bulgaria
S. Shrestha
Present address: Washington College, Chestertown, MD, USA
Y. Tayalati
Present address: Institute of Applied Physics, Mohammed VI Polytechnic University, Ben Guerir, Morocco
L. Tompkins
Present address: Department of Physics, Stanford University, Stanford, CA, USA
T. Turtuvshin
Present address: Institute of Physics and Technology, Mongolian Academy of Sciences, Ulaanbaatar, Mongolia
Deceased: J. Khubua.
Deceased: U. Mallik.
Deceased: I. P. J. Shipsey.

Authors and Affiliations

CPPM, Aix-Marseille Université, CNRS/IN2P3, Marseille, France
G. Aad, M. Barbero, R. Bertrand, Y. Coadou, F. Djama, A. Duperrin, L. Feligioni, M. J. V. Fernoux, M. Fujimoto, G. D. Hallewell, C. Mavungu Tsava, E. Monnier, S. Muanza, E. Nagy, E. Petit, A. Rozanov, L. Splendori, T. Strebler, M. Talby, T. Theveneaux-Pelzer & G. Tolkachev
Department for Physics and Technology, University of Bergen, Bergen, Norway
E. Aakvaag, T. Buanes, G. Eigen, A. S. Grefsrud, S. Hassan, S. Hellesund, T. S. Hillersoy, S. K. Huiberts, D. Larsen, A. Lipniacka, B. Martin dit Latour, I. Slazyk & B. Stugu
Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK, USA
B. Abbott, V. Balakrishnan, A. A. Gerwin, P. Gutierrez, M. P. Kawale, M. Marjanovic, J. D. Nichols, E. Pompa Pacchi, B. T. Saifuddin, H. Severini, B. Shrestha, P. Skubic, M. Strauss, J. Stupak, L. Vozdecky & C. H. Waits
New York University Abu Dhabi, Abu Dhabi, United Arab Emirates
S. Abdelhameed, M. Elsawy, M. Losada & B. Ngair
II. Physikalisches Institut, Georg-August-Universität Göttingen, Göttingen, Germany
K. Abeling, W. Alkakhi, M. Bindi, M. P. Drescher, S. Eggebrecht, A. Gaa, J. Grosse-Knetter, H. L. Joos, M. K. Kingston, A. Kirchhoff, K. Köneke, S. Korn, S. Lai, A. H. Melo, M. Niemeyer, A. Quadt, P. Rincke, E. Shabalina, S. Sindhu, A. Skaf & S. Wozniewski
Fakultät Physik, Technische Universität Dortmund, Dortmund, Germany
N. J. Abicht, M. Baselga, T. Bisanz, C. D. Burgard, L. Cremer, C. M. Delitzsch, S. Dungs, B. Gocke, A. Gupta, A. Knue, K. Kroeninger, T. Kupfer, D. M. Mattern, A. Rej, S. Ruscelli, A. Van Der Graaf, J. Weingarten & B. Wendland
Physics Department, Brookhaven National Laboratory, Upton, NY, USA
S. H. Abidi, K. Assamagan, M. Begel, D. Boye, E. Brost, V. Cavaliere, H. Chen, G. D’amen, S. J. Das, J. Elmsheuser, Y. Go, G. Iakovidis, A. Klimentov, E. Lançon, A. Li, D. Lynn, H. Ma, T. Maeno, J. L. Nagle, P. Nilsson, D. Oliveira Damazio, D. V. Perepelitsa, M.-A. Pleier, S. Rajagopalan, A. Sciandra, P. Sharma, M. V. Silva Oliveira, S. Singh, S. Snyder, P. Steinberg, S. A. Stucci, A. Tishelman-Charny, A. Tricoli, E. N. Umaka, A. Undrus, I. Veliscek, C. Weber, T. Wenaus & S. Ye
Physics Department, Southern Methodist University, Dallas, TX, USA
M. Aboelela, S. Bataju, C. S. Billingsley, A. M. Deiana, M. H. Klein, K. J. C. Leney, T. Moskalets, A. C. Mullins, E. A. Narayanan, A. Ryzhov, A. C. Schaffer, R. Stroynowski & R. E. Thornberry
Faculté des sciences, Université Mohammed V, Rabat, Morocco
A. Aboulhorma, M. Ait Tamlihat, R. Cherkaoui El Moursli, F. Fassi, Z. Soumaimi & Y. Tayalati
Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
H. Abramowicz, C. Appelt, L. Barak, G. Bella, Y. Benhammou, B. Chen, E. Etzion, Y. Y. Frid, S. Galantzan, G. Ninio, A. Salvador Salas, A. Soffer, N. M. Tamir & D. Vannicola
Department of Physics, New York University, New York, NY, USA
Y. Abulaiti, Z. M. Bhatti, M. Drnevich, A. Haas, J. K. K. Liu, A. I. Mincer, P. Rieck & E. J. Weik
INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
B. S. Acharya, M. Cobal, M. Faraj, M. P. Giordani, G. Giugliarelli, C. Merlassino, S. Monzani, N. Nitika, G. Panizzo, M. Pinamonti, L. Pintucci, L. Primomo, B. Ricci & L. Toffolin
ICTP, Trieste, Italy
B. S. Acharya & M. Faraj
Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
A. Ackermann, M. J. Backes, L. M. Baltes, F. Bartels, M. Dunford, S. Franchino, T. Junkermann, T. Mkrtchyan, D. F. Rassloff, L. Sanfilippo, H-C. Schultz-Coulon, V. Sothilingam, R. Stamen, S. M. Weber & M. Wessels
LAPP, Université Savoie Mont Blanc, CNRS/IN2P3, Annecy, France
C. Adam Bourdarios, O. Arnaez, R. Balasubramanian, N. Berger, L. Boudet, N. Brahimi, A. Carnelli, F. L. Castillo, T. Cavaliere, F. Costanza, J. Couthures, M. Delmastro, L. Di Ciaccio, M. Dubau, T. Hryn’ova, I. Koletsou, O. Kurdysh, J. Levêque, D. J. Lewis, N. Lorenzo Martinez, E. Sauvan & Z. Wu
Faculty of Physics and Applied Computer Science, AGH University of Krakow, Krakow, Poland
L. Adamczyk, P. Balek, T. Bold, K. M. Ciesla, W. Dabrowski, K. Domijan, M. Dyndal, A. K. Gilbert, I. Grabowska-Bold, S. Koperny, K. Maj, B. Mindur, P. Moszkowicz, P. A. Potepa, M. Przybycien & P. Rybczynski
SLAC National Accelerator Laboratory, Stanford, CA, USA
S. V. Addepalli, T. Barklow, R. Bartoldus, C. Bernius, P. Bhattarai, B. A. Bullard, S. Cheong, R. B. Garg, J. L. Gonski, P. Grenier, M. Kagan, M. Kocian, E. H. Miller, L. Pereira Sanchez, A. Salnikov, B. Schlag, A. Schwartzman, R. Smith, D. Su, L. Tompkins, M. D. Vassilev, C. Vernieri, C. Wagner, M. Wittgen, C. Young & Z. Zheng
School of Physics and Astronomy, University of Manchester, Manchester, UK
M. J. Addison, J. S. Allen, M. Aly, M. Amerl, V. A. Austrup, D. A. Baron Moreno, C. Da Via, C. Doglioni, P. Dougan, M. D’uffizi, T. Fitschen, A. C. Forti, T. G. Hitchings, B. P. Honan, P. Jawahar, H. Li, G. T. Marsden, J. Masik, A. E. May, A. M. Mendes Jacques Da Costa, F. J. Munoz Sanchez, A. Oh, J. R. Pater, R. F. Y. Peters, A. D. Pilkington, D. Price, D. Qichen, M. Queitsch-Maitland, S. M. Shaw, E. L. Simpson, S. Sinha, J. L. Smith, V. Vecchio, P. Wang, B. J. Wilson, D. J. Wilson & T. R. Wyatt
Department of Physics, Northern Illinois University, DeKalb, IL, USA
J. Adelman, H. De la Torre, W. H. Kostecka, A. C. Kraus, A. N. Lancaster, I. Maznas, G. Mercado, A. M. Rodríguez Vera, K. Sedlaczek, H. Shaddix & C. Varni
Department of Physics, Istanbul University, Istanbul, Türkiye
A. Adiguzel
Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
T. Adye, J. T. Baines, J. P. Biswal, W. Buttinger, J. Dopke, D. Emeliyanov, S. M. Farrington, B. J. Gallop, R. Z. Hasan, B. P. Kerridge, J. Kirk, T. A. Martin, S. Martin-Haugh, S. J. McMahon, R. P. Middleton, W. J. Murray, R. E. Owen, J. G. Panduro Vazquez, P. W. Phillips, D. P. C. Sankey, C. Sawyer, B. H. Smart, J. Walder & M. Wielers
Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA, USA
A. A. Affolder, M. Battaglia, V. Fadeyev, M. Gignac, A. A. Grillo, M. Hance, J. W. Johnson, N. J. Kang, D. Liu, S. M. Mazza, J. Nielsen, S. S. Roberts, H. F-W. Sadrozinski, B. A. Schumm, H. R. Schwartz, A. Seiden, G. H. Stark, A. Z. Wang & M. C. Wong
Enrico Fermi Institute, University of Chicago, Chicago, IL, USA
Y. Afik, A. Badea, K. F. Di Petrillo, K. M. Dona, R. W. Gardner, Y. K. Kim, M. N. Mantinan, D. W. Miller, J. T. Offermann, M. J. Oreglia, J. L. Rainbolt, B. J. Rosser, M. J. Shochet, C. Tosciri, E. M. Villhauer, I. Vukotic & P. J. Windischhofer
Institut de Física d’Altes Energies (IFAE), Barcelona Institute of Science and Technology, Barcelona, Spain
M. N. Agaras, A. Azzam, A. Berrocal Guardia, D. Bogavac, M. Bosman, J. I. Carlotto, M. P. Casado, L. Castillo Garcia, V. Gautam, S. Grinstein, J. Harrison, J. Jimenez Pena, A. Juste Rozas, N. Kakoty, I. Korolkov, A. Lopez Solis, J. Mamuzic, M. Martinez, P. Martinez Suarez, L. M. Mir, J. Montejo Berlingen, H. Moyano Gomez, G. Oliveira Correa, A. Pacheco Pages, C. Padilla Aranda, J. Pinol Bel, Y. Qin, I. Riu, A. Sonay, S. Terzo, P. M. Tricarico & T. Vazquez Schroeder
Institut für Physik, Universität Mainz, Mainz, Germany
A. Aggarwal, M. Akbiyik, A. Alvarez Fernandez, J. Balz, A. Basan, J. Blumenthal, V. Büscher, J. Damp, C. C. Delogu, D. Fakoudis, F. Fiedler, R. Gugel, M. E. Hesping, Y. Huang, C. Kahra, G. Lamprinoudis, J. C. MacDonald, L. Masetti, E. Meuser, H. Mildner, S. Rave, M. Robles Manzano, U. Schäfer, K. Schmieden, C. Schmitt, N. Schmitt, H. Smitmanns, A. Stein, D. Ta, S. Tapprogge, E. Tzovara, A. Vgenopoulos, O. Vujinovic & C. Wang
Department of Physics, Alexandru Ioan Cuza University of Iasi, Iasi, Romania
C. Agheorghiesei & P. Postolache
Affiliated with an international laboratory covered by a cooperation agreement with CERN, Geneva, Switzerland
F. Ahmadov, I. N. Aleksandrov, A. Amirkhanov, A. V. Anisenkov, V. A. Bednyakov, V. S. Bobrovnikov, I. R. Boyko, A. R. Buzykaev, G. A. Chelkov, A. Cheplakov, M. V. Chizhov, D. V. Dedovich, M. Demichev, A. R. Didenko, F. Dubinin, S. Filimonov, M. I. Gostkin, S. N. Karpov, Z. M. Karpova, U. Kruchonak, O. Kuchinskaia, V. Kukhtin, Y. Kulchitsky, E. Ladygin, V. Lyubushkin, T. Lyubushkina, S. Malyukov, A. L. Maslennikov, M. Mineev, E. Plotnikova, I. N. Potrap, E. Ramakoti, O. L. Rezanova, N. A. Rusakovich, M. Shiyakova, I. Shreyber, A. A. Snesarev, E. Yu. Soldatov, A. Soloshenko, Yu. A. Tikhonov, A. Tropina, P. V. Tsiareshka, T. Turtuvshin, A. Vasyukov, I. Yeletskikh, A. Zhemchugov & N. I. Zimine
Department of Physics, Royal Holloway University of London, Egham, UK
S. Ahuja, A. M. Aslam, T. Berry, V. Boisvert, E. Canonero, G. Cowan, T. A. Elliot, L. S. Evans, S. George, S. M. Gibson, E. J. Hampshire, R. Z. Hasan, D. Malito, F. Pastore, P. Teixeira-Dias, D. W. Thomas & S. Waterhouse
School of Physics, Zhengzhou University, Zhengzhou, China
X. Ai
INFN Sezione di Roma Tor Vergata, Rome, Italy
G. Aielli, P. Camarri, R. Cardarelli, L. Cerrito, U. De Sanctis, A. Di Ciaccio, F. Giuli, B. Liberti, A. Prades Ibanez, F. Raffaeli, A. Rocchi & M. Vanadia
Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
G. Aielli, P. Camarri, L. Cerrito, U. De Sanctis, A. Di Ciaccio, F. Giuli, A. Prades Ibanez, F. Raffaeli, A. Rocchi & M. Vanadia
Instituto de Física Corpuscular (IFIC), Centro Mixto Universidad de Valencia - CSIC, Valencia, Spain
A. Aikot, K. R. Amos, N. Bouchhar, S. Cabrera Urbán, J. Cantero, V. Castillo Gimenez, M. Chitishvili, M. J. Costa, F. Curcio, M. Didenko, C. Escobar, L. Fiorini, J. Fuster, C. García, J. E. García Navarro, A. J. Gomez Delegido, S. González de la Hoz, J. Hofer, M. Jimenez Ortega, C. Lacasta, M. Lanzac Berrocal, S. Marti-Garcia, P. Martinez Agullo, D. Melini, V. A. Mitsou, L. Monsonis Romero, M. Moreno Llácer, D. Munoz Perez, J. Navarro-Gonzalez, J. Poveda, A. Rubio Jimenez, A. Ruiz-Martinez, A. Saibel, J. Salt, J. Sánchez, V. Sanchez Sebastian, V. Senthilkumar, U. Soldevila, E. Torró Pastor, A. Valero, E. Valiente Moreno, J. A. Valls Ferrer, L. Varriale, M. Villaplana Perez, M. Vincent, M. Vos, K. Wandall-Christensen & T. Zakareishvili
Faculté des Sciences Ain Chock, Université Hassan II de Casablanca, Casablanca, Morocco
B. Aitbenchikh, D. Benchekroun, F. Bendebba, K. Bouaouda, A. El Moussaouy, S. Ezzarqtouni, H. Imam, Y. Khoulaki, F. Z. Lahbabi, M. Noury & I. Zahir
Fysiska institutionen, Lunds universitet, Lund, Sweden
T. P. A. Åkesson, K. S. V. Astrand, L. Calic, C. Doglioni, P. A. Ekman, V. Hedberg, H. Herde, B. Konya, E. Lytken, R. Poettgen, O. Smirnova, N. Sur & E. J. Wallin
Departments of Physics and Astronomy, Stony Brook University, Stony Brook, NY, USA
A. V. Akimov, E. Antipov, H. Arnold, C. P. Bee, S. Bhatta, V. Dao, A. Dimri, Y. Hernández Jiménez, J. Hobbs, J. Jia, S. F. Lin, M. M. Lyukova, G. Piacquadio, M. Rijssenbeek, R. D. Schamberger, M. Tanasini, F. Tsai & D. Tsybychev
Waseda University, Tokyo, Japan
D. Akiyama, H. Ito & K. Yorita
Physikalisches Institut, Universität Bonn, Bonn, Germany
N. N. Akolkar, A. Bandyopadhyay, S. Bansal, P. Bauer, P. Bechtle, F. Beisiegel, F. U. Bernlochner, I. Brock, K. Desch, J. Dingfelder, C. Grefe, S. Gurbuz, M. Hamer, Y. T. Harris, L. M. Herrmann, F. Hinterkeuser, M. Huebner, F. Huegging, E. Karentzos, C. Kirfel, F. Kirfel, O. Kivernyk, P. Kramer, H. Krüger, K. Lantzsch, T. Lenz, M. Mucha, C. Nass, J. Pampel, M. Schott, L. Vomberg, E. Von Toerne & N. Wermes
Department of Physics, Bogazici University, Istanbul, Türkiye
S. Aktas, H. Denizli, B. Gokturk, S. Istin & V. E. Ozcan
INFN Sezione di Bologna, Bologna, Italy
G. L. Alberghi, F. Alfonsi, E. Ballabene, L. Bellagamba, G. Bianco, E. Bisceglie, D. Boscherini, A. Bruni, G. Bruni, M. Bruschi, Y. Cai, G. Carratta, A. Cervelli, F. A. Corchia, D. Cremonini, S. De Castro, F. Fabbri, L. Fabbri, M. Franchini, A. Gabrielli, B. Giacobbe, F. Lasagni Manghi, B. Leban, G. Levrini, S. Nechaeva, M. Negrini, L. Pezzotti, A. Polini, L. Rinaldi, M. Romano, E. Sanzani, C. Sbarra, A. Sbrizzi, N. Semprini-Cesari, A. Sidoti, M. Sioli, S. Valentinetti, M. Villa, I. Vivarelli & A. Zoccoli
Department of Physics and Astronomy, University of Victoria, Victoria, BC, Canada
J. Albert, L. M. Brown, C. Camincher, E. M. Carlson, B. Chen, K. Hamano, R. Keeler, J. M. Kelly, R. Kowalewski, J. E. Lambert, M. Lefebvre, J. P. Mc Gowan, R. A. McPherson, J. Pretel, J. C. Rivera Vergara, H. L. Russell, M. J. Shroff & R. Sobie
Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
U. Alberti, H. P. Beck, D. Dal Santo, M. Glazewska, L. Halser, S. Mobius, L. G. Mollier, A. P. O’Neill, M. M. Schefer, F. G. Sciacca & M. S. Weber
INFN e Laboratori Nazionali di Frascati, Frascati, Italy
P. Albicocco, M. Antonelli, C. Arcangeletti, M. Beretta, G. Cesarini, V. Chiarella, Z. Chubinidze, G. Mancini, C. Paraskevopoulos, D. Pudzha, A. Sansoni, M. Testa, L. Vannoli & E. Vilucchi
LPSC, Université Grenoble Alpes, CNRS/IN2P3, Grenoble INP, Grenoble, France
G. L. Albouy, J. Collot, S. Crépé-Renaudin, J. B. De Vivie De Regie, P. A. Delsart, M. H. Genest, F. Ledroit-Guillon, F. Malek, C. E. Pandini, L. Selem & T. Wojtkowski
SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
S. Alderweireldt, J. F. Allen, P. J. Clark, J. R. Curran, D. Duda, S. M. Farrington, Y. Gao, J. M. Gargan, R. Y. González Andana, C. Jiang, C. Leonidopoulos, M. Firdaus M. Soberi, V. J. Martin, L. Mijović, E. A. Pender, T. Qiu, J. M. Silva, A. L. Sopio, F. Ustuner, H. Watson, B. M. Wynne & Z. Xu
Department of Physics, Oklahoma State University, Stillwater, OK, USA
Z. L. Alegria, V. S. Bhopatkar, J. E. Crosby, S. Goswami, J. Haley, A. Khanov, Y. Ma, S. Mohiuddin, F. Rizatdinova, J. R. Stewart, E. R. Vandewall & L. M. Vaughan
CERN, Geneva, Switzerland
M. Aleksa, C. Amelung, C. Antel, N. A. Asbah, G. Avolio, M-S. Barisits, J. F. Beirer, F. Bernon, P. Bokan, J. Boyd, V. M. M. Cairo, N. Calace, S. Camarda, T. Carli, M. Carnesale, A. Catinaccio, S. Cella, T. Dado, D. Dannheim, A. Dell’Acqua, A. Di Girolamo, G. Di Gregorio, F. Dittus, A. Dudarev, M. Dührssen, B. S. Dziedzic, H. El Jarrari, N. Ellis, M. Elsing, F. Ernst, L. Flores Sanz De Acedo, E. Fortin, D. Francis, V. Franco Lima, N. Fritzsche, D. Froidevaux, P. Gadow, P. Gessinger-Befurt, M. Goblirsch-Kolb, L. Goossens, B. Gorini, C. A. Gottardo, G. Guerrieri, S. Guindon, R. J. Hawkings, A. M. Henriques Correia, L. Hervas, A. Hoecker, M. Holzbock, M. Huhtinen, J. P. Iddon, H. L. Joos, J. J. Junggeburth, E. F. Kay, T. Klioutchnikova, A. Kotsokechagia, A. Koulouris, S. Kuehn, F. Lanni, M. Lassnig, G. Lehmann Miotto, J. H. Lindon, J. Lunde, M. S. Lutz, T. Manoussos, S. Manzoni, A. Marzin, E. Mazzeo, M. Mentink, A. Milic, M. Mlynarikova, S. Morgenstern, P. Moschovakos, R. Müller, A. M. Nairz, M. Nessi, J. Niermann, N. Nikiforou, M. L. Ojeda, T. Pauly, E. Perez Codina, H. Pernegger, B. A. Petersen, K. Petukhova, L. Pfaffenbichler, A. J. Pfleger, L. Pontecorvo, A. Poreba, M. E. Pozo Astigarraga, R. Pozzi, B. Ravina, M. Raymond, C. Rembser, S. Rettie, P. Riedler, M. Rimoldi, S. Rodriguez Bosca, S. Roe, J. T. Roemer, R. A. Rojas, A. Rummler, A. Salzburger, L. Santi, C. Sauer, S. Schlenker, C. D. Sebastiani, M. Shamim, A. Sharma, R. Simoniello, I. Siral, C. A. Solans Sanchez, A. Stefl, G. A. Stewart, M. C. Stockton, A. Swoboda, G. Tarna, G. Unal, T. Vafeiadis, M. Valente, M. Van Rijnbach, W. Vandelli, C. Vittori, B. Vormwald, M. Vozak, R. Vuillermet, T. Wengler, H. G. Wilkens, J. Wollrath, X. Yang, C. J. S. Young, A. Zografos & L. Zwalinski
Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest, Romania
C. Alexa, A. Chitan, D. A. Ciubotaru, I-M. Dinu, O. A. Ducu, A. E. Dumitriu, M. S. Filip, A. Jinaru, V. S. Martoiu, J. Maurer, D. Pietreanu, H. Rasheed, M. Renda, M. Rotaru, G. Stoicea, A. Tudorache, V. Tudorache & M. E. Vasile
Physics Department, National Technical University of Athens, Zografou, Greece
T. Alexopoulos, M. Arampatzi, I. Drivas-koulouris, E. N. Gazis, S. Maltezos & M. Perganti
Département de Physique Nucléaire et Corpusculaire, Université de Genève, Geneva, Switzerland
M. Algren, M. Alves Cardoso, K. Axiotis, L. Bezio, L. Bozianu, V. Cepaitis, A. Clark, D. Della Volpe, M. Drozdova, D. Ferrere, S. Franchellucci, A. Froch, T. Golling, S. Gonzalez-Sevilla, D. Harada, G. Iacobucci, S. B. Klein, P. Kontaxakis, M. Leigh, C. Moreno Martinez, I. Oleksiyuk, L. Paolozzi, A. Pirttikoski, G. Quetant, J. A. Raine, J. A. Sabater Iglesias, C. Scheulen, S. Schramm, T. Schroer, D. Sengupta, A. Sfyrla, O. Theiner, Y. Tian & S. Zambito
Department of Physics, University of Warwick, Coventry, UK
M. Alhroob, R. A. Ashby Pickering, K. Becker, S. Chakraborty, J. Davidson, M. Ghani, E. Guilloton, P. F. Harrison, A. Mitra, W. J. Murray, C. S. Pollard & K. Potamianos
Czech Technical University in Prague, Prague, Czech Republic
B. Ali, K. Augsten, B. Bergmann, P. Fiedler, Z. Hubacek, P. Jacka, V. Lysenko, S. Mondal, M. Myska, R. Novotny, V. Petousis, S. Pospisil, K. Smolek, P. Smolyanskiy, A. Sopczak, V. Vacek, P. Vokac & O. Zaplatilek
Physics Department, Lancaster University, Lancaster, UK
H. M. J. Ali, Z. M. K. Alsolami, A. E. Barton, G. Borissov, E. V. Bouhova-Thacker, B. Fernandez Barbadillo, J. Ferrando, H. Fox, A. I. Hagan, R. W. L. Jones, V. Kartvelishvili, P. A. Love, E. J. Marshall, L. F. Mcelhinney, L. Meng, E. Sampson, M. Smizanska & A. M. Wharton
California State University, Fresno, CA, USA
S. Ali, K. Grimm, J. Moss & J. Veatch
Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
S. W. Alibocus, J. K. Anders, S. Burdin, J. Carmignani, J. Degens, P. Dervan, B. Dixit, M. D’Onofrio, C. B. Gwilliam, H. S. Hayward, R. K. Irwin, T. J. Jones, U. Klein, J. Kretzschmar, C. M. Mcpartland, A. Mehta, J. Newell, N. Rompotis & M. J. Sullivan
Department of Mechanical Engineering Science, University of Johannesburg, Johannesburg, South Africa
M. Aliev, M. P. Connell, S. H. Connell, M. G. D. Gololo, N. Govender, L. L. Leeuw, P. T. Mafa, X. Mapekula & L. Truong
INFN Sezione di Milano, Milan, Italy
G. Alimonti, A. Andreazza, A. Carbone, L. Carminati, B. Cervato, M. Citterio, S. Coelli, S. D’Auria, L. Dell’Asta, M. Fanti, D. Giugni, T. Lari, M. Lazzaroni, C. Marcon, C. Meroni, L. Nasella, A. R. Petri, F. Ragusa, S. Resconi, A. Sala, G. F. Tartarelli, R. Turra & R. Zanzottera
IJCLab, Université Paris-Saclay, CNRS/IN2P3, Orsay, France
C. Allaire, A. Bassalat, L. Cadamuro, R. Chakkappai, L. Duflot, M. Escalier, L. Fayard, D. Fournier, J.-F. Grivaz, S. E. D. Hammoud, T. Hsu, Z. Huang, L. Iconomidou-Fayard, Z. Liu, A. Lounis, M. Lu, V. Maiboroda, N. Makovec, M. Markovitch, A. J. Maury, M. Mihovilovic, N. Morange, D. Rousseau, A. C. Schaffer, L. Serin, S. Simion, R. Tanaka, D. Varouchas, D. Zerwas & Z. Zhang
Department of Physics and Astronomy, University of Sussex, Brighton, UK
B. M. M. Allbrooke, M. A. Aparo, S. Biryukov, B. M. Cunnett, A. De Santo, Z. O. Earnshaw, D. M. Jones, J. J. Kempster, G. Löschcke Centeno, S. S. Mandarry, J. A. Mcfayden, K. M. Piper, F. Salvatore, K. Shaw, H. Simpson, T. J. Stevenson, M. R. Sutton & C. L. Yardley
School of Physics and Astronomy, University of Birmingham, Birmingham, UK
P. P. Allport, P. Bellos, J. Bracinik, D. G. Charlton, A. S. Chisholm, A. Dimitrievska, L. Gonella, F. Gonnella, C. M. Hawkes, S. J. Hillier, K. Krizka, E. H. L. Liu, J. D. Lomas, T. J. Neep, P. R. Newman, E. Skorda, J. P. Thomas, P. D. Thompson, A. T. Watson, M. F. Watson & C. Wu
INFN Sezione di Napoli, Naples, Italy
A. Aloisio, M. G. Alviggi, V. Canale, G. Carlino, P. Casolaro, F. Cirotto, F. Conventi, A. D’Avanzo, R. De Asmundis, M. Della Pietra, C. Di Donato, A. D’Onofrio, A. Doria, P. Iengo, V. Izzo, P. Massarotti, E. Rossi, G. Sekhniaidze, M. Sessa & B. Spisso
Dipartimento di Fisica, Università di Napoli, Naples, Italy
A. Aloisio, M. G. Alviggi, V. Canale, P. Casolaro, F. Cirotto, A. D’Avanzo, M. Della Pietra, C. Di Donato, A. D’Onofrio, P. Iengo, P. Massarotti, E. Rossi, M. Sessa & B. Spisso
Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
F. Alonso, J. Y. Beaucamp, M. T. Dova, F. Monticelli, F. Sili & H. Wahlberg
Department of Physics, University of Washington, Seattle, WA, USA
C. Alpigiani, Q. Buat, Y. Chou, A. Cordeiro Oudot Choi, A. Garabaglu, A. G. Goussiou, S.-C. Hsu, E. E. Khoda, C. Lewis, Q. Liu, H. J. Lubatti, T. Ovsiannikova, A. P. Pereira Peixoto, M. L. Proffitt, J. Schaarschmidt, G. Watts, Y. Xu, Y. Zhang & H. Zhao
Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
Y. Amaral Coutinho, L. E. Balabram Filho, L. P. Caloba, J. V. Da Fonseca Pinto, N. M. J. Nunes De Moura Junior, J. M. Seixas, I. Silva Ferreira & M. Verissimo De Araujo
Department of Physics, McGill University, Montreal, QC, Canada
A. Ambler, F. Corriveau, R. Hulsken, X. Li, C. Nelson, B. Vachon & A. Warburton
Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
C. G. Ames, O. Biebel, V. D’Amico, G. Duckeck, S. A. Gotz, N. M. Hartmann, R. Hertenberger, E. V. Kumar, L. Linden, A. M. Lory, A. Mann, S. Mehlhase, K. E. Penski, D. Schaile, N. A. Schneider, C. Stauch, C. Valderanis, F. Vogel & R. Walker
LPNHE, Sorbonne Université, Université Paris Cité, CNRS/IN2P3, Paris, France
T. Amezza, T. Beau, L. S. Boggia, G. Calderini, R. Camacho Toro, P. M. Chabrillat, F. Crescioli, L. Delagrange, F. Derue, Y. A. R. Khwaira, M. W. Krasny, D. Lacour, B. Laforge, B. Malaescu, I. Nikolic-Audit, J. Ocariz, L. Panwar, A. E. Pinto Pinoargote, L. Poggioli, M. Ridel, C. P. A. Roland, L. Roos & S. Trincaz-Duvoid
Department of Physics, University of Michigan, Ann Arbor, MI, USA
D. Amidei, T. M. Baer, T. Dai, E. B. Diehl, C. Ferretti, P. Fleischmann, L. Guan, J. A. M. Guhit, Y. Guo, C. Hayes, D. D. Hofer, N. G. Kyriacou, C. Li, H. Lin, S. P. Mc Kee, G. Myers, K. Nelson, J. Qian, T. A. Schwarz, M. Tsai, Z. Wang, T. Xu, M. Yuan, B. Zhou & J. Zhu
Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany
B. Amini, D. Bahner, N. K. Bhalla, K. D. Bhide, M. Boehler, O. Burlayenko, C. Heidegger, K. K. Heidegger, G. Herten, K. Jakobs, P. Jenni, I. Kalaitzidou, R. Kuesters, O. Kuprash, U. Landgraf, V. S. Lang, A. Markhoos, B. Moser, Ö. O. Öncel, U. Parzefall, L. Rossini, B. Rottler, Z. Rurikova, D. Sammel, M. Schumacher, K. Solovieva, D. Sperlich, J. M. Webb, Y. Wei, C. Weiser & B. T. Winter
Department of Physics, University of Toronto, Toronto, ON, Canada
K. Amirie, C. Clarry, L. S. Colangeli, C. De Almeida Rossi, J. H. Foo, A. Gabrielli, C. A. Garner, E. Hill, N. Ilic, T. M. Knight, P. Krieger, E. Lodhi, O. Miu, D. P. Mungo, R. S. Orr, S. Roy-Garand, P. Savard, P. Sinervo, J. J. Teoh, R. J. Teuscher, L. M. Veloce & C. Wu
Laboratório de Instrumentação e Física Experimental de Partículas - LIP, Lisbon, Portugal
S. P. Amor Dos Santos, M. G. Barros Teixeira, A. Berti, N. F. Castro, R. F. Coelho Barrue, P. Conde Muiño, N. Dos Santos Fernandes, G. Evans, L. F. Falda Ulhoa Coelho, M. C. N. Fiolhais, I. L. Gavrilenko, A. Gomes, R. Gonçalo, M. Kholodenko, A. Maio, I. Ochoa, L. F. Oleiro Seabra, A. Onofre, R. Pedro, B. C. Pinheiro Pereira, H. Santos, J. G. Saraiva, M. Stolarski, F. Veloso & H. Wolters
Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
D. Amperiadou, S. Argyropoulos, K. Bachas, D. Iliadis, E. Kasimi, K. Kordas, C. Lampoudis, A. Leisos, A. Marantis, S. Merianos, C. Petridou, D. Sampsonidis, A. Tsiamis, A. Tsirigotis, M. Tsopoulou & S. Tzamarias
KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
S. An, M. Aoki, Y. Enari, K. Hanagaki, Y. Ikegami, K. Itabashi, K. Nagano, Y. Nakahama, K. Nakamura, H. Oide, O. Sasaki, S. Shimizu, Y. Takubo, M. Togawa, M. Tomoto, S. Tsuno, Y. Uematsu, L. Vaslin, C. Wanotayaroj & Y. Yamaguchi
Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
C. Anastopoulos, D. Costanzo, M. C. Hodgkinson, P. Johansson, S. D. Lawlor, L. Lewitt, K. Lohwasser, H. Maguire, M. B. Norfolk, M. A. Postill, S. R. Pradhan, J. E. Puddefoot, N. P. Readioff, D. R. Tovey, T. Vickey, O. E. Vickey Boeriu, D. F. Zhang & T. G. Zorbas
Department of Physics, University of Texas at Austin, Austin, TX, USA
T. Andeen, K. Choi, M. Contreras Cossio, L. Larson, P. U. E. Onyisi, D. K. Panchal, M. Tost & C. Wang
SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, UK
A. C. Anderson, R. L. Bates, A. Blue, A. G. Borbély, D. Britton, A. G. Buckley, P. J. Bussey, C. M. Buttar, G. Callea, W. R. Cunningham, A. T. Doyle, J. Friend, M. Habedank, J. Howarth, J. Jamieson, T. Maurin, M. Miralles Lopez, M. Owen, A. S. Reed, A. G. Rennie, A. Robson, Z. M. A. Rozario, D. P. Spiteri, K. Walkingshaw Pass, N. Warrack, E. Watton, K. Wraight & S. Yan
Dipartimento di Fisica, Università di Milano, Milan, Italy
A. Andreazza, A. Carbone, L. Carminati, B. Cervato, S. D’Auria, L. Dell’Asta, M. Fanti, M. Lazzaroni, C. Meroni, L. Nasella, A. R. Petri, F. Ragusa, A. Sala & R. Zanzottera
Physics Department, National and Kapodistrian University of Athens, Athens, Greece
S. Angelidakis, D. Fassouliotis, L. Fountas, I. Gkialas, C. Kourkoumelis & K. Sioulas
Nevis Laboratory, Columbia University, Irvington, NY, USA
A. Angerami, G. Brooijmans, E. L. Busch, B. Cole, B. J. Gilbert, D. A. Hangal, R. Kopeliansky, J. D. Long, S. L. Mason, S. Mohapatra, K. R. Park, J. A. Parsons, B. D. Seidlitz, A. C. Smith, P. M. Tuts, D. M. Williams & E. L. Woodward
INFN Sezione di Pisa, Pisa, Italy
A. Annovi, A. Cerri, G. Chiarelli, G. D’anniballe, P. Francavilla, S. Leone, P. Mastrandrea, C. Roda, F. Scuri & M. Verducci
INFN Sezione di Roma, Rome, Italy
F. Anulli, G. Artoni, P. Bagnaia, M. Bauce, A. Betti, C. Bini, N. Bruscino, L. Corazzina, M. Corradi, A. De Salvo, A. Di Domenico, S. Falciano, D. Fiacco, P. Gauzzi, S. Giagu, G. Gustavino, V. Ippolito, F. Lacava, C. Luci, L. Martinelli, F. Morodei, A. Nisati, G. Padovano, E. Pasqualucci, S. Perrella, S. Rosati, G. Russo, F. Safai Tehrani, R. Vari & S. Veneziano
International Center for Elementary Particle Physics and Department of Physics, University of Tokyo, Tokyo, Japan
T. Aoki, S. Asai, W. Y. Chan, A. Cortes-Gonzalez, M. Furukawa, S. Ganguly, Y. Hayashi, R. Iguchi, Y. Iiyama, T. Iizawa, M. Ishino, W. Jang, T. Kaji, Z. Li, M. Morinaga, R. Nagasaka, Y. Narukawa, T. Nobe, Y. Okumura, M. Saito, T. Saito, R. Sawada, A. Tanaka, J. Tanaka, G. Tateno, K. Terashi, J. Wu, E. Yamashita, Y. Yang, J. Zang & T. Zhang
Deutsches Elektronen-Synchrotron DESY, Hamburg and Zeuthen, Germany
L. Aperio Bella, J.-H. Arling, M. Barakat, L. T. Bayer, J. K. Behr, L. Beresford, I. Bloch, B. Brüers, M. Caspar, S. E. Clawson, F. Dattola, N. De Biase, S. Díez Cornell, L. Ferencz, L. Franconi, G. Glemža, M. V. Gonzalez Rodrigues, I. M. Gregor, L. Guo, S. S. Gurdasani, Y. He, S. Heim, C. A. Hugli, P. Jain, S. Jiggins, F. A. Jolly, E. Jones, J. Katzy, J. A. Kremer, T. Kuhl, N. Kumari, E. M. Lobodzinska, E. Loiacono, O. Majersky, M. Marinescu, S. Marium, T. C. Mclachlan, F. Meloni, K. Mönig, A. L. Moreira De Carvalho, C. Mwewa, I. Ninca, S. Oerdek, P. Pani, K. Peters, K. Ran, F. Renner, A. L. Rescia, D. Rousso, C. O. Sander, S. Schmitt, C. Seitz, S. Sinha, E. Sitnikova, D. South, W. Stanek-Maslouska, M. M. Stanitzki, B. Stapf, N. A. Styles, K. Tackmann, X. Wang, C. J. Wells & S. D. Worm
Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Física, y CONICET, Instituto de Física de Buenos Aires (IFIBA), Buenos Aires, Argentina
M. Apicella, L. T. Bazzano Hurrell, G. Otero y Garzon, R. Piegaia, M. Toscani & F. I. Winkel
Department of Physics, Brandeis University, Waltham, MA, USA
A. Apyan, D. Camarero Munoz, F. Capocasa, M. P. Cardiff, E. R. Duden, G. Frattari, S. Gupta, M. N. Mancini, K. Reeves, G. Sciolla, S. N. Singh, S. Solomon, D. A. Trischuk & D. T. Zenger Jr
Institute of Nuclear Physics Polish Academy of Sciences, Krakow, Poland
S. J. Arbiol Val, E. Banas, S. Bashiri, P. A. Bruckman de Renstrom, J. J. Chwastowski, D. Derendarz, D. Ernani Martins Neto, M. K. Juzek, A. Kaczmarska, T. Komarek, K. Korcyl, M. P. Lewicki, Pa. Malecki, T. G. Mroz, F. Ozturk, P. Patel, M. Slawinska, E. Stanecka, R. Staszewski, M. Trzebinski, A. Trzupek, M. W. Wolter, B. K. Wosiek, K. W. Woźniak, B. Zabinski & Z. K. Zak
Department of Physics, Duke University, Durham, NC, USA
A. T. H. Arce, A. T. Goshaw, A. Kotwal, M. C. Kruse, J. J. Mullin, U. M. Patel, N. Ribaric & K. Vorobev
Group of Particle Physics, University of Montreal, Montreal, QC, Canada
J-F. Arguin, S. Epari, D. Godin, H. D. N. Nguyen & M. Usman
Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
G. Artoni, P. Bagnaia, M. Bauce, A. Betti, C. Bini, N. Bruscino, L. Corazzina, M. Corradi, A. Di Domenico, D. Fiacco, P. Gauzzi, S. Giagu, G. Gustavino, V. Ippolito, F. Lacava, C. Luci, L. Martinelli, F. Morodei, G. Padovano, S. Perrella & G. Russo
Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
H. Asada, Y. Horii, Y. Mitsumori, Y. Osumi & M. Tomoto
Ochanomizu University, Bunkyo-ku, Tokyo, Japan
K. Asai, T. Kono & K. Tsuri
Yerevan Physics Institute, Yerevan, Armenia
S. Asatryan, S. Harkusha & A. Semushin
Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
R. Astalos, P. Bartos, A. Dohnalova, M. Dubovsky, B. Eckerova, L. Keszeghova, M. Kostov, D. Suchy, I. Sykora, S. Tokár & T. Ženiš
Department of Physics and Astronomy, University of California Irvine, Irvine, CA, USA
S. Atashi, M. J. Fenton, A. Ghosh, R. M. Gleason, K. T. Greif, A. J. Lankford, R. Lazaridou, I. Longarini, K. Ntekas, J. L. Oliver, D. R. Smith, A. Taffard, G. Unel, M. Vessella & D. Whiteson
Department of Physics, University of Cape Town, Cape Town, South Africa
R. J. Atkin, C. M. Garvey, J. M. Keaveney & S. Yacoob
Institute of Applied Physics, Mohammed VI Polytechnic University, Ben Guerir, Morocco
H. Atmani & Y. Bimgdi
Department of Physics, University of Pennsylvania, Philadelphia, PA, USA
P. A. Atmasiddha, G. L. Gardner, T. C. Gosart, L. F. Gutierrez Zagazeta, M. D. Hank, J. G. Heinlein, A. Kahn, J. Kroll, E. Lipeles, S. Lu, B. S. Lunday, R. P. McGovern, L. M. Osojnak, N. Proklova, D. S. Rankin, J. D. Shahinian, K. Sugizaki, E. Thomson, A. Wall, H. H. Williams & R. Xu
LPC, Université Clermont Auvergne, CNRS/IN2P3, Clermont-Ferrand, France
A. D. Auriol, D. Boumediene, D. Calvet, S. Calvet, L. D. Corpe, L. D’Eramo, J. Donini, A. Haddad, A. Lafarge, R. Madar, E. Mayer, B. Pascual Dias, C. Santoni & O. V. Solovyanov
Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
D. Babal, F. Sopkova, P. Strizenec & J. Urban
IRFU, CEA, Université Paris-Saclay, Gif-sur-Yvette, France
H. Bachacou, F. Balli, M. Boonekamp, E. Chapon, L. Chevalier, F. Deliot, P. M. Fitzhugh, A. Formica, P. F. Giraud, J. F. Laporte, M. Liberatore, J-P. Meyer, R. Nicolaidou, H. Pang, M. Saimpert, L. Schoeffel, Ph. Schune & Ph. Schwemling
Department of Physics, Carleton University, Ottawa, ON, Canada
A. Bachiu, A. Bellerive, P. Calfayan, J. R. Dandoy, M. Diamantopoulou, D. Duvnjak, D. Gillberg, K. Graham, J. Heilman, C. E. Jessiman, S. Kaur, J. S. Keller, C. Klein, T. Koffas, J. H. Lepage Bourbonnais, L. S. Miller, B. J. Norman, D. A. Pizzi, I. A. Ramirez-Berend, W. F. Rettie, P. G. Scholer, M. B. Smith, E. J. Staats, M. G. Vincter, I. K. Vyas & Y. Zhao
Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
E. Bachmann, A. Berthold, M. Gutsche, A. Hadef, M. Helbig, T. Herrmann, M. Kobel, O. Kolay, T. Kresse, J-E. Nitschke, F. Siegert, P. Sommer, M. V. Stange, A. Straessner & J. C. Voigt
Institut für Physik, Humboldt Universität zu Berlin, Berlin, Germany
M. Bahmani, D. Battulga, D. Guest, A. Guida, C. Issever, T. J. Khoo, H. Lacker, C. E. Leitgeb, T. Lohse, A. Nayaz, V. H. Ruelas Rivera, C. Scharf & H. A. Weber
Institute for Fundamental Science, University of Oregon, Eugene, OR, USA
K. Bai, J. E. Brau, A. M. Carroll, G. Gaycken, M. Glisic, J. J. Heinrich, L. Jeanty, D. M. Koeck, O. Kovanda, W. Kozanecki, S. Majewski, T. T. Mathew, F. Piazza, D. Reikher, D. Sampsonidou, D. M. Strom, E. Torrence, F. Winklmeier, A. Xiong & N. D. Young
Department of Physics and Astronomy, Queen Mary University of London, London, UK
L. Baines, A. J. Bevan, U. Blumenschein, M. Bona, I. Dawson, K. Ghorbanian, J. M. Hays, N. B. Heatley, J. M. Inglis, M. P. J. Landon, S. L. Lloyd, J. P. Mandalia, R. R. Marcelo Gregorio, P. S. Miyagawa, G. Poddar, E. Rizvi, C. Vergis & S. Zenz
Department of Physics, Yale University, New Haven, CT, USA
O. K. Baker, S. Demers, J. N. Farr, A. G. Garcia Caffaro, T. Lagouri, E. M. Le Boulicaut, R. Li, J. Pan, G. D. Penn, G. Pezzullo, C. O. Shimmin, P. Tipton & M. Varma
Institute of Physics, University of Belgrade, Belgrade, Serbia
E. Bakos, L. J. Beemster, J. Jovicevic, V. Maksimovic, E. Maricic, Dj. Sijacki, N. Vranjes, M. Vranjes Milosavljevic & L. Živković
Department of Physics, University of Texas at Arlington, Arlington, TX, USA
D. Bakshi Gupta, B. Burghgrave, J. C. J. Cardenas, K. De, A. Farbin, H. K. Hadavand, K. S. Jones, S. Kandel, A. J. Myers, N. Ozturk, G. Usai & A. White
Affiliated with an institute formerly covered by a cooperation agreement with CERN, Geneva, Switzerland
E. M. Baldin, S. Barsov, K. Beloborodov, A. G. Bogdanchikov, I. S. Bordulev, S. P. Denisov, A. Ezhilov, R. M. Fakhrutdinov, O. L. Fedin, A. Gavrilyuk, L. K. Gladilin, D. Golubkov, A. N. Karyukhin, V. F. Kazanin, A. G. Kharlamov, T. Kharlamova, N. Korotkova, A. S. Kozhin, V. A. Kramarenko, A. Kupich, Y. A. Kurochkin, A. Kurova, M. Levchenko, R. Makhmanazarov, V. P. Maleev, D. A. Maximov, A. A. Minaenko, A. G. Myagkov, I. Naryshkin, P. Y. Nechaeva, V. Nikolaenko, S. V. Peleganchuk, M. Penzin, V. A. Schegelsky, P. B. Shatalov, L. N. Smirnova, E. A. Starchenko, V. V. Sulin, L. Sultanaliyeva, A. A. Talyshev, S. Timoshenko, I. I. Tsukerman & O. Zenin
Dipartimento di Fisica e Astronomia A. Righi, Università di Bologna, Bologna, Italy
E. Ballabene, G. Bianco, E. Bisceglie, Y. Cai, G. Carratta, F. A. Corchia, D. Cremonini, S. De Castro, F. Fabbri, L. Fabbri, M. Franchini, A. Gabrielli, B. Leban, G. Levrini, S. Nechaeva, L. Pezzotti, L. Rinaldi, E. Sanzani, A. Sbrizzi, N. Semprini-Cesari, M. Sioli, S. Valentinetti, M. Villa, I. Vivarelli & A. Zoccoli
Cavendish Laboratory, University of Cambridge, Cambridge, UK
W. K. Balunas, G. A. Bird, O. Brandt, J. D. Chapman, N. Fomin, L. B. A. H. Hommels, S. Huang, P. Jones, C. G. Lester, M. Maheshwari, A. J. Mullin, A. Plebani, C. J. Potter, M. M. Revering, D. Robinson, S. Rutherford Colmenares, A. H. Shah, P. N. Swallow, J. F. Wack, J. J. H. Wilkinson & S. Williams
United Arab Emirates University, Al Ain, United Arab Emirates
I. Bamwidhi, M. Belfkir & S. Nasri
Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA, USA
M. Bandieramonte, R. M. Bianchi, J. Boudreau, H. Cai, B. T. Carlson, R. Gupta, T. M. Hong, R. A. Khan, J. Mueller, H. J. Stelzer & R. Xue
School of Physics, University of Melbourne, Melbourne, VIC, Australia
E. L. Barberio, I. B. Carr, S. Goldfarb, E. F. McDonald, T. Pham & G. N. Taylor
University of California, Berkeley, CA, USA
D. Barberis, M. Santana Queiroz & B. Yeo
Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, The Netherlands
M. Z. Barel, L. Brenner, E. Cherepanova, V. Croft, P. de Jong, F. A. Dias, T. A. du Pree, Z. Feng, P. Ferrari, A. Garcia Alonso, T. Giani, G. Gilles, R. L. Hayes, O. Karkout, P. Kluit, B. Kortman, A. E. McDougall, C. Nellist, J. O. Rieger, A. C. Sidley, H. L. Snoek, D. R. Van Arneman, I. Van Vulpen, W. Verkerke, J. C. Vermeulen, A. Visibile, M. Vreeswijk & Z. Wolffs
Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
T. Barillari, J. B. Beacham, S. Bethke, S. Bharthuar, D. Britzger, D. Buchin, D. Cieri, F. Fallavollita, M. Greco, S. G. Grewe, N. M. Hartman, L. Heinrich, J. Hessler, M. E. Horstmann, M. Kado, A. E. Kiryunin, S. Kluth, O. Kortner, S. Kortner, E. Kourlitis, H. Kroha, C-Q. Li, S. Menke, R. Nisius, T. H. Park, G. Proto, D. Rafanoharana, R. Richter, E. Schmidt, M. Spalla, S. Stonjek, A. Verbytskyi, M. Vigl, E. Voevodina, N. S. Wenke & J. Wuerzinger
Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic
P. Baron, P. Berta, M. Biros, C. Chauhan, T. Davidek, M. Divisek, Z. Dolezal, J. Faltova, P. Federic, M. Haviernik, N. Hidic, Y. Huang, S. Jankovych, P. Kodyš, R. Leitner, G. Martinovicova, J. Matousek, A. Ogrodnik, F. Pauwels, T. Petru, V. Pleskot, S. Polacek, P. Reznicek, M. Rybar, D. Scheirich, M. Spousta, M. Sykora, T. Sykora, P. Tas, D. Timoshyn, S. Todorova-Nova, P. Vana & R. Vavricka
Department of Modern Physics and State Key Laboratory of Particle Detection and Electronics, University of Science and Technology of China, Hefei, China
A. Baroncelli, Z. Chen, Y. Ding, D. Du, Y. El Ghazali, A. Giannini, L. Han, Q. Hu, T. Kawamoto, H. Li, Z. Li, M. Liu, M. Y. Liu, X. Liu, Y. W. Liu, K. Ma, W. Ma, H. Ren, S. Su, X. Su, C. Tian, A. Wang, T. Wang, Y. Wang, C. Wei, X. Wu, Y. Wu, M. Xie, H. Xu, L. Xu, H. T. Yang, S. Yang, Y. Yang, X. Ye, Y. Yu, M. Zaazoua, L. Zhang, Y. Zhang, Z. Zhao, X. Zheng & Y. Zhu
Department of Physics, Oxford University, Oxford, UK
A. J. Barr, D. Bortoletto, T. L. Bruckler, M. Chen, E. I. Conroy, A. M. Cooper-Sarkar, T. Dingley, M. A. Draguet, G. H. Eberwein, J. A. Frost, E. J. Gallas, R. P. Grabarczyk, C. Gwenlan, F. Haslbeck, C. P. Hays, B. H. Hodkinson, V. Homsak, T. B. Huffman, K. Karava, S. F. Koch, U. Molinatti, K. Nagai, L. Nedic, R. B. Nickerson, H. A. Pacey, E. Rossi, A. Ruggiero, I. P. J. Shipsey, D. M. S. Sultan, S. B. Tuncay, G. H. A. Viehhauser, A. R. Weidberg & T. P. Yildirim
Department of Physics and Astronomy, University College London, London, UK
J. D. Barr, J. M. Butterworth, M. Campanelli, N. Clarke Hall, H. Cui, P. K. Duckett, G. Facini, C. Gutschow, E. H. Haines, M. L. E. Hart, Y. He, N. Kimura, N. Konstantinidis, A. Korn, N. N. Lad, W. S. Lai, T. Madula, J. Martin, A. C. Martyniuk, D. J. Mclaughlin, M. Mlinarevic, T. Mlinarevic, N. I. Pond, T. Scanlon, P. Sherwood, L. Shi, A. Vaitkus, S. Van Stroud, P. Wang, B. M. Waugh, Y. Yeh, M. R. Yexley, L. Yue & Y. Zhang
Departamento de Física Teorica C-15 and CIAFF, Universidad Autónoma de Madrid, Madrid, Spain
F. Barreiro, S. Batlamous, P. Collado Soto, A. Cueto, J. Del Peso, C. Glasman, L. Pascual Dominguez, M. A. Principe Martin & J. Terron
Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
J. Barreiro Guimarães da Costa, X. Chu, Y. Fan, Y. Fang, F. Guo, S. Han, M. He, X. Huang, Y. Huang, X. Jia, K. Li, S. Li, Z. Li, S. Liang, Z. Liang, B. Liu, P. Liu, X. Lou, Q. Sha, L. Y. Shan, X. Shi, W. Sun, K. Tariq, S. Wang, W. Wang, S. Wu, D. Xu, X. Yang, J. Ye, J. Yuan, H. Zeng, M. Zhai, G. Zhang, K. Zhang, P. Zhang & X. Zhuang
TRIUMF, Vancouver, BC, Canada
M. J. Basso, L. M. Brown, S. V. Chekulaev, E. K. Filmer, N. P. Hessey, L. L. Kurchaninov, K. Pachal, D. M. Portillo Quintero, B. Stelzer, O. Stelzer, M. Swiatlowski, R. Tafirout, I. M. Trigger & S. Tsigaridas
Department of Physics, University of British Columbia, Vancouver, BC, Canada
R. Bate, C. Gay, C. M. Helling, H. Jia, A. Lister, C. C. McCracken, R. P. Quinn, A. S. Sharma & Z. Tao
Universität Innsbruck, Department of Astro and Particle Physics, Innsbruck, Austria
M. Bauer, E. Kneringer, A. Romaniouk & A. Thaler
Department of Physics and Astronomy, Tufts University, Medford, MA, USA
P. H. Beauchemin, N. Garelli, V. K. Gassmann, F. I. Kaya, M. Klassen & C. I. Pazos
Istinye University, Sariyer, Istanbul, Türkiye
A. J. Beddall, O. Bulekov, E. Celebi, S. A. Cetin, S. Ozturk, A. Petukhov, M. Sahinsoy, S. Simsek, Y. Smirnov, V. Tikhomirov & Z. Uysal
Rio de Janeiro State University, Rio de Janeiro, Brazil
M. Begalli, M. Donadelli, G. Inacio Goncalves, A. Malvezzi Lopes & B. S. Peralva
Department of Physics, Indiana University, Bloomington, IN, USA
C. D. Bellgraph, A. J. Brooks, H. Evans, J. J. Hong, S. Lammers, H. Lien, J. D. Little, F. Luehring, C. Meyer, R. Omar, G. Palacino, D. Ponomarenko, S. Sottocornola, O. Toldaiev & K. Zhukov
Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA, USA
K. C. Benkendorfer, L. E. Bruce, S. Francescato, M. Franklin, J. Huth, G. V. Kehris, J. Ling, M. Morii, A. E. Mulski, G. Rabanal Bolanos, L. P. Rossi, R. Wang, A. S. White & K. Zoch
Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
E. Bergeaas Kuutmann, R. Brenner, T. Ekelof, V. Ellajosyula, M. Ellert, A. Ferrari, A. L. Gallen, R. Gonzalez Suarez, H. Hamdaoui, G. A. Mullier, P. Rincke, G. Ripellino & O. Sunneborn Gudnadottir
Physics Division, Lawrence Berkeley National Laboratory, Berkeley, CA, USA
J. Beringer, P. Calafiura, F. Cerutti, J. Chan, A. Ciocio, S. D. Diefenbacher, G. I. Dyckes, K. Einsweiler, I. Ene, D. E. Fellers, A. W. Fortman, L. Foster, L. G. Gagnon, M. Garcia-Sciveres, H. M. Gray, C. Haber, T. Heim, M. Hu, C. E. Hultquist, X. Ju, L. T. Le Pottier, C. Leggett, Z. Marshall, M. Mironova, B. P. Nachman, D. Noll, S. Pagan Griso, M. Pettee, E. Pianori, A. Rastogi, E. Reynolds, B. R. Roberts, M. Shapiro, B. Stanislaus, E. A. Thompson, V. Tsulaia, J. M. Wagner, T. Wamorkar, H. Wang, J. Xiong, T. Yamazaki & W-M. Yao
APC, Université Paris Cité, CNRS/IN2P3, Paris, France
G. Bernardi, M. Bomben, T. Li, A. Maloizel, G. Marchiori & K. Nakkalil
INFN Sezione di Roma Tre, Rome, Italy
M. Biglietti, B. Di Micco, R. Di Nardo, A. Farilla, M. Iodice, F. Montereali, D. Orestano & R. Orlandini
Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
A. Bingham, G. Brandt, F. Ellinghaus, M. Errenst, T. Flick, M. E. Geyik, T. Harenberg, D. Hirschbuehl, J. W. Kraus, L. Kretschmann, J. A. Reidelsturz, M. Sandhoff, J. Schmeing, M. A. Schmidt, M. Stratmann, W. Wagner, S. Wahdan & C. Zeitnitz
Department of Physics Engineering, Gaziantep University, Gaziantep, Türkiye
A. Bingul
Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot, Israel
M. Birman, R. Brener, S. Bressler, K. L. Chu, Z. H. Citron, E. Dreyer, E. Duchovni, E. Gross, N. Hod, A. Ivina, T. Jakoubek, N. Kakati, D. Kobylianskii, L. J. Levinson, I. M. Maniatis, D. C. Mankad, G. Mikenberg, A. Milov, L. Moleri, Y. Moyal, I. Ravinovich, B. Sahoo, A. Santra, V. Smakhtin & N. Soybelman
Department Physik, Universität Siegen, Siegen, Germany
D. Biswas, M. Cristinziani, C. Diez Pardos, I. Fleck, A. Ghosal, G. Gomes Da Silva, J. J. Hahn, V. V. Kostyukhin, N. B. Krengel, A. Petrukhin, E. Schopf, K. Voss, W. Walkowiak, A. L. Warnerbring & M. Ziolkowski
Dipartimento di Fisica, Università di Genova, Genoa, Italy
L. Boccardo, R. Bouquet, M. J. Da Cunha Sargedas De Sousa, M. D’Andrea, F. A. Di Bello, G. Gagliardi, F. Parodi, L. Rambelli, S. Ravera, M. Ressegotti, C. Schiavi, F. Sforza, S. Turchikhin & A. Zaio
INFN Sezione di Genova, Genoa, Italy
L. Boccardo, R. Bouquet, A. Coccaro, M. J. Da Cunha Sargedas De Sousa, G. Darbo, F. A. Di Bello, G. Gagliardi, C. Gemme, P. Morettini, F. Parodi, S. Passaggio, L. Rambelli, S. Ravera, M. Ressegotti, C. Schiavi, F. Sforza, S. Turchikhin & A. Zaio
Fakultät für Physik und Astronomie, Julius-Maximilians-Universität Würzburg, Würzburg, Germany
B. Boehm, M. Haleem, G. Khoriauli, L. Klein, R. Ströhmer, T. Swirski & T. Trefzger
Ohio State University, Columbus, OH, USA
A. Boveia, B. M. Cote, K. K. Gan, A. Gekow, N. M. Harrison, R. Joshi, H. Kagan, M. Montella, Z. B. Pollock, R. Rosten & S. Shrestha
Department of Physics, University of Massachusetts, Amherst, MA, USA
B. Brau, R. Coelho Lopes De Sa, C. Dallapiccola, M. L. Harris, D. L. Humphreys, M. Javurkova, A. Krasznahorkay, A. K. Kvam, W. A. Leight, M. K. Maroun, V. I. Martinez Outschoorn, E. J. W. Moyse, G. Perera, M. J. Veen, S. Willocq & Z. Yan
INFN-TIFPA, Trento, Italy
G. Brianti, M. Cristoforetti, A. Di Luca, F. M. Follega, R. Iuppa, D. Mascione & E. Ricci
Università degli Studi di Trento, Trento, Italy
G. Brianti, M. Cristoforetti, A. Di Luca, F. M. Follega, R. Iuppa, D. Mascione & E. Ricci
Department of Physics and Astronomy, Michigan State University, East Lansing, MI, USA
R. Brock, C. J. Buxo Vazquez, B. Dong, T. Farooque, W. C. Fisher, Y. Fu, J. P. Gombas, R. Hauser, D. Hayden, J. R. Hinds, J. Huston, S. Kazakos, K. S. Krowpman, H. D. M. Le, R. Les, R. Qian, R. Schwienhorst & A. Tarek Abouelfadl Mohamed
Department of Physics and Astronomy, York University, Toronto, ON, Canada
E. M. Brooks, J. Kerr, P. Kumari, T. F. Lee & W. Taylor
Department of Physics, Stockholm University, Stockholm, Sweden
D. Brunner, C. Clement, K. Dunne, S. Hellman, T. Ingebretsen Carlson, D. W. Kim, X. Lou, D. A. Milstead, A. Montella, S. Richter, E. M. Riefel, S. B. Silverstein, J. Sjölin, S. Strandberg, A. Strubig & E. Valdes Santurio
Oskar Klein Centre, Stockholm, Sweden
D. Brunner, C. Clement, K. Dunne, S. Hellman, T. Ingebretsen Carlson, D. W. Kim, X. Lou, D. A. Milstead, A. Montella, S. Richter, E. M. Riefel, J. Sjölin, S. Strandberg, A. Strubig & E. Valdes Santurio
L2IT, Université de Toulouse, CNRS/IN2P3, UPS, Toulouse, France
A. M. Burger, J. Manjarres Ramos, J. Stark, M. J. Tartarin, A. S. Tegetmeier, H. Torres, A. Vallier & S. Zhang
Department of Physics, University of Illinois, Urbana, IL, USA
J. Burleson, Y. Cao, C. Fan, A. M. Hodges, B. H. Hooberman, M. C. Hoppesch, M. R. Housenga, R. Longo, M. S. Neubauer, Y. W. Y. Ng, S. Parajuli, A. C. Romero Hernandez, A. M. Sickles, A. C. Tate, X. Wang, J. C. Zeng, K. Zheng & D. Zhong
Department of Physics, Simon Fraser University, Burnaby, BC, Canada
J. C. Burzynski, J. Chen, M. Danninger, H. Hanif, A. Poley, D. J. Sheppard, B. Stelzer & M. C. Vetterli
Department of Physics, Boston University, Boston, MA, USA
J. M. Butler & A. B. Lux
II. Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
D. Caforio, M. Düren & H. Stenzel
University of Chinese Academy of Science (UCAS), Beijing, China
Y. Cai, X. Chu, Y. Fang, F. Guo, M. He, X. Huang, X. Jia, S. Li, Z. Li, S. Liang, Y. Liu, X. Lou, K. Ran, J. Yuan, M. Zhai, K. Zhang & P. Zhang
Department of Physics, Nanjing University, Nanjing, China
Y. Cai, Y. Che, H. Chen, S. J. Chen, A. De Maria, Z. Duan, L. Han, Z. Jia, S. Jin, F. L. Lucio Alves, Y. Miao, T. Min, Y. Wang, Z. Wu, L. Xia, L. Zhang, R. Zhang, Y. Zhang, J. Zheng & Y. Zhou
Department of Physics, Ankara University, Ankara, Türkiye
O. Cakir, A. C. Canbay, H. Duran Yildiz, S. Kuday & I. Turk Cakir
Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
A. Camplani, M. Dam, J. B. Hansen, P. H. Hansen, A. Morancho Tarda, T. C. Petersen, C. Wiglesworth & S. Xella
Dipartimento di Fisica, Università della Calabria, Rende, Italy
M. Capua, G. Carducci, G. Crosetti, G. Falsetti, A. Mastroberardino, E. Meoni, M. Schioppa & E. Tassi
INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
M. Capua, G. Carducci, G. Crosetti, G. Falsetti, I. Gnesi, A. Mastroberardino, E. Meoni, M. Schioppa & E. Tassi
Institute for Mathematics, Astrophysics and Particle Physics, Radboud University/Nikhef, Nijmegen, The Netherlands
S. Caron, E. Y. S. Chow, N. De Groot, P. Ferrari, F. Filthaut, L. Franco, W. Leinonen, M. C. Missio, P. Moskvitina, D. Pyatiizbyantseva & M. Wu
Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
E. Carquin, S. Fuenzalida Garrido, R. Pezoa, S. Tapia Araya & N. Viaux Maira
INFN Sezione di Pavia, Pavia, Italy
S. Carrá, T. Cresta, R. Ferrari, G. Gaudio, G. Introzzi, A. Kourkoumeli-Charalampidi, A. Lanza, G. Manco, A. Negri, A. Pareti, G. Polesello, D. M. Rebuzzi & E. Romano
Dipartimento di Fisica, Università di Pavia, Pavia, Italy
S. Carrá, T. Cresta, G. Introzzi, A. Kourkoumeli-Charalampidi, G. Manco, A. Negri, A. Pareti, D. M. Rebuzzi & E. Romano
Departamento de Física, Escola de Ciências, Universidade do Minho, Braga, Portugal
N. F. Castro & A. Onofre
Department of Physics, University of Oslo, Oslo, Norway
J. R. Catmore, E. Gramstad, R. Guevara, E. S. Haaland, O. K. B. Langrekken, J. Malamant, F. Ould-Saada, M. Pedersen, A. L. Read, O. Røhne, H. Sandaker, D. R. Shope & I. Sliusar
Departamento de Física, Universidad Nacional de Colombia, Bogotá, Colombia
L. J. Caviedes Betancourt, M. A. Garcia Ruiz, J. M. Moreno Perez & C. Sandoval
Joint Laboratory of Optics, Palacký University, Olomouc, Czech Republic
K. Cerny, M. Hrabovsky, J. Kvita, L. Nozka & R. Privara
Departamento de Engenharia Elétrica, Universidade Federal de Juiz de Fora (UFJF), Juiz de Fora, Brazil
A. S. Cerqueira, M. Hufnagel Maranha De Faria & L. Manhaes de Andrade Filho
Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
A. Cerri, G. D’anniballe, P. Francavilla, P. Mastrandrea, C. Roda & M. Verducci
High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
B. Chargeishvili, T. Djobava, A. Durglishvili, J. Khubua, I. A. Minashvili & M. Mosidze
High Energy Physics Division, Argonne National Laboratory, Lemont, IL, USA
S. Chekanov, W. H. Hopkins, J. Hoya, D. Kim, N. A. Luongo, C. A. Mc Lean, J. Metcalfe, A. S. Mete, A. Paramonov, J. Proudfoot, L. R. Simpson, P. Van Gemmeren, R. Wang & J. Zhang
State Key Laboratory of Dark Matter Physics, School of Physics and Astronomy, Shanghai Jiao Tong University, Key Laboratory for Particle Astrophysics and Cosmology (MOE), SKLPPC, Shanghai, China
J. Chen, X. Chen, J. Guo, J. Li, L. Li, S. Li, D. Liu, K. Liu, Q. Liu, L. Mao, Q. Shen, N. K. Vu, X. Wang, H. J. Yang, R. Yuan, N. Zhou & Y. Zhu
Faculty of Science, Kyoto University, Kyoto, Japan
S. Chen, C. Kawamoto, Y. Mino, T. Sano & Y. Tsujikawa
Physics Department, Tsinghua University, Beijing, China
X. Chen, H. Li, S. Peng, M. Xia & Y. Zhou
Department of Physics, University of Wisconsin, Madison, WI, USA
C. L. Cheng, K. Cranmer, M. Feickert, A. Held, W. Islam, T. M. Pham, J. A. Sandesara, S. Sun, W. Wiedenmann & S. L. Wu
Department of Physics, Chinese University of Hong Kong, Shatin, N.T., Hong Kong, China
H. C. Cheng, M. C. Chu, L. R. Flores Castillo, K. Y. Fung & T. Pan
Department of Physics, University of Arizona, Tucson, AZ, USA
E. Cheu, Z. Cui, A. Ghosh, R. Hyneman, K. A. Johns, W. Lampl, R. E. Lindley, P. Loch, N. A. Lopez-canelas, J. P. Rutherfoord, J. Sardain, E. W. Varnes, H. Zhou & Y. Zhou
Department of Physics, National Tsing Hua University, Hsinchu, Taiwan
K. Cheung & P. J. Hsu
INFN Sezione di Lecce, Lecce, Italy
G. Chiodini, R. Coluccia, F. De Santis, E. Gorini, S. Grancagnolo, F. G. Gravili, A. Palazzo, M. Primavera, S. Spagnolo & A. Ventura
Institute of Physics of the Czech Academy of Sciences, Prague, Czech Republic
J. Chudoba, P. Federicova, J. Hejbal, O. Kepka, J. Kroll, A. Kupco, R. Lysak, M. Marcisovsky, M. Mikestikova, B. Mondal, F. Nechansky, S. Nemecek, O. Penc, P. Sicho, P. Staroba, M. Svatos & M. Tasevsky
Department of Experimental Particle Physics, Jožef Stefan Institute and Department of Physics, University of Ljubljana, Ljubljana, Slovenia
V. Cindro, J. Debevc, A. Filipčič, J. Gavranovic, A. Gorišek, B. Hiti, A. S. Howard, B. P. Kerševan, G. Kramberger, M. Mali, I. Mandić, B. Maček, M. Mikuž, M. Muškinja, J. Novak, T. Novak & I. Velkovska
Dipartimento Politecnico di Ingegneria e Architettura, Università di Udine, Udine, Italy
M. Cobal, M. P. Giordani, G. Giugliarelli, C. Merlassino, S. Monzani, N. Nitika, G. Panizzo, M. Pinamonti, L. Pintucci, L. Primomo, B. Ricci & L. Toffolin
Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
R. Coluccia, F. De Santis, E. Gorini, S. Grancagnolo, F. G. Gravili, A. Palazzo, S. Spagnolo & A. Ventura
Departamento de Fisica, Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal
P. Conde Muiño
Institute of Physics, Academia Sinica, Taipei, Taiwan
S. Dahbi, K. Farman, S. Hou, Y. J. Lu & S. M. Wang
Department of Physics, University of Adelaide, Adelaide, SA, Australia
A. M. Desai, M. P. Fewell, J. Gallagher, C. M. Grant, M. J. Green, P. Jackson, A. X. Y. Kong, J. Kull, H. D. Pandya, H. I. Purnell, T. A. Ruggeri, S. Saha, E. X. L. Ting & M. J. White
Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
B. Di Micco, R. Di Nardo, F. Montereali, D. Orestano & R. Orlandini
Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
M. A. Diaz, F. M. Garay Walls & P. Urrejola
Millennium Institute for Subatomic physics at high energy frontier (SAPHIR), Santiago, Chile
M. A. Diaz, F. M. Garay Walls, S. Kuleshov, S. Yu. Smirnov, O. J. Soto Sandoval & P. A. Ulloa Poblete
Department of Physics, Royal Institute of Technology, Stockholm, Sweden
C. Dimitriadi, A. Leopold, O. Lundberg, C. C. Ohm, R. Shaheen, J. Strandberg, U. M. Vande Voorde & R. Wierda
Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
S. J. Dittmeier, A. Nandi, A. Schoening, L. Vigani & J. Zinsser
Federal University of Bahia, Salvador, Bahia, Brazil
I. A. Dos Santos Luz, E. Egidio Purcino De Souza, E. Furtado De Simas Filho, J. Lieber Marin & P. C. Machado De Abreu Farias
Faculty of Physics, University of Bucharest, Bucharest, Romania
I. Duminica
Faculté des Sciences, Université Ibn-Tofail, Kénitra, Morocco
S. El Farkh, M. Gouighri & M. Hidaoui
Departamento de Física, Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
G. Evans, A. Gomes, A. Maio & H. Santos
Department of Physics, University of Hong Kong, Hong Kong, China
K. Y. Fan, Q. Jiang, D. Paredes Hernandez, L. Pizzimento, K. C. Tam & Y. Tu
Louisiana Tech University, Ruston, LA, USA
Z. Farazpay, L. Sawyer & M. Wobisch
Institute of Frontier and Interdisciplinary Science and Key Laboratory of Particle Physics and Particle Irradiation (MOE), Shandong University, Qingdao, China
C. Feng, J. Han, C. Jia, B. Li, H. Li, X. Liu, Y. L. Liu, L. L. Ma, J. Zhang, Z. Zhang, T. Zhao & C. G. Zhu
Centro Nacional de Microelectrónica (IMB-CNM-CSIC), Barcelona, Spain
P. Fernandez Martinez
Departamento de Física, Universidade de Coimbra, Coimbra, Portugal
M. C. N. Fiolhais, F. Veloso & H. Wolters
National Institute of Physics, University of the Philippines Diliman (Philippines), Quezon City, Philippines
M. Flores
University of Sharjah, Sharjah, United Arab Emirates
S. Gaid, K. A. Saoucha & P. Starovoitov
Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM, USA
A. D. Gentry, M. H. Mohamed Farook, S. C. Seidel & J. D. Sorenson
National Centre for Scientific Research “Demokritos”, Agia Paraskevi, Greece
T. Geralis, A. Psallidas, G. Stavropoulos & O. Zormpa
Marian Smoluchowski Institute of Physics, Jagiellonian University, Krakow, Poland
D. T. Gil, T. Procter, W. W. Przygoda, E. Richter-Was & Yu. Volkotrub
Department of Physics, University of Alberta, Edmonton, AB, Canada
D. M. Gingrich & J. L. Pinfold
University of Georgia, Tbilisi, Georgia
A. Gongadze
West University in Timisoara, Timisoara, Romania
P. M. Gravila
School of Science, Shenzhen Campus of Sun Yat-sen University, Guangzhou, China
L. Guo, Y. Huang, B. X. Liu, Y. Liu & M. Wu
Department of Physics, Shinshu University, Nagano, Japan
Y. Hasegawa & K. Kawade
Graduate School of Science, University of Osaka, Osaka, Japan
M. Hirose, T. Masubuchi, H. Nanjo & L. Wickremasinghe
Division of Physics and Tomonaga Center for the History of the Universe, Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
S. Hirose, S. Kita, K. Sato, H. Suzuki, F. Ukegawa, S. Wada & H. Yamauchi
National University of Science and Technology Politechnica, Bucharest, Romania
R. Hobincu
Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
N. Huseynov
Instituto de Investigación Multidisciplinario en Ciencia y Tecnología, y Departamento de Física, Universidad de La Serena, La Serena, Chile
S. A. Infante Cabanas, O. J. Soto Sandoval & P. A. Ulloa Poblete
E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
J. Jejelava, V. Tsiskaridze & E. G. Tskhadadze
Department of Physics, Institute of Science, Tokyo, Japan
O. Jinnouchi, M. Kuze, I. R. Sotarriva Alvarez & K. Todome
Instituto de Alta Investigación, Universidad de Tarapacá, Arica, Chile
S. Kabana & M. Schernau
Department of Physics, Technion, Israel Institute of Technology, Haifa, Israel
E. Kajomovitz, Y. Rozen & S. Tarem
School of Physics, University of the Witwatersrand, Johannesburg, South Africa
D. Kar, B. Kibirige, M. Kumar, R. Mazini, R. P. Mckenzie, B. R. Mellado Garcia, G. Mokgatitswane, O. Mtintsilana, N. P. Rapheeha, E. Sideras Haddad, A. A. Solodkov & H. Z. Van Der Schyf
Department of Physics and Astronomy, Iowa State University, Ames, IA, USA
N. Krumnack
Department of Physics, Universidad Andres Bello, Santiago, Chile
S. Kuleshov & J. A. Zamora Saa
Graduate School of Science, Kobe University, Kobe, Japan
H. Kurashige, J. Maeda, A. Ochi & Y. Yamazaki
Instituto de Física, Universidade de São Paulo, São Paulo, Brazil
M. A. L. Leite & G. T. Saito
State Key Laboratory of Dark Matter Physics, Tsung-Dao Lee Institute, Shanghai Jiao Tong University, Shanghai, China
S. Li, D. Liu, K. Liu, K. Liu, Q. Liu, N. K. Vu, Z. Wang, H. J. Yang, R. Yuan & X. Zhu
Department of Physics and Institute for Advanced Study, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
K. Lie, K. Prokofiev, J. Wang & T. Yang
Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
A. Maio & J. G. Saraiva
University of Iowa, Iowa City, IA, USA
U. Mallik & W. T. Wang
Research Center for Advanced Particle Physics and Department of Physics, Kyushu University, Fukuoka, Japan
M. Moritsu, H. Otono, S. Shirabe & J. Tojo
LPMR, Faculté des Sciences, Université Mohamed Premier, Oujda, Morocco
A. Moussa, M. Ouchrif, H. Riani & S. Ridouani
Facultad de Ciencias y Centro de Investigaciónes, Universidad Antonio Nariño, Bogotá, Colombia
G. Navarro & Y. Rodriguez Garcia
iThemba Labs, Cape Town, Western Cape, South Africa
E. K. Nkadimeng
School of Physics, University of Sydney, Sydney, NSW, Australia
T. Nommensen, H. Potti, K. E. Varvell & B. Yabsley
Transilvania University of Brasov, Brasov, Romania
S. Popa
Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj-Napoca, Romania
G. A. Popeneciu
University of West Attica, Athens, Greece
E. Sideras Haddad
Khalifa University of Science and Technology, Abu Dhabi, United Arab Emirates
R. Soualah
Division of Physics, TOBB University of Economics and Technology, Ankara, Türkiye
S. Sultansoy
Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
R. Ushioda

Consortia

The ATLAS Collaboration

G. Aad
, E. Aakvaag
, B. Abbott
, S. Abdelhameed
, K. Abeling
, N. J. Abicht
, S. H. Abidi
, M. Aboelela
, A. Aboulhorma
, H. Abramowicz
, Y. Abulaiti
, B. S. Acharya
, A. Ackermann
, C. Adam Bourdarios
, L. Adamczyk
, S. V. Addepalli
, M. J. Addison
, J. Adelman
, A. Adiguzel
, T. Adye
, A. A. Affolder
, Y. Afik
, M. N. Agaras
, A. Aggarwal
, C. Agheorghiesei
, F. Ahmadov
, S. Ahuja
, X. Ai
, G. Aielli
, A. Aikot
, M. Ait Tamlihat
, B. Aitbenchikh
, M. Akbiyik
, T. P. A. Åkesson
, A. V. Akimov
, D. Akiyama
, N. N. Akolkar
, S. Aktas
, G. L. Alberghi
, J. Albert
, U. Alberti
, P. Albicocco
, G. L. Albouy
, S. Alderweireldt
, Z. L. Alegria
, M. Aleksa
, I. N. Aleksandrov
, C. Alexa
, T. Alexopoulos
, F. Alfonsi
, M. Algren
, M. Alhroob
, B. Ali
, H. M. J. Ali
, S. Ali
, S. W. Alibocus
, M. Aliev
, G. Alimonti
, W. Alkakhi
, C. Allaire
, B. M. M. Allbrooke
, J. S. Allen
, J. F. Allen
, P. P. Allport
, A. Aloisio
, F. Alonso
, C. Alpigiani
, Z. M. K. Alsolami
, A. Alvarez Fernandez
, M. Alves Cardoso
, M. G. Alviggi
, M. Aly
, Y. Amaral Coutinho
, A. Ambler
, C. Amelung
, M. Amerl
, C. G. Ames
, T. Amezza
, D. Amidei
, B. Amini
, K. Amirie
, A. Amirkhanov
, S. P. Amor Dos Santos
, K. R. Amos
, D. Amperiadou
, S. An
, C. Anastopoulos
, T. Andeen
, J. K. Anders
, A. C. Anderson
, A. Andreazza
, S. Angelidakis
, A. Angerami
, A. V. Anisenkov
, A. Annovi
, C. Antel
, E. Antipov
, M. Antonelli
, F. Anulli
, M. Aoki
, T. Aoki
, M. A. Aparo
, L. Aperio Bella
, M. Apicella
, C. Appelt
, A. Apyan
, M. Arampatzi
, S. J. Arbiol Val
, C. Arcangeletti
, A. T. H. Arce
, J-F. Arguin
, S. Argyropoulos
, J.-H. Arling
, O. Arnaez
, H. Arnold
, G. Artoni
, H. Asada
, K. Asai
, S. Asai
, S. Asatryan
, N. A. Asbah
, R. A. Ashby Pickering
, A. M. Aslam
, K. Assamagan
, R. Astalos
, K. S. V. Astrand
, S. Atashi
, R. J. Atkin
, H. Atmani
, P. A. Atmasiddha
, K. Augsten
, A. D. Auriol
, V. A. Austrup
, G. Avolio
, K. Axiotis
, A. Azzam
, D. Babal
, H. Bachacou
, K. Bachas
, A. Bachiu
, E. Bachmann
, M. J. Backes
, A. Badea
, T. M. Baer
, P. Bagnaia
, M. Bahmani
, D. Bahner
, K. Bai
, J. T. Baines
, L. Baines
, O. K. Baker
, E. Bakos
, D. Bakshi Gupta
, L. E. Balabram Filho
, V. Balakrishnan
, R. Balasubramanian
, E. M. Baldin
, P. Balek
, E. Ballabene
, F. Balli
, L. M. Baltes
, W. K. Balunas
, J. Balz
, I. Bamwidhi
, E. Banas
, M. Bandieramonte
, A. Bandyopadhyay
, S. Bansal
, L. Barak
, M. Barakat
, E. L. Barberio
, D. Barberis
, M. Barbero
, M. Z. Barel
, T. Barillari
, M-S. Barisits
, T. Barklow
, P. Baron
, D. A. Baron Moreno
, A. Baroncelli
, A. J. Barr
, J. D. Barr
, F. Barreiro
, J. Barreiro Guimarães da Costa
, M. G. Barros Teixeira
, S. Barsov
, F. Bartels
, R. Bartoldus
, A. E. Barton
, P. Bartos
, A. Basan
, M. Baselga
, S. Bashiri
, A. Bassalat
, M. J. Basso
, S. Bataju
, R. Bate
, R. L. Bates
, S. Batlamous
, M. Battaglia
, D. Battulga
, M. Bauce
, M. Bauer
, P. Bauer
, L. T. Bayer
, L. T. Bazzano Hurrell
, J. B. Beacham
, T. Beau
, J. Y. Beaucamp
, P. H. Beauchemin
, P. Bechtle
, H. P. Beck
, K. Becker
, A. J. Beddall
, V. A. Bednyakov
, C. P. Bee
, L. J. Beemster
, M. Begalli
, M. Begel
, J. K. Behr
, J. F. Beirer
, F. Beisiegel
, M. Belfkir
, G. Bella
, L. Bellagamba
, A. Bellerive
, C. D. Bellgraph
, P. Bellos
, K. Beloborodov
, D. Benchekroun
, F. Bendebba
, Y. Benhammou
, K. C. Benkendorfer
, L. Beresford
, M. Beretta
, E. Bergeaas Kuutmann
, N. Berger
, B. Bergmann
, J. Beringer
, G. Bernardi
, C. Bernius
, F. U. Bernlochner
, F. Bernon
, A. Berrocal Guardia
, T. Berry
, P. Berta
, A. Berthold
, A. Berti
, R. Bertrand
, S. Bethke
, A. Betti
, A. J. Bevan
, L. Bezio
, N. K. Bhalla
, S. Bharthuar
, S. Bhatta
, P. Bhattarai
, Z. M. Bhatti
, K. D. Bhide
, V. S. Bhopatkar
, R. M. Bianchi
, G. Bianco
, O. Biebel
, M. Biglietti
, C. S. Billingsley
, Y. Bimgdi
, M. Bindi
, A. Bingham
, A. Bingul
, C. Bini
, G. A. Bird
, M. Birman
, M. Biros
, S. Biryukov
, T. Bisanz
, E. Bisceglie
, J. P. Biswal
, D. Biswas
, I. Bloch
, A. Blue
, U. Blumenschein
, J. Blumenthal
, V. S. Bobrovnikov
, L. Boccardo
, M. Boehler
, B. Boehm
, D. Bogavac
, A. G. Bogdanchikov
, L. S. Boggia
, V. Boisvert
, P. Bokan
, T. Bold
, M. Bomben
, M. Bona
, M. Boonekamp
, A. G. Borbély
, I. S. Bordulev
, G. Borissov
, D. Bortoletto
, D. Boscherini
, M. Bosman
, K. Bouaouda
, N. Bouchhar
, L. Boudet
, J. Boudreau
, E. V. Bouhova-Thacker
, D. Boumediene
, R. Bouquet
, A. Boveia
, J. Boyd
, D. Boye
, I. R. Boyko
, L. Bozianu
, J. Bracinik
, N. Brahimi
, G. Brandt
, O. Brandt
, B. Brau
, J. E. Brau
, R. Brener
, L. Brenner
, R. Brenner
, S. Bressler
, G. Brianti
, D. Britton
, D. Britzger
, I. Brock
, R. Brock
, G. Brooijmans
, A. J. Brooks
, E. M. Brooks
, E. Brost
, L. M. Brown
, L. E. Bruce
, T. L. Bruckler
, P. A. Bruckman de Renstrom
, B. Brüers
, A. Bruni
, G. Bruni
, D. Brunner
, M. Bruschi
, N. Bruscino
, T. Buanes
, Q. Buat
, D. Buchin
, A. G. Buckley
, O. Bulekov
, B. A. Bullard
, S. Burdin
, C. D. Burgard
, A. M. Burger
, B. Burghgrave
, O. Burlayenko
, J. Burleson
, J. C. Burzynski
, E. L. Busch
, V. Büscher
, P. J. Bussey
, J. M. Butler
, C. M. Buttar
, J. M. Butterworth
, W. Buttinger
, C. J. Buxo Vazquez
, A. R. Buzykaev
, S. Cabrera Urbán
, L. Cadamuro
, D. Caforio
, H. Cai
, Y. Cai
, Y. Cai
, V. M. M. Cairo
, O. Cakir
, N. Calace
, P. Calafiura
, G. Calderini
, P. Calfayan
, L. Calic
, G. Callea
, L. P. Caloba
, D. Calvet
, S. Calvet
, R. Camacho Toro
, S. Camarda
, D. Camarero Munoz
, P. Camarri
, C. Camincher
, M. Campanelli
, A. Camplani
, V. Canale
, A. C. Canbay
, E. Canonero
, J. Cantero
, Y. Cao
, F. Capocasa
, M. Capua
, A. Carbone
, R. Cardarelli
, J. C. J. Cardenas
, M. P. Cardiff
, G. Carducci
, T. Carli
, G. Carlino
, J. I. Carlotto
, B. T. Carlson
, E. M. Carlson
, J. Carmignani
, L. Carminati
, A. Carnelli
, M. Carnesale
, S. Caron
, E. Carquin
, I. B. Carr
, S. Carrá
, G. Carratta
, A. M. Carroll
, M. P. Casado
, P. Casolaro
, M. Caspar
, F. L. Castillo
, L. Castillo Garcia
, V. Castillo Gimenez
, N. F. Castro
, A. Catinaccio
, J. R. Catmore
, T. Cavaliere
, V. Cavaliere
, L. J. Caviedes Betancourt
, E. Celebi
, S. Cella
, V. Cepaitis
, K. Cerny
, A. S. Cerqueira
, A. Cerri
, L. Cerrito
, F. Cerutti
, B. Cervato
, A. Cervelli
, G. Cesarini
, S. A. Cetin
, P. M. Chabrillat
, R. Chakkappai
, S. Chakraborty
, J. Chan
, W. Y. Chan
, J. D. Chapman
, E. Chapon
, B. Chargeishvili
, D. G. Charlton
, C. Chauhan
, Y. Che
, S. Chekanov
, S. V. Chekulaev
, G. A. Chelkov
, B. Chen
, B. Chen
, H. Chen
, H. Chen
, J. Chen
, J. Chen
, M. Chen
, S. Chen
, S. J. Chen
, X. Chen
, X. Chen
, Z. Chen
, C. L. Cheng
, H. C. Cheng
, S. Cheong
, A. Cheplakov
, E. Cherepanova
, R. Cherkaoui El Moursli
, E. Cheu
, K. Cheung
, L. Chevalier
, V. Chiarella
, G. Chiarelli
, G. Chiodini
, A. S. Chisholm
, A. Chitan
, M. Chitishvili
, M. V. Chizhov
, K. Choi
, Y. Chou
, E. Y. S. Chow
, K. L. Chu
, M. C. Chu
, X. Chu
, Z. Chubinidze
, J. Chudoba
, J. J. Chwastowski
, D. Cieri
, K. M. Ciesla
, V. Cindro
, A. Ciocio
, F. Cirotto
, Z. H. Citron
, M. Citterio
, D. A. Ciubotaru
, A. Clark
, P. J. Clark
, N. Clarke Hall
, C. Clarry
, S. E. Clawson
, C. Clement
, Y. Coadou
, M. Cobal
, A. Coccaro
, R. F. Coelho Barrue
, R. Coelho Lopes De Sa
, S. Coelli
, L. S. Colangeli
, B. Cole
, P. Collado Soto
, J. Collot
, R. Coluccia
, P. Conde Muiño
, M. P. Connell
, S. H. Connell
, E. I. Conroy
, M. Contreras Cossio
, F. Conventi
, A. M. Cooper-Sarkar
, L. Corazzina
, F. A. Corchia
, A. Cordeiro Oudot Choi
, L. D. Corpe
, M. Corradi
, F. Corriveau
, A. Cortes-Gonzalez
, M. J. Costa
, F. Costanza
, D. Costanzo
, B. M. Cote
, J. Couthures
, G. Cowan
, K. Cranmer
, L. Cremer
, D. Cremonini
, S. Crépé-Renaudin
, F. Crescioli
, T. Cresta
, M. Cristinziani
, M. Cristoforetti
, V. Croft
, J. E. Crosby
, G. Crosetti
, A. Cueto
, H. Cui
, Z. Cui
, B. M. Cunnett
, W. R. Cunningham
, F. Curcio
, J. R. Curran
, M. J. Da Cunha Sargedas De Sousa
, J. V. Da Fonseca Pinto
, C. Da Via
, W. Dabrowski
, T. Dado
, S. Dahbi
, T. Dai
, D. Dal Santo
, C. Dallapiccola
, M. Dam
, G. D’amen
, V. D’Amico
, J. Damp
, J. R. Dandoy
, M. D’Andrea
, D. Dannheim
, G. D’anniballe
, M. Danninger
, V. Dao
, G. Darbo
, S. J. Das
, F. Dattola
, S. D’Auria
, A. D’Avanzo
, T. Davidek
, J. Davidson
, I. Dawson
, K. De
, C. De Almeida Rossi
, R. De Asmundis
, N. De Biase
, S. De Castro
, N. De Groot
, P. de Jong
, H. De la Torre
, A. De Maria
, A. De Salvo
, U. De Sanctis
, F. De Santis
, A. De Santo
, J. B. De Vivie De Regie
, J. Debevc
, D. V. Dedovich
, J. Degens
, A. M. Deiana
, J. Del Peso
, L. Delagrange
, F. Deliot
, C. M. Delitzsch
, M. Della Pietra
, D. Della Volpe
, A. Dell’Acqua
, L. Dell’Asta
, M. Delmastro
, C. C. Delogu
, P. A. Delsart
, S. Demers
, M. Demichev
, S. P. Denisov
, H. Denizli
, L. D’Eramo
, D. Derendarz
, F. Derue
, P. Dervan
, A. M. Desai
, K. Desch
, F. A. Di Bello
, A. Di Ciaccio
, L. Di Ciaccio
, A. Di Domenico
, C. Di Donato
, A. Di Girolamo
, G. Di Gregorio
, A. Di Luca
, B. Di Micco
, R. Di Nardo
, K. F. Di Petrillo
, M. Diamantopoulou
, F. A. Dias
, M. A. Diaz
, A. R. Didenko
, M. Didenko
, S. D. Diefenbacher
, E. B. Diehl
, S. Díez Cornell
, C. Diez Pardos
, C. Dimitriadi
, A. Dimitrievska
, A. Dimri
, Y. Ding
, J. Dingfelder
, T. Dingley
, I-M. Dinu
, S. J. Dittmeier
, F. Dittus
, M. Divisek
, B. Dixit
, F. Djama
, T. Djobava
, C. Doglioni
, A. Dohnalova
, Z. Dolezal
, K. Domijan
, K. M. Dona
, M. Donadelli
, B. Dong
, J. Donini
, A. D’Onofrio
, M. D’Onofrio
, J. Dopke
, A. Doria
, N. Dos Santos Fernandes
, I. A. Dos Santos Luz
, P. Dougan
, M. T. Dova
, A. T. Doyle
, M. A. Draguet
, M. P. Drescher
, E. Dreyer
, I. Drivas-koulouris
, M. Drnevich
, M. Drozdova
, D. Du
, T. A. du Pree
, Z. Duan
, M. Dubau
, F. Dubinin
, M. Dubovsky
, E. Duchovni
, G. Duckeck
, P. K. Duckett
, O. A. Ducu
, D. Duda
, A. Dudarev
, E. R. Duden
, M. D’uffizi
, L. Duflot
, M. Dührssen
, I. Duminica
, A. E. Dumitriu
, M. Dunford
, S. Dungs
, K. Dunne
, A. Duperrin
, H. Duran Yildiz
, M. Düren
, A. Durglishvili
, D. Duvnjak
, G. I. Dyckes
, M. Dyndal
, B. S. Dziedzic
, Z. O. Earnshaw
, G. H. Eberwein
, B. Eckerova
, S. Eggebrecht
, E. Egidio Purcino De Souza
, G. Eigen
, K. Einsweiler
, T. Ekelof
, P. A. Ekman
, S. El Farkh
, Y. El Ghazali
, H. El Jarrari
, A. El Moussaouy
, V. Ellajosyula
, M. Ellert
, F. Ellinghaus
, T. A. Elliot
, N. Ellis
, J. Elmsheuser
, M. Elsawy
, M. Elsing
, D. Emeliyanov
, Y. Enari
, I. Ene
, S. Epari
, D. Ernani Martins Neto
, F. Ernst
, M. Errenst
, M. Escalier
, C. Escobar
, E. Etzion
, G. Evans
, H. Evans
, L. S. Evans
, A. Ezhilov
, S. Ezzarqtouni
, F. Fabbri
, L. Fabbri
, G. Facini
, V. Fadeyev
, R. M. Fakhrutdinov
, D. Fakoudis
, S. Falciano
, L. F. Falda Ulhoa Coelho
, F. Fallavollita
, G. Falsetti
, J. Faltova
, C. Fan
, K. Y. Fan
, Y. Fan
, Y. Fang
, M. Fanti
, M. Faraj
, Z. Farazpay
, A. Farbin
, A. Farilla
, K. Farman
, T. Farooque
, J. N. Farr
, S. M. Farrington
, F. Fassi
, D. Fassouliotis
, L. Fayard
, P. Federic
, P. Federicova
, O. L. Fedin
, M. Feickert
, L. Feligioni
, D. E. Fellers
, C. Feng
, Z. Feng
, M. J. Fenton
, L. Ferencz
, B. Fernandez Barbadillo
, P. Fernandez Martinez
, M. J. V. Fernoux
, J. Ferrando
, A. Ferrari
, P. Ferrari
, R. Ferrari
, D. Ferrere
, C. Ferretti
, M. P. Fewell
, D. Fiacco
, F. Fiedler
, P. Fiedler
, S. Filimonov
, M. S. Filip
, A. Filipčič
, E. K. Filmer
, F. Filthaut
, M. C. N. Fiolhais
, L. Fiorini
, W. C. Fisher
, T. Fitschen
, P. M. Fitzhugh
, I. Fleck
, P. Fleischmann
, T. Flick
, M. Flores
, L. R. Flores Castillo
, L. Flores Sanz De Acedo
, F. M. Follega
, N. Fomin
, J. H. Foo
, A. Formica
, A. C. Forti
, E. Fortin
, A. W. Fortman
, L. Foster
, L. Fountas
, D. Fournier
, H. Fox
, P. Francavilla
, S. Francescato
, S. Franchellucci
, M. Franchini
, S. Franchino
, D. Francis
, L. Franco
, V. Franco Lima
, L. Franconi
, M. Franklin
, G. Frattari
, Y. Y. Frid
, J. Friend
, N. Fritzsche
, A. Froch
, D. Froidevaux
, J. A. Frost
, Y. Fu
, S. Fuenzalida Garrido
, M. Fujimoto
, K. Y. Fung
, E. Furtado De Simas Filho
, M. Furukawa
, J. Fuster
, A. Gaa
, A. Gabrielli
, A. Gabrielli
, P. Gadow
, G. Gagliardi
, L. G. Gagnon
, S. Gaid
, S. Galantzan
, J. Gallagher
, E. J. Gallas
, A. L. Gallen
, B. J. Gallop
, K. K. Gan
, S. Ganguly
, Y. Gao
, A. Garabaglu
, F. M. Garay Walls
, C. García
, A. Garcia Alonso
, A. G. Garcia Caffaro
, J. E. García Navarro
, M. A. Garcia Ruiz
, M. Garcia-Sciveres
, G. L. Gardner
, R. W. Gardner
, N. Garelli
, R. B. Garg
, J. M. Gargan
, C. A. Garner
, C. M. Garvey
, V. K. Gassmann
, G. Gaudio
, V. Gautam
, P. Gauzzi
, J. Gavranovic
, I. L. Gavrilenko
, A. Gavrilyuk
, C. Gay
, G. Gaycken
, E. N. Gazis
, A. Gekow
, C. Gemme
, M. H. Genest
, A. D. Gentry
, S. George
, T. Geralis
, A. A. Gerwin
, P. Gessinger-Befurt
, M. E. Geyik
, M. Ghani
, K. Ghorbanian
, A. Ghosal
, A. Ghosh
, A. Ghosh
, B. Giacobbe
, S. Giagu
, T. Giani
, A. Giannini
, S. M. Gibson
, M. Gignac
, D. T. Gil
, A. K. Gilbert
, B. J. Gilbert
, D. Gillberg
, G. Gilles
, D. M. Gingrich
, M. P. Giordani
, P. F. Giraud
, G. Giugliarelli
, D. Giugni
, F. Giuli
, I. Gkialas
, L. K. Gladilin
, C. Glasman
, M. Glazewska
, R. M. Gleason
, G. Glemža
, M. Glisic
, I. Gnesi
, Y. Go
, M. Goblirsch-Kolb
, B. Gocke
, D. Godin
, B. Gokturk
, S. Goldfarb
, T. Golling
, M. G. D. Gololo
, D. Golubkov
, J. P. Gombas
, A. Gomes
, G. Gomes Da Silva
, A. J. Gomez Delegido
, R. Gonçalo
, L. Gonella
, A. Gongadze
, F. Gonnella
, J. L. Gonski
, R. Y. González Andana
, S. González de la Hoz
, M. V. Gonzalez Rodrigues
, R. Gonzalez Suarez
, S. Gonzalez-Sevilla
, L. Goossens
, B. Gorini
, E. Gorini
, A. Gorišek
, T. C. Gosart
, A. T. Goshaw
, M. I. Gostkin
, S. Goswami
, C. A. Gottardo
, S. A. Gotz
, M. Gouighri
, A. G. Goussiou
, N. Govender
, R. P. Grabarczyk
, I. Grabowska-Bold
, K. Graham
, E. Gramstad
, S. Grancagnolo
, C. M. Grant
, P. M. Gravila
, F. G. Gravili
, H. M. Gray
, M. Greco
, M. J. Green
, C. Grefe
, A. S. Grefsrud
, I. M. Gregor
, K. T. Greif
, P. Grenier
, S. G. Grewe
, A. A. Grillo
, K. Grimm
, S. Grinstein
, J.-F. Grivaz
, E. Gross
, J. Grosse-Knetter
, L. Guan
, G. Guerrieri
, D. Guest
, R. Guevara
, R. Gugel
, J. A. M. Guhit
, A. Guida
, E. Guilloton
, S. Guindon
, F. Guo
, J. Guo
, L. Guo
, L. Guo
, Y. Guo
, A. Gupta
, R. Gupta
, S. Gupta
, S. Gurbuz
, S. S. Gurdasani
, G. Gustavino
, P. Gutierrez
, L. F. Gutierrez Zagazeta
, M. Gutsche
, C. Gutschow
, C. Gwenlan
, C. B. Gwilliam
, E. S. Haaland
, A. Haas
, M. Habedank
, C. Haber
, H. K. Hadavand
, A. Haddad
, A. Hadef
, A. I. Hagan
, J. J. Hahn
, E. H. Haines
, M. Haleem
, J. Haley
, G. D. Hallewell
, L. Halser
, K. Hamano
, H. Hamdaoui
, M. Hamer
, S. E. D. Hammoud
, E. J. Hampshire
, J. Han
, L. Han
, L. Han
, S. Han
, K. Hanagaki
, M. Hance
, D. A. Hangal
, H. Hanif
, M. D. Hank
, J. B. Hansen
, P. H. Hansen
, D. Harada
, T. Harenberg
, S. Harkusha
, M. L. Harris
, Y. T. Harris
, J. Harrison
, N. M. Harrison
, P. F. Harrison
, M. L. E. Hart
, N. M. Hartman
, N. M. Hartmann
, R. Z. Hasan
, Y. Hasegawa
, F. Haslbeck
, S. Hassan
, R. Hauser
, M. Haviernik
, C. M. Hawkes
, R. J. Hawkings
, Y. Hayashi
, D. Hayden
, C. Hayes
, R. L. Hayes
, C. P. Hays
, J. M. Hays
, H. S. Hayward
, M. He
, Y. He
, Y. He
, N. B. Heatley
, V. Hedberg
, C. Heidegger
, K. K. Heidegger
, J. Heilman
, S. Heim
, T. Heim
, J. G. Heinlein
, J. J. Heinrich
, L. Heinrich
, J. Hejbal
, M. Helbig
, A. Held
, S. Hellesund
, C. M. Helling
, S. Hellman
, A. M. Henriques Correia
, H. Herde
, Y. Hernández Jiménez
, L. M. Herrmann
, T. Herrmann
, G. Herten
, R. Hertenberger
, L. Hervas
, M. E. Hesping
, N. P. Hessey
, J. Hessler
, M. Hidaoui
, N. Hidic
, E. Hill
, T. S. Hillersoy
, S. J. Hillier
, J. R. Hinds
, F. Hinterkeuser
, M. Hirose
, S. Hirose
, D. Hirschbuehl
, T. G. Hitchings
, B. Hiti
, J. Hobbs
, R. Hobincu
, N. Hod
, A. M. Hodges
, M. C. Hodgkinson
, B. H. Hodkinson
, A. Hoecker
, D. D. Hofer
, J. Hofer
, M. Holzbock
, L. B. A. H. Hommels
, V. Homsak
, B. P. Honan
, J. J. Hong
, T. M. Hong
, B. H. Hooberman
, W. H. Hopkins
, M. C. Hoppesch
, Y. Horii
, M. E. Horstmann
, S. Hou
, M. R. Housenga
, A. S. Howard
, J. Howarth
, J. Hoya
, M. Hrabovsky
, T. Hryn’ova
, P. J. Hsu
, S.-C. Hsu
, T. Hsu
, M. Hu
, Q. Hu
, S. Huang
, X. Huang
, Y. Huang
, Y. Huang
, Y. Huang
, Y. Huang
, Z. Huang
, Z. Hubacek
, M. Huebner
, F. Huegging
, T. B. Huffman
, M. Hufnagel Maranha De Faria
, C. A. Hugli
, M. Huhtinen
, S. K. Huiberts
, R. Hulsken
, C. E. Hultquist
, D. L. Humphreys
, N. Huseynov
, J. Huston
, J. Huth
, R. Hyneman
, G. Iacobucci
, G. Iakovidis
, L. Iconomidou-Fayard
, J. P. Iddon
, P. Iengo
, R. Iguchi
, Y. Iiyama
, T. Iizawa
, Y. Ikegami
, D. Iliadis
, N. Ilic
, H. Imam
, G. Inacio Goncalves
, S. A. Infante Cabanas
, T. Ingebretsen Carlson
, J. M. Inglis
, G. Introzzi
, M. Iodice
, V. Ippolito
, R. K. Irwin
, M. Ishino
, W. Islam
, C. Issever
, S. Istin
, K. Itabashi
, H. Ito
, R. Iuppa
, A. Ivina
, V. Izzo
, P. Jacka
, P. Jackson
, P. Jain
, K. Jakobs
, T. Jakoubek
, J. Jamieson
, W. Jang
, S. Jankovych
, M. Javurkova
, P. Jawahar
, L. Jeanty
, J. Jejelava
, P. Jenni
, C. E. Jessiman
, C. Jia
, H. Jia
, J. Jia
, X. Jia
, Z. Jia
, C. Jiang
, Q. Jiang
, S. Jiggins
, M. Jimenez Ortega
, J. Jimenez Pena
, S. Jin
, A. Jinaru
, O. Jinnouchi
, P. Johansson
, K. A. Johns
, J. W. Johnson
, F. A. Jolly
, D. M. Jones
, E. Jones
, K. S. Jones
, P. Jones
, R. W. L. Jones
, T. J. Jones
, H. L. Joos
, R. Joshi
, J. Jovicevic
, X. Ju
, J. J. Junggeburth
, T. Junkermann
, A. Juste Rozas
, M. K. Juzek
, S. Kabana
, A. Kaczmarska
, M. Kado
, H. Kagan
, M. Kagan
, A. Kahn
, C. Kahra
, T. Kaji
, E. Kajomovitz
, N. Kakati
, N. Kakoty
, I. Kalaitzidou
, S. Kandel
, N. J. Kang
, D. Kar
, K. Karava
, E. Karentzos
, O. Karkout
, S. N. Karpov
, Z. M. Karpova
, V. Kartvelishvili
, A. N. Karyukhin
, E. Kasimi
, J. Katzy
, S. Kaur
, K. Kawade
, M. P. Kawale
, C. Kawamoto
, T. Kawamoto
, E. F. Kay
, F. I. Kaya
, S. Kazakos
, V. F. Kazanin
, J. M. Keaveney
, R. Keeler
, G. V. Kehris
, J. S. Keller
, J. M. Kelly
, J. J. Kempster
, O. Kepka
, J. Kerr
, B. P. Kerridge
, B. P. Kerševan
, L. Keszeghova
, R. A. Khan
, A. Khanov
, A. G. Kharlamov
, T. Kharlamova
, E. E. Khoda
, M. Kholodenko
, T. J. Khoo
, G. Khoriauli
, Y. Khoulaki
, J. Khubua
, Y. A. R. Khwaira
, B. Kibirige
, D. Kim
, D. W. Kim
, Y. K. Kim
, N. Kimura
, M. K. Kingston
, A. Kirchhoff
, C. Kirfel
, F. Kirfel
, J. Kirk
, A. E. Kiryunin
, S. Kita
, O. Kivernyk
, M. Klassen
, C. Klein
, L. Klein
, M. H. Klein
, S. B. Klein
, U. Klein
, A. Klimentov
, T. Klioutchnikova
, P. Kluit
, S. Kluth
, E. Kneringer
, T. M. Knight
, A. Knue
, M. Kobel
, D. Kobylianskii
, S. F. Koch
, M. Kocian
, P. Kodyš
, D. M. Koeck
, T. Koffas
, O. Kolay
, I. Koletsou
, T. Komarek
, K. Köneke
, A. X. Y. Kong
, T. Kono
, N. Konstantinidis
, P. Kontaxakis
, B. Konya
, R. Kopeliansky
, S. Koperny
, K. Korcyl
, K. Kordas
, A. Korn
, S. Korn
, I. Korolkov
, N. Korotkova
, B. Kortman
, O. Kortner
, S. Kortner
, W. H. Kostecka
, M. Kostov
, V. V. Kostyukhin
, A. Kotsokechagia
, A. Kotwal
, A. Koulouris
, A. Kourkoumeli-Charalampidi
, C. Kourkoumelis
, E. Kourlitis
, O. Kovanda
, R. Kowalewski
, W. Kozanecki
, A. S. Kozhin
, V. A. Kramarenko
, G. Kramberger
, P. Kramer
, M. W. Krasny
, A. Krasznahorkay
, A. C. Kraus
, J. W. Kraus
, J. A. Kremer
, N. B. Krengel
, T. Kresse
, L. Kretschmann
, J. Kretzschmar
, P. Krieger
, K. Krizka
, K. Kroeninger
, H. Kroha
, J. Kroll
, J. Kroll
, K. S. Krowpman
, U. Kruchonak
, H. Krüger
, N. Krumnack
, M. C. Kruse
, O. Kuchinskaia
, S. Kuday
, S. Kuehn
, R. Kuesters
, T. Kuhl
, V. Kukhtin
, Y. Kulchitsky
, S. Kuleshov
, J. Kull
, E. V. Kumar
, M. Kumar
, N. Kumari
, P. Kumari
, A. Kupco
, T. Kupfer
, A. Kupich
, O. Kuprash
, H. Kurashige
, L. L. Kurchaninov
, O. Kurdysh
, Y. A. Kurochkin
, A. Kurova
, M. Kuze
, A. K. Kvam
, J. Kvita
, N. G. Kyriacou
, C. Lacasta
, F. Lacava
, H. Lacker
, D. Lacour
, N. N. Lad
, E. Ladygin
, A. Lafarge
, B. Laforge
, T. Lagouri
, F. Z. Lahbabi
, S. Lai
, W. S. Lai
, J. E. Lambert
, S. Lammers
, W. Lampl
, C. Lampoudis
, G. Lamprinoudis
, A. N. Lancaster
, E. Lançon
, U. Landgraf
, M. P. J. Landon
, V. S. Lang
, O. K. B. Langrekken
, A. J. Lankford
, F. Lanni
, K. Lantzsch
, A. Lanza
, M. Lanzac Berrocal
, J. F. Laporte
, T. Lari
, D. Larsen
, L. Larson
, F. Lasagni Manghi
, M. Lassnig
, S. D. Lawlor
, R. Lazaridou
, M. Lazzaroni
, H. D. M. Le
, E. M. Le Boulicaut
, L. T. Le Pottier
, B. Leban
, F. Ledroit-Guillon
, T. F. Lee
, L. L. Leeuw
, M. Lefebvre
, C. Leggett
, G. Lehmann Miotto
, M. Leigh
, W. A. Leight
, W. Leinonen
, A. Leisos
, M. A. L. Leite
, C. E. Leitgeb
, R. Leitner
, K. J. C. Leney
, T. Lenz
, S. Leone
, C. Leonidopoulos
, A. Leopold
, J. H. Lepage Bourbonnais
, R. Les
, C. G. Lester
, M. Levchenko
, J. Levêque
, L. J. Levinson
, G. Levrini
, M. P. Lewicki
, C. Lewis
, D. J. Lewis
, L. Lewitt
, A. Li
, B. Li
, C. Li
, C-Q. Li
, H. Li
, H. Li
, H. Li
, H. Li
, H. Li
, J. Li
, K. Li
, L. Li
, R. Li
, S. Li
, S. Li
, T. Li
, X. Li
, Z. Li
, Z. Li
, Z. Li
, S. Liang
, Z. Liang
, M. Liberatore
, B. Liberti
, K. Lie
, J. Lieber Marin
, H. Lien
, H. Lin
, S. F. Lin
, L. Linden
, R. E. Lindley
, J. H. Lindon
, J. Ling
, E. Lipeles
, A. Lipniacka
, A. Lister
, J. D. Little
, B. Liu
, B. X. Liu
, D. Liu
, D. Liu
, E. H. L. Liu
, J. K. K. Liu
, K. Liu
, K. Liu
, M. Liu
, M. Y. Liu
, P. Liu
, Q. Liu
, X. Liu
, X. Liu
, Y. Liu
, Y. L. Liu
, Y. W. Liu
, Z. Liu
, S. L. Lloyd
, E. M. Lobodzinska
, P. Loch
, E. Lodhi
, T. Lohse
, K. Lohwasser
, E. Loiacono
, J. D. Lomas
, J. D. Long
, I. Longarini
, R. Longo
, A. Lopez Solis
, N. A. Lopez-canelas
, N. Lorenzo Martinez
, A. M. Lory
, M. Losada
, G. Löschcke Centeno
, X. Lou
, X. Lou
, A. Lounis
, P. A. Love
, M. Lu
, S. Lu
, Y. J. Lu
, H. J. Lubatti
, C. Luci
, F. L. Lucio Alves
, F. Luehring
, B. S. Lunday
, O. Lundberg
, J. Lunde
, N. A. Luongo
, M. S. Lutz
, A. B. Lux
, D. Lynn
, R. Lysak
, V. Lysenko
, E. Lytken
, V. Lyubushkin
, T. Lyubushkina
, M. M. Lyukova
, M. Firdaus M. Soberi
, H. Ma
, K. Ma
, L. L. Ma
, W. Ma
, Y. Ma
, J. C. MacDonald
, P. C. Machado De Abreu Farias
, R. Madar
, T. Madula
, J. Maeda
, T. Maeno
, P. T. Mafa
, H. Maguire
, M. Maheshwari
, V. Maiboroda
, A. Maio
, K. Maj
, O. Majersky
, S. Majewski
, R. Makhmanazarov
, N. Makovec
, V. Maksimovic
, B. Malaescu
, J. Malamant
, Pa. Malecki
, V. P. Maleev
, F. Malek
, M. Mali
, D. Malito
, U. Mallik
, A. Maloizel
, S. Maltezos
, A. Malvezzi Lopes
, S. Malyukov
, J. Mamuzic
, G. Mancini
, M. N. Mancini
, G. Manco
, J. P. Mandalia
, S. S. Mandarry
, I. Mandić
, L. Manhaes de Andrade Filho
, I. M. Maniatis
, J. Manjarres Ramos
, D. C. Mankad
, A. Mann
, T. Manoussos
, M. N. Mantinan
, S. Manzoni
, L. Mao
, X. Mapekula
, A. Marantis
, R. R. Marcelo Gregorio
, G. Marchiori
, M. Marcisovsky
, C. Marcon
, E. Maricic
, M. Marinescu
, S. Marium
, M. Marjanovic
, A. Markhoos
, M. Markovitch
, M. K. Maroun
, G. T. Marsden
, E. J. Marshall
, Z. Marshall
, S. Marti-Garcia
, J. Martin
, T. A. Martin
, V. J. Martin
, B. Martin dit Latour
, L. Martinelli
, M. Martinez
, P. Martinez Agullo
, V. I. Martinez Outschoorn
, P. Martinez Suarez
, S. Martin-Haugh
, G. Martinovicova
, V. S. Martoiu
, A. C. Martyniuk
, A. Marzin
, D. Mascione
, L. Masetti
, J. Masik
, A. L. Maslennikov
, S. L. Mason
, P. Massarotti
, P. Mastrandrea
, A. Mastroberardino
, T. Masubuchi
, T. T. Mathew
, J. Matousek
, D. M. Mattern
, J. Maurer
, T. Maurin
, A. J. Maury
, B. Maček
, C. Mavungu Tsava
, D. A. Maximov
, A. E. May
, E. Mayer
, R. Mazini
, I. Maznas
, S. M. Mazza
, E. Mazzeo
, J. P. Mc Gowan
, S. P. Mc Kee
, C. A. Mc Lean
, C. C. McCracken
, E. F. McDonald
, A. E. McDougall
, L. F. Mcelhinney
, J. A. Mcfayden
, R. P. McGovern
, R. P. Mckenzie
, T. C. Mclachlan
, D. J. Mclaughlin
, S. J. McMahon
, C. M. Mcpartland
, R. A. McPherson
, S. Mehlhase
, A. Mehta
, D. Melini
, B. R. Mellado Garcia
, A. H. Melo
, F. Meloni
, A. M. Mendes Jacques Da Costa
, L. Meng
, S. Menke
, M. Mentink
, E. Meoni
, G. Mercado
, S. Merianos
, C. Merlassino
, C. Meroni
, J. Metcalfe
, A. S. Mete
, E. Meuser
, C. Meyer
, J-P. Meyer
, Y. Miao
, R. P. Middleton
, M. Mihovilovic
, L. Mijović
, G. Mikenberg
, M. Mikestikova
, M. Mikuž
, H. Mildner
, A. Milic
, D. W. Miller
, E. H. Miller
, L. S. Miller
, A. Milov
, D. A. Milstead
, T. Min
, A. A. Minaenko
, I. A. Minashvili
, A. I. Mincer
, B. Mindur
, M. Mineev
, Y. Mino
, L. M. Mir
, M. Miralles Lopez
, M. Mironova
, M. C. Missio
, A. Mitra
, V. A. Mitsou
, Y. Mitsumori
, O. Miu
, P. S. Miyagawa
, T. Mkrtchyan
, M. Mlinarevic
, T. Mlinarevic
, M. Mlynarikova
, S. Mobius
, M. H. Mohamed Farook
, S. Mohapatra
, S. Mohiuddin
, G. Mokgatitswane
, L. Moleri
, U. Molinatti
, L. G. Mollier
, B. Mondal
, S. Mondal
, K. Mönig
, E. Monnier
, L. Monsonis Romero
, J. Montejo Berlingen
, A. Montella
, M. Montella
, F. Montereali
, F. Monticelli
, S. Monzani
, A. Morancho Tarda
, N. Morange
, A. L. Moreira De Carvalho
, M. Moreno Llácer
, C. Moreno Martinez
, J. M. Moreno Perez
, P. Morettini
, S. Morgenstern
, M. Morii
, M. Morinaga
, M. Moritsu
, F. Morodei
, P. Moschovakos
, B. Moser
, M. Mosidze
, T. Moskalets
, P. Moskvitina
, J. Moss
, P. Moszkowicz
, A. Moussa
, Y. Moyal
, H. Moyano Gomez
, E. J. W. Moyse
, T. G. Mroz
, O. Mtintsilana
, S. Muanza
, M. Mucha
, J. Mueller
, R. Müller
, G. A. Mullier
, A. J. Mullin
, J. J. Mullin
, A. C. Mullins
, A. E. Mulski
, D. P. Mungo
, D. Munoz Perez
, F. J. Munoz Sanchez
, W. J. Murray
, M. Muškinja
, C. Mwewa
, A. G. Myagkov
, A. J. Myers
, G. Myers
, M. Myska
, B. P. Nachman
, K. Nagai
, K. Nagano
, R. Nagasaka
, J. L. Nagle
, E. Nagy
, A. M. Nairz
, Y. Nakahama
, K. Nakamura
, K. Nakkalil
, A. Nandi
, H. Nanjo
, E. A. Narayanan
, Y. Narukawa
, I. Naryshkin
, L. Nasella
, S. Nasri
, C. Nass
, G. Navarro
, J. Navarro-Gonzalez
, A. Nayaz
, P. Y. Nechaeva
, S. Nechaeva
, F. Nechansky
, L. Nedic
, T. J. Neep
, A. Negri
, M. Negrini
, C. Nellist
, C. Nelson
, K. Nelson
, S. Nemecek
, M. Nessi
, M. S. Neubauer
, J. Newell
, P. R. Newman
, Y. W. Y. Ng
, B. Ngair
, H. D. N. Nguyen
, J. D. Nichols
, R. B. Nickerson
, R. Nicolaidou
, J. Nielsen
, M. Niemeyer
, J. Niermann
, N. Nikiforou
, V. Nikolaenko
, I. Nikolic-Audit
, P. Nilsson
, I. Ninca
, G. Ninio
, A. Nisati
, R. Nisius
, N. Nitika
, J-E. Nitschke
, E. K. Nkadimeng
, T. Nobe
, D. Noll
, T. Nommensen
, M. B. Norfolk
, B. J. Norman
, M. Noury
, J. Novak
, T. Novak
, R. Novotny
, L. Nozka
, K. Ntekas
, N. M. J. Nunes De Moura Junior
, J. Ocariz
, A. Ochi
, I. Ochoa
, S. Oerdek
, J. T. Offermann
, A. Ogrodnik
, A. Oh
, C. C. Ohm
, H. Oide
, M. L. Ojeda
, Y. Okumura
, L. F. Oleiro Seabra
, I. Oleksiyuk
, G. Oliveira Correa
, D. Oliveira Damazio
, J. L. Oliver
, R. Omar
, Ö. O. Öncel
, A. P. O’Neill
, A. Onofre
, P. U. E. Onyisi
, M. J. Oreglia
, D. Orestano
, R. Orlandini
, R. S. Orr
, L. M. Osojnak
, Y. Osumi
, G. Otero y Garzon
, H. Otono
, M. Ouchrif
, F. Ould-Saada
, T. Ovsiannikova
, M. Owen
, R. E. Owen
, V. E. Ozcan
, F. Ozturk
, N. Ozturk
, S. Ozturk
, H. A. Pacey
, K. Pachal
, A. Pacheco Pages
, C. Padilla Aranda
, G. Padovano
, S. Pagan Griso
, G. Palacino
, A. Palazzo
, J. Pampel
, J. Pan
, T. Pan
, D. K. Panchal
, C. E. Pandini
, J. G. Panduro Vazquez
, H. D. Pandya
, H. Pang
, P. Pani
, G. Panizzo
, L. Panwar
, L. Paolozzi
, S. Parajuli
, A. Paramonov
, C. Paraskevopoulos
, D. Paredes Hernandez
, A. Pareti
, K. R. Park
, T. H. Park
, F. Parodi
, J. A. Parsons
, U. Parzefall
, B. Pascual Dias
, L. Pascual Dominguez
, E. Pasqualucci
, S. Passaggio
, F. Pastore
, P. Patel
, U. M. Patel
, J. R. Pater
, T. Pauly
, F. Pauwels
, C. I. Pazos
, M. Pedersen
, R. Pedro
, S. V. Peleganchuk
, O. Penc
, E. A. Pender
, S. Peng
, G. D. Penn
, K. E. Penski
, M. Penzin
, B. S. Peralva
, A. P. Pereira Peixoto
, L. Pereira Sanchez
, D. V. Perepelitsa
, G. Perera
, E. Perez Codina
, M. Perganti
, H. Pernegger
, S. Perrella
, K. Peters
, R. F. Y. Peters
, B. A. Petersen
, T. C. Petersen
, E. Petit
, V. Petousis
, A. R. Petri
, C. Petridou
, T. Petru
, A. Petrukhin
, M. Pettee
, A. Petukhov
, K. Petukhova
, R. Pezoa
, L. Pezzotti
, G. Pezzullo
, L. Pfaffenbichler
, A. J. Pfleger
, T. M. Pham
, T. Pham
, P. W. Phillips
, G. Piacquadio
, E. Pianori
, F. Piazza
, R. Piegaia
, D. Pietreanu
, A. D. Pilkington
, M. Pinamonti
, J. L. Pinfold
, B. C. Pinheiro Pereira
, J. Pinol Bel
, A. E. Pinto Pinoargote
, L. Pintucci
, K. M. Piper
, A. Pirttikoski
, D. A. Pizzi
, L. Pizzimento
, A. Plebani
, M.-A. Pleier
, V. Pleskot
, E. Plotnikova
, G. Poddar
, R. Poettgen
, L. Poggioli
, S. Polacek
, G. Polesello
, A. Poley
, A. Polini
, C. S. Pollard
, Z. B. Pollock
, E. Pompa Pacchi
, N. I. Pond
, D. Ponomarenko
, L. Pontecorvo
, S. Popa
, G. A. Popeneciu
, A. Poreba
, D. M. Portillo Quintero
, S. Pospisil
, M. A. Postill
, P. Postolache
, K. Potamianos
, P. A. Potepa
, I. N. Potrap
, C. J. Potter
, H. Potti
, J. Poveda
, M. E. Pozo Astigarraga
, R. Pozzi
, A. Prades Ibanez
, S. R. Pradhan
, J. Pretel
, D. Price
, M. Primavera
, L. Primomo
, M. A. Principe Martin
, R. Privara
, T. Procter
, M. L. Proffitt
, N. Proklova
, K. Prokofiev
, G. Proto
, J. Proudfoot
, M. Przybycien
, W. W. Przygoda
, A. Psallidas
, J. E. Puddefoot
, D. Pudzha
, H. I. Purnell
, D. Pyatiizbyantseva
, J. Qian
, R. Qian
, D. Qichen
, Y. Qin
, T. Qiu
, A. Quadt
, M. Queitsch-Maitland
, G. Quetant
, R. P. Quinn
, G. Rabanal Bolanos
, D. Rafanoharana
, F. Raffaeli
, F. Ragusa
, J. L. Rainbolt
, J. A. Raine
, S. Rajagopalan
, E. Ramakoti
, L. Rambelli
, I. A. Ramirez-Berend
, K. Ran
, D. S. Rankin
, N. P. Rapheeha
, H. Rasheed
, D. F. Rassloff
, A. Rastogi
, S. Rave
, S. Ravera
, B. Ravina
, I. Ravinovich
, M. Raymond
, A. L. Read
, N. P. Readioff
, D. M. Rebuzzi
, A. S. Reed
, K. Reeves
, J. A. Reidelsturz
, D. Reikher
, A. Rej
, C. Rembser
, H. Ren
, M. Renda
, F. Renner
, A. G. Rennie
, A. L. Rescia
, S. Resconi
, M. Ressegotti
, S. Rettie
, W. F. Rettie
, M. M. Revering
, E. Reynolds
, O. L. Rezanova
, P. Reznicek
, H. Riani
, N. Ribaric
, B. Ricci
, E. Ricci
, R. Richter
, S. Richter
, E. Richter-Was
, M. Ridel
, S. Ridouani
, P. Rieck
, P. Riedler
, E. M. Riefel
, J. O. Rieger
, M. Rijssenbeek
, M. Rimoldi
, L. Rinaldi
, P. Rincke
, G. Ripellino
, I. Riu
, J. C. Rivera Vergara
, F. Rizatdinova
, E. Rizvi
, B. R. Roberts
, S. S. Roberts
, D. Robinson
, M. Robles Manzano
, A. Robson
, A. Rocchi
, C. Roda
, S. Rodriguez Bosca
, Y. Rodriguez Garcia
, A. M. Rodríguez Vera
, S. Roe
, J. T. Roemer
, O. Røhne
, R. A. Rojas
, C. P. A. Roland
, A. Romaniouk
, E. Romano
, M. Romano
, A. C. Romero Hernandez
, N. Rompotis
, L. Roos
, S. Rosati
, B. J. Rosser
, E. Rossi
, E. Rossi
, L. P. Rossi
, L. Rossini
, R. Rosten
, M. Rotaru
, B. Rottler
, D. Rousseau
, D. Rousso
, S. Roy-Garand
, A. Rozanov
, Z. M. A. Rozario
, Y. Rozen
, A. Rubio Jimenez
, V. H. Ruelas Rivera
, T. A. Ruggeri
, A. Ruggiero
, A. Ruiz-Martinez
, A. Rummler
, Z. Rurikova
, N. A. Rusakovich
, S. Ruscelli
, H. L. Russell
, G. Russo
, J. P. Rutherfoord
, S. Rutherford Colmenares
, M. Rybar
, P. Rybczynski
, A. Ryzhov
, J. A. Sabater Iglesias
, H. F-W. Sadrozinski
, F. Safai Tehrani
, S. Saha
, M. Sahinsoy
, B. Sahoo
, A. Saibel
, B. T. Saifuddin
, M. Saimpert
, G. T. Saito
, M. Saito
, T. Saito
, A. Sala
, A. Salnikov
, J. Salt
, A. Salvador Salas
, F. Salvatore
, A. Salzburger
, D. Sammel
, E. Sampson
, D. Sampsonidis
, D. Sampsonidou
, J. Sánchez
, V. Sanchez Sebastian
, H. Sandaker
, C. O. Sander
, J. A. Sandesara
, M. Sandhoff
, C. Sandoval
, L. Sanfilippo
, D. P. C. Sankey
, T. Sano
, A. Sansoni
, M. Santana Queiroz
, L. Santi
, C. Santoni
, H. Santos
, A. Santra
, E. Sanzani
, K. A. Saoucha
, J. G. Saraiva
, J. Sardain
, O. Sasaki
, K. Sato
, C. Sauer
, E. Sauvan
, P. Savard
, R. Sawada
, C. Sawyer
, L. Sawyer
, C. Sbarra
, A. Sbrizzi
, T. Scanlon
, J. Schaarschmidt
, U. Schäfer
, A. C. Schaffer
, D. Schaile
, R. D. Schamberger
, C. Scharf
, M. M. Schefer
, V. A. Schegelsky
, D. Scheirich
, M. Schernau
, C. Scheulen
, C. Schiavi
, M. Schioppa
, B. Schlag
, S. Schlenker
, J. Schmeing
, E. Schmidt
, M. A. Schmidt
, K. Schmieden
, C. Schmitt
, N. Schmitt
, S. Schmitt
, N. A. Schneider
, L. Schoeffel
, A. Schoening
, P. G. Scholer
, E. Schopf
, M. Schott
, S. Schramm
, T. Schroer
, H-C. Schultz-Coulon
, M. Schumacher
, B. A. Schumm
, Ph. Schune
, H. R. Schwartz
, A. Schwartzman
, T. A. Schwarz
, Ph. Schwemling
, R. Schwienhorst
, F. G. Sciacca
, A. Sciandra
, G. Sciolla
, F. Scuri
, C. D. Sebastiani
, K. Sedlaczek
, S. C. Seidel
, A. Seiden
, B. D. Seidlitz
, C. Seitz
, J. M. Seixas
, G. Sekhniaidze
, L. Selem
, N. Semprini-Cesari
, A. Semushin
, D. Sengupta
, V. Senthilkumar
, L. Serin
, M. Sessa
, H. Severini
, F. Sforza
, A. Sfyrla
, Q. Sha
, E. Shabalina
, H. Shaddix
, A. H. Shah
, R. Shaheen
, J. D. Shahinian
, M. Shamim
, L. Y. Shan
, M. Shapiro
, A. Sharma
, A. S. Sharma
, P. Sharma
, P. B. Shatalov
, K. Shaw
, S. M. Shaw
, Q. Shen
, D. J. Sheppard
, P. Sherwood
, L. Shi
, X. Shi
, S. Shimizu
, C. O. Shimmin
, I. P. J. Shipsey
, S. Shirabe
, M. Shiyakova
, M. J. Shochet
, D. R. Shope
, B. Shrestha
, S. Shrestha
, I. Shreyber
, M. J. Shroff
, P. Sicho
, A. M. Sickles
, E. Sideras Haddad
, A. C. Sidley
, A. Sidoti
, F. Siegert
, Dj. Sijacki
, F. Sili
, J. M. Silva
, I. Silva Ferreira
, M. V. Silva Oliveira
, S. B. Silverstein
, S. Simion
, R. Simoniello
, E. L. Simpson
, H. Simpson
, L. R. Simpson
, S. Simsek
, S. Sindhu
, P. Sinervo
, S. N. Singh
, S. Singh
, S. Sinha
, S. Sinha
, M. Sioli
, K. Sioulas
, I. Siral
, E. Sitnikova
, J. Sjölin
, A. Skaf
, E. Skorda
, P. Skubic
, M. Slawinska
, I. Slazyk
, I. Sliusar
, V. Smakhtin
, B. H. Smart
, S. Yu. Smirnov
, Y. Smirnov
, L. N. Smirnova
, O. Smirnova
, A. C. Smith
, D. R. Smith
, J. L. Smith
, M. B. Smith
, R. Smith
, H. Smitmanns
, M. Smizanska
, K. Smolek
, P. Smolyanskiy
, A. A. Snesarev
, H. L. Snoek
, S. Snyder
, R. Sobie
, A. Soffer
, C. A. Solans Sanchez
, E. Yu. Soldatov
, U. Soldevila
, A. A. Solodkov
, S. Solomon
, A. Soloshenko
, K. Solovieva
, O. V. Solovyanov
, P. Sommer
, A. Sonay
, A. Sopczak
, A. L. Sopio
, F. Sopkova
, J. D. Sorenson
, I. R. Sotarriva Alvarez
, V. Sothilingam
, O. J. Soto Sandoval
, S. Sottocornola
, R. Soualah
, Z. Soumaimi
, D. South
, N. Soybelman
, S. Spagnolo
, M. Spalla
, D. Sperlich
, B. Spisso
, D. P. Spiteri
, L. Splendori
, M. Spousta
, E. J. Staats
, R. Stamen
, E. Stanecka
, W. Stanek-Maslouska
, M. V. Stange
, B. Stanislaus
, M. M. Stanitzki
, B. Stapf
, E. A. Starchenko
, G. H. Stark
, J. Stark
, P. Staroba
, P. Starovoitov
, R. Staszewski
, C. Stauch
, G. Stavropoulos
, A. Stefl
, A. Stein
, P. Steinberg
, B. Stelzer
, H. J. Stelzer
, O. Stelzer
, H. Stenzel
, T. J. Stevenson
, G. A. Stewart
, J. R. Stewart
, M. C. Stockton
, G. Stoicea
, M. Stolarski
, S. Stonjek
, A. Straessner
, J. Strandberg
, S. Strandberg
, M. Stratmann
, M. Strauss
, T. Strebler
, P. Strizenec
, R. Ströhmer
, D. M. Strom
, R. Stroynowski
, A. Strubig
, S. A. Stucci
, B. Stugu
, J. Stupak
, N. A. Styles
, D. Su
, S. Su
, X. Su
, D. Suchy
, K. Sugizaki
, V. V. Sulin
, M. J. Sullivan
, D. M. S. Sultan
, L. Sultanaliyeva
, S. Sultansoy
, S. Sun
, W. Sun
, O. Sunneborn Gudnadottir
, N. Sur
, M. R. Sutton
, H. Suzuki
, M. Svatos
, P. N. Swallow
, M. Swiatlowski
, T. Swirski
, A. Swoboda
, I. Sykora
, M. Sykora
, T. Sykora
, D. Ta
, K. Tackmann
, A. Taffard
, R. Tafirout
, Y. Takubo
, M. Talby
, A. A. Talyshev
, K. C. Tam
, N. M. Tamir
, A. Tanaka
, J. Tanaka
, R. Tanaka
, M. Tanasini
, Z. Tao
, S. Tapia Araya
, S. Tapprogge
, A. Tarek Abouelfadl Mohamed
, S. Tarem
, K. Tariq
, G. Tarna
, G. F. Tartarelli
, M. J. Tartarin
, P. Tas
, M. Tasevsky
, E. Tassi
, A. C. Tate
, G. Tateno
, Y. Tayalati
, G. N. Taylor
, W. Taylor
, A. S. Tegetmeier
, P. Teixeira-Dias
, J. J. Teoh
, K. Terashi
, J. Terron
, S. Terzo
, M. Testa
, R. J. Teuscher
, A. Thaler
, O. Theiner
, T. Theveneaux-Pelzer
, D. W. Thomas
, J. P. Thomas
, E. A. Thompson
, P. D. Thompson
, E. Thomson
, R. E. Thornberry
, C. Tian
, Y. Tian
, V. Tikhomirov
, Yu. A. Tikhonov
, S. Timoshenko
, D. Timoshyn
, E. X. L. Ting
, P. Tipton
, A. Tishelman-Charny
, K. Todome
, S. Todorova-Nova
, L. Toffolin
, M. Togawa
, J. Tojo
, S. Tokár
, O. Toldaiev
, G. Tolkachev
, M. Tomoto
, L. Tompkins
, E. Torrence
, H. Torres
, E. Torró Pastor
, M. Toscani
, C. Tosciri
, M. Tost
, D. R. Tovey
, T. Trefzger
, P. M. Tricarico
, A. Tricoli
, I. M. Trigger
, S. Trincaz-Duvoid
, D. A. Trischuk
, A. Tropina
, L. Truong
, M. Trzebinski
, A. Trzupek
, F. Tsai
, M. Tsai
, A. Tsiamis
, P. V. Tsiareshka
, S. Tsigaridas
, A. Tsirigotis
, V. Tsiskaridze
, E. G. Tskhadadze
, M. Tsopoulou
, Y. Tsujikawa
, I. I. Tsukerman
, V. Tsulaia
, S. Tsuno
, K. Tsuri
, D. Tsybychev
, Y. Tu
, A. Tudorache
, V. Tudorache
, S. B. Tuncay
, S. Turchikhin
, I. Turk Cakir
, R. Turra
, T. Turtuvshin
, P. M. Tuts
, S. Tzamarias
, E. Tzovara
, Y. Uematsu
, F. Ukegawa
, P. A. Ulloa Poblete
, E. N. Umaka
, G. Unal
, A. Undrus
, G. Unel
, J. Urban
, P. Urrejola
, G. Usai
, R. Ushioda
, M. Usman
, F. Ustuner
, Z. Uysal
, V. Vacek
, B. Vachon
, T. Vafeiadis
, A. Vaitkus
, C. Valderanis
, E. Valdes Santurio
, M. Valente
, S. Valentinetti
, A. Valero
, E. Valiente Moreno
, A. Vallier
, J. A. Valls Ferrer
, D. R. Van Arneman
, A. Van Der Graaf
, H. Z. Van Der Schyf
, P. Van Gemmeren
, M. Van Rijnbach
, S. Van Stroud
, I. Van Vulpen
, P. Vana
, M. Vanadia
, U. M. Vande Voorde
, W. Vandelli
, E. R. Vandewall
, D. Vannicola
, L. Vannoli
, R. Vari
, M. Varma
, E. W. Varnes
, C. Varni
, D. Varouchas
, L. Varriale
, K. E. Varvell
, M. E. Vasile
, L. Vaslin
, M. D. Vassilev
, A. Vasyukov
, L. M. Vaughan
, R. Vavricka
, T. Vazquez Schroeder
, J. Veatch
, V. Vecchio
, M. J. Veen
, I. Veliscek
, I. Velkovska
, L. M. Veloce
, F. Veloso
, S. Veneziano
, A. Ventura
, A. Verbytskyi
, M. Verducci
, C. Vergis
, M. Verissimo De Araujo
, W. Verkerke
, J. C. Vermeulen
, C. Vernieri
, M. Vessella
, M. C. Vetterli
, A. Vgenopoulos
, N. Viaux Maira
, T. Vickey
, O. E. Vickey Boeriu
, G. H. A. Viehhauser
, L. Vigani
, M. Vigl
, M. Villa
, M. Villaplana Perez
, E. M. Villhauer
, E. Vilucchi
, M. Vincent
, M. G. Vincter
, A. Visibile
, C. Vittori
, I. Vivarelli
, E. Voevodina
, F. Vogel
, J. C. Voigt
, P. Vokac
, Yu. Volkotrub
, L. Vomberg
, E. Von Toerne
, B. Vormwald
, K. Vorobev
, M. Vos
, K. Voss
, M. Vozak
, L. Vozdecky
, N. Vranjes
, M. Vranjes Milosavljevic
, M. Vreeswijk
, N. K. Vu
, R. Vuillermet
, O. Vujinovic
, I. Vukotic
, I. K. Vyas
, J. F. Wack
, S. Wada
, C. Wagner
, J. M. Wagner
, W. Wagner
, S. Wahdan
, H. Wahlberg
, C. H. Waits
, J. Walder
, R. Walker
, K. Walkingshaw Pass
, W. Walkowiak
, A. Wall
, E. J. Wallin
, T. Wamorkar
, K. Wandall-Christensen
, A. Wang
, A. Z. Wang
, C. Wang
, C. Wang
, H. Wang
, J. Wang
, P. Wang
, P. Wang
, R. Wang
, R. Wang
, S. M. Wang
, S. Wang
, T. Wang
, T. Wang
, W. T. Wang
, W. Wang
, X. Wang
, X. Wang
, X. Wang
, Y. Wang
, Y. Wang
, Z. Wang
, Z. Wang
, Z. Wang
, C. Wanotayaroj
, A. Warburton
, A. L. Warnerbring
, N. Warrack
, S. Waterhouse
, A. T. Watson
, H. Watson
, M. F. Watson
, E. Watton
, G. Watts
, B. M. Waugh
, J. M. Webb
, C. Weber
, H. A. Weber
, M. S. Weber
, S. M. Weber
, C. Wei
, Y. Wei
, A. R. Weidberg
, E. J. Weik
, J. Weingarten
, C. Weiser
, C. J. Wells
, T. Wenaus
, B. Wendland
, T. Wengler
, N. S. Wenke
, N. Wermes
, M. Wessels
, A. M. Wharton
, A. S. White
, A. White
, M. J. White
, D. Whiteson
, L. Wickremasinghe
, W. Wiedenmann
, M. Wielers
, R. Wierda
, C. Wiglesworth
, H. G. Wilkens
, J. J. H. Wilkinson
, D. M. Williams
, H. H. Williams
, S. Williams
, S. Willocq
, B. J. Wilson
, D. J. Wilson
, P. J. Windischhofer
, F. I. Winkel
, F. Winklmeier
, B. T. Winter
, M. Wittgen
, M. Wobisch
, T. Wojtkowski
, Z. Wolffs
, J. Wollrath
, M. W. Wolter
, H. Wolters
, M. C. Wong
, E. L. Woodward
, S. D. Worm
, B. K. Wosiek
, K. W. Woźniak
, S. Wozniewski
, K. Wraight
, C. Wu
, C. Wu
, J. Wu
, M. Wu
, M. Wu
, S. L. Wu
, S. Wu
, X. Wu
, Y. Wu
, Z. Wu
, Z. Wu
, J. Wuerzinger
, T. R. Wyatt
, B. M. Wynne
, S. Xella
, L. Xia
, M. Xia
, M. Xie
, A. Xiong
, J. Xiong
, D. Xu
, H. Xu
, L. Xu
, R. Xu
, T. Xu
, Y. Xu
, Z. Xu
, R. Xue
, B. Yabsley
, S. Yacoob
, Y. Yamaguchi
, E. Yamashita
, H. Yamauchi
, T. Yamazaki
, Y. Yamazaki
, S. Yan
, Z. Yan
, H. J. Yang
, H. T. Yang
, S. Yang
, T. Yang
, X. Yang
, X. Yang
, Y. Yang
, Y. Yang
, W-M. Yao
, C. L. Yardley
, J. Ye
, S. Ye
, X. Ye
, Y. Yeh
, I. Yeletskikh
, B. Yeo
, M. R. Yexley
, T. P. Yildirim
, K. Yorita
, C. J. S. Young
, C. Young
, N. D. Young
, Y. Yu
, J. Yuan
, M. Yuan
, R. Yuan
, L. Yue
, M. Zaazoua
, B. Zabinski
, I. Zahir
, A. Zaio
, Z. K. Zak
, T. Zakareishvili
, S. Zambito
, J. A. Zamora Saa
, J. Zang
, R. Zanzottera
, O. Zaplatilek
, C. Zeitnitz
, H. Zeng
, J. C. Zeng
, D. T. Zenger Jr
, O. Zenin
, T. Ženiš
, S. Zenz
, D. Zerwas
, M. Zhai
, D. F. Zhang
, G. Zhang
, J. Zhang
, J. Zhang
, K. Zhang
, L. Zhang
, L. Zhang
, P. Zhang
, R. Zhang
, S. Zhang
, T. Zhang
, Y. Zhang
, Y. Zhang
, Y. Zhang
, Y. Zhang
, Z. Zhang
, Z. Zhang
, H. Zhao
, T. Zhao
, Y. Zhao
, Z. Zhao
, Z. Zhao
, A. Zhemchugov
, J. Zheng
, K. Zheng
, X. Zheng
, Z. Zheng
, D. Zhong
, B. Zhou
, H. Zhou
, N. Zhou
, Y. Zhou
, Y. Zhou
, Y. Zhou
, C. G. Zhu
, J. Zhu
, X. Zhu
, Y. Zhu
, Y. Zhu
, X. Zhuang
, K. Zhukov
, N. I. Zimine
, J. Zinsser
, M. Ziolkowski
, L. Živković
, A. Zoccoli
, K. Zoch
, A. Zografos
, T. G. Zorbas
, O. Zormpa
& L. Zwalinski

Contributions

All authors have contributed to the publication, being variously involved in the design and the construction of the detectors, in writing the software, calibrating subsystems, operating the detectors and acquiring data and finally analysing the processed data. The ATLAS Collaboration members discussed and approved the scientific results. This Article was prepared by a subgroup of authors appointed by the ATLAS Collaboration and subjected to an internal collaboration-wide review process. All authors reviewed and approved the final version of the paper.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Thomas Kuhr, Spandan Mondal and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

University of South Africa, Department of Physics, Pretoria, South Africa.

University of Zululand, KwaDlangezwa, South Africa.

Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Morocco.

Departamento de Física Téorica y del Cosmos, Universidad de Granada, Granada, Spain

Universidad San Sebastian, Recoleta, Chile

Supplementary information

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

The ATLAS Collaboration. Transforming jet flavour tagging at ATLAS. Nat Commun 17, 541 (2026). https://doi.org/10.1038/s41467-025-65059-6

Download citation

Received: 27 May 2025
Accepted: 07 October 2025
Published: 14 January 2026
Version of record: 14 January 2026
DOI: https://doi.org/10.1038/s41467-025-65059-6