Introduction

There are a number of approaches to the design of electronic replicas of biological neurons and their networks. Such engineered systems select configurable models of biological elements and create electronic implementations of the models. For example, reduced models may implement leaky integrate-and-fire (LIF) units1,2, while more mechanistic models instantiate Hodgkin–Huxley dynamics3,4. Most work focuses on specific models of biological processes—e.g., the sophistication of the neuron model5,6,7, the dynamics of the synapse8,9,10, or local learning rules11,12,13.

No matter what computational model the electronic systems implement, a cross-cutting system-level issue that must be resolved in neuromorphic systems is the representation of time. How should one unit of time in a biological system be represented in the electronic model? Early neuromorphic systems represented time in an implicit fashion, whereby the progression of physical time in the biological system corresponded to the progression of physical time in the electronic model. A constant scale factor was sometimes applied so that time in the electronic system corresponded to a scaled version of biological real time. Numerous platforms including BrainScaleS14, SpiNNaker15, Neurogrid16, and Braindrop17 use this implicit approach.

While this idea is appealing and can be successfully applied to small-scale neuromorphic systems, the implicit approach faces three major challenges when we scale up the number of neurons and synapses in the system. First, electronic systems are wire-limited—the number of wires needed to directly model the connectivity in a biological network is prohibitive in a practical, cost-effective setting. This forces large-scale neuromorphic systems to use time-multiplexed wires to emulate the connectivity of biological networks. This multiplexing introduces a sharing constraint—individual wires are used for multiple connections between axons and dendrites. In turn, this means that the communication of a spike may have to be delayed due to a shared wire being actively used for another spike. As a result, spike arrival times at synapses may be perturbed in a way that does not correspond to the underlying computation—violating the requirement of implicit time representation. This problem can be mitigated by over-designing the communication infrastructure to reduce the timing jitter18,19,20, but the underlying issue is fundamental. The second issue is that computation multiplexing in some designs adds another source of unpredictability, with each core’s processing time varying according to its input activity. Third, changes in operating conditions of the electronics (voltage, temperature, and manufacturing uncertainty) impact delays and timing. In the case of voltage and temperature, the same physical electronic system may behave differently in different environments. With manufacturing variability, inconsistencies in neural coding may arise across different chips. These effects are particularly pronounced in subthreshold electronics that are widely used in the implicit approach. Because of this unpredictability, large-scale neuromorphic systems with implicit time are difficult to deploy in applications that require repeatable results.

An alternate approach is to model time explicitly. In the standard realization of this approach, the neuromorphic system includes a mechanism to synchronize the operations of all neurons and synapses. The TrueNorth system uses an externally controlled signal that is distributed to all the hardware components of the architecture21. This signal, typically operating with a frequency of 1 kHz, is used to advance time for all components of the system. The C2 large-scale cortical software simulator implemented on the Blue Gene/P architecture uses barrier synchronization to advance time, taking advantage of hardware features of the Blue Gene/P supercomputer22. Intel’s Loihi and Loihi 2 architectures also implement barrier synchronization to advance time23,24. Tianjic uses a global clock for all its coordination processes, including advancing time25. Representing time explicitly means that all the issues due to multiplexing and uncertainty outlined earlier no longer arise, and the hardware model can be made deterministic. This, in turn, vastly simplifies developing applications using the hardware since any errors encountered during algorithm development are repeatable.

A drawback of the current implementations of explicit time is that they either directly or indirectly rely on global synchronization, which limits the scalability of the overall system. In the 2D (or 3D) physical realization of an electronic system, global synchronization requires \({{{\mathcal{O}}}}(\sqrt{N})\) (or \({{{\mathcal{O}}}}(\root 3 \of {N})\)) delay because the synchronization signal has to touch all N neurons26. This means that the delay for one time step will increase by the same scaling factor. Hence, as the system size grows to hundreds of millions of neurons or more27, global synchronization will reduce system performance even though the modeled biological system has no such limitation.

We present a distributed protocol for maintaining deterministic execution in neuromorphic systems. We exploit a simple insight: as long as neurons and synapses that are directly connected are synchronized in time, we can still correctly model a biological network without global barrier synchronization. Our approach can be viewed as an extension of work in the distributed systems literature on maintaining a consistent distributed notion of time28, adapted to meet the additional requirements imposed by neuromorphic systems, such as bounded on-chip buffers for communication. Unlike prior models that rely on a central controller to detect and resolve deadlocks, our protocol utilizes local, bidirectional synchronization to prevent deadlocks entirely and scale efficiently (Supplementary Notes). We describe NeuroScale, a neuromorphic architecture that realizes our protocol in asynchronous hardware, and present hardware as well as simulation results that demonstrate the functionality and scalability of the protocol. We show that our approach provides significant benefits when the system size is scaled up compared to the global barrier approaches of TrueNorth and Loihi/Loihi 2.

When the overall system is implemented with asynchronous circuits, it eliminates the \({{{\mathcal{O}}}}(\sqrt{N})\) (or \({{{\mathcal{O}}}}(\root 3 \of {N})\)) scaling limitation; instead, our system is only limited by the same scaling laws that would apply to the biological network being modeled. In summary, our work presents a scalable approach to neuromorphic systems design.

Results

For ease of exposition, we assume that time in the neuromorphic architecture is integer-valued. When we use the phrase time or simulation time, we refer to time in the biological network being modeled; we will use wall-clock time to refer to the progression of physical time in the electronic system.

Time synchronization

To understand the requirements of time synchronization in neuromorphic systems, consider two neurons A and B where the output from neuron A is connected to neuron B. When the computation starts at wall-clock time t = 0.0, all neurons begin with identical local times of 0—i.e., \({t}_{{{{\rm{A}}}}}^{\nu }(t)=0\) and \({t}_{{{{\rm{B}}}}}^{\nu }(t)=0\) where \({t}_{{{{\rm{A}}}}}^{\nu }:{\mathbb{R}}\to {{\mathbb{Z}}}_{\ge 0}\) and \({t}_{{{{\rm{B}}}}}^{\nu }:{\mathbb{R}}\to {{\mathbb{Z}}}_{\ge 0}\) map wall-clock time to the simulation time for neurons A and B, respectively, in the neuromorphic architecture.

For correct operation, a neuron cannot advance in time until it has received all its inputs up to its current time. In other words, neuron B must have received the entire history of its possible inputs to advance in time. In particular, this means that \({t}_{{{{\rm{B}}}}}^{\nu }(t)\) can advance by one only if \({t}_{{{{\rm{A}}}}}^{\nu }(t)\ge {t}_{{{{\rm{B}}}}}^{\nu }(t)\), and B has received any output produced by A up to and including time \({t}_{{{{\rm{B}}}}}^{\nu }(t)\). If the neuromorphic architecture’s communication network guarantees first-in first-out message-passing semantics between two neurons, we can satisfy this requirement by having A send a done message to B after all the spike outputs at each time step. We remark that this network property is true for typical deterministic, lossless routing architectures such as the ones used in TrueNorth and Loihi/Loihi 2.

A second constraint that arises in neuromorphic systems is the magnitude of the gap \({t}_{{{{\rm{A}}}}}^{\nu }(t)-{t}_{{{{\rm{B}}}}}^{\nu }(t)\). If A is operating ahead of B, then B would have to buffer the entire history of spikes generated by A in time \([{t}_{{{{\rm{B}}}}}^{\nu }(t),{t}_{{{{\rm{A}}}}}^{\nu }(t)]\)—a potentially unbounded amount of state. Since hardware is finite, we must bound how far ahead A can be with respect to B. The maximum permitted value of \({t}_{{{{\rm{A}}}}}^{\nu }(t)-{t}_{{{{\rm{B}}}}}^{\nu }(t)\) is dependent on the local memory capacity and is an architecture-specific parameter, Tadv. This requirement can be enforced by having B send an advance message to A at the beginning of every simulation time step.

Note that at each time step, a neuron evaluates its spiking condition once and can spike at most once in our architecture. In summary, the operation of each neuron N can be described as the repetition of the following steps (Supplementary Fig. 1):

  • Sends advance messages to all neurons in the direct fan-in.

  • Waits for advance messages that indicate that every neuron Fo in its direct fan-out has time \({t}_{{{{{\rm{F}}}}}_{{{{\rm{o}}}}}}^{\nu }(t)\ge {t}_{{{{\rm{N}}}}}^{\nu }(t)-{T}_{{{{\rm{adv}}}}}\).

  • Updates the neuron state and produces any necessary spikes.

  • Sends done messages to all neurons in the direct fan-out.

  • Waits for done messages that indicate that every neuron Fi in its direct fan-in has time \({t}_{{{{{\rm{F}}}}}_{{{{\rm{i}}}}}}^{\nu }(t)\ge {t}_{{{{\rm{N}}}}}^{\nu }(t)\) and it has received all the spikes for time step \({t}_{{{{\rm{N}}}}}^{\nu }(t)\).

  • Advances the time step \({t}_{{{{\rm{N}}}}}^{\nu }(t)\) by one.

The value of Tadv captures how far out of step the neurons in the architecture can be with respect to each other. Also, observe that for the first Tadv time steps, the inequality \({t}_{{{{{\rm{F}}}}}_{{{{\rm{o}}}}}}^{\nu }(t)\ge {t}_{{{{\rm{N}}}}}^{\nu }(t)-{T}_{{{{\rm{adv}}}}}\) is always satisfied because the right hand side is non-positive. Hence, the second step only waits if a neuron has not received the appropriate advance message when \({t}_{{{{\rm{N}}}}}^{\nu }(t) > {T}_{{{{\rm{adv}}}}}\).

For efficiency, neuromorphic architectures are typically organized into cores distributed across a silicon chip, where each core contains a collection of neurons and their associated synapses. NeuroScale adopts the same approach, where all neurons within one core operate as a single synchronization unit and share the same simulation time step; hence, the synchronization messages outlined above are not required between individual neurons but between cores. The sequence of steps is thus applied at the core level rather than at the level of individual neurons.

We implement NeuroScale in Communicating Hardware Processes (CHP), an asynchronous hardware description language based on Hoare’s CSP29. We use the Asynchronous Circuit Tools (ACT) for designing digital asynchronous circuits30,31. For comparison, we also implement the barrier synchronization approaches of TrueNorth and Loihi, while maintaining the same underlying core architecture as NeuroScale (see Methods).

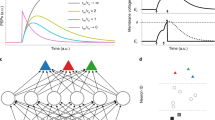
In TrueNorth, barrier synchronization advances the simulation time at regular intervals via a system-wide synchronization trigger (Fig. 1a). During each tick interval, cores read spikes from input buffers, distribute them across axons, update neuron membrane potentials, and generate output spikes. All computational operations must complete within the fixed tick duration before the next synchronization signal arrives, forcing the entire system to operate at the worst-case speed. Loihi implements a two-phase mesh-level barrier synchronization mechanism (Fig. 1b). After completing computation, cores initiate synchronization by exchanging barrier messages with neighboring cores in two phases. The first step flushes any in-flight spikes throughout the mesh network to ensure message delivery completion. The second step involves propagating a time-step-advance notification throughout the entire system, instructing cores to advance to the next time step. In contrast to TrueNorth and Loihi, NeuroScale adopts a distributed synchronization approach that eliminates the need for explicit barrier synchronization phases (Fig. 1c). Cores advance their local time steps independently through direct message passing between connected cores. This approach enables performance scaling without the global coordination overhead inherent in barrier-based methods.

Fig. 1: Comparison of synchronization protocols in NeuroScale, Loihi, and TrueNorth.
figure 1

Gray squares represent cores in the system. a TrueNorth barrier synchronization protocol. Cores begin their computation phase upon receiving a global trigger signal to advance time. This phase involves updating the states of the neurons and communicating spikes. All communication and computation must be completed within a fixed wall-clock interval. b Loihi barrier synchronization protocol. Each core exchanges barrier messages that flush any spikes in flight with its neighbors after the computation phase. This is followed by a global time-step-advance notification propagated to all cores. c NeuroScale distributed synchronization protocol. Computation and synchronization occur concurrently in a distributed fashion.

Full size image

Determinism and FPGA prototype

In addition to our CHP design, we develop a Field-Programmable Gate Array (FPGA) prototype of NeuroScale using an automated approach for emulating asynchronous hardware on commercial FPGA platforms32 (see Methods). In the following, we present the results of both FPGA measurements and hardware simulations.

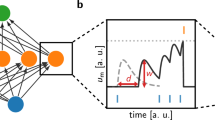
To verify NeuroScale’s deterministic execution, we compare spikes generated by our hardware prototype and hardware simulation against those generated by a software reference model. We use a recurrent neural network configuration similar to the one used to demonstrate deterministic execution in the TrueNorth design33. The network comprises 200 neurons, each with a bias of one and a threshold of 100, connected as a random graph with connection probability p = 0.2, where each synapse has a weight of one. The network is mapped onto four cores. The experimental validation is conducted on the FPGA-based hardware platform (Fig. 2a), where spike data is collected through Universal Asynchronous Receiver-Transmitter (UART) communication with the host CPU. Figure 2b illustrates the spiking activity of the network. Initially, after 100 time steps, all neurons spike simultaneously due to the same bias and threshold. This spike burst desynchronizes subsequent spikes due to random network connectivity. Over time, the spiking activity becomes irregular as excitatory inputs dominate the constant bias. Despite the complex pattern of activity, the software and hardware simulations, along with the FPGA implementation, show identical spiking activity. This 1:1 equivalence between software and hardware is crucial as it decouples algorithm design from hardware processes, enabling developers to build applications without having to contend with non-determinism in the hardware.

Fig. 2: NeuroScale hardware prototype and deterministic execution.
figure 2

a Photograph of the FPGA board during operation. The FPGA board communicates with the host CPU via the UART port, marked with a red outline. b Comparison of spiking activity between software model (dots), hardware model (orange circles), and hardware prototype (blue circles), running the same recurrent neural network. The two simulations and FPGA implementation have identical spike times, verifying deterministic execution in NeuroScale and equivalence between software and hardware. The software model is run on the Fugu SNN simulator40. The functionally equivalent Verilog model of the CHP description is generated by ACT2FPGA32.

Full size image

Scaling study

One of the key features of NeuroScale is that the architecture readily scales as the size of the system increases. Such a study cannot be performed on real hardware, since the hardware being compared corresponds to a system with a large number of chips for each different type of machine and would be prohibitively expensive. Hence, we use a detailed hardware simulation approach to compare the scaling properties of NeuroScale, TrueNorth, and Loihi.

For our scaling study, we configure a locally connected lattice network where each core communicates its spikes to itself, and to neighboring cores one hop away in the routing mesh (see Methods). With this setup, we progressively increase the total number of cores in the system and measure the total wall-clock time required to run 100 time steps. Figure 3a illustrates a pronounced scaling advantage of NeuroScale over Loihi and TrueNorth. As shown, the wall-clock time of NeuroScale remains roughly constant as the system size increases, while the wall-clock times of both TrueNorth and Loihi continuously increase with system size. This scaling advantage results from the fact that cores in NeuroScale synchronize through the exchange of local messages, unaffected by the overall system size. In contrast, cores in Loihi and TrueNorth rely on system-wide synchronization messages at every time step. As the system size (i.e., number of cores) grows, these global messages must traverse longer distances across the layout, leading to longer wall-clock times and slower execution speeds. With 16,384 cores in the system, NeuroScale outperforms Loihi and TrueNorth by more than a factor of four.

Fig. 3: Comparison of scalability in NeuroScale, Loihi, and TrueNorth.
figure 3

a Wall-clock times for systems with increasing number of cores. As the number of cores increases, the wall-clock time of NeuroScale remains steady (\({{{\mathcal{O}}}}(1)\) scaling), while the wall-clock times of Loihi and TrueNorth gradually increase (\({{{\mathcal{O}}}}(\sqrt{n})\) scaling, where n is the core count). Wall-clock times are normalized to the wall-clock time of a 256-core NeuroScale system. For a 16,384-core system, NeuroScale is over four times faster than Loihi and TrueNorth. Note that Intel’s recently announced Hala Point system has 140,544 cores. b Wall-clock times of a fixed-size network spanning 256 cores on systems of increasing size. As the system size increases, the wall-clock time of NeuroScale stays constant (\({{{\mathcal{O}}}}(1)\) scaling), while that of Loihi and TrueNorth keeps increasing (\({{{\mathcal{O}}}}(\sqrt{n})\) scaling). c Effect of locality on the speedup of NeuroScale compared to Loihi and TrueNorth. A more significant speedup is achieved when communicating cores are placed in closer physical proximity (higher locality). d Effect of activity sparsity. NeuroScale achieves higher speedup with sparser spiking activity. Sparsity is measured as the average time interval between spikes.

Full size image

Next, we evaluate a configuration in which only a small portion of the system is utilized, leaving the rest idle—a common scenario in applications prioritizing minimal energy consumption. In these situations, the goal is often to develop a network that solves a problem of interest with as few neural and synaptic resources as possible, thereby minimizing active energy consumption across the system. To compare NeuroScale, Loihi, and TrueNorth under these conditions, we use the same lattice network configuration as in Fig. 3a, and increase system size while utilizing only 256 cores out of the total. Once again, NeuroScale exhibits a significant scaling advantage, with wall-clock time remaining roughly constant as the total number of cores increases (Fig. 3b). In contrast, the wall-clock times of Loihi and TrueNorth rise progressively with system size, even though only a small fraction of the system is active in this setup.

The scaling advantage of NeuroScale, as discussed above, arises from the local synchronization between neuromorphic cores. In the network configuration of Fig. 3a, b, each core communicates with cores one hop away in the routing mesh. To examine the effects of communication distance, we vary the hop distance between one to nine, thereby varying the locality of synchronizing messages. Figure 3c presents the speedup of NeuroScale over Loihi and TrueNorth for five networks, each configured in a 128 × 128 core layout (in total 16,384 cores) with different degrees of locality. We define locality as (href − h)/(href − 1), where h is the number of hops between communicating cores and href equals nine (the maximum h tested in this setup). As shown, NeuroScale achieves greater speedup with higher locality. Automated mapping algorithms21,34,35,36 for mapping networks on neuromorphic systems often have locality as a primary objective because reducing the distance between communicating cores lowers communication traffic across the system, thereby lowering energy consumption and increasing processing speed. The trend observed in Fig. 3c underscores the importance of locality in these mapping algorithms.

Next, we examine the impact of spiking activity levels on performance. We set up a lattice network (same configuration as Fig. 3a, b) across a 128 × 128 core layout and vary spiking activity levels by adjusting the probability of neural spiking in each core. We find that the speedup of NeuroScale over Loihi and TrueNorth increases as activity levels become sparser (Fig. 3d). This occurs because the global synchronization processes in Loihi and TrueNorth, performed at the end of each time step, become a larger fraction of the overall running time when spiking activity is sparse.

Synchronization behavior

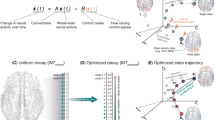
In TrueNorth and Loihi, all cores advance simulation time in unison. In contrast, NeuroScale allows cores to run ahead of one another as the dynamics of the configured network unfold. At any given wall-clock time, different NeuroScale cores may operate at different simulation times. For instance, core A may have advanced to time t, core B to time t − δt, and core C to time t + δt. The identities of leading and lagging cores can change over wall-clock time; for example, core B may catch up and overtake core A as the simulation progresses, depending on the connectivity and changing activity levels. Despite the time disparities, NeuroScale’s synchronization protocol ensures correctness of computation across the system, with all cores converging to the same time by the end of the simulation.

We illustrate the effect using a recurrent neural network consisting of sixteen neural populations P1–P16. Each population consists of a group of neurons that are recurrently connected to one another and to neurons in the subsequent population. The network is configured in an 8 × 8 core layout with each population mapped to 2 × 2 adjacent cores. Each population is configured to generate spikes at a distinct rate, thus producing a gradient of spiking activity across the multi-core system (see Methods). Cores that have higher activity run slower due to heavier load on their computation and communication circuits, whereas cores with lower activity run ahead. Different parts of the system thus maintain different measures of time, with the lagging cores eventually catching up and synchronizing with the rest by the end of the simulation (Fig. 4a). Figure 4b, c illustrate the progressive advance of simulation time in TrueNorth, Loihi, and NeuroScale, with one core selected from each of the sixteen populations described above. Each dot in the plot represents a simulation time increment for a core. As shown, TrueNorth enforces strict synchronization, requiring cores to advance time at regular intervals. Loihi introduces some optimization by allowing cores to advance time at intervals determined by system-wide activity levels, with lower activity leading to faster execution. However, similar to TrueNorth, Loihi relies on a global coordination process with all cores advancing time synchronously. Neither system can exploit connectivity and variations in local activity levels to accelerate computations. In contrast, NeuroScale cores adaptively advance simulation time, enabling the system to complete the simulation (represented by the final dot in Fig. 4b) significantly faster than Loihi and TrueNorth.

Fig. 4: Comparison of synchronization behavior in NeuroScale, Loihi, and TrueNorth.
figure 4

a Adaptive synchronization in NeuroScale. The large square represents the array of cores at a particular moment in wall-clock time. Colors indicate simulation time within each core, and arrows show the progression of wall-clock time. Cores with lower spiking activity advance time faster. b Progression of simulation time in the three systems, shown with normalized wall-clock time. Each dot represents a simulation time increment for a core. c A magnified view of subplot (b). TrueNorth cores advance time synchronously at fixed intervals. Loihi cores also advance time synchronously, but the synchronization intervals vary based on system-wide activity levels (e.g., compare the first interval with the last). NeuroScale cores advance time asynchronously, enabling them to adapt to local changes in computational loads.

Full size image

Computational overhead

NeuroScale’s distributed synchronization approach introduces modest computational overheads compared to TrueNorth and Loihi. The architecture incurs a 4.51% memory overhead per core due to temporal buffering and local synchronization management. For the lattice network configuration with 16,384 cores described in Section “Scaling study”, NeuroScale achieves 4.27× and 4.11× speedups over TrueNorth and Loihi, respectively, with energy overheads of 24.97% and 17.40%. These penalties arise from additional message hops and memory access operations for synchronization. The results demonstrate favorable performance-overhead trade-offs. A detailed breakdown and quantitative analysis are provided in Supplementary Table 1 and Supplementary Notes.

Application benchmark: maze navigation

We compare the performance of NeuroScale, Loihi, and TrueNorth in a maze navigation problem which involves an agent planning the shortest collision-free path between a source and a destination within a maze containing irregular obstacles (see Methods). Figure 5a shows an example maze, where the black sections represent obstacles and the white sections represent feasible paths. The agent finds the shortest path from the source to the destination, making the correct decision at all intersections. This problem provides a benchmark for neuromorphic systems as the solution involves fine-grained parallel computations using spike-timing dependent mechanisms37,38. In Loihi, the solution is a hundred times faster than a conventional algorithm running on a CPU26. Figure 5b shows that NeuroScale consistently outperforms Loihi and TrueNorth, achieving increasing speedup for increasing system size.

Fig. 5: Maze navigation problem.
figure 5

a An example maze. The black color represents irregular obstacles or boundaries. An agent finds the shortest collision-free path (red dashed line) from the source (S) to the destination (T). Yellow arrows depict correct decisions made at every intersection. b Speedup of NeuroScale over Loihi and TrueNorth. We test mazes of increasing size that map to 256, 1024, 4096, and 16,384 core systems respectively. NeuroScale consistently outperforms Loihi and TrueNorth. For each system size, five randomly generated mazes and selected pairs of source and destination points are tested (hollow) and the results are averaged (solid).

Full size image

Discussion

We present NeuroScale, a scalable and decentralized neuromorphic architecture that utilizes distributed synchronization to support networks of arbitrary size. Previous systems, such as TrueNorth and Loihi, rely on global synchronization to maintain deterministic execution, which results in performance limitations as system sizes increase. NeuroScale’s local synchronization mechanism leads to efficiency and high speed, and its adaptive representation of time suggests hitherto unexplored strategies for algorithm design.

We implement a software-to-hardware stack and conduct analysis from multiple perspectives to demonstrate NeuroScale’s advantages. These advantages arise from sparse and local communication, achieved through network design and mapping. In scenarios where dense communication spans the entire system, the performance advantage becomes moderate as computation time dominates synchronization overhead, reducing the relative benefit of NeuroScale’s optimized synchronization protocol (Supplementary Methods and Supplementary Fig. 2). To support both communication patterns, NeuroScale provides configurable options that modify only the core-to-core synchronization logic while keeping all other modules unchanged. Users can select between distributed and barrier synchronization protocols. Based on this observation, we are currently developing a hybrid approach that combines them as a balanced solution, addressing the shortcomings of each method and enhancing overall system performance.

Methods

NeuroScale architecture

Similar to Loihi, NeuroScale features a multi-core 2D mesh architecture. All point-to-point inter-core communication occurs in a packetized format, with messages distributed by a Network-on-Chip (NoC) that employs a destination-based dimension-order routing algorithm. Both spike messages and synchronization messages include the message type and relative address between the source core and destination core, denoted as \({{{{\rm{addr}}}}}_{{{{\rm{core}}}}}\). Additionally, spike messages carry a destination axon ID, represented as idaxon.

The NeuroScale core is the basic building block of the system and consists of several units depicted in Fig. 6. These units manage two types of memories: memory tables and memory records. Memory tables store network information and dynamics. Memory records are bit-vectors that encode binary activity, where a value of one indicates the presence of an event and zero indicates its absence. Annotations associated with the memories indicate the number of logical addresses. Multiple memories span T time steps for ramping activity and future retention, and each includes a pointer to the current local time step. The following hardware resource parameters for each core constrain the mapping of the network: up to Ncin fan-in cores, Naxin input axons, Nsyn synapses, Nn neurons, Naxout core-to-core fan-out edges, and Ncout fan-out cores. In the simulations presented in Section “Results”, we set T = 8, Ncin = Ncout = 32, Naxin = Naxout = 4096, Nsyn = 16,384, and Nn = 1024.

Fig. 6: The NeuroScale core architecture.
figure 6

The dashed box marks a single NeuroScale core that communicates with other cores through a Network-on-Chip (NoC). Memories are labeled with their logical address sizes. The components of the core are as follows. IN: receives messages, manages synchronization between cores, and sends advance messages to the core’s direct fan-ins. SYNAPSE: records incoming spikes and reads out corresponding synaptic weights. DENDRITE: accumulates synaptic inputs. NEURON: updates neural states and evaluates spiking status. FANOUT: generates spike and done messages to the core’s direct fan-outs. LEARNING: collects activity information and adjusts synaptic weights stored in the SYNAPSE unit based on learning rules with a two-time-step window. MANAGER: serves as the central coordinator, directing all units through an event-driven protocol that uses notification signals and First-In-First-Out buffers (FIFOs) to manage the sequence of steps described in Methods.

Full size image

The IN unit manages synchronization between cores with two hash tables: one for done messages from fan-ins and the other for advance messages from fan-outs. The keys are the \({{{{\rm{addr}}}}}_{{{{\rm{core}}}}}\) carried in the synchronization messages, while the values—tcin in the Fanin Hash Table and tcout in the Fanout Hash Table—function as time gap counters. Upon receiving a done message, the associated value tcin in the Fanin Hash Table increments by one. Then, if the values for all fan-ins are positive, they are each decremented by one, and a token is enqueued into the Done FIFO. The same rule applies to advance messages, the Fanout Hash Table, and the Advance FIFO. Regarding a spike message, the value tcin is processed and the pair (tcin, idaxon) is sent to the SYNAPSE unit. Additionally, the IN unit generates an advance message to each fan-in when it receives a notification signal from the MANAGER unit.

The SYNAPSE unit manages synaptic connections in the Input Axon Table and maintains active axon records in the Input Axon Records. When it receives a (tcin, idaxon) pair from the IN unit, it updates the record and acquires the synapses linked to the idaxon, forwarding (tcin, idneuron, weight) pairs to the DENDRITE unit. It also adjusts synaptic weights based on learning packets from the LEARNING unit and generates (tcin, idneuron, δweight) pairs to correct the future dendritic accumulations if needed.

The DENDRITE unit maintains records of active dendrites and accumulates synaptic inputs from the SYNAPSE unit in its Dendritic Accumulation Table. The NEURON unit accesses this table at each time step to update membrane potentials.

The NEURON unit implements a LIF neuron model. Note that other spiking neuron models can also be utilized in the architecture. The Neuron State Table holds the dynamics of every neuron in the core. The NEURON unit checks the spiking status and sends the identities of the spiking neurons idneuron to both the FANOUT and LEARNING units.

The FANOUT unit stores information of every neuron’s fan-out edges, including idaxon and idremote of destination cores, in the Fanout Table. When a neuron spikes, the Remote Table translates each idremote to the actual relative address \({{{{\rm{addr}}}}}_{{{{\rm{core}}}}}\) in the spike messages. After sending out all spike messages at the current time step, a done message is generated for each fan-out core.

The LEARNING unit tracks activity records over a two-time-step window to apply the spike-timing dependent plasticity (STDP) learning rule. The idneuron from the NEURON unit is recorded for the current time step. Combining spiking records and dendritic records, the LEARNING unit indicates to the SYNAPSE unit whether the neurons undergo learning.

To coordinate the units, the MANAGER unit follows this sequence of steps:

  • Instructs the LEARNING unit to complete the pre-before-post learning phase.

  • Advances the memory pointers to the next time step, as follows:

    • Notifies the IN unit to block inbound messages from NoC.

    • Informs SYNAPSE, DENDRITE, and LEARNING units to shift the memory pointers.

    • Notifies the IN unit to unblock inbound messages from NoC and generate advance messages to fan-ins.

  • Instructs the LEARNING unit to complete the post-before-pre learning phase.

  • Dequeues a token from the Advance FIFO, waiting if necessary.

  • Instructs the NEURON unit to update neuron states and evaluate spiking status, generating spike messages and done messages to fan-outs.

  • Dequeues a token from the Done FIFO, waiting if necessary.

While the MANAGER unit dequeues tokens from the FIFOs, the IN unit handles enqueueing operations based on synchronization message arrivals, which can occur at any point during execution when the conditions are met. Initially, the Advance FIFO contains Tadv tokens, where Tadv = T−2 with a two-time-step learning window, and the Done FIFO is empty.

In configurations where ramping activity is not needed, NeuroScale supports an alternative implementation that reduces memory usage and relies solely on Input Axon Records to manage future incoming spikes. At each time step, before the NEURON unit assesses the spiking status of neurons, (idneuron, weight) pairs are read from the Input Axon Table and accumulated in the DENDRITE unit based on the complete Input Axon Record for the current time step. Consequently, the DENDRITE unit receives only (idneuron, weight) pairs from the SYNAPSE unit, and (idneuron, δweight) pairs for correcting future accumulation are omitted. When architectures are configured without ramping activity, the memory overhead of NeuroScale is reduced to 4.35% compared to TrueNorth and Loihi (Supplementary Table 1 and Supplementary Notes).

Network configurations

In the lattice network studied in Fig. 3, each core consists of 200 neurons, spiking with a probability of 0.01 at each time step. If one time step models 1 ms of neural activity, this configuration corresponds to a spike rate of 10 Hz. The total wall-clock time required to run 100 time steps is measured for the configured networks. For the configuration with 16,384 cores, 20 time steps are simulated as a reference due to limitations in computational resources.

The recurrent neural network studied in Fig. 4 consisted of 16 recurrently-connected neural populations (P1-P16), with each population containing 200 neurons. Populations 1 through 16 have biases of 1 through 16, respectively, with a fixed threshold of 100. Higher bias results in denser spiking activity. Connections are formed uniformly at random within populations with a probability of 0.1, and between populations with a probability of 0.05. All synaptic connections have a weight of one. The 16 populations are mapped onto an 8 × 8 core layout in adjacent sectional order.

The navigation problem of Fig. 5 uses 2D grid mazes of varying sizes: 400 × 400, 800 × 800, 1600 × 1600, and 3200 × 3200. Each maze contains obstacles occupying 40% of the grid points. Obstacle positions are selected uniformly at random, with the remaining locations forming feasible paths. The source and destination points are also selected uniformly at random. The grid is mapped to a graph, where each non-obstacle point is represented by a node, and edges are added between adjacent nodes. Due to computational resource constraints, simulations are limited to a maximum of 100 time steps.

Simulation and timing methodology

After mapping to the chip layout, network information is stored in a JSON file, which includes parameters specifying neurons, synapses, and connectivity. The CHP simulator loads and processes this file to program the chip, initializing all on-chip memories with a sequence of programming packets.

For comparing the architectures, we measure the wall-clock time required to complete a specified number of time steps. We define wall-clock time as the physical time elapsed from the moment a notification signal is sent to all cores until the moment every core completes its final time step. The CHP simulation is configured with specific timing weights based on the relative cost of operations to model wall-clock time. Note that absolute wall-clock times are technology-dependent. Our focus here is on demonstrating the scaling properties and synchronization behavior that reveal the fundamental performance characteristics of different architectures.

In each of our simulations, we set the fixed synchronization interval in TrueNorth to the longest synchronization interval in Loihi, consistent with TrueNorth’s synchronization approach.

FPGA prototyping

For FPGA emulation, we use an automated approach, ACT2FPGA32, to translate our asynchronous design into a synthesizable Verilog model with equivalent functionality. For the results of Fig. 2, we use the Digilent Genesys 2 board (XC7K325T-2FFG900C) and Vivado 2021.2 for synthesis and implementation. The FPGA board runs at 100 MHz.