Hundred-layer photonic deep learning

Abstract

In the artificial intelligence era propelled by complex computational models, photonic computing represents a promising approach for energy-efficient machine learning; however, error accumulation inherent to the analog nature limits their depth to around ten layers, restricting advanced computing capabilities towards large language models (LLMs). In this study, we identify that such error accumulation arises from propagation redundancies. By introducing perturbations on-chip to decouple computational correlations, we eliminate the redundancy and develop deep photonic learning with a single-layer photonic computing (SLiM) chip that exhibits error tolerance. The SLiM chip overcomes the depth limitations of optical neural networks, allowing for error rates to be constrained across more than 200 layers, and extends spatial depth from millimeter to hundred-meter scale, enabling a three-dimensional chip cluster. We experimentally constructed a neural network with 100 layers for image classification, along with a 0.345-billion-parameter LLM with 384 layers for text generation, and a 0.192-billion-parameter LLM with 640 layers for image generation, all achieving performances comparable to ideal simulations at 10-GHz data rate. This error-tolerant single-layer chip initiates the advancement of state-of-the-art deep learning models on efficient analog computing hardware.

Introduction

Notable progress has been witnessed in the field of artificial intelligence (AI), primarily driven by the advancement of deep learning^1,2,3,4. It is known that by extending the depth of neural network layers and the complexities of the neural network structures, a renaissance of AI debuts, and large models are developed for generating contents close to human level^{5,6,7,8,9,10,11,12,13,14}. However, the ever-increasing demand for deeper models also exacerbates the speed and energy exhaustion on digital electronic computational devices, which are unfortunately reaching their extremes^15,16,17,18.

One promising route in the saturating digital intelligence era is physical intelligence, which computes with efficient physical media, including photonics, electronics, spintronics^{19,20,21,22,23,24,25,26,27,28}. Especially, exploiting the large bandwidth and high parallelism of optics, the optical neural network (ONN) is prosperous and has potential in high-performance AI computing. In free-space lens systems and photonic integrated circuits, the spatial and temporal computing approaches have yielded prototypes in linear ONNs^29,30, multi-layer all-optical ONNs^31,32, and optoelectronic nonlinear neural networks^33,34,35,36. These neural networks facilitate sequence^34,37, image^38,39,40, video^25,32, and three-dimensional (3D) volumetric scene^41,42 processing in the optical domain. Notably, based on the evolution of integration, the silicon photonic platform represents the most mature platform to be exploited to map neural networks for the processing of the signals intelligently^{30,37,43,44,45}. The large bandwidth of the silicon photonic chip proves an ideal analog machine learning module for high-speed signal processing in the radio frequency domain^46,47.

However, existing ONNs cannot achieve the deep structures necessary for the advanced AI tasks. The primary reason is that, due to the analog nature of physical computing, numerical errors accumulated during deep-layer propagation cause the computed results to deviate significantly from the ideal simulation (Fig. 1a, left). One solution is to reach precise numerical operations by carefully calibrating the transmission properties of the system⁴⁸, or by employing multiple steps for asymptotically approaching the high-precision results^49,50. However, these approaches would require extensive spatial and temporal overhead, proving infeasible for large models containing hundred layers and billion-scale parameters. In addition, even if these approaches improve the precision of system calibration, the inherent data noise in direct proportion to the input speed remains hardly compensated⁵¹. As a result, it is still elusive to realize deep models with a high data rate based on existing analog computing methods.

Fig. 1: Single-layer photonic computing.

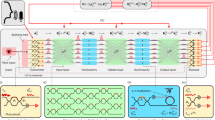
a Due to the on-chip redundancies, error accumulation arises and precludes optical neural networks (ONNs) of large depth. We propose single-layer photonic chip (SLiM) removing these redundancies and realizing bounded error rate across over 100 layers. b By injecting the propagation perturbation on chip, we decorrelate the weights for arbitrary matrices, thus eliminating the redundant propagations to minimize the error accumulation. Perturbation is further injected into the detection process and decorrelate the signals from the errors, alleviating the error-prone nonlinear layers. The single-layer propagation and detection lead to an error-tolerant photonic chip shown at the bottom panel. c The single-layer computing connects chips in the three-dimensional (3D) hundred-meter space for the execution of billion-parameter deep neural networks, supporting advanced tasks like sentence completion, image recognition, and image generation. NL, nonlinearity, MUX, wavelength multiplexing, Scalebar, 1 mm.

Instead of striving for ultrahigh precision operations with the physical architecture, it is more practical to accommodate the errors as part of the ONN and tolerate these errors during the computing^52,53. Nonetheless, realizing an error-tolerant architecture remains technically challenging. Firstly, the spread and accumulation of the noise-induced error should be inhibited. Existing photonic chip designs utilizing the MZI mesh, cross-bar mesh, and diffractive metalines require multilayer propagation for one linear matrix-vector multiplication^37,54,55,56. The multi-layer structure inevitably exacerbates the issue of error accumulation. Also, the commonly used nonlinear layers like the rectified linear unit, sigmoid⁵⁷, or optical analog activation functions^33,34,58 are not resilient to the errors and amplify the noise with detection processes, which disseminates the errors to the subsequent layers. To achieve very deep neural network architectures, it would be necessary to minimize the error propagation and bound the error rate throughout the entire ONN.

Here we report a single-layer photonic computing (SLiM) chip that removes all the error-prone propagation layers, targeting ONNs with a hundred-layer depth working at tens of GHz data rate. To realize SLiM, we incorporate perturbations within the photonic chip design, which breaks the on-chip wavelength correlation to realize arbitrary matrices and decorrelates the signal from the error with the detection-based activation function. The single-layer photonic chip minimizes the error propagation and guarantees bounded errors regardless of the number of network layers, surpassing the depth limit (DL) of ONNs. The arbitrary error-tolerant computing with single-layer propagation and detection facilitates chip clusters with computational connections at hundred-meter spatial depth. Experiments were conducted at 10 GHz to build 100-layer residual network, classifying the full ImageNet-1000 (photonic accuracy 85.2%, digital accuracy 85.9%). Transformer-based error-tolerant ONN of 384 and 640 layers with billion-scale parameters (0.345B and 0.192B) were then experimentally evaluated to generate prompted language (photonic loss function value 3.04, digital loss function value 2.96) and conditioned image (photonic loss function value 7.32, digital loss function value 7.28).

Results

Error tolerance with single-layer photonic computing

Conventionally, implementing one layer of ONN on-chip consists of multiple layers of physical propagations and nonlinear activations, which is formulated as $Y=f({\prod }_{{{\rm{i}}}=1}^{{{\rm{L}}}}{W}_{{{\rm{i}}}}X)$ with X, Y, f, and W_i denoting the input, output, nonlinear, and propagation layers (Fig. 1a, left). Taking the per-layer error into account, the final error distorted model is expressed as $Y+\Delta Y=f\left({\prod }_{{{\rm{i}}}=1}^{{{\rm{L}}}}\left({W}_{{{\rm{i}}}}+\Delta {W}_{{{\rm{i}}}}\right)\left(X+\Delta X\right)\right)$, where the relative error ${Var}(\Delta Y/Y) \sim {\sum }_{{{\rm{i}}}=1}^{{{\rm{L}}}}\left({Var}(\Delta {W}_{{{\rm{i}}}}/{W}_{{{\rm{i}}}})\right)$, meaning that the error is amplified by a factor of L after propagation. As a result, the extra layers, including the second to the final linear layer and the error-prone nonlinear function, exacerbate the error accumulation. However, in view of the computation, these layers are indispensable as the propagation layer number L in direct proportion to the output dimensions M supports a fully tunable matrix and the nonlinear layers facilitate the neuron activations. Here, we eliminate these error-prone ONN propagations and nonlinear layers by proposing a photonic chip implementing error-tolerant matrix-vector multiplications with only a single propagation layer, achieving bounded error even when deeply concatenated (Fig. 1a, right). The detailed error model is presented in [Supplementary Note 1 The error model of ONN].

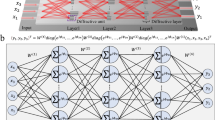
As illustrated in the Fig. 1b, in SLiM chip, the inputs ${x}_{{{\rm{i}}}}$ are assigned to specific wavelengths ${\lambda }_{{{\rm{i}}}}$. Multi-wavelength light is multiplexed into a single fiber channel and coupled into an input loading chip for the configuration of inputs ${x}_{{{\rm{i}}}}$ onto corresponding light intensities. To realize the computing matrix W, the transmission channels are modulated on chip by exerting wavefront Φ, derived from the equation $W={|G}\varPhi {|}^{2}$, where G represents chip-to-chip propagation. However, because of the spectral proximity, the wavefront Φ and the transmission matrix G both exhibit a high correlation, resulting in linear dependence on the right-hand side of the equation that does not guarantee a solution. We introduce on-chip perturbative noise to break the correlation, mathematically represented as ${{\hat{\varPhi }}_{{{\rm{k}}}}=\varPhi }_{{{\rm{k}}}}\cdot {e}^{{\mathrm{jn}}2{\mathrm{\pi \varDelta k}}/{{{\rm{\lambda }}}}_{{{\rm{i}}}}}$, where k symbolizes the waveguide coordinate with corresponding noise $\Delta k$. The linearly correlated equations are now reformulated as

$${W}_{{{\rm{i}}}}={\left|{G}_{0}{\widehat{\varPhi }}_{{{\rm{i}}}}\right|}^{2},1\le i\le N$$

(1)

The set includes N linearly independent equations, enabling the realization of arbitrary matrices. In realization of the target weight matrix W, the modulation wavefront ${\hat{\varPhi }}_{{{\rm{i}}}}$ is first solved with the calibrated propagation matrix G, after which the corresponding modulation coefficients are loaded onto the single-layer chips.

To further preclude the dissemination of these minimal errors, it necessitates a nonlinear function to decorrelate the output errors from the signals. The error-isolating function features zero gradient with respect to the error, $\partial f=0$. However, the solutions easily degenerate to trivial constant-valued functions, nullifying the contributions of subsequent layer. We inject noise to the gradient so that signal diversity is maintained while the errors are only transmitted to the subsequent layer through finite positions. The solution can be formulated as the Kronecker delta function through $f=\int \delta (x-\Delta f)$, where $\Delta f$ represents the noise position in the nonlinear function. Note that this activation function can be implemented at the detection with the analog-to-digital conversion ${\left({{\boldsymbol{\cdot }}}\right)}_{{{\rm{D}}}}$, by assigning the error-distorted values to the nearest signal levels. As an illustration in Fig. 1b, with single-layer computing, despite the input errors, fluctuation of the propagation is minimized and the outputs are then pushed towards the correct levels. It can be theoretically proved that the proposed SLiM constrains the error rate by adhering to the following inductive error bounding criterion,

$${{\mathcal{E}}}\left({\left(\left(W+\Delta W\right)\left(X+\Delta X\right)\right)}_{{{\rm{D}}}}\right)\le {{{\mathcal{E}}}}_{0},{if} \, {{\mathcal{E}}}\left(X\right)\le {{{\mathcal{E}}}}_{0}.$$

(2)

Analysis shows that the SLiM could tolerate input error with standard deviation (Std) as high as 44% ([Supplementary Note 3 Error-bounding with SLiM]). We adopted the injected propagation noise as $k\Delta d$ for $\Delta k$, and $\Delta d=20\,{{\rm{\mu }}}{{\rm{m}}}$ showed the largest rank for the 256 elements on chip, which was selected for photonic chip fabrication. The injected detection noise $\Delta x$ is data-dependent and determined during the training process. The details of the chips are provided in [Methods “Implementation of single-layer chips”]. For detailed derivations please refer to [Supplementary Note 1 The error model of ONN] and [Supplementary Note 2 Formulations of the SLiM].

The single-layer photonic chips lift the computational dimension from on-chip computing to chip-to-chip connections, such that large numbers of photonic chips can be connected to compute in the 3D space to execute billion-parameter large models (Fig. 1c), which enables the advanced AI tasks, including text completion, image recognition, and image generation.

Deep matrix multiplication with single-layer computing

We first confirm that perturbation injection of the SLiM chip facilitates matrices of any size while enabling full DOFs, which is essential for achieving error-tolerant matrix-vector multiplication (refer to Fig. 2a). The phase-voltage dynamics influenced by perturbation are measured (Fig. 2b). Leveraging the symmetric structure of the designed error-tolerant chip, an analysis was conducted on 128 spatial waveguide channels using driving voltages with 0-4 V modulation range. Four distinct wavelengths are highlighted, each demonstrating random starting phases across both spatial and spectral domains. To illustrate the decorrelated transmission properties, matrices were created using one-hot vectors derived from the wavelength channels at 1530, 1540, 1550, and 1560 nm. In Fig. 2c, the first row showcases example [${e}_{2}$, ${e}_{1}$, ${e}_{4}$, ${e}_{3}$], where ${e}_{{{\rm{i}}}}$ symbolizes the vector with the $i-{th}$ wavelength active and the others nullified. The entries can be reconfigured flexibly, with the final row represented as [${e}_{3}$, ${e}_{4}$, ${e}_{1}$, ${e}_{2}$]. The average ratios of active to inactive states were determined to be 215.16 in simulations and 244.32 in experimental conditions. This independent propagation makes it possible to implement matrices with diverse sizes and values. As illustrated in the upper section of Fig. 2d, various combinations of input sizes and output channel numbers were tested, with each iteration focusing on 100 random matrix samples. The matrices displaying full DOFs were extracted and displayed in the lower section of the figure. By gradually increasing the input size, the normalized mean square error (NMSE) recorded were found to be 0.41% (with input size 2)/0.46% (with input size 4)/0.25% (with input size 8)/0.03% (with input size 16), respectively. In contrast, the NMSEs rose significantly to 4.59%/5.77%/11.22%/17.57% without the perturbation incorporation.

Fig. 2: Realizing arbitrary matrices towards deep layers.

a The single-layer chip realizes matrices with arbitrary dimension, with entry values fully reconfigurable. The right subfigure exemplifies the single-layer chip after packaging. b The experimentally calibrated dispersive characteristics of 128 channels. The perturbation on chip leads to random initial phase. c Examples showing the decorrelated outputs with dispersive perturbation. Light of different wavelengths could be independently focused onto arbitrary positions. First to third rows designate [${e}_{2}$, ${e}_{1}$, ${e}_{4}$, ${e}_{3}$], [${e}_{1}$, ${e}_{2}$, ${e}_{3}$, ${e}_{4}$], [${e}_{4}$, ${e}_{2}$, ${e}_{1}$, ${e}_{3}$], [${e}_{3}$, ${e}_{4}$, ${e}_{1}$, ${e}_{2}$]. d Matrices with arbitrary dimension and full degree-of-freedom (DOF). The relative error is quantitatively evaluated by sweeping the input dimensions as well as the output dimensions, where the error with full DOF as delineated with dashed lines, were plotted against the method without redundancy elimination. With redundancy elimination, the relative error dropped from ~10 to ~0.1%. e Experimental relative errors for matrix multiplication with 8 outputs channels. f Analysis of the temporal stability within 10 hours. g Deep matrix multiplications across 200 layers with and without error tolerance at varying noise levels. h Maximum error rates with varying noise levels across 200 layers. Shaded area, 2 Stds. NMSE, normalized mean square error. Scalebar, 3 mm.

To experimentally assess error tolerance, we configured the output channel number as 8 and examined all possible 256 occasions. The findings indicate maximum mean error being 0.16% (Fig. 2e). Additionally, we evaluated temporal stability. During 10-hour measurements, the mean error of W for the 8-dimensional outputs stayed less than 1.0%, with highest absolute deviation being 0.90% (Fig. 2f). To verify error bounding criterion of Eq. (1), we examined the multiplication error across 200 layers by employing the perturbed propagations and detections. The resulting error rates were analyzed under varying levels of Gaussian noise ΔX at 5%/10%/20% (Fig. 2g). In contrast to the perturbed single-layer outcomes, the multi-layer results without perturbation progressively worsened, ultimately hitting 41.5%/48.8%/50.7% due to error accumulation. Meanwhile, the errors from single-layer multiplication remained below 0.76%/33.5%/44.5%. The peak error rates associated with distinct system noise levels were calculated (Fig. 2h), where the error rate with multi-layer photonic computing reached 50% once the noise level exceeded 6.5% standard deviation, indicating that performance degraded to random guessing under high-speed conditions. In comparison, the errors ${{{\mathcal{E}}}}_{0}$ resulting from error-tolerant multiplications were effectively constrained below 33.5%/41.3%/44.5% across noise levels of 10%/15%/20% standard deviation over 200 layers. Statistical assessments corroborated by proof in [Supplementary Note 3 Error-bounding with SLiM] indicate that a standard deviation of 44.3% in the inputs leads to a 47.1% error tolerance in the network, which aligns with the theoretical limit of 50% random-guess error tolerance. The implementation of single-layer computing operations thus facilitates the functioning of deep ONNs.

Deep single-layer computing beyond the spatial depth limit

The interchip computing of SLiMs can be interconnected to create an expansive ONN chip cluster (see Fig. 3a). Here we demonstrate these chip-to-chip connections can span distances ranging from centimeters up to hundreds of meters. By combining K chips into a single unit, the DOFs increase K-fold, and the spatial depth can further extend to kilometers, making it feasible to develop an ONN chip cluster with 3D computational connection. For illustration, a two-layer ONN was developed to classify the MNIST dataset as a means of assessing the spatial capabilities of the error-tolerant computing configuration ([Methods “Dataset preparation”; Methods “Network architecture and training methods”]). This experimental setup utilized five relays to extend the transmission distance between 0.1 and 45 m (Fig. 3a, right and Fig. S2; [Methods “Spatial depth of SLiM computing”]). The neural network featured inputs and hidden neurons, both with 64 dimensions. In Fig. 3b, we investigated the classification accuracies at various receiver sizes, with four detectors evenly distributed. For accuracy rates above 95%, the upper (and lower) thresholds were 8 m (0.02 m)/28 m (0.8 m)/80 m (2.5 m) determined based on 5, 20, and 70 mm aperture sizes. Furthermore, Fig. 3c highlights results from three distinct experiments at spatial depths of 0.1 m/5 m/45 m, achieving accuracies of 95.75%/95.76%/95.53%, which are close to the simulated accuracy of 95.78%. It is important to note that the findings in Fig. 3b, c are constrained by the spatial propagation depth limitations associated with individual chips. The spatial DL is defined by the equation ${\mathrm{DL}}={D}_{{\mathrm{in}}}{D}_{{\mathrm{out}}}/\lambda$, where ${D}_{{\mathrm{in}}}$, ${D}_{{\mathrm{out}}}$, and ${\mathrm{DL}}$ refer to the input aperture, output aperture, and the spatial DL, respectively. For the three aperture sizes, the spatial DLs were calculated to be 17, 65, and 230 m. When the target detectors are evenly spaced within the receiver aperture, the effective computing depth with the 4-D output is expected to be a third of the DLs (5.7, 21.7, and 76.7 m, Fig. 3b), aligning well with the effective ranges identified during classification tests (8, 28, and 80 m).

Fig. 3: Deep single-layer computing beyond the spatial depth limit.

a The computational connection between single-layer chips enable a cluster composed of extensive ONN chips. By assembling multiple chips, both the spatial depth and computational capabilities become scalable. A folded-space experimental setup was developed to assess the scalability of spatial deep computing (right panel). b Accuracies for MNIST image classification are demonstrated across varying spatial depth and receiver sizes using a two-layer ONN, with DL indicating the spatial depth limit. c Experimentally measured results are showcased for spatial depths of 0.1 m/5 m/45 m, with accuracies of 95.75%/95.76%/95.53%. d The DOF can be expanded from 256 up to 256 K by utilizing spatial ensemble techniques. The top panel displays the ensemble configuration of K = 16. e The chip ensemble can be adjusted by varying the chip ensemble size K and the gap distance H between them, which significantly enhances accuracy from 17.05 to 95.78% when adopting ensemble K to be 16, effectively surpassing the limitations of a single chip’s performance. This framework can further support kilometer-scale distances, accommodating millions of error-tolerant chips. Scalebar, 2 mm.

Since the SLiM operates with spatial-spectral propagation, it facilitates the integration of multiple chips to perform computational tasks with greater DOFs and extended operational range. As illustrated in Fig. 3d, inputs can be loaded onto numerous chips, which are interconnected and function as a single computational unit. By combining K chips, the DOFs increase by a factor of K, resulting in a total computing capability that is K times greater. The upper section of Fig. 3d displays an ensemble comprising 16 chips post-fabrication and packaging, with inter-chip gaps of 30 mm. Consequently, the cumulative DOFs rise to 4096, resulting in a computing performance of 335.54 PetaOPS. Spatial propagation depth was also enhanced by optimizing the emission aperture via a tunable configuration. The diffraction resolution can be expressed as ${\mathrm{DL}}={{\mathrm{ED}}}_{{\mathrm{in}}}{D}_{{\mathrm{out}}}/\lambda$, where E represents the tunable enhancement factor, which can be adjusted by modifying the inter-chip distance (H). By assembling 2/4/8/16 chips, the classification accuracies improved to 85.27%/94.67%/95.34%/95.78%, respectively (Fig. 3e). The tunable ensemble increased the accuracies further to 93.80%/95.78%/95.78%/95.78%, which extends the spatial depth to kilometers. Given that each chip is on a millimeter scale, such an ensemble could create an ONN chip cluster comprising chips towards million scale, elevating performance to ZettaOPS.

Reaching ONNs beyond the depth limit for advanced artificial intelligence

The error-tolerant SLiM computational propagations were then integrated to form deep ONNs with over 100 layers (see Fig. 4a). For demonstration purposes, we created deep networks aimed at image classification using the full ImageNet-1000 dataset ([Methods “Dataset preparation”; Methods “Network architecture and training methods”]). Both error-tolerant (single-layer computing) and non-error-tolerant (multi-layer computing) ONNs with residual connections were developed at depths of 18/34/100 layers, with detailed structural information outlined in Fig. S3. Figure 4b illustrates the parameter convergence for the error-tolerant ONNs with downsampling for visualization. To assess error tolerance, varying levels of noise were introduced as the layer depth increased, and the classification accuracies under these conditions are presented (Fig. 4c). In a scenario without noise (where noise-distorted layers were configured to zero), both single-layer and multi-layer networks obtained top-5 accuracies as high as 85.9% and 93.0%, respectively. However, when 5%-Std Gaussian noise was introduced, the accuracy of multi-layer networks plummeted to 37.0%. Increasing the noise standard deviation to 10%/20% further reduced their accuracies to 2.2%/1.2% at the 2nd/10th layers, respectively. In contrast, the single-layer networks exhibited accuracies of 85.5%/85.6%/81.2%. Notably, a significant decline in accuracy for the single-layer networks to 16.4% was only recorded when the noise reached a 50% standard deviation.

Fig. 4: 100-layer error-tolerant ONN.

a Deep ONNs were constructed using inter-chip computational propagation. High-speed inputs, organized into an 8-channel modulator array, were directed to the transmitter (inset) and loaded onto the single-layer chip. b Deep ONNs were trained for the complete ImageNet-1000 classification, with parameters including perturbed weights and perturbed nonlinearity downscaled to a 120-dimensional representation here. The grids in white/gray represent weights +1/−1, respectively. c Analysis was conducted for the deep ONNs involved in classifying the ImageNet-1000 dataset. The networks were tested against various levels of Gaussian noise featuring different standard deviations (Stds), focusing on both the ONNs with single-layer and multi-layer chip implementation as noise gradually distorted the layers. d Experiments with different depths and operational frequencies. The results indicate consistent improvements in performance with increased network depth for the ONN based on the single-layer chip, in stark contrast to the significant decline in classification accuracy seen in multi-layer ones at elevated frequencies. Error bars represent twice the Stds., with detailed values provided in [Supplementary Note 4 Computing capabilities of single-layer photonic chip]. A.u., arbitrary unit.

Utilizing error tolerance, we assessed the performance of the developed deep ONNs at high speeds. In the experiments, the operations in ONN were decomposed to 8 × 8 matrix computations, with inputs being loaded onto an 8-channel input array before being sent to the transmitter array ([Methods “Deep neural network with SLiM chips”]). Figure S11 illustrates the measured high-speed characterization with eye diagrams, covering frequency ranges from 1 to 10 GHz. From Fig. 4d, we observe that the error-tolerant ONNs with 18/34/100 layers operate at 1/5/10 GHz, stably achieving high accuracies of 80.9%/83.8%/85.9% and 80.7%/83.8%/85.7% at the 1 and 5-GHz settings, respectively. Even at the maximum speed of 10 GHz, the accuracies remained relatively high at 80.4%/83.2%/85.4%, showing only a slight decline by up to 0.48% from the ideal simulations. In contrast, the multi-layer ONNs experienced significant performance degradation, recording accuracies of only 3.6%/10.6%/15.5% at 1 GHz, with further declines to 0.58%/1.2%/1.4% and 0.46%/0.62%/0.34% at 5 and 10 GHz, respectively. Intermediate activation results are provided in Fig. S3. The error evaluation throughout the entire deep ONN indicated that the analog noise at the highest frequency of 10 GHz is equal to Gaussian noise with Stds ranging from 20 to 50%. This noise could be effectively mitigated in the single-layer photonic chip.

To illustrate the SLiM chips in larger AI models, we developed several variations of ONN models akin to GPT (generative pretrained transformer), featuring parameters of 5 million/30 million/60 million/0.117 billion/0.345 billion, which correspond to network depths of 8/16/32/48/96 layers and the error-tolerant matrix multiplications were employed (Fig. S4, [Methods “Dataset preparation”; Methods “Network architecture and training methods”]). Figure 5a presents the experimental outcomes from 356 token samples from the evaluation dataset ([Methods “Deep neural network with SLiM chips”]). As the model size increased, the average loss (with standard deviation) decreased from 4.91 (0.4108) for the 5-million-parameter model to 4.10 (0.4844)/3.72 (0.4950)/3.34 (0.5753)/3.04 (0.5864) for the 30-million/60-million/0.117-billion/0.345-billion-parameter models, respectively. Concurrently, the token prediction accuracies improved significantly, rising from 28.58 to 34.51%/37.29%/40.14%/43.92%. To further assess the predictable performance enhancements realized by enlarging the model size, we examined the trend of the scaling law. We specifically fitted the number of parameters (in millions) and their corresponding loss values to the function $L=\beta {N}^{-{{\rm{\alpha }}}}$. The analysis revealed a strong Pearson correlation of 0.9956, with parameters β as 5.97 and α as 0.116. We also provided standard input prompts that were not included in the training or testing datasets to the language model, which in turn generated human-like responses (Fig. 5b). At each generation step, the error-tolerant single-layer chips produce a token pool with top 80% probability threshold (highlighted in green) and a token was generated. The full sentence was constructed based on four recursive generations. The output token closely matched the ideal simulations, displaying only minor variations in individual probabilities. Figure S4 provides a comprehensive overview of the parameters in the whole network along with the intermediate activations for the tested sentences.

Fig. 5: Billion-parameter error-tolerant ONNs with single-layer photonic chip.

a The scaling behavior of the large language ONN models constructed with single-layer computing is illustrated alongside experimental results. As the network size increases from 5 million to 30 million, 60 million, 0.117 billion, and up to 0.345 billion parameters, there is a noticeable decrease in loss from 4.91 down to 3.04, accompanied by a rise in accuracy from 28.58% up to 43.92%, with error bars measuring half the Std derived from the experiments, while the scaling law is described by the solid line indicating the fitting power function. b The generated outputs based on sentence prompts were chosen from the token pool, which was created by the language models, maintaining the top 80% probability; individual probabilities are indicated in brackets. A complete sentence consists of four output steps. c In the conditional image generation, two examples were drawn from six categories, all produced via the single-layer photonic chip. d The bounded error rate across 640 layers during a 10-step image generation process. e The FID (Fréchet inception distance) features of the images generated was analyzed, with numerical calculations made to measure the feature distances from the true ImageNet distribution for the single-layer photonic computing models under noise-free conditions, as well as under 0.2-Std and 0.5-Std noise distortions.

An error-tolerant SLiM model containing 16 blocks and 64 layers was then developed to produce conditional images each with 256 × 256 pixels, utilizing the ImageNet dataset for training (see Fig. S5). After the training phase, the error-tolerant chips generated images across six categories (Fig. 5c). In the experiments, the error rates remained within 37.2%/38.6%/40.2%/38.8%/42.1%/39.1% for these categories (Fig. 5d). For the assessment of the fidelity of these generated images against the actual dataset, we randomly evaluated 24,000 images from the trained model across three noise conditions numerically: zero, 0.2-Std (akin to the noise level observed from the 10-GHz experiments, [Supplementary Note 3 Error-bounding with SLiM], Fig. S3), and 0.5-Std (strongly distorted inputs). Following standard procedures, FID (Fréchet inception distance) features with 2048-D were computed for each input image. We then compared the averaged features exhibiting different noise levels to those from the actual ImageNet dataset. The average errors for the models with zero noise and 0.2-Std noise were 0.019/0.012, with Stds of 0.027/0.028, respectively (Fig. 5e). In comparison, the model with 0.5-Std noise showed a larger average error of −0.078 with a Std of 0.089. This indicates that while the outputs from the noise-free and low-noise models remain close to the ideal simulation, the absence of error tolerance results in significant divergence in output features when higher noise levels are encountered.

Discussion

In summary, we introduce deep error-tolerant SLiM, which benefits from both scalable reconfigurability and robust error correction capabilities. Given that current optical computing systems still struggle with shallow depths, the approach of SLiM represents a significant advancement toward practical applications of physics-based analog machine learning systems by enabling deep ONNs with over 100 layers. Our findings demonstrate a substantial model comprising billion-level parameters for general-purpose generation in diverse modalities with similar performances to the digital implementations, which aligns well with the requirements of sophisticated machine learning frameworks. The SLiM could use universal data transmission channels, allowing the chip to harness the inherent computational capacity of physical processes with extra modulators for matrix construction. With a calibrated modulation efficiency of 1.7 µW/π (VπL = 0.753 V-cm, as elaborated in [Methods “Low-power phase modulation”] and Fig. S6), the chip could realize competitive energy efficiency. Additional calculations are detailed in [Supplementary Note 4 Computing capabilities of single-layer photonic chip]. See [Supplementary Table S1 Comparisons of deep AI performances] for comparison with existing techniques.

The introduction of the error-tolerant single chip breaks the spatial barriers and represents a pivotal step toward universal computing. In essence, we introduce the photonic version of chiplets with SLiM, where the error-tolerant chip eliminates spatial limitations through post-manufacturing ensembles. The showcased setup of 16-chiplets ensemble is capable of executing Peta operations per second at a frequency of 10 GHz. Remarkably, the system’s error tolerance can endure input noise levels of at least 20% standard deviation, and even up to 44% standard deviation, as confirmed in [Supplementary Note 3 Error-bounding with SLiM]. This resilience aligns well with the signal fluctuations encountered in sub-THz optoelectronic devices, suggesting the potential to enhance the computing capabilities of each chip by 10 up to 100 times through faster data transmission⁵⁹. Additionally, the ensemble of chips supports scalable computing over distances ranging from centimeters up to kilometers, with the potential to develop ZettaOPS (10²¹ operations per second) supercomputing cluster with million-scale chips. This evolution moves beyond the limitations of existing chiplet technologies mostly with planar connections. By capitalizing on the widespread nature of data propagation, the single-layer chip can leverage the inherent computational capacity of physical processes, potentially integrating trillions of physical nodes, thus transforming into a ubiquitous intelligent computing network.

Methods

Implementation of single-layer chips

Chip fabrication

The SLiM chips were designed and produced using a silicon-on-insulator platform to showcase their capabilities effectively. The primary single-layer chip integrated both transmitter and emitter functions, serving a critical role in propagation-based data processing. Light was input through waveguide edge couplers, then split via multi-modal interferometers and subsequently routed to a 256-element array. During the propagation of signals on chip, dispersive perturbation was introduced by progressively extending guided-wave distances. Thermal-optical phase shifters enabled independent phase adjustments for each element in the array, with routing made possible by a grating coupler array. The receiver component comprised 256 on-chip germanium photodiodes, each individually connected to the printed circuit board (PCB). The circuit diagram of the SLiM chip is displayed in Fig. S14. A separate low-power modulator chip was fabricated using the same process, which featured an 8 × 8 transmitter array. Each modulator was designed as an all-pass carrier-based ring structure associated with an emission grating. To optimize the efficiency of phase modulation while minimizing energy consumption, the modulators operated in an over-coupling mode. The input-loading chip included interconnected ring modulators arranged in a cascade, linked through a shared bus waveguide. Each modulator demonstrated a 3-dB bandwidth exceeding 35 GHz as confirmed by process control monitoring assessments; however, due to the limitations of the testing equipment, measurements indicated a bandwidth of only 10 GHz. Tapered edge couplers were utilized to facilitate input and output connections.

Chip packaging. Electrical packaging

PCB boards were designed and manufactured to serve as the interface for the chip. By employing gold wire bonding technology, electrical connections were formed between the chip bond pads and the pins on the PCB board. This setup facilitated the interface for the 256-channel phase shifter and receiver array on each chip. Seven multichannel connectors (Samtec ERF8-040-05.0) were mounted on the PCB bottom layer to enhance electrical connectivity. The input-loading chip was wire-bonded onto a high-frequency PCB (Rogers RO3006) to minimize gold wire lengths and reduce parasitic inductance. This high-frequency PCB utilized a grounded coplanar waveguide structure to maintain a transmission line impedance of 50 ohms. Additionally, a grounding structure and shielding vias were incorporated between channels to ensure electromagnetic shielding. Multi-channel signals were subsequently interfaced through side-mounted high-speed connectors (Gwave SMA-KHD7) (see Fig. S8b). Die Bonding: the assembly of the PCB and metal substrate was secured using M2.5 screws. The error-tolerant chip and NTC thermistor were then affixed to the metal substrate with silver epoxy, finalizing the die bonding process after curing the epoxy at 110 degrees Celsius. Optical Packaging: for optical signal transmission, an 8-channel fiber array (FA) with a 127 μm pitch was employed, formed by fusing single-mode fibers with ultra-high numerical aperture (NA) fibers to convert the mode field diameter from 3 to 9 μm. The optical interface of the error-tolerant chip featured a 7-channel edge coupler array with pitches aligned to the FA. Straight waveguides were added on both ends, serving as the alignment aids, ensuring precise coupling between the error-tolerant chip and the FA through motorized 6-axis stages. The measured alignment loss between the chip and the FA was 3.1 dB per facet, and the FA was securely attached to the chip with UV curing. The input-loading chip utilized single-lensed fibers for edge coupling, resulting in an alignment loss of 1.5–2.0 dB per facet. Packaging was conducted using a 1550-nm light source. Thermal Control: to effectively manage heat dissipation, thermal silicone grease (Thermalright TF8) was applied to attach the Peltier cooler and heat sink fins to the metal substrate of the error-tolerant chip. The Peltier cooler and NTC thermistor (B3950 10 K) were connected to a TEC controller, enabling precise temperature regulation through proportional–integral–derivative control. Furthermore, a fan mounted on the heat sink enhanced heat dissipation from the chip module.

Chip calibration

To evaluate the modulation characteristics of the phase modulation array, we implemented an on-axis interference system. As shown in Fig. S9a, b, the input laser beam was split using a fiber splitter, with one path directed to the chip and the other collimated to serve as the reference beam. The interference pattern resulting from this setup was captured using an infrared sensor (ARTCAM-991SWIR), as illustrated in Fig. S9c. We then applied a control voltage to each individual phase shifter, varying it from 0 to 4 volts. By fitting the resulting data to a sinusoidal function, as demonstrated in Fig. S9d, we extracted the initial phase values and the relationship between phase and voltage. The modeling of the modulators is based on the recognition that the phase shift, $\Delta \phi$, induced by the grating is influenced by the refractive index change, n, which is proportional to the applied voltage V from the Ohm’s law. This relationship can be expressed as $\Delta \phi \propto \Delta n\propto \Delta {V}^{2}$. Furthermore, the phase variation is related to the intensity of interference between the signal and reference beams, represented by a sinusoidal function. The detected intensity is parameterized as $I(\phi )={p}_{1}\sin \left({p}_{2}{V}^{2}+{p}_{3}\right)+{p}_{4}$, where these four parameters, ${p}_{1},{p}_{2},{p}_{3},{p}_{4}$ denote the signal amplitude, modulation coefficients, the initial phase, and background light, respectively. After measuring interference intensities at various voltages, an iterative fitting process employing the nonlinear least squares method was applied to determine all parameters, enabling us to calculate the phase terms from ${p}_{2}$ to ${p}_{3}$. This calibration process was conducted repeatedly for all wavelengths analyzed in the study using a tunable laser (TSL-570, Santec). The experiments spanned a wavelength range from 1480 to 1640 nm, with 10 nm stepsize to demonstrate performance across a broad spectrum. Modulation curves for 24 wavelengths spanning ITU channels C13 to C59 were measured for these experiments (as illustrated in Fig. S13). High-speed calibration to assess the on-chip signal quality across various input frequencies, we calibrated optical signals within the range of 1–10 GHz. A 25-GHz waveform generator (Keysight M8195A) produced non-return-to-zero signal sequences, which were fed into the ring modulator. Signal detection was performed using a germanium photodetector from an error-tolerant chip and a commercial InGaAs photodetector. The resulting photocurrents were recorded with a 10-GHz oscilloscope (Tektronix MSO64B). To ensure the modulator and detectors were appropriately biased, we employed 40-GHz bias tees (Anritsu K251) for high-speed signals transmission and detection. Figure S11 displays the eye diagrams obtained from the experiments. Both the on-chip photodetector and the germanium photodetector showcased distinctly defined open eye patterns at frequencies of 1, 5, and 10 GHz. However, at the frequency of 10 GHz, some distortion in the eye pattern was noted, which was due to the limitations of the testing setup. Nevertheless, the system effectively demonstrated signal transmission and detection capabilities up to 10 GHz. Following detailed bandwidth evaluations, deep neural networks were studied, designed for tasks including image classification and general-purpose generation (Figs. 4, 5 and S1).

Dedicated control board

To demonstrate the integration of control and detection-based nonlinear functionalities, we developed a specialized application-specific integrated circuit (ASIC) interface that links the modules and performing the detection perturbation and perturbed weight loading. Upon receiving signals, an analog-to-digital converter (ADC) transition the analog signals into the digital domain. The detected signals are the perturbed with biases implemented on board with parallel access to registers, effectively implementing the nonlinear functions and bypassing the need for memory read/write operations. Figure S10 presents an illustrative example of the packaged chip featuring the ASIC interface.

Specifically, the ADC, equipped with 256 channels, digitized the detected analog signals after they pass through 249-K gain transimpedance amplifiers. The resulting digital signals are subsequently processed by the application-specific unit, capable of executing nonlinear activation functions. These functionalities are tailored for the detection perturbations, with the perturbation data stored directly on the board, thus facilitating processing tasks while minimizing the memory access. The results from detection perturbation are then converted again to analog regime for the driving of the subsequent propagation modules. The controller board is designed with two driving arrays: one array drives the propagation modulators using 256 digital-to-analog converters (DACs) for perturbed weight loading, while the other DACs manage the ring modulators, transmitting signals to subsequent processing layers.

Low-power phase modulation

To achieve minimized energy consumption, we introduced a strategy that employs ring resonators along with electrical modulation-induced carrier plasma dispersion. This design capitalizes on resonance within the ring cavity to improve phase modulation effectiveness while simultaneously minimizing amplitude modulation via over-coupling of the ring structure. The approach involves the application of electro-optical modulation for phase shifting. A chip featuring an array of ring resonators was fabricated to conduct experiments on electro-optic modulation. The assembled chip, as shown in Fig. S6, underwent both electrical and optical packaging processes. Noteworthy elements of modulation, especially the NP-doped ring structure, are illustrated in Fig. S6b. The emitted pattern from the chip, captured through a focal plane arrangement (Fig. S6c), illustrated the phase modulation process, which was further analyzed through interference patterns in conjunction with a reference beam (Fig. S6d). By varying the input voltage from 0 to 4.0 V, we attained a phase shift of 0.07 radians, registering a power consumption of about 18.96 nW at an input of 4.0 V. Through mode-coupling analysis, it was determined that a π-phase shift would correspondingly consume approximately 1.7 µW.

Dataset preparation

Language corpus dataset

The language corpus dataset was derived from a selection of text pages from the Wikipedia dump dated 20240220 (available at https://dumps.wikimedia.org/enwiki/20240220/). Sentences shorter than 64 characters were omitted, and the tokenized dataset consists of a vocabulary of 8000 tokens. This dataset was divided into training and evaluation sets, containing 2,172,312 and 241,370 sentences, respectively. During the training process, initial tokens from the training sentences were input to predict subsequent tokens. The predicted tokens were then compared with the actual tokens to compute losses, which guided the model’s training. For evaluation, a total of 356 samples from ten different sentences were utilized, and the average accuracies, loss values, and standard deviations of loss are presented in Fig. 5a.

ImageNet-dataset

The ImageNet dataset⁶⁰ comprises labeled images that encompass 1000 different object categories. It contains a training set of 1,281,167 samples and a testing set of 50,000 samples, with each image having 224 × 224 pixels. Data augmentation techniques applied to the training set include random resizing, cropping, horizontal flipping, and color adjustments (brightness, contrast, and saturation variations of 0.4). For the testing set, a center crop was used. In the context of 1000-category recognition, each sample was encoded into multi-wavelength light input. The categories were grouped into 10 sets of 100, each having 500 testing samples. Figure 4d presents the average accuracies alongside their corresponding standard deviations. For the image generation experiments, six data categories were utilized for training. The dataset includes 7800 training samples and 300 testing samples, with each resized to an image of 256 × 256 pixels, serving as the ground truth of training.

MNIST-dataset

The MNIST dataset comprises handwritten digits across ten categories, containing 60,000 samples for training and 10,000 samples for testing. Each image, with a resolution of 28 × 28 pixels, was converted into 64 dimensions through principal component analysis. For the evaluation of deep single-layer chip cluster, each sample from the ten categories was transformed into an input encoded with multi-wavelength light intensity. The findings from this analysis are documented in Fig. 3.

Network architecture and training methods

ImageNet classification

To tackle the ImageNet classification task, we developed a deep neural network architecture comprising up to 100 layers. This architecture, which includes 18-layer, 34-layer, and 100-layer networks, is based on a residual connection framework. Each of these networks contains four blocks with sizes structured as [3, 8, 35, 3] for the 100-layer version (and [2, 2, 2, 2] for the 18-layer version, and [3, 4, 6, 3] for the 34-layer version). Each block is equipped with two error-tolerant convolutional layers, each utilizing a kernel size of 3, in addition to the residual connections. The convolutional operations are decomposed into fundamental matrix-vector multiplications, which are executed by encoding the input vector onto light intensity across eight different wavelengths. Subsequently, the light at these wavelengths is modulated with pre-trained arbitrary weight matrices. The combined effect of these multiplications facilitates the required convolution operations within the deep learning framework. We employed a cross-entropy loss function together with a stochastic gradient descent (SGD) optimizer, initialized with a learning rate of 0.4 (which was reduced by a factor of 10 every 30 epochs), a momentum of 0.9, and a weight decay of 2 × 10⁻⁵, to train the networks over a span of 90 epochs across all three architectures. We also evaluated digital models of the same size to the 100-layer SLiM network. For both networks with 11.475 MegaByte parameters, the SLiM network reached 85.4% accuracy, while the network of same size with 32-bit floating point weights reached 79.19% accuracy.

Large language model

The foundational components of the deep neural networks utilized in the language models were built on transformers, organized into four error-tolerant linear layers and one attention block. The attention mechanism was structured into multiple heads, enabling multi-head attention. We closely adhered to the specifications of the GPT-2 model regarding the number of layers, dimensions, and attention heads, assigning configurations of 2, 4, 8, 12, and 24 attention blocks, with dimensions set to 256, 512, 640, 768, 1024, and head counts of 4, 8, 10, 12, 16, resulting in a total of 4, 16, 32, 48, and 96 layers, respectively. The training employed a cross-entropy loss function alongside the SGD optimizer, initialized at a learning rate of 0.001 (which decayed proportionally to the current step relative to the total steps) and a weight decay value of 1 × 10⁻². The networks were trained until convergence, requiring 11, 18, 79, 132, and 240 GPU hours for their respective configurations.

Conditioned image generation

The ONN designed for conditioned generation was based on a transformer architecture, comprising four error-tolerant linear layers alongside the attention block. This network specifically featured 16 attention blocks, each with 1024-D inputs and 16 heads. The vocabulary for image generation was segmented into 4096 words using VQ-VAE⁶¹, while a GPT training methodology was utilized to generate subsequent tokens in the following scale. Commencing with one token with a class-conditioned embedding at the 1 × 1 scale, the network processes this through all 16 blocks to predict the generation of subsequent tokens, following a scaling order of 1, 2, 3, 4, 5, 6, 8, 10, 13, and 16. The resultant 16 × 16 tokens were decoded into an image with a resolution of 256 × 256 × 3. The employed loss function was cross-entropy, and the AdamW optimizer was utilized with parameters β₁ = 0.9, β₂ = 0.95, learning rate set to 0.0005 (decreasing proportionally to the ratio of current steps to total steps), and batch size set to 128. The training process took around 576 GPU-hours to reach convergence.

Scalable photonic neural network

For the centimeter- to hundred meter-scale photonic AI computing experiment, we constructed a two-layer fully connected (FC) network composed of fault-tolerant matrices sized (64, 64) and (64, 10). The output from this network is a 10-dimensional classification result. Implementing the error-tolerant two-layer FC structure required the decomposition of matrix-vector multiplications into smaller groups of 4 × 4 matrix units. Each unit was encoded by modulating the input’s intensity across multi-wavelength light, which was then adjusted according to pre-trained weights to achieve the necessary arbitrary matrix multiplications. A cross-entropy loss function was utilized, and the SGD optimizer, configured with an initial learning rate of 0.01 and a momentum of 0.9 was employed for 60 epochs to fine-tune the network parameters.

Spatial depth of SLiM computing

In our demonstration of a deep single-layer chip cluster (Fig. S2), we utilized a packaged chip that was connected to a specialized control board, facilitating rapid electrical adjustments. After modulation, the emitted light was directed through a grating, which featured unique initial phases and amplitudes. A plano-convex cylindrical lens (LJ1636L2-C, Thorlabs) was employed to collimate the divergent light from a one-dimensional array of 128 emitters, maintaining a consistent horizontal separation of 15 mm between the chip and the lens, corresponding to the lens’s focal length. This configuration effectively reduced light divergence in the transverse direction, thereby concentrating energy along the grating array.

The setup incorporated a series of five mirrors (PF20-03-G01, Thorlabs) with reflectance greater than 95%, allowing for wireless transmission through five successive reflections, which significantly extended the propagation distance. This enabled long-range experiments covering distances from centimeters to nearly one hundred meters. Upon propagation, the light was captured by a camera lens (Nikon 50 mm 1.8D) aimed at the detector array to analyze the resulting propagation outcomes across various receiving ranges, ranging from 5 to 70 mm. Figure S12 presents four distinct matrices observed at propagation distances of 0.5, 5.0, and 45 m before lens imaging, all demonstrating relative errors within 2% (0.97%, 1.14%, and 0.86%, respectively).

The integration of multiple SLiM chips using an ensemble method significantly enhances both the spatial depth and scale, as well as the computational flexibility. The maximum spatial scale, identified as the spatial DL, can be deduced by examining the diffraction behavior. The diffraction limit of the system’s receiver aperture, denoted as ${D}_{{\mathrm{out}}}$, is mathematically represented as ${D}_{{\mathrm{out}}}=0.5\cdot \lambda /N.A.$, where N.A. signifies the NA derived from the emission aperture, De, and the propagation distance, represented as N.A. = (1/2)${D}_{{\mathrm{in}}}/{\mathrm{DL}}$. Therefore, the relationship ${\mathrm{DL}}={D}_{{\mathrm{in}}}{D}_{{\mathrm{out}}}/\lambda$, is established. Implementing the ensemble method with integrated chips not only broadens the spatial scale by increasing aperture sizes but enhances the DOFs as well, thus augmenting the overall computational capacity. This scalable spatial and computational ability paves the way for the development of extensive computing clusters utilizing error-tolerant chips. As illustrated in Fig. 3, an ensemble of 16 chips demonstrates a computing capability of 335.54 Peta OPS, and the potential incorporation of millions of chips over distances spanning kilometers could elevate the system’s performance into the ZettaOPS domain.

Deep neural network with SLiM chips

During the construction of the deep network, to avoid the non-differentiable issue of the perturbed nonlinear activations, in the gradient propagation phase, gradients for weights exceeding an absolute value of one were clipped, while gradients within bounds navigated past the nonlinear layers. Specifically, the forward nonlinear function is delineated as (x)_D = 1 for x ≥ 0 and −1 for x < 0. The adjusted gradient for this procedure is expressed as (x)’_D = 1 for −1 ≤ x ≤ 1 and 0 otherwise. This tailored gradient descent framework proficiently facilitates the training of deep ONNs through the noise perturbed nonlinearities. After training to determine the neural network parameters, we decompose the inference processes into elementary matrix-vector multiplications. We segment extensive matrix operations into a series of smaller operational units. During the experimental phase, the network was executed using 8 × 8 elemental matrix cores (Figs. 4 and 5), with input data allocated across eight ITU wavelength channels (multi-channel lasers CBDX-NC-NC-NC-NC, Fig. S13) facilitated by a dense wavelength division multiplexing multiplexer, across a propagation distance of 0.5 m. The phase terms for realizing each matrix are realized by trained offline, taking 0.167 s on one 3090 Ti GPU. High-speed input and output signals were managed and detected using arbitrary waveform generators (Keysight M8195A) and oscilloscopes (Tektronix MSO64B), with perturbed weights loaded by the controller board. The illustration of the experiment system is presented in Fig. S1. The outputs are captured and activated by feeding the result to the dedicated control board.

In our deep network evaluations, the standard deviations of the observed errors ranged from 6% to 20% of signal intensity; however, due to SLiM operations, the error-affected inputs transformed into noise-reduced activations, facilitating their transfer to subsequent layers. This error mitigation occurs at each layer, enhancing the resilience of the network within the context of a 100-layer deep neural network. As depicted in Fig. 4d, the experimental measurements reveal standard deviations at operational frequencies of [1 G/5 G/10 G] corresponding to values of [5.757%/5.845%/6.240%], [5.182%/5.331%/5.893%], and [4.454%/4.352%/4.776%] for 18-layer, 34-layer, and 100-layer SLiM networks, respectively. Conversely, the standard deviations for multi-layer chips were recorded at [1.482%/0.494%/0.482%], [2.432%/1.071%/0.533%], and [2.922%/0.660%/0.297%]. The intermediate outputs from the 100-layer neural network and the ideal simulated results are illustrated in Fig. S3. These intermediate results are rescaled by a factor of 110 and adjusted for uniform column widths for presentation. The per-layer error rates are detailed in the upper section of Fig. S3b, indicating that the experimental outcomes at speeds of 1, 5, and 10 G achieved average error rates of 9.04%, 9.22%, and 10.34%, respectively. These error rates align within the established error assessment range influenced by Gaussian noise standard deviations, as presented in the lower section of Fig. S3b, yielding error rates of 10.48%, 11.56%, and 18.78% under 15%, 20%, and 50% standard deviations of noise, respectively.