Electromagnetic viscosity supported anomalous electric field in the electron diffusion region of collisionless magnetic reconnection

Abstract

Kinetic-scale electromagnetic fluctuations are frequently observed in the reconnection electron diffusion region. However, their potential to accelerate magnetic reconnection through anomalous effects remains a topic of debate, with a lack of direct in-situ observational evidence. Using the unprecedented high-resolution data from Magnetospheric Multiscale mission, we directly and systematically calculate the secular field-particle energy exchange rate and anomalous electric fields associated with electromagnetic fluctuations within 13 electron diffusion regions observed in Earth’s magnetotail. Our findings reveal that the electromagnetic anomalous viscosity is the primary contributor to the anomalous electric field induced by electromagnetic fluctuations within the electron diffusion region. The maximum contribution of the anomalous viscosity can account for up to ~ 20% of the fast reconnection electric field, though it is typically less than 5% in most cases. We further find that locally growing electromagnetic fluctuations tend to accelerate reconnection, while locally damping electromagnetic fluctuations inhibit it. These results offer insights into the coupling between kinetic-scale electromagnetic fluctuations and magnetic reconnection in collisionless plasmas.

Introduction

Magnetic reconnection is a fundamental process responsible for fast energy conversion in astrophysical, space, and laboratory plasma systems^1,2,3. It is implicated in explosive phenomena such as fast radio bursts and X-ray bursts^4,5,6, solar flares^7,8, and planetary substorms^9,10. A long-standing question in magnetic reconnection is how the plasma decouples from magnetic fields in the electron diffusion region (EDR). In collisional plasmas, Coulomb collisions provide the resistivity necessary for the decoupling of magnetic fields and plasmas, and for energy dissipation within the diffusion region^11,12,13. However, in collisionless plasmas, Coulomb collisions between particles are negligible due to the large mean free path compared to the characteristic system size^14,15,16,17. Therefore, alternative dissipation mechanisms must be considered in collisionless magnetic reconnection.

The electron pressure gradient and electron inertial effect in the electron momentum equation are two candidate mechanisms for breaking magnetic field lines in collisionless EDR^18,19. Recent particle-in-cell (PIC) simulations have shown that the electron pressure gradient term can support the reconnection electric field in fast collisionless reconnection^20,21. This finding has been corroborated by high-resolution spacecraft observations^22,23,24. In addition, wave-particle interactions have been proposed as another possible dissipation mechanism. Field-particle interactions associated with electromagnetic (EM) fluctuations can participate in reconnection via effective particle scattering and diffusion, providing anomalous resistivity resembling Coulomb collisions²⁵. These interactions, termed anomalous effects, include anomalous drag, viscosity, and transport, and are proposed to affect the temporal behavior of fast reconnection in collisionless plasmas^{26,27,28,29,30}. The relevant waves or instabilities that contribute to anomalous effects involve lower-hybrid drift instabilities^31,32, whistler waves^28,29,33,34, drift kink instabilities³⁵, Buneman instabilities³⁶, electron Kelvin-Helmholtz instabilities^37,38,39, and plasmoid-induced turbulence^40,41.

Fluctuations near the lower-hybrid frequency (LHF) have drawn considerable attention as a candidate responsible for anomalous effects⁴². Electrostatic (ES) LHF fluctuations are typically observed at boundaries with a strong density gradient, both in symmetric and asymmetric reconnection. These ES fluctuations primarily emerge in the low plasma β region away from the EDR. Although ES LHF fluctuations can also survive at the center of reconnecting current sheets when a large guide field reduces the β value therein^32,43, EM LHF fluctuations are more frequently detected near and within the EDR^{28,29,39,44,45,46,47,48}. It is commonly recognized that anomalous electric field contributed by LHF fluctuations are negligible compared to the electron pressure gradient term within the EDR^21,49. However, there are still some studies that suggest that an anomalous electric field arising from LHF fluctuations is significant^{28,29,30,32,50,51}. One of the reasons for the emergence of these different viewpoints is that the PIC simulations are constrained by artificial parameters, making it difficult to achieve realistic ion-to-electron mass ratios and large electron plasma to gyrofrequency ratios (ω_pe/ω_ce)^42,52. Although the anomalous effects have been quantified in asymmetric reconnection by in-situ observation⁵³, comparable evidence for their importance within the EDR of symmetric reconnection is still lacking. Therefore, it is essential to directly quantify and systematically assess the anomalous effects within the EDR of symmetric reconnection using high-resolution in-situ measurements, in order to better understand the role of EM fluctuations in reconnection.

Here, we use data from the Magnetospheric Multiscale (MMS) mission⁵⁴ (see Methods section) to directly characterize the secular field-particle energy exchange rate and anomalous effects of EM fluctuations within 13 EDRs of symmetric reconnection observed in the Earth’s magnetotail. These EM fluctuations appear near the local LHF range. The results show that the EM fluctuations can provide anomalous effects within EDRs and are primarily through the EM anomalous viscosity term ${{{\boldsymbol{T}}}}_{{\mathrm{EM}}}=-\frac{ < \delta (n{{\bf{V}}})\times \delta {{\bf{B}}} > }{ < n > }$. The maximum contribution of ${{{\boldsymbol{T}}}}_{{\mathrm{EM}}}$ is up to approximately 20% of the reconnection electric field, while it is less than 5% inside most EDRs. The positive/negative effects of these EM fluctuations on the reconnection electric field are closely related to the growing/damping state of these EM fluctuations.

Results

Observations of electromagnetic fluctuations inside EDR

Table 1 presents 13 EDR events associated with EM fluctuations in the magnetotail (see Methods section)⁵⁵. An EDR of magnetotail reconnection was encountered by the MMS spacecraft at approximately 20:24:07 UT on June 17, 2017, when the spacecraft were positioned around [−19.3, −11.1, 3.6] R_E in Geocentric Solar Magnetospheric (GSM) coordinates^56,57,58. Figure 1b–i illustrate MMS2 observations during this reconnecting current sheet crossing in the local current sheet (LMN) coordinate system. The reversal of B_L from negative to positive (Fig. 1b) and the positive electron jet V_eL (Fig. 1c) suggest that MMS crossed the reconnecting current sheet from the +L side of the reconnection X-line, as depicted in Fig. 1a. The reconnection electric field E_R is directed along the +M direction in this LMN coordinate system, and a large out-of-plane electron jet was observed along the −M direction with V_eM ~−1800 km/s. The magenta rectangle marks the EDR of this reconnection event (see Methods section), where the electron frozen-in condition is broken, i.e., ${{{\bf{E}}}}^{{\prime} }={{\bf{E}}}+{{{\bf{V}}}}_{{{\rm{e}}}}\times {{\bf{B}}}\ne 0$, and concomitant observed non-zero energy dissipation ${{\bf{J}}}\cdot {{\bf{E}}}{\prime}$, crescent-shaped electron velocity distribution⁵⁶, the enhancement of electron agyrotropy and thermal Mach number⁵⁹.

Fig. 1: First column: EM fluctuations were observed in the vicinity of the electron diffusion region (EDR 2 in Table 1).

During this interval, the four MMS spacecraft formed a tetrahedron with a quality factor of ~0.984. The average spacing among the four spacecraft was about 26 km ~4 d_e, where 1 d_e is 7 km given an average electron density of 0.56 cm⁻³. a illustrates the spacecraft trajectory and propagating of EM fluctuations, b three components of magnetic field, c electron bulk velocity, d electric field fluctuations, e spectrum of E, f magnetic field fluctuations, g spectrum of B, h ellipticity, i electron beta ${\beta }_{e}$. The vectors are shown in local boundary normal (LMN) coordinates, refer to Wang et al.⁵⁵, and references therein, where L is along the reconnecting magnetic field direction, N is the normal direction of the current sheet, M is the out-of-plane direction of the current sheet, and N = L × M completes the right-hand coordinate system. To perform statistical analysis, we uniformly adjust the +M of all EDR events to the direction of the reconnection electric field, i.e., E_R > 0 in all EDR events in this work. The second and third columns: estimated frequency-wave number (f-k) power spectrum of EM fluctuations in the vicinity of the reconnection site. j–l show the f-k_L, f-k_M, and f-k_N of EM fluctuations in the B_L < 0 side (20:24:03-20:24:07 UT) of the reconnecting current sheet, while m–o show the f-k_L, f-k_M, and f-k_N of E_M fluctuations in the B_L > 0 side (20:24:07-20:24:11 UT). The wave number k has been normalized by $\sqrt{{\rho }_{e}{\rho }_{i}}$, where ${\rho }_{e}$ and ${\rho }_{i}$ are the electron and ion gyration radii, respectively. The dashed lines denote the fit of the linear dispersion relation $f=\frac{{V}_{{ph}}}{2\pi }{{\bf{k}}}$.

Table 1 EDR events list

EM fluctuations with frequencies between ~1 and 16 Hz, near the local LHF, were enhanced in the vicinity of the EDR (Fig. 1e, g). The electric field fluctuations ${{\rm{\delta }}}{{\bf{E}}}$ are dominated by $\delta {E}_{N}$ with a maximum amplitude of ~5 mV/m (Fig. 1d), while the magnetic field fluctuations ${{\rm{\delta }}}{{\bf{B}}}$ show similar amplitudes in three directions with a maximum amplitude of ~1 nT (Fig. 1f). These EM fluctuations are mainly inclined to right-handed circular polarization (Fig. 1h), indicating they may be whistler-branch waves. The EM fluctuations primarily exist in the center of the reconnecting current sheet, where ${\beta }_{e}$ is greater than 1 (Fig. 1i). These features are consistent with the EM turbulence in the EDR observed in three-dimensional PIC simulations²⁹ and laboratory plasmas²⁸.

Figure 1j–o presents the estimated dispersion relation (f-k) spectra of the EM fluctuations using spectral phase differences analysis based on multiple spacecraft measurements^{34,47,60,61,62}. Figure 1j–l displays the estimated f-k spectra and phase velocity V_ph of EM fluctuations on the −N (B_L < 0) side of the current sheet along the L, M, and N directions, respectively. Figure 1m–o has the same format as Fig. 1j–l except for the +N (B_L > 0) side of the current sheet. These results show that EM fluctuations primarily propagate in the −N (+N) direction on the B_L < 0 (B_L > 0) side with V_phN ~−1500 km/s (V_phN ~ 800 km/s) as shown in Fig. 1a. Additionally, there is another weaker wave mode at a higher frequency range (f ~ 6–15 Hz, marked by a red dashed line), suggesting that EM fluctuations are composed of several wave modes or the phase speeds may be quite uncertain. The wavenumber $k\sqrt{{\rho }_{i}{\rho }_{e}} \sim 1$ (Fig. 1j–o) of these EM fluctuations indicates they are long-wavelength LHF wave modes^47,63. Furthermore, the EM fluctuations propagate along the +L and −M directions, matching the direction of the outflow and out-of-plane electron jets, respectively. The phase velocity of EM fluctuations along the −M direction, V_phM ~−2500 km/s, is close to the ion-electron relative drift velocity in the −M direction, V_d ~ V_eM ~−2000 km/s (Fig. 2b), which implies a possible interaction between the EM fluctuations and the out-of-plane electron jet²⁸.

Fig. 2: Secular filed-particle energy exchange.

a three components of the magnetic field, b electron bulk velocity, c total secular field-particle energy exchange rate, d spectrum of secular field-particle energy exchange rate $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{c}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$, e spectrum of secular field-particle energy exchange rate $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{p}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$, f secular filed-electron energy exchange rate. g–i distribution functions of secular field-electron energy exchange in velocity phase space in L, M, and N directions, respectively.

Secular field-particle energy exchange

To elucidate the field-particle interaction, we calculated the secular field-particle energy exchange rate between the EM fluctuations and plasma, denoted as $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ (see Methods section). This metric helps determine whether these EM fluctuations are growing or damping in the EDR^64,65,66. Figure 2d, e present the spectra of $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$, estimated from the current density derived via the curlometer technique, ${{{\bf{J}}}}_{{{\rm{c}}}}=\nabla \times {{\bf{B}}}/{\mu }_{0}$, and from plasma moments, ${{{\bf{J}}}}_{{{\rm{p}}}}={en}({{{\bf{V}}}}_{{{\rm{i}}}}-{{{\bf{V}}}}_{{{\rm{e}}}})$, respectively. Both spectra show significantly negative $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ values associated with EM fluctuations in the 1–16 Hz range. Figure 2c displays the secular field-particle energy exchange rates, $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{c}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t\right)$ (red curve) and $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{p}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t\right)$ (black curve), integrated from 1 to 16 Hz, derived from the $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{c}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ and $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{p}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ spectra, respectively. Both the black and red curves exhibit negative values with a peak around −5 pW/m³, which indicates that the plasma moments data and results are reliable, and the EM fluctuations gain energy from the plasma. Wang et al.⁵⁵ proposed that these EM fluctuations, initially generated along the direction of the electric current (the Y direction in the GSM coordinates), propagate toward a tilted current sheet with the normal direction of the current sheet points primarily along Y_GSM, hence the waves appear to propagate along this local normal direction. In contrast, our results show that the LHF EM fluctuations grow locally within the EDR, suggesting that they originate from the center of the reconnecting current sheet and then propagate outward (Fig. 1a). This local growth may be related to the pinching of the current sheet as proposed by Yoon et al.⁶⁷, which could act as a source of fluctuating energy.

The integrated secular field-electron energy exchange rates, $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{e}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t\right)$ (green curve in Fig. 2c, f), estimated from the electron current density ${{{\bf{J}}}}_{{{\rm{e}}}}$, align well with the black curve, as the current density in the EDR is primarily carried by electrons, ${{{\bf{J}}}}_{{{\rm{p}}}}\approx {{{\bf{J}}}}_{{{\rm{e}}}}$. This means that the EM fluctuations gain energy directly from electrons rather than ions in the EDR. To identify electrons in which phase space are involved in these interactions, Fig. 2g–i shows the distributions of the secular energy exchange rates in one-dimensional electron velocity phase space along the L, M, and N directions (see Methods section). We see that intense secular field-electron energy exchange occurs within a broad range of $[-{\mathrm{3.5,3.5}}]\times {10}^{4}$ km/s in all three directions in velocity phase space. This contrasts with the classical resonance interaction scenario, where energy exchange occurs only around resonance velocities; hence, we suggest that non-resonant interactions are important in the EDR⁶⁸. The intense field-electron energy exchange in the EDR may result in efficient electron scattering and associated anomalous effects in reconnection^28,29,39.

Anomalous effects of electromagnetic fluctuations

The anomalous effects induced by wave-particle interactions can be quantified by examining ensemble averaged second-order terms in the electron momentum equation, which can be written as^34,53,69:

$$ < {{\bf{E}}} > + < {{{\bf{V}}}}_{{{\rm{e}}}} > \times < {{\bf{B}}} > =-\frac{\nabla \cdot < {{{\bf{P}}}}_{{{\rm{e}}}} > }{e < {n}_{e} > }-\frac{{m}_{e}}{e < {n}_{e} > }\nabla \\ \cdot \left( < {n}_{e} > < {{{\bf{V}}}}_{{{\rm{e}}}} > < {{{\bf{V}}}}_{{{\rm{e}}}} > \right)+{{\bf{D}}}+{{\bf{T}}}+{{\bf{I}}}$$

(1)

where D, ${{\bf{T}}}={{{\bf{T}}}}_{{{\rm{ES}}}}+{{{\bf{T}}}}_{{{\rm{EM}}}}$, and I are the anomalous drag (resistivity), anomalous viscosity (momentum transport), and anomalous Reynold’s stress, respectively. These quantities are defined as:

$${{\bf{D}}}=-\frac{ < \delta {n}_{e}{{\rm{\delta }}}{{\bf{E}}} > }{ < {n}_{e} > }$$

(2)

$${{{\bf{T}}}}_{{{\rm{ES}}}}=-\frac{ < \delta {n}_{e}{{\rm{\delta }}}{{{\bf{V}}}}_{{{\bf{e}}}} > \times < {{\bf{B}}} > }{ < {n}_{e} > }$$

(3)

$${{{\bf{T}}}}_{{{\rm{EM}}}}=-\frac{ < {{\rm{\delta }}}({n}_{e}{{{\bf{V}}}}_{{{\bf{e}}}})\times {{\rm{\delta }}}{{\bf{B}}} > }{ < {n}_{e} > }$$

(4)

$${{\bf{I}}}=-\frac{{m}_{e}}{e < {n}_{e} > }[\nabla \cdot \left({n}_{e}{{{\bf{V}}}}_{{{\bf{e}}}}{{{\bf{V}}}}_{{{\bf{e}}}}\right)-\nabla \cdot ( < {n}_{e} > < {{{\bf{V}}}}_{{{\bf{e}}}} > < {{{\bf{V}}}}_{{{\bf{e}}}} > )]$$

(5)

The contributions of I are neglected in our analyses since it is generally much smaller than D and T due to it being related to the specific charge of the electron⁴². The anomalous viscosity T is split into two components ${{{\bf{T}}}}_{{{\rm{ES}}}}$ and ${{{\bf{T}}}}_{{{\rm{EM}}}}$, here. ${{{\bf{T}}}}_{{{\rm{ES}}}}$ (the ES anomalous viscosity term) is the anomalous Lorentz force due to the background magnetic field $< {{\bf{B}}} >$ and this term exactly cancels with D for frozen-in electrons, such as in the ES lower hybrid drift waves^53,70. ${{{\bf{T}}}}_{{{\rm{EM}}}}$ (the EM anomalous viscosity term) corresponds to the anomalous Lorentz force due to fluctuating magnetic field ${{\rm{\delta }}}{{\bf{B}}}$, i.e., the classical EM anomalous viscosity term⁴¹. The total anomalous electric field is defined as ${{\bf{R}}}={{\bf{D}}}+{{{\bf{T}}}}_{{{\rm{ES}}}}+{{{\bf{T}}}}_{{{\rm{EM}}}}$.

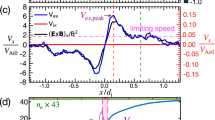
Figure 3 illustrates the anomalous effects of EM fluctuations along the out-of-plane direction (M direction), estimated using the spectral average method (see Methods section). The EM anomalous viscosity term $< {n}_{e} > {T}_{{EM},M}$ (Fig. 3e) exhibits significant positive values corresponding to EM fluctuations in the EDR, whereas $< {n}_{e} > {D}_{M}$ (Fig. 3c) and $< {n}_{e} > {T}_{{ES},M}$ (Fig. 3d) do not show clear enhancement. Figure 3b presents the anomalous electric fields in the M direction, which are integrated from the spectra within the 1–16 Hz frequency range (see Table 1). The total anomalous electric field R_M reaches a positive peak of approximately 0.025 mV/m inside the EDR. It is in the same direction as the out-of-plane reconnection field; however, its magnitude is only 3% of the reconnection electric field (see Table 1). The increase in R_M is primarily contributed by T_EM,M of EM fluctuations at frequencies near the lower hybrid frequency (f_LH). The anomalous drag D_M and the ES anomalous viscosity term T_ES,M are negligible in comparison to T_EM,M. This is different from previous observations of ES fluctuations⁵³ in asymmetric reconnection at the magnetopause. Notably, D_M and T_ES,M show an anti-correlated change within the EDR, even though electrons are not entirely frozen-in, similar to the ideal electron-magnetohydrodynamic nature seen in PIC simulations⁷⁰ and recent observations⁵³.

Fig. 3: Anomalous effects of EM fluctuations in the M direction of the reconnecting current sheet.

a three components of the magnetic field, b total anomalous electric fields R_M (black), anomalous drag D_M (blue), anomalous viscosity ${T}_{{ES},M}$ (red) and ${T}_{{EM},M}$ (green) in M direction. The colored shaded regions associated with the anomalous terms represent the uncertainty in the calculation based on the uncertainties in the particle moments and electric field. The values of ${T}_{{EM},M}$ within this EDR are larger than its uncertainty (see Methods section). c Spectra of anomalous drag term $< {n}_{e} > {D}_{M}$, d ES anomalous viscosity term $< {n}_{e} > {T}_{{ES},M}$, e EM anomalous viscosity term $< {n}_{e} > {T}_{{EM},M}$.

Figure 4 details the other two EDRs (events 7 and 10 in Table 1), which are associated with strong EM fluctuations near the LHF observed in the magnetotail on 2018-08-27 (Fig. 4a–h) and 2017-07-11 (Fig. 4i–p), respectively. The secular field-particle energy exchange $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ in EDR 7 is predominantly negative at the central region and slightly positive at the edges (Fig. 4c, d), indicating that the EM fluctuations are growing within this EDR. The total anomalous electric field in the M direction R_M during EDR 7 shows a positive peak of ~0.371 mV/m at the center, with smaller negative peaks at the edges of the EDR (Fig. 4e). This feature resembles the anomalous electric fields observed in recent three-dimensional simulations^41,48. The positive peak magnitude of R_M is up to 18% of the reconnection electric field in this EDR, much larger than that of EDR 2. Figures 4f–h present the time-frequency spectra of the anomalous effects, with the positive peak of T_EM,M attributed to EM fluctuations around the LHF.

Fig. 4: Secular filed-particle energy exchange and anomalous electric fields in M direction of other two EDR events.

a, i three components of the magnetic field, b, j electron bulk velocity, c, k total secular filed-particle energy exchange rate corresponding to fluctuations, d, l spectra of $< {{\rm{\delta }}}{{{\bf{J}}}}_{{{\rm{p}}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$, e, m total anomalous electric fields R_M (black), anomalous drag D_M (blue), anomalous viscosity ${T}_{{ES},M}$ (red) and ${T}_{{EM},M}$ (green) in M direction. The colored shaded regions associated with the anomalous terms represent the uncertainty in the calculation based on the uncertainties in the particle moments and the electric field. f–h, n–p spectra of anomalous effects.

In contrast, the secular field-particle energy exchange $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)$ for EDR 10 is positive (Fig. 4k, l), hence the EM fluctuations are damping within this EDR. The anomalous electric field in the M direction R_M for EDR 10 shows a positive peak of ~0.036 mV/m, only ~1% of the reconnection electric field, at the center and negative values at the EDR edges as well (Fig. 4m). One can see that fluctuations in the anomalous electric fields are observed both inside and outside the EDR. The intense secular field-particle energy exchange and associated larger anomalous electric field occur outside the EDR in this event, differing from the above two EDRs. Interestingly, in these events, R_M is predominantly contributed by T_EM,M, while D_M is small and counterbalanced by T_ES,M in most regions.

Statistical results

Columns 5 and 6 of Table 1 display the maximum total anomalous electric field R_M,max and the maximum average non-ideal electric field ${ < {E}^{{\prime} } > }_{M,\max }$ in the M direction for all EDR events, where $< {{{\bf{E}}}}^{{\prime}} > = < {{\bf{E}}} > + < {{{\bf{V}}}}_{{{\rm{e}}}} > \times < {{\bf{B}}} >$. In all events, the EM fluctuations contribute a positive anomalous electric field in the +M direction, which can support the reconnection electric field. To assess the relative significance of the anomalous electric field to the reconnection electric field, we calculate the ratio of R_M,max to ${ < {E}^{{\prime} } > }_{M,\max }$, denoted as ${P={R}_{M,\max }/ < {E}^{{\prime} } > }_{M,\max }$, as shown in Column 7 of Table 1. The maximum contribution of the anomalous electric field associated with EM fluctuations can reach up to ~20% of the reconnection electric field, but it is less than 5% in approximately 70% of the events.

For each event, we normalize ${R}_{M}$, ${T}_{{EM},M}$, ${T}_{{ES},M}$ and ${D}_{M}$ by the maximum absolute values of the total anomalous electric field ${|{R}_{M}|}_{\max }$. Figure 5a shows the statistical results of the normalized anomalous electric field ${R}_{M}/{|{R}_{M}|}_{\max }$ and the normalized anomalous viscosity term ${T}_{{EM},M}/{|{R}_{M}|}_{\max }$ for all EDRs. All data points are clustered around the line of ${R}_{M}/{|{R}_{M}|}_{\max }={T}_{{EM}}/{|{R}_{M}|}_{\max }$ (black line), with a positive correlation coefficient of approximately r = 0.98, indicating that the anomalous electric fields within all EDRs are mainly contributed by the EM viscosity term T_EM. Figure 5b shows the normalized anomalous drag ${D}_{M}/{|{R}_{M}|}_{\max }$ and the normalized ES viscosity term ${T}_{{ES},M}/{|{R}_{M}|}_{\max }$. These two terms are smaller than T_EM,M and nearly cancel each other out within the EDRs, with a correlation coefficient of approximately r = −0.64 between them.

Fig. 5: Correlation analysis.

a relation between anomalous electric field ${R}_{M}/{|{R}_{M}|}_{\max }$ and anomalous viscousity ${T}_{{EM},M}/{|{R}_{M}|}_{\max }$, b the relation between anomalous drag ${D}_{M}/{|{R}_{M}|}_{\max }$ and anomalous viscosity ${T}_{{ES},M}/{|{R}_{M}|}_{\max }$. Data points in a, b are from all 13 EDRs. The black lines in (a, b) denote ${R}_{M}/{|{R}_{M}|}_{\max }={T}_{{EM}}/{|{R}_{M}|}_{\max }$ and ${T}_{{ES},M}/{|{R}_{M}|}_{\max }=-{D}_{M}/{|{R}_{M}|}_{\max }$, respectively. c, d show the correlation between the normalized secular field-particle energy exchange and anomalous electric field, i.e., $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > /{| < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > |}_{\max }$ and ${R}_{M}/{|{R}_{M}|}_{\max }$. Data points in c are from EDR events 1–9, while data points in d are from EDR events 10–13. Different colors and markers are used to represent different EDR events.

Does the evolution stage (growing or damping) of these EM fluctuations correlate with their roles in the reconnection process? Fig. 5c, d examines the statistical relationship between $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} >$ and R_M across all EDR events. For each event, we normalize $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} >$ and R_M by their maximum absolute values, $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > /{| < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > |}_{\max }$ and ${R}_{M}/{|{R}_{M}|}_{\max }$. Figure 5c shows a scatter plot of $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > /{| < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > |}_{\max }$ and ${R}_{M}/{|{R}_{M}|}_{\max }$ from events 1–9. A clear inverse correlation is observed, with a correlation coefficient of approximately −0.68. In these events, negative (positive) secular field-particle energy exchange correlates with a positive (negative) anomalous electric field in the M direction, and the intensity of $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > /{| < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > |}_{\max }$ can influence the magnitude of ${R}_{M}/{|{R}_{M}|}_{\max }$. This suggests that the growing or damping state of EM fluctuations is a key factor in determining whether they contribute to or inhibit the reconnection electric field. In contrast, Fig. 5d shows the scatter plot of $< {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > /{| < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > |}_{\max }$ and ${R}_{M}/{|{R}_{M}|}_{\max }$ from events 10–13, where no clear correlation is evident. These findings indicate that while the growing or damping state of EM fluctuations significantly influences their anomalous effect on the reconnection electric field, it is not the sole determinant.

Discussion

In this work, we employed a spectral average method to accurately determine the secular field-particle energy exchange and the anomalous electric field associated with EM fluctuations from in-situ data. This method provides a perspective on understanding the coupling between kinetic-scale fluctuations and symmetric reconnection in collisionless plasmas. The results directly demonstrate that EM LHF fluctuations can locally grow and damp within the EDR. The anomalous electric fields of EM fluctuations within the EDR are mainly contributed by the EM anomalous viscosity term T_EM,M, rather than by anomalous drag D_M or the ES anomalous viscosity term T_ES,M. Additionally, although electrons are not entirely frozen-in within the EDR, the anomalous drag D_M and the ES anomalous viscosity T_ES,M are mutually restrained, similar to the effects induced by ES lower-hybrid drift waves in asymmetric reconnection, where electrons are approximately frozen-in^53,70.

The guide field B_g and the normal component of the magnetic field B_N in reconnection are two additional potential factors influencing the role of anomalous effects. In these EDRs, B_N is much smaller than the asymptotic inflow magnetic field B₀ (i.e., B_N < 0.1 B₀) and can therefore be neglected. The guide fields B_g in these events range from 0 to 0.5 B₀, as shown in Column 8 of Table 1, yet the ratio P = R_M,max/<E’ > _M,max (Column 7 of Table 1) appears uncorrelated with B_g, with a correlation coefficient r ~ −0.02. Another possible factor is the asymmetry across the current sheet. For instance, intense ES LHF waves are driven by strong density gradients across the magnetopause reconnecting current sheet, where the anomalous drag ${{\bf{D}}}$ is approximately balanced by ${{{\bf{T}}}}_{{{\rm{ES}}}}$, while ${{{\bf{T}}}}_{{{\rm{EM}}}}$ can be neglected⁵³. Here we find that the EDR of symmetric reconnection in the magnetotail is mainly characterized by EM LHF fluctuations rather than ES fluctuations, and the dominant contribution to the anomalous electric field is the EM viscosity term ${{{\bf{T}}}}_{{{\rm{EM}}}}$. The asymmetry of the current sheet primarily affects the type of waves generated, but may not directly change the magnitude of the anomalous electric field. Further investigations are required to identify and quantify other contributing factors.

The maximum contribution of anomalous electric fields provided by EM anomalous viscosity can be up to about 20% of the fast reconnection electric field. This maximum contribution in low guide field (B_g ~ 0.05) symmetric reconnection is comparable to the role played by the anomalous drag of ES lower-hybrid drift waves reported in laboratory symmetric reconnection with a large guide field (B_g ~ 0.7 B₀)³². However, the contribution of anomalous electric fields is less than 5% in most events. This is consistent with the prevailing consensus that anomalous effects generally do not significantly influence the reconnection rate⁴⁹. The proportion of anomalous electric field varies significantly across different EDRs and appears to be independent of the guide field strength, which may suggest that the role of anomalous effects driven by kinetic-scale EM fluctuations may evolve over time during reconnection. For example, the viscosity term may become important at later stages of reconnection^29,51,71. However, spacecraft observations cannot continuously monitor the full temporal evolution of a single reconnection event or clearly distinguish the different stages among separate events. Therefore, future work should include detailed comparisons between in-situ observations and simulations performed under more realistic parameters.

Methods

MMS data

The data used in this study are from the following instruments onboard MMS: the Fluxgate Magnetometer (FGM)⁷²; the Fast Plasma Investigation (FPI)⁷³; the Electric Double Probes (EDP)^74,75. Since the frequency ranges of these EM fluctuations in the EDR events are mainly less than 16 Hz, the burst mode magnetic fields from FGM with a sampling rate of 128 Hz, the fast mode electric fields from EDP with a sampling rate of 32 Hz, and the burst mode electron data from FPI with the resolution of 0.03 s–33 Hz are used in this paper.

The magnetic fields, electric fields, and plasma moments used to calculate the spectra of the time-averaged quantities in this study have been averaged over multiple spacecraft. Note that not all four MMS spacecraft have valid data for each event. For example, the FPI on MMS4 was out of order after June 2018, resulting in a lack of electron moments data from MMS4 after June 2018. Therefore, for events 1, 2, 5, 10, 11, and 12, the fields and plasma moments were averaged over all four MMS spacecraft, while for the other events, the average values are calculated using the data from only three MMS spacecraft.

In the magnetotail, the electron counts are low, and internal photoelectrons may significantly affect the reliability of the plasma moments. The L2 electron moments data from MMS have been corrected to eliminate photoelectron contamination. The L2 data are deemed reliable in events 1–5 and 8–12, as the electron moments data are almost identical to the partial moments data, which excludes low-energy electrons that are likely influenced by photoelectrons. For these events, both the electron moments and the corresponding uncertainty data are used. However, the L2 data for events 6, 7, and 13 are considered unreliable. Therefore, partial moments data with energy greater than 50 eV are used for these events to enhance the quality of the electron moments. One should be noted that there is no uncertainty data available in the partial moments data product.

Definition and time window of EDRs

Most EDR events in our list have been reported in previous studies, as shown by Wang et al.⁵⁵, and the references therein. In this paper, we employ six parameters to identify the EDR: (1) electron agyrotropy as defined by Swisdak⁷⁶; (2) agyrotropy of the measured electron pressure tensor based on Scudder et al.⁵⁹; (3) electron thermal Mach number following Scudder et al.⁵⁹; (4) energy dissipation as proposed by Zenitani et al.⁷⁷; (5) energy gain per cyclotron period based on Scudder et al.⁵⁹; and (6) the relative strength of electric and magnetic forces in the electron fluid rest frame, also based on Scudder et al.⁵⁹. Although not every case exhibits increase in all of the six parameters, at least three parameters show significant enhancements. These observations indicate that all the analyzed events correspond to EDR crossings.

Moreover, we find that the electron thermal Mach number increases significantly in all EDR events. Therefore, we primarily use the enhancement of this parameter to determine the time windows for each EDR. Considering that the EM fluctuations near the EDRs typically have a minimum frequency close to 1 Hz, we determine the EDR windows (i.e., begin and end time) with a temporal resolution of 1 s.

Calculate the spectrum of the time-averaged quantities

The spectral average method

The spectrum of secular filed-particle energy exchange rate as a function of time and frequency is defined as^64,65,66

$$ < {{\rm{\delta }}}{{\bf{J}}}\cdot {{\rm{\delta }}}{{\bf{E}}} > \left(t,f\right)=\frac{1}{4}[{{\rm{\delta }}}{{\bf{J}}}(t,f)\cdot {{{\rm{\delta }}}{{\bf{E}}}\left(t,f\right)}^{*}+{{{\rm{\delta }}}{{\bf{J}}}(t,f)}^{*}\cdot {{\rm{\delta }}}{{\bf{E}}}(t,f)]$$

(6)

where ${{\rm{\delta }}}{{\bf{J}}}(t,f)$, ${{{\rm{\delta }}}{{\bf{J}}}(t,f)}^{*}$, ${{\rm{\delta }}}{{\bf{E}}}(t,f)$, ${{{\rm{\delta }}}{{\bf{E}}}\left(t,f\right)}^{*}$ represent the wavelet spectra and corresponding conjugate counterparts of the current density ${{\bf{J}}}(t)$ and electric field ${{\bf{E}}}(t)$, respectively.

The secular energy exchange rates in one-dimensional electron velocity phase space

The time series of the reduced one-dimensional (1D) electron velocity distribution functions are expressed as ${f}_{e}\left(t,{V}_{k}\right)=\iint {f}_{e}\left(t,{{\bf{V}}}\right){{dV}}^{2}$, where $k=L,M,N$ denotes the directions in the LMN coordinate system. Based on the definition of electron current density, ${J}_{e,k}=-{en}{V}_{e,k}$, the time series of 1D electron current density distribution in velocity phase space can be expressed as

$${J}_{e,k}\left(t,{V}_{k}\right)=-e{V}_{k}{f}_{e}(t,{V}_{k})d{V}_{k}$$

(7)

Taking $k=M$ as an example, for each velocity V_M = V₀, we have an associated electron current density ${J}_{e,M}\left(t,{V}_{0}\right)$ and its wavelet spectrum $\delta {J}_{e,M}\left(t{,V}_{0},f\right)$. Using Eq. (6) in the main text, we derive the secular energy conversion spectrum corresponding to this current density, $< \delta {J}_{e,M}\delta {E}_{M} > \left(t,{V}_{0},f\right)$. Integrating this spectrum over the frequency range of the EM fluctuations yields the secular energy conversion rate $< \delta {J}_{e,M}\delta {E}_{M} > (t,{V}_{0})$, representing the contribution from electrons with velocity V_M = V₀.

Repeating the above process across all velocities in the 1D velocity phase space yields the 1D distribution of field–electron secular energy exchange rates in the 1D velocity phase space, $< \delta {J}_{e,M}\delta {E}_{M} > (t,{V}_{M})$, as shown in Fig. 2h. The same computational procedure is applied to the $k=L,N$ to obtain $< \delta {J}_{e,L}\delta {E}_{L} > \left(t,{V}_{L}\right)$ and $< \delta {J}_{e,N}\delta {E}_{N} > \left(t,{V}_{N}\right)$ as shown in Fig. 2g, i, respectively.

Spectra of anomalous terms

The quantities of anomalous effects in Eq. (1) are computed from an ensemble average ideally. In this work, we use the four-spacecraft average and the spectra time-average method provided in Eq. (6) to estimate the spectra of anomalous terms. First, we calculate the four-spacecraft average fields and plasma moments, i.e., E, B, n_e, V_e, and (n_eV_e). Second, we calculate their wavelet spectra, i.e., ${{\rm{\delta }}}{{\bf{E}}}$, ${{\rm{\delta }}}{{\bf{B}}}$, $\delta {n}_{e}$, ${{\rm{\delta }}}{{{\bf{V}}}}_{{{\rm{e}}}}$, and ${{\rm{\delta }}}({n}_{e}{{{\bf{V}}}}_{{{\rm{e}}}})$ and corresponding conjugate counterparts, i.e., ${{{\rm{\delta }}}{{\bf{E}}}}^{*}$, ${{{\rm{\delta }}}{{\bf{B}}}}^{*}$, ${\delta {n}_{e}}^{*}$, ${{{\rm{\delta }}}{{{\bf{V}}}}_{{{\rm{e}}}}}^{*}$, and ${{{\rm{\delta }}}({n}_{e}{{{\bf{V}}}}_{{{\rm{e}}}})}^{*}$. Then, calculate the spectra of anomalous terms via

$$ < {n}_{e} > {{\bf{D}}}(t,f)=-\frac{1}{4}[\delta {n}_{e}{{\rm{\delta }}}{{{\bf{E}}}}^{*}+\delta {{n}_{e}}^{*}{{\rm{\delta }}}{{\bf{E}}}]$$

(8)

$$ < {n}_{e} > {{{\bf{T}}}}_{{{\rm{ES}}}}(t,f)=-\frac{1}{4}[\delta {n}_{e}{{{\rm{\delta }}}{{{\bf{V}}}}_{{{\bf{e}}}}}^{*}+{\delta {n}_{e}}^{*}{{\rm{\delta }}}{{{\bf{V}}}}_{{{\bf{e}}}}]\times < {{\bf{B}}} > $$

(9)

$$ < {n}_{e} > {{{\bf{T}}}}_{{{\rm{EM}}}}(t,f)=-\frac{1}{4}[\delta ({n}_{e}{{{\bf{V}}}}_{{{\rm{e}}}})\times {{{\rm{\delta }}}{{\bf{B}}}}^{*}+{\delta ({n}_{e}{{{\bf{V}}}}_{{{\rm{e}}}})}^{*}\times {{\rm{\delta }}}{{\bf{B}}}]$$

(10)

where $< {n}_{e} >$ and $< {{\bf{B}}} >$ are the background electron density and magnetic field calculated via the low-pass filter below the frequency of EM fluctuations⁵³, for example, it is 1 Hz for event 2.

The uncertainties of anomalous terms are estimated using the spectral average method as well, which incorporates uncertainties from the electron moments and assumes a 10% uncertainty in the gain of the electric field⁵³. The results indicate that the uncertainty of ${{{\bf{T}}}}_{{{\rm{EM}}}}$ is generally smaller than that of ${{{\bf{T}}}}_{{{\rm{ES}}}}$ and ${{\bf{D}}}$ terms, as shown in Figs. 3b and 4e, m. The values of ${{{\bf{T}}}}_{{{\rm{EM}}}}$ within the EDR are greater than their associated uncertainties, suggesting that the results are reliable.