Generalizable morphological profiling of cells by interpretable unsupervised learning

Murthy, Rashmi Sreeramachandra; Stassen, Shobana V.; Siu, Dickson M. D.; Lo, Michelle C. K.; Yip, Gwinky G. K.; Tsia, Kevin K.

doi:10.1038/s41467-025-66267-w

Download PDF

Article
Open access
Published: 11 December 2025

Generalizable morphological profiling of cells by interpretable unsupervised learning

Nature Communications volume 16, Article number: 11465 (2025) Cite this article

2839 Accesses
2 Altmetric
Metrics details

Subjects

Abstract

The intersection of advanced microscopy and machine learning is transforming cell biology into a quantitative, data-driven field. Traditional cell profiling depends on manual feature extraction, which is labor-intensive and prone to bias, while deep learning provides alternatives but faces challenges with interpretability and reliance on labeled data. We present MorphoGenie, an unsupervised deep-learning framework for single-cell morphological profiling. By combining disentangled representation learning with high-fidelity image reconstruction, MorphoGenie creates a compact, interpretable latent space that captures biologically meaningful features without annotation, overcoming the “curse of dimensionality.” Unlike previous models, it systematically links latent representations to hierarchical morphological attributes, ensuring semantic and biological interpretability. It also supports combinatorial generalization, enabling robust performance across diverse imaging modalities (e.g., fluorescence, quantitative phase imaging) and experimental conditions, from discrete cell type/state classification to continuous trajectory inference. This provides a generalized, unbiased strategy for morphological profiling, revealing cellular behaviors often overlooked by expert visual examination.

A deep learning approach for morphological feature extraction based on variational auto-encoder: an application to mandible shape

Article Open access 06 July 2023

Orientation-invariant autoencoders learn robust representations for shape profiling of cells and organelles

Article Open access 03 February 2024

MorphoSim: an efficient and scalable phase-field framework for accurately simulating multicellular morphologies

Article Open access 17 February 2023

Introduction

Recent advances in microscopy have revolutionized cell biology by transforming it into a data-driven science. This transformation allows researchers to explore the rich structural and functional traits of cell morphology, providing valuable insights into cell health, disease mechanisms, and cellular responses to chemical and genetic perturbations. In recent years, we have witnessed remarkable growth in open image data repositories^1,2,3,4,5 and the development of powerful machine learning methods for analyzing cellular morphological fingerprints (or profiles). There is mounting evidence that these morphological profiles can reveal critical information about cell functions and behaviors, often remaining hidden in molecular assays. Notably, it has been shown that cell morphology and gene expression profiling provide complementary information in genetic and chemical perturbations^6,7,8.

Traditional morphological profiling methods rely on manual feature extraction, which can be labor-intensive, require domain expertise, and often lack scalability and generalizability across different imaging modalities. Conventionally, features are crafted based on cellular shape, size, texture, and pixel intensities to assign a unique identity to each cell. Extracting hundreds to thousands of morphological features from a single image allows the investigation of complex cellular properties with high discriminative power, such as responses to drug treatments^9,10. However, manual feature extraction methods are susceptible to the “curse of dimensionality” and may introduce biases, as the selected features might not fully represent the data.

Deep learning techniques that employ supervised or weakly supervised learning have shown promise in delivering more accurate image classification¹¹. However, these methods require large-scale, expert labeling or annotation of training datasets, which can be time-consuming and subject to human biases¹². Additionally, the performance of deep learning is often hindered by its lack of interpretability. An ideal cell morphology profiling strategy should generate features without overly depending on human knowledge, making inferences based solely on the images themselves, free from any a priori assumptions. Adopting such an approach has proven to be effective in extracting subtle cellular features that are obscured through manual feature extraction; and to offer a more unbiased analysis of cellular morphology, overcoming the limitations associated with manual annotation and expert knowledge. At the same time, the deep-learned morphological profile should effectively be interpretable (or explainable) in order to improve the deep learning model transparency and gain credibility, which is particularly important in biomedical diagnosis^13,14.

Unsupervised deep generative networks, notably variational autoencoders or VAEs¹⁵, have gained widespread success in learning interpretable latent representations for downstream analysis and providing insights into neural network model learning. Autoencoders learn to compress input data into a lower-dimensional representation (encoding) and then reconstruct the input image data from this lower-dimensional representation (decoding), while learning the latent representations. Despite their potential, autoencoders often face limitations in lossy image reconstructions - making it difficult to assess how well the model can learn a good probabilistic latent representation of the image data. While previous works have employed VAE variants for unsupervised and self-supervised learning of cellular image datasets to reveal cellular dynamics and attempted to interpret the learned latent space^16,17,18, they have not established a direct and systematic mapping between the learned latent space and interpretable morphological features. This highlights the need for further research to overcome these limitations and enhance the morphological profiling of cells.

We present MorphoGenie, a deep-learning framework for unsupervised, interpretable single-cell morphological profiling and analysis to address the abovementioned challenges. MorphoGenie distinguishes itself from previous works with three key attributes: (1) High-fidelity Image Reconstruction: MorphoGenie utilizes a hybrid architecture that capitalizes on the unparalleled strengths of the variant of VAEs and generative adversarial networks (GANs) to achieve interpretable, high-quality cell image generation¹⁹. (2) Interpretability: MorphoGenie learns a compact, interpretable, and transferable disentangled representation for single-cell morphological analysis. In contrast to the prior work on disentangled deep-learning^20,21,22, we propose a technique for interpreting the disentangled latent representations by mapping them to different classes of hierarchical spatial features, extracted from reconstructed images, through a process called visual latent traversals. (3) Generalizability: The strategy of gaining interpretability in MorphoGenie mimics the concept of combinatorial generalization in human intelligence that assemble different hierarchical spatial attributes from diverse image data to learn the unseen image data - thus facilitating the discovery of biologically meaningful inferences, especially the heterogeneities of cell types and lineages. Indeed, MorphoGenie is widely adaptable across various imaging modalities and experimental conditions, promoting cross-study comparisons and reusable morphological profiling results. The model generalizes to unseen single-cell datasets and different imaging modalities while providing explanations for its predictions. Overall, MorphoGenie could spearhead new strategies for conducting comprehensive morphological profiling and make biologically meaningful discoveries across a wide range of imaging modalities.

Results

Overview of MorphoGenie

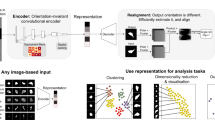
The learning part of MorphoGenie employs a hybrid neural network architecture, enabling the generation of a “disentangled representation” within its latent space—a model’s internal, high-dimensional conceptualization of data—while also facilitating the reconstruction of high-fidelity cellular images (Fig. 1). Disentangled representation is a concept that involves segregating and identifying independent variables (or factors of variation) that constitute the diversity observed within image data. In other words, a representation where a change in one latent dimension corresponds to a change in one factor of variation, while being relatively invariant to changes in other factors. In the context of cell morphology, these variables can be related to quantifiable attributes such as cell/nuclear size, texture of the cytoplasm, or specific cellular spatial patterns.

**Fig. 1: Overview of the MorphoGenie framework.**

In MorphoGenie’s latent space, each disentangled dimension corresponds to one of these variations independently. Hence, it allows for visual latent traversal, a process that modifies only one chosen variable, with other factors remaining unchanged, thus enabling visual inspection of how individual features impact cell morphologies (Fig. 1). This capacity for selective alteration is crucial in deconvoluting the complexities of cellular morphology and understanding the distinct contributions of each morphological aspect.

Prior research has utilized VAEs for unsupervised learning in single-cell imaging, such as the use of VQ-VAE to predict cell state transitions^16,23. These approaches, however, often result in discrete and non-continuous latent spaces that lack the desired disentanglement, complicating the interpretation of morphological changes. Another work explored adversarial autoencoder (AAE) models for classification and identifying metastatic melanoma, but it, too, yielded entangled representations, impeding clear and direct downstream analysis¹⁷.

These previous methodologies highlight the inherent trade-offs faced when seeking disentangled representations with VAEs. Techniques such as β-VAE and other factorized approaches have been proposed to enhance interpretability by creating a more structured latent space^20,21. However, the compact nature of these VAE-derived latent representations often leads to a loss in the quality of reconstructed images, presenting significant hurdles in mapping the disentangled latent factors to visually interpretable and biologically relevant features. In contrast, GANs excel in generating realistic reconstructions but typically result in a more entangled latent representation, which can obscure the direct interpretability required for precise morphological analysis. Also, GANs are known to suffer from training instability²⁴.

MorphoGenie is built upon bringing two generative models (VAE and GAN) into a hybrid architecture (Fig. 2a, and Supplementary Fig. S1). The overall rationale is to jointly optimize the objectives of disentanglement learning and high-fidelity image generation by a dual-step training approach. Initially, a VAE variant, called FactorVAE (Methods), is employed to effectively learn the disentangled representations (in the latent space) from real image space, using a probabilistic encoder²⁰. Subsequently, image reconstruction from the latent representation is accomplished through a decoder. During optimization, the objective is to minimize the disparity between the reconstructions and real images while at the same time learning the latent disentangled representations. FactorVAE is proven to provide a better trade-off between disentanglement and reconstruction performance than the state-of-the-art VAE models, notably the popular β-VAE²¹. In the second step, the disentangled representation learned from the first step is transferred to the GAN and trained by the generator to generate synthetic images, which are then assessed by a discriminator for differentiating between the generated (fake) and real images. By transferring the inference model, which provides a disentangled latent distribution, rather than a commonly used simple Gaussian prior, to GAN, this joint sequential learning approach could allow the overall hybrid model to learn latent representation by first learning the main disentangled factors by VAE, then learning additional (entangled) nuisance factors by GAN. Also, it allows a more accurate and detailed reconstruction than VAEs alone can achieve (See Methods).

Prior work has highlighted that the disentangled factors could, to a certain extent, support combinatorial generalization - the ability to understand and generate novel combinations of familiar elements—a core attribute of human intelligence²⁵. The idea is to capture the compositional information of the images through disentangled representation learning, and reuse (and recombine) a finite set of these representations to generate a novel understanding of the image in different scenarios (e.g., different imaging modalities as demonstrated in this work), thereby bridging the gap between human and machine intelligence^22,26. To this end, we attempt to systematically investigate the inter-relationship between the disentangled latent representation and the morphological descriptors of single cells extracted from a spatially hierarchical analysis (Fig. 1). Inspired by that the disentangled representations learned by some VAE variants have been shown effective for learning a hierarchy of abstract visual concepts²², we define a hierarchy of single-cell morphological features segmented for this mapping analysis (using the classical mathematical/statistical metrics): from the fine-grained textures and their local multi-order moment statistics to the coarse-grained features such as cell body size, cell/organelle shape, cell mass density distribution and so on (Fig. 1). Based on this method, we establish a single-cell morphological profile in a hierarchy that allows us to gain semantic and biologically relevant interpretation of the disentangled representation—unraveling the factors governing single-cell generative attributes. This makes the model not only interpretable, as each latent dimension can be understood and visualized in isolation, but also transferable, as the learned representation can be applied to new, unseen data more effectively.

Image reconstruction in MorphoGenie

We first assessed the performance of MorphoGenie in cell image reconstruction (Fig. 2b). High-quality image reconstruction in generative models is crucial for validating model accuracy, ensuring the encoded latent space captures and preserves the essential details of the input image data. Moreover, accurate image reconstructions allow users to make informed interpretability based on the model outputs. They also serve as a reliable reference for downstream applications, where the integrity of subsequent analyses depends heavily on the initial reconstruction’s fidelity. Importantly, we investigated how the hybrid architecture of VAE and GAN improves the reconstruction performance in MorphoGenie, compared to the case in which only VAE is included. We chose four distinctly different image datasets for the assessments, including quantitative phase images (QPI) of suspension cells and fluorescence images of adherent cells (Fig. 2b). In the case of multi-color fluorescence images captured by the Cell-Painting drug assays, in which morphologies of the key subcellular organelles can separately be analyzed, e.g., nucleus, mitochondria, nucleoli, actin, endoplasmic reticulum (ER), we trained MorphoGenie with the multi-color image inputs, i.e., superimposing images of 5 fluorescence channels (i.e., dimensions 256 × 256 × 5) (See Methods for training details).

In general, the VAE-only model (based on FactorVAE) can only manage to preserve overall attributes such as shapes, sizes, and overall pixel intensities in both QPI and fluorescence images (Fig. 2b). However, the intricate local texture variations within cellular structures are generally lost. In contrast, MorphoGenie, which involves dual-stage training based on both VAE and GAN, effectively preserves the subcellular textural details in both QPI and fluorescence imaging scenarios (Fig. 2b).

We also compared MorphoGenie’s image reconstruction performance with the state-of-the-art models (VQ-VAE²³ and AAE²⁷) adopted for cellular morphological analysis on the different cell image datasets, i.e., covering diverse complex morphologies (both in suspension and adherent cell formats) and different imaging modalities (QPI and fluorescence imaging) (See the description of datasets in Methods) (Fig. 2c). To facilitate disentangled representation learning that can be easily interpretable (as discussed later), the latent space in MorphoGenie is kept to have only 10 dimensions, significantly smaller than the AAE (512 dimensions)²⁷ and VQ-VAE (1024 dimensions)²³ used in the prior work. For a fairer comparison, we also evaluated lower-dimensional versions of VQ-VAE (16 dimensions) and AAE (10 dimensions), aligning their latent space sizes with MorphoGenie’s configuration.

MorphoGenie’s image reconstruction outperformed these methods and achieved comparable performance to high-dimensional models across most datasets. Importantly, we find that reducing the latent dimensionality of VQ-VAE and AAE to match MorphoGenie leads to a significant decline in their image reconstruction performance. These assessments were based on a comprehensive set of metrics, including Structural Similarity Index (SSIM), Mean Squared Error (MSE), and Fréchet Inception Distance (FID) values (Fig. 2c, Supplementary Figs. S2, 3, Table S1). Notably, we note that FactorVAE—while prioritizing interpretability over reconstruction quality—benefits from MorphoGenie’s incorporation of a GAN, which enables MorphoGenie to achieve both strong reconstruction performance and a disentangled, interpretable latent space.

To validate the importance as well as the robustness of the dual-stage training in ensuring high-fidelity image reconstruction, we further compared the reconstruction performance of the FactorVAE-only model and MorphoGenie across a wide range of a hyperparameter ${\gamma }$ used in training for improving the representation disentanglement (Methods). Clearly, not only can MorphoGenie consistently demonstrate significant improvement in reconstruction performance compared to the FactorVAE-only model, but also exhibit relatively more stable image reconstruction performance (in terms of SSIM, MSE, and FID) across two orders-of-magnitude of ${\gamma }$ (Supplementary Fig. S3). We further evaluated the role of the GAN in MorphoGenie by assessing downstream performance using GAN-generated images. The 2D visualizations obtained from these images showed that they preserve biologically relevant information and closely match those from real images, whereas 2D visualizations obtained from decoder-reconstructed images exhibit clear differences (Supplementary Fig. S28).

Disentangled representation learning and interpretation in MorphoGenie

Accurate image reconstruction by generative models is a complex task that does not inherently lead to disentangled and interpretable latent representations. MorphoGenie is designed to produce such disentangled representations (e.g., D1 and D2 in Fig. 3a), enabling the isolation and visual identification of key factors of variation in cell morphology. As mentioned earlier, the value in each disentangled dimension, which corresponds to one of these variations, is varied (e.g., vary D1), with other factors remaining unchanged (e.g., fix D2) - a process called latent traversal. Using MorphoGenie’s decoder to reconstruct the image, one can further perform visual inspection of how changes in individual dimensions (latent traversal) impact cell morphologies (Fig. 3a).

**Fig. 3: Disentangled representation learning in MorphoGenie.**

It should be noted that our work does not aim to benchmark various existing disentanglement metrics, among which no single disentanglement standard has proven consistently applicable across varied data types^{20,21,28,29,30}. Instead, we focus on evaluating the separability of latent features in relation to three key visual hierarchical concepts/primitives: bulk, global textures, and local textures (Fig. 1). Bulk-level features primarily focus on cell size, shape, and deformation, while global texture features are based on the holistic textural characteristics of pixel intensities using multi-order moment statistics. Local texture features are extracted using spatial texture filters at various kernel sizes, quantifying local textural characteristics at both coarse and fine scales (Supplementary Tables S2, S3)^10,31,32. This approach is motivated by the demonstrated effectiveness of VAE models in learning hierarchical abstractions of visual concepts²².

In order to assess how these hierarchical features can be discerned within the latent space, we introduce an interpretation heatmap that correlates the variability of hierarchical single-cell morphological features with that in the latent space dimensions (e.g., D1 is highly correlated with cell size changes shown in Fig. 3a). Based on the categorization of the three hierarchical primitives, we further devised a disentanglement scoring system (from the interpretation heatmap) that rewards higher separability of factors across different latent dimensions and penalizes scenarios with coexisting or entangled features within the same latent dimension (Methods). The disentanglement across the three hierarchical primitive factors can further be summarized by a bubble plot (Fig. 3b), in which we can gain further insights into the separability of the three visual primitive factors across the latent dimensions by highlighting the predominant factors of variation encoded in MorphoGenie. Thus, one can evaluate the extent of entanglement/disentanglement between the bulk, local, and global factors within each dimension of the latent space (Methods).

The overall approach of disentanglement learning assessment also provides a practical visual guide for the selection of the best-disentangled model, which can be determined through a grid search, tuning a hyperparameter that controls the degree of disentanglement in VAEs (Fig. 3b, Supplementary Fig. S4). In this case, the evolution of the disentanglement learning process can clearly be visualized by both the interpretation heatmap and bubble plot. In the initial training steps, the latent dimensions predominantly comprise entangled features (Fig. 3b). However, as the training progresses, there is a noticeable transition during which the latent space becomes increasingly disentangled.

For interpretability evaluation, we benchmark MorphoGenie against the key VAE variants, including VAE, AAE, ${{{\rm{\beta }}}}$-VAE, Guided VAE, CC${{{\rm{\beta }}}}$-VAE, and FactorVAE^{15,20,21,27,33}, all with a 10-dimensional latent space. These VAEs operate on continuous latent spaces, where the latent variables are sampled from an aggregated posterior distribution. Although AAE is not specifically designed to have a disentangled representation, AAE learns continuous latent space typically employ larger latent space. To facilitate the comparisons, we also include it in our qualitative and quantitative evaluation, using a reduced 10-dimensional latent space (Supplementary Figs. S4, S5). We also recognize VQ-VAE and JointVAE as the notable approaches for disentangled representation learning—VQ-VAE using a discrete codebook²³, and JointVAE using a combination of continuous and discrete latent variables³⁴. However, our interpretability assessment is specifically tailored for continuous latent spaces, where each dimension can be systematically traversed and interpreted. Therefore, we do not benchmark VQ-VAE or JointVAE in this context. Comparing different VAE models based on the disentanglement scores, Factor-VAE is chosen in MorphoGenie because of its consistently superior disentanglement performance across diverse image datasets (Fig. 3c and Supplementary Figs. S4, 5).

We next demonstrate the MorphoGenie’s ability to learn the disentangled representations in two distinctly different image contrasts and cell formats - label-free QPI of three different lung cancer cell subtypes in suspension (Fig. 3d–g); and fluorescence adherent cell images of a Cell-Painting drug assay¹² (Fig. 3h–k). The disentangled latent profiles generated by MorphoGenie show distinct groups associated with specific cell types (i.e., small cell lung carcinoma (SCLC), squamous cell carcinoma (LUSC) and adenocarcinoma (LUAD)) or the presence of drug treatment (Human osteosarcoma U2OS cell line treated with glucocorticoid receptor agonist) (Fig. 3d, h).

Based on these profiles, we generated the latent traversal maps from which we can identify qualitatively the key factors of variations in the latent space (Fig. 3e, i). For instance, in the lung cancer cell dataset, Dimensions 0, 1, and 3 show distinct changes in the textural distribution of phase. In contrast, Dimension 7 displays a significant shift in overall cell shape (Fig. 3e). In the Cell Painting dataset, Dimension 4 exhibits a noticeable change in overall cell size/shape. In contrast, Dimension 7 contributes to drastic textural modification within the cell (Fig. 3i).

To investigate further how MorphoGenie learns to disentangle cell morphological features, we employed the interpretation heatmap to illustrate the grouping/clustering of specific hierarchical visual primitive features corresponding to the disentangled latent dimensions. In both datasets, hierarchical features can effectively be segregated into different latent dimensions with minimal redundancy - indicating that the latent representations are disentangled according to the spatial hierarchy (Fig. 3f, j). Specifically, we observed that Dimensions 0, 3, and 7 in the lung cancer datasets, which are among the top-ranked (top 5) latent features for classifying the three cell types (Supplementary Fig. S6a), are primarily linked to the local texture, global texture and bulk mass/optical density features, respectively (Fig. 3f). We also note that, across all feature categories, the distributions of the most significant manually extracted features closely align with those of their corresponding latent representations, as visualized in violin plots (Supplementary Figs. S7, S8), demonstrating that MorphoGenie effectively captures the underlying feature distributions in its latent space.

Similarly, in the Cell-Painting dataset, predominant texture feature variation is observed, with Dimensions 1 and 5 emphasizing more on the local textural aspects and Dimension 7 highlighting global textural features. On the other hand, Dimensions 3 and 4 are more related to the bulk cell shape (Fig. 3f, j). Hence, these observations suggest that the most significant morphological features sensitive to drug perturbation are closely linked to the local and global textural changes, whereas the bulk aspects are comparatively less significant.

We note that only some latent features always display clear factors of variations in the 10-dimensional latent space. For instance, Dimensions 4 and 9 in the lung cancer dataset, the minor important features for cell-type classification (Fig. 3e), show no apparent morphological variability in the latent traversal maps. This observation is consistent with the latent feature ranking analysis (Supplementary Fig. S6) and thus their negligible contribution to the interpretation heatmap (Fig. 3f) and the bubble plot (Fig. 3g). Based on these analyses, we can disentangle the relevant morphological features learned by MorphoGenie, and further provide an interpretable assessment of their contributions to classification tasks (which are further detailed in the next section), based on the three hierarchical visual primitives.

We highlight the crucial role of the GAN in enhancing the interpretability of MorphoGenie. As shown in Supplementary Fig. S9a, GAN-generated images capture finer and richer textures than those produced by the VAE decoder. When traversing individual latent dimensions, GAN reconstructions reveal clear textural variations that are not apparent in VAE outputs (Supplementary Fig. S9b). These variations are effectively detected and visualized in the bubble plots, demonstrating that specific latent dimensions correspond to distinct morphological features. Overall, the GAN not only improves image fidelity but also augments the ability of MorphoGenie to disentangle and interpret complex morphological patterns (Supplementary Fig. S9c), providing deeper insights into underlying biological processes.

We note that all the components in our interpretation pipeline, from the latent traversal reconstructions, the disentangled latent profile, the interpretation heatmap, the features ranking, to the bubble plot, are arranged/aligned in the same order of latent dimensions (Fig. 3d–g and h–k). This alignment allows feature interpretation to be easily approached in a bi-directional manner. Firstly, the user can select dimensions based on qualitative assessment and investigate deeper into the profiles and corresponding interpretation heatmaps. Alternatively, they can pick the targeted disentangled dimensions, assess the dimensions based on the feature rankings, and visually identify the morphologically varying factors learned by MorphoGenie.

MorphoGenie enables interpretable downstream analysis: cell type/state classification

Previously, we demonstrated that a biophysical phenotyping method based on a deep neural network model, which was trained with the manually extracted hierarchical morphological features, could effectively identify three distinct histologically differentiated subtypes of lung cancers¹¹. In contrast to this supervised learning method, we evaluate whether the unsupervised disentangled representation learning in MorphoGenie can also support such downstream biophysical image-based analyses¹⁰.

Therefore, we performed dimensionality reduction using the uniform manifold approximation and projection (UMAP) algorithm based on the set of MorphoGenie’s disentangled representations (i.e., the profile shown in Fig. 3d) learned from all single-cell lung cancer QPI. Visualizing the MorphoGenie’s latent space in UMAP reveals the clear clustering of the three major lung cancer subtypes based on their label-free biophysical morphologies: LUSC, (H2170), LUAD (H1975), and SCLC (H526). (Fig. 4a). Using these disentangled representations to train a decision-tree-based classifier (Methods) also yields high label-free classification accuracies among three cell types (77%-94%) (Fig. 4b). In comparison, supervised convolutional neural network (CNN) mode of classification, achieves an overall accuracy of 88% (Supplementary Fig. S10). We note that even the dimensionality of MorphoGenie is kept at 10 dimensions only, which displays high degree of disentanglement (compared to higher dimensional latent space (Supplementary Fig. S11)), significantly smaller than the AAE (512-dimensional)¹⁷ and VQ-VAE (1024-dimensional)¹⁶, MorphoGenie is still able to cluster clearly in UMAP different lung cancer cell types (Fig. 4a).

**Fig. 4: Downstream morphological analysis based on the disentangled representation learnt from MorphoGenie.**

Further analysis of disentangled representations shows that the latent dimensions particularly influential in lung cancer cell-type classification, such as Dimensions 0, 3, and 7 (i.e., the dimensions that are more related to the three different hierarchical visual primitive morphological aspects (Fig. 3f, g)), display heterogeneities when color-coded in UMAP, confirming their discriminative power (Fig. 4c). We further observed that the patterns of the expressions (i.e., the normalized values) of disentangled representations among the three subtypes align very well with the manually extracted biophysical features falling under the same hierarchical attributes. For instance, Dimension 3 (primarily attributable to global texture of mass/optical density, as shown in Fig. 3f, g) shows the same pattern of variation as the global textural feature GlobalInt3 (Intensity Skewness in the intensity histogram) (See the box-plot comparisons in Fig. 4d). This agreement suggests that MorphoGenie’s representations are not simply statistically significant but also readily interpretable in label-free lung cancer subtype classification.

Apart from label-free QPI, we proceeded to test the downstream analysis with the fluorescence cellular images (based on the Cell Painting dataset shown in Fig. 4e–g). Clearly, the disentangled representations learned from MorphoGenie can show the morphological change/shift due to the bioactive compound treatment (Fig. 4e). To further identify the organelle-specific morphological variations, we subsequently trained MorphoGenie with separate fluorescence channels (Methods). We observed that MorphoGenie is indeed able to delineate the impacts on different organelles’ morphologies due to the drug treatment (Fig. 4f, g). Our decision-tree classifier trained with the disentangled latent representations showed that actin and nucleoli have the most distinct difference in morphology (AUC: 0.87 for actin; 0.83 for nucleoli) as AUC values (Fig. 4f). We also observed that the shifts in the drug-treated cell population from the control condition (mock) is more pronounced in the cases of actin and nucleoli, compared to other organelles (Fig. 4g). To further demonstrate MorphoGenie’s ability to detect and track variations induced by drug treatment in different organelles across five channels, we included three additional treatments Supplementary Fig. S12 and performed similar analyses as shown in Fig. 4e–g. Notably, MorphoGenie detected treatment effects in multiple channels, with the known mechanisms of action (MOA) for each of the three treatments. We also evaluated F1 scores for drug-treatment classification alongside the AU-ROC analysis and included the results in the Supplementary Fig. S26.

In terms of classification tasks, we also note that MorphoGenie in general outperforms other VAE-only models, including (“disentangled” VAEs and “non-disentangled” VAEs) as well as CellProfiler (i.e., hand-crafted feature extraction method) across all the datasets studied in this work (Supplementary Figs. S13, S14). Hence, it further substantiates the advantages of MorphoGenie over other state-of-the-art VAE models from the perspectives of image reconstructions and downstream analysis, with the extra benefit of having disentangled representation (Supplementary Figs. S15, S16).

MorphoGenie enables interpretable downstream analysis: cellular progression tracking

We next investigated if MorphoGenie could extend beyond static cell type/state classification to enable dynamic tracking of cellular progression. Morphological profiling of continuous cellular progressions and dynamics could provide valuable insights into deciphering complex cellular development, e.g., cell growth, differentiation, and the mechanisms behind various physiological and pathological conditions. Here we put MorphoGenie to the test, evaluating its capacity to monitor morphological changes during cellular events such as epithelial-to-mesenchymal transition (EMT) and cell-cycle progression (Fig. 5).

**Fig. 5: Downstream trajectory inference from MorphoGenie’s disentangled representations.**

EMT is a critical process underlying various biological phenomena, including embryonic development, tissue regeneration, and cancer progression^35,36. EMT includes dynamic changes in cellular organization leading to functional changes in mobility. Here, we utilized MorphoGenie to analyze time-lapse live-cell fluorescence imaging data from the A549 cell line, labeled with endogenous vimentin–red fluorescent protein (VIM-RFP). As vimentin, an intermediate filament, is a key mesenchymal marker, the expression and morphological changes of fluorescently-labeled vimentin could be indicative of the process of EMT, induced by transforming growth factor–β (TGF-β) in this study³⁷.

Furthermore, the disentangled representations derived from VIM-RFP-expressing cell images by MorphoGenie were scrutinized using a novel trajectory inference tool called StaVia³⁸. It is an unsupervised graph-based algorithm that initially organizes single-cell data into a cluster graph^39,40. Subsequently, it applies a high-order probabilistic approach based on a random walk with memory to calculate pseudo-time trajectories, mapping out cellular pathways within the graph structure. StaVia also offers intuitive graph visualization “Atlas View” that simultaneously captures the nuanced details of cellular development at single-cell resolution and the overall connectivity of cell lineages in an edge-bundle graph format⁴⁰ (Fig. 5b, k). Through the integration of MorphoGenie and StaVia, we aim to provide a robust framework for providing holistic visual understanding of the continuous cellular processes with different complexities, as EMT and cell cycle progression studied in this work.

MorphoGenie’s disentangled representations (Supplementary Fig. S17a) successfully recapitulate chronology of the TGF-β-induced EMT into three different stages, i.e., epithelial (E), intermediate (I), and mesenchymal (M) (Methods) (Fig. 5a), annotated in the previous study³⁷. Furthermore, MorphoGenie also reveals the heterogeneity in the single-cell EMT trajectories (Fig. 5b), in which three distinct EMT pathways leading to the separate terminal clusters (Fig. 5c). This is in contrast to the two pathways previously reported³⁷.

To validate this observation, we investigate the images of the mesenchymal populations in these three pathways, identifying discernible morphological differences (Fig. 5d). Particularly, we observe that the cells toward the end of pathway 2 and 3 (M) tend to show elongated spear shapes, characteristic changes of EMT³⁷. This is compared to the cells at the terminal cluster of pathway 1 (I) are still in more or less round shapes.

Our trajectory inference analysis showcases differentially expressed disentangled representations (Fig. 5e-g) (notably Dimensions 3, 5, and 4) in the three pathways (Fig. 5h). We note that the representation trends in Pathway 3 are more deviated from the Pathway 1 and 2. Our interpretation heatmap highlights that Dimensions 3, 5, and 4 are more closely related to bulk, global texture, and local texture features of the cell morphology, respectively (Fig. 5f, g). On the other hand, our feature ranking suggests the dimensions that rank higher are pertaining to the shape-size morphologies and global intensity (Supplementary Fig. S6c). The above analyses thus provide a multifaceted description that suggests that the discriminative factors for EMT states are primarily associated with cell shape and size morphologies, and vimentin global textures, associated with subtle changes in local textures - consistent with the previous findings³⁷.

We further verified that the variations of the three disentangled representations (Dimension 3, 5 and 4) across three lineages correlate strongly with the corresponding hierarchical visual attributes (Fig. 5i). The distinct change patterns in Dimension 3 and 5 across lineages are highly consistent with the changes of aspect ratio (bulk AR) and the global intensity values (GlobalInt3- Skewness of the intensity levels of the image pixels). The small variation in Dimension 4 across lineages is concordant with similar insensitive changes in local texture features (LocalTextFib2- Radial distribution of fiber texture in the image).

We further explored MorphoGenie’s potential to predict cell cycle progression based on biophysical morphologies. For this purpose, we utilized our recently developed high-throughput imaging flow cytometer, FACED^41,42. FACED operates at speeds surpassing traditional imaging flow cytometry (IFC) by at least 100 times, offering a rapid and efficient alternative for cell cycle analysis, which typically relies solely on fluorescence intensity measurements from DNA dyes. Recent IFC advancements have demonstrated that label-free imaging can predict DNA content, and hence cell cycle phases, in live cells. MorphoGenie aims to expand on this capability by extracting biologically relevant information from large-scale single-cell FACED-QPI data and analyzing subcellular biophysical texture changes throughout the cell cycle (Methods).

In this study, our FACED platform captured a set of multimodal image contrasts, including fluorescence and QPI. These contrasts provide high-resolution insights into the biophysical properties of cells, such as mass and optical density, which are often challenging to assess through conventional methods. Utilizing QPI images from FACED, MorphoGenie generated disentangled representation profiles of live human breast cancer cells (MDA-MB231) as they progressed through the cell cycle (Fig. 5j, see latent traversal in Supplementary Fig. S17b).

Furthermore, using StaVia, our pseudotime analysis based on MorphoGenie’s disentangled representations reveals a well-defined progression (Fig. 5j), both in terms of pseudotime reconstruction (Fig. 5k) and lineage probability (Fig. 5l) - consistent with the chronology of G1, S and G2 phases, independently defined by the fluorescently labeled DNA images in the same FACED imaging system (Fig. 5j, see Methods).

Based on our feature interpretation analysis (Fig. 5m–o), we can interpret that MorphoGenie’s disentangled representations captures general characteristics of changes in both cell size and local textures (Dimension 3), cell shape (Dimension 7), global textures (Dimension 4), composite changes in local/global textures (Dimensions 6 and 9) (Fig. 5n–o). In the pseudotime analysis, we indeed observed that Dimension 3, which captures simultaneous variability of cell size and local texture features, displays a significant progression through the G1-S-G2 phases (Fig. 5p). This finding aligns with established knowledge of cell growth in bulk size and mass during the cell cycle⁴¹. Moreover, Dimensions 4, 6 and 9, which are indicative of global/local phase intensity and relate to the dry mass density textures of cellular components like chromosomes and cytoskeletons⁴⁰, exhibit a slow-down during the G1/S transition (Fig. 5p) (Supplementary Fig. S18). This trend is in agreement with the slower rate of protein accumulation observed during the S phase⁴³.

This finding is further validated by the correlational analysis between the actual DNA content from the fluorescently labeled DNA images and the predicted DNA (Fig. 5q). In this analysis, Latent Dimension 3 shows a high correlation, with a pearson correlation coefficient of $R$ = 0.82, compared to other dimensions, which exhibit lower correlation coefficients. The dimension-wise correlation analysis is illustrated in Supplementary Fig. S19. This suggests that dimension 3 is related to dry mass density growth relevant to cell-cycle progression. The strength of MorphoGenie, as demonstrated by these findings, lies in its ability to interpret the intricate biophysical morphology of cells captured by FACED and to provide a predictive analysis of cell cycle progression.

Generalizability of MorphoGenie across imaging modalities

The wealth of morphological data generated by current microscopy technologies poses a challenge for interoperable analysis, a key attribute for cross-modality correlative analysis, such as QPI-fluorescence imaging. For generative morphological profiling, achieving this interoperability necessitates a model with a high degree of generalizability. In the case of MorphoGenie, this means that the disentangled representations should encapsulate fundamental cellular image features and be transferable across diverse cellular image contrasts.

To assess MorphoGenie’s generalizability, we trained the model on a dataset from one imaging modality and tested its performance on unseen datasets with different image contrasts. We aimed to determine whether MorphoGenie could apply its trained latent representations to perform accurate downstream analyses and predictions on these new test datasets, without any retraining.

The robustness of a pre-trained MorphoGenie model is illustrated in Fig. 6, where we demonstrate its ability to carry forward the learned insights as disentangled representations and make precise predictions in the unseen novel contexts. We evaluated four distinct models, each initially trained on a unique dataset. When tasked with analyzing three additional datasets, each with significant variations in single-cell analytical problems (from discrete cell state/type classification to continuous trajectory inference), cellular morphology (adherent versus suspension cells), and image contrasts (fluorescence, and QPI), the models produced visualizations with consistent global and local structures, whether viewed in UMAP or StaVia’s Atlas View (Fig. 6a)

**Fig. 6: MorphoGenie’s generalizability performance.**

For example, a model pre-trained on the Cell-Painting assay (CPA) dataset, which involved classifying morphological changes in adherent cells, was capable of classifying suspension lung cancer cells using label-free QPI images. Furthermore, it provided insightful trajectory inferences for cell cycle progression and EMT. The performance of such generalization, as evident from the F1 scores, is preserved across different model training scenarios (Fig. 6b).

To further evaluate the generalizability of MorphoGenie, we extended the cross-modality/dataset tests to a wider range of unseen scenarios/datasets (Supplementary Fig. S20, Methods). They include delineation of sub-types of primary human T-cells and their activation states (QPI), classification of lung cancer cell sub-type captured from multiple experimental batches, monitoring of morphological responses of lung cancer to anticancer drug treatment (bright-field); cell-type classification from a recently published large-scale dataset of label-free live cells (phase-contrast). Again, we observed that all 8 models pre-trained respectively by different datasets can be used to produce consistent downstream analysis performance (across 8 diverse imaging scenarios), as evident from both data visualizations in UMAP and F1 scores (Supplementary Fig. S20).

We next evaluated how the disentanglement, and thus the interpretation of the latent space of a pre-trained model could be impacted when it is tested with the new unseen datasets. This evaluation was conducted in two primary ways. First, we assessed the performance of a trained model when applied to a new dataset, comparing the interpretation heatmaps of the original and generalized models. This comparison is facilitated by measuring the variance using latent traversals to construct the interpretation heatmaps (Fig. 6b). The results indicate that the model generalizes well and accurately reconstructs images that are similar in appearance, in a notable case, such as the Cell-Cycle (Ccy) versus the Lung Cancer (LC) datasets. The bubble plot further supports this finding, highlighting Dimensions 7, 4, and 3 in both the main and generalized heatmaps as corresponding to the bulk, global, and local categories, respectively (Fig. 6c). We note that the disentanglement of the model can moderately be generalized to not only similar imaging modality but also new modality. For instance, models trained solely with QPI datasets preserve the disentanglement even they are tested with the Cell-Painting (fluorescence) dataset (Fig. 6d). We also note that such models, pretrained solely with single dataset/modality, is sometimes compromised when it is tested with the unseen datasets which have significantly different morphological shape or different color scales (Fig. 6d). We anticipate that the disentanglement could better be generalized if different model training paradigms can be adopted, such as transferring learning with more diverse datasets captured from multiple modalities.

We further assessed MorphoGenie’s latent space by comparing representations for a lung cancer (LC) dataset using two different pretrained models: one trained on the LC dataset itself and another on a distinct cell cycle progression (Ccy) dataset (Fig. 6e). We evaluated how the bulk, global, and local textural morphological categories were represented in both models by calculating latent-feature-wise correlations and visualizing them as correlation bubble plots. The analysis revealed that corresponding latent features exhibited substantial correlations between the two models, and that the distributions of the key morphological categories (bulk, global, and local textures) were highly similar. Moreover, the distributions of these categories remained consistent with the original manually defined features, underscoring the interpretability of the learned representations. This encouraging level of transferability suggests that MorphoGenie learns core morphological primitives from a single dataset that generalize to new contexts. Nonetheless, we anticipate that pretraining on a more diverse array of cell types and imaging modalities could further enhance the model’s generalizability and robustness across different datasets.

Discussion

Supercharged by the advances in computer vision, learning morphological features of cells through deep learning has gained considerable interest in the last decade. We introduced MorphoGenie, a deep-learning framework for profiling cell morphologies that effectively handles data from various microscopy modalities, including standard fluorescence, QPI, and imaging flow cytometry. Through comprehensive evaluations (from model performance to generalization), we demonstrated that MorphoGenie distinguishes itself from the current state-of-the-art with the following key attributes.

In contrast to the prior work¹⁹, MorphoGenie not only achieves high-fidelity image synthesis but also provides a comprehensive and flexible pipeline for the quantification and interpretation of disentangled latent features. Through extensive benchmarking, interpretability analyses, and generalizability testing, MorphoGenie establishes itself as a robust tool for uncovering both known and novel morphological patterns in single-cell imaging data.

The generalizable latent space, visualized as an interpretation heatmap, enables the identification of factors contributing to multiple cell states and conditions. The model’s main strength is in extracting the compositional essence of cell morphology, distilling this into a limited set of key representations that can be flexibly interpreted to uncover novel insights across different imaging scenarios. This approach not only minimizes complexity but also enhances the alliance between human intuition and machine intelligence. Comparatively modest in dimensionality (Supplementary Fig. S11), MorphoGenie operates within a 10-dimensional latent space—significantly more concise than the expansive feature sets generated by manual extraction methods (e.g., Cell-Profiler: ~1700 dimensions⁹) or other generative models (e.g., AAE: 512 dimensions; and VQ-VAE: 1024 dimensions). Our evaluations illustrate its compatibility in a broad spectrum of single-cell image analyses, ranging from discrete cell-type classification to intricate trajectory inference. Compared to other state-of-the-art autoencoder models, MorphoGenie offers advantages of accurate image reconstruction (Fig. 2, and Supplementary Fig. S2, 3), clear visual and quantitative data analysis across diverse data types (Supplementary Fig. S13–S16), disentanglement representation learning (Fig. 3c and Supplementary Fig. S4, 5), and generalizable cross-modality learning (Fig. 6, Supplementary S20, S21). MorphoGenie’s strength lies in its focused distillation of critical morphological information, avoiding the clutter of excessive features that can hinder meaningful interpretation.

Comparing MorphoGenie with traditional morphological feature extraction methods highlights distinct advantages in single-cell image analysis. While both MorphoGenie and CellProfiler achieve comparable results in downstream analyses, MorphoGenie offers significant benefits in several key aspects. Notably, MorphoGenie excels at tracking morphological changes, such as smooth transitions during EMT and distinguishing distinct cell lineages (Supplementary Figs. S21 and S22). In addition, MorphoGenie extracts features significantly faster than CellProfiler (CellProfiler-v4.2.8) (Supplementary Table S4)⁹. While CellProfiler offers built-in segmentation tools for simple tasks and integrates external tools like CellPose and Stardist as plugins for more complex tasks, MorphoGenie also leverages external tools such as CellPose and intensity threshold-based algorithms for segmentation^44,45. Notably, MorphoGenie requires only a single training session on single cell segmented images, generalizing to any dataset without significant modifications. In contrast, CellProfiler demands manual parameter tuning for each run.

MorphoGenie’s interpretability is further refined through a systematic investigation into the interplay between its disentangled latent space and the morphological descriptors of single cells, derived from a spatially hierarchical analysis. This analysis stratifies morphological features into a structured hierarchy from the nuanced textures (and their statistical analyses) to the more discernible attributes like cell size, shape, and mass/optical density textural distribution. Employing this hierarchical framework, MorphoGenie constructs a morphological profile that facilitates semantic and biological interpretations of the disentangled representations. It should be noted that it is not the purpose of MorphoGenie to seek for a universal interpretation that can offer a complete disentanglement among spatial hierarchical groups of cellular features - which is unlikely to occur in complex biological processes. Instead, MorphoGenie provides a practical reductionist framework to distill the key morphological features and their changes that can be explainable by the hierarchical features defined in this work.

In some cases, bulk cellular features (such as size and shape) naturally overlap with global or local texture variations, as visualized in our bubble plots (e.g., Figs. 3–6, and Supplementary Fig. S4). Rather than contradicting the principle of disentanglement, these overlaps reflect inherent correlations in biological systems—for example, larger cells often exhibit increased intracellular space and dry mass. By contextualizing morphology within such a spatial hierarchy, our approach enables researchers to systematically reveal how different latent dimensions correspond to biologically meaningful properties, even when these properties are not strictly independent. Building on this, our framework is not confined to predefined feature sets; it can be extended to incorporate new and complementary descriptors, such as fractality⁴⁶, Fourier decomposition of cell shape⁴⁷ or other geometric and statistical descriptors⁴². As long as these features facilitate biological interpretation, MorphoGenie’s disentangled representation learning process can flexibly accommodate and reveal new insights into cellular morphology. For example, we demonstrate this flexibility by integrating fractal features for enhanced interpretability, as shown in Supplementary Fig. S29.

Beyond correlating latent features with manual annotations, we aim to develop user-friendly tools that integrate disentanglement, interpretability, and explainability to reveal morphological changes across conditions and phenotypic transitions. To overcome the limitations of supervised disentanglement metrics, which often rely on incomplete or biased ground-truth labels particularly in biological datasets, we propose using unsupervised methods such as UDR^48,49. UDR assesses disentanglement quality by comparing model representations in pairs and has been shown to align well with supervised evaluation methods.

Importantly, interpretability is not just about selecting models with high disentanglement scores; it also requires clear, biologically meaningful explanations of the learned representations to be able to communicate and deploy. Recent methods enhance interpretability by applying perceptual similarity and spatial constraints, making latent features more aligned with human-understandable concepts and assess disentanglement without supervision⁵⁰. MorphoGenie lays the groundwork for building intuitive, interactive tools that enable automated interpretation of biological data with minimal human input.

Moreover, the generalizability of MorphoGenie is evidenced by its capacity to learn from one dataset and accurately predict morphological features in completely unseen datasets, regardless of the imaging modality, cell morphological formats and problems of interest. This adaptability demonstrated the model’s robustness and its potential as an interoperable analytical tool. It enables consistent cross-modality analysis, facilitating comparisons and integrations across studies, which is invaluable for the progression of biological research and understanding of cellular heterogeneity. MorphoGenie demonstrates flexibility in model selection, allowing for the integration of new disentanglement strategies and generative algorithms^50,51. Incorporating these disentangled models with improved image generation quality enhances both interpretability and generalizability. This adaptability ensures that MorphoGenie remains at the forefront of technological advancements, continually improving its ability to extract meaningful insights from complex biological data.

In summary, MorphoGenie provides several key advantages, including improved interpretability of cellular morphology, enhanced generalizability across different datasets, and increased scalability for processing large datasets. It also overcomes the curse of dimensionality by capturing primary factors of variation and offers flexibility in its interpretation pipeline. Additionally, MorphoGenie enables the discovery of novel morphological features that may be correlated with specific biological processes or perturbations. MorphoGenie’s ability to reproduce biologically meaningful information in generated images, and consequently in downstream visualizations (Supplementary Fig. S28), underscores its potential for applications such as data compression, while future GAN enhancements are expected to further enable cross-modality image translation.

Looking forward, there are a number of avenues for further development of MorphoGenie. (1) MorphoGenie’s capabilities can extend beyond individual cells. By learning factors that are not confined to hierarchical single-cell features, MorphoGenie can capture more fundamental insights in tissue images, related to cell spatial organization, cell-cell interactions, protein localization, and other critical cellular processes. This expansion of scope enables the framework to provide deeper insights into the dynamics of multicellular systems, paving the way for broader applications in complex biological environments where understanding collective cellular behavior is essential. (2) 3D cellular imaging: Extending MorphoGenie to interpret three-dimensional cellular images will unlock a deeper comprehension of spatial cellular dynamics, benefiting from the volumetric data (e.g., confocal, multi-photon, and light-sheet imaging techniques). (3) Batch effect correction: Tackling batch effects could improve the model’s precision, minimizing technical noise and enhancing the biological signal in morphological data⁵². Leveraging the recent advancements in self-supervised/weakly supervised learning for this purpose will potentially improve the reproducibility and accuracy of phenotype classifications across different datasets. (4) Image reconstruction and translation: High-fidelity image reconstruction capabilities of MorphoGenie could augment the applicability of label-free imaging, such as translating QPI to fluorescence images. This could build a bridge between molecular specificity and morphological phenotypes, enriching our label-free understanding with detailed molecular insights. (5) Broadened interpretability: The framework currently categorizes features into bulk, global, and local textures. Expanding this taxonomy will capture a wider range of cellular features. It could be readily achievable in MorphoGenie, thanks to its ability to adapt to new domains where it can be fine-tuned to less-represented scenarios, potentially uncovering novel morphological features and contributing to the discovery of new cellular phenotypes or pathological states.

Methods

Disentangled representation learning in MorphoGenie

MorphoGenie is a deep-learning pipeline that generates the cellular morphological profiles and images of cells through disentanglement representation learning in an unsupervised manner. It can subsequently offer interpretation of the morphological profile through hierarchical feature mapping. Specifically, it employs a hybrid neural-network architecture built upon two generative models (VAE and GAN) (Figs. 1–2) that jointly optimizes the objectives of disentanglement learning and high-fidelity image generation by a dual-step training approach. In principle, while different VAE variants could be adopted in MorphoGenie, our comparative analyses have shown that FactorVAE stands out in accurately learning the disentangled representations in the latent space and reconstructing the cell images (Fig. 3, Supplementary Fig. S2). For the sake of clarity, we first describe the key features of different state-of-the-art VAE models tested in this work including the vanilla VAE, β-VAE and FactorVAE:

Variational autoencoder (VAE)

Consider a dataset consisting of N discrete or continuous variables x.

$$X=\left\{{x}^{i}\right\}i=1..N$$

(1)

The encoder of a VAE initially maps the input data X to a probability distribution ${q}_{e}$, which is modeled as a multivariate Gaussian distribution ${{{\mathscr{N}}}}$ representing the latent space. The encoder learns to approximate the variables z of the K-dimensional latent space which is represented as a posterior approximation according to the Bayesian rule¹⁵.

$$z \sim {q}_{e}({z|}{x}_{i})={{{\mathscr{N}}}}({z;}{\mu }_{i},{{\sigma }_{i}}^{2})$$

(2)

where ${\mu }_{i},{\sigma }_{i}$ (mean, variance) are the outputs of encoder. On the other hand, the decoder of the VAE samples the variable z from $z \sim {q}_{e}\left({x}_{i}\right)$ to generate the observed data point x, which is given by

$$x{\prime} \sim {P}_{d}({x|z})$$

(3)

Assuming the data $X{\prime}$ is generated by continuous hidden representation z, by formulating a generative model Eq. (4)

$$X{\to }^{e}Z{\to }^{d}X{\prime}$$

(4)

The above two approximations are optimized jointly by a single objective function:

$$L\left(d,{e;}{x}^{\left(i\right)}\right)=-{D}_{{KL}}\left[{q}_{e}({z|}{x}^{\left(i\right)}){||P}(z)\right]+{{\mathbb{E}}}_{{q}_{e}({z|x})}[\log {P}_{d}({x}^{\left(i\right)}{|z})]$$

(5)

where $P\left(z\right)$ is the prior which is a K-dimensional normal distribution ${{{\mathscr{N}}}}({{\mathrm{0,1}}})$. The Kullback–Leibler divergence (KL divergence, ${D}_{{KL}}\left[{q}_{e}\left(z,|,{x}^{\left(i\right)}\right){||P}(z)\right]$ is introduced to assess the divergence of the two distributions ${q}_{e}({z|}{x}^{\left(i\right)})$ and $P(z)$. The above term of the LHS is optimized and differentiated to estimate the variational parameters “e”, and the generative parameters “d”. However, it is practically infeasible to estimate the parameter “e” as it is not differentiable which is overcome by reparameterization trick¹⁵.

β-VAE

It extends the standard VAE by an additional hyperparameter ${{{\rm{\beta }}}}$. ${{{\rm{\beta }}}}$-VAE is deigned to achieve a disentangled latent representation by controlling beta ${{{\rm{\beta }}}}$. When ${{{\rm{\beta }}}}=1$ it represents a standard VAE and varying ${{{\rm{\beta }}}}$ > 1 improves disentanglement at the cost of data reconstruction. However, higher values of ${{{\rm{\beta }}}}$ allow interpretation of the latent space by varying dimensions, leading to an objective function²¹:

$$L\left(d,{e;}{x}^{\left(i\right)},\beta \right)=-{\beta*D}_{{KL}}\left[{q}_{e}\left(z,|,{x}^{\left(i\right)}\right){||P}(z)\right]+{{\mathbb{E}}}_{{q}_{e}({z|x})}[\log {P}_{d}({x}^{\left(i\right)}{|z})]$$

(6)

FactorVAE

FactorVAE (see Supplementary Fig. S23) addresses the tradeoff in ${{{\rm{\beta }}}}$-VAE, in which penalizing the KL term with weight $\beta$ encourages disentanglement at the same time. It leads to poor reconstruction as it reduces the amount of information of x in z. To address this, in FactorVAE, the KL term in the objective of VAE is split as

$${D}_{{KL}}\left[{q}_{e}\left(z,|,{x}^{\left(i\right)}\right){||P}(z)\right]=I\left(x,z\right)+{KL}\left(\right.q((z){||p}(z))$$

(7)

where, $I\left(x,z\right)$ is the mutual information between the observation x and the latent variable z. However, penalizing the KL term in the above equation leads to pushing the posterior towards the factorized prior and, hence achieving a better disentangled independent latent factor. Therefore, the objective function of FactorVAE can be expressed as:

$$L\left(d,{e;}{x}^{\left(i\right)},\gamma \right)= {{\mathbb{E}}}_{{q}_{e}({z|x})}[\log {P}_{d}({x}^{\left(i\right)}{|z})]-{D}_{{KL}}({q}_{e}({z|x}){||}{P}_{d}(z))\\ -{{{\rm{\gamma }}}}{D}_{{KL}}(q\left(z\right){||}\bar{q}(z))$$

(8)

where,

$$\bar{q}\left(z\right)=q\left(z\right)\mathop{\prod }_{j=1}^{d}q\left({z}_{j}\right)$$

(9)

where ${z}_{j}$ corresponds to one underlying factor of variation in the latent space. ${\gamma }$ in Eq. 8 directly encourages independence in the latent distribution and ${D}_{{KL}}(q\left(z\right){||}\bar{q}(z))$ is known as a total correlation term, being intractable and is optimized by employing an alternate method called density-ratio trick, which involves training a classifier/discriminator (Supplementary Fig. S24) to approximate the density ratio present in the KL term²⁰.

FactorVAE is also modeled as a two-step generative process. First, a latent variable z is sampled from a factorized distribution $p(z)$, where each dimension of z corresponds to an independent factor of variation (e.g., size, intensity, texture). Second, observations (images) are generated from $p(x|z)$. The goal of disentanglement is to encode these factors of variation independently in a latent vector.

1.
Standard Gaussian prior ${{{\rm{p}}}}({{{\rm{z}}}})={{{\rm{N}}}}(0,{{{\rm{I}}}}),$ chosen for its factorized distribution.
2.
Decoder ${{{{\rm{p}}}}}_{{{{\rm{d}}}}}({{{\rm{x}}}}|{{{\rm{z}}}})$, parameterized by a neural network.
3.
Variational posterior ${{{{\rm{q}}}}}_{{{{\rm{e}}}}}({{{\rm{z}}}}|{{{\rm{x}}}})$ with mean and variance produced by the encoder, also parameterized by a neural network.

Observations ${{{\rm{x}}}}({{{\rm{i}}}})\in {{{\rm{X}}}}$ are generated by combining K underlying factors ${{{\rm{f}}}}=({{{{\rm{f}}}}}_{1},...,{{{{\rm{f}}}}}_{{{{\rm{k}}}}})$. These observations are modeled using a real-valued latent/code. The use of a factorized prior encourages orthogonality among latent factors in the aggregated posterior, allowing each latent dimension to represent an independent morphological feature without imposing excessive constraints on the learned representations.

Generative model in MorphoGenie

Disentanglement learning in VAEs often compromises the quality of generated images due to the strict constraints imposed to ensure that the latent variables are fully factorized (independent of each other). Our goal is to enhance VAE-based models by improving the quality of generated images while maintaining their ability to learn disentangled representations. To achieve this, we adopt a hybrid VAE-GAN architecture that separates the tasks of learning disentangled representations and generating realistic images into two distinct but sequential steps. First, we use FactorVAE to learn a disentangled representation of the data, ensuring that the latent variables are independent and capture distinct factors of variation. Next, we train a second network with a higher capacity for image generation by a GAN’s generator. This network takes the disentangled representation learned by the FactorVAE and decodes it into a high-quality, realistic image in the observation space. By decomposing these objectives, we leverage the strengths of both FactorVAEs and GANs: the FactorVAE focuses on disentangling the latent space, while the GAN enhances the quality of the generated images.

Our objective is to build a generative model (Supplementary Fig. S25) that learns the generative parameter ω to produce high-fidelity output x with an interpretable latent code z (i.e., disentangled representation):

$${{{{\rm{G}}}}}_{{{{\rm{\omega }}}}}:{{{\rm{z}}}}\to {{{\rm{X}}}}$$

(10)

The idea is to decompose the objectives of the disentanglement learning and high-fidelity image generation as two different tasks¹⁹. Formally, let z = (s, c) denote the latent variable composed of the disentangled variable c and the nuisance variable s capturing independent and correlated factors of variation, respectively. Depending on which VAE model is used, the VAE model is first trained based on Eqs. (5), (6) or (8) to learn disentangled latent representations of data, where each observation x can be projected to c by the learned encoder ${q}_{e}(z|x)$ after the training. Then in the second stage, encoder ${q}_{e}(z|x)$ is fixed to train a generator ${G}_{\omega }\left(z\right)={G}_{\omega }(s,c)$ for high-fidelity synthesis while distilling the learned disentanglement by optimizing the following objective:

$${\min }_{G}{\max }_{D}{L}_{{GAN}}\left(D,G\right)-\lambda {R}_{{Distill}}(G)$$

(11)

The GAN loss, ${L}_{{GAN}}\left(D,G\right)$ is optimized adversarially, enabling the discriminator to distinguish between real and fake images, while simultaneously improving the generator’s ability to produce realistic images from random noise.

$${L}_{{GAN}}\left(D,G\right)={E}_{x \sim P(x),c \sim {q}_{e}(c)}[\log \left(\right.D\left(x\right)]+{E}_{s \sim P\left(s\right),c \sim q\left(c\right)}[\log \{1-D(G(s,c))\}]$$

(12)

The alignment of the GAN’s reconstruction with the disentangled representation is accomplished by ${R}_{{Distill}}(G)$. And the ${R}_{{Distill}}$ term aims to maximize the mutual information between the latent variable c and the generator output, ${I}({c;c}^{{\prime} })$ where, ${c \sim q}_{e}(z|x)$ and the ${{c}^{{\prime} } \sim q}_{e}(z|{{{\rm{G}}}}\left({{{\rm{s}}}},{{{\rm{c}}}}\right))$. Notably, $c$ and ${c}^{{\prime} }$ is sampled from the aggregated posterior distribution ${q}_{e}(z|x)$, rather than the prior distribution$q\left(c\right)$. Dotted lines in Fig. 2a indicates the input to the fixed encoder (from which $c$ and ${c}^{{\prime} }$ is sampled), which is not updated during the training and is optimized with respect to the generator only. This distills disentangled information into the GAN, enhancing the alignment between latent vector sampling for real and generated images. This joint sequential learning approach enables the hybrid model to minimize the disparity between reconstructions and real images while learning disentangled latent representations.

Image reconstruction through the decoder and generator of MorphoGenie

Reconstructing images from latent representations

The Decoder reconstructs images from a 10-dimensional latent vector c sampled by the Encoder. In contrast, the Generator produces reconstructions by combining the latent representation c with a random noise vector s. Specifically, the GAN generates images based on the 266-dimensional input vector (c, s), where c is the 10-dimensional latent vector sampled from the aggregated posterior, and s is a 256-dimensional random noise vector. As shown in Fig. 2a and Supplementary Fig. S1, the GAN architecture effectively utilizes this input to produce realistic reconstructions, demonstrating its ability to generate high-quality images from the latent representation.

Traversing latent dimensions to generate images

To generate images that vary in a specific factor, we traverse one latent dimension while keeping the remaining dimensions unchanged. This approach allows us to modify one factor corresponding to the traversed dimension, resulting in generated images that exhibit variations in that particular factor while keeping the other factors unchanged. Given a trained Variational Autoencoder (VAE) with a 10-dimensional latent space, sampling from the aggregated posterior ${c \sim q}_{e}({z|x})$ yields a 10-dimensional disentangled latent vector, denoted as ${{{\rm{c}}}}=({l}_{1},{l}_{2},{l}_{3},{l}_{4},{l}_{5},{l}_{6},{l}_{7},{l}_{8},{l}_{9},{l}_{10})$. This vector is fed into the decoder or generator to reconstruct an image. To generate images with a specific variation corresponding to a single latent dimension, we modify only that dimension while keeping the others constant (as shown in Fig. 3a for a 2 dimensional latent representation). For instance, to traverse the first latent dimension, we change its value ${l}_{1}$ in linear steps, resulting in: ${c}_{11}=({l}_{1}+0.5,{l}_{2},{l}_{3},{l}_{4},{l}_{5},{l}_{6},{l}_{7},{l}_{8},{l}_{9},{l}_{10})$, ${c}_{12}=({l}_{1}+1,{l}_{2},{l}_{3},{l}_{4},{l}_{5},{l}_{6},{l}_{7},{l}_{8},{l}_{9},{l}_{10})$, ${c}_{13}=({l}_{1}+1.5,{l}_{2},{l}_{3},{l}_{4}{l}_{5},{l}_{6},{l}_{7},{l}_{8},{l}_{9},{l}_{10})$ and so on. By extrapolating one dimension ${l}_{1}$, we generate images that vary according to the factor captured by that latent dimension, while the remaining dimensions ${l}_{2},{l}_{3},{l}_{4},{l}_{5},{l}_{6},{l}_{7},{l}_{8},{l}_{9},{l}_{10}$ retain their original values from the vector sampled by the encoder. This process is repeated for each of the 10 dimensions, allowing us to visualize the effect of each latent factor on the generated images.

MorphoGenie training

The latent space dimension of the VAE models studied in this work is set as 10 (Supplementary Fig. S11). The encoder is trained with images of size 256 × 256 × 3. Encoder and decoder (Supplementary Fig. S23) and discriminator (Supplementary Fig. S24) of the FactorVAE is optimized using adam optimizer with decay parameters ${\beta }_{1}$ = 0.9, ${\beta }_{2}$ = 0.999 at a learning rate of 0.0001. On the other hand, the discriminator of the GAN in MorphoGenie is optimized with the decay parameters ${\beta }_{1}$ = 0.5, ${\beta }_{2}$ = 0.9 at a learning rate of 0.0001 and a batch size of 32. The generator of the GAN consisting of the residual blocks is trained with the latent vector (10-dimensional) and a random noise vector called as nuisance vector, which has 256 dimensions¹⁹. Generator and discriminator are trained at learning rate if 0.0001 using RMS prop optimizer, with a batch size of 32 (Supplementary Fig. S25).

Model selection for MorphoGenie

Model selection for MorphoGenie is performed through a grid search over the hyperparameters that control the strength of disentanglement in VAE variants (including β-VAE and FactorVAE). All models are trained in a fully unsupervised manner: no labels or feature category information are used during training. The model learns to represent the underlying structure of the data solely from the input images. After training, models are evaluated based on two criteria: (1) the degree to which the learned latent dimensions separate the three hierarchical primitive feature categories (bulk, global texture, and local texture) in the latent space and (2) downstream performance. This assessment uses predefined feature categories for interpretability, serving as a supervised evaluation step to benchmark how well the unsupervised representations align with biologically meaningful factors. Importantly, this evaluation does not influence the training process or hyperparameter optimization, which remain entirely unsupervised. The top-performing models, as determined by these evaluations, (Supplementary Fig. S27) are then interpreted using interpretation heatmaps. Since the optimal level of disentanglement can vary between datasets, hyperparameters should be tuned accordingly for each dataset during model selection.

Datasets

The datasets selected in this work comprise of a wide range of cell lines for initial model training. Datasets are both open source and those imaged in-house to demonstrate the applicability of our approach to the datasets that are diverse in multiple aspects. The rationale of dataset types is driven by the needs for showcasing the versatility of MorphoGenie - adapting to multiple major imaging modalities, spanning fluorescence, bright-field, phase contrast, and QPI. On the other hand, our choice of datasets also includes distinctly different biological conditions such as multiclass cell type classification (Lung cancer cell type (LC)) cellular response to drug treatment (CPA), and those showing continuous biological processes such as cell-cycle progression (CCy) and EMT. Furthermore, inclusion of different imaging conditions, namely adherent cells (in EMT and CPA datasets) and cells in suspension (in CCy and LC datasets).

To further evaluate the generalizability of MorphoGenie, we include the additional datasets. These comprise Quantitative Phase Imaging (QPI) images of lung cancer cell lines captured in multiple experimental batches. We also include bright-field images of a lung cancer cell line, which capture cellular phenotypic responses to anticancer drug treatment. Furthermore, in addition to cell line datasets we added a new primary human T-cell image dataset. See the detailed descriptions of these datasets in the sections below.

Cell painting assay (CPA)

This is a subset of BBBC022, which is a publicly available fluorescence Cell Painting image dataset, consisting of U2O2 cells treated with one of the 1600 bioactive compounds. In this dataset, images consisting of 5 channels tagged with 6 dyes characterizing 7 organelles (nucleus, golgi-complex, mitochondria, nucleoli, cytoplasm, actin, endoplasmic reticulum). The dataset is provided with annotation of the plate locations corresponding to the compound and the mechanism of action^12,53. One of the treatments annotated as glucocorticoid receptor agonist named Clobetasol Propionate is used in this study for training and testing MorphoGenie. To test perturbation due to the chosen bioactive compound treatment, training is performed in two different ways. First, we overlaid multiple fluorescence channels of the images with the dimension of 256 × 256 × FL, wherein FL can be more than 1 or can be extended up to the maximum number of fluorescence channels available in the dataset. Second, the models are trained separately by using the 5 different channels in the dataset.

Epithelial to mesenchymal transition (EMT)

This dataset consists of fluorescence images of adherent live cell image data (A549 cell line, labeled with endogenous vimentin–red fluorescent protein (VIM-RFP)) to study the morphological changes in response to TGF-β-induced EMT process³⁷. In this dataset, the morphological dynamics of vimentin is quantified by extracting fluorescence texture features (Haralick features). The TGF-β treatment showed a shift in distribution for nearly all Haralick related features (i.e., texture features), with only two trajectories during EMT process were reported. A basic morphological operation has been performed in this work to annotate epithelial and mesenchymal cells by measuring the aspect ratio³⁷. Elongated mesenchymal cell population is generally different from epithelial cells which are generally round and small. The remaining cells are categorized as the population in the intermediate state between the epithelial and mesenchymal states.

Cell-cycle progression

This dataset was captured using another novel, in-house ultrafast QPI technique based on free-space angular-chirp-enhanced delay (FACED). It is an ultrafast laser-scanning technique that allows for high imaging speed at the scale orders of magnitude greater than the current technologies. More specifically, this FACED imaging system is integrated with a microfluidic flow cytometer platform enabling synchronized and co-registered single-cell QPI and fluorescence imaging at an imaging throughput of 77,000 cells/s with sub-cellular resolution^41,42,54. This dataset was collected in an assay for cell-cycle progression tracking of human breast cancer cells (MDA-MB231) in microfluidic suspension. Annotations of the cell-cycle stages (G1, S, and G2) in this dataset were provided by quantitatively tracking the content of DNA labeled with Vybrant Dye orange stain (Invitrogen).

Primary human T-cells dataset

This dataset contains high-resolution, label-free QPI of primary human CD4⁺ and CD8⁺ T cells in resting and activated states. Healthy donor buffy coat samples were obtained from the Hong Kong Red Cross and processed within 24 h. The research protocol was approved by the Institutional Review Board of the University of Hong Kong (IRB Reference No.: UW 17-219) and complied with the Declaration of Helsinki and acts in accordance with ICH GCP guidelines, local regulations and Hospital Authority and the University policies. T cells were isolated through two consecutive negative isolation steps, MACSprep™ PBMC Isolation Kit (130-115-169, Miltenyi Biotec) and follow with Human Pan T Cell Isolation Kit (130-096-535, Miltenyi Biotec) according to manufacturer protocols. All the T cells were then resuspended in RPMI-1640 medium (Gibco) supplemented with 10% FBS and 1% Antibiotic-Antimycotic. Cells were seeded into 48-well plates (32048, SPL Life Science) at a cell density of 2.5 × 10⁶/ml (in each well) under standard culture condition (37 °C, 95% relative humidity). T cell activation was induced using Anti-Biotin MACSiBead Particles conjugated with CD2, CD3, and CD28 antibodies (130-091-441, Miltenyi Biotec) at a 1:2 bead-to-cell ratio. Control wells were maintained without bead addition. Images of T-cells were acquired with the multi-ATOM high-throughput QPI flow cytometer. We use these data to evaluate whether label-free QPI can distinguish T-cell subtypes and their activation states.

Human lung cancer cells treated with anti-cancer drug

This collection comprises bright-field images of NCI-H1975 non-small-cell lung cancer cells treated with a platinum-based anticancer drug, captured on our in-house multi-ATOM system. The platform enables large-scale screening across hundreds of wells—each holding thousands of live, adherent cells. Cells were seeded on fibronectin-coated plates and incubated for 24 h before imaging.

Lung cancer cell types with multiple experimental batches

This dataset comprises of images of various lung cancer cell types, with multiple experimental batches, allowing for the assessment of batch-to-batch variability⁵². The dataset includes 7 lung cancer cell lines imaged by multi-ATOM and analyzed on 7 different days, resulting in 3 batches of ~120,000 cells per cell line, totaling over 1,000,000 single-cell images⁴⁴. Each image consists of two label-free contrasts: Bright Field (BF) and QPI. For this study, a subset of the QPI image dataset was used, including 4 cell lines and 3 batches, representing three major lung cancer types: Lung Squamous Cell Carcinoma (LUSC) with cell line H2170, Adenocarcinoma (LUAD) with cell lines H358 and H1975, and Small Cell Carcinoma (SCLC and cell line H69).

LiveCell

LIVECell is a large scale dataset consisting of phase-contrast microscopy images of 5239 manually annotated, expert-validated, with a total of 1,686,352 individual cells annotated from eight different cell types⁵⁵. The dataset consists of cell types with varying shape morphologies and size, spanning round and neuronal-like structures. Our results include analysis on 4 chosen cell types (A172, BV2, MCF7, SkBr3) with diverse morphologies and sizes.

Lung cancer cell-types (LC):

This dataset consists of single-cell images (QPI) of three major histologically differentiated subtypes of lung cancer amongst seven cell lines, i.e., Three adenocarcinoma (H1975), squamous cell carcinoma cells (H2170), small cell lung cancer cell lines (H526). This data was collected by an in-house high-throughput microfluidic QPI flow cytometry system called multi-ATOM. Detailed experimental setup and protocols can be referred to ref. ¹¹. Using intensity-only measurements, multi-ATOM retrieves the complex-field information of light transmitting through the cell and yields two image contrasts at subcellular resolution: bright-field (BF: amplitude of the complex-field), and quantitative phase (i.e., QPI). BF images essentially display the distribution of light attenuation (or optical density) within the cell whereas QPI presents dry-mass density distribution within the cell¹¹.

Image pre-processing

Our image preprocessing pipeline involves segmentation, background noise removal, and aligning cells to the center of the image frame. We employ different segmentation approaches depending on the image type. For single-cell images captured using a high-speed imaging flow cytometer, intensity threshold-based segmentation is used (Lung Cancer, Cell Cycle datasets)^11,41. In contrast, for images of cells in culture plates with multiple cells in the field of view, Cellpose (Cellpose v2.1.1) is utilized for batch processing of image segmentation, specifically leveraging the ‘cyto2’ model for segmenting images (Cell Painting dataset and EMT)⁴⁵. The images are then cropped into single-cell images, followed by background noise removal, preserving cell body information, and center cropping to reduce the image size to 256 × 256 pixels. Finally, the cells are aligned to the center to prevent positional features from influencing the analysis.

Interpretation heatmap

The latent space of MorphoGenie effectively encodes information of cell morphology within its disentangled dimensions. By traversing the latent space and reconstructing images from MorphoGenie, we can observe variations in the morphological features encoded within each latent dimension (Figs. 1, 2a).

Furthermore, we can investigate how these latent features can be interpreted through a set of hierarchical cellular information. In detail, we manually defined and extracted a total of M = 35 morphological features from the latent traversal images, encompassing bulk, global textural, and local textural characteristics of cell morphology, i.e., ${Feat}={ \{ {{feat}_{1}},\ldots .{{feat}_{M}} \} }.$The chosen latent space dimension is K = 10, which shows high degree of disentanglement (Supplementary Fig. 11). For each dimension, we computed Q ( = 10) steps of latent traversal and visualized the morphological variations across each traversal step. We calculated the statistical variance for each of the M ( = 35) features in each latent traversal of the k^th dimension, resulting in a 1 × M vector (Fig. 3a). This process is repeated for all K ( = 10) latent dimensions, generating K such 1 × M vectors. These vectors are then stacked to create a K × M matrix. We then performed hierarchical clustering in this matrix to identify the relationships between the K latent dimensions and M manually extracted morphological features in a heatmap representation. We refer to this clustered heatmap as the “interpretation heatmap”. This heatmap serves as a reference guide for our MorphoGenie feature analysis. For latent traversal of K = 10 latent dimensions and a total number of features extracted is M = 35, the interpretation heatmap (matrix) can be represented as

$${Var}=\left[\begin{array}{ccc}{{Var}}_{{{trav}}_{1},{{feat}}_{1}} & \cdots & {{Var}}_{{{trav}}_{1},{{feat}}_{35}}\\ \vdots & \ddots & \vdots \\ {{Var}}_{{{trav}}_{10},{{feat}}_{1}} & \cdots & {{Var}}_{{{trav}}_{10},{{feat}}_{35}}\end{array}\right]$$

(13)

Var is a K x M (i.e., 10 x 35 in this example) matrix that is subjected to hierarchical clustering. Each element in the matrix (${{Var}}_{{{trav}}_{k},{{feat}}_{m}}$) is the variance of the feature (${{feat}}_{m}$) extracted from all Q steps across the k^th dimension traversal, which is computed as:

$${{Var}}_{{{trav}}_{k},{{feat}}_{m}}={{Var}}_{{{trav}}_{k}}({{feat}}_{m1},{{feat}}_{m2}\ldots ..{{feat}}_{{mQ}})$$

(14)

${{feat}}_{{mi}}$, where i = {1:Q}, is the feature value of ${{feat}}_{m}$ extracted from the i^th traversal step. Based on these formulations, the interpretation heatmap provides valuable insights into the encoded features and their variations within the disentangled latent space, aiding our understanding of model predictions and generalization capabilities.

Summarized disentanglement score

Various methods of defining and assessing disentanglement have been proposed in the previous studies^{20,21,28,29,30}. Notably, β-VAE and FactorVAE metrics follow a supervised approach in which the annotations of the factors of variation in a dataset are predefined. However, in practical real-world datasets, whose annotations are not known, unsupervised disentanglement metrics are necessary. While there is no universal definition of disentanglement, we here investigate and interpret disentanglement of MorphoGenie’s latent representations broadly in the context of three hierarchical primitive categories (factors), i.e., bulk, global texture and local texture features.

$${{{\rm{Feat}}}}={ \{ {{feat}_{1}},\ldots .{{feat}_{M}}\}}=\{ {Bulk},{Global},{Local} \}$$

(15)

$${{Bulk}}=\{ {{featB}_{1}},{{featB}_{2}}..{{featB}_{{Nb}}} \}$$

(16)

$${{Global}}=\{ {{featG}_{1}},{{featG}_{2}}..{{featG}_{{Ng}}} \}$$

(17)

$${{Local}}=\{ {{featL}_{1}},{{featL}_{2}}..{{featL}_{{Nl}}} \}$$

(18)

N_b, N_g and N_l are the number of features in the hierarchical feature category of Bulk, Global and Local textures, respectively. Following Eq. (13), we can then define a matrix S that summarizes the significance of the hierarchical primitive factor/category in each latent dimension:

$${{{\rm{S}}}}=\left[\begin{array}{c}\begin{array}{ccc}\frac{1}{{N}_{b}}{\sum }_{n=1}^{{N}_{b}}{{Var}}_{{{trav}}_{1},{{featB}}_{n}} & \frac{1}{{N}_{g}}{\sum }_{n=1}^{{N}_{g}}{{Var}}_{{{trav}}_{1},{{featG}}_{n}} & \frac{1}{{N}_{l}}{\sum }_{n=1}^{{N}_{l}}{{Var}}_{{{trav}}_{1},{{featL}}_{n}}\\ \frac{1}{{N}_{b}}{\sum }_{n=1}^{{N}_{b}}{{Var}}_{{{trav}}_{2},{{featB}}_{n}} & \frac{1}{{N}_{g}}{\sum }_{n=1}^{{N}_{g}}{{Var}}_{{{trav}}_{2},{{featG}}_{n}} & \frac{1}{{N}_{l}}{\sum }_{n=1}^{{N}_{l}}{{Var}}_{{{trav}}_{2},{{featL}}_{n}}\end{array}\\ \vdots \\ \begin{array}{ccc}\frac{1}{{N}_{b}}{\sum }_{n=1}^{{N}_{b}}{{Var}}_{{{trav}}_{K},{{featB}}_{n}} & \frac{1}{{N}_{g}}{\sum }_{n=1}^{{N}_{g}}{{Var}}_{{{trav}}_{K},{{featG}}_{n}} & \frac{1}{{N}_{l}}{\sum }_{n=1}^{{N}_{l}}{{Var}}_{{{trav}}_{K},{{featL}}_{n}}\end{array}\end{array}\right]$$

(19)

where K = 10 is the latent dimension in this work. In fact, the matrix S can be represented as the bubble plots shown in Figs. 3 and 5. This matrix computes, in each latent dimension, the mean of the variances of all the features groups in the three hierarchical primitive categories. The features exhibiting higher variance values spotlight the factors of variation tied to the latent dimension. This approach helps us understand the specific attributes that contribute significantly to the variations within the latent space. Hence, matrix S essentially displays the importance of each category in each latent dimension.

Based on this matrix S, we can compute a disentanglement score which reflects how the three hierarchical primitive categories can be separated to different latent dimensions. Specifically, the maximum value in each column (i.e., each hierarchical primitive category) corresponding to either bulk, global and local texture attributes in matrix S, i.e., ${{MaxVar}}_{{Bulk}},$ ${{{{\rm{Max}}}}{Var}}_{{Global}},{Max}{{Var}}_{{Local}}$ is regarded as the key bulk, global texture and local texture attributes respectively and the mean of the three variances is computed as the disentanglement score.

$${Score}=\frac{1}{3} ({{MaxVar}}_{{Bulk}}+{{{{\rm{Max}}}}{Var}}_{{Global}}+{Max}{{Var}}_{{Local}})$$

(20)

The model is said to be more entangled if two categories having maximum mean values in the same latent dimension, resulting in a lower disentanglement score.

Other performance metrics

Mean square error (MSE)

MSE is a metric used to evaluate the accuracy of image reconstruction. It calculates the average of the squared differences between actual and predicted pixel values. In the context of MorphoGenie, $y$ and $\hat{y}$ is the pixel values of the real image and the generated image. With N as total number of pixels in the image, MSE is computed as:

$${MSE}=\frac{1}{N}\sum {(y-\hat{y})}^{2}$$

(21)

Fréchet inception distance (FID)

FID is a metric used to evaluate the quality of images generated by generative models, such as VAEs and GANs. It measures how similar the latent representations of generated images are to those of real images. Specifically, FID calculates the distance between these distributions, with lower values indicating closer resemblance and better performance of the model in generating realistic images.

Classification accuracy

F1 score is used to measure the classification accuracy of the model based on the true positive (TP), false positive (FP) and false negative (FN) values from the confusion matrix of a tree-based decision classifier:

$$F1=\frac{2*{precision}*{recall}}{{precision}+{recall}}$$

(22)

$${precision}=\frac{{TP}}{{TP}+{FP}}$$

(23)

$${recall}=\frac{{TP}}{{TP}+{FN}}$$

(24)

SSIM

SSIM is a metric used to evaluate the similarity between two images by analyzing their luminance, contrast, and structural characteristics. It ranges from 0 to 1, where 1 indicates perfect similarity. In this work, SSIM is applied to compare real and reconstructed images, averaging over 500 reconstructions, to assess the efficiency of the deep learning model in image reconstruction.

Feature ranking

Importance of disentangled latent representations is measured by decision tree-based classifier. This basically works by computing how much impurity is reduced by each feature and hence determining the importance of every feature in classifying the samples according to given labels. Impurity here refers to presence of samples of one category under the label of another category.

StaVia

StaVia is a computational framework for trajectory inference and visualization based on the diverse single-cell multi-omics as well as image data, including time-series data. StaVia uses higher-order random walks with teleportation and lazy-walk characteristics, which consider cells’ past states, to deduce cell fates, differentiation pathways, and gene (or morphological feature) trends, without imposing the assumptions about the underlying data structure. Built on the VIA framework³⁸, StaVia performs trajectory inference at both the single-cell and cluster-graph levels, handling complex non-tree topologies in large-scale datasets efficiently, even with millions of cells and modest computational resources. StaVia can also visualize inferred trajectories using an “Atlas View,” a cartographic approach that provides intuitive graph visualization at large scale. This view captures detailed cellular development at single-cell resolution while also illustrating broader cell lineage connectivity, such as cell cycle progression and epithelial-mesenchymal transition (EMT).

Computational resource for training MorphoGenie

To enhance the time efficiency and scalability of MorphoGenie, we parallelized the training pipeline across two separate computers equipped with GPUs for training FactorVAE: NVIDIA GeForce RTX 1080, 6 Cores, 64GB RAM and GAN: NVIDIA GeForce RTX 4090, 8 Cores, 64GB RAM. This optimization yielded computational efficiency, particularly during our grid-search for selecting the best disentangled models, where multiple models were trained concurrently. The computational time for training Factor-VAE and GAN models using two GPUs is documented in Supplementary Table S5 of the supplementary section. This highlights MorphoGenie’s ability to scale effectively to large datasets, facilitating the learning of universal single-cell morphological features and to achieve efficient generalizability.

Statistics and reproducibility

Lung cancer cell type and cell cycle tracking experiments shown in Fig. 2b (top left and bottom left) were performed in-house and independently repeated at least three times with consistent results. The EMT data in the bottom right were adapted from ref. ³⁷, where three independent repeats were reported. The top right cell-painting micrographs, as provided in the original dataset include imaging of multiple sites (nine per well) to enhance robustness and statistical power⁵³.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

Datasets used to reproduce the results in the main text and Supplementary Information have been fully deposited on Figshare https://doi.org/10.6084/m9.figshare.30040564. The Lung Cancer and CellCycle datasets, together with associated metadata, are available on the same Figshare DOI⁵⁶. The EMT dataset was accessed under restricted conditions with permission from the authors of the original publication. The Cell Painting image dataset used in this study is available through the Broad Bioimage Benchmark Collection (https://bbbc.broadinstitute.org/BBBC022)⁵⁷. The LIVECell dataset, used in the Supplementary Information, is available at https://sartorius-research.github.io/LIVECell/ and https://doi.org/10.6084/m9.figshare.14931555⁵⁸. Source data are provided with this paper, and all data generated in this study are available in the Source Data file. Source data are provided with this paper.

Code availability

The code used to develop the model, perform the analyses and generate results in this study is publicly available and has been deposited in MorphoGenie at https://github.com/rashmisrm/MorphoGenie, under GNU General Public License. The specific version of the code associated with this publication is archived in Zenodo and is accessible via https://zenodo.org/records/17009401⁵⁹.

References

Ljosa, V., Sokolnicki, K. L. & Carpenter, A. E. Annotated high-throughput microscopy image sets for validation. Nat. Methods 9, 637–637 (2012).
Article CAS PubMed PubMed Central Google Scholar
Williams, E. et al. Image data resource: a bioimage data integration and publication platform. Nat. methods 14, 775–781 (2017).
Article CAS PubMed PubMed Central Google Scholar
Thul, P. J. et al. A subcellular map of the human proteome. Science 356, 820–820 (2017).
Article CAS Google Scholar
Cho, N. H. et al. OpenCell: endogenous tagging for the cartography of human cellular organization. Science 375, eabi6983 (2022).
Article CAS PubMed PubMed Central Google Scholar
Viana, M. P. et al. Integrated intracellular organization and its variations in human iPS cells. Nature 613, 345–354 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Way, G. P. et al. Morphology and gene expression profiling provide complementary information for mapping cell state. Cell Syst. 13, 911–923.e9 (2022).
Gerbin, K. A. et al. Cell states beyond transcriptomics: integrating structural organization and gene expression in hiPSC-derived cardiomyocytes. Cell Syst. 12, 670–687 (2021).
Lazar, N. H. et al. High-resolution genome-wide mapping of chromosome-arm-scale truncations induced by CRISPR-Cas9 editing. Nat. Genet. 56, 1482–1493 (2024).
Article CAS PubMed PubMed Central Google Scholar
Carpenter, A. E. et al. CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 7, R100–R100 (2006).
Article PubMed PubMed Central Google Scholar
Lee, K. C. M., Guck, J., Goda, K. & Tsia, K. K. Toward deep biophysical cytometry: prospects and challenges. Trends Biotechnol. 39, 1249–1262 (2021).
Article CAS PubMed Google Scholar
Siu, D. M. D. et al. Deep-learning-assisted biophysical imaging cytometry at massive throughput delineates cell population heterogeneity. Lab Chip 2, 3696–378 (2020).
Article Google Scholar
Bray, M.-A. et al. Cell Painting, a high-content image-based assay for morphological profiling using multiplexed fluorescent dyes. Nat. Protoc. 11, 1757–1774 (2016).
Article CAS PubMed PubMed Central Google Scholar
Samek, W., Montavon, G. G., Vedaldi, A., Hansen, L. K. & Müller, K.-R. Explainable AI: interpreting, explaining and visualizing deep learning. Explainable Artificial Intelligence. https://doi.org/10.1007/978-3-030-28954-6 (2019).
Tjoa, E. & Guan, C. A Survey on Explainable Artificial Intelligence (XAI): Toward Medical XAI. IEEE transaction on neural networks and learning systems, vol. 32, pp. 4793–4813. https://doi.org/10.1109/TNNLS.2020.3027314 (2021).
Kingma, D. P. & Welling, M. Auto-Encoding Variational Bayes, CoRR, vol. abs/1312.6114 (2013).
Wu, Z. et al. DynaMorph: self-supervised learning of morphodynamic states of live cells. Mol. Biol. cell 33, ar59–ar59 (2022).
Article CAS PubMed PubMed Central Google Scholar
Zaritsky, A. et al. Interpretable Deep Learning of Label-free Live Cell Images Uncovers Functional Hallmarks of Highly-Metastatic Melanoma (ed Cold Spring Harbor) (Cold Spring Harbor Laboratory Press, 2021).
Kobayashi, H., Cheveralls, K. C., Leonetti, M. D. & Royer, L. A. Self-supervised deep learning encodes high-resolution features of protein subcellular localization. Nat. methods 19, 995–1003 (2022).
Article CAS PubMed PubMed Central Google Scholar
Vedaldi, A., Bischof, H., Brox, T. & Frahm, J.-M. High-Fidelity Synthesis with Disentangled Representation Vol. 12371, (Lecture Notes in Computer Science). 157–174 (Springer International Publishing AG, 2020).
Kim, H. & Mnih, A. Disentangling by Factorising. International Conference on Machine Learning (2018).
Burgess, C. P. et al. Understanding disentangling in $\beta$-VAE. https://doi.org/10.48550/arxiv.1804.03599 (2018).
Higgins, I. et al. SCAN: Learning Hierarchical Compositional Visual Concepts. https://doi.org/10.48550/arxiv.1707.03389 (2017).
Oord, A. v. d., Vinyals, O. & Kavukcuoglu K. Neural Discrete Representation Learning. In Neural Information Processing Systems (2017).
Xiang, W., Gong, B., Liu, Z., Lu, W. & Wang, L. Improving the improved training of Wasserstein GANs: a consistency term and its dual effect. arXiv.org, https://doi.org/10.48550/arxiv.1803.01541 (2018).
Vankov, I. I. & Bowers, J. S. Training neural networks to encode symbols enables combinatorial generalization. Philos. Trans. R. Soc. Lond. Ser. B. Biol. Sci. 375, 20190309–20190309 (2020).
Google Scholar
Montero, M. L., Bowers, J. S., Costa, R. P., Ludwig, C. J. H. & Malhotra, G. Lost in Latent space: disentangled models and the challenge of combinatorial generalisation. https://doi.org/10.48550/arxiv.2204.02283 (2022).
Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I. & Frey, B. Adversarial autoencoders. https://doi.org/10.48550/arxiv.1511.05644 (2015).
Kumar, A., Sattigeri, P. & Balakrishnan, A. Variational inference of disentangled latent concepts from unlabeled observations. https://doi.org/10.48550/arxiv.1711.00848 (2017).
Locatello, F. et al. Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations. In International Conference on Machine Learning (2018).
Chen, R. T. Q., Li, X., Grosse, R. & Duvenaud, D. Isolating sources of disentanglement in variational autoencoders. https://doi.org/10.48550/arxiv.1802.04942 (2018).
Chandrasekaran, S. N., Ceulemans, H., Boyd, J. D. & Carpenter, A. E. Image-based profiling for drug discovery: due for a machine-learning upgrade? Nat. Rev. Drug Discov. 20, 145–159 (2021).
Article CAS PubMed Google Scholar
Siu, D. M. D. et al. Optofluidic imaging meets deep learning: from merging to emerging. Lab Chip 23, 111–133 (2023).
Article Google Scholar
Ding, Z. et al. Guided Variational Autoencoder for Disentanglement Learning. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7917–7926 (2020).
Dupont, E. Learning disentangled joint continuous and discrete representations. Proceedings of the 32nd International Conference on Neural Information Processing Systems, (Montréal, Canada, 2018).
Yang, J. et al. Guidelines and definitions for research on epithelial–mesenchymal transition, Nat. Rev. Mol. Cell Biol. 21, 341–352 (2020).
Nieto, M. A., Huang, R. ubyY.-J., Jackson, R. ebeccaA. & Thiery, J. eanP. EMT: 2016. Cell 166, 21–45 (2016).
Article CAS PubMed Google Scholar
Wang, W. et al. Live-cell imaging and analysis reveal cell phenotypic transition dynamics inherently missing in snapshot data. Sci. Adv. 6, eaba9319 (2020).
Article ADS CAS PubMed PubMed Central Google Scholar
Stassen, S. V., Kobashi, M., Huang, Y., Ho, J. W. K. & Tsia, K. StaVia: Spatially and Temporally Aware Cartography with Higher Order Random Walks for Cell Atlases, Genome Biol. 25, 224 (2024).
Stassen, S. V. et al. PARC: ultrafast and accurate clustering of phenotypic data of millions of single cells. Bioinformatics 36, 2778–2786 (2020).
Article MathSciNet CAS PubMed PubMed Central Google Scholar
Stassen, S. V., Yip, G. G. K., Wong, K. K. Y., Ho, J. W. K. & Tsia, K. K. Generalized and scalable trajectory inference in single-cell omics data with VIA. Nat. Commun. 12, 5528–5528 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Yip, G. G. K. et al. Multimodal FACED imaging for large-scale single-cell morphological profiling. APL Photonics 6, 70801–070801-10 (2021).
Article Google Scholar
Lai, Q. T. K. et al. High-speed laser-scanning biological microscopy using FACED. Nat. Protoc. 16, 4227–4264 (2021).
Article ADS CAS PubMed Google Scholar
Kafri, R. et al. Dynamics extracted from fixed cells reveal feedback linking cell growth to cell cycle. Nature 494, 480–483 (2013).
Article ADS CAS PubMed PubMed Central Google Scholar
Lee, K. C. M. et al. Multi-ATOM: ultrahigh-throughput single-cell quantitative phase imaging with subcellular resolution. J. Biophotonics 12, e201800479 (2019).
Article PubMed PubMed Central Google Scholar
Stringer, C., Wang, T., Michaelos, M. & Pachitariu, M. Cellpose: a generalist algorithm for cellular segmentation. Nat. methods 18, 100–106 (2021).
Article CAS PubMed Google Scholar
Zhang, Z. et al. Morphological profiling by high-throughput single-cell biophysical fractometry. Commun. Biol. 6, 449–449 (2023).
Article CAS PubMed PubMed Central Google Scholar
Fregin, B. et al. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun. 10, 415–415 (2019).
Article ADS CAS PubMed PubMed Central Google Scholar
Duan, S. et al. Unsupervised model selection for variational disentangled representation learning. https://doi.org/10.48550/arxiv.1905.12614 (2019).
Carbonneau, M.-A., Zaidi, J., Boilard, J. & Gagnon, G. Measuring disentanglement: a review of metrics. IEEE Trans. Neural Netw. Learn. Syst. PP, 1–15 (2022).
Google Scholar
Zhu, X., Xu, C. & Tao, D. Where and What? Examining Interpretable Disentangled Representations. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5857–5866 (2021).
Rotem, O. et al. Visual interpretability of image-based classification models by generative latent space disentanglement applied to in vitro fertilization. Nat. Commun. 15, 7390–19 (2024).
Article ADS CAS PubMed PubMed Central Google Scholar
Lo, M. C. K. et al. Information-distilled generative label-free morphological profiling encodes cellular heterogeneity. Adv. Sci. 11, e2307591–n/a (2024).
Article Google Scholar
Gustafsdottir, S. M. et al. Multiplex Cytological profiling assay to measure diverse cellular states. PLoS ONE 8, e80999 (2013).
Article ADS PubMed PubMed Central Google Scholar
Wu, J.-L. et al. Ultrafast laser-scanning time-stretch imaging at visible wavelengths. Light, Sci. Appl. 6, e16196–e16196 (2017).
Article ADS CAS PubMed Google Scholar
Edlund, C. et al. LIVECell—a large-scale dataset for label-free live cell segmentation. Nat. methods 18, 1038–1045 (2021).
Article CAS PubMed PubMed Central Google Scholar
Murthy, R. S. et al. Generalizable Morphological Profiling of Cells by Interpretable Unsupervised Learning [Online] Available: https://doi.org/10.6084/m9.figshare.30040564 (in press)
Gustafsdottir, S. M. et al. BBBC022v1 Dataset, [Online] Available: https://bbbc.broadinstitute.org/BBBC022 (2013).
Edlund, C. et al. LiveCell, [Online] Available: https://figshare.com/articles/dataset/LIVECell_dataset/14931555 (2021).
Murthy, R. S. et al. Generalizable Morphological Profiling of Cells by Interpretable Unsupervised Learning, MorphoGenie [Online] Available: https://zenodo.org/records/17009401 (In press)

Download references

Acknowledgements

The work is supported by Advanced Biomedical Instrumentation Center, the Research Grants Council and the Innovation and Technology Commission of the Hong Kong Special Administrative Region of China (Grant nos. 17125121, 17208918, RFS2021-7S06, and ITS/318/22FP), Platform Technology Funding of the University of Hong Kong.

Author information

Authors and Affiliations

Department of Electrical and Electronic Engineering, The University of Hong Kong, Pokfulam, Hong Kong
Rashmi Sreeramachandra Murthy, Shobana V. Stassen, Dickson M. D. Siu, Michelle C. K. Lo, Gwinky G. K. Yip & Kevin K. Tsia
Advanced Biomedical Instrumentation Centre, Hong Kong Science Park, Shatin, New Territories, Hong Kong
Dickson M. D. Siu, Michelle C. K. Lo & Kevin K. Tsia
School of Biomedical Engineering, The University of Hong Kong, Pokfulam, Hong Kong
Kevin K. Tsia

Authors

Rashmi Sreeramachandra Murthy
View author publications
Search author on:PubMed Google Scholar
Shobana V. Stassen
View author publications
Search author on:PubMed Google Scholar
Dickson M. D. Siu
View author publications
Search author on:PubMed Google Scholar
Michelle C. K. Lo
View author publications
Search author on:PubMed Google Scholar
Gwinky G. K. Yip
View author publications
Search author on:PubMed Google Scholar
Kevin K. Tsia
View author publications
Search author on:PubMed Google Scholar

Contributions

K.K.T. and R.S.M. conceived the project. R.S.M. developed the algorithm and software to analyze the data. K.K.T. and R.S.M., S.V.S., and M.C.K.L. analyzed data. D.M.D.S. and G.G.K.Y. performed the imaging experiments and generated QPI datasets. R.S.M. and K.K.T. wrote the paper. All authors commented on and edited the text.

Corresponding author

Correspondence to Kevin K. Tsia.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Murthy, R.S., Stassen, S.V., Siu, D.M.D. et al. Generalizable morphological profiling of cells by interpretable unsupervised learning. Nat Commun 16, 11465 (2025). https://doi.org/10.1038/s41467-025-66267-w

Download citation

Received: 17 September 2024
Accepted: 29 October 2025
Published: 11 December 2025
Version of record: 29 December 2025
DOI: https://doi.org/10.1038/s41467-025-66267-w