Heterogeneous ensemble enables a universal uncertainty metric for atomistic foundation models

Abstract

Universal machine-learning interatomic potentials (uMLIPs) are emerging as foundation models for atomistic simulation, offering near-ab initio accuracy at far lower cost. Their safe, broad deployment is limited by the absence of reliable, general uncertainty estimates. We present a unified, scalable uncertainty metric, U, built from a heterogeneous ensemble that reuses existing pretrained MLIPs. Across diverse chemistries and structures, U strongly tracks true prediction errors and robustly ranks configuration-level risk. Using U, we perform uncertainty-aware distillation to train system-specific potentials with far fewer labels: for tungsten, we match full density-functional-theory (DFT) training using 4% of the DFT data; for MoNbTaW, a dataset distilled by U supports high-accuracy potential training. By filtering numerical label noise, the distilled models can in some cases exceed the accuracy of the MLIPs trained on DFT data. This framework provides a practical reliability monitor and guides data selection and fine-tuning, enabling cost-efficient, accurate, and safer deployment of foundation models.

Introduction

For decades, quantum-mechanical simulations, with density functional theory (DFT) at the forefront, have defined the benchmark for predicting materials’ properties. However, the emergence of data-driven strategies in the AI-for-Science paradigm has led to machine-learned interatomic potentials (MLIPs) that achieve near-DFT accuracy at a fraction of computational cost¹. Recent advances in high-performance computing and deep-learning architectures have enabled the development of universal MLIPs (uMLIPs), or atomistic foundation models, which are trained on hundreds of millions of configurations spanning metals, organic molecules, and inorganic solids^2,3. The field is advancing at an unprecedented pace: platforms such as Matbench Discovery now catalog more than twenty distinct uMLIP models⁴, including M3GNet⁵, CHGNet², MACE⁶, Orb⁷, SevenNet⁸, and EquiformerV2 (eqV2)⁹, which exhibit strong transferability across most of the periodic table and a wide range of chemical environments.

The primary application of uMLIPs lies in replacing DFT calculations for direct property prediction. However, their accuracy can degrade for specialized systems or defect-rich configurations. Systematic softening behaviors, for instance, have been reported in uMLIPs¹⁰, while predictions of surface energies, vacancy formation energies, and interface properties remain particularly challenging^11,12. These limitations are typically mitigated through fine-tuning on small, system-specific DFT datasets^13,14. A second challenge stems from computational efficiency: conventional uMLIPs are generally restricted to systems of thousands of atoms¹², limiting their applicability to large-scale simulations. Recent advances in model distillation have enabled the training of compact student potentials that replicate the performance of high-capacity teacher uMLIPs, preserving accuracy while accelerating inference by one to two orders of magnitude^15,16. Despite these promising developments, skepticism persists regarding the accuracy and reliability of uMLIPs in fully autonomous applications. This raises a critical question: how can the uncertainty of uMLIP predictions be rigorously quantified in the absence of reference DFT calculations?

Although a range of uncertainty quantification (UQ) methods exists for system-specific MLIPs (sMLIPs), which are faster than uMLIPs but typically applicable to only a small number of elements^{17,18,19,20,21,22,23}, robust and general strategies for uMLIPs remain scarce. This represents a critical gap, as uMLIPs require reliable extrapolation across diverse chemistries and structures due to their broader deployment scope. Current probabilistic approaches show limitations: The Orb model introduces a dedicated confidence head to estimate atomic force variances⁷, while Bilbrey et al.²⁴ apply quantile regression within MACE to generate confidence intervals, though both methods demonstrate limited effectiveness for out-of-distribution (OOD) detection. Feature-space distance metrics, particularly latent space distances in graph-based uMLIPs such as eqV2 and GemNet^21,25, show strong correlation with prediction errors. However, these methods face challenges in interpretability and scalability when applied to large, multi-element datasets. Ensemble methods have proven effective for sMLIPs²⁶, but their application to uMLIPs yields mixed results. Shallow MACE ensembles can identify some OOD configurations yet systematically underestimate errors²⁴. The Mattersim framework²⁷ employs five independently initialized models with identical architectures to estimate uncertainty through prediction variance, but still shows systematic underestimation. Recent work by Musielewicz et al.²⁵ suggests bootstrap ensembles offer a favorable cost-accuracy balance, whereas architectural ensembles provide greater diversity at increased computational cost.

Collectively, these observations reveal the absence of a universally accepted UQ framework for uMLIPs that correlates robustly with prediction errors. The development of an uncertainty metric on an absolute, transferable scale therefore remains a pressing challenge. Addressing this challenge bolsters the safety and reliability of uMLIP deployment in critical applications while providing essential guidance for fine-tuning, model distillation, and dataset extension.

This work introduces a heterogeneous ensemble approach for universal UQ in uMLIPs, as schematically illustrated in Fig. 1. By strategically combining architecturally diverse uMLIPs, our method generates reliable uncertainty estimates without requiring additional training or calibration. The resulting metric exhibits strong linear correlation with prediction errors across material classes, and consistent transferability between chemical spaces. Comprehensive validation employs the Open Materials 2024 (OMat24) inorganic materials dataset³, supplemented by systematic testing across diverse DFT-derived datasets to establish robust uncertainty thresholds. Practical applications demonstrate uncertainty-aware distillation of interatomic potentials for both elemental tungsten (W) and the MoNbTaW high-entropy alloy, achieving comparable accuracy to teacher models with significantly reduced computational cost. This framework provides a critical foundation for uncertainty-aware development throughout the MLIP ecosystem, enabling reliable model distillation, dataset expansion, and more trustworthy computational materials discovery.

Fig. 1: Universal uncertainty metric U for atomistic foundation models.

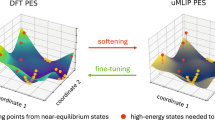
The proposed metric U is constructed from a heterogeneous ensemble of over ten uMLIPs with diverse architectures. In the schematic energy landscape, the color band illustrates the spread of model predictions around the mean, reflecting epistemic uncertainty. On the OMat24 test set, this deviation shows strong correlation with true DFT errors, enabling U to reliably separate low-uncertainty from high-uncertainty predictions. This universal metric facilitates four key applications: using uMLIPs as DFT surrogates, guiding fine-tuning, enabling uncertainty-aware model distillation, and identifying high-uncertainty configurations for targeted dataset extension.

Results

Universal uncertainty metric U via heterogeneous ensemble

Conventional ensemble methods face fundamental scalability challenges when applied to uMLIPs. Training even one single high-accuracy uMLIP, such as eqV2 with hundreds of millions of parameters on more than 100 million atomic configurations, requires prohibitive computational resources. The challenge escalates dramatically for state-of-the-art models like Universal Models for Atoms (UMA)²⁸ from Meta FAIRChem, a mixture-of-experts graph network with 1.4 billion parameters trained on billions of atoms. With future uMLIPs expected to grow larger in both model size and training data, the conventional approach of training multiple independent models for UQ becomes computationally intractable. Conversely, academia and industry have spent millions of GPU-hours training over twenty uMLIP architectures⁴. Given the immense computational investment behind each model and the ever-growing catalog on Matbench Discovery, developing an uncertainty metric that leverages model reuse is particularly desirable.

Here we introduce a heterogeneous ensemble framework for UQ in uMLIPs, leveraging the uMLIP models available in Matbench Discovery⁴. Owing to their broad architectural and parametric diversity, the predictive accuracies of the models vary markedly (Table S1), and lower-accuracy members may introduce larger random errors that can distort ensemble estimates. To mitigate this, we assign weights to each model proportional to its accuracy, thereby preserving ensemble diversity while limiting the influence of less reliable contributors.

This leads to a weighted formulation of uncertainty:

$${U}_{i}^{(1)}=\sqrt{\sum _{k}{w}_{k}{\left[{\max }_{j}\left\Vert {{\bf{F}}}_{i,j,k}-\langle {{\bf{F}}}_{i,j}\rangle \right\Vert \right]}^{2}},$$

(1)

where subscripts i, j, and k index the configurations, atoms within a configuration, and the individual uMLIP, respectively. 〈F_i,j〉 denotes the average force vector. The weight w_k assigned to each uMLIP model is given by

$${w}_{k}=\frac{{{\rm{RMSE}}}_{F,k}^{-1}}{\mathop{\sum }\nolimits_{k^{\prime} = 1}^{K}{{\rm{RMSE}}}_{F,k^{\prime} }^{-1}}\,.$$

(2)

where RMSE_F,k is the root-mean-square error (RMSE) in the force predictions produced by model k. If uniform weights w_k = 1/K are used instead, Eq. (1) degrades to the conventional equal-weight uncertainty metric (denoted as U⁽⁰⁾).

Additionally, we evaluate an alternative formulation that incorporates inverse-RMSE weighting during the force-averaging step:

$${U}_{i}^{(2)}=\sqrt{\sum _{k}{w}_{k}{\left[{\max }_{j}\left\Vert {{\bf{F}}}_{i,j,k}-\widetilde{\langle {{\bf{F}}}_{i,j}\rangle }\right\Vert \right]}^{2}},$$

(3)

where

$$\widetilde{\langle {{\bf{F}}}_{i,j}\rangle }=\sum _{k}{w}_{k}\,{{\bf{F}}}_{i,j,k}.$$

(4)

The force error between the uMLIP predictions and DFT for configuration i is defined as

$$\Delta {F}_{i}={\max }_{j}\left\Vert {{\bf{F}}}_{i,j}^{{\rm{DFT}}}-\langle {{\bf{F}}}_{i,j}^{{\rm{uMLIP}}}\rangle \right\Vert ,$$

(5)

where j indexes the atoms within the configuration, and $\langle {{\bf{F}}}_{i,j}^{{\rm{uMLIP}}}\rangle$ denotes the ensemble-averaged force predicted by all uMLIP members.

With these definitions, all uncertainties U⁽⁰⁾, U⁽¹⁾, and U⁽²⁾ carry units of eV/Å, consistent with those of force and force error. Having defined the uncertainty estimator, the next critical step is to select which uMLIP models to include in Eqs. (1) and (3). To ensure generality across chemistries and structures, we evaluate candidate ensembles on the public OMat24 test set, which contains more than one million configurations. Because the full OMat24 benchmark comprises over one hundred million DFT-labeled configurations and spans a wide range of elements, bonding types, phases, and thermodynamic conditions³, strong performance on its test split provides a stringent and broadly representative assessment of the generality of our uncertainty metric. We then construct the heterogeneous ensemble incrementally by ranking available models by force RMSE and adding them sequentially, beginning with the five most accurate ones (Fig. 2a). Performance is quantified using Spearman’s rank correlation coefficient ρ between predicted uncertainties and the force errors with respective to DFT.

Fig. 2: Uncertainty quantification methods and their performance on the OMat24 dataset.

a Shows names of the 18 uMLIP models used, sorted by force RMSE (low to high); more accurate models are prioritized in uncertainty estimation. b Shows performance of three uncertainty metrics evaluated by Spearman’s ρ as the number of uMLIPs varies; the selected model is marked with a red circle (as Eq. (1), referred as U), and corresponding uMLIPs are highlighted in a. c is parity plot of force error vs. U; color indicates point density, showing strong alignment along y = x. d Shows force error vs. Orb-confidence (see⁷). (e, f) show force (e) and energy (f) RMSE after removing high-uncertainty configurations, as identified by U or Orb-confidence. The x-axis shows the remaining data coverage. Results are shown for both the 〈uMLIP〉 average and the efficient eqV2-31M-omat model. U leads to faster error reduction and outperforms Orb-confidence.

Figure 2b shows Spearman’s ρ for U⁽⁰⁾, U⁽¹⁾ and U⁽²⁾ as a function of ensemble size. For U⁽⁰⁾, optimal performance is obtained with six uMLIP models (ρ = 0.82); adding further models reduces the correlation between estimated uncertainty and true error, indicating that equal weighting allows less accurate models to degrade performance. Both U⁽¹⁾ and U⁽²⁾ outperform U⁽⁰⁾, reaching local maxima of ρ = 0.87 and ρ = 0.86, respectively, at an ensemble size of eleven (the red dashed circle in Fig. 2b). This underscores the effectiveness of inverse-RMSE weighting in suppressing noise from lower-accuracy members. The eleven models included in the optimal ensemble are highlighted by the red dashed box in Fig. 2a. Notably, ρ for U⁽¹⁾ decreases slightly up to fourteen models and then increases as additional lower-accuracy models are added, demonstrating that the diversity contributed by less accurate members can also enhance performance. These findings underscore the value of harnessing the architectural diversity of existing uMLIP models to improve UQ. In comparison with U₂, U₁ consistently outperforms it. Therefore, we propose the U⁽¹⁾ metric, computed from an ensemble of eleven uMLIPs, as a universal uncertainty metric for general inorganic materials, hereafter denoted U. The weights for each model are shown in Table S1.

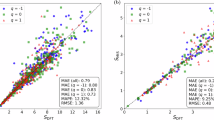
Figure 2c shows a hexbin parity plot of the predicted uncertainty U against the actual force error on the OMat24 test set. The density of points closely follows the ideal y = x (orange dashed line), with Spearman’s ρ = 0.87, indicating a strong monotonic relationship between uncertainty and error. Notably, the conditional spread around the diagonal remains within a single order of magnitude, even when spanning nearly five orders of magnitude in U (10⁻³–10² eV/Å). This indicates that low-uncertainty predictions almost never yield large errors, whereas high-uncertainty cases consistently signal catastrophic deviations. This tight, nearly unbiased clustering demonstrates that U directly corresponds to force error without the need for post hoc calibration.

Figure 2d shows a hexbin plot of the Orb-confidence against the true force error on the OMat24 test set⁷, directly comparable to the ensemble-based U in Fig. 2c. Here the force error is similar to Eq. (5) except that $\langle {{\bf{F}}}_{i,j}^{{\rm{uMLIP}}}\rangle$ is replaced by the force predicted by the single Orb-v3-c-inf-omat model. While both metrics achieve a Spearman’s ρ = 0.87, Orb-confidence exhibits a much narrower horizontal spread (only ~2–3 decades of confidence values) and a large vertical dispersion: at a single confidence level, the force error can vary by up to two orders of magnitude. In particular, some configurations labeled with moderate confidence (10–20) still show catastrophic errors (>10 eV/Å), indicating that Orb-confidence cannot reliably flag its worst failures. This improved calibration of U relative to Orb-confidence translates into tangible gains, as shown by the accuracy-coverage curves for total energies and atomic forces (Fig. 2e, f). For U, all RMSE values are computed using the ensemble mean of an eleven-member uMLIP, denoted 〈uMLIP〉. For Orb-confidence, RMSE values are calculated solely by Orb. In these plots, configurations are ranked by their predicted uncertainty, and those with the highest uncertainty are progressively excluded from the dataset. The remaining configurations are then used to calculate the RMSE. Accordingly, the horizontal axis (“coverage”) represents the fraction of data retained after excluding the most uncertain points, while the vertical axis denotes the corresponding prediction error. A well-performing uncertainty metric should produce a monotonic improvement in accuracy (i.e., decreasing RMSE) with increasing coverage, ideally showing a sharp initial drop that indicates configurations with higher predicted uncertainty indeed correspond to larger true errors. Up to approximately 80% coverage, U maintains the energy RMSE below 0.05 eV/atom and the force RMSE below 0.06 eV/Å. In sharp contrast, Orb-confidence can only achieve the same accuracy below roughly 25% coverage for energy and 40% for force. Beyond these thresholds, its error rises rapidly, particularly when the most challenging ~10% of configurations are included (around 90% coverage), highlighting the substantial advantage of U in identifying high-error cases.

Building on our analysis of uncertainty calibration, we next consider whether to use the ensemble mean or a single top-performing model to replace DFT. In principle, averaging a homogeneous ensemble can cancel random noise and improve accuracy, but our uMLIP ensemble is heterogeneous, so this effect may not hold. Accordingly, we compare accuracy-coverage curves computed with 〈uMLIP〉 against those obtained using the single most accurate model, eqV2-31M-omat. Figure 2e, f show that eqV2-31M-omat matches or outperforms the ensemble mean at nearly every coverage level, maintaining lower RMSE values. Accordingly, we adopt eqV2-31 M-omat as the surrogate for DFT reference to calculate forces and eqV2-31M-OAM to calculate energy in all subsequent sections.

Validation of U across diverse materials

To further establish the universality of our uncertainty metric U, we evaluate it across an extensive suite of PBE-level DFT datasets that have underpinned prior sMLIP development and span diverse materials classes (see Supplementary Note 1 and Table S2). The metals-and-alloys corpus includes pure elements (e.g., Fe, Mg), the complete transition-metal set (TM23; see Fig. S1), and medium- to high-entropy alloys—CrCoNi, VCoNi, MoNbTaVW, MoNbTaTi, WTaCrV—as well as the M16 binary alloys, totaling 264,383 configurations and 13,701,879 atoms (see Fig. S2). The inorganic-compounds collection comprises interstitial and stoichiometric systems that combine light elements (H, C, N, O) with metals, including FeH, LiH, FeC, MoNbTaWH, HfO₂, Ga₂O₃, and GaN (49,092 configurations; 4,412,916 atoms). The remaining datasets encompass carbon, metal–organic frameworks (MOFs), ionic covalent organic frameworks (ICOFs), surface-catalytic structures, perovskites, and battery-relevant chemistries such as LiPS, Li₄P₂O₇, and representative cathode compositions (64,464 configurations; 4,868,199 atoms).

Figure 3a shows the predicted uncertainty U against the true force error for each of the three dataset categories. Compared to the OMat24 test set (Fig. 2c), both U and the force error now span an even broader range (10⁻⁷–10⁶ eV/Å). Nevertheless, a strong monotonic relationship persists: Spearman’s ρ is 0.92 for metals and alloys, 0.88 for inorganic compounds, and 0.82 for the remaining materials, demonstrating that higher U values reliably correspond to larger errors across all categories. Notably, the metals and alloys attain a higher correlation than the OMat24 benchmark (ρ = 0.87; Fig. 2c), underscoring the robustness of U in comparatively uniform systems and contrasting with the greater heterogeneity of the other two categories. Figure 3b shows mirror-histograms of the predicted uncertainty U (top) and the actual force error (bottom) for each material category. The close symmetry of each color-coded distribution around the horizontal axis demonstrates that U faithfully captures the error spread across all systems. Moreover, the histograms reveal distinct accuracy regimes. Metals and alloys (red) concentrate almost entirely below 10⁰ eV/Å, indicating relatively high accuracy. Inorganic compounds (blue) span a wider range and dominate above 10⁰, reflecting a broader spread in both uncertainty and error. The “others” group (green) occupies an intermediate region around 10⁻²–10⁰. These differences underscore that, beyond uncertainty, the baseline uMLIP accuracy varies significantly by material class, with metals and alloys achieving the best performance, consistent with recent benchmarking studies²⁹.

Fig. 3: Performance of the uncertainty indicator U on additional datasets.

a Scatter plot of uncertainty U versus force error (Eq. (5)) across various datasets. The data are grouped into three categories based on their origin: metals and alloys, inorganic compounds, and others (including MOFs, perovskites, etc.). The distribution is centered along the diagonal y = x, indicating a strong correlation between uncertainty and error. b Histograms of U and force error, shown above and below the x-axis, respectively, for the three data categories. The distributions of uncertainty and error closely resemble each other within each group. Green shaded regions indicate force RMSE lower than 0.1 eV/Å. Vertical lines correspond to U_c = 1 eV/Å. c–h For each dataset, configurations with U higher than uncertainty criteria U_c are gradually removed, and the RMSE of the remaining “low-uncertainty” configurations is plotted as a function of dataset coverage (c, e, g) and U_c (d, f, h).

Figure 3c, e, g display coverage-accuracy curves in which we progressively discard the highest-uncertainty configurations and record the resulting force RMSE on the remaining data. The shaded green region denotes RMSE < 0.1 eV/Å, a common requirement for developing reliable sMLIPs. For every material class, removing even a small fraction of the most uncertain points produces a clear, monotonic drop in error. The most dramatic improvements occur in systems with large initial RMSE: in the W-Ta-Cr-V alloy (brown line in Fig. 3c), discarding under 5% of configurations brings the RMSE down from 10 eV/Å to below 0.1 eV/Å. Similarly, steep declines are seen for CrCoNi, Ga₂O₃, FeH and FeC, confirming that uMLIP yields high-accuracy predictions for the vast majority of structures, with only a handful of OOD points driving the worst errors. Datasets whose baseline RMSE already lies inside the green region show nearly flat curves, indicating uniformly reliable performance of the uMLIP. Dataset Carbon (C) is an exception, as its RMSE remains elevated until more than 70% of the data are retained, suggesting that uncertainty and error are less tightly coupled in this compositionally simple but structurally varied system.

Practical workflows often lack access to true DFT errors and instead must rely on an a priori uncertainty cutoff U_c to flag unreliable uMLIP predictions. Figure 3d, f, h show how the force RMSE of the retained subset varies as a function of U_c. The point where each curve intersects the horizontal target line at RMSE = 0.1 eV/Å defines the U_c threshold below which uMLIP predictions can be trusted and catastrophic errors on OOD configurations can be avoided. For both metals and alloys (Fig. 3d) and inorganic compounds (Fig. 3f), these intersection points fall at or above U_c = 1 eV/Å, with only a few outliers (e.g., TM23, FeC) requiring slightly lower U_c. In the “Others” category (Fig. 3h), which contains a larger fraction of OOD configurations, the required cutoff shifts marginally below U_c = 1 eV/Å, indicating that dataset-specific tuning may improve performance in these more challenging regimes. Given the broad compositional and structural diversity tested, the consistency of this threshold is striking. We therefore recommend U_c = 1 eV/Å as a general rule of thumb for selecting configurations that uMLIP can predict with RMSE ≤0.1 eV/Å. Users may adjust this cutoff to meet more stringent or relaxed accuracy requirements; for example, setting U_c = 0.3 eV/Å yields an RMSE of approximately 0.05 eV/Å.

Uncertainty-aware model distillation for W

Building on the demonstrated efficacy of U for quantifying uncertainty in uMLIP ensembles, we now turn to its most direct application: guiding the distillation of predictive accuracy into streamlined sMLIP models. In this section, we introduce an uncertainty-aware model distillation (UAMD) framework that leverages U to adaptively construct the training dataset by retaining low-U configurations using the most accurate predictions in place of expensive DFT references, and by flagging high-U configurations for targeted DFT calculations. As discussed below, UAMD drastically reduces and in some cases entirely eliminates the need for expensive DFT calculations compared to conventional sMLIP development workflows. Furthermore, unlike standard model distillation techniques, UAMD uses uncertainty estimates to explicitly control and constrain error propagation from the uMLIP ensemble, ensuring that the resulting sMLIP meets its target accuracy with a minimal amount of reference data.

To demonstrate the UAMD framework, we first consider the tungsten (W) system as a case study. The primary configuration set comprises 1026 structures from ref. ³⁰, covering a broad spectrum of defects. To extend this set into the extreme deformation regime relevant to radiation damage, we augment it with 13 dimer and 100 short-range configurations from Byggmästar et al.³¹. These highly distorted structures with huge forces lie outside the standard uMLIP training domain and thus serve as challenging OOD test cases for UAMD.

Figure 4a shows the predicted uncertainty U against the true force error for the W configurations. The dimer and short-range points lie predominantly in the high-U, high-error quadrant, confirming that these OOD geometries are correctly identified as challenging. In contrast, the bulk of the general dataset clusters at low U and low error, with many samples below 10⁻² eV/Å. Despite spanning over seven orders of magnitude in U (10⁻⁴–10³ eV/Å), the points follow the y = x diagonal closely, with only a few outliers dropping below the y = 0.1x reference lines. This tight, nearly linear trend demonstrates that U provides a robust, physically meaningful measure of prediction error even for extreme deformations.

Fig. 4: Validation of uncertainty-aware model distillation for W.

a The uncertainty U shows a strong correlation with force errors (Eq. (5)) across 1139 configurations of W. Dimer and short-range configurations (in red and green, respectively) exhibit both high uncertainty and high errors. b Mixed datasets are constructed using different uncertainty thresholds U_c: configurations with U < U_c use uMLIP predictions, while those with U≥U_c are labeled using DFT. The x-axis indicates the fraction of DFT data. Blue solid and green dashed lines represent the RMSE of the dataset and ACE training error, respectively. Red dash-dot and purple dotted lines denote ACE performance on training and test sets, respectively. c Force and energy RMSE of ACE potentials trained by mixed datasets on the test set reported in³⁰ (Fig. S5). For each dataset, 20 independent models are trained, and the standard deviations of energy and force RMSEs are shown as error bars. d Relative errors (%) for basic physical properties predicted by the ACE model trained on hybrid datasets (ACE_UAMD), compared with the ACE model trained on full DFT data (ACE_DFT). Error bars indicate the standard deviation across five independently trained models. e Comparison of phonon dispersion curves predicted by ACE_UAMD, ACE_DFT, and DFT. f Stress-strain curves from uniaxial tension simulations of Σ3 tilt (above) and twist (below) grain boundaries. ACE_DFT and ACE_UAMD model with U_c = 1.0 eV/Å produce nearly identical results.

We then apply a series of uncertainty thresholds U_c to partition all configurations into high- and low-U subsets. Configurations with U > U_c are assigned true DFT labels, while those with U ≤ U_c use uMLIP predictions. For consistency with prior benchmarks²⁹, we employ eqV2-31M-OAM for energies and eqV2-31M-omat for forces. We evaluate six thresholds: U_c = ∞ (i.e., trust uMLIP for all points), 10, 1, 0.5, 0.1, and 0 (i.e., full DFT). Higher U_c values correspond to more permissive use of uMLIP labels, whereas lower values increasingly rely on the DFT reference. For each mixed dataset, we train an ACE potential (see Methods) and report the resulting errors in Fig. 4b. The fraction of DFT-labeled configurations (measured by atomic environments) is indicated along the bottom of the x-axis, while the corresponding U_c values are shown on the top x-axis. The blue solid line shows the error of the constructed mixed dataset relative to DFT values. Incorporating only about 4% of the configurations as DFT references reduces the energy RMSE from over 1 eV to below 0.01 eV and the force RMSE from more than 10 eV/Å to approximately 0.1 eV/Å. These remaining errors reflect the propagation of data error from the uMLIP predictions into the distilled sMLIP. The green dashed line shows the ACE training error, defined as the RMSE between ACE predictions and the mixed dataset. Introducing approximately 4% of DFT references leads a sharp drop in training error, and by 4% the training error stabilizes.

The relatively high training error for the full uMLIP dataset arises from the energy–force inconsistency of the eqV2 models, in which the predicted forces are not exact derivatives of the corresponding energy. Using the small-perturbation method, the degree of energy–force inconsistency is found to correlate positively with the model uncertainty, as shown in Fig. S3 and discussed in Supplementary Note 2. For the W dataset, dimer and short-range configurations exhibit particularly strong energy–force inconsistency. Comparing the cases with U_c = ∞ and U_c = 1, labeling the dimer and short-range configurations with eqV2 significantly increases the overall training error. Another indication of the impact of energy–force inconsistency is that, for the fully uMLIP-labeled dataset, the ACE training process often terminates prematurely due to instability in loss convergence. The plateau in training error beyond 4% reflects the irreducible errors inherent to the ACE training process. Furthermore, we evaluate each ACE potential on both the full DFT dataset and an independent test set that includes complex plasticity and crack propagation scenarios, as shown in Fig. S5 and sourced from ref. ³⁰, to assess their generalization performance. Figure 4b shows that when U_c < 1 (i.e., more than 4% of the configurations are labeled with DFT), the errors on the full DFT set (red dash-dotted line) and the test set (purple dotted line) converge to nearly the same value. This pattern demonstrates that the final accuracy of the ACE model is determined by two primary contributions: the intrinsic data error of the training labels (blue solid line) and the training error during fitting (green dashed line). Importantly, the observed test error on the independent DFT dataset is not simply the sum of the training-data error and the fitting error; rather, it is governed by whichever contribution is dominant, and the two can partially offset each other. In energy predictions, the test error primarily reflects the training-data error, whereas in force predictions, where the fitting error is larger, the test error closely follows the training-loss curve.

To investigate the impact of the uncertainty threshold U_c, and thus the fraction of DFT-labeled data, on model performance, we plot energy and force RMSEs for ACE_UAMD trained with different U_c values in Fig. 4c. Figure 4a shows that raising U_c (i.e., trusting more uMLIP-generated labels) admits additional high-error configurations, which might naively be expected to worsen accuracy. Instead, Fig. 4c reveals that the lowest RMSEs occur at intermediate DFT fractions (~4% to 39%), not with either full DFT or full uMLIP labels. This behavior reflects a trade-off between label bias and label noise. DFT labels provide low-bias physical information yet carry stochastic numerical noise, arising from finite plane-wave cutoffs, k-point sampling, and incomplete convergence^32,33. In contrast, uMLIP predictions are smooth and effectively free of the non-physical numerical fluctuations, but they exhibit systematic bias in regions of large model error. An optimal mixture corrects the uMLIP bias while limiting exposure to DFT-induced noise: below ≈ 4% DFT coverage residual uMLIP bias dominates, whereas above ≈39% the increasing DFT noise and overfitting begin to degrade performance. Selecting U_c = 1 eV/Å (yielding about 4% DFT labels) achieves this balance, reducing the number of expensive DFT calculations while improving fidelity beyond conventional fully DFT-labeled training.

To substantiate the critical observation in Fig. 4c, we first establish the presence and scale of DFT label noise and its interaction with model variance. Recomputing a subset with a tighter k-mesh (see Fig. S4 and Supplementary Note 3) shows energy noise concentrated around ~2 meV/atom with a non-negligible tail > 10 meV/atom, i.e., up to ~2× the ACE training energy error in Fig. 4c. The force noise is near zero for elastic deformation of a 2-atom unit cell but can reach ~60 meV/Å for larger or more complex configurations, about one third of the ACE training force error. Under pure-DFT supervision, ACE is prone to overfitting training-specific DFT fluctuations (high variance, as indicated by the error bars in Fig. 4c), which lowers training error but degrades generalization. Introducing a moderate amount of uMLIP energy supervision acts as a shrinkage prior, reducing variance and improving test accuracy. The stronger improvement in energy relative to force follows from both the noise magnitudes and the training objective. Energies are global quantities whose label noise is comparable to, or larger than, the training energy error, whereas forces are local gradients with smaller label noise relative to the training force error. Moreover, the loss is energy-dominated, L = (1 − κ)L_E + κL_F with κ = 0.01, directing optimization to preferentially reduce energy discrepancies. Consequently, denoising and variance reduction yield a conspicuous gain in the global energy metric, while the local force RMSE remains nearly unchanged until excessive substitution reduces DFT fidelity.

While Fig. 4b, c presents RMSE comparisons between ACE and DFT, it is essential to validate the accuracy of ACE_UAMD across several static and dynamic physical properties. These results are compared against the ACE_DFT model, which is trained on fully DFT-labeled data. Figure 4d shows the relative errors on several basic properties of W with various U_c. For each U_c, we independently trained five ACE models. The markers denote the mean predictions over these models. The lattice constant a remains exceptionally stable across all U_c, with relative deviations below 0.1%. Surface energies γ₁₀₀ and vacancy formation energy E_vac also show minor sensitivity, with relative errors around 3% and other surface energies below 1%. In contrast, elastic properties such as C₁₁, C₁₂, C₄₄, bulk modulus B, and Poisson’s ratio ν display greater dependence on U_c, with relative errors approaching 10% at U_c = 1. This increased sensitivity likely arises because elastic constants are second derivatives of the potential energy, making them more sensitive to numerical fluctuation during calculation.

Figure 4e compares the phonon spectra predicted by ACE_UAMD and ACE_DFT against reference DFT data^34,35. Both ACE variants produce nearly identical curves that track the DFT results closely, with a slight systematic underestimation of vibrational frequencies. The close agreement between ACE_UAMD and ACE_DFT indicates that adding more high-accuracy DFT data beyond the UAMD threshold does not yield significant gains for these properties, suggesting diminishing returns for further improvement in data accuracy. Figure 4f shows stress-strain curves of bicrystal tensile molecular dynamics (MD) simulation using the ACE_UAMD potential (with U_c = 1.0 eV/Å) and the ACE_DFT reference. Two Σ3 grain boundary (GB) geometries are studied: a symmetric tilt boundary and a twist boundary, see Methods. Each loading simulation is repeated three times with different random velocity seeds to confirm reproducibility. The details of deformation mechanisms are shown in Fig. S6. The ACE_UAMD model reliably captures the contrasting deformation modes seen with the ACE_DFT potential, namely localized plastic slip at the tilt boundary and brittle cleavage along the twist boundary. Both the yield stresses and the strains at which plastic flow or fracture start agree closely between the two potentials, demonstrating that UAMD-trained potentials can reliably reproduce complex mechanical responses.

Taken together, the W case study demonstrates that an ACE potential trained with only 4% of configurations labeled by DFT (U_c = 1.0 eV/Å) matches the accuracy of fully DFT-trained models across energetic, structural, and mechanical benchmarks.

Uncertainty-aware model distillation for MoNbTaW alloys

We next apply UAMD to develop sMLIPs for the prototypical refractory high-entropy alloy (HEA) MoNbTaW. Conventional sMLIPs for HEAs are typically trained on narrow composition ranges and include only limited defect types in pure metals, leaving them unable to capture the full chemical and structural complexity of real microstructures³⁶. In principle, a truly general-purpose HEA potential would require an exhaustive DFT dataset that samples every composition, chemical interaction, and defect configuration, a requirement that becomes infeasible as each additional element exponentially expands the combinatorial space and the associated DFT workload. UAMD promises to overcome this bottleneck by drastically reducing the number of required DFT calculations.

We benchmark UAMD on a curated dataset of 17,654 MoNbTaW configurations, which includes ground-state structures, finite elastic strains, ab initio molecular dynamics (AIMD) snapshots, and a wide variety of point and extended defects across the full compositional space³⁷. Similar to the workflow applied to OMat24 and W, we first examine the relationship between U and the force prediction error. As shown in Fig. 5a, a strong monotonic correlation is observed, with Spearman’s ρ = 0.91. High values of U reliably identify configurations with large force errors, while the majority of points occupy the low-U, low-error region (<10⁻¹ eV/Å). Importantly, no configuration exceeds the critical threshold U_c = 1 eV/Å, and both the force errors and uncertainties remain small for the overwhelming amount of data. This robust performance allows us to replace DFT labels with uMLIP predictions for all configurations (eqV2-31M-OAM model for energy and eqV2-31M-omat for force), without any DFT calculation. These surrogate labels form the training data for ACE_UAMD. For comparison, we also train ACE_DFT on the full DFT dataset. To ensure statistical robustness, each ACE model variant is trained five times with different random initializations.

Fig. 5: Validation of uncertainty-aware model distillation in MoNbTaW HEA systems.

a Correlation between force error (Eq. (5)) and predicted uncertainty; each point represents a configuration. The color shows the density of points. b Energy (top) and force (bottom) RMSEs across various scenarios. The dashed lines indicate the RMSEs of ACE models trained solely on DFT data. c Correlation of per-atom errors between ACE models trained on DFT data and those trained via UAMD, both evaluated against raw DFT references. Each point represents an atom. d Relative errors (%) of mechanical properties predicted by ACE_DFT and ACE_UAMD. Error bars denote the standard deviation across five independently trained ACE_UAMD models. e Validation of monovacancy diffusion barriers (E_b) in Mo₂₅Nb₂₅Ta₂₅W₂₅, based on 500 independent NEB calculations with randomly shuffled atomic positions. Error bars reflect the spread from five independently trained ACE models. f Validation in bicrystal tensile simulations. For both DFT- and UAMD-derived ACE models, five different potentials are tested. Cross markers indicate simulation failure due to atom loss.

The performance of the resulting models is quantified by energy and force RMSEs, as shown in Fig. 5b. We compare four scenarios: (i) ACE_DFT predictions against DFT references; (ii) uMLIP predictions against DFT references; (iii) ACE_UAMD predictions against uMLIP outputs; and (iv) ACE_UAMD predictions against DFT references. We observe three key findings. First, the uMLIP used for data distillation outperforms ACE_DFT in both energy and force prediction, which is consistent with our recent study²⁹. Second, ACE_UAMD aligns more closely with the uMLIP predictions than ACE_DFT does with DFT, suggesting that uMLIP outputs provide a smoother target that reduces numerical noise and simplifies ACE training. Third, when evaluated against true DFT data, ACE_UAMD exhibits only slightly higher energy RMSE (7.25 vs. 5.69 meV/atom) and maintains a force RMSE comparable to that of ACE_DFT (118.82 meV/Å vs. 119.83 meV/Å). These results confirm that error propagation from the uMLIP teacher to the ACE student remains well controlled even in the absence of DFT labels. Figure 5c shows the density of per-atom force errors for ACE_DFT versus ACE_UAMD on a logarithmic scale, with both models evaluated against the same DFT reference. The pronounced symmetry about the y = x diagonal indicates that neither potential holds a systematic advantage: configurations where ACE_UAMD has larger error than ACE_DFT are balanced by the opposite case. Similar trends are observed in Fig. S7b, c when comparing the absolute errors ∣ACE_DFT − DFT∣ vs. ∣uMLIP − DFT∣ and ∣ACE_UAMD − uMLIP∣ vs. ∣uMLIP − DFT∣, indicating that the random-error distributions are similar across these sources. Formally, the error of ACE_UAMD decomposes into its residual fitting error to the uMLIP teacher (training error) plus the teacher’s zero-mean numerical noise from DFT (data error, as shown in Fig. S7a). In contrast, ACE_DFT fits the raw DFT labels directly under identical model capacity and regularization, making it susceptible to numerical errors. By training on the inherently smoother uMLIP ensemble predictions, ACE_UAMD effectively filters out these DFT fluctuations, much like deliberate noise injection, which is known to suppress overfitting and improve generalization³⁸. In regions where the opposite interplay occurs, the two methods counterbalance one another, yielding statistically indistinguishable fidelity to forces prediction, as illustrated in Fig. 5b. These results are consistent with the case for W in Fig. 4.

To further validate the efficacy of the distilled model, we use ACE_UAMD to predict key properties of Mo₂₅Nb₂₅Ta₂₅W₂₅, including the lattice constant a, lattice distortion (LD), independent elastic constants C₁₁, C₁₂, C₄₄, and the statistics of unstable stacking fault energies (γ_USF,ave, γ_USF,std) and maximum restoring forces (τ_USF,ave, τ_USF,std), which are critical to determine the solid solution strengthening of HEAs³⁹. As shown in Fig. 5d, all of these quantities agree closely with the corresponding ACE_DFT predictions, exhibiting only minor deviations. We then benchmark monovacancy migration barriers (Fig. 5e), where ACE_UAMD and ACE_DFT produce virtually identical energy profiles. Bicrystal tensile simulations (Fig. 5f) using ACE_UAMD and ACE_DFT reveal highly consistent stress-strain behavior, showing close agreement from the elastic regime through yield and into plastic flow.

It should be noted that early termination due to atom loss occurred in 3/5 ACE_UAMD runs and 1/5 ACE_DFT runs in Fig. 5f. Although this suggests a higher failure frequency for ACE_UAMD, we do not regard it as evidence of an intrinsic stability deficit. Both families were trained on the same data and thus have a similar domain of validity; under the extreme-loading conditions considered here, failures consistently arise at very large strains in low-coordination, surface- and crack-tip-like environments that are underrepresented in the training set. Consistent with this view, the stress-strain responses up to failure are comparable across the two families, and we do not observe a reproducible shift in onset strain or failure mode indicative of method-specific instability. Augmenting the training data to better cover such configurations substantially mitigates catastrophic failures for both families (Fig. 6).

Fig. 6: Application of UAMD-derived general-purpose potential in modeling high-entropy MoNbTaW alloys.

a Uncertainty quantification distribution using conventional ensemble learning based on ACE_UAMD models for 7000 newly generated configurations. b Distribution of the new uncertainty metric U for the same dataset. c Performance comparison between ACE_UAMD and ACE_UAMD,g on independent test datasets. d Stress-strain curves of bicrystal fracture for random solid solution (RSS) and chemically short-range ordered (SRO) systems. The inset shows the bicrystal model with a center crack, highlighting Nb segregation at both the crack surface and grain boundary (GB). e, f Per-atom atomic shear strain in final snapshots for RSS and SRO cases, highlighting critical deformation mechanisms including deformation twinning, cleavage, GB migration, and dislocation emission.

General-purpose potential for MoNbTaW alloys

Although the 17,654-configuration MoNbTaW dataset provides a rigorous benchmark, it does not span the full spectrum of microstructural motifs required for general-purpose modelling, including arbitrary GBs, dislocation-GB interactions, and fracture. As illustrated in Fig. 5f, MD simulations of bicrystal tension can terminate prematurely with the LAMMPS “Atom lost” error. The strength of the UAMD framework is its capacity to explore vast configurational spaces without incurring the cost of additional DFT calculations. To demonstrate this capability, we begin with the recently published defect genome for W³⁰, which systematically samples general plasticity, surfaces, and crack tips. We then apply the maximum-volume algorithm in the MLIP-2 package⁴⁰ to introduce increasing chemical complexity into each topological motif across the full MoNbTaW compositional space (see Supplementary Note 4). In total, we generate 7000 defect configurations, providing broad coverage for general-purpose modelling of MoNbTaW alloys.

We first use the original ACE_UAMD ensemble, trained on 17,654 configurations, to evaluate the 7000 newly generated structures. Figure 6a shows that all of these configurations lie outside the distribution spanned by the original dataset. We then compute the uncertainty U for each new configuration and find that every value falls below the threshold U_c = 1 eV/Å (Fig. 6b), confirming that the uMLIP predictions remain reliable. We merge these configurations with the original dataset, and assign uMLIP labels to all 24,654 configurations. From this augmented set, we train a general-purpose ACE potential, denoted ACE_UAMD,g. We then benchmark both ACE_UAMD,g and the original ACE_UAMD on two independent DFT test sets: GB-deform, which probes severe GB deformations, and Crack, which examines crack propagation, across varying compositions. Remarkably, ACE_UAMD,g achieves substantially lower errors on both test sets compared to ACE_UAMD as shown in Fig. 6c, despite relying solely on uMLIP-generated labels. The improvement in the prediction accuracy of ACE_UAMD,g is comparable to that reported for the W system with fully DFT-labeled defect genomes³⁰, demonstrating that UAMD can efficiently extend sMLIPs to new regions of configuration space without incurring costly DFT calculations.

Finally, we apply the ACE_UAMD,g potential to large-scale MD simulations of bicrystal fracture in MoNbTaW alloys, capturing coupled chemical and mechanical effects on crack propagation. We first use hybrid Monte Carlo/molecular dynamics (MC/MD) to probe chemical short-range order (SRO) in a bicrystal model containing a central crack. After equilibration, the inset of Fig. 6d shows pronounced segregation of Nb atoms to the GB and crack surfaces. The details of SRO formation are presented in Fig. S8a–d. The stress-strain curves in Fig. 6d compare the mechanical response of bicrystals with a random solid solution (RSS) and with SRO. We find that SRO has little influence on the elastic regime, slightly reduces the yield stress, and substantially diminishes ductility, with loss of load-bearing capacity occurring at only 8% tensile strain. Figure 6e, f show the per-atom strain fields at the end of tensile loading for the two cases. In the RSS case, deformation twinning initiates at the right crack tip, whereas brittle cleavage nucleates at the left tip. The twin boundary then interacts with the non-crack grain boundary, triggering a new crack. The twin band thickens, and the GB migrates substantially to accommodate plastic deformation. These mechanisms are consistent with the sustained stress beyond 8% strain in Fig. 6d. In contrast, SRO markedly alters the deformation pathway: twinning is suppressed, only two dislocations are emitted from the crack in the presence of Nb segregation at the crack tip and the GB, and complete cleavage fracture is observed, as shown in Fig. 6f.

To validate the reliability of these simulations, we monitor the per-atom extrapolation grade throughout the tensile deformation. As shown in Fig. S8f, g, most of atomic environments remain within the interpolation domain of the training data, indicating that no significant extrapolation occurs. This confirms that ACE_UAMD,g reliably describes complex deformation involving GBs, dislocations, deformation twinning, and cracks.

Discussion

The rapid advancement of uMLIPs has transformed computational materials science, enabling high-throughput simulations across diverse applications. Although many studies have demonstrated uMLIP accuracy in specific systems, validation remains challenging and circular: one needs DFT calculations to assess uMLIP predictions, yet the availability of reliable DFT data would obviate the need for uMLIPs. This dilemma highlights the urgent requirement for DFT-free UQ methods at every stage, from initial development through fine-tuning and model distillation. To address this, we propose an ensemble learning strategy that combines architecturally diverse uMLIP models with varying performance levels. By assigning weights to each ensemble member based on its test-error statistics on the comprehensive OMat24 dataset, we construct a universal and sustainable uncertainty metric that can be applied to general material systems.

Critically, the proposed metric U not only provides a universal and reliable indicator of uMLIP prediction error but also enables a demonstrably sustainable approach to atomistic modelling. First, our workflow avoids the need to train or calibrate new uMLIP models, thereby eliminating the GPU-years of computation and kilolitres of cooling water that modern AI training typically requires. Second, by reusing more than twenty uMLIPs already available in the MatBench Discovery repository, we leverage their existing carbon footprint instead of creating redundant emissions. Third, the weighting scheme in Eq. (1) allows any future, higher-accuracy uMLIP to be incorporated simply by evaluating its test errors on the OMat24 dataset, improving the uncertainty metric without additional training cycles. Finally, when combined with the UAMD protocol, U eliminates the vast majority of new DFT calculations: we demonstrate a 96% reduction in DFT use for W potential development and complete avoidance of DFT in the expanded MoNbTaW dataset. Because the computational cost of running the eleven-member uMLIP ensemble (Fig. 2a) is negligible compared to DFT²⁹, our method significantly reduces both the GPU/CPU compute time for training and the electricity consumption of energy-intensive DFT calculations, offering a truly low-carbon pathway for generating accurate interatomic potentials at scale.

Beyond its accessibility, the strong performance of the proposed heterogeneous ensemble has both theoretical and empirical support. In the field of UQ for neural networks employing ensemble learning, a key principle for improving UQ performance is to maximize the diversity among individual models⁴¹. This principle has been confirmed in recent systematic studies of uMLIPs²⁵, where architecture ensembles (e.g., GemNet-OC, eSCN, and EquiformerV2) were found to yield the best correlation between predicted uncertainty and true error compared with ensembles trained on varying datasets or with different parameter sizes. Our results are consistent with these findings: increasing the architectural diversity of ensemble members improves the correlation between uncertainty and error (Spearman’s ρ), while even models of moderate accuracy contribute valuable variance that enhances the identification of high-error configurations. Similar conclusions have been drawn for system-specific MLIPs, where heterogeneous ensembles outperform homogeneous ones⁴².

The proposed U is highly transferable and readily accommodates newly developed uMLIPs. For new models that already include OMat24 in training (e.g., Nequip-OAM-L and Allegro-OAM-L⁴³), their test-set errors on OMat24 can be used directly in the U formulation without any additional adjustments. The computational burden of obtaining these metrics is negligible compared with DFT: uMLIP inference is typically 10³–10⁵ times faster than DFT evaluation²⁹ and scales more favorably with system size, and, in many cases, standardized OMat24 RMSEs are reported by the model developers, requiring no new calculations. Moreover, if more comprehensive benchmark suites become available, the same weighting strategy extends seamlessly by substituting the corresponding test-set errors of uMLIPs on those benchmarks, again with negligible extra cost.

Our UAMD framework unlocks the full potential of sMLIPs for atomistic modelling by addressing key limitations of existing model distillation approaches. Existing model distillation from uMLIPs offers no mechanism to filter or correct errors inherited from the teacher⁴⁴. Fine-tuning can mitigate this issue by retraining on new data^15,16, but it still demands substantial additional DFT calculations and GPU-intensive training, and it carries the risk of catastrophic forgetting, which can degrade the original capability of uMLIPs¹⁴. In contrast, UAMD uses uncertainty estimates to selectively supplement the teacher’s labels with targeted DFT references, minimizing both numerical error and computational cost while preserving the extrapolation ability of uMLIPs.

Our case studies on W and MoNbTaW alloys reveal several critical insights on model distillation. First, the accuracy of the student model (sMLIP) hinges on the fidelity of the uMLIP-generated labels, while stochastic fitting errors during sMLIP training tend to cancel out against random data noise. Therefore, it is essential to choose the most accurate uMLIP as the surrogate for DFT and to replace any configurations with high uncertainty with true DFT calculations. Although uMLIPs are inherently slower than sMLIPs²⁹, their computational cost can be mitigated by subsequent distillation into lightweight sMLIPs. Consequently, prioritizing uMLIP accuracy outweighs further improvements in computational efficiency. Second, UAMD can outperform direct training on raw DFT data (as illustrated in Fig. 4c) because uMLIP predictions are inherently smoother owing to their advanced network architectures. Raw DFT labels contain non-physical numerical noise^32,33. The expressive power and regularization built into uMLIPs effectively filter out these fluctuations, yielding higher-quality surrogate labels for sMLIP training. This denoising effect is particularly valuable for challenging configurations⁴⁵, such as large-scale or highly distorted structures, where uMLIP predictions can even surpass the fidelity of DFT calculations.

Additionally, our uncertainty metric U enables three complementary capabilities beyond model distillation, addressing both immediate practical needs and long-term development of uMLIPs. First, by embedding uncertainty estimation into each prediction, outputs are accompanied by a uncertainty measure and configurations with U above a user-defined threshold can be flagged for targeted DFT recalculation, ensuring reliability in critical simulations such as defect energetics or phase transformations. Second, U facilitates efficient fine-tuning by identifying only the highest-U configurations for additional DFT labels. Third, systematic UQ-driven dataset expansion leverages U to discover novel structures beyond existing dataset (for example, OMat24), guiding the gradual construction of ever more comprehensive training sets. Over successive cycles, this approach promises to converge on a truly universal potential that delivers near-DFT fidelity across a broad spectrum of materials challenges.

In summary, this study develops an error-weighted UQ metric via the heterogeneous ensemble approach. Our validation across the diverse DFT datasets highlights its exceptional performance in estimating the prediction errors of uMLIPs without any DFT calculations and additional model training. In particular, we show that the derived UAMD can unleash the power of machine learning in atomistic modeling by avoiding the great computational cost of DFT, yet reach comparable accuracy. The new UQ method is shown to offer significant advantages for a wide range of uMLIP applications.

Methods

Atomic cluster expansion potential development

We employ pacemaker⁴⁶ to develop ACE potentials for bcc W and MoNbTaW. For ACE, we adopt a highly non-linear per-atom energy${E}_{i}=\varphi +\sqrt{\varphi }+{\varphi }^{1/8}+{\varphi }^{1/4}+{\varphi }^{3/8}+{\varphi }^{3/4}+{\varphi }^{7/8}+{\varphi }^{2}$, following ref. ⁴⁷. For the ACE basis, we use 72 functions (801 parameters) for W and 3656 functions (30,868 parameters) for MoNbTaW. As the radial basis, we employ Bessel functions. During fitting, we set the force-to-energy weight ratio to κ = 0.01. We optimize the models using the BFGS algorithm for 2000 steps. The cutoff distance is 5Å for both W and MoNbTaW.

DFT calculations

We use the Vienna ab initio Simulation Package (VASP)⁴⁸ to perform DFT calculations for W dimer and short-range configurations. Exchange-correlation effects are described within the generalized-gradient approximation using the Perdew-Burke-Ernzerhof (PBE) functional⁴⁹. Electron-ion interactions are treated with the projector-augmented-wave (PAW) method using the standard VASP PAW datasets. Electronic self-consistency is converged to 10⁻⁶ eV, and the plane-wave cutoff is 520 eV. k-point meshes are generated with VASPKIT⁵⁰ using Monkhorst-Pack grids, with a reciprocal-space resolution of 2π × 0.03Å⁻¹ applied consistently across the dataset.

Atomistic simulations

We perform all atomistic simulations with LAMMPS⁵¹. Atomic configurations are visualized and post-processed with OVITO⁵² (e.g., dislocation analysis). Together, these tools provide an integrated workflow for investigating the vacancy diffusion barriers, mechanical properties, and plastic-deformation mechanisms of BCC W and MoNbTaW alloys.

We perform bicrystal tensile simulations under fully periodic boundary conditions, with GB models constructed following ref. ⁵³. The Σ3 tilt GB $\left(109.4{7}^{\circ }\,[110]\,(1\overline{1}2)\right)$ model measures 66 × 203 × 108 ų and contains approximately 90,000 atoms. The Σ3 twist GB $\left(60.0{0}^{\circ }\,[111]\,(111)\right)$ model measures 85 × 210 × 74 ų and contains about 82,000 atoms. In both cases, the distance between the two GBs exceeds 10nm. Before loading, each system is energy-minimized and equilibrated at 300K for 20ps. Uniaxial tension is applied normal to the GB plane at a engineering strain rate of 5 × 10⁸s⁻¹, while the temperature is maintained at 300K using a Nose-Hoover thermostat. For the tilt GB model, deformation proceeds to 50% engineering strain. For the twist GB model, the simulation is terminated upon a brittle fracture.

We perform similar tensile simulations for MoNbTaW bicrystals with and without an initial crack. For the crack-free models shown in Fig. 5f, the initial bicrystal measures 132 × 203 × 108 ų and contains 18,000 atoms. The bicrystal incorporates a $\Sigma 3\,109.4{7}^{{\rm{o}}}[110](1\overline{12})$ tilt GB. The strain rate and loading manner are the same as that for W. For the cracked case in Fig. 6e, the simulation cell measures 280 × 207 × 46 ų and contains 154,750 atoms, retaining the same Σ3 tilt GB and loading protocol. The initial crack measures 60 × 9.5 × 46 ų.

The MC/MD simulations are conducted to generate chemical short range order (SRO) at 300 K by LAMMPS⁵¹. The samples are initially relaxed and equilibrated at 300 K and zero pressure under the isothermal-isobaric (NPT) ensemble through MD. After that, MC steps consisting of attempted atom swaps are conducted, hybrid with the MD. In each MC step, a swap of one random atom with another random atom of a different type is conducted based on the Metropolis algorithm in the canonical ensemble. 100 MC swaps are conducted at every 1000 MD steps with a time step of 0.001 ps during the simulation. 1 × 10⁶ MD steps are conducted in MC/MD simulations.