Main

Multiplexed imaging of tissue at single-cell resolution has been transformative in the understanding of disease through the discovery of novel biomarkers, regulators of immunity and mechanisms of drug resistance1,2,3. Single-cell analyses have unveiled fundamental concepts in biological systems, proving an invaluable tool in both basic research and translational settings4. Many multiplex imaging technologies exist, each with unique advantages and caveats. Immunofluorescence (IF) microscopy, for instance, can reach high multiplexity and resolution in a cyclic format but is limited by autofluorescence, and successive rounds of bleaching (or antibody removal) and imaging can undermine tissue integrity and introduce artifacts5,6. These effects, combined with the need for image registration, make the interpretation of subcellular physiology challenging. The emerging Deep Visual Proteomics platform combines IF-guided microdissection with mass spectrometry for deep proteome coverage but currently lacks the spatial precision to resolve subcellular compartments7. IMC uses tissue laser ablation of metal isotope-labeled antibodies and mass spectrometry-based detection and thereby avoids autofluorescence and cycling artifacts due to its one-shot staining and imaging workflow. The technique, however, suffers from lower resolution than that of fluorescence imaging, challenging its application to subcellular biology8. To enable subcellular analysis by IMC, new methods need to be developed to address these trade-offs.

The ability to resolve any structure by a given technology is determined by the so-called Nyquist limit, according to which a structure can be captured if the resolution of the technology is at least half the size of its smallest feature9. Currently, the laser ablation resolution of IMC is 1 µm, meaning that IMC resolves single cells and subcellular compartments such as the nucleus and the cytoplasm but subcellular structures below 2 µm such as mitochondria and nucleoli cannot be resolved. Achieving a higher laser ablation resolution in IMC is feasible but technically challenging due to difficulties associated with laser stability, tissue penetration and thermal degradation when using submicrometer laser beams10. As an alternative, computational approaches may overcome these limitations and achieve higher resolution in existing IMC systems. Recent computational strategies, such as blind deconvolution (for example, SpiDe-SR11) and cross-modality deep learning12, have shown promise but rely on strong prior assumptions or high-resolution training data. Here we present a new method to increase resolution in IMC, based on oversampling coupled with image deconvolution. We demonstrate that HR-IMC enables the mapping of subcellular marker distribution at steady state and under perturbation, improves cell segmentation and can be used to characterize subcellular compartments in cell types of interest within tissue.

Results

Tissue oversampling and deconvolution enable submicrometer-resolution IMC

We achieved HR-IMC using a standard 1-µm laser spot to sample tissue at a submicrometer step size, resulting in partially redundant (that is, overlapping) ablation areas (Fig. 1a). To achieve this oversampling, we reduced the laser energy per pass, thereby obtaining a signal from several laser passes over any given tissue region (Extended Data Fig. 1a). Multiple overlapping shots thus subdivide individual 1-µm pixels into multiple subpixels; the number and size of subpixels for a given oversampled acquisition will depend on the step size used, for example, nine subpixels for the 333-nm step size in the example shown (Extended Data Fig. 1b, left). In oversampled IMC, we assume that the signal from a given 1-µm pixel upon sampling with a single laser shot contains information from these subpixels, leading to image blur. To address this, we extracted information from the central subpixel by correcting for the effect of border subpixels using deconvolution methods (Extended Data Fig. 1b, left). In classical microscopy, deconvolution is typically achieved by methods such as Richardson–Lucy (RL) or Wiener deconvolution, which approximate a high-resolution image by using a point spread function (PSF)13. Such techniques have been applied to fluorescence and superresolution imaging to reduce blur and resolve fine structures14,15. By repeating deconvolution for each overlapping shot, we could reconstruct a high-resolution image. This procedure yielded IMC images at a resolution exceeding the limits imposed by the laser spot size (Fig. 1a).

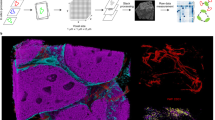
Fig. 1: HR-IMC enables imaging of subcellular structures.
figure 1

a, Schematic overview comparing classic (1 µm) and high-resolution (for example, 500 nm) IMC. In HR-IMC, the laser ablates tissue in 1-µm spots but the tissue is sampled at smaller step sizes (500 nm as shown here or adapted to the desired resolution). Ablated ions are measured by a time-of-flight mass cytometer; images are reconstructed from ion count information and further processed for image analysis. CyTOF, cytometry by time of flight. b(i)–b(iii), Representative IMC images of the same cell, nucleus and nucleolus. Data were acquired at 333-nm steps using 1-µm laser shots (b(ii)) and transformed to a resolution of 333 nm using RL deconvolution (b(iii)). Data were artificially convolved to 1 µm (b(i)), and an IF image was acquired on the same section (b(iv)). Overlapping 1-µm laser shots (b(ii)) are separated and visualized consecutively; thus, each unit in the image represents the data from a single laser shot. Intensities were 0–1 normalized. Scale bars, 1 µm. c, Spearman correlation between 0–1 normalized HR-IMC count values (1 µm, 333 nm before RL deconvolution, 333 nm after RL deconvolution) and 0–1 normalized IF intensity values observed at IF-IMC aligned nucleolar regions. Center lines of the box plot represent median values, box limits show the first and third quartiles, and whiskers extend to 1.5 times the interquartile range. The mean is represented as \(\hat{\upmu}\). Points display individual data points from different images (n = 3). Significance was assessed using a two-sided t-test. d, Representative images of a section of tonsil tissue imaged with ×40 IF (top) and HR-IMC (bottom). Similar results were observed in six different image pairs. Scale bars, 30 µm. e, Representative images of high-grade serous ovarian cancer tissue measured with HR-IMC compared to representative examples of the same subcellular structures measured with classical IMC from different images. Iridium 191 (191Ir), DNA intercalation marker; Ki-67, proliferation marker. Scale bars, 5 µm.

Full size image

The effect of a border subpixel on the recorded signal for a given laser shot depends on two factors. First, it depends on the fraction of total pixel area covered by the border subpixel, which can be mathematically modeled by intersecting circle geometry (Extended Data Fig. 1b, left). Second, the effect of a border subpixel depends on the number of laser passes it has undergone before acquiring the pixel. Because IMC is destructive, tissue that has undergone multiple rounds of ablation from previous overlapping shots will contribute less signal. The number of laser passes for a given border subpixel can be determined based on its position in the laser pass map, as the direction of laser movement and the step size are known (Extended Data Fig. 1b, right). For instance, in our exemplary scenario using a laser step size of 333 nm, designed to achieve a resolution of 333 nm, a given analyzed region will receive signal from one to nine laser passes. We estimated signal loss per laser pass in separate experiments by repeated sampling of a tissue region in the identical experimental setup, followed by mathematical modeling of the signal loss (Extended Data Fig. 1c). Spatial correlation of markers was high between consecutive laser passes, indicating that signals were preserved between passes, despite an indication of some loss over all passes (Extended Data Fig. 1d). We then estimated the PSF for our experimental setup and the 333-nm step size by multiplying the proportional area of the contribution of each subpixel by the signal expected given the number of passes across these areas (Extended Data Fig. 1e).

We compared oversampled HR-IMC data to the same HR-IMC data artificially convolved to a resolution of 1 µm. We used these artificially convolved data as a comparator rather than separately acquired IMC data to enable comparison on the identical section, given the destructive nature of the technique. As expected, this analysis revealed high-density, detailed images compared to the convolved HR-IMC data. However, oversampling alone failed to accurately represent the underlying structure of the nucleolus (Fig. 1b,c). PSF-based deconvolution of these data improved performance, reassigning pixel values in the nucleolar cavity while accentuating the nucleolar periphery (Fig. 1b,c). We found that the first seven laser passes were critical for deconvolution while the last two passes contributed minimally (Extended Data Fig. 1f). Notably, the convolved data had a signal-to-noise ratio (SNR) comparable to that of classic IMC on the sequential section (Extended Data Fig. 1g,h) and showed good spatial correlation for markers of large-scale structures (that is, smooth muscle actin (SMA) (blood vessels) and CD20 (germinal centers); Extended Data Fig. 1i), indicating that the convolved data are an adequate reference for benchmarking. Next, we examined the accuracy of our technique by comparing its performance to that of standard IF microscopy on the same section of formalin-fixed paraffin-embedded (FFPE) tissue. In each case, we stained the tissue section with a lanthanide-conjugated antibody but first imaged it using a fluorophore-labeled secondary antibody. The same section was then imaged with IMC. Comparing the two imaging modes for several markers (vimentin, SMA, mitochondrial membrane ATP synthase (ATP5A) and GLUT1) and tissue types (tonsil, lung adenocarcinoma, placenta, colorectal cancer, lung or bronchus, and kidney) showed that HR-IMC measured at 333 nm captures details as well as routine tissue IF (Fig. 1d and Extended Data Fig. 2a). As demonstrated on a SMA+ blood vessel, HR-IMC improved resolution also in fresh-frozen tissue in comparison to classical IMC (Extended Data Fig. 2b).

HR-IMC results were more similar to the IF pattern than classic IMC data from an adjacent region (Extended Data Fig. 2a) and showed better pixel-wise spatial correlation of markers to same-section IF data than did classic IMC data (Fig. 1c and Extended Data Fig. 2c). In a more visual assessment, HR-IMC enabled better delineation of SMA fibers in muscle tissue, offering improved structural separation compared to classical IMC (Extended Data Fig. 1j). Furthermore, in an exploration of subcellular structures undetectable with classical IMC, analysis of high-grade serous ovarian carcinoma (HGSOC) tissue with HR-IMC revealed highly resolved features, including submicrometer-level structures such as mitochondrial networks encircling nuclei and stretching into the cytoplasm, filamentous SMA fibers traversing stromal cells, and fine cell membranes (Fig. 1e). In addition, we observed nucleolus-resembling structures and Ki-67 foci in nuclei of interphase cells (Fig. 1e). These data show that HR-IMC unveils known subcellular structures across multiple tissue types.

Owing to the reduction in laser energy per pass, HR-IMC had lower overall signal intensity than classical IMC, but notably this was not at the expense of SNR (Extended Data Fig. 1g). For many markers, deconvolution improved the SNR because averaging multiple passes reduced noise while retaining signal (Extended Data Figs. 2d and 3a). Typically, the higher the resolution of HR-IMC and the higher the starting SNR of the marker, the stronger was this effect (Extended Data Fig. 3b), and some markers (for example, FOXP3) fell below the detection limit in HR-IMC. Furthermore, while our studies were primarily carried out on the newer, more sensitive Hyperion XTi instrument, we achieved comparable HR-IMC performance on the Hyperion+ system, albeit with a resolution limit of 500 nm due to its poorer stage precision and at slower imaging speeds (Extended Data Fig. 3c–e). While the SNR of many markers was within the same range as for the Hyperion XTi, lower-abundance markers such as CD11b or FOXP3 were less interpretable or even no longer detected on the Hyperion+ (Extended Data Fig. 3f,g).

HR-IMC improves segmentation and cell phenotyping in densely packed tissues

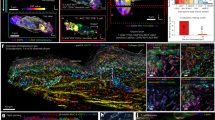
Beyond measuring subcellular structures in high multiplex, HR-IMC should also enable better segmentation of cells in proximity to one another. For instance, the tonsil is a difficult tissue to segment, packed with small, interacting immune cells. We compared nuclear segmentation masks between HR-IMC and classic IMC on the tonsil and found that convolved HR-IMC data underestimated cell numbers and merged adjacent nuclei (Fig. 2a,b). Ground truth comparisons with hematoxylin and eosin (H&E)-stained images of the same sections showed that HR-IMC more accurately separated individual cells and better distinguished mutually exclusive markers in a pixel-level analysis, in both cases compared to classic IMC (Fig. 2a,c–f). Previous IMC publications detail so-called ‘BnT’ cells, representing interacting B and T cells that could not be separated by segmentation3,16. To assess whether HR-IMC could mitigate this problem, we imaged an FFPE tonsil section at a resolution of 333 nm and then segmented single cells from both HR-IMC data and classic IMC (Fig. 2g). The proportion of these ‘BnT’ cells was over threefold greater in classical IMC than in HR-IMC (Fig. 2h). These data show that HR-IMC improves tissue segmentation in comparison to classical IMC.

Fig. 2: HR-IMC improves segmentation and cell phenotyping.
figure 2

a, Representative images comparing nuclear boundaries in the tonsil measured with HR-IMC versus with convolved HR-IMC data as a model of classical IMC. Colors indicate merged, matched or split cell masks between the two data types. Stacked bar plots represent relative mask contribution. H&E images of the same section serve as ground truth. b, Total number of cells segmented in HR-IMC (333 nm) data, in the respective image convolved to the resolution of classical IMC (1 µm), and in a same-section brightfield H&E image (×40); data are presented as mean ± s.e.m.). Points display individual images (n = 4). c, The proportion of segmentation masks that could not be mapped to equivalent masks on the same-section H&E image (presented as mean ± s.e.m.). Proportions were compared between the HR-IMC (333 nm) images and convolved equivalents. Points display individual images (n = 4). Significance was assessed using a two-sided t-test. d, Proportion of pixels that were deemed positive for both CD20 and CD3 based on a Gaussian mixture model (presented as mean ± s.e.m.). Proportions were compared between the HR-IMC (333 nm) images and convolved equivalents. Points display individual images (n = 4). Significance was assessed using a two-sided t-test. e, Same-section H&E and HR-IMC (333 nm) staining of human colon, lung adenocarcinoma and tonsil FFPE tissues. Scale bars, 100 µm. f, Representative images of B and T cells in close proximity in HR-IMC (333 nm) and classical IMC acquired on a consecutive section. g, Heatmap of mean marker expression of annotated immune subtypes. Expression values are scaled, and relative abundance is compared between HR-IMC (333 nm) and classical IMC (acquired on the consecutive section). h, The proportion of total B and T cells that were classified as BnT cells compared between HR-IMC (333 nm) and classical IMC on the consecutive section (presented as mean ± s.e.m.). Points display individual images (n = 4). Significance was assessed using a paired two-sided t-test.

Full size image

HR-IMC enables analysis of subcellular phenomena in high-grade serous ovarian cancer

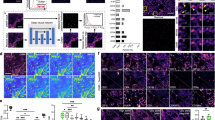
To further probe subcellular phenomena with HR-IMC, we applied it to patient-derived HGSOC cells cultured in 3D, aiming to compare chemotherapy response captured with both high-resolution and classical IMC (Fig. 3a). We built a 25-plex antibody panel visualizing chemotherapy response markers and subcellular structures (Fig. 3b and Extended Data Fig. 4a) and used this panel to image cells cultured in the presence and absence of combined chemotherapy using carboplatin and paclitaxel (Extended Data Fig. 4a–c). We then artificially convolved the high-resolution data to a resolution of 1 µm to simulate classical IMC and performed pixel-level clustering of the HR-IMC data and the convolved data to identify regions within cells exhibiting shared marker profiles. For the HR-IMC data, this yielded 13 distinct clusters (Extended Data Fig. 4d), with marker expression patterns corresponding to known subcellular structures (Fig. 3c,d). We annotated cluster 4 as mitochondrial regions based on expression of ATP5A and heat shock protein 10 (HSP10) and also annotated eight nuclear clusters that included DNA repair regions, replication foci and DNA damage (Fig. 3d). The same pixel-level clustering on the artificially convolved image recovered similar patterns but with less distinct marker separation, and we could also reproduce the HR-IMC clusters using a different clustering approach (Extended Data Fig. 4e,f). Using both global and local cluster quality metrics (Methods), we found that HR-IMC showed enhanced separation of clusters based on subcellular markers compared to convolved data as a model for classical IMC (Fig. 3e and Extended Data Fig. 4g–i).

Fig. 3: HR-IMC reveals changes in subcellular organization of ovarian cancer cells in response to chemotherapy.
figure 3

a, Schematic overview of the experimental workflow. b, Targets of the antibody panel grouped by subcellular location and with their associated functions indicated. Cl., cleaved. p-, phospho. c, t-distributed stochastic neighborhood embedding (t-SNE) visualization of tumor cell-derived pixels. Each dot represents a pixel, and colors represent pixel clusters. d, Heatmap of mean marker expression (exprs) of each flowSOM pixel cluster. Expression values are scaled, and markers as well as clusters are separated by nuclear or nonnuclear localization. Cluster annotations were made based on mean marker expression and biological knowledge. e, Comparison of cluster quality based on silhouette width (SW), neighborhood purity (NP) and Davies-Bouldin index (DBI) between clusters. The plot compares pixel-level clusters at a resolution of 333 nm from Fig. 2d and data artificially convolved to a resolution of 1 µm from Extended Data Fig. 5f. f, Representative image of cells comparing localization of pixel clusters and key marker expression on original images. Depicted are representative examples of membrane (cluster 6, GLUT1), mitochondria (cluster 4, ATP5A) and nucleus (cluster 8, Ki-67). Scale bars, 5 µm. g, Log (fold change (FC)) in the absolute frequency of subcellular clusters upon treatment with carboplatin and paclitaxel (CP) relative to the dimethylsulfoxide (DMSO) control, determined by differential abundance testing using edgeR. Significantly changing clusters are indicated (P < 0.05, Benjamini–Hochberg-adjusted likelihood ratio tests). h, Changes in marker colocalization within cells upon chemotherapy treatment. Spearman correlations of marker expression within each cell were computed, and the mean difference with and without chemotherapy was plotted pairwise for significant changes (Benjamini–Hochberg-adjusted P value < 0.05) and where the difference in colocalization exceeded 0.05; this threshold was chosen for clarity in the visualization. Red and blue lines indicate positive and negative changes in correlation, respectively. Thickness of lines reflects the extent of the change. All nonredundant markers were included in this analysis. Examples of marker colocalization between DNA damage foci (p-H2AX) and open chromatin regions (H3K4me2) upon chemotherapy treatment are depicted below. Scale bars, 10 µm.

Full size image

Annotated clusters showed spatial colocalization with subcellular compartments that were consistent with biological expectations (Fig. 3f). For instance, cluster 8, associated with proliferation, corresponded to Ki-67 foci, while cluster 4, representing mitochondrial pixels, was characterized by ATP5A staining localized to the mitochondria (Fig. 3f). To examine whether HR-IMC can recover known effects of chemotherapy on the subcellular level, we analyzed the differential abundance of clusters after treatment. This analysis showed an upregulation of DNA damage and repair foci and a downregulation of proliferative clusters in treated cells, consistent with the classical chemotherapy response (Fig. 3g). Changes of marker colocalizations upon chemotherapy furthermore suggested a loss of Ki-67 nuclear localization and a significant gain of phosphorylated histone H2AX (p-H2AX) in regions of open transcription marked by histone methylation and acetylation variants, which we could confirm in the corresponding images (Fig. 3h). These experiments illustrate that HR-IMC identifies features that are not detectable with classical IMC and detects shifts on the subcellular level in these compartments after drug perturbation, showcasing its value in studying intracellular processes.

Finally, we took advantage of our unique combination of highly multiplex and subcellular resolution imaging to examine subcellular architecture of different cell types in situ, within their tissue context. We defined tumor cells, immune cells and fibroblasts in HR-IMC-imaged ovarian tumor tissue based on marker expression patterns (Fig. 4a), identified mitochondrial pixel clusters and networks marked by ATP5A and HSP10 expression (Fig. 4b,c and the Methods) and then compared these mitochondrial networks across different cell types. As expected, tumor cells displayed higher mitochondrial density and larger mitochondrial networks than the other cell types (Fig. 4d,e). Also, hypoxic (CAIX+) tumor cells showed reduced mitochondrial content and increased GLUT1 expression compared to normoxic cells (Fig. 4f,g). This approach holds great potential for mapping subcellular structures in different cell types and states in situ.

Fig. 4: HR-IMC links subcellular features to cell types and states.
figure 4

a, Heatmap of mean marker expression of annotated tumor, immune and endothelial cells and fibroblasts. Expression values are scaled. panCK, pan-cytokeratin. b, Example HR-IMC (333 nm) images of in situ HGSOC (n = 3) demonstrating pixel-level clustering to detect mitochondrial pixels and subsequent mitochondrial patch detection. c, Heatmap of mean expression of the mitochondrial markers HSP10 and ATP5A in pixel-level clusters. Expression values are scaled. d, Box plot comparing mean size of mitochondrial patches (mitochondrial interconnectivity, left) and number of mitochondria normalized to cell area (mitochondrial density, right) across different cell types. Center lines of the box plots represent median values, box limits show the first and third quartiles, and whiskers extend to 1.5 times the interquartile range. Points display individual cells across regions of interest (ROIs) (n = 3 ROIs). Significance was assessed using a two-sided, paired t-test comparing the average value for each cell type, calculated per ROI. e, Representative images of panCK+ tumor cells with high mitochondrial load and SMA+FAP+ fibroblasts with less mitochondria. Scale bar, 30 µm. f, Box plots comparing GLUT1 expression (left), mean size of mitochondrial patches (mitochondrial interconnectivity, middle) and number of mitochondria normalized to cell area (mitochondrial density, right) between normoxic (N) and hypoxic (H) tumor cells. Tumor hypoxia status was determined by Gaussian mixture modeling of carbonic anhydrase expression. Points display individual cells across ROIs (n = 3 ROIs). Center lines of the box plot represent median values, box limits show the first and third quartiles, and whiskers extend to 1.5 times the interquartile range. Significance was assessed using a two-sided, paired t-test comparing the average value for each cell type, calculated per ROI. g, Representative images of adjacent normoxic and hypoxic tumor regions showing differential mitochondrial (ATP5A) and GLUT1 expression. Scale bar, 60 µm.

Full size image

Discussion

This work demonstrates the application of submicrometer-level UV laser positioning to approximate and reconstruct image details at a resolution greater than that achievable with standard IMC in the tissue types studied. By modeling and optimizing laser energy settings, we could deconvolve the HR-IMC signal in a manner uniquely tailored to the characteristics of IMC. We have thus established a new acquisition mode for IMC that enhances resolution while remaining compatible with current instrumentation.

While a host of superresolution methods have shown enhanced resolution in IF data, these methods have limited application to IMC. Many require considerable computational resources as well as pairs of high- and low-resolution training data, with the latter thus far not available for IMC. Recently described self-supervised blind deconvolution strategies for IMC data are constrained by the need for post hoc inference of information that has not been experimentally measured11,12. By contrast, our HR-IMC approach primarily relies on technical innovation at the image acquisition stage rather than on inference alone. By precisely altering the physical characteristics of ablation, we record dense, richer imaging data that can be deconvolved with a PSF specifically tailored for IMC. Moreover, the data generated using HR-IMC could be useful for the development of superresolution technologies specifically adapted for IMC.

Currently the resolution of HR-IMC is limited by the precision of tissue ablation and stage movement, the decrease in signal intensity and the increase in imaging times (Extended Data Fig. 3). As the speed of laser ablation and the precision of stage movement improve, these technical limitations can be addressed. Furthermore, the loss of signal intensity observed in HR-IMC could be overcome by signal amplification methods such as SABER-IMC17. On the other hand, the computational processing of oversampled data could be achieved with a range of deconvolution strategies. For instance, we modeled laser aperture as an evenly ablating circle, thus not accounting for crater effects or tissue density. Craters arise from the Gaussian profile of most laser beams, because the center delivers more energy than the edges. Incorporating these factors into the calculations or developing spatially variant PSFs to account for local tissue composition may provide a more accurate representation of the tissue in the near future.

In summary, we provide a new approach to analyze cell biology at the intracellular level. HR-IMC can capture spatial distribution of proteins within cells, identify organelle-specific signaling events and characterize subtle morphological features that correlate with function or disease state. In the future, this might facilitate discovery of complex cellular architectures and new cell phenotypes. Together, these advances establish HR-IMC as a new high-resolution, multiplexed imaging method capable of mapping the subcellular structures that underpin fundamental biological processes.

Methods

Ethics

Ethical approval was granted by the Ethical Committee of Northwest and Central Switzerland (EKNZ, BASEC IDs 2017-01900 and 2023-00988).

High-resolution IMC

HR-IMC data were acquired with the Hyperion XTi or Hyperion+ imaging system. While HR-IMC does not require hardware modification of the instrument, the step size parameter was adjusted to a value of either 0.5 µm or 0.33 µm in the instrument’s acquisition mode settings and the laser energy was reduced accordingly to allow multiple rounds of tissue ablation. Detailed instructions for practical implementation are available in Extended Data Fig. 5. To deconvolve overlapping signals, we calculated the expected overlap between 1-µm ablations with a circular laser aperture (Extended Data Fig. 1b). Each pixel was divided into a number of subpixels based on intersecting circle geometry. Briefly, circles were superimposed (at either 500-nm or 333-nm steps) in vector graphics-based software to replicate the laser scanning pattern. The areas of these intersects were approximated using ImageJ18. The signal contribution of each subpixel was calculated by multiplication of the proportional area of the subpixel and the observed signal of the pixel. To account for subpixels that had been ablated several times from the overlapping acquisition above and to the left of the pixel of interest, overlaps were annotated with pass numbers. The resulting laser pass map depends on the direction of the scanning laser (classically left to right and top to bottom). For each successive laser shot, regions corresponding to the newest ablation were labeled with the number of previous passes they had received. The signal was then corrected based on the expected signal remaining given the number of passes received. Correction was based on an experimentally derived inverse sigmoidal loss function at −10 dB of laser energy. The calculated contributions were summarized in a skewed 3 × 3 PSF by multiplying the signal of each subpixel by its relative area contribution, resulting in upper subpixels contributing less signal, given that their overlapping area was measured in regions that experienced greater pass numbers (Extended Data Fig. 1e).

Laser energy optimization and deconvolution

Signal loss was measured for different laser energies to select an energy that permitted signal recovery after nine rounds of ablation. To do this, a 500 × 500-µm area of the tissue was repeatedly ablated for a total of ten passes at laser energies of 0, −1, −10, −15 and −20 dB. Pixel values from the iridium channel (191Ir and 193Ir) were summed for each pass and for each energy, to measure intensity loss. The signal loss function was defined as:

$$\mathrm{Intensity}\left(x\right)={I}_{0}-\frac{{I}_{0}}{1+\exp \left(-\left(x-{x}_{0}\right)\right)},$$

where intensity(x) represents the estimated intensity at pass x, I0 is the maximum intensity and x0 is the inflection point (the pass number at which signal begins to rapidly decline). Model parameters were estimated using nonlinear least-squares fitting implemented in R (version 4.3.2) using the nsl2 package. After modeling each energy, we selected −10 dB as the optimal laser energy for our experimental setup.

For multiplexed analyses, the calculation was carried out for each channel, where I0 represented the maximum marker signal and remained constant across channels. This ensured that correction was carried out on a marker, rather than image-specific, level. To recover higher-resolution images, RL deconvolution was implemented in Python using the richardson_lucy function of the skimage.restoration (version 0.16.2) module. The raw images were split into respective channels, and each was deconvolved with the predefined PSF using seven iterations to achieve convergence. The number of iterations was determined based on empirical testing to balance restoration quality and noise amplification. A three-pixel border was removed from the image after processing, as the PSF is designed to take into account the effect of surrounding pixels that are partially absent in border pixels. Our approach uses classic RL deconvolution, which is well suited for Poisson noise as present in IMC data. It is important to note that we focused on optimizing the PSF for nonuniformly ablated oversampled IMC data. By contrast, Wiener deconvolution is optimized for Gaussian noise. To avoid noise amplification during the iterative process, we monitored the increase in the log likelihood of the Poisson model after each iteration. The optimal number of iterations was chosen based on the flattening of the log likelihood curve combined with visual inspection of the images, confirming enhanced resolution without the introduction of artifacts or noise.

Tissue staining

Tissue samples were preserved using formalin fixation and paraffin embedding at the university hospitals of Basel and Zurich. Antibody staining was performed according to a standardized IMC protocol, with specific antibody clones and concentrations listed in Supplementary Table 1. All antibodies underwent a two-step validation process by detection of the unconjugated antibody using secondary IF staining and IMC analysis of the metal-conjugated antibody. Images were compared to staining patterns from the Human Protein Atlas using positive and negative control tissues. First, the tissue slides were deparaffinized by incubation in Histo-Clear (Biosystems) for 10 min each over three consecutive rounds. They were then rehydrated by dipping them in 100% ethanol twice for 5 min each, followed by exposure to a series of ethanol solutions diluted with deionized water (96%, 90%, 80% and 70% ethanol) for 3 min each. Heat-induced epitope retrieval was carried out by incubating the slides in Tris-EDTA buffer (pH 9) at 95 °C for 30 min using a NxGen decloaking chamber (Biocare Medical). After cooling for 20 min, the slides were blocked in TBS-T buffer (20 mM Tris, pH 7.6, 150 mM NaCl, 0.1% Tween) containing 3% BSA for 1 h to minimize nonspecific antibody binding. The tissue samples were incubated overnight at 4 °C with a full panel of metal-tagged antibodies. The next day, the slides were washed with TBS buffer three times for 5 min each and subsequently incubated with 0.5 μM Cell-ID Intercalator-Ir (Standard BioTools) for 5 min to detect DNA. After another wash with TBS and a dip in deionized water, the slides were dried using pressurized air.

To perform combined IF and IMC staining, tissue samples were first stained overnight at 4 °C with primary antibodies (Supplementary Table 1), followed by the use of fluorophore-labeled secondary antibodies. After washing twice with TBS buffer, fluorescently labeled or metal-conjugated secondary antibodies targeting the host species of primary antibodies were applied for 1 h at room temperature. For IF, a coverslip was mounted using 85% glycerol to perform immunofluorescent imaging. Images were acquired using a CELENA X microscope (Logos Biosystems) with a ×40 objective. After this imaging step, the coverslip was removed using TBS, and the slides were washed, dried and prepared for laser ablation and analysis by IMC.

To perform combined IMC with H&E staining, an additional H&E staining step was included after heat-induced epitope retrieval. Briefly, sections were stained according to standard protocols, mounted with a coverslip with 85% glycerol and imaged using a ZEISS Axio slide scanner at ×40 in brightfield mode. Immediately after imaging, the coverslip was removed using TBS, and the standard IMC staining protocol was continued as previously described.

Immunofluorescence comparison

IF staining was carried out on FFPE-embedded tonsil, lung adenocarcinoma, placenta, lung or bronchus, kidney and colorectal cancer tissues using a fluorophore-labeled secondary antibody. HR-IMC data were acquired from the same section after imaging, detecting the metal-labeled primary antibody using the ZEISS Axioscan 7 at ×40. To align the data modalities, a transformation matrix was generated with the Napari affinder plugin. For nucleolar comparison, IF pixel coordinates were transformed into IMC space, and each pixel was assigned to its nearest IMC pixel based on a k-nearest-neighbor search using the R package RANN (version 4.0.16). For comparison to IF staining across larger tissue areas in lung adenocarcinoma, placenta, lung or bronchus, kidney and colorectal tissues, pixels were assigned by directly binning those that shared the same coordinates. Spearman’s correlation (using the stats package (version 4.3.1)) was then calculated on a subset of the image focused on nucleolar structures in the tonsil or across the whole image for other tissue types. Correlation was calculated using normalized expression values from the DNA, GLUT1, SMA, ATP5A or vimentin channel.

Data processing

Multiplexed tissue images were processed using the Steinbock toolkit and workflow19, available at https://github.com/BodenmillerGroup/steinbock. Briefly, raw mcd files from the Hyperion Imaging System were converted to TIFF format and preprocessed by applying a hot pixel filter with a threshold of 50. Cell segmentation was performed using the pretrained neural network DeepCell, with min–max normalization applied to each channel and an adjusted pixel size parameter of 0.33. Cytoplasmic channels were assigned as panCK, E-cadherin and TUBB3 for the ex vivo and in situ analysis and as VIM and CD45 for tonsil segmentation. Nuclear channels were set as H3K4me2, 191Ir and 193Ir for ex vivo and in situ analysis and as 191Ir and 193Ir for tonsil segmentation. Single-cell segmentation masks were overlaid on the TIFF images, enabling the extraction of both spatial features and mean marker expression levels, which were summarized as the mean count values for each channel across pixels within a given cell. For downstream analysis, cells with an area smaller than 55 µm2 or greater than 555 µm2 were removed, as they most likely result from segmentation artifacts.

Data transformation and normalization

To correct for signal spillover, pure spots of each metal-tagged antibody were measured, and compensation was performed using the CATALYST R package (version 1.26.1)20. The raw counts were adjusted by applying a 99th-percentile cutoff and then subjected to arc-sinh transformation with a cofactor of 1. For visualization and clustering, the transformed data were normalized to a scale ranging from 0 to 1. All further analyses were conducted using the arc-sinh transformed data.

Image convolution

HR-IMC images were artificially convolved to lower resolution to provide demonstrative same-slide low-resolution data. Convolution was performed in R (version 4.0.16), where pixels were binned into 3×3 superpixels and raw count values were summed.

Segmentation comparison

Segmentation quality was assessed by phenotyping immune cells in the tonsil and direct comparison of cell masks in convolved and HR-IMC data. HR-IMC (333 nm) images were convolved, and both images underwent nuclear segmentation using DeepCell as previously outlined. Each mask was assigned to its nearest mask in the corresponding image based on a nearest-neighbor search using the R package RANN (version 4.0.16) (RRID:SCR_024297). Masks identified at a distance greater than the major axis of the matched cell were discounted. Multiple masks that aligned to a single mask were annotated as ‘split’, with the corresponding mask annotated as ‘merged’. To assess the accuracy of segmentation in these data, H&E images were segmented using QuPath (version 0.4.4) cell detection (threshold, 0.05; sigma, 0.5; minimum area, 8 µm; background radius, 20 µm; and standard settings), aligned using the Napari affinder plugin (version 0.5.6) and assigned to corresponding cell masks as previously outlined.

Cell phenotyping was assessed in the tonsil by comparing the ratio of ‘BnT’ cells in consecutive sections of the tonsil measured with HR-IMC (333 nm) and classical IMC. Cells were classified by independent clustering of the image-normalized expression values. The Rphenograph algorithm21 was used to construct a shared nearest-neighbor graph (k = 20) using Euclidean distance, implemented in the R package Rphenograph (version 0.99.1) (RRID:SCR_022603). To refine edge weights in the shared nearest-neighbor graph, Jaccard similarity was applied to pairs of cells. Louvain community detection was then applied to optimize cluster modularity based on the resulting graph. The resulting clusters were annotated as either B cells, BnT cells, CD4+ T cells, CD8+ T cells or ‘other’, based on canonical immune cell markers. Proportions of the shared cell types were compared between images. To assess clustering stability, the image-normalized expression values were independently clustered using k-means clustering (k = 10) with the R package clvalid (version 0.7). To determine pixel double positivity, images were converted into image matrices and Gaussian mixture models were implemented for the scaled expression values of CD3 and CD20 with the densityMclust function in the R package mclust (version 6.1.1).

Quantification of signal intensity and signal-to-noise ratio

To quantify pixel signal intensities, pixel counts were extracted from each channel of raw TIFF images acquired at different resolutions (1,000 nm, 500 nm, 333 nm and 200 nm). Pixel classification into background and foreground was performed using Otsu thresholding, implemented via the EBImage R package (version 4.44.0). Otsu’s method determines an optimal threshold by minimizing the variance within each class. We verified that the number of pixels classified as foreground remained consistent across conditions and visually inspected all thresholded images to exclude the occurrence of artifacts. Mean pixel intensity was then calculated as the average signal intensity across foreground pixels, while total pixel intensity was determined by summing the intensities of the foreground pixels. The SNR was computed by dividing the mean intensity of the foreground pixels by the mean intensity of the background pixels. It should be noted that this quantification may be influenced by variations in cell density and size within the images.

Three-dimensional patient-derived ovarian cancer culture

Three-dimensional patient-derived ovarian cancer cultures were performed according to previously published protocols22. The tissue sample from a patient with high-grade serous ovarian cancer was processed within 30 min after surgery. Cultures were treated with DMSO or a combination of 100 µM carboplatin (Labatec Pharma) and 100 nM paclitaxel (Merck).

Cell- and pixel-level clustering approaches

For pixel-level clustering of ex vivo and in situ data, single-pixel expression profiles were extracted from TIFF files and pixels outside segmentation masks were excluded. Pixels were aggregated across conditions and clustered into subcellular clusters using the flowSOM algorithm23 as implemented in the CATALYST package (version 1.26.1)24 (RRID:SCR_017127) and suggested by the Pixie workflow25. Normalized marker expression values were used for this clustering step to minimize the impact of brightness variation between markers. Next, the mean expression profile of each cluster was determined and metaclustered using consensus hierarchical clustering based on z-scored expression values. The number of metaclusters was initially selected based on cluster stability (Extended Data Fig. 4d), and a final higher k value was selected to enable resolution of subcellular structures. Resulting clusters were manually annotated using biological knowledge. To simulate traditional IMC data, HR-IMC data were artificially convolved to a resolution of 1 µm and clustered using the same approach. For pixel-level clustering in the ex vivo analysis, additionally unsupervised clustering was performed using the Rphenograph algorithm with k = 600 to construct a k-nearest-neighbor graph and identify community structure. Due to computational constraints, the dataset was downsampled to 30,000 pixels for this analysis. All random sampling steps were controlled with fixed seeds to ensure reproducibility. For cell-level clustering in the ex vivo analysis, the Rphenograph algorithm (k = 20) was applied, and resulting clusters were annotated to cell types based on their scaled marker expression profiles.

Comparison of cluster qualities

To evaluate cluster quality of HR-IMC data compared to that simulated traditional IMC data, the average distance between cluster means and the silhouette width were computed. For the average distance, the Euclidean distance between the centroids (means) of all cluster pairs was calculated in the scaled marker expression space. The distances were averaged to quantify how well separated the clusters were. Larger average distances indicate better separation. The silhouette width was calculated for each individual pixel to evaluate how well each pixel matched its assigned cluster compared to other clusters26,27. It is determined by comparing the average distance of a pixel to other pixels within its own cluster (intracluster distance) with the average distance to pixels in the nearest neighboring cluster (nearest-cluster distance). The overall clustering quality was summarized by averaging the silhouette widths of all pixels, allowing for a direct comparison between HR-IMC and simulated traditional IMC datasets. In addition, neighborhood purity was computed as the percentage of the ten nearest neighbors that belonged to the same cluster28. Davies–Bouldin index was computed using the index.DB function implemented in the clusterSim package29. The R package bluster was used for implementation of all other cluster quality metrics.

Differential abundance analysis

To assess significant differences in the proportions of subcellular clusters between untreated cells and those exposed to chemotherapy, differential abundance analysis was performed using the edgeR R package (version 4.0.16)30 (RRID:SCR_012802). Cluster 3 showed no marker expression, suggestive of background pixels, and was therefore excluded from this analysis. This differential abundance analysis includes dispersion estimation to account for variability in the data and fitting a negative binomial generalized linear model to the cluster counts. A design matrix was created to represent the relationship between cluster counts and treatment conditions, enabling a comparison of chemotherapy-treated cells with the DMSO-treated reference group. The log (fold change) of each subcellular cluster was computed, and significance was evaluated by performing quasi-likelihood F-tests. A false discovery rate threshold of <0.05 was applied using the Benjamini–Hochberg method to adjust for multiple comparisons.

Pixel-level correlation analysis

To investigate colocalization of proteins, we conducted a pixel-level correlation analysis of markers. Spearman correlation coefficients were computed for each marker pair within cells using the stats package (version 4.3.1) and aggregated to mean correlation values for each treatment condition. To assess changes in correlation structures between conditions, Wilcoxon testing was used to compare the Spearman correlation coefficients between DMSO and chemotherapy (carboplatin and paclitaxel) conditions. The Benjamini–Hochberg method for multiple-comparison adjustment was used to control the false discovery rate, and P values < 0.05 were considered statistically significant. The final results visualize significant changes in protein colocalization induced by chemotherapy, represented as the difference in mean correlation between the two conditions.

Detection of mitochondria via patch analysis

To identify mitochondrial structures at the pixel level, we employed patch detection. First, a spatial interaction graph was constructed on the pixel level using the buildSpatialGraph function from the imcRtools package, with a one-pixel threshold for neighborhood expansion. Patch detection was then performed using the patchDetection function, which grouped spatially connected mitochondrial pixels (within the defined graph) into contiguous patches. Mitochondrial pixels were defined as those expressing the markers ATPTA and HSP10, and the detection was restricted to pixels of interest without additional spatial expansion. Patches were then summarized at the single-cell level by calculating the number of distinct mitochondrial patches per cell and the average number of mitochondrial pixels per patch.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.