Introduction

There is no doubt that optimization methods have now become an intrinsic part of the microwave design process. For many classes of circuits, rough initial designs can usually be obtained by means of the traditional, e.g., circuit theory methods (either in the form of explicit analytical formulas1, or equivalent networks2). Notwithstanding, conventional techniques and circuit models lack the accuracy whenever phenomena like dielectric and radiation losses or electromagnetic (EM) cross-coupling, have non-negligible effects on the system characteristics. Securing the best achievable performance requires cautious tuning of circuit dimensions3. Intricacy of modern microwave systems made experience-driven parametric studies virtually obsolete. Instead, rigorous numerical optimization is recommended4, which enables efficient handling of multiple variables, objectives, and constraints5,6. Unfortunately, optimization of microwave devices faces serious difficulties on its own. On the one hand, it is often necessary to handle large numbers of system variables, which is numerically demanding. On the other hand, accurate evaluation of circuits often involves CPU intensive full-wave EM analysis. Both factors contribute to considerable costs associated with parameter tuning7, as well as limited efficacy of conventional algorithms8. These problems are particularly pronounced for compact passive components constructed by meandering transmission lines (TL)9,10,11,12,13, compact microwave resonant cells (CMRCs)14, slow-wave phenomenon15, defected ground structures (DGS)16,17, electronic bandgap structures (EBG)18,19, or a variety of geometrical alterations (slots20, stubs21, shorting pins22, etc.). Miniaturization using the aforementioned approaches multiplies the number of degrees of freedom within the structures (e.g., a typical CMRC unit is described by at least four parameters versus two for a TL), which further exacerbates their design process, including optimization. In many cases, local algorithms23 have to be replaced by global procedures24,25,26,27,28,29, often leading to unmanageable computational expenses.

The literature provides a plethora of algorithmic solutions primarily aiming at the improvement of both the computational efficiency and reliability of the EM-driven optimization procedures. Acceleration methods include the incorporation of techniques for fast evaluation of circuit response gradients (adjoint sensitivities30,31, mesh deformation32, parallelization33), replacing numerical derivatives by updating formulas34, as well as utilization of sparse sensitivity updates35,36,37. In a more generic setting, surrogate-assisted procedures have been gaining considerable attention38,39,40,41, both in the context of physics-based (space mapping42, adaptive response scaling43, manifold mapping44), and data-driven models (radial basis functions45, kriging46, artificial neural networks47, ensemble learning48, support vector regression49), along with variable-resolution methods (co-kriging50, Bayesian model fusion51). Surrogate-based methods are applied for both local52, 90,91,92,93 and global optimization53,54,55, but also multi-criterial design56,57,58,59, and uncertainty quantification60,61,62. In terms of reliability improvements, in some cases combined with acceleration, some of the worth-mentioning techniques include efficient global optimizers (EGO)63, machine learning frameworks64, response feature technology65, cognition-driven design66, frequency-based regularization67, or adaptive design specification strategies68. Some of these approaches aim at facilitating exploration of the parameter space63,69, whereas others alleviate the difficulties pertinent to local routines (e.g., sensitivity to initial design67,68).

A particular type of an optimization task, which is of significant practical importance, is a re-design of a given microwave component to a different set of operating conditions (e.g., center frequency, power division ratio, etc.) or material parameters (e.g., substrate permittivity or thickness). The need for re-design may arise due to employing a circuit in a new application area, or implementing it on a different substrate. The associated numerical challenges are similar to those elaborated on at the beginning of this section: high computational cost, and potential reliability issues, especially for local search, or when the structure is to be scaled for operating parameters considerably misaligned with those at the current design. A number of frameworks have been developed to facilitate the dimension scaling process, including analytical design curves70, utilization of inverse surrogate models71,72, response features73, as well as more sophisticated frameworks that enable control of both the major operating conditions (e.g., center frequencies) and supplementary performance figures (e.g., power split ratios)74. The major drawback of the aforementioned techniques constitutes a high initial cost necessary to construct the surrogate models, which are typically rendered using pre-optimized reference designs71. Utilization of generic surrogate modeling techniques is another option75,76,77,78; however, setting up dependable metamodels over extended ranges of cicuit dimensions and material parameters (otherwise necessary to ensure design utility) is exacerbated by the curse of dimensionality and highly nonlinear microwave components characteristics. A possible workaround is a utilization of performance-driven modeling methods, which permit a rendition of accurate surrogates at a fraction of CPU costs incurred by conventional techniques79,80,81.

This article introduces a novel technique for fast and reliable re-design of passive microwave devices. Our methodology employs a concurrent scaling of geometry parameters, which is interleaved with local tuning. The role of the scaling stage is to perform large-scale design relocation of the circuit operating frequency at low computational cost. The tuning stage aims at improving the performance parameters of the circuit before launching the next scaling step. Eventually, i.e., upon relocating the operating frequency near the target, the process defaults to gradient-based optimization. The efficacy of the introduced technique is verified using several compact microstrip couplers, which are re-designed for center frequencies distant from those at the initial designs. Comparative experiments also indicate that straightforward local search normally fails under these conditions. Apart from its reliability, the proposed framework exhibits other attractive features, including simple implementation, easy handling, in particular, the lack of problem-dependent control parameters that need to be tuned, and low cost. The latter is related to the fact that our method does not utilize any surrogate models, and, consequently, there is no initial cost associated with the acquisition of either training data or pre-optimized reference designs.

Circuit re-design using concurrent scaling and intermittent local tuning

This section explains the constituent parts of the introduced re-design methodology. We start by formulating the design problem in Sect. "Problem statement". Section "Concurrent parameter scaling" discusses the concurrent parameter scaling stage. Section "Intermittent local tuning" describes the local (gradient-based) tuning step, which is carried out to ensure sufficient performance of the circuit before executing the subsequent scaling step. The complete optimization procedure has been summarized in Sect. "Complete optimization procedure".

Problem statement

In the following, x = [x1 … xn]T represents the vector of design parameters of the considered circuit (i.e., its dimensions). We will also denote by S(x) the EM-simulated scattering parameters. For individual S-parameters, we will use the symbol Sjk(x,f) to denote the value of Sjk at the design x and frequency f. Finally, we denote by Ft = [Ft.0 Ft.1 … Ft.N]T the target vector of operating parameters with the first entry, Ft.0, being the operating frequency. The remaining entries denote the target values for other figures of interest, such as bandwidth, footprint area, power split ratio, material parameters of the substrate the circuit is to be implemented on, etc. At this point, it should be emphasized that the optimization technique introduced in this paper pertains to single-band structures. A generalization for multi-band systems will be discussed elsewhere.

The quality of design x with respect to the target vector Ft is quantified using the objective function U(x,Ft), which should be defined so that lower values of U correspond to better designs, i.e., those that meet the design specifications to the fuller extent. Having the objective function, the optimization task is formulated as

$${\boldsymbol{x}}^{*} = U^{*} ({\boldsymbol{F}}_{t} ) = \arg \mathop {\min }\limits_{{{\boldsymbol{x}} \in X}} U({\boldsymbol{x}},{\boldsymbol{F}}_{t} )$$
(1)

Here x* is the optimum design to be identified. The optimum solution is sought for in the design space X, which is normally delimited using the lower bounds l = [l1 … ln]T and the upper bound u = [u1 … un]T for the system parameters, i.e., lk ≤ xk ≤ uk, k = 1, …, n. In some cases, we also have additional constraints: inequality or equality ones. However, in the following, we assume for simplicity that the only geometrical constraints are those related to l and u.

Table 1 gathers a few exemplary design tasks for microwave components. Note that in the presented formulations, some of the design objectives are treated as constraints, and handled using a penalty function approach82. For more information about penalty functions see, e.g.,82,83.

Table 1 Selected examples of design tasks for passive microwave components.
Full size table

Concurrent parameter scaling

The physical size of conventional (transmission-line-based) microstrip components affects the guided wavelength1, 2. Consequently, approximate re-design of circuit parameters, aimed at relocating the operating frequency of the system, can be achieved through a concurrent dimension scaling, i.e., jointly increasing or decreasing the geometry parameters. In this work, we describe this process as a transformation MS(x,α), defined as

$$M_{S} ({\boldsymbol{x}},\alpha ) = M_{S} ([x_{1} \;...\;x_{n} ]^{T} ,\alpha ) = \left[ {\min (u_{1} ,\max (l_{1} ,\alpha x_{1} ))\;\;...\;\;\min (u_{n} ,\max (l_{n} ,\alpha x_{n} ))} \right]^{T}$$
(2)

Recall that l = [l1 … ln]T and u = [u1 … un]T stand for the lower and upper bounds for geometry parameters. The transformation MS is defined to ensure that the scaling process leaves the design within the assumed design space X.

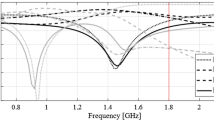
Let fa.0(x) be the actual center frequency of the circuit at hand at a certain design x. It can be extracted from the EM-simulated system responses, and defined depending on the particular type of a circuit. Typically, it would be the arithmetic average of the frequencies corresponding to the specific features of the system responses, e.g., the minima of the matching and isolation response for a coupler (cf. Figure 1a), or the frequencies determining the bandwidth for a broadband impedance transformer (cf. Figure 1b).

Figure 1
figure 1

Extracting approximate center frequency fa.0 of a circuit: (a) microwave coupler: fa.0 = (fm1 + fm2)/2, where fm1 and fm2 are the frequencies of the minima of |S11| and |S41|, respectively; (b) impedance matching transformer: fa.0 = (fm1 + fm2)/2, where fm1 and fm2 are the frequencies corresponding to the left- and right-hand-side edges of the –20 dB bandwidth of the circuit, respectively.

Full size image

Here, the concurrent dimension scaling is executed to re-align the operating frequency of the circuit with its target value Ft.0. The scaling coefficient α is computed as

$$\alpha = \min \left\{ {\alpha_{\max } ,\max \left\{ {\alpha_{\min } ,\frac{{f_{a.0} ({\boldsymbol{x}})}}{{F_{t.0} }}} \right\}} \right\}$$
(3)

where αmin and αmax are user-defined lower and upper bounds. These are introduced to avoid excessive scaling, which may be detrimental to the shape of the circuit characteristics. This is particularly important for compact structures, where interrelations between geometry parameters and electrical responses are rather complex. Concurrent scaling usually leads to response distortion if carried out using α which is significantly different from the unity. Figure 2 illustrates this for an exemplary microstrip coupler scaled using α = 1.2, 1.4, and 1.6. Typically, we would set αmin = 0.7, and αmax = 1/αmin, to be on a safe side.

Figure 2
figure 2

Concurrent dimension scaling of a compact branch-line coupler. EM-simulated S-parameters at: (a) initial design x, (b) design obtained as MS(x,1.2), (c) design obtained as MS(x,1.4), (d) design obtained as MS(x,1.6). Note increasing distortion of electrical characteristics, especially for α > 1.4.

Full size image

Concurrent scaling is followed by the extraction of the center frequency fa.0. If the extraction is impossible due to heavy distortion of the circuit characteristics, the scaling is repeated with an updated coefficient α/mα (for α > 1) or mαα (for α < 1), where mα is a control parameter, normally set to αmax1/2. If repeated scaling still fails, it is abandoned altogether in a current iteration of the optimization process, and the design is improved using local tuning (cf. Sect. "Intermittent local tuning") before attempting the scaling process again.

Intermittent local tuning

Local tuning is executed after applying the concurrent dimension scaling of Sect. "Concurrent parameter scaling". Its role is to improve the quality of the current design before launching the scaling again, or to finalize the optimization process if the current operating frequency fa.0 is sufficiently close to the target Ft.0. The tuning is realized as the iterative gradient-based algorithm with numerical derivatives84.

Given the design x(i) obtained using the scaling procedure (or the previous application of the tuning routine), the new candidate design x(i+1) is rendered as

$${\boldsymbol{x}}^{(i + 1)} = \arg \mathop {\min }\limits_{\substack{ {\boldsymbol{x}} \in X \\ ||{\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} || < d^{(i)} } } U_{L} ({\boldsymbol{x}},{\boldsymbol{F}}_{a} )$$
(4)

where the objective function UL is defined similarly as the original function U (cf. Sect. "Problem statement"); yet, it is calculated using the linear expansion model of the circuit characteristics

$${\boldsymbol{L}}^{(i)} ({\boldsymbol{x}}) = {\boldsymbol{S}}({\boldsymbol{x}}^{(i)} ) + {\boldsymbol{J}}_{S} ({\boldsymbol{x}}^{(i)} ) \cdot ({\boldsymbol{x}} - {\boldsymbol{x}}^{(i)} )$$
(5)

The Jacobian matrix JS is evaluated using finite differentiation85. The vector Fa is the current target objective vector, defined as

$${\boldsymbol{F}}_{a} = \left[ {f_{a.0} \;F_{t.1} \;...\;F_{t.N} } \right]^{T}$$
(6)

i.e., it coincides with Ft except the first entry, which is replaced by the existent operating frequency of the circuit extracted at the design x(i). As mentioned before, the tuning step (4), (5) aims at improving the design quality in terms of its performance parameters with respect to the current operating parameters, and prior to executing another round of concurrent scaling.

The size d(i) of the search region is adaptively adjusted contingent upon the gain ratio r = [U(x(i+1),Fa) – U(x(i),Fa)]/[UL(x(i+1),Fa) – UL(x(i),Fa)] (i.e., increased if r is close to 1, and decreased if it is close to zero84). Also, the tried design is retained if r > 0, i.e., the improvement of the original objective function U (computed using EM simulation data) has been observed.

If fa.0 is sufficiently close to Ft.0, concurrent scaling is no longer executed, and the tuning process (4), (5) is continued until convergence. Here, the termination condition is ||x(i+1) – x(i)||< εx (when converging in argument), or d(i) < εx (search region reduction); we set εx = 10–3.

Complete optimization procedure

This section puts together the entire optimization procedure involving the concurrent scaling of Sect. "Concurrent parameter scaling", and local tuning of Sect. "Intermittent local tuning". The major assumption here is that the initial design x(0) is of sufficient quality to allow successful scaling, i.e., so that the scaled circuit has identifiable operating frequency (cf. Sect. "Concurrent parameter scaling"). This assumption normally holds, because the purpose of the described procedure is circuit re-design. Otherwise, the execution of the procedure should be preceded by local optimization with respect to the current (actual) operational frequency of the circuit.

Table 2 gathers the control parameters of the presented algorithm. It should be noted that we only have three independent parameters αmin, εx, and dF0. None of these is critical. For example, setting αmin sufficiently close to unity is a safer option (to avoid abrupt design relocations), and the performance of the optimization process will be more or less invariant of the choice. The second parameter decides upon the resolution of the optimization process, whereas the last one can be set as a small fraction (e.g., five percent) of Ft.0. As a matter of fact, setting dF0 to anything less than half of the expected circuit bandwidth is normally sufficient to ensure adequate operation of the procedure.

Table 2 Proposed optimization procedure: Control parameters.
Full size table

Figure 3 presents the pseudocode of the re-design procedure. It can be noted that the concurrent scaling is only performed (Step 6) if the actual center frequency is too far from to the target, i.e., if |fa.0 – Ft.0|> dF0. If the scaling is unsuccessful, that is, the operating frequency cannon be extracted at the candidate design, it is repeated with the updated scaling coefficient αupdate (Step 8).

Figure 3
figure 3

Pseudocode of the proposed re-design algorithm with concurrent parameter scaling and intermittent local tuning.

Full size image

The next stage is local tuning (Step 11), which aims at improving the design quality in terms of the objective function value. At this stage, the circuit is optimized using the objective function U computed for the current center frequency fa.0. Local tuning is performed intermittently, following subsequent rounds of concurrent scaling. If the operating frequency of the circuit becomes sufficiently close to the target, concurrent scaling is no longer executed, and the final design is produced through local optimization. For additional explanation, Fig. 4 provides a flow diagram of the proposed algorithm.

Figure 4
figure 4

Flow diagram of the proposed re-design algorithm with concurrent parameter scaling and intermittent local tuning.

Full size image

Verification case studies

This section summarizes the results of the numerical experiments conducted to demonstrate the operation and performance of the introduced optimization technique. The experiments were designed to verify the capability of our procedure to handle circuit re-design over wide range of operating frequencies, with the initial design corresponding to the center frequency significantly different from the target one. Under such conditions, conventional local tuning normally fails, which was also corroborated by carrying out the appropriate optimization runs. A remark should be made that all of the benchmark microwave components have been already experimentally validated (both in the source papers86,87,88,89, as well as in our previous work, e.g.,81). Thus, the experimental validation of the optimized designs has not been provided, as being immaterial to the scope of the paper.

Verification circuits

Verification experiments have been performed using four compact microstrip couplers shown in Fig. 5. The computational models are implemented and simulated using the time-domain solver of CST Microwave Studio. The important data concerning the structures in Fig. 5 (material parameters of the substrate, independent and dependent geometry parameters, target operating frequencies, initial designs) have been shown in Fig. 6. For all verification structures, we aim at re-designing the circuit from the given initial design to the center frequency listed in the table as Ft.0. The design task is formulated as in Table 1 (second row). For Circuits I through III, the target power split ratio is 0 dB, whereas for Circuit IV, it is 3 dB. The target operating vector is Ft = [Ft.0 Ft.1 Ft.2]T, where Ft.0 = f0 is the center frequency, Ft.1 = K is the target power split ratio, whereas Ft.2 = εr is the substrate permittivity.

Figure 5
figure 5

Microstrip couplers employed as verification case studies to validate the re-design procedure proposed in this work: (a) Circuit I: miniaturized branch-line coupler (BLC)86, (b) Circuit II: rat-race coupler of transmission lines folded87, (c) Circuit III: BLC with microstrip cells88, (d) Circuit IV: compact BLC (non-equal power split)89.

Full size image
Figure 6
figure 6

Microwave couplers used for validating of the proposed re-design procedure.

Full size image

Observe that the proposed optimization method is a general one and may be successfully applied for design optimization of verification structures other than those presented in Fig. 5, such as, e.g., antenna structures. The sole limitation of the introduced optimization technique is that it is capable of handling single-band structures. A generalization for multi-band systems will be a focus of the future work.

Numerical results and discussion

The procedure of Sect. "Circuit re-design using concurrent scaling and intermittent local tuning" along with the conventional gradient-based search84 have been applied to optimization of Circuits I, II, III, and IV. In all cases, local tuning starting from the initial designs listed in Table 3 failed, i.e., the algorithm was unable to identify the designs featuring the required operating frequency. On the other hand, the proposed procedure turned successful for all circuits. Table 3 provides information about the final designs, as well as the actual operating conditions therein.

Table 3 Optimization results for Circuits I through IV.
Full size table

It can be observed that both the operational frequency as well as power split ratio are well aligned with the targets. The misalignment of the center frequency is less than one percent, whereas the power division error is below or equal to 0.15 dB (it is much lower for Circuits III and IV). It should also be emphasized that the latter can be further reduced by increasing the penalty coefficient associated with the power-split-related penalty function (at the expense of slightly misaligned center frequency). At the same time, the circuit matching and isolation is also well controlled (typically, |S11| and |S41| are well below –20 dB at the target frequency Ft.0). Finally, computational efficiency of our algorithm is excellent. The cost of the optimization process corresponds to only 104, 130, 61, and 135 EM simulations of Circuits I through IV, respectively (the average of 107). This corresponds to the typical cost of local gradient-based tuning. These expenses are low given significant relocation of the designs, normally achievable with the use of global search procedures.

A comment should be made concerning the scalability of the presented method. Based on the presented evidence of four test cases of the dimensionality ten, six, nine, and twelve parameters, as well as the cost of design optimization procedure (104, 130, 61 and 135 EM analyses per design), it might be estimated that the computational expenses are around ten times larger than the number of the design variables, which can be considered as low. In general, our procedure exhibits complexity typical for gradient-based algorithms employing first-order sensitivities, i.e., the dependence of the computational cost on the number of design variables is slightly higher than linear. In other words, the cost of the proposed procedure is comparable to that of the local optimization routines, and, as such, may be considered as practically acceptable, even for problems described by as high as twenty parameters.

Figures 7, 8, 9 and 10 show the circuit responses at the initial and final designs, as well as the responses at the designs obtained by the first round of concurrent scaling, along with the evolution of the current operational frequency of the coupler throughout the optimization run. It should be emphasized that despite large discrepancies between the operating frequency at the initial designs and the targets, the proposed algorithm ensures good alignment of fa.0 and Ft.0 after just five iterations. The remaining computational budget is utilized to improve the objective function value at Ft.0. Finally, it should also be mentioned that the results are consistent for all considered circuits. On the one hand, this demonstrates the overall efficacy of the presented framework. On the other hand, it shows that problem-specific tuning of the control parameters (cf. Table 2) is not necessary.

Figure 7
figure 7

Optimization results for Circuit I: (a) EM-evaluated S-parameters at the optimized (black) and initial design (grey); (b) evolution of the operating frequency fa.0; (c) S-parameters upon first concurrent scaling (black) versus responses at the initial design (grey).

Full size image
Figure 8
figure 8

Optimization results for Circuit II: (a) EM-evaluated S-parameters at the optimized (black) and initial design (grey); (b) evolution of the operating frequency fa.0; (c) S-parameters upon first concurrent scaling (black) versus responses at the initial design (grey).

Full size image
Figure 9
figure 9

Optimization results for Circuit III: (a) EM-evaluated S-parameters at the optimized (black) and initial design (grey); (b) evolution of the operating frequency fa.0; (c) S-parameters upon first concurrent scaling (black) versus responses at the initial design (grey).

Full size image
Figure 10
figure 10

Optimization results for Circuit IV: (a) EM-evaluated S-parameters at the optimized (black) and initial design (grey); (b) evolution of the operating frequency fa.0; (c) S-parameters upon first concurrent scaling (black) versus responses at the initial design (grey).

Full size image

The procedure introduced in this work has been developed for handling single-band structures. Its generalization for multi-band circuits poses certain challenges, because concurrent parameter scaling as described in Sect. "Concurrent parameter scaling" would be inadequate here, due to synchronized relocation of the operating bands it would incur. The aim of the forthcoming work will be to generalize this stage of the process to allow “orthogonal” scaling of geometry variables in order to enable independent control over several center frequencies.

Conclusion

The paper outlined a novel technique for reliable re-design of microwave passives over broad ranges of operating frequencies. Our methodology utilizes a scope-controlled concurrent scaling of geometry parameters interleaved with local tuning. The former enables large design relocations at minimum computational expenses, whereas the latter allows for a continuous improvement of the design with regard to the assumed performance figures. Both mechanisms have been incorporated into an optimization framework controlled by a few user-defined and easily adjustable parameters. Comprehensive verification involving four compact microstip couplers demonstrated superior efficacy of the procedure, both in terms of reliability, and computational efficiency. In particular, it permits a precise control of the center frequencies and other electrical performance figures (here, a power division ratio), while being able to re-design the structures to operating frequencies distant from those at the initial designs. The cost of the optimization procedure slightly exceeds one hundred EM evaluations of the device under design, thus, it is equivalent to the expenses associated with a local gradient-based search. At the same time, straightforward local optimization failed for all test circuits, which indicates, that—for the considered design scenarios—global search routines would normally be necessary.

The presented technique has been developed to handle single-band circuits, which is a practical limitation as contemporary applications often require dual-, triple-, or even quad-band structures. Generalization of the method for multi-band systems poses considerable challenges. In particular, simple concurrent parameter scaling results in more-or-less synchronized adjustment of the operating bands. Enabling independent control requires more sophisticated strategies, involving a number of scaling directions, which are “orthogonal” to each other in terms of their effects on particular operating frequencies. The focus of the future work will be the conceptual development and implementation of the respective design framework, as well as its verification using real-world test cases.