An ultra-high gain boost converter with low switching stress for integrated multi-energy storage systems

Abstract

In this paper, a high-gain low-switching-stress coupled-inductor with high voltage step-up voltage multiplier cells quadratic boost converter (VMC-QBC) is proposed. The turn ratio of the coupled inductors and the switch duty cycle increase the dynamic gain, and the two degrees of freedom adjustment and modularity of the voltage multiplier cells (VMC) make the structure more flexible. The use of the same drive signal for both switches makes control easier. While achieving multi-stage boosting and multiplication boosting from low to medium duty cycle, the passive clamping circuit absorbs the energy leaked by the coupled inductor, thus reducing the stress on the switching tube and alleviating the diode reverse recovery problem. A non-ideal model with parasitic parameters is developed to analyse the real voltage gain and the converter losses to give design guidelines. A 300 W prototype is designed and tested. The state space model of the converter is established and the working principle is analysed. Compared to other high-gain quadratic boost converters, the proposed converter has continuous input current, common ground characteristics, and high voltage gain at low to medium duty cycles to accommodate integrated multi-energy storage systems.

Introduction

With the decreasing of non-renewable energy sources such as oil, coal, and natural gas, and the increasing warming of global climate, it has become a global consensus to replace these non-renewable energies with renewable new energy sources to achieve carbon peak and carbon neutrality, thereby suppressing global warming^1,2,3. Traditional fossil fuel power stations have a low efficiency of about 30% and consume about 70% of the energy in boilers and turbine generators. Meanwhile, a lot of carbon dioxide is emitted during combustion, which will lead to global warming.

Renewable energy sources (hydrogen fuel cells, photovoltaics) have become the main alternatives to traditional energy sources due to their sustainability, low pollution, and low noise. Hydrogen fuel cells can directly convert chemical energy into electrical energy through electrochemical reactions^4,5,6. The product of hydrogen fuel cells is water, which has no impact on the environment and can be directly discharged. Therefore hydrogen fuel cells have high efficiency and low emission. However when hydrogen fuel cells are directly used, there are several problems: the output voltage is at low level (10–50 V), and the output characteristic is soft, which means that the output voltage will decrease with the increase of the output current^7,8. When hydrogen fuel cells are used for grid connected power generation or as power sources for electric vehicles, the required DC voltage (usually higher than 250 V) is much higher than the power generation voltage of fuel cells. Although hydrogen fuel cells cascading can raise this voltage level and realize high voltage output, the reliability of the whole hydrogen fuel cell power generation system is reduced and the overall structural complexity and cost is increased.

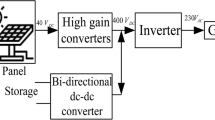
Photovoltaic power generation converts light energy into electricity through the photovoltaic effect of semiconductor materials, in which the output voltage of a single solar panel is about (10–20 V). Therefore, the series connection of multiple solar panels is required to superimpose the voltage for output. Photovoltaic energy storage systems are widely recognized for their sustainability and low cost, in addition, photovoltaic energy storage systems can be used to solve the problem of power supply in different geographic environments and climates, especially in remote areas^9,10. Lithium batteries are commonly used in the field of electric vehicles because of their small size, high energy density, high monomer voltage, and long cycle life¹¹. Supercapacitors store and release energy through the adsorption and release of charge on the dielectric, because of the high power density of supercapacitors, the ability to fast charge and discharge, and the ability to store large amounts of energy and release large currents, they are often used in electric vehicles with frequent starts and stops, especially plug-in hybrid electric vehicles¹². From the above two renewable energy generation devices and two electrical energy storage devices, an integrated multi-energy energy storage system can be constructed, as shown in Fig. 1. It shows the application areas of the power supply system with a high gain step-up DC-DC converter as the boost unit, which includes photovoltaic energy system, Hydrogen fuel cell power system, Li-ion batteries energy storage, and supercapacitor energy storage, etc. Renewable energy and energy storage devices all have low output voltages Therefore a voltage step-up converter is required to convert the low voltage power from these into high voltage used by consumers^13,14,15.

Fig. 1

Integrated multi-energy storage systems. (In the integrated multi-energy storage system contains photovoltaic power generation energy system, hydrogen fuel cell energy system, lithium battery energy system, and supercapacitor energy system. They generate a low voltage level after their respective generators, so a high gain DC-DC converter is needed to boost the voltage level and connect to the DC bus.).

A large number of techniques such as utilizing staggered parallel connection^16,17, coupled inductors (CL)^18,19,20], switched capacitors (SC)²¹, switched inductors (SI)²², and cascading^23,24,25 are commonly proposed to achieve high step-up voltage gain, therefore a lot of new high gain converters have been proposed.

In¹⁶, a two coupled inductors interleaving based quadratic converter is proposed. This converter greatly reduces the input current ripple in the structure, reduces the current stress of the components, and improves the device lifetime. In¹⁸, scalable diode-capacitor voltage multiplier cells are proposed to realize the zero-voltage switching-on conditions of the switches with high voltage gain and efficiency, but excessive constituent elements increase the overall cost and converter size and reduce the power density. In¹⁹, a quadratic converter based on the combination of coupled inductor and voltage doubler is proposed to realize zero-current switching-off of the output diode and to increase the overall efficiency by absorbing the leakage inductance through the active clamping circuit, but the high switching stress leads to the reduced reliability and increased cost. In²¹, the proposed converter with switched capacitor technology still has a high voltage gain at the low duty cycle and reduces the losses of circuit components and semiconductor devices, but the efficiency and output power are low and only suitable for low power devices. In²², a switched inductor technique is utilized to construct a high step-up boost converter with fewer components and a simple structure, but the voltage gain is significantly reduced at low voltage inputs with low efficiency due to the hard-switching work condition. The quadratic boost is one of the basic high step-up converters and can obtain high voltage gain due to its unique quadratic structure, but low efficiency, high duty cycle, and increased cost at ultra-high voltage gain. The voltage multiplier cells (VMC), which consist only of diodes and capacitors without semiconductor switches, are one of the most optimal ways to increase the voltage gain of the converter with great positional flexibility and easy modularization. In addition, it offers the advantages of increased efficiency and reduced component voltage stress. In addition to these converters, some new converters utilize a combination of these techniques further to improve the voltage gain^26,27,28,29. These converters have a high voltage gain, but due to the large forward voltage drop of the diode itself, coupled with the lack of optimization of switching tube losses, resulting in lower efficiency, in order to obtain a sufficiently high voltage gain, it is necessary to use more cascade units, the cost and the overall complexity of the circuit structure will also increase.

To further improve the voltage gain of the DC-DC converter and reduce the switching stress, a new high voltage step-up voltage multiplier cells quadratic boost converter (VMC-QBC) is proposed in this paper. The proposed converter combines the quadratic, coupled inductor (CL), and VMC techniques to achieve ultra-high voltage gain and low switching stress even at the low duty cycle. The VMC provides fixed static gain, and the duty cycle and coupled inductor turns ratio enhances dynamic gain for flexible gain adjustment. The low input current ripple and low switching stress extend the converter’s life. The energy leaked from the leakage inductor is also absorbed during the multistage boost to alleviate the diode reverse recovery problem and reduce the switching voltage stress, which improves the overall efficiency. The stability of the system is verified by building a state-space model of the converter, the overall loss and real voltage gain are calculated using a non-ideal circuit model containing parasitic parameters, and the output dynamic characteristics are verified by varying the input voltage and load.

Proposed converter: description and analysis

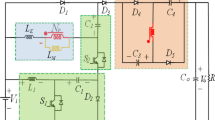
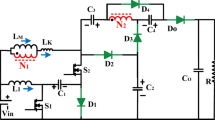
The proposed converter consists of two power switches S₁ and S₂, two energy storage inductors L₁ and L₂, two storage capacitors C₁ and C₂, a voltage multiplier unit consisting of C_o2, C_o3, and C_o4, three diodes D_o2, D_o3, and D_o4, and a coupled inductor consisted of N₁ and N₂. It can be roughly divided into the quadratic boost converter (QBC), and the voltage multiplier cells (VMC). The simplified circuit model of the proposed converter is shown in Fig. 2. The operating waveforms of the proposed converter. is shown in Fig. 3.

Fig. 2

Structure of the proposed converter. Structure of the proposed converter. (The proposed converter consists of a quadratic boost unit in the front stage and a VMC in the back stage. There are two inductors, six capacitors, five diodes, and two switches).

Operation analysis

The proposed converter has four operating modes, mode I-mode III is in continuous conduction mode (CCM), and mode IV is a special kind of CCM. the current paths in this mode are L₂, C₂, L_m, and V_in, thus forming a kind of self-circulating mod, but no matter how much the inductance values of L₁ and L₂ are reduced, no current to 0 occurs, so it is called quasi- discontinuous conduction mode (DCM).

Fig. 3

Operating waveforms Operating waveforms (Contains switch drive, current and voltage waveforms, inductor current waveforms, diode voltage and current waveforms, current waveforms for leakage and excitation inductance).

Fig. 4

The proposed converter (a) Mode I (b) Mode II (c) Mode III. The proposed converter (a) Mode I (b) Mode II (c) Mode III. (Give the different operations of the proposed converter within a perimeter apparatus).

Mode -I operation (Fig. 4a, t0-t1): When both switches S₁ and S₂ are on, continuity diode D₁, output diodes D_o1, and D_o4 are off and the converter is in the charging mode. The input voltage source V_in charges inductor L₁; capacitor C₁ and V_in together charge inductor L₂. Meanwhile, the magnetizing inductance L_m is energized by capacitors C₁ and C₂, and the output capacitors C_o1 and C_o2 energize the load, ignoring the voltage drop across the leakage inductance L_k. The equation for the voltage gain of the converter and the voltage stresses on the components of the converter are easily derived from the principle of volt-second balance of inductance.

The expression in mode I is obtained according to Kirchhoff’s Voltage Law (KVL) as:

$$\:\left\{\begin{array}{l}{V}_{L1}={V}_{in}\\\:{V}_{L2}={V}_{in}+{V}_{C1}\\\:{V}_{Lm}={V}_{C1}+{V}_{C2}\\\:{V}_{o}={V}_{Co1}+{V}_{Co2}\end{array}\right.$$

(1)

Mode -II Operation (Fig. 4b, t1-t2): When both switches S₁ and S₂ turn off, diodes D_o2 and D_o3 are off and the converter is in output mode. The energy stored in L₁ charges C₁, inductor L₂ charges capacitor C₂, and provides energy to capacitors C_o1, C_o3, and C_o4 through output diode D_o1. At the same time, the coupled inductor N₁ transfers energy to N₂, and the energy in N₂ transfers energy to capacitor C_o2 and the load together with capacitors C_o3 and C_o4. Ignoring the voltage drop across the leakage inductor L_k, the ratio between the primary and secondary of the coupled inductor will be 1: n. It is worth noting that the energy leaked from the coupling inductor is transferred to C_o1 via the output diode D_o1 and then supplied to the load, reducing switching stress and suppressing voltage spikes of the switches. The expression in this mode is:

$$\:\left\{\begin{array}{l}{V}_{Lm}={V}_{Co1}-{V}_{C2}\\\:{V}_{Co2}={V}_{n2}+{V}_{Co3}+{V}_{Co4}\\\:{V}_{Co3}={V}_{Co4}=\frac{1}{n}\left({V}_{C1}+{V}_{C2}\right)\end{array}\right.$$

(2)

Mode -III Operation (Fig. 4c, t2-t3): The diode D_o1 is turned off in the CCM state in mode III, and at this time it can be divided into CCM and quasi-DCM modes according to the current state of the inductor L₂, and the equivalent circuit diagram at this time is shown in Fig. 4c.

Mode -IV Operation (Fig. 4c, t3-t4): The off state of L₂ in quasi-DCM mode occurs when the switching signal is turned off, at this time the current path is a self-circulating state, and due to the large inductance value of L_m, the current in it can be equated to a constant current source, so no matter how the inductance value of L₂ becomes smaller, the current passing through it can not be reduced to 0. Therefore mode IV is a quasi-DCM state. the expression for the current of L₂ is shown in Eq. 3.

$$\left\{ {\begin{array}{*{20}{l}} {\frac{{{d_{i{L_2}}}}}{{{d_{t0 - t1}}}}=\frac{{{V_{in}}+{V_{C1}}}}{{{L_2}}}} \\ {\frac{{{d_{i{L_2}}}}}{{{d_{t1 - t2}}}}=\frac{{{V_{in}} - {V_{Lm}} - {V_{C2}}}}{{{L_2}}}} \end{array}} \right.$$

(3)

The quasi-DCM mode is generated when the L_m current is equal to the L₂ current, Eq. 4 can be obtained:

$$\:{I}_{Lm}+\frac{{V}_{in}+{V}_{C1}}{{L}_{2}}DT+\frac{{V}_{in}-{V}_{Lm}-{V}_{C2}}{{L}_{2}}t={I}_{Lm}$$

(4)

$$\:t=\frac{{V}_{in}+{V}_{C1}}{{V}_{in}-{V}_{Lm}-{V}_{C2}}DT$$

(5)

It can be obtained that the quasi-DCM mode exists at t < 1-DT, and the converter is in mode III when t > 1-DT, so the appearance of quasi-DCM is related to the value of L₂ inductance, is shown in Eq. 5.

Voltage stress analysis

This section describes the voltage stresses of components and the voltage gains of the converter. The following equations can be obtained by applying the volt-second equilibrium law to the inductors L₁ and L₂:

$$\:\left\{\begin{array}{l}{\int\:}_{0}^{DT}{V}_{in}\:dt+{\int\:}_{DT}^{T}{V}_{in}-{V}_{C1}\:dt=0\\\:{\int\:}_{0}^{DT}{V}_{in}+{V}_{C1}\:dt+{\int\:}_{DT}^{T}{V}_{in}-{V}_{Co1}\:dt=0\end{array}\right.$$

(6)

Where D is the duty cycle of the switching, T is the switching cycle, V_C2=V_in.

Based on Eq. (6), the steady-state analysis results of the proposed converter in the CCM mode are:

$$\:\left\{\begin{array}{l}{V}_{C1}=\frac{{V}_{in}}{1-D}\\\:{V}_{Lm}=\frac{D{V}_{in}(2-D)}{\left(1-D\right)^{2}}\\\:{V}_{Co1}=\frac{{V}_{in}}{\left(1-D\right)^{2}}\\\:{V}_{Co2}=\frac{n{V}_{in}\left(6-4D+{\text{D}}^{2}\right)}{{\left(1-D\right)}^{2}}\\\:{V}_{Co4}={V}_{Co3}=\frac{{nV}_{in}(2-D)}{\left(1-D\right)}\end{array}\right.$$

(7)

The voltage gain of the proposed converter can be derived from Eq. 7 as:

$$\:M=\frac{{V}_{o}}{{V}_{in}}=\frac{1+n(2-D)^{2}}{\left(1-D\right)^{2}}$$

(8)

From the above equations, it can be seen that the voltage gain is not only related to the duty cycle of the power switching devices but also to the coupled inductor turn of the coupled inductor.

The voltage gain by considering the leakage inductance influent is:

$$\:M=\frac{{V}_{o}}{{V}_{in}}=\frac{1+kn(2-D)^{2}}{\left(1-D\right)^{2}}$$

(9)

Where $\:\:k=\frac{{L}_{m}}{{L}_{k}+{L}_{m}}$

The switching semiconductor devices will be subjected to a reverse turn-off voltage when it is turned off. The maximum reverse turn-off voltage to which the device is subjected during the switching cycle is the voltage stress on the device. Since all the diodes are reverse biased during mode I, the voltage stress on the diodes can be obtained as:

$$\:\left\{\begin{array}{l}{V}_{D1}={V}_{C1}=\frac{{V}_{in}}{1-D}\\\:{V}_{Do1}={V}_{C1}+{V}_{Co1}=\frac{(2{-D)V}_{in}}{{\left(1-D\right)}^{2}}\\\:{V}_{Do2}={V}_{Do3}={V}_{Do4}=\frac{2n(2{-D)V}_{in}}{(1-D)}\end{array}\right.$$

(10)

In mode II, the power switches are in disconnected state, so the voltage stress can withstand as:

$$\:\left\{\begin{array}{l}{V}_{S1}={V}_{C1}=\frac{{V}_{in}}{1-D}\\\:{V}_{S2}={V}_{Co1}=\frac{{V}_{in}}{(1-D)^{2}}\end{array}\right.$$

(11)

The variation of switching voltage stress due to the variation of coupled inductor turns ratio is shown in Fig. 5.

Fig. 5

Normalized voltage stress of (a) S₁, and (b) S₂ with D = 0.5. Normalized voltage stress of (a) S₁, and (b) S₂ with D = 0.5. (Three-dimensional pattern of S₁ and S₂ with respect to coupled inductor turns and switching stress at 0.5 duty cycle).

Current stress analysis

The average current stress of the switching devices is the average value of the current in one cycle. To facilitate the current stress analysis, the power loss of the proposed converter and the current ripple of the inductor are ignored. At this time, the actual state of inductance L_k, L_m does not meet the requirements of continuous operation in CCM mode, so the root-mean-square (rms) values of the excitation inductance L_m and the leakage inductance L_k are selected for calculation. The application of the principle of the ansatz equilibrium to capacitance C₁ and C_o2 yields the current stress of the circuit elements in CCM mode as:

$$\:\left\{\begin{array}{l}{\int\:}_{0}^{DT}{(-I}_{Lm}+{I}_{L2})dt+{\int\:}_{DT}^{T}{I}_{L1}\:dt=0\\\:{\int\:}_{0}^{DT}-{I}_{o}\:dt+{\int\:}_{DT}^{T}\frac{{L}_{m\left(rms\right)}-{I}_{Lk\left(rms\right)}}{n}\:dt=0\end{array}\right.$$

(12)

Based on the fact that the output power is approximately equal to the input power in the CCM state, it can be obtained as:

$$\:{I}_{L1}+{I}_{L2}={I}_{o}M$$

(13)

According to the above equations, the average current stress of inductors L₁, L₂ and L_m can be obtained as:

$$\:\left\{\begin{array}{l}{I}_{L1}=\frac{D\left({I}_{Lm}+{I}_{L2}\right)}{1-D}\\\:{I}_{L2}=\frac{D{I}_{Lm}}{1-D}\\\:{I}_{Lm}=n{I}_{o}\end{array}\right.$$

(14)

Since the voltage multiplier cells (VMC) current magnitude is determined by I_Lm, and also, L_m and I_o are connected through a transformer, the relationship conforms to that of transformer ratio. Therefore, I_lm=nI_o is valid regardless of the mode in which the converter is operated.

When switching transistors S₁ and S₂ are in the conduction state, the peak current stress and average current of the switching transistor are:

$$\:\left\{\begin{array}{l}{I}_{S1}={I}_{L2}+{I}_{Lk\left(rms\right)}\\\:{I}_{S2}={I}_{L2}+{I}_{S1}\\\:{I}_{S1\_avg}=D({I}_{L2}+{I}_{Lk\left(rms\right)})\\\:{I}_{S{2\_}_{avg}}=D({I}_{L2}+{I}_{S1})\end{array}\right.$$

(15)

The output voltage of the proposed converter is composed of V_Co1 and V_Co2, assuming that the average current of C_o2 is equal to the average current of N₂. The coupled inductor primary and secondary turn ratio is 1: n. When the converter is in the steady state, the following diode current stress can be derived:

$$\:\left\{\begin{array}{l}{I}_{D1}=\left(1-D\right){I}_{L1}\\\:{I}_{Do1}={I}_{Do4}={I}_{o}\\\:{I}_{Do2}={I}_{Do3}=\frac{{I}_{Lm\left(rms\right)}-{I}_{Lk\left(rms\right)}}{2n}\end{array}\right.$$

(16)

Converter losses analysis and comparison

Real voltage gain

In this section, the effects of component parasitic parameters on output voltage and efficiency are analyzed by building a non-ideal loss model of the proposed converter. Figure 6 shows the converter circuit with parasitic parameters, where the inductor equivalent series resistance (ESR) is r_L1, r_L2, switch on resistance r_S1, r_S2, diode forward bias voltage drop V_D1, V_Do1, V_Do2, V_Do3, V_Do4, diode internal resistance r_D1, r_Do1, r_Do2, r_Do3, r_Do4, diode internal resistance capacitor series resistance r_C1, r_C2, r_Co1, r_Co2, r_Co3, r_Co4.

The voltage gain of the proposed converter in the actual operating state is similar to the working principle of the non-ideal voltage gain containing parasitic resistive losses, and according to the equivalent model of the circuit containing parasitic parameters established in Fig. 6, the real voltage gain in the non-ideal state can be derived as Eqs. (17) and (18):

Fig. 6

Non-ideal loss modelling of converters (By establishing a non-ideal model of the proposed converter containing parasitic parameters, the parasitic parameters of each component are analyzed and the voltage gain with parasitic parameters is given).

$$\:M=\frac{{V}_{o}}{{V}_{in}}=\frac{3}{1+[a{r}_{L2}+b\left({r}_{S1}+{r}_{C1}\right)+c{r}_{S2}+d{r}_{L2}+e{(r}_{C1}+{r}_{D1}+\frac{{r}_{L1}}{1-D})+f{r}_{Do2}+j{r}_{Co3}+h{r}_{Co2}+i{r}_{Do4}+\beta\:]\frac{1}{R}}$$

(17)

$$ \left\{ {\begin{array}{*{20}l} {a = \frac{{1 - n}}{{1 - D}}} \hfill & {f = \frac{{3 - 5D + 2D^{2} }}{{\left( {1 - D} \right)}}} \hfill \\ {b = \frac{{3\left( {1 - n^{2} } \right)}}{{2\left( {1 - D} \right)}}} \hfill & {j = \frac{{3 - 4D}}{{2\left( {1 - D} \right)}}} \hfill \\ {c = \frac{{1 - n + D - 2n^{2} D + n^{2} D^{2} }}{{2\left( {1 - D} \right)}}} \hfill & {h = \frac{D}{{1 - D}}} \hfill \\ {d = \frac{{3\left( {1 - n} \right)}}{{2\left( {1 - D} \right)}}} \hfill & {\alpha = 2V_{{Do2}} \left( {1 - D} \right) + V_{{Do4}} - V_{{Do1}} \left( {1 - D} \right) - V_{{D1}} \left( {1 - D} \right)} \hfill \\ {e = \frac{{D\left( {1 - n^{2} } \right)}}{{2\left( {1 - D} \right)}}} \hfill & {\beta = \frac{\alpha }{{V_{o} }}} \hfill \\ \end{array} } \right. $$

(18)

Losses analysis

As it can be concluded from the non-ideal model containing parasitic resistances described in the previous section, the presence of parasitic resistances affects the efficiency and performance of the converter, and therefore the power losses in the converter need to be considered and calculated. The power loss of the converter mainly exists in the including switching transistor losses, capacitance losses, magnetic component (inductance and coupled inductance) losses, and diode losses. This section will analyze each of these losses and explain how they are calculated. The parasitic parameters in this section are shown in Table 1.

The switching loss is divided into conduction loss and switching loss. The conduction loss is mainly generated by the loss flowing through the switch parasitic resistance in the switch conduction state. The switching loss is generated by the switch voltage drop V_S1 and the switch current I_S1. Equation 19 can be obtained.

$$\:\left\{\begin{array}{l}{P}_{SC}={R}_{dS1\left(on\right)}{I}_{S1\left(rms\right)}^{2}+{R}_{dS2\left(on\right)}{I}_{S2\left(rms\right)}^{2}\\\:{P}_{SW}=\frac{1}{2}{V}_{S1\left(on\right)}{I}_{S1\left(\text{r}\text{m}\text{s}\right)}({t}_{on}+{t}_{off}){f}_{s}+\frac{1}{2}{V}_{S2\left(on\right)}{I}_{S2\left(\text{r}\text{m}\text{s}\right)}({t}_{on}+{t}_{off}){f}_{s}\end{array}\right.$$

(19)

Where P_SC is the conduction loss, P_SW is the switch conduction state, Rds1(on) is the S₁ on-resistance; Is1(rms) is the S₁ switching current; Rds2(on) is the S₂ on-resistance; Is2(rms) is the S₂ switching current. V_S1(on) is the voltage of the switch, I_S1(rms) is the current flowing through the switch, the switch on and off times are t_on, t_off, f_s is the switching frequency.

There is a fixed parasitic resistance in the capacitor that cannot be eliminated, so there is a power loss when current passes through the parasitic resistance, calculated as follows:

$$\:{P}_{C}={R}_{C}{I}_{C\left(rms\right)}^{2}$$

(20)

Where P_C is the capacitor loss; R_C is the capacitor impedance; I_C(rms) is the capacitor current.

Magnetic component loss consists of core loss and its inductive loss, inductive power loss is calculated as follows:

The loss of magnetic components consists of magnetic loss and copper loss. Magnetic loss is mainly the loss generated by the core material, which is a fixed loss and only related to the core material. Copper loss is the current flowing through the coil and the loss generated by the parasitic resistance of the copper wire. Specifically calculated as Eqs. 21, 22

$$\:{P}_{CL}={R}_{L1}{I}_{L1\left(avg\right)}^{2}+{R}_{L2}{I}_{L2\left(avg\right)}^{2}$$

(21)

Where P_L for inductive loss; R_L1 for L₁ reactance; I_L1(avg) for inductive L₁ average current; R_L2 for L₂ reactance; I_L2(avg) for inductive L₂ average current. The core power loss is:

$$ P_{M} = K_{{Fe}} f_{s} \left( {\frac{{\Delta B}}{2}} \right)^{\alpha } V_{e} $$

(22)

Where P_M for magnetic loss, K_Fe and α are determined by the core model and material; ∆B is related to the current ripple of the inductor; V_e is the volume of the core, f_s is the switching frequency.

The power loss of the diode is generated by the current flowing through the diode on-resistance, and the conduction loss is generated by the diode forward voltage drop and the average current, the losses of all diodes in the proposed converter are calculated by Eq. 20, which is given as follows.

$$\:{P}_{D}={I}_{D\left(avg\right)}{V}_{f}+{R}_{D}{I}_{D\left(rms\right)}^{2}$$

(23)

Where I_D(avg) is the average diode current, V_f is the diode forward voltage drop, R_D is the diode on-resistance, I_D(rms) is the diode rms current.

In order to analyze the losses of the converter more intuitively, detailed equations for the losses of each device are given in this section. Finally, the total power loss and efficiency of the converter are given. As shown in Eqs. 24, 25.

$$\:{P}_{T}={P}_{SC}+{P}_{SW}+{P}_{C}+{P}_{CL}+{P}_{M}+{P}_{D}$$

(24)

$$\:\eta\:=\frac{{P}_{O}}{{P}_{O}+{P}_{T}}\times\:100\text{\%}$$

(25)

State space representation

This section gives the state space model of the proposed converter. Where the state variables of the converter include: inductor currents (iL₁(t), iL₂(t), iL_m(t)),capacitor voltages (v_C1(t), v_C2(t), v_Co1(t), v_Co2(t), v_Co3(t)). The input variable is the input voltage V_in(t).

The differential equation can be obtained by modal I analysis as:

$$\:\left\{\begin{array}{l}{L}_{1}\frac{d{i}_{L1}\left(t\right)}{dt}={V}_{in}\\\:{L}_{2}\frac{d{i}_{L2}\left(t\right)}{dt}={V}_{in}+{v}_{C1}\left(t\right)\\\:{L}_{m}\frac{d{i}_{Lm}\left(t\right)}{dt}={v}_{C1}\left(t\right)+{v}_{C2}\left(t\right)\\\:{L}_{k}\frac{d{i}_{Lk}\left(t\right)}{dt}={v}_{C1}\left(t\right)+{v}_{C2}\left(t\right)-{v}_{Co3}\left(t\right)\\\:{C}_{1}\frac{d{v}_{C1}\left(t\right)}{dt}=-{i}_{L2}\left(t\right)-{i}_{Lk}\left(t\right)\\\:{C}_{2}\frac{d{v}_{C2}\left(t\right)}{dt}=-{i}_{Lk}\left(t\right)\\\:{{C}_{o}}_{1}\frac{d{v}_{Co1}\left(t\right)}{dt}=-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{2}\frac{d{v}_{Co2}\left(t\right)}{dt}=-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{3}\frac{d{v}_{Co3}\left(t\right)}{dt}=\frac{{i}_{Lk}\left(t\right)-{i}_{Lm}\left(t\right)}{2n}\end{array}\right.$$

(26)

The differential equation can be obtained by modal II analysis as:

$$\:\left\{\begin{array}{l}{L}_{1}\frac{d{i}_{L1}\left(t\right)}{dt}={V}_{in}-{v}_{C1}\left(t\right)\\\:{L}_{2}\frac{d{i}_{L2}\left(t\right)}{dt}={V}_{in}-{v}_{Co1}\left(t\right)\\\:{L}_{m}\frac{d{i}_{Lm}\left(t\right)}{dt}=-\frac{{v}_{Co2}\left(t\right)-2{v}_{Co3}\left(t\right)}{n}\\\:{L}_{k}\frac{d{i}_{Lk}\left(t\right)}{dt}={v}_{C2}\left(t\right)-{v}_{Co1}\left(t\right)+\frac{{v}_{Co2}\left(t\right)-2{v}_{Co3}\left(t\right)}{n}\\\:{C}_{1}\frac{d{v}_{C1}\left(t\right)}{dt}={i}_{L1}\left(t\right)\\\:{C}_{2}\frac{d{v}_{C2}\left(t\right)}{dt}=-{i}_{Lk}\left(t\right)\\\:{{C}_{o}}_{1}\frac{d{v}_{Co1}\left(t\right)}{dt}={i}_{L2}\left(t\right)+{i}_{Lk}\left(t\right)-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{2}\frac{d{v}_{Co2}\left(t\right)}{dt}=\frac{{i}_{Lm}\left(t\right)-{i}_{Lk}\left(t\right)}{n}-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{3}\frac{d{v}_{Co3}\left(t\right)}{dt}=\frac{{i}_{Lk}\left(t\right)-{i}_{Lm}\left(t\right)}{n}\end{array}\right.$$

(27)

The differential equation can be obtained by modal III analysis as:

$$\:\left\{\begin{array}{l}{L}_{1}\frac{d{i}_{L1}\left(t\right)}{dt}={V}_{in}-{v}_{C1}\left(t\right)\\\:({L}_{2}+{L}_{k})\frac{d{i}_{L2}\left(t\right)}{dt}=-({L}_{2}+{L}_{k})\frac{d{i}_{Lk}\left(t\right)}{dt}={V}_{in}-{v}_{C2}\left(t\right)-\frac{{v}_{Co3}\left(t\right)}{n}-\frac{{v}_{Co2}\left(t\right)-2{v}_{Co3}\left(t\right)}{n}\\\:{L}_{m}\frac{d{i}_{Lm}\left(t\right)}{dt}=-\frac{{v}_{Co2}\left(t\right)-2{v}_{Co3}\left(t\right)}{n}\\\:{C}_{1}\frac{d{v}_{C1}\left(t\right)}{dt}={i}_{L1}\left(t\right)\\\:{C}_{2}\frac{d{v}_{C2}\left(t\right)}{dt}=-{i}_{Lk}\left(t\right)\\\:{{C}_{o}}_{1}\frac{d{v}_{Co1}\left(t\right)}{dt}=-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{2}\frac{d{v}_{Co2}\left(t\right)}{dt}=\frac{{i}_{Lm}\left(t\right)-{i}_{Lk}\left(t\right)}{n}-\frac{{v}_{o}\left(t\right)}{R}\\\:{{C}_{o}}_{3}\frac{d{v}_{Co3}\left(t\right)}{dt}=\frac{{i}_{Lk}\left(t\right)-{i}_{Lm}\left(t\right)}{n}\end{array}\right.$$

(28)

The transfer function of the proposed converter can be derived from the duty cycle and output voltage using the above differential equation. The average state space model can be written as:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}\left( t \right) = Ax\left( t \right) + Bu\left( t \right)} \\ {y\left( t \right) = Cx\left( t \right)} \\ \end{array} } \right. $$

(29)

where the coefficient matrices A, B and C are:

$$\:\begin{array}{c}\left[A\right]={A}_{1}{d}_{1}+{A}_{2}{d}_{2}+{A}_{3}{d}_{3}\\\:\left[B\right]={B}_{1}{d}_{1}+{B}_{2}{d}_{2}+{B}_{3}{d}_{3}\\\:d={d}_{1}+{d}_{2}+{d}_{3}=1\end{array}$$

(30)

The state space of the high voltage step-up voltage multiplier cells quadratic boost converter (VMC-QBC) is modelled as:

$$\begin{aligned}\left[\begin{array}{l}{\dot{i}_{L1}}\left(t\right)\\\:{\dot{i}_{L2}}\left(t\right)\\\:{\dot{i}_{Lm}}\left(t\right)\\\:{\dot{i}_{Lk}}\left(t\right)\\\:{\dot{v}_{C1}}\left(t\right)\\\:{\dot{v}_{C2}}\left(t\right)\\\:{\dot{v}_{Co1}}\left(t\right)\\\:{\dot{v}_{Co2}}\left(t\right)\\\:{\dot{v}_{Co3}}\left(t\right)\end{array}\right] & =\left[\begin{array}{ccccccccc}0& \:0& \:0& \:0& \:-\frac{{d}_{2}+{d}_{3}}{{L}_{1}}& \:0& \:0& \:0& \:0\\\:0& \:0& \:0& \:0& \:\frac{{d}_{1}}{{L}_{2}}& \:-\frac{{d}_{3}}{{L}_{2}+{L}_{k}}& \:-\frac{{d}_{2}}{{L}_{2}}& \:-\frac{{d}_{3}}{n({L}_{2}+{L}_{k})}& \:\frac{{d}_{3}}{n({L}_{2}+{L}_{k})}\\\:0& \:0& \:0& \:0& \:\frac{{d}_{1}}{{L}_{m}}& \:\frac{{d}_{1}}{{L}_{m}}& \:0& \:-\frac{{d}_{2}+{d}_{3}}{n{L}_{m}}& \:\frac{2({d}_{2}+{d}_{3})}{n{L}_{m}}\\\:0& \:0& \:0& \:0& \:\frac{{d}_{1}}{{L}_{k}}& \:\frac{{d}_{1}+{d}_{2}}{{L}_{k}}+\frac{{d}_{3}}{{L}_{2}+{L}_{k}}& \:-\frac{{d}_{2}}{{L}_{k}}& \:\frac{{d}_{2}}{n{L}_{k}}+\frac{{d}_{3}}{n({L}_{2}+{L}_{k})}& \:-\frac{n{d}_{1}+2{d}_{2}}{n{L}_{k}}-\frac{{d}_{3}}{n({L}_{2}+{L}_{k})}\\\:\frac{{d}_{2}+{d}_{3}}{{C}_{1}}& \:-\frac{{d}_{1}}{{C}_{1}}& \:0& \:-\frac{{d}_{1}}{{C}_{1}}& \:0& \:0& \:0& \:0& \:0\\\:0& \:0& \:0& \:-\frac{1}{{C}_{2}}& \:0& \:0& \:0& \:0& \:0\\\:0& \:\frac{{d}_{2}}{{C}_{o1}}& \:0& \:\frac{{d}_{2}}{{C}_{o1}}& \:0& \:0& \:0& \:0& \:0\\\:0& \:0& \:\frac{{d}_{2}+{d}_{3}}{n{C}_{o2}}& \:-\frac{{d}_{2}+{d}_{3}}{n{C}_{o2}}& \:0& \:0& \:0& \:0& \:0\\\:0& \:0& \:-\frac{{d}_{1}+2{d}_{2}+2{d}_{3}}{2n{C}_{o3}}& \:\frac{{d}_{1}+2{d}_{2}+2{d}_{3}}{2n{C}_{o3}}& \:0& \:0& \:0& \:0& \:0\end{array}\right]\\ & \quad \left[\begin{array}{c}{i}_{L1}\left(t\right)\\\:{i}_{L2}\left(t\right)\\\:{i}_{Lm}\left(t\right)\\\:{i}_{Lk}\left(t\right)\\\:{v}_{C1}\left(t\right)\\\:{v}_{C2}\left(t\right)\\\:{v}_{Co1}\left(t\right)\\\:{v}_{Co2}\left(t\right)\\\:{v}_{Co3}\left(t\right)\end{array}\right] +\left[\begin{array}{c}\frac{1}{{L}_{1}}\\\:\frac{{d}_{1}+{d}_{2}}{{L}_{2}}+\frac{{d}_{3}}{{L}_{2}+{L}_{k}}\\\:0\\\:-\frac{{d}_{3}}{{L}_{2}+{L}_{k}}\\\:0\\\:0\\\:-\frac{1+n(2-D{)}^{2}}{{C}_{o1}(1-D{)}^{2}R}\\\:-\frac{1+n(2-D{)}^{2}}{{C}_{o1}(1-D{)}^{2}R}\\\:0\end{array}\right]{V}_{in}\left(t\right) \end {aligned}$$

(31)

$$\:y\left(t\right)={v}_{o}\left(t\right)=\left[\begin{array}{ccccccccc}0&\:0&\:0&\:0&\:0&\:0&\:1&\:1&\:0\end{array}\right]\left[\begin{array}{c}{i}_{L1}\left(t\right)\\\:{i}_{L2}\left(t\right)\\\:{i}_{Lm}\left(t\right)\\\:{i}_{Lk}\left(t\right)\\\:{v}_{C1}\left(t\right)\\\:{v}_{C2}\left(t\right)\\\:{v}_{Co1}\left(t\right)\\\:{v}_{Co2}\left(t\right)\\\:{v}_{Co3}\left(t\right)\end{array}\right]$$

(32)

Design process

This section gives a paper selection range of the proposed converter components to design a low cost, high gain boost converter. After selecting the appropriate input voltage, output voltage, and duty cycle, the turns ratio of the coupled inductor is determined after simulation and physical verification as:

$$n\frac{{M(1 - D)^{2} - 1}}{{(2 - D)^{2} }}$$

(33)

At this time, the value of the excitation inductance is:

$$\:{L}_{m}=\frac{{V}_{Lm\_on}{DT}_{s}}{{2I}_{Lm\_avg}}$$

(34)

Where V_{Lm_on}for the excitation inductor turn-on time voltage; I_{Lm_avg}for the excitation inductor average current.

Because to meet the efficiency requirements of the proposed converter, the inductance ensures CCM operation as much as possible, the values of inductors L₁ and L₂ are:

Since there are two conduction states, CCM and quasi-DCM, for the inductors of the proposed converter, the critical conditions for the conduction of inductors L₁ and L₂ are given, as well as specific formulas for the current ripple. Where the inductor L₁ can be simplified as a boost circuit, the critical conditions of inductors L₁ and L₂ and the current ripple are given by Eqs. 13, 14.

$$ \left\{ {\begin{array}{*{20}l} {L_{1} = \frac{{MD\left( {1 - D} \right)^{{2V_{{in}} }} }}{{2I_{o} f_{s} }}} \\ {L_{2} = \frac{{\left( {2 - D} \right)V_{{in}} }}{{2I_{o} f_{s} }}} \\ \end{array} } \right. $$

(35)

$$ \left\{ {\begin{array}{*{20}l} {\Delta L_{1} = \frac{{2I_{o} }}{{MD\left( {1 - D} \right)^{2} }}} \\ {\Delta L_{2} = \frac{{\left( {D + \frac{1}{{1 - D}}} \right)2nI_{o} }}{{2 - D}}} \\ \end{array} } \right. $$

(36)

Where M is the voltage gain, D is the duty cycle, V_in is the input voltage, n is the turns ratio, I_o is the output current, f_s is the switching frequency.

Due to the presence of ripple in the capacitor, the capacitor voltage should be kept at a reasonable value, assuming that the maximum voltage ripple rate of the capacitor is X_ci%, so the capacitance value of the capacitor is:

$$\:{C}_{i}\ge\:\frac{{\int\:}_{0}^{{T}_{ci}}{I}_{ci}\:dt}{{V}_{ci}{X}_{ci}\text{\%}}$$

(37)

Where T_ci and I_ci are the charging time and charging current of the capacitor respectively; V_ci is the capacitor voltage.

Fig. 7

Experimental set-up of the proposed converter Experimental set-up of the proposed converter. (Pictures of the proposed converter while performing the experiment, proving the authenticity of the experiment and giving the names of the components).

Fig. 8

Comparison with other converter. Comparison with other converter (Comparison of voltage gain with the same type of converter, voltage gain curve under the same conditions).

Table 1 Characteristics of the implemented prototype (the specific parameters of each component of the proposed converter are introduced, including frequency, voltage, turn ratio, inductance value and capacitance value).

Comparison with other converters

This section compares the proposed converter with other VMC-QBC converters of the same type to highlight the advantages and enhancements of the proposed converter. The voltage gain, voltage stress of switches, input current ripple, common ground between input and output, and number of components for each topology are analyzed from key data in Table 2. Figure 7 shows the experimental set-up of the proposed converter.

As the quadratic boost converter is mostly combined with other units, it leads to the higher number of components while enhancing the voltage gain. The converter proposed in^15,19 uses too many semiconductor devices which increases the cost and leads to impairment of overall efficiency. In^18,28 the converter has a large input current ripple, which shortens the life of the input and reduces the efficiency, and²⁸ does not have an input-output common ground characteristic, which reduces the stability and reliability of the system and is not conducive to resistance to noise and interference. In²⁶, the proposed converter has low input current ripple and common ground characteristics and has a wide voltage output, but the high switching stress tends to affect the converter life. In²⁷ excessive energy storage components such as inductors and capacitors are used, which results in a large amount of losses during energy transfer and greatly reduces the converter efficiency. Shown in Fig. 8. Shows the comparison of voltage gain with other converters. It is known that the voltage gain of the proposed converter is highest at low to medium duty cycle and the gain-duty cycle balance is also best. In addition, the input-output common ground feature enhances the resistance to noise and interference and has a wider range of application scenarios.

Table 2 Detailed parameters of the proposed converter (the proposed converter is compared with the same type of converter, including voltage gain, switching voltage stress, input current ripple, number of devices, and whether they are common ground).

Fig. 9

(a) I_L1, V_Co2 (b) V_Co1, I_L2, V_C1 (c) V_Co3 (d) V_o, V_in (e) V_D1, I_D1 (f) V_Do1, I_Do1 (g) V_Do2, I_Do2 (h) V_Do3, I_Do3 (i) V_Do4, I_Do4 (j) input voltage 15 V burst to 20 V and output voltage, (k) load 2 kΩ Burst to 1 kΩ input voltage and output voltage (l) load 1 kΩ Burst to 2 kΩ input voltage and output voltage. (The picture shows the experimental waveform graph. Experimental verification of the dynamic response of input current ripple, diode voltage current, capacitor voltage, variable input voltage and load is made).

Experimental results and discussion

A 300 W experimental prototype is developed as shown in Fig. 7. Table 1 gives the detailed parameters of the developed experimental prototype. The experimental prototype was tested with 50 kHz at CCM.

The capacitor voltage waveforms of V_C1, V_Co1, V_Co2, V_Co3, and V_Co4 are shown in Fig. 9a–c, where V_Co3 = V_Co4, and are consistent with the theoretical calculation of Eq. (7). The current waveforms of I_L1 and I_L2 are shown in Fig. 9a, b, which are in agreement with Eq. (14). It is worth noting that the smaller the input current ripple is, the more stable the converter’s operating state is and the longer its lifetime is. The voltage and current waveforms of D₁, D_o1, D_o2, D_o3, and D_o4 are shown in Fig. 9e–i, where the voltages and currents of D_o2, D_o3 are equal, which is in agreement with the theoretical calculation of Eq. (13). These properties of V_Co3, V_Co4, D_o2 and D_o3 depend on the symmetry of the voltage multiplier cells (VMC). (j), (k), and (l) are the dynamic response pictures for input mutation and load mutation respectively, it can be seen that when the input voltage is mutated from 15 to 20 V, the output voltage response is faster and the output is still stable. (k) and (l) are the load mutated from 2 to 1 kΩ and 1 to 2 kΩ, and the input and output do not change drastically, which shows that the proposed converter has good output stability.

Fig. 10

(a) switching pules(V_SW1), V_S1, I_S1, (b) switching pules(V_SW2), V_S2, I_S2. (Experimental verification of the switches S1 and S2 is carried out to analyse the driving waveforms, voltage and current waveforms to verify the correctness of the theoretical analysis).

The driving waveforms, voltages and currnts of switches S₁ and S₂ are shown in Fig. 10a, b, where the same driving signals are used for the switching waveforms of S₁ and S₂, which is conducive to simplifying the control. The voltage and current of S₂ is twice as much as that of S₁ due to the multiplication boost. It is worth noting that the voltage of V_S1 is only 1/10 of the output voltage, and the very small switching stress helps to improve the life of the converter.

Figure 11 shows the efficiency of the proposed converter measured under the same load with different output powers, where the average efficiency is 92% and the maximum efficiency is 92.7%, which indicates stable output and smooth efficiency. The real voltage gain curve in Fig. 12 is obtained from the experiment, which shows the voltage gain when the Vin = 5v and the duty cycle is 0.1–0.7, to highlight that the converter has a high voltage gain. The difference between the real voltage gain and the theoretical voltage gain is explained.

Fig. 11

Efficiency versus Output power. Efficiency versus Output power. (The efficiency graph of 50–300 W measured by changing the load size at a certain input voltage, the average value of the efficiency is about 92%).

Fig. 12

Real voltage gain and theoretical voltage gain. (Compare the real voltage gain with the theoretical voltage gain in this figure).

Conclusion

In this paper, a coupled inductor voltage multiplier cells quadratic boost converter (VMC-QBC) with high gain and low switching stress is proposed. The multistage boost is achieved by using voltage multiplier cells and quadratic boost technique at low to medium duty cycle, and the passive clamp circuit absorbs the energy leaked by the coupled inductor, which is conducive to improving efficiency. The steady-state analysis of the CCM state is discussed in detail, state-space models with parasitic parameters and non-ideal models are developed, and detailed design guidelines are given. Finally, a 300 W prototype was fabricated and tested. When V_in= 25 V, the duty cycle is 0.5, then V_o = 549 V and the voltage gain is 22. In the experiment, when V_in= 25 V, the duty cycle is 0.5, the V_o = 547 V, the voltage gain is 21.8, which is 0.3% lower than the theoretical calculated value. At the same time, the test capacitor voltage, diode voltage and current, switching drive signal, voltage and current waveforms, the experimental results are more consistent with the theoretical analysis. The tests were conducted under different input and load conditions to verify that the converter has stable output characteristics. In addition, the proposed converter has low input current ripple, high voltage gain, low switching stress, and common ground characteristics, which makes it suitable for integrated multi-energy storage systems.