Introduction

According to reports, HIV infections impair the immune system of their human hosts and harm internal organs including the heart, brain and kidneys, which finally causes death. Although yet no treatment is designed for this infectious disease, but there are other effective retroviral treatments that can greatly improve the health of patients. However, the excessive use of these medications can lead to adverse side effects. On the report of studies, HIV infection is the most hazardous virus in the world, having an impact on a variety of industries. In 2017, 1.8 million people were living with HIV, and 940,000 of them passed away. Presently, a greater number of individuals are engaging in therapy compared to previous times. Some individuals have manifested symptoms resembling headaches, rashes, sore throats, influenza, and fevers on certain occasions. In some cases the symptoms including weight gain, coughing, fever, enlarged lymph nodes and diarrhoea are dangerous. The significance of treatment is paramount, given its critical role in enhancing individual health outcomes, mitigating disease progression and transmission, and improving quality of life1,2,3. Additionally, treatment supports public health initiatives and fosters economic and medical advancements4,5. Although various treatments have been developed, there is still a need for more effective therapies to manage this infectious disease.

Mathematical modeling of HIV and the immune system continues to be an important tool in understanding the disease and improving treatment outcomes. These models provide enough details and key factors of the transmission route of diseases. The authors in6 proposed the use of compartment models as a viable way to combat HIV infection in humans. The immune deficiency virus’s dynamics during the whole infection process were examined by Duffin et al.7. The influence of HIV testing, treatment, and control on HIV transmission in Kenya was mathematically modeled by the researchers8. In9, the researchers modelled the transmission of HIV with treatment and pathogenics to investigate the intricate phenomena of the infection. In 1999, some researchers constructed an HIV model and statistically identified the most beneficial control measures10. Multiple models were subsequently developed by the authors in11,12,13 to explore the dynamics of HIV infection, incorporating important elements such as intracellular delays and viral mutation. The study in14 examined two transmission methods: direct cell-to-cell transfer and infection by free virions. In15, a model with four distinct classes of \({\text{CD}}4^{ + }\) T-cell populations infected by HIV was employed to analyze their interrelationships. In16, Perelson and Nelson employed a dynamical model and a parameter estimation approach to identify key aspects of HIV-1 infection dynamics. The model initially proposed by Perelson and Nelson was subsequently examined by Raun and Callshaw17, who categorized it into three compartments: free virus, healthy \({\text{CD}}4^{ + }\) T-cells, and infected \({\text{CD}}4^{ + }\) T-cells. Further, the existence theory of an HIV-1 infection model was explored in18 to enhance the understanding and analysis of HIV-1 dynamics. Furthermore, a multistage Homotopy Perturbation Method (HPM) was introduced for path tracking of damped oscillations in a model of HIV infection in CD4+ T cells19. In20, computational solutions were presented for the fractional mathematical model of HIV-1 infection in \({\text{CD}}4^{ + }\) T-cells, which causes AIDS, taking into account the impact of antiviral drug therapy. The main objective of this work is to elucidate the impact of input factors on the system’s dynamics to identify the most sensitive parameter for controlling the infection.

It is eminent that different mathematical frameworks have been employed in the literature to represent the dynamics of biological processes21,22,23. In the realm of disease modeling, fractional calculus offers significant advantages over classical approaches24,25. Fractional derivatives offer a powerful and versatile mathematical tool for modeling and understanding the intricate behaviors observed in biological systems26,27. Their ability to capture memory effects, non-local interactions, and complex structures makes them invaluable for advancing our knowledge and developing practical applications in biology and medicine. By embracing fractional calculus, researchers can achieve more accurate and comprehensive models, leading to better predictions and innovations in the biological sciences28,29. Although fractional calculus includes numerous operators, we chose to analyze our model using the Atangana-Baleanu and Caputo-Fabrizio operators. These fractional operators effectively captures real-world processes characterized by non-local and non-singular properties. Therefore, we choose to model the dynamics of HIV infection with nonlocal and nonsingular kernels to achieve more accurate and precise results.

The rest of the work is organized as follows: In section "Formulation of HIV model", we structure the dynamics of HIV and \({\text{CD}}4^{ + }\)" T cells with non-integer derivatives involving nonsingular and nonlocal kernel. The basic concepts and main results of the fractional calculus is presented in Sect. "Results and concepts of fractional theory for the analysis of the model. In section "Solution of the HIV system", a numerical schemes are introduced to visualize the dynamical behavior of the recommended system of HIV. Through numerical simulations, we visualized the chaotic natural and the solution pathways in section "Results and discussion" of the this research work. We have shown the impact of different input factors on the output of the system. The limitations of this work have been acknowledged and potential future directions are outlined in section " Limitations of the work". In section " Conclusion", we presented the conclusion remarks.

Formulation of HIV model

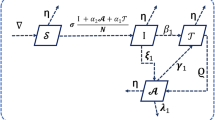
We organised the HIV transmission phenomena to show the interlink of infected T-cells \(\mathcal {I}\), healthy T-cells \(\mathcal {T}\) and HIV-free virus \(\mathcal {V}\). A number of researchers have developed and tested the dynamics of HIV in the past to explain the intricate dynamics of HIV30,31,32. The authors in19 developed the following model for the dynamics of HIV:

$$\begin{aligned}&\frac{d \mathcal {T}}{dt}=\rho -\beta _{T} \mathcal {T}+\eta \mathcal {T} (1-\frac{\mathcal {T}+\mathcal {I}}{\mathcal {T_{\max }}})-\nu \mathcal{V}\mathcal{T},\nonumber \\&\frac{d \mathcal {I}}{dt}=\nu \mathcal{V}\mathcal{T}-\beta _{I}\mathcal {I},\nonumber \\&\frac{d \mathcal {V}}{dt}=\mu \beta _{I}\mathcal {I}-\beta _{V} \mathcal {V}, \end{aligned}$$
(1)

where \(\rho\) is the rate at which the body recruits new T-cells, \(\beta _{T}\) is the death rate of T-cells while \(\beta _{V}\) and \(\beta _{I}\) are the rates at which HIV and infected T-cells dies, respectively. The parameter \(\nu\) signifies the infection rate affecting healthy T-cells, while \(\mu\) denotes the reproduction number associated with cells as a consequence of infected T-cells. The rate associated with the growth of healthy T-cells is indicated by \(\eta\). The model presented in33 is given below

$$\begin{aligned}&\frac{d \mathcal {T}}{dt}=\eta \mathcal {T}\left( 1-\frac{\mathcal {T}}{\mathcal {T_{\max }}}\right) -\frac{\sigma \mathcal{V}\mathcal{T}}{1+\delta \mathcal {V}},\nonumber \\&\frac{d \mathcal {I}}{dt}=\frac{\sigma \mathcal{V}\mathcal{T}}{1+\delta \mathcal {V}}-\beta _{I} \mathcal {I},\nonumber \\&\frac{d \mathcal {V}}{dt}=\mu \beta _{I} \mathcal {I}-\beta _{V} \mathcal {V}, \end{aligned}$$
(2)

in which the saturation incidence rate would allow HIV and infected T-cells to infect healthy \({\text{CD}}4^{ + }\) T-cells. The model of HIV infection with variable recruitment for the healthy T-cells illustrated in34 is presented as:

$$\begin{aligned}&\frac{d \mathcal {T}}{dt}=\rho \exp (-\xi \mathcal {V}) -\beta _{T} \mathcal {T}+\eta \mathcal {T}\left( 1-\frac{\mathcal {T}}{\mathcal {T_{\max }}}\right) -\nu \mathcal{V}\mathcal{T}-\delta \mathcal{I}\mathcal{T},\nonumber \\&\frac{d \mathcal {I}}{dt} = \nu \mathcal{V}\mathcal{T}+\delta {IT}-\beta _{I} \mathcal {I},\nonumber \\&\frac{d \mathcal {V}}{dt} = \mu \beta _{I} \mathcal {I}-\beta _{V} \mathcal {V}- \nu \mathcal{V}\mathcal{T}, \end{aligned}$$
(3)

where \(\delta\) is the effectiveness of a protease inhibitor while \(\nu\) is the rate of cellular infection. Numerous fresh definitions of non-integer derivatives have been put out recently and utilised to create mathematical models for a wide range of real-world systems that involve memory, history, or nonlocal effects. We illustrate the above recommended model of HIV infection through CF derivative as

$$\begin{aligned}& ^{CF}_0 D^{\upsilon }_t \mathcal {T}=\rho \exp (-\xi \mathcal {V}) -\beta _{T} \mathcal {T}+\eta \mathcal {T}\left( 1-\frac{\mathcal {T}}{\mathcal {T_{\max }}}\right) -\nu \mathcal{V}\mathcal{T}-\delta \mathcal{I}\mathcal{T},\nonumber \\&^{CF}_0 D^{\upsilon }_t \mathcal {I} = \nu \mathcal{V}\mathcal{T}+\delta {IT}-\beta _{I} \mathcal {I},\nonumber \\&^{CF}_0 D^{\upsilon }_t \mathcal {V} = \mu \beta _{I} \mathcal {I}-\beta _{V} \mathcal {V}- \nu \mathcal{V}\mathcal{T}, \end{aligned}$$
(4)

where \(\upsilon\) is order of CF derivative. Since it is commonly known that the definite integral lacks a regular kernel, many definitions have included both kinds of kernels. The ABC derivative, which was first presented by the researcher in 2016, is one of the significant concepts that has lately received attention. The dynamics of HIV in the framework of ABC derivative is given by

$$\begin{aligned}&^{ABC}_0 D^{\upsilon }_t \mathcal {T}=\rho \exp (-\xi \mathcal {V}) -\beta _{T} \mathcal {T}+\eta \mathcal {T}\left( 1-\frac{\mathcal {T}}{\mathcal {T_{\max }}}\right) -\nu \mathcal{V}\mathcal{T}-\delta \mathcal{I}\mathcal{T},\nonumber \\&^{ABC}_0 D^{\upsilon }_t \mathcal {I} = \nu \mathcal{V}\mathcal{T}+\delta {IT}-\beta _{I} \mathcal {I},\nonumber \\&^{ABC}_0 D^{\upsilon }_t \mathcal {V} = \mu \beta _{I} \mathcal {I}-\beta _{V} \mathcal {V}- \nu \mathcal{V}\mathcal{T}, \end{aligned}$$
(5)

where \(^{ABC}_0 D^{\upsilon }_t\) indicate Atangana-Baleanu derivative. These operators are more attractive for the researchers and scientists due to nonlocal and nonsingular kernel. In the following section of the work, we introduce some concepts and results of CF and ABC fractional operators.

Results and concepts of fractional theory

Here, we list the essential notions of fractional theory for the examination of recommended system. Below are some of the key findings and theories of CF and ABC:

Definition 1

Assume that \(q \in \mathfrak {H}^1(a_{1}, a_{2})\), where \(a_{2} > a_{1}\), then the CF derivative35 of order \(\upsilon\) can be stated as

$$\begin{aligned} D^{\upsilon }_{t}(q(t))=\frac{\mathcal {W}(\upsilon )}{1-\upsilon }\int ^{t}_{a_{1}}q'(x)\exp \Big [-\upsilon \frac{t-x}{1-\upsilon }\Big ]dx, \end{aligned}$$
(6)

where \(\upsilon \in [0, 1]\) and \(\mathcal {W}(\varkappa )\) represent normality with \(\mathcal {W}(0) = \mathcal {W}(1) = 1\)35. If \(q \notin \mathfrak {H}^1(a_{1}, a_{2})\), then we obtain

$$\begin{aligned} D^{\upsilon }_{t}(q(t))=\frac{\upsilon \mathcal {W}(\upsilon )}{1-\upsilon }\int ^{t}_{a_{1}}(q(t)-q(x))\exp \Big [-\upsilon \frac{t-x}{1-\upsilon }\Big ]dx. \end{aligned}$$
(7)

Remark 1

Suppose that \(\varphi =\frac{1-\upsilon }{\upsilon }\in [0, \infty )\) and \(\upsilon =\frac{1}{1+\varphi }\in [0, 1]\), then Eq. (7) can also be stated as

$$\begin{aligned} D^{\upsilon }_{t}(q(t))=\frac{ \mathcal {A}(\varphi )}{\varphi }\int ^{t}_{a_{1}}q'(x) e^{[-\frac{t-x}{\varphi }]} dx,~\mathcal {A}(0)=\mathcal {A}(\infty )=1. \end{aligned}$$
(8)

Moreover,

$$\begin{aligned} \lim _{\varphi \longrightarrow 0}\frac{1}{\varphi }\exp \Big [-\frac{t-x}{\varphi }\Big ]=\varpi (x-t). \end{aligned}$$
(9)

The definition of fractional integral is given as follows:

Definition 2

Let us assume any function q then the fractional integral can be defined as

$$\begin{aligned} I^{\upsilon }_t(q(t))=\frac{2(1-\upsilon )}{(2-\upsilon )\mathcal {W}(\upsilon )}q(t)+\frac{2\upsilon }{(2-\upsilon )\mathcal {W}(\upsilon )}\int ^t_0 q(v)dv, \ \ \ t\ge 0, \end{aligned}$$
(10)

where \(\upsilon\) indicate the order of fractional integral and \(0<\upsilon <1\).

Remark 2

Further modified form of Definition 2 is given as

$$\begin{aligned} \frac{2(1-\upsilon )}{(2-\upsilon )\mathcal {W}(\upsilon )}+\frac{2\upsilon }{(2-\upsilon )\mathcal {W}(\upsilon )}=1, \end{aligned}$$
(11)

which gives \(\mathcal {W}(\upsilon )=\frac{2}{2-\upsilon }\),  \(0<\upsilon <1\). Utilizing Eq. (11), Nieto and Losada obtained Caputo derivative of order \(\upsilon\), which is stated as

$$\begin{aligned} D^{\upsilon }_t(q(t))=\frac{1}{1-\upsilon }\int ^t_0 q'(x)\exp \Big [\upsilon \frac{t-x}{1-\upsilon }\Big ]dx, \ \ \ 0< \upsilon < 1. \end{aligned}$$
(12)

Definition 3

Consider a function g such that \(g\in \mathfrak {H}^1(b_{1},b_{2})\), \(b_{2}>b_{1}\), and \(z \in [0,1],\) then ABC represent the AB fractional operator in Liouville-Caputo structure defined as

$$\begin{aligned} ^{{ABC}}_{b_{1}}D^{z}_{t}g(t)= \frac{B(z)}{1-z}\int _{b_{1}}^t g'(\varepsilon )E_z \bigg [-z\frac{(t-\varepsilon )^z}{1-z}\bigg ]d\varepsilon . \end{aligned}$$

Definition 4

\(^{{ABC}}_{b_{1}}I^{z}_{t}g(t)\) represent the integral of AB derivative stated as follows

$$\begin{aligned} ^{{ABC}}_{b_{1}}I^{z}_{t}g(t)= \frac{1-z}{B(z)}g(t)+\frac{z}{B(z)\gimel (z)}\int _{b_{1}}^t g(\varepsilon )(t-\varepsilon )^{z-1}d\varepsilon . \end{aligned}$$

Obviously, we get the initial function as the fractional-order z tends to 0.

Theorem 1

Suppose a continuous function g such that \(g \in C[b_{1},b_{2}]\), then the the resulting outcome satisfies the condition36

$$\begin{aligned} \Vert ^{{ABC}}_{b_{1}}D^{z}_{t}(g(t))\Vert <\frac{B(z)}{1-z}\Vert g(t)\Vert , \;where\; \Vert g(t)\Vert =max_{b_{1}\le t\le b_{2}}|g(t)|. \end{aligned}$$

Furthermore, the Lipschitz condition holds for the newly developed ABC derivative as

$$\begin{aligned} \Vert ^{{ABC}}_{b_{1}}D^{z}_{t}g_1(t)- ^{{ABC}}_{b_{1}}D^{z}_{t}g_2(t)\Vert <\mathcal {\varrho }_1 \Vert g_1(t)-g_2(t)\Vert . \end{aligned}$$

Theorem 2

The equation for the fractional differential system is given as36

$$\begin{aligned} ^{{ABC}}_{b_{1}}D^{z}_{t}g(t)=w(t), \end{aligned}$$

which yields a unique solution as

$$\begin{aligned} {g(t)=\frac{1-z}{B(z)}w(t)+\frac{z}{B(z)\gimel (z)}\int _{b_{1}}^t w(\varepsilon )(t-\varepsilon )^{z-1}d\varepsilon .} \end{aligned}$$

Solution of the HIV system

Here, our primary objective is to illustrate numerical method to demonstrate the solution pathways of the recommended system. These numerical schemes will be utilized to visualize the dynamics of the system and to illustrate the chaotic phenomena of the system.

Solution through Caputo-Fabrizio

The solution analysis of a fractional system plays a pivotal role in enhancing our understanding of system behavior, validating models, making predictions, optimizing performance, and informing decision-making across diverse fields of study. There are many numerical methods available, but we will use the method developed in37 to analyze our recommended fractional system (4) for HIV infection. We start by looking at the first equation of our system:

$$\begin{aligned} \mathcal {J}_1(t)-\mathcal {J}_1(0)= \frac{1-\upsilon }{\mathcal {W}(\upsilon )} \textrm{V}_1 (t,\mathcal {J}_1)+\frac{\upsilon }{\mathcal {W}(\upsilon )} \int _0^t \textrm{V}_1 (\chi , \mathcal {J}_1) d \chi . \end{aligned}$$
(13)

Let \(t=t_{\ell +1}, \ell =0,1, \dots ,\) so we obtain

$$\begin{aligned} \mathcal {J}_1(t_{\ell +1})-\mathcal {J}_{1}(0)= \frac{1-\upsilon }{\mathcal {W}(\upsilon )} \textrm{V}_1 (t_\ell ,\mathcal {J}_1(t_\ell ))+\frac{\upsilon }{\mathcal {W}(\upsilon )} \int _0^{t_{\ell +1}} \textrm{V}_1 (t, \mathcal {J}_1) d t, \end{aligned}$$
(14)

and

$$\begin{aligned} \mathcal {J}_1(t_{\ell })-\mathcal {J}_{1}(0)= \frac{1-\upsilon }{\mathcal {W}(\upsilon )} \textrm{V}_1 (t_{\ell -1},\mathcal {J}_1(t_{\ell -1}))+\frac{\upsilon }{\mathcal {W}(\upsilon )} \int _0^{t_{\ell }} \textrm{V}_1 (t, \mathcal {J}_1) d t. \end{aligned}$$
(15)

The successive terms difference is stated below

$$\begin{aligned} \mathcal {J}_{1_{\ell +1}}-\mathcal {J}_{1_\ell }= \frac{1-\upsilon }{\mathcal {W}(\upsilon )} \bigg (\textrm{V}_1 (t_\ell ,\mathcal {J}_{1_\ell })-\textrm{V}_1 (t_{\ell -1},\mathcal {J}_{1_{\ell -1}}) \bigg )+\frac{\upsilon }{\mathcal {W}(\upsilon )} \int _\ell ^{t_{\ell +1}} \textrm{V}_1 (t, \mathcal {J}_1) d t. \end{aligned}$$
(16)

Now we approximate the function \(\textrm{V}_1 (t, \mathcal {J}_1)\) in the time interval \([t_\kappa ,t_{\kappa +1}]\) by utilizing interpolation polynomial and obtain

$$\begin{aligned} \mathcal {P}_\kappa (t)\cong \frac{\textrm{V}_1 (t_\kappa , \mathcal {J}_\kappa )}{q} (t-t_{\kappa -1})- \frac{\textrm{V}_1 (t_{\kappa -1}, \mathcal {J}_{\kappa -1})}{q} (t-t_{\kappa }), \end{aligned}$$
(17)

where q represent the time spent and \(q=t_\ell -t_{\ell -1}\). The above stated \(\mathcal {P}_\kappa (t)\) is utilized to obtain

$$\begin{aligned} \int _\ell ^{t_{\ell +1}} \textrm{V}_1 (t, \mathcal {J}_1) d t&= \int _\ell ^{t_{\ell +1}} \bigg ( \frac{\textrm{V}_1 (t_\ell , \mathcal {J}_{1_\ell })}{q} (t-t_{\ell -1})-\frac{\textrm{V}_1 (t_{\ell -1}, \mathcal {J}_{1_{\ell -1}})}{q} (t-t_{\ell }) \bigg ) dt,\nonumber \\&=\frac{3q}{2} \textrm{V}_1 (t_\ell , \mathcal {J}_{1_\ell })-\frac{q}{2} \textrm{V}_1 (t_{\ell -1}, \mathcal {J}_{1_{\ell -1}}). \end{aligned}$$
(18)

Here, putting Eq. (29) in Eq. (16), yield the following result

$$\begin{aligned} \mathcal {J}_{1_{\ell +1}}&= \mathcal {J}_{1_\ell }+\bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{3\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg ) \textrm{V}_1 (t_\ell , \mathcal {J}_{1_\ell }) \nonumber \\&\quad - \bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg )\textrm{V}_1 (t_{\ell -1}, \mathcal {J}_{1_{\ell -1}}), \end{aligned}$$
(19)

which is required solution for the first equation of the system. In the same way, we can determine for the second and third equation of (4) given by

$$\begin{aligned} \mathcal {J}_{2_{\ell +1}}&= \mathcal {J}_{2_\ell }+\bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{3\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg ) \textrm{V}_2 (t_\ell , \mathcal {J}_{2_\ell }) \nonumber \\&\quad - \bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg )\textrm{V}_2 (t_{\ell -1}, \mathcal {J}_{2_{\ell -1}}), \end{aligned}$$
(20)

and

$$\begin{aligned} \mathcal {J}_{3_{\ell +1}}&= \mathcal {J}_{3_\ell }+\bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{3\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg ) \textrm{V}_3 (t_\ell , \mathcal {J}_{3_\ell }) \nonumber \\&\quad - \bigg ( \frac{1-\upsilon }{\mathcal {W}(\upsilon )}+\frac{\upsilon q}{2 \mathcal {W} (\upsilon )} \bigg )\textrm{V}_3 (t_{\ell -1}, \mathcal {J}_{3_{\ell -1}}). \end{aligned}$$
(21)

The two-step Adams-Bashforth approach (ABA) used in this method for the CF takes into consideration the nonlinearity of the kernel as well as the exponential decay rule for the CF.

Solution through Atangana-Baleanu

Here, we will represent the solution pathways of our system (5) of HIV infection. We initially adopt the following fractional system to develop the necessary numerical method for our fractional model as follows:

$$\begin{aligned} ^{{ABC}}_{0}D^{\upsilon }_{t}\mathcal {J}(t)=f(t,\mathcal {J}(t)), \end{aligned}$$

using the theory of fractional calculus, we attain

$$\begin{aligned} \mathcal {J}(t)-\mathcal {J}(0)= \frac{1-\upsilon }{ABC(\upsilon )} f (t,\mathcal {J}(t))+\frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \int _0^t (t-\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa . \end{aligned}$$
(22)

Take \(t=t_\zeta\), then we obtain

$$\begin{aligned} \mathcal {J}(t_\zeta )-\mathcal {J}(0)= \frac{1-\upsilon }{ABC(\upsilon )} f (t_{\zeta -1},\mathcal {J}(t_{\zeta -1}))+\frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \int _0^{t_\zeta } (t_\zeta -\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa . \end{aligned}$$
(23)

and for \(t_{\zeta +1}\), we get

$$\begin{aligned} \mathcal {J}(t_{\zeta +1})-\mathcal {J}(0)= \frac{1-\upsilon }{ABC(\upsilon )} f (t_{\zeta +1},\mathcal {J}(t_{\zeta +1}))+\frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \int _0^{t_{\zeta +1}} (t_{\zeta +1}-\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa . \end{aligned}$$
(24)

We get the difference for above equation as

$$\begin{aligned} \mathcal {J}(t_{\zeta +1})-\mathcal {J}(t_\zeta )&= \frac{1-\upsilon }{ABC(\upsilon )} \bigg [ f (t_{\zeta },\mathcal {J}(t_{\zeta }))-f (t_{\zeta -1},\mathcal {J}(t_{\zeta -1})) \bigg ]+ \frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \nonumber \\&\int _0^{t_{\zeta +1}} (t_{\zeta +1}-\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa -\int _0^{t_{\zeta }} (t_{\zeta }-\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa . \end{aligned}$$
(25)
$$\begin{aligned} \mathcal {J}(t_{\zeta +1})-\mathcal {J}(t_\zeta )&= \frac{1-\upsilon }{ABC(\upsilon )} \bigg [ f (t_{\zeta },\mathcal {J}(t_{\zeta }))-f (t_{\zeta -1},\mathcal {J}(t_{\zeta -1})) \bigg ]+ B_{\upsilon ,1}-B_{\upsilon , 2}. \end{aligned}$$
(26)

where

$$\begin{aligned} B_{\upsilon ,1}= \frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \int _0^{t_{\zeta +1}} (t_{\zeta +1}-\varkappa )^{\upsilon -1} f (\varkappa , \mathcal {J}(\varkappa )) d \varkappa . \end{aligned}$$

Using approximation we obtain

$$\begin{aligned} P(t)\cong \frac{f (t_\zeta , \mathcal {J}_\zeta )}{q} (t-t_{\zeta -1})- \frac{f (t_{\zeta -1}, \mathcal {J}_{\zeta -1})}{q} (t-t_{\zeta }), \end{aligned}$$
(27)

where \(q=t_\ell -t_{\ell -1}\). Then, we get the following

$$\begin{aligned} B_{\upsilon ,1}&= \frac{\upsilon }{ABC(\upsilon ) \gimel (\upsilon )} \int _0^{t_{\zeta +1}} (t_{\zeta +1}-\varkappa )^{\upsilon -1} \bigg [ \frac{f (t_\zeta , \mathcal {J}_\zeta )}{q} (t-t_{\zeta -1})- \frac{f (t_{\zeta -1}, \mathcal {J}_{\zeta -1})}{q} (t-t_{\zeta }) \bigg ] d \varkappa \nonumber \\&= \frac{\upsilon }{ABC(\upsilon )\gimel (\upsilon )} \int _0^{t_{\zeta +1}} (t_{\zeta +1}-\varkappa )^{\upsilon -1} \bigg [ \frac{f (t_\zeta , \mathcal {J}_\zeta )}{q} (t-t_{\zeta -1})- \frac{f (t_{\zeta -1}, \mathcal {J}_{\zeta -1})}{q} (t-t_{\zeta }) \bigg ] d \varkappa , \end{aligned}$$
(28)
$$\begin{aligned} B_{\upsilon ,1}&= \frac{\upsilon f(t_\zeta ,\mathcal {J}_\zeta )}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{2qt_{\zeta +1}^{\upsilon }}{\upsilon }-\frac{t_{\zeta +1}^{\upsilon +1}}{\upsilon +1} \bigg ]-\frac{\upsilon f(t_{\zeta -1},\mathcal {J}_{\zeta -1})}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{qt_{\zeta +1}^{\upsilon }}{\upsilon }-\frac{t_{\zeta +1}^{\upsilon +1}}{\upsilon +1} \bigg ]. \end{aligned}$$
(29)

Similarly, we obtain

$$\begin{aligned} B_{\upsilon ,2}=\frac{\upsilon f(t_\zeta ,\mathcal {J}_\zeta )}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{q t^\upsilon _\zeta }{\upsilon }-\frac{t_\zeta ^{\upsilon +1}}{\upsilon +1} \bigg ]- \frac{ f(t_{\zeta -1},\mathcal {J}_{\zeta -1})}{ABC(\upsilon )\gimel (\upsilon )q}, \end{aligned}$$

so, we get the following result

$$\begin{aligned} \mathcal {J}(t_{\zeta +1})-\mathcal {J}(t_\zeta )&= \frac{1-\upsilon }{ABC(\upsilon )} \bigg [ f (t_{\zeta },\mathcal {J}(t_{\zeta }))-f (t_{\zeta -1},\mathcal {J}(t_{\zeta -1})) \bigg ]+ \frac{\upsilon f(t_\zeta ,\mathcal {J}_\zeta )}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{2qt_{\zeta +1}^{\upsilon }}{\upsilon }-\frac{t_{\zeta +1}^{\upsilon +1}}{\upsilon +1} \bigg ] \nonumber \\&\quad -\frac{\upsilon f(t_{\zeta -1},\mathcal {J}_{\zeta -1})}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{qt_{\zeta +1}^{\upsilon }}{\upsilon }-\frac{t_{\zeta +1}^{\upsilon +1}}{\upsilon +1} \bigg ]-\frac{\upsilon f(t_\zeta ,\mathcal {J}_\zeta )}{ABC(\upsilon )\gimel (\upsilon )q} \bigg [ \frac{q t^\upsilon _\zeta }{\upsilon }-\frac{t_\zeta ^{\upsilon +1}}{\upsilon +1} \bigg ]\nonumber \\&\quad +\frac{ f(t_{\zeta -1},\mathcal {J}_{\zeta -1})}{ABC(\upsilon )\gimel (\upsilon )q}. \end{aligned}$$
(30)

The above yields that

$$\begin{aligned} \mathcal {J}(t_{\zeta +1})&= \mathcal {J}(t_\zeta )+ f(t_\zeta ,y_\zeta ) \bigg [ \frac{1-\upsilon }{ABC(\upsilon )}+ \frac{\upsilon }{ABC(\upsilon )q} \bigg \{ \frac{2qt^{\upsilon }_{\zeta +1}}{\upsilon }-\frac{t^{\upsilon +1}_{\zeta +1}}{\upsilon +1} \bigg \} \nonumber \\&\quad - \frac{\upsilon }{ABC(\upsilon )\gimel (\upsilon )q} \bigg \{ \frac{qt_{\zeta }^{\upsilon }}{\upsilon }-\frac{t_{\zeta }^{\upsilon +1}}{\upsilon +1} \bigg \} \bigg ] +f(t_{\zeta -1},y_{\zeta -1}) \times \nonumber \\&\quad - \bigg [\frac{\upsilon -1}{ABC(\upsilon )}-\frac{\upsilon }{ABC(\upsilon )\gimel (\upsilon )q} \bigg \{ \frac{qt_{\zeta +1}^{\upsilon }}{\upsilon }-\frac{t_{\zeta +1}^{\upsilon +1}}{\upsilon +1} +\frac{ t^{\upsilon +1}}{q ABC(\upsilon )\gimel (\upsilon )} \bigg \} \bigg ]. \end{aligned}$$
(31)

The method described above is for the ABC fractional derivative. Here, we run different simulations to see how different factors affect the relationship between HIV and T-cells. The settings we use for the parameters in this section are meant to highlight the chaotic and up-and-down behavior of the system (5) through simulations.

Results and discussion

The choice between CF and AB kernels depends on the specific requirements of the model and the nature of the system being studied. The effectiveness of CF fractional derivatives is evident in their ability to provide accurate, stable, and computationally efficient modeling of systems with memory effects. Their non-singular nature, exponential decay properties, and simplicity make them a powerful tool in various scientific and engineering fields. On the other hand, the AB kernel, with its complex memory effects via the Mittag-Leffler function, is better suited for systems requiring a more nuanced representation of memory and hereditary properties. By using both kernels, researchers can leverage the strengths of each to develop more robust and accurate models.

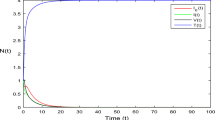
Despite extensive international efforts to mitigate HIV/AIDS, the disease continues to exert a substantial burden on affected families. Elevated healthcare expenses, diminished employment income, and the depletion of resources exacerbate the income-to-expenditure gap, underscoring the persistent challenges. Consequently, an examination of the fundamental causes of HIV infection is imperative to mitigate these adverse consequences. The primary objective of this research phase is to elucidate the chaotic behavior and time series dynamics of the system, aiming to enhance comprehension of the diverse factors influencing it. Employing various numerical scenarios, we explore how input elements contribute to the dynamics of HIV. For numerical purposes, parameter values are derived from Table 1, and initial conditions for state variables are assumed as \(\mathcal {T}(0)=300, \mathcal {I}(0)=200\), and \(\mathcal {V}(0)=120\).

Table 1 List of input variables of the proposed system of HIV infection.
Full size table

In Figs. 1, 2, 3, we visually depict the oscillatory behavior inherent in the system. Notably, the solution pathways of the system exhibit a significant dependence on the fractional parameter. The findings of these simulations indicate that the order of the fractional derivative positively influences HIV dynamics, suggesting its potential utility as a preventive measure. The chaotic nature of the system is demonstrated in Figs. 4, 5, 6, where diverse values of input factors lead to varied system outputs. The interplay between the oscillatory and chaotic aspects is intricately linked by the non-linearity of the model, inducing unstable states within the system. Policymakers are urged to consider the input parameter, as it has been empirically shown to exert a remarkable impact on the system’s output. This insight underscores the importance of incorporating fractional parameters in policy decisions related to HIV dynamics.

Fig. 1
figure 1

Illustration of the time series of the recommended model of HIV infection with the input parameter \(\upsilon =1.00\) and \(\rho =0.1\).

Full size image
Fig. 2
figure 2

Plotting the dynamical behaviour of the recommended model of HIV infection with the input parameter \(\upsilon =0.75\) and \(\rho =0.1\).

Full size image
Fig. 3
figure 3

Illustration of the solution pathways of the suggested system of HIV infection with input values \(\upsilon\) and \(\rho =0.1\).

Full size image
Fig. 4
figure 4

Graphical view of chaotic nature of the recommended model of HIV infection with input values \(\rho =1.0, \upsilon =0.8\) and \(\eta =3.0\).

Full size image
Fig. 5
figure 5

Graphical view of chaotic nature of the recommended model of HIV infection with input values \(\rho =5.0, \upsilon -0.8\) and \(\eta =3.0\).

Full size image
Fig. 6
figure 6

Graphical view of chaotic nature of the recommended model of HIV infection with input values \(\eta =1.0, \upsilon =0.8\) and \(\rho =1.0\).

Full size image

Chaos theory delves into nonlinear phenomena characterized by inherent unpredictability and difficulty in control. This field focuses on the deterministic principles and fundamental patterns of dynamical systems, particularly sensitive to initial values of state variables, challenging the prior belief of their wholly unpredictable chaotic states. The significance of these conditions lies in the valuable insights they offer into the HIV infection system. The chaotic behavior observed in the system illustrates the profound impact of minor perturbations, leading to substantial changes. The instability of the system is vividly portrayed in these chaotic plots, underscoring its susceptibility to initial conditions and inherent uncertainty. Our research underscores that the nonlinearity of the system significantly amplifies chaos and oscillation, rendering the system inherently unstable. This revelation contributes to a deeper understanding of the intricate dynamics of the HIV infection system and emphasizes the importance of considering nonlinear factors in system analysis and intervention strategies.

Limitations of the work

The importance of this research lies in its potential to deepen the understanding of HIV dynamics, particularly the interaction between HIV and CD\(4^+\) T-cells. By utilizing fractional derivatives and exploring the chaotic and oscillatory behaviors within the system, this research addresses a critical gap in current HIV studies. The identification of chaotic behavior and the influence of fractional-order dynamics on disease progression provide new insights that could lead to more effective treatment strategies. This work not only contributes to the scientific community’s knowledge of HIV but also has practical implications for developing interventions that could enhance patient outcomes and inform global health policies.

Future work

  • Despite the promising insights provided by this study, a notable limitation is the lack of validation using clinical data or published datasets to substantiate the application of the Atangana-Baleanu and Caputo-Fabrizio derivatives. Future research should address this limitation by incorporating clinical data or relevant published datasets for model validation. Such validation would enhance the reliability of the models and ensure that the theoretical predictions align with real-world HIV infection dynamics, thereby strengthening the overall impact and applicability of the research.

  • Future research could focus on enhancing the model by integrating a broader spectrum of biological and environmental factors, such as the impact of antiretroviral therapy and the influence of co-infections. Additionally, expanding the model to account for individual variability in immune responses and viral characteristics would increase its relevance and applicability to a wider range of patients.

Conclusion

HIV infection weakens the body’s immune defenses by attacking the immune system and destroying T-cells, presenting a major challenge to global public health. Although recent data suggest a decline in HIV infections, thorough research is essential to fully understand the complex interactions between viruses and T-cells. To tackle this issue, we have meticulously analyzed the intricate relationship between \({\text{CD}}4^{ + }\) T-cells and HIV using non-integer derivatives. We considered the relation between infected T-cells, uninfected T-cells and HIV viruses in our system. The recommended HIV model is demonstrated through CF and ABC fractional derivatives. We investigated the solution pathways and chaotic dynamics of the proposed system using numerical methods. Various simulations were conducted to examine the critical conditions of the system. Our findings confirm the presence of chaotic behavior within the model. We observed that fractional-order dynamics influence the solution pathways of the HIV infection system. The impact of different input factors has been shown on tracking path behavior of the system. We identified a significant correlation between chaotic and oscillatory behaviors. Further work will focus on assessing the impact of medical advancements on the progression of the virus and developing more effective treatment strategies. We aim to extend the current model to analyze the effects of treatment and vaccination on HIV infection.