Introduction

According to the world health organization, chronic obstructive pulmonary disease (COPD) and lower respiratory infections were the third and fourth leading causes of death worldwide, respectively1. A wide range of inhaled therapies is available for respiratory diseases such as COPD and asthma, dispensed via a variety of devices. Each of these drug-device combinations interacts differently with patient specific characteristics influencing the amounts of drug delivered to the desired location within the lung, and consequently leading to associated variability in exposure, absorption and, potentially, efficacy2,3.

Inhaled substances may be administered in the form of liquid or powdered aerosols using an inhaler. The three main types of inhalers are dry powder inhalers (DPIs), nebulizers, and metered-dose inhalers (MDIs). DPIs use dry powder as the inhaled substance, and the patient’s inhalation is the primary force that propels the powder4. Nebulizers deliver liquid aerosols, which can be propelled either by the patient’s inhalation and/or by external assistive forces5. In MDIs, the liquid aerosols are propelled partly by pressurized propellant and partly by the patient’s inhalation4.

Until recently, patient-specific drug deposition within the lungs was assessed only by means of scintigraphic imaging using radiolabeled compounds6,7, a process with high costs and complexity precluding widespread adoption in clinic. Newer approaches utilizing computational fluid dynamic (CFD) simulation of particle deposition in patient-specific airway geometry models extracted from standard-of-care computed tomography (CT) images have shown promise delivering highly accurate predictions8,9,10,11. The time required for CFD simulation of air flow and aerosols in airways depends on model settings and hardware characteristics, and may vary between some hours to several days12,13,14. Therefore, the CFD approach remains computationally expensive and time-consuming due to the high dimensionality of the models, and thus largely inaccessible outside research institutions.

One option to expedite deposition evaluations is the use of one-dimensional whole-lung models. These models simplify human airways as a one-dimensional lumped “trumpet” model with a variable cross-sectional area15. While the models provide insights on idealized correlation between deposition and aerosol sizes, evidently, they oversimplify the problem by neglecting airways complexity and inter-patient variability16,17.

Artificial neural networks have been used previously to predict aerosol deposition in human airways. However, they were limited to prediction of mono-disperse aerosols18,19 and limited inhalation patterns20. Similarly, while artificial intelligence has been used in 3D airway model segmentation for over ten years21,22,23,24,25, its recent contribution in the aerosol deposition field have focused on improving simulation time26, or have been limited to idealized airway geometry models27,28 and mono-dispersed aerosols28.

In this article, a rapid deposition analysis (RDA) is presented that has been developed based on dimensional analysis of the parameters involved in deposition of inhaled medications. Dimensionless correlations for total, regional, and lobar depositions are formulated using a database of solutions derived from CFD simulations. Dimensional analysis is a technique widely used in fluid dynamics and heat transfer29. By identifying the relevant physical parameters and grouping them into dimensionless variables, dimensional analysis helps simplify the problem and reduce the number of variables in a phenomenon. Dimensionless correlations can then be developed to predict physical phenomena. From prediction of forced convection condensation30 and deposition of frost on cooled surfaces31 to estimate cooling efficiency of cooling towers32 and natural convection from plates33, all benefited from dimensional analysis.

The trust in any data-driven approach, whether utilizing neural networks, artificial intelligence, or dimensional analysis, is directly linked to the size of its training dataset. To our knowledge, this research on aerosol deposition in human lungs is the first of its kind, built upon a dataset of over 3400 previously conducted CFD simulation results. The deposition results predicted by the RDA model were compared with CFD results. We also compared lobe-wise deposition predicted by RDA with the single-photon emission computed tomography (SPECT)/CT data for 6 subjects studies using a radiolabeled inhaled compound.

Methods

The historical CFD simulations were performed on airway geometry models extracted from chest CT data of real patients or healthy volunteers from historical clinical trials, for a range of pulmonary indications including both restrictive and obstructive physiologies, of varying etiologies and severities. Relevant institutional review boards have approved the protocols of the tests in the corresponding clinical trials. The Institutional Review Board at University Hospital Antwerp approved the study protocol of the SPECT tests. All methods and research were performed in accordance with relevant regulations. All patients gave their signed informed consent. The CFD analysis were performed on airway geometry models of patients and healthy volunteers representing age ranged from 5 to 85 years old. High Resolution (HR) CT scans were utilized to generate 3-dimensional representations of the airways and lobes. Airway geometries were extracted from the HRCT scan at total lung capacity (TLC) using a semi-automatic algorithm. The segmentation and 3-dimensional reconstruction were performed, and the segmented airway model was smoothed with a volume compensation algorithm. Additionally, the lung lobes at both functional residual capacity (FRC), and TLC were extracted. Further information is available in Ref8,34,35.

The CFD analyses involved different inhaler device including DPIs, nebulizers, and MDIs and formulations. Several types of patient and/or device specific and idealized inhalation profiles were investigated. In the simulations, to describe the flow and aerosol motion the Navier -Stokes equations were solved, which are based on the conservation of mass, momentum, and energy36. To represent real-life conditions, patient-specific boundary conditions were applied in the CFD simulations using in silico Functional Respiratory Imaging (FRI) technology37,38. Lobe volumes and airway geometry models were extracted from inspiratory and expiratory HRCT scans of each patient. The ventilated air from each lobe determined the correct flow rate, incorporating peripheral resistance and regional compliance automatically. Aerodynamic particle size distribution (APSD) data were used to simulate particle motion and predict airway deposition for various inhalation profiles. In the CFD studies, particles (discrete phase) were injected from the devices. For MDIs, they were introduced using a cone nozzle setup with an initial velocity and cone angle specific to each inhaler. For DPIs and nebulizers, the particles were released with zero velocity and were carried by the airflow momentum during inhalation. The historical simulations were performed using ANSYS® Fluent software. The database includes 3434 CFD simulation results for 526 subjects, 184 formulation characteristics, and 98 patient specific or idealized inhalation patterns.

Dimensional analysis is applied to the CFD based database including all inputs (independent variables) and results (dependent variables). Dimensional analysis is a mathematical method employed in fluid dynamics to analyze units and dimensions, and solve problems involving physical quantities29. Its fundamental principle involves scrutinizing the units of measurement associated with different physical quantities39. Buckingham theorem is a key element in dimensional analysis40. The theorem offers a method for determining a collection of dimensionless groups, which cover the solution space, based on measurement variables and parameters41.

A primary group was formed containing all variables influencing aerosol deposition in airways with total number of 36 (n), which are listed in the second column of Table 1. Using dimensional analysis and Buckingham Theorem, dimensionless numbers were constructed. The primary dimension(s) of each variable in the primary group was determined i.e. M (mass), L (length), t (time) and Θ (temperature). The number (j) of primary dimensions in the primary group was determined (4 primary dimensions M, L,T, Θ). Based on the Buckingham Theorem, the minimum number (k) of dimensionless numbers is k = n-j, and therefore 36–4 = 32.

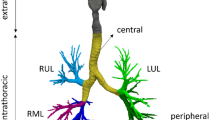
The dimensionless numbers (πi) were placed in the dimensionless correlation in the form of π0 = c0 × π1c1 × π2c2 × π3c3 ×…. × πkck, where deposition in a zone (see all zones in Fig. 1) is represented as π0 (dependent dimensionless variable), and π1 to πk are the independent dimensionless variables. Each c of c1 to ck is an exponent of the dimensionless numbers and c0 is a multiplier of the correlation. For each zone shown in Fig. 1, a dimensionless correlation is obtained.

Table 1 Influencing input parameters in simulation of aerosol deposition in airway within the three main groups of Functional respiratory imaging (FRI), inhalation and device/active pharmaceutical ingredient (API), and their combinations.
Full size table
Fig. 1
figure 1

Zones of deposition: extrathoracic (mouth and upper airways, gray), central (trachea and main bronchi, yellow), distal (visible small airways, indigo, purple, blue, pink, and green), peripheral (invisible airway, i.e., doses exiting outlets), intrathoracic (sum of central, distal, and peripheral depositions). Total lobe deposition: right upper lobe (RUL), right middle lobe (RML), right lower lobe (RLL), left upper lobe (LUL), left lower lobe (LLL).

Full size image

Total deposition zones within a representative set of airways (Fig. 1) are extrathoracic and intrathoracic regions. The extrathoracic zone comprises the mouth and upper airways, while the intrathoracic region starts at the trachea and extends down through the remaining airways. Within the intrathoracic airways, the yellow-shaded area (including the trachea and main bronchi) represents the central zone. The distal zone is composed of airways visible on a CT scan, with diameters of 1 to 2 mm or more, highlighted in indigo, purple, blue, pink, and green colors. The peripheral zone is defined by airway diameter; it includes the small airways less than 1 to 2 mm in diameter, which are not detectable on a CT scan. Particles exiting the domain from airway outlets contribute to peripheral deposition.

Non-linear least square regression was used to select the dimensionless parameters which best predicted deposition to construct a model for RDA. Specifically, the Levenberg-Marquardt approach42 was used to derive the best correlation for total (extrathoracic and intrathoracic), regional (central, distal and peripheral), and lobar deposition based on the historical CFD based results.

As the number of independent dimensionless variables (k) in each correlation increases, the accuracy of the results may be improved. A sub-study is performed to determine the optimum number of independent variables in the dimensionless correlations by monitoring the intraclass correlation coefficient (ICC) versus k. ICC is a statistical estimate that measures the extent of agreement between two or more quantitative measurements. In addition to assessing agreement, the ICC evaluates reliability, consistency, and stability43. The technique for calculating the ICC is based on the analysis of variance and the estimation of various variance components44. The dataset was divided into training and test sets, with 80% allocated to the training set and 20% to the test set. This split ensured a balanced approach for model development and evaluation.

After identifying all input parameters involved in CFD simulations, three main groups and their combinations of dimensionless parameters were derived using the Buckingham method. The main groups are: FRI parameters, inhalation flow, and device and active pharmaceutical ingredients (API). The FRI parameters include the information extracted from CT scans of a patient such as airway volume, functional residual capacity (FRC), and total lung capacity (TLC)35. The input parameters in each group are listed in Table 1.

The predictions of RDA are compared to the CFD predictions and single-photon emission computed tomography (SPECT) data for 6 asthma patients. The in-vivo and CFD data on regional deposition for six mild asthma patients were collected from the previous research by Sadafi et al.9. The inhaled radiolabeled aerosols with an average diameter of approximately 1.32 μm were delivered via SmartVent nebulizer.

Moreover, the deposition of inhaled corticosteroids (ICS) delivered via Nexthaler® DPI was predicted using RDA, and compared with the results of CFD evaluation on 77 patients diagnosed with asthma or COPD. The patients’ ages ranged from 21 to 77 years, and their heights ranged from 149 to 181 cm. To evaluate the RDA predictions, the accuracy percentage is calculated. Accuracy percentage is calculated as the absolute difference between RDA and CFD predicted values divided by the CFD values multiplied by 100 and then subtract this result from 100.

The RDA predictions of intrathoracic deposition in 20 independent studies are compared with the associated CFD results. Table 2 shows the device and API, peak inhaled flow, MMAD, GSD, FPF, and number of patients in those studies. All CFD studies were performed using real patient airway geometry models and applying patient specific internal airflow distribution. Airflow was simulated through the inhalers, as well as the realistic mouth and throat for each patient.

Table 2 Device and active pharmaceutical ingredient (API), peak inhaled flow (PIF), mass median aerodynamic diameter (MMAD), geometrical standard geometry (GSD), fine particle fraction (FPF), and number of patients in 20 independent studies used for comparing rapid deposition analysis (RDA) and computational fluid dynamic (CFD) results
Full size table

Results

Figure 2 shows the intraclass correlation coefficient (ICC) for intrathoracic deposition. The ICC is calculated for 80% of the training dataset (2747 datapoints) and 20% of the test data (687 datapoints). Both ICC values derived from both RDA and CFD predictions stand at 0.92. The ICC between RDA and CFD for all zones shown in Fig. 1 are presented in Table 3.

Table 3 Intraclass correlation coefficient (ICC) between rapid deposition analysis (RDA) and computational fluid dynamics (CFD) calculated for all zones shown in Fig. 1. Right upper and right middle lobes (RUL + RML), right lower lobe (RLL), left upper lobe (LUL), left lower lobe (LLL).
Full size table
Fig. 2
figure 2

Intrathoracic deposition (as the percentage of delivered dose) obtained rapid deposition analysis (RDA) and computational fluid dynamics (CFD) methods. The total number of the training data is 2747, and the number of independent test data is 687 (20% of total). The intraclass correlation coefficient (ICC) for the training and the test data is 0.93.

Full size image

Figure 3 shows that the lobar mean difference between RDA and CFD results is 1.275%. The mean difference between RDA and SPECT is 1.325%.

Fig. 3
figure 3

Loba-wise deposition in six asthma patients obtained from in-vivo single-photon emission computed tomography (SPECT), computational fluid dynamics (CFD), and rapid deposition analysis (RDA). % of DD: as a percentage of delivered dose. Lobar depositions: right upper and right middle lobes (RUL + RML), right lower lobe (RLL), left upper lobe (LUL), left lower lobe (LLL). The values for SPECT and CFD are taken from9.

Full size image

Figure 4 compares the deposition of inhaled corticosteroids (ICS) delivered via Nexthaler® DPI predicted by CFD and RDA. For total and regional zones the accuracy of RDA is above 90.2% when compared to CFD results.

Fig. 4
figure 4

Total, regional and lobar deposition of inhaled corticosteroids (ICS) delivered via Nexthaler® dry powder inhaler predicted by computational fluid dynamics (CFD), and rapid deposition analysis (RDA). % of DD: as a percentage of delivered dose. Lobar depositions: right upper and right middle lobes (RUL + RML), right lower lobe (RLL), left upper lobe (LUL), left lower lobe (LLL).

Full size image

Regional deposition predicted by RDA was compared to 20 independent studies with available CFD simulations and results. As shown in Table 4, the average accuracy between the RDA and CFD results for intrathoracic deposition was 92.5%.

Table 4 Comparison of intrathoracic deposition predicted by computational fluid dynamics (CFD), and rapid deposition analysis (RDA) for 20 studies on airway geometries of real patients. API: active pharmaceutical ingredients, % DD: percentage of delivered dose, accuracy is calculated as the absolute difference between RDA and CFD predicted values divided by the CFD values and multiplied by 100 then subtract the results by 100.
Full size table

Figure 5 shows that the average calculation time of RDA is less than 0.05% of a CFD calculation, which is a comparison between few seconds and several hours.

Fig. 5
figure 5

calculation times for rapid deposition analysis (RDA) versus computational fluid dynamics (CFD).

Full size image

Figure 6 shows the asymptotic improvement of ICC by number of dimensionless variables (π) for intrathoracic, central + distal, and peripheral zones. The optimum number of independent variables is 18 for nebulizers, and 20 for DPIs and MDIs due to the larger number of influencing variables. Further inclusion of dimensionless variables does not lead to a significant improvement in the ICC values.

Fig. 6
figure 6

Intraclass correlation coefficient (ICC) for dimensionless correlations of intrathoracic, central + distal, and peripheral zones (refer to Fig. 1) versus number of independent dimensionless variables (π) in a correlation.

Full size image

Discussion

CFD simulations have long been a go-to tool for accurately modelling airflow and drug deposition patterns within the lungs8,45,46,47. However, their extensive computational demands and lengthy processing times pose significant limitations, especially in clinical settings where rapid evaluations are essential12,13,14. These simulations often require specialized hardware and deep expertise in fluid dynamics, making them impractical for routine use by clinicians who need to make quick decisions about patient care. Consequently, the complex nature and slow pace of CFD simulations can delay treatment planning, ultimately affecting patient outcomes.

To address these challenges, RDA may offer a promising solution. This approach provides a faster and more efficient means of evaluating lung deposition, delivering a reasonable accuracy. The speed and precision of the RDA model make it a potential choice for clinical practice, where timely and reliable assessments are crucial for guiding patient treatment. It is patient-, device- and inhalation flow-specific, and does not require specialized training in fluid dynamics or access to high-performance computing resources.

In RDA, dimensional analysis is applied to a large database of aerosol deposition in human airways with CFD simulation based results. To the best of our knowledge, this is the first research applying dimensional analysis as a well-known method in fluid dynamics30,31,32,33,48,49,50,51,52 on this context. As an inter-disciplinary domain, the application of fluid dynamics in the respiratory field is new relative to the heat transfer, aerospace53,54, or automative industry55,56. Moreover, a sufficiently large database is necessary to perform a reliable dimensional analysis. The extensive database, which includes various diseases, patient-specific airway geometry models, and their associated CFD analyses, provided the foundation for this pioneering application. Buckingham Theorem40 is a key element in dimensional analysis performed in most studies. Some apply the approach for comparing two or more systems based on similarity principles57,58 and some other develop further and propose dimensionless correlations using regression analysis59,60, such the present study.

Patients with various respiratory conditions can benefit from RDA for effectiveness of their medications at points of care. Non-adherence to inhaled treatment regimens61 and improper use of both pMDIs and DPIs62 are common issues. RDA may allow clinicians to quickly assess how well medications are being delivered and distributed throughout the lungs. For patients with asthma, COPD, or other respiratory disorders, RDA may guide personalized adjustments to treatment plans, ensuring that the medication reaches the intended areas of the lungs with optimal efficacy. By providing immediate feedback, clinicians may tailor drug formulations, dosages, and delivery methods to each patient’s unique needs, improving symptom management and overall health outcomes63. Additionally, this analysis may help identify any potential issues with medication delivery, enabling quick interventions that can prevent exacerbations and improve patient quality of life. All these were not possible with CFD due to long simulation times and the need for fluid dynamics expertise, but may now be achievable with RDA because of its rapid assessment time.

In addition to its clinical applications, RDA has potential benefits for the drug discovery process, where after several years of research the chance of success is one in 30,00064. By providing quick and reasonably accurate data on drug deposition patterns, researchers can use the RDA model to optimize drug formulations and delivery methods more efficiently. Digitalization of drug development cycles optimizes the results and accelerates the introduction of new treatments to the market65. The versatility and speed of the RDA model may position it as a valuable tool in both clinical practice and pharmaceutical research, offering improvements over traditional CFD simulations.

The speed and efficiency of the RDA model also offer improvements over traditional CFD simulations in clinical settings. Healthcare providers can use RDA to quickly assess the effectiveness of different medications for individual patients, allowing for more personalized treatment plans. This level of customization can improve patient outcomes and enhance the overall quality of care.

Limitations

When comparing two devices/formulations with very limited difference such as in a bio-equivalence assessment, RDA nay not deliver the required accuracy and a full CFD analysis should be used. RDA treats two inhalation profiles with similar general characteristics including but not limited to mean and peak flows and the slope at the onset of inhalation the same regardless of the details of the profiles and curvatures. Additional physical phenomena, such as evaporation and hygroscopic effects, may be considered in CFD analysis but are neglected in both the RDA and the CFD training data in the current study.

Conclusion

Rapid deposition analysis (RDA) provides a quicker alternative to full computational fluid dynamics (CFD) simulations, which require substantial hardware resources and involve long computation times. After identifying the input parameters influencing aerosol deposition in human airways, they were divided into three primary groups based on their origin: data from patient CT scans, inhalation maneuver characteristics, and device/medication specifications. Through dimensional analysis and non-linear least square regression on a comprehensive database of CFD simulations and results, dimensionless correlations for predicting total, regional, and lobar deposition are derived. These correlations are tailored to the patient, flow, and device/medication, and calculate deposition in a few seconds. The intraclass correlation coefficient between RDA and CFD is 0.92, indicating strong agreement between the two methods. This rapid and reasonably accurate evaluation of deposition has significant potential for providing personalized information on medication effectiveness and choice in clinical practice. Moreover, RDA can play a role in the drug discovery cycle by quickly providing insights that inform and guide research and development efforts and are a precursor for more detailed and accurate CFD simulations.