A geometric formulation to measure global and genuine entanglement in three-qubit systems

Abstract

We introduce a purely geometric formulation for two different measures addressed to quantify the entanglement between different parts of a tripartite qubit system. Our approach considers the entanglement–polytope defined by the smallest eigenvalues of the reduced density matrices of the qubit-components. The measures identify global and genuine entanglement, and are respectively associated with the projection and rejection of a given point of the polytope on the corresponding biseparable segments. Solving the so called ‘inverse problem’, we also discuss a way to force the system to behave in a particular form, which opens the possibility of controlling and manipulating entanglement for practical purposes.

Introduction

Entanglement is the most interesting nonclassical correlation of multipartite quantum systems. It represents an important resource in quantum computing, quantum information processing and quantum teleportation^1,2,3. However, the characterization and quantification of multipartite entanglement is still an open question^4,5. Even in the three-qubit system case it has been pointed out that different forms of entanglement may be present^6,7,8,9. This can be seen from the fact that there is no unified notion of a maximally entangled state for more than two-qubits⁶. In fact, considering the most widely used measures¹⁰, different requirements comprise different characteristics of the nonlocal properties that a given system must satisfy to exhibit maximal entanglement.

In this sense, entanglement measures based on the geometry of the state space or the appropriate projective space are of particular interest. For example, the geometric measure of entanglement (GME) evaluates the distance from a target state to its closest separable state in a given Hilbert space^11,12. Although its immediate geometric interpretation, the GME demands a non-trivial optimization so it becomes a nondeterministic polynomial (NP) problem¹³. Indeed, the amount of information that must be processed suggests that sooner or later it will be inevitable to resort to numerical methods¹². Other examples include the entanglement of minimum bipartite entropy¹⁴, which quantifies the distance of a given state with its nearest state with no three-way entanglement, and robustness¹⁵.

With respect to the geometry of projective spaces, for permutation invariant states, the Majorana representation leads to the identification of maximal symmetric n-qubit states^16,17; it has also been reported an entanglement measure associated with the barycenter of the Majorana constellation¹⁶. More recently, the triangle whose edges correspond to the squared bipartite concurrence of a three-qubit system has been considered as a useful tool to quantify entanglement¹⁸. It has been shown that the genuinely multipartite concurrence defined in¹⁹ is exactly the square root of the shortest edge length of such a triangle, and that its perimeter is nothing else than the global entanglement measure considered in^20,21. Remarkably, the concurrence triangle area, computed through the Heron’s formula, is associated with a genuine entanglement measure referred to as the concurrence fill¹⁸. Geometric simplices (tetrahedra) can be used to quantify GME²², a generalization of the Peres-Horodeckis criterion applies also for multiqubit, continuous-variable, and hybrid systems²³, and even entropic measures derived from experimental correlations are useful to quantify tripartite entanglement²⁴.

It is notable that the three qubit entanglement–polytope permits the introduction of some criteria for the characterization and detection of entanglement^{25,26,27,28,29,30,31,32,33,34}. To deepen the understanding of entanglement classification, the relationship between the entanglement types introduced in^7,8 and some subsets of the polytope^27,28 has been analyzed. In this context, a relationship between the linear entropy of entanglement^20,21 and the Euclidean distance to one of the vertices of the polytope has been observed^26,35. However, most of the characterization of the entanglement–polytope studied so far has been done qualitatively.

In this work, we study the entanglement between different parts of a tripartite qubit system from a purely geometric perspective. Our approach considers the entanglement polytope defined by the smallest eigenvalues of the reduced density matrices. We introduce a mapping from the state space to the polytope that leads to identifying some relationships between tripartite quantum states and points with clear geometric interpretation in the polytope. Then, fully separable, bi-separable and non-separable states are associated with concrete subsets (vertices, edges, facets, etc) of the polytope, providing a geometric identification of entanglement.

The most striking feature of our approach is to find that the projection of a given point of the polytope along the edges that represent biseparable states encodes a quantification of both, global and genuine entanglement.

As a byproduct, we look for a way to force the system to behave in a particular form. The cornerstone is provided by solutions to the inverse problem: given a point on the polytope in a region that characterizes very specific entanglement properties, the quantum state that satisfies such a profile must be found. We show that this approach offers interesting challenges and a much broader perspective on nonclassical correlations since it opens the possibility of controlling and manipulating entanglement for practical purposes.

In Section 2 we review the convex structure of the three-qubit polytope and some entanglement properties are characterized qualitatively. A quantitative description of the three-qubit entanglement is provided in Section 3, where we propose two distance-based entanglement measures, one quantifying the global entanglement and the other characterizing the three-qubit genuine entanglement. Section 4 is addressed to solve the inverse problem. Some conclusions are given in Section 5.

Qualitative characterization of entanglement

Let $\mathcal {H} = \mathcal {H}_2 \otimes \mathcal {H}_2 \otimes \mathcal {H}_2$ be the Hilbert space of a three-qubit system, with $\mathcal {H}_2$ the two-dimensional space of states for a single qubit. Given a pure state $\vert \psi \rangle \in \mathcal {H}$, written in the standard form^7,8,

$$\begin{aligned} \vert \psi \rangle = b_{0} \vert 000 \rangle + b_{1} e^{i \omega } \vert 100 \rangle + b_{2} \vert 101 \rangle + b_{3} \vert 110 \rangle + b_{4} \vert 111 \rangle , \quad b_{\ell } \ge 0, \quad \sum _{\ell =0}^{4} b_{\ell }^{2}=1, \end{aligned}$$

(1)

with $0 \le \omega \le \pi$, we will pay attention to the vector $\vec {\lambda }_{\psi } = \left( \lambda _{1}, \lambda _{2}, \lambda _{3} \right) ^{T}$, where $\lambda _k$ is the smallest eigenvalue of the density matrix $\rho _k$ associated to the kth qubit.

Looping through all allowed values of $b_{\ell }$ and $\omega$ in (1), vector $\vec {\lambda }_{\psi }$ localizes the points of a convex polytope $\mathcal {P} \subset \mathbb {R}^3$ that encodes the degree of entanglement between the different parts of a tripartite qubit system^26,27,28. Therefore, we consider the mapping

$$\begin{aligned} \begin{array}{ll} \Lambda : & \mathcal {H} \rightarrow \mathcal {P} \subset \mathbb {R}^{3}\\ & \mathinner {|{\psi }\rangle } \mapsto \Lambda \left( \psi \right) = \vec {\lambda }_{\psi }, \end{array} \end{aligned}$$

(2)

together with the inequalities²⁹:

$$\begin{aligned} \lambda _i\le \lambda _j+\lambda _k, \quad 0\le \lambda _i\le \tfrac{1}{2}, \quad i,j,k =1,2,3. \end{aligned}$$

(3)

System (3) characterizes $\mathcal {P}$ as the geometric scenario where the marginal problem defined by the pure state $\vert \psi \rangle$ finds solutions with physical meaning²⁶. That is, among all possible states of one-qubit, $\lambda _k$ in (3) selects those that can be achieved as the reduced one-qubit density matrix $\rho _k = {\text {Tr}}_{i,j} \left( \vert \psi \rangle \langle \psi \vert \right)$, with $k \ne i \ne j$. No state of one-qubit that is not linked to $\vert \psi \rangle$ in this way is included in $\mathcal {P}$. Indeed, (3) is a system of triangle inequalities that completely characterize the possible reduced one-qubit states of $\vert \psi \rangle$²⁹.

Figure 1 shows the entanglement–polytope $\mathcal {P}$ that we are dealing with. It is a body that resembles two tetrahedra, joined at their base, embedded in a cube with edges of length equal to 1/2, located at the first octant of $\mathbb {R}^3$. To be concrete, $\mathcal {P}$ is defined by the convex combination of its vertices

$$\begin{aligned} \begin{array}{ccc} \vec {S}=(0,0,0)^T, \quad \vec {B}_1= \left( 0, \tfrac{1}{2} , \tfrac{1}{2} \right) ^T, \quad \vec {B}_2 = \left( \tfrac{1}{2} , 0, \tfrac{1}{2} \right) ^T,\\ \vec {B}_3 = \left( \tfrac{1}{2}, \tfrac{1}{2}, 0 \right) ^T, \quad \vec {G}= \left( \tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2} \right) ^T. \end{array} \end{aligned}$$

(4)

Characterizing multipartite entanglement in terms of entanglement–polytopes is very useful since only one-particle information is required^25,26, see also²⁷ and³⁰. Remarkably, this picture finds immediate application in detection processes of entanglement since its predictions do not require the measurement of correlations between the parts. For example, the experimental detection of entanglement–polytopes for three- and four-qubit genuine entanglement occurring in quantum optics has been reported in^31,32, a fact that shows the practical usefulness of the method.

Fig. 1

Entanglement–polytope $\mathcal {P} \subset \mathbb {R}^3$ associated with the three-qubit states (1). It is a body that resembles two tetrahedra, joined at their base, embedded in a cube with edges of length equal to 1/2. The parameter $\lambda _k$ (defining the corresponding axis) is the smallest eigenvalue of the density matrix associated with the kth qubit. Vertex $\vec {S}$ represents the entire set of fully separable states while $\vec {G}$ corresponds to the Greenberger–Horne–Zeilinger state. The vertices $\vec {B}_i$ correspond to bi-separable states $\vert \phi _i \rangle \vert \phi _{jk} \rangle$, with $\vert \phi _i \rangle$ the state of the ith qubit and $\vert \phi _{jk} \rangle$ a Bell state in the bipartition $i-jk$.

Considering the separability properties of $\vert \psi \rangle$, as it is written in (1), and remembering that local-unitary transformations preserve entanglement properties³⁶, one can identify different entangled pure states in terms of the coefficients $b_{\ell } \ne 0$, see details in Supplementary Information file. Our classification coincides with the results reported in^7,8, and is summarized in Table 1.

For completeness, in Table 1 we have included a set of states that is not obtained directly from (1). These states are classified as type 4d and are represented by the linear combination³⁷:

$$\begin{aligned} \vert \psi _{4d} \rangle = c_{0} \vert 001 \rangle + c_{1} \vert 010 \rangle + c_{2} \vert 100 \rangle + c_{3} \vert 111 \rangle , \quad c_{k} \ge 0, \quad \sum _{k=0}^3 c_k^2 =1. \end{aligned}$$

(5)

Note that unlike $\vert \psi \rangle$, these additional states embrace only four basis vectors. Their usefulness will become clear in the following sections.

Next, based on the results reported in²⁷, we show that this classification results in the identification of concrete convex subsets of $\mathcal {P}$ under the mapping $\Lambda$.

Table 1 The number of basis elements of $\mathcal {H} = \mathcal {H}_2 \otimes \mathcal {H}_2 \otimes \mathcal {H}_2$ that are included in the linear superposition (1) gives rise to a classification of three-qubit states^7,8. Some of the representative states generated by such basis elements are associated with specific convex subspaces of the entanglement–polytope $\mathcal {P} \subset \mathbb {R}^3$ shown in Figure 1, see²⁷ and discussion in the main text. The class of fully separable states is represented by $\vert 000 \rangle$ as a generic case, see details in Supplementary Information file. States of type 4d are represented by the vector $\vert \psi _{4d} \rangle$ defined in (5).

The simplest class, called type 1, refers to fully separable states, hereafter written $\vert \psi _{{\text {sep}}} \rangle = \mathinner {|{\phi _{1}}\rangle } \mathinner {|{\phi _{2}}\rangle } \mathinner {|{\phi _{3}}\rangle }$, with $\vert \phi _{i} \rangle \in \mathcal {H}_{2}$. These states are generically represented by $\vert 000 \rangle$ in Table 1, since they are local-unitary equivalent to such state. Furthermore, in this case the smallest eigenvalue $\lambda _k$ of $\rho _k$ is equal to zero for all $i=1,2,3$. Thus, the entire set of vectors $\vert \psi _{{\text {sep}}} \rangle$ is associated with the vertex $\vec {S} \in \mathcal {P}$, which is a 0-dimensional convex set.

Type 2 includes linear superpositions (1) with two coefficients different from zero as well as any other state $\vert \psi \rangle$ that can be transformed into any of these superpositions by means of local-unitary transformations, see Supplementary Information file for details. We identify two different subclasses, called 2a and 2b.

Type 2a is subdivided into three different categories, called 2a-1, 2a-2 and 2a-3, whose generic states are characterized by the pairs $\{b_2, b_3\}$, $\{b_0, b_2\}$ and $\{b_0, b_3\}$, respectively. These states are bi-separable, written $\mathinner {|{\psi _{{\text {bi}}}}\rangle } = \mathinner {|{\phi _{i}}\rangle } \mathinner {|{\phi _{jk}}\rangle }$, with $\mathinner {|{\phi _{jk}}\rangle }$ a non-separable state shared by the jth and kth qubits (the sub labels are cyclic). They correspond to the one-dimensional convex subsets of $\mathcal {P}$ generated by the vertices $\vec {S}$ and $\vec {B}_i$. That is, type 2a states are associated with the line-segments (edges) $\overline{SB_1}$, $\overline{SB_2}$ and $\overline{SB_3}$ of $\mathcal {P}$. For instance, if $\mathinner {|{\psi _{{\text {bi}}}}\rangle } = b_{2} \mathinner {|{101}\rangle } + b_{3} \mathinner {|{110}\rangle }$, then $\vec {\lambda }_{\psi _{{\text {bi}}}} = (1-2\lambda ) \vec {S} + 2 \lambda \vec {B}_{1}$, where $\lambda = ( 1 - \sqrt{1-4 b_{2}^{2} b_{3}^{2}} )/2$. Similarly for types 2a-2 and 2a-3. Stellar members of type 2a are the bi-separable states linked to the vertices $\vec {B}_i \in \mathcal {P}$, for which $\mathinner {|{\phi _{jk}}\rangle }$ is one of the Bell–basis elements $\sqrt{2} \vert \Phi ^{\pm } \rangle = \vert 00 \rangle \pm \vert 11 \rangle$, $\sqrt{2} \vert \Psi ^{\pm } \rangle = \vert 01 \rangle \pm \vert 10 \rangle$.

The generic type 2b state is characterized by the pair $\{b_0, b_4\}$. This class of states is associated with the one-dimensional convex subset generated by the extremal points $\vec {S}$ and $\vec {G}$ (the line-segment $\overline{SG}$). Explicitly, $\vec {\lambda }_{\psi _{2b}} = (1-2\lambda ) \vec {S} + 2\lambda \vec {G}$, where $\lambda = (1-\sqrt{1-4b_{0}^{2}b_{4}^{2}})/2$. The Greenberger–Horne–Zeilinger (GHZ) state

$$\begin{aligned} \vert GHZ \rangle = \frac{1}{\sqrt{2}} \left( \vert 000 \rangle + \vert 111 \rangle \right) \end{aligned}$$

corresponds to the extremal point $\vec {G}$.

Generic states of type 3 involve three coefficients different from zero in the linear superposition (1). They are associated with two-dimensional convex subsets of $\mathcal {P}$, as we indicate below.

The type 3a refers to generic vectors that can be written in the form

$$\begin{aligned} \vert \psi _\textrm{3a} \rangle = \sqrt{\gamma } \vert 000 \rangle + \sqrt{\alpha } \vert 101 \rangle + \sqrt{\beta } \vert 110 \rangle , \quad 0\le \alpha ,\beta \le 1, \quad \gamma = 1-\alpha -\beta . \end{aligned}$$

(6)

Therefore, the components of $\vec {\lambda }_{\psi _\textrm{3a}}$ are as follows

$$\begin{aligned} \lambda _1= \tfrac{1}{2} - \left| \gamma - \tfrac{1}{2} \right| , \quad \lambda _2 = \tfrac{1}{2} -\left| \beta - \tfrac{1}{2} \right| , \quad \lambda _3 = \tfrac{1}{2} - \left| \alpha - \tfrac{1}{2} \right| . \end{aligned}$$

Fig. 2

The parameters $\alpha$ and $\beta$ completely define the state $\vert \psi _{3a} \rangle$ introduced in Eq. (6). The constraints on these parameters give rise to the convex set $\mathcal {M}$, a right triangle with legs of one unit on the plane $\mathbb {R}^2$. The extreme points, $(\alpha , \beta ) = (0,0)$, (0, 1) and (1, 0), characterize $\vert \psi _{3a} \rangle$ as a fully separable state. The middle points, (1/2, 1/2), (1/2, 0) and (0, 1/2), produce the bi-separable states $\vert 0 \rangle _i \vert \Psi ^+ \rangle _{jk}$, where $\vert \Psi ^+ \rangle _{jk}$ stands for the Bell state $\vert \Psi ^+ \rangle$ shared by the jth and kth qubits. The convex combinations of extreme and middle points yield four different convex subsets (regions) of $\mathcal {M}$ that permit a classification of entanglement for $\vert \psi _{3a} \rangle$.

Figure 2 shows the convex set $\mathcal {M} \subset \mathbb {R}^2$ that arises from the constraints on the parameters $\alpha$ and $\beta$ in Eq. (6). It is a right triangle with legs of one unit. The extreme points, $(\alpha , \beta ) = (0,0)$, (0, 1) and (1, 0), define fully separable states that are mapped onto the vertex $\vec {S}$ of $\mathcal {P}$. In turn, the middle points, (1/2, 1/2), (1/2, 0) and (0, 1/2), produce the bi-separable states that are mapped onto the vertices $\vec {B}_i$ of $\mathcal {P}$. The data shown in Figure 2 is obtained from (6), after the appropriate local unitary transformation. The convex combinations of extreme and middle points yield four different convex subsets (regions) of $\mathcal {M}$ that permit a classification of entanglement for the state $\vert \psi _{3a} \rangle$.

Region I. The convex set $\alpha \in [1/2, 1]$, $\beta \in [0, 1-\alpha ]$, represented in Figure 2 as the right triangle in blue, yields the parametrization

$$\begin{aligned} \vec {\lambda }_{\psi _\textrm{3a}} = \kappa _{1} \vec {S} + \kappa _{2} \vec {B}_{1} + \kappa _{3} \vec {B}_{2}, \end{aligned}$$

(7)

where $\kappa _{1} = 2 \alpha - 1$, $\kappa _{2} = 2 \beta$, and $\kappa _{3} = 1- \kappa _{1} - \kappa _{2}$. Vectors (7) localize the points on the triangle $\triangle _{SB_{1}B_{2}} \in \mathcal {P}$, see Figure 3(a).

Fig. 3

The four different regions of the convex set $\mathcal {M}$ illustrated in Figure 2 are associated with the faces of the lower tetrahedron of the polytope $\mathcal {P}$. The color-code corresponds to the colors of the right-triangles in Figure 2. (a) Region I. (b) Region II. (c) Region III. (d) Region IV.

Region II. The right triangle in orange of Figure 2 corresponds to the convex set $\alpha \in [0,1/2]$, $\beta \in [0, 1/2 - \alpha ]$, and gives

$$\begin{aligned} \vec {\lambda }_{\psi _\textrm{3a}} = \kappa _{1} \vec {S} + \kappa _{2} \vec {B}_{2} + \kappa _{3} \vec {B}_{3}, \end{aligned}$$

(8)

with $\kappa _2=2\alpha$, $\kappa _3=2\beta$ and $\kappa _1=1-\kappa _2-\kappa _3$. In this case, the vectors (8) localize the points on the triangle $\triangle _{SB_{2}B_{3}} \in \mathcal {P}$, see Figure 3(b).

Region III. The right triangle in pink of Figure 2 represents the convex set $\alpha \in [0, 1/2]$, $\beta \in [1/2, 1 - \alpha ]$. This yields

$$\begin{aligned} \vec {\lambda }_{\psi _\textrm{3a}} = \kappa _{1} \vec {S} + \kappa _{2} \vec {B}_{1} + \kappa _{3} \vec {B}_{3}, \end{aligned}$$

(9)

with $\kappa _1=2\alpha -1$, $\kappa _2=2\beta$ and $\kappa _3=1-\kappa _1-\kappa _2$. The points on the triangle $\triangle _{SB_{1}B_{3}} \in \mathcal {P}$ of Figure 3(c) are localized by the vectors (9).

Region IV. The right triangle in light-purple of Figure 2 stands for the convex set $\alpha \in [0, 1/2]$, $\beta \in [1/2 - \alpha , 1/2]$. The corresponding vectors

$$\begin{aligned} \vec {\lambda }_{\psi _\textrm{3a}} = \kappa _{1} \vec {B}_1 + \kappa _{2} \vec {B}_{2} + \kappa _{3} \vec {B}_{3}, \end{aligned}$$

(10)

with $\kappa _2=1-2\beta$, $\kappa _3=1-2\alpha$ and $\kappa _1=1-\kappa _2-\kappa _3$, localize the points on the triangle $\triangle _{B_{1} B_2 B_{3}} \in \mathcal {P}$ shown in Figure 3(d).

The latter case is of particular relevance. Making $\alpha = \beta = 1/3$ we have the state

$$\begin{aligned} \vert \psi _\textrm{3a} \rangle = \tfrac{1}{\sqrt{3}} \left( \mathinner {|{000}\rangle } + \mathinner {|{101}\rangle } + \mathinner {|{110}\rangle } \right) , \end{aligned}$$

which is local unitary equivalent to the well-known W–state,

$$\begin{aligned} \vert W \rangle = \tfrac{1}{\sqrt{3}} \left( \mathinner {|{001}\rangle } + \mathinner {|{010}\rangle } + \mathinner {|{100}\rangle } \right) . \end{aligned}$$

(11)

Explicitly, $\vert \psi _\textrm{3a} \rangle = \left( \sigma _{x} \otimes \mathbbm {1} \otimes \mathbbm {1} \right) \vert W \rangle$, with $\sigma _{x}$ the x–Pauli matrix and $\mathbbm {1}$ the identity operator in $\mathcal {H}_2$. Since the smallest eigenvalues are local unitary invariant^38,39 both, $\vert \psi _\textrm{3a} \rangle$ and $\vert W \rangle$, are mapped onto the same point $\vec {\lambda }_{W} = \left( 1/3,1/3, 1/3 \right) ^{T} \in \mathcal {P}$, which is the geometric center of the triangle $\triangle _{B_{1}B_{2}B_{3} }\subset \mathcal {P}$.

On the other hand, the type 3b includes three different families of generic vectors, given by the expressions

$$\begin{aligned} \begin{array}{l} \vert \psi _\mathrm{3b-1} \rangle = b_{0} \vert 000 \rangle + b_{1} e^{i\omega } \vert 100 \rangle + b_{4} \vert 111 \rangle ,\\[2ex] \vert \psi _\mathrm{3b-2} \rangle = b_{0} \vert 000 \rangle + b_{2} \vert 101 \rangle + b_{4} \vert 111 \rangle ,\\[2ex] \vert \psi _\mathrm{3b-3} \rangle = b_{0} \vert 000 \rangle + b_{3} \vert 110 \rangle + b_{4} \vert 111 \rangle . \end{array} \end{aligned}$$

(12)

They correspond respectively to the triangles $\triangle _{SB_{1}G}$, $\triangle _{SB_{2}G}$, and $\triangle _{SB_{3}G}$, see Figure 4.

Fig. 4

The type 3b-i states (12) are associated with the two-dimensional convex subsets that are different from the faces of the tetrahedra that form the polytope $\mathcal {P}$. (a) Type 3b-1. (b) Type 3b-2. (c) Type 3b-3.

The generic type 4 states, referring to superpositions (1) that admit four non-zero coefficients, correspond to three-dimensional convex subsets of $\mathcal {P}$ that are subdivided into four different classes.

Type 4a, with $b_4=0$, is restricted to the lower tetrahedron of $\mathcal {P}$, written $SB_{1}B_{2}B_{3}$, where $\lambda _{1} + \lambda _{2} + \lambda _{3} \le 1$²⁷. The identity in this inequality is saturated by the points on the triangle $\triangle _{B_{1}B_{2}B_{3}}$.

Type 4b is subdivided into two different categories, called b-1 (with $b_2=0$) and b-2 (with $b_3=0$). They are respectively mapped into a subset of $SB_{1}B_{3}G$ and $SB_{1}B_{2}G$, see Figure 5.

Fig. 5

Type 4b states. Following²⁸, the values of the Fourier coefficients have been discretized to identify the image of the states. (a) Type 4b-1. (b) Type 4b-2.

For states of type 4c (with $b_1=0$), the image covers region $SB_{1}B_{2}B_{3} \cup SB_{2}B_{3}G$. To identify states that are mapped to the faces of the upper tetrahedron of $\mathcal {P}$ we fix $b_0 = 1/\sqrt{2}$, and consider the linear superposition

$$\begin{aligned} \mathinner {|{\psi _{4c-1} }\rangle }= \tfrac{1}{\sqrt{2}} \mathinner {|{000}\rangle } + b_{2} \mathinner {|{101}\rangle } + b_{3} \mathinner {|{110}\rangle } + b_{4} \mathinner {|{111}\rangle }, \end{aligned}$$

(13)

where $b_{2}^{2} + b_{3}^{2} + b_{4}^{2} = 1/2$. In this case, the vector

$$\begin{aligned} \vec {\lambda }_{\psi _\mathrm{4c-1}} = \kappa _{1} \vec {B}_{2} + \kappa _{2} \vec {B}_{3} + \kappa _{3} \vec {G}, \end{aligned}$$

(14)

with

$$\begin{aligned} \kappa _{1} = 2 \sqrt{b_{2}^{2} \left( \tfrac{1}{2} - b_{3}^{2} \right) }, \quad \kappa _{2} = 2 \sqrt{b_{3}^{2} \left( \tfrac{1}{2} - b_{2}^{2} \right) }, \quad \kappa _{3} = 1 - \kappa _{1} -\kappa _{2}, \end{aligned}$$

(15)

localizes the points on the triangle $\triangle _{B_2B_3G}$. The appropriate permutations transform (13) into a pair of additional states of type 4c. Namely,

$$\begin{aligned} \begin{array}{ll} \mathinner {|{\psi _{4c-2}}\rangle } = \frac{1}{\sqrt{2}} \mathinner {|{000}\rangle } + b_{2} \mathinner {|{110}\rangle } + b_{3} \mathinner {|{011}\rangle } + b_{4} \mathinner {|{111}\rangle },\\[2ex] \mathinner {|{\psi _{4c-3}}\rangle } = \frac{1}{\sqrt{2}} \mathinner {|{000}\rangle } + b_{2} \mathinner {|{011}\rangle } + b_{3} \mathinner {|{101}\rangle } + b_{4} \mathinner {|{111}\rangle }, \end{array} \end{aligned}$$

(16)

where $\sum b_{i}= 1/2$. It is immediate to show that these states are mapped into the triangles $\triangle _{B_1B_3G}$ and $\triangle _{B_1B_2G}$, respectively. That is, with type 4c-i states, $i=1,2,3$, we cover the three faces of the upper tetrahedron in $\mathcal {P}$, see Figure 6.

Fig. 6

The type 4c-i states, $i=1,2,3$, are associated with the faces of the upper tetrahedron of the polytope $\mathcal {P}$. (a) Type 4c-1. (b) Type 4c-2. (c) Type 4c-3.

The generic type 4d state is expressed in an alternative canonical form³⁷, given in (5). This class of states is associated with points along the entire polytope $\mathcal {P}$. The relationship between types 4b, 4c, 4d and the polytope has been numerically studied in²⁸.

Quantitative characterization of entanglement

Consider two different points in the entanglement–polytope, $\vec {\lambda }_{\psi _k} \in \mathcal {P}$, $k=1,2$. We know that there is at least one state $\vert \psi _k \rangle$ in $\mathcal {H}$ that is associated with each $\vec {\lambda }_{\psi _k}$ through the mapping $\Lambda$.

Assuming that $\vert \psi _1 \rangle$ and $\vert \psi _2 \rangle$ have a certain degree of entanglement, what it does mean to say that one of them is more entangled than the other?

The notion of entanglement measure gives diverse quantitative answers to such a question^{2,3,4,5,9,10,40}. Most of them are based on the distance measures of quantum states, which quantify how close two states are (static case), or how well information has been preserved during a dynamic process (dynamic case)¹. In any case, it is required a measure standard, a state (or set of states) for which the measure is equal to 1, and a state (or set of states) that provides a result equal to 0. For three-qubit entanglement, it is usual to associate $\vert GHZ \rangle$ with measure 1, and the fully separable states with measure 0. Within this standard, any entanglement measure of the states included in Table 1 should range between 0 and 1.

How do the entanglement properties of $\vert \psi _k \rangle$ affect point $\vec {\lambda }_{\psi _k}$?

Suppose $\vert \psi _1 \rangle$ is the GHZ–state and that $\vert \psi _2 \rangle$ is to be determined. Since $\vert GHZ \rangle$ corresponds to the vertex $\vec {G} = \vec {\lambda }_{\psi _1}$, if we wanted $\vert \psi _2 \rangle$ to be as entangled as possible, we would look for the point $\vec {\lambda }_{\psi _2}$ to be in the vicinity of $\vec {G}$. The closer $\vec {\lambda }_{\psi _2}$ is to $\vec {G}$, the state $\vert \psi _2 \rangle$ will be more ‘similar’ to $\vert GHZ \rangle$.

The problem is to define the notion of proximity between two points in $\mathcal {P}$ that corresponds to some entanglement measure in $\mathcal {H}$.

Next, we provide two different options, one addressed to quantify global entanglement and the other characterizing genuine entanglement.

Global entanglement is usually quantified in terms of bipartite entanglement measures^15,20,36. An example is the measure Q introduced in²⁰, which is the sum of concurrences between a single qubit and the remaining qubits in the system. However, Q does not distinguish between fully inseparable states and entangled states that are separable according to some set of subsystems⁴⁰. On the other hand, one says that a pure state is genuinely entangled if it cannot be written as the product of simpler entangled states¹⁹, the canonical examples are states $\vert GHZ \rangle$ and $\vert W \rangle$. In general, a given measure quantifies genuine entanglement if (a) it returns the result zero for fully separable states as well as for bi-separable states and (2) it is positive for non-biseparable states^18,19,22.

Let us project the vector $\vec {\lambda }_{\psi } \in \mathcal {P}$ on the line segments $\overline{SB_{i} } \subset \mathcal {P}$. In each case one has

$$\begin{aligned} \vec {\lambda }_{\psi } = \vec {p}_{i} + \vec {q}_{i}, \quad \vec {p}_i = \left( \vec {\lambda }_{\psi } \cdot \textbf{e}_{B_i} \right) \textbf{e}_{B_i} , \quad \textbf{e}_{B_i} = \sqrt{2} \vec {B}_i, \quad i=1,2,3. \end{aligned}$$

(17)

The above decomposition is illustrated in Figure 7. Vectors $\vec {p}_i$ and $\vec {q}_i$ are the projection of $\vec {\lambda }_{\psi }$ on $\vec {B}_{i}$ and rejection of $\vec {\lambda }_{\psi }$ from $\vec {B}_{i}$, respectively. Their norms, written in terms of the components of $\vec {\lambda }_{\psi }$, read as follows

$$\begin{aligned} p_{i} = \tfrac{1}{\sqrt{2}} \left( \lambda _{j} + \lambda _{k} \right) , \quad q_{i}= \sqrt{\lambda _{i}^{2} + \tfrac{1}{2} \left( \lambda _{j} - \lambda _{k} \right) ^{2} }, \quad i,j,k =1,2,3. \end{aligned}$$

(18)

Fig. 7

Partial section of the entanglement–polytope $\mathcal {P}$ along the plane $\Pi _i$ defined by the vertices $\vec {S}$, $\vec {B}_i$ and $\vec {G}$. The orthogonal projection of $\vec {\lambda }_{\psi } \in \mathcal {P}$ on the line-segment $\overline{SB_i} \subset \mathcal {P}$ (written $\vec {p}_i$), as well as the rejection of $\vec {\lambda }_{\psi }$ from $\overline{SB_i}$ (denoted $\vec {q}_i$) are useful for introducing diverse entanglement measures (see discussion in the main text). If $\vec {\lambda }_{\psi }$ is located in $\Pi _i$ (as shown in the figure), then $\vec {q}_i$ is also located in $\Pi _i$. In general, both $\vec {q}_i$ and $\vec {\lambda }_{\psi }$ localize the same (arbitrary) point of $\mathcal {P}$, the former from $\vec {p}_i$ on the line-segment $\overline{SB_i}$, the latter from the vertex $\vec {S}$.

Clearly $\vec {\lambda }_{\psi } = \vec {S}$ produces $p_i = q_i = 0$, since $\lambda _i=0$ for all $i=1,2,3$. Avoiding this simple case, the identity $\vec {\lambda }_{\psi } = \vec {B}_i$ for some $i=1,2,3$, provides null rejection $q_i = 0$, and vice versa. We have seen already that these points, distributed along the line segment $\overline{SB_{i} }$, yield the bi-separable states $\vert \psi _{{\text {bi}}} \rangle = \mathinner {|{\phi _{i}}\rangle } \mathinner {|{\phi _{jk}}\rangle }$.

On the other hand, if $\lambda _i = \lambda$ for all $i=1,2,3$, then $p_i = \sqrt{2} \lambda$ and $q_i = \lambda$. Vectors $\vec {\lambda }_{\psi }$ satisfying this condition localize points along the line-segment $\overline{SG}$. In this case, the largest rejection $q_i = 1/2$ and largest projection $p_i= {1}/{\sqrt{2}}$ are attributed to the vertex $\vec {\lambda }_{\psi } = \vec {G}$, see Figure 7.

It is notable that the norm of the projection $\vec {p}_i$ is proportional to the average (arithmetic mean) of $\lambda _j$ and $\lambda _k$, we write $p_i = \sqrt{2} {\text {Av}} (\lambda _j, \lambda _k)$. Although the eigenvalue $\lambda _i$ seems to be missing here, it plays a significant role to define the decomposition (17). Indeed, $\lambda _i$ determines the length of $q_i$ (and the length of $p_i$ as well).

If we make $\lambda _i =0$, the inequalities (3) imply $\lambda _j = \lambda _k \equiv \lambda$ (by necessity), so that $q_i=0$. That is, as noted above, $\lambda _i =0$ produces the bi-separability of the three-qubit state by isolating the ith qubit. Moreover, if $\lambda _i =0$ then $p_i = \sqrt{2} \lambda$. Therefore $p_i \in [0, {1}/{\sqrt{2}} ]$, as expected for the bi-separable states $\vert \psi _{{\text {bi}}} \rangle = \mathinner {|{\phi _{i}}\rangle } \mathinner {|{\phi _{jk}}\rangle }$.

In addition, since $\lambda _i = 1/2$ means that $\rho _{i}$ is maximally mixed, the corresponding three-qubit state (in the bipartition $i-jk$) is maximally entangled. This configuration imposes the number ${1}/{(2 \sqrt{2})}$ as a lower bound on the values of $p_i$, for which we find maximally entangled states. As a consequence, the projection domain is restricted to the second half of the previous case, $p_i \in [{1}/{(2 \sqrt{2})}, {1}/{\sqrt{2}}]$.

The previous analysis shows that the norm of $\vec {p}_i$ encodes sensitive information about the entanglement of the three-qubit system.

Looking for a global treatment, where all the components of $\vec {\lambda }_{\psi }$ intervene at the same time, we propose the following arithmetic mean

$$\begin{aligned} \xi (\psi ) = \tfrac{\sqrt{2}}{3} \left( p_1 + p_2 + p_3 \right) = \tfrac{2}{3} \left( \lambda _1 + \lambda _2 + \lambda _3 \right) , \end{aligned}$$

(19)

which vanishes for fully separable states ($\lambda _{1,2,3}=0$), and is normalized to 1 for the GHZ–state ($\lambda _{1,2,3}=1/2$).

Fig. 8

The arithmetic mean $\xi (\psi )$ introduced in Eq. (19) vanishes for fully separable states and is normalized to 1 for the GHZ–state. (a) The points $\vec {\lambda }_{\psi } \in \mathcal {P}$ average higher values $\xi$ as they get closer to the vertex $\vec {G} \in \mathcal {P}$. (b) Condition $\xi (\psi ) = \xi _0$, with $\xi _0 = {\text {constant}}$, defines planes transverse to the line segment $\overline{SG}$ whose points represent states $\vert \psi \rangle \in \mathcal {H}$ with the same degree of entanglement. The $\xi _0$–planes shown in the figure correspond to $\xi _0 = 1/3, 2/3$, and 5/6.

Figure 8(a) shows the distribution of points $\vec {\lambda }_{\psi }$ according to $\xi (\psi )$. Clearly, these points average better values $\xi$ as they get closer to the vertex $\vec {G}$.

Of particular interest, if $\lambda _i = \lambda$ for all $i=1,2,3$, then $p_i = \sqrt{2} \lambda$, $q_i = \lambda$, and $\xi (\psi ) = 2 \lambda$. In this case $\vec {\lambda }_{\psi }$ localizes points along the line-segment $\overline{SG}$. Then the projection $p_i$ ($={1}/{\sqrt{2}}$), the rejection $q_i$ ($=1/2$) and the measure $\xi$ ($=1$) reach their maximum when $\vec {\lambda }_{\psi } = \vec {G}$.

A very versatile property of the average (19) arises by imposing the condition $\xi (\psi ) = {\text {constant}}$, since this defines a plane transverse to the line segment $\overline{SG}$ whose points represent states $\vert \psi \rangle \in \mathcal {H}$ with the same degree of entanglement. Indeed, assume that such a plane cuts the line segment $\overline{SG}$ at the point localized by $\vec {\lambda }_0$. We write $\vec {\lambda }_0 = \xi _0 \vec {G}$, with $\xi _0\in [0,1]$. If $\vec {\lambda }$ localizes another point on the plane, then $\vec {\lambda } - \vec {\lambda }_0$ must be orthogonal to the unitary vector $\textbf{n} = \vert \vert \vec {G} \vert \vert ^{-1} \vec {G}$, so we arrive at the equation

$$\begin{aligned} {\hat{n}}\cdot (\vec {\lambda }-\vec {\lambda }_0)=0. \end{aligned}$$

(20)

The solution of (20) is easily found, it is given by $\xi _0 = \xi (\psi )$.

Figure 8(b) shows some $\xi _0$–planes. Among them, the triangle $\triangle _{B_1B_2B_3}$ coincides with the plane $\xi _0 = 2/3$ and contains the W–state at its geometric center, as indicated above. That is, $\vert W \rangle$ is $\xi = 1/3$ distant from $\vert GHZ \rangle$.

The decomposition (17) offers another possibility to quantify entanglement. As we have seen, the rejection $\vec {q}_i$ is very sensitive to the eigenvalue $\lambda _i$ (its norm $q_i$ cancels if $\lambda _i=0$), and vice versa. Then, we may use $q_i$ to quantify the ‘transverse distance’ between $\vec {\lambda }_{\psi }$ and $\overline{SB_i}$ since vector $\vec {\lambda }_{\psi }$ is as ‘close’ to $\overline{SB_i}$ as the rejection $q_i$ (equivalently, $\lambda _i$) approaches zero. In this context, we introduce the function

$$\begin{aligned} \mu (\psi ) = 2 \min (q_1,q_2,q_3), \end{aligned}$$

(21)

which quantifies the transverse–distance from $\vec {\lambda }_{\psi }$ to the nearest line segment $\overline{SB_i}$.

Figure 9(a) shows the distribution of points $\vec {\lambda }_{\psi }$ according to the function $\mu$. Similar to the previous case, condition $\mu (\psi ) = \mu _0 = {\text {const}}$ provides a collection of points that represent pure states $\vert \psi \rangle$ with the same degree of entanglement. Figure 9(b) shows the regions of $\mathcal {P}$ associated with two different values of $\mu _0$.

Fig. 9

(a) The transverse–distance measure $\mu (\psi )$ introduced in (21) gives 0 for separable states and 1 for the GHZ–state. In addition, this also gives 0 for bi-separable states, so it discriminates bi-separability from genuine entanglement. Notably, $\mu$ gives the same value as $\xi$ for the W–state, which confirms that $\vert W \rangle$ is $\xi = \mu = 1/3$ distant from $\vert GHZ \rangle$. (b) Regions of constant measure $\mu (\psi ) = \mu _0$ for $\mu _0 = 4/5$ (closest to vertex G) and $\mu _0 = 1 - \sqrt{13}/5$ (closest to vertex S).

The standard of $\mu (\psi )$ is as follows: it vanishes for separable states, attains its maximum value ($=1$) for the GHZ–state, and carries out the value $\mu = 2/3$ for the W–state. Incidentally, $\mu (\psi )$ gives the same value as $\xi (\psi )$ for the W–state, reinforcing our previous statement that $\vert W \rangle$ is $\xi = \mu = 1/3$ distant from $\vert GHZ \rangle$, see Figure 10.

As $q_i=0$ is a condition for bi-separability, in contrast with $\xi$, the measure $\mu$ also gives the value 0 for bi-separable states, see Figure 10. Indeed, $\mu$ is a measure of genuine multipartite entanglement since it satisfies the requirements reported in, for example,¹⁸.

Fig. 10

Entanglement measures $\xi (\psi )$, $\mu (\psi )$, $F_{123} (\psi )$ and $\mathcal {C}_{GME} (\psi )$ for states $\vert \psi _{{\text {sep}}} \rangle$, $\vert \psi _{{\text {bi}}} \rangle = \vert 0 \rangle _i \vert \Psi ^+ \rangle _{jk}$, $\vert W \rangle$ and $\vert GHZ \rangle$. All the measures give 0 for fully separable states. Measure $\xi$ does not discriminate bi-separability from genuine entanglement since it averages a value different from 0 for bi-separable states. Among these measures, $\mu$ gives the lowest results for the four states.

Figure 10 shows the values provided by the measures $\xi$ and $\mu$ for states $\vert \psi _{{\text {sep}}} \rangle$, $\vert \psi _{{\text {bi}}} \rangle =\vert 0 \rangle _i \vert \psi ^+ \rangle _{jk}$, $\vert W \rangle$ and $\vert GHZ \rangle$. These results are compared with the values that can be obtained in terms of the concurrence–fill $F_{123}$ and the genuine multipartite concurrence $\mathcal {C} _{{\text {GME}}}$. The former measure is defined as¹⁸:

$$\begin{aligned} F_{123} (\psi ) = \left[ 8 Q(\psi ) \left( \frac{3}{2} Q(\psi ) - \mathcal {C}_{1}^{2} \right) \left( \frac{3}{2} Q(\psi ) - \mathcal {C}_{2}^{2} \right) \left( \frac{3}{2} Q(\psi ) - \mathcal {C}_{3}^{2} \right) \right] ^{1/4}, \end{aligned}$$

where $Q \left( \psi \right) = \frac{1}{3} \sum _{i=1}^{3} \mathcal {C}_{i}^{2} \left( \psi \right)$. The I concurrence $\mathcal {C}_{i}$ is a measure of entanglement between the ith qubit and the subsystem composed of qubits j and k⁴¹. In turn, the measure $\mathcal {C}_{GME}$ is defined as¹⁹:

$$\begin{aligned} C_{GME} (\psi ) = \min \lbrace \mathcal {C}_{1}, \mathcal {C}_{2}, \mathcal {C}_{3} \rbrace . \end{aligned}$$

With exception of $\xi$, these measures give 0 for bi-separable states. That is, $\xi$ does not discriminate bi-separability from genuine entanglement, so it is a measure of global entanglement. On the other hand, among these measures, $\mu$ averages the lowest results for the four states. In other words, $\mu$ defines a lower bound for measuring genuine entanglement.

To compare in more detail both the properties and the behavior of the measures $\xi$ and $\mu$, let us consider the type 3a state

$$\begin{aligned} \vert \psi _{\alpha } \rangle = \cos \alpha \vert 100 \rangle + \sin \alpha \vert 0 \rangle _1 \vert \Psi ^+ \rangle _{23}, \quad 0 \le \alpha \le \tfrac{\pi }{2}. \end{aligned}$$

(22)

It is a matter of substitution to verify that $\vert \psi _{\alpha =0} \rangle =\vert 100 \rangle$ and $\vert \psi _{\alpha =\pi /2} \rangle = \vert 0 \rangle _1 \vert \Psi ^+ \rangle _{23}$. That is, at the ends of the $\alpha$-domain, the state $\vert \psi _{\alpha } \rangle$ becomes fully separable and bi-separable, respectively. Additionally, making $\alpha = \alpha _0= \arccos ({1}/{\sqrt{3}})$, one gets $\vert \psi _{\alpha _0} \rangle = \vert W \rangle$.

Fig. 11

(a) When the parameter $\alpha$ sweeps the domain $[0, \alpha _{**} ] \equiv [0, \pi /2]$, the state $\vert \psi _{\alpha } \rangle$ introduced in (22) describes a path $\vec {\lambda }_{\psi _{\alpha }}$ on the lower tetrahedron of $\mathcal {P}$. The trajectory goes first from the vertex $\vec {S}$ to the midpoint of $\overline{B_{2}B_{3}}$ (at $\alpha = \alpha _* = \pi /4$), and then to the vertex $\vec {B}_1$ (at $\alpha = \alpha _{**}$) on the triangle $\triangle _{B_1B_2B_3}$. In this last journey, $\vec {\lambda }_{\psi _{\alpha }}$ passes through the geometric center of $\triangle _{B_1B_2B_3}$, at $\alpha = \alpha _0 = \arccos ({1}/{\sqrt{3}})$, which houses state $\vert W \rangle$. (b) Measures $\xi$ and $\mu$ for state $\vert \psi _{\alpha } \rangle$, the former gives $\xi _0 = 2/3$ for $\alpha \in [\alpha _*, \alpha _{**}]$ whereas the latter cancels at the ends of the $\alpha$-domain. In contrast with $\xi$, the measure $\mu$ also distinguishes among the points living on $\triangle _{B_1B_2B_3}$. That is, points $\vec {\lambda }_{\psi _{\alpha }}$ closer to the center of $\triangle _{B_1B_2B_3}$ will correspond to more $\mu$-entangled states $\vert \psi _{\alpha } \rangle$.

Parameterized by $\alpha$, the vector $\vec {\lambda }_{\psi _{\alpha }}$ describes a path in the entanglement–polytope $\mathcal {P}$ that follows a trajectory from $\vec {S}$ (at $\alpha =0$) to $\vec {B}_1$ (at $\alpha = \pi /2$), see Figure 11(a). Looping through values in the first half of the $\alpha$-domain, $\vec {\lambda }_{\psi _{\alpha }}$ draws a straight line on the triangle $\triangle _{SB_2B_3}$, from $\vec {S}$ to the midpoint of segment $\overline{B_2B_3}$ (at $\alpha = \pi /4$). From there, the vector continues in a straight line on triangle $\triangle _{B_1B_2B_3}$ to vertex $\vec {B}_1$. In this last journey, $\vec {\lambda }_{\psi _{\alpha }}$ passes through the geometric center of $\triangle _{B_1B_2B_3}$ (at $\alpha = \alpha _0$), which houses state $\vert W \rangle$.

Remember that mesure $\xi$ averages the constant value $\xi _0= 2/3$ for any point on the triangle $\triangle _{B_1B_2B_3}$, see Figure 8(b). Then, the values averaged by $\xi$ would indicate that the degree of entanglement of $\vert \psi _{\alpha } \rangle$ is conserved during the second part of the path described above, just as it is shown in Figure 11(b). In turn, $\mu$ gives 0 for both separable and bi-separable states, so it cancels at the ends of the $\alpha$-domain. That is, with the values given by $\mu$ we find that $\vert \psi _{\alpha } \rangle$ increases its degree of entanglement during the first half of the journey, and decreases it during the second half to remain as at the beginning. According to $\mu$, the maximum degree of entanglement is reached at $\alpha = \alpha _0$, where $\vert \psi _{\alpha } \rangle$ coincides with $\vert W \rangle$. Indeed, $\mu$ averages two local maxima, the one at $\alpha =\alpha _0$, and another at $\alpha =\alpha _* = \pi /4$, see Figure 11(b). Between $\alpha _*$ and $\alpha _0$ (the transit from $\overline{B_2B_3}$ to the geometric center of $\triangle _{B_1B_2B_3}$) there is still an increase of $\mu$ that connects these maxima. This last result shows that, in contrast with $\xi$, the measure $\mu$ also distinguishes among the points living on $\triangle _{B_1B_2B_3}$. The points $\vec {\lambda }_{\psi _{\alpha }}$ closer to the center of $\triangle _{B_1B_2B_3}$ will correspond to more $\mu$-entangled states $\vert \psi _{\alpha } \rangle$.

Let us verify the universality of measure $\mu$ to quantify genuine multipartite entanglement. Consider the state

$$\begin{aligned} \vert \psi _{\theta } \rangle = N(\theta ) \left[ \cos ^2 \left( \tfrac{\theta }{2} \right) \vert 111\rangle + \tfrac{1}{\sqrt{3}} \sin ^2 \left( \tfrac{\theta }{2} \right) \vert W \rangle \right] , \quad \theta \in [0, \pi ], \end{aligned}$$

(23)

where

$$\begin{aligned} N(\theta ) = \left[ \cos ^4 \left( \tfrac{\theta }{2} \right) + \tfrac{1}{3} \sin ^4 \left( \tfrac{\theta }{2} \right) \right] ^{-1/2} \end{aligned}$$

stands for the normalization constant. It is immediate to verify the identities $\vert \psi _{\theta =0} \rangle = \vert 111 \rangle$, $\vert \psi _{\theta = \pi } \rangle = \vert W \rangle$ and $\vert \psi _{\theta = \theta _0} \rangle = \vert \varphi \rangle$, with $\theta _0 = 2 \pi /3$. The latter state is given in Eq. (31), which has been shown to be local unitary equivalent to the GHZ–state. The measures $\mu$ and $F_{123}$ are respectively given by

$$\begin{aligned} \mu (\psi _{\theta }) = 1-\frac{2}{3} \bigg \vert \frac{3+5\cos \theta + \cos 2\theta }{3+2\cos \theta +\cos 2\theta }\bigg \vert , \end{aligned}$$

(24)

and

$$\begin{aligned} F_{123}(\psi _{\theta })= \frac{8 (16 \cos \theta + 5 \cos 2\theta +15)}{9(2\cos \theta +\cos 2\theta +3)} \sin ^4 \left( \frac{\theta }{2} \right) . \end{aligned}$$

(25)

In turn, the GME–concurrence reads $\mathcal {C}_{{\text {GME}}} (\psi _{\theta }) = \sqrt{F_{123}(\psi _{\theta })}$.

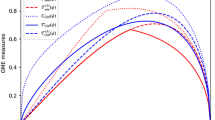
The above functions are plotted in Figure 12. They range between 0 and 1, with $\mu$ defining the lower bound for any $\theta \ne \theta _0$. At $\theta _0$, the three measures give the result 1.

Fig. 12

Entanglement measures $\mu (\psi )$, $F_{123} (\psi )$ and $\mathcal {C}_{{\text {GME}}} (\psi )$ for the state $\vert \psi _{\theta } \rangle$ given in Eq. (23). At $\theta =0$ the state becomes $\vert 111 \rangle$, so it is fully separable. However, it is maximally entangled at $\theta = \theta _0 = 2\pi /3$, since it is local unitary equivalent to the GHZ–state. At $\theta = \pi$ the state is equal to $\vert W \rangle$. Consistently, the measures range between 0 and 1, reaching their maximum ($=1$) at $\theta _0$. Measure $\mu$ defines a lower bound, as it produces lower values than the results of the other two measures, except at $\theta = \theta _0$.

Note that $\mu$ defines a lower bound on the degree of entanglement that could be measured in the state $\vert \psi _{\theta } \rangle$, as it produces lower values than the results of the other two measures.

The inverse problem

One of the advantages of working with the geometric representation of quantum states is that the classification of entanglement becomes visual and simple. If a given three-qubit state $\vert \psi \rangle \in \mathcal {H}$ exhibits a certain amount of entanglement, this is linked to a very concrete point of the entanglement–polytope $\mathcal {P}$ throughout the vector $\vec {\lambda }_{\psi }$.

The question in the opposite direction offers even more interesting challenges and a much broader perspective on entanglement.

Given a point $\vec {\lambda } \in \mathcal {P}$, what three-qubit state (or class of states) can be mapped from $\mathcal {H}$ to precisely $\vec {\lambda }$?

This dilemma is an example of the inverse problem of quantum mechanics⁴², where one seeks to manipulate systems in order to force them to behave in a particular way (some applications can be found in^{43,44,45,46,47,48}). In the present case, it is about choosing a point of the polytope in a region that characterizes very specific entanglement properties, and searching for the quantum state that satisfies such a profile.

Some of the possibilities of the inverse problem for states of types 1 to 4a have been explored in²⁷ (although the authors of such work do not use the terminology of the inverse problem nor exploit all the potential of the method). However, as a matter of fact, the solutions to the inverse problem for three-qubit systems are far from being exhausted. For example, to the best of our knowledge, the inverse problem for the facets $B_{1}B_{2}G$, $B_{1}B_{3}G$ and $B_{2}B_{3}G$, remains unsolved.

To contribute to this topic, let us solve the problem of determining the states that can be associated with a given point $\vec {\lambda }$ on the triangle $\triangle _{B_{2}B_{3}G} \in \mathcal {P}$.

The states that we are looking for belong to type 4c-1, so they are written in the form of Eq. (13). Since $\vec {\lambda }_{\psi _{4c-1}}$ must be provided in advance, we assume that we know every one of the coefficients of the convex combination (14). Then, we solve the parameter system (15) to fix the coefficients of $\vert \psi _{4c-1} \rangle$ in (13). The acceptable solutions are as follows

$$\begin{aligned} \begin{array}{l} b_{2}^{2} = \frac{1}{4} \left( 1 + \kappa _{1}^{2} - \kappa _{2}^{2} - \sqrt{ \left( 1 - \kappa _{1}^{2} + \kappa _{2}^{2} \right) ^{2} - 4 \kappa _{2}^{2} } \right) ,\\[3ex] b_{3}^{2} = \frac{1}{4} \left( 1 - \kappa _{1}^{2} + \kappa _{2}^{2} - \sqrt{ \left( 1 - \kappa _{1}^{2} + \kappa _{2}^{2} \right) ^{2} - 4 \kappa _{2}^{2} } \right) ,\\[3ex] b_{4}^{2} = \frac{1}{2} \left( 1 - \sqrt{ \left( 1 - \kappa _{1}^{2} + \kappa _{2}^{2} \right) ^{2} - 4 \kappa _{2}^{2} } \right) . \end{array} \end{aligned}$$

(26)

Thus, coefficients (26) are determined by the parametrization $\kappa _1$, $\kappa _2$ and $1-\kappa _1 - \kappa _2$, which also defines the facet $B_{2}B_{3}G$.

The inverse problem for facets $B_{1}B_{3}G$ and $B_{1}B_{2}G$ finds a similar solution, this time using the states (16).

In a more general picture, any point $\vec {\lambda } \in \mathcal {P}$ can be written as a convex combination of the extremal points,

$$\begin{aligned} \vec {\lambda } = \kappa _{0} \vec {S} + \kappa _{1} \vec {B}_{1} + \kappa _{2} \vec {B}_{2} + \kappa _{3} \vec {B}_{3} + \kappa _{4} \vec {G}, \quad \kappa _q \ge 0, \quad \sum _{q=0}^{4} \kappa _{q} =1. \end{aligned}$$

(27)

This expression is universal for three-qubit systems in the sense that any of the states reported in Table 1 can be associated with $\vec {\lambda }$.

For example, knowing that states of type 4d are mapped to points along the entire entanglement–polytope $\mathcal {P}$, let us consider $\vert \psi _{4d} \rangle$ as it is given in Eq. (5). Making $c_{r}^{2} = v_{r}$, the corresponding smallest eigenvalues are

$$\begin{aligned} \begin{array}{ll} \lambda _{1} = \frac{1}{2} \left[ 1 - \sqrt{1 - 4 (v_{2}+v_{3}) \left( 1-v_{2}-v_{3} \right) } \right] ,\\ \lambda _{2} = \frac{1}{2} \left[ 1 - \sqrt{1 - 4 (v_{1}+v_{3}) \left( 1-v_{1}-v_{3} \right) } \right] ,\\ \lambda _{3} = \frac{1}{2} \left[ 1 - \sqrt{1 - 4 (v_{0}+v_{3}) \left( 1-v_{0}-v_{3} \right) } \right] . \end{array} \end{aligned}$$

(28)

Since these eigenvalues define the vector $\vec {\lambda }$, from (27) and (28) we see that the coefficients of $\vert \psi _{4d} \rangle$ can be expressed in terms of $\kappa _i$, $i=0,1,2,3$, as follows

$$\begin{aligned} \begin{array}{cc} v_{0} = \frac{1}{2} \left[ 1 - 2 v_{3} \pm (\kappa _{0}+\kappa _{3}) \right] ,\quad v_{1} = \frac{1}{2} \left[ 1 - 2 v_{3} \pm (\kappa _{0}+\kappa _{2}) \right] ,\\ v_{2} = \frac{1}{2} \left[ 1 - 2 v_{3} \pm (\kappa _{0}+\kappa _{1}) \right] , \quad v_3 + v_2 + v_1 + v_0 =1. \end{array} \end{aligned}$$

(29)

Only four of the set of solutions above are admissible for our purposes. In particular, the case ‘$+$’ yields

$$\begin{aligned} c_{0}^2 = \tfrac{1}{2} \left( \kappa _{3} + \tfrac{\kappa _4}{2} \right) , \quad c_{1}^2 = \tfrac{1}{2} \left( \kappa _{2} + \tfrac{\kappa _{4}}{2} \right) , \quad c_{2}^2 = \tfrac{1}{2} \left( \kappa _{1} + \tfrac{\kappa _{4} }{2} \right) , \quad c_{3}^2= \tfrac{1}{2} \left( 1+\kappa _{0}- \tfrac{\kappa _{4} }{2} \right) . \end{aligned}$$

(30)

The set (30) constitutes the solution to the inverse problem of the entanglement–polytope $\mathcal {P}$ that we are dealing with. By providing purely geometric information, through the parameters $\kappa _i$, the state $\vert \psi _{4d} \rangle$ is completely determined, with very specific entanglement properties that can be defined on demand.

To verify the universality of the above solution, first consider the vertex $\vec {S}$. That is, $\kappa _{0} = 1$. Then $c_{3} = 1$ and $c_{0} = c_{1} = c_{2} = 0$. In this case we arrive at the fully separable state $\vert 111 \rangle$. Another immediate example arises if $\kappa _{4} = 1$ (the vertex $\vec {G}$), then $c_{0}=c_{1}=c_{2}=c_{3}= 1/2$, and

$$\begin{aligned} \vert \varphi \rangle = \frac{1}{2} \left( \sqrt{3} \vert W \rangle + \vert 111 \rangle \right) . \end{aligned}$$

(31)

This state is local unitary equivalent to the GHZ state. Indeed,

$$\begin{aligned} \vert \varphi \rangle = \left( \sigma _x H \otimes \sigma _x H \otimes \sigma _x H \right) \vert GHZ \rangle , \end{aligned}$$

with H the Hadamard operator.

More interesting configurations are obtained when two or more $\kappa$-parameters are different from zero. In the extreme case, where $\kappa _i \ne 0$ for all $i=0,1,2,3,4$, one can pay attention to the barycenter of the simplex $\triangle _{B_1B_2B_3}$ (where state $\vert W \rangle$ is located). The inverse problem solution leads to the state

$$\begin{aligned} \vert \chi \rangle = \tfrac{1}{\sqrt{2}}\left( \vert W \rangle + \vert 111 \rangle \right) . \end{aligned}$$

(32)

It is remarkable that $\vert \chi \rangle$ is not local unitary equivalent to $\vert W \rangle$, although these two states are mapped into the same point of the entanglement–polytope $\mathcal {P}$. The difference is notable considering that the three-tangle of $\vert W \rangle$ is equal to zero⁴⁹, while the three-tangle of $\vert \chi \rangle$ is equal to $4/(3\sqrt{3})$.

The above case shows the generality that the inverse problem introduces in the determination of quantum states. In the conventional (direct) problem, every state $\vert \psi \rangle \in \mathcal {H}$ is mapped to one and only one point of $\mathcal {P}$. However, the fact that two or more elements of $\mathcal {H}$ can be mapped to the same point of $\mathcal {P}$ usually goes unnoticed because, in the direct problem, attention is paid to a specific state. The inverse problem considers all possibilities in $\mathcal {H}$ that can be associated with $\vec {\lambda } \in \mathcal {P}$ in a single move. The latter means that the solution to the inverse problem usually associates a family of states, rather than a single state, with such a point.

As we have seen, the solution (30) provides universality to the state $\vert \psi _{4d} \rangle$ in Eq. (5). Once the coefficients $c_k$ of $\vert \psi _{4d} \rangle$ are parametrized with purely geometric information, obtained from the entanglement–polytope $\mathcal {P}$, the entanglement properties of such state become manipulable. Furthermore, the strength of set (30) lies in the fact that any other selection of solutions (29) is local unitary equivalent to (30). For example, taking the roots ‘$+, -, -$’, from (29) we have

$$\begin{aligned} c_0^2 =\tfrac{1}{2} \left( 1+\kappa _{0}- \tfrac{\kappa _{4} }{2} \right) , \quad c_1^2 =\tfrac{1}{2} \left( \kappa _{1} + \tfrac{\kappa _{4} }{2} \right) , \quad c_2^2 =\tfrac{1}{2} \left( \kappa _{2} + \tfrac{\kappa _{4} }{2} \right) , \quad c_3^2=\tfrac{1}{2} \left( \kappa _{3} + \tfrac{\kappa _{4} }{2} \right) . \end{aligned}$$

The state $\vert \widetilde{\psi }_{4d} \rangle$ that results from these coefficients is local unitary equivalent to $\vert \psi _{4d} \rangle$ through the transformation $U_1=\sigma _{x} \otimes \sigma _{x} \otimes \mathbbm {1}$. Similarly, the roots ‘$-,+,-$’ and ‘$-,-,+$’ provide states of type 4d that can be transformed into the form $\vert \psi _{4d} \rangle$ by using the unitary operators $U_2=\sigma _{x} \otimes \mathbbm {1} \otimes \sigma _{x}$ and $U_3=\mathbbm {1} \otimes \sigma _{x} \otimes \sigma _{x}$, respectively.

We have chosen type 4d states to exemplify, in a more or less general way, the applicability and power of the inverse problem. Therefore, we must emphasize that this method is applicable to any point $\vec {\lambda }_{\psi } \in \mathcal {P}$, in connection with the states included in Table 1.

We can also pose the inverse problem in another context. Suppose you are interested in determining a collection of points that describe a given path in $\mathcal {P}$. Say, the path follows one of the surfaces determined by $\mu = \mu _0 ={\text {const}}$. It can be shown that a particular solution is obtained after making $b_{\ell } = 1/\sqrt{5}$, $\ell =0,1,2,3,4$, in (1). Looping through all the domain $[0, \pi ]$ of $\omega$, we obtain the path shown in Figure 13(a). In a given interval of $\omega$, the path overflows the $\mu _0$-region towards vertex S. That is, entanglement is constant for $\omega \in [\omega _0, \pi ]$ and decreases as $\omega$ goes from $\omega _0$ to zero. Our assertion is verified in Figure 13(b), where we show the measures $\mu$, $\xi$, $F_{123}$ and $\mathcal {C}_{GME}$ for the $\omega$-dependent solution we have found to the above inverse problem.

Fig. 13

A particular solution to the inverse problem of finding a set of points in $\mathcal {P}$ that follows a path with entanglement measure $\mu = \mu _0 = {\text {const}}$, see Figure 9(b), is obtained after making $b_{\ell } = 1/\sqrt{5}$ in (1). The pure state $\vert \psi \rangle$ is parameterized by the phase $0 \le \omega \le \pi$ and is projected onto the path $\vec {\lambda }_{\psi (\omega )}$ in $\mathcal {P}$ . (a) $\vec {\lambda }_{\psi (\omega )}$ starts and finishes at $\left( {\mu _{0}}/{2}, \varepsilon , \varepsilon \right)$ and $\left( {\mu _{0}}/{2}, 2/5, 2/5 \right)$, respectively. Here $\mu _{0} = 1 - {\sqrt{13}}/{5}$ and $\varepsilon = \tfrac{1}{2} \left( 1 - {\sqrt{17}}/{5} \right)$. In the interval $[0, \omega _0]$, with $\omega _0 = \pi /3$, the path overflows the $\mu _0$-region. (b) Measures $\mu$, $\xi$, $F_{123}$ and $\mathcal {C}_{GME}$ as functions of $\omega$. Only $\mu$ and $\mathcal {C}_{GME}$ maintain constant in the interval $[\omega _0, \pi ]$, with values $\mu = 1 - {\sqrt{13}}/{5}$ and $\mathcal {C}_{GME} = {12}/{25}$.

In general, the versatility of the solutions of the inverse method could extend to the practical aspects of entanglement. For example, the creation and measurement of three-qubit entanglement associated with states of type  4c-2 have been reported in³¹. Since these results are parametrized by data obtained from the optical bench in the laboratory, information like this could be translated to the entanglement–polytope $\mathcal {P}$ to give it measurable properties.

Conclusions

We have studied the degree of entanglement between the different parts of a tripartite qubit system from a purely geometric perspective. After constructing a convex polytope $\mathcal {P} \subset \mathbb {R}^3$ formed by points $\vec {\lambda } = (\lambda _1, \lambda _2, \lambda _3)$, where $\lambda _k$ is the smallest eigenvalue of the reduced matrix associated with the kth qubit^26,27,28,29, we have considered a map $\Lambda : \mathcal {H} \rightarrow \mathcal {P}$ to identify some relationships between the tripartite quantum states $\vert \psi \rangle \in \mathcal {H}$ and the points of the projective space $\mathcal P$.

In agreement with the conditions reported in²⁷, we have shown that the classification of entangled states introduced in^7,8 results in the identification of concrete subsets of $\mathcal {P}$ under the mapping $\Lambda$. The emphasis in the present study has been on the states mapped into the facets of the polytope $\mathcal {P}$.

Considering the geometric properties of the polytope $\mathcal {P}$, we have introduced two different entanglement measures, denoted $\xi$ and $\mu$. They are respectively associated with the projection and rejection of the point $\vec {\lambda }$ on the biseparable segments of $\mathcal {P}$; the former quantifies global entanglement while the latter measures genuine entanglement. When compared with some previously reported measures of entanglement, it is found that $\xi$ and $\mu$ establish a lower bound for the type of entanglement to which they refer (excluding the GHZ–state for which both measurements return the value 1, as would be expected).

The above results can be extended in several directions. For example, one may consider the projection of $\vec {\lambda }$ onto different subsets of $\mathcal {P}$ in such a way that different entanglement information is provided. In general, the definition of $\xi$ and $\mu$ can be directly extended to the multi-qubit case, since the points of the corresponding entanglement–polytope (the dimension of the space that contains it does not matter) can always be projected onto the appropriate subsets of biseparable points.

The advantages of working with the geometric representation of quantum states, as we have done here, become more evident when considering the possibility of controlling and manipulating entanglement.

As we have shown, by solving the inverse problem we can force the system to behave in a particular way. In particular, given a point of the polytope in a region that characterizes very specific entanglement properties, the quantum state that satisfies such a profile is sought. As a matter of fact, the solution to the inverse problem associates a family of states in $\mathcal {H}$, rather than a single state, with such a point. The latter provides information of the space of states $\mathcal {H}$ that cannot be obtained by solving the conventional (direct) problem, where a given state in $\mathcal {H}$ is mapped to one and only one point of $\mathcal {P}$.

Setting the value of $\xi$ or $\mu$ identifies regions of the entanglement–polytope $\mathcal {P}$ whose points represent states with exactly the same degree of entanglement. These regions allow us to presuppose various evolutions of the tripartite system, associated with trajectories on some hypersurface of $\mathcal {P}$, which are characterized by leaving the degree of initial entanglement invariant. The inverse problem allows us to determine the type of operations that must be applied on the states of the system to induce said trajectories in $\mathcal {P}$. Even better, it opens the possibility of inducing an increase in the degree of entanglement by identifying operations that correspond to transitions between the different hypersurfaces of $\mathcal {P}$ that are characterized by the entanglement measures $\xi$ and $\mu$. Work in this direction is in progress and will be published elsewhere.