Enhancing load frequency control and automatic voltage regulation in Interconnected power systems using the Walrus optimization algorithm

Abstract

This paper introduces the Walrus Optimization Algorithm (WaOA) to address load frequency control and automatic voltage regulation in a two-area interconnected power systems. The load frequency control and automatic voltage regulation are critical for maintaining power quality by ensuring stable frequency and voltage levels. The parameters of fractional order Proportional-Integral-Derivative (FO-PID) controller are optimized using WaOA, inspired by the social and foraging behaviors of walruses, which inhabit the arctic and sub-arctic regions. The proposed method demonstrates faster convergence in frequency and voltage regulation and improved tie-line power stabilization compared to recent optimization algorithms such as salp swarm, whale optimization, crayfish optimization, secretary bird optimization, hippopotamus optimization, brown bear optimization, teaching learning optimization, artificial gorilla troop optimization, and wild horse optimization. MATLAB simulations show that the WaOA-tuned FO-PID controller improves frequency regulation by approximately 25%, and exhibits a considerable faster settling time. Bode plot analyses confirm the stability with gain margins of 5.83 dB and 9.61 dB, and phase margins of 10.8 degrees and 28.6 degrees for the two areas respectively. The system modeling and validation in MATLAB showcases the superior performance and reliability of the WaOA-tuned FO-PID controller in enhancing power system stability and quality under step, random step load disturbance, with nonlinearities like GDC and GDB, and system parameter variations.

Introduction

The interconnected power network stability is a multi-variable multi-objective control problem whose dynamic performance is affected by any disparity between the generation and demand. This disparity is a crucial indicator of power network stability. The stability of any power network can be broadly classified into three categories: frequency, voltage, and rotor angle stability. Frequency stability is influenced by changes in active power, whereas voltage stability is primarily affected by reactive power imbalance. Frequency stability relies on the system’s capacity to reestablish balance between generation and load demand while minimizing load losses¹. On the other hand, voltage stability is the capability of a power system to keep voltages close to their nominal values at all buses throughout the system, even after experiencing a disturbance². Active and reactive power can be kept stable by modifying the speed governor settings in the LFC loop and adjusting the exciter in the AVR loop. Combining both LFC and AVR is commonly referred to as automatic generation control^3,4.

Several classical controllers have been used in past to design LFC and AVRs. This includes integral control (I)⁵, PI control⁶, PID control^7,8, PID controllers with and without serial compensator⁹, fuzzy and neuro-fuzzy based PI and PID controllers^10,11,12, LMI based PID approach¹³, LQR controller¹⁴including many others. In last decade, the structure of PID controller has been translated into different forms such as PID plus double derivative¹⁵, 1 + PD-PID cascade controller¹⁶, tilt integral derivative¹⁷, hybrid fuzzy FO-PI-FO-PD controller¹⁸, cascade FO with filter (${I^\lambda }{D^\mu }N$) controller¹⁹, FO-PID controller^20,21to address specific challenges and improve the dynamic performance. Apart from PID controller and its several derivatives, other control strategies like model predictive control^22,23, sliding mode control^24,25,26, event triggered control²⁷, optimal and adaptive controls^28,29, active disturbance rejection control³⁰ including many others are present in the literature. There are several limitations associated with the use of the aforementioned controllers, such as, slow response, complex tuning process, limited adaptability, high complexity and computation, and model dependency.

Significant advancements in optimization and computation theory has helped in achieving the best performance of LFC and AVR controllers by optimally selecting the design parameters. Researchers have employed various optimization techniques depending upon different objective functions (also known as cost function) to select the gains of the controllers optimally. These optimization techniques are inspired from metaheuristic approaches. Unlike conventional optimization algorithms, metaheuristic optimization algorithms are simple in design and easy to implement. Metaheuristic optimization algorithms are highly effective for tackling multi-extremum problems to identify the global optimal solution. Their results are not influenced by initial conditions, they operate independently of the solution domain, and they exhibit strong robustness. Over the past few years, metaheuristic optimization methods have drawn inspiration from evolutionary phenomena, human behavior and intelligence, nature, biological science, physical laws, game rules including many others. PI/PID controllers for LFC and AVR based on genetic algorithm³¹, differential evolution³², harmony search algorithm³³have been reported among evolution inspired approach. Metaheuristic optimization algorithms such as particle swarm optimization³⁴, grey wolf optimization³⁵, artificial bee colony³⁶, ant colony optimization³⁷, firefly algorithm³⁸, whale optimization algorithm³⁹, bacteria foraging optimization⁴⁰, invasive weed optimization algorithm⁴¹, salp swarm optimization⁴², cuckoo search⁴³, ant lion optimization⁴⁴, brown bear Optimization⁴⁵, moth flame optimization⁴⁶, grasshopper optimization algorithm⁴⁷, mountain gazelle optimization⁴⁸, wild horse optimization⁴⁹, artificial gorilla troop optimization^50,51, including many others are present in literature. While many optimization methods show promise, they often face limitations in convergence speed, robustness, and handling non-linearity or dynamic constraints in different scenarios. By enhancing existing techniques or developing hybrid methods, researchers have found a way to improve accuracy, computational efficiency, and adaptability to diverse problem sets as reported in^{52,53,54,55,56,57}.

Motivation

Any metaheuristic optimization approach has three main components, decision variable, constraints, and cost function. The fundamental working principle of any optimization approach is to quantify the decision variable so as to minimize/maximize the cost while respecting the constraints. Despite the rise of numerous optimization techniques, the quest for enhanced performance persists. Researchers continually seek improvements in convergence speed, accuracy, robustness, and computational efficiency. The validation of NFL theorem also asserts that no single optimization technique can achieve a global solution for all optimization problems. In other words, no single optimization algorithm can effectively solve all or even most optimization problems. In addition, the literature survey indicates that numerous researchers have employed PI/PID controllers, enhanced by optimization methods, to achieve frequency stability in both single-area and multi-area power systems. However, it is surprising to note that only a few studies address both frequency and voltage stability using optimization methods. This study explores the use of a metaheuristic optimization approach to analyze both LFC and AVR with FO-PID controller. Ensuring both frequency and voltage stability is essential for preventing widespread outages, protecting infrastructure, and ensuring the smooth operation of the power grid.

Contribution

In this work, a maiden application of WaOA is demonstrated for LFC and AVR using FO-PID controller. The WaOA is inspired by the social and foraging behaviors of walruses. Walruses are large marine mammals distinguished by their long tusks, stubbles, and significant blubber reserves. They inhabit the cold arctic regions and are typically found on ice floes or in shallow waters. Walruses are known for their social behavior, often living in large herds. The WaOA is inspired by the complex and adaptive behaviors of walruses, translating their social structure, foraging strategies, movement patterns, and adaptability into an effective optimization framework. The primary goal is to achieve frequency and voltage stability using FO-PID controllers. The gains of the FO-PID controllers are tuned using the WaOA, with the integral time square error (ITSE) as the objective function. The frequency response is compared with other new and popular population based metaheuristic optimization approaches like SSA, WOA, COA, SBOA, HOA, BBOA, TL, GTO, and WHO. Results obtained using MATLAB simulation demonstrate improved frequency and voltage stability using the proposed methodology. The key contributions of the work are:

• Maiden application of WaoA is studied for LFC and AVR in two area interconnected power system using FO-PID controller. The LFC and AVR loops are cross coupled making the modelling more significant and practical.

• MATLAB simulations show that the WaOA-tuned FO-PID controller improves frequency regulation by approximately 25%, and exhibits a considerable faster settling time.

• The proposed designs exhibit robustness under random load disturbance, with parameter uncertainties, and typical energy system nonlinearities like GRC and GDB.

• The proposed design demonstrates effectiveness and superiority over other population based metaheuristic optimization approaches.

• The stability of the proposed design is studied based on frequency response analysis.

Layout

The remaining work is outlined as follows: Sect. 2 discusses the two area interconnected LFC and AVR model. In Sect. 3, FO-PID controller is discussed along with the optimization algorithm which is used to tune the controller parameters. Section 4 discusses the simulation results under different case studies. Finally, the article ends with conclusion and scope for future research in Sect. 5.

Problem formulation

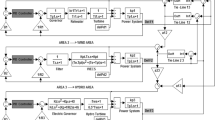
Figure 1 depicts a two area block diagram model of LFC and AVR along with schematic diagram in Fig. 2. A typical LFC model consists of a governor which adjusts the input to the turbine based on the frequency abnormality from the schedule value, ensuring that the system responds to changes in load demand, turbine which converts the mechanical energy into electrical energy, and the load represents the power demand that the system must meet. The two areas are connected via tie-lines to assist power exchange between areas during normal operation. Any disparity between generation and demand in any area has potential to cause oscillations in frequency in all the connected areas. The LFC loop dynamics are given as below²⁷,

$$\Delta \dot {f}= - \frac{{\Delta f}}{{{T_P}}}+\frac{{{K_P}}}{{{T_P}}}\Delta {P_G} - \frac{{{K_P}}}{{{T_P}}}\Delta {P_e} - \frac{{{K_P}}}{{{T_P}}}\Delta {P_{tieline}} - \frac{{{K_P}}}{{{T_P}}}\Delta {P_{Load}}$$

(1)

$$\Delta {\dot {P}_G}= - \frac{1}{{{T_T}}}\Delta {P_G}+\frac{1}{{{T_T}}}\Delta {X_G}$$

(2)

$$\Delta {\dot {X}_G}= - \frac{1}{{R{T_G}}}\Delta f - \frac{1}{{{T_G}}}\Delta {X_G}+\frac{1}{{{T_G}}}u$$

(3)

$$\Delta {\dot {P}_{tielin{e_{i,j}}}}=2\pi \,{T_{i,j}}\left( {\Delta {f_i} - \Delta {f_j}} \right)$$

(4)

Fig. 1

LFC and AVR model⁴.

Fig. 2

LFC and AVR schematic diagram⁵⁸.

where $\Delta f$, $\Delta {P_g}$, $\Delta {X_G}$, $\Delta {P_{tielin{e_{i,j}}}}$are deviations in frequency (Hz), power output (p.u.), governor valve position (p.u.), and tie line power (p.u.) respectively. The parameters ${T_P}$, ${T_T}$, ${T_G}$, $R$, and ${K_B}$ are time constants of load (sec), turbine (sec) and governor (sec), speed regulation coefficient (Hz/p.u.), frequency bias factor (p.u/Hz) respectively. The area control error (ACE) denoted by $e\left( t \right)$ which acts as an input to the FO-PID is a constituent of linear combination of frequency and tie line power as given below,

$$e\left( t \right)={K_B}\Delta f+\Delta {P_{tielin{e_i}}}$$

(5)

Frequency is typically managed through appropriate governor actions, while terminal voltage is regulated by adjusting the generator’s excitation. Deviation in active power causes frequency to change. Any change in frequency influences the terminal voltage because the internal electromotive force of the generator is directly proportional to the frequency. Given that the time constant of the AVR loop is smaller compared to that of the LFC loop, the impact of LFC on AVR is minimal, while the impact of AVR on LFC is significant. Consequently, in practical scenarios, it is necessary to cross-couple the LFC and AVR loops to ensure comprehensive stability and optimal performance of the power system. The parameters ${\alpha _1}$, ${\alpha _2}$, ${\alpha _3}$, ${\alpha _4}$ and ${\beta _s}$ are coefficients of cross coupling between the LFC and AVR model. The AVR system consists of four essential components: the amplifier, exciter, generator field, and sensor. The terminal voltage is continuously monitored and compared to the reference voltage. The resulting error signal act as an input to the FO-PID controller. After amplification, the control input is sent to the excitation system to regulate the generator field excitation. A small change in frequency causes change in rotor angle $\left( \delta \right)$, the real power is given as^1,58,

$$\Delta {P_e}={P_s}\Delta \delta +{K_1}E$$

(6)

The change in terminal voltage is given as,

$$\Delta V={K_2}\Delta \delta +{K_3}E$$

(7)

The generator field transfer function is given as,

$$E=\frac{{{K_F}}}{{1+s{T_F}}}\left( {{E_e} - {K_4}\Delta \delta } \right)$$

(8)

In order to design the FOPID controller, two different objective functions have been designed separately for LFC and AVR,

$${J_1}=\int\limits_{0}^{t} {t\,\left( {{{\left( {\Delta f} \right)}^2}+{{\left( {\Delta {P_{tieline}}} \right)}^2}} \right)} \,dt$$

(9)

$${J_2}=\int\limits_{0}^{t} {t\,\left( {{{\left( {\Delta {V_1}} \right)}^2}+{{\left( {\Delta {V_2}} \right)}^2}} \right)} \,dt$$

(10)

The final objective function for the optimal designing of FOPID controller is linear combination of (9) and (10), $J={J_1}+\gamma {J_2}$ where $\gamma$ is the weighing factor and is $\gamma <1$.

Optimization algorithm

Fractional order PID controller

Fractional calculus was first introduced to scientific community about three centuries ago by Gottfried Leibniz. Unlike conventional calculus, fractional calculus provides different application in science and engineering to achieve robust performance. The concept of fractional calculus in addition with PID controller was first brought into attention by I. Podlubny in 1994⁵⁹. The FO-PID is an advance variant of conventional PID controller, incorporating fractional calculus to enhance control precision and adaptability. In contrast to traditional PID controllers, FO-PID controllers are less affected by parameter variations, can easily achieve iso-damping characteristics, and are well-suited for nonlinear multivariable systems while demonstrating high robustness. However, tuning a FO-PID controller presents a challenge due to the additional two parameters that need to be adjusted compared to a traditional PID controller. The design of FO-PID controller involves five parameters namely proportional gain $\left( {{K_P}} \right)$, integral gain$\left( {{K_I}} \right)$, derivative gain $\left( {{K_D}} \right)$, order of integration$\left( \lambda \right)$, and order of differentiation $\left( \mu \right)$. The differential equation of FO-PID controller is given as,

$$u\left( t \right)={K_P}e\left( t \right)+{K_I}D_{t}^{{ - \lambda }}e\left( t \right)+{K_D}D_{t}^{\mu }e\left( t \right)$$

(11)

Using Laplace transform, one can obtain,

$${G_c}\left( s \right)={K_P}+{K_I}{s^{ - \lambda }}+{K_D}{s^\mu }$$

(12)

where ${G_c}\left( s \right)={{U\left( s \right)} \mathord{\left/ {\vphantom {{U\left( s \right)} {E\left( s \right)}}} \right. \kern-0pt} {E\left( s \right)}}$, and $\lambda$, $\mu$ may not necessarily be an integer. It should be noted that for $\lambda =\mu =1$, (12) takes the form of a transfer function of traditional PID controller. The process of determining the optimal values for the parameters in (12) is outlined in the following sections.

Optimization algorithm

Walruses are large marine mammals known for their distinctive tusks, stubbles, and blubbery body⁶⁰. Found primarily in the arctic regions, walruses inhabit shallow coastal waters and ice floes. Walruses are highly social creatures, frequently assembling in large groups known as herds. They primarily consume benthic invertebrates like clams and mussels, using their sensitive stubbles to discover prey on the ocean floor. Their tusks, which can grow up to three feet long, are used for various purposes, including defense, dominance displays, and aiding in hauling themselves onto ice. Walruses are vital to the arctic ecosystem and hold considerable cultural significance for indigenous communities. Drawing inspiration from the social interactions, foraging patterns, and exploratory behaviors of walruses, WaOA aims to solve complex optimization problems by effectively balancing exploration and exploitation⁶¹. Here, each walrus signifies a prospective solution, and the population evolves over time as walruses interact, forage locally, and explore new areas. This approach enables the WaOA to effectively explore the search space, adaptively modifying its strategies to identify optimal or near-optimal solutions across various applications. Figure 3 illustrate the control methodology.

Fig. 3

Control approach block diagram (The walrus image used in this figure was generated using DALL·E, version 3, OpenAI).

The WaOA is a population-based metaheuristic optimization approach where the search agents are modelled as walruses. In WaOA, each walrus corresponds to a potential solution for the optimization problem, with its location in the search space indicating the values of the problem variables. Consequently, each walrus is represented as a vector, and the entire population of walruses can be mathematically described using a population matrix. The optimization begins with random initialization of the members based on the upper and lower bound of the problem using (13),

$${x_{i,j}}={l_j}+rand \cdot \left( {{u_j} - {l_j}} \right)\,\,;\,\,i=1,2,3 \ldots .\,N\,;\,j=1,2,3 \ldots.\,D$$

(13)

where ${x_{i,j}}$ denotes the value of the ${j^{th}}$ design variable specified by the ${i^{th}}$ population member, $N$ denotes number of population (walruses), $D$ is the total number of design variables also known as dimension, $rand$ is a random number in the range $\left[ {0,\,1} \right]$, ${u_j}$ and ${l_j}$ are the upper and lower bound of ${j^{th}}$ design variables respectively. The population matrix$X$with rows representing candidate solution and columns representing problem variables is shown below,

$$X=\left[ {\begin{array}{*{20}{c}} {{X_1}} \\ \vdots \\ {{X_i}} \\ \vdots \\ {{X_N}} \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} {{x_{1,1}}}& \cdots &{{x_{1,j}}}& \cdots &{{x_{1,D}}} \\ \vdots & \ddots &{}&{}& \vdots \\ {{x_{i,1}}}& \cdots &{{x_{i,j}}}& \cdots &{{x_{i,D}}} \\ \vdots &{}&{}& \ddots & \vdots \\ {{x_{N,i}}}& \cdots &{{x_{N,j}}}& \cdots &{{x_{N,D}}} \end{array}} \right]_{N \times D}}$$

(14)

The estimated objective function values derived from the walruses are provided in (15),

$$J=\left[ {\begin{array}{*{20}{c}} {{J_1}} \\ \vdots \\ {{J_i}} \\ \vdots \\ {{J_N}} \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} {J\left( {{X_1}} \right)} \\ \vdots \\ {J\left( {{X_i}} \right)} \\ \vdots \\ {J\left( {{X_N}} \right)} \end{array}} \right]_{N \times 1}}$$

(15)

In WaOA, the update process for walrus positions is modelled in three distinct phases, each reflecting the natural behaviours of these animals.

Phase I: exploration phase

The walrus with the tallest tusk is considered to be the strongest and leader for rest of the walruses. It helps others in the group to guide for the food. The food includes clams and mussels, worms, crustaceans, sea cucumbers and urchins, and other benthic invertebrates. In walruses, tusk length is analogous to the superiority of objective function values for candidate solutions. Thus, the strongest walrus in the population is the one which has the best objective function value. This search behaviour enables exploration of different regions within the search space, improving the WaOA’s global search capabilities. The position update process for walruses is mathematically modelled based on their feeding patterns, guided by the dominant member of the group, as outlined in (16) and (17). At the start, using (16), a fresh position for a walrus is generated. This fresh position changes the previous one if it improves the objective function’s value, as modelled in (17)⁶¹.

$$x_{{i,j}}^{{{p_1}}}={x_{i,j}}+ran{d_{i,j}} \cdot \left( {{p_j} - {I_{i,j}} \cdot {x_{i,j}}} \right)\,$$

(16)

where $x_{{i,j}}^{{{p_i}}}$ is the new status of the ${i^{th}}$ walrus in the ${j^{th}}$ dimension based on the first phase, $ran{d_{i,j}}$ is any random number in the interval $\left[ {0,\,1} \right]$, ${p_j}$ is the best solution considering the strongest walrus in the ${j^{th}}$ dimension, ${I_{i,j}}$ is any random number used to improve the algorithm’s exploration ability which is equal to one or two. If the new objective function value is better than the previous in that position, the new position for a walrus $X_{i}^{{{p_1}}}$is accepted. This process is modelled as follow,

$${X_i}=\left\{ {\begin{array}{*{20}{c}} {X_{i}^{{{p_1}}}\,,\,J_{i}^{{{p_1}}}<{J_i}} \\ {{X_i}\,,else} \end{array}} \right.$$

(17)

Equation (17) is responsible to drive the algorithm towards global optimal solution within the search space.

Phase 2: Migration

During the summer, walruses migrate to rocky beaches as the air warms. In WaOA, this migration behaviour is leveraged to direct the walruses toward promising regions in the search space. This behavioural mechanism is represented by (18) and (19). The model assumes that each walrus moves to the position of another randomly chosen walrus located in a different area of the search space. As a result, a new proposed position is initially generated according to (18). If this new position improves the value of the objective function, it replaces the walrus’s previous position as per (19)⁶².

$$x_{{i,j}}^{{{p_2}}}=\left\{ {\begin{array}{*{20}{c}} {{x_{i,j}}+ran{d_{i,j}} \cdot \left( {{x_{k,j}} - {I_{i,j}} \cdot {x_{i,j}}} \right);\,{J_k}<{J_i}} \\ {{x_{i,j}}+ran{d_{i,j}} \cdot \left( {{x_{i,j}} - {I_{k,j}}} \right),else,} \end{array}} \right.$$

(18)

$${X_i}=\left\{ {\begin{array}{*{20}{c}} {X_{i}^{{{p_2}}}\,,\,J_{i}^{{{p_2}}}<{J_i}} \\ {{X_i}\,,else,} \end{array}} \right.$$

(19)

where $X_{i}^{{{p_2}}}$ is the new position of the ${i^{th}}$ walrus after the second phase, $x_{{i,j}}^{{{p_2}}}$ is its ${j^{th}}$ dimension, $J_{i}^{{{p_2}}}$ is the value of objective function, ${X_k},\mathop k\limits_{{k \ne i}} \in \left\{ {1,2, \ldots N} \right\}$ is the location of selected walrus to migrate the ${i^{th}}$ walrus towards it, ${x_{k,j}}$ is its ${j^{th}}$ dimension, and ${J_k}$ is its objective function valuE

Phase 3: exploitation phase

Walruses frequently face threats from polar bears and killer whales. Their natural responses to evade and confront these predators result in shifts in their positions within their current area. By simulating this behaviour, WaOA improves its local search capabilities around candidate solutions. In the simulation, a neighbourhood is defined around each walrus, and a new position is randomly generated within this neighbourhood using (20) and (21). If this new position yields a better objective function value, it replaces the previous position according to (22)^61,62.

$$x_{{i,j}}^{{{P_3}}}={x_{i,j}}+\left( {l_{{local,j}}^{t}+\left( {u_{{local,j}}^{t} - rand \cdot l_{{local,j}}^{t}} \right)} \right)$$

(20)

$$Local \ Bounds: \ \left\{ {\begin{array}{*{20}{c}} {l_{{local,j}}^{t}=\frac{{{l_j}}}{t}} \\ {u_{{local,j}}^{t}=\frac{{{u_j}}}{t}} \end{array}} \right.$$

(21)

$${X_i}=\left\{ {\begin{array}{*{20}{c}} {X_{i}^{{{P_3}}},\,J_{i}^{{{p_3}}}<{J_i}} \\ {{X_i},\,else} \end{array}} \right.$$

(22)

where $X_{i}^{{{p_3}}}$ is the new position of the ${i^{th}}$ walrus after third phase, $x_{{i,j}}^{{{P_3}}}$ is its ${j^{th}}$ dimension, $J_{i}^{{{p_3}}}$ is its objective function value, $t$ is the iteration count, $l_{{local,j}}^{t}$ and $u_{{local,j}}^{t}$ are the local upper and lower bounds allowable for the ${j^{th}}$ variable to simulate local search in the neighbourhood of the candidate solutions. After updating the walrus positions based on three phases, one iteration of WaOA is finished. The algorithm then recalculates both the positions of the walruses and their objective function values. This iterative process of refining candidate solutions continues until the final iteration according to the steps defined in WaOA, as detailed by (16) to (22). At the end, WaOA determines the best candidate solution found during the process as the optimal solution to the problem. The flowchart and pseudo code for WaOA are illustrated in Fig. 4 and Table 1, respectively.

Fig. 4

WaOA flowchart⁶².

Table 1 Walrus optimization algorithm pseudo code.

Case studies

The simulation results presented in this study detail the tuning process of a FO-PID controller using the WaOA, executed within the MATLAB environment. The optimization algorithm is initialized with following details which include, population size (number of walruses) = 50; dimension (number of tunable parameters) = 20; lower and upper bound of tunable parameters = 0 and 1 respectively; and maximum iteration as 20. The system parameter values for LFC and AVR are given in Tables 2 and 3 respectively.

Table 2 Two area LFC parameter values²⁴.

Table 3 AVR system parameter values^4,34.

Study 1

In this case, 2% and 1.5% change in load demand is assumed to have occurred at $t=0$ seconds in area 1 and 2 respectively. The simulation results reveal that both LFC and AVR perform exceptionally well using the FO-PID controller tuned with WaOA. Compared to other recently introduced population-based metaheuristic optimization algorithms such as SSA, WOA, SBOA, HOA, BBOA, TL, GTO, and WHO, the response achieved with WaOA exhibits significantly reduced undershoot and overshoot. The controller parameter values for are all the optimization approaches considered for comparison is shown in Table 4. This superior performance indicates that the FO-PID controller, optimized by WaOA, ensures more stable and reliable frequency and voltage regulation. Figure 5(a) and (b) illustrate the frequency regulation in two areas of an interconnected power system, while Fig. 5(c) displays minimum/maximum deviation in frequency for different optimization algorithms. The deviations in terminal voltages in areas 1 and 2 are shown in Fig. 6. The WaOA’s enhanced tuning capability provides a robust controller that effectively mitigates transient deviations, maintaining system stability. Additionally, these results underscore the efficiency of WaOA in achieving optimal control performance, highlighting its potential as a promising solution for complex power system applications. The overall system response demonstrates the algorithm’s effectiveness in ensuring precise and consistent LFC and AVR operations, crucial for the stability and reliability of interconnected power systems. Simulation results also indicate that the tie-line power stabilization is significantly improved using the WaOA when compared to above mentioned optimization algorithms as shown in Fig. 7. The best cost versus iteration graph is shown in Fig. 8 which illustrates the convergence behavior of the algorithm over successive iterations. The graph typically shows a rapid decrease in the best cost value during the initial iterations, indicating effective exploration and quick identification of promising solutions. As iterations progress, the graph flattens out, signifying the algorithm’s transition from exploration to exploitation, refining the solutions to reach the optimal or near-optimal cost. This smooth convergence curve demonstrates WaOA’s efficiency in optimizing the objective function and its ability to achieve high-quality solutions within a reasonable number of iterations. The best cost value is numerically shown for each iteration and optimization algorithms in Fig. 9.

Fig. 5

$\Delta f\left( t \right)$ for area 1 and 2 using FO-PID controller.

Fig. 6

$\Delta V\left( t \right)$ for area 1 and 2 using FO-PID controller.

Fig. 7

Power exchange between interconnected areas.

Fig. 8

Best cost vs. iteration.

Fig. 9

Best cost values for each iteration over different algorithms.

Table 4 Controller parameter values.

Study 2

The results of the proposed design for random changes in load disturbance in power systems shows that the frequency remains within an acceptable range, ensuring system stability and reliability (see Fig. 10). This confirms the design’s effectiveness in maintaining frequency regulation under varying load conditions. Random changes in disturbance are essential for testing the system’s resilience to unpredictable load variations that can occur in real-world scenarios due to sudden increase or decrease in demand. In addition, the design is also validated with system parameter variations. System parameter variations are critical for evaluating the control design’s adaptability to potential fluctuations in system parameters, such as speed regulation factor, governor and turbine time constants, which can affect overall performance. In the simulink environment, these system parameters are assumed to be affected by $\pm 20\,\%$ from the nominal values. Figure 11 depicts frequency stabilization with system parameter variations. These comprehensive tests ensure the proposed design’s applicability, reliability, and robustness in dynamic and uncertain operational environments.

Fig. 10

Frequency deviation using proposed approach against random disturbance.

Fig. 11

Frequency deviation using proposed approach with system parameter variations.

Study 3

Frequency stability in power systems is challenged by typical nonlinearities such as GRC and GDB (see Fig. 12(a)). The modelling of this nonlinearities is discussed in⁶³. The value of GRC and GDB considered for simulation is ${{ \pm 3\% } \mathord{\left/ {\vphantom {{ \pm 3\% } {\hbox{min} }}} \right. \kern-0pt} {\hbox{min} }}$and 0.036 Hz respectively. These nonlinearities can cause significant overshoot and undershoot as seen from the Fig. 12(b), impacting the system’s ability to maintain steady frequency. Despite these challenges, the proposed design effectively compensates for these nonlinearities, ensuring that frequency stabilization is achieved. The design’s robustness and adaptability allow it to counteract the adverse effects of GRC and GDB, maintaining frequency within acceptable limits. This capability demonstrates the design’s potential to provide reliable frequency regulation even in the presence of common nonlinear disturbances in power systems.

Fig. 12

Frequency deviation using proposed approach with nonlinearities.

Study 4

The stability analysis of the proposed design to stabilize frequency and voltage under load disturbances is conducted using Bode plot analysis. The gain margin (GM) and phase margin (PM) are critical parameters in this analysis. For area 1, the GM is found to be 5.83 dB and the PM to be 10.8 degrees, indicating sufficient robustness against gain variations and phase shifts (see Fig. 13(a)). In area 2, the GM is higher at 9.61 dB, and the PM is significantly larger at 28.6 degrees, suggesting an even greater stability margin (see Fig. 13(b)). These values collectively reveal that the proposed design is stable and capable of effectively maintaining system performance despite load disturbances, thereby ensuring reliable frequency and voltage regulation.

Fig. 13

Stability analysis using bode plot.

Conclusion and future research directions

This study introduced the WaOA as an innovative solution for optimizing the FO-PID controllers in LFC and AVR within a two-area interconnected power system. The WaOA, inspired by the social and foraging behaviors of walruses, was tested against several established optimization techniques, including SSA, WOA, COA, SBOA, HOA, BBOA, TL, GTO, and WHO. The simulation results demonstrated that the WaOA significantly enhances the stability and performance of power systems. Specifically, the WaOA-tuned FO-PID controller achieved superior frequency and voltage regulation, with reduced overshoot and undershoot, faster settling times, and robust performance under varying load disturbances, nonlinearitites, and system parameter variations. The stability of the proposed approach was validated through Bode plot analyses, which showed strong gain and phase margins. The WaOA’s ability to maintain frequency and voltage deviations underlines its effectiveness in handling the inherent nonlinearities and uncertainties of power systems. These improvements contribute to the overall stability and reliability of interconnected power systems, making the WaOA a valuable tool for modern power quality management.

While the WaOA has shown superior performance compared to many recent optimization techniques, the authors do not claim it to be universally the best solution for all engineering challenges. Similar to other optimization methods, WaOA has its limitations, primarily due to its random search mechanism, which means there’s no certainty of always reaching the global optimum. In line with the NFL theorem, there is a continuous need to design new algorithms that can deliver better results for specific problems. Future work could focus on extending WaOA to multi-objective and binary optimization variants, enhancing its applicability to diverse fields. Combining WaOA with other optimization techniques in hybrid models could help leverage the strengths of multiple algorithms, improving performance and convergence speed. Moreover, integrating advanced energy storage systems like battery energy storage systems and supercapacitors could offer fast, precise frequency control during transient disturbances. These systems provide immediate grid support when mismatches occur, enhancing frequency stability.