Enhanced artificial hummingbird algorithm with chaotic traversal flight

Abstract

Tackling the shortcomings of slow convergence, imprecision, and entrapment in local optima inherent in traditional meta-heuristic algorithms, this study presents the enhanced artificial hummingbird algorithm with chaotic traversal flight (CEAHA), which employs chaotic ergodicity within the foundational framework of the conventional artificial hummingbird algorithm. This approach implements chaotic motion within local regions of the solution space, ensuring a thorough exploration of potential optima and preventing algorithmic stagnation at local maxima by guaranteeing a non-repetitive traversal of all search states. This study also analyzes the intrinsic mechanisms by which eight different chaotic mappings affect optimization performance, from the perspectives of invariant measures and traversal efficiency of ergodic chaotic motion. In comparative tests with 21 meta-heuristic algorithms on the CEC2014, CEC2019, and CEC2022 benchmark suites across various dimensions, CEAHA demonstrates superior optimization performance. Furthermore, the practicability and robustness of CEAHA have been confirmed in mechanical design optimization problems through 4 engineering instances: pressure vessel, gear trains, speed reducers, and piston levers.

Introduction

Meta-heuristic optimization algorithms, simulating natural or biological behaviors, aim to effectively avoid local optima and achieve global ones. They outperform in handling a range of complex decision-making scenarios involving nonlinear, high-dimensional, non-convex variables such as path planning, resource allocation, neural network architecture search, optimal control, and parameter identification. For instance, the enhanced sand cat swarm optimization algorithm (ESCSO)¹ that combines adaptive social neighborhood search with Lévy flights is used to improve the accuracy and response speed of unmanned aerial vehicle (UAV) path planning and real-time obstacle avoidance, enhance the quality of samples generated under the interfered fluid dynamical system, and find optimal weights and biases for multi-layer perceptrons. The basic behavioral rules of Boids model²-separation, alignment, and cohesion-are merged with deep reinforcement learning to develop a control framework for UAV pursuit-evasion in dynamic and complex environments. A multi-objective particle swarm optimization algorithm addresses distribution issues during refined oil shortages, minimizing operational costs and maximizing gas station satisfaction³. IEGQO-AOA⁴, building on the original AOA, effectively addresses practical engineering design problems of solar photovoltaic parameter extraction by integrating information exchange, adaptive Gaussian distribution, and quasi-opposition based learning. Additionally, more effective strategies for optimizing PID controller gains include an improved stochastic fractal search algorithm (ISFS)⁵ with a piecewise linear chaotic map (PLCM), an improved symbiotic organisms search algorithm (ISOS)⁶ integrating quasi-oppositional based learning with chaotic local search, and a modified salp swarm algorithm (mSSA)⁷ that adds chaotic map, leader information exchange, and randomness to enhance diversity. Notably, ISOS and mSSA have also shown exceptional performance in solving constrained engineering problems such as compression springs, pressure vessels, automatic voltage regulators, and cantilever beams.

Figure 1

Classification of meta-heuristic optimization algorithms.

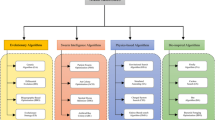
Moreover, meta-heuristic optimization algorithms, depending on their simulation objects and methodologies^8,9, can be classified into four main categories (Fig. 1): evolution-based, physics-based, human-based and swarm-based methods. Evolution-based algorithms are inspired by Darwin and Mendel’s theories of natural evolution, simulating the selection and reproduction processes of biological entities in their environment. Some of the most popular algorithms are genetic algorithm (GA)¹⁰, differential evolution (DE)¹¹, genetic programming (GP)¹², evolutionary mating algorithm (EMA)¹³, gene expression programming (GEP)¹⁴. And some enhanced versions of DE are also widely used in engineering optimal design, such as self-adaptive differential evolution with neighborhood search (SaNSDE)¹⁵ and adaptive differential evolution with optional external archive (JADE)¹⁶.

Physics-based optimization algorithms mimic certain rules and phenomena observed within physical systems. Some of the most widely accepted algorithms are gravitational search algorithm (GSA)¹⁷, multi-verse optimizer (MVO)¹⁸, flow direction algorithm (FDA)¹⁹, ray optimization (RO)²⁰, electrostatic discharge algorithm (ESDA)²¹, Henry gas solubility optimization (HGSO)²², nuclear reaction optimization (NRO)²³, big-bang big-crunch (BBBC)²⁴ and sinh cosh optimizer (SCHO)^25,26.

Human-based algorithms attempt to construct global optimization mechanisms by utilizing characteristics of human social and cognitive activities. Some of the most typical algorithms are teaching-learning-based optimization (TLBO)²⁷, human mental search (HMS)²⁸, league championship algorithm (LCA)²⁹, imperialist competitive algorithm (ICA)³⁰, human evolutionary optimization algorithm (HEOA)³¹, student psychology based optimization (SPBO)³², social cognitive optimization (SCO)³³ and circulatory system based optimization (CSBO)³⁴.

Swarm-based methods attempt to simulate the habitat, foraging, survival laws and movement characteristics of biological communities. Some of the most popular algorithms are particle swarm optimization (PSO)³⁵, whale optimization algorithm (WOA)³⁶, electric eel foraging optimization (EEFO)³⁷, artificial vortex optimization algorithm (AVOA)³⁸, grasshopper optimization algorithm (GOA)³⁹, salp swarm algorithm (SSA)⁴⁰, gorilla troops optimizer (GTO)⁴¹, crayfish optimization algorithm (COA)⁴² and the recently emerged artificial hummingbird algorithm (AHA)⁴³.

The artificial hummingbird algorithm (AHA), stands out in the meta-heuristic realm through its unique bionic approach. Emulating hummingbird-flights and foraging strategies, AHA enables agents to explore and exploit the solution space with some efficiency. Distinctively, agents in AHA possess a memory system to track their visits to other hummingbirds’ locations, highlighting intelligent behavior. With fewer control parameters, AHA offers simplicity and flexibility, making it widely used in various applications, such as new energy system design⁴⁴, the coordinated scheduling of wind-solar-thermal generation⁴⁵, and searching for neural network optimal architectures⁴⁶. Yet, AHA still faces difficulties achieving precision and convergence in non-convex, high-dimensional complex problems with a wide search domain⁴⁷.

It’s worth noting that balancing exploration and exploitation represents a critical challenge in meta-heuristic algorithm design^48,49. Exploration, driven by diversity, is essential for surveying the search space and pinpointing probable zones for optimal solutions. Conversely, exploitation involves intensive probing within these zones to hasten convergence to the optimum. Lack of exploration may weaken performance and risk local optima traps, whereas poor exploitation may impair the precise pinpointing of the best solution. Employing chaos theory has emerged as a favored method for refining heuristic algorithms to overcome this dilemma^50,51.

Chaos is a type of deterministic nonlinear system with aperiodic behavior characterized by extreme sensitivity to initial conditions, rendering long-term prediction impractical⁵². It has been widely applied in various scientific disciplines, such as the design of pseudo-random number generators, construction of chaotic neural networks, and establishment of secure communication⁵³. Earlier studies indicated that the global search capacities of certain chaotic sequences have been highly effective in enhancing the performance of metaheuristic optimization algorithms^54,55. For example, a chaotic enhanced adaptive hybrid butterfly particle swarm optimization algorithm⁵⁶ and an improved chaotic nonlinear dynamic inertia weight PSO algorithm⁵⁷ have been utilized for target localization and secure path planning, respectively. Chaotic motion facilitates the traversal of every state around attractors, allowing meta-heuristic algorithms to explore more extensively and avoid local optima. Based on these properties, the chaotic optimization algorithm (COA) was proposed, utilizing the Logistic map⁵⁸. This strategy underwent further refinement in 2018, resulting in the creation of the niche chaotic optimization algorithm (NCOA)⁵⁹, which partitions the entire solution space into smaller parts to facilitate chaotic search within each parts. Some studies have developed new search strategies by alternating the search behavior of COA with traditional meta-heuristic algorithms, thereby enhancing solution quality. For instance, ISOS⁶ employed PLCM with a uniform invariant probability density to perform chaotic local search (CLS) around the globally optimal individual, naturally reducing the search radius as iterations progress. Compared to the original SOS, ISOS only added one parameter-the number of CLS iterations-yet significantly improved performance. Similarly, accelerated particle swarm optimization with chaotic search (APSOC)⁶⁰, by examining the impact of ten different chaotic maps on iterative search, found that integrating Circle map with APSO yielded better optimization results. However, this approach required adjustments to the chaotic search radius and shrinkage coefficient, complicating the parameter tuning process. Furthermore, chaotic evolution (CE)^61,62 was developed to simulate the rapid blending and diffusive movements of chaos in the process of crossover and mutation of intelligent individuals, leading to faster convergence.

Additionally, integrating chaotic sequences into traditional meta-heuristic algorithms could increase population diversity and prevent premature convergence. Such strategies were implemented in several algorithms, including the chaotic dwarf mongoose optimization algorithm (CDMO) for feature selection⁶³, the chaotic African vultures optimization algorithm (CAOVA)⁶⁴ for achieving optimal power flow with real devices and stochastic wind power, and the chaotic Runge Kutta optimization (CRUN) for solving constrained engineering problems⁶⁵. Specifically, ISFS⁵ analyzed the impact of Logistic, PLCM, Iterative, and Sine maps on the first statistical process of the original SFS and found that PLCM notably enhanced population diversity and facilitated a smooth transition from exploration to exploitation, effectively optimizing automatic generation control in power systems. In mSSA⁷, the main control parameter for exploration and exploitation underwent systematic, ergodic chaotic changes through the embedding of a sinusoidal map, ensuring that the algorithm maintained an effective balance between exploration and exploitation from the first to the last iteration.

Although various chaotic systems have been applied to explore solution spaces, it remains unclear which types possess superior search efficiency or are better suited for optimization strategy design. Additionally, the underlying mechanisms of chaotic optimization warrant further investigation to ensure continuous advancement in theoretical design.

The No Free Lunch Theorem of Optimization⁶⁶ theorizes that it is impossible for any single algorithm to effectively solve all optimization problems, and such an algorithm will never emerge. This theorem motivates ongoing innovation and the proposal of more efficient meta-heuristic optimization techniques. Recently, some enhanced versions of the AHA algorithm incorporating chaos theory have been proposed, such as DGSAHA algorithm⁶⁷, which is based on the golden sine factor and integrates the concepts of differential evolution crossover and mutation; LCAHA algorithm⁴⁷, which combines Lévy flight and sinusoidal chaotic map; and IAHA algorithm⁶⁸, which utilizes Chebyshev map for population initialization settings. These researches all employ chaotic sequences generated from chaotic maps to determine initial population positions. Furthermore, other algorithmic designs, such as the chaotic whale optimization algorithm (CWOA)⁶⁹, hyper-chaos cuckoo search (HCS)⁷⁰, demonstrate that relying solely on pseudo-random sequences from chaos maps for initializing population positions can enhance optimization performance. However, the limitations of these enhancement strategies are evident in their failure to effectively utilize chaotic maps during the exploration and exploitation phases of the algorithm. Additionally, in real-world engineering optimization instances, most heuristic algorithms may encounter diminished performance or weakened convergence. Hence, to address various engineering scenarios, there is an ongoing requirement to refine and advance optimization strategies.

Motivated by the factors mentioned above, this paper introduces an innovative chaotic optimization strategy grounded in the classical AHA algorithm - namely, the enhanced artificial hummingbird with chaotic traversal flight (CEAHA). An in-depth examination of the invariant probability measures and traversal efficiency within chaotic sequences is conducted, aiming to reveal how different chaotic maps fundamentally influence the optimization performance of meta-heuristic algorithms. This further expands the research frontier concerning the chaotic motion of intelligent agents within the field of optimization algorithms. The novelties and primary contributions of CEAHA are as follows:

• The concept of a chaotic traversal efficiency has been introduced as a novel metric based on spatial ergodicity to delve into the internal mechanics of chaotic optimization.

• A novel strategy for chaotic optimization has been developed, integrating a chaos traversal flight approach into the framework of the AHA algorithm.

• Through comparative analysis, it has been shown that chaotic maps characterized by various invariant probability measures demonstrate significantly diverse optimization effects.

• An extensive set of numerical experiments has been conducted. Comparing CEAHA against 21 other meta-heuristic algorithms across CEC2014, CEC2019, and the most recent single objective benchmark test suite CEC2022, the experiments substantiate CEAHA’s superior optimization capabilities.

• Through tests on 4 machine design problems, including pressure vessel, gear train, speed reducer, and piston lever, the superior practicability and robustness of CEAHA are verified.

The rest of this paper is organized as follows. “Overview of artificial hummingbird algorithm” section presents a brief overview of the traditional artificial hummingbird algorithm. “Traversal efficiency of chaotic maps” section discusses the traversal efficiency of chaotic maps. “A novel enhanced artificial hummingbird algorithm” section proposes the structure of CEAHA. “Experimental results and discussion” section provides the experimental results, along with in-depth discussions and analyses of these outcomes. Finally, in the “Conclusions” section, a summary is provided, and potential directions for future research are pointed out.

Overview of artificial hummingbird algorithm

Given n food sources randomly, hummingbird population is randomly initialized:

$$\begin{aligned} {x_i} = Lb + rand(0,1) \cdot (Ub - Lb), i = 1,2, \ldots ,n \end{aligned}$$

(1)

where Ub and Lb are the upper and lower boundaries, respectively. rand(0.1) is a random vector in range [0, 1], $x_i$ represents the i-th candidate solution. Initialize the visit table for food sources as follows:

$$\begin{aligned} V{T_{i,j}} = \left\{ {\begin{array}{*{20}{c}} 0& {i \ne j}\\ {null}& {i = j} \end{array}} \right. ,i = 1,2, \ldots ,n;j = 1,2, \ldots ,n \end{aligned}$$

(2)

where for i = j, $V{T_{i,j}}=null$ signifies that the i-th hummingbird is feeding at its designated source; for $i \ne j$, $V{T_{i,j}}=0$ denotes the i-th hummingbird’s recent visit to the j-th food source in the current iteration.

The hummingbird’s three flight skills (including axial flight, diagonal flight, and omnidirectional flight) are perfectly expressed, all with the help of the direction tangent vector. The specific expressions of hummingbird’s flight skills in d-dimension (d-D) space are as follows:

Axial flight:

$$\begin{aligned} D_{Af}^{(i)} = \left\{ {\begin{array}{*{20}{c}} 1& {i = randi([1,d])}\\ 0& {others} \end{array}} \right. \end{aligned}$$

(3)

Diagonal flight:

$$\begin{aligned} D_{Df}^{(i)} = \left\{ {\begin{array}{*{20}{c}} 1& {i = P(i),j \in [1,k]}\\ 0& {others} \end{array}} \right. \end{aligned}$$

(4)

where,

$$\begin{aligned} P = randperm(k),k \in [2,\lceil {r_{1}} \cdot (d - 2) \rceil + 1] \end{aligned}$$

(5)

Omnidirectional flight:

$$\begin{aligned} \begin{array}{*{20}{c}} {D_{Of}^{(i)} = 1,}&{i = 1, \ldots ,d} \end{array} \end{aligned}$$

(6)

randi([1, d]) generates random integers from [1, d], randperm(k) produces a random permutation from 1 to k, $r_1$ is a random number within (0, 1], and d signifies the spatial dimension of the target problem. Moreover, AHA emulates hummingbird foraging strategies: guided, territorial, and migratory.

Guided foraging:

$$\begin{aligned} {v_i}(t + 1) = {x_{i,tar}}(t) + \alpha \cdot {D_t} \cdot ({x_i}(t) - {x_{i,tar}}(t)), \alpha \sim N(0,1) \end{aligned}$$

(7)

Territorial foraging:

$$\begin{aligned} {v_i}(t + 1) = {x_i}(t) + b \cdot {D_t} \cdot {x_i}(t), b \sim N(0,1) \end{aligned}$$

(8)

where ${x_i}(t)$ represents the i-th hummingbird’s position at time t, ${x_{i,tar}}(t)$is the targeted source for the i-th hummingbird, and $\alpha \sim N(0,1)$ is a normally distributed guiding factor. $D_t \in \{ D_{Af},D_{Df},D_{Of}\}$ indicates the flight skill employed: axial, diagonal, or omnidirectional.

When mod(t,2n)=0, the hummingbird with worst flight position update to new food source through migratory foraging:

$$\begin{aligned} {x_{wor}}(t + 1) = Low + r \cdot (Up - Low) \end{aligned}$$

(9)

where ${x_{wor}}$ is the worst candidate solution.

The updating method for the hummingbird’s position is as follows:

$$\begin{aligned} {x_i}(t + 1) = \left\{ {\begin{array}{*{20}{c}} {{x_i}(t)}& {f({x_i}(t)) \le f({v_i}(t + 1))}\\ {{v_i}(t + 1)}& {f({x_i}(t)) > f({v_i}(t + 1))} \end{array}} \right. \end{aligned}$$

(10)

where $f({x_i}(t))$ and $f({v_i}(t + 1))$ represent the fitness values of the candidate solution ${x_i}(t)$ and the updated solution ${v_i}(t + 1)$, respectively. Although the unique flight skills and design of the visit table in AHA significantly enhance its optimization performance compared to earlier meta-heuristic algorithms, there are still some weaknesses. For example, as the iterations progress, the population diversity of AHA gradually declines, and its local exploitation ability weakens accordingly. This leads to a slow convergence rate, making it challenging to accurately find the optimal solution, and it may easily fall into the predicament of local optima.

Traversal efficiency of chaotic maps

While numerous studies have highlighted chaos as an effective method to improve the performance of meta-heuristic algorithms, how to integrate chaotic maps into algorithmic optimization design continues to be an area of active research. The statistical properties of chaotic maps are known to play a crucial role in influencing global search efficiency and computational effectiveness^61,71,72,73. Detailed investigations into chaotic optimization^{60,74,75,76,77} have considered the factors like the discreteness, probability density functions, and Lyapunov exponents of chaotic sequences, with particular attention to the Tent map’s notable advantages in population initialization and global search. These findings are further supported by empirical results obtained from the chaotic accelerated particle swarm optimization⁶⁰, chaotic whale optimization algorithm⁶⁹ and chaotic dwarf mongoose optimization algorithm⁶⁴.

Table 1 Equations of chaotic maps.

In order to further explore the internal mechanism of chaotic optimization, eight common chaotic maps are documented in Table 1, detailing their formulations, values of control parameters, experimental parameter values, and associated Lyapunov exponents (LEs). The positive LEs under the parameters listed in Table 1 indicate that these motion equations have all entered a state of chaotic behavior.

Consider the countable subset ${ {C^n}({x_0})}$ produced by a chaotic map, as listed in Table 1, starting from any initial value ${x_0}$ within the chaotic regime X. And $\{ {C^n}({x_0})\}$ forms a semi-flow on the measured space $(X,\mathcal{B},\mu )$ if it adheres to the conditions: (1) the mapping ${{C^n}:X \rightarrow X,}$ for $\forall n \in {R^ + }$; (2) ${{C^{t + s}} = {C^t} \circ {C^s}}$, for ${t,s \in {R^ + }}$, ${x_0 \in X}$; (3) the function: $C^n(x):X \times {R^ + } \rightarrow X$ is continuous with respect to each n⁸².

By a measure on X, any probability measure defined on the Borel $\sigma$-algebra $\mathcal{B}(X)$ subsets of X is referred. A measure $\mu$ is invariant under a transformation C, if $\mu (A) = \mu (C_t^{ - 1}(A))$ holds for each $t \in {R^ + }$ and $\forall A \in \mathcal{B}$. Under the assumption that $(X,\mathcal{B},\mu )$ is a $\sigma$-finite measure space, the Birkhoff Ergodic Theorem⁸³ assures that, for any function f in ${L^1}(\mu )$, the time average $\frac{1}{n}\sum \limits _{i = 0}^{n - 1} {f({C^i}(x))}$ a.e. converges to a function $f^* \in {L^1}(\mu )$, if $C:(X,\mathcal{B},\mu ) \rightarrow (X,\mathcal{B},\mu )$ is measure-preserving, where ${L^1}(X,\mathcal{B},\mu )$ is a Banach space with the norm $||f|{|_1} = \int {|f|} d\mu$. Similarly, $\int \limits _X {{f^*}d\mu = \int {Xfd\mu } }$ is true, if a.e. ${{f^*} \circ C = {f^*}}$ and $\mu (x) < \infty$. Of course, when $C:(X,\mathcal{B},\mu ) \rightarrow (X,\mathcal{B},\mu )$ exhibits ergodicity, The invariant measure $f^*$ is almost everywhere constant and does not depend on the initial conditions of the chaotic maps. The invariant probability measure functions $f^*$ of each chaotic map, which are scaled into the (0, 1) interval to facilitate comparison, are shown in Fig. 2. It is intuitive to see from Fig.2, these maps can be categorized into three types: those exhibiting uniform distribution characteristics (including Tent, Bernoulli, and piecewise linear chaotic map (PLCM)), which are shown in Fig. 2a; those with U-shaped distribution characteristics (including Logistic, Chebyshev and Cubic), which are shown in Fig. 2b; and those demonstrating Spike and Gaussian-like distributions (including 2D-NHM and Circle), which are shown in Fig. 2b.

Figure 2

Analysis of invariant probability measure functions $f^*$ for 8 chaotic maps.

The objective solution space X is assumed to be uniformly divided into N subintervals, where N represents the population size of the metaheuristic optimization algorithm. To achieve a point set ${ {C^n}({x_0})}$ that perfectly fills these N subintervals, the ratio of the number of elements $\mu$ in set ${ {C^n}({x_0})}$ to the number of subintervals N is defined as the traversal efficiency (TE) of the chaotic map. The “Perfect filling” refers to the condition where if $\mu ({C^n}({x_0}))$ decreases by one, there is exactly one subinterval without any elements in ${C^n}({x_0})$. The lower the ratio, the higher the traversal efficiency, which can be expressed by the following mathematical formula:

$$\begin{aligned} TE = \frac{1}{k}\sum \limits _{i = 1}^k {\frac{{\mu ({C^n}({x_0}))}}{N}} \end{aligned}$$

(11)

where k represents the average value taken over multiple experimental results.

Figure 3

Comparison curves of the TE and $\beta$ for 8 chaotic maps across different values of the population size N.

As illustrated in the left image of Fig. 3, the comparison curves of the traversal efficiency for eight chaotic maps in Table 1 across different values of N demonstrate that the chaotic maps with an invariant probability measure of $f^*=1$ (i.e., PLCM, Bernoulli, and Tent maps) exhibit the highest efficiency in traversing space. The U-shaped distribution maps like Chebyshev, Logistic, and Cubic follow, while the 2D-NHM and Circle maps show relatively lower traversal efficiency. Therefore, using chaotic maps with $f^*=1$ for population initialization is the optimal choice to lay the groundwork for subsequent spatial exploration by intelligent agents. Moreover, the left image of Fig. 3 reveals that the traversal efficiency curves conform to a power-law distribution $TE \in {N^\beta }$, allowing the expression of the traversal efficiency exponent $\beta$ ($0<\beta <1$) to be represented as:

$$\begin{aligned} \beta = \mathop {\lim }\limits _{N \rightarrow \infty } {\log _N}(TE)= \mathop {\lim }\limits _{N \rightarrow \infty } \left( {{{\log }_N}\left( {\sum \limits _{i = 1}^k {\mu ({C^n}({x_0}))} } \right) - {{\log }_N}k - 1} \right) \end{aligned}$$

(12)

Under the definition of the measure $\beta$, the traversal efficiency becomes an inherent feature of the chaotic map. The right image of Fig. 3 shows the calculated values of $\beta$ for various chaotic maps, which reveal that the exponent $\beta$ exhibits the same three patterns as TE; specifically, chaotic maps with an invariant probability measure of $f^*=1$ offer optimal traversal in the solution space. And although the Tent, PLCM, and Bernoulli all have an $f^*$ value of 1, there are still slight differences in their values of TE and $\beta$. For instance, with a population size of $N=50$, the TE for Tent is better than PLCM and surpasses Bernoulli (see Fig. 3). And an in-depth analysis of the optimization effects that these three types of chaotic systems have on algorithm performance is conducted in the “Efficiency of CEAHA with different chaotic maps” section.

A novel enhanced artificial hummingbird algorithm

In order to further improve the performance of AHA, a novel enhanced artificial hummingbird algorithm with chaotic traversal flight (CEAHA) is proposed. Given that the experiments in this paper are set with a population size of 50 and and taking into account the conclusions of Section, Section will employ the Tent map for population initialization and migratory foraging, laying the groundwork for iterative updates and exploration of the solution space in the algorithm.

Algorithm 1

Pseudo-code of CEAHA

The equation of Tent map is shown in the first row of Table 1. Place N hummingbird population on N food sources and use chaos numbers $T^t(i,d) \in \{ {C^t}({x_0})\}$ generated by Tent map to initialize the population, as shown in the equation below:

$$\begin{aligned} {x_i} = Lb + T^t(i,d) \cdot (Ub - Lb) \end{aligned}$$

(13)

where $T^t(i,d)$ denotes the d-dimensional chaotic vector generated by the i-th hummingbird at time t within the d-dimensional solution space.

During the migratory foraging process of hummingbirds, a chaos mechanism for global mutation is introduced to update the position of the individuals ranked last. This behavior prevents the worst individuals from lingering long on scarce and sterile food sources, and aids in the implementation of a chaotic traversal search throughout the global space. The expression of migratory foraging based on Tent map is presented in Eq. (14).

$$\begin{aligned} {x_{wor}}(t + 1) = Lb + T^t(i,d) \cdot (Ub - Lb) \end{aligned}$$

(14)

To reduce the overlapping movement of individuals and enhance search efficiency in algorithm, the chaotic traversal flight strategy leverages chaotic motion’s ergodicity and non-repetitive properties for thoroughly exploiting local solution spaces. consider a population of N hummingbirds uniformly distributed across the solution space, where each bird has a unique spatial flight domain defined by $(Ub - Lb)/(N - 2 + 2 \cdot rand)$. The equation for chaotic domain traversal flight behavior, which is based on the chaotic map, can be formulated as follows:

$$\begin{aligned} {v_i}(t + 1) = {H_i}(t,d)\cdot (Ub - Lb)/(N - 2 + 2*rand) \cdot {D_t} \cdot {x_i}(t) + {x_i}(t) \end{aligned}$$

(15)

where $D_t \in \{ D_{Af},D_{Df},D_{Of}\}$, and ${H_i}(t,d)$ represents the d-dimensional chaotic vector produced by the i-th hummingbird at time t within the d-dimensional solution space, following the equation in Table 1. To determine the most apt chaotic system from Table 1 for chaotic traversal flight, this work will assess and contrast the efficacy of various CEAHA algorithm incarnations with integrated chaotic maps in “Efficiency of CEAHA with different chaotic maps”.

During chaotic traversal flights, candidate solutions identified are logged in a visit table and updated accordingly according to Eq. (10). If a hummingbird discovers a superior solution, its corresponding visit table entry is promptly upgraded to the highest level, directing the next phase of the population’s guided foraging toward these high-value locations. Conversely, if the i-th hummingbird fails to find an improved solution post-chaotic traversal, the visit levels for the rest of the agents increase by 1, refocusing efforts on unexplored areas and reducing the likelihood of getting trapped in local optima. Therefore, the memory and search capabilities of the hummingbirds are expanded, ensuring a comprehensive examination of available food sources. The pseudo-code and algorithmic workflow diagram of the proposed CEAHA are illustrated in Algorithm 1 and Fig. 4.

In Algorithm 1, ${f_{cur}}({x_i})$ and ${f_{pre}}({x_i})$ denote the visit levels of a hummingbird at the current and previous moments, respectively. As shown in Eq. (16), if the visit level at a hummingbird’s location remains unchanged, (i.e., ${f_{cur}}({x_i}) - {f_{pre}}(x) = 0$), indicating a loss of activity, chaotic traversal flight behavior is initiated to enhance diversity and facilitate precise exploitation of nearby optimal solutions.

$$\begin{aligned} {x_i}(t + 1) = \left\{ {\begin{array}{*{20}{c}} {{v_i}(t + 1)}&{\begin{array}{*{20}{c}} {if}& {{f_{cur}}({x_i}) - {f_{pre}}(x) = 0} \end{array}}\\ {{x_i}(t)}& {others} \end{array}} \right. \end{aligned}$$

(16)

Figure 4

The workflow diagram of the proposed CEAHA.

Table 2 Unimodal benchmark functions used in the algorithm performance test experiments.

Table 3 Multimodal benchmark functions used in the algorithm performance test experiments.

Table 4 Fixed-dimension multimodal benchmark functions used in the algorithm performance test experiments.

Figure 5

Comparative images (F1–F8) of the average convergence and diversity curves of 8 CEAHA variants with distinct chaotic maps versus the original AHA. Left 1 and 2 are the 3D plots and 2D contour maps of the test function, respectively, with a red asterisk (*) indicating the optimal solution. Left 3 and 4 illustrate the average convergence and diversity curves, respectively.

Figure 6

Comparative images (F9–F16) of the average convergence and diversity curves of 8 CEAHA variants with distinct chaotic maps versus the original AHA. Left 1 and 2 are the 3D plots and 2D contour maps of the test function, respectively, with a red asterisk (*) indicating the optimal solution. Left 3 and 4 illustrate the average convergence and diversity curves, respectively.

Figure 7

Comparative images (F17–F23) of the average convergence and diversity curves of 8 CEAHA variants with distinct chaotic maps versus the original AHA. Left 1 and 2 are the 3D plots and 2D contour maps of the test function, respectively, with a red asterisk (*) indicating the optimal solution. Left 3 and 4 illustrate the average convergence and diversity curves, respectively.

Table 5 Statistical results of eight CEAHA versions with eight different chaotic maps on 23 test functions.

Experimental results and discussion

To rigorously evaluate the optimization performance of the eight chaotic maps in Table 1 and the efficacy of the CEAHA, this study devises two sets of experiments. The first experiment is designed to investigate the performance variations when integrating 8 different chaotic maps into the CEAHA algorithm, using a comprehensive assessment with 23 standard test functions⁴². These 23 functions included unimodal (F1–F7), multimodal (F8–F13), and fixed-dimension multimodal functions (F14–F23), with their formulas and expressions presented in Table 2, 3 and 4. Moreover, this part delves into the inherent mechanics of chaotic search, considering the ergodicity of chaotic sequences and their effects on population diversity.

In the second experiment, the best-performing variant of CEAHA from the first set is benchmarked against 21 popular meta-heuristic algorithms (see Table 6, where the parameter values for each algorithm are extracted from the respective original publications) on the recent single-objective optimization test suite CEC2022⁸⁴, and supplemented with additional benchmarks on CEC2014⁴³ and CEC2019⁸⁵ suites due to CEC2022’s category limitations.

To ensure fairness, all algorithms in this study are configured with a population size of 50 and a maximum iteration count of 500 ($T_{max}=500$). Each algorithm is run independently 30 times to evaluate average convergence and robustness. And the maximum number of fitness evaluation for each algorithm is 25000. The hardware configuration of the computer used in this study is an AMD Ryzen 7-5800H CPU with Radeon Graphics @ 3.20 GHz, and the simulation platform used for implementing all the algorithms and comparative experiments mentioned in this paper is MATLAB R2021b. Detailed experimental procedures and analysis are elaborated in the following sections.

Efficiency of CEAHA with different chaotic maps

Figures 5, 6, and 7 present the average convergence and average population diversity curves for the eight versions of CEAHA compared with the original AHA, after 30 independent runs on 23 standard benchmark functions. Diversity is defined as the distance between solutions or clusters of solutions within the search space⁸⁶. To effectively execute meta-heuristic algorithms, intelligent agents must be broadly distributed across the entire search space during the exploration phase, while remaining focused during the exploitation phase. During the later stages of algorithm iteration, efforts should be made to minimize excessive clustering of intelligent agents to prevent the entire population from prematurely converging on local optima, an undesirable event. This paper employs the diversity measure formula proposed in the literature⁸⁶, which is as follows:

$$\begin{aligned} Di{v_z}= & \frac{1}{N}\sum \limits _{i = 1}^N {\left| {median({x^z}) - x_i^z} \right| } \end{aligned}$$

(17)

$$\begin{aligned} Div= & \frac{1}{d}\sum \limits _{z = 1}^d {Di{v_z}} \end{aligned}$$

(18)

In Eqs. (17) and 18, N is population size, and d is the dimension of the solution space. $x_i^z$ refers to the solution of the i-th hummingbird individual in the z-dimensional direction, while $median({x^z})$ denotes the median position of the entire population in the same d-dimensional space. $Di{v_z}$ represents the diversity of the population in specific z-dimension direction, and Div signifies the diversity index of the population across all dimensions. The larger the value of Div, the richer the diversity of the population. The rightmost columns of Figs. 5, 6 and 7 display the curves of average diversity over iterations for the eight different versions of CEAHA and the original AHA when addressing 23 test functions.

From the convergence curves of Figs. 5, 6 and 7, it is observed that the eight versions of CEAHA all outperform the original AHA across 23 standard benchmark functions. A detailed analysis of unimodal problems reveals that CEAHA must swiftly guide the population to resource-rich regions in the early stages, avoiding prolonged stagnation in flat or locally optimal areas. From F1 to F4 and F6, chaotic maps with U-shaped distributions exhibit rapid convergence due to their diversity curves quickly narrowing toward the optimal regions. For problems like F5 with large flat zones, the Circle map shows superior search performance.

For complex multimodal problems, featuring numerous local optima and high-dimensional challenges, maintaining a high level of diversity among the intelligent agents in the solution space is crucial. The results from F7, F9 to F12, and F16 to F18 indicate that the three chaotic maps with U-shaped distributions not only demonstrate better search performance but also maintain higher population diversity. For F13, however, the 2D-NHM chaotic system, characterized by its Spike distribution, shows a faster convergence rate and a slower convergence of population diversity. As for F17, with optima at the edge, the Logistic map succeeds in finding the best solution due to consistently highest population diversity. Since F19 and F20 are similar, as are F21, F22 and F23, with their search convergence and diversity curves nearly identical, only F19 and F23 are illustrated in Fig. 7. These problems are marked by significant differences between the minimum and other values, which is why, despite Chebyshev, Logistic, and Cubic maps maintaining high levels of population diversity, the 2D-NHM and Circle mappings exhibit better search convergence behavior.

Additionally, the Wilcoxon rank-sum test is utilized to evaluate the performance differences in solving 23 test functions among CEAHA-Cubic, the other seven versions of CEAHA, and the original AHA, as shown in Table 5. Initially, it is observed that the Cubic map, along with Logistic and Chebyshev maps, exhibits remarkably similar optimization performances. Subsequently, compared to other versions of CEAHA, the CEAHA version that incorporates the Cubic map demonstrates superior performance on all unimodal test problems and some multimodal test problems.

In summary, chaotic maps with U-shaped distributions, such as the Logistic, Chebyshev, and Cubic maps that engender chaotic traversal flight behavior, show outstanding performance in accelerating convergence while also maintaining population vitality and diversity. The traversal flight behavior with these chaotic maps significantly enhances the robustness and adaptability of the algorithms.

Table 6 CEAHA and 21 meta-heuristic optimization algorithms used for comparative analysis.

Table 7 Statistical results of CEAHA compared with other optimization algorithms in CEC2014 (100D).

Table 8 Statistical results of CEAHA compared with other optimization algorithms in CEC2019.

Table 9 Statistical results of CEAHA compared with other optimization algorithms in CEC2022(10D).

Table 10 Statistical results of CEAHA compared with other optimization algorithms in CEC2022(20D).

Table 11 Statistical results of CEAHA compared with other optimization algorithms in CEC2022(20D).

Performance of CEAHA with cubic map

The conclusion from previous section suggests that chaotic maps with a U-shaped distribution of the invariant probability measure $f^*$ are more suitable for the design of chaotic traversal flights. Although the Cubic, Chebyshev, and Logistic exhibit similar curve shapes, there are slight differences in traversal efficiency when the population size is set to $N=50$, with Cubic marginally outperforming Chebyshev, which in turn slightly surpasses Logistic (see Fig. 3). Therefore, Cubic map is selected to be the baseline pattern for the CEAHA chaotic traversal flight strategy. Concurrently, this version of CEAHA is comprehensively compared with three newly proposed AHA-based enhanced Hummingbird algorithms and other 17 meta-heuristic algorithms on the CEC2014, CEC2019, and the latest single-objective test suite CEC2022. Table 6 provides detailed listings of the names and parameter settings for 22 algorithms, with the parameter values for 21 competitive algorithms extracted from their respective original publications.

Wilcoxon rank sum test

To comprehensively assess the performance of the CEAHA, the Wilcoxon signed-rank test⁹¹ is employed for comparative analysis. The significance level is set to $p=0.05$. Here, “$\approx$” denotes no significant difference in the statistical sense, “+” to suggest that the corresponding CEAHA has surpassed the original AHA in performance, and “-” indicates the reverse situation. All considered algorithms are compared using the mean (Mean) and standard deviation (Std) of the best solutions obtained so far as two evaluation criteria. The formulas of Mean and Std are as follows:

$$\begin{aligned} Mean = \frac{1}{T}\sum \limits _{i = 1}^T {P_i^*} \end{aligned}$$

(19)

$$\begin{aligned} Std = \sqrt{\frac{1}{T}{{(P_i^* - Mean)}^2}} \end{aligned}$$

(20)

where ${P_i^*}$ represents the best-so-far solution obtained in the i-th independent experimental run, and T denotes the number of independent experimental runs. The smaller the mean, the closer the feasible solution obtained by the algorithm is to the standard solution (true value), indicating that the algorithm possesses superior average performance. Moreover, the smaller the standard deviation, the more stable and reliable the feasible solution provided by the algorithm.

Figure 8

Fitness curves and box plots of CEAHA and other 21 algorithms used for comparative analysis on CEC2019.

Figure 9

Fitness curves and box plots of CEAHA and other 21 algorithms used for comparative analysis on CEC2022 (20D).

Table 7 showcases the assessment results on the 100-dimensional CEC2014 benchmark suite, with CEAHA outperforming AHA, DGSAHA, IAHA, LCAHA, COA, EEFO, and SHCO in nearly two-thirds of the test cases. Despite slightly lagging behind CSBO, SaNSDE, SSA, SPBO, and GTO in a few instances, CEAHA’s performance is significantly superior to these algorithms on most test cases, especially when compared to AOA, CS, EMA, JADE, and GOA. Table 8 documents the performance of the algorithms on the CEC2019 test suite at specific dimensions, with CEAHA excelling in over half of the test cases compared to AHA, DGSAHA, IAHA, LCAHA. And CEAHA outstrips the other competitors on most of the CEC2019 problems.

On the 10-dimensional CEC2022 benchmark suite, as indicated in Table 9, CEAHA falls short of JADE in 7 out of 12 cases but leads AHA, DGSAHA, IAHA, LCAHA, EEFO, EMA, GOA, GTO, SPBO, SSA, and JADE in nearly two-thirds of the cases and outperforms AOA, WOA, and SHCO in the majority. Tables 10 and 11 reveal that on the 20-dimensional CEC2022 test suite, CEAHA’s performance improves compared to the 10-dimensional case, slightly outdoing JADE in 8/12 cases, COA in 6/12 cases, and surpassing DGSAHA and GOA in nearly 9/12 of the cases, outperforming all other competitor algorithms in most cases. It is evident that CEAHA generally exhibits superior optimization capability when facing high-dimensional test problems.

Convergence and robustness analysis

To assess the convergence speed and robustness of various algorithms during the evolutionary process, Figs. 8 and 9 display the best fitness curves from 30 independent runs of CEAHA and 21 other competitive algorithms on the CEC2019 and CEC2022 test suites, all conducted with the same number of fitness evaluations (FES). Additionally, these figures also present box plots at the final fitness evaluation to demonstrate their performance outcomes. Additionally, to ensure fairness in comparison, all algorithms start from the same initial points, with a population size set at 50, and undergo 25,000 FES.

For the unimodal functions F1, F2, F5, and F9 within the CEC2019 suite, algorithms including CEAHA, DGSAHA, IAHA, LAHA, COA, GTO, EEFO and SCSSA exhibits rapid convergence. Notably, CEAHA demonstrates the highest optimization stability with the lowest median and narrowest interquartile range in its box plots. For F2, although SCSSA exhibited a superior best convergence curve earlier compared to CEAHA, and also performed exceptionally well in terms of robustness, this is merely an isolated extreme case. This is because, across other test functions, CEAHA generally shows better convergence performance and robustness than SCSSA. In the multimodal functions F3, F4, and F6 to F8, and F10 of CEC2019 test suite, CEAHA significantly shows the fastest convergence rate, consistently finding the optimal solutions, and also maintains superior stability in its box plots compared to other competitors. Specially, CEC2019-F7 is the Modified Schwefel’s Function, characterized by its asymmetric search space which leads to unbalanced optimization paths and a global optimum not located at the center. In this problem, CEAHA quickly finds the optimal solution, followed by EEFO, EMA, and IAHA. CEAHA outperforms other algorithms on CEC2019-F7, demonstrating its ability to effectively handle asymmetry. CEC2019-F8 is the Expanded Schaffer’s F6 Function, notable for the drastic and periodic changes in terrain near the global optimum area, which may cause cyclic search paths. CEAHA rapidly pinpoints the optimal solution in this case, while AHA gradually finds the solution after CEAHA’s convergence. CEC2019-F10 is the Ackley Function, with a relatively flat central area challenging the algorithm’s capability to explore regions with minor gradients. CEAHA, AHA, LCAHA, and EEFO manage to find the optimal solution within a limited number of function evaluations, and CEAHA has the best convergence rate compared with other competitive algorithms.

CEC2022 encompasses unimodal functions (F1), multimodal functions (from F2 to F5), composite functions (from F6 to F8), and constrained optimization functions (from F9 to F12). While CEAHA’s convergence speed for F2 trails slightly behind IAHA, and its box plot shows a marginally higher stability compared to IAHA, DGSAHA, LCAHA, and SaNSDE, which indicates that CEAHA is still competitive. In the test functions F1, F3, F4, F5, F7, F9, and F12, CEAHA, IAHA, DGSAHA, and LCAHA demonstrated faster convergence speeds and more stable optimization performance compared to other competing algorithms such as JADE, SaNSDE, WOA, SSA, PSO, PDO, GTO, GOA, EMA, and AOA. A detailed analysis of Fig. 10 reveals that CEAHA’s fitness evaluation curve converges the fastest, and its box plot at the 25,000th function evaluation shows the narrowest interquartile range, highlighting CEAHA’s significant advantages in enhancing the convergence rate and robustness of performance in the artificial hummingbird algorithm. From these 12 test cases, it is evident that regardless of whether the problems are unimodal, multimodal, composite, or constrained optimization issues, CEAHA consistently maintains superior convergence speed and robustness.

Figure 10

The column chart of Friedman’s mean rank among CEAHA and other algorithms in CEC2014.

Figure 11

The column chart of Friedman’s mean rank among CEAHA and other algorithms in CEC2019 and CEC2022.

Friedman test

To comprehensively and visually evaluate CEAHA against 21 other meta-heuristic competitor algorithms on CEC2014, CEC2019, and CEC2022 test suites, the Friedman test⁹² is conducted. Figure 10 presents a bar chart of Friedman’s mean ranks for CEAHA and its competitors across four dimensions (10D, 30D, 50D, and 100D) of the CEC2014 suite. CEAHA consistently ranks at the forefront across all tested dimensions with average ranks of 2.75, 3.5, 3.5, and 2.9, respectively, followed by IAHA, LCAHA, DGSAHA, EEFO, SaNSDE, GTO, CSBO, among others. Notably, as the dimension of problems increases, the average ranks of AOA, CSBO, EEFO, EMA, SPBO, SaNSDE, and JADE trend upward, while CEAHA maintains a strong performance with an average rank of only 2.9 in the challenging 100D tests, demonstrating its robust performance in high-dimensional optimization spaces.

Figure 11 depicts the Friedman’s mean rank bar charts for CEAHA and competing algorithms on CEC2019 and the two dimensions (10D, 20D) of CEC2022. The data in the chart indicates that CEAHA leads the ranking, with an average rank of only 1.75 in CEC2019 and with average ranks of 3.33 and 3.67 in the 10D and 20D dimensions of CEC2022, respectively. These comparative results highlight that CEAHA shows exceptional potential and applicability in tackling non-convex problems in CEC2022, whether they are unimodal, multimodal, composite, or constrained optimization tasks.

Figure 12

Structure of pressure vessel design problem.

Engineering cases analysis

To further validate the effectiveness of CEAHA in handling constrained global optimization problems, this section selects four practical engineering design challenges from existing literature. These problems include the design of pressure vessels, gear train, speed reducer, and piston lever. These design problems have been solved using various other optimization techniques. By comparing the results obtained with CEAHA to those achieved with other methods, this paper demonstrates the superiority of the proposed algorithm. In addressing these mechanical design issues, penalty functions are utilized to manage the various constraints, ensuring the generality and practicality of the algorithm. Specifically, suppose the optimization problem includes an objective function f(X) and multiple constraints, including inequality constraints ${g_i}(X) \le 0$ and equality constraints ${h_i}(X) = 0$, thereby allowing the construction of a new objective function $\Phi (X)$:

$$\begin{aligned} \Phi (X) = f(X) + \sum \nolimits _{i = 1}^m {{P_i} \cdot \max (0,{g_i}(X))} + \sum \nolimits _{j = 1}^n {{Q_j} \cdot |{h_j}(x)|} \end{aligned}$$

(21)

where, f(X) represents the original objective function, $g_i(X)$ denotes the i-th inequality constraint, and $h_j(X)$ represents the j-th equality constraint. $P_i$ and $Q_i$ are the corresponding penalty coefficients, which reflect the severity of the penalty for violating each respective constraint. The detailed analyses of four constrained mechanical design problems are presented as follows.

Design of pressure vessel

Table 12 Statistical results of 30 independent runs of the pressure vessel design optimization problem.

The objective of this issue is to minimize the manufacturing cost of a pressure vessel, with its parameter structure illustrated in Fig. 12. The problem comprises 4 design variables (i.e., thickness of the shell ($x_1$), thickness of the head ($x_2$), inner radius ($x_3$), length of the cylindrical section of the vessel ($x_4$)). The penalty coefficient vector is denoted as $[{P_1},{P_2},{P_3},{P_4},Q] = [12{,}000,8000,1,1,1]$, with an additional constant constraint $h=0$. The mathematical model of pressure vessel is as follows:

Minimize:

$$\begin{aligned} f(X) = 0.6224{x_1}{x_3}{x_4} + 1.7781{x_2}x_3^2 + 3.1661x_1^2{x_4} + 19.84x_1^2{x_3} \end{aligned}$$

(22)

Subject to:

$$\begin{aligned} \left\{ {\begin{array}{l} {{g_1}(X) = - {x_1} + 0.0193{x_3} \le 0}\\ {{g_2}(X) = - {x_2} + 0.00954{x_4} \le 0}\\ {{g_3}(X) = - \pi x_3^2{x_4} - \frac{4}{3}\pi x_3^3 + 1{,}296{,}000 \le 0}\\ {{g_4}(X) = {x_4} - 240 \le 0} \end{array}} \right. \end{aligned}$$

(23)

Among these variables, $x_1$ and $x_2$ are discrete, expressed as integer multiples of 0.0625. Conversely, $x_3$ and $x_4$ are continuous. Their respective lower and upper bounds specified below:

$$\begin{aligned} & 1 \times 0.0625 \le {x_1},{x_2} \le 99 \times 0.0625, \nonumber \\ & \quad 10 \le {x_3},{x_4} \le 200 \end{aligned}$$

(24)

The solution results for this design challenge obtained by CEAHA and competing algorithms are displayed in Table 12. It can be observed that CEAHA, ISOS, mSSA, SNS, AOA-NM, GEA, and RCGA all have the potential to find the optimal solution; however, CEAHA achieves a lower mean solution value and a smaller standard deviation than SNS, AOA-NM, GEA, RCGA, and other competitors. It is worth noting that although the fitness function values obtained by AHA, LAA, mDE, SCSO, and WaOA are relatively small, these results are infeasible. The infeasibility arises because the design variables $x_1$ and $x_2$ they solved do not meet the discretization requirement of being integer multiples of 0.0625. Although CEAHA does not perform as well as ISOS in terms of mean and standard deviation when addressing the pressure vessel problem, it demonstrates a clear competitive advantage over other algorithms such as SNS, AOA-NM, GEA, BBO, RCGA, CPSO, MVO, ASO, EBO, and AOA, providing an effective new solution for solving the pressure vessel issue.

Design of gear train

Figure 13

Structure of gear train design problem.

The issue of gear train design (Fig. 13) represents an unconstrained discrete design problem within the field of mechanical engineering. The objective is to minimize the gear ratio, which is defined as the ratio of the angular velocity of the output shaft to that of the input shaft. Numbers of teeth on the gears, denoted as ${n_A}( = {x_1})$, ${n_B}( = {x_2})$, ${n_C}( = {x_3})$ and ${n_D}(={x_4})$, are considered as design variables, with their mathematical model as follows:

Minimize:

$$\begin{aligned} f(X) = {\left( \frac{1}{{6.931}} - \frac{{{x_3}{x_2}}}{{{x_1}{x_4}}}\right) ^2} \end{aligned}$$

(25)

Variable range:

$$\begin{aligned} {x_i} \in \{ 12,13,14, \ldots ,60\}, i = 1,2,3,4 \end{aligned}$$

(26)

The penalty coefficient vector is denoted as $[{P_1},{P_2},{P_3},Q] = [1,1,1,1]$, with an additional constant constraint $h=0$. Analysis of the data presented in Table 13 indicates that for the gear train design problem, CEAHA, SNS, GEA, ABC, and RCGA all have the potential to find the optimal solution across 30 independent runs. However, CEAHA exhibited the best average performance among all the algorithms and the least standard deviation, demonstrating higher efficiency and stability in solving this design challenge. It is worth noting that although LAA achieves relatively low fitness function values, these results are infeasible. The reason is that the design variables $n_A$, $n_B$, $n_C$, and $n_D$ solved by LAA do not meet the requirements for discretization into positive integers.

Table 13 Statistical results of 30 independent runs of the gear train design optimization problem.

Table 14 Statistical results of 30 independent runs of the speed reducer design optimization problem.

Design of speed reducer

Figure 14

Structure of speed reducer problem.

The speed reducer (Fig. 14) is a crucial component of the gearbox, applicable to a variety of uses. The weight of the reducer will be minimized under 11 constraint conditions. The problem involves seven variables: the width of the tooth surface $b( = {x_1})$, the module of the tooth surface $m( = {x_2})$, the number of teeth in the small gear $z( = {x_3})$, the length of the first shaft between bearings ${l_1}( = {x_4})$, the length of the second shaft between bearings ${l_2}( = {x_5})$, the diameter of the first shaft ${d_1}( = {x_6})$ and the diameter of the second shaft ${d_2}( = {x_7})$. The penalty coefficient vector is denoted as $[{P_1},{P_2}, \ldots ,{P_{11}},Q] = [50,10,1,1,1,20,1,300,1,1,50,1]$, with an additional constant constraint $h=0$. The mathematical formulas for this problem are as follows:

Minimize:

$$\begin{aligned} \begin{array}{*{20}{c}} {f(X) = 0.7845{x_1}x_2^2(3.3333x_3^2 + 14.9334{x_3}} {- 43.0934) - 1.508{x_1}(x_6^2 + x_7^2)} {+ 7.4777(x_6^3 + x_7^3) + 0.7854({x_4}x_6^2 + {x_5}x_7^2)} \end{array} \end{aligned}$$

(27)

Subject to:

$$\begin{aligned} {g_1}(X)&= \frac{{27}}{{{x_1}x_2^2{x_3}}} - 1 \le 0 \end{aligned}$$

(28)

$$\begin{aligned} {g_2}(X)&= \frac{{397.5}}{{{x_1}x_2^2x_3^2}} - 1 \le 0 \end{aligned}$$

(29)

$$\begin{aligned} {g_3}(X)&= \frac{{1.93x_4^3}}{{{x_2}x_6^4{x_3}}} - 1 \le 0 \end{aligned}$$

(30)

$$\begin{aligned} {g_4}(X)&= \frac{{1.93x_5^3}}{{{x_2}x_7^4{x_3}}} - 1 \le 0 \end{aligned}$$

(31)

$$\begin{aligned} {g_5}(X)&= \frac{{\sqrt{{{(745{x_4}/({x_2}{x_3}))}^2} + 16.9 \times {{10}^6}} }}{{110x_6^3}} - 1 \le 0 \end{aligned}$$

(32)

$$\begin{aligned} {g_6}(X)&= \frac{{\sqrt{{{(745{x_5}/({x_2}{x_3}))}^2} + 157.5 \times {{10}^6}} }}{{85x_7^3}} - 1 \le 0 \end{aligned}$$

(33)

$$\begin{aligned} {g_7}(X)&= \frac{{{x_2}{x_3}}}{{40}} - 1 \le 0 \end{aligned}$$

(34)

$$\begin{aligned} {g_8}(X)&= \frac{{5{x_2}}}{{{x_1}}} - 1 \le 0 \end{aligned}$$

(35)

$$\begin{aligned} {x_9}(X)&= \frac{{{x_1}}}{{12{x_2}}} - 1 \le 0 \end{aligned}$$

(36)

$$\begin{aligned} {g_{10}}(X)&= \frac{{1.5{x_6} + 1.9}}{{{x_4}}} - 1 \le 0 \end{aligned}$$

(37)

$$\begin{aligned} {g_{11}}(X)&= \frac{{1.1{x_7} + 1.9}}{{{x_5}}} - 1 \le 0 \end{aligned}$$

(38)

Variable range:

$$\begin{aligned} \begin{array}{*{20}{c}} {2.6 \le {x_1} \le 3.6}\\ {0.7 \le {x_2} \le 0.8}\\ {{x_3} \in \{ 17.18.19, \ldots ,28\} }\\ {7.3 \le {x_4},{x_5} \le 8.3}\\ {2.9 \le {x_6} \le 3.9}\\ {5.0 \le {x_7} \le 5.5} \end{array} \end{aligned}$$

(39)

Analysis of the data from Table 14 reveals that in addressing the gear train design problem, CEAHA, mDE, SNS, AHA, and EABOA all have the potential to find the optimal solution in 30 independent runs. However, CEAHA demonstrates the best average performance among all the algorithms. Although EABOA exhibits the smallest variance in the context of gearbox design optimization, its ability to find the optimal solution is inferior to that of CEAHA.

Figure 15

Structure of piston lever problem.

Design of piston lever

The primary objective of this problem is to minimize the itinerary when raising the piston lever from ${0^ \circ }$ to ${45^ \circ }$, by positioning components $H( = {x_1})$, $B( = {x_2})$, $D( = {x_3})$ and $X( = {x_4})$ of the piston lever (Fig. 15). The penalty coefficient vector is denoted as $[{P_1},{P_2},{P_3},{P_4},Q] = [1,1,1,100,1]$, with an additional constant constraint $h=0$. The mathematical formulas for the problem are as follows:

Minimize:

$$\begin{aligned} \begin{array}{*{20}{c}} f(X) = \frac{1}{4}\pi x_3^2({L_2} - {L_1}) \end{array} \end{aligned}$$

(40)

Subject to:

$$\begin{aligned} {g_1}(X)&= QL\cos \theta - R \times F \le 0 \end{aligned}$$

(41)

$$\begin{aligned} {g_2}(X)&= Q(L - {x_4}) - {M_{\max }} \le 0 \end{aligned}$$

(42)

$$\begin{aligned} {g_3}(X)&= 1.2({L_2} - {L_1}) - {L_1} \le 0 \end{aligned}$$

(43)

$$\begin{aligned} {g_4}(X)&= \frac{{{x_3}}}{2} - {x_2} \le 0 \end{aligned}$$

(44)

where,

$$\begin{aligned} \begin{aligned} R&= \frac{{| - {x_4}({x_4}\sin \theta + {x_1}) + {x_1}({x_2} - {x_4}\cos \theta )|}}{{\sqrt{{{({x_4} - {x_2})}^2} + x_1^2} }} \\ F&= \frac{{\pi Px_3^2}}{4} \\ {L_1}&= \sqrt{{{({x_4} - {x_2})}^2} + x_1^2} \\ {L_2}&= \sqrt{{{({x_4}\sin \theta + {x_1})}^2} + {{({x_2} - {x_4}\cos \theta )}^2}} \\ \theta&= {45^ \circ } \\ Q&= 10,000lbs \\ L&= 240in \\ {M_{\max }}&= 1.8 \times {10^6}lbs in \\ P&= 1500psi \\ \end{aligned} \end{aligned}$$

(45)

Variable range:

$$\begin{aligned} \begin{aligned} 0.05&\le {x_1},{x_2},{x_4} \le 500 \\ 0.05&\le {x_3} \le 200 \\ \end{aligned} \end{aligned}$$

(46)

An analysis of the data in Table 15 indicates that, when addressing the piston lever design problem, the algorithms CEAHA, SNS, AOA-NM, EBO, and MVO all exhibit the potential to find the optimal solution across 30 independent runs. However, CEAHA has demonstrated exceptional average optimization performance and lower standard deviations. Although the best fitness value of SNS is slightly lower than that of CEAHA, CEAHA outperforms SNS in terms of mean, worst-case performance, and standard deviation. This suggests that CEAHA exhibits greater robustness in the context of piston lever design optimization.

Table 15 Statistical results of 30 independent runs of the piston lever design optimization problem.

It can be observed from these four mechanical design problems, characterized by composite constraints, that CEAHA not only possesses commendable average performance but also exhibits excellent robustness, capable of achieving cost-minimized solutions with limited computational resources.

Conclusions

In this study, the ergodic chaotic motion mechanism is applied within the artificial hummingbird algorithm (AHA) framework to develop an enhanced version, termed CEAHA, which incorporates chaotic traversal flight. This study introduces the concept of traversal efficiency by chaotic intelligent entities within the solution space for the first time, and examines the impact of eight chaotic maps capable of generating centrally symmetric distributions on the convergence speed and population diversity of optimization algorithms. It is shown that the Cubic mapping significantly aids algorithmic agents in escaping local optima. This paper provides an in-depth analysis of the global search role of the Tent mapping with an invariant probability measure of 1 and the benefits of the U-shaped Cubic mapping in escaping local optima, enhancing population diversity, and comprehensively exploiting the solution space. By integrating chaotic dynamics, CEAHA effectively synergizes exploration and exploitation in optimization processes. Performance evaluations on 23 standard test functions, the CEC2014 and CEC2019 test suites, the latest single-objective test suite CEC2022, and four mechanical design cases (including pressure vessel, gear train, speed reducer, and piston lever designs) demonstrate CEAHA’s exceptional convergence capabilities and robustness. These findings underscore the substantial potential for including chaotic mappings in meta-heuristic optimization algorithm design. Additionally, the deterministic nature of chaos, with its inherent randomness, is well-suited to population movement patterns and is expected to significantly improve metaheuristic algorithms’ performance in solving complex optimization problems through accelerated convergence, enhanced solution quality, and reduced resource consumption. However, for specific scenarios, how to combine different chaotic motion laws to design diverse chaotic optimization strategies to adapt to various optimization tasks remains an urgent topic for exploration.