Introduction

Structural integrity and safety are primary criterions for reliable and durable functioning in civilian structures at the time of severe shocks and seismic inputs. During any seismic excitation, traditional structures without any control scheme rely on the inherent structural damping for the dissipation of the induced seismic energy. To enhance the dissipative capabilities of a structure, various active and passive control devices have been investigated and utilized. Active devices for vibration suppression utilize control feedback schemes for the optimal control1,2. The main drawbacks for such devices include their stability, robustness, complexity and energy consumption making them more challenging than passive vibration absorbers to be adopted. On the other hand, passive vibration reduction devices suppress the structural vibration amplitudes without mandating additional power requirements3. However, the linear passive vibration suppression devices (i.e. the tuned mass damper) can only operate in narrowband frequency range. Therefore, they cannot function effectively during multi-frequency transient disturbances which impedes their applicability for broadband frequency-energy inputs. In order to alleviate such drawbacks, the concept of nonlinear energy sinks (NESs) was introduced in4. The functioning of NESs is based on the passive targeted energy transfer (TET), described in5, wherein there is an irreversible unidirectional passive redistribution of input energy from the main structure to the NES. Moreover, the presence of nonlinear stiffness in the NES is associated with a broadband nonlinear frequency components, thereby allowing single or cascade of resonance captures between the NES and the modes of the structure6. The TET was also found to be achieved by the NES action of transferring energy from low-frequency to high-frequency modes which results in more effective energy dissipation by the inherent structural modal damping7. This low to high TET was recently named as an intermodal targeted energy transfer (IMTET) in8. The single-sided vibro-impact (SSVI NES) was found to be the most effective NES to redistribute the input energy from the low frequency mode of the primary structure to its high frequency modes7. Accordingly, a substantial number of structural modes engage in TET by the SSVI NES nonlinear action. The NESs has found various applications across the literature, some of these include, but not limited to, the suppressing of aeroelastic flutter instabilities9,10,11, vortex induced vibrations12,13, vibrations in beams14,15 and wind turbines16. Additional information about various types of NESs and their respective applications can be found in17.

Seismic mitigation capabilities of NESs have been an active area of research in the past two decades. In18, a two-dimensional NES was proposed to study the efficacy of the NES in suppressing the induced seismic excitation vibration in two translationally-coupled directions of the structure motion. A numerical optimization procedure was applied to enhance the TET along the transverse and the longitudinal directions of the motion of the primary structure. The bistable nonlinear coupling force in NESs was firstly applied in19 where robust and high performance in impulsive vibration suppression was achieved for broad range of input energies induced into the primary linear structure. Later, the frequency-energy analysis of this Bistable NES (BNES) was thoroughly studied in the frequency-energy plot (FEP)20. Several studies later explored the various applications of the BNESs. As an example, a magnetic BNES (MBNES) was utilized in21 and 22 for structural seismic control. The proposed MBNES utilized permanent magnets to generate the bistability in the NES coupling force. Accordingly, a comparative study between MBNES, cubic NES and a tuned mass damper (TMD) was conducted in21. A cascade of transient internal resonance captured by the MBNES was found to result in a faster vibration suppression. In22, cyclic-loading tests and shake table tests were employed to analyze the response of the MBNES subjected to seismic excitations on a single-story structure. Based on the tests, it was concluded that the bistability property is influenced by the spatial configuration of the magnets. Seismic mitigation using a sliding BNES (SBNES) placed on a one degree-of-freedom system was studied in23 and for a 4 m four-story building structure in24. The MBNES and the SBNES models are extensions of the BNES and the magnet-based NESs that were firstly proposed in19 and 25, respectively.

The pendulum tuned mass dampers (PTMD) was applied in various structures because of its simplicity. The PTMD essentially consists of a tip mass, pendulum, and a damper element. The nonlinear effects of PTMDs on mitigation of vibration for one degree-of-freedom system undergoing harmonic excitation was analyzed in26. One conclusion from this study was that the nonlinear effect of the PTMD can be ignored when the rotational angle is less than 9°. A pendulum-type nontraditional TMD was proposed in27 for seismic mitigation purposes. The system acted as an inverted rocking system with connection to the primary structure at the top end and dampers at the base. The resultant system was found to reduce both the inter-story drift and the floors’ absolute acceleration in a six-story structure. The system was later extended in28 to a twenty five-story structure. The study in29 employed an array of pendulums as vibration absorbers for single degree-of-freedom primary structure. The authors were able to enhance the frequency bandwidth of vibration suppression by tuning the pendulums at different natural frequencies. A pendulum-type tuned vibration absorber was also analyzed in30 and coupled with a system incorporating multiple modes. The proposed vibration absorber was designed as two dynamic masses that are oscillating about a pendulum axis and was found to suppress vibration in broadband frequency range. The method of direct partition of motion was employed in31 to study the dynamics of a spring-mass-pendulum system. The global system consisted of a simple pendulum that is connected to a mass on a spring (moving horizontally). The authors also assumed the global system to be such that the respective spring stiffness of the linear oscillator (LO) is very large, resulting in a frequency of the uncoupled oscillator to be an order of magnitude higher than that of the uncoupled pendulum. The dynamics of a spring-pendulum and the corresponding exchange of energy during coupling between the pendulum and LO was analyzed in32. During a strong coupling, the pendulum and the LO move as a coherent unit. However, during a weak coupling, the interactions were minimal between the two components. The strong coupling was observed for low magnitude and negative total energy. Moderate and weak coupling was observed for higher magnitude and intermediate values of total energy, respectively. Structural vibration suppression using spring-pendulum with impact on a 53.9 m high power transmission tower was studied in33. The proposed model had a better suppression than the case of simple pendulum and a spring-pendulum without impact. A spring-mass inverted pendulum-like vibration absorber was proposed in34 for a primary structure that also resembled an inverted pendulum with applications in robotics and civil engineering. The vibration suppression capabilities of a spring-pendulum system representing a ship’s rolling motion using a tuned transverse absorber was studied in35. The authors studied the dynamics of two modes of the vibration absorber system subjected to multi-parameter excitations using multiple scale perturbation technique. Moreover, the absorber was changed to a longitudinal configuration in36. In35, the authors were able to attenuate the steady-state amplitude of the two modes to 0.08% and 0.2% of its maximum values, whereas in36, the reduction was 0.012% and 10% of its maximum values respectively. In another set of publications in37,38,39,40, different NESs configurations were introduced and investigated for vibration suppression. A nonlinear vibration absorber, that incorporates a synergy between linear and nonlinear cubic stiffness NES dynamics, was introduced and investigated in37 for vibration suppression in harmonically excited circular ring. A lever-type vibration absorber was proposed in38 to suppress the induced vibration by harmonic base excitation. In this configuration, the left end of the pivoted massless lever is coupled with the linear system while the right one is coupled with the NES. This configuration allowed for obtaining maximum transmissibility of vibration energy at lower mass than that of the cubic stiffness NES. Another NES configuration, which was based on employing an inerter in the cubic stiffness NES, was also explored in39 for isolation of the induced vibration energy by harmonic based excitation. This design was also aimed to reduce the reliance on additional mass for obtaining optimal performance in the cubic stiffness NES. In a recent publication40, the concept of hybrid vibration absorber in37 was employed for vibration energy isolation from a rectangular plate attached to an arbitrary boundary. Accordingly, the vibration energy is transferred to the coupled rigid body with the plate through a set of four hybrid-coupling elements where each one incorporates linear and nonlinear stiffness components.

From the surveyed literature above, it can be said that the main advantages of NESs include their broader frequency-energy range of operation and their capability of modal energy redistribution by the TET mechanism. However, the utilization of bistable spring-loaded inverted pendulum, as NES, was not considered in the literature up-to-date. The stability characteristics of the supported inverted pendulum by a restoring torsional stiffness can be either stable or bistable depending on the gravity and torsional stiffness resultant moments. Accordingly, if the moment of the torsional stiffness force is less than that of the gravity force moment, then system becomes bistable and generates two stable and one critically stable equilibria. Therefore, in the present study, a spring-loaded inverted pendulum NES (SLIP NES) is proposed for vibration mitigation purposes to suppress impulsive, seismic and forced vibration. The proposed SLIP NES configuration is adaptable to resemble the dynamics of the stiffness-based NES with purely cubic stiffness and the bistable NES (BNES) with negative and non-negative stiffness content. This new NES configuration incorporates a synergetic mechanism between the inertial and bistable nonlinear coupling dynamics. Significant enhancement in the performance is obtained by this proposed configuration compared with the well-known cubic stiffness NESs, the TMD and many other existing types of NESs.

Mathematical model of the SLIP NES

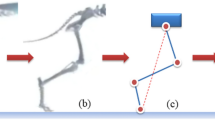
The torsional SLIP NES possesses both nonlinear inertial and dynamical coupling with the primary LO. The dynamic coupling is incorporated in the inertial coupling as it will be observed in the equations of motion. This dynamic coupling assists the inertial coupling to generate both stable and bistable nonlinear coupling forces. The SLIP NES is shown in the schematic diagram Fig. 1a. This SLIP NES of mass \(m\), coupling rigid and massless rod of length \(\ell\), torsional spring of stiffness coefficient \(k_{\beta }\) and torsional damping of viscous damping coefficient \(\lambda_{\beta }\) is coupled with the LO as shown in Fig. 1b. The physical parameters of the LO are the mass M, the linear spring stiffness coefficient \(k\) and the linear viscous damping coefficient \(\lambda\).

Fig. 1
figure 1

The SLIP NES configuration in (a) and the coupled LO with the SLIP NES in (b).

Full size image

To verify the stable and bistable forces in the SLIP, the equation of motion is obtained as

$$m\ell^{2} \ddot{\beta } + k_{\beta } \beta - mg\ell \sin \beta = 0$$
(1)

Accordingly, from Eq. (1), the nonlinear coupling force in the SLIP is expressed by

$$f\left( \beta \right) = k_{\beta } \beta - mg\ell \sin \beta$$
(2)

The force in Eq. (2) is rewritten as

$$f\left( \beta \right) = k_{\beta } \left( {\beta - \alpha \sin \beta } \right)$$
(3)

where, \(k_{\beta }\) is the SLIP torsional stiffness coeffecient and \(\alpha = mg\ell /k_{\beta }\). The SLIP NES force in Eq. (3) resembles the odd-power stiffness components in the stiffness-based NES. The equivalent stiffness-based force can be represented, up to 5th power, by

$$\overline{f}\left( \beta \right) = a\beta + b\beta^{3} + c\beta^{5}$$
(4)

The effect of the quantity \(\alpha\) on the type of the force \(f\left( \beta \right)\) in Eq. (3) is shown in Fig. 2 at \(k_{\beta } = 1\) for \(\alpha = 2\),\(\alpha = 1\), \(\alpha = 0.5\) and \(\alpha = - 1\). In addition, the corresponding stiffness-based forces \(\overline{f}\left( \beta \right)\) in Eq. (4) are plotted on the same figure. For \(\alpha \le 1\), the obtained force resembles the stable nonlinear NES coupling force in which one stable equilibrium position appears19,20. However, at \(\alpha > 1\) the SLIP NES generates four equilibrium positions (two stable and two critically stable at \(\beta = 0\) and \(\beta = \pi\)) where the force resembles the bistable NES force for the angles of rotation \(0 < \beta < \pi\). Therefore, the SLIP NES can be simply realized and designed to serve dual purpose as either stable or bistable NES which can be achieved at fixed mass by either adjusting the arm length or the torsional stiffness to alter the magnitude of \(\alpha\)(i.e. \(\alpha \le 1\) for the stable case and \(\alpha > 1\) for the bistable case).

Fig. 2
figure 2

The SLIP NES force \(f\left( \beta \right)\) and its corresponding force \(\overline{f}\left( \beta \right)\) for \(k_{\beta } = 1\) in (a) at \(\alpha = 2\), in (b) at \(\alpha = 1\), in (c) at \(\alpha = 0.5\) and in (d) at \(\alpha = - 1\).

Full size image

The SLIP NES force in Eq. (3) resembles stiffness-based NESs as represented by Eq. (4) where the corresponding polynomial coefficients of the equivalent stiffness-based force are provided in Table 1. For \(\alpha = 2\), the SLIP NES force is dominated by negative and nonnegative cubic stiffness terms which resembles the bistable NES in the literature (i.e.,19,20,21,22,23,24). For \(\alpha = 1\), the SLIP NES force is dominated by the nonnegative cubic stiffness term which resembles the well-known Type I NES in the literature (i.e.,4,5,6). For \(\alpha = 0.5\), the SLIP NES force is dominated by the nonnegative linear and cubic stiffness terms which resembles the quasi-zero stiffness nonlinear vibration absorber that firstly addressed (i.e.,41,42,43). For negative values of \(\alpha\), the nonlinear SLIP NES coupling force exhibits stiffness softening as shown in Fig. 2d where the force is dominated by nonnegative linear and negative cubic stiffness terms as in44. Accordingly, the SLIP NES configuration is adaptable to serve as an alternative to different kinds of NESs based on its parameter \(\alpha\).

Table 1 The corresponding stiffness-based force coefficients.
Full size table

Therefore, depending on the parameter \(\alpha\) and the torsional stiffness \(k_{\beta }\) values, the resembled four kinds of nonlinear vibration absorbers or NESs are shown in Table 2 based on the new proposed SLIP NES configuration.

Table 2 Different NES configurations resembled by the NES force in Eq. (3).
Full size table

Application with Impulsive Input

The equations of motion of the coupled LO with the SLIP NES are obtained by Euler–Lagrange methods as

$$\begin{gathered} \left( {M + m} \right)\ddot{x} + m\ell \ddot{\beta }\cos \beta - m\ell \dot{\beta }^{2} \sin \beta + \lambda \dot{x} + kx = 0 \hfill \\ m\ell^{2} \ddot{\beta } + m\ell \ddot{x}\cos \beta + \lambda_{\beta } \dot{\beta } + k_{\beta } \beta - mg\ell \sin \beta = 0 \hfill \\ \end{gathered}$$
(5)

These equations are rewritten in non-dimensional form by letting \(u = \frac{x}{\ell }\), \(\omega_{0} = \sqrt {\frac{k}{M + m}}\), \(\tau = \omega_{o} t\), and \(\varepsilon = \frac{m}{M + m}\). In addition, the angle \(\beta \left( t \right)\) in dimensional time is represented by \(\theta \left( \tau \right)\) in the non-dimensional time to be distinguished between dimensional and non-dimensional time scales. Accordingly, the equation of motion in terms of the non-dimensional degrees of freedom \(u\left( \tau \right)\) and \(\theta \left( \tau \right)\) are rewritten as

$$\begin{aligned} \ddot{u} & = \frac{{ - \hat{\lambda }\dot{u} - u + \hat{\lambda }_{\theta } \dot{\theta }\cos \theta + \varepsilon \cos \theta \hat{k}_{\theta } \left( {\theta - \alpha \sin \theta } \right) + \varepsilon \dot{\theta }^{2} \sin \theta }}{{(1 - \varepsilon \cos^{2} \theta )}} \\ \ddot{\theta } & = - \ddot{u}\cos \theta - \frac{{\hat{\lambda }_{\theta } }}{\varepsilon }\dot{\theta } - \hat{k}_{\theta } \left( {\theta - \alpha \sin \theta } \right) \\ \end{aligned}$$
(6)

where \(\hat{\lambda } = \frac{\lambda }{{\omega_{0} \left( {M + m} \right)}}\), \(\hat{\lambda }_{\theta } = \frac{{\lambda_{\beta } }}{{\ell^{2} \omega_{0} \left( {M + m} \right)}}\), \(\hat{k}_{\theta } = \frac{{k_{\beta } }}{{\ell^{2} \omega_{0}^{2} \left( {M + m} \right)}}\), and \(\alpha = \frac{\varepsilon g}{{\ell \omega_{0}^{2} \hat{k}_{\theta } }}\). The derivation of the equations of motion in non-dimensional form in Eq. (6) is provided in Appendix A in the supplementary material based on the non-dimensional energy equations. The equations of motion has inertial coupling by the term \(\ddot{u}\cos \theta\) and dynamic coupling by the term \(\hat{k}_{\theta } \left( {\theta - \alpha \sin \theta } \right)\), which is similar to the SLIP force in Eq. (3).

The SLIP NES optimized parameters (\(\alpha\), \(\hat{k}_{\theta }\) and \(\hat{\lambda }_{\theta }\)) are determined based on optimizing the energy transfer from the LO by the nonlinear action of the SLIP NES and completely dissipated by its damping content. Therefore, the three optimized parameters, especially the quantity \(\alpha\), makes the SLIP NES adjustable to work with any system by mainly adjusting its arm length \(\ell\) at the optimized values of \(\hat{k}_{\theta }\) and \(\hat{\lambda }_{\theta }\). In the following sections, the proposed SLIP NES is applied for translational vibration generated by impulsive input, and harmonic and seismic ground motion inputs. In addition, the proposed SLIP NES is applied here for torsional vibration suppression.

Application with Harmonic and Seismic Inputs

The non-dimensional equations of motion in Eq. (6) of the attached LO with the bistable SLIP NES (B-SLIP) NES are rewritten in matrix form as

$$\left[ {\begin{array}{*{20}c} 1 & {\varepsilon \cos \theta } \\ {\varepsilon \cos \theta } & \varepsilon \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{u}} \\ {\ddot{\theta }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\hat{\lambda }} & 0 \\ 0 & {\hat{\lambda }_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{\theta }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {\varepsilon \hat{k}_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ \theta \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varepsilon \dot{\theta }^{2} \sin \theta } \\ {\varepsilon \hat{k}_{\theta } \alpha \sin \theta } \\ \end{array} } \right] + {\text{F}}_{input}$$
(7)

where, \({\text{F}}_{input} = [\begin{array}{*{20}c} {\gamma f\cos \omega t} & 0 \\ \end{array} ]^{\text{T}}\) is employed for harmonic excitation input and \({\text{F}}_{input} = - \left[ {\begin{array}{*{20}c} 1 & \varepsilon \\ \end{array} } \right]^{\text{T}} \gamma \ddot{u}_{g}\) for the seismic ground motion with \(\ddot{u}_{g}\) being the ground acceleration while \(\gamma\) incorporates scaling and non-dimensional effect to the input force.

Application with torsional vibration

The equations of motion of the torsional vibration system in Fig. 3 that incorporates a disk attached to an elastic rod and coupled with the SLIP NES are obtained in non-dimensional form as

$$\begin{gathered} \ddot{\phi } + \hat{\lambda }\dot{\phi } + \phi - \hat{\lambda }_{\theta } \left( {\dot{\theta } - \dot{\phi }} \right) - \hat{k}_{\theta } \left( {\theta - \phi } \right) = 0 \hfill \\ \varepsilon \ddot{\theta } + \hat{\lambda }_{\theta } \left( {\dot{\theta } - \dot{\phi }} \right) - \hat{k}_{\theta } \phi + \hat{k}_{\theta } \left( {\theta - \hat{\alpha }\sin \left( \theta \right)} \right) = 0 \hfill \\ \end{gathered}$$
(8)

where \(\omega_{0} = \sqrt {\frac{{k_{\phi } }}{J}}\),\(\tau = \omega_{o} t\),\(\varepsilon = \frac{{m\ell^{2} }}{J}\), \(\hat{\lambda } = \frac{{\lambda_{\phi } }}{{J\omega_{0} }}\), \(\hat{\lambda }_{\theta } = \frac{{\lambda_{\theta } }}{{J\omega_{0} }}\) and \(\hat{k}_{\theta } = \frac{{k_{\theta } }}{{J\omega_{0}^{2} }}\), and \(\hat{\alpha } = \frac{\varepsilon g}{{\omega_{0}^{2} \ell \hat{k}_{\theta } }}\).

Fig. 3
figure 3

Coupled torsional system with the B-SLIP NES.

Full size image

The derivation of equations of motion in Eq. (8) is provided in Appendix B in the supplementary material. These equations are rewritten in matrix form for harmonic excitation input \({\text{F}}_{input} = [\begin{array}{*{20}c} {\gamma f\cos \omega t} & 0 \\ \end{array} ]^{\text{T}}\) as

$$\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & \varepsilon \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{\phi }} \\ {\ddot{\theta }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\hat{\lambda } + \hat{\lambda }_{\theta } } & { - \hat{\lambda }_{\theta } } \\ { - \hat{\lambda }_{\theta } } & {\hat{\lambda }_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\phi }} \\ {\dot{\theta }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {1 + \hat{k}_{\theta } } & { - \hat{k}_{\theta } } \\ { - \hat{k}_{\theta } } & {\hat{k}_{\theta } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \phi \\ \theta \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {\hat{k}_{\theta } \alpha \sin \theta } \\ \end{array} } \right] + {\text{F}}_{input}$$
(9)

Application with impulsive input to the LO system

The non-dimensional parameters of the considered B-SLIP NES are obtained by employing the multi-objective optimization method. The optimization is carried out at LO initial velocity of \(\dot{u}\left( 0 \right) = 0.25\) for \(\alpha\) values ranges between \(1 < \alpha \le 2\) for the B-SLIP NES. Accordingly, The obtained optimized parameters of the this NES, using minimum energy dissipation by the LO as an objective function, are \(\hat{\lambda }_{\theta } = 0.0021\), \(\hat{k}_{\theta } = 14.1\), and \(\alpha = 1.29\).

The non-dimensional equations of motion in Eq. (6) are solved numerically at \(\varepsilon = 0.05\) and LO damping coefficient of \(\hat{\lambda } = 0.005\). Accordingly, the results in Fig. 4, in which the values of \(\alpha\) at the optimized B-SLIP NES parameter \(\hat{\lambda }_{\theta }\) and \(\hat{k}_{\theta }\) are plotted, 99% of the energy induced into the LO is transferred and dissipated by the B-SLIP NES action.

Fig. 4
figure 4

Energy dissipation performance for different values of \(\alpha\) of the B-SLIP NES at its optimized parameters.

Full size image

The responses at these optimized B-SLIP NES parameters for \(\dot{u}\left( 0 \right) = 0.25\), are shown in Fig. 5 where 99% of the energy induced into the LO is transferred and rapidly dissipated by the B-SLIP NES nonlinear action. A significant portion of this transferred energy from the LO is dissipated by the torsional damping of the B-SLIP NES. It is also observed that the B-SLIP NES significantly reduces the second half of the first cycle of oscillation and the first half of the second cycle of oscillation. This rapid vibration suppression is achieved via a strong 1:1 resonance capture between the B-SLIP NES and the LO responses as shown in the wavelet transform in Fig. 5d.

Fig. 5
figure 5

The LO displacement in (a), the B-SLIP NES force in (b), its angle \(\theta \left( \tau \right)\) in (c) and the wavelet frequency spectrum of \(\theta \left( \tau \right)\) in (d), at the optimized B-SLIP NES parameters \(\hat{\lambda }_{\theta } = 0.0021\) and \(\hat{k}_{\theta } = 14.1\) at \(\alpha = 1.29\) and LO initial velocity \(\dot{u}\left( 0 \right) = 0.25\), and damping \(\hat{\lambda } = 0.005\).

Full size image

The bistability content in the considered B-SLIP NES generates a double-well potential due to the negative stiffness content in the coupling NES force with the LO. Consequently, the considered B-SLIP NES is associated with two stable and one unstable equilibria which results in achieving the snap-through mechanism by which the NES escapes from one stable potential well to another as shown in Fig. 5c. Accordingly, two complete cycles of oscillation by the B-SLIP NES between the two stable equilibria are observed before it get engaged with in-well oscillation at one of the stable equilibrium positions. During the first double-well regime of oscillation, significant portion of the induced vibration energy is rapidly transferred into the NES via a strong 1:1 resonance capture with the LO as shown from the wavelet transform spectrum in Fig. 5d. This transferred energy by the passive TET mechanism is localized in the NES and dissipated by its damping.

To analyze the energy transfer by the B-SLIP NES, the instantaneous mechanical energy and the energy dissipated by damping in the system are represented, respectively, by the following equations

$$\begin{aligned} E_{Mech} \left( t \right) & = \frac{1}{2}\dot{u}\left( t \right)^{2} + \frac{1}{2}\varepsilon \left( {\dot{\theta }\left( t \right)^{2} + 2\dot{u}\left( t \right)\dot{\theta }\left( t \right)\cos \theta \left( t \right)} \right) + \frac{1}{2}u\left( t \right)^{2} + \frac{1}{2}\varepsilon \hat{k}_{\theta } \left( {\theta \left( t \right)^{2} - 2\alpha \left( {1 - \cos \theta \left( t \right)} \right)} \right) \\ E_{dissip} \left( t \right) & = E_{LO} \left( t \right) + E_{NES} \left( t \right) = \int\limits_{0}^{t} {\left( {\hat{\lambda }\dot{u}\left( t \right)^{2} + \hat{\lambda }_{\theta } \dot{\theta}\left( t \right)^{2} } \right)\,} dt \\ \end{aligned}$$
(10)

After sufficient simulation time \(t_{end} > > 0\), the quantities \(u\left( {t_{end} } \right) \cong 0\) ,\(\dot{u}\left( {t_{end} } \right) \cong 0\),\(\dot{\theta }\left( {t_{end} } \right) \cong 0\) and \(\theta \left( {t_{end} } \right) \cong \pm \theta_{s}\) where \(+\) and \(-\) indicates the right and left equilibrium positions of the B-SLIP NES, respectively. Therefore, a portion of the energy transferred from the LO by the B-SLIP NES is the pre-stored energy at the critical equilibrium position. This amount of initial energy is represented, according in Eq. (10) when the B-SLIP NES settles at stable equilibrium position, by the following equation

$$E_{PS} = \frac{1}{2}\varepsilon \hat{k}_{\theta } \left( {\theta_{s} - 2\alpha \left( {1 - \cos \theta_{s} } \right)} \right)$$
(11)

Since the B-SLIP NES has a similar behavior to the BNES in19,20, the \(E_{PS}\) is kind of a prestored energy caused by the critical stable position at \(\theta = 0\). Therefore, this energy is immediately released when the B-SLIP NES starts its initial motion at \(\theta = 0\) where it becomes negative in-well potential at the stabile equilibria. Therefore, this energy is included in the net input energy calculation at \(t = 0\) to keep 100% energy balance between the net input energy, mechanical energy, and the energy dissipation by damping. Accordingly, the calculations of the input energy into the LO by impulsive, harmonic excitation and seismic ground motion are performed, respectively, by the following equations

$$\begin{gathered} E_{input} \left( 0 \right) = \frac{1}{2}\dot{u}\left( 0 \right)^{2} - E_{PS} {\text{ (Impulsive input)}} \hfill \\ E_{input} \left( t \right) = \int\limits_{0}^{t} {\gamma \dot{u}\left( t \right)f\left( t \right)} dt - E_{PS} {\text{ (Harmonic excitation input)}} \hfill \\ E_{input} \left( t \right) = - \int\limits_{0}^{t} {\gamma \left( {\dot{u}\left( t \right) + \varepsilon \dot{\theta }\left( t \right)} \right)\ddot{u}_{g}^{{}} \left( t \right)^{2} } dt - E_{PS} {\text{ (Siesmic ground motion input)}} \hfill \\ \end{gathered}$$
(12)

The two stable equilibria of the B-SLIP NES are obtained from solving Eq. (3) at \(\alpha = 1.29\) which are \(\theta_{S} = \pm 1.204{\text{ rad (}} \pm {69}^{{\text{o}}} {)}\). At these values the residual energy is calculated from Eq. (10) as \(E_{residual} \cong - 0.076869\) at \(E_{input} = 0.04\) where \(E_{residual} + E_{PS} \cong 0\) at \(t_{end} > > 0\). Accordingly, the energy analysis is shown in Fig. 6. The balance between \(E_{input}\) and \(E_{Mech} \left( t \right) + E_{dissp} \left( t \right)\) is verified in Fig. 6a. It is clear from Fig. 6b that the energy dissipated by the LO damping \(\left( {E_{LO} } \right)\) is minimal. However, the BSLIP-NES dissipates up to 99.2% of the induced energy into the LO by its viscous damping. The energy converges to zero when the B-SLIP NES mass captures the in-well dynamics and settles at one of its stable equilibria. This B-SLIP NES nonlinear action makes it outperform the reported NESs in the literature based on its optimum performance in terms of vibration suppression in dynamical structures.

Fig. 6
figure 6

Energy plots in (a) for the balance between \(E_{input}\) and \(E_{Mech} + E_{dissp}\), and in (b) for mechanical energy \(E_{Mech}\) and energy dissipation by the LO \(\left( {E_{LO} } \right)\) and by the B-SLIP NES \(\left( {E_{NES} } \right)\).

Full size image

Furthermore, when the LO damping content is changed to \(\hat{\lambda } = 0.01\) and \(\hat{\lambda } = 0.05\), as shown in Fig. 7, the B-SLIP NES is found maintaining its performance even at high LO damping content.

Fig. 7
figure 7

The LO displacement and the B-SLIP NES angular displacement at the optimized B-SLIP NES parameters in (a) and (b) for \(\hat{\lambda } = 0.01\), and in (c) and (d) for \(\hat{\lambda } = 0.05\).

Full size image

The B-SLIP NES performance is compared with the TMD and the cubic stiffness NES (Type I NES) in Fig. 8. The Type I NES optimized parameters are \(\hat{\lambda }_{NES} = 0.012\) and \(\hat{k}_{NES} = 0.304\) while the TMD optimized parameters are \(\hat{\lambda }_{TMD} = 0.011\) and \(\hat{k}_{TMD} = 0.048\). At the optimized B-SLIP NES, Type I NES, and TMD parameters, the results in the figure clearly show that the B-SLIP NES significantly reduces the vibration amplitudes in the first two-cycle of oscillation compared with the Type I NES and the TMD. Exceeding the performances of the TMD and Type I NES in terms of vibration suppression by the B-SLIP NES is an important advantage considering its simple design that can be easily realized for real-life applications.

Fig. 8
figure 8

Comparison between B-SLIP NES, Type I NES and TMD at their optimized parameters at \(\dot{u}\left( 0 \right) = 0.25\).

Full size image

Application with seismic input to the LO system

The attached B-SLIP NES with LO is also applied with seismic ground motion input into the LO. The considered Kobe and Northridge earthquakes data, shown in Fig. 9, are scaled by the parameter \(\gamma\) and applied to the LO as in Eq. (7). The optimized B-SLIP NES parameters are also obtained by employing the multi-objective optimization method where the objective function can be either minimizing the potential energy in the LO or minimizing the root-mean-square (\(RMS\)) of the LO displacement. Both functions result in nearly similar optimum parameters of the considered NESs in this study. Accordingly, the obtained optimized parameters are \(\hat{\lambda }_{\theta } = 0.009\), \(\hat{k}_{\theta } = 58.8\), and \(\alpha = 1.013\) at \(\gamma = 0.5\). Moreover, the B-SLIP NES performance is evaluated at different \(\gamma\) values as shown in Fig. 10 where the vibration levels of the LO are significantly reduced starting from the second half of the first cycle of oscillation.

Fig. 9
figure 9

Ground acceleration data in (a) for Kobe and in (b) for Northridge earthquakes.

Full size image
Fig. 10
figure 10

Effect of the B-SLIP NES on Kobe seismic input vibration in the LO at its optimized parameters \(\hat{\lambda }_{\theta } = 0.009\),\(\hat{k}_{\theta } = 58.8\) and \(\alpha = 1.013\) for \(\gamma = 0.25\) in (a), \(\gamma = 0.5\) in (b), and \(\gamma = 0.75\) in (c).

Full size image

The performance of the B-SLIP NES is compared with that of the TMD and the Type I NES in Fig. 11 during seismic ground motion input. The optimized parameters of Type I NES are \(\hat{\lambda }_{NES} = 0.005\) and \(\hat{k}_{NES} = 2.38\) while the TMD optimized parameters are \(\hat{\lambda }_{TMD} = 0.008\) and \(\hat{k}_{TMD} = 0.04\) at \(\gamma = 0.5\). At the optimized B-SLIP NES, Type I NES, and TMD parameters, the results in the figure clearly show that the B-SLIP NES provides better performance in vibration suppression than Type I and the TMD at the two selected values of \(\gamma\).

Fig. 11
figure 11

Comparison between SLIP NES, Type I NES and TMD for Kobe seismic input at their optimized parameters in (a) at \(\gamma = 0.25\) and in (b) at \(\gamma = 0.5\).

Full size image

The energy analysis according to Eqs. (10)-(12) is provided in Fig. 12. Accordingly, the balance between \(E_{input} \left( t \right)\) and \(E_{Mech} \left( t \right) + E_{dissp} \left( t \right)\) is verified in Fig. 12a. It is also clear in Fig. 12b that the nonlinear action of the B-SLIP NES considerably minimized the energy dissipation by the LO damping \(\left( {E_{LO} } \right)\). In addition, the B-SLIP NES dissipated high percentage of the energy, induced into the LO, by its viscous damping \(\left( {E_{NES} } \right)\). The mechanical energy converges to zero when the B-SLIP NES mass settles at one of its stable equilibria. The energy analysis verifies the equations of motion and the robust performance of the B-SLIP NES.

Fig. 12
figure 12

Energy plots in (a) for the balance between \(E_{input}\) and \(E_{Mech} + E_{dissp}\), and in (b) for mechanical energy \(E_{Mech}\) and energy dissipation by the LO \(\left( {E_{LO} } \right)\) and by the B-SLIP NES \(\left( {E_{NES} } \right)\).

Full size image

The B-SLIP NES is also investigated with the previously given Northridge earthquake data in Fig. 9b. Accordingly, the LO and B-SLIP NES responses are shown in Fig. 13a and Fig. 13b, respectively, at \(\gamma = 1\). The induced seismic vibration to the LO is significantly suppressed as shown in the Fig. 13a. In addition, the bistability effect is clear in the B-SLIP NES response in Fig. 13b where it completes three cycles of in-well oscillation at its right stable equilibrium position before jumping through the critical stability position to continue with in-well oscillation on its left stable equilibrium position to settle there. This regime of motion is achieved by the synergetic mechanism between the inertial and bistable nonlinear actions in the B-SLIP NES.

Fig. 13
figure 13

Effect of the B-SLIP NES on Northridge seismic input vibration in the LO at its optimized parameters \(\hat{\lambda }_{\theta } = 0.009\),\(\hat{k}_{\theta } = 62.8\) and \(\alpha = 1.05\) for LO response in (a), and B-SLIP NES in (b).

Full size image

Application with forced torsional vibration

Analytical analysis

To further investigate and validate the performance of the B-SLIP NES in suppression the forced vibration of the system in Eq. (8) and its relevant numerical simulation results in Figs. 13 and 14, the analytical solution is obtained by applying the complexification averaging (CX-A) method that introduced in47 and48. The nonlinear NES force \(\hat{k}_{\theta } \left( {\theta - \alpha \sin \theta } \right)\) in Eq. (8) is replaced by its equivalent polnomial force \(a\theta + b\theta^{3}\) according to the analysis in section "Mathematical model of the SLIP NES" where \(a = - 0.0162\) and \(b = 0.0196\). Therfore, the equations of motion in Eq. (8) are rewritten as

$$\begin{gathered} \ddot{\phi } + \left( {\hat{\lambda } + \hat{\lambda }_{\theta } } \right)\dot{\phi } + \left( {1 + \hat{k}_{\theta } } \right)\phi - \hat{\lambda }_{\theta } \dot{\theta } - \hat{k}_{\theta } \theta = \gamma f\sin \omega t \hfill \\ \varepsilon \ddot{\theta } + \hat{\lambda }_{\theta } \dot{\theta } - \hat{\lambda }_{\theta } \dot{\phi } - \hat{k}_{\theta } \phi + a\theta + b\theta^{3} = 0 \hfill \\ \end{gathered}$$
(13)
Fig. 14
figure 14

The B-SLIP NES steady-state analytical solution amplitudes at \(\varepsilon = 0.05\) for the undamped LO-NES system in (a) and for the damped version at the optimized B-SLIP NES parameters in (b).

Full size image

For the application of the CX-A method, new complex variables are introduced as \(\psi_{1} = \dot{\phi } + j\phi\) and \(\psi_{1} = \dot{\theta } + j\theta\) for \(j = \sqrt { - 1}\)47. Accordingly,

$$\begin{aligned} \phi & = \frac{{\psi_{1} - \psi_{1}^{*} }}{2j\omega },\quad \dot{\phi } = \frac{{\psi_{1} + \psi_{1}^{*} }}{2},\quad \ddot{\phi } = \dot{\psi }_{1} - \frac{1}{2}j\omega \left( {\psi_{1} + \psi_{1}^{*} } \right) \\ \theta & = \frac{{\psi_{2} - \psi_{2}^{*} }}{2j\omega },\quad \dot{\theta } = \frac{{\psi_{2} + \psi_{2}^{*} }}{2},\quad \ddot{\theta } = \dot{\psi }_{2} - \frac{1}{2}j\omega \left( {\psi_{2} + \psi_{2}^{*} } \right) \\ \end{aligned}$$
(14)

The steady-state periodic solution is obtained by setting \(\psi_{1} = \varphi_{1} e^{j\omega t}\) and \(\psi_{2} = \varphi_{2} e^{j\omega t}\) and imposing \(\dot{\varphi }_{1} = 0\) and \(\dot{\varphi }_{2} = 0\) according to49 and 50. Therfore, the equations of motion in Eq. (13) become

$$\begin{gathered} \frac{1}{2}j\omega \varphi_{1} + \frac{1}{2}\left( {\hat{\lambda } + \hat{\lambda }_{\theta } } \right)\varphi_{1} + \left( {1 + \hat{k}_{\theta } } \right)\frac{{\varphi_{1} }}{2j\omega } - \hat{\lambda }_{\theta } \frac{{\varphi_{2} }}{2} - \hat{k}_{\theta } \frac{{\varphi_{2} }}{2j\omega } = \frac{\gamma f}{{2j}} \hfill \\ \frac{1}{2}j\varepsilon \omega \varphi_{2} + \hat{\lambda }_{\theta } \frac{{\varphi_{2} }}{2} - \hat{\lambda }_{\theta } \frac{{\varphi_{1} }}{2} - \hat{k}_{\theta } \frac{{\varphi_{1} }}{2j\omega } + a\frac{{\varphi_{2} }}{2j\omega } - \frac{3bj}{{8\omega^{2} }}\left| {\varphi_{2} } \right|^{2} \varphi_{2} = 0 \hfill \\ \end{gathered}$$
(15)

By substituting \(\varphi_{1} = y_{1} + jy_{2}\) and \(\varphi_{2} = y_{3} + jy_{4}\) into Eq. (15), the following st of equations is obtained

$$\begin{aligned} & - \frac{{y_{2} \omega }}{2} + \frac{{\left( {\hat{\lambda } + \hat{\lambda }_{\theta } } \right)y_{1} }}{2} + \frac{{\left( {1 + \hat{k}_{\theta } } \right)y_{2} }}{2\omega } - \frac{{\hat{k}_{\theta } y_{4} }}{2\omega } - \frac{{\hat{\lambda }_{\theta } y_{3} }}{2} = 0 \\ & \frac{{y_{1} \omega }}{2} + \frac{{\left( {\hat{\lambda } + \hat{\lambda }_{\theta } } \right)y_{2} }}{2} - \frac{{\left( {1 + \hat{k}_{\theta } } \right)y_{1} }}{2\omega } + \frac{{\hat{k}_{\theta } y_{3} }}{2\omega } - \frac{{\hat{\lambda }_{\theta } y_{4} }}{2} + \frac{\gamma f}{2} = 0 \\ & - \frac{{\varepsilon y_{4} \omega }}{2} + \frac{{\hat{\lambda }_{\theta } y_{3} }}{2} - \frac{{\hat{k}_{\theta } y_{2} }}{2\omega } - \frac{{\hat{\lambda }_{\theta } y_{1} }}{2} + \frac{{ay_{4} }}{2\omega } + \frac{{3by_{4} \left( {y_{3}^{2} + y_{4}^{2} } \right)}}{{8\omega^{3} }} = 0 \\ & \frac{{\varepsilon y_{3} \omega }}{2} + \frac{{\hat{\lambda }_{\theta } y_{4} }}{2} + \frac{{\hat{k}_{\theta } y_{1} }}{2\omega } - \frac{{\hat{\lambda }_{\theta } y_{2} }}{2} - \frac{{ay_{3} }}{2\omega } - \frac{{3by_{3} \left( {y_{3}^{2} + y_{4}^{2} } \right)}}{{8\omega^{3} }} = 0 \\ \end{aligned}$$
(16)

These equations are numerically solved at the previously given parameters of the system to obtain \(y_{1}\), \(y_{2}\), \(y_{3}\) and \(y_{4}\). Therefore, the steady-state response of the LO and the B-SLIP NES is analytically obtained from the following equation

$$\begin{aligned} \phi & = \frac{{\left| {\varphi_{1} } \right|}}{\omega }\sin \left( {\omega t + \beta_{1} } \right) \\ \theta & = \frac{{\left| {\varphi_{2} } \right|}}{\omega }\sin \left( {\omega t + \beta_{2} } \right) \\ \end{aligned}$$
(17)

where.

\(\left| {\varphi_{1} } \right| = \sqrt {y_{1}^{2} + y_{2}^{2} }\), \(\left| {\varphi_{2} } \right| = \sqrt {y_{3}^{2} + y_{4}^{2} }\), \(\beta_{1} = \tan^{ - 1} \left( {\frac{{y_{2} }}{{y_{1} }}} \right)\) and \(\beta_{2} = \tan^{ - 1} \left( {\frac{{y_{4} }}{{y_{3} }}} \right)\).

The steady-state response amplitudes which are represented by the steady-state amplitude \(\left| {\varphi_{1} } \right|\) of the LO and \(\left| {\varphi_{2} } \right|\) of the NES are plotted in Fig. 14a for the undamped sytem and Fig. 14b of the damped system. The unstable branch which is represented by red dots in Fig. 14a is identified According to50 based on the numerical simulation response. In addition, this unstable analytical solution is not physically realizable. The effect of the LO and the B-SLIP NES damping content resulted in a stable steady solution for the considered forcing frequency range. It is observed in Fig. 14b that the B-SLIP NES is capable of transferring and localizing the instatanous induced vibration energy at steady-state over broad excitation frequency range. This localization becomes obvious at frequencies above the resonance frequency of the system where the B-SLIP NES exhibits much higher steady-state vibration amplitude than the LO. In addition, the B-SLIP NES steady-state response is at strong resonance capture near the to resonance frequency.

The steady-state nalytical solution amplitudes of the damped LO-NES system for B-SLIP NES locked and locked cases are provided in Fig. 15 for wide range of forcing frequencies and various forcing amplitudes. Significant amount of the induced energy into the LO by harmonic excitation is passively transferred into the B-SLIP NES by its synergitic nonlinear action where it is locaized in the NES as observed from the analytical response amplitudes.

Fig. 15
figure 15

The LO analytical solution amplitudes for B-SLIP NES locked and unlocked cases at \(\varepsilon = 0.05\) and \(\gamma = 0.05\) in (a), \(\gamma = 0.1\) in (b), \(\gamma = 0.15\) in (c), and \(\gamma = 0.2\) in (d).

Full size image

The analytical results indicated to the robustness of the B-SLIP NES in steady-state vibration energy transfer and localization in the NES. However, the depicted analytical results in Figs. 14 and 15 are only based on an approximate analytical solution where the robustness of these observations requires a numerical simulation validation which is coverd in the following section.

Numerical simulation

In the present section, the torsional vibration suppression capabilities of the B-SLIP NES is also explored using the equations of motion given in Eq. (9). The optimized parameters for the harmonic excitation input \({\text{F}}_{input} = [\begin{array}{*{20}c} {\gamma f\cos \omega t} & 0 \\ \end{array} ]^{\text{T}}\) at \(f = 1\), \(\omega = 1\) and \(\gamma = 0.05\) are obtained as \(\hat{\lambda }_{\theta } = 0.017\) and \(\hat{k}_{\theta } = 0.127\) at \(\alpha = 1.16\). At similar forcing input parameters, the optimized Type I NES and TMD parameters are, respectively obtained as \(\hat{\lambda }_{NES} = 0.017\), \(\hat{k}_{NES} = 0.115\), \(\hat{\lambda }_{TMD} = 0.0013\) and \(\hat{k}_{TMD} = 0.05\). Accordingly, the \(RMS\) values of the LO torsional system angular displacements are plotted in Fig. 16 for the B-SLIP NES, Type I NES, and the TMD. It is apparent from Fig. 16a that the B-SLIP NES is more robust in forced torsional vibration suppression for the selected range of forcing frequency ratios at \(\gamma = 0.05\) during which all the considered vibration absorbers’ parameters are optimized. Moreover, at the same parameters, both TMD and Type I NES fails to maintain their performance when \(\varepsilon\) is reduced from 0.05 to 0.02 as shown in Fig. 16b. This is a significant finding regarding the B-SLIP NES compared with TMD and Type I NES. The B-SLIP NES keeps its robust performance at low mass (i.e. low values of \(\varepsilon\)) which is an important factor for real NES design. Therefore, compared with TMD, Type I NES and many other reported NESs in the literature, the B-SLIP NES appears to be one of highly effectual vibration absorbers for torsional vibration.

Fig. 16
figure 16

The \(RMS\) of \(\phi \left( \tau \right)\) of the B-SLIP NES, Type I NES and TMD at their optimized parameters and at \(\gamma = 0.05\) in (a) at \(\varepsilon = 0.05\), and in (b) at \(\varepsilon = 0.02\).

Full size image

The performance of the B-SLIP NES at \(\varepsilon = 0.02\) in the neighborhood of resonance (\(\omega /\omega_{0} = 0.98\) and \(\omega /\omega_{0} = 1.02\)) is verified in Fig. 17. The significant reduction in the forced torsional vibration amplitudes is clear when compared with the case of locked B-SLIP NES. This vibration suppression dynamics affects both transient and steady state response of the LO. For the frequency ratio of 0.98 in Fig. 17b, the double-well oscillation continuous in the B-SLIP NES between its two stable equilibria, which indicates to the strong nonlinear bistability action in TET. For the frequency ratio of 1.02 in Fig. 17d, the double-well oscillation takes place for a short time until the B-SLIP NES gets engaged with in-well oscillation at 1:1 resonance capture with the LO. Accordingly, this high performance in energy transfer from the harmonically excited LO to the B-SLIP NES takes place by the synergetic action in the B-SLIP NES where the induced excitation energy is instantaneously transferred and localized in the B-SLP NES without bouncing back to the LO.

Fig. 17
figure 17

The LO and B-SLIP NES angular displacements at \(\hat{\lambda }_{\theta } = 0.017\),\(\hat{k}_{\theta } = 0.127\),\(\alpha = 1.16\) ,\(\gamma = 0.05\), and \(\varepsilon = 0.02\) in (a) and (b) for \(\omega /\omega_{0} = 0.98\), and in (c) and (d) for \(\omega /\omega_{0} = 1.02\).

Full size image

According to the obtained analytical and numerical analysis results, the B-SLIP NES can be more suitable for torsional vibration suppression due to its simpler and more synchronous design with the LO than the TMD, Type I NES, and other existing types of NESs.

Concluding remarks

The current study investigates a new NES configuration which is based on a spring-loaded inverted pendulum. The proposed B-SLIP NES resembles the dynamical behavior of the stiffness-based BNES. It is associated with two stable and two critically stable equilibrium positions. The B-SLIP NES configuration is successfully applied in the present study to effectively suppress the impulsive, harmonic and seismic ground motion vibration inputs. The proposed B-SLIP NES is able to transfer and dissipate over 99% of the input energy, which is the highest achieved energy dissipation in comparison with the existing NESs in the literature. The obtained numerical simulation and analytical CX-A response results have verified the robustness of this new kind of NES in terms of energy transfer and vibration suppression when compared with the cubic stiffness Type I NES and TMD. Both the Type I NES and the TMD failed to maintain their performance during certain seismic or harmonic energy inputs. However, for the considered energy inputs to the linear oscillator, the B-SLIP NES has maintained its high performance in vibration suppression. Moreover, the B-SLIP NES can be easily realized compared with several other types of NESs due to its simple design and its capability to be adjusted between stable and bistable states.