Introduction

Tires are one of the most critical components of a vehicle, and their quality directly affects driving safety. X-ray imaging detection technology, by utilizing X-rays to penetrate tires, can capture internal structural information and clearly present it. Timely detection and elimination of tire defects before they leave the factory is a crucial step in ensuring that defective products do not enter the market1,2. Currently, industrial non-destructive testing technology has been widely applied in various fields such as construction3,4, metallurgy5, textiles6, and semiconductors7. As shown in Fig. 1, However, tires consist of multiple layers of different composite materials, which have varying absorption capacities for X-rays, leading to uneven brightness and saturation in the imaging and thus affecting the quality of the image8. Moreover, the complex texture of tires results in a non-linear distribution of image grayscale. The multitude of tire defect types, complex defect locations, and the high similarity of some defects to the background, all contribute to the low accuracy in identifying tire defects based on X-ray imaging9.

Fig. 1
figure 1

X-ray image of tire.

Full size image

Defects are typically defined as areas of absence or irregularities that differ from normal samples10. Radial tires, influenced by their own structure, production equipment, and manufacturing processes, are prone to a variety of defects. As shown in Fig. 2, these defects can be broadly categorized into grayscale defects and texture defects. Grayscale defects are characterized by uneven distribution of grayscale in the image, such as foreign objects in the tread and sidewall, and air bubbles. Texture defects are identified based on changes in the internal steel wire structure of the tire, including tread cracks, sparse cords, and cord overlap. The detection of these two types of defects is crucial for ensuring the quality and safety of tires. Figure 2 shows the examples of tire defects.

Fig. 2
figure 2

Examples of tire defects.

Full size image

Currently, manual visual inspection for tire defects remains widely used on production lines. However, this method is inefficient, yields poor detection results, and poses serious risks to workers’ health. In addition to manual inspection, machine vision methods are increasingly being applied in industrial non-destructive testing. Traditional machine vision methods typically utilize shallow features for image analysis, which can roughly be categorized into projection-based, filter-based, and transform-based methods. Liu et al.11 proposed a tire defect detection method based on Radon transform, while Cui et al.12 introduced a tire X-ray image defect detection method based on principal component analysis and inverse transformation. This method reconstructs the remaining defect image by inverse transforming the principal component residuals. To precisely locate the defective area, statistical methods are used for binarization on the residual image with upper and lower thresholds. However, this approach is not suitable for large-scale defects. Furthermore, Guo et al.13 proposed a method using weighted texture distinctiveness to detect tire defects. This method captures anomalies by leveraging the feature similarity of tire images, making it applicable to both sidewall and tread images.

In summary, although the experts and scholars mentioned above have designed specialized methods for different tire defects that have achieved relatively ideal results, it is important to consider the complexity and variability of tire defects. Using dedicated methods for each specific defect would greatly increase computation time and reduce transferability, which is not conducive to large-scale industrial applications.

With the advancement of artificial intelligence and the enhancement of computing power, deep learning algorithms have been successfully applied in various fields14. Unlike the traditional machine vision methods mentioned earlier, which rely on manually extracting shallow image features, deep learning methods can utilize deep convolutional neural networks to extract deeper-level information from images, making them highly suitable for tire non-destructive defect detection.

In the field of tire defect detection, deep learning-based methods are flourishing. For instance, Wang et al.15 proposed an unsupervised learning approach using generative adversarial networks for tire defect detection. This method does not require a large dataset with defective images for support; instead, it only needs defect-free images for training. However, this method can only determine the presence of defects in tires and cannot differentiate between different types of defects, thus limiting its applicability in industrial scenarios. On the other hand, Li et al.16 developed a high recall tire defect classification algorithm in 2021: TireNet. The algorithm uses ResNet-50 and ResNet-101 as backbone networks, and the results show a detection omission rate of only 0.17%. However, for defects such as bubbles that have indistinct differences from the background, feature extraction using other methods is still necessary, resulting in lower generality of this method. Additionally, Wang et al.8 proposed a fully convolutional network for tire defect detection based on VGG16 in 2019. This network has the capability of pixel-wise prediction, enabling simultaneous defect localization and segmentation. However, this method did not compare with existing deep learning methods, thus lacking convincing power.

Current research generally relies on mainstream object detectors, including two-stage detectors like Faster R-CNN17 and single-stage detectors like YOLO18,19,20. Professor Wu Zeju’s21 team at Qingdao University of Technology optimized the Faster R-CNN by improving the network and pyramid structure, resulting in enhanced detection accuracy. However, the detection results for some ambiguously bounded bubble defects were relatively poor. On the other hand, Peng22 and colleagues used YOLO as the base detector, striking a balance between accuracy and real-time performance, yet their performance was inadequate for detecting some elongated defects . Zhao et al.23 on the other hand, developed a multi-scale self-attention feature enhancement model (MSAM) based on YOLOv4-tiny. This model aims to extract feature maps with rich multi-scale contextual information. They also proposed a pyramid pooling layer based on MSAM and CBAM, achieving higher precision.

In summary, using deep learning methods for defect detection has effectively improved the accuracy and efficiency of detection. However, due to the unique characteristics of tire defects, this poses special challenges for defect detection:

1. The original tire data has high resolution, while the defect targets are relatively small. Using them directly as input would result in large memory usage, slow training speeds, and susceptibility to overfitting.

2. Some defect types exhibit elongated shapes, which regular convolution operations cannot adapt to, resulting in single defects being misidentified as multiple independent entities and thus reducing detection accuracy.

3. There is significant variation in the sizes of defects, with small targets accounting for a large proportion. Therefore, detectors need to have a high level of sensitivity to accurately identify defects of various sizes.

In response to these challenges, we propose an efficient tire X-ray defect non-destructive detection method Dynamic Snake Convolution YOLO model (DSC-YOLO) based on YOLOv5. The main contributions of this paper are as follows:

1. We propose an efficient tire defect detection network DSC-YOLO based on the YOLOv5 single-stage object detector. This network model can effectively identify multi-scale targets in complex tire X-ray texture backgrounds, achieving a balance between accuracy and efficiency.

2. We design snake convolution for tire defect detection, considering the snake morphology of defect pipe structures. We introduce constraints during the free learning process to enhance the perception of elongated pipe structures.

3. Combining the uniqueness of tire defects, we design a new attention scale sequence fusion model and introduce CBAM on this basis. This model integrates effective feature maps from different resolutions, better preserving the image’s detailed information.

4. We establish a comprehensive tire X-ray dataset, including four types of defects, and conduct comparative experiments and ablation experiments on this dataset to verify the effectiveness of the proposed method.

The remaining chapters of the paper are organized as follows: the second section describes the algorithm of the paper in detail; the third section gives the results and discussion of the comparison and ablation experiments; and finally the fourth section summarizes the whole paper.

Materials and methods

Overall framework

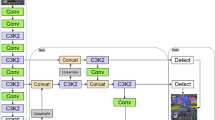
In this paper, we aim to construct a tire defect detection network model that balances accuracy and efficiency. To achieve this, considering the YOLOv5 detector has demonstrated good detection accuracy and real-time performance in various industrial fields, and is easy to deploy on machines, we chose it as the base model for our network. Building upon YOLOv5, we fully consider the uniqueness of tire defect detection. Under the premise of fully utilizing the base network, we make improvements to it. Figure 3 illustrates the overall network architecture we proposed.

Fig. 3
figure 3

Architecture of the proposed method.

Full size image

YOLOv5 encompasses the advantages of many algorithms and performs well in balancing detection accuracy and speed, making it one of the most widely used object detection algorithms. YOLOv5 comes in four versions: s, m, l, and x. While these architectures are consistent, they differ in depth and width, resulting in increased computational complexity. As a result, accuracy increases but real-time performance decreases. Considering the practical needs of tire non-destructive testing, we chose the YOLOv5m model as the base model for this paper.

As shown in the Fig. 4, YOLOv5m network architecture diagram, the network structure is divided into three parts: Backbone, Neck, and Head. The Backbone network is responsible for downsampling at different scales, extracting effective features, and generating feature maps of different sizes, which are then inputted to the Neck to build the feature pyramid. The Neck network merges features from different levels using Feature Pyramid Network (FPN) and Path Aggregation Network (PAN). The Head network is designed with three detection layers of different sizes, each used for predicting the category and bounding box regression of large, medium, and small targets.

Fig. 4
figure 4

Architecture of YOLOv5.

Full size image

Dynamic Snake Convolution

Ordinary convolution is used to extract local features, and based on this, scholars have proposed dilated convolution24 and deformable convolution25, which effectively increase the receptive field and adapt to different target shapes. However, these types of convolutions allow the network to learn geometric transformations freely, which may cause the perception region to deviate from the target, especially in the case of elongated tubular structures. In 2023, Qi et al.26 proposed the Dynamic Snake Convolution (DSConv), which stretches the convolution kernel in the x and y directions for targets with elongated and curved characteristics, such as blood vessels and distant roads, achieving remarkable results. In tire defect detection, both belt overlap and belt missing are elongated defects. Inspired by the aforementioned work, this paper designs a Dynamic Snake Convolution module specifically for elongated tire defects. The Dynamic Snake Convolution module learns deformations based on the input feature map, and with an understanding of the tubular structure morphology, it adaptively focuses on the local features of elongated and curved structures. Schematic diagram of snake convolutional deformation is shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of snake convolutional deformation.

Full size image

In a convolution with a convolution kernel of 9, each grid axis direction can be expressed as \(K_{i \pm c} = (x_{i \pm c} ,y_{i \pm c} )\), where takes the value of \(\{ 1,2,3,4\}\), which is expressed as the distance to the center grid. Each grid position \(K_{i + 1}\) in the convolution kernel K adds an offset \(\Delta = \{ \delta |\delta \in [ - 1,1]\}\) relative to \(K_{i}\), so the offsets need to be summed to ensure that the convolution kernel follows a linear morphological structure. formula(1) represents how each point in the convolution kernel is computed for horizontal offsets:

$$K_{i \pm c} = \left\{ {\begin{array}{*{20}l} {(x_{i + c} ,y_{i + c} ) = (x_{i} + c,y_{i} + \sum_{i}^{i + c} \Delta y),} \hfill \\ {(x_{i - c} ,y_{i - c} ) = (x_{i} - c,y_{i} + \sum_{i - c}^{i} \Delta y),} \hfill \\ \end{array} } \right.$$
(1)

where \(\sum\limits_{i}^{i + c} \Delta y\) denotes the cumulative vertical offset from the center point yi to the current point of the convolution kernel.

Similar to the above equation, formula (2) denotes the formula for calculating the coordinates of each point when the convolution kernel is vertically shifted

$$K_{j \pm c} = \left\{ {\begin{array}{*{20}l} {(x_{j + c} ,y_{j + c} ) = (x_{j} + \Sigma_{j}^{j + c} \Delta x,y_{j} + c),} \hfill \\ {(x_{j - c} ,y_{j - c} ) = (x_{j} + \Sigma_{j - c}^{j} \Delta x,y_{j} - c),} \hfill \\ \end{array} } \right.$$
(2)

where \(\sum\limits_{i}^{i + c} \Delta x\) denotes the cumulative horizontal offset from the center point \(x_{i}\) to the current point of the convolution kernel.

Since the convolution kernel may be located at a non-integer coordinate position after deformation, bilinear interpolation is used to estimate the pixel value at this position. The specific formula is expressed as shown in formula (3).

$$K = \sum\limits_{{K^{\prime}}} B (K^{\prime},K) \cdot K^{\prime},$$
(3)

where \(K^{\prime}\) is the set of all possible integer pixel coordinate points that form the possible area covered by the deformation of the convolution kernel. \(B(K^{\prime},K)\) denotes the bilinear interpolation kernel, where the pixel value at each \(K^{\prime}\) position is multiplied with the corresponding bilinear interpolation kernel \(B(K^{\prime},K)\) and then accumulated to obtain the final pixel value. The bilinear interpolation kernel is shown in formula (4):

$$B(K,K^{\prime}) = b(K_{x} ,K^{\prime}_{x} ) \cdot b(K_{y} ,K^{\prime}_{y} )$$
(4)

where b denotes the one-dimensional interpolation kernel.

This paper designs a C3 module based on the Dynamic Snake Convolution (DSConv), and the specific details of the module are illustrated in the Fig. 6: (a)represents the DSConv module. The input feature map first passes through an offset_conv convolutional layer to learn the offset for each position. The learned offsets are then normalized through a Batch Normalization (BN) layer. Subsequently, the normalized offsets are passed through a tanh activation function to limit them to the range of −1 to 1. Using the DSC module, a coordinate mapping is created based on these normalized offsets, and bilinear interpolation is performed to deform the feature map. The deformed feature map is then subjected to convolution operations along the x or y direction, followed by a Group Normalization (GN) layer for feature normalization. Finally, the normalized features go through a ReLU activation function for non-linear transformation, resulting in the final output feature map. Building upon (a), the DySnakeConv module is designed as shown in (b). This module splits the input feature map into two branches. One branch undergoes regular convolution, while the other branch passes through two DSConv layers successively. The outputs of the two branches are then concatenated using the Concatenation module and passed through a 1 × 1 convolutional kernel to generate the output feature map. (c) and (d)represent the improved Bottleneck module and C3 module respectively.

Fig. 6
figure 6

Architecture of DSConv and DSConv-based moules. (a) DSConv; (b) DySnakeConv; (c) Bottleneck_DySnake; (d) C3_DySnake.

Full size image

Attention module

When processing visual information, the human brain does not evenly attend to all parts of the visual field; instead, it selectively focuses on certain areas. The attention mechanism imitates this selective focus behavior, making machine learning models more aligned with human visual perception when performing visual tasks.

The CBAM27 module sequentially infers two-dimensional attention maps (channel and spatial) on intermediate feature maps, then multiplies these attention maps with the input feature map for adaptive feature refinement. CBAM is a lightweight and versatile module that can seamlessly integrate into any CNN architecture and can be trained end-to-end with the base CNN.

The CBAM module consists primarily of two parts: the Channel Attention Module and the Spatial Attention Module. Each module includes three components: aggregation of information, computation of attention, and weighted operations.

As shown in Fig. 7, For the input feature map \(F \in {\mathbb{R}}^{C \times H \times W}\), C, H, W represent the number of channels, height and width of the feature map, respectively. Firstly, two feature descriptors are obtained by aggregating the spatial information through global average pooling and global maximum pooling: \(F_{avg}^{c}\) and \(F_{max}^{c}\).The former captures the global spatial information; the latter highlights the most salient features.

Fig. 7
figure 7

Diagram of Channel Attention Module.

Full size image

Next, these two feature descriptors are fed into a shared multilayer perceptron (MLP), which contains a hidden layer of size \({\mathbb{R}}^{C \times 1 \times 1}\), where r is the dimensionality reduction ratio. The output of the MLP is normalized by a sigmoid function to obtain the channel attention map Mc, which is denoted by the formula (5):

$$\begin{aligned} M_{c} (F) & = \sigma (MLP(AvgPool(F)) + MLP(MaxPool(F))) \\ & = \sigma (W_{1} (W_{0} (F_{avg}^{c} )) + W_{1} (W_{0} (F_{\max }^{c} ))) \\ \end{aligned}$$
(5)

where σ denotes the sigmoid function and \(W_{0} \in {\mathbb{R}}^{{{C \mathord{\left/ {\vphantom {C r}} \right. \kern-0pt} r} \times C}}\), \(W_{1} \in {\mathbb{R}}^{C \times C/r}\) denote the weights of MLP.

Finally, the channel attention map \(M_{c}\) is subjected to an element-wise multiplication operation with the original feature map F to obtain the channel-weighted feature map \(F^{\prime}\), which is denoted by the formula (6):

$$F^{\prime} = M_{c} (F) \otimes F$$
(6)

As shown in Fig. 8, For the channel-weighted feature map \(F^{\prime}\), the average pooling and maximum pooling operations are first applied on the channel axes to obtain two 2D maps \(F_{avg}^{s}\) and \(F_{max}^{s}\) ,which are spliced and fed into a convolutional layer to generate a spatial attention map \(M_{s} (F)\), which is denoted by the formula (7):

$$\begin{aligned} M_{s} (F) & = \sigma (f^{7 \times 7} ([AvgPool(F);MaxPool(F)])) \\ & = \sigma (f^{7 \times 7} ([F_{avg}^{s} ;F_{\max }^{s} ])), \\ \end{aligned}$$
(7)

where \(f^{7 \times 7}\) represents the 7 × 7 convolution, AvgPool represents average pooling, and MaxPool represents maximum pooling.

Fig. 8
figure 8

Diagram of Spatial Attention Module.

Full size image

Finally, the spatial attention map \(M_{s}\) and the channel-weighted feature map \(F^{\prime}\) are multiplied at the element wise level to obtain the refined feature map, which is denoted by the formula (8):

$$F^{\prime\prime} = M_{c} (F^{\prime}) \otimes F^{\prime},$$
(8)

Attentional scale sequence fusion with CBAM

Existing literature uses a feature pyramid structure for feature fusion, which only fuses pyramid features using summation or splicing. However, the structure of various feature pyramid networks cannot effectively utilize the correlation between all pyramid feature maps. scale sequence feature fusion module(SSFF)28 used in this paper can combine the high-dimensional information of deep feature maps with the detailed information of shallow feature maps.

A series of Gaussian filters are utilized to generate images with different scales as inputs to the SSFF module, this process is represented by the following formula (9):

$$F_{\sigma } (w,h) = G_{\sigma } (w,h) \times f(w,h),$$
(9)

where, \(F_{\sigma } (w,h)\) is the image after smoothing by Gaussian filter. \(G_{\sigma } (w,h)\) is a 2D Gaussian filter, which can be expressed by formula (10):

$$G_{\sigma } (w,h) = \frac{1}{{2\pi \sigma^{2} }}e^{{ - (w^{2} + h^{2} )/2\sigma^{2} }}$$
(10)

where \(\sigma\) is the standard deviation of the Gaussian filter. \(f(w,h)\) denotes the width and height of the original input image.

In this way, it is possible to generate images with the same resolution but different scales that can be considered as part of the scale space.

The structure of the SSFF module is shown in Fig. 9. The SSFF module receives P3, P4 and P5 feature maps from the YOLO backbone network. These feature maps may differ in spatial dimensions and feature depth. In order to fuse these feature maps, they need to be first resized to the same size and stacked in the depth dimension.

Fig. 9
figure 9

The overview of improved YOLOv5v model.

Full size image

The P4 and P5 feature maps are upsampled using the nearest neighbor interpolation method to match their dimensions to the P3 feature map. Convert each feature map from a three-dimensional tensor to a four-dimensional tensor, i.e., add a depth dimension, by the unsqueeze operation. The adjusted P3, P4 and P5 feature maps are stacked along the depth dimension to form a four-dimensional feature tensor. 3D convolution, 3D batch normalization and SiLU activation function are applied to the stacked four-dimensional feature tensor in order to complete the extraction of scale sequence features.

With this approach, the SSFF module is able to integrate multi-scale information from different network layers, thus providing richer feature representations for subsequent cell instance segmentation tasks. This fusion strategy helps the model to better understand the small-scale details and large-scale contextual information in the cell image, thus improving the accuracy and robustness of segmentation.

The TFE module captures detailed information about small targets by stitching feature maps of different sizes in spatial dimensions. As shown in Fig. 10, the TFE module receives feature maps of different sizes from the backbone network and first performs a convolution operation on the large-size feature maps and downsamples the feature maps through a hybrid structure of maximum pooling and average pooling in order to preserve the validity and diversity of the high-resolution features and defects images. A convolution operation is performed on the small-size feature maps and up-sampling is performed by the nearest neighbor interpolation method to maintain the local feature richness of the resolution image and to prevent the loss of small target feature information.

Fig. 10
figure 10

The structure of TFE module.

Full size image

The adjusted large-size, medium-size, and small-size feature maps are spliced in the channel dimension, and the features of each feature map are integrated into a unified feature representation.

Finally the spliced feature images have the same resolution and three times the number of channels, which ensures that no scale information is lost in the fusion process.

The whole process can be expressed by formula (11):

$$F_{TFE} = Concat(F_{l} ,F_{m} ,F_{s} )$$
(11)

where FTFE denotes the feature map output from the TFE module, Concat denotes the splicing operation, and \(F_{l} ,F_{m} ,F_{s}\) denote the large, medium, and small size feature maps, respectively.

Soft-NMS

In object detection, redundant candidate boxes often appear around the target, so Non-maximum suppression (NMS) is needed to remove some redundant candidate boxes. The core idea of NMS is to select the candidate box with the highest confidence score, and then calculate the Intersection over Union (IoU) with the candidate box that has the next highest score. If the IoU between the two boxes is greater than a pre-set threshold, it is considered that these two candidate boxes identify the same object. At this point, the candidate box with the lower score is discarded, and this process continues until the final result is obtained. This algorithm can be represented by the following formula (12):

$$s_{i} = \left\{ {\begin{array}{*{20}c} {s_{i} ,\;\;iou(M,b_{i} ) < N_{t} } \\ {0,\;\;iou(M,b_{i} ) \ge N_{t} } \\ \end{array} } \right.$$
(12)

where si represents the score of the current candidate box, iou represents the Intersection over Union, M represents the box with the highest score, bi represents the candidate box generated during detection, and \(N_{t}\) represents the threshold of iou.

However, Non-maximum suppression (NMS) has some problems. The issue with NMS is that it forcefully sets the confidence score of adjacent detection boxes to zero. If a real object appears in the overlapping area, it cannot be correctly detected, leading to a decrease in detection accuracy. Additionally, determining the threshold for NMS is not straightforward; a threshold that is too large can result in false positives, while a threshold that is too small can lead to false negatives. To address these issues, many scholars have proposed different solutions.

Soft-NMS29 is an improvement upon NMS. Its core idea is that when a detection box is suppressed, instead of immediately setting its score to zero, it is multiplied by a coefficient to gradually decrease its score, which can be expressed by formula (13).

$$s_{i} = \left\{ {\begin{array}{*{20}c} {s_{i} ,\;\;iou(M,b_{i} ) < N_{t} } \\ {s_{i} (1 - iou(M,b_{i} )),\;\;iou(M,b_{i} ) \ge N_{t} } \\ \end{array} } \right.$$
(13)

The above function addresses the drawback of traditional NMS by linearly decaying the score. As a result, detection boxes that are far from M are not affected, while those very close to M are significantly influenced and penalized. However, because the function is not continuous in terms of overlap degree, it suddenly has an effect when the threshold \(N_{t}\) is reached. To address this issue, we can use the following Gaussian penalty function for the update step, which can be expressed by formula (14):

$$s_{i} = s_{i} e^{{ - \frac{{i\sigma w(M,b_{i} )^{2} }}{\sigma }}} ,\forall b_{i} \notin D$$
(14)

where D represents the set of final detection results.

The Flowchart of Soft-NMS is shown in Fig. 11.

Fig. 11
figure 11

Flowchart of Soft-NMS.

Full size image

Experiments and discussions

Dateset

Since there is no public dataset applied to tire defect detection, we made our own dataset applied to this scenario, which contains four common tire defects, the specific number of each category of the dataset is shown in the table.

The resolution of the tire X-ray image obtained from the production line is 1819*11,400, and the input of large resolution images will have problems such as large memory occupation, slow training speed, and easy overfitting during deep learning training. Therefore, during deep learning training, some operations such as cropping and scaling are usually performed on the image to reduce the image resolution and decrease the computation and memory consumption. For a tire X-ray image, as shown in Fig. 12, this paper divides the image into a number of sheets along the height direction with the width as the benchmark, and in addition, in order to prevent the defects from being cropped at the same time as cropping the image, which leads to incomplete defects, the overlapping region segmentation is used in the division. Finally, the image is cropped to get a sheet with a resolution of 1819 × 1819.

Fig. 12
figure 12

Schematic of cross cropping of tire images.

Full size image

Rich data is the basis of deep learning, for better training results, we perform data enhancement on the basis of the cropped images. The data enhancement methods include horizontal and vertical inversion, random angle rotation, increasing noise, etc. These data enhancement methods act on the image alone or in combination. The result of data enhancement is shown in Fig. 13.

Fig. 13
figure 13

Image enhancement effect. (a) Normal; (b-d) random rotation, noice.

Full size image

After cropping and data enhancement operations, the final dataset is shown in Table 1. Dataset information. Finally, the dataset is divided into training set, validation set and test set in the ratio of 8:1:1.

Table 1 Dataset information.
Full size table

In order to improve the performance of the detector in a targeted way, we categorized the defects into large, medium, and small targets according to COCO’s classification method30. Among them, large targets accounted for 57% medium targets accounted for 10% small targets accounted for 33%, the specific distribution and data statistics of the three sizes are shown in Fig. 14. As can be seen from (a), the overall aspect ratio of defects in the dataset is large, the size distribution of defects XBJO and defects XTFM is relatively uniform, and the defects XFM is small overall, while the defects XBJO is moderate in size but large in aspect ratio.

Fig. 14
figure 14

Distribution of target sizes and statistics on the number of small, medium and large targets. (a) Distribution; (b) statictics.

Full size image

Experimental settings

Hyperparameters are essential settings that adjust model training, and selecting the appropriate hyperparameters can significantly enhance the performance of an object detection model. The default hyperparameters of the YOLOv5 model are configured based on the COCO dataset; however, the tire X-ray dataset employed in this study differs considerably from COCO, necessitating hyperparameter optimization to better suit the task of tire defect detection. Given the large number of hyperparameters in the YOLO model, traditional optimization methods, such as grid search, are impractical. Consequently, this experiment employs a genetic algorithm for hyperparameter optimization.

The genetic algorithm, an optimization approach inspired by natural selection, effectively addresses the exponential growth issue in traditional methods and efficiently finds optimal solutions within high-dimensional spaces. The core operations of the genetic algorithm include selection, crossover, and mutation, following these steps: The genetic algorithm optimizes the hyperparameters by defining individual solutions within a population, evaluating them using a fitness function based on accuracy, recall, and mAP0.5, applying crossover and mutation to generate new solutions, and iteratively selecting the fittest individuals for continuous evolution.

In this paper, we use Windows 10 operating system, the compiler is Python 3.8.10, Pytorch 1.9.0 , CUDA 11.1, torch 1.9.0, torchvison 0.10.0. All models are trained, validated, and reasoned on NVIDIA RTX4090 (24 GB), and the hyperparameters for training are shown in Table 2.

Table 2 Hyperparameters for training.
Full size table

The mean Average Precision (mAP), Parameters (Params), and GFLOPs evaluation metrics were selected to accurately assess the detection performance of the improved algorithm. mAP0.5 represents the mean average precision of all target categories at an IoU threshold of 0.5. mAP0.5:0.95 represents the average of the detection precision at all 10 IoU thresholds calculated with a step size of 0.05 for IoU thresholds ranging from 0.5 to 0.95. Higher IoU thresholds indicate more stringent requirements on the detection capability of the model. If the detection index of the model is higher under the high threshold, it means that the detection performance of the model is better, then the detection results of the model are more satisfying for practical applications. Params represents the number of parameters of the model, which is used to measure the overhead of computational memory resources. GFLOPs is the number of floating-point operations at 1 billion times per second, which is used to measure the computational complexity of the model when it is being trained.

The mAP integrates the two indicators of model precision and recall, which is one of the most important indicators for evaluating the model, and the specific formula (15) is as follows:

$$mAP = \frac{1}{N}\sum\limits_{n = 1}^{N} {P_{n} } \times R_{n} \times 100\% ,$$
(15)

where TP denotes true positive, FP denotes false positive, TN denotes true negative, FN denotes false negative, which can be expressed by formula (16).

$$\left\{ {\begin{array}{*{20}l} {P = \frac{TP}{{TP + FP}},} \hfill \\ {R = \frac{TP}{{TP + FN}},} \hfill \\ \end{array} } \right.$$
(16)

where TP denotes true positive, FP denotes false positive, TN denotes true negative, FN denotes false negative.

In order to verify the superiority of the method proposed in this paper, comparison experiments are conducted with the method proposed in this paper and the current mainstream detection algorithms. The accuracy and model complexity of the algorithm model are mainly tested using mAP and Param and GFLOPS as evaluation indexes.

Comparison experiment

From the Table 3 Comparison of different detection algorithms, it can be seen that compared to the two-stage detection algorithm Faster-RCNN, the single-stage detection algorithm occupies an obvious advantage in tire defect detection accuracy: Faster-RCNN’s mAP0.5 is only 33.4%, and the mAP0.5:0.95 is only 17.7%, which is only half of the accuracy of the single-stage detection algorithm, and in the model parameter of the model, the mAP0.5:0.95is only 17.7%, which is only half of that of the single-stage detection algorithm. The detection accuracy is only half of that of the single-stage target detection algorithm, and it is also not superior in terms of the number and complexity of model parameters. In terms of the single-stage target detection algorithm, the mAP0.5 of SSD30031 reaches 59.4%, and the mAP0.5:0.95 reaches 30.4%, which is higher than that of the Faster-RCNN, but there is still a big gap compared with the YOLO model.

Table 3 Results of the comparison experiment.
Full size table

For YOLOv5 series detectors, YOLOv5m and YOLOv5l have the same number of parameters and floating-point operations, but mAP0.5 and mAP0.5:0.95 are 0.5% and 0.9% higher than the latter, so the choice of using YOLOv5m model as the basis of the study is reasonable. Although YOLOv5s has a smaller number of parameters, there is a considerable gap in accuracy compared to YOLOv5m. Compared with the latest algorithms YOLOv732 and YOLOv8, which are introduced by the YOLO series in 2023, the algorithm in this paper is 6.1% and 3.2% higher than the former two in mAP0.5, 10% and 1.7% higher in mAP0.5:0.95, and the number of floating-point operations is smaller than both of them.

Ablation experiments

In order to verify the improvement effect, this paper selects YOLOv5m as the benchmark model, and evaluates the impact on target detection performance when different modules and methods are combined with each other through ablation experiments under the same experimental conditions, and the convergence of the loss in the ablation experiments is shown in Fig. 15. It can be seen that the losses in the ablation experiments have all converged.

Fig. 15
figure 15

Comparison of losses from ablation experiments.

Full size image

From the results of the table ablation experiments, shown in Table 4, it can be seen that both the modules and the model improvement methods proposed in this paper provide some improvement in defect detection accuracy. As far as a module alone is concerned, experiment B introduces soft-NMS in the post-processing stage of the model, and the mAP0.5 is improved by 4.8 percentage points, and the mAP0.5:0.95 is improved by 3.7 percentage points, which indicates that the use of Soft-NMS can effectively compensate for the shortcomings of the traditional NMS that forces the confidence level to zero, and improves the problem of the increase of leakage due to the mutual occlusion of the targets, and drastically improves the detection accuracy of the model without adding additional training parameters. C experiments use snake convolution instead of ordinary convolution, compared with the basic network in mAP0.5 increased by 0.4 percentage points, mAP0.5:0.95 increased by 0.6 percentage points, indicating that the snake convolution gives full play to its advantages for slender targets, but at the same time increases the number of model parameters and the number of floating-point operations. number. D experiment improves the FPN structure of the network model, mAP0.5 increases by 2.4 percentage points, and mAP0.5:0.95 is basically the same as the original network. SSFF module can combine the high-dimensional information of the deep feature maps with the detailed information of the shallow feature maps, and the TFE module splices the feature maps with different sizes in the spatial dimensions to capture the detailed information of the small targets. E experiment introduces the CBAM, mAP0.5 improves by 2.4 percentage points and mAP0.5:0.95 improves by 0.5 percentage points, which indicates that the channel and spatial information in the feature maps can be effectively weighted so as to enhance the network’s focus on important features and suppress unimportant features, and ultimately achieve adaptive refinement of features.

Table 4 Results of the ablation experiment.
Full size table

In terms of different modules combining with each other, the F experiment combines soft-NMS and DSConv, and the combination of the two gives full play to their respective advantages, with mAP0.5 improving by 4.9 percentage points and mAP0.5:0.95 improving by 4.7 percentage points, both of which are higher than the detection accuracy when acting alone. Based on the F experiment, the G experiment used the ASF structure, which improved mAP0.5 by 5.3 percentage points and mAP0.5:0.95 by 5.6 percentage points, and the number of model parameters was somewhat reduced compared to the F experiment. Finally, the H-experiment shows that by combining all the improvements in this paper, the final detection accuracy is improved compared with that when acting alone. mAP0.5 is improved by 5.9 percentage points, and mAP0.5:0.95 is improved by 5.7 percentage points, which proves that the improved model can effectively accomplish the task of detecting tire defects.

Visual analysis

Figure 16 shows the detection results of the model trained by this method on the X-ray defect map, there are two defects in Figure (a), the code questions are XBJO and XTFM respectively, the shape of these two defects are elongated, the algorithm proposed in this paper can accurately determine the type and location of the defects, which indicates that the snake convolution based method proposed in this paper is very suitable for the detection of this type of defects; Figure (b) is the code name of the XFM defect, this type of defect is smaller, and it is more testing for the detector’s performance on small targets, this paper improves the neck network structure, which can effectively increase the focus on small targets, and the effectiveness of the method is also proved in the actual detection; Figure (c) demonstrates the defects of similar types, both of which are elongated and have high gray values, but the method proposed in this paper can clearly distinguish between the two different defects, and the detection accuracy are very high; Figure (d) in the defect and the background is very similar, are elongated and low gray value, this paper’s algorithm can accurately distinguish between the target and the background, with an objective detection effect.

Fig. 16
figure 16

Example of test results.

Full size image

Conclusions

In this paper, we propose a tire X-ray defect detection method DSC-YOLO, which is based on the mainstream target detector YOLOv5, and puts forward a series of targeted improvement measures based on the comprehensive consideration of tire X-ray photos and the special characteristics of defects.

First, for the existence of a large number of elongated defects in tire defects, we adopt dynamic snake convolution to adaptively focus on elongated and curved local features, and design a C3 module based on dynamic snake convolution, which increases the focus on elongated defects such as overlapping cords and missing cords, and improves the accuracy of the model.

Secondly, to address the problem that defects have a large proportion of small targets and conventional detectors are not effective in detecting small targets, we introduce SSFF and TFE modules in the model neck to integrate multi-scale information from different network layers and integrate CBAM in it by embedding the CBAM attention module, which weakens the independent features of the complex anisotropic texture background of tires, and enhances the useful features of the defects in tire characterization. Subsequently, the Soft-NMS algorithm is used to further optimize the processing of candidate frames to improve the model’s detection accuracy for small targets with dense occlusions.

Finally, ablation experiments and comparison experiments are conducted on our own created tire X-ray defect dataset, and the results show that our algorithm achieves a balance between detection accuracy and model size, and can meet the requirements of visual inspection in tire production lines.

Although the method proposed in this paper achieves better detection than the base network in our dataset, there are still cases of poor detection. In the Fig. 17 shows the failure case where the defect was not detected due to the fact that this defect is very similar to the background in both gray value and shape, and the small size of this target leads to a significant reduction of features when the model is downsampled, so the detector mistook it for the background. In subsequent research, focus could be on increasing the attention to this type of defect.

Fig. 17
figure 17

Example of failure case.

Full size image