Introduction

Swarm intelligence (SI) algorithms, which mimic animal group behaviors, serve as effective metaheuristic optimizers1. They are widely applied to address complex engineering problems2,3,4,5,6. Optimizing parameter control for these algorithms in specific applications continues to be an active research area, with recent enhancements including refined versions of the harmony search grey wolf optimizer, and cuckoo search algorithms7,8,9,10,11 designed to meet industry-specific demands.

The beetle antennae search (BAS) algorithm, a single-individual optimization algorithm, models the foraging and courtship behaviors of beetles12. Utilizing their antennae to sense pheromone concentration variations, beetles navigate towards areas of higher concentration. They adjust their direction based on antennal pheromone readings, favoring left or right movement accordingly. This sensory integration efficiently guides them to food sources. BAS is celebrated for its strong directional sense, straightforward coding, and ease of implementation13. These attributes have facilitated BAS’s application across a spectrum of domains, including robot trajectory planning14, ship collision prediction15, and case prediction16.

However, the BAS algorithm still has some drawbacks, such as slow convergence speed, easy to fall into local optima, insufficient convergence accuracy and over-dependence on parameters when dealing with high-dimensional problems. Various improved BAS algorithms are proposed to overcome these shortcomings. Addressing the challenge of local optimization, Liao et al.17 introduced a nonlinear-activated BAS, and Lin et al.18 enhanced the algorithm by implementing a linearly decreasing inertia weight. Wang et al.19 proposed a beetle swarm antennae search (BSAS) algorithm based on the feedback step-size update strategy and combined with the population search concept to overcome the influence of random beetle direction. Xu et al.20 presented an improved BAS algorithm based on levy flight and adaptive strategy (LABAS) by integrating the concept of group search and combined the elite individual reverse learning strategy and levy flight strategy. Zhao et al.21 improved the BAS algorithm based on versoria distributed inertia weights and random attenuation factors. Shao et al.22 improved the BAS algorithm based on the elite selection mechanism and the neighbor mobility strategy (ENBAS), which is used to generate new individuals in the global search and local search stages to diversify search patterns. Lyu et al.23 proposed an improved BAS (IBAS) by using adaptive step-size strategy and adjusting the flight distance, and IBAS is applied to track the location of the jamming attack point and deploy security defense mechanism, a minimum covered circle jamming attack localization algorithm with lower error rate, better positioning performance.

The above improved algorithms have different shortcomings, and new algorithm of high performance is needed to solve complex problems and engineering application. This manuscript proposes ABSAS-CS-GSA, an enhanced Beetle Antennae Search (BAS) algorithm integrating Golden Sine Algorithm (Gold-SA)24, Vertical and Horizontal Crossover Strategy (VHCS)25, and dynamic step-size adjustment. These improvements overcome limitations from individual search in BAS, such as limited global search efficiency, and sensitivity to local optima. Applied to Wireless Sensor Networks (WSNs), ABSAS-CS-GSA aims to achieve high coverage-rate. The development of ABSAS-CS-GSA is detailed in three phases. Initially, the BAS is refined by transitioning from a single individual to a population-based approach, updating step-size with optimal individual to increase diversity and stability. Subsequently, Gold-SA24 is integrated with BAS to improve calculation accuracy through population update. Lastly, VHCS25 is employed to perturb the population, maintaining better fitness and enhancing the escape from local optima. Performance validation of ABSAS-CS-GSA is conducted using 12 benchmark functions and the Wilcoxon test, comparing ABSAS-CS-GSA against other algorithms. ABSAS-CS-GSA demonstrates superior performance across individual and aggregate optimization outcomes. Finally, the algorithm is applied to WSNs, where it is evaluated against others in optimizing network coverage with 30 and 50 sensor nodes. ABSAS-CS-GSA shows excellent results, further confirming its effectiveness.

Standard BAS

As previously stated, the BAS algorithm emulates the method by which beetles forage for food in nature. The objective of optimization is to identify the optima for fitness functions, analogous to the natural foraging behavior of beetles searching for food. In this analogy, the independent variables of the function correspond to the beetle's spatial position, while the fitness function value represents the intensity of the food's odor. The algorithm's search for an optimal solution mirrors the beetle's search for food.

During the optimization process, tackling an unknown problem entails searching for a solution within an undefined dimensional space. This involves the random generation of the beetle's position and orientation.

The direction vector is quantized as,

$${r}_{d}=\frac{rands(dim,pop)}{\Vert rands(dim,pop)\Vert }$$
(1)

where rands(·) is the random function, \({r}_{d}\), dim and pop represent the direction of the beetle, the dimensions of the problem to be optimized, the number of beetle populations, respectively.

The position of the beetle’s tentacle is calculated as,

$$\left\{\begin{array}{c}{x}_{r}={x}^{t}-{d}^{t}\times \frac{{r}_{d}}{2}\\ {x}_{l}={x}^{t}+{d}^{t}\times \frac{{r}_{d}}{2}\end{array}\right.$$
(2)

where \({x}_{r}\), \({x}_{l}\) respectively represent the position of the right and left tentacle of the beetle. \({x}^{t}\) and \({d}^{t}\) represent the position of the beetle in the solution space and the distance between the two tentacles at time t respectively.

The beetle’s position in the solution space at time t + 1 is updated as,

$${x}^{t+1}={x}^{t}+{\delta }^{t}\times {r}_{d}\times sign(f({x}_{r})-f({x}_{l}))$$
(3)
$$sign(x)=\left\{\begin{array}{c}1 ,x>0\\ 0 ,x=0\\ -1 ,x<0\end{array}\right.$$
(4)

where \({\delta }^{t}\) is the step-size of the beetle at time t, \(f({x}_{r})\) and \(f({x}_{l})\) represent the fitness of two tentacles.

Once updating of the beetle position, \({\delta }^{t+1}\) and \({d}^{t+1}\) are updated as,

$${\updelta }^{\text{t}+1}={\updelta }^{\text{t}}\times {\upvarepsilon }_{\text{s}}$$
(5)
$${\text{d}}^{\text{t}+1}={\text{d}}^{\text{t}}\times {\upvarepsilon }_{\text{d}}+{\text{d}}_{0}$$
(6)

where \({\varepsilon }_{s}\) and \({\varepsilon }_{d}\) are respectively the step-size attenuation factor of the beetle search and the attenuation factor of the distance between the two tentacles, \({d}_{0}\) is a constant artificially set to prevent the pair from being too close to detect, \({\delta }^{t+1}\) is the step-size of the beetle at time t + 1, \({d}^{t+1}\) is the distance between the two tentacles at time t + 1.

The beetle will repeatedly compare and update the position according to the fitness of the left and right tentacles until it finds the optimal solution or reaches the stop condition.

Proposed ABSAS-CS-GAS

To improve the convergence speed, accuracy and the capacity to evade local optima in the complex problems, the ABSAS-CS-GAS utilizes a population-based initialization and dynamic step-size adjustment, integrates the golden sine algorithm for position updates, and employs a vertical and horizontal crossover strategy to perturb the population distribution, thereby facilitating escape from local optima.

Dynamic step-size adjustment strategy

While the single-individual approach in BAS accelerates convergence for simple problems, it may compromise accuracy and increase the likelihood of local optima in complex scenarios. The algorithm's efficacy hinges on the accurate setting of initial antenna length and step-size parameters. To optimize performance across diverse optimization challenges, these parameters need be meticulously adjusted. To address these challenges, the ABSAS-CS-GAS introduces a multi-individual strategy and adaptive step-size, enhancing population diversity. The beetle population is now represented in matrix form, as detailed below,

$$X=\left[\begin{array}{ccc}\begin{array}{cc}{x}_{\text{1,1}}& {x}_{\text{1,2}}\end{array}& \begin{array}{cc}\cdots & \cdots \end{array}& {x}_{1,d}\\ \begin{array}{cc}{x}_{\text{2,1}}& {x}_{\text{2,2}}\\ \vdots & \vdots \end{array}& \begin{array}{cc}\cdots & \cdots \\ \vdots & \vdots \end{array}& \begin{array}{c}{x}_{2,d}\\ \vdots \end{array}\\ \begin{array}{cc}{x}_{n,1}& {x}_{n,2}\end{array}& \begin{array}{cc}\cdots & \cdots \end{array}& {x}_{n,d}\end{array}\right]$$
(7)

where n represents the number of beetles, d represents the dimension of the variables to be optimized.

The population of beetle is changed to improved the performance of BAS. The population experiment is shown in Fig. 1.

Fig. 1
figure 1

Population analyse (dim = 30). BAS-1 is the BAS algorithm with population 1, BAS-10 is the BAS algorithm with population 10, BAS-30 is the BAS algorithm with population 30, BAS-1 is the BAS algorithm with population 50.

Full size image

Figure 1 illustrates that the population size can enhance the efficiency of the BAS up to a certain threshold. However, the performance does not improve significantly once the population size reaches 50 individuals. The population-based adaptive parameter strategy is introduced to address the issue of the indeterminate step-size for individual populations as the population size increases.

Population-based search methods elevate the probability of identifying the global optimum, thereby avoiding entrapment in local optima, and are adept at addressing complex problem sets. The step-size is dynamically calibrated based on the proximity to the globally optimal solution; it expands when the current solution is distant from the best-known beetle position and contracts as it approaches. The step-size \({\delta }_{i}^{t}\) at time t of the i-th beetle is updated as,

$${\delta }_{i}^{t}=\lambda \sqrt{\sum_{j=1}^{dim}{\left({x}_{best,j}^{t}-{x}_{i,j}^{t}\right)}^{2}}$$
(8)

where dim and \(\lambda\) are the dimension of the function to be optimized and the step-size reduction factor, \({x}_{best,j}^{t}\) and \({x}_{i,j}^{t}\) represent the j dimension of the position of the global optimal individual and the i-th beetle at time t, respectively.

The distance between the two tentacles affects the scope of the beetle exploration. To ensure that the beetle can explore a larger range, the distance between the two tentacles is determined by the step-size. The distance is updated as,

$${d}_{i}^{t}={\delta }_{i}^{t}/2$$
(9)

where \({d}_{i}^{t}\) is the distance between the two tentacles at time t of the i-th beetle.

Population position update strategy

The BAS algorithm, relying solely on antennae fitness and a fixed step-size for position updates, potentially undermines swarm diversity and computational accuracy. To mitigate this, we integrate the Golden Section Algorithm (Gold-SA) to enhance swarm diversity by updating the positions of beetles. Gold-SA, introduced by Tanyildizi et al.24 in 2017, is a meta-heuristic algorithm that adeptly navigates the solution space through the use of the golden section ratio. This characteristic, when combined with BAS, ensures both localized individual search and global swarm exploration. The collaborative position updates of Gold-SA and BAS are intended to improve the search for global optima and increase computational accuracy. Thereby, the beetle’s position \({x}_{i}^{t+1}\) is updated as,

$$x_{i}^{{t + 1}} = \left\{ {\begin{array}{*{20}l} {x^{t} + \delta ^{t} \times r_{d} \times sign(f(x_{r} ) - f(x_{l} ))} & {r \le 0.5} \\ {x_{i}^{t} \left| {sin(r_{1} )} \right| - r_{2} sin(r_{1} )\left| {x_{1} x_{{best}}^{t} - x_{2} x_{i}^{t} } \right|} & {r> 0.5} \\ \end{array} } \right.$$
(10)

where \({r}_{1}\) and \({r}_{2}\) are random numbers,\({r}_{1}\)∈[0,2 \(\uppi\)] and \({r}_{2}\)∈[0,\(\uppi\)], \({x}_{1}\) and \({x}_{2}\) are the coefficients of golden-section to narrow the search space and gradually bring the individual closer to the optima respectively, and they are given as,

$${x}_{1}=-\pi *(1-t)+\pi *t$$
(11)
$${x}_{2}=-\pi *t+\pi *(1-t)$$
(12)

where t is the number of golden-section, and it is calculated as,

$$\text{t}=\left(\sqrt{5}-1\right)/2$$
(13)

Population disturbance strategy

The Variable Horizontal and Vertical Crossing Strategy (VHCS) refines the beetle population, enhancing avoidance of local optima and the efficiency of global search. VHCS includes Horizontal Crossing Search (HCS)26 and Vertical Crossing Search (VCS)26, which together mitigate search blind spots and counteract premature convergence, thereby allowing dimensions to escape local optima. The interaction of HCS and VCS enhances optimization accuracy and accelerates convergence.

HCS is an arithmetical crossing of all dimensions between two different individuals. The individuals of the beetle swarm are paired, and then the two paired individuals are crossed horizontally. Suppose \({M}_{i1}^{P}\) and \({M}_{i2}^{P}\) are crosswise parent individuals, \({M}_{i1}^{C}\) and \({M}_{i2}^{C}\) are the horizontal crossed offspring, the offspring are obtained as,

$${M}_{i1j}^{C}={r}_{1}{M}_{i1j}^{P}+(1-{r}_{1}){M}_{i2j}^{P}+{c}_{1}({M}_{i1j}^{P}-{M}_{i2j}^{\text{P}})$$
(14)
$${M}_{i2j}^{C}={r}_{2}{M}_{i2j}^{P}+(1-{r}_{2}){M}_{i1j}^{P}+{c}_{2}({M}_{i2j}^{P}-{M}_{i1j}^{P})$$
(15)

where \({M}_{i1j}^{P}\), \({M}_{i2j}^{P}\), \({M}_{i1j}^{C}\) and \({M}_{i2j}^{C}\) represent the j dimension of the parent individuals and the offspring individuals, respectively. \({r}_{1}\), \({r}_{2}\), \({c}_{1}\) and \({c}_{2}\) are uniformly distributed random numbers, \({r}_{1}\),\({r}_{2}\)∈(0,1),\({c}_{1}\),\({c}_{2}\)∈(− 1,1). The generated offspring individuals compare with the parent individuals, and the individual with larger fitness value is retained.

VCS implements an arithmetic crossover between all individuals across two distinct dimensions, with each individual updating a single dimension while others remain constant. This method provides stagnant dimensions the opportunity to escape local optima without impacting dimensions that are already optimal or close to the global optimum. Suppose \({M}_{i}^{P}\) is the parent individual and takes \({j}_{1}\) and \({j}_{2}\) as the dimensions of the individual to be crossed subsequently. \({M}_{i}^{C}\) is the offspring individual and to be calculated as,

$${M}_{ij1}^{C}=r{M}_{ij1}^{P}+(1-r) {M}_{ij2}^{P}$$
(16)

where \({M}_{ij1}^{C}\) represents the offspring individual \({M}_{i}^{C}\) in dimension \({j}_{1}\), \({M}_{ij1}^{P}\) and \({M}_{ij2}^{P}\) represent parent individuals \({M}_{i}^{P}\) in dimension \({j}_{1}\) and dimension \({j}_{2}\), r is a uniformly distributed random number in (0,1). \({M}_{i}^{C}\) is compared with \({M}_{i}^{P}\), and the individual with larger fitness value is retained.

Ablation experiment

The ablation experiment is performed to evaluate the efficacy of the aforementioned strategies. This involves systematically removing or reintroducing one or more strategies to assess whether there is a discernible impact on the algorithm’s performance. The result is shown in Fig. 2.

Fig. 2
figure 2

Ablation experiment (dim = 30). BAS1 is the BAS with adaptive step-size based population, BAS2 is the BAS with adaptive step-size and VHCS, BAS3 is the BAS with adaptive step-size and Gold-SA, BAS4 is the BAS with Gold-SA, BAS5 is the BAS with VHCS, BAS6 is the BAS with Gold-SA and VHCS, ABSAS_CS_GSA is the BAS with all strategies.

Full size image

Figure 2 clearly indicates that the implemented strategies have enhanced the performance of the BAS to a notable degree. The Gold-SA and adaptive step-size can improve the performance speed through BAS4, and the Gold-SA and VHCS strategies can improve greatly the convergence accuracy of the algorithm through BAS4 and BAS5.

Algorithm description

The flowchart of ABSAS-CS-GSA is shown in Fig. 3, and the pseudocode is provided in Algorithm 1.

Fig. 3
figure 3

Flowchart of ABSAS-CS-GSA.

Full size image
Algorithm 1
figure a

ABSAS-CS-GSA.

Full size image

Time complexity

The function is assumed that the dimension is D and the population size is N, the worst time complexity of the algorithm is analyzed as follows.

Firstly, the time complexity required to initialize population and to calculate the fitness of the beetles are all \({\rm O}(N\times D)\), the time complexity required to calculate the step-size of the beetles is \({\rm O}(N\times F(D))\). Then, in each iteration, the time complexity required to update the position of the beetles is \({\rm O}(N\times D)\), to update the population by HCS and by VHS are \({\rm O}(N/2\times D)\) and \({\rm O}\left(N\times 2\right)\), to update d is \({\rm O}(1)\).

In summary, the total time complexity of T iterations is \({\text{O}}\left( {T \times N \times D} \right) + {\text{O}}\left( {T \times N \times D} \right) + {\text{O}}\left( {T \times N \times F\left( D \right)} \right) + {\text{O}}\left( {T \times N \times D} \right) + {\text{O}}\left( {T \times N/2 \times D} \right) + \)\({\text{O}}\left( {T \times N \times 2} \right) + {\text{O}}(T) \approx {\text{O}}\left( {T \times N \times \left( {D + F\left( D \right)} \right)} \right)\).

Methods

Environment and parameter description

The experiment was carried out on desktop computer with Gen Intel(R) Core(TM) i5-12400F @2.50 GHz, 16 GB RAM and Window10 operating system, using Python 3.8 programming language.

To verify the performance of the algorithm, ABSAS-CS-GSA was compared with the standard BAS12 algorithm and whale optimization algorithm (WOA)3, particle swarm search (PSO) algorithm2, and four BAS variants with better performance. The variants respectively are LABAS19 IBAS23, BSAS19 and ENBAS22 algorithms. The parameter settings of the 8 algorithms are shown in Table 1.

Table 1 Algorithm parameter settings.
Full size table

The benchmark test functions are usually used to verify performance of algorithm, and refer to the website (http://www.sfu.ca/~ssurjano/). The No Free Lunch27 theorem underscores that no single algorithm excels universally across all problems. Consequently, a judicious selection of benchmark functions is essential for performance assessment. The 12 benchmark functions with wide universality to verity the performance of ABSAS-CS-GSA are shown in Table 2.

Table 2 Benchmark functions.
Full size table

Results and discussion

Experimental results and analysis

To evaluate the accuracy and stability of the algorithm, Mean and Standard Deviation (std) serve as the metrics. Each algorithm was run 30 times independently, not exceeding 2000 iterations per run. Mean evaluates the algorithm's accuracy, with lower mean indicating higher accuracy. Std evaluates stability, with smaller std denoting greater stability. Table 3 details the comparative results from these experiments across 8 algorithms on 12 benchmark functions, where 'Dim' indicates the problem dimension. Experimental results exceeding 1.00e-300 are recorded as such; results below this value are recorded as 0.

Table 3 Comparison on experiments’ result.
Full size table

Seen from Table 3, for F1, F3 and F9-F12, ABSAS-CS-GSA all gets the \({f}_{min}\), and except for the following two cases, the mean and std of ABSAS-CS-GSA are significantly lower than or equal to that of the other seven algorithms.

For unimodal function F2 in both 30 and 50, the mean of ABSAS-CS-GSA is slightly higher than that of ENBAS.

For multimodal function F8 in both 30 and 50, the mean of ABSAS-CS-GSA is slightly higher than that of WOA and ENBAS.

Therefore, it can be concluded that the accuracy and stability of ABSAS-CS-GSA are superior to the other seven algorithms.

Despite outperforming other algorithms on functions F2-F8, the ABSAS-CS-GSA falls short of achieving the theoretical optimum. The Gold-SA effectively enhances the algorithm’s precision, and the inherent randomness of the VHCS strategy in escaping local optima leads to the population’s inability to fully break free from local optima.

The convergence curves of the above eight algorithms in the performance tests of 12 benchmark functions are shown in Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15.

Fig. 4
figure 4

Performance comparison on F1.

Full size image
Fig. 5
figure 5

Performance comparison on F2.

Full size image
Fig. 6
figure 6

Performance comparison on F3.

Full size image
Fig. 7
figure 7

Performance comparison on F4.

Full size image
Fig. 8
figure 8

Performance comparison on F5.

Full size image
Fig. 9
figure 9

Performance comparison on F6.

Full size image
Fig. 10
figure 10

Performance comparison on F7.

Full size image
Fig. 11
figure 11

Performance comparison on F8.

Full size image
Fig. 12
figure 12

Performance comparison on F9.

Full size image
Fig. 13
figure 13

Performance comparison on F10.

Full size image
Fig. 14
figure 14

Performance comparison on F11.

Full size image
Fig. 15
figure 15

Performance comparison on F12.

Full size image

Seen from Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15, for all functions F1-F12, the convergence speed of ABSAS-CS-GSA is faster than that of the other seven algorithms. The algorithm’s rapid convergence is attributed to the population swiftly converging towards the optimal individual.

Wilcoxon test

The Wilcoxon test is conducted on the mean of the 30 running results of each algorithm. The statistical results are shown in Table 4. In the Wilcoxon test, ' + ' means that the proposed algorithm is superior to the selected algorithm, ' − ' means that the proposed algorithm is worse to the selected algorithm, and ' = ' means that the two algorithms get the same result.

Table 4 The results of the Wilcoxon test.
Full size table

Seen from Table 4, the number of ‘\(-\)’ is six. It means that the improved algorithm is better than these seven algorithms in most cases. The results show that ABSAS-CS-GSA is superior to the selected swarm intelligence algorithm, standard BAS, and the variants.

Application in coverage of WSNs

Model of WSNs coverage

Many SI algorithms are optimized the coverage of WSNs with better result28,29,30,31. Then coverage of WSNs is suited to verify the applicability and superiority of the improved algorithm. The ABSAS-CS-GSA has better ability to jump out of the local optimal and find the global optimal through the above experiments, and the ABSAS-CS-GSA can solve complex problem. Then ABSAS-CS-GSA has certain advantages to solve the problem of WSNs coverage.

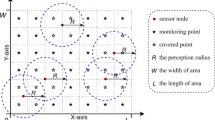
The model32 of solving the WSNs coverage in two-dimensional space is used to verify the performance of the proposed algorithm. In detail, the perception radius of each node is \({R}_{s}\) the same as the communication radius \({R}_{c}\), and \({R}_{s}{\le R}_{c}\). The coverage area of each sensor node is self-centered, \({R}_{s}\) is a circular area of radius. The monitoring area is \(M\times N\), and divide the area into \(M\times N\) grids. A random point in each grid is the monitoring node \(O=\left\{{o}_{1},{o}_{2},...,{o}_{M\times N}\}\right.\), n sensor nodes are randomly deployed in the monitoring area, \(S=\{{s}_{1},{s}_{2},...,{s}_{n}\}\). The distance between any sensor node and any monitoring node is calculated as,

$$d({s}_{i},{o}_{j})=\sqrt{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}}$$
(17)

where \(d(\cdot )\) represents the distance from monitoring node to sensor node, (\({x}_{i}\), \({\text{y}}_{\text{i}}\)) and (\({x}_{j}\), \({y}_{j}\)) represent the position of the sensor node and the monitoring node, respectively.

The non-probability expression formula of whether the monitoring node \({o}_{j}\) is covered by the sensor node \({s}_{i}\). The formula (18) is used to judge whether a single monitoring node is covered.

$$p(s_{i} ,o_{j} ) = \left\{ {\begin{array}{*{20}l} {1,} & {if\,d(s_{i} ,o_{j} ) \le R_{c} } \\ {0,} & {otherwise} \\ \end{array} } \right.$$
(18)

where \(p(\cdot )\) represents the probability of a monitor is detected with one sensor.

Any monitoring node can be covered by multiple sensors at the same time. The formula (19) is used to calculate the joint probability of the monitoring node \(S=\{{s}_{1},{s}_{2},...,{s}_{n}\}\) being covered by the sensor node.

$${C}_{p}(S,{o}_{j})=1-\prod_{i=1}^{n}(1-\text{p}({\text{s}}_{\text{i}},{\text{o}}_{\text{j}}))$$
(19)

where \({C}_{p}(\cdot )\) is the joint probability of a single sensor node.

The coverage-rate of the monitoring area is noted \({R}_{cov}\), it is the ratio of the sum of probabilities of all monitoring nodes in monitoring area, and calculated by formula (20).

$${R}_{cov}=\frac{\sum_{j=1}^{M\times N}{C}_{p}(S,{o}_{j})}{M\times N}$$
(20)

where \({R}_{cov}\) represents the coverage-rate of the all sensor nodes.

The WSNs coverage model is shown in Fig. 16.

Fig. 16
figure 16

WSNs coverage model.

Full size image

Figure 16 clearly shows the relationship between the monitoring point, the sensor node and the sensor radius.

Flowchart of WSNs coverage optimization

The flowchart of ABSAS-CS-GSA is shown in Fig. 17.

Fig. 17
figure 17

Flowchart of WSNs coverage optimization.

Full size image

Experiment of WSNs coverage optimization section

Set the monitoring area to a 50 m x 50 m square, each monitoring node is a random point in the square, the sensor sensing radius is 5 m, the communication radius is 10 m, and the number of test sensor nodes is 30 and 50 respectively. Table 5 shows the coverage of ABSAS-CS-GSA with the other seven algorithms at 30 and 50 nodes.

Table 5 WSNs overlay optimization simulation results.
Full size table

Seen from the Table 5, compared with BAS, PSO, WOA, LABAS, IBAS, BSAS and ENBAS, in the case of 30 nodes, the optimal coverage-rate of ABSAS-CS-GSA is increased by 6.04%, 8.68%, 8.84%, 8.16%, 17.40%, 6.28% and 11.04%, respectively, and the average coverage-rate is increased by 10.94%, 10.79%, 12.68%, 11.29%, 21.96%, 7.42% and 12.23%, respectively; in the case of 50 nodes, the optimal coverage-rate of ABSAS-CS-GSA is increased by 9.2%, 8.16%, 9.52%, 9.72%, 16.20%, 6.04% and 9.92%, respectively, and the average coverage-rate is increased by 10.87%, 11.88%, 14.84%, 10.80%, 21.14%, 7.75% and 11.38%, respectively.

The convergence curves of ABSAS-CS-GSA and the other seven algorithms in 30 wireless sensor nodes and 50 wireless sensor nodes are shown in Figs. 18, 19.

Fig. 18
figure 18

Coverage convergence curve (30 Nodes).

Full size image
Fig. 19
figure 19

Coverage convergence curve (50 Nodes).

Full size image

From the Figs. 18, 19, ABSAS-CS-GSA is superior to the other seven algorithms in convergence speed and convergence accuracy. In network with 30 nodes, both the coverage accuracy and speed of ABSAS-CS-GSA outperform other algorithms. In network with 50 nodes, ABSAS-CS-GSA exhibits slower coverage-rate compared to the BSAS algorithm during the initial iterations. However, in the later iterations, it achieves higher optimization speed and accuracy compared to other algorithms. The experimental results show that ABSAS-CS-GSA demonstrates superior performance in wireless sensor network coverage optimization compared to the other seven algorithms.

Figures 20, 21, 22, 23, 24, 25, 26 and 27 show the coverage models of ABSAS-CS-GSA and the other seven algorithms in 30 and 50 sensors in the monitoring area, respectively.

Fig. 20
figure 20

BAS’s coverage of WSNs.

Full size image
Fig. 21
figure 21

WOA’s coverage of WSNs.

Full size image
Fig. 22
figure 22

PSO’s coverage of WSNs.

Full size image
Fig. 23
figure 23

LABAS’s coverage of WSNs.

Full size image
Fig. 24
figure 24

IBAS’s coverage of WSNs.

Full size image
Fig. 25
figure 25

BSAS’s coverage of WSNs.

Full size image
Fig. 26
figure 26

ENBAS’s coverage of WSNs.

Full size image
Fig. 27
figure 27

ABSAS_CS_GSA’s coverage of WSNs.

Full size image

The Figs. 20, 21, 22, 23, 24, 25, 26 and 27 clearly illustrate that the sensor nodes deployed by ABSAS-CS-GSA are more uniformly spread across the monitoring area, resulting in a broader coverage. It is evident that ABSAS-CS-GSA achieves a more even distribution and wider coverage, regardless of whether there are 30 or 50 nodes.

The figures indicate that the ABSAS-CS-GSA has effectively explored the majority of the search space, but there are still some unmulched areas. The ABSAS-CS-GSA has an inherent randomness that may result in certain regions being missed during the search process.

Conclusions

The proposed ABSAS-CS-GSA integrates GSA and VHCS for addressing the limitations of the standard BAS, including lower accuracy, slower convergence speed, and easier to be trapped in local optima in solving complex problems. The experiment is structured into two main sections to verify the performance of the proposed algorithm. Initially, ABSAS-CS-GSA is developed with a time complexity of \({\rm O}(T\times N\times (D+F(D))\), and performed with superior accuracy and swift convergence through experimental results on 12 benchmark functions. Subsequently, to further verify the applicability and superiority, ABSAS-CS-GSA is applied to optimize the coverage of WSNs, and the experimental outcomes confirm that ABSAS-CS-GSA outperforms other algorithms compared with it in terms of coverage-rate.

The experiments are found that the performance of BAS algorithm still has spare to improve and to solve more engineering application problems. Moreover, the inherent randomness of the ABSAS-CS-GSA’s search process have challenging in addressing engineering issues of robust stability and interpretability. Then the stability is important for the algorithm, and the VHCS has certain limitations in jumping out of local optima, and the other strategies can use to improve the ability of avoiding local optima. The ABSAS-CS-GSA’s high convergence precision and rapid convergence rate make it well-suited for optimization tasks of paramount sheer accuracy and efficiency. In the future, the algorithm can be used to solve problem of absolute high precision. Then the proposed algorithm will be utilized to optimize the deep learning model in future work.