Introduction

Lateral cephalometric analysis, originally proposed by Broadbent in 1931 to assess anteroposterior and vertical skeletal morphology, is a fundamental diagnostic tool in orthodontics and an integral part of orthodontic treatment planning1. Cephalometric analysis relies on identifying radiological landmarks and subsequent measurements of various angles, distances, and ratios to delineate anatomical structures in the craniofacial region2. Remarkably, manual landmark plotting continues to be the standard practice, even when utilizing professional software within the orthodontic field3. Hence, the quality of cephalometric analysis heavily relies on the orthodontist’s knowledge and experience, which can result in variability among different raters4. The recognition of the value of automated landmark detection for cephalometric analysis is growing, driven by it potential to streamline the labor-intensive nature and reduce reliance on experienced orthodontists5,6.

In recent years, the application of artificial intelligence (AI) in the medical field, particularly computer vision and AI-based image analysis, has gained significant traction. Deep learning (DL), a subset of machine learning, and the use of convolutional neural networks (CNN) have been notably advocated for their suitability in computer vision tasks7. One prevalent approach is supervised learning, where an algorithm is trained on data pairs and corresponding labels8. During the training phase, the algorithm learns the statistical relationships between input data and labels to predict new, unseen data2.

Efforts have been made to create specialized datasets for automated cephalometric analysis and incorporate them into DL models for landmark detection9,10. However, despite promising initial results, challenges persist, particularly those related to the accuracy of landmark detection, which still needs to be improved11. Additionally, concerns about X-ray exposure persist, particularly in cephalograms and cone beam computed tomography (CBCT) used in maxillofacial procedures12. These concerns highlight the need to study alternative techniques for orthodontic pre-treatment examinations that reduce or eliminate X-ray exposure.

Conversely, facial landmark detection involves localizing predefined facial landmarks such as the eyes, nose, mouth, and chin in facial images. Previous studies have utilized models such as the active shape model (ASM)13 and constrained local model (CLM)14. However, these models have struggled to maintain robustness against appearance variations. To address these challenges, studies have explored the cascade regression approach15; however, this approach has limitations regarding accuracy improvement16. Deep neural networks (DNN) have recently emerged as a potent alternative17, with CNN-based approaches, including the hourglass structure18 and heat-map-based regression19,20,21, demonstrating outstanding results. Sun et al. introduced the high-resolution network V2 (HRNetV2)22, designed to preserve high resolution throughout the network while reducing parameters and computational costs compared to conventional methods. Other studies have focused on architecture-agnostic learning algorithms, such as ADNet, based on LAB and Awing, which achieved high performance19,23,24. Other methods of improved accuracy are called fine-tuning. It is the process of adjusting the parameters of a model that has been pre-trained with a large amount of data by learning additional data according to the target task to perform. Combining pre-training and fine-tuning has the advantage of providing AI with high-quality learning even when there is insufficient training data, and is used in AI development.

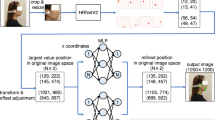
Our previous study has developed a novel approach to estimating cephalometric landmarks for cephalon analysis from lateral facial photographs by using CNN-based algorithm25. Even though landmark estimation was performed from lateral facial photographs, this method showed outstanding accuracy, surpassing the previously reported accuracy of landmark estimation from X-ray cephalograms. A two-stage learning method wherein HRNetV2 is employed for cephalometric landmark localization, and a multilayer perceptron (MLP) is used to refine the positions of the landmarks in our algorithm, thereby enhancing accuracy. However, this study’s results, which achieved high accuracy, were conducted using data from patients with normal occlusion after orthodontic treatment as training data.

Given the potential clinical applications, where orthodontists often need to analyze malocclusions, it becomes crucial to investigate further whether a similarly high level of accuracy can be achieved in malocclusion patients with skeletal Class II malocclusion and skeletal Class III malocclusion. this is a critical step towards the clinical implementation of our novel approach.

Therefore, by adding malocclusion data to the algorithm in the previous study25, this study was conducted to evaluate the accuracy and reliability of detecting estimated cephalometric landmarks from lateral facial photographs using a modified our algorithm that can adapt to malocclusion.

Additionally, it evaluated the accuracy and reliability of cephalometric analysis values derived from the estimated cephalometric landmarks.

Material and methods

The study protocol was approved by the Tokyo Dental College Ethics Committee (No. 1091). All experiments were conducted in accordance with the principles of the Declaration of Helsinki and the relevant guidelines and regulations. Informed written consent, including facial images, was obtained from all patients.

Data preparation

Patients with malocclusion who underwent orthodontic treatment, including surgical orthodontic treatment, at Tokyo Dental College between September 1981 and September 2021 were recruited, and their pre-treatment data were collected for analysis. All participants included in the study exhibited an ANB angle of 4° or more, indicating skeletal Class II malocclusion (CL II group) or an ANB angle of 1° or less, and a Wits appraisal of -1 mm or less, indicative of Skeletal Class III mallocclusion (CL III group) (Table 1).

Table 1 Details of the participants of this study.
Full size table

The exclusion criteria included patients with congenital abnormality such as cleft lip and palate, all syndromes that cause maxillofacial deformity, patients with missing molars or multiple missing teeth of more than 3 teeth, and those with a history of maxillofacial trauma. A total of 200 patients were selected for each group, and the lateral cephalograms were obtained during participants examinations.

Lateral cephalograms were acquired using a CX-150S (ASAHIROENTGEN, Tokyo, Japan), and lateral facial photographs were captured in the JPEG format using an EOS Kiss X90 camera (Canon, Tokyo, Japan). The acquisition of lateral cephalograms adhered to globally recognized standards1. The cartridge was positioned parallel to the mid-sagittal plane of the head, and the head was stabilized using ear rods so that the central axis of the X-ray beam passed through the axis of the left and right ear rods. The distance from the X-ray tube to the mid-sagittal plane of the head was 150 cm, and the distance from the mid-sagittal plane of the head to the cartridge was 15 cm. For the lateral facial photographs, the camera-to-mid-sagittal plane distance was maintained at 150 cm, and ear rods were used to secure the head for capturing images.

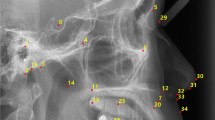
The plotting and transfer of landmarks from the cephalogram to lateral facial photographs were performed according to the guidelines reported in a previous study25. A brief description of this process is as follows. A total of 23 landmarks were selected as representative landmarks of the skeleton and teeth (Fig. 1, Supplementary information 1). These are the main landmarks used in major cephalometric analyses, such as Downs, Northwestern, and Ricketts26,27,28, and the landmarks were plotted and tracing soft tissue using Quick Ceph Studio (version 5.0.2, Quick Ceph Systems, San Diego, California). A line traced from the forehead to the upper lip on the cephalogram was matched to a corresponding line on the lateral facial photograph in the software. This alignment ensured that the magnification and position of the cephalogram and the lateral facial photograph matched (Fig. 2.)

Fig. 1
figure 1

Twenty-three landmarks plotted on the cephalometric radiograph.

Full size image
Fig. 2
figure 2

Procedure for plotting landmarks and superimposing the cephalometric tracing on the facial profile image. (a) cephalogram. (b) plotting landmark and tracing on cephalogram. Landmarks and tracing are excluded from cephalograms. (c) lateral facial photograph. (d) superimposition of landmarks, tracing and lateral facial photograph

Full size image

Error analysis for the landmarks plotting on the cephalogram and transferred landmarks on the lateral facial photograph

Two manual procedures were conducted: (1) plotting the landmarks and (2) transferring the landmarks from the cephalogram to the lateral facial photograph. These error tests were based on the methods reported in25. A brief description of this process is as follows. Prior to each manual procedure, an error test was conducted to validate the precision of each task. To assess the repeatability and reproducibility errors in landmark plotting, 23 landmarks from five randomly selected patients were plotted three times for each case, with a two-week interval between repetitions. Plotting and tracing for this study were performed by two orthodontists: one orthodontic specialist with five years of experience and one orthodontic supervisor with 15 years of experience. The accuracy of plotting and tracing was subsequently verified by another orthodontist: an orthodontic supervisor with 36 years of experience and a board member of the Japanese Orthodontic Society. The Shapiro–Wilk test was employed for normality checks to calculate the intraclass correlation coefficients (ICC) (Supplementary information 2). The results indicated that both repeatability and reproducibility errors remained within a 1-mm range, and the ICC was above 0.9 for all landmarks. Consequently, No problems were identified related to errors with the plotted landmarks29. Subsequently, error tests were conducted to superimpose trace lines on the lateral facial photographs at five landmarks (sella, porion, menton, gonion, and basion). The error distances between and within each landmark were measured consistently. The findings revealed that the errors were within a 1-mm range, and the ICC was above 0.9, indicating that the superimposition errors were negligible30. Each image has 1200 × 1200 pixels and the pixel size was 0.35 mm and each cephalograms has 1980 × 1648 pixels and the pixel size was 0.15 mm. The cephalograms is then matched to the pixel size of the lateral facial photograph.

Input of training data and estimation of test data

In this study, a computer equipped with a GeForce GTX 1080, a 3.70 GHz Intel(R) Core (TM) i7-8700 K CPU, and 16 GB of memory was used. For the landmark estimation, we adopted the neural network used in25, which consisted of two stages: HRNetV2 and MLP. The training dataset comprised 160 randomly selected participants from the CL II group (n = 200) and 160 randomly selected participants from the CL III group (n = 200). The fine-tuning process was applied as a learning process in this study. (Fig. 3). The test data comprised the remaining 40 from the CL II group and CL III group that were not included in the training dataset. Five-fold cross-validation was performed on all images in this study, and the results were averaged across five estimations.

Fig. 3
figure 3

Overview of the proposed model. The image data used for training was randomly selected from two groups: 160 individuals from the CL II group (n = 200) and 160 individuals from the CL III group (n = 200). Subsequently, a fine-tuning process was performed, and these datasets were used for training.

Full size image

Accuracy assessment of the estimated landmark

To validate the accuracy of landmarks estimation from lateral facial photographs using AI, we calculated the mean radial error (MRE) according to the methodology proposed in31. Furthermore, we assessed the displacement in the horizontal (x) and vertical (y) directions. The radial error was defined as R (R = \(\sqrt{\Delta {x}^{2}+\Delta {y}^{2}}\)) , where Δx and Δy the Euclidean distance between the estimated landmarks and the actual landmarks along the respective x and y axes. The MRE can be defined as follows:

$$MRE=\sqrt{\frac{{\sum }_{i=1}^{N}Ri}{n}},$$

Where Ri represents the radial error for the ith landmark, and n denotes the total number of detected landmarks. The success detection rate (SDR) is the proportion of estimated landmarks within a predefined threshold, and it is defined as follows:

$$SDR= \frac{{n}_{d}}{n} \times 100\%,$$

Where, nd represents the number of successfully detected landmarks. The thresholds were set to 2.0, 2.5, 3.0, and 4.0-mm, respectively. The average SDR for all images at each threshold was calculated.

Accuracy cephalometric of analysis using estimated landmarks

  1. 1)

    Accuracy: Using the estimated landmarks, we conducted angle and distance landmarks for the cephalometric analysis of skeletal and denture patterns. Student’s t-test was used to compare the cephalometric analysis results between the estimated and actual landmarks in the two groups.

  2. 2)

    Agreement: Brand-Altman analysis was performed to examine the agreement of cephalometric analysis values by AI.

  3. 3)

    Correlation: To investigate the influence of anterior–posterior and vertical positional discrepancies in the 23 landmarks of skeletal malocclusions, we examined the bivariate correlations with the ANB angle, wits appraisal, and FMA for each group. The Kolmogorov–Smirnov test was used to determine whether the data were normally distributed; we used Pearson’s correlation coefficient for correlation analysis. All statistical analysis was conducted using IBM SPSS Statistics software (version 27.0, IBM, Armonk, New York).

Results

Accuracy of landmark estimation

Figure 4 shows an example of the results of landmark estimation on training data, and Tables 2 and 3 list the estimation accuracy of 23 landmarks of the mean MRE and the SDR for each threshold.

Fig. 4
figure 4

Examples of landmark estimation result. (A) Example of skeletal Class II malocclusion. (B) Example of skeletal Class III malocclusion. Red dots: actual landmark. Green dots: estimated landmark.

Full size image
Table 2 Comparison of the estimate accuracy by each landmark in the CL II Group.
Full size table
Table 3 Comparison of the estimate accuracy by each landmark in the CL III group.
Full size table

In the CL II group, the mean MRE was 0.42 ± 0.15 mm, with values lower than 0.35 mm for Or and Pt, indicating high accuracy. However, landmarks such as Pog, Ar, and R3 show values above 0.5 mm. The SDR showed 100.00% at all thresholds. In the CL III group, the mean MRE was 0.46 ± 0.16 mm. High accuracy (< 0.35 mm) was observed for Po, Pt, and ANS, whereas landmarks such as S, N, A, B, Pog, Is, Ar, and U1-R showed values above 0.5 mm. The SDR was 99.96% at a mean of all landmarks for the 2.0-mm threshold and 100.00% for other thresholds.

Evaluation of cephalometric analysis using estimated measurement points by AI from the lateral facial photograph

  1. 1)

    Accuracy: We conducted a cephalometric analysis using the estimated landmarks and examined the differences with the actual data. In both groups, no significant differences were observed for any of the data. In the Cl II group, the error was approximately less than 0.1° for convexity, ANB angle, U1 to FH, less than 0.1 mm for L1 to Apo (mm), and approximately 0.5°for facial, gonial, and interincisal angles, and FMIA. In the CL III group, the error was less than 0.1° for the cant of occlusal plane, SNB angle, SNP angle, facial axis, and U1 to FH, and approximately 1.0°for interincisal angle and FMIA (Tables 4 and 5).

  2. 2)

    Agreement: In the horizontal (x) direction of the CL II group, random errors were detected at N, Or, Po, and Ba. Fixed errors were detected as S, A, B, Pog, Me, Gn, Go, Ii, Is, Cc, Pt, R1, PNS, ANS, Ar, R3, U1-R, and L1-R biased in the negative direction, and R3 biased in the positive direction. Proportional errors were detected in Mo. For the CL II group in the vertical direction (y), random errors were detected in S, N, Or, A, Pog, Me, Gn, Go, Is, PNS, ANS, Ar, Mo, and L1-R. Fixed errors were detected for Po in the positive direction and for B, Ii, Ba, Cc, Pt, R1, R3, and U1-R in the negative direction. For the CL III group in the horizontal direction (x), random errors were detected for N, Or, Ii, Cc, Pt, R3, and Mo. Fixed errors were positively biased at S and negatively biased at A, B, Pog, Gn, Go, R1, PNS, ANS, Ar, U1-R, and L1-R. Proportional errors were detected for Po, Me, and Ba. Random errors were detected in Po, A, Me, Gn, Go, Pt, R1, and L1-R in the vertical direction (y) of the CL III group. Fixed errors were observed in the positive direction for S and N and the negative direction for Or, B, Pog, Ii, Is, Ba, PNS, R3, and U1-R. Proportional errors were detected for Cc, ANS, Ar, and Mo (Tables 6 and 7 and Supplementary information 3).

  3. 3)

    Correlation: Bivariate correlation coefficients between the average MRE at each landmark and the measured values of the ANB angle, wits appraisal, and FMA were determined. A positive correlation (r = 0.485) was observed between the ANB angle and Is in the CL II group (Table 8).

Table 4 Mean of the actual and estimation data with differences in the CL II group.
Full size table
Table 5 Mean of the actual and estimation data with differences in the CL III group.
Full size table
Table 6 Type of error for each landmark in the CL II group using the Bland–Altman analysis.
Full size table
Table 7 Type of error for each landmark in the CL III group using the Bland–Altman analysis.
Full size table
Table 8 Correlations skeletal deviation and error for each landmark in the CL II group.
Full size table

Limited correlation was observed between Wits appraisal and any of the measurement points. However, a negative correlation (r = − 0.495) was observed between FMA and Cc.

In the CL III group, negative correlations were observed between the ANB angle and A (r = − 0.464), Go (r = − 0.436), and Ii (r = − 0.482) (Table 9).

Table 9 Correlations between the skeletal deviation and the error for each landmark in the CL III group.
Full size table

Regarding Wits appraisal, a negative correlation was observed with A (r = − 0.492) and Ii (r = − 0.479). In FMA, weak positive correlations were observed with Po (r = 0.364) and B (r = 0.364), whereas weak negative correlations were noted with Cc (r = − 0.319) and Ar (r = − 0.379).

Discussion

This study enabled the acquisition of a highly accurate cephalometric analysis value from the lateral facial photographs of malocclusion patients.

The proposed algorithm and the accuracy of landmarks estimation

The algorithm implemented in this study is based on our previous work25, where we predicted landmarks from lateral facial photographs of patients with normal occlusion. This algorithm comprises two stages: HRNetV2 and MLP. Initially, we used HRNetV2 for heatmap regression to estimate the positions of all landmarks in the input image. HRNetV2 applies multiple convolutional layers, enabling a precise understanding of the spatial relationships between each landmark and facial structures. In this step, the model learns the relationship between the local features of the face and landmarks. Subsequently, we introduced coordinate regression using MLP, which significantly improved the accuracy of landmark estimation. Learning complex spatial relationships with only MLP might not be accurate; however, combination of MLP and HR NetV2 can improve the accuracy of landmark estimation. Moreover, MLP can integrate input position information effectively because it is fully connected from the input to the output layer. This enables the model to learn underlying spatial relationships. Therefore, MLP can estimate the structural features between landmarks, i.e., it can estimate the relative positions of landmarks. In this study, the two-stage approach, comprising the coarse estimation through HRNetV2 heatmap regression and the fine estimation through MLP, enabled the accurate detection of all landmarks25.

Even though our study inferred landmarks from lateral facial photographs, the results outperformed those of previous studies that inferred landmarks from cephalograms32,33,34,35. This outcome may be unexpected from the perspective of humans; however, for the AI, it is possible that the HR NetV2 heatmap regression-based methods could capture facial soft tissue features such as eyes, nose, and mouth, in color facial photographs than in radiograph images36.

In our previous study25, we used lateral facial photographs of patients with normal occlusion after orthodontic treatment as the training data and the test data, and the mean MRE for each landmark was 0.61 ± 0.50 mm. In contrast, this study focused on pre-treatment patients with skeletal Class II and III malocclusion. Malocclusion data are considered more variable than that of normal occlusion, which may lead to greater variability in the prediction of landmarks. However, as a result, the mean MRE for each landmark in patients with the CL II group was 0.42 ± 0.15 mm, and that in patients with the CL III group was 0.46 ± 0.16 mm, which is even more accurate than those of normal occlusion. Moreover, there were almost no differences between each landmark.

In this study, several methods were attempted as a preliminary step in the research, using the algorithms from our previous study to learn and estimate data on malocclusion (Table 10). The methods include learning only skeletal Class II malocclusion data to predict skeletal Class II malocclusion, learning only skeletal Class III malocclusion data to predict skeletal Class III malocclusion, learning a combination of normal occlusion data and skeletal Class II malocclusion and skeletal Class III malocclusion data to predict the mixed data, and adding fine-tuning methods to these methods. Fine-tuning is the process of selecting pre-trained data, adding new layers tailored to the target task, and retraining the entire model with these new layers for refinement37,38. After conducting these preliminary steps, finally, we adopted method 6, because it achieved the most accurate estimation of the landmarks. This study was able to predict landmarks more accurately than the previous study for several reasons. One reason is that we employed fine-tuning methods to improve accuracy, and the other is that the constructed AI algorithms were additionally trained with malocclusion data. We obtained more precise results because we attempted several fine-tuning processes and selected the one with the highest accuracy. This can be considered an advancement in machine learning.

Table 10 Methods to improve the accuracy of training data.
Full size table

Cephalometric measurements

  1. 1)

    Accuracy: Most skeletal cephalometric measurements based on estimated landmarks revealed a discrepancy of approximately 0.5° between the actual and estimated values. Clinically, an error of less than 1° in skeletal measurements is considered acceptable39.

  2. 2)

    Agreement: Using a Bland–Altman analysis, we evaluated the agreement and error trends between the actual and estimated values. Measurements contain errors, which can be either random or systematic errors. A random error occurs in the true value and is caused by uncontrollable causes.

In this analysis, the influence of individual participant differences was removed by considering the difference between the two measurement methods (the actual data and the estimated data) for each participant. Systematic errors, which have a certain biased tendency toward the true value and are caused by controllable factors (e.g., the habit of the measurer or the inadequacy of the measuring instrument), were further classified into fixed and proportional errors. Fixed errors are those that have a constant bias in a specific direction, regardless of the true value. A proportional error is an error that occurs in a specific direction with respect to the true value. A scatter plot was created to investigate these systematic errors. The scatter plot considered the difference between the estimated and actual values on the vertical axis and the average of the estimated and actual values on the horizontal axis. Then, the vertical (Y-direction) and anterior–posterior (X-direction) errors were classified in this study, and the limit of agreement (LOA) of errors was calculated to ensure the reliability of our findings.

  1. 3)

    Correlation: We selected the ANB angle, Wits appraisal, and FMA as the skeletal type measurement items in this study to examine the relationship between skeletal deformity and the error of each landmark. The ANB angle and Wits appraisal are generally used to indicate the anteroposterior position of the skeleton, with the ANB angle being more relevant than the Wits appraisal, particularly in skeletal Class II malocclusion and the Wits appraisal being more relevant than the ANB angle in skeletal Class III malocclusion40,41. FMA was selected for this study because it is associated with vertical position of the skeleton.

In skeletal Class II malocclusion, the greater the anteroposterior skeletal deformity, namely, the larger the ANB angle, the larger is the error in the position estimation of the upper incisor edge. In contrast, in skeletal Class III malocclusion, the more significant the anteroposterior skeletal deformity, namely, the smaller the Wits appraisal, the larger is the error in the position estimation of the lower incisor edge. Notably, errors in locating the incisor edge of the forward-positioned in overjet could cause errors in inclination. This might be because the position of incisor teeth located forward of overjet is prone to errors in estimated position due to the thickness of the lips42,43. Therefore, the results suggest that the greater the anterior–posterior skeletal deviations, the greater is the error in estimating the incisal position of the anterior teeth.

Regarding the skeletal structure, the results indicated that the larger the skeletal Class III malocclusion, the more the position of A shifted. As noted in the results of this study, the direction of the error was mainly horizontal, and the error was in the backward direction. These findings indicated the similar tendency in both ANB angle and Wits appraisal. Moreover, in skeletal vertical positioning, the greater the tendency for a long face in skeletal Class II malocclusion, the smaller is the error in estimating the position of the condylar head.

However, all landmarks had errors of less than 0.5 mm, which is considered a suitable accuracy level for clinical applications44.

Study limitation

A previous study reported that the greater the sample size of the training data, the greater is the accuracy45. Although no studies have yet been reported on detecting landmarks from photographs, Moon et al.46 estimated the landmarks from the cephalogram and reported that 2300 is the optimal sample size for training data. Arik et al.2, Gilmour et al.32, Li et al.33, Kwon et al.34, and Oh et al.35 used a total of 400 data, and Kim et al.9 used total data counts of 2075 (Table 11).

Table 11 Comparison of MRE and SDR for another automated cephalometric analysis system.
Full size table

In this study, we additionally trained using the Takahashi et al. algorithm25, thus using 160 skeletal Class II malocclusion and 160 skeletal Class III malocclusion patients in addition to the 2000 patients from the previous study. Thus, 2320 patients were used as the number of training data. Therefore, based on these related reports, we consider this number as the optimum sample size for the number of training data.

In this study, as several researchers worked on the task, assessing both repeatability and reproducibility errors was crucial. A previous study reported that errors between landmarks in the cephalometric analysis are acceptable in the range of 2 mm46. The errors calculated in the present study were, on average less, than 0.5 mm. Furthermore, this value is considerably smaller than the acceptable errors among orthodontists reported previously, as the inter-measurement error between the two orthodontists in this study was within 1 mm. This result implies that the training data already has an error of at least 1 mm. Namely, the accuracy estimated by the algorithm in this study is considered suitable and high.

Furthermore, this research includes manual steps in the preparation of the test data. These are the plotting of landmarks and the transfer of landmarks from cephalograms to lateral photographs. The methodology in this manual are likely affects the accuracy of the prediction, so it was necessary for us to be highly sensitive in this point.

The training data used in this study consisted mainly of participants of Japanese descent, representing a specific racial background. Hence, errors may arise when facial photographs of participants from different races are used as test data for inference, as there will be differences in the facial morphology, soft tissue, and skeletal structures of the lateral facial photographs. Therefore, to implement the approach for various races, the training data of various races must be considered, and the accuracy must be improved. Thus, we plan to add more training data from various races and conduct further research.

Conclusion

This study developed a machine learning algorithm by adding skeletal Class II and III malocclusion data to the previous algorithm using normal occlusion data. As a result, this algorithm can be applied not only to those with normal occlusion but also to Class II Class III patients. Furthermore, the predictive algorithm was highly accurate, suggesting that a clinically accurate cephalometric analysis could be performed without conventional lateral cephalograms. The findings of this study provide a practical approach to automating cephalometric analysis solely using patients’ lateral facial photographs, thereby eliminating the need for X-ray exposure. Given prevalent concerns regarding X-ray radiation exposure, this development could benefit patients, particularly children. The results of this study have considerable clinical significance.