Non-invasive blood glucose monitoring using PPG signals with various deep learning models and implementation using TinyML

Abstract

Accurate and continuous blood glucose monitoring is essential for effective diabetes management, yet traditional finger pricking methods are often inconvenient and painful. To address this issue, photoplethysmography (PPG) presents a promising non-invasive alternative for estimating blood glucose levels. In this study, we propose an innovative 1-second signal segmentation method and evaluate the performance of three advanced deep learning models using a novel dataset to estimate blood glucose levels from PPG signals. We also extend our testing to additional datasets to assess the robustness of our models against unseen distributions, thereby providing a comprehensive evaluation of the models’ generalizability and specificity and accuracy. Initially, we analyzed 10-second PPG segments; however, our newly developed 1-second signal segmentation technique proved to significantly enhance accuracy and computational efficiency. The selected model, after being optimized and deployed on an embedded device, achieved immediate blood glucose estimation with a processing time of just 6.4 seconds, demonstrating the method’s practical applicability. The method demonstrated strong generalizability across different populations. Training data was collected during surgery and anesthesia, and the method also performed successfully in normal states using a separate test dataset. The results showed an average root mean squared error (RMSE) of 19.7 mg/dL, with 76.6% accuracy within the A zone and 23.4% accuracy within the B zone of the Clarke Error Grid Analysis (CEGA), indicating a 100% clinical acceptance. These findings demonstrate that blood glucose estimation using 1-second PPG signal segments not only outperforms the traditional 10-second segments, but also provides a more convenient and accurate alternative to conventional monitoring methods. The study’s results highlight the potential of this approach for non-invasive, accurate, and convenient diabetes management, ultimately offering improved health management.

Introduction

Diabetes is a chronic metabolic disorder that affects millions of people worldwide^1,2,3. It arises when the body either inadequately produces insulin or develops resistance to its effects⁴. Insulin, a hormone produced by the pancreas, plays a crucial role in regulating blood glucose levels by facilitating its uptake into cells for energy production². Inadequate insulin production or action results in elevated blood glucose levels (hyperglycemia), which, over time, can lead to severe complications, such as cardiovascular disease⁵, kidney damage⁶, nerve damage⁷, and vision problems^3,4. According to the World Health Organization (WHO), diabetes is a growing global health concern with significant implications for individuals, families, and healthcare systems⁸. As of 2021, an estimated 422 million people worldwide are living with diabetes, nearly four times the number in 1980⁴. Furthermore, WHO reports that in 2019 alone, approximately 1.5 million deaths were directly attributed to this metabolic disorder⁸. The International Diabetes Federation (IDF) predicts that by the year 2045, the global prevalence of diabetes will rise to around 700 million individuals⁴. This alarming increase can be attributed to various factors such as population growth, aging societies, urbanization trends leading to sedentary lifestyles and unhealthy dietary habits⁹. Consequently, there is a pressing need for effective prevention strategies as well as innovative diagnostic tools and treatment options to manage existing cases efficiently while minimizing complications⁴.

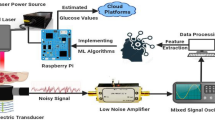
Monitoring blood glucose levels is essential in the effective management of diabetes. Traditionally, blood glucose level (BGL) measurement has been performed using invasive methods like finger stick testing, which requires a small blood sample obtained through skin puncture¹⁰. However, this approach can be painful and inconvenient for patients leading to non-compliance with recommended monitoring schedules¹¹. To address these challenges, researchers have been investigating non-invasive techniques that allow for more comfortable and user-friendly ways of measuring BGL^12,13,14. Photoplethysmography (PPG) is one such promising method gaining attention in recent years^12,13,14. PPG utilizes optical sensors to detect changes in blood volume by emitting light into the skin and measuring the amount of light absorbed or reflected by blood vessels¹⁵. Since blood glucose concentration affects various factors including tissue transparency and local hemodynamics, it may influence PPG signal characteristics as well¹⁶. By analyzing specific features within acquired PPG signals using advanced algorithms, it becomes possible to estimate BGL without causing discomfort or requiring any direct contact with bodily fluids¹². This non-invasive approach has potential benefits not only for improving patient adherence but also facilitating continuous monitoring systems enabling better glycemic control and reduced risk of complications¹⁷. Also PPG is a versatile technique that has applications beyond blood glucose level estimation. By capturing subtle changes in blood volume using optical sensors, researchers have been able to explore its potential for predicting various health parameters and conditions. Stress detection is one area where PPG has shown promising results¹⁸. As stress can trigger physiological responses such as increased heart rate and altered blood flow patterns, these variations can be detected by analyzing the characteristics of the PPG signal^18,19. Similarly, studies have demonstrated the feasibility of estimating blood pressure non-invasively using PPG data²⁰. By examining specific features within the acquired signals like pulse transit time or waveform morphologies, it becomes possible to estimate systolic and diastolic blood pressure values without relying on traditional cuff based measurements¹².

Machine Learning (ML) and Artificial Intelligence (AI) have the potential to significantly enhance the utility of PPG for BGL estimation^{12,21,22,23,24}. These technologies can be used to develop sophisticated algorithms capable of analyzing complex PPG signals and accurately estimating BGLs. ML and AI can help in identifying and learning the intricate patterns in PPG signals associated with changes in BGLs, which may not be discernible through traditional analysis methods. Furthermore, they can be used to create predictive models that can adapt to individual physiological variations, thereby improving the accuracy of BGL estimation. The integration of ML and AI in PPG-based BGL monitoring systems could lead to more reliable, personalized, and user-friendly solutions for diabetes management^21,22,23,24. In this work, we address the challenge of estimating BGL from raw PPG signals. While previous studies have explored the use of raw PPG for BGL estimation^25,26, they often suffer from limited sample sizes and lack of diversity in subjects. To overcome these limitations, we present a novel approach that incorporates a larger and more diverse dataset by using a 10-second and 1-second segmentation of PPG signals. This segmentation technique significantly increases the size of our dataset, enabling us to train a more robust and accurate model. We are conducting a comparative study between traditional 10-second segmentation and a novel approach that processes and converts these segments into 1-second intervals. This comparison utilizes two distinct datasets: one influenced by anesthesia and the other unaffected, demonstrating the model’s robustness in handling diverse clinical scenarios. Our analysis highlights the model’s generalizability, effectively predicting BGL from PPG data across conditions with and without anesthesia. Furthermore, we trained this model on the largest dataset ever utilized for BGL prediction by PPG, emphasizing the scale and relevance of our research. Additionally, we successfully implemented the best performing model on an embedded device, showcasing its practical applicability with a swift processing time of only six seconds. This research not only proves the efficacy of advanced segmentation techniques but also enhances the model’s utility in real world settings.

Furthermore, our proposed model outperforms previous approaches that rely solely on PPG signal and deep learning models^25,26. Through rigorous experimentation and evaluation, we demonstrate the superior performance of our method in estimating blood glucose levels from PPG signals. This work represents an important advancement in the field and has the potential to contribute to the development of more effective and reliable non-invasive BGL estimation techniques.

To conclude the introduction of this paper, we highlight the main contributions of our research, which set it apart from existing studies and signify its impact in the field of non-invasive blood glucose estimation:

• 1. Innovative segmentation technique: We introduce a novel preprocessing method that converts traditional 10-second PPG signal segments into more granular 1-second segments. This finer segmentation allows for more detailed analysis and potentially increases the sensitivity and accuracy of BGL estimations.

• 2. Extensive dataset utilization: Our study is distinguished using the largest dataset ever deployed for BGL prediction using PPG technology. This extensive dataset includes a diverse range of subjects and scenarios, enhancing the robustness and generalizability of our findings.

• 3. Cross-condition applicability: We rigorously test our model across two different datasets: one influenced by anesthesia and the other not, effectively demonstrating the model’s capability to deliver reliable performance under varied physiological conditions.

• 4. Real world implementation: We successfully implement our best performing model on an embedded device, achieving rapid BGL estimations in just six seconds. This achievement underscores the practical applicability of our approach for real time, continuous monitoring.

• 5. Superior performance metrics: Through meticulous experimentation and validation, our approach not only meets but exceeds the accuracy of previous methods, as evidenced by a remarkable average root mean squared error (RMSE) of 19.7 mg/dL and a 100% accuracy in clinical acceptance zones (A zone + B zone).

The rest of this paper is structured as follows: “Related works” section reviews existing studies on BGL estimation using PPG signals and various modeling techniques. “Datasets” section describes the datasets used in this study. “Data preprocessing and signal segmentation” section details the preprocessing and segmentation steps for the PPG and BGL data. “Model architecture” section discusses the deep learning models evaluated, including ResNet34, VGG16, and a hybrid CNN-LSTM with Attention. The metrics section explains the metrics used to assess model performance. “Results” section presents the comparative performance of the models and segmentation methods. “The optimizing model deployment on embedded devices” section covers the deployment of ResNet34 on the STM32H743IIT6 micro-controller, including model optimization techniques. Finally, the “Discussion” section addresses the findings, limitations, and effectiveness of the segmentation methods, and the “Conclusion” summarizes key findings and suggests future research directions.

Related works

Several studies have explored the prediction of BGL using PPG signals, employing various approaches and techniques. Some of these studies focused on feature extraction techniques to enhance the accuracy of BGL prediction models^12,27,28. These methods involve extracting relevant features from PPG signals, such as pulse rate, pulse amplitude, and waveform characteristics, to capture the physiological variations associated with glucose levels^12,14. By incorporating these extracted features into predictive models, researchers aimed to improve the accuracy and reliability of BGL estimation. Additionally, some studies incorporated auxiliary or helper features, such as HbA1c (glycated hemoglobin) levels, in their predictive models. HbA1c provides an indication of average blood glucose levels over the past two to three months, making it a potentially useful factor for BGL prediction²⁶. However, it is important to acknowledge the limitations of relying solely on HbA1c. HbA1c provides an overview of long term glycemic control, but it may not capture immediate changes in BGL or reflect short term variations that can be captured by real time monitoring using PPG signals. Moreover, some studies utilizing raw PPG signals alone to estimate BGL²⁶. They leveraged the inherent information present in the PPG waveform to extract meaningful features directly, without resorting to additional data or feature extraction methods^12,26. The simplicity of using raw PPG signals is advantageous as it reduces complexity and computational overhead.

Despite the usefulness of feature extraction techniques and auxiliary features like HbA1c²⁶, there are compelling reasons to consider using raw PPG signals as the primary data source for BGL prediction models. The main advantage lies in the ease of obtaining PPG signals through wearable sensors or commonly available mobile devices^29,30. This accessibility makes PPG signals a practical choice for continuous monitoring and enables real time estimation of BGL without the need for additional tests or complex procedures. One critical aspect to consider in the development of models for BGL estimation using PPG is the robustness of these models, particularly when data availability is limited. While PPG-based BGL estimation shows promise, the accuracy and reliability of the models can be affected by the quantity and diversity of the data used for training. One challenge that researchers face is the scarcity of data²⁵, especially in studies involving a low number of subjects. In some cases, the available datasets may only consist of a few individuals, making it difficult to capture the full range of physiological variations and inter-individual differences.

This limitation can impact the generalizability of the developed models, as they may not adequately account for the variability present in the broader population of individuals with diabetes. On the other end of the spectrum, studies with a higher number of subjects, such as the one involving 2,538 individuals, may have their own challenges. While a larger dataset offers more diversity and potential for robust model development, it introduces complexities related to data management, computational requirements, and potential biases. Handling and processing such large volumes of data require efficient algorithms, computational resources, and careful consideration of potential confounding factors.

Datasets: detailed overview of VitalDB and MUST sources

VitalDB dataset: comprehensive data collection for BGL estimation

The dataset described in the paper “VitalDB: A Public Dataset for Perioperative Biosignal Research” is a comprehensive resource for studying perioperative patient care and developing biosignal algorithms. It encompasses high resolution biosignal data collected from multiple monitoring devices used during surgery and anesthesia, with sampling frequencies ranging from 64Hz to 500Hz. The dataset includes vital signs data, such as electrocardiography, blood pressure, oxygen saturation, and body temperature, along with derived parameters like anesthesia depth index and cardiac output. This dataset provides detailed waveform and numeric data, enabling accurate interpretation of biosignals and facilitating algorithm development. The data collection was performed using the Vital Recorder program, which integrates various anesthesia devices and captures time synchronized data. Notably, the dataset incorporates PPG signals, which measure blood volume changes in peripheral tissues and offer cardiovascular information.

Moreover, the dataset encompasses glucose monitoring during surgery, allowing for real time monitoring of glucose levels. This dataset presents valuable opportunities for research in biosignal analysis, algorithm development, and investigating the impact of intraoperative variables on patient outcomes³¹. The collection of BGL and PPG signals from a patient’s fingertip using a TramRac4A device is described. The BGL and PPG data are subsequently transmitted to a monitoring system, which is used to track the patient’s vital signs. Additionally, the dataset contains 6388 subjects, and we use 70% of the segments for training, 15% for validation, and the remaining 15% for testing. Statistics and information regarding the distribution of the VitalDB dataset are presented in Tables 1 and 2.

Table 1 Summary Statistics of Variables Before Preprocessing.

Table 2 Summary Statistics of Variables After Preprocessing.

MUST dataset: university of science and technology of Iran, Mazandaran data collection

The dataset in question was collected by the digital systems research team at the University of Science and Technology in Mazandaran, Behshahr, Iran (MUST)³². It contains 67 raw PPG signals, sampled at a frequency of 2175 Hz. Each entry in the dataset is accompanied by labels for age, gender, and invasively measured blood glucose levels, making it suitable for further research and the development of learning algorithms in non-invasive blood glucose monitoring. This dataset is used solely for testing purposes.

Data prepossessing and signal segmentation

Efficient data handling through downsampling

Considering the high sampling rate of the original PPG signal (500 Hz)³¹, we decided to down sample the signal to reduce computational load and processing time. The PPG signal was resampled to a lower frequency of 100 Hz, striking a balance between capturing relevant information and reducing data dimensionality.

Synchronizing PPG signals with BGL measurements

During this stage, we focused on aligning the PPG signal with the corresponding BGL measurements The BGL measurements were recorded at specific time points and indexes denoted by tm and the sampling index respectively. To synchronize the PPG signal and BGL measurements. we calculated the corresponding time for each sampling index using the formula:

$$\begin{aligned} t_m = \frac{ \text {sampling index}}{\text {sample rate}} \end{aligned}$$

(1)

This step ensured temporal alignment between PPG and BGL.

Focused analysis with targeted data cropping

Moving on to the cropping stage, we focused on analyzing the PPG signal within specific time intervals. We defined a time interval, denoted as tm, which served as a reference point for analysis. The PPG signal was cropped 8 minutes before and after the tm point. This segmentation allowed us to examine the relationship between the PPG signal and BGL measurements during this time window (Fig. 1). Based on feedback from VitalDB correspondents, we understood that the patients status was stable and they were fasting. Therefore, the BGL did not change 8 minutes before and after the tm point, allowing us to assume that BGL remained constant during that window. This assumption does not affect the reliability of the measurements.

Fig. 1

This figure illustrates the stages of processing PPG signals. The plot shows a 16-minute segment of the signal centered around the measurement point (t_m), including 8 minutes before and after. It also displays the filtered signal, demonstrating the removal of noise and artifacts using the described methods in Refining signals with advanced filtering techniques.

Refining signals with advanced filtering techniques

During the crop process, some BGL measurements were excluded if they were recorded at a time point where an 8-minute interval before or after was not available. Additionally, segments of the cropped PPG signal within the 8-minute intervals before and after the t_m point, which had missing values for the entire 16-minute duration, were removed from further analysis. In situations where individual data points within the PPG signal were missing, the forward filling method was used to fill in these missing values, ensuring continuity in the signal.

To eliminate undesired noise and artifacts from the PPG signal, a Butterworth filter was applied. The filter settings included a low cut frequency of 0.5 Hz and a high cut frequency of 8 Hz, which aimed to retain the relevant frequency components associated with physiological variations in the signal. A third order design was employed to achieve a smooth frequency response while preserving the integrity of the signal. The data underwent rigorous cleaning using the Nerukit2 tool, which ensures data quality and reliability²⁸.

Advanced segmentation techniques for enhanced data analysis

Comprehensive window segmentation: converting 8-minute windows into 10-second intervals

We use the 8 minutes windows and then we segmented this 8 minute to 10 seconds segments with the selected BGL for the whole 8 minutes signal. We chose the 10-second segments based on trial and error, understanding that this segmentation was more useful than segments of longer durations. The dataset used in this study comprised a total of 6388 subjects. Within this dataset, there were 35358 BGL records. With the implementation of the segmentation approach, the number of data points increased significantly, resulting in a total of 699072 segmented data points for further analysis.

As the number of data points increased through the segmentation process, It is expected that the distribution of various variables such as BGL, age, BMI (body mass index), and sex may undergo changes, as shown in Tables 1 and 2. However, these changes are minimal and can be safely ignored for the purposes of this analysis. These changes can provide valuable insights into the characteristics of the dataset and the population it represents. These preprocessing and segmentation steps were crucial in preparing the PPG and BGL data for subsequent analysis, ensuring accurate interpretation and meaningful insights into the relationship between biosignals and blood glucose levels.

Precision interval segmentation: condensing signals to 1-second windows

In this approach, we aim to retain the most informative portion of the signal while reducing the computational complexity of the model. To achieve this, we condense the original 10-second PPG signal into a 1-second window. However, directly segmenting the 10-second signal into ten 1-second segments may be suboptimal, as certain segments could lack essential information. Consequently, we focus on isolating the systolic and diastolic peaks within a 1-second window, as these peaks are the most informative components of the photoplethysmogram (PPG) signal (see Fig. 2).

Fig. 2

One-second segment of a PPG signal, highlighting the characteristic waveform typically used for analysis in BGL prediction.

The process begins by detecting the systolic and diastolic peaks in the PPG signal. These points represent significant physiological events during the cardiac cycle. For each detected peak, we extract a 1-second window centered around the peak to capture the key features of the PPG waveform. To ensure that both systolic and diastolic peaks are included, the window may be expanded slightly beyond the initial 1-second boundary.

Detecting peaks in the PPG signal

Peaks in the PPG signal correspond to significant events in the cardiac cycle, namely the systolic peak, which is the largest peak and indicates maximum blood volume during the heartbeat, and the diastolic peak, which follows as a secondary wave. We employ a mathematical approach to detect these peaks using the concept of local maxima.

A point in the signal $f(t)$ is identified as a peak if its value is greater than its neighboring points. Mathematically, a peak at time $t_i$ satisfies the Eq. (2):

$$\begin{aligned} f(t_{i-1}) < f(t_i) > f(t_{i+1}) \end{aligned}$$

(2)

where $f(t_i)$ represents the PPG signal at sample $t_i$, and $f(t_{i-1})$ and $f(t_{i+1})$ are the signal values at the neighboring points. This local maximum condition forms the basis for peak detection in the signal. To refine peak detection, two additional conditions are applied:

• Height Threshold: This filters out noise and small fluctuations, ensuring that only peaks above a certain amplitude are considered. Mathematically, for a peak at $t_i$, the condition is (Eq. 3):

  $$\begin{aligned} f(t_i) > H_{\text {min}} \end{aligned}$$

  (3)

  where $H_{\text {min}}$ is the minimum height threshold.

• Distance Threshold: To avoid detecting multiple peaks in close proximity, a minimum distance between consecutive peaks is enforced. If two peaks are detected within a short time interval, only the more prominent peak is retained. This requirement is expressed as (Eq. 4):

  $$\begin{aligned} | t_i - t_j | > D_{\text {min}}, \quad \forall i \ne j \end{aligned}$$

  (4)

  where $D_{\text {min}}$ is the minimum allowable distance between peaks $t_i$ and $t_j$.

By applying these thresholds, the detected peaks are ensured to be both physiologically meaningful and appropriately spaced, reducing the chance of false positives caused by noise or rapid fluctuations in the signal.

Window selection and template matching

Once the peaks have been detected, 1-second windows are extracted, each centered around the detected peak. These windows ensure that key features of the PPG waveform, particularly systolic and diastolic peaks, are captured for further analysis.

To validate the quality of these windows, we employ a matching filter to compare each window with a predefined template. The template is computed as the mean of all detected windows, representing the typical PPG waveform. This allows us to filter out windows that deviate significantly from the expected waveform.

The similarity between each window and the template is quantified using cosine similarity (Eq. 5), a measure of the angle between two vectors. The cosine similarity between a window $W_i$ and the template $T$ is defined as:

$$\begin{aligned} \text {cosine\_similarity}(W_i, T) = \frac{W_i \cdot T}{\Vert W_i \Vert \Vert T \Vert } \end{aligned}$$

(5)

where $W_i \cdot T$ is the dot product of the window and the template, and $\Vert W_i \Vert$ and $\Vert T \Vert$ are their Euclidean norms. Cosine similarity ranges from -1 to 1, where a value of 1 indicates perfect similarity, and values close to 0 indicate low similarity.

To retain only high-quality segments, we discard any window whose cosine similarity with the template falls below 85%. This threshold is a hyperparameter that can be adjusted depending on the specific requirements of the model. By filtering out low-quality windows, we focus on the most informative segments of the signal, enhancing the overall performance of the model by reducing noise and irrelevant data.

This process effectively condenses the PPG signal into 1-second windows that capture the most critical information, reducing computational load while retaining key features of the waveform. To illustrate the methodology, we present the pseudocode (Algorithm 1 ) for the precision interval segmentation process. The algorithm involves peak detection, window extraction, template computation, and cosine similarity filtering, as described in the previous sections.

Algorithm 1

Precision Interval Segmentation

Model architecture: customizing and implementing advanced deep learning models for PPG signal analysis

In this study, we utilize three distinct deep learning models ResNet34, VGG16, and a hybrid CNN-LSTM with attention mechanisms-to enhance the accuracy and efficiency of PPG-based blood glucose monitoring. The rationale behind selecting these models lies in their unique capabilities. ResNet34, known for its robust architecture with residual connections, has been customized with one-dimensional convolution (Conv1D) layers to capture the temporal dynamics of PPG signals, addressing the vanishing gradient problem while leveraging deep feature extraction. VGG16, chosen for its simplicity and computational efficiency, also employs Conv1D layers, making it suitable for scenarios with limited computational resources while maintaining effective temporal pattern recognition. Lastly, the hybrid CNN-LSTM-ATTENTION model integrates convolutional layers for hierarchical feature extraction with bidirectional LSTM and attention mechanisms to enhance temporal dependency capture and focused learning. We aim to explore and demonstrate their complementary strengths in providing a comprehensive solution for accurate and efficient PPG signal analysis for blood glucose prediction.

Tailoring ResNet34 for enhanced PPG signal analysis

ResNet34³³ is a deep convolutional neural network primarily designed for image classification tasks. However, we adapt this architecture to the domain of biosignal analysis, specifically PPG signals, by leveraging 1D convolutional layers, referred to as Conv1D. Conv1D layers are specifically designed to process sequential data, such as time series signals, by applying filters along the temporal dimension. Unlike Conv2D layers used for image processing, Conv1D layers possess a single spatial dimension, which makes them suitable for capturing patterns and dependencies in the temporal sequence of PPG signals. In the standard ResNet34 architecture, Conv2D layers are typically employed to process 2D image data^33,34. However, to accommodate our 1D PPG signal data, we modify the architecture by replacing these Conv2D layers with Conv1D layers. This customization allows the model to effectively learn relevant features and capture the specific temporal dynamics present in PPG signals. Moreover, ResNet34 utilizes residual connections, also known as skip connections, to address the vanishing gradient problem and enable the training of deep networks³³. These skip connections play a critical role in the successful training of ResNet34 and are preserved in our modified version that incorporates Conv1D layers. By utilizing Conv1D layers within the ResNet34 architecture, we can effectively capture the temporal patterns and variations inherent in PPG signals, leading to improved blood glucose prediction performance. This modified architecture utilizes the strengths of Conv1D layers in processing sequential data while retaining the proven benefits of ResNet34’s deep structure and skip connections.

Our customized version of the ResNet34 architecture, tailored for PPG signal analysis, represents a novel adaptation of the original ResNet34 model. It demonstrates how state of the art architectures can be customized and repurposed to suit the specific requirements of biosignal analysis tasks, in this case, accurate blood glucose prediction from PPG signals. In the modified ResNet34 (Figs. 3 and 4) architecture implemented in this paper, the input PPG signal data undergoes the following layers and connections:

• Input Layer: The model takes PPG signal data as input.

• Conv1D Layer: The initial Conv1D layer processes the input data with 64 filters, a kernel size of 3, and a stride of 1. It uses the ’same’ padding and is followed by batch normalization and ReLU activation. This layer extracts lower level features from the PPG signals.

• BatchNorm1d Layer: Following the first Conv1D layer, a BatchNorm1d layer with 64 features is used.

• Residual Blocks: The model consists of multiple residual blocks that incorporate Conv1D layers, batch normalization, and ReLU activation. Each residual block takes the previous output and applies Conv1D layers with specific filter sizes, kernel sizes, and strides. These residual blocks enable the model to capture higher level representations and long term dependencies in the PPG signals. The number of residual blocks can be adjusted based on the requirements of the task. In the model structure, there are three residual blocks with 64 filters and four residual blocks each with 128, and six block with 256 filters, and three of 512 filters, respectively.

• Flatten Layer: Following the last residual block, a Flatten layer is used to reshape the output into a one dimensional vector, preparing it for the subsequent dense layers.

• Dense Layers: The flattened output is fed into three dense layers. The first dense layer consists of 256 units with ReLU activation, allowing for the extraction of higher level features and representations. The second dense layer has 128 units with ReLU activation. The final layer has a single unit with a linear activation function that predicts the BGL value.

Fig. 3

Resnet34 model diagram.

Fig. 4

Architecture of the residual block used in the modified ResNet34 model for PPG signal analysis, showing the flow of data through 1d-CNN layers, batch normalization, and ReLU activation, with a skip connection to combat the vanishing gradient problem.

Using VGG16 for processing of 1d biosignal data

The VGG16³⁵ (Fig. 5) , renowned for its simplicity and effectiveness, proves to be a suitable candidate for processing 1D biosignal data such as PPG signals. By leveraging Conv1D layers tailored to analyze temporal sequences, VGG16 can capture the intricate temporal patterns and dependencies inherent in PPG signals. Additionally, its relatively smaller size compared to ResNet makes VGG16 a practical choice for applications with limited computational resources, without compromising performance, as further detailed in accompanying visual representations.

Fig. 5

VGG16 model diagram adapted for PPG signal analysis.

Enhanced biosignal interpretation with hybrid CNN-LSTM and attention mechanisms

The proposed model combines convolutional neural network (CNN), bidirectional LSTM unit (Bi-LSTM), and attention mechanisms for robust analysis of 1D biosignal data, particularly PPG signals. Initially, Conv1D layers are utilized to extract hierarchical features from the input signal, allowing for the capture of temporal dependencies. Batch normalization and ReLU activation further enhance feature extraction, followed by max pooling to reduce spatial dimensions and retain salient features. Subsequently, the model incorporates a bidirectional long short term memory (Bi-LSTM) layer to effectively capture temporal dynamics and dependencies bidirectionally. Dropout regularization is employed to mitigate over-fitting and enhance model generalization.

Furthermore, an attention mechanism is introduced to dynamically weight the importance of each time step’s representation in the Bi-LSTM output sequence, facilitating focused learning and improving predictive performance. Finally, a dense output layer predicts the blood glucose level from the attended BiLSTM output, offering a comprehensive solution for accurate biosignal analysis. This architecture demonstrates a holistic approach, leveraging both temporal and hierarchical features present in PPG signals for improved blood glucose prediction.

Comprehensive evaluation metrics for predictive model assessment

In the model evaluation metrics section, we assess the performance of our model for blood glucose estimation using several key metrics. These metrics provide quantitative measures to evaluate the accuracy, precision, and reliability of the model’s predictions.

Key quantitative metrics for evaluating blood glucose prediction accuracy

In predictive modeling, particularly in the context of blood glucose prediction, several key quantitative metrics are used to assess the accuracy of the predictions. Let $Y$ represent the reference or true blood glucose values, $Y_i$ the individual reference value for the $i^{th}$ observation, and $Y_i'$ the corresponding predicted value for the same observation. The total number of observations is denoted by $n$. The following metrics provide insights into different aspects of prediction accuracy:

Mean squared error

Mean squared error (MSE)³⁶ is a common loss function (Eq. 6) used to measure the average squared difference between the predicted blood glucose values and the corresponding reference values. It provides an overall measure of the model’s prediction accuracy, with lower values indicating better performance.

$$\begin{aligned} MSE = \frac{1}{n} \Sigma ^{n}_{i=1} (Y_i - Y_i^\prime )^2 \end{aligned}$$

(6)

Mean absolute error

MAE³⁷ (Eq. 7) calculates the average absolute difference between the predicted and reference blood glucose values. It provides a measure of the model’s average prediction error and is useful for assessing the model’s precision

$$\begin{aligned} MAE = \frac{1}{n} \Sigma ^{n}_{i=1} \mid Y_i - Y_i^\prime \mid \end{aligned}$$

(7)

Coefficient of determination

Coefficient of determination ($R^2$ )³⁸ (Eq. 8) is a statistical measure that indicates the proportion of variance in the blood glucose values that can be explained by the model. It ranges from 0 to 1, where a value closer to 1 indicates a better fit of the model to the data.

$$\begin{aligned} R^2 = 1 - \frac{ \Sigma _{i} (Y_i - Y_i^\prime )^2}{ \Sigma _{i} (Y_i - \bar{Y_i})^2} \end{aligned}$$

(8)

Mean absolute relative difference

Mean absolute relative difference (MARD)³⁹ (Eq. 9) measures the average relative difference between the predicted and reference blood glucose values, expressed as a percentage. It assesses the model’s accuracy in capturing the relative magnitude of the blood glucose levels.

$$\begin{aligned} MARD = \frac{1}{n} \Sigma (\frac{\mid Y_i - Y_i^\prime \mid }{Y_i}) \times 100 \end{aligned}$$

(9)

Root mean squared error

Root mean squared error (RMSE)⁴⁰ (Eq. 10) is the square root of the MSE and provides an estimate of the average prediction error in the original units of the blood glucose measurements. It is a commonly used metric for evaluating the overall performance of predictive models.

$$\begin{aligned} RMSE = \sqrt{\frac{1}{n} \Sigma ^{n}_{i=1} (Y_i - Y_i^\prime )^2} \end{aligned}$$

(10)

Clinical accuracy assessment using clarke error grid analysis

Clarke error grid (CEG) is a powerful tool used to evaluate the clinical accuracy of our predictive model for blood glucose prediction⁴¹. It provides a comprehensive assessment by comparing predicted and reference blood glucose values and categorizing them into five distinct zones: A, B, C, D, and E. Each zone represents a different level of clinical risk associated with the predictions.

• Zone A: This zone represents clinically accurate predictions, where both the predicted and reference blood glucose values fall within a clinically acceptable range. Specifically, Zone A includes values where the reference blood glucose level is below 70 mg/dL and the predicted value is also below 70 mg/dL, or where the predicted value is within 20% of the reference value (i.e., between 80% and 120% of the reference)⁴¹. Predictions in this zone indicate a high level of accuracy and clinical approval.

• Zone B: In this zone, the predicted blood glucose values deviate from the reference values but the discrepancies are clinically benign and would not result in inappropriate treatment decisions. Zone B applies to predictions that do not fall into the more clinically risky zones but still deviate from the 20% range of the reference value. These discrepancies are minor and do not significantly affect patient management⁴¹.

• Zone C: This zone includes predictions that may lead to unnecessary treatment. Predictions fall into this zone if the reference value is between 70 and 290 mg/dL, and the predicted value deviates by more than 110 mg/dL above the reference value. Additionally, if the reference value is between 130 and 180 mg/dL, predictions that fall below a threshold defined by the formula $(7/5) \times \text {reference} - 182$ also belong to Zone C. The deviations in this zone could result in overly cautious or inappropriate treatment⁴¹.

• Zone D: Predictions in this zone indicate a potentially dangerous failure to detect hypoglycemia or hyperglycemia. This zone applies when the reference value is above 240 mg/dL, but the predicted values fall between 70 and 180 mg/dL, or when the reference value is below approximately 58 mg/dL (175/3) and the predicted value is between 70 and 180 mg/dL. Additionally, if the reference value is between approximately 58 and 70 mg/dL, predictions that are greater than 120% of the reference fall into Zone D. These errors may lead to dangerous clinical outcomes and require further refinement of the prediction model⁴¹.

• Zone E: This zone represents the most critical prediction errors, where confusion in treatment may occur. Predictions fall into Zone E if the reference value is above 180 mg/dL and the predicted value is below 70 mg/dL, or if the reference value is below 70 mg/dL and the predicted value is above 180 mg/dL. These severe deviations could lead to incorrect treatment, such as mistaking hypoglycemia for hyperglycemia, and result in harmful clinical decisions⁴¹.

It is important to note that while predictions falling within Zone B are generally considered acceptable, the goal is to minimize the number of predictions in Zones C, D, and E to ensure optimal clinical performance and patient safety⁴¹. CEG serves as a valuable tool for assessing the clinical relevance and safety of our predictive model by providing insights into the level of agreement between predicted and reference blood glucose values and guiding further improvements to enhance clinical accuracy.

Comparative results and performance analysis

Table 3 indicates parameter counts and Table 4 presents a detailed comparison of the performance of three models across two segmentation methods: 1-second segmentation with a matching filter and 10-second segmentation for test dataset of Vital DB. It includes key metrics such as RMSE, MAE, MSE, MARD, and R² for the test sets. This table facilitates an easy evaluation of each model’s accuracy and error metrics across different datasets, offering valuable insights into their predictive accuracy and error estimation capabilities.

Table 3 Comparison of Parameter Counts in Different Models.

Table 4 Comparative performance of three models using 1-second and 10-second segmentation methods: evaluation metrics across test sets.

Table 5 represents the distribution of predictions over test dataset of Vital DB across various zones according to CEG. The CEG zones categorize predictions based on their level of agreement with reference values, ranging from no risk to potentially dangerous. This table displays the percentages of predictions in each zone for the three models, providing a visual representation of each model’s accuracy and highlighting potential risks associated with their predictions. Figures 6, 7, 8, 9, 10, and 11 illustrate the assessment of clinical risk levels using the Clarke Error Grid by distinguishing zones and data points for the test sets of three models across two segmentation methods. These figures provide a graphical representation of the agreement between predicted and reference values, visualizing the distribution of predictions within the CEG zones to clarify the models’ accuracy and identify potential areas for improvement. Additionally, Figs. 12 and 13 display the training and validation loss history throughout the training for three models using 10-second and 1-second segmentation methods. These figures offer a detailed view of the loss metrics, illustrating performance improvements and convergence behaviors of the models during the training phases.

Table 5 Clarke error grid analysis for three models using 1-second and 10-second segmentation methods.

Fig. 6

Assessment of clinical risk levels for 1-second ResNet34 predictions.

Fig. 7

Assessment of clinical risk levels for 10-second ResNet34 predictions.

Fig. 8

Assessment of clinical risk levels for 1-second VGG16 predictions.

Fig. 9

Assessment of clinical risk levels for 10-second VGG16 predictions.

Fig. 10

Assessment of clinical risk levels for 1-second CNN-LSTM-ATTENTION predictions.

Fig. 11

Assessment of clinical risk levels for 10-second CNN-LSTM-ATTENTION predictions.

Fig. 12

Training and validation loss for different models using 10-second segments. The plot compares the performance of ResNet34, VGG16, and CNN-LSTM with Attention models.

Fig. 13

Training and validation loss across different models for 1-second segments.

In addition, we evaluated our optimal model ResNet34 designed for 1-second segments on the MUST dataset. The dataset comprises recordings from 23 subjects, each providing multiple 10-second signal segments accompanied by corresponding BGL test results. Initially, these signals were resampled to a frequency of 100Hz. Subsequently, following the procedures outlined in the data processing and segmentation section, these 10-second segments were meticulously processed to isolate special 1-second segments. These targeted segments were specifically chosen to contain both systolic and diastolic peaks, aligning with the critical events of interest as defined in our study protocol. Table 6 presents the performance metrics obtained with the ResNet34 model, while Table 7 details the results from the CEG analysis.

Table 6 Performance of 1-second ResNet34 using quantitative metrics for MUST dataset.

Table 7 Accuracies of CEG zones on MUST dataset.

Moreover, Figure 14 displays the residual plot, from which it can be concluded that there is an absence of any discernible pattern, indicating excellent model predictions. Furthermore, Figure 15 illustrates the CEG plot, with the detailed results documented in Table 7. Additionally, Figs. 16, 17, and 18 demonstrate the superior performance of our proposed method, which benefits from a significantly larger dataset involving three times more subjects than the nearest competitor, which included 2538 subjects. This extensive dataset has enabled us to refine our model further, resulting in enhanced accuracy as evidenced by our superior results in both the A zone of the Clarke Error Grid and RMSE metrics. This robust performance underlines the effectiveness of our approach in delivering precise and reliable BGL estimates, setting a new benchmark in the field. Table 8 summarizes these comparisons, highlighting the distinguishing features of our approach. Our study leverages a significantly larger and more diverse dataset, with 6,388 training and testing subjects (70% train, 15% validation and 15% test) and 67 testing subjects spanning an age range from 0.3 to 94 years. This broad range improves the generalizability of the model across different age groups, which is an advantage over many prior studies that often utilize smaller datasets or more limited age groups. Furthermore, our model is compatible with STM32 microcontrollers, enabling real-time, embedded BGL monitoring-setting it apart from previous works which generally lack embedded compatibility or are designed for non-real-time applications.

Fig. 14

Residual plot for predicted blood glucose levels using the MUST dataset. The plot shows the residuals (difference between predicted and actual values) against the predicted values, helping to assess the accuracy and consistency of the model predictions.

Fig. 15

Assessment of clinical risk levels for MUST dataset predictions.

Fig. 16

Comparing the number of subjects in the study to the number of subjects in previous studies.

Fig. 17

RMSE comparison with previous studies.

Fig. 18

Comparative analysis of model performance in zone A.

Table 8 Comparison of related works with our method.

When comparing the clinical accuracy of our method to previous studies, we achieve 72.6% accuracy in Zone A and 25.9% in Zone B, according to the clarke error grid analysis (CEGA). While our performance in Zone B is lower than some previous works, the versatility and real-time applicability of our approach offer substantial practical advantages for continuous BGL monitoring in various clinical settings. Additionally, we report a RMSE of 19.7 mg/dL and a MAE of 14.8 mg/dL in our testing results (Table 6). Our model’s performance, particularly in terms of RMSE and MAE, highlights the trade-off between clinical accuracy and practical implementation in resource-constrained environments. In contrast to prior works that often rely on more complex, offline systems, low number of subjects, our embedded approach with STM32 microcontrollers provides a solution that can be deployed in real-world, resource-constrained environments. This capability is particularly beneficial for continuous, accessible BGL monitoring, making it applicable in low-cost, portable devices that can be used in diverse settings, from home care to clinical environments.

Optimizing model deployment on embedded devices: strategies and implementation

Model training and inference typically occur on high performance servers equipped with GPUs^46,47.The workflow depicted in Figure 19 highlights the integration of advanced computing and security technologies to deploy efficient and secure machine learning models on embedded devices. It involves intensive computational tasks on powerful GPUs, followed by model optimization and secure data transfer, culminating in direct execution from external flash memory. This approach enhances both performance and operational security, demonstrating a sophisticated strategy to apply machine learning effectively in power-sensitive environments like IoT and edge devices.

Fig. 19

Workflow of embedded systems development: This diagram illustrates the process of inferencing on an embedded device, beginning with data collection and processing. The workflow involves utilizing a remote server (Secure Shell (SSH) is employed for secure communication between the local computer and the remote server) with a 3090 GPU for training and validating models. The selected model undergoes optimization through pruning and quantization, followed by compilation into a binary format using C++ compilers, preparing it for execution on the STM32 MCU. The model binary is then transferred from the internal memory of the STM32H743IIT6 to the external flash memory (W25Q256), enabling direct execution using the ’Execute in Place’ (XIP) function.

However, deploying these models on wearable devices presents challenges due to constraints like limited battery life, RAM capacity, processing power, and potential latency issues⁴⁶. These factors are critical in scenarios where the model must be accessible for public and medical purposes. Edge computing tackles these obstacles by facilitating model inference directly on the local device⁴⁸, enhancing responsiveness and reducing the need for continuous cloud connectivity.

However, deploying deep networks on resource limited edge devices necessitates substantial optimization of compute and memory demands. Networks are generally trained on well resourced servers and subsequently refined for efficient operation on edge hardware. Primary optimization strategies involve model compression, utilization of lower numerical precision, and hardware aware adaptation to ensure effective performance within these constraints⁴⁶. So, in this section, we discuss the implementation of the ResNet34 model, which was selected as our optimal model for 1-second segmentation, on the STM32H743IIT6 micro-controller.

Essential technical requirements for efficient tinyML execution on micro-controllers

TinyML optimizes machine learning for low power devices like microcontrollers⁴⁹, enhancing local processing in wearables and sensors while ensuring privacy and reducing cloud dependency. These models prioritize energy efficiency by optimizing neural network operations and minimizing data transfers. Despite their benefits, challenges related to limited computational power, memory, and energy persist. Trade-offs between performance attributes such as power, speed, and accuracy are critical in selecting suitable micro-controllers. The ARM Cortex-M series⁴⁶. The STM32H743IIT6 micro-controller is particularly effective, combining adequate memory, energy efficiency, and cost effectiveness to support applications like real time BGL estimation. Additionally, Fig. 20 illustrates the three key specifications of the STM32H743IIT6: power consumption, processing power, and memory and storage.

Fig. 20

Key specifications of the STM32H743IIT6 microcontroller, highlighting its processing power, memory and storage capacity, and efficient power consumption, making it suitable for TinyML applications.

Given the size of the model, which exceeds the capacity of the internal flash memory, we utilized QSPI flash memory alongside the microcontroller to accommodate the model⁴⁶. This implementation highlights the modifications necessary to adapt the model to the constraints of an embedded system. We applied quantization and pruning techniques to reduce the model size, making it feasible for deployment on the embedded device⁴⁶.

Experimental results for model deployment on embedded devices

In this subsection, we present the experimental results of deploying our optimized ResNet34 model on the STM32H743IIT6 microcontroller. Due to the constraints of our experimental setup, we inferred the results through the serial port on the STM32H743IIT6 microcontroller, processing and visualizing the predictions on a connected computer. This setup was effective in displaying the glucose prediction results in real-time, although we did not use an external monitor directly connected to the microcontroller.

Table 9, provided in this subsection, details the model size before and after these modifications and includes the inference time of the model on the device. Additionally, we present performance metrics to demonstrate the effectiveness of the model in this constrained environment. Also, Figs. 21 and 22 illustrate the process and comparison of the base model, the pruned model, and the pruning-preserving quantization-aware training (PQAT). These figures show the MSE loss and the model size, respectively, highlighting the benefits of each approach.

Table 9 ResNet34 model information for embedded devices.

Fig. 21

Mean Squared Error (MSE) loss comparison of three different model types: Base Model, Pruned Model, and PQAT Model, showing the performance differences in predicting blood glucose levels.

Fig. 22

Size comparison of three different model types: Base Model, Pruned Model, and PQAT Model, showing the differences in model size in megabytes.

While the base model is shown in the figures as a reference, it is too large to be deployed directly on microcontrollers due to memory constraints. The PQAT model, however, provides a significant advantage over the pruned-only model. As demonstrated in the figures, PQAT reduces the model size while preserving accuracy, as it incorporates quantization during the training process. This makes the PQAT model the optimal choice for deployment on resource-constrained microcontrollers, as it strikes the best balance between size, performance, and efficiency. We conclude that the PQAT model is the recommended approach for efficient execution in TinyML environments.

Discussion

In this study, we present several key innovations that distinguish our approach in the field of non-invasive BGL estimation using PPG signals. One of the primary advantages is the introduction of a novel preprocessing technique that shifts from the traditional 10-second segmentation to a more granular 1-second segmentation. This finer segmentation allows for capturing crucial physiological details, such as systolic and diastolic peaks, leading to more sensitive and accurate predictions. Additionally, this 1-second segmentation simplifies and speeds up the processing on embedded devices, making real-time BGL estimation more feasible in resource-constrained environments. We tested two methods of segmentation with different time intervals to determine their effectiveness in predicting BGL from PPG signals. Our analysis showed that using 1-second segments, which include both systolic and diastolic peaks (one complete cardiac cycle), yielded good results. This suggests that the sequence of cycles does not significantly impact the prediction accuracy, indicating that longer segments do not necessarily improve performance.

Moreover, our findings revealed that sequential models like the hybrid CNN-LSTM-Attention, which rely on the order of data points, are not as effective in this context as deeper models, such as ResNet34, that can capture more complex patterns within each cycle. Deeper models demonstrated better performance in predicting BGL from PPG signals. Additionally, the robustness and generalizability of our model were enhanced by utilizing the largest dataset ever deployed for BGL prediction using PPG technology. This extensive dataset, which includes a wide variety of subjects and conditions, helped demonstrate that our model performs consistently across different physiological states, including cases influenced by anesthesia and normal states. The successful deployment of the model on an embedded device, achieving real-time BGL estimation within just six seconds, further underscores the practical applicability of our approach.

A key novelty of this work lies in the successful implementation of the model on an embedded device, the STM32H743IIT6 microcontroller. The deployment of the model achieved real-time BGL estimation within just six seconds, which demonstrates not only the accuracy but also the practical applicability of our approach in real-world, resource-constrained environments. The ability to achieve such rapid processing on an embedded system is a significant advantage for continuous and non-invasive glucose monitoring applications.

Despite these strengths, the study also has some limitations. The system’s performance in predicting extreme BGL values, such as in cases of hypo- and hyperglycemia, may have been limited by the insufficient representation of abnormal glucose levels in the dataset, which could affect accuracy in critical scenarios. While the model performed well within normal glucose ranges, its ability to generalize to rare and extreme cases remains an area for improvement.

The current dataset, although comprehensive, had a distribution that favored normal glucose levels, which may have limited the model’s ability to learn from and predict rare abnormal values. Future research should focus on collecting a more diverse range of data, especially including more abnormal BGL cases, to further enhance the model’s performance. Finally, refining the balance between short- and long-term signal information will be necessary to improve the system’s overall reliability, especially in predicting dynamic changes in glucose levels.

Conclusion

This research has successfully demonstrated the practical application of ResNet34 in enhancing non-invasive glucose monitoring using PPG signals. Our study systematically evaluated three deep learning models, with ResNet34 emerging as particularly effective in processing and analyzing PPG data, which was collected under diverse clinical conditions to ensure robustness and accuracy. By adapting ResNet34 for embedded devices, we achieved rapid and accurate blood glucose estimations, addressing key challenges in diabetes management, such as the invasiveness and inconvenience of traditional monitoring methods. The implementation of the model on an embedded device not only provided real time analytics but also maintained high accuracy, crucial for patient trust and regulatory approval.

The study underscores the importance of comprehensive dataset utilization and continuous model validation . The use of a novel preprocessing technique that segments PPG signals into more precise intervals significantly enhanced the model’s predictive accuracy, demonstrating the critical role of fine tuning and optimization in deploying deep learning models in medical applications. In conclusion, the findings from this research point towards a future where non-invasive, continuous glucose monitoring can be seamlessly integrated into everyday life, offering a significant improvement in the quality of life for individuals with diabetes. Future work will focus on expanding dataset diversity, refining model architectures, and enhancing the computational efficiency of these systems to further improve their deployment in clinical and real world settings.