An efficient trustworthy cyberattack defence mechanism system for self guided federated learning framework using attention induced deep convolution neural networks

Abstract

As cyberattacks become more advanced, conventional centralized threat intelligence models often fail to keep up with these threats’ growing complexity and frequency, highlighting the requirement for innovative approaches to strengthen cybersecurity resilience. Federated learning (FL), a decentralized machine learning (ML) model, provides a promising solution by permitting spread objects to train techniques on local data collaboratively without distributing sensitive data. The efficiency of FL in enhancing attack intelligence skills emphasizes its probability of driving a novel period of robust and privacy-protecting cybersecurity practices. Furthermore, combining FL into cybersecurity structures can strengthen attack intelligence models by permitting real upgrades and adaptive learning mechanisms. Recently, ML and Deep Learning (DL) approaches have drawn the study community to advance security solutions for cyberattack defence mechanism models. Conventional ML and DL techniques that function with data kept on a federal server increase the main privacy issues for user information. This manuscript presents a Cyberattack Defence Mechanism System for Federated Learning Framework using Attention Induced Deep Convolution Neural Networks (CDMFL-AIDCNN) technique. The CDMFL-AIDCNN model presents an improved structure incorporating self-guided FL with attack intelligence to improve defence mechanisms across varied cybersecurity applications in distributed systems. Initially, the data preprocessing stage utilizes Z-score normalization to transform input data into a beneficial format. The Dung Beetle Optimization (DBO) technique is used in the feature selection process to identify the most relevant and non-redundant features. Furthermore, the fusion of convolutional neural networks, bidirectional long short-term memory, gated recurrent units, and attention (CBLG-A) models are employed to classify cyberattack defence mechanisms. Finally, the parameter tuning of the CBLG-A approach is performed by the growth optimizer (GO) approach. The CDMFL-AIDCNN technique is extensively analyzed using the CIC-IDS-2017 and UNSW-NB15 datasets. The comparison analysis of the CDMFL-AIDCNN technique portrayed a superior accuracy value of 99.07% and 98.64% under the CIC-IDS-2017 and UNSW-NB15 datasets.

Introduction

Cybersecurity threats are malicious and deliberate activities considered as threat detection, and actors of such threats utilize Intrusion Detection Systems (IDS), which is vital and essential for security defence groups to reduce the loss caused¹. Anomaly recognition is the main technique utilized in IDS design. The fast development of computer networks and systems increases the speed, variety, and volume of data being processed and collected by anomaly-based IDS². In progressively connected digital organizations, the landscape faces an increasing wave of cyber-attacks, jeopardizing sensitive data and threatening operational dependability and integrity³. Classical cybersecurity processes, often dependent on centralized data analysis and processing, have proven inadequate for addressing novel cyber-attack difficulties and dynamic nature. These approaches overlook the possible collaborative organizations to pool their intelligence and source without compromising sensitive data⁴. FL is a feasible solution for improving attack intelligence while maintaining data privacy. This shift model signifies an essential departure from traditional centralized ML methods, allowing organizations to communally improve their cybersecurity abilities without sharing sensitive data⁵. FL enables decentralized training of ML methods by permitting several organizations to cooperate in the learning process without transmitting their information to a central server. This novel method mitigates the risks related to data privacy and leakage violations, addressing dual crucial problems in the cybersecurity realm⁶.

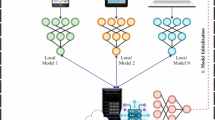
As per a recent analysis, over 60% of organizations stated that inadequate data privacy processes are the main difficulty of ineffectual attack intelligence distribution. The capability of FL to respect data locality but still remove meaningful visions from combined efforts represents an opportunity to improve the mitigation and detection of advanced cyber-attacks⁷. Likewise, incorporating FL into cybersecurity structures can bolster attack intelligence methods by allowing adaptive learning mechanisms and real-world updates. Figure 1 portrays the general structure of FL. DL methods have been developed recently, which show substantially more excellent performance than traditional ML anomaly recognition methods to process large-scale higher complexity datasets⁸. The FL attains immense achievement and is broadly utilized in several regions, for example, vehicle communications, Intrusion detection, mobile edge network optimization, and more⁹. Thus, various cyber security investigators have difficulty discovering the top learning type, FL or centralized, to evaluate and test their projected security approaches in IoT applications, and choosing a suitable federated DL approach is a vital concern in this area. Classical IDS have struggled with higher false positive rates and are inefficient in recognizing unknown or new threat vectors¹⁰. However, FL presents a promising alternative by permitting organizations to train methods on local data while helping from the collectively aggregated knowledge.

Fig. 1

General structure of FL.

This manuscript presents a Cyberattack Defence Mechanism System for Federated Learning Framework using Attention Induced Deep Convolution Neural Networks (CDMFL-AIDCNN) technique. The CDMFL-AIDCNN model presents an improved structure incorporating self-guided FL with attack intelligence to improve defence mechanisms across varied cybersecurity applications in distributed systems. Initially, the data preprocessing stage utilizes Z-score normalization to transform input data into a beneficial format. The Dung Beetle Optimization (DBO) technique is used in the feature selection process to identify the most relevant and non-redundant features. Furthermore, the fusion of convolutional neural networks, bidirectional long short-term memory, gated recurrent units, and attention (CBLG-A) models are employed to classify cyberattack defence mechanisms. Finally, the parameter tuning of the CBLG-A approach is performed by the growth optimizer (GO) approach. The CDMFL-AIDCNN technique is extensively analyzed using the CIC-IDS-2017 and UNSW-NB15 datasets. The major contribution of the CDMFL-AIDCNN technique is listed below.

• The CDMFL-AIDCNN model utilizes Z-score normalization to standardize the data, ensuring that all features are comparable. This process transforms the data by centring it around a mean of zero and scaling it by the standard deviation. As a result, the model’s learning process becomes more efficient, improving the overall classification performance.

• The CDMFL-AIDCNN approach employs DBO-based feature selection to detect the dataset’s most relevant and non-redundant features. This technique eliminates irrelevant or duplicate features, improving the model’s efficiency and accuracy. This results in a more streamlined and effective cyberattack detection process.

• The integration of the CNN, Bi-LSTM, GRU, and CBLG-A models enables effective classification of cyberattack defence mechanisms. This incorporation employs every technique’s merits to capture spatial and temporal patterns in attack data. As a result, the model achieves more accurate and robust detection of complex cyber threats.

• The CDMFL-AIDCNN methodology implements GO-based tuning to enhance the model’s performance by refining hyperparameters for optimal results. This technique effectively adjusts parameters to improve accuracy and efficiency in detecting cyberattacks. It assists in fine-tuning the model for better generalization and robustness in real-world applications.

• The CDMFL-AIDCNN model presents a novel hybrid model that integrates multiple advanced techniques, comprising CNN, BiLSTM, GRU, and an attention mechanism, for robust and efficient cyberattack classification. It introduces a unique feature selection process optimized by DBO to identify the most relevant features. Also, hyperparameter tuning through GO improves model performance, ensuring superior accuracy and efficiency in detecting cyberattacks. This integration of techniques provides a highly adaptive and effective solution for evolving cybersecurity challenges.

Related works

Taheri et al.¹¹ present an Artificial Neural Networks (ANNs)-based method to change FL-trust to non-independent and identically distributed (non-IID) data. The ANN is intended as an intellect abnormality modification control approach, applying a dynamic recurrent neural network (RNNs) with exogenic input. This research also takes the general effects of VPP and poisoning threats on the disseminated supportive controller at the secondary control stage. In Ref.¹², a privacy-preserving disseminated malware recognition method with irregular customers, which utilizes a deep CNN-based FL method, is presented. A data augmentation approach was used to balance malware information for local training. A deep CNN structure utilized intensified characteristics to accomplish local training and create Local Model Updates (LMU). Afterwards, LMUs are sent to the overall server for the aggregating method. In Ref.¹³, a complete FL-based deep abnormality recognition structure designed for reliable, privacy, and practical preserving energy theft recognition is presented. In the projected structure, user train local deep AE-based indicators on their private power usage of data and share only their trained detector hyper-parameter with an EUC aggregation server to make a worldwide abnormality detection. In Ref.¹⁴, a FL is presented. This work first examines the vulnerability of classical electricity stealing classifiers trained by FL to EAs for data consumption. Afterwards, it examines the efficiency of AT in securing the detection of electricity theft against EAs. Then, wide-ranging experiments are organized to validate the cruelty of these projected threats.

Kalapaaking et al.¹⁵ present a verifiable and auditable Decentralized FL (DFL) structure. This paper first improves a smart-contract-based observing method for DFL members. This observing method is then employed by every DFL member and performed when the local training method is started. The observing method records essential data for auditing goals during the local training. Then, every DFL participant sends the monitoring and local model to the Blockchain (BC) node. The BC nodes demonstrating every DFL participant alter the local methods and usage of the observing method to validate every local method. Husnoo et al.¹⁶ present FeDiSa, a new Semi-asynchronous FL structure for power method flaws and a distinct cyber threat that considers communication straggler and latency. This work presents a collective training of deep AE by the Data Acquisition and Supervisory Control sub-system that uploads their local method upgrades to a control centre and then accomplishes a semi-asynchronous method. Namakshenas et al.¹⁷ project the IP2FL method, an Interpretation-based Privacy-Preserving FL method made for ICPS. This method associates Additive Homomorphic Encryption (AHE) for privacy with developed Shapley Values (SV) and feature selection approaches for improved interpretability. The projected resolution mitigates privacy issues in FL, while classical methods fall short owing to the absence of interpretability and computational restrictions. By incorporating AHE, the IP2FL method reduces computational overhead and guarantees data privacy. Jiang et al.¹⁸ present a novel method to attack intelligence distribution called Blockchain and FL for sharing attack recognition methods as Cyber Threat Intelligence (BFLS), whereas BC-based CTI sharing frameworks are utilized for privacy and security. FL technology is accepted for accessible ML applications, like threat recognition.

The limitations of the existing studies include the potential vulnerability of FL models to diverse attacks, such as poisoning and data consumption attacks, which could compromise model accuracy and reliability. Additionally, many approaches depend on specific data types or centralized servers, which may limit scalability and generalization across various real-world scenarios. While privacy-preserving techniques like AHE are utilized, they often introduce computational overhead that may reduce the efficiency of the models. Furthermore, some studies do not fully address the challenge of handling non-IID data in FL, which affects model performance in practical environments. Research gaps exist in enhancing model robustness, improving privacy-preserving techniques without compromising computational efficiency, and addressing the challenges posed by real-world, dynamic attack scenarios. Future work should develop more resilient and effectual FL models capable of handling diverse, non-IID data while ensuring privacy and security in distributed settings.

Proposed methodology

This manuscript presents a CDMFL-AIDCNN technique. The CDMFL-AIDCNN model has an improved structure that incorporates self-guided FL with attack intelligence to improve defence mechanisms across varied cybersecurity applications in distributed systems. The CDMFL-AIDCNN model involves various phases: data preprocessing, feature selection, classification model, and hyperparameter fine-tuning process. Figure 2 denotes the overall workflow process of the CDMFL-AIDCNN model.

Fig. 2

Overall working process of CDMFL-AIDCNN technique.

Z-score normalization

At first, the data preprocessing stage applied Z-score normalization to convert input data into a beneficial format¹⁹. This is chosen for its capability to standardize the dataset, ensuring that all features contribute equally to the model’s performance. By transforming the data into a standard scale with a mean of 0 and a standard deviation of 1, this technique prevents features with more extensive ranges from dominating the learning process. Unlike other scaling methods, Z-score normalization is robust to outliers and allows the model to operate effectively with various data distributions. It ensures better convergence in optimization algorithms and improves the overall efficiency of ML models, specifically when dealing with datasets having varying units or magnitudes.

It is also named standardization, an arithmetic model utilized to convert features by measuring them to ensure a standard deviation of one and a mean of zero. In a cyberattack defence mechanism system, this technique aids in standardizing input data throughout distinct nodes or devices, confirming comparability and consistency in their feature. By eliminating biases owing to dissimilar data distributions, Z-score normalization improves the system’s capability to identify cyber threats precisely. Also, it supports FL by accepting methods from numerous resources to be aggregated well, enhancing the sturdiness of the defence mechanism. This normalization develops model stability and convergence, specifically in heterogeneous surroundings.

DBO-based feature selection process

For the feature selection process, the DBO method is employed to identify the most relevant and non-redundant features²⁰. This process was chosen because of its ability to effectively identify appropriate and non-redundant features from a high-dimensional dataset. DBO replicates the dung beetles’ behaviour, which efficiently explores and selects features, giving a robust search for optimal subsets. DBO is less likely to get stuck in local optima than other feature selection methods due to its dynamic exploration-exploitation balance. Its global search capability enhances the model’s performance by choosing the most informative features while mitigating dimensionality. This improves accuracy and reduces computational complexity, making it appropriate for large-scale datasets with noisy or irrelevant features. Figure 3 specifies the DBO architecture.

Fig. 3

Overall structure of the DBO model.

The DBO method is a swarm intelligence optimizer model based on the behavioural features of dung beetles. This method mimics several behaviours of DBs, namely dancing, foraging, rolling, breeding, and stealing, and strategies a series of updated rules and tactics. All DB groups comprise four dissimilar agent categories: rolling, breeding (breeding balls), small, and stealing beetles.

Rolling beetles

DBs roll dung balls to desirable places. While rolling, signals are utilized to keep a direct route. To pretend these behaviours are in the method, DBs must move in a specified way inside the search area. In the rolling procedure, the locations of this beetle are upgraded, and their location modifications are exposed in Eqs. (1) and (2):

$$\:{x}_{i}\left(t+1\right)={x}_{i}\left(t\right)+\alpha\:k{x}_{i}\left(t-1\right)+b\varDelta\:x$$

(1)

$$\:\varDelta\:x=\left|{x}_{i}\left(t\right)-{X}^{w}\right|,$$

(2)

whereas $\:t$ characterizes the iteration counts; $\:X\left(t\right)$ specifies the location information of the $\:i\:th$ DB at iteration $\:t$; $\:\alpha\:$ embodies the standard coefficient, allocated the value of 1 or $\:-1$. Suppose $\:\alpha\:=1$ or $\:\alpha\:=-1$; both specify no deviation and deviation from the direction. $\:Ke(\text{0,0.2}$) signifies the defection coefficient; $\:b$ specifies the constant value attributed to $\:\left(\text{0,1}\right)$, $\:{X}^{w}$ characterizes the globally poor location, and $\:\varDelta\:x$ has been applied to pretend modifications in the intensity of light. Once these DBs meet a problem preventing their route, they may utilize their dancing behaviour to reevaluate their way. In such cases, the location-updated equation for these DBs is exposed in Eq. (3):

$$\:{x}_{i}\left(t+1\right)={x}_{i}\left(t\right)+\text{t}\text{a}\text{n}\left(\theta\:\right)\left|{x}_{i}\left(t\right)-{x}_{i}\left(t-1\right)\right|$$

(3)

whereas $\:\theta\:e[0,\pi\:]$ characterizes the defection angle. If $\:\theta\:=0,\frac{\pi\:}{2}$, and $\:\pi\:$, the location of the DB may not be upgraded.

Breeding beetles (breeding balls)

To securely breed their offspring, DBs roll the dung balls to a safe place and conceal them confidential wherever they lay eggs. Hence, the boundary selection tactic for the DBs is exposed in Eqs. (4) and (5):

$$\:{b}_{L}^{\text{*}}=\text{m}\text{a}\text{x}\left({X}^{\text{*}}\left(1-R\right),{b}_{L}\right)$$

(4)

$$\:{b}_{U}^{\text{*}}=\text{m}\text{i}\text{n}\left({X}^{\text{*}}\left(1+R\right),{b}_{U}\right)$$

(5)

whereas $\:{b}_{U}^{\text{*}}$and$\:\:{b}_{L}^{\text{*}}$ characterize the upper and lower borders of the egg-laying area, correspondingly $\:{X}^{\text{*}}$ signifies the present optimum position,$\:\cdot\:$ $\:R=1-t/{T}_{\text{m}\text{a}\text{x}},$ $\:{T}_{\text{m}\text{a}\text{x}}$ designate the maximal iteration counts; and $\:{b}_{L}$ and $\:{b}_{U}$ characterize the upper and lower limits of the optimizer issue, correspondingly.

When the position of the laying egg zone is decided, female DBs will select the breeding ball in that laying egg zone. Every female DB lays a single egg only for each execution. As discussed in Eqs. (4) and (5), the borders of these laying egg zones are dynamic and based on the $\:R$-value. As a result, the location of the breeding ball additionally varies with dynamism in the iterations, which is characterized as shown:

$$\:{B}_{i}\left(t+1\right)={X}^{\text{*}}+{b}_{1}\left({B}_{i}\left(t\right)-{b}_{L}^{\text{*}}\right)+{b}_{2}\left({B}_{i}\left(t\right)-{b}_{U}^{\text{*}}\right)$$

(6)

Here, $\:B\left(t\right)$ denotes the location of the $\:i\:th$ dung ball at the iteration $\:t$; $\:{b}_{1}$ refers to a $\:D$-dimension arbitrary vector resulting in the standard distribution, and $\:{b}_{2}$ characterizes a $\:D$‐dimensional arbitrary vector in the interval of $\:\left[\text{0,1}\right].$

Small beetles

After a while, larvae grow to adult DBs and originate from the field foraging; they’re related to smaller beetles. The borders of their optimum foraging region are described as shown:

$$\:{b}_{L}^{b}=\text{m}\text{a}\text{x}\left({X}^{b}\left(1-R\right),{b}_{L}\right),$$

(7)

$$\:{b}_{U}^{b}=\text{m}\text{i}\text{n}\left({X}^{b}\left(1+R\right),{\:b}_{U}\right),$$

(8)

whereas $\:{b}_{L}^{b}$ and $\:{b}_{U}^{b}$ characterize the upper and lower limits of the optimum foraging region for smaller beetles, $\:{X}^{b}$ signifies the globally optimal location. Hence, the location updated for the smaller beetles is as demonstrated:

$$\:{x}_{i}(t+1)={x}_{i}\left(t\right)+{C}_{1}\left({x}_{i}\left(t\right)-{b}_{L}^{b}\right)+{C}_{2}\left({x}_{i}\left(t\right)-{b}_{U}^{b}\right),$$

(9)

Here, $\:{x}_{i}\left(t\right)$ characterizes the location information of $\:i\:th$ smaller beetles at iteration $\:t$; $\:{C}_{1}$ specifies randomly generated numbers after standard distributions; and $\:{C}_{2}$ symbolizes randomly formed vectors characterized by the range $\:\left(\text{0,1}\right)$.

Stealing beetles

Some DBs would steal dung balls from another beetle, and this dung-thieving beetle is discussed as a theft beetle in Eqs. (7) and (8), it is detected that $\:{X}^{b}$ signifies the finest source of food. As a result, they might consider that the region close $\:{to\:X}^{b}$ represents the optimum position for a food challenge. In the iteration procedure, the locations of the stealing beetles are constantly upgraded and are designated as shown:

$$\:{x}_{i}\left(t+1\right)={x}^{b}+S\times\:g\left(\left|{x}_{i}\left(t\right)-{X}^{\text{*}}\right|+\left|{x}_{i}\left(t\right)-{X}^{b}\right|\right)$$

(10)

Now $\:X\left(t\right)$ characterizes the location information of $\:i\:th$ thief at iteration $\:t$; $\:g$ specifies arbitrary vector size $\:1\times\:D$ succeeding normal distributions; and $\:S$ means constants. While the DBO method is carried out over other models in optimization, showing robust optimizer ability and quick convergence speed, it continues to encounter differences in local exploitation and global exploration while challenging composite difficulties. It might result in the threat of getting captured by local targets and direct poor global exploration capability. As a result, to improve the exploration capability of DBO, enhancements are completed to the recent optimizer method by combining Bernoulli mapping tactics, implanting an enhanced sine algorithm tactic, and using adaptable Gaussian Cauchy mutation perturbations to tackle this disadvantage.

Before the development, the population initialization of the method was performed utilizing arbitrary generation. The limitations of these models include the unequal distribution of the beetles’ locations, poor globally recognized possibilities, lower population diversity, and a trend of getting stuck in local goals. Conversely, chaotic mapping associations randomness and determinism, categorized by non-periodicity and randomness. Initialization of Chaotic can improve the extensiveness of search optimizer methods and can be applied to tackle global optimizer issues. There are different kinds of chaotic mappings, and the Bernoulli mapping is one. It might substitute the population’s arbitrary number initialization during the optimization area, enhancing the population DB’s distribution characteristic and improving global searching ability. As a result, Bernoulli mapping is utilized to initialize the locations of the DBs. Initially, the values gained over the Bernoulli mapping relative to the space of the chaotic variable are designed. Formerly, the resultant chaotic values are maps in the first area of the method over linear transformation. The particular representation for the Bernoulli mapping is as demonstrated:

$$\:{z}_{n+1}=\left\{\begin{array}{l}\frac{{z}_{-}}{1-\beta\:},\:0\le\:{z}_{n}\le\:1-\beta\:\\\:\frac{{z}_{n}-\left(1-\beta\:\right)}{\beta\:},\:1-\beta\:\le\:{z}_{n}\le\:{1}^{{\prime\:}}\end{array}\right.$$

(11)

Now, $\:\beta\:$ denotes the mapping parameter, $\:\beta\:e\left(\text{0,1}\right)$, fixed to $\:\beta\:=0.518,{z}_{0}=0.326$ to attain optimum value performance.

The fitness function (FF) imitates the classifier precision and the sum of the chosen features. It increases the classifier accuracy and decreases the set size of the chosen features. Thus, the FF mentioned in Eq. (12) is used to evaluate a specific solution. This function plays a significant role in determining the quality of the solution based on the defined criteria, ensuring that only the most optimal solutions are selected for further processing.

$$\:Fitness=\alpha\:*\:ErrorRate+\left(1-\alpha\:\right)*\frac{\#SF}{\#All\_F\:}$$

(12)

Here, $\:ErrorRate$ indicates a classification rate of error using the chosen feature. $\:ErrorRate$ is the ratio of incorrectly classified features, with a value between 0 and 1. $\:\#SF$ denotes the number of nominated features, and $\:\#All\_F$ refers to the total number of features in the original dataset. $\:\alpha\:$ is employed to restrain the consequence of classifier attribute and sub-set length. In the tests, $\:\alpha\:$ is set as 0.9.

CBLG-A-based classification model

Likewise, the hybrid of the CBLG-A model for classifying cyberattack defence mechanisms²¹. This technique is chosen because it can handle complex, sequential, and spatial patterns in cybersecurity data. CNN outperforms in extracting local spatial features, while BiLSTM and GRU capture temporal dependencies, making the model effectual in dynamic environments like cyberattack detection. The attention mechanism enhances the focus on significant data parts, improving model interpretability and decision-making. This hybrid approach outperforms conventional models by effectively incorporating the merits of every technique, ensuring high accuracy and robustness in classifying cyberattacks. It also adapts well to real-time and evolving threat landscapes, giving superior performance to models relying on individual techniques. Figure 4 depicts the architecture of the BiLSTM technique.

Fig. 4

Structure of BiLSTM model.

The hybrid model features a superior structure to uphold cybersecurity attack recognition. It is attained by combining numerous complex neural network structures to create a complete analytic structure. The model’s design tackles the intricate features and combines numerous specified networks, such as BiLSTM, CNN, Gated GRUs, and Attention mechanisms. The model employs CNN to handle input data, advancing from their capability for recognizing spatial order and pattern. BiLSTMs were utilized to realize time-based dependencies, delivering a hidden perception of the successive network flow data features. Also, GRUs are employed, enhancing the method’s capability for controlling data over time with higher effective parameterization than conventional LSTM. An attention network was combined to select essential data parts, improving the method’s attention and interpretability about the most significant feature of the recognition task. These systems unite at a Concatenation Layer, uniting the distinct feature map into a merged depiction, followed by a Dense Layer that merges the discovered feature for the last classification.

CNNs were crucial networks for removing classified features from spatial data. The main process at the basis of CNN contains using a convolution filter to input data, resulting in a feature map that acquires models in an input area. The CNN element is essential in obtaining spatial features from the dataset. The proposed method uses a 128-filter CNN layer with a kernel size 3. A $\:ReLU$ activation function was employed to establish non-linearity and enable the removal of features. Lastly, a Dense layer with 64 units was presented to aid as a fully connected (FC) layer for understanding the CNN feature. Exactly, it includes utilizing a filter $\:\left(W\right)$ and an input $\:\left(X\right)$ for performing a convolution process at an exact spatial position $\:\left(i,j\right)$, which is mathematically mentioned below:

$$\:F(i,\:j)={\sum\:}_{m}{\sum\:}_{n}X\left(i+m,\:j+n\right)W\left(m,\:n\right),$$

(13)

$\:F(i,j)$ signifies the feature mapping produced by employing a convolution filter $\:W$ to an input $\:X.$ The sequential layer inserts non-linearity and decreases sizes. It contains $\:ReLU$ and a pooling layer. The BiLSTM layer is one of the LSTM structures intended to examine information in both backward and forward routes, enhancing the system’s capability to take dependencies among time-based sequences.

The below mentioned are the set of formulations which define the primary structure of the LSTM unit:

Forget gate:

$$\:{f}_{t}=\sigma\:\left({W}_{f}\cdot\:\left[{h}_{t}-1,\:{x}_{t}\right]+{b}_{f}\right),$$

(14)

Input gate:

$$\:{i}_{t}=\sigma\:\left({W}_{i}\cdot\:\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{j}\right),$$

(15)

Cell state update:

$$\:{C}_{t}=\text{t}\text{a}\text{n}\text{h}\left({W}_{c}\cdot\:\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{c}\right),$$

(16)

Final cell state:

$$\:{C}_{t}={f}_{t}\text{*}{C}_{t-1}+{i}_{t}\text{*}{C}_{t},$$

(17)

Output gate:

$$\:{o}_{t}=\sigma\:\left({W}_{o}\cdot\:\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{o}\right),$$

(18)

Hidden state:

$$\:{h}_{t}={\text{o}}_{t}\text{*}\text{t}\text{a}\text{n}\text{h}\left({C}_{t}\right),$$

(19)

Here, $\:\sigma\:$ signifies the activation function of the sigmoid, $\:\text{*}$ denotes element-wise multiplication, and b and $\:W$ represent the biases and weights. The model combines progressed BiLSTM and GRU models to take time-based dependencies. The BiLSTM layer is proposed to recognize sequential patterns by handling data backwards and forward. On the other hand, the GRU layer simplifies the recurrent structure by protecting its capability to take longer‐term dependencies. The layer of BiLSTM contains 64 units, and another layer of BLSTM has 32 units, which enhances the feature’s time-based extraction. A Dense layer with 64 units is then employed to understand the BiLSTM output. GRUs are one of the neural network structures that make up the LSTM framework. The architecture of GRU unites the functionality of input and forget gates into a single update gate. The generalization outcomes in a more effective and efficient neural network. The process of GRU is demonstrated below in the mathematical formula:

Update gate:

$$\:{u}_{t}=\sigma\:\left({W}_{u}\cdot\:\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{i}\right),$$

(20)

Reset gate:

$$\:{v}_{t}=\sigma\:\left({W}_{v}\cdot\:\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{v}\right),$$

(21)

Candidate activation:

$$\:{\stackrel{\sim}{h}}_{\text{t}}=\text{t}\text{a}\text{n}\text{h}\:\left(W\left[{v}_{t}\cdot\:{h}_{t-1},\:{x}_{t}\right]+b\right),$$

(22)

Final output:

$$\:{h}_{t}=(1-{u}_{t})\text{*}{h}_{t-1}+{u}_{t}\text{*}{\stackrel{\sim}{h}}_{t}.$$

(23)

The layers of GRU and Dense have 64 units, which handle time-series data for recognizing developing attack patterns. The attention network has been fundamental in improving attention to substantial parts of the data. It calculates context‐aware representation by allocating weights to diverse input parts, permitting the method to highlight related data. The device has been included afterwards in the embedding layer, with the following compressing and a Dense layer to make alert signals. Throughout the forecast stage, the attention mechanism permits the method to concentrate on related portions of input data. To compute the attention score for context $\:e$ and an assigned input $\:{x}_{i}$, the below-mentioned formulation is mathematically expressed below:

$$\:{a}_{i}=\frac{\text{e}\text{x}\text{p}\left(score\left({x}_{i},e\right)\right)}{{\sum\:}_{j}\text{e}\text{x}\text{p}\left(score\left({x}_{j},e\right)\right)},$$

(24)

The “$\:score$” indicates a device that assesses how well an input is aligned with the adjacent context. The output of the attention layer is a core of input, weighted depending upon their relevant attention score. The handled features from the BiLSTM, CNN, Attention components, and GRU are united at a layer of Concatenation, which unites the diverse feature map into a single unified representation, capturing context-aware, sequential, and spatial data. Then, the concatenated feature goes over the Dense layer, processing the feature representation and making the data classification.

Hyperparameter tuning process

Finally, the GO model implements the parameter tuning of the CBLG-A approach²². This model effectively balanced exploration and exploitation during the hyperparameter optimization process. Unlike conventional optimization techniques, GO utilizes an adaptive strategy that progressively grows the population, enabling it to escape local optima and find better solutions in complex search spaces. Its flexibility in tuning various parameters makes it highly effective for models like neural networks, where hyperparameter selection significantly impacts performance. The capability of the GO model to enhance convergence speeds and improve model robustness makes it superior for real-time cyberattack detection. The model outperforms other techniques by ensuring optimal parameter configurations that directly influence the efficiency and accuracy of the classification. Figure 5 depicts the steps involved in the GO method.

Fig. 5

Steps involved in the GO technique.

The arithmetic basis of the Growth Optimizer (GO), its framework, movement, and features from other human meta-heuristic models are explained below. Remarkably, this technique only tackles the issue of minimization. Dual stages are accessible, such as the learning stage, which creates the initial segment, whereas the reflection stage makes up the next. The learning stage is when an individual fills the gaps another human being leaves. Then, the reflection stage is when the human utilizes numerous models to recognize and precisely pinpoint their faults.

Learning stage

Opposing and examining the gaps among them and inspecting and realizing them noticeably helps a person’s advancement. The four common gaps were accurately demonstrated in the learning stage of GO: $\:\overrightarrow{Ga{p}_{1}}$ amongst the elite and the leader, $\:\overrightarrow{Ga}{p}_{2}$ amongst the bottom and the leader, $\:\overrightarrow{Ga{p}_{3}}$ amongst the bottom and the elite, and $\:Ga{p}_{4}$ among dual randomly generated people. Equation (25) expresses the mathematical technique for every group of gaps.

$$\:\left\{\begin{array}{l}\overrightarrow{Ga{p}_{1}}\:={\overrightarrow{x}}_{best}-{\overrightarrow{x}}_{better}\\\:\overrightarrow{Ga{p}_{2}}={\overrightarrow{x}}_{best}-{\overrightarrow{x}}_{worse}\\\:\overrightarrow{Ga{p}_{3}}={\overrightarrow{x}}_{better}-{\overrightarrow{x}}_{worse}\\\:\overrightarrow{Ga{p}_{4}}={\overrightarrow{x}}_{L1}-{\overrightarrow{x}}_{L2}\end{array}\right.$$

(25)

Here, the leader of society is symbolized by $\:{\overrightarrow{x}}_{best}$, and the subsequent P1-1 finest people, who were indicated as elite, were denoted by $\:{\overrightarrow{x}}_{better}$. At the bottom of the social ladder, $\:\overrightarrow{x}$ is between the P_1 lower-rank individuals in the populace. Randomly generated individuals discrete from the $\:ith$ individual are signified as $\:{\overrightarrow{x}}_{L2}$ and $\:{\overrightarrow{x}}_{L1}$. The distance among dual humans is stated as $\:\overrightarrow{Ga}{p}_{k}\left(k=1.2.3.and\:4\right).\overrightarrow{\:Ga}{p}_{k}$ permits pupils to accurately realize and acquire the advantages of the differences amongst dual people. The GR must be set in ascending order in the present iteration $\:\left(It\right)$ of the GO technique. There are four disparity measurements, and a learning factor $\:\left(LF\right)$ was included for accounting for the fluctuation $\:LF$ that was demonstrated as exposed in Eq. (26) and will impact the individual’s learning on$\:\:the\:Kth\:set\:gap$.

$$\:LF_{k} = \frac{{\left\| {G\vec{a}p_{k} } \right\|}}{{\sum\nolimits_{{k = 1}}^{4} {\left\| {G\vec{a}p_{k} } \right\|} \:}},\:\left( {k = {\text{1,2}},{\text{3,4}}} \right)$$

(26)

If $\:G\overrightarrow{a}{p}_{k}$, the $\:kth$ group gap is symbolized by a ratio of normalized $\:L{P}_{k}$ within the interval of [0,1]. The $\:ith$ individual will acquire expertise from $\:the\:kth$ gap when a $\:kth$ set gap is more significant, and $\:L{F}_{k}$ will be more prominent. Human beings perceive themselves inversely based on the developing procedure. The $\:ith$ individual defines the level of normal expertise by utilizing $\:S{F}_{i}$. A high $\:S{F}_{i}$ signifies that to advance himself, an individual $\:i$ has to study more. Equation (27) exhibits$\:\:sF.$

$$\:S{P}_{i}=\frac{G{R}_{i}}{G{R}_{\text{m}\text{a}\text{x}}}$$

(27)

While, $\:G{R}_{max}$ denotes the maximum progression resistance of every and $\:G{R}_{i}$ signifies the growth resistance of $\:ith$ person. Usually, a lesser $\:G{R}_{i}$ signifies that a person will obtain and understand expertise more so that his level is more significant. As an outcome, the individual should get a decreased $\:S{F}_{i}$, which is biased near appealing in local exploitation practice. When $\:G{R}_{i}$ is bigger, it suggests that an $\:i$ndividual is inadequate and a person wants to adjacent the knowledge gap. As an outcome, the individual was inclined to implement global exploration patterns and should get a greater $\:S{F}_{i}.$ The person $\:I$ discovered somewhat from the $\:kth$ set of gap $\:G{\overrightarrow{ap}}_{k}$, and this data is a $\:kth$ group of knowledge acquisition $\:K{\overrightarrow{A}}_{k}$. Equation (28) defines the model by which $\:L{F}_{k}$ and $\:S{F}_{i}$ function on the $\:kth$ set gap to attain $\:K{\overrightarrow{A}}_{k}$ for the $\:ith$ individual.

$$\:K{\overrightarrow{A}}_{k}=S{F}_{i}\cdot\:L{F}_{k}\cdot\:G{\overrightarrow{ap}}_{k},\:(k=\text{1,2},\text{3,4})$$

(28)

Here, the knowledge that the $\:ith$ being from the $\:kth$ set of the gap has been discovered is indicated by $\:K{\overrightarrow{A}}_{k},\:L{F}_{k}$ assesses the exterior environment, and $\:S{F}_{i}$ estimates its interior situation. The $\:ith$ person concludes the learning procedure by defining his individual required knowledge $\:(K{\overrightarrow{A}}_{k}$ from $\:G{\overrightarrow{ap}}_{k}$) as an outcome of both evaluations’ effects. The $\:ith$ individual concludes a richer expertise accumulation procedure by recognizing the gaps among distinctive individuals; the $\:ith$ individual’s expert learning method was delivered by Eq. (29).

$$\:{\overrightarrow{x}}_{i}^{It+1}={\overrightarrow{x}}_{i}^{It}+K{\overrightarrow{A}}_{1}+K{\overrightarrow{A}}_{2}+K{\overrightarrow{A}}_{3}+K{\overrightarrow{A}}_{4}$$

(29)

$\:It$ denotes the number of present iterations, and $\:{\overrightarrow{x}}_{i}$ signifies the $\:ith$ individual who learns the expertise obtained throughout the learning stage to develop. By following the adjustment of the learning stage, every individual’s candidate resolution quality might further or retreat. The individual’s $\:G{R}_{i}$ will decline, and its position will grow when the development has been achieved. The $\:ith$ individual has a higher opportunity of dropping part, which have educated when they revert. In this situation, $\:{P}_{2}$ is a rate of control. Equation (30) explains this process.

$$\:{x}_{i}^{\to\:It+1}=\left\{\begin{array}{l}\to\:It+1\:if\:f\left({x}_{i}^{\to\:it+1}\right)<f\left({x}_{i}^{\to\:ii}\right)\\\:\{\to\:It+1\:if\:{r}_{1}<{P}_{2}\\\:\to\:It\end{array}\right.$$

(30)

Here, $\:{P}_{2}$ determines whether the recently learned data is retained when the $\:ith$ individual drops to upgrade, $\:{r}_{1}$ refers to an evenly distributed randomly generated number within the range of [0,1], and $\:ind\:\left(i\right)\:$denotes placing $\:an\:ith$ individual in ascending order. $\:{P}_{2}$ in this situation is 0.001. The complete restricted judgment record for controlling the recently learned data is delivered here due to space restrictions in Eq. (31):

$$\:{r}_{1}<{P}_{2}\:\&\&\:ind\left(i\right)\sim\:=ind$$

(31)

This guarantees that the existent global optimum solution cannot be substituted, which prevents the technique from convergence. When a distinct upgrade fails, the individual contains a 0.001 likelihood of merging the population of the mentioned creation.

Reflection phase

As an outcome, an individual should obtain both reflecting and learning skills. They must acquire knowledge from elevated people regarding their adverse traits while preserving their positive character. Equations (32) and (33) deliver a calculation method of the reflecting method of GO.

$$\:{x}_{i}^{It+1}=i\left\{\begin{array}{l}\left\{\begin{array}{c}lb+{r}_{4}\times\:\left(ub-lb\right)\:if\:{r}_{3}<AF\\\:{x}_{i}^{\text{I}t}+{r}_{5}\times\:\left({R}_{j}-{x}_{i}^{\text{I}t}\right)\:if{r}_{2}<{p}_{3}\end{array}\right.\\\:\{{x}_{i,j}^{\text{I}t}\end{array}\right.$$

(32)

$$\:F=0.01+0.99\times\:\left(1-\frac{FEs}{\:\text{M}\text{a}\text{x}FEs}\right)$$

(33)

Here, $\:{r}_{2},{r}_{3},{r}_{4}$, and $\:{r}_{5}$ are evenly spread random values within the range of [0,1], $\:ub$ and $\:lb$ indicate upper and lower limits, respectively. The reflection is defined by $\:{P}_{3}$, which is fixed at 0.3. The present maximum number of evaluations $\:\left(MaxFEs\right)$ and the number of assessments $\:\left(FEs\right)$ unite to create the attenuation factor $\:\left(AF\right)$. The value of $\:AF$ will gradually converge to 0.01 when the technique goes over. A higher-level individual $\:\left(\overrightarrow{R}\right).\overrightarrow{R}$. will assist$\:\:th$e individual $\:jth$ feature throughout this stage. This represents a higher level of distinction and performs as a model for absorbed learning for the current individual $\:I$. The $\:jth$ feature of $\:{R}_{=}$ is indicated by $\:{R}_{j}$. When $\:the\:jth$ feature of $\:ith$ individual genuinely wants to be realized from others, a higher-level distinct as $\:\overrightarrow{R}$ leads it. Since $\:\overrightarrow{R}$ is indicated as the topmost $\:{P}_{1}+1$ individual among the inhabitants, the similarity is authentic for the learning phase after completing his reflection.

Fitness selection (FS) is a substantial factor in persuading the performance of GO. The hyperparameter range method contains the solution-encoded model to estimate the effectiveness of the candidate solution. The GO reflects accuracy as the general principle for projecting the FF. Its mathematical formulation is expressed below:

$$\:Fitness\:=\:\text{m}\text{a}\text{x}\:\left(P\right)$$

(34)

$$\:P=\frac{TP}{TP+FP}$$

(35)

Here, $\:TP$ denotes the positive value of true, and $\:FP$ indicates the positive value of false.

Experimental analysis

The experimental analysis of the CDMFL-AIDCNN technique is examined under dual datasets such as CIC-IDS-2017²³ and UNSW-NB15²⁴. The CIC-IDS-2017 dataset contains 25,500 counts under 11 traffic types, as exhibited in Table 1.

Table 1 Details of the CIC-IDS-2017 dataset.

Figure 6 presents the classifier results of the CDMFL-AIDCNN approach under the CIC-IDS-2017 dataset. Figure 6a,b demonstrates the confusion matrix with correct recognition and classification of all classes under 70%TRPH and 30%TSPH. Figure 6c shows the PR analysis, representing superior performance across all class labels. At the same time, Fig. 6d exemplifies the ROC analysis, signifying capable results with high ROC values for different classes.

Fig. 6

CIC-IDS-2017 dataset (a,b) confusion matrix, (c) curve of PR, and (d) curve of ROC.

Table 2; Fig. 7. signify the classifier result of the CDMFL-AIDCNN technique under the CIC-IDS-2017 dataset. The outcome implies that the CDMFL-AIDCNN technique correctly recognized the samples. With 70%TRPH, the CDMFL-AIDCNN technique presents an average $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}$, $\:{F}_{measure}$, and $\:{G}_{mean}$ of 99.05%, 94.74%, 94.38%, 94.55%, and 94.55%, respectively. Additionally, with 30%TRPH, the CDMFL-AIDCNN method presents an average $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}$, $\:{F}_{measure}$, and $\:{G}_{mean}$ of 99.07%, 94.75%, 94.56%, 94.65%, and 94.65%, correspondingly.

Table 2 Classifier outcome of CDMFL-AIDCNN method under CIC-IDS-2017 dataset.

Fig. 7

Average of CDMFL-AIDCNN method under CIC-IDS-2017 dataset.

In Fig. 8, the training (TRA) $\:acc{u}_{y}$ and validation (VAL) $\:acc{u}_{y}$ analysis of the CDMFL-AIDCNN methodology under the CIC-IDS-2017 dataset is exemplified. The $\:acc{u}_{y}\:$analysis is calculated within the 0-100 epochs range. The figure highlights that the TRA and VAL $\:acc{u}_{y}$ analysis displays a rising tendency, which informed the capacity of the CDMFL-AIDCNN methodology with superior outcomes over multiple iterations. At the same time, the TRA and VAL $\:acc{u}_{y}$ remainders closer through the epochs, which identifies inferior overfitting and displays the maximal performance of the CDMFL-AIDCNN model, guaranteeing reliable prediction on unseen samples.

Figure 9 demonstrates the TRA loss (TRALOS) and VAL loss (VALLOS) curves of the CDMFL-AIDCNN approach under the CIC-IDS-2017 dataset. The loss values are computed across an interval of 0-100 epochs. It is denoted that the TRALOS and VALLOS values demonstrate a decreasing tendency, informing the ability of the CDMFL-AIDCNN technique to balance a trade-off between generalization and data fitting. The constant reduction in loss values further guarantees the better performance of the CDMFL-AIDCNN technique and tunes the prediction results over time.

Fig. 8

$\:Acc{u}_{y}$ curve of CDMFL-AIDCNN method under CIC-IDS-2017 dataset

Fig. 9

Loss curve of CDMFL-AIDCNN method under CIC-IDS-2017 dataset.

Table 3; Fig. 10 study the comparison analysis of the CDMFL-AIDCNN approach under the CIC-IDS-2017 dataset with the existing models^25,26, and²⁷. The outcomes emphasized that the MLP, BBB-BAE-Homo, MCD-BAE-Hetero-Last, LSTM, 1D-CNN, Deep-GFL, and DBN models have described lower performance. Meanwhile, the ENIDS-IV approach has attained closer outcomes with corresponding $\:pre{c}_{n}$, $\:rec{a}_{l},$ $\:acc{u}_{y},\:{and\:F1}_{score}$ of 93.07%, 92.55%, 98.27%, and 93.11%. Followed by, the CDMFL-AIDCNN method exhibited better performance with higher $\:pre{c}_{n}$, $\:rec{a}_{l},$ $\:acc{u}_{y},\:{and\:F1}_{score}$ of 94.75%, 94.56%, 99.07%, and 94.65%, respectively.

Table 3 Comparative analysis of the CDMFL-AIDCNN method under the CIC-IDS-2017 dataset^25,26, and²⁷.

Fig. 10

Comparative analysis of the CDMFL-AIDCNN method under the CIC-IDS-2017 dataset.

The UNSW-NB15 dataset contains 21,000 counts of nine traffic types, as described in Table 4.

Table 4 Details of the UNSW-NB15 dataset.

Figure 11 signifies the classifier results of the CDMFL-AIDCNN approach under the UNSW-NB15 dataset. Figure 11a and b demonstrates the confusion matrices with accurate recognition and classification of all classes under 70%TRPH and 30%TSPH. Figure 11c displays the PR curve, indicating maximal performance across all class labels. Besides, Fig. 11d illustrates the ROC curve, signifying proficient outcomes with better ROC values for dissimilar classes.

Fig. 11

UNSW-NB15 dataset (a,b) confusion matrix, (c) curve of PR and (d) curve of ROC.

Table 5; Fig. 12. indicate the classifier results of CDMFL-AIDCNN methodology under the UNSW-NB15 dataset. The outcomes imply that the CDMFL-AIDCNN methodology correctly recognized the samples. With 70%TRPH, the CDMFL-AIDCNN methodology presents an average $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}$, $\:{F}_{measure}$ and $\:{G}_{mean}$ of 98.64%, 93.82%, 93.52%, 93.65%, and 93.66%, respectively. In addition, with 30%TSPH, the CDMFL-AIDCNN model presents an average $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}$, $\:{F}_{measure}$ and $\:{G}_{mean}$ of 98.59%, 93.55%, 93.25%, 93.39%, and 93.40%, correspondingly.

Table 5 Classifier outcome of CDMFL-AIDCNN method under UNSW-NB15 dataset.

Fig. 12

Average of CDMFL-AIDCNN method under UNSW-NB15 dataset.

Figure 13 illustrates TRA $\:acc{u}_{y}$ and VAL $\:acc{u}_{y}$ outcomes of the CDMFL-AIDCNN technique under the UNSW-NB15 dataset. The $\:acc{u}_{y}\:$values are computed within the range of 0-100 epochs. The figure highlights that the TRA and VAL $\:acc{u}_{y}$ analysis demonstrated a rising tendency, which informed the capacity of the CDMFL-AIDCNN methodology with better outcomes over several iterations. At the same time, the TRA and VAL $\:acc{u}_{y}$ remain closer over the epochs, which identifies lower overfitting and illustrates maximum outcomes of the CDMFL-AIDCNN methodology, guaranteeing reliable prediction on hidden samples.

In Fig. 14, TRALOS and VALLOS analysis of the CDMFL-AIDCNN technique under the UNSW-NB15 dataset is demonstrated. The loss values are computed over the range of 0-100 epochs. It is denoted that the TRALOS and VALLOS values exemplify a diminishing tendency, informing the ability of the CDMFL-AIDCNN technique to balance a trade-off between data fitting and generalization. The continuous reduction in loss values guarantees the improved outcome of the CDMFL-AIDCNN technique and tunes the prediction results over time.

Fig. 13

$\:Acc{u}_{y}$ curve of CDMFL-AIDCNN method under UNSW-NB15 dataset

Fig. 14

Loss curve of CDMFL-AIDCNN method under UNSW-NB15 dataset.

Table 6; Fig. 15 study the comparison analysis of the CDMFL-AIDCNN methodology under the UNSW-NB15 dataset with the existing approaches. The results highlighted that the DT, RF, DT-XGB, Random Forest-FS, LR, KNN + XGBoost, and SVM models have gained minimal results. Simultaneously, the CDMFL-AIDCNN approach reported maximal performance with maximum $\:pre{c}_{n}$, $\:rec{a}_{l},$ $\:acc{u}_{y},\:{and\:F}_{measure}$ of 93.82%, 93.52%, 98.64%, and 93.65%, respectively. These results highlight the efficiency of the CDMFL-AIDCNN approach in balancing precision, recall, and accuracy, demonstrating its robustness across various evaluation metrics.

Table 6 Comparative analysis of CDMFL-AIDCNN method under the UNSW-NB15 dataset^25,26, and²⁷.

Fig. 15

Comparative analysis of CDMFL-AIDCNN method under UNSW-NB15 dataset.

Conclusion

This manuscript presents a CDMFL-AIDCNN technique. The CDMFL-AIDCNN model presents an improved structure incorporating self-guided FL with attack intelligence to improve defence mechanisms across varied cybersecurity applications in distributed systems. At first, the data preprocessing stage applied Z-score normalization to convert input data into a beneficial format. The DBO technique is employed to identify the most relevant and non-redundant features for the feature selection process. Furthermore, the hybrid of the CBLG-A model is used to classify cyberattack defence mechanisms. Finally, the GO model implements parameter tuning of the CBLG-A approach. The CDMFL-AIDCNN technique is extensively analyzed using the CIC-IDS-2017 and UNSW-NB15 datasets. The comparison analysis of the CDMFL-AIDCNN technique portrayed a superior accuracy value of 99.07% and 98.64% under the CIC-IDS-2017 and UNSW-NB15 datasets. The limitations of the CDMFL-AIDCNN technique comprise its reliance on specific datasets, which may not fully capture the diversity of cyberattack scenarios in real-world environments. While the model depicts promising results, it may encounter threats when exposed to novel or unseen attack types. The computational complexity of the proposed approach could limit its scalability for large-scale systems, specifically in real-time applications. Additionally, the model’s performance may degrade with incomplete or noisy data, which is common in practical cybersecurity situations. Future work could expand the model’s generalizability across diverse attack vectors, enhance its efficiency for real-time use, and integrate continuous learning mechanisms to adapt to emerging threats. Moreover, further research into optimizing the robustness and scalability of the technique will be crucial for practical deployment.