Introduction

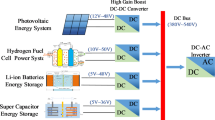
Over the last few decades, the need to utilize renewable energy sources has literally been increasing. Global crises such as air pollution and increase in fossil fuel price have pushed us towards clean and inexpensive form of energy sources such as photovoltaic and fuel cells. Versatility, ease of access, and low-cost maintenance, along with the increasing development of technologies in the renewable energies are among their significant advantages. However, the low magnitude of the voltage value provided by the renewable energy sources is one of their drawbacks. To overcome this issue, the high step-up DC-DC converters are proposed as a solution. In recent decades, diverse structures have been introduced as voltage boost converters for various applications such as DC bus regulation in micro sources1 or as an intermediate interface for feeding micro inverters2. There are various well-known techniques such as switched inductors, switched capacitors, coupled inductors in non-isolated structures3,4 or using isolated transformers in high frequency converters which are used frequently in different applications. Bidirectional structures are another type of DC-DC converters that can transfer energy in both directions and are widely used in electric vehicles and renewable energy systems5. However, there are some advantages and disadvantages to each of these methods. The conventional converters based on switched inductors and switched capacitors have been widely used in many applications to provide high voltage gain6, although in general, the low efficiency of these structures along with high current demand from the source and high fluctuation of the output voltage are considered as serious disadvantages7,8. The boost converters based on cascaded structures can be another choice, however, the need for a large number of components and low efficiency due to voltage drop in semiconductors are among the disadvantages of such structures9,10. In latest few decades, the interleaved configuration has been introduced as another choice for step-up DC-DC structures. Interleaved configuration utilized on some type of converters have good advantages such as low ripple on both input and output ports, leading to lower losses and lower output filter sizes11,12,13. Moreover, voltage stress is significantly reduced on the components in the interleaved converters14. Although, some undesired constraints are included such as power limitation at high voltage gain15,16. Meanwhile, as another drawback of interleaved topologies, the need for additional current control loops to balance the active current literally increase the complexity of control7,17. Furthermore, in recent years, some other type of interleaved structures without using of transformers have been proposed which have the advantage of simple and expandable design18,19,20,21. The Z-source and quasi Z-source converters are proposed in22. The lack of common ground feature along discontinuity in the current of input source are two major drawbacks of Z-source structures. Although, the issue of discontinuous current has been solved in quasi Z-source converter, but it operates under lower voltage gain due to the limitation of duty cycle23. Quadratic boost converters (QBC) are another type of topologies which can operate under continuous input current while also providing low voltage/current stress on the components1,24,25.

The non-isolated converters based on QBC structure are literally cost-saving designed to be more compact and light weight. Moreover, common ground feature is counted as another advantage of QBC structures which are widely used in many applications26,27. In ref24. a high step- up converter integrated of a quadratic boost structure along a voltage doubler is proposed. The voltage doubler cell is implemented with cascading method along a high frequency transformer. However, implementing a large number of components such as power diodes and capacitors in the structure of these converters lead to deterioration of the efficiency. Generally, extra power loss due to transformer is imposed to the converter, moreover, the power density limitation seems as another drawback for this converter.

The combination of QBC structure with switched-capacitor cells are recently become an attractive solution for DC-DC converters. The switched capacitor cells are useful to obtain compact and light-weight converters with high efficiency and high voltage gain in moderate duty cycles. In addition, as another advantage, in the converters consisted of SC cells, the electromagnetic interface (EMI) issues are significantly less18.

In this study, a new optimized non-isolated step-up DC/DC converter which inspired by QBC structure and taking advantage of combination of coupled inductor and voltage multiplier cell is introduced. Ultra-high voltage gain, using lower components, reduced voltage stress on power switches and diodes, soft-switching operation for both power switches along three out of five power diodes and high efficiency performance of the converter are the main features. Moreover, the leakage energy of CI is recovered and perfectly delivered to the output load to optimize the efficiency of the proposed converter performance. The proposed soft switching step-up DC-DC converter is designed for low power range applications and can be applied in small-scale renewable energy systems such as residential solar panels, fuel cells and small off-grid systems. High efficiency and reduced EMI are two major parameters obtained in ZCS performance. In addition, soft switching improves efficiency by reducing heat losses in PV systems. It is possible to re-design the components value in order to be utilized for higher power range of such applications. To assess the performance of the proposed converter, first of all, in Sects. 2 and 3, the proposed converter is analyzed in steady state mode in order to obtain major parameters such as, the voltage gain, the normalized voltage stresses of the components and the averaged and rms current values which are needed to determine the theoretical efficiency. Then, in comparison section, the proposed converter has been compared to some other step-up converters by details. Additionally, to demonstrate the stability and controllability of the proposed converter, the dynamic model analysis based on state space averaged (SSA) method is applied to extract the state equations of the system28,29. Next, to evaluate the reliability of the proposed system, a robust control strategy using pole-placement method is applied and the results are obtained. Eventually, in the experimental section, a prototype of the converter is built and tested in laboratory in order to provide and compare experimental result with theoretical estimations. Finally, in the last section of the study, a brief conclusion is provided.

Proposed converter topology

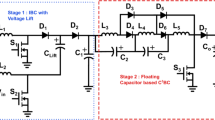
The power circuit of the proposed topology is shown in (Fig. 1). The suggested DC-DC structure is implemented based on a switched capacitor cell (SC), non-isolated CI and a VM cell. The CI implemented in the proposed structure is consisted with the primary turns of NP and secondary turns of NS. The proposed converter is included of two power switches which are placed near the source and on the primary windings side of the CI in order to alleviate the voltage stresses on them. The inductor L1 is embedded between the source and SC cell to collaborate as the first boost stage. Furthermore, the CI, and the second SC cell as the second boost stage, are integrated in suggested topology. The power diode D1 and capacitor C2 are clamped to primary windings side. At the secondary windings side of CI, VM cell is implemented as voltage lift to increase the ultimate higher voltage gain. The power switches S1 and S2 operate synchronously with same duty ratio which results in a simple control unit. At the first step, to avoid complexity of the theoretical analysis, following assumptions can be considered as:

  • All power components used in the converter are totally assumed ideal. So, the efficiency is considered to be 100%.

  • The input voltage is considered as an ideal DC source without fluctuations.

  • All capacitors and inductors are large enough with no fluctuations in the voltage of capacitors and the current inductors.

  • In order to achieve an exact analysis, the CL is modelled and divided into three parts including a magnetizing inductor Lm, a leakage inductor Lk and finally the structure itself as an ideal transformer.

  • Turns ratio of CL is n = NS/NP.

  • The coupling coefficient of the CL is k, which is obtained as: \(k=\frac{{Lm}}{{Lm+Lk}}\)

Fig. 1
figure 1

The schematic of proposed structure.

Full size image

Principle of operation modes

The operation of the suggested structure is applied in one switching period (TS). When the power switches are on-state, DTS is considered first time interval and when are off-state, (1-D)TS is considered second time interval. Figure 2 shows all the equivalent sequences of the proposed topology in CCM (continuous conductance mode) operation.

Mode 1 [\(t_{0} \le t \le t_{1}\)]

In this mode, the power switches S1 and S2 are in ON-state.

All the power diodes are in forward biased except D2 and D3. In the first step, the inductor L1 is charged by the input voltage source. Simultaneously, the magnetizing inductor Lm, the leakage inductor Lk and capacitor C2 are charged. In this interval, the current of both magnetizing inductor and also leakage inductor are linearly increased. Meanwhile, capacitors C3 and C4 are charged by the secondary winding of coupled inductor (NS). During this mode, output load is being supplied by the capacitor CO which has been charged in previous interval. In the beginning of this mode, the power diodes D1, D4 and D5 are turned on with ZCS. Additionally, both switches are turned on under ZCS operation which is considered as soft switching. The following equations using KVL and KCL can be written for this mode as follows:

$${V_{Lm}}=k{V_1}{\text{ (}}k{\text{ is }}coupling{\text{ }}coefficient)$$
(1)
$$- {V_i}+VL1=0 \Rightarrow VL1={V_i}$$
(2)
$$V1 - VC1 - VL1=0$$
(3)
$${V_{C2}} - {V_1}=0{\text{ }} \Rightarrow {V_{C2}}={V_1}$$
(4)
$${V_{NS}}=nk{V_1}$$
(5)
$${V_{C3}}={V_{C4}}=nkV1$$
(6)
$${V_{Co}}={V_O}$$
(7)
$$- {i_{C1}}={i_{in}} - {i_{L1}} \Rightarrow {\text{ }}{i_{C1}}={i_{L1}} - {i_{in}}$$
(8)
$${i_{Lk}}={i_{Lm}}+{i_{N1}}$$
(9)
$${i_{C2}}= - {i_{C1}} - {i_{Lk}}$$
(10)
$${i_{in}}={i_{L1}}+{i_{Lk}}+{i_{C2}}$$
(11)
$${i_{C3}}={i_{C4}}=\frac{{{i_{N2}}}}{2}$$
(12)
$${i_{Co}}= - {I_O}$$
(13)

Mode 2 [\({t_1} \le t \le {t_2}\)]

Due this mode, the power switches S1 and S2 are still in ON-state. The power diodes D1, D2 and D3 are all in reversed biased while the other remained diodes, D4 and D5 are in forward biased. The capacitor C1 discharges and releases its energy through S1 into input source. The capacitor C2 is open-circuited due to turned-off diodes D1 and D3. The capacitors C3 and C4 are charged by the secondary winding of coupled inductor. During this mode, output load is still being supplied by capacitor CO. The following equations can be written for this mode as:

$$- {V_i}+VL1=0 \Rightarrow VL1={V_i}$$
(14)
$$VLK+VLm - VC1 - VL1=0$$
(15)
$${V_{C3}}={V_{NS}}=nkV1$$
(16)
$${V_{C4}}={V_{NS}}=nkV1$$
(17)
$${V_{Co}}={V_O}$$
(18)
$$- {i_{C1}}={i_{in}} - {i_{L1}} \Rightarrow {\text{ }}{i_{C1}}= - {i_{in}}+{i_{L1}}$$
(19)
$${i_{Lk}}={i_{Lm}}+{i_{Np}}$$
(20)
$${i_{in}}={i_{L1}}+{i_{Lk}}$$
(21)
$${i_{C3}}={i_{C4}}=\frac{{{i_{NS}}}}{2}$$
(22)
$${i_{Co}}= - {I_O}$$
(23)

Mode 3 [\({t_2} \le t \le {t_3}\)]

In this short interval, all the conditions are same as previous mode 2 except diodes D4 and D5 which are turned off under ZCS condition. Two power switches S1 and S2 are still in ON-state. Similarly to mode 2, the above equations are valid for this interval.

Mode 4 [\({t_3} \le t \le {t_4}\)]

In this mode, both S1 and S2 are turned OFF. All power diodes are in reverse biased condition except Diodes D2 and D3 which are in forward biased mode. The magnetizing inductor Lm and the leakage inductor Lk and all the capacitors C2, C3 and C4 are being discharged into the output load RL. Consequently, during this mode, the load is directly being supplied by the input source. At the end of this interval, due to the beginning of mode 1, the power diodes D1, D4 and D5 will be turned on with ZCS. The following equations can be written:

$$- {V_i}+VL1+VC1=0 \Rightarrow VL1={V_i} - VC1$$
(24)
$$VLK+VLm=V1$$
(25)
$$- {V_i}+{V_1} - {V_{C2}} - {V_{C3}}+nk{V_1} - {V_{C4}}+{V_O}=0$$
(26)
$${V_{Co}}={V_O}$$
(27)
$${V_{NS}}=nk{V_1}$$
(28)
$${i_{Lk}}= - {i_{C2}}= - {i_{C3}}= - {i_{C4}}={i_{Co}}+{I_O}$$
(29)
$${i_{in}}={i_{L1}}+{i_{Lk}}$$
(30)
$${i_{C1}}={i_{L1}}$$
(31)
$${i_{C1}}={i_{in}} - ({i_{Co}}+{I_O})$$
(32)
Fig. 2
figure 2

The equivalent circuit of the proposed converter at CCM operation, (a) mode 1, (b) mode 2, (c) mode 3, (d) mode 4.

Full size image

Steady state analysis

By assuming that converter has reached its steady state, the volt second balance law for inductors can be used as follows:

$${\left\langle {{V_{L1}}} \right\rangle _{{T_S}}}=0$$
(33)
$${\left\langle {{V_{Lm}}} \right\rangle _{{T_S}}}={\left\langle {{V_{NP}}} \right\rangle _{{T_S}}}=0$$
(34)
$${\left\langle {{V_{NS}}} \right\rangle _{{T_S}}}=n{\left\langle {{V_{Lm}}} \right\rangle _{{T_S}}}=0$$
(35)

Substituting Eqs. (1)–(32) into Eqs. (33)–(35) the voltages of the capacitors in terms of duty cycle are calculated as follows:

$${V_{C1}}=\frac{1}{{1 - D}}{V_i}$$
(36)
$${V_{C2}}=\frac{{2 - D}}{{1 - D}}{V_i}$$
(37)
$${V_{C3}}={V_{C4}}=\frac{{nk(2 - D)}}{{1 - D}}{V_i}$$
(38)

Based on Eqs. (36)–(38), the voltage gain of the proposed converter in CCM operation can be expressed by:

$$M=\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}}{{{{(1 - D)}^2}}}$$
(39)

By assumption the CL is ideal, the coupling coefficient can be considered as (k=1). Therefore, the ideal voltage gain relation of the proposed converter in can be expressed as follows:

$$M=\frac{{{V_{out}}}}{{{V_{in}}}}=\frac{{{D^2}\left( {n+1} \right) - D\left( {4n+3} \right)+4n+3}}{{{{(1 - D)}^2}}}$$
(40)

Figure 3 illustrates the main waveforms of the proposed topology in one switching period.

Fig. 3
figure 3

The main waveforms of the proposed converter in CCM operation.

Full size image

Calculation the voltage/current stress across the power switch, the efficiency of proposed converter and capacitor/inductor design

The voltage stress across semiconductors

The voltage stress across the semiconductors can be obtained using the equivalent circuits when they are switched off or blocked. Hence, using the Eqs. (36)–(38), the voltage stress across the diodes can be expressed as below:

$${V_{D1}}=\frac{{D(2k - kD+D - 3)+2}}{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}} \times {V_o}$$
(41)
$${V_{D2}}={V_{C1}}=\frac{{(1 - D)}}{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}} \times {V_o}$$
(42)
$${V_{D3}}=\left( {1 - \frac{{nk(2 - D)}}{{M(1 - D)}} - \frac{1}{M}} \right) \times {V_o}$$
(43)
$${V_{D4}}={V_{D5}}=\frac{1}{M}\left( {\frac{{nk(2 - D)}}{{(1 - D)}} - \frac{{nkD(D - 2)}}{{{{(1 - D)}^2}}}} \right) \times {V_o}$$
(44)

Also, the per-unit (normalized) voltage stresses on power switches are calculates as follow:

$$\frac{{{V_{S1}}}}{{{V_o}}}=\frac{{(1 - D)}}{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}}$$
(45)
$$\frac{{{V_{S2}}}}{{{V_o}}}=\frac{{{{(1 - D)}^2} - kD(D - 2)}}{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}}$$
(46)

The current calculation and current stress across semiconductors

According to the capacitor charge balance (CCB) law, the average of a capacitor current in one switching period is zero.

Assuming the ideal condition due to zero power loss, the current gain relation can be obtained from Eqs. (39), (40). Considering CCB law, following averaged currents are obtained:

$${I_{Np}}=n{I_{Ns}}=n{I_o}$$
(47)
$${P_{in}}={P_{out}}{\text{ }} \Rightarrow {\text{ }}\frac{{{I_i}}}{{{I_o}}}=\frac{{{V_{out}}}}{{{V_{in}}}}=M{\text{ }} \Rightarrow {\text{ }}{I_i}=M{I_o}$$
(48)
$${I_{L1,avg}}=D \times \left( {\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}}{{{{(1 - D)}^2}}}} \right){I_{out}}$$
(49)
$${I_{Lm,avg}}=\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 5n - 4} \right)+3n+2}}{{(1 - D)}}{I_o}$$
(50)
$${I_{S1}}=\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+(4n+3)}}{{{{(1 - D)}^2}}}{I_o}$$
(51)
$${I_{S2}}=\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 4} \right)+4n+2}}{{(1 - D)}}{I_o}$$
(52)

Additionally, to calculate rms (root mean squared) currents of the both power switches over a conduction period, considering the averaged values in one period, the following equations are valid:

$$rms=\sqrt {\frac{1}{{{T_S}}}\int\limits_{0}^{{Ts}} {{{\left[ {{I_S}(t)} \right]}^2}dt} } =\sqrt {\frac{1}{{{T_S}}}\int\limits_{0}^{{DTs}} {{{\left[ {{I_{S,avg}}} \right]}^2}dt} }$$
(53)
$${I_{S1,rms}}=\sqrt D {\text{ }}M{I_{out}}$$
(54)
$${I_{S2,rms}}=\sqrt D {\text{ }}M{I_{out}}(1 - D){\text{ }}$$
(55)

To estimate the rms current value of the inductor L1 and and the magnetizing inductor Lm, the peak currents of both inductors are calculated by considering the half of the current ripple over a period which can be expressed as below:

$${I_{L1}}^{{peak}}={I_{L1,avg}} \pm \frac{{{V_{in}}D}}{{2{L_1}{f_S}}}$$
(56)
$${I_{Lm}}^{{peak}}={I_{Lm,avg}} \pm \frac{{{V_{Lm}}D}}{{2{L_m}{f_S}}}$$
(57)

Considering the triangle waveform of the inductors current over one period according Fig. 3, from Eqs. (49), (50) and (56), (57), the rms current values can be calculated as follows:

$${I_{L1,rms}}=\sqrt {{{\left( {D \times \left( {\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+4n+3}}{{{{(1 - D)}^2}}}} \right){I_{out}}} \right)}^2}+{{\left( {\frac{{{V_{in}}D}}{{2\sqrt 3 {L_1}{f_S}}}} \right)}^2}}$$
(58)
$${I_{Lm,rms}}=\sqrt {{{\left( {\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 5n - 4} \right)+3n+2}}{{(1 - D)}}{I_o}} \right)}^2}+{{\left( {\frac{{{V_{Lm}}D}}{{2\sqrt 3 {L_m}{f_S}}}} \right)}^2}}$$
(59)

Calculation the efficiency of proposed converter

The following parameters are considered to calculate the efficiency (\({\eta _{Converter}}\)) of the proposed converter:

  • rD: the internal resistors of diodes.

  • rS: the internal resistors of switches.

  • rLm: the internal resistors of inductors.

  • VFD: the forward drop voltage of diodes.

  • VFS: the forward drop voltage of switches.

The overall efficiency is defined as follow:

$${\eta _{Converter}}=\frac{{{P_o}}}{{{P_o}+{P_{losses}}}}$$
(60)

According to refs.5,8, to accurately determine the total power loss, the losses of switches and diodes (which are calculated by sum of switching and conduction loss) can be obtained as follow:

$${P_{S,Tot}}={P_{Cond,{S_1}}}+{P_{SW,{S_1}}}+{P_{Cond,{S_2}}}+{P_{SW,{S_2}}}$$
(61)
$$\begin{gathered} {P_{D,Tot}}={P_{Cond,{D_1}}}+{P_{Cond,{D_2}}}+{P_{Cond,{D_3}}}+{P_{Cond,{D_4}}}+{P_{Cond,{D_5}}} \hfill \\ {\text{ }}+{P_{SW,{D_1}}}+{P_{SW,{D_2}}}+{P_{SW,{D_3}}}+{P_{SW,{D_4}}}+{P_{SW,{D_5}}} \hfill \\ \end{gathered}$$
(62)

To calculate the conduction losses, the rms current values are expected as determined from (54–55)&(58–59). Assuming the turn ratio of CI as (n = 1.5), the conduction and switching losses of the power switches are calculated as following, respectively:

$$\begin{gathered} {P_{Cond,{S_1}}}=\frac{1}{{{T_s}}}\int\limits_{0}^{{D{T_s}}} {\left( {{V_{F{S_1}}}{I_{{S_1}}}} \right)dt+{r_{{S_1}}}I_{{{S_1},rms}}^{2}} = \hfill \\ D \times \left[ {0.6 \times \frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 6n - 5} \right)+(4n+3)}}{{{{(1 - D)}^2}}}{I_o}} \right]+\left[ {{r_{{S_1}}} \times {{\left( {\sqrt D {\text{ }}M{I_{out}}} \right)}^2}} \right]= \hfill \\ {P_{Cond,{S_1}}}=2.335{\text{W}} \hfill \\ \end{gathered}$$
(63)
$${P_{Cond,{S_2}}}=1.247\;W$$
(64)
$${P_{SW,{S_1}}}=\frac{1}{2}\left( {\frac{1}{{{T_s}}}\int\limits_{0}^{{{t_{on}}}} {({V_{{S_1}}}{I_{S1 - (ON)}})dt+} \frac{1}{{{T_s}}}\int\limits_{0}^{{{t_{off}}}} {({V_{{S_1}}}{I_{S1 - (ON)}})dt={f_s}{V_{{S_1}}}{I_{S1 - (ON)}}} ({t_{on}}+{t_{off}})} \right)=0.825{\text{ }}W$$
(65)
$${P_{SW,{S_2}}}=0.821{\text{ }}W$$
(66)

The conduction losses of power diodes are calculated as:

$${P_{Cond,{D_1}}}=\frac{1}{{{T_s}}}\int\limits_{0}^{{(23/50)D{T_s}}} {{V_{F{D_1}}}{I_{{D_1},avg}}+{r_{{D_1}}}I_{{{D_1},rms}}^{2}} dt=0.323{\text{ }}W$$
(67)
$${P_{Cond,{D_2}}}=1.469{\text{ }}W$$
(68)
$${P_{Cond,{D_3}}}=0.318{\text{ }}W$$
(69)
$${P_{Cond,{D_4}}}=0.319{\text{ }}W$$
(70)
$${P_{Cond,{D_5}}}=0.319{\text{ }}W$$
(71)

The conduction loss of the both L1 and Lm using Eqs. (58), (59) is obtained as:

$${P_{Cond,L1}}={r_{L1}}{\left( {{I_{L1,rms}}} \right)^2}=0.438{\text{ }}W$$
(72)
$${P_{Cond,Lm}}={r_{Lm}}{\left( {{I_{Lm,rms}}} \right)^2}=0.494{\text{ }}W$$
(73)

The core power loss formula related to inductor L1 and CI is obtained as:

$${P_C}=kf_{s}^{\alpha }B_{m}^{\beta }$$
(74)

The power loss (PC) is determined in SI unit as W/kg. α, β and k are called Steinmetz parameters which usually provided by manufacturers for different core materials. Typical values of α can vary from 1 to 2 for ferrite materials (1 ≤ α ≤ 2). According to, Faraday’s Law, which is as follows:

$${V_L}=N\frac{{d\varphi (t)}}{{dt}}=N{A_c}\frac{{dB(t)}}{{dt}}$$
(75)

The Ac parameter is the core area which has been presented by manufactures for different types of magnetic cores. N is the number of windings turn of inductor. Therefore, the peak flux density of ΔB for coupled inductor is expressed as:

$$\Delta B=\frac{1}{{N{A_c}}}\int\limits_{0}^{{D{T_s}}} {{V_{core}}dt=} \frac{{{V_{core}}D{T_s}}}{{{N_p}{A_c}}}=\frac{{{V_{core}}D}}{{{N_p}{A_c}{f_s}}}$$
(76)

The core loss formula related to the inductor is equal to PCore=PCM, where M is mass of the core. By considering Bm = ΔB/2, the core loss of coupled inductor is calculated as:

$${P_{Core}}=kf_{s}^{\alpha }{\left( {\frac{{{V_{core}}D}}{{2{N_p}{A_c}{f_s}}}} \right)^\beta }M$$
(77)

Now, the core power losses can be simplified as follows:

\({P_{Core\_total}}={P_{Core\_CI}}+{P_{Core\_L1}}=kf_{s}^{\alpha }B_{m}^{\beta }M\)

$$=kf_{s}^{\alpha }M\left\{ {{{\left( {\frac{{{V_{Lm}}D}}{{2{N_p}{A_c}{f_s}}}} \right)}^\beta }} \right\}+kf_{s}^{\alpha }M\left\{ {{{\left( {\frac{{{V_{L1}}D}}{{2{N_p}{A_c}{f_s}}}} \right)}^\beta }} \right\}=0.461+0.025=0.486{\text{ }}W$$
(78)

Finally, the total power loss PLoss is calculated as:

$${P_{Losses}}={P_{S,Tot}}+{P_{D,Tot}}+{P_{Cond,Lm}}+{P_{Cond,L1}}+{P_{Core\_total}}=9.4{\text{ }}W$$
(79)

The overall efficiency of the suggested converter is intended as follows:

$${\eta _{Converter}}=\frac{{{P_o}}}{{{P_o}+{P_{losses}}}} \times 100\% =\frac{{162}}{{162+9.4}} \times 100\% =94.51\%$$
(80)

According to (79–80), the graphs of the theoretical efficiency versus duty cycle and output power are depicted in (Figs. 4 and 5), respectively.

As shown in (Fig. 4), the efficiency of the proposed converter is plotted for both (n = 1.5) and (n = 2) turn ratios versus output power, simultaneously. The maximum efficiency is achieved for 150 W output power, furthermore, the proposed converter is obtained nearly more than 94% of efficiency for rated output power of 400 W. Figure 5 represents the efficiency of the proposed converter for a constant load (R = 800 ohm) versus the wide change of duty cycles. As it illustrated in (Fig. 5), in the range of duty cycles from 0.25 to 0.65, the proposed converter is managed to operate 92 and 91% for n = 1.5 and n = 2, respectively. To observe the contribution of each element, the distribution of power losses is depicted in (Fig. 6). As shown, the contribution of power switches in total loss is the highest compared to the others, followed by the conduction loss of the power diodes. It is necessary to be mentioned that the power loss of switching devices is calculated without considering soft-switching performance in the proposed converter. Therefore, in the condition of considering the ZCS performance, the losses of the switches and the diodes are obviously reduced.

Fig. 4
figure 4

Curve of the theoretical efficiency vs. (W).

Full size image
Fig. 5
figure 5

Curve of the theoretical efficiency vs. (D).

Full size image
Fig. 6
figure 6

Power loss distribution.

Full size image

Desired values of passive components

Capacitors design

The value of the capacitors mainly depends on the switching frequency, duty cycle, output current and permitted voltage ripple (\({x_C}\)). Hence, for proper design, the desired values of capacitors are calculated according to Eqs. (36)–(38) as follows:

$${x_C}\left( \% \right)=\frac{{\Delta V}}{{{V_C}}} \times 100$$
(81)
$${C_1} \ge \frac{{{I_o}MD{{(D - 1)}^2}}}{{{f_s} \times {V_i} \times {x_C}\% }}$$
(82)
$${C_2} \ge \frac{{(1 - D){I_o}}}{{{d_1} \times {f_s}(2 - D){V_i} \times {x_C}\% }}$$
(83)
$${C_3}={C_4} \ge \frac{{(1 - D){I_o}}}{{{f_s}(2 - D)nk{V_{in}} \times {x_C}\% }}$$
(84)

Inductor design

To determine the suitable value for L1 in terms of inductor’s desirable current ripple (\({x_L}\)), following calculation is obtained:

$${x_L}\left( \% \right)=\frac{{\Delta I}}{{{I_L}}} \times 100$$
(85)
$${L_1} \ge \frac{{{R_L}}}{{{f_s} \times {M^2} \times {x_L}_{\% }}}$$
(86)

Calculation of CI specifications

The design procedure of the utilized CI is similar to the inductor design. Therefore, in order to obtain the minimum value of the magnetizing inductor in terms of desirable current ripple (\({x_{Lm}}\)) and by using (50), following calculation is expressed:

$${x_{Lm}}\left( \% \right)=\frac{{\Delta I}}{{{I_{Lm}}}} \times 100$$
(86-1)
$${L_m} \ge \frac{{KD(2 - D) \times {R_L}}}{{{f_s} \times M \times \left( {{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 5n - 4} \right)+3n+2} \right) \times {x_L}_{\% }}}$$
(86-2)

As represented in Table 2, the obtained value of leakage inductor Lk is 3µH. The value of magnetizing inductor using coupling coefficient of CI is calculated as follows:

$${L_m}=\frac{{k \times {L_k}}}{{1 - k}}=\frac{{3k \times {{10}^{ - 6}}}}{{1 - k}}$$
(87)

The type of magnetic core used for the CI is E55/28/25. Hence, based on the dimensions presented in the core datasheet, the core air gap of the coupled inductor can be calculated as:

$$\begin{gathered} {l_g}=\frac{{{L_m}{I_{Lm}}^{2}{\mu _0}}}{{{B_m}^{2}{A_{Air{\text{ Gap}}}}}}= \hfill \\ \frac{{\frac{{3k \times {{10}^{ - 6}}}}{{1 - k}} \times {{(\frac{{{D^2}\left[ {2n+2 - k(n+1)} \right]+D\left( {2k+2nk - 5n - 4} \right)+3n+2}}{{(1 - D)}}{I_o})}^2} \times 4\pi \times {{10}^{ - 7}}}}{{{{0.1}^2} \times [(17.2+18.7) \times 25 \times {{10}^{ - 6}}]}} \hfill \\ \end{gathered}$$
(88)

As a result, the number of primary windings turns of the CI can be obtained by using the following equation:

$${N_p} \ge \sqrt {{L_m} \times \frac{{{l_g}}}{{{\mu _0}A_{{Air{\text{ Gap}}}}^{{Equivalent}}}}}$$
(89)

The turn’s ratio of the CI is assumed as n = Ns/Np. Likewise, the number of secondary windings turns of the CI can be calculated in terms of its turn ratio:

$${N_s}=n \times {N_p}=\frac{3}{2} \times {N_p}$$
(90)

Review of stability and controller design

Dynamic model using the SSA method

To discuss reliability of the proposed converter, the major issue is the stability of the converter. A proper solution to model the system and achieve a suitable control method is the goal of this section. In Ref29, the decoupling method is suggested for a MIMO DC-DC converter which appears a suit solution. However, as applied in28, the pole-placement method for SISO (single-input single-output) systems due to flexibility and precise control is an appropriate solution. Hence, for the proposed converter the pole-placement method is applied. In single-input single-output converters, to provide an accurate output load power, it is necessary to have a suitable dynamic model of the system in order to design and implement an optimum control strategy. For this purpose, to form the dynamic equation systems, following assumptions are considered. All the power switches, the inductors, and the capacitors are assumed to be ideal. To provide more accuracy, for both leakage and magnetizing inductors, the parasitic series resistors rL1 and rLm are considered. Moreover, parasitic series resistors of capacitors (ESR) are implemented as rC. The effect of parallel capacitors with switching elements are neglected due to their very small values. Then, the average model and the small-signal model can be obtained by using the SSA method28. In this method, the system equations are achieved in all operating states, and averaged during one commutation period by taking into account the time interval of each state. The SSA equations of the proposed converter are obtained as follows:

$$\frac{{d{I_{L1}}}}{{dt}}=\frac{{ - {r_{L1}}+{r_{C1}}(D - 1)}}{{{L_1}}}{I_{L1}}+\frac{{(D - 1)}}{{{L_1}}}{V_{C1}}+\frac{1}{{{L_1}}}{V_{in}}$$
(91)
$$\left\{ \begin{gathered} \frac{{dI_{{Lm}} }}{{dt}} = \frac{{DKr_{C} }}{{L_{m} }}I_{{L1}} + D\,\left[ {\frac{{ - Kr_{{Lm}} }}{{L_{m} }}\, - \frac{K}{{L_{m} (nK + 1)}} \times \frac{{( - r_{{Lm}} (n + 1) - 3r_{C} )}}{{n + 1}}} \right] + \frac{K}{{L_{m} (nK + 1)}} \times \frac{{( - r_{{Lm}} (n + 1) - 3r_{C} )}}{{n + 1}}I_{{Lm}} \hfill \\ + \frac{{KD}}{{L_{m} }}V_{{C1}} + \left( {\frac{{ - KD}}{{L_{m} (nK + 1)}} + \frac{K}{{L_{m} (nK + 1)}}} \right)V_{{C2}} + \left( {\frac{{ - KD}}{{L_{m} (nK + 1)}} + \frac{K}{{L_{m} (nK + 1)}}} \right)V_{{C3}} + \left( {\frac{{ - KD}}{{L_{m} (nK + 1)}} + \frac{K}{{L_{m} (nK + 1)}}} \right)V_{{C4}} \hfill \\ + \left( {D\left[ {\frac{{ - KMr_{C} }}{{L_{m} R_{{Load}} }} + \frac{K}{{L_{m} (nK + 1)}}} \right] - \frac{K}{{L_{m} (nK + 1)}}} \right)V_{{Cout}} + \frac{{nK^{2} D + K}}{{L_{m} (nK + 1)}}V_{{in}} \hfill \\ \end{gathered} \right.$$
(92)
$$\begin{aligned} \frac{{dV_{{C1}} }}{{dt}} = & \left( {D\left[ {\frac{{ - {\text{0}}{\text{.46}}}}{{2C_{1} }} + \frac{{{\text{0}}{\text{.54}}}}{{C_{1} }} + \frac{1}{{C_{1} (n + 1)}}} \right] - \frac{1}{{C_{1} (n + 1)}}} \right)I_{{Lm}} - \frac{{{\text{0}}{\text{.46D}}}}{{2r_{C} C_{1} }}V_{{C1}} + D\left[ {{\text{0}}{\text{.46}}\left( {\frac{{1 - 2n^{2} K}}{{2r_{C} C_{1} }}} \right) + {\text{0}}{\text{.54}}\frac{{ - 2n^{2} K}}{{r_{C} C_{1} }}} \right]V_{{C2}} \\ & + \left[ {\frac{{{\text{0}}{\text{.46}}nD}}{{2r_{C} C_{1} }} + \frac{{{\text{0}}{\text{.54}}nD}}{{r_{C} C_{1} }}} \right](V_{{C3}} + V_{{C4}} ) + \frac{{M(1 - D)}}{{C_{1} R_{{Load}} }}V_{{Cout}} - \frac{{{\text{0}}{\text{.46D}}}}{{r_{C} C_{1} }}V_{{in}} \\ \end{aligned}$$
(93)
$$\begin{aligned} \frac{{dV_{{C2}} }}{{dt}} & = \left( {D\left[ {\frac{{ - {\text{0}}{\text{.46}}}}{{2C_{2} }} + \frac{1}{{C_{2} (n + 1)}}} \right] - \frac{1}{{C_{2} (n + 1)}}} \right)I_{{Lm}} + \frac{{{\text{0}}{\text{.46D}}}}{{2r_{C} C_{2} }}V_{{C1}} + \frac{{{\text{0}}{\text{.46D}}( - 1 - 2n^{2} K)}}{{2r_{C} C_{2} }}V_{{C2}} \\ & + \frac{{{\text{0}}{\text{.46}}nD}}{{2C_{2} r_{C} }}\left( {V_{{C3}} + V_{{C4}} } \right) + \frac{{M(D - 1)}}{{C_{2} R_{{Load}} }}V_{{Cout}} + \frac{{{\text{0}}{\text{.46D}}}}{{2C_{2} r_{C} }}V_{{in}} \\ \end{aligned}$$
(94)
$$\frac{{d{V_{C3}}}}{{dt}}=\frac{{D - 1}}{{{C_3}(n+1)}}{I_{Lm}}+\frac{{nDk}}{{{r_C}{C_3}}}{V_{C2}} - \frac{D}{{{r_C}{C_3}}}{V_{C3}}+\frac{{M(D - 1)}}{{{C_3}{R_{Load}}}}{V_{Cout}}$$
(95)
$$\frac{{d{V_{C4}}}}{{dt}}=\frac{{D - 1}}{{{C_4}(n+1)}}{I_{Lm}}+\frac{{nDk}}{{{r_C}{C_4}}}{V_{C2}} - \frac{D}{{{r_C}{C_4}}}{V_{C4}}+\frac{{M(D - 1)}}{{{C_4}{R_{Load}}}}{V_{Cout}}$$
(96)
$$\frac{{d{V_{Cout}}}}{{dt}}=\frac{{1 - D}}{{{C_{out}}(n+1)}}{I_{Lm}} - \frac{D}{{{C_{out}}{R_{Load}}}}{V_{Cout}}$$
(97)

The SSA method is considered to provide the small signal model which is required to design a closed loop controller for the proposed topology. Therefore, the state variables and the control inputs which are consisted of two fixed parts (\(\bar {X},\bar {D}\)) and small variables of the states (\(\tilde {x},\tilde {d}\)) parts, are described as:

$$\left\{ \begin{gathered} X=\bar {X}+\tilde {x} \hfill \\ D=\bar {D}+\tilde {d} \hfill \\ \end{gathered} \right.$$
(98)

Afterward, by implementing the SSA model and neglecting the second order values, the small signal model is obtained as:

$$\left\{ \begin{gathered} \dot {\tilde {x}}=A\tilde {x}+B\tilde {u} \hfill \\ y=C\tilde {x}+D\tilde {u} \hfill \\ \end{gathered} \right.$$
(99)

The variable states (\(\tilde {x}\)), control input (\(\tilde {u}\)), and the output signals (y) are determined as below:

$${\tilde {x}^T}=\left[ {\begin{array}{*{20}{c}} {{{\tilde {i}}_{L1}}}&{{{\tilde {i}}_{Lm}}}&{{{\tilde {v}}_{C1}}}&{{{\tilde {v}}_{C2}}}&{{{\tilde {v}}_{C3,4}}}&{{{\tilde {v}}_{Cout}}} \end{array}} \right]$$
(100)
$$\tilde {u}=\left[ {\tilde {d}} \right]$$
(101)
$${y^T}=\left[ {\begin{array}{*{20}{c}} {{I_{L1}}}&{{I_{Lm}}}&0&0&0&{{V_{Cout}}} \end{array}} \right]$$
(102)

The pole-placement method implementation

It is important to clarify that both C3 and C4 capacitors which embedded in VM cell, form a capacitor loop due to the same values and the schematic of the proposed converter where depicted in (Fig. 2). Consequently, as calculated in (95) and (96), the state equations of both C3 and C4 are equal which leads to the reduction of one state. According to pole-placement method, poles of a closed-loop system can be located at any desired location, provided that the mentioned system has been assumed completely state-controllable. The controllability matrix of the suggested converter can be written in the following form:

$${\Phi _C}=\left[ {B \vdots AB \vdots {A^2}B \vdots \cdots \vdots {A^{n - 1}}B} \right]$$
(103)

For this system, if rank(\({\Phi _C}\)) = n = 6 (rank of \({\Phi _C}\)equals to number of variable states (\(\tilde {x}\))), the system would be completely state-controllable. Next, two further integral states are obtained as follows:

$$\left\{ \begin{gathered} {{\dot {q}}_1}(t)={r_1}(t) - {y_1}(t)={r_1}(t) - {{\tilde {i}}_{L1}}(t) \hfill \\ {{\dot {q}}_2}(t)={r_2}(t) - {y_2}(t)={r_2}(t) - {{\tilde {i}}_{Lm}}(t) \hfill \\ {{\dot {q}}_3}(t)={r_3}(t) - {y_3}(t)={r_3}(t) - {{\tilde {v}}_{Cout}}(t) \hfill \\ \end{gathered} \right.$$
(104)

The Eq. (104) can be re-written as follows:

$$\left\{ \begin{gathered} {{\dot {q}}_1}(t)={I_{L1,ref}} - {I_{L1}}(t) \hfill \\ {{\dot {q}}_2}(t)={I_{Lm,ref}} - {I_{Lm}}(t) \hfill \\ {{\dot {q}}_3}(t)={V_{Cout,ref}} - {V_{Cout}}(t) \hfill \\ \end{gathered} \right.$$
(105)

Subsequently, the new integral states, the state and output equations can be expressed as:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {\dot{\tilde{x}}(t)} \\ \cdots \\ {\dot{q}(t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} A & \vdots & 0 \\ \cdots & \vdots & \cdots \\ { - C} & \vdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} B \\ \cdots \\ 0 \\ \end{array} } \right]\tilde{u}(t) + \left[ {\begin{array}{*{20}c} 0 \\ \cdots \\ I \\ \end{array} } \right]r(t) \hfill \\ y(t) = \left[ {\begin{array}{*{20}c} C & \vdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(106)

In (106), r(t) is the input reference vector which is determined as:

$$r(t)={\left[ {\begin{array}{*{20}{c}} {{I_{L1,ref}}}&{{I_{Lm,ref}}}&{{V_{C1,ref}}}&{{V_{C2,ref}}}&{{V_{C3,4,ref}}} \end{array}{\text{ }}{V_{Co,ref}}} \right]^T}$$
(107)

Considering (106), the new matrices \(\bar {A}\) and \(\bar {B}\) are defined as:

$$\bar{A} = \left[ {\begin{array}{*{20}c} A & \vdots & 0 \\ \cdots & \vdots & \cdots \\ { - C} & \vdots & 0 \\ \end{array} } \right],\bar{B} = \left[ {\begin{array}{*{20}c} B \\ \cdots \\ 0 \\ \end{array} } \right]$$
(108)

The controllability matrix for the system (\({\bar {\Phi }_C}\)) in (106) can be arranged as:

$${\bar {\Phi }_C}=\left[ {\begin{array}{*{20}{c}} B& \vdots &{A{\Phi _C}} \\ \cdots & \vdots & \cdots \\ 0& \vdots &{ - C{\Phi _C}} \end{array}} \right]=\underbrace {{\left[ {\begin{array}{*{20}{c}} B& \vdots &A \\ \cdots & \vdots & \cdots \\ 0& \vdots &{ - C} \end{array}} \right]}}_{M}\left[ {\begin{array}{*{20}{c}} I& \vdots &0 \\ \cdots & \vdots & \cdots \\ 0& \vdots &{{\Phi _C}} \end{array}} \right]$$
(109)

Considering \({\Phi _C}\) is complete-rank, the system defined in (106) would be completely state-controllable under the condition that the rank of the matrix M is n + m (n and m are the number of the variable states (\(\tilde {x}\)) and output signals (y), respectively. Using the code in MATLAB to place the eigenvalues by entering the matrices and determining the location of the eigenvalues of the closed loop as follows:

$$\begin{gathered} {\text{K}}=\left[ {{{\text{K}}_{\text{x}}},{\text{ }}{{\text{K}}_{\text{q}}}} \right]\,=\,{\text{place }}\left( {\hat {A}^{\prime},\hat {B}^{\prime},\hat {\lambda }} \right) \hfill \\ {\text{K}}=\left[ {{{\text{K}}_{\text{x}}},{\text{ }}{{\text{K}}_{\text{q}}}} \right]\,=\,{\text{place }}\left( {{{\hat {A}}^{}}} \right) \hfill \\ \end{gathered}$$
(110)
Fig. 7
figure 7

Bode diagram and closed loop control of the proposed converter, (a) Bode diagrams for the transfer functions of the inductor currents, (b) Closed-loop control of the suggested topology.

Full size image

Consequently, the control coefficients matrices Kx and Kq can be obtained. It should be mentioned that since the type of the designed control system is one (due to presence of an integrator), it tracks the input references\({I_{L1,ref}}\)and \({I_{Lm,ref}}\) without steady-state error by the poles which have been assigned by the matrices Kx and Kq at the desired places. Therefore, there is a matrix K which satisfies the following equation:

$$\tilde{u}(t) = - K\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {K_{x} } & \vdots & {K_{q} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right]$$
(111)

Substituting (111) in (106) the following equation can be written as:

$$\left[ {\begin{array}{*{20}c} {\dot{\tilde{x}}(t)} \\ \cdots \\ {\dot{q}(t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A - BK_{x} } & \vdots & { - BK_{q} } \\ \cdots & \vdots & \cdots \\ { - C} & \vdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ \cdots \\ I \\ \end{array} } \right]r(t){\text{ , }}y(t) = \left[ {\begin{array}{*{20}c} C & \vdots & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} \\ \cdots \\ {q(t)} \\ \end{array} } \right]$$
(112)

Eventually, the point is to find the control signal \(\tilde {u}(t)\)using state feedback gain matrix K, so that the closed-loop system eigenvalues are placed at the desired locations. There are some practical methods to establish the system controller matrix K=[Kx, Kq]. The control systems toolbox of the MATLAB software provides a useful pole-placement function, which inputs the system (106) and the desired eigenvalues locations to find the state feedback gain matrices. Ultimately, using the trial & error method, the desired values for gain margin and phase margin (GM ≥ 10 and 60 ≤ PM ≤ 80) are ascertained and determined. The result is depicted in (Fig. 7a), which represents the bode diagram of the control system. As shown in Fig. 7a, the value of gain margin for the magnetizing inductor Lm is limitless (inf) and greater than 10, also, the phase margin (closed loop) path is 70 (deg) which is greater than 60. Therefore, both values are within the allowed range.

The block diagram of the closed-loop control is depicted in Fig. 7b which has been implemented for the proposed converter.

Comparison study

In this section, to discuss the advantages and disadvantages of the proposed converter, it is compared to some other similar structures presented in1,2,3,4,6,7,8,10,15,16,18,20,30. All the converters are consisted of at least one coupled inductor and also the selected topologies are similar to the proposed converter. Table 1 covers the detailed information of all selected converters including the number of components, voltage gain versus duty cycle, normalized voltage stress of switches, maximum voltage stress of diodes, maximum efficiency and input current ripple respectively. The comparison results are shown in Fig. 8 in terms of all structures features.

In order to obtain a strict result of the comparison, turns ratio of the implemented CI in the proposed structure is considered once as (n = 2) and again as (n = 1.5) while all other structures are kept with a constant turns ratio of (n = 2). This would be a fair comparison to evaluate the proposed converter capability under a same condition and also with less turn ratio of the CI compared to the others.

1) As depicted in Fig. 8a, the voltage gain of the proposed converter with (n = 2) is explicitly higher than all other structures. Although, the voltage gain obtained by1,7 is obviously higher for the range D ≥ 0.5 and D ≥ 0.7, respectively. However, due to higher values of duty cycles, the conduction losses are increased extremely which leads to lower efficiency. Considering (n = 1.5) for the proposed converter as shown in Fig. 8a simultaneously, it still provides a reasonable higher voltage gain compared to the other structures listed in (Table 1). In this case, for D ≤ 0.7, the voltage gain obtained by the proposed converter is higher than converters presented in refs2,3,6,7,10,15,18,20,30. In the range of D ≥ 0.7, only two converters presented in7,20 acquire higher voltage gain with a slight difference. The converter presented in4 achieves a better performance of voltage gain due to duty cycles higher than 50%. However, its optimal operating point to obtain the maximum efficiency is calculated under D = 0.43 condition which clearly acquires literally same result of voltage gain compared to the proposed structure. In total, the suggested topology exhibits a robust performance even due to wide changes of duty cycle rate specifically at lower duty cycles rate which provides less conduction loss in order to obtain better performance and maximum efficiency.

Fig. 8
figure 8

Comparison between the proposed converter and other structures. (a) Voltage gain versus duty-cycle, (b) Normalized voltage stress across power switches versus duty-cycle, (c) Normalized voltage stress across power diodes versus duty-cycle.

Full size image

As represented in Table 1; Fig. 8, the proposed converter provides following advantages:

2) As shown in Fig. 8b, the normalized voltage stress curves of the power switches versus duty cycle are presented. The voltage stress of power switches in refs2,6,15,30. is obviously severe compared to other topologies which is considered as a major drawback. As an advantage, the voltage stress across the switch (S1) of the proposed converter along the converters presented in4,8,16,18 obtain the lowest values. Additionally, in the previously mentioned converters, the changes in the voltage stress rate are relatively constant in term of the duty cycle increment, however, for the switch (S1) of the proposed converter, the slope of the stress curve is reduced due to higher values of duty cycles that is considered as another advantage. In the range of (D ≥ 0.5), the switch (S1) obtains the lowest voltage stress compared to all other converters. As illustrated in Fig. 8b, in the range of (D ≤ 0.55), the voltage stress of (S2) in the proposed converter compared to1,2,3,6,7,10,15,30 acquires the lowest values. Although, considering to the range (D ≥ 0.7), the voltage stress of power switch (S2) increases slightly which leads to pass7,10,20.

3) In Fig. 8c, the normalized voltage stress of power diodes is plotted. Refs3,8,16,18. obtain the lowest values. The maximum voltage stress of diodes in the load side of the proposed converter is applied to power diodes (D4 & D5). In comparison with1,2,4,6,7,10,15,20,30, the proposed converter obtains the lowest values as an advantage. Moreover, the constant slope of the voltage stress for the proposed converter is considered as another advantage due to higher duty ratios. The voltage stress of power diodes of converters presented in2,15,30 obtain the highest values compared to others which is considered as a drawback. Finally, the approximate stability of voltage stress values for power diodes in a wide range of different duty cycles is another advantage for the suggested converter.

Another comparison is illustrated in Fig. 9, which represents the normalized RMS current flowing through the switching devices at a given voltage gain of the proposed converter. The converters in10,15,20 are selected to be compared due to their topology similarity. The converter in20 has the most similar structure along the equal number of components to the proposed converter compared to10,15. Regarding to Fig. 9, in the entire range of voltage gain, the switch S1 of20 tolerates the highest current stress compared to other converters.

Additionally, the current stress for power switches S2 from20 and S1 from proposed converter has lower values and almost similar to each other. The current stress value for S1 of the proposed converter ranks third after15,20 in the voltage range lower than 20, meanwhile for gain values greater than 20, switch S1 of the proposed converter retains the second place after20. However, by inspecting Fig. 8a, the proposed converter has the greater voltage gain value in the whole range of duty cycles compared to15,20 which considered as an advantage. The both power switches used in the converter10 are obtained the lowest current stress compared to all others. Nevertheless, by inspecting Fig. 8a, the proposed converter along the converters in15,20 are obtained higher gain values compared to10, prospectively. As it shown in Fig. 9, the rms current across all power diodes of the proposed converter are plotted. In comparison with all power diodes implemented in the proposed converter, D2 reaches slightly higher values compared to the rest. The power diode D1 used in10 has the lowest value along D1, D3, D4 and D5 of the proposed converter which all are nearly equal. However, power diode D1 used in15 has reached the highest current stress compared to all other structures as a major disadvantage.

The input current ripple comparison is presented in the last column on the (Table 1). As it shown, regarding to the simulator results and also as illustrated in the experimental section Fig. 11j, the input current ripple of the proposed converter is obtained in medium range compared with other structures in this section. The observed input current ripple range for Refs1,3,4,6,7,8,10,15,16. are considered as low ripple while high ripple range is obtained for refs.20,30.

Table 1 Comparison between the proposed converter and other topologies.
Full size table
Fig. 9
figure 9

Comparison between the normalized rms currents of switching elements versus the voltage gain.

Full size image

Experimental results

To investigate the functionality of the proposed topology and evaluate its actual performance, a prototype is built and tested in laboratory. The prototype is tested with input voltage of 20 V under rated power of 150 W. All the characteristics of the prototype converter are given in Table 2 including the selected type of the MOSFET switches, the power diodes, the capacitors and designed values for the inductor and turn ratio of the CI. As depicted in (Fig. 10k), the output voltage is measured about 345 V.

Table 2 Characteristics of the power components.
Full size table

Considering the actual losses, the obtained voltage value is almost close to the theoretical analysis based on Eq. (39), which is calculated by substituting the parameters determined in Table 2 and estimated output voltage of 358 V. The voltage value of the capacitor C1 is about 36 V as illustrated in (Fig. 10b). The Fig. 10c shows the voltage of capacitor C2 which is about 53 V. As shown in Fig. 10d, the voltage values of the both capacitors C3 and C4 are measured 78 V which are identical due to the loop law for capacitors. The observed all values are nearly close to the calculated equations from (36) to (38). By replacing the parameters from Table 2, the estimated voltages are 36.3, 56.36 and 84 V respectively.

As depicted in (Fig. 11a, d), the power diodes D1 and D4 are turned on under ZCS condition, the power diode D4 is turned off under pseudo ZCS condition, furthermore, the power diode D5 is turned off under ZCS condition. The soft-switching capability is in compliance with (Fig. 3). Additionally, as shown in (Fig. 11a–f), the voltage stresses of the diodes D1, D2, D3, D4 and D5 are measured 99, 34.3, 245, 140 and 140 V, respectively. The measured voltages are almost in accordance with Eqs. (41–44), which utilizing the parameters given in Table 2, the estimated values for D1, D2, D3, D4 and D5 are 102.2, 36.36, 256, 150.8 and 150.8 respectively. As illustrated in (Fig. 11f, g) the voltage stress of S1 and S2 is measured 35 V and 64 V, correspondingly. The observed values are almost match with Eqs. (45), (46) where using the parameters presented in Table 2, the theoretical values for S1 and S2 are estimated to be 36.36 V and 65.84 V, respectively. Furthermore, the current/voltage waveforms of the power switches are illustrated in (Fig. 11f, g) where both S1 and S2 are turned on under ZCS condition. The soft-switching performance of S1 and S2 are in accordance with (Fig. 3). In Fig. 11h, i, the current waveforms of the leakage inductor Lk and inductor L1 are shown. As shown in Fig. 11i, considering ripple current of the inductor L1 which is less than 20%, the designed value of 300 µH for L1 seems appropriate. Additionally, as depicted in (Fig. 11j), the continuous waveform of the input current is clearly observed which proves the theoretical analysis. The output voltage/current waveforms are shown in (Fig. 11k). As illustrated, the prototype operates under 150 W full load in steady state where output current and voltage results are obtained. By inspecting Fig. 11k, the obtained output voltage is estimated 345 V which represents actual value for voltage gain about 17.25 under 0.45 of duty cycle. The dynamic response of a DC-DC converter is a predominant factor to determine the stability and reliability of its performance. As shown in Fig. 12, the dynamic response of the proposed converter during a sudden change in load is illustrated. In Fig. 12a, the output power immediately drops from 246.24 to 136.8 W, which means a 55% reduction in power load. Next, as shown in Fig. 10b, the output power is increased 55% again. In both cases, the output voltage change is very small in the manner that capable to be stabilized in fewer than 300 milliseconds which means a robust performance of the proposed converter.

The acquired experimental efficiency under the rated power of 150 W is obtained 93%. In the comparison of theoretical approximation which is calculated 94.51% based on Eq. (80), represents a reasonable performance of the proposed converter.

Eventually, by investigating the entire experimental results, the theoretical analysis of the proposed converter has a good accordance with actual lab results.

Fig. 10
figure 10

The voltage waveforms of the capacitors, (a) C1, (b) C2, (c) C3, (d) C4.

Full size image
Fig. 11
figure 11

The experimental waveforms of the inductors current, semiconductors, input current, output voltage/current, (a) VD1, iD1 (b) VD2, iD2 (c) VD3, iD3 (d) VD4, iD5 (e) VD5,, iD5 (f) iS1, VS1, (g) iS2, VS2, (h) iLk, (i) iL1, (j) iin, (k) iout ,Vout.

Full size image
Fig. 12
figure 12

The dynamic response of the proposed converter, (a) with 55% increasing changes in the load, (b) with 55% decreasing change in the load.

Full size image

Conclusions

An ultra-high step-up DC/DC converter inspired from QBC topology consisted of a non-isolated coupled inductor alongside a voltage multiplier cell is suggested. The proposed structure is equipped with three main boost stages which utilized with two simultaneous power switches to achieve high voltage gain with simple control capability. An input inductor is embedded in the primary winding side of CI along with two other boost stage cells, afterward the third boost stage as VM cell is placed in the secondary winding side to deliver ultimate volage gain into the output port. The design of the proposed converter successfully reduces voltage stress on power MOSFETs and diodes along with soft-switching performance for enhanced efficiency. The presence of common ground and continuous input current features make the converter particularly suitable for renewable energy systems. High voltage gain, low rms current stress on switching devices, moderated number of components and low-cost solution are among the advantages of the proposed converter. The overall efficiency of the proposed converter is estimated about 94.51% for high power level. Furthermore, dynamic modeling and implementation of pole-placement method has been carried out to investigate the robust performance of the proposed converter. Eventually, the proposed structure is built and tested in the laboratory to evaluate the theoretical analysis of the proposed converter. All the experimental results are compared and interpreted to confirm the proper performance of the proposed structure.