Combined contour error control method for five-axis machine tools based on digital twin

Abstract

Contour error is a critical factor influencing machining quality. This paper proposes a combined contour error control method for five-axis machine tools based on digital twin. The proposed method combines pre-compensation implemented in digital twin with feedback control in the real-time controller. After obtaining the tool path input, the digital twin performs interpolation and applies model predictive pre-compensation control to the interpolated commands to control modeled errors. The pre-compensated commands and interpolation data are sent to the real-time controller where contour error is estimated and controlled in each control cycle through feedback control to control unmodeled errors. Using the S-shaped curve as the test case, the maximum tool tip position contour error is reduced by 77.78%, with an average reduction of 83.90%. The maximum tool orientation contour error decreased by 79.05%, with an average reduction of 86.66%. The experimental results demonstrate that the proposed method significantly reduces tool contour error.

Introduction

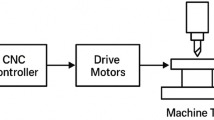
Five-axis machine tools are widely used for machining complex parts. The limited dynamic bandwidth of servo axes leads to tracking errors during motion. These tracking errors are kinematically transferred to the tool of five-axis machine tools and result in tool deviations from the intended tool path. These deviations are defined as contour error.

Improving the bandwidth of each axis can reduce contour error indirectly but cannot address the dynamic performance mismatches between axes. Therefore, direct control of contour error is currently the focus of research, which can be divided into two directions: contour error estimation (CEE) and contour error control (CEC).

For CEE, since real-time controllers operate in discrete systems, discrete interpolation points are typically used to approximate the ideal curve for contour error estimation. Yang et al.¹ proposed a fast iterative method that approximates the ideal contour as a straight line. Yang et al.² used three interpolation points to fit an intended arc for calculating the contour error. Chen et al.³ conducted a comparative analysis of the computational efficiency of various approximation methods, including straight lines, arcs, and their linear combinations. Pi et al.⁴ used Ferguson curves to refit the interpolation points. Liu et al.⁵ proposed a CEE method based on Taylor series expansion and the Frenet-Serret frame to consider the effects of curvature and torsion. Yang et al.⁶ identified high-curvature regions and modified the contour error vector to avoid abrupt changes. Wang et al.⁷ proposed an iterative method with Aitken acceleration. Li et al.⁸ employed a moving window method to compare reference positions and search for the optimal solution. Ghaffari et al.⁹ proposed a dynamic CEE algorithm based on the Newton update algorithm.

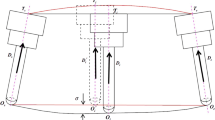
For CEC, typical control methods include feedback control, pre-compensation control, and predictive control¹⁰. Control structures of these three methods are illustrated in Fig. 1.

Fig. 1

Three contour error control methods: (a) feedback control; (b) pre-compensation control; (c) predictive control.

Feedback control calculates the current contour error in each control cycle, decomposes the contour error into each axis, and compensates it by adjusting the control inputs of each axis in the next cycle. Lu et al.¹¹ designed a single-neuron adaptive cross-coupled controller, which dynamically adjusts its weights through a single-neuron learning algorithm to enhance control precision. Zhao et al.¹² proposed a controller that integrates feedforward, feedback, and cross-coupled control. Feedback control is simple to implement and can handle the effects of unknown disturbances. However, feedback control always lags the contour error. To address these limitations, researchers have investigated pre-compensation control. Pre-compensation control optimizes control commands in advance through simulation or modeling, enabling compensation before contour errors occur. Pre-compensation control does not rely on the real-time state of the system, so it can be completed in offline conditions. Xu et al.¹³ proposed a 1DCNN-BiLSTM-Attention model to predict and compensate contour errors. Wang et al.¹⁴ proposed an iterative pre-compensation method based on a predictive model. Xiao et al.¹⁵ proposed a model predictive contour error pre-compensation method. Wang et al.¹⁶ analyzed the composition of contour errors in three-axis machine tools and designed a pre-compensation controller. Pi et al.¹⁷ further considered the influence of cutting force disturbances. Lyu et al.¹⁸ and Duong et al.¹⁹ achieved pre-compensation by offline adjustment of servo control gains. Although pre-compensation method can control contour error in advance, its effectiveness depends on the model accuracy which is not easy to fulfill. Recently, predictive control methods such as MPC^20,21,22 and generalized predictive control (GPC)^5,23 have been applied to contour error control. Based on the current state of the machine tool, predictive control solves multi-objective optimization problems by predicting future states over multiple steps, thereby obtaining the optimal control commands for the current cycle. Compared with pre-compensation control, predictive control compensates based on the system’s current actual state, so it can compensate for errors caused by unmodeled disturbances. Compared with feedback control, predictive control compensates through multi-step prediction and rolling optimization, so the compensation does not lag the occurrence of errors. However, predictive control involves numerous matrix calculations, which result in a significant computational load on the real-time controller. The application of MPC and GPC in contour error control is mainly focused on two-axis or three-axis platforms. Therefore, it is necessary to consider combining those methods to fully leverage the advantages of each.

As a digital mirror of the real world, digital twin technology has obtained significant attention in recent years²⁴. Many scholars have explored the application of digital twin in CNC machine tools for commissioning^25,26, virtual machining^27,28, optimization^29,30,31,32 and monitoring^33,34. However, in the above research, digital twin primarily optimizes the machining process by adjusting feedrate override and few studies have explored combining digital twins with real-time controllers for contour error control. Digital twin can synchronously update with physical machine tools^35,36 and handle greater computational loads through cloud computing service³⁷, which meets the requirements of model precision and computation capability of MPC. Therefore, developing a combined contour error control method based on the digital twin effectively meets the requirements for both control accuracy and computational load.

This paper presents a combined contour error control method based on the digital twin. After obtaining the tool path input, the digital twin performs interpolation and applies model predictive pre-compensation control (MPCC) to the interpolated commands to control modeled errors. The pre-compensated commands and interpolation data are sent to the real-time controller which estimates and controls contour error in each control cycle by feedback control to control unmodeled errors.

The remaining sections of this paper are organized as follows: “Principle of proposed method” introduces the principle of the proposed method. Section “Digital twin for contour error control” describes the software architecture of the digital twin, as well as the servo dynamic model and the machine kinematics model. Section “Combined contour error control method” presents the offline model predictive pre-compensation control and the online feedback control method. Finally, “Experiment” demonstrates the experimental results and discusses their implications.

Principle of proposed method

The combined contour error control method for five-axis machine tools based on digital twin is shown in Fig. 2. The contour error control is divided into two steps: offline pre-compensation implemented in the digital twin and online control executed in the real-time controller.

The NURBS toolpath and processing information generated by CAM are input into the digital twin. The NURBS direct interpolator of the digital twin processes the tool path to generate interpolation commands. Subsequently, the simulation module, which includes the machine tool kinematics model and servo dynamics model, executes simulations of the interpolation commands. Meanwhile, the pre-compensation module simultaneously compensates for the interpolation commands and ultimately generates the pre-compensated commands. Then the interpolation commands, the pre-compensated commands, and other required data are sent to the real-time controller via the Beckhoff Automation Device Specification (ADS) protocol.

In the real-time controller, the online controller estimates the contour error in each control cycle and generates compensation commands. The resulting commands are then transmitted via the industrial ethernet to the servo drives. The real-time data (axis position, axis velocity, axis current, etc.) sampled at each interpolation cycle is also transmitted to the digital twin adapter via EtherCAT and formatted into structured data. Then the formatted data is sent to the database as machining history data for storage via ethernet. The machine status data is transmitted to the digital twin monitoring module via ADS every 100 ms. The digital twin periodically reads machining historical data from the database, analyzes machining performance and updates simulation model parameters through parameter identification module. If the machining quality still fails to meet requirements, the feedrate and toolpath can be further optimized using methods from the reference^30,38,39,40 to enhance the accuracy of subsequent machining processes.

Fig. 2

Schematic diagram of combined contour error method for five-axis machine tools based on digital twin.

Digital twin for contour error control

Architecture of the digital twin

The functional architecture of the digital twin developed in this paper is shown in Fig. 3. The software was developed using C + + on the Visual Studio 2019 platform, with the visualization interface implemented using Qt 5.

Fig. 3

Architecture of the digital twin.

Servo dynamic model

Currently, the servo feed axis commonly employs proportional-proportional-integral (PPI) control. The control model of servo axis is illustrated in Fig. 4.

Fig. 4

Servo dynamic model.

Where $\:{K}_{\text{p}}$ is the proportional gain coefficient of the position loop. $\:{K}_{\text{v}}$ is the proportional gain coefficient of the velocity loop. $\:{K}_{\text{i}\text{v}}$ is the integral gain coefficient of the velocity loop. $\:{K}_{\text{t}}\:$is the torque constant of motor. $\:{J}_{\text{m}}$ is the equivalent mass. $\:{C}_{m}$ is the equivalent damping coefficient and $\:{r}_{\text{g}}$ is the transmission coefficient. $\:{T}_{\text{l}\text{o}\text{a}\text{d}}$ is the external load torque including Coulomb friction $\:{f}_{\text{c}}$. $\:{p}_{\text{c}\text{m}\text{d}}$ is the command input position, $\:{p}_{\text{a}\text{c}\text{t}}$ is the actual response position, $\:{\omega\:}_{\text{a}\text{c}\text{t}}$ is the actual angular velocity, $\:{o}_{\text{a}\text{c}\text{t}}$ is the output of the velocity loop integrator. Let the state vector be $\:\varvec{x}={\left[\begin{array}{ccc}{p}_{\text{a}\text{c}\text{t}}&\:{\omega\:}_{\text{a}\text{c}\text{t}}&\:{o}_{\text{a}\text{c}\text{t}}\end{array}\right]}^{\text{T}}$, output vector be $\:\varvec{y}=\left[{p}_{\text{a}\text{c}\text{t}}\right]$, input vector be $\:\varvec{u}=\left[{p}_{\text{c}\text{m}\text{d}}\right]$ and disturbance vector be $\:\varvec{d}=\left[{T}_{\text{l}\text{o}\text{a}\text{d}}\right]$, the above system can be described as Eq. (1).

$$\:\begin{array}{c}\left\{\begin{array}{c}\dot{\varvec{x}}={\varvec{A}}_{\text{c}}x+{\varvec{B}}_{\text{c}}u+{\varvec{F}}_{\text{c}}d\\\:y=Cx\end{array}\right.\end{array}$$

(1)

where

$$\:{\varvec{A}}_{\text{c}}=\left[\begin{array}{ccc}0&\:{r}_{\text{g}}&\:0\\\:-\frac{{K}_{\text{p}}{K}_{\text{v}}{K}_{\text{t}}}{{J}_{\text{m}}}&\:-\frac{{K}_{\text{v}}{K}_{\text{t}}+{C}_{\text{m}}}{{J}_{\text{m}}}&\:\frac{{K}_{\text{t}}}{{J}_{\text{m}}}\\\:-{K}_{\text{p}}{K}_{\text{i}\text{v}}&\:-{K}_{\text{i}\text{v}}&\:0\end{array}\right],{\varvec{B}}_{\text{c}}=\left[\begin{array}{c}0\\\:\frac{{K}_{\text{p}}{K}_{\text{v}}{K}_{\text{t}}}{{J}_{\text{m}}}\\\:{K}_{\text{p}}{K}_{\text{i}\text{v}}\end{array}\right],\varvec{C}=\left[\begin{array}{ccc}1&\:0&\:0\end{array}\right],{\varvec{F}}_{\text{c}}=\left[\begin{array}{c}0\\\:-\frac{1}{{J}_{\text{m}}}\\\:0\end{array}\right]$$

Assuming that $\:\varvec{u}$ and $\:\varvec{d}$ remain constant in an interpolation cycle, the system described by Eq. (1) can be discretized using a zero-order hold (ZOH). The resulting discrete system can be expressed as Eq. (2):

$$\:\begin{array}{c}\left\{\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right)+Fd\left(k\right)\\\:y\left(k\right)=Cx\left(k\right)\end{array}\right.\end{array}$$

(2)

where

$$\:\varvec{A}={\text{e}}^{{\varvec{A}}_{\text{c}q}{T}_{s}},\varvec{B}=\left({\int\:}_{0}^{{T}_{s}}{\text{e}}^{{\varvec{A}}_{\text{c}}t}\text{d}t\right){\varvec{B}}_{\text{c}},\varvec{F}=\left({\int\:}_{0}^{{T}_{s}}{\text{e}}^{{\varvec{A}}_{\text{c}}t}\text{d}t\right){\varvec{F}}_{\text{c}}$$

The position loop proportional gain coefficient, velocity loop proportional gain coefficient, velocity loop integral gain coefficient, and torque constant in the above model can typically be obtained directly from the servo driver. Parameters such as mass, viscous friction, and Coulomb friction can be identified using the methods described in references^4,41.

Machine tool kinematic model

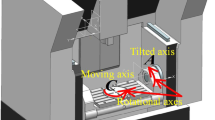
As illustrated in Fig. 5, this paper uses an AC head-type CNC machine tool as an example. The forward and inverse kinematics transformations are established using the method described in reference⁴².

Fig. 5

AC head-type motion platform.

Let the tool tip coordinates be denoted as $\:{\left[{p}_{\text{t}x},{p}_{\text{t}y},{p}_{\text{t}z}\right]}^{\text{T}}$, the tool orientation vector as $\:{\left[{O}_{\text{t}i},{O}_{\text{t}j},{O}_{\text{t}k}\right]}^{\text{T}}$. and servo axis coordinates as $\:{\left[{p}_{\text{m}x},{p}_{\text{m}y},{p}_{\text{m}z},{p}_{\text{m}a},{p}_{\text{m}c}\right]}^{\text{T}}$ The forward kinematics transformation is expressed in Eq. (3).

$$\:\begin{array}{c}\left\{\begin{array}{c}{p}_{\text{t}x}={p}_{\text{m}x}-{x}_{0}+Lsin{p}_{\text{m}a}sin{p}_{\text{m}c}\\\:{p}_{\text{t}y}={p}_{\text{m}y}-{y}_{0}-Lsin{p}_{\text{m}a}cos{p}_{\text{m}c}\\\:{p}_{\text{t}z}={p}_{\text{m}z}-{z}_{0}+Lcos{p}_{\text{m}a}\\\:{O}_{\text{t}i}=-sin\left({p}_{\text{m}a}-{a}_{0}\right)sin\left({p}_{\text{m}c}-{c}_{0}\right)\\\:{O}_{\text{t}j}=sin\left({p}_{\text{m}a}-{a}_{0}\right)cos\left({p}_{\text{m}c}-{c}_{0}\right)\\\:{O}_{\text{t}k}=-cos\left({p}_{\text{m}a}-{a}_{0}\right)\end{array}\right.\end{array}$$

(3)

where $\:{x}_{0},{y}_{0},{z}_{0},{a}_{0},{c}_{0}$ are the zero offsets from the workpiece coordinate system (WCS) to the machine coordinate system (MCS).$\:L$ is the tool length and in this paper $\:L=75\:\text{m}\text{m}$.

From Eq. (3), the inverse kinematics equations can be obtained as Eq. (4).

$$\:\begin{array}{c}\left\{\begin{array}{c}{p}_{\text{m}a}=arccos\left(-{O}_{\text{t}k}\right)\\\:{p}_{\text{m}c}=arctan\left(-\frac{{O}_{\text{t}i}}{{O}_{\text{t}j}}\right)\\\:{p}_{\text{m}x}={p}_{\text{t}x}+{x}_{0}-Lsin{p}_{\text{m}a}sin{p}_{\text{m}c}\\\:{p}_{\text{m}y}={p}_{\text{t}y}+{y}_{0}+Lsin{p}_{\text{m}a}cos{p}_{\text{m}c}\\\:{p}_{\text{m}z}={p}_{\text{t}z}+{z}_{0}-Lcos{p}_{\text{m}a}\end{array}\right.\end{array}$$

(4)

Combined contour error control method

Definition of contour error

As shown in Fig. 6, $\:\varvec{C}\left(u\right)$ is the ideal tool tip position path, and $\:{\varvec{P}}_{\text{r}\text{t}},{\varvec{O}}_{\text{r}\text{t}}$ are the ideal interpolation tool tip position (TTP) and tool orientation (TORI) vectors. $\:{\varvec{P}}_{\text{a}\text{t}}\left(k\right),{\varvec{O}}_{\text{a}\text{t}}\left(k\right)$ represent the actual TTP and TORI at the k-th cycle. The five-axis contour error encompasses both TTP error and TORI error. In current research, contour error is often defined as the shortest distance or normal distance from the actual position to the ideal trajectory. The point on the ideal trajectory closest to the actual position is identified as the foot point $\:{\varvec{P}}_{\text{f}}$, with the corresponding tool orientation being $\:{\varvec{O}}_{\text{f}}$. Considering computational stability and efficiency, this paper employs the iterative method proposed in reference¹ to find $\:{\varvec{P}}_{\text{f}}$.

Fig. 6

Schematic diagram of contour error.

Since the interpolation cycle is typically very short, the command trajectory between two adjacent interpolation points can be approximated as a straight line. At this time, $\:{\varvec{P}}_{\text{f}}$ lies on the line $\:\overrightarrow{{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right){\varvec{P}}_{\text{r}\text{t}}\left(i\right)}$ formed by the two adjacent interpolation points $\:{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right),{\varvec{P}}_{\text{r}\text{t}}\left(i\right)$, and can be expressed as

$$\:\begin{array}{c}{\varvec{P}}_{\text{f}}={\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)-{h}_{i}\left({\varvec{P}}_{\text{r}\text{t}}\left(i\right)-{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)\right)\end{array}$$

(5)

where

$$\:{h}_{i}=\frac{\overrightarrow{{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right){\varvec{P}}_{\text{f}}}}{\overrightarrow{{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right){\varvec{P}}_{\text{r}\text{t}}\left(i\right)}}$$

From the geometric relationship, it is known that $\:\overrightarrow{{\varvec{P}}_{\text{a}\text{t}}\left(k\right){\varvec{P}}_{\text{f}}}\perp\:\overrightarrow{{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right){\varvec{P}}_{\text{r}\text{t}}\left(i\right)}$, i.e., $\:{\left(\overrightarrow{{\varvec{P}}_{\text{a}\text{t}}\left(k\right){\varvec{P}}_{\text{f}}}\right)}^{\text{T}}\cdot\:\left(\overrightarrow{{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right){\varvec{P}}_{\text{r}\text{t}}\left(i\right)}\right)=0$. Substituting into Eq. (5), we have

$$\:\begin{array}{c}{h}_{i}=-\frac{{\left({\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)-{\varvec{P}}_{\text{a}\text{t}}\left(k\right)\right)}^{\text{T}}\left({\varvec{P}}_{\text{r}\text{t}}\left(i\right)-{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)\right)}{{\left({\varvec{P}}_{\text{r}\text{t}}\left(i\right)-{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)\right)}^{\text{T}}\left({\varvec{P}}_{\text{r}\text{t}}\left(i\right)-{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)\right)}\end{array}$$

(6)

During the search process, the value of $\:{h}_{i}$ can be categorized into five cases, as illustrated in Fig. 7. When $\:0\le\:{h}_{i}\le\:1$, it indicates that $\:{\varvec{P}}_{\text{f}}$ lies between $\:{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right),{\varvec{P}}_{\text{r}\text{t}}\left(i\right)$. If $\:{h}_{i}<0$ occurs, the search is restarted forward to determine whether $\:{\varvec{P}}_{\text{f}}$ is located between $\:{\varvec{P}}_{\text{r}\text{t}}\left(i-2\right),{\varvec{P}}_{\text{r}\text{t}}\left(i-1\right)$, and this iteration continues until the situations shown in Fig. 7(a) or (d) are satisfied. Conversely, if $\:{h}_{i}>1$, the search proceeds backward until the conditions shown in Fig. 7(a) or (e) are satisfied. The process can start from the current cycle command point and the previous cycle command point, $\:{\varvec{P}}_{\text{r}\text{t}}\left(k\right)$ and $\:{\varvec{P}}_{\text{r}\text{t}}\left(k-1\right)$.

After identifying the interval where $\:{\varvec{P}}_{\text{f}}$ lies, the value of $\:{\varvec{P}}_{\text{f}}$ can be determined by Eq. (5). The tool orientation vector $\:{\varvec{O}}_{\text{f}}$ corresponding to $\:{\varvec{P}}_{\text{f}}$ can be obtained through spherical linear interpolation of the tool orientation at the two interpolation points in the interval, as shown in Eq. (7)

$$\:\begin{array}{c}{\varvec{O}}_{\text{f}}=\frac{\text{s}\text{i}\text{n}\left(\left(1-{h}_{i}\right)\theta\:\right)}{\text{s}\text{i}\text{n}\theta\:}{\varvec{O}}_{\text{r}\text{t}}\left(i-1\right)+\frac{\text{s}\text{i}\text{n}\left({h}_{i}\theta\:\right)}{\text{s}\text{i}\text{n}\theta\:}{\varvec{O}}_{\text{r}\text{t}}\left(i\right)\end{array}$$

(7)

where $\:\theta\:$ is the angle between $\:{\varvec{O}}_{\text{r}\text{t}}\left(i-1\right)$ and $\:{\varvec{O}}_{\text{r}\text{t}}\left(i\right)$.

After obtaining $\:{\varvec{P}}_{\text{f}}$ and $\:{\varvec{O}}_{\text{f}}$, the TTP contour error and TORI contour error can be calculated by Eq. (8)

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varepsilon\:}_{\text{p}}=\|{\varvec{P}}_{\text{a}\text{t}}-{\varvec{P}}_{\text{f}}\|\\{\varepsilon\:}_{\text{o}}=arccos\frac{{\varvec{O}}_{\text{f}}\cdot\:{\varvec{O}}_{\text{a}\text{t}}}{\|{\varvec{O}}_{\text{f}}\|\cdot\:\|{\varvec{O}}_{\text{a}\text{t}}\|}\end{array}\right.\end{array}$$

(8)

Fig. 7

Different situations when searching for the foot point.

Contour error model predictive pre-compensation control

The principle of model predictive pre-compensation control is shown in Fig. 8. In the digital twin, the predictive controller reads the interpolation commands from the interpolator, optimizes axis commands via predictive control and then outputs the pre-compensated commands for the real-time controller.

Fig. 8

Principle of model predictive pre-compensation control.

As analyzed in the previous section, the tool contour error is not equivalent to the tool tracking error. It depends not only on the command point but also on the characteristics of the nearby curve. And calculating the contour error often requires information from several adjacent command points and iterative computations, making it impossible to express it as a linear combination of the position of each axis. However, since the tool command posture must lie on the ideal contour, the tracking error of the current point $\:{\varvec{P}}_{\text{a}\text{t}}\left(k\right)$ relative to its corresponding command point $\:{\varvec{P}}_{\text{r}\text{t}}\left(k\right)\:$serves as the upper bound of its contour error. Therefore, reducing the tool tracking error remains beneficial for minimizing the tool contour error. Additionally, the tool tracking error can be conveniently linearized to facilitate pre-compensation control.

Assuming that the disturbance changes slowly compared to the sampling control cycle, the incremental form can be used to eliminate its influence. Define $\:\varDelta\:{\varvec{u}}_{q}\left(k\right)={\varvec{u}}_{q}\left(k\right)-{\varvec{u}}_{q}\left(k-1\right),\varDelta\:{\varvec{x}}_{q}\left(k\right)=\:{\varvec{x}}_{q}\left(k\right)-{\varvec{x}}_{q}\left(k-1\right),\:\:\varDelta\:{\varvec{y}}_{q}\left(k\right)=\:{\varvec{y}}_{q}\left(k\right)-{\varvec{y}}_{q}\left(k-1\right),(q=X,Y,Z,A,C)$. Then Eq. (2) can be written as Eq. (9):

$$\:\begin{array}{c}\left\{\begin{array}{c}\varDelta\:{\varvec{x}}_{q}\left(k+1\right)={\varvec{A}}_{q}\varDelta\:{\varvec{x}}_{q}\left(k\right)+{\varvec{B}}_{q}\varDelta\:{\varvec{u}}_{q}\left(k\right)\\\:\varDelta\:{\varvec{y}}_{q}\left(k\right)={\varvec{C}}_{q}\varDelta\:{\varvec{x}}_{q}\left(k\right)\end{array}\right.\end{array}$$

(9)

For a machine tool with five coordinate axes(X/Y/Z/A/C), let its state be $\:{\varvec{x}}_{\text{m}}={\left[{\varvec{x}}_{X}^{\text{T}}\:\:{\varvec{x}}_{Y}^{\text{T}}\:\:{\varvec{x}}_{Z}^{\text{T}}\:\:{\varvec{x}}_{A}^{\text{T}}\:\:{\varvec{x}}_{C}^{\text{T}}\right]}^{\text{T}}$, the output be the positions of each coordinate axis, i.e., $\:{\varvec{y}}_{\text{m}}={\left[{\varvec{y}}_{X}^{\text{T}}\:\:{\varvec{y}}_{Y}^{\text{T}}\:\:{\varvec{y}}_{Z}^{\text{T}}\:\:{\varvec{y}}_{A}^{\text{T}}\:\:{\varvec{y}}_{C}^{\text{T}}\right]}^{\text{T}}$, and the input be the command positions of each axis, i.e., $\:{\varvec{u}}_{\text{m}}={\left[{\varvec{u}}_{X}^{\text{T}}\:\:{\varvec{u}}_{Y}^{\text{T}}\:\:{\varvec{u}}_{Z}^{\text{T}}\:\:{\varvec{u}}_{A}^{\text{T}}\:\:{\varvec{u}}_{C}^{\text{T}}\right]}^{\text{T}}$. Then, expressing the machine state in incremental form, we have

$$\:\begin{array}{c}\left\{\begin{array}{c}\varDelta\:{\varvec{x}}_{\text{m}}\left(k+1\right)={\varvec{A}}_{\text{m}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k\right)\\\:\varDelta\:{\varvec{y}}_{\text{m}}\left(k\right)={\varvec{C}}_{\text{m}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)\end{array}\right.\end{array}$$

(10)

where

$$\:{\varvec{A}}_{\text{m}}=\text{d}\text{i}\text{a}\text{g}\left({\varvec{A}}_{X},{\varvec{A}}_{Y},{\varvec{A}}_{Z},{\varvec{A}}_{A},{\varvec{A}}_{C}\right)$$

$$\:{\varvec{B}}_{\text{m}}=\text{d}\text{i}\text{a}\text{g}\left({\varvec{B}}_{X},{\varvec{B}}_{Y},{\varvec{B}}_{Z},{\varvec{B}}_{A},{\varvec{B}}_{C}\right)$$

$$\:{\varvec{C}}_{\text{m}}=\text{d}\text{i}\text{a}\text{g}\left({\varvec{C}}_{X},{\varvec{C}}_{Y},{\varvec{C}}_{Z},{\varvec{C}}_{A},{\varvec{C}}_{C}\right)$$

Since the rotational axes generally rotate at a slower speed, it is assumed that the angular increment within an interpolation cycle is very small. Under this assumption, the approximations $\:\text{s}\text{i}\text{n}\left(\theta\:+\varDelta\:\theta\:\right)\approx\:\text{s}\text{i}\text{n}\theta\:+\varDelta\:\theta\:\text{c}\text{o}\text{s}\theta\:$ and $\:\text{c}\text{o}\text{s}\left(\theta\:+\varDelta\:\theta\:\right)=\text{c}\text{o}\text{s}\theta\:-\varDelta\:\theta\:\text{s}\text{i}\text{n}\theta\:$ can be applied. Taking $\:{p}_{\text{t}x}$ in Eq. (3) as an example, we obtain

$$\:\begin{array}{c}\begin{array}{c}\varDelta\:{p}_{\text{t}x}\left(k\right)\approx\:{p}_{\text{t}x}\left(k\right)-{p}_{\text{t}x}\left(k-1\right)=\varDelta\:{p}_{\text{m}x}+L\left(\text{s}\text{i}\text{n}\left({p}_{\text{m}a}+\varDelta\:{p}_{\text{m}a}\right)\text{s}\text{i}\text{n}\left({p}_{\text{m}c}+\varDelta\:{p}_{\text{m}c}\right)-\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}\right)\\\:=\varDelta\:{p}_{\text{m}x}+L\left(\varDelta\:{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}+\varDelta\:{p}_{\text{m}c}\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}+\varDelta\:{p}_{\text{m}a}\varDelta\:{p}_{\text{m}c}\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}\right)\end{array}\#\end{array}$$

(11)

Since the angular increment is very small, $\:\varDelta\:{p}_{\text{m}a}\varDelta\:{p}_{\text{m}c}$ can be regarded as higher-order infinitesimal quantities relative to the angular increment. Therefore, Eq. (11) can be approximated as Eq. (12).

$$\:\begin{array}{c}\varDelta\:{p}_{\text{t}x}\left(k\right)\approx\:\varDelta\:{p}_{\text{m}x}+L\left(\varDelta\:{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}+\varDelta\:{p}_{\text{m}c}\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}\right)\end{array}$$

(12)

Equation (3) can be approximated and expressed in incremental form as shown in Eq. (13).

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varDelta\:p}_{\text{t}x}=\varDelta\:{p}_{\text{m}x}+L\left(\varDelta\:{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}+\varDelta\:{p}_{\text{m}c}\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}\right)\\\:{\varDelta\:p}_{\text{t}y}=\varDelta\:{p}_{\text{m}x}-L\left(\varDelta\:{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}-\varDelta\:{p}_{\text{m}c}\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}\right)\\\:{\varDelta\:p}_{\text{t}z}={\varDelta\:p}_{\text{m}z}-L\varDelta\:{p}_{\text{m}a}sin{p}_{\text{m}a}\\\:{\varDelta\:O}_{\text{t}i}=-\varDelta\:{p}_{\text{m}a}cos{p}_{\text{m}a}sin{p}_{\text{m}c}-\varDelta\:{p}_{\text{m}c}sin{p}_{\text{m}a}cos{p}_{\text{m}c}\\\:{\varDelta\:O}_{\text{t}j}=\varDelta\:{p}_{\text{m}a}cos{p}_{\text{m}a}cos{p}_{\text{m}c}-\varDelta\:{p}_{\text{m}c}sin{p}_{\text{m}a}sin{p}_{\text{m}c}\\\:{\varDelta\:O}_{\text{t}k}=\varDelta\:{p}_{\text{m}a}sin{p}_{\text{m}a}\end{array}\right.\end{array}$$

(13)

Equation (13) can be written as Eq. (14):

$$\:\begin{array}{c}\varDelta\:{\varvec{y}}_{\text{t}}=\left[\begin{array}{c}\varDelta\:{p}_{\text{t}x}\\\:\varDelta\:{p}_{\text{t}y}\\\:\varDelta\:{p}_{\text{t}z}\\\:\varDelta\:{O}_{\text{t}i}\\\:\varDelta\:{O}_{\text{t}j}\\\:\varDelta\:{O}_{\text{t}k}\end{array}\right]=\left[\begin{array}{cc}{\varvec{I}}_{3\times\:3}&\:-L{\varvec{T}}_{\text{R}}\\\:{0}_{3\times\:3}&\:{\varvec{T}}_{\text{R}}\end{array}\right]\left[\begin{array}{c}\varDelta\:{p}_{\text{m}x}\\\:\varDelta\:{p}_{\text{m}y}\\\:\varDelta\:{p}_{\text{m}z}\\\:\varDelta\:{p}_{\text{m}a}\\\:\varDelta\:{p}_{\text{m}c}\end{array}\right]={\varvec{C}}_{\text{t}}\varDelta\:{\varvec{x}}_{\text{m}}\end{array}$$

(14)

where

$$\:{\varvec{T}}_{\text{R}}=\left[\begin{array}{cc}-\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}&\:-\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}\\\:\text{c}\text{o}\text{s}{p}_{\text{m}a}\text{c}\text{o}\text{s}{p}_{\text{m}c}&\:-\text{s}\text{i}\text{n}{p}_{\text{m}a}\text{s}\text{i}\text{n}{p}_{\text{m}c}\\\:\text{s}\text{i}\text{n}{p}_{\text{m}a}&\:0\end{array}\right]$$

Then the incremental form of the system can be written as Eq. (15).

$$\:\begin{array}{c}\left\{\begin{array}{c}\varDelta\:{\varvec{x}}_{\text{m}}\left(k+1\right)={\varvec{A}}_{\text{m}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k\right)\\\:\varDelta\:{\varvec{y}}_{\text{m}}\left(k\right)={\varvec{C}}_{\text{m}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)\\\:\varDelta\:{\varvec{y}}_{\text{t}}\left(k\right)={\varvec{C}}_{\text{t}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)\end{array}\right.\end{array}$$

(15)

This paper employs MPC method to implement pre-compensation control. By looking ahead N steps and using the incremental form, the system state can be expressed as Eq. (16).

$$\:\begin{array}{c}\left\{\begin{array}{c}\varDelta\:{\varvec{x}}_{\text{m}}\left(k+1\right)={\varvec{A}}_{\text{m}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{m}\left(k\right)\\\:\varDelta\:{\varvec{x}}_{\text{m}}\left(k+2\right)={\varvec{A}}_{\text{m}}^{2}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k+1\right)\\\: \vdots \\\:\begin{array}{c}\varDelta\:{\varvec{x}}_{\text{m}}\left(k+N\right)={\varvec{A}}_{\text{m}}^{N}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{A}}_{\text{m}}^{N-1}{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k\right)+\cdots\:\\\:+{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k+N-2\right)+{\varvec{B}}_{\text{m}}\varDelta\:{\varvec{u}}_{\text{m}}\left(k+N-1\right)\end{array}\end{array}\right.\end{array}$$

(16)

Let the N-step ahead prediction state be defined as $\:{\varvec{X}}_{\text{m}}\left(k+N\right)={\left[\begin{array}{cccc}{\varvec{x}}_{\text{m}}^{\text{T}}\left(k+1\right)&\:{\varvec{x}}_{\text{m}}^{\text{T}}\left(k+2\right)&\:\cdots\:&\:{\varvec{x}}_{\text{m}}^{\text{T}}\left(k+M\right)\end{array}\right]}^{\text{T}}$, and the N-step ahead control command as $\:{\varvec{U}}_{\text{m}}\left(k+N\right)={\left[\begin{array}{cccc}{\varvec{u}}_{\text{m}}^{\text{T}}\left(k+1\right)&\:{\varvec{u}}_{\text{m}}^{\text{T}}\left(k+2\right)&\:\cdots\:&\:{\varvec{u}}_{\text{m}}^{\text{T}}\left(k+M\right)\end{array}\right]}^{\text{T}}$. Then we have

$$\:\begin{array}{c}\varDelta\:{\varvec{X}}_{\text{m}}\left(k+N\right)={\varvec{A}}_{\text{f}\text{x}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{f}\text{x}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)\end{array}$$

(17)

where

$$\:{\varvec{A}}_{\text{f}\text{x}}=\left[\begin{array}{c}{\varvec{A}}_{\text{m}}\\\:{\varvec{A}}_{\text{m}}^{2}\\\:\vdots \\\:{\varvec{A}}_{\text{m}}^{N}\end{array}\right],{\varvec{B}}_{\text{f}\text{x}}=\left[\begin{array}{cccc}{\varvec{B}}_{\text{m}}&\:0&\:\cdots\:&\:0\\\:{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}+{\varvec{B}}_{\text{m}}&\:{\varvec{B}}_{\text{m}}&\:\cdots\:&\:0\\\:\vdots &\:\vdots &\:\ddots\:&\:\vdots \\\:\sum\:_{i=0}^{N-1}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\sum\:_{i=0}^{N-2}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:{\varvec{B}}_{\text{m}}\end{array}\right]$$

The N-step ahead output incremental state can be described as Eq. (18):

$$\:\begin{array}{c}\left\{\begin{array}{c}\varDelta\:{\varvec{Y}}_{\text{m}}\left(k+N\right)={\varvec{A}}_{\text{f}\text{y}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{f}\text{y}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)\\\:\varDelta\:{\varvec{Y}}_{\text{t}}\left(k+N\right)={\varvec{A}}_{\text{f}\text{t}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{f}\text{t}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)\end{array}\right.\end{array}$$

(18)

where

$$\:{\varvec{A}}_{\text{f}\text{y}}=\left[\begin{array}{c}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}\\\:{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{2}\\\:\vdots \\\:{{\varvec{C}}_{\text{m}}\varvec{A}}_{\text{m}}^{N}\end{array}\right],{\varvec{B}}_{\text{f}\text{x}}=\left[\begin{array}{cccc}{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:0&\:\cdots\:&\:0\\\:{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}+{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:0\\\:\vdots &\:\vdots &\:\ddots\:&\:\vdots \\\:\sum\:_{i=0}^{N-1}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\sum\:_{i=0}^{N-2}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}\end{array}\right]$$

$$\:{\varvec{A}}_{\text{f}\text{t}}=\left[\begin{array}{c}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}\\\:{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{2}\\\:\vdots \\\:{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{N}\end{array}\right],{\varvec{B}}_{\text{f}\text{t}}=\left[\begin{array}{cccc}{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:0&\:\cdots\:&\:0\\\:{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}+{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:0\\\:\vdots &\:\vdots &\:\ddots\:&\:\vdots \\\:\sum\:_{i=0}^{N-1}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\sum\:_{i=0}^{N-2}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}\end{array}\right]$$

The N-step ahead output states are:

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varvec{y}}_{\text{m}}\left(k+j\right)={\varvec{y}}_{\text{m}}\left(k\right)+\sum\:_{i=1}^{j}\varDelta\:{\varvec{y}}_{\text{m}}\left(k+i\right)\\\:{\varvec{y}}_{\text{t}}\left(k+j\right)={\varvec{y}}_{\text{t}}\left(k\right)+\sum\:_{i=1}^{j}\varDelta\:{\varvec{y}}_{\text{t}}\left(k+i\right)\end{array}\right.\end{array}$$

(19)

Therefore, we have

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varvec{Y}}_{\text{m}}\left(k+N\right)={\varvec{H}}_{\text{m}}{\varvec{y}}_{\text{m}}\left(k\right)+{\varvec{A}}_{\text{F}\text{y}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{F}\text{y}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)\\\:{\varvec{Y}}_{\text{t}}\left(k+N\right)={\varvec{H}}_{\text{t}}{\varvec{y}}_{\text{t}}\left(k\right)+{\varvec{A}}_{\text{F}\text{t}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{F}\text{t}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)\end{array}\right.\end{array}$$

(20)

where

$$\:{\left\{{\varvec{H}}_{\text{m}}\right\}}_{5N\times\:5N}=\text{d}\text{i}\text{a}\text{g}\left({\varvec{I}}_{5\times\:5},{\varvec{I}}_{5\times\:5},\cdots\:,{\varvec{I}}_{5\times\:5}\right),{\left\{{\varvec{H}}_{\text{t}}\right\}}_{6N\times\:6N}=\text{d}\text{i}\text{a}\text{g}\left({\varvec{I}}_{6\times\:6},{\varvec{I}}_{6\times\:6},\cdots\:,{\varvec{I}}_{6\times\:6}\right)$$

$$\:{\varvec{A}}_{\text{F}y}=\left[\begin{array}{c}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}\\\:{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{2}+{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}\\\:\vdots \\\:\sum\:_{i=1}^{N}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{i}\end{array}\right],{\varvec{B}}_{\text{F}y}=\left[\begin{array}{cccc}{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:0&\:\cdots\:&\:0\\\:{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}+{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:0\\\:\vdots &\:\vdots &\:\ddots\:&\:\vdots \\\:\sum\:_{i=1}^{N-1}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\sum\:_{i=1}^{N-2}{\varvec{C}}_{\text{m}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:{\varvec{C}}_{\text{m}}{\varvec{B}}_{\text{m}}\end{array}\right]$$

$$\:{\varvec{A}}_{\text{F}t}=\left[\begin{array}{c}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}\\\:{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{2}+{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}\\\:\vdots \\\:\sum\:_{i=1}^{N}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{i}\end{array}\right],{\varvec{B}}_{\text{F}t}=\left[\begin{array}{cccc}{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:0&\:\cdots\:&\:0\\\:{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}{\varvec{B}}_{\text{m}}+{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:0\\\:\vdots &\:\vdots &\:\ddots\:&\:\vdots \\\:\sum\:_{i=1}^{N-1}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\sum\:_{i=1}^{N-2}{\varvec{C}}_{\text{t}}{\varvec{A}}_{\text{m}}^{i}{\varvec{B}}_{\text{m}}&\:\cdots\:&\:{\varvec{C}}_{\text{t}}{\varvec{B}}_{\text{m}}\end{array}\right]$$

Define pre-compensation increment $\:\varvec{v}{\left(k\right)}_{5N\times\:1}$, the final reference command is defined as $\:{\varvec{u}}_{\text{r}}\left(k\right)={\varvec{u}}_{\text{m}}\left(k\right)+\varvec{v}\left(k\right)$. Equation (20) can be rewritten as:

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varvec{Y}}_{\text{m}}\left(k+N\right)={\varvec{H}}_{\text{m}}{\varvec{y}}_{\text{m}}\left(k\right)+{\varvec{A}}_{\text{F}\text{y}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{F}\text{y}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)+{\varvec{B}}_{\text{F}\text{y}}V\left(k+N\right)\\\:{\varvec{Y}}_{\text{t}}\left(k+N\right)={\varvec{H}}_{\text{t}}{\varvec{y}}_{\text{t}}\left(k\right)+{\varvec{A}}_{\text{F}\text{t}}\varDelta\:{\varvec{x}}_{\text{m}}\left(k\right)+{\varvec{B}}_{\text{F}\text{t}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)+{\varvec{B}}_{\text{F}\text{y}}V\left(k+N\right)\end{array}\right.\end{array}$$

(21)

where $\:\varvec{V}\left(k+N\right)={\left[\begin{array}{cccc}{\varvec{v}}^{\text{T}}\left(k\right)&\:{\varvec{v}}^{\text{T}}(k+1)&\:\cdots\:&\:{\varvec{v}}^{\text{T}}(k+N)\end{array}\right]}^{T}$

Let the desired positions of each axis and the desired tool posture be denoted as $\:{\varvec{Y}}_{\text{m}\text{r}}\left(k+N\right),{\varvec{Y}}_{\text{m}\text{t}}\left(k+N\right)$, respectively. The cost function is taken as

$$\begin{aligned} & J = \underbrace {{{\left[ {{Y_{{\text{mr}}}}\left( {k + M} \right) - {Y_{\text{m}}}\left( {k + M} \right)} \right]}^{\text{T}}}{Q_{\text{m}}}\left[ {{Y_{{\text{mr}}}}\left( {k + M} \right) - {Y_{\text{m}}}\left( {k + M} \right)} \right]}_{{\text{axis~tracking~error}}} \nonumber\\ & + \underbrace {{{\left[ {{Y_{{\text{tr}}}}\left( {k + M} \right) - {Y_{\text{t}}}\left( {k + M} \right)} \right]}^{\text{T}}}{Q_{\text{t}}}\left[ {{Y_{{\text{tr}}}}\left( {k + M} \right) - {Y_{\text{t}}}\left( {k + M} \right)} \right]}_{{\text{tool~tracking~error}}} \nonumber \\ & + \underbrace {\Delta {V^{\text{T}}}\left( k \right){Q_{\text{u}}}\Delta V\left( k \right)}_{{\text{pre}} - {\text{compensation~increment}}} \end{aligned}$$

(22)

where $\:{\left\{{\varvec{Q}}_{\text{m}}\right\}}_{5N\times\:5N},{\left\{{\varvec{Q}}_{\text{t}}\right\}}_{6N\times\:6N},{\left\{{\varvec{Q}}_{\text{u}}\right\}}_{5N\times\:5N}$ are weight matrices. The diagonal elements of these matrices represent the weights assigned to each predicted quantity, all of which are real numbers greater than 0, while the off-diagonal elements are set to 0.

Equation (22) indicates that the cost function incorporates the tracking errors of each axis, the tool tracking errors, and the pre-compensation increment. The next step involves determining its minimum value.

Let

$$\:{\varvec{E}}_{m}\left(k\right)={\varvec{Y}}_{mr}\left(k+M\right)-{\varvec{H}}_{m}{\varvec{y}}_{m}\left(k\right)-{\varvec{A}}_{\text{F}\text{y}}\varDelta\:{\varvec{x}}_{m}\left(k\right)-{\varvec{B}}_{\text{F}\text{y}}\varDelta\:{\varvec{U}}_{\text{m}}\left(k+N\right)$$

$$\:{\varvec{E}}_{t}\left(k\right)={\varvec{Y}}_{tr}\left(k+M\right)-{\varvec{H}}_{t}{\varvec{y}}_{t}\left(k\right)-{\varvec{A}}_{\text{F}\text{t}}\varDelta\:{\varvec{x}}_{m}\left(k\right)-{\varvec{B}}_{\text{F}\text{t}}\varDelta\:{\varvec{U}}_{\text{m}}(k+N)$$

Taking the derivative of Eq. (22), we have

$$\:\begin{array}{c}\frac{\partial\:J}{\partial\:\varvec{V}\left(k\right)}=-2{\varvec{B}}_{y}^{\text{T}}{\varvec{Q}}_{m}\left[{\varvec{E}}_{m}-{\varvec{B}}_{y}\varDelta\:\varvec{U}\left(k\right)\right]-2{\varvec{B}}_{yt}^{\text{T}}{\varvec{Q}}_{t}\left[{\varvec{E}}_{t}\left(k\right)-{\varvec{B}}_{yt}\varDelta\:\varvec{U}\left(k\right)\right]+2{\varvec{Q}}_{u}V\left(k\right)\end{array}$$

(23)

Let $\:\partial\:J/\partial\:\varvec{V}=0$, we have

$$\:\begin{array}{c}V\left(k\right)={\left({\varvec{B}}_{y}^{\text{T}}{\varvec{Q}}_{m}{\varvec{B}}_{y}+{\varvec{B}}_{yt}^{\text{T}}{\varvec{Q}}_{t}{\varvec{B}}_{yt}+{\varvec{Q}}_{u}\right)}^{-1}\left[{\varvec{B}}_{y}^{\text{T}}{\varvec{Q}}_{m}{\varvec{E}}_{m}+{\varvec{B}}_{yt}^{\text{T}}{\varvec{Q}}_{t}{\varvec{E}}_{t}\left(k\right)\right]\end{array}$$

(24)

In each cycle, only the first set of commands in $\:\varvec{V}\left(k\right)$ is taken as the output for the current cycle. Therefore, the final reference command for this cycle is

$$\:\begin{array}{c}{\varvec{u}}_{\text{r}}\left(k\right)={\varvec{u}}_{\text{m}}\left(k-1\right)+\varDelta\:{\varvec{u}}_{\text{m}}\left(k\right)+v\left(k\right)\end{array}$$

(25)

where

$$\:\varvec{v}\left(k\right)={\left[\begin{array}{cc}{\varvec{I}}_{5\times\:5}&\:{0}_{5\times\:5\left(N-1\right)}\end{array}\right]}_{5\times\:5N}\varvec{V}\left(k\right)$$

Contour error online feedback control

After obtaining the pre-compensation command, this paper further designs an online contour error feedback controller to achieve more precise control of contour error. In the real-time controller, the foot point can be located using the contour error calculation method described earlier. Once the tool position and orientation at the foot point, $\:{\varvec{P}}_{\text{f}}$ and $\:{\varvec{O}}_{\text{f}}$, are obtained, the corresponding positions of each axis can be determined through inverse kinematics using Eq. (4). The difference between these positions and the current axis coordinates yields the components of the contour error projected onto each servo axis, denoted as $\:{\varvec{\epsilon\:}}_{\text{m}}={\left[\begin{array}{ccccc}{\epsilon\:}_{x}&\:{\epsilon\:}_{y}&\:{\epsilon\:}_{z}&\:{\epsilon\:}_{a}&\:{\epsilon\:}_{c}\end{array}\right]}^{\text{T}}$.

This component is utilized as the compensation amount $\:\varDelta\:{u}_{\text{e}}$. To prevent system oscillation, a gain coefficient $\:{K}_{\text{c}\text{e}}\:$is introduced, and a limiter is applied to ensure system stability. The final reference control increment is:

$$\:\begin{array}{c}\varDelta\:{u}_{\text{r}q}\left(k\right)=\left\{\begin{array}{cc}-\varDelta\:{u}_{\text{m}\text{a}\text{x}q},&\:{K}_{\text{c}\text{e}}\varDelta\:{u}_{\text{e}q}\left(k\right)<-\varDelta\:{u}_{\text{m}\text{a}\text{x}q}\\\:{K}_{\text{c}\text{e}}\varDelta\:{u}_{\text{e}q}\left(k\right),&\:-\varDelta\:{u}_{\text{m}\text{a}\text{x}q}\le\:{K}_{\text{c}\text{e}}\varDelta\:{u}_{\text{e}q}\left(k\right)\le\:\varDelta\:{u}_{\text{m}\text{a}\text{x}q}\\\:\varDelta\:{u}_{\text{m}\text{a}\text{x}q},&\:{K}_{\text{c}\text{e}}\varDelta\:{u}_{\text{e}q}\left(k\right)>-\varDelta\:{u}_{\text{m}\text{a}\text{x}q}\end{array}\right.,q=X,Y,Z,A,C\end{array}$$

(26)

The principle of online feedback control is shown in Fig. 9:

Fig. 9

Schematic diagram of the contour error online feedback control.

Experiment

To validate the method proposed in this paper, an experimental system was constructed, as illustrated in Fig. 10. The system includes a five-axis motion platform, a real-time controller, and a digital twin. The control system of this platform is developed by TwinCAT 3 and runs on a Windows 7 industrial computer with an Intel^® Core™ i7-6700 CPU @ 3.40 GHz. And the control cycle sets to 2ms.The digital twin platform runs on a workstation with Windows 11, powered by an Intel^® Core™ i9-12900 CPU @ 2.40 GHz.

Fig. 10

Experimental equipment.

The model parameters of the five-axis motion control platform are shown in Table 1:

Table 1 Parameters of the five-axis motion platform.

This paper adopts an S-shaped curve as the input curve as depicted in Fig. 11. And the curve information is shown in Appendix A, Table A1.The interpolator and the velocity, acceleration, and jerk constraints for each axis are configured according to the settings described in reference⁴³. The feedrate is set to 50 mm/s. The interpolation results are illustrated in Figs. 12 and 13.

Fig. 11

S-shaped curve: (a) Tool tip position trajectory; (b) Tool orientation trajectory.

Fig. 12

Digital twin interpolation positions: (a) X-axis; (b) Y-axis; (c) Z-axis; (d) A-axis; (e) C-axis.

Fig. 13

Digital twin interpolation velocities: (a) tool tip position feedrate; (b) X-axis velocity; (c) Y-axis velocity; (d) Z-axis velocity; (e) A-axis velocity; (f) C-axis velocity.

As indicated in reference⁴⁴, the MPCC prediction control cycle should exceed the system time constant to achieve optimal control performance. Therefore, in the offline MPCC stage, the prediction step length is set to $\:N=10$, $\:{\varvec{Q}}_{\text{m}}=5{\varvec{I}}_{50\times\:50},{\varvec{Q}}_{\text{t}}=5{\varvec{I}}_{60\times\:60},{\varvec{Q}}_{\text{u}}={\varvec{I}}_{60\times\:60}$. For online control $\:\varDelta\:{u}_{\text{m}\text{a}\text{x}q}$ is set to 0.02 mm (or rad). The linear encoder resolution of X, Y and Z are both 0.1 μm while the rotator encoder resolution of A and C are 2²⁰ pulses/rev and 2¹⁷ pulses/rev. The sampling period is 0.002 s.

To verify the effectiveness of the control methods and the impact of the online feedback control gain $\:{K}_{\text{c}\text{e}}$ on the control results, the following groups of experiments are compared: (1) no compensation is performed (case 1); (2) only MPCC (case 2); (3) MPCC and online feedback control with $\:{K}_{\text{c}\text{e}}=0.1$(case 3) ; (4) MPCC and online feedback control with $\:{K}_{\text{c}\text{e}}=0.2$ (case 4); (5) MPCC and online feedback control with $\:{K}_{\text{c}\text{e}}=0.25$ (case 5); (6) MPCC and online feedback control with $\:{K}_{\text{c}\text{e}}=0.3$ (case 6). The final tool positions and orientations of those cases are shown in Fig. 14.

Fig. 14

Experiment results of tool tip position and tool orientation: (a) tool tip position; (b) partial enlargement of tool tip position; (c) tool orientation; (d) partial enlargement of tool orientation.

The tool tracking error is presented in Table 2; Fig. 15. Here, the TTP tracking error and TORI tracking error are defined according to Eq. (8), with the foot point replaced by the command of the current cycle.

Table 2 Tool tracking error under different cases.

It can be observed that after pre-compensation, the tool tracking error of case 2 is significantly reduced than case 1, which achieves the goal of pre-compensation. However, since online feedback control does not account for tool tracking errors, no further improvement in tool tracking error is observed in case 3 – case 6. In terms of average TORI tracking error, case 3 – case 6 have a slight increment compared to case 2. This situation is caused by the different objectives of contour error control and tracking error control. If the dynamic performance of a certain axis is poor, tracking error control will not adjust the response of other axes. However, contour error control will adjust the response of other axes to minimize the contour error, such as reducing the speed of other axes, which may result in a larger tracking error. Considering that tool contour error is a more effective indicator of machining quality, the slight increase in the average tool orientation tracking error is considered acceptable.

Fig. 15

Tool tracking error under different cases: (a) Tool tip position tracking error; (b) partial enlargement of tool tip position tracking error; (c) Tool orientation tracking error; (d) partial enlargement of tool orientation tracking error.

The contour error is illustrated in Fig. 16; Table 3. Compared to case 1, pre-compensation significantly reduces TTP contour error and TORI contour error. Specifically, the maximum TTP error is reduced by 72.71%, and its average value is reduced by 80.00%. Similarly, the maximum TORI error is reduced by 74.95%, and its average value is reduced by 83.43%.

Compared to the results of case 2, online control can further reduce the contour error. As $\:{K}_{\text{c}\text{e}}$ increases, the contour error control effect improves. However, when $\:{K}_{\text{c}\text{e}}$ is set to 0.3, the system oscillates. Therefore, in this experiment, $\:{K}_{\text{c}\text{e}}$ = 0.25 (case 5) is more reasonable. The maximum TTP error of case 5 is reduced by 18.58% compared to case 2, and its average value is reduced by 19.48%. The maximum TORI error is reduced by 16.37%, and its average value is reduced by 19.47%. Using this combined method, compared to the uncompensated scenario, the maximum TTP error is reduced by 77.78%, its average value is reduced by 83.90%, the maximum TORI error is reduced by 79.05%, and its average value is reduced by 86.66%. These results demonstrate that the method proposed in this paper effectively reduces contour error. Meanwhile, the iterations required to calculate the contour error are reduced after MPCC, as shown in Table 4. It indicates that pre-compensation control can provide a better basis for online control, effectively reducing the computational load of online control and enhancing the applicability of the control system.

Fig. 16

Tool contour error under different cases: (a) tool tip position contour error; (b–d) partial enlargement of tool tip position contour error; (e) tool orientation contour error; (f–h) partial enlargement of tool orientation contour error.

Table 3 Tool contour error under different cases.

Table 4 Average number of iterations for foot point search under different cases.

Conclusion

Digital twin has garnered significant attention from both academia and industry. This paper proposes a combined contour error control method for five-axis machine tools based on digital twin. The digital twin established in this paper includes NURBS interpolator, machine kinematic model and servo dynamic model. When get tool path as input, the digital twin process interpolation and model predictive pre-compensation control, generating the pre-compensated command to reduce modeled error. The pre-compensated command with interpolated command and other required commands are sent to the real-time controller. An online feedback control is designed to reduce the unmodeled error. Using the S-shaped curve as an example, the method proposed in this paper reduces the maximum tool tip position contour error by 77.78% and its average value by 83.90%. Similarly, the maximum tool orientation contour error is reduced by 79.05%, and its average value is reduced by 86.66%. Additionally, real-time data (axis position, axis velocity, axis current, etc.) is also transmitted to the digital twin for analyzing machining performance and updating simulation model parameters. For situations where precision requirements are not met, the digital twin can adjust the feedrate during subsequent machining to achieve an overall closed-loop optimization. In this study, a smaller proportional gain was employed to prevent system oscillation, which somewhat limited the effectiveness of online control. Future research could explore more robust online control methods. Furthermore, future work could integrate tool path planning and speed planning into the digital twin closed-loop optimization framework to further enhance performance. Meanwhile, considering cutting force during the MPCC stage can enhance contour error control during actual machining and improve machining accuracy.