Medical image segmentation model based on local enhancement driven global optimization

Abstract

In medical image segmentation, it is a challenging task to identify and locate the boundary of pathological tissue accurately. In response to this issue, this paper proposes a medical image segmentation model, named Local Enhancement Driven Global Optimization Network (LEGO-Net), and specially develops an Detail and Contour Recognition Module (DCRM) to accurately identify the boundaries of lesion tissue. Specifically, the DCRM has the following two main contributions: Firstly, it improves the network’s capability to identify the boundaries of diseased tissue by examining the intricate spatial relationships between row and column elements on the feature map. Secondly, by integrating local modeling with global modeling, the network is able to not only capture the detailed local structural information of the lesion area but also take into account the tissue’s overall structure, thereby enhancing the network’s capability to delineate the boundaries of the lesion tissue more effectively. Furthermore, to further augment the network’s capacity to discern lesion information, this paper introduces a Channel Feature Enhancement Module (CFEM). the CFEM can highlight the importance of elements that are beneficial to foreground feature discrimination. The outcomes demonstrate that the network architecture proposed in this paper is capable of effectively identifying and segmenting the boundaries of pathological tissues.

Introduction

By segmenting different different tissues or lesions in medical images, medical image segmentation technology can help doctors observe abnormal areas more intuitively and clearly. As an indispensable part of medical diagnosis, medical image segmentation technology not only improves the accuracy and efficiency of diagnosis, but also provides a scientific and quantitative evaluation method for patients’ personalized treatment¹.

In recent years, Convolutional Neural Networks (CNNs) have attracted widespread attention in the field of medical image processing, mainly due to their outstanding performance in feature extraction^2,3. In 2015, Ronneberger et al. proposed U-Net⁴ in a groundbreaking work. This is a network architecture that combines an encoder and a decoder with skip connections, and its emergence extends the fully convolutional network (FCN)⁵. Following U-Net, a multitude of medical image segmentation networks have embraced the U-shaped architectural design, such as ResUNet⁶, R50 U-Net⁷, R50 Att-UNet⁷, Att-UNet⁸, UNet++⁹, UNet3+¹⁰, R2U-Net¹¹. Despite the robust performance of these networks across various medical image segmentation challenges, they continue to exhibit limitations in accurately identifying the boundaries of lesion tissues. The specific reasons are as follows: (1) The segmentation model is capable of extracting features and progressively expanding its receptive field through a sequence of convolutional operations. This design can capture contextual information on a wider range, but it may also lead to a decrease in the model’s ability to perceive small lesions or fine edges of lesions. (2) In medical image segmentation tasks, pooling operations can enable the network to learn more abstract feature representations by reducing the scale of feature maps. However, this operation is often accompanied by the loss of spatial information, especially in terms of fine boundary information of lesions. (3) While convolutional neural networks are adept at capturing local features within medical images, their ability to incorporate global contextual information is limited. Therefore, these networks often struggle to effectively identify both the fine boundaries and overall structure of lesions simultaneously.

Recently, researchers have adapted the Transformer, a robust global modeling framework originally developed for Natural Language Processing (NLP)^12,13, for use in the field of computer vision. The Vision Transformer (ViT)¹⁴, proposed in 2020, leverages self-attention mechanisms¹⁵ to effectively extract contextual semantic information, becoming a research hotspot in computer vision tasks. Some scholars have attempted to utilize the Transformer solely as a feature extractor, such as nnFormer¹⁶, DaeFormer¹⁷, and MissFormer¹⁸, among others. In addition, some researchers have integrated Transformer into CNN to jointly serve as feature extractors. TransUNet¹⁹ was the initial endeavor to incorporate the Transformer architecture into the domain of medical image segmentation. Subsequently, a host of other network architectures such as TransUNet++²⁰, MT-UNet²¹, TransBTS²², TransClaw U-Net (TransClaw)²³, Conformer²⁴, and TranFuse²⁵ have emerged for medical image segmentation. Although Transformer has powerful global modeling ability, it still shows some shortcomings in the task of lesion edge recognition. The specific reasons are as follows: (1) In the case of too much background information, the learning focus of the model cannot be focused on the lesion area when Transformer calculates the correlation between global elements. (2) Although the Transformer model performs well in extracting global contextual information, its insufficient local modeling ability results in poor performance in identifying lesions with complex boundaries and shapes. (3) The lesion structures in medical images often have long-distance correlation, and the self-attention mechanism of Transformer model can not effectively deal with long-distance information transmission. This leads to the performance degradation of the model in segmenting lesion structures with complex shapes.

To enhance the segmentation network’s capability to identify lesion boundaries, we have developed a novel medical image segmentation model that incorporates a Detail and Contour Recognition Module (DCRM) designed to improve the network’s precision in differentiating lesion boundaries. The key contributions of our work are as follows:

• 1) By synchronizing local modeling and global modeling, the Detail and Contour Recognition Module (DCRM) can not only capture the local fine structure information of the lesion area, but also comprehensively consider the overall structure of the tissue.

• 2) By analyzing the inter relationships between pixels across the channel dimension, the Channel Feature Enhancement Module (CFEM) can highlight the importance of lesion features.

• 3) In order to alleviate that the decoder can’t completely recover the fine boundary details lost in the down-sampling process, the Detail and Contour Recognition Module (DCRM) transmits the captured lesion edge information to the decoder as much as possible at the skip connection.

Related work

CNN based methods

From manual to automatic, computer-aided diagnostic systems are becoming increasingly prevalent in the field of medicine. The innovation of Fully Convolutional Networks (FCNs)⁵ marked the initialization of convolutional neural networks for image segmentation purposes. The progression from the U-Net architecture to its numerous variants has collectively showcased the proficiency of CNNs in medical image segmentation. For instance, UNet++⁹ enhances the interplay of information across diverse levels by integrating densely connected and nested encoder-decoder subnetworks, effectively mitigating the semantic disparities between low-level and high-level features. In sequence, models such as 3D-UNet²⁶ and V-Net²⁷ have demonstrated remarkable applicability and efficiency in the domain of 3D medical image segmentation. Specifically, 3D-UNet leverages a 3D convolutional neural network architecture to tackle the challenges associated with volumetric image segmentation. As an improved version of 3D-UNet, V-Net has realized the effective segmentation of prostate tissue volume under magnetic resonance imaging (MRI) by applying loss function based on Dice coefficient, data augmentation strategy and residual learning method.

In addition, Lin et al.²⁸ introduced a novel 2D network named CFANet for CT image segmentation. CFANet features two enhanced modules: the pyramid fusion module (PFM) and the parallel divergent convolution module (PDCM). Among them, the PFM effectively merges context information from various levels of the encoder through jumping connection, which enriches the decoder with comprehensive global context from the original image and enhances the identification of indistinct boundary targets. The PDCM is appended at the encoder’s output, utilizing convolutions with varying dilation rates to extract multi-scale features, thereby improving the network’s capability to pinpoint small targets. The presence of similar local features, intricate artifacts, and ambiguous boundaries within medical images poses significant challenges to achieving precise image segmentation. To address these challenges, Liu et al. introduced the Long Strip Kernel Attention Network (LSKANet)²⁹ and developed two effective modules: the Dual-block Large Kernel Attention module (DLKA) and the Multiscale Affinity Feature Fusion module (MAFF). The DLKA employs strip convolutions with different topological structures (both cascade and parallel) to diminish false segmentations arising from similar local features. In the MAFF, an affinity matrix derived from multi-scale feature maps is utilized as weights for feature fusion, aiding in resolving artifact interference by suppressing the activation of irrelevant regions. To enhance the segmentation model’s capability to identify lesion boundaries, Ma et al. introduced the Multi-scale Detail Enhanced network (MSDEnet)³⁰. The Multi-scale detail enhanced (MSDE) module within MSDEnet is designed to detect subtle changes in feature information more acutely by contrasting central and peripheral details of the feature map. Furthermore, the Channel Multi-scale (CMS) module of MSDEnet diminishes the redundant information produced by the encoder through its independent and parallel multi-scale structure across channels, effectively addressing the issue of lesion boundary information becoming diluted by the network. To counteract the loss of boundary information due to successive pooling layers and convolution stride sizes, Tang et al. developed UG-Net, an automatic medical image segmentation network³¹. UG-Net comprises a Coarse Segmentation Module (CSM), an Uncertainty Guided Module (UGM), and a Feature Refinement Module (FRM) that incorporates several Dual Attention (DAT) blocks. The CSM is responsible for producing initial segmentation results and generating an uncertainty map during training. The UGM utilizes the uncertainty map to extract distinctive features from the CSM encoder. Finally, the FRM employs DAT blocks to produce a finely detailed and reliable final segmentation by utilizing meaningful features from the CSM decoder and the discriminative features of the UGM.

Despite the various strategies employed by the aforementioned networks to enhance the segmentation model’s ability to recognize lesion boundaries, the feature extractor within these networks does not account for the global pixel correlations in the feature map when extracting features at multiple scales. This limitation hampers the network’s capability to effectively capture and consolidate the comprehensive contour information of the lesion.

CNN and transformer based methods

The remarkable success of Transformers in natural language processing has spurred an increasing number of researchers to adapt this architecture for visual tasks. Chen et al. were among the first to investigate the potential of Transformers in medical image segmentation, introducing the TransUNet network¹⁹. TransUNet leverages convolutional kernels at the initial stages of the encoder to capture local feature details, while employing Transformers at deeper layers to model global context. The experiment shows that the combination of convolutional kernels and Transformers can improve the network’s capability to identify lesions. However, neither convolutional kernels nor Transformers are adept at simultaneously handling local and global modeling tasks. Consequently, TransUNet may not achieve optimal segmentation results for certain intricate pathological tissues. Furthermore, Cao et al. introduced SwinUNet³², a network architecture that integrates convolutional kernels and Swin Transformer blocks. The novelty of SwinUNet lies in its use of two consecutive Transformer blocks with distinct window configurations (employing shifting windows to decrease computational demands) to effectively capture contextual information from neighboring windows. Despite the Swin Transformer blocks in SwinUNet significantly reducing computational complexity, they still struggle to capture the correlation of all elements across the feature map. Additionally, Wang et al. proposed UCTransNet³³, which primarily comprises convolutional kernels and channel transformers (CTrans). CTrans leverages Transformers to determine the relation between feature maps at varying depths. Following this, Azad et al. introduced Dae-Former¹⁷, which computes correlations not only along the channel dimension of the feature map but also across the spatial dimension. While this approach allows for the measurement of correlations within both the channel and spatial dimensions, it substantially raises the computational complexity of the network. For example: TransDeepLab³⁴, HiFormer³⁵, DSGA-Net³⁶. While these networks are capable of efficiently performing both global and local modeling, they do so at the expense of increased computational complexity. Furthermore, the inherent limitation remains that convolutional kernels and Transformers alone cannot accomplish local and global modeling simultaneously.

In addition, in order to automatically detect the curve structure of lesion structure from biomedical images, Mou et al.³⁷ proposed a medical segmentation network (CS2-Net). Specifically, two self-attention mechanisms proposed by CS2-Net are used to generate expressive features of attention perception in channels and spaces. They can enhance the network’s ability to capture long-range correlations and leverage multi-channel spatial information for feature representation and normalization, thereby facilitating more effective classification of lesion area boundaries from the background. Addressing the challenges in segmentation due to variations in lesion shape, size, and the presence of blurred boundaries and noise interference, Cao et al. proposed the Pyramid Transformer Inter-pixel Correlation (PTIC) module and the Local Neighborhood Metric Learning (LNML) module³⁸. The PTIC module employs a pyramid Transformer and a fully connected layer to capture multi-level non-local context information and to model the global correlation between pixels. On the other hand, the LNML module utilizes metric learning to model the semantic relationship between pixels in the local neighborhood between the target lesion and the background class. These two modules work together to guide the network in learning more distinctive feature representations, thereby significantly enhancing the segmentation model’s capability to discern the lesion boundary. To effectively capture intricate details such as small targets and irregular boundaries, Yang et al. introduced the Pyramid Fourier Deformable Network (PFD-Net)³⁹. PFD-Net employs a PVT v2-based Transformer as the primary encoder to gather global information. Additionally, the proposed Fast Fourier Convolution Residual (FFCR) module is utilized to further refine both local and global feature representations. Furthermore, this paper introduces the Dilated Deformable Improvement (DDR) module and the Cross-level Fusion Block with Deformable Transformation (CLFB) to extract intricate structural information of lesions and refine their boundary details, respectively. To address issues such as inaccurate polyp localization and ambiguous boundary segmentation, Li et al. proposed the Cross-level Information Fusion and Guidance (CIFG-NET) network for polyp segmentation⁴⁰. Similarly, the CIFG-NET leverages a PVT v2-based Transformer as its primary encoder to capture global information. Moreover, to refine the feature information processed by the encoder, this paper introduces an Edge Feature Processing Module (EFPM) and a Cross-level Information Processing Module (CIPM). The EFPM focuses on enhancing the boundary information within polyp features, while the CIPM is designed to aggregate and process multi-scale features from various encoder layers. By utilizing multi-level features, the CIPM aims to resolve the issue of inaccurate polyp positioning by providing precise positional information. To differentiate between normal tissues and polyps with unclear and highly similar boundaries, Yin et al. developed the Regional Self-Attention Enhancement Network (RSAformer)⁴¹. Unlike other segmentation models, RSAformer utilizes a double decoder structure to generate diverse feature maps, offering greater flexibility and detail in feature extraction compared to the traditional single-decoder approach. Furthermore, RSAformer incorporates the Region Self-Attention Enhancement Module (RSA), which fosters interaction between low-level and high-level features to achieve a more precise delineation of the lesion area.

These segmentation models achieve the integration of local details and global context information; however, the modeling of local and global information occurs independently at different stages, posing a challenge for the segmentation model to simultaneously capture the fine tissue and overall structure information of the lesion. To sum up, this paper puts forward a medical image segmentation model LEGO-Net, which can synchronously model locally and globally. Specifically, LEGO-Net uses CFEM in the encoder to make the network highlight the importance of lesion features as much as possible, and then uses DCRM at the skip connection to synchronously extract the overall contour and edge details of the lesion. In this way, LEGO-Net can better identify the edge element information of the lesion.

Methodology

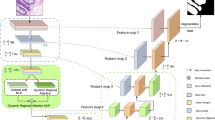
As shown in Fig. 1, the structure of LEGO-Net’s encoder primarily incorporates the Channel Feature Enhancement Module (CFEM). For the decoder, it employs a bilinear interpolation method to elevate the feature map’s resolution to match that of the original image. To minimize the loss of lesion border detail during downsampling, we interpose the Detail and Contour Recognition Module (DCRM) between the encoder and decoder. This module works to concurrently harvest local detail and comprehensive structural data of the lesion. A detailed discussion of each module’s architecture and their respective functions will ensue.

Fig. 1

Overall architecture diagram of LEGO-Net.

Encoder

Illustrated in Fig. 2, the Encoder employs convolutional kernels to extract semantic features from the input imagery. Here, Stage0, Stage1, Stage2, and Stage3 denote the network’s progression through convolutional kernels of $3\times 3$ size with a stride of 2, effectively diminishing the scale of the feature map at each stage. The CFEM enhances the network’s ability to identify lesions by calculating the inter channel relationships between feature elements. Next, we will explain its working principle in detail.

Fig. 2

Example diagram of the Encoder.

Channel feature enhancement module (CFEM)

To enhance the extraction of semantic information from the feature map, this section delves into the inter-channel correlations within the encoder component. As depicted in Fig. 2, the input feature map is denoted as $\text {F} \in \text {R}^{h \times w \times c}$. Subsequently, the input feature maps are segmented along the channel axis into k distinct groups of feature maps, represented as $\left\{ F_1, F_2 \ldots , F_k\right\}$.

$$\begin{aligned} \left\{ F_1, F_2 \ldots F_k\right\} =\text {{ Split}}(F) \quad \left\{ F_1, F_2 \ldots F_k\right\} \in R^{h \times w \times c / k} \end{aligned}$$

(1)

Then, we continue to group the feature graphs $\left\{ F_1, F_2 \ldots , F_k\right\}$ from the channel dimension to get r feature graphs. Among them, $\left\{ F_{11}, F_{12} \ldots F_{1r}\right\}$ can be obtained by grouping the feature graph $F_1$. Other feature maps and so on.

$$\begin{aligned} \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} =\text {{ Split}}\left( F_i\right) \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} \in R^{h \times w \times c / k / r} ; 1 \ll i \le k \end{aligned}$$

(2)

Next, we use convolution kernels of size $1 \times 1$ and $3 \times 3$ to extract features from feature maps $\left\{ F_{i1}, F_{i2} \ldots F_{i r}\right\}$, and obtain feature maps $\left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\}$.

$$\begin{aligned} \left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\} =\text {{ conv}3}\left( \text {{ conv}1} \left( \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} \right) \right) \left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\} \in R^{h \times w \times c^{\prime } / k } \end{aligned}$$

(3)

Then, input the feature map $\left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\}$ into the Spilt Attention module to calculate the relationship between feature map channels and output the feature map $T_i$.

$$\begin{aligned} T_i= \text{ SpiltAttention } \left( \left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\} \right) \quad T_i \in R^{h \times w \times c^{\prime } / k} \end{aligned}$$

(4)

Following this, the feature maps $\left\{ T_1, T_2 \ldots , T_k\right\}$ are merged along the channel axis to produce the output feature map T.

$$\begin{aligned} T= \text{ concatenate } \left( T_1, T_2 \ldots T_k\right) \quad T \in R^{h \times w \times c^{\prime }} \end{aligned}$$

(5)

Finally, the feature map T is convolved and fused with the original feature map F.

$$\begin{aligned} \text{ out } =\text {{ conv}1} (T)+F \quad \text{ out } \in R^{h \times w \times c} \end{aligned}$$

(6)

The following section will elaborate on the precise functioning of the Split Attention module. As depicted in Fig. 3, we consider that the feature maps $\left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\}$ entering the Split Attention module have a dimension of $R^{h \times w \times c}$. Initially, these feature maps $\left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\}$ are combined by means of an addition operation to generate the integrated feature map $F_i$ with dimensions $R^{h \times w \times c}$.

$$\begin{aligned} F_i=F_{i 1}^{\prime }+F_{i 2}^{\prime }+\cdots +F_{i r}^{\prime } \quad F_i \in R^{h \times w \times c} \end{aligned}$$

(7)

Fig. 3

Example diagram of the spilt attention.

Then, the feature map $F_i \in R^{h \times w \times c}$ undergoes global maximum pooling operation.

$$\begin{aligned} F_i= \text{ Globalpooling } \left( F_i\right) \quad F_i \in R^{1 \times 1 \times c} \end{aligned}$$

(8)

Next, the feature map $F_i \in R^{1 \times 1 \times c}$ goes through convolution operation (convolution kernel with size of $1 \times 1$), normalization operation (BatchNorm2d) and activation of function mapping (Rule) operation.

$$\begin{aligned} F_i=\text {{ Relu}}\left( B N\left( \text {{ conv}1} \left( F_i\right) \right) \right) \quad F_i \in R^{1 \times 1 \times c^{\prime }} \end{aligned}$$

(9)

Subsequently, the semantic content of the feature map $F_i \in R^{1 \times 1 \times c}$ is harvested through the application of r concurrent convolutional kernels (each of size $1 \times 1$), resulting in the derivation of r distinct feature maps $\left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\}$.

$$\begin{aligned} \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} =\text {{ conv}1} \left( F_i\right) \quad \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} \in R^{1 \times 1 \times c} \end{aligned}$$

(10)

Then, the channel dimensions of feature graphs $\left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\}$ are calculated by using Softmax function, and the corresponding channel coefficients are obtained.

$$\begin{aligned} \partial _{i t}=\left\{ \partial _{i 1}, \partial _{i 2} \ldots \partial _{i r}\right\} =Softmax \left( \left\{ F_{i 1}, F_{i 2} \ldots F_{i r}\right\} \right) =\frac{e^{F_{i t}}}{\sum _{p=1}^{p=r} e^{F_{i p}}} \quad 1 \le t \le r ; \left\{ \partial _{i 1}, \partial _{i 2} \ldots \partial _{i r}\right\} \in R^{1 \times 1 \times c} \end{aligned}$$

(11)

Channel coefficient $\left\{ \partial _{i 1}, \partial _{i 2} \ldots \partial _{i r}\right\}$ is multiplied by feature map $\left\{ F_{i 1}^{\prime }, F_{i 2}^{\prime } \ldots F_{i r}^{\prime }\right\}$, and then added to output the feature map.

$$\begin{aligned} \text{ out } =\partial _{i 1} \times F_{i 1}^{\prime }+\partial _{i 2} \times F_{i 2}^{\prime }+\cdots +\partial _{i r} \times F_{i r}^{\prime } \quad \text{ out } \in R^{h \times w \times c} \end{aligned}$$

(12)

In order to achieve encapsulation, this strategy first divides the feature map into multiple subsets along the channel dimension and repeats the processing twice for each subset to extract valuable information from these subsets. Subsequently, these feature maps are passed to the segmentation attention module for channel attention coefficient calculation. Finally, the attention coefficient is multiplied with the feature map to highlight the criticality of specific channel feature maps. Through this method, CFEM enhances the importance of channel feature maps with high lesion information ratios.

The CFEM module introduces a multi-path feature extraction mechanism to segment the feature map into multiple sub paths, and independently applies attention mechanisms on each sub path. This strategy not only enhances the model’s ability to perceive local details in images, but also improves its efficiency in capturing global structural information. This unique architecture design enables CFEM to construct richer and multi-level feature representations during the feature learning phase, providing a more accurate and discriminative feature foundation for subsequent classification or other tasks. Compared with attention mechanisms such as CBAM model³⁶ and SE model³⁷, the CFEM module has stronger expressiveness and flexibility in processing complex image features.

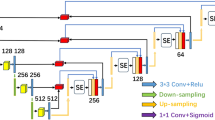
Detail and Contour Recognition Module (DCRM)

Illustrated in Fig. 4, the functionality of the DCRM is delineated in this section. To commence, we specify the dimensions of the input feature map X as $R^{c \times h \times w}$. For the sake of clarity, we establish $c=1$ and $h=w=4$, thereby rendering the input feature map with a size of $R^{1 \times 4 \times 4}$. Next, we use the Softmax activation function to act on the input feature graph to get two attention coefficient matrices $\alpha \in R^{1 \times 4 \times 4}=\left[ \begin{array}{llll}\alpha _1 & \alpha _2 & \alpha _3 & \alpha _4 \\ \alpha _5 & \alpha _6 & \alpha _7 & \alpha _8 \\ \alpha _9 & \alpha _{10} & \alpha _{11} & \alpha _{12} \\ \alpha _{13} & \alpha _{14} & \alpha _{15} & \alpha _{16}\end{array}\right]$ and $\beta \in R^{1 \times 4 \times 4}=\left[ \begin{array}{cccc}\beta _1 & \beta _2 & \beta _3 & \beta _4 \\ \beta _5 & \beta _6 & \beta _7 & \beta _8 \\ \beta _9 & \beta _{10} & \beta _{11} & \beta _{12} \\ \beta _{13} & \beta _{14} & \beta _{15} & \beta _{16} \end{array}\right]$. Among them, $\alpha _i(1 \le i \le 16)$ is obtained by calculating the correlation between column elements, and $\beta _i(1 \le i \le 16)$ is obtained by calculating the correlation between row elements. The specific calculation formulas of $\alpha _1$ and $\beta _1$ are as follows.

$$\begin{aligned} \alpha _1= & \frac{e^{X_1}}{e^{X_1}+e^{X_2}+e^{X_3}+e^{X_4}} \end{aligned}$$

(13)

$$\begin{aligned} \beta _1= & \frac{e^{X_1}}{e^{X_1}+e^{X_5}+e^{X_9}+e^{X_{13}}} \end{aligned}$$

(14)

It can be seen that the $\alpha _1$ in the coefficient matrix $\alpha$ is obtained by calculating the correlations among the elements $X_1$, $X_2$ , $X_3$ and $X_4$ in the input feature map. Similarly, $\alpha _2$, $\alpha _3$ and $\alpha _4$ are also obtained by calculating the correlation among $X_1$, $X_2$ , $X_3$ and $X_4$, and other coefficients are analogized in turn. At this time, the values of $\alpha _i$ within the coefficient matrix $\alpha$ are determined through the computation of correlations among the columnar elements of the input feature map.

Fig. 4

Example diagram of the DCRM.

The distinction lies in how the coefficients $\beta _1$, $\beta _5$, $\beta _9$, and $\beta _{13}$ within the matrix $\beta$ are derived. These values are the result of analyzing the correlations among specific elements $X_1$, $X_5$, $X_9$, and $X_{13}$ of the input feature map. Essentially, each $\beta _i$ in the matrix $\beta$ is calculated by examining the relationships between the row-wise elements of the input feature map.

Subsequently, the input feature map is combined with the coefficient matrix, and the resulting feature map undergoes a dimensional transformation, yielding two distinct feature maps, Q with dimensions $R^{1 \times 16 \times 1}$ and K with dimensions $R^{1 \times 1 \times 16}$.

$$\begin{aligned} & \text {{ Q}}=\text {{ Reshape}}(\alpha \times \text{ X } ) \quad Q \in R^{1 \times 16 \times 1} \end{aligned}$$

(15)

$$\begin{aligned} & \text {{ K}}=\text {{ Reshape}}(\beta \times \text{ X } ) \quad K \in R^{1 \times 1 \times 16} \end{aligned}$$

(16)

Following this, the feature maps Q and K are convolved through matrix multiplication, yielding an elemental matrix $M_1$. The entries of this elemental matrix are derived from the correlations between row and column elements of the input feature map. For instance, the specific element $Q_1 K_1$ in the elemental matrix is calculated based on the elements $\left\{ X_1, X_2, X_3, X_4, X_5, X_9, X_{13}\right\}$ from the input feature map.

$$\begin{aligned} Q_1 K_1=Q_1 \times K_1=\frac{e^{X_1} \times X_1}{e^{X_1}+e^{X_2}+e^{X_3}+e^{X_4}} \times \frac{e^{X_1} \times X_1}{e^{X_1}+e^{X_5}+e^{X_9}+e^{X_{13}}} \end{aligned}$$

(17)

In like manner, every element within the elemental matrix is computed by assessing the correlations between elements from corresponding rows and columns of the input feature map. Through this method, the DCRM enhances the network’s capability to identify the anomalous contours of lesions.

Fig. 5

Example diagram of the Sigmoid derivative.

Subsequently, we determine the Euclidean distance between each element and the diagonal elements within the elemental matrix, thereby constructing a similarity matrix.

$$\begin{aligned} \begin{aligned} N_{i j}=Q_i K_j-Q_i K_i\{1 \le i, j \le 9\} \mid \end{aligned} \end{aligned}$$

(18)

This similarity matrix is then converted into a self-attention coefficient matrix through the application of the Sigmoid activation function’s derivative.

$$\begin{aligned} \lambda _{i,j}=1-\left( \frac{e^{N_{i, j}}-e^{-N_{i, j}}}{e^{N_{i, j}}+e^{-N_{i, j}}}\right) ^2=1-\left( \frac{e^{Q_i K_j-Q_i K_i}-e^{-\left( Q_i K_j-Q_i K_i\right) }}{e^{Q_i K_j-Q_i K_i}+e^{-\left( Q_i K_j-Q_i K_i\right) }}\right) ^2 \quad 1 \le i, j \le 9 \end{aligned}$$

(19)

Among them, $\lambda _{i, j}$ represents the self-attention coefficient of a certain spatial position, and $\left( Q_i K_j-Q_i K_i\right)$ represents the concrete calculation formula for converting a certain point element in the element matrix into a similarity value by using euclidean distance.

As shown in Fig. 5, we present an example graph of Sigmoid derivatives. It can be seen that when two pixels are more similar, the similarity value obtained through Euclidean distance is smaller, and the attention coefficient obtained through function mapping is also larger. So, we use the Sigmoid derivative as the mapping function for the transformation from similarity values to attention coefficients.

Next, the self-coefficient matrix is matrix-multiplied with the feature map $V \in R^{1 \times 4 \times 4}$ to output the feature map Y.

$$\begin{aligned} \begin{aligned} Y_i=\lambda _{i,1} \times v_1+\lambda _{i,2} \times v_2+\ldots +\lambda _{i,15} \times v_{15} +\lambda _{i,16} \times v_{16} \end{aligned} \end{aligned}$$

(20)

Observably, every element $Y_i$ in the resulting feature map is produced through the involvement of all elements from the feature graph V in the computation. Moreover, the coefficient $\lambda _{i,j}$ is derived from the correlation analysis of row and column elements within the input feature map. In essence, the DCRM exhibits both local and global modeling capabilities. By doing so, the DCRM effectively focuses on both the nuanced details within the lesion area and the comprehensive structural information.

The core function of Non-local blocks⁴² is to directly capture remote dependencies by calculating the interaction between any two positions, allowing for direct modeling of global information. RSAFormer⁴¹ significantly improves the performance of medical image segmentation models by utilizing region self attention mechanism and dual decoder structure. However, their single feature extraction method to some extent overlooks the importance of the interaction between local and global features. In sharp contrast, the DCRM module not only achieves synchronous collection of local and global information, but also promotes effective interaction between the two. Compared to their feature extraction methods, the DCRM module significantly improves the overall performance of the segmentation model.

Decoder

In the decoder segment, LEGO-Net incorporates a structure that parallels U-Net for generating the predicted image. As depicted in Fig. 6, the profound features produced by the DCRM are transmitted to the decoder. The decoder initiates the process by employing convolutional operations to distill semantic data from the feature map. It then applies bilinear interpolation to elevate the spatial resolution of the feature map, facilitating pixel-wise predictions. However, as the network depth intensifies, the spatial resolution of the feature map progressively diminishes, which can result in the loss of crucial information. To mitigate this challenge, LEGO-Net integrates skip connections, blending features from both the encoder and decoder stages.

Fig. 6

Example diagram of the decoder.

Loss function

Since the number of organs in the datasets selected in this paper is unbalanced and there are many categories, the combined Dice loss and CrossEntoryLoss loss is chosen as the loss function, please refer to Formula (21).

$$\begin{aligned} \begin{aligned} L_{\text{ Loss }}=0.5\times L_{\text{ Dice }}+0.5\times L_{\text{ CrossEntropyLoss } } \end{aligned} \end{aligned}$$

(21)

The formulas for $L_{Dice}$ and $L_{CrossEntropyLoss}$ are as follows (22) and (23):

$$\begin{aligned} \begin{aligned} L_{\text{ Dice } }=1-2 \times \frac{P_{i} G_{i}}{P_{i}+G_{i}} \end{aligned} \end{aligned}$$

(22)

Where $P_i$ is the probe value of the ith factor value in the forecast graph of belonging to a given category of prospects. $G_i$ is the true factor value of the ith factor in the labeling graph.

$$\begin{aligned} \begin{aligned} L_{\text{ CrossEntropyLoss } }=-\frac{1}{H \times W} \sum _{i=1}^{H \times W} \log \left( P_{i( \text{ correct } )}\right) \end{aligned} \end{aligned}$$

(23)

Where $P_{i(correct)}$ quantifies the probability of accurately predicting the value of a specific element at a point within an item, while $H \times W$ specifies the resolution of the resulting forecasted image.

Experiments

To assess the approach introduced in this paper, we selected three datasets that are popular and have different imaging modalities with different number of categories for validation under the same experimental parameters. We also present and analyze the experimental results.

Datasets

Synapse Multi-Organ Segmentation Dataset (Synapse): This dataset, compiled from 30 cases, encompasses 3779 clinical CT images, with each image including segmentations of 8 abdominal organs: Aorta, Gallbladder, Kidney (left), Kidney (right), Liver, Pancreas, Spleen, and Stomach. We allocated 2211 images for training and utilized the remainder for testing purposes. The dataset can be accessed via https://www.synapse.org/#!Synapse:syn3193805/wiki/217789.

Automated Cardiac Diagnostic Challenge Dataset (ACDC): Derived from MRI scans of 100 individuals, this dataset comprises 1579 images, each annotated with segmentations for the left ventricle, right ventricle, and myocardium. For training purposes, 1539 images were employed, while the remaining 40 were reserved for testing. The dataset can be found at https://www.creatis.insa-lyon.fr/Challenge/acdc/.

Myeloma Plasma Cell Segmentation Dataset (SegPC-2021): Comprising 497 images, each featuring numerous myeloma plasma cells requiring segmentation of the cytoplasm and nucleus, this dataset was utilized with 398 images designated for training and 99 for testing. The dataset can be accessed via https://www.kaggle.com/datasets/sbilab/segpc2021dataset.

International Skin Imaging Collaboration Dataset (ISIC2017): Comprising 2600 images, each containing lesion and normal tissue regions. Among them, 2000 of the images are used for training and 600 is used for testing. The dataset can be accessed via https://challenge.isic-archive.com/data/#2017.

Implementation details

The training of all experiments detailed in this paper was conducted using a solitary NVIDIA Tesla V100 GPU, equipped with 16 GB of memory. The software environment consisted of Python 3.8 and Pytorch 1.11.0. The input images were resized to $224\times 224$ pixels, and the batch size for training was set to 16. For the optimization process, we utilized the SGD optimizer with an initial learning rate of 0.01, a momentum factor of 0.9, and a weight decay coefficient of 1e-4.

Evaluation metrics

To thoroughly evaluate the efficacy of the algorithm put forth in this study, we have selected the Dice Similarity Coefficient (DSC) and Hausdorff Distance (HD) as the primary metrics for assessment. The formula for calculating DSC is presented in Eq. (24):

$$\begin{aligned} \begin{aligned} DSC=\frac{(2*TP)}{(2*TP+FP+FN)} \end{aligned} \end{aligned}$$

(24)

In this formula, TP represents the count of samples correctly predicted as positive; FP indicates the number of samples incorrectly predicted as positive; and FN signifies the number of samples incorrectly predicted as negative.

HD quantifies the maximum discrepancy between the predicted and actual segmentation outcomes, providing a measure of their similarity. The computation formula is expressed in Eq. (25):

$$\begin{aligned} HD(A,B)=max{(h(A,B),h(B,A))} \end{aligned}$$

(25)

Where A and B denotes the forecast segmentation result and the true segmentation result respectively. h(A, B) denotes the maximum value of the shortest distance from each point in A to B, i.e Formula (26):

$$\begin{aligned} h(A,\, B)=max\{ min(d(a,b))\} \end{aligned}$$

(26)

Where d(a, b) denotes the Euclidean distance between point a to point b.

$$\begin{aligned} Jaccard =\frac{T P}{F N+T P+F P} \end{aligned}$$

(27)

Jaccard is used to measure the degree of overlap between predicted results and true labels.

$$\begin{aligned} Precision =\frac{T P}{T P+F P} \end{aligned}$$

(28)

Precision is used to test the probability of predicting a certain category correctly.

$$\begin{aligned} Recall =\frac{T P}{T P+F N} \end{aligned}$$

(29)

Recall measures the proportion of positive samples correctly identified by the model to all actual positive samples.

Comparative test results and visualization

To confirm the capabilities and utility of the aforementioned approaches, we chose a variety of models encompassing CNN-based, attention mechanism-based, CNN-Transformer hybrid, and Transformer-based architectures to conduct comparative and ablation studies across three datasets. We will present the findings in sequence, starting with the Synapse dataset, followed by the ACDC dataset, and concluding with the SegPC-2021 dataset.

Table 1 Comparison of experimental outcomes among various networks on the Synapse dataset.

Fig. 7

Visualization results of selected comparison experiments on the Synapse dataset.

Table 1 presents a comparison of our method with other networks on the Synapse dataset. It is worth noting that LEGO-Net performs better in HD scores, indicating its superior ability to delineate lesion boundaries. In addition, LEGO-Net exhibits a higher overall Dice coefficient, indicating its stronger ability to accurately identify the integrity of lesions. Overall, LEGO-Net can improve the network’s ability to learn lesion information from feature maps by effectively combining DCRM and CFEM.

As shown in the first line of the image in Fig. 7, other network architectures are not satisfactory in the task of distinguishing between Liver from Kidney (left). In contrast, LEGO-Net can accurately distinguish their respective categories, highlighting its significant effectiveness in capturing the overall structure of organs or lesions of interest. What deserves special attention is the second line of Fig. 7, where the close proximity between Gallbladder and Liver creates an indistinguishable boundary. To effectively differentiate between the two types of organs, the network must be capable of precisely identifying the adjacent boundary elements between these organs in the image. At this point, LEGO-Net shows better performance than other networks of the same type. It clearly distinguishes Gallbladder from Liver, even if its boundary is very close. Generally speaking, LEGO-Net shows better overall segmentation ability than other network models, which shows its excellent ability in identifying the edge and overall structure of lesions.

Table 2 Comparison of experimental outcomes among various networks on the ACDC dataset.

Table 2 shows the segmentation results of LEGO-Net and other networks in the ACDC dataset. Due to the close connectivity of the three types of organs in the ACDC dataset, this increases the recognition pressure on the segmentation model. The LEGO-Net model introduced in this paper outperforms existing segmentation models on the ACDC dataset, demonstrating its superior capability in edge detection within image segmentation tasks. In addition, it can be seen from the table that introducing transformers alone or using pure transformers will not produce satisfactory results.

As shown in Fig. 8, there are close spatial links between myocardium and right ventricle and left ventricle. In order to accurately segment these three organs, the network needs to be able to clearly distinguish the elements located at the boundary of each type of lesion tissue area. Compared with other networks, LEGO-Net shows excellent performance in segmenting these three kinds of foreground organs. This result further proves that LEGO-Net can effectively distinguish the boundary elements of diseased tissues. This achievement emphasizes the critical role of accounting for the interplay between local contextual details and global information within feature maps during the design of neural networks for medical image segmentation tasks.

Fig. 8

Visualization of some of the comparison experiments on the ACDC dataset.

Table 3 Comparison of experimental outcomes among various networks on the SegPC-2021 dataset.

The data presented in Table 3 clearly leads to the following observations: LEGO-Net is superior to other comparison models in the task of distinguishing Cytoplasm from Nucleus. By thoroughly extracting and analyzing local details as well as global information from the feature map, the DCRM has markedly enhanced the network’s capability to recognize the characteristics of foreground structures. LEGO-Net’s score on HD index shows that the network has high accuracy in depicting the boundary contour of cytoplasm and nucleus. In addition, the performance of LEGO-Net in Dice index further confirms the vital importance of LEGO-Net in improving the accuracy of identifying cell properties.

Fig. 9

Visualization of some of the comparison experiments on the SegPC-2021 dataset.

Table 4 Comparison of experimental outcomes among various networks on the ISIC2017 dataset.

The results shown in Fig. 9 clearly demonstrate the excellent ability of the LEGO-Net network to extract tissue features of interest and restore their boundary contours. Especially in the first line, the contour of the organ reconstructed by LEGO Net is very consistent with the real anatomical structure. As shown in the fourth row of the figure, LEGO-Net can also reliably identify the main organ elements in scenes with sparse regions of interest. Overall, among all the compared segmentation models, LEGO-Net performed the best in the segmentation tasks of cytoplasm and nucleus. This strongly proves that the LEGO-Net proposed in this paper greatly improves the accuracy of boundary pixel model recognition.

The data in Table 4 clearly demonstrate that the segmentation performance of the LEGO Net network on the skin disease segmentation dataset far exceeds that of other compared networks. Firstly, CFEM can highlight the importance of lesion features by analyzing the interrelationships between pixels in the channel dimension. Secondly, DCRM can not only capture detailed local structural information of the lesion area, but also comprehensively consider the overall structure of the lesion. More importantly, by mining the spatial relationships between row and column elements in the feature map, DCRM significantly enhances the network’s ability to capture local detail information, especially the contour of lesion tissue edges.

Comparison of ablation experiments

Table 5 Results of ablation experiments on the Synapse dataset. Among them, DSC (M+SD) represents the mean and standard deviation of DSC. DSC (CI) represents the 95% confidence interval of DSC. HD (M+SD) represents the mean and standard deviation of HD.

Next, we will verify the related ablation experiments of DCRM and CFEM in LEGO-Net on three datasets. Among them, “Without DCRM+CFEM” means LEGO-Net doesn’t use DCRM and CFEM. “Only DCRM” means that LEGO-Net uses DCRM in the deepest layer of the encoder and at two jumping connections. “Only CFEM” means that LEGO-Net uses CFEM in three different positions in the encoder at the same time. DCRM 1+CFEM represents LEGO-Net using CFEM at three different positions in the encoder and DCRM after the encoder output. DCRM 2+CFEM represents LEGO-Net using CFEM at three different positions in the encoder and DCRM at the deepest jump connection. DCRM 3+CFEM represents LEGO-Net using CFEM at three different positions in the encoder and DCRM at the second layer jump connection. As depicted in Fig. 1, DCRM+CFEM stands for LEGO-Net.

As illustrated in Table 5, the inclusion of CFEM at three distinct positions within the encoder, labeled “Only CFEM,” significantly enhances the segmentation model’s capability to recognize the entire lesion area when compared to the “Without DCRM+CFEM” condition. This demonstrates that CFEM effectively emphasizes the significance of elements that facilitate the differentiation of foreground features. The “Only DCRM” module has yielded the highest HD score, thereby verifying that DCRM is instrumental in enhancing the model’s proficiency in detecting lesion boundaries. Deploying DCRM at various locations within LEGO-Net has yielded diverse segmentation outcomes, indicating that DCRM’s processing of feature maps across various scales influences the network’s focal points of learning. When CFEM and DCRM are simultaneously applied at different positions, the network attains the best overall performance.

Table 6 Results of ablation experiments on the ACDC dataset. Among them, DSC (M+SD) represents the mean and standard deviation of DSC. DSC (CI) represents the 95% confidence interval of DSC. HD (M+SD) represents the mean and standard deviation of HD.

Table 7 Results of ablation experiments on the SegPC-2021 dataset. Among them, DSC (M+SD) represents the mean and standard deviation of DSC. DSC (CI) represents the 95% confidence interval of DSC. HD (M+SD) represents the mean and standard deviation of HD.

Table 6 displays that when LEGO-Net employs CFEM and DCRM at various positions within the ACDC dataset, it achieves Dice and HD scores of 83.26% and 1.03, respectively. Utilizing both CFEM and DCRM for feature extraction, denoted as “DCRM+CFEM,” results in superior extraction of detailed tissue and overall structural information of lesions. Given the close proximity of the three types of foreground organs in the ACDC dataset, the network must possess robust capabilities for distinguishing local information and recognizing edge pixels to accurately classify each pixel. The improvements seen when using either CFEM or DCRM individually, as compared to the “Without DCRM+CFEM” condition, effectively validates the efficacy of both CFEM and DCRM.

Table 7 presents the outcomes of ablation studies conducted on the SegPC-2021 dataset. The table reveals that while employing DCRM and CFEM separately can enhance the model’s segmentation performance, the “Only DCRM” approach yields a superior Dice and HD score. This finding underscores the advantage of DCRM in distinguishing the lesion’s edge and overall structural information through its synchronized local and global modeling techniques.

In addition, as shown in Tables 5, 6, and 7, the mean and standard deviation of the proposed algorithm on the DSC index indicate significant performance advantages and higher stability. Given that the confidence interval of the algorithm in this study is relatively narrow, this further confirms the reliability and accuracy of its performance evaluation. These statistical results collectively indicate that this algorithm provides more accurate and reliable performance in related tasks.

Comparison of number of participants

To comprehensively evaluate the model’s performance, it is essential to consider not only the enhancement of segmentation efficacy but also the comparison of the model’s parameter count. As detailed in Table 8, the number of parameters in LEGO-Net is contrasted against several mainstream models, including those based on Convolutional Neural Networks (CNN) like U-Net and R50 U-Net, models that leverage attention mechanisms like R50 Att-UNet and Att-UNet, models that integrate CNN and Transformer technologies such as TransUNet, MT-UNet, and TransClaw, and models that are entirely built upon the Transformer architecture like TransDeepLab and SwinUNet. The results of this comparison clearly indicate that our proposed network demonstrates superior performance in terms of parameter count, highlighting its ability to enhance segmentation accuracy while effectively managing the model’s parameters. Nevertheless, the utilization of DCRM and CFEM to compute correlations between pixels in the feature map space and pixels in the channel dimension does increase the computational complexity of the network. In addition, the comprehensive evaluation of GPU usage and inference time shows that the algorithm proposed in this study has the fastest inference speed. This result highlights the significant advantage of our algorithm in inference efficiency, providing strong evidence for its performance in practical applications.

Table 8 Number of parameters for different network architectures. Among them, Inference Time (M) represents the time required for the algorithm to reason about the test set in the Synapse dataset, and M represents minutes.

Conclusions

Medical image segmentation is a complex task, particularly when it comes to identifying and localizing the boundaries of pathological tissues. Given the intricate interplay of human organs and tissues and the ambiguous demarcation between diseased and healthy regions, the segmentation algorithm must possess high recognition acumen and overall performance. To address these challenges, this paper introduces a novel medical image segmentation model, LEGO-Net, which incorporates a DCRM (Detail and Contour Recognition Module) to achieve precise delineation of pathological tissue boundaries. The DCRM plays a pivotal role in the model’s innovation and offers two significant contributions. Firstly, by deeply analyzing the spatial correlation of elements in the feature map, the DCRM enhances the model’s capability to differentiate boundary elements of diseased tissue. Secondly, the DCRM not only captures and leverages local details of the lesion area but also considers the overall tissue structure by integrating local and global perspectives, enabling more accurate contouring of lesion tissues. Additionally, the CFEM (Channel Feature Enhancement Module) is introduced to analyze the correlation of elements along the channel dimension, thereby enhancing the model’s ability to distinguish regions of interest and backgrounds. Through a series of meticulous experimental validations, the segmentation network proposed in this paper demonstrates its effectiveness in delineating the boundaries of pathological tissues.

In summary, this algorithm effectively addresses the shortcomings of existing models in terms of synchronization between local and global modeling. However, there are also several areas for improvement in this algorithm. In the feature extraction stage, this algorithm is still unable to automatically quantify the importance of local and global information, making it difficult to automatically adjust the weights of local and global modeling according to different application scenarios. We will further optimize and improve the relevant mechanisms in future research to address this issue.