Research on the electro-magnetic-thermal–mechanical characteristics of shearer cables

Abstract

Cables provide power and control signals for the shearer, playing a crucial role in ensuring the reliable operation of the shearer. Utilizing MCP0.66–1.14 (3*95 + 1*35) and control wire core cross-sectional areas of 4mm², 6 mm², and 10 mm² as the specifications for shearer cables, a 3D model of the cable is developed utilizing the theta and trajpar functions. A four-field coupling simulation model for the electrical, magnetic, and thermal characteristics of shearer cables is established based on the fundamental principles of electric and magnetic fields, temperature fields, and structural mechanics. An orthogonal experiment was designed to investigate the electromagnetic loss characteristics of cable control wire core under various influencing factors. The results suggest that among the three factors: cable pitch-to-diameter ratio, cross-sectional area, and current-carrying capacity, the cross-sectional area significantly affects the magnetic flux density mode, current density mode, and volume loss density of the control wire core. A cable motion simulation experiment was conducted with a shearer traction speed of 6 m/min along cable to obtain the characteristics of cables of different specifications. The variation patterns of these characteristics were then analyzed. The research results indicate that: During the straight segment of the cable, as the cross-sectional area of the control wire core conductor increases, the equivalent stress, temperature, current density mode, and volumetric loss density gradually decrease, while the magnetic flux density mode shows a slight increase. In the bending segment of the cable, an increase in the cross-sectional area of the control wire core conductor leads to a gradual increase in equivalent stress, while temperature, magnetic flux density mode, volumetric loss density, and current density mode all gradually decrease. Using cables of the same specifications, the influence of the cable section-to-diameter ratios (4, 5, 6, 7, and 8) on cable characteristics was investigated. The results indicate that as the cable section-to-diameter ratio increases, equivalent stress increases, temperature decreases, and magnetic flux density mode, current density mode, and volumetric loss density slightly decrease. Experiments were conducted using the cable bending test machine developed by the Yankuang Group. The experimental results demonstrated a strong agreement between measured and simulated values of the cable’s outer sheath surface temperature and equivalent stress. The maximum deviation between experimental and simulated values for the outer sheath surface temperature was 2.40%, and for the equivalent stress, 4.66%. These findings are significant for improving the overall performance of shearer cables and provide theoretical guidance for their design and development.

Introduction

The operational environment of a shearer is challenging and complex. Cables play a crucial role in transmitting power and control signals, significantly impacting the reliability of the shearer. As the installed capacity of coal mining equipment increases, the utilization of mining power cables has also risen, leading to a proportional increase in cable failure rates^1,2. The "Guiding Opinions on Accelerating the Intelligent Development of Coal Mines," jointly issued by the National Development and Reform Commission, the Energy Administration, and eight other ministries and commissions, emphasize that addressing the comprehensive technological challenges of fully mechanized mining operations is key to supporting the rapid transformation of the coal industry and advancing high-quality development³. In recent years, numerous scholars have conducted research on cables using multi-physics field coupling technology to reduce cable faults in shearers, improve operational efficiency, and enhance the intelligence level of shearers⁴. Tai Baoyu et al.⁵ conducted simulations on the temperature of the internal insulation layer of high-voltage cables using multi-physics field coupling technology. Their findings revealed that incorporating air outlets or introducing ventilation equipment during cable installation can significantly reduce cable temperature and improve its current-carrying capacity. Niu Jing⁶ used COMSOL Multiphysics software to develop an electromagnetic-thermal multiphysics coupling model for mining fiber optic composite high-voltage cables. The study focused on analyzing the temperature correlation between the cable wire core and the temperature-measuring fiber under abnormal operating conditions. Li Jilai et al.⁷ conducted a study on electrical faults in optoelectronic composite submarine cables by integrating multiple physical fields of electricity and heat. Their research established a theoretical foundation for monitoring the degradation of Cross-Linked PolyEthyline(XLPE) insulation layers. Qu Mingxin et al.⁸ used the COMSOL simulation platform to develop a multiphysics field coupling model for AC three-core and DC single-core submarine cables. They performed calculations on the current-carrying capacity, providing a foundation for the strategic selection of submarine cable installation schemes. Zhu Jiang⁹ developed a temperature field monitoring system for power cables using multiphysics field coupling. The system obtained the temperature distribution of power cables under various laying conditions, providing a foundation for the sensor layout of the monitoring system.Wang Yanwen et al.¹⁰ introduced a method for calculating the surface temperature of a cable’s outer sheath, enabling the prediction of the cable wire core temperature and fault detection.Wang Yannan et al.¹¹ investigated the effects of laying depth and the thermal conductivity of thermal backfill on cable temperature, using the coupling characteristics of multiple physical fields. The findings indicate that selecting the appropriate laying depth and thermal conductivity can enhance cable heat dissipation and ensure cable reliability.Gavin D. Scott et al.¹² presented a numerical calculation method for the magnetic field model of offshore power cables based on electromagnetic field coupling technology.Bai Xue et al.¹³ developed a simulation model using ANSYS based on the theory of power cable discharge and analyzed the magnetic field characteristics of single-core cables. This work established a foundation for using magnetic field measurement methods to detect partial discharge in power cables.Artur Cywiński et al.¹⁴ introduced a finite element-based multiphysics field method to simulate the temperature distribution in cables. The results highlighted the significant impact of uneven current distribution on heat exchange conditions, including proximity and skin effects. Liang Yongchun¹⁵ used COMSOL simulation software to establish a multiphysics field coupling model for the electric, magnetic, and thermal properties of power cable wire core. This approach provided an effective method for calculating the temperature field and current-carrying capacity of laid power cable groups. Professor Lijuan Zhao’s research team^16,28 at Liaoning Technical University developed a parametric model of a shearer cable using Rhino-Grasshopper. The dynamic characteristics of the cable during normal operation were analyzed based on the Absolute Nodal Coordinate Method (ANCM), while its mechanical properties were investigated using ANSYS-LS-DYNA software. A Temporal Convolutional Network—Bidirectional Long Short-Term Memory-Squeeze-and-Excitation Attention(TCN-BiLSTM-SEAttention)model was employed to predict the cable’s mechanical properties, and a Bi-LSTM model was used to forecast its temperature. Additionally, the influence of the cable-dragging system on the cable’s dynamic behavior was examined. This study provides a solid foundation for future research on the electromechanical, electromagnetic, thermal, and structural coupling characteristics of shearer cables.

Previous studies have laid the foundation for investigating the electro-magnetic-thermal–mechanical characteristics of shearer cables. However, most of these studies focus on submarine cables and consider only individual physical fields, without fully accounting for multi-physics coupling effects. Moreover, research on the mobile flexible cables of shearers remains in its early stages.

To address these gaps, this study builds on prior research by the project team and selects MCP0.66–1.14(3*95 + 1*35) cables with control wire core cross-sectional areas of 4 mm², 6 mm², and 10 mm² as research subjects. A 3D model of the cable is developed using the theta and trajpar functions; Orthogonal experiments are designed to explore the effects of cable control wire core pitch-to-diameter ratios, cross-sectional area, and current-carrying capacity on electromagnetic loss characteristics. The results indicate that the control wire core cross-sectional area significantly influences cable performance; Furthermore, a four-field coupled simulation model, incorporating electromagnetic, thermal, and structural interactions, is constructed to analyze the Electro-Magnetic-Thermal–Mechanical characteristics of the cable in both straight and bending segments under normal operating conditions. The impact of different total pitch-to-diameter ratios on cable Electro-Magnetic-Thermal–Mechanical characteristics is also examined. Finally, experimental validation is conducted using a cable bending test machine at Yankuang Group, verifying the accuracy of the 3D model and COMSOL numerical simulations. The findings provide a novel approach for the development of mining cables and contribute to improving their overall performance.

Construction 3D model and multiphysics field coupling model of cable

Structure of shearer cable

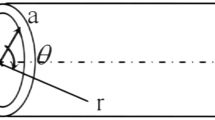
The shearer cables experience continuous motion and frequent bending during operation, which requires them to possess strong mechanical properties and an extended service life. The structural modeling parameters of the cables are listed in Table 1, while Fig. 1a) provides a schematic diagram of the cable cross-Section^16,17.

Table 1 Modeling parameters of cable structure.

Fig. 1

Schematic diagram of cable model. (a) Schematic diagram of cable cross-section. (b) Cable 3D solid model.

Construction of the 3D cable model

When constructing the cable’s layered structure using Creo Parametric, it is essential to determine the relative positions of each component to enhance modeling efficiency and accuracy. The positional relationships among the various units of the cable are illustrated in Fig. 2.

Fig. 2

Cable structure positioning relationship diagram.

Where r is the distance from the center of the wire core to the center of the cable,mm,d is the outer diameter of the strand,mm, h is pitch, theta is the angle between the line connecting the origin of the cylindrical coordinate system and the origin of the Cartesian coordinate system and the X-axis,°.

Construct a spiral using the theta function, with its mathematical model represented in Eq. (1).¹⁶.

$$\left\{ \begin{gathered} r = r_{1} \hfill \\ theta = 360 \cdot L/(d \cdot \delta ) \cdot t \hfill \\ z = W*t \hfill \\ \end{gathered} \right.$$

(1)

where, L is the length of the cable model, mm, and $\delta$ is the pitch diameter ratio.

Utilizing the trajpar function²² to define a single strand of the core cable, the mathematical model is presented in Eq. (2).

$$sd = \beta + trajpar \times 360 \times \left[ {L/\left( {d \times \delta } \right)} \right]$$

(2)

where sd is the rotation angle,°,$\beta$ is the starting angle,°, and trajpar is an independent variable that varies from 0 to 1.

Based on the structural parameters of the cable presented in Eqs. (1) and (2), as well as in Table 1, a 3D model of the cable is developed, as illustrated in Fig. 1b).

Multiphysics field coupling

The study of the mechanical properties of shearer cables involves the coupled calculation of multiple physical fields, including electric, magnetic, thermal, and structural fields, as illustrated in Fig. 3. The flow of current within the cable generates electric and magnetic fields as well as Joule heating. As the cable moves along the working face with the shearer, the electric and magnetic fields exert electric and magnetic forces, respectively. The structural field produces strain and displacement, while the temperature field influences changes in the electrical conductivity of the conductor due to temperature rise. Thermal expansion can also induce thermal stress, resulting in the coupling between these multiple physical fields.

Fig. 3

Interaction process of coupling multiple physical fields.

Simulation conditions

The cable clamp moves continuously with the operation of the shearer, causing the cable to slide along the working face due to friction. With the traction speed of the shearer set at 6 m/min, three cable specifications with control wire core cross-sectional areas of 4 mm², 6 mm², and 10 mm² are selected for electrical-magnetic-thermal-structural coupling simulations. The continuous current-carrying capacity of conductors with varying cross-sectional areas at 25 °C is presented in Table 2²³, while the mechanical performance parameters of the cable are detailed in Table 3.

Table 2 Continuous current carrying capacity of conductors with different cross-sectional areas at 25 ℃

Table 3 Mechanical property parameters of cables.

Construction of a mathematical model for multi physics field coupling

A mathematical model of the cable is formulated based on the fundamental equations and constitutive relationships of electric and magnetic field theories, the first law of thermodynamics, Fourier’s law, and the continuity equation. This model incorporates internal heating, solid heat transfer, thermoelectric coupling, and electromagnetic field modules.

The equation for the internal heating of the cable is given in Eq. (3)²⁴.

$$\left\{ \begin{gathered} \rho C_{\rho } \cdot \nabla T = \nabla \cdot \left( {k\nabla T} \right) + Q_{e} \hfill \\ Q_{e} = J \cdot E \hfill \\ \end{gathered} \right.$$

(3)

where $\nabla$ is a Hamiltonian operator, due to the establishment of a 3D model,$\nabla = \partial /\partial x + \partial /\partial y + \partial /\partial z$; $\rho$ is the density of the conductor, ${\text{kg/m}}^{{3}}$, $C_{\rho }$ is the constant pressure heat capacity, ${\text{J/}}\left( {{\text{kg}} \cdot {\text{K}}} \right)$, $T$ is the conductor temperature, $^\circ C$, $k$ is the thermal conductivity coefficient, W/(m °C)and $Q_{e}$ is the heat source heat per unit length of the cable,${\text{W/m}}$.

The equation for solid heat transfer is given in Eq. (4)²⁵.

$$\left\{ \begin{gathered} \nabla \cdot q + \rho_{1} C_{\rho 1} \frac{\partial T}{{\partial t}} = Q_{1} \hfill \\ q = - k\nabla T \hfill \\ \end{gathered} \right.$$

(4)

where q is the heat flux density, ${\text{W/m}}^{{2}}$, $\rho_{{1}}$ is the density of the solid on the heat transfer path, ${\text{kg/m}}^{{3}}$, $C_{\rho 1}$ is the constant pressure heat capacity, ${\text{J/}}\left( {{\text{kg}} \cdot {\text{K}}} \right)$, and $Q_{1}$ is the heat conduction per unit length path, ${\text{W/m}}$.

The control equation for the heat transfer module is given in Eq. (5)²⁶.

$$\rho C_{p} u \cdot \nabla T = \nabla \cdot \left( {\lambda \nabla T} \right) + Q$$

(5)

where $\rho$ is the density of the material, ${\text{kg/m}}^{{3}}$, $C_{p}$ is the atmospheric heat capacity of the material, ${\text{J/}}\left( {{\text{kg}} \cdot {\text{K}}} \right)$, $u$ is the velocity vector of the material, ${\text{m/s}}$, $T$ is the temperature of the material, ${\text{K}}$, $\lambda$ is the thermal conductivity of the material, ${\text{W/}}\left( {{\text{m}} \cdot {\text{K}}} \right)$,and $Q$ is the heating power per unit volume of the heat source, ${\text{W/m}}$.

The equation governing the electric-thermal coupling module is shown in Eq. (6)²⁷.

$$\begin{gathered} \rho C\frac{\partial T}{{\partial t}} + \rho Cu \cdot \nabla T = \nabla \cdot \left( {\lambda \nabla T} \right) + Q \hfill \\ = \nabla \cdot \left( {\lambda \nabla T} \right) + J \cdot E \hfill \\ \end{gathered}$$

(6)

The equation for the electromagnetic field module is provided in Eq. (7)²⁸.

$$\begin{gathered} \nabla \times H = J \hfill \\ B = \nabla \times A \hfill \\ J = \sigma E + j\omega D + \sigma v \times B + J_{e} \hfill \\ E = - j\omega A \hfill \\ \end{gathered}$$

(7)

where $H$ is the magnetic field strength, ${\text{A/m}}$, $J$ is the current density vector, ${\text{A/m}}^{{3}}$, $B$ is the magnetic flux density, ${\text{T}}$, $A$ is the external magnetic potential,${\text{T/m}}$, $\sigma$ is the conductivity, ${\text{S/m}}$, $E$ is the electric field strength, ${\text{V/m}}$, $\omega$ is the angular frequency, ${\text{rad/s}}$, $D$ is the angular frequency, ${\text{C/m}}^{{2}}$, v is the velocity, ${\text{m/s}}$, and $J_{e}$ is the external injection current density, ${\text{A/m}}^{{3}}$.

Analysis of multiple factors influencing the electrical magnetic loss characteristics of cable control wire core

During the normal operation of the shearer cable, the internal evolution process is characterized by a complex, time-varying, and multifactor coupling effect. The structural design of the control wire core makes it a vulnerable component within the cable system. Various factors influence the configuration of control wire cores.Utilizing the characteristics of the orthogonal experimental method, which include 'uniform dispersion and comparability,' this study focuses primarily on the control wire core of the cable. Since the strand pitch-to-diameter ratio, cross-sectional area, and current-carrying capacity significantly influence the structure of the control wire core, this research examines the distribution characteristics of magnetic flux density mode, current density mode, and volume loss density under the influence of these three factors. The results aim to provide a theoretical foundation for cable development.

Scheme design

The MCP0.66–1.14 (3*95 + 1*35) model shearer cable control wire core was selected as the subject of study, and various cable models were generated by adjusting the cable’s pitch-to-diameter ratio (4, 5, and 6), cross-sectional area (4 mm², 6 mm², and 10 mm²), and current-carrying capacity (37A, 46A, and 63A). These three variables pitch-to-diameter ratio, cross-sectional area, and current-carrying capacity,were identified as experimental factors, labeled A, B, and C, respectively. A three-factor, three-level orthogonal experiment was conducted^29,30, with the factor levels presented in Table 4.

Table 4 Factor level table.

Using the L9(3³) orthogonal table, The values of each factor were replaced with corresponding level codes, resulting in nine orthogonal test schemes. Using Creo Parametric, cable models with different structures required for the tests were established.Electromagnetic loss simulation was conducted on the nine experimental designs, resulting in data for the magnetic flux density mode, current density mode, and volume loss density of the control wire core conductor. The experimental design is presented in Table 5.

Table 5 Experimental configuration plan and orthogonal test results.

Analysis of orthogonal experimental results

Using Minitab, the sum of factor levels (K), mean (k), range (R), and variance (S) were calculated for each factor at different levels. The results of the orthogonal experiment is presented in Table 6.

Table 6 Analysis of the degree of influence of factors.

The range (R) quantifies data dispersion and variability. The results of the analysis regarding the influence of various factors are summarized in Table 6. The examination of the mean magnetic flux density mode in Table 6, reveals the relationship R_B > R_C > R_A. Among the three factors:cable pitch-to-diameter ratio, cross-sectional area, and current carrying capacity,the cross-sectional area has the most significant impact on the magnetic flux density mode, followed by current carrying capacity, while the cable pitch-to-diameter ratio exerts the least influence. In the analysis of the current density mode, the relationship R_B > R_C > R_A is observed, indicating that the cross-sectional area has the greatest effect, followed by the current carrying capacity, with the cable pitch-to-diameter ratio having the smallest effect. In the volume loss density analysis, the relationship R_B > R_C > R_A is again found, demonstrating that the cross-sectional area has the most substantial impact, followed by current carrying capacity, and with the cable pitch-to-diameter ratio having the least influence.

Variance (S) as a significance test for mean differences between samples, with higher variance indicating a more substantial effect on the cable control wire core. The analysis presented in Table 6 for magnetic flux density mode reveals the relationship S_B > S_C > S_A, signifying that the cross-sectional area has a notable impact, followed by current carrying capacity, while the cable pitch-to-diameter ratio has the least influence. In the current density mode analysis, the relationshipS_B > S_C > S_A is observed, indicating that the cross-sectional area exerts a significant impact, followed by current carrying capacity, and the cable pitch-to-diameter ratio has the lowest effect. For the volume loss density analysis, the relationshipS_B > S_C > S_A is confirmed, demonstrating that the cross-sectional area has a significant impact, followed by current carrying capacity, and the cable pitch-to-diameter ratio has the least influence.

In conclusion, both the range (R) and variance (S) are effective tools for assessing the influence levels of factors, and the results are consistent.

The influence trends of different factor levels on magnetic flux density mode, current density mode, and volume loss density were analyzed using Minitab. The factors considered were cable section diameter ratio, cross-sectional area, and current carrying capacity, which were plotted on the x-axis, while the magnetic flux density mode, current density mode, and volume loss density were plotted on the y-axis, as illustrated in Fig. 4.

Fig. 4

Analysis of factors influencing trends.

According to the curve for factor A in Fig. 4a), an increase in the pitch-to-diameter ratio of the cable results in a decrease in the mean magnetic flux density mode, with a small amplitude of change, indicating a relatively minor impact. Analysis of the factor B curve shows that an increase in the cross-sectional area leads to the most significant decrease in the mean magnetic flux density mode. Furthermore, the factor C curve demonstrates that an increase in current carrying capacity causes the mean magnetic flux density mode to rise. The order of influence on the mean magnetic flux density mode, from most to least significant, is as follows: cross-sectional area, current carrying capacity, and cable pitch-to-diameter ratio.

According to the curve for factor A in Fig. 4b), the average current density mode initially increases and then decreases as the cable pitch-to-diameter ratio rises, displaying a small amplitude of change and a relatively minor impact. The factor B curve indicates that an increase in the cross-sectional area results in the most significant decrease in the mean current density mode, suggesting a trend toward linearity. Furthermore, the factor C curve illustrates that an increase in current carrying capacity leads to a rise in the average current density mode. The order of influence of the three factors on the average current density mode, from most to least significant, is as follows: cross-sectional area, current carrying capacity, and cable pitch-to-diameter ratio.

In Fig. 4c), the factor A curve demonstrates that as the cable pitch-to-diameter ratio increases, the average volume loss density also increases, albeit with a small amplitude of change, resulting in a relatively minor impact. Conversely, the factor B curve reveals that an increase in the cross-sectional area leads to the most significant decrease in average volume loss density, exerting a substantial impact. Furthermore, the factor C curve shows that an increase in current carrying capacity results in a rise in average volume loss density. The order of influence of the three factors on average volume loss density, from most to least significant, is as follows: cross-sectional area, current carrying capacity, and cable pitch-to-diameter ratio.

In summary, the strand pitch-to-diameter ratio, cross-sectional area, and current-carrying capacity all have varying degrees of influence on magnetic flux density mode, current density mode, and volume loss density. Regarding magnetic flux density mode, an increase in the pitch-to-diameter ratio results in a slight decrease in the average value, indicating a minimal effect. However, a larger cross-sectional area significantly reduces the average magnetic flux density mode, making it the most influential factor, while an increase in current-carrying capacity leads to a rise in the average value. For current density mode, the pitch-to-diameter ratio initially increases the average value before causing a decrease, having a small impact. A larger cross-sectional area leads to a significant and linear reduction in the average current density, while an increase in current-carrying capacity raises the average value. Lastly, the average volume loss density increases slightly with the pitch-to-diameter ratio, showing a small effect, while a larger cross-sectional area markedly reduces the average value, representing the most significant influence. An increase in current-carrying capacity also raises the average value.

A comprehensive analysis of the orthogonal experiments reveals that the cross-sectional area has the greatest impact on the magnetic flux density, current density, and volume loss density of the control cores. Therefore, selecting cables with varying control core cross-sectional areas based on coal seam conditions and actual working conditions in the mining face can effectively reduce electromagnetic losses, prolong cable life, and increase coal mining efficiency.

The cross-sectional area, the pitch-diameter ratio, and the current-carrying capacity of the cable control wire core are interdependent factors that influence cable performance. First, increasing the cross-sectional area reduces electrical resistance, thereby minimizing power loss and heat generation while enhancing current-carrying capacity. However, a larger cross-sectional area also increases the cable’s weight and cost, potentially affecting installation efficiency. Second, the pitch-diameter ratio significantly impacts the cable’s mechanical properties and heat dissipation. A smaller pitch-diameter ratio enhances conductor compactness, reduces air gaps, and improves heat dissipation, thereby increasing the current-carrying capacity. However, if the pitch-diameter ratio is too small, mechanical strength may decrease, negatively affecting the cable’s flexibility and service life. Additionally, the cross-sectional area and pitch-diameter ratio must be optimized together, as a larger cross-sectional area generally requires an appropriate pitch-diameter ratio to ensure structural stability and electrical performance. Therefore, cable design must comprehensively consider these three factors to balance electrical, mechanical, and thermal properties for optimal performance. Orthogonal experiments indicate that the cross-sectional area of the control wire core has the most significant impact on cable performance. Hence, Chapter 3 focuses on investigating its influence on the Electro-Magnetic-Thermal–Mechanical characteristics of the cable.

Analysis of cable characteristics based on electro-magnetic-thermal-structural multiphysics coupling

Based on the aforementioned orthogonal experimental study, the cross-sectional area of the control wire core significantly affects the equivalent stress, temperature, current density mode, magnetic flux density mode, and volumetric loss density of the cable. Therefore, this chapter investigates the impact of the control wire core’s cross-sectional area on the Electro-Magnetic-Thermal–Mechanical characteristics of the cable.

Structural field simulation analysis

The electric and magnetic field forces, calculated from their respective fields, are treated as volume forces in the structural field. The temperature rise distribution, obtained from the thermal field simulation, is incorporated into the material properties of the structural field. The equivalent stress distribution of the cable under normal operating conditions is then computed, The equivalent stress of the cable in the straight segment during motion is shown in Fig. 5.

Fig. 5

Equivalent stress cloud diagram of the straight segment of the cable.

During typical linear motion of the cable, as shown in Fig. 5, the highest equivalent stress is concentrated near the wire core conductor of the control wire core. As the cross-sectional area of the control wire conductor increases, the maximum equivalent stress in the cable gradually decreases, stabilizing at 85.5 MPa, 83.1 MPa, and 75.7 MPa, respectively, all within the allowable stress limits. The equivalent stress distribution cloud diagram of the cable in the bending segment during motion is shown in Fig. 6.

Fig. 6

Equivalent stress cloud diagram of the bending segment of the cable.

As shown in Fig. 6, the maximum equivalent stress points of the control wire core conductor are located at the initial bending segment of the cable. As the cross-sectional area of the control wire core conductor increases, the maximum equivalent stress in the cable also increases, reaching 83.6 MPa, 96.1 MPa, and 141 MPa, respectively.

Temperature field simulation analysis

The underground working conditions in coal mines are complex, with copper conductors in cables demonstrating relatively high thermal conductivity. In contrast, the insulation layer model of EPDM(Ethylene-Propylene-Diene Monomer) rubber and the outer sheath of chloroprene rubber have low thermal conductivity, resulting in insufficient heat dissipation a rapid rise in cable temperature.

Cable straight segment temperature distribution shown in Fig. 7, indicates that the highest temperature within the cable is concentrated near the core of the control wire. Additionally, increasing the cross-sectional area of the control wire core conductor results in a slight decrease in the cable’s peak temperature, eventually stabilizing at 83.7 °C, 81.5 °C, and 78.7 °C, respectively. Prolonged exposure to excessive temperatures, while the shearer continues to pull the cable, can significantly reduce the cable’s operational lifespan.

Fig. 7

Cable straight segment temperature distribution.

The temperature distribution of the control wire core during the cable bending segment is shown in Fig. 8.

Fig. 8

Cable bending segment temperature distribution.

As shown in Fig. 8, the highest temperature of the cable is concentrated near the control wire core at the initial bending segment. As the cross-sectional area of the control wire core conductor increases, the maximum cable temperature decreases slightly, measuring 98.8 °C, 97.2 °C, and 94 °C, respectively. Prolonged exposure to high temperatures during continuous cable dragging by the shearer can reduce the cable’s service life.

Electromagnetic field simulation analysis

In the multi-physics field coupling analysis, the current transmission frequency is set at 50 Hz. Figures 9, 10 and 11 depict the distribution of magnetic flux density mode, current density mode, and volume loss density in the cable wire core conductor. These figures illustrate a significant uneven distribution of current within the cable wire core. Specifically, the current density mode is higher where the conductors are in close proximity and lower where they are farther apart, a phenomenon attributed to the skin effect and proximity effect.

Fig. 9

Magnetic flux density mode distribution of straight segment cable core conductor.

Fig. 10

Current density mode distribution of straight segment cable core conductor.

Fig. 11

Distribution of volume loss density of straight segment cable wire core conductor.

Moreover, the analysis of Figs. 9, 10 and 11 indicates that as the cross-sectional area of the control wire core increases, the magnetic flux density modes are measured at 7.29 mT, 7.34 mT, and 7.48 mT, respectively. Correspondingly, the current density modes are 12.50 A/mm², 11.00 A/mm², and 7.44 A/mm², while the volume loss densities are 2.61 MW/m³, 2.04 MW/m³, and 0.932 MW/m³.As the cross-sectional area of the control wire core expands, the magnetic flux density mode increases, resulting in a decrease in both current density mode and volume loss density. The distributions of the magnetic flux density modulus, current density modulus, and volumetric loss density of the control wire core conductor during the cable bending segment are shown in Figs. 12, 13 and 14.

Fig. 12

Magnetic flux density mode distribution of bending segment cable core conductor.

Fig. 13

Current density mode distribution of bending segment cable core conductor.

Fig. 14

Distribution of volume loss density of bending segment cable wire core conductor.

As shown in Figs. 12, 13 and 14, the maximum magnetic flux density occurs where the cable initially enters the bend, while the maximum current density and volumetric loss density are found at the cable end. With control wire core cross-sectional areas of 4 mm², 6 mm², and 10 mm², the corresponding magnetic flux densities in the cable’s control wire core conductors are 19.6 mT, 17.3 mT, and 13.7 mT, respectively. The current densities are 26 A/mm², 15.4 A/mm², and 9.11 A/mm², respectively, and the volumetric loss densities are 11.3 MW/m³, 4.02 MW/m³, and 1.4 MW/m³. In other words, as the cross-sectional area of the control wire core increases, the magnetic flux density, current density, and volumetric loss density decrease.

To make the trends of equivalent stress, temperature, magnetic flux density, current density, and volumetric loss density changes more intuitive, the simulation results of the straight and bent sections of the cable are summarized in Table 7.

Table 7 Summary of simulation data.

Table 7 summarizes the simulation data. As the cross-sectional area of the control wire cores increases to 4 mm², 6 mm², and 10 mm², the equivalent stress in the straight segment cable decreases to 85.5 MPa, 83.1 MPa, and 75.7 MPa, respectively. Correspondingly, the temperature decreases to 83.7 °C, 81.5 °C, and 78.7 °C, while the magnetic flux density increases to 7.29 mT, 7.34 mT, and 7.48 mT. The current density also decreases to 12.50 A/mm², 11.00 A/mm², and 7.44 A/mm², and the volume loss density declines to 2.61 MW/m³, 2.04 MW/m³, and 0.932 MW/m³. As the cross-sectional area of the control wire cores increases to 4 mm², 6 mm², and 10 mm², the equivalent stress in the bending segment cable decreases to 83.6 MPa, 96.1 MPa, and 141 MPa, respectively. Correspondingly, the temperature decreases to 98.8 °C, 97.2 °C, and 94 °C, while the magnetic flux density increases to 19.6 mT, 17.3 mT, and 13.7 mT. The current density also decreases to 26 A/mm², 15.4 A/mm², and 9.11 A/mm², and the volume loss density declines to 11.3 MW/m³, 4.02 MW/m³, and 1.4 MW/m³.

It can be concluded that, during the bending segment of the cable’s motion, the equivalent stress, temperature, current density, magnetic flux density, and volumetric loss density are all higher than those during the straight segment. Additionally, as the cross-sectional area of the conductor in the control wire core increases, the equivalent stress, temperature, current density, and volumetric loss density decrease during the straight segment cable, while the magnetic flux density slightly increases. In the bending segment, the temperature, magnetic flux density, current density, and volumetric loss density decrease, while the equivalent stress increases. This is because, when the cable initially enters the bending segment, it experiences compression on the inside and tension on the outside, which leads to a higher equivalent stress at the point of bending.

The influence of the total pitch diameter ratio on the characteristics of cables

Based on the preceding multi-physics field simulation analysis, cables with identical specifications and total cable pitch-to-diameter ratios of 4, 5, 6, 7, and 8 were selected for further simulation. Figure 15 illustrates the variations in equivalent stress, temperature, magnetic flux density mode, current density mode, and volume loss density in relation to the total cable pitch-to-diameter ratio.

Fig. 15

The relationship between equivalent stress, temperature, magnetic flux density mode, current density mode, and volume loss density with the variation of cable pitch diameter ratio.

As shown in Fig. 15, as the total cable pitch-to-diameter ratio increases, the equivalent stress rises to 72.5 MPa, 73.2 MPa, 74.3 MPa, 74.8 MPa, and 75.7 MPa, respectively. Simultaneously, the temperature decreases to 82.7 °C, 81.4 °C, 80.2 °C, 79.5 °C, and 78.7 °C, respectively. The magnetic flux density mode slightly decreases to 7.92 mT, 7.78 mT, 7.73 mT, 7.58 mT, and 7.48 mT, respectively. Likewise, the current density mode marginally declines to 8.85 A/mm², 8.73 A/mm², 8.65 A/mm², 8.33 A/mm², and 7.44 A/mm². Additionally, the volume loss density experiences a slight decrease to 1.410 MW/m³, 1.355 MW/m³, 1.265 MW/m³, 1.071 MW/m³, and 0.932 MW/m³, respectively. These results indicate that appropriately reducing the total cable-to-diameter-ratio can enhance the cable’s mechanical properties while slightly increasing the temperature, magnetic flux density mode, current density mode, and volume loss density. Furthermore, an excessively small total cable cable pitch-to-diameter ratio may raise the cable’s manufacturing costs. Therefore, the optimal total cable cable pitch-to-diameter ratio should be determined comprehensively based on coal seam conditions and the actual working environment of the coal mining face.

As shown in Fig. 15, as the total cable pitch-to-diameter ratios increases, the equivalent stress of the cable rises, while the cable temperature decreases. Additionally, the mode of magnetic flux density, current density, and volume loss density exhibit a slight reduction. According to Reference ¹⁶, an increase in the lay pitch diameter ratio leads to an increase in equivalent cable stress, though the maximum value remains below 80 MPa. Based on the general provisions for mobile soft cables used in coal mines²³ and the findings in References²⁰ and²⁶, the maximum operating temperature of shearer cables under normal working conditions is 75 ± 8 °C. In this study, the maximum cable temperature does not exceed 77 °C, and it gradually decreases with an increasing lay pitch diameter ratio. Furthermore, as indicated in Reference²⁶, the volume loss density of the cable decreases as the total cable pitch-to-diameter ratios increases, with a maximum volumetric loss density remaining within 1.5 MW/m³ and showing minimal variation. The mode of magnetic flux density and current density serve as key parameters for describing the electromagnetic characteristics of the cable. Their variation trends align with those of the volumetric loss density, with maximum values remaining within 8 mT and 9 A/mm², respectively, and exhibiting only minor fluctuations.

The variation trends and maximum values of the parameters analyzed in Fig. 15 are consistent with the references cited, thereby validating the accuracy of the proposed model and simulation method.

Straight segment outer sheath experimental validation

During the normal operation of the straight segment of the shearer cable with a control wire core cross-sectional area of 10 mm², the equivalent stress and temperature of the cable outer sheath remain relatively low. The distribution of equivalent stress and temperature is shown in Fig. 16.

Fig. 16

Equivalent stress and temperature distribution cloud diagrams of the cable outer sheath.

As shown in Fig. 16, the maximum stress of the cable outer sheath is 30.8 MPa, and the highest temperature is 43 °C. The primary reason for this is that the outer sheath is relatively thick and made of neoprene, which has a low thermal conductivity. As a result, during normal operation, the outer sheath can absorb some of the stress while also having difficulty dissipating internal heat, leading to relatively low equivalent stress and temperature.To evaluate the operational status of the cable, a bending test was conducted using the Yankuang Group’s cable bending testing machine, with a traction speed of 6 m/min. The cable with a control wire core cross-sectional area of 10 mm² was selected as the test subject. When the testing machine detected a circuit failure in the cable, it issued an alarm and ceased loading. Existing cable bending test machines can only monitor the stress and temperature of the cable’s outer sheath by placing strain gauges and temperature sensors on its surface. In this experiment, the temperature sensors and strain gauges were positioned between the cable and the cable clamp, directly attached to the outer sheath. The experimental setup is shown in Fig. 17.

Fig. 17

Test equipment diagram.

Ten sets of temperature and equivalent stress data from the normal operation of a straight segment cable were randomly selected for comparison between COMSOL simulation results and experimental data, as shown in Table 8.

Table 8 Comparison of experimental and simulated values.

As shown in Table 8, the experimental values of the cable’s outer sheath temperature and equivalent stress closely align with the simulation results. The maximum error between the experimental and simulation values for the outer sheath temperature is 2.40%, while the maximum error for the equivalent stress is 4.66%. These experimental results validate the accuracy of the developed three-dimensional simulation model and further confirm the reliability of COMSOL simulations. Additionally, they provide new insights for the multiphysics coupling analysis of cable temperature in shearer applications.

Conclusion

This study investigates the Electro-Magnetic-Thermal–Mechanical characteristics of the mobile soft cable in shearers using multiphysics coupling technology. It lays a solid foundation for researching intelligent fiber-optic sensing cables and holds significant practical implications for advancing the automation of coal mines. The specific conclusions are as follows:

• (1) Utilizing Minitab design, orthogonal experiments were conducted to investigate the multifactorial influence on the electrical-magnetic loss characteristics of cable control wire cores. The study revealed that among the three factors, the cross-sectional area has a significant impact on the magnetic flux density mode, current density mode, and volume loss density of the control wire cores.

• (2) A four-field coupling simulation model for the electrical-magnetic-thermal structure of cables was established using COMSOL Multiphysics field coupling simulation technology. The results indicate that during the straight segment of the cable, as the cross-sectional area of the control wire core conductor increases, the equivalent stress of the cable gradually decreases to 85.5 MPa, 83.1 MPa, and 75.7 MPa, respectively. The conductor temperature of the cable also decreases progressively, reaching 83.7 °C, 81.5 °C, and 78.7 °C. Meanwhile, the magnetic flux density mode exhibits a slight increase, measuring 7.29mT, 7.34mT, and 7.48mT. Conversely, the current density mode gradually decreases to 12.5A/mm², 11A/mm², and 7.44A/mm², while the volumetric loss density also declines, reaching 2.61 MW/m³, 2.04 MW/m³, and 0.932 MW/m³, respectively. During the bending segment of the cable, as the cross-sectional area of the control wire core conductor increases, the equivalent stress of the cable gradually increases to 83.6 MPa, 96.1 MPa, and 141 MPa, respectively. The conductor temperature of the cable decreases progressively, reaching 98.8 °C, 97.2.5 °C, and 94 °C. Meanwhile, the magnetic flux density mode exhibits decrease, measuring 19.6mT, 17.3mT, and 13.7mT. Conversely, the current density mode gradually decreases to 26A/mm², 15.4A/mm², and 9.11A/mm², while the volumetric loss density also declines, reaching 11.3 MW/m³,4.02 MW/m³, and 1.4 MW/m³, respectively.

• (3) This study investigates the Electro-Magnetic-Thermal–Mechanical characteristics of cables by selecting cables of the same specification with varying cable pitch-to-diameter ratio of 4, 5, 6, 7, and 8. The results indicate that as the cable p pitch-to-diameter ratio increases, the equivalent stress slightly rises to 72.5 MPa, 73.2 MPa, 74.3 MPa, 74.8 MPa, and 75.7 MPa, respectively. Simultaneously, the temperature decreases slightly to 82.7 °C, 81.4 °C, 80.2 °C, 79.5 °C, and 78.7 °C. The magnetic flux density mode exhibits a slight decrease to 7.92 mT, 7.78 mT, 7.73 mT, 7.58 mT, and 7.48 mT, while the current density mode decreases slightly to 8.85 A/mm², 8.73 A/mm², 8.65 A/mm², 8.33 A/mm², and 7.44 A/mm². Furthermore, the volume loss density decreases slightly to 1.410 MW/m³, 1.355 MW/m³, 1.265 MW/m³, 1.071 MW/m³, and 0.932 MW/m³.

• (4) The cable was tested using the bending testing machine from Yankuang Group. After the testing was halted, Ten sets of temperature and equivalent stress data from the normal operation of a straight cable segment were randomly selected for comparison between COMSOL simulation results and experimental data. The results indicate that the experimental values of the cable’s outer sheath temperature and equivalent stress closely align with the simulation results. The maximum error between the experimental and simulation values for the outer sheath temperature is 2.40%, while the maximum error for the equivalent stress is 4.66%.