Artificial intelligence for streamflow prediction in river basins: a use case in Mar Menor

Abstract

Streamflow prediction is crucial for efficient water resource management, flood forecasting and environmental protection. This is even more important in areas particularly vulnerable to environmental changes such our study area—the Mar Menor basin in the Region of Murcia, Spain—with a specific emphasis on the Albujón watercourse, a significant contributor to the Mar Menor. Utilizing data from stream gauge stations, nearby rain gauge stations, and piezometers, our research forecasts streamflow at two critical points: “La Puebla” and “Desembocadura” along the watercourse. Targeting short-term forecasts of 1, 12, and 24 hours, our study employs Machine and Deep Learning techniques after data preprocessing, which includes station selection, data granularity adjustment, and feature selection. A state-of-the-art data augmentation technique was used to balance periods of low and high streamflow. Results show that Random Forest slightly outperforms LSTM for 1-hour forecasts (NSE > 0.89, MAE < 0.01), while Long Short Term Memory with data augmentation excels for 12 and 24-hour forecasts (NSE > 0.12, MAE < 0.05). This is noteworthy in areas with torrential rains causing rapid streamflow increases, a more challenging yet less studied scenario in forecasting. The findings contribute to addressing the challenges associated with streamflow prediction in vulnerable regions.

Introduction

Accurate and timely predictions of streamflow are essential to support informed decision-making processes¹ for effective water resource management, flood forecasting, and environmental protection. These predictions are particularly crucial in regions like the Mar Menor basin in the Region of Murcia, Spain. This basin includes the Albujón watercourse, which stands out as one of the most critical contributors to the Mar Menor lagoon’s water quality and its ecological balance. The Albujón’s highly variable streamflow, characterized by torrential rains and low baseline flows, presents unique challenges for prediction, making it an ideal focus for this study.

Traditional hydrological models, while foundational, often encounter limitations in capturing the intricate nonlinear relationships inherent in river systems. Variabilities arising from land use changes, precipitation patterns, and the dynamic interactions of surface and groundwater further compound the challenges of precise streamflow prediction. Recent advancements in Artificial Intelligence (AI), specifically Machine Learning (ML) and Deep Learning (DL) techniques, have shown considerable promise in overcoming these limitations. These techniques excel in identifying complex patterns in large datasets, making them particularly suitable for streamflow prediction in regions with challenging hydrological conditions².

Despite extensive research into hydrological modeling and AI applications in water management, studies explicitly focusing on short-term streamflow prediction in ephemeral or highly variable watercourses remain scarce. Existing works on the Mar Menor basin have predominantly addressed broader ecological concerns, such as eutrophication³, water quality monitoring, and lagoon dynamics⁴. While these studies underscore the basin’s environmental significance, they do not address the critical need for precise streamflow forecasts to manage water resource challenges effectively.

The considerable volume of water that the Albujón watercourse carries, especially during periods of increased precipitation or runoff events and the fact that it reaches regions characterized by diverse land uses, including agricultural lands, urban areas, and natural habitats, makes it the most important contributor to the Lagoon in terms of water influx. In that sense, in this study, we focus on two of its critical points: “La Puebla” and “Desembocadura” for several horizons within 24 h.

The structure of the paper is as follows: Section “Related work” analyzes and describes the state of the art regarding streamflow forecasting and the Mar Menor ecosystem. Then, in Sect. “Materials and methods” a detailed description of the study area is provided, the process of data collection and the ML algorithms used, and Sect. “Methodology” presents our AI-based methodology. Section “Experiments and results” describes the results of the models applied to the locations of interest. The paper concludes in Sect. “Conclusions and future work” and suggests future lines of research.

Related work

Predicting streamflow in river basins is a crucial task in hydrology, necessary for efficient water resource management, flood forecasting, and environmental protection. The field has experienced a paradigm shift from traditional hydrological models to more advanced, data-driven approaches, thanks to the advent of sophisticated computational techniques. This section reviews recent advancements in streamflow prediction, highlighting the methodologies, achievements, and challenges in this field.

The application of AI has become increasingly popular in the past two decades as it has exhibited significant progress in forecasting and modeling non-linear hydrological applications. Reference² identified Artificial Neural Networks (ANN), Support Vector Machines (SVM), and other ML algorithms as suitable for capturing the complexity inherent in hydrological data. In addition, the review from⁵ compared ANNs, SVMs and Adaptative Neuro-Fuzzy Inference Systems (ANFIS) to traditional physics-deterministic models, concluding that AI-based modeling frameworks are overcoming the limitations faced by traditional methods. Afterward⁶, highlighted the transition from basic ML models to more sophisticated hybrid, modular and ensemble approaches. Hence, enhanced ML algorithms and the newer DL approaches seem to be the most promising ways for the purpose of streamflow predictions.

The Mar Menor lagoon and its surrounding areas have been extensively studied across various ecological disciplines. In⁷, the lagoon was analyzed to mitigate issues such as eutrophication, a topic also explored by⁸ in its estimates of chlorophyll-a levels. Additional research has already been conducted using satellite imagery to address eutrophication, map the distribution of water quality indicators, and assess dissolved oxygen levels^4,9,10. Therefore, numerous studies have been conducted on the Mar Menor coastal lagoon and its surrounding ecosystem, and while some of these utilize ML and AI, none specifically focuses on predicting streamflow.

Streamflow forecasting involves a wide range of methodologies and contexts, including various locations, features, time horizons, data sources, and algorithms. Streamflow prediction models are applied across diverse geographical settings, from snow-fed rivers in mountainous regions to rain-dependent streams in flatlands, each with its unique hydrological characteristics. These models incorporate different features to provide a comprehensive view of the factors that influence river behaviour. The time horizons for predictions vary significantly, ranging from short-term forecasts crucial for flood management to long-term projections essential for water resource planning. The models rely on a variety of data sources, such as in-situ measurements, remote sensing data, and historical hydrological records. The complexity and adaptability of streamflow prediction models are underscored by the rich diversity in locations, features, time horizons, data sources, and algorithms. These models cater to the specific needs and challenges of different hydrological environments. In the following paragraphs, the literature that addresses these factors is reviewed, commencing with publications that investigate larger time horizons and progressing to those focused on shorter durations.

Beginning with forecasts for extended prediction horizons, Liu et al.¹¹ explores the application of the Relevance Vector Machine (RVM) for long-term streamflow forecasting, specifically over a one-year period. The study compares the performance of RVM with that of Support Vector Machines (SVMs), a model commonly used in hydrology and water resources research, as discussed below. Similarly, in their study on long-term forecasting, Waqas et al.¹² collected data from up to eight stations along the basin and employed algorithms such as Tree Boost (TB), Decision Tree Forest (DTF), Single Decision Tree (SDT), and Multilayer Perceptron Network (MLP) to generate predictions with both annual and seasonal time horizons.

Monthly time horizons are widely used in streamflow forecasting, particularly in studies with sufficient data availability. Yaseen et al.¹³ explores the potential of the Extreme Learning Machine (ELM) for forecasting monthly streamflow discharge rates and compares its performance to that of Support Vector Regression (SVR) and the Generalized Regression Neural Network (GRNN). Other AI techniques, such as ANFIS and ANN, are incorporated by¹⁴ for the same purpose. Similar to the previous study, prior streamflow values were used as inputs, but cyclic terms were also included. In another comparison of ML techniques, Patel and Ramachandran¹⁵ uses daily discharge as input for Auto-Regressive Integrated Moving Average (ARIMA), ANN, and SVR, concluding that ARIMA models were less effective in capturing nonlinear dynamics compared to SVR and ANN. This aligns with the findings of¹⁶, which conclude that ARIMA underestimates real runoff.

Other studies also explore the monthly time horizon but with enhanced variations of ML algorithms. Mohammadi et al.¹⁷ evaluates the performance of two process-driven conceptual rainfall-runoff models and several hybrid models based on AI methods for simulating streamflow, using streamflow and precipitation data as inputs. Although AI demonstrated better overall performance, hybrid models improved streamflow accuracy in watersheds with limited data. In¹⁸, a selection of lagged streamflow values is taken as input from 1 up to 24 months, demonstrating the potential of fuzzy logic when using only lags from the target variable, especially for low flows. A different approach is presented in¹⁹, which incorporates different timescales of the data to represent seasonality and irregularity, resulting in improved forecasting performance for peak values with a modified ANN. Continuing with the improvement of ML techniques, Guo et al.²⁰ modifies a SVM to enhance its resilience to noise in the streamflow time series. Further improving SVMs, Luo et al.¹⁶ proposes a framework that integrates factor analysis, time series decomposition, data regression, and error suppression to enhance the accuracy of monthly streamflow forecasting. This framework introduces the integration of Grey Correlation Analysis (GCA), the Seasonal-Trend Decomposition Procedure Based on Loess (STL), and Support Vector Regression (GCA-STL-SVR) and employs the Autocorrelation Function (ACF) for feature selection of multiple lagged streamflow times. Other hybrid models are investigated in Fathian et al.²¹, which integrates two time series analysis approaches with three artificial intelligence models, concluding that hybrid models perform best when using monthly river flow as input.

Typically, the primary goal of long-term forecasts is effective water resource management, particularly in the context of climate variability and increasing demand, followed by flood mitigation and the development of safety measures. While this approach is reasonable, in an environment like the Albujón watercourse-characterized by heavy rains-such a time horizon is too long to provide a timely response in a rapidly changing scenario. Therefore, it is essential to focus on shorter timeframes.

The other widely studied time horizon is one day (24 h). In²², two scenarios for input variables are presented: one using only lagged streamflow and another incorporating external variables such as rainfall, water level, and others. The best performance is achieved by an enhanced ELM, which is proposed as a suitable model for hydrological forecasting in tropical river systems. Rivers in cold-humid and humid climates are studied in²³, where the M5 model tree (M5Tree) and MARS models are enhanced with ensemble empirical mode decomposition (EEMD). The EEMD-MARS model achieves high efficiency in forecasting, with significant improvements in accuracy over standalone models. Moreover, Khand et al.²⁴ concludes that increasing the complexity of LSTM by adding layers does not necessarily improve predictions. In line with the goal of improving existing algorithms, Yilmaz et al.²⁵ reinforces statistical methods with an ANN to mitigate errors, and uses a method that considers donor basins streamflow, enhancing its suitability for streamflow prediction in regions with limited data. Another variation of ELM for daily forecasts is presented in²⁶, which evaluates its results in two basins. The study finds that the best results are obtained using two previous time lags of streamflow and precipitation for one basin, while in the other basin, precipitation does not significantly influence the forecast. Parisouj et al.²⁷ examines both monthly and daily forecasts using SVR, ANN, and ELM in four rivers, one of which has a Mediterranean climate. The results indicate that SVR exhibits the best overall performance, whereas ANN-BP is the weakest. Another study, Karran et al.²⁸, conducted in watersheds with Mediterranean, Oceanic, and Hemiboreal climates²⁹, applies ANN, SVR, Wavelet ANN, and Wavelet SVR, using as inputs daily streamflow, daily precipitation, minimum and maximum temperature, and their lags from one to three days, in addition to high- and low-frequency components derived from wavelet transformation. For the Mediterranean scenario, lagged precipitation exhibits the highest correlation with streamflow, which appears to be subject to rapid peaks and declines. In fact, these rapid peaks are typically the most challenging points to predict, especially in ephemeral streamflows such as the Albujón watercourse.

Lastly, the hourly time horizon is examined in Campolo et al.³⁰ for forecasting with ANN using rainfall, water level, and power production data in a basin regulated by two artificial reservoirs. Hourly intervals are studied up to 12 hours, with ANN effectively predicting water levels up to 6 hours ahead, but yielding the best results for 1-hour-ahead predictions. The reliability of ANNs, along with Long Short Term Memory (LSTM), ANFIS, and the physical model SOBEK, is evaluated in³¹, concluding that LSTM performs well for average streamflow simulation in tidal rivers, while ANFIS demonstrates the highest accuracy for peak streamflow simulation. Dehghani et al.³² also found that LSTM performed better in smaller basins with well-distributed rainfall stations, whereas CNN and ConvLSTM were more effective in larger river basins with moderate to high streamflow when forecasting 1, 3, and 6 hours into the future. Continuing with LSTMs and their variants, Lin et al.³³ presents a hybrid model composed of a first-order difference, a feedforward neural network, and an LSTM, named DIFF-FFNN-LSTM, which outperforms MLR, autoregressive (AR), ARIMA, and each component individually. Furthermore, in their particular case, it was found that inputs closer to the prediction time do not necessarily have a greater impact on accuracy. The studies mentioned so far use only hourly lags of streamflow and precipitation as inputs. In contrast, Xiang and Demir³⁴ additionally incorporates forecasts of precipitation and evapotranspiration and proposes a Neural Runoff Model (NRM), which outperforms the Generalized Recurrent Unit (GRU), Ridge Regression, and Random Forest (RF). In another scenario involving multiple gauge stations, Sit et al.³⁵ utilizes data from eight sensors along the stream to predict streamflow at the final station and proposes a GRU variant for predictions up to 36 hours. Table 1 presents a summary of daily and hourly studies, including the study location, algorithms and features used, the best-performing model, and performance metrics. Additionally, Supplementary Tables 1 and 2 contain the same summary, along with monthly and yearly studies, as well as the data source for all the studies.

The inclusion of studies with diverse forecasting horizons serves to contextualize the different methodologies available for streamflow prediction and to identify their respective strengths and limitations. These studies highlight the evolution of predictive models, from traditional hydrological approaches to AI-based techniques, as well as their application across different temporal resolutions. While these studies provide valuable insights, they often focus on either long-term predictions or larger, perennial water systems. Few studies address the unique challenges of short-term streamflow prediction in ephemeral or intermittent watercourses, such as the Albujón watercourse in the Mar Menor basin. These gaps underscore the need for models tailored to regions where streamflow is highly variable, with sudden peaks caused by torrential rains. Our work specifically addresses this gap.

Table 1 Daily and hourly summary table.

Materials and methods

This section describes the study area, data sources, and gathered data, followed by a brief mathematical explanation of the algorithms of interest is provided. Also, the metrics used to evaluate the experiments are presented.

Study area and data

Mar Menor is a coastal lagoon located in the Region of Murcia, Spain, with a surface area of 170 km², a coastline length of 73 km, and a maximum depth of 7 m. The lagoon is separated from the Mediterranean Sea by a narrow strip of land known as La Manga.

The lagoon is characterized by its shallow waters, which are typically warmer than the adjacent Mediterranean Sea. The climate is semi-arid and characterized by hot, dry summers where daytime temperatures range from 30 to 40 degrees Celsius. Winters are mild, with temperatures between 10 and 20 degrees Celsius, and frost or snow is rare.

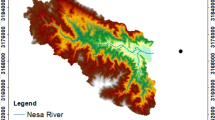
In this study, the source data are extracted from the Automatic Hydrological Information System (SAIH) of the Segura River Hydrographic Basin. It provides information on the levels and flows of the major rivers and tributaries, the levels and volumes impounded in the dams, the flows released through spillways, valves and gates, the precipitation at numerous points, and the flows withdrawn by the major water uses in the basin. As shown in Fig. 1, two main types of locations are used for this study. The stream gauge areas (stations starting with the code 06A*), in which the variables streamflow $\hbox {(m}^{3}\hbox {/s)}$ and rain gauges (mm) are selected to develop this work, and the piezometers (also referred to as Sondeos and start with the code 06Z*), in which the piezometric level (msnm) is used. All variables used in this study are publicly available at https://www.chsegura.es/es/cuenca/redes-de-control/saih/ivisor/ (Accessed December 4, 2023) and are measured every five minutes. Measurements are obtained from the Confederación Hidrográfica del Segura (CHS), the official Spanish authority responsible for managing water resources in the Segura River basin. CHS ensures high-quality measurement standards and the maintenance of sensors and devices throughout the basin. A Python script is implemented to download the required data from the web page and then save it in Parquet format for more efficient data storage.

Fig. 1

Map of all the sites used in this study in the Region of Murcia. The yellow points indicate the piezometers and the blue points the stream gauge stations. The blue line represents the Albujón watercourse. Map generated by the authors using Folium³⁶, an interactive mapping library for Python based on Leaflet.js. The specific map layer used is Esri.NatGeoWorldMap from Leaflet Providers³⁷.

Regarding the distribution of stream gauge station, location 06A18 (Desembocadura Rambla de Albujón) is the primary contributor to the Mar Menor, followed by location 06A01 (La Puebla) due to their proximity to the basin. For this work, data from a total of 12 stream gauge stations was used, with the importance of the stream gauge decreasing as one moves away from the main entrance to the Mar Menor. On the other hand, the piezometers are located to the west of the Mar Menor coast, with a total of 19 points. The stream gauge data cover a spatial area of 423.12 km², with records starting from January 8, 2016, while the piezometer data cover 41.06 km², with records starting from December 13, 2019. To develop reliable predictive models, data from March 8, 2021 (12:00 PM) to November 18, 2023 (11:55 PM) was isolated, ensuring a sufficient availability of streamflow records at the two focal points.

Methods

In this subsection, the ML and DL models employed in our study are outlined, including their respective definitions and parameter configurations.

Decision trees (DT) and random forest (RF)

A Decision Tree is a tree-like model used for both classification and regression. It partitions the data into subsets based on the features’ values, creating a tree structure where each node represents a feature, and each branch represents a decision rule. For a given observation $x_i$ with m features each decision node $j$ in a tree applies a split on a feature $f_j$ using a threshold $t_j$ as follows: $\text {if } x_i[f_j] \le t_j \text { then } \text {left branch, else right branch}$. Terminal nodes (leaves) contain the predicted value.

Random Forest was first introduced by³⁸ and is an ensemble learning method that constructs a multitude of DTs during training. It outputs the average prediction of individual trees for regression tasks or uses voting for classification. Each tree in the forest is trained on a random subset of the dataset, introducing randomness to enhance performance and reduce overfitting.

For regression tasks, the predicted output $\hat{Y}$ for a new observation $x$ is calculated as the average of predictions from individual trees. For classification tasks, it operates through a process of majority voting among the trees.

K-nearest neighbors (KNN)

KNeighbors is one of the fundamental algorithms in ML. KNN is an instance-based learning algorithm used for both classification and regression tasks. KNN utilizes the entire training dataset for both classification and regression tasks. When a new data point needs to be classified or assigned a value, KNN identifies the k closest neighbors to this point from the training dataset³⁹. In classification tasks, it calculates the distance between the new point and the existing ones using metrics like Euclidean, Manhattan, or other distance measures and once the k nearest neighbours are identified, the most frequently occurring class label among them is assigned to the new point. In regression tasks, the process is similar, but instead of assigning a class label, KNN assigns the new point the average value of its k nearest neighbors. KNN has been previously applied in marine science-related problems⁴⁰.

Linear regression (LR) and Ridge regression (L2)

Linear Regression is a fundamental statistical technique that models the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data.

Ridge Regression, also known as L2 regression, is a regularized linear regression technique that adds a penalty term proportional to the square of the magnitude of coefficients, thus helps control overfitting by shrinking the coefficients toward zero⁴¹. The formula is as follows:

$\text {Minimize } \sum _{i=1}^{n} \left( y_i - (\beta _0 + \beta _1x_{i1} + \beta _2x_{i2} + \cdots + \beta _px_{ip}) \right) ^2 + \lambda \sum _{j=1}^{p} \beta _j^2$, where

• $y_i$: Represents the observed value of the dependent variable for the $i^{th}$ observation.

• $x_{i1}, x_{i2}, \ldots , x_{ip}$: Represent the values of independent variables for the $i^{th}$ observation.

• $\beta _0, \beta _1, \ldots , \beta _p$: Are the coefficients to be estimated.

• p: Denotes the number of independent variables.

• $\lambda$: Is the regularization parameter controlling the penalty term. An increase in $\lambda$ leads to stronger regularization and greater shrinkage of coefficients.

Gradient boosting (GB) and extreme gradient boosting (XGB)

Gradient Boosting is an ensemble technique that builds a model in a stage-wise manner by combining weak learners, typically decision trees, to improve predictive accuracy. It minimizes errors by iteratively fitting new models to the residual errors of previous models.

Extreme Gradient Boosting is an optimized and efficient implementation of Gradient Boosting designed for speed and performance⁴². It employs a more regularized model formalization to control overfitting and provides various hyperparameters for fine-tuning.

Neural networks for time series: long-short term neural network (LSTM)

LSTMs are a type of recurrent neural network (RNN) architecture designed to handle the vanishing and exploding gradient problems that are present in more traditional RNNs. The original paper presenting the standard LSTM cell concept was published in 1997⁴³. LSTMs excel at capturing long-range dependencies in sequential data, making them well-suited for time series analysis, natural language processing, and other sequential tasks. LSTMs contain memory cells that maintain information over extended time intervals, selectively remembering or forgetting information through specialized gates. They consist of input, forget, and output gates, enabling the model to regulate the flow of information within the network.

The forget gate, introduced by⁴⁴, determines which information is retained or discarded from the cell state. When the forget gate value, $f_t$, is 1, the information is retained; when it is 0, the information is discarded. Figure 2, illustrates the structure of an LSTM with a forget gate. The LSTM cell can be mathematically expressed as follows:

$$\begin{aligned} f_t&= \sigma (W_f \cdot h_{t-1} + W_f \cdot x_t + b_f), \end{aligned}$$

(1)

$$\begin{aligned} i_t&= \sigma (W_{ih} \cdot h_{t-1} + W_{ix} \cdot x_t + b_i), \end{aligned}$$

(2)

$$\begin{aligned} \tilde{c}_t&= \tanh (W_{\tilde{c}h} \cdot h_{t-1} + W_{\tilde{c}x} \cdot x_t + b_{\tilde{c}}), \end{aligned}$$

(3)

$$\begin{aligned} c_t&= f_t \cdot c_{t-1} + i_t \cdot \tilde{c}_t, \end{aligned}$$

(4)

$$\begin{aligned} o_t&= \sigma (W_{oh} \cdot h_{t-1} + W_{ox} \cdot x_t + b_o), \end{aligned}$$

(5)

$$\begin{aligned} h_t&= o_t \cdot \tanh (c_t). \end{aligned}$$

(6)

Fig. 2

Architecture of LSTM with a forget gate. Image extracted from⁴⁵.

Throughout our experiments, these ML models were implemented and automatically tuned with appropriate hyperparameters to address our research objectives and optimize predictive performance.

The selection of algorithms was based on their ability to handle the complexities of the data. Specifically, RF is robust in capturing nonlinear relationships and has demonstrated success in short-term streamflow prediction studies⁴⁶. LSTM networks were chosen due to their architecture’s capability to process sequential data, making them ideal for capturing temporal dependencies in streamflow time series²⁴. Finally, other algorithms, such as Gradient Boosting, K-Nearest Neighbors, and Linear Regression, were included to serve as comparative benchmarks, highlighting the advantages of ensemble and sequential models.

Metrics

This work assesses model accuracy using the following error metrics: the Nash–Sutcliffe Model Efficiency Coefficient (NSE)⁴⁷, the reformulation of Willmott’s Index of agreement⁴⁸, Root-Mean-Square Error (RMSE), Coefficient of the Variation of the Root Mean Square Error (CVRMSE) and Mean Absolute Error (MAE).

NSE is usually defined as:

$$\begin{aligned} \text {NSE} = 1 - \frac{\sum _{i=1}^{n}(Q_{o}- Q_{p})^2}{\sum _{i=1}^{n}(Q_{o}- \bar{Q}_{o})^2} \end{aligned}$$

(7)

where $\bar{Q}_{o}$ is the mean value of observed streamflow, $Q_p$ is the predicted streamflow and $Q_{o}$ is the real streamflow. A perfect model would have an NSE of 1. An NSE of 0 means the model has the same predictive capacity as the mean of the time series, while a negative NSE indicates that the mean is a better predictor than the model.

The Willmott’s Index (WI) is calculated as follows:

$$\begin{aligned} \text {WI} = 1 - \frac{\sum _{i=1}^{n} (Q_{o} - Q_{p})^2}{\sum _{i=1}^{n} (| Q_{p} - \bar{Q}_{o}| + |Q_{o} - \bar{Q}_{o}|)^2} \end{aligned}$$

(8)

This index can take values between 0 and 1 and it represents the ratio of the mean square error and the potential error. Since NSE and WI consider square differences both metrics are overly sensitive to extreme values.

The RMSE is computed using the predictions $Q_{p}$ and the real values $Q_{o}$:

$$\begin{aligned} \text {RMSE} = \sqrt{\frac{1}{n}\sum _{t=1}^{n}\left( Q_{p} - Q_{o}\right) ^2} \end{aligned}$$

(9)

It has the same units as the predicted variable, allowing an intuitive understanding of prediction error magnitude.

CVRMSE can be computed with the RMSE:

$$\begin{aligned} \text {CVRMSE} = \frac{RMSE}{\bar{{Q}_{o}}}\times 100 \end{aligned}$$

(10)

CVRMSE is a dimensionless measure, where values close to 0 indicate better model performance. For example, a CVRMSE of 5% means that the mean unexplained variation in the real magnitude is 5% of its mean value⁴⁹.

Finally, calculate the MAE as:

$$\begin{aligned} \text {MAE} = \frac{1}{n}\sum _{i=1}^{n}|Q_{p}-Q_{o}| \end{aligned}$$

(11)

Like RMSE, MAE has the same scale as the evaluated values, but it should not be used to compare predictions across different scales.

Methodology

Fig. 3

Flowchart of the study.

The following section describes the procedures carried out to prepare the data for optimal training. These steps include data preprocessing, classification to detect streamflow peaks for dataset balancing (data augmentation), feature and algorithm selection, and final performance evaluation using the metrics described above. Figure 3 depicts the study workflow.

Data preprocessing

The data preprocessing methodology in this study focuses on extracting comprehensive insights from attributes and locations, specifically considering two key points of the Albujón watercourse: “La Puebla” (06A01) and “Desembocadura” (06A18). Given the presence of multiple sensors and locations-8 stream gauges, 12 rain gauges, and 19 piezometric level sensors-our dataset consists of diverse time series with varying start and end dates. To ensure consistency, data from all available locations and features were isolated between March 8, 2021 (12:00 PM) and November 18, 2023 (11:55 PM), guaranteeing the availability of accurate streamflow records at the two focal points. Next, we assessed the frequency of missing data (NAs) for each location and feature. Due to a high prevalence of missing values (> 50% of the values), we strategically removed certain features, including one stream gauge, two piezometric level sensors, and two rain gauge stations. For the remaining missing values, we applied two imputation strategies:

• Piezometric level and rain gauge features: Forward fill (propagating the last valid observation).

• Streamflow features: Backward fill (using the next available observation).

To facilitate ML experiments, the dataset-originally recorded at 5-min intervals was resampled into 1-hour aggregated values. For each feature, we computed statistical aggregates: mean, maximum, minimum, and standard deviation within each interval. We then shifted the index by 1 to 6 periods in the positive direction and applied rolling calculations for forecast horizons of 1 h, 6 h, 12 h, and 24 h, using rolling windows of 6 h, 12 h, 18 h, and 24 h. This preprocessing resulted in a structured dataset with 3570 features for ML models.

For deep learning (DL) experiments, we employed a simpler approach, resampling features into hourly mean values only. The resulting dataset contained 33 features, optimized for LSTM networks. The scripts needed to perform the preprocessing are available for reproducibility at https://github.com/auroragonzalez/streamflow_prediction.

Data augmentation

Within our context, that is time series prediction for streamflow, the inclusion of a dummy variable to signify streamflow peaks is imperative for a comprehensive and accurate modeling approach. Streamflow peaks represent exceptional events that deviate significantly from the regular flow dynamics and possess the potential to exert a profound influence on the overall behavior of the time series, especially in these complex scenarios. If a model neglects those peaks, its performance could be significantly reduced.

Peak values can be seen as outliers. In order to identify such points, a z-score approach is used. First, we normalize the data with respect to its mean and standard deviation, and data points where the absolute z-score exceeds a specified threshold are considered outliers or peaks.

To address consecutive outliers, a windowing approach is used. It iterates through the outlier indices, grouping consecutive indices that are within the specified window. For each group, it selects the index with the maximum corresponding data value as the representative outlier index. This is done to identify the peak value within a cluster of outliers, assuming that the highest point in the cluster is the most representative. The pseudocode of this process can be seen in Algorithm 1.

Algorithm 1

Algorithm to detect streamflow peaks

When attempting to predict peak streamflow for the test set, it was found that the problem was highly unbalanced. Several data augmentation techniques are used in our training set and then the results are evaluated on the test set. The techniques employed were: the regular resampling with sklearn, Synthetic Minority Oversampling Technique (SMOTE)⁵⁰ and Identical Partitions for Imbalanced Problems (IPIP). IPIP was previously used to train ML models on an imbalanced COVID-19 dataset⁵¹.

IPIP is an imbalance-aware and ensemble-based ML method. We split $20\%$ of the data into a test set and used the remaining data for the train set, ensuring that each set contained the same class proportion as the original set. IPIP obtains a number $b_s$ of balanced subsets by randomly subsampling the training set over the majority of class instances. Each subset contains $75\%$ of the minority class samples and has a balanced class proportion of 55–45%. The number of subsets generated, $b_s$, is determined by the minimum number needed to represent all samples of the minority class at least once. We required $b_s=7$ subsets for our datasets. A new ML model is generated for each subset and integrated into an ensemble through majority voting if it outperforms the previous ensemble, as measured by commonly used metrics for imbalanced problems such as Cohen’s Kappa⁵² and Balanced Accuracy. If not, random resampling is performed, and a new model is trained up to a predefined maximum number of attempts or models. The ensemble is evaluated at each iteration using test data. For each of the $b_s$ subsets, the ensemble classifies an observation as a member of the majority class if at least $75\%$ of the models in the ensemble classify it as negative. The final ensemble is composed of the ensembles trained on each of the p subsets. A sample is classified as negative if $50\%$ of the ensembles classify it as negative. The code required to reproduce the IPIP algorithm is available at https://github.com/antoniogt/ipip.

Feature and algorithm selection for prediction

Initially, a comparative analysis between various ML algorithms for regression using sklearn⁵³ and a Deep Learning (DL) algorithm was conducted, specifically the LSTM using keras⁵⁴, to find the best model to forecast streamflow in several time horizons. The algorithms under comparison included Random Forest (RF), KNeighbors (KNN), Linear Regression (LR), Gradient Boosting (GB), Decision Tree (DT), Ridge Regression (L2), and Extreme Gradient Boosting (XGB). To assess their performance, a time series cross-validation methodology utilizing the time series split function from the sklearn library is employed. Our approach entailed a 3-fold parameter configuration, utilizing the 25% of the dataset to evaluate and compare various error metrics. We performed feature selection for the ML algorithms due to the large number of features, selecting the top 100 features based on the k highest scores (SelectKBest). Features are scaled using RobustScaler, which allowed to scale features using statistics that are robust to outliers.

Due to the nature of our problem, obtaining negative streamflow values was not feasible; streamflow could only be 0 or positive. Nevertheless, on rare occasions, the LSTM model produced negative values. To address this issue, a straightforward function was devised to convert such negative values to 0. Furthermore, to prevent overfitting during LSTM training, we implemented early stopping with a patience of 20 epochs, restoring the model weights from the epoch with the best monitored value. We showed the effect of this technique in supplementary figure 1. Early stopping is a regularization technique that halts training once validation performance begins to degrade, rather than running for a fixed number of epochs. This approach helps the model avoid memorizing noise and enhances generalization.

Experiments and results

Fig. 4

Partitioning of streamflow for each focal point, resampled at hourly intervals for ML algorithms. (a) Streamflow from ‘La Puebla’. (b) Streamflow from ‘Desembocadura’. The blue represents the training set, while the orange represents the test set.

Fig. 5

Partial autocorrelation for both target variables. (a) Shows the partial autocorrelation of streamflow from ‘La Puebla’. (b) Represents the partial autocorrelation of streamflow from ‘Desembocadura’. The X-axis represents lags on an hourly basis, while the Y-axis indicates the value of the partial autocorrelation.

In this section, the experiments conducted are described. All necessary functions and scripts are available at https://github.com/auroragonzalez/streamflow_prediction to ensure reproducibility. The experiments were run on a VM with O.S. Ubuntu 22.04.2 LTS implemented on QEmu with 8 vCPU and 68 GB of RAM on a host with a Xeon Silver 4214R CPU @2.4GHz, and the algorithms were programmed in Python 3.11.4. The dataset is stored on an SSD-accelerated ZFS volume. Further implementation details can be found in the referenced GitHub repository.

Before presenting a detailed analysis of the ML and DL experiments and their results, the streamflow series from the two key locations along the Albujón watercourse (“La Puebla” 06A01 and “Desembocadura” 06A18) were partitioned, covering the period from March 8, 2021, to November 18, 2023. This partitioning aimed to ensure representative events and values in the test set, allocating a split of 75% for training and 25% for testing, as depicted in Fig. 4. Correspondingly, for the LSTM model, we utilized a split of 55% for training, 20% for validation, and maintained the same 25% test set. To ensure a fair comparison, evaluated both models were evaluated on the same test set (25% of the total data). The test set remained untouched during training and validation for both approaches, providing a direct and unbiased assessment of generalization performance. This setup facilitated result comparisons among algorithms.

When analyzing the target variables along the Albujón watercourse (streamflow at “La Puebla” and “Desembocadura”), a partial autocorrelation exceeding 0.9 at both locations was observed within a 1-hour time horizon, whereas autocorrelation was nearly negligible (close to 0) over a 24-hour horizon (see Fig. 5). Additionally, the Barlett’s test was conducted to assess the homogeneity of variances for both time series. The results of this test confirmed that both streamflow time series did not exhibit homogeneity. The lack of homogeneity in variances suggests that the data’s dispersion changes over time. This is a common feature of nonlinear and nonstationary time series, making it harder for linear models to provide consistent predictions.

Data augmentation results

As can be observed, the nature of our problem is highly imbalanced, a characteristic inherent to the Albujón watercourse. In most instances, streamflow remains consistently low; however, with occasional rapid increases following specific events. To account for these dynamics, a mathematical algorithm based on z-scores (see pseudocode in Algorithm 1) was applied to detect sudden streamflow increases. This was combined with an algorithm designed to handle imbalanced data, enabling the classification of these events as 0 or 1 based on the occurrence of rapid streamflow increases. The resulting classification was then incorporated as a feature in the analysis.

Table 2 Prediction of the streamflow peaks on the test set using data augmentation.

Table 2 presents the Balanced Accuracy obtained by combining different data augmentation techniques with the best-performing classification method. In most cases, applying IPIP to the training set and using Logistic Regression to predict peaks in the test set resulted in the highest accuracy. The only exception was the 1-hour predictive horizon at the “Desembocadura” gauge station, though the difference was minimal. IPIP is a metric-based approach for adding models to an ensemble. In this study, both Cohen’s Kappa and Balanced Accuracy were evaluated as selection criteria, finding that Balanced Accuracy yielded superior results in all cases. While other classifiers, such as Random Forest, were included in the pipeline, Logistic Regression consistently outperformed them. Also, it is to be noted that performing data augmentation in the 24H horizon brings a very small improvement in Balanced Accuracy. Notably, performing data augmentation for the 24-hour horizon led to only a slight improvement in Balanced Accuracy. This suggests that incorporating predicted peaks as an input variable in the streamflow prediction model has a limited impact on accuracy, contributing only a marginal increase.

As shown in Fig. 6, the data augmentation technique leads the classification algorithm to identify significantly more points than those detected by Algorithm 1. This is not necessarily a drawback, as peak detection is intended to support the subsequent streamflow estimation stage. To assess whether there was a significant difference between the values of predicted peaks and non-peak points, an independent t-test was initially considered. However, normality and homoscedasticity assumptions were not met⁵⁵, making this approach unsuitable. Instead, its nonparametric counterpart was applied, the Mann-Whitney U test, with results presented in Fig. 6 for each predictive horizon and both gauge stations. The test revealed significant differences between predicted peaks and non-peaks for the 1-hour and 12-hour horizons. However, no significant differences were observed in the 24-hour horizon.

Fig. 6

Observed and predicted streamflow peak values on the test set using the augmentation technique IPIP on the train set across 1, 12, and 24-hour time horizons for both focal points. Real streamflow values are represented in blue, computed peaks in a red cross and estimated with IPIP and Logistic Regression with a pink dot. A Mann-Whitney U test was run to determine if there were differences between the values predicted as peaks and those that were not.

Table 3 Experiments La Puebla.

Table 4 Experiments Desembocadura.

Streamflow prediction results and discussion

To identify the most effective algorithm for streamflow forecasting, multiple time horizons (1h, 12h, and 24h) were initially evaluated. After data preprocessing, feature selection, and model training using a 3-fold time series split for machine learning algorithms, we obtained test error metrics for each method. The results are presented in Table 3 for the “La Puebla” focal point and Table 4 for the “Desembocadura” focal point. Additionally, these tables include an assessment of LSTM performance in streamflow prediction. The reported values for the LSTM experiments include the mean and standard deviation after conducting training 10 times for each location (“La Puebla” and “Desembocadura”), across three time horizons (1 h, 12 h, 24 h), both with and without the IPIP algorithm. This resulted in a total of 120 training experiments with different random seeds. Figure 7 presents a visual representation of the results, allowing for an intuitive comparison of model performance. In these graphs, values near the center of the radius have been adjusted to avoid displaying extremely negative values, keeping the figure as clean as possible. A vertex at the center indicates that the corresponding value falls outside a reasonable range.

Fig. 7

Radar plots for each scenario. Each plot contains the results of all metrics for each model.

Among ML algorithms, RF achieved the best performance for streamflow forecasting at the 1-hour time horizon for the “La Puebla” point. However, for “Desembocadura,” RF yielded the lowest MAE and WI, LR outperformed in terms of RMSE, CVRMSE, and NSE, as can be seen by looking at the dark blue pentagon in subfigures a) and d) from Fig. 7, respectively. For the 12-hour and 24-hour time horizons, ML algorithms exhibited generally poor performance. In contrast, among all evaluated models-including both DL and ML approaches-LSTM with categorical data derived from IPIP (LSTM_IPIP) achieved the best results for streamflow forecasting at both the 12-hour and 24-hour horizons, which is clearly illustrated by the yellow polygon in subfigures c) to f) from Fig. 7. There, one can also observe the improvement from the regular LSTM to LSTM_IPIP by comparing with the red and yellow pentagons. After testing different LSTM architectures, the optimal configuration consisted of the following layers: (1) LSTM (128 units) and tahn activation function; (2) Dense (64 units) and linear activation function; (3) Dense (32 units) and relu activation function; (4) Dense (1 unit) and linear activation function. Additionally, LSTM_IPIP demonstrated strong predictive performance for the 1-hour horizon at both focal points. In contrast, incorporating categorical data from the IPIP-based data augmentation pipeline did not improve the performance of ML algorithms. Based on these findings, LSTM_IPIP was selected as the optimal model for our task. Figure 8 presents the observed and predicted values for LSTM_IPIP across the 1-hour, 12-hour, and 24-hour time horizons for both focal points.

Fig. 8

Observed and predicted streamflow values of LSTM_IPIP across 1, 12, and 24-hour time horizons for both focal points. Real streamflow values are represented in blue, while predicted streamflow values are in orange. Panels (a) and (b) display streamflow for the 1-hour time horizon for the “La Puebla” and “Desembocadura” focal points, respectively. Panels (c) and (d) depict the same for the 12-hour time horizon, and Panels (e) and (f) illustrate the 24-hour time horizon.

To contextualize our findings, the results described above and detailed in Tables 3 and 4 are compared with the most relevant studies summarized in Table 1 for each time horizon. This comparison allows us to assess the performance of our models relative to existing literature and highlight their significance in the scarcely studied field of ephemeral watercourse streamflow prediction. Starting with the 24-hour horizon, it has been observed that in other studies, NSE ranges between 0.33 and 0.85, while WI exceeds 0.9 in cases where it was computed. To provide proper context, these studies focus on large basins and rivers with abundant streamflow, unlike our watercourse of interest, which is much more susceptible to sudden changes. The regions where these studies were conducted have streamflows that generally range between 100 and 500 m³/s, whereas the Albujón watercourse has a streamflow between 0 and 15 m³/2. In addition, time series from larger streamflows, like those studied in the literature, tend to be more stable than the problem addressed in this work. Furthermore, it has been suggested that this watercourse can be classified as an intermittent or ephemeral stream⁵⁶, as illustrated in Fig. 4, where streamflow is frequently close to zero. The fact that NSE and WI are highly sensitive to extreme values suggests that, although the values obtained at both gauge stations may initially appear low, they are reasonable results, particularly at Desembocadura, where NSE is 0.22 and WI exceeds 0.58. CVRMSE is also affected by outliers, producing values that may not be entirely appropriate for assessing model performance. The key metrics to consider are RMSE and MAE; however, since they are scale-dependent, direct comparisons with other publications are inappropriate. Given our study’s scale, RMSE and MAE yield remarkable results, with errors in the tenths or hundredths. For the 12-hour horizon, the prediction shows a considerable improvement compared to the 24-hour forecast. This aligns with studies that indicate NSE improves over shorter time horizons, with the best values occurring at the nearest horizon. Unfortunately, studies specifically addressing the 12-hour horizon have not been found; therefore, further discussion is not possible. Lastly, in relevant studies for the 1-hour horizon, NSE values exceed 0.9, aligning with the results obtained at both gauge stations. Placing these values in the context of the study’s scale suggests that the WI and NSE results could be considered outstanding. Turning to RMSE and MAE, we observe a significant improvement, with errors in the hundredths and even thousandths. Additionally, in this scenario, CVRMSE also improves and falls within a more acceptable range.

Regarding the models used, an analysis of Table 1 and the frequency of use of each model reveals that LSTM and its variants are the most commonly used for this type of problem. In many cases, they also yield the best results^31,32,33. Our findings align with this, as LSTM and its variant-specifically the IPIP version-outperform the other options in the majority of scenarios.

Regarding the physical insights and the relationship with the models, a clear trend was observed: the closer a point in the watercourse is to the lagoon, the better the obtained results. “Desembocadura (06A18)” is the final point of the watercourse and is closer to the lagoon than “La Puebla (06A01),” which, in turn, is closer than the other four stations in the Albujón watercourse. Several factors could explain this trend. First, it is logical that as we collect data from upstream points, we gain more insights into future streamflow downstream. This suggests that previous points are useful for predicting subsequent ones due to the natural delay in the watercourse. Another key factor is the volume of water available for streamflow prediction. As previously explained, the Albujón watercourse is almost ephemeral for most upstream points and dates. However, “Desembocadura (06A18)” has the highest streamflow and remains active almost 100% of the time. The volume and variability of streamflow are crucial characteristics for ML and DL models to make accurate predictions. Finally, in areas closer to the lagoon, we also have data from piezometric level sensors. This information is more directly related to locations near the basin, ensuring a minimum level of streamflow, which further enhances prediction accuracy.

The interpretation of the results as remarkable is supported by the representation of real and predicted time series as shown Fig. 8 where two aspects can be highlighted: first, the models do not return false positives, meaning that they only predict a significant rise of streamflow when this event actually happens and secondly, when the peaks do occur, the models are able to predict adequately the situation but not capable of fully reflect the increase in streamflow.

Conclusions and future work

In conclusion, our study on streamflow prediction in the Albujón watercourse within the Mar Menor basin has provided valuable insights into the dynamics of this critical water resource. The significance of accurate streamflow predictions is particularly high, especially in regions facing environmental vulnerabilities like the Mar Menor basin.

Our research focused on two gauge stations, “La Puebla” and “Desembocadura,” employing a combination of Machine and Deep Learning techniques to address the challenges posed with torrential rainfall and sudden increases in streamflow. The study aimed to contribute to efficient water resource management, flood forecasting, and environmental protection in the endangered areas of the Mar Menor basin.

As previously mentioned, the Mar Menor lagoon and Albujón watercourse are unique due to their specific ecosystem and weather conditions. However, similar sensor-based data collection and modeling approaches could be applied to other lagoon basins worldwide. Notable examples include Étang de Thau and Étang de Vaccarès (France), Laguna de Rocha (Uruguay), Laguna Madre (Mexico/USA), Laguna Ojo de Liebre and Laguna Guerrero Negro (Mexico), and Laguna de Aveiro (Portugal), among others, where such methods could be valuable for understanding key watercourses.

The key findings indicate that Random Forest slightly outperforms other models for the short-term 1-hour time horizon, while the LSTM model, coupled with the data augmentation process, yields superior results for the 12 and 24-hour forecasts. This suggests the importance of selecting appropriate models based on the forecasting horizon, highlighting the need for a nuanced approach to streamflow prediction.

The results reveal that Random Forest yields an NSE greater than 0.89 and an MAE less than 0.01 for both gauge stations in the short-term 1-hour time horizon. Conversely, longer predictions (12h and 24h) with LSTM result in an NSE of 0.121 and 0.223 for ‘La Puebla’ and ‘Desembocadura’, respectively. Although these results for the 12 and 24-hour forecasts may not initially appear highly positive, considering the inherent characteristics of the Albujon watercourse, we regard our findings as satisfactory. We addressed a challenge involving ephemeral waterflow, characterized by streamflow registers near zero most of the time and sudden peaks several times the baseline waterflow. Given the high sensitivity of NSE and WI to extreme values^57,58, the obtained values are understandably modest. This is particularly evident in the NSE, which can be strongly penalized by small discrepancies between observed and predicted values during peak events. In our case, the streamflow time series exhibits a strong asymmetry, with prolonged periods of low streamflow interrupted by isolated and pronounced peaks. These high-flow events, although rare, dominate the variance of the series, causing the NSE to drop significantly even when the model performs well during the majority of the time series. Consequently, the relatively low or even negative NSE values observed in some cases-which occur only for the ML models-do not necessarily reflect poor model performance but rather the disproportionate influence of a few misestimated extremes. This interpretation is supported by the exceptionally low MAE and RMSE values, as well as the generally consistent predictions shown in the time series plots. Together, these metrics reinforce the reliability of the model outputs and highlight the importance of using multiple complementary metrics for evaluating model performance, particularly when dealing with highly skewed hydrological series. Figure 7 allows for a straightforward analysis to understand in which metrics each model stands out and, since the ranges of each axis are shared for each time horizon, the viewer can also compare the model differences between locations.

The methodology included careful data preprocessing, feature selection, and the application of state-of-the-art data augmentation techniques to address the imbalance between low and high streamflow periods. These steps were crucial in enhancing the overall performance and reliability of the predictive models.

Our research not only advances the academic understanding of streamflow prediction but also provides practical benefits for water resource managers and environmental agencies operating in the Mar Menor basin. The ability to anticipate streamflow variations with greater accuracy and efficiency supports better decision-making, resource allocation, and timely responses to potential flood events.

In this context, the LSTM model has been used to predict streamflow in a real-world scenario within a future digital twin of the Mar Menor Lagoon, which is currently under development. This system can be accessed by clicking on points 06A01 and 06A18 on the 2D map available at http://155.54.95.167/. By continuously monitoring this watercourse, we can anticipate future drainage into the lagoon and mitigate risks associated with extreme events, such as floods. A relevant example is the severe flooding that occurred in Valencia on October 29, 2025, a region geographically close to ours.

As with any study, there are limitations. Specifically, despite the use of data augmentation techniques such as IPIP and SMOTE, efficiently classifying peak events remains a challenge, particularly for longer prediction horizons. The model performs better at Desembocadura (06A18) than at La Puebla (06A01), likely due to a more stable and continuous water presence, suggesting that predictions may not generalize well to locations with different streamflow patterns. While our study demonstrates that short-term (1-hour) predictions achieve good accuracy, performance degrades significantly for longer horizons (12-hour, 24-hour), highlighting the need for further testing at intermediate horizons (e.g., 3 h, 6 h) to identify an optimal balance between stability and accuracy. Additionally, a key limitation is the limited availability of extreme event data, as our dataset spans only approximately 3 years, which may impact the model’s ability to generalize to rare and high-impact events. To mitigate this, our data partitioning strategy was not entirely random; instead, we ensured that all subsets contained at least some extreme events, allowing the model to be trained and evaluated under such conditions.

Future research could focus on refining model parameters, incorporating additional data sources, and integrating real-time data to enhance predictive capabilities. Expanding the range of environmental variables, such as satellite-derived rainfall, soil moisture, and vegetation indices, could improve streamflow prediction accuracy, particularly for longer-term forecasts where hydrological processes play a significant role. Additionally, leveraging advanced data augmentation techniques, such as Generative Adversarial Networks (GANs) or Variational Autoencoders (VAEs), could help synthesize rare extreme events, addressing the challenge of limited training data. Furthermore, implementing attention mechanisms within LSTM architectures may enhance the model’s ability to focus on the most relevant past events, improving its ability to capture temporal dependencies and refine predictions under varying streamflow conditions.

Even if there are limitations and open lines of research, our findings mark a significant step forward in addressing the challenges associated with streamflow prediction in vulnerable regions, ultimately contributing to more resilient and sustainable water resource management practices.